Detecting high-emitting methane sources in oil/gas fields using satellite observations

Methane emissions from oil/gas fields originate from a large number of relatively small and densely clustered point sources. A small fraction of high-mode emitters can make a large contribution to the total methane emission. Here we conduct observation system simulation experiments (OSSEs) to examine the potential of recently launched or planned satellites to detect and locate these high-mode emitters through measurements of atmospheric methane columns. We simulate atmospheric methane over a generic oil/gas field (20–500 production sites of different size categories in a 50×50 km² domain) for a 1-week period using the WRF-STILT meteorological model with 1.3×1.3 km² horizontal resolution. The simulations consider many random realizations for the occurrence and distribution of high-mode emitters in the field by sampling bimodal probability density functions (PDFs) of emissions from individual sites. The atmospheric methane fields for each realization are observed virtually with different satellite and surface observing configurations. Column methane enhancements observed from satellites are small relative to instrument precision, even for high-mode emitters, so an inverse analysis is necessary. We compare L₁ and L₂ regularizations and show that L₁ regularization effectively provides sparse solutions for a bimodally distributed variable and enables the retrieval of high-mode emitters. We find that the recently launched TROPOMI instrument (low Earth orbit, 7×7 km² nadir pixels, daily return time) and the planned GeoCARB instrument (geostationary orbit, 2.7×3.0 km² pixels, 2 times or 4 times per day return times) are successful (> 80 % detection rate, < 20 % false alarm rate) at locating high-emitting sources for fields of 20–50 emitters within the 50×50 km² domain as long as skies are clear. They are unsuccessful for denser fields. GeoCARB does not benefit significantly from more frequent observations (4 times per day vs. 2 times per day) because of a temporal error correlation in the inversion, unless under partly cloudy conditions where more frequent observation increases the probability of clear sky. It becomes marginally successful when allowing a 5 km error tolerance for localization. A next-generation geostationary satellite instrument with 1.3×1.3 km² pixels, hourly return time, and 1 ppb precision can successfully detect and locate the high-mode emitters for a dense field with up to 500 sites in the 50×50 km² domain. The capabilities of TROPOMI and GeoCARB can be usefully augmented with a surface air observation network of 5–20 sites, and in turn the satellite instruments increase the detection capability that can be achieved from the surface sites alone.

1 Introduction

Anthropogenic methane emissions from oil/gas fields originate from a large number of relatively small and densely clustered point sources (Allen et al., 2013). For example, the Barnett Shale in Texas has over 20 000 well pads spread over a 300×300 km² domain, contributing 40 % of total oil/gas emissions from the region (Lyon et al., 2015). It has been estimated that 7 % of the wells contribute 50 % of the total well emissions (Rella et al., 2015; Zavala-Araiza et al., 2015). Identifying such high-emitting wells is of both economic and environmental interest. We present here observing system simulation experiments (OSSEs) to examine the potential of using satellite observations of atmospheric methane for this purpose.

Satellites measure backscattered solar radiation in the shortwave infrared (SWIR) from which atmospheric columns of methane can be retrieved with near-uniform sensitivity down to the surface under clear-sky conditions (Jacob et al., 2016). The satellite record for SWIR methane began with the SCIAMACHY instrument (2003–2012; Frankenberg et al., 2005), which provided coarse-resolution measurements (30×60 km² in nadir). The currently operating GOSAT instrument (2009-; Kuze et al., 2016) has finer resolution (10 km diameter pixels) but sparse coverage (individual pixels 250 km apart). The TROPOMI instrument, launched in October 2017, provides complete daily coverage at 7×7 km² nadir resolution (Hu et al., 2018). The geostationary GeoCARB instrument, to be launched in the early 2020s, is currently planned to provide 2.7×3 km² pixel resolution with a return time that may range from 1 to 4 times per day (Polonsky et al., 2014; O'Brien et al., 2016). Other geostationary methane satellite missions have been proposed with various combinations of more frequent coverage, finer pixel resolution, and higher instrument precision (Fishman et al., 2012; Butz et al., 2015; Xi et al., 2015; Propp et al., 2017).

A number of studies have examined the value of satellite observations for quantifying methane sources. Inverse analyses of SCIAMACHY and GOSAT data have focused on quantifying emissions at ∼100 km regional scales (Bergamaschi et al., 2013; Wecht et al., 2014a; Alexe et al., 2015; Turner et al., 2015). OSSEs have shown the potential for TROPOMI and GeoCARB to effectively constrain emissions at the 25–100 km scale without the multiyear averaging required by SCIAMACHY and GOSAT (Wecht et al., 2014b; Sheng et al., 2018a). Other OSSEs have examined the potential for satellites to quantify large point sources from plume observations (Buchwitz et al., 2013; Rayner et al., 2014; Varon et al., 2018). A recent study by Turner et al. (2018) evaluated the capability of TROPOMI and GeoCARB to quantify emissions in the Barnett Shale down to the kilometer scale for a 1-week observing period. They found that GeoCARB should have some capability for constant sources over a 1-week period but not for transient sources. Hase et al. (2017) simulated surface and aircraft pseudo-observations over North America and used them to constrain North American emissions at 1^∘×1^∘ resolution. They found that sparse optimization better constrained local methane hot spots than the standard Bayesian approach.

Here we target a different problem. Given a population of production sites (wells) in an oil/gas field, can satellites localize high-mode emitters to enable corrective action? In this problem, quantifying emissions is not as important as identification of the high-mode emitters. The location of the individual point sources is known, but their mode of emission (normal, low mode or high mode) is unknown. Once a well starts emitting in the high mode, it continues doing so until corrective action is taken. Satellites offer an attractive monitoring approach for identifying high-mode emitters but their capability may be limited by return frequency, cloud cover, pixel resolution, error in the atmospheric transport model needed to relate the plume to the location of emission, or limitations in the inverse method for identifying sparse high-mode sources. Here we will evaluate the potential of different satellite observing configurations and inverse methods to address this problem with application to TROPOMI, GeoCARB, and finer-resolution geostationary data. We will also examine whether the information from satellites can be usefully complemented with a supporting network of surface observations.

2 Observing system simulation experiment

We consider a hypothetical oil/gas field of dimension 50×50 km² with 20, 50, 100, or 500 randomly placed production sites (wells), corresponding to site densities of 0.008, 0.02, 0.04, and 0.2 km⁻², respectively. The latter case corresponds to the average site density in the Barnett Shale. We create a large ensemble of emission scenarios in each case where different random subsets of sites of different production size categories (small: 10–100 million cubic feet per day (Mcf day⁻¹), where 1 Mcf day${}^{-\mathrm{1}}=\mathrm{0.028}$ Mm³ day⁻¹; medium: 100–1000 Mcf day⁻¹; large: 1000+ Mcf day⁻¹) are in the high-emission mode, and we simulate the resulting atmospheric methane concentration fields with the WRF meteorological model at 1.3×1.3 km² resolution. We then sample this pseudo-atmosphere with different satellite and surface observing configurations and apply different inverse methods to detect the high emitters. Detection success is evaluated for each observing configuration and inverse method using statistics for the ensemble of emission scenarios. We describe the different elements of the OSSE in this section.

2.1 Constructing an ensemble of emission fields

Production sites within the 50×50 km² domain are randomly placed on the 1.3×1.3 km² WRF model grid, with at most one site per grid cell. Emission statistics for the sites are based on observations from the Barnett Shale Coordinated Campaign (Lyon et al., 2015). For each scenario we randomly assign a production size category to each site with 23 % of the sites as small, 62 % as medium, and 15 % as large (Rella et al., 2015). We then assign an emission rate for each site by randomly sampling the bimodal probability density functions (PDFs) describing low-mode emissions and high-mode emissions for each size category (Lan et al., 2015; Rella et al., 2015; Yacovitch et al., 2015). We assume no other sources in the domain.

Figure 1 shows the PDFs of methane emissions for each production site size category. We flag production sites to be in the high-emission mode if they exceed an emission threshold of 40 kg h⁻¹ (axis break in Fig. 1), which corresponds on average to 5 % of all the sites. High-mode emissions from small facilities are much lower, centered around 24 kg h⁻¹, and would be difficult to distinguish from the normal (low) emission mode. Thus we do not attempt to detect them as high-mode emitters.

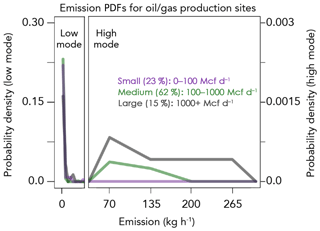
Figure 1 Probability density functions (PDFs) of emissions for oil/gas production sites of different production size categories (small, medium, and large) taken from Barnett Shale observations (Lan et al., 2015; Rella et al., 2015; Yacovitch et al., 2015). Note the difference in y-axis scales between the left (low mode) and right (high mode) panels. The axis break at 40 kg h⁻¹ represents the threshold for flagging an emitter as high.

Figure 2 shows a sample realization of the oil/gas field with 24 small production sites, 67 medium sites, and 9 large sites (100 total) within the 50×50 km² domain. In this realization there are five sites in the high-emission mode. We generate 500 emission scenarios in the same fashion as Fig. 2 by randomly assigning size categories for each site (small, medium, large) and randomly sampling the emission PDFs from Fig. 1.

2.2 Constructing pseudo-observations of atmospheric methane

We use the meteorological simulation previously generated by Turner et al. (2018) for a 1-week period (19–25 October 2013) in the Barnett Shale. This simulation applied the Weather Research and Forecasting Model (WRF; Skamarock et al., 2008) at 1.3 km horizontal resolution to drive the Stochastic Time-Inverted Lagrangian Transport (STILT) model (Nehrkorn et al., 2010). STILT is a receptor-oriented Lagrangian particle dispersion model that defines the source footprints for individual atmospheric observations. Turner et al. (2018) applied it to generate 1.3×1.3 km² hourly footprints for any daytime surface or atmospheric column observation in a 70×70 km² domain. Footprints for each column were obtained by releasing and tracking back in time 100 particles from vertical levels centered at 28, 97, 190, and 300 m above ground, and 8 additional levels up to 14 km altitude spaced evenly on a pressure grid. The column footprints were weighted with a typical near-uniform SWIR averaging kernel for satellite observations (Worden et al., 2015). Surface observations are taken in the lowest model layer (centered at 28 m above ground) and the corresponding footprints are obtained by releasing and tracking back in time 100 particles at the observation location and time. We use the ensemble of footprints generated by Turner et al. (2018) and add to it hourly footprints for surface observations at night. The 70×70 km² observing domain encompasses our 50×50 km² oil/gas field plus 10 km outside the boundaries (Fig. 2) to account for plume transport.

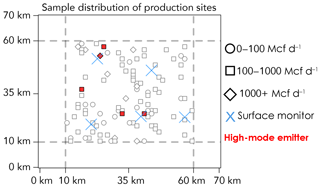
Figure 2 Sample realization of emissions from a hypothetical oil/gas production field with 100 production sites of different production size categories (symbols) within a 50×50 km² domain (dashed line). Different production size categories are shown with symbols. Red shading indicates high-mode emitters. Blue symbols mark the locations of five surface air monitoring sites placed according to the k-means algorithm.

The 70×70 km² archive of WRF-STILT footprints allows us to immediately compute the time-dependent methane concentration field associated with any emission scenario. Figure 3 shows a sample footprint, expressing the sensitivity of atmospheric concentrations at a given location and time i to the emission field upwind. Column footprints are about an order of magnitude smaller than surface footprints because surface signal is weakened for receptors (e.g., satellites) with total column sensitivity. Taking the footprints to represent the true atmospheric transport relating emissions to atmospheric concentrations for that location and time, we can combine them with any realization of our emission field (Sect. 2.1) to generate the true time-dependent methane concentrations in the domain to be sampled by the instruments.

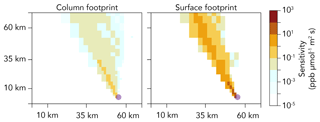
Figure 3 Sample sensitivities of observed atmospheric concentrations (column and surface) to surface emissions upwind, defining the emission footprint for that observation. Values are shown here for a particular observation point (purple dot) and time (19 October 2013 at 09:00 LT). Concentrations are in mixing ratio units of ppb (dry column mean mixing ratio for the column) and emissions are in units of µmol m⁻² s⁻¹.

Satellite observations of methane column concentrations are conventionally expressed in units of dry column mean mixing ratio (ppb), which is the ratio of the vertical column density of methane to the vertical column density of dry air (Jacob et al., 2016). The footprint for location and time i is mathematically represented as ${\mathit{h}}_i=(\partial y_i/\partial \mathit{x}{)}^T$ (units: ppb µmol⁻¹ m² s) where y_i is the methane concentration (ppb) for that location and time, and x (µmol m⁻² s⁻¹) is a vector of dimension n describing the emission field for the n emitters in the domain. The vector h_i is also a vector of n dimension. The true atmospheric concentration can be immediately constructed for any emission field x as $y_i={\mathit{h}}_i\cdot \mathit{x}+b$, where ⋅ denotes the scalar product and b is a background assumed here to be constant.

A given methane observing configuration makes m observations of the domain over the 1-week simulation period. The true methane concentrations for that observation ensemble can be assembled as an m-dimensional vector ${\mathit{y}}_{\mathrm{true}}=\mathbf{H}\mathit{x}+b$, where $\mathbf{H}=\partial {\mathit{y}}_{\mathrm{true}}/\partial \mathit{x}$ is the m×n Jacobian matrix of footprints with rows ${\mathit{h}}_i^T$. The pseudo-observations are then generated as $\mathit{y}={\mathit{y}}_{\mathrm{true}}+\mathit{\sigma }\mathit{\epsilon }$, where σ is the instrument precision (1 standard deviation) and the vector ε is a random realization of Gaussian noise with mean value of zero and standard deviation of unity for each vector element. SWIR instruments may also suffer from systematic errors but we do not account for those here in the absence of information. The largest source of systematic error on our scale would likely be the inhomogeneity in surface reflectivity (Pfister et al., 2005).

The mean daytime 10 m horizontal wind speed inside the observing domain during the simulated week is 5.4 m s⁻¹. Stronger winds could further dilute plumes within an observing domain, making the ability for satellite detection of emitters more difficult; on the other hand, the model transport error is less for stronger winds (Varon et al., 2018).

Table 1 Observing configurations considered in this work.

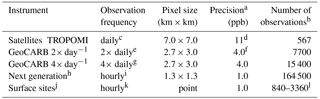
^ar Dry column mean mixing ratio for the satellite observations, local mixing ratio for the surface observations. ^b One week of clear-sky conditions in the 70×70 km² domain. ^c 13:00 LT (local time). ^d Butz et al. (2012). ^e 12:00 and 16:00 LT. ^f O'Brien et al. (2016). ^g 10:00, 12:00, 14:00, and 16:00 LT. ^h Aspirational instrument combining the characteristics of instruments currently at the proposal stage (Fishman et al., 2012; Butz et al., 2015; Xi et al., 2015). ⁱ Between 08:00 and 17:00 LT. ^j In situ measurements of surface air concentrations. ^k Day and night. ^l For 5 to 20 surface sites.

2.3 Satellite and surface observing configurations

Table 1 describes the different satellite observing configurations evaluated in this work including TROPOMI, GeoCARB with 2 or 4 return times per day, and an aspirational next-generation geostationary instrument with 1.3×1.3 km² pixel resolution, 1 ppb precision, and hourly return frequency between 08:00 and 17:00 LT (local time). Successful methane retrievals from satellites require a clear sky. The probability of clear sky in a partly cloudy domain depends greatly on pixel size (Remer et al., 2012). Results for a partly cloudy condition would depend on the particular cloud configuration and would be difficult to generalize. Here we assume clear-sky conditions to avoid this complication, but the detection probability for high-mode emitters should then be viewed as an upper limit. In particular, it should be recognized that no detection from satellite is possible for a cloudy domain.

We also wish to determine the benefit of a well-positioned surface air monitoring network for supplementing the satellite observations. Assuming that we have M fixed monitoring instruments to deploy measuring surface air methane concentrations in situ. We want to place them in a configuration that maximizes the information that they would provide, assuming an isotropic wind for generality. A trivial solution would be to place an instrument at each production site, in which case the monitoring problem would be fully solved, but this solution may not be practical for a large number of production sites. Given a known spatial distribution of emitters (the locations of the production sites), we use the k-means spatial clustering approach (Hartigan and Wong, 1979) to select monitoring site locations minimizing the distances to emitter locations. Figure 2 shows the selected locations for five surface monitoring sites. We assume that these sites report hourly data with 1 ppb precision and that the background concentration in surface air is constant, consistent with the assumption made for satellite observations. A variable background would complicate the problem but could be retrieved as part of the inversion (Wecht et al., 2014b).

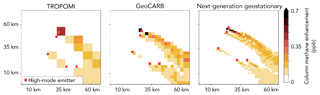
Figure 4 Simulated noiseless methane column enhancement for sampling by single overpasses of TROPOMI, GeoCARB, and a next-generation high-resolution geostationary satellite (Table 1). Emission field is that of Fig. 2. The locations of the five high-mode emitters in that field are indicated. Values are for 22 October 2013 at 13:00 LT.

An important consideration in the interpretation of satellite observations is that methane column enhancements from individual point sources are typically small relative to instrument precision, even in the high-emitting mode (Jacob et al., 2016; Varon et al., 2018). Figure 4 shows the pixel-resolved distribution of atmospheric methane column enhancements above the background for a single pass of the different satellite instruments sampling the emission field of Fig. 2. The enhancements are less than 1 ppb even for 1.3×1.3 km² pixels and are weaker at coarser pixel resolution. This is less than the single-scene precision of the satellite instruments (Table 1). Successful detection of high-mode emitters thus requires the sampling of many pixels, across the plume and/or through repeated sampling, to reduce the noise. This is less of an issue for surface air measurements, where methane enhancements are an order of magnitude higher (Fig. 3). On the other hand, surface monitoring sites are spatially sparse. For both satellite and surface air observations, a formal inverse analysis of the ensemble of atmospheric observations accounting for plume transport is required for detection of the high-mode emitters.

2.4 Inverse methods

Given a set of observations y and Jacobian matrix H, we need an inverse method to determine the best solution $\widehat{\mathit{x}}$ of the emission field x at predetermined locations. We use the same matrix H for both pseudo-observation construction and the inversion. The inversion should be able to detect the small fraction of sources in the high-emitting mode, with detection being more important than quantification. This is known as a sparse-solution problem, where most elements of the emission field x are very small (for which an optimized value of zero would be acceptable), and a few of the elements are relatively large. We use regularized least squares regression (e.g., Hansen, 2010), also known as Tikhonov regularization, where the solution is found by minimizing the cost function J(x),

$$\begin{array}{}\text{(1)}& {\displaystyle }J\left(x\right)={\left(\mathbf{H}\mathit{x}-\mathit{y}\right)}^T{\mathbf{R}}^{-\mathrm{1}}\left(\mathbf{H}\mathit{x}-\mathit{y}\right)+\mathit{\lambda }{∥\mathit{x}∥}_L^p.\end{array}$$

Here the first term on the right-hand side represents the ordinary least-squares cost function, such that the solution would minimize the residuals between the prediction Hx and the observations weighted by the observational error covariance matrix R. The second term represents an adjustable parameter λ and the L-norm of x, which is a measure of the magnitude of the vector x defined as the following:

$$\begin{array}{}\text{(2)}& {\displaystyle }{∥\mathit{x}∥}_L=\sqrt[L]{{\mathrm{\Sigma }}_{k=\mathrm{1}}^n{\left|x_k\right|}^L}.\end{array}$$

Adding this second term in the cost function penalizes the total magnitude of x in the solution, which reduces overfitting to noise and regularizes the solution. When L=1 and p=1, this is known as L₁ regularization or the least absolute shrinkage and selection operator (LASSO; Tibshirani, 1996), and Eq. (1) takes the form

$$\begin{array}{}\text{(3)}& {\displaystyle }J\left(\mathit{x}\right)={\left(\mathbf{H}\mathit{x}-\mathbf{y}\right)}^T{\mathbf{R}}^{-\mathrm{1}}\left(\mathbf{H}\mathit{x}-\mathit{y}\right)+\mathit{\lambda }\sum _{k=\mathrm{1}}^n\left|x_k\right|.\end{array}$$

When L=2 and p=2 , Eq. (1) takes the form known as L₂ regularization or ridge regression (Evgeniou et al., 2000):

$$\begin{array}{}\text{(4)}& {\displaystyle }J\left(\mathit{x}\right)={\left(\mathbf{H}\mathit{x}-\mathit{y}\right)}^T{\mathbf{R}}^{-\mathrm{1}}\left(\mathbf{H}\mathit{x}-\mathit{y}\right)+\mathit{\lambda }{\mathit{x}}^T\mathit{x}.\end{array}$$

Equation (4) is equivalent to the standard Bayesian optimization (Rodgers, 2000) assuming Gaussian distributions, a prior emission estimate of zero, and uniform prior error variance of λ⁻¹.

The observational error covariance matrix R=(r_ij) adds and accounts for both instrument and model transport errors. Representation errors are negligible due to the model grid resolution being finer or the same resolution as the instrument pixels (Turner et al., 2018). The diagonal terms add the corresponding error variances in quadrature:

$$\begin{array}{}\text{(5a)}& {\displaystyle }{r}_{ii}={\mathit{\sigma }}_{\mathrm{I}}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{M}}^{\mathrm{2}},\end{array}$$

where σ_I is the instrument error standard deviation as given by the precision in Table 1, and σ_M is the model transport error standard deviation previously estimated to be 4 ppb for methane columns (Turner et al., 2018). Given the order of magnitude difference in sensitivity between satellite columns and surface measurements (Fig. 3), we assume σ_M to be 40 ppb for surface measurements. Off-diagonal terms account for model transport error correlation between different observations. Following Turner et al. (2018), we assume a temporal error correlation length scale (τ) of 2 h and a spatial error correlation length scale (ℓ) of 40 km:

$$\begin{array}{}\text{(5b)}& {\displaystyle }{r}_{ij}={\mathit{\sigma }}_{\mathrm{M}}^{\mathrm{2}}\exp \left\{-{\displaystyle \frac{d}{l}}\right\}\exp \left\{-{\displaystyle \frac{t}{\mathit{\tau }}}\right\}\mathrm{for}i\ne j,\end{array}$$

where d and t are the distance and elapsed time, respectively, between observations y_i and y_j.

Additional model transport error correlation applies when combining satellite and surface air observations in the inversion, since the footprints can be similar (Fig. 3). To quantify this error correlation, we use the work of Sheng et al. (2018b) who jointly compared column (TCCON) and surface air (NOAA) measurements of methane at Lamont, Oklahoma, with GEOS-Chem transport model simulations. By correlating the model–observation differences for coincident column (i) and surface air (j) observations we find a model transport error correlation coefficient cor($i,j)=\mathrm{0.65}$ that we apply to the corresponding off-diagonal terms:

$$\begin{array}{}\text{(5c)}& {\displaystyle }{r}_{ij}=\mathrm{cor}\left(i,j\right){\mathit{\sigma }}_{Mi}{\mathit{\sigma }}_{Mj}\exp \left\{-{\displaystyle \frac{d}{l}}\right\}\exp \left\{-{\displaystyle \frac{t}{\mathit{\tau }}}\right\}.\end{array}$$

Inverse solutions derived using L₁ regularization produce sparser solutions than the L₂ counterpart (Tibshirani, 1996), which is desirable for our application and has previously been shown to produce good results for constraining methane hot spots (Hase et al., 2017). Here we will perform both L₁ and L₂ inversions and compare the results. Minimization of J(x) in Eqs. (3) and (4) to obtain the solution $\widehat{\mathit{x}}$ corresponding to $\mathrm{d}J/\mathrm{d}x=\mathrm{0}$ is done numerically using coordinate gradient descent (Friedman et al., 2009). The regularization parameter λ is chosen so that the mismatch between model and observations is small, but not so small that the solution $\widehat{\mathit{x}}$ is over fit to random noise, which would occur when λ=0. We use the process of 5-fold cross-validation to select an optimal λ value (Arlot and Celisse, 2010). This process randomly samples H and y into a training and validation set. Minimization of J is done on the training set using an array of λ values. The process is repeated five times, and the value of λ that on average minimizes the residual error in the validation set is retained.

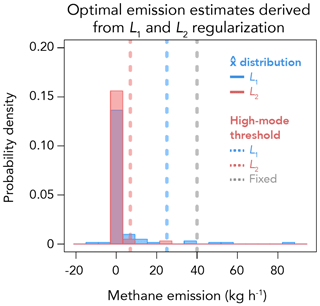
Figure 5 An example distribution of the optimal emission estimate $\widehat{x}$ for a realization of the emission inventory (100 sites), GeoCARB 4× day⁻¹ pseudo-observations, and L₁ or L₂ regularization. Dashed lines represent the thresholds to classify an emitter as high-mode, determined either from the distribution $\widehat{x}$ (S=2) or from a fixed prior value (here 40 kg h⁻¹).

Figure 5 shows the distribution $\widehat{\mathit{x}}$ from a single realization of emissions, GeoCARB 4 times per day (denoted as 4× day⁻¹) pseudo-observations, and both L₁ and L₂ regularization. In this simulation, L₁ regularization enables the retrieval of high-mode emitters while L₂ regularization is more restrictive in allowing excursions from the low-mode mean.

2.5 Detection of high-emission modes

Success in the detection of high-mode emitters from the distribution of $\widehat{\mathit{x}}$ can be determined by comparison to the actual occurrence and location of these emitters as defined in Sect. 2.1 and illustrated in Fig. 2. In a real-world application we would not know the actual PDFs of emissions (Fig. 1), so we need to diagnose the occurrence of high-mode emitters on the basis of anomalies in the distribution of $\widehat{\mathit{x}}$. We define high-mode elements as being more than S standard deviations from the mean of the $\widehat{\mathit{x}}$ distribution, where S is varied in the 1.65–2.5 range to examine the associated sensitivity. Using anomaly detection on $\widehat{\mathit{x}}$ instead of a fixed threshold (e.g., 40 kg h⁻¹) allows for generalization to other emission fields where the mean normal and high modes may be different than the Barnett Shale. Figure 5 shows thresholds for classifying high-mode emitters using anomaly detection and a fixed value of 40 kg h⁻¹. The L₁ threshold is larger than the L₂ threshold, but smaller than 40 kg h⁻¹. Had the fixed threshold been used, some high-mode emitters (relative to $\widehat{\mathit{x}}$) would not have been classified as such.

The detection of high-mode emitters by the inversion is graded into four categories: (1) true positives (TP), or the inversion correctly identifying the locations of the high-mode emitters; (2) true negatives (TN), or the inversion correctly identifying the locations of the low-mode emitters; (3) false positives (FPs), or the inversion signaling a high-mode emitter when in reality the emitter is in the low mode; and (4) false negatives (FNs), or the inversion signaling a low-mode emitter when in reality the emitter is in the high mode.

We compile these grades into three overall performance metrics (Brasseur and Jacob, 2017). The probability of detection (POD) is defined as the ratio of true positives to true positives plus false negatives:

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathrm{POD}={\displaystyle \frac{\mathrm{\Sigma }\mathrm{TP}}{\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FN}}}.\end{array}$$

This metric measures the ability to detect high-mode emitters. The false alarm ratio (FAR) is defined as the ratio of false positives to false positives plus true positives:

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathrm{FAR}={\displaystyle \frac{\mathrm{\Sigma }\mathrm{FP}}{\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FP}}}.\end{array}$$

This metric measures the reliability of high-mode emission occurrences detected by the inversion.

A perfect observing system would have a POD of 1 and a FAR of 0. Here we define a successful observing system as achieving a POD of 0.8 (80 %) and a FAR of 0.2 (20 %). These criteria, although somewhat arbitrary, allow us to succinctly summarize the success of each observing configuration.

We combine the POD and FAR metrics into one overall performance metric called the equitable threat score (ETS; Wang, 2014):

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathrm{ETS}={\displaystyle \frac{\mathrm{\Sigma }\mathrm{TP}-\mathit{\alpha }}{\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FP}+\mathrm{\Sigma }\mathrm{FN}-\mathit{\alpha }}},\end{array}$$

where α is the number of TP predictions that are expected by chance:

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathit{\alpha }={\displaystyle \frac{\left(\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FP}\right)\left(\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FN}\right)}{\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FP}+\mathrm{\Sigma }\mathrm{FN}+\mathrm{\Sigma }\mathrm{TN}}}={\displaystyle \frac{\mathrm{1}}{N}}{\displaystyle \frac{\mathrm{\Sigma }\mathrm{FP}}{\mathrm{FAR}}}{\displaystyle \frac{\mathrm{\Sigma }\mathrm{TP}}{\mathrm{POD}}}\end{array}$$

and $N=\mathrm{\Sigma }\mathrm{TP}+\mathrm{\Sigma }\mathrm{FP}+\mathrm{\Sigma }\mathrm{FN}+\mathrm{\Sigma }\mathrm{TN}$. The ETS measures how well the high-mode emitters detected by the observing system correspond to the actual occurrences, beyond what could be achieved by chance. A perfect observing system has an ETS of 1, and a system performing worse than chance would have a negative ETS. An observing system with POD of 0.8 and FAR of 0.2 has an ETS of 0.65 for a field where 5 % of emitters are in the high mode. We take this as our ETS criterion for successful detection.

3 Results and discussion

3.1 Performance of different satellite and surface observing systems

We begin by testing the ability of each satellite configuration of Table 1 to detect high-mode emitters from fields of 20 to 500 randomly scattered production sites within the 50×50 km² domain. For a given number of sites, we conduct each test for 500 different realizations of the emission field randomly assigning each production site to a size category (small, medium, large) and randomly sampling the PDFs of Fig. 1. Emitter locations are fixed across all 500 realizations. Figure 6 shows the POD, FAR, and ETS results for a field of 100 emitters and compares the results of L₁ and L₂ regularizations. The values represent the mean results for the ensemble of 500 realizations, and the error bars represent the range of results when the high-mode detection threshold S is varied from 1.65 to 2.5. We find that L₁ regularization provides better predictions for all cases. This is especially the case for the next-generation satellite, where L₁ regularization produces a POD of 0.85 with a near-perfect FAR of 0.04. L₂ regularization is more conducive to spreading emissions across a broader array of state vector elements. The better performance of L₁ regularization is also observed for other site densities (not shown). We use L₁ regularization in what follows.

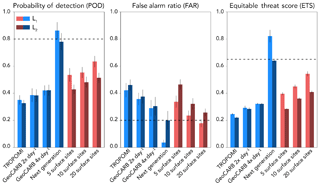
Figure 6 Probability of detection (POD), false alarm ratio (FAR), and equitable threat score (ETS) of high-mode emitters for each satellite and surface observing configuration. Each bar represents the mean of 500 observing system simulation experiments (OSSEs), where 100 production sites in a 50×50 km² domain were used to construct 500 random realizations of an emission field including different subsets of high-mode emitters. For each observing configuration, the left bar (lighter color) shows results for the inversion with L₁ regularization, and the right bar (darker color) is for the L₂ regularization. The dashed lines represent the POD, FAR, and ETS criteria for successful observing systems. Here, and in following figures, the vertical lines measure the sensitivity to the choice of threshold for diagnosing high-mode emitters in the inversion.

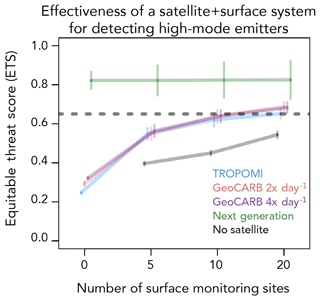
Figure 6 also compares the performances of the satellite observing systems to those of an ensemble of 5–20 optimally placed (k means) surface sites. We find that the surface observing system performs comparably to GeoCARB. We explore combining satellite and surface observations into a single prediction in Sect. 3.3.

The results from Fig. 6 show that TROPOMI and GeoCARB are unsuccessful in locating high-mode emitters for a field of 100 production sites (0.04 sites km⁻²). We examine the sensitivity of this result to site density. Figure 7 compares the detection results for fields of 20, 50, 100, and 500 production sites within the 50×50 km² domain. For a field of only 20 emitters, TROPOMI is successful and GeoCARB produces near-perfect results. For a field of 50 emitters, TROPOMI is no longer successful, but GeoCARB is still marginally successful due to finer pixel resolution and higher instrument precision. We find in general that GeoCARB gains little by sampling 4 times a day (4× day⁻¹) vs. 2× day⁻¹. This is due to the temporal model error correlation between successive GeoCARB observations. Accounting for cloud cover would show more benefit from 4× day⁻¹ observations, since a higher frequency of observations allows for a greater chance of sampling clear-sky conditions, although the benefit depends on the cloud persistence timescale (Sheng et al., 2018a).

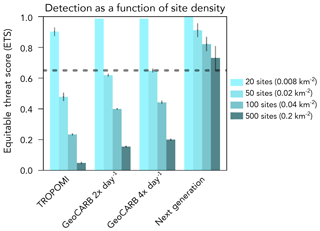
Figure 7 Equitable threat score (ETS) for each satellite observing configuration, varying the density of production sites (20–500 sites in 50×50 km² domain). Results are from the L₁ inversion. The dashed line represents the ETS criterion for successful observation.

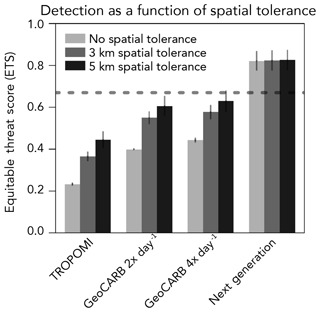
Figure 8 Effect of introducing spatial tolerance in the detection of high-mode emitters. Spatial tolerance is the radius within which a high-mode emitter must be located in order for a prediction to be called true positive (TP). The results are for an emission field with 100 production sites in the 50×50 km² domain. Only results from the L₁ inversion method are shown. The dashed line represents the ETS success criterion.

The ability of a satellite observing configuration to localize high-mode emitters thus depends not only on repeat time, resolution, precision, and cloud cover, but also on the density of emitters within a field. For the high-density fields of 100 and 500 production sites considered here (0.04 and 0.2 sites km⁻²), we find that only the next-generation satellite instrument is successful. Actual fields can be even denser but we are limited in our investigation by the 1.3×1.3 km² resolution of the WRF simulation. Detecting individual high-mode emitters in denser fields would require geostationary satellite observations with sub-kilometer pixels but this is beyond the scope of current proposals.

3.2 Spatial tolerance in detection of high-mode emitters

The results from Fig. 7 are somewhat pessimistic regarding the ability of near-future satellite observations (TROPOMI and GeoCARB) to detect the locations of high-mode emitters in fields of 100+ wells. It may be acceptable to relax the localization criterion. If the observing system detects a false positive that is sufficiently close to the actual location of a high-mode emitter, then the detection may still have some value. In our OSSE setup, localization is effectively limited by the 1.3×1.3 km² grid resolution of the WRF simulation. To examine the sensitivity to localization, we repeated the analysis allowing for 3–5 km tolerance of false predictions. Figure 8 shows the results for a field of 100 emitters. We find that spatial tolerance significantly improves the performance of GeoCARB but still falls short of our success criterion. The FAR decreases below 0.2 for 3 km tolerance and below 0.1 for 5 km tolerance, but the POD only improves to 0.7 and thus the ETS remains below 0.65.

Figure 9 Effectiveness of a combined satellite and surface observing system for detecting high-mode emitters in an oil/gas field of 100 emitters over a 50×50 km² domain, as determined from joint inversion of the observations. The dashed line represents the ETS success criterion.

3.3 Combining satellite and surface observations

We saw in Sect. 3.1 that only the next-generation satellite instrument can successfully detect high-mode emitters when the site density is high. Here we examine if a combination of satellite and surface observations can improve detection, i.e., if TROPOMI and GeoCARB could benefit from an in situ supporting surface network and vice versa. This is addressed with a joint inversion of the satellite and surface observations, taking into account the error correlation between the two as described in Sect. 2.4.

Figure 9 shows the results for a field of 100 emitters. The already successful next-generation instrument shows no benefit from added surface sites, and the uncertainty increases slightly with the number surface sites. This increase is due to imperfect accounting of correlated error between satellite and surface measurements. On the other hand, the surface sites provide greatly added value to TROPOMI and GeoCARB. Adding 10–20 surface sites enables near-successful detection of the high-mode emitters. At the same time, TROPOMI and GeoCARB data add significantly to the performance of a surface observing system alone by providing observations with more spatial coverage. We find that TROPOMI and GeoCARB perform similarly when added to surface sites, and that their main benefit is to decrease the FAR. Accounting for clouds would show more benefit for GeoCARB because the finer pixels allow for more frequent clear-sky observations (Sheng et al., 2018a).

4 Conclusions

We performed observing system simulation experiments (OSSEs) to test the ability of near-future satellite instruments measuring atmospheric methane (TROPOMI, GeoCARB, next-generation geostationary) to detect high-mode point-source emitters among a field of individual point sources, alone or supported by a surface monitoring network. We focused on the practical problem of detecting high-mode emitters in an oil/gas production field with a high density of wells. Remote detection from satellites, combined with operator knowledge, could supplement on-site leak detection and repair (LDAR) programs to identify and fix unexpected high emitters. Our results in these meteorological conditions can be usefully summarized in terms of answers to questions that a field manager might have:

“Can I rely on satellite data alone to detect high-mode emitters among the production sites in my oil/gas field?” We find that TROPOMI and GeoCARB can detect high-mode emitters as long as the density of point sources is relatively small (20 sites within our 50×50 km² domain, or a density of 0.008 km⁻²) and skies are clear. GeoCARB shows little difference in success rate (equitable threat score, ETS, > 0.65) for 2 or 4 overpasses per day. GeoCARB is marginally successful for 50 sites (0.02 km⁻²) but fails for 100 sites (0.04 km⁻²). A next-generation geostationary satellite instrument with ∼1 km pixel resolution and hourly return time would deliver precise detection in dense fields up to 500 sites (0.2 km⁻²). Allowing for a 5 km spatial error tolerance for localization, we find that GeoCARB comes close to successful detection in a field of 100 sites.

“How should I analyze the satellite observations to detect high-mode emitters?” Detection of high-mode emitters from satellite observations is not a simple matter of flagging hot spots because the methane column enhancements are typically small compared to instrument precision, even for high-mode emitters. Repeated clear-sky observation combined with inverse analysis using an atmospheric transport model is needed. We find that an inversion with L₁ regularization produces better results than L₂ regularization. This is expected since the L₁ regularization method is designed to recover sparse signals.

“Can I usefully supplement satellite information with surface monitoring?” Both TROPOMI and GeoCARB significantly add to the information provided by a surface monitoring network of 5–20 sites within the 50×50 km² domain, and conversely the addition of a surface network significantly enhances the information that can be retrieved from TROPOMI and GeoCARB. The combination of these satellite instruments with the surface monitors can deliver successful detection of high-mode emitters through a joint inversion. Adding surface sites provides no benefit to the next-generation geostationary instrument, which can successfully detect high-mode emitters on its own as long as skies are clear.