Direct Lagrangian tracking simulation of droplet growth in vertically developing cloud

We present a direct Lagrangian simulation that computes key warm-rain processes in a vertically developing cloud, including cloud condensation nuclei (CCN) activation, condensational growth, collisional growth, and droplet gravitational settling. This simulation, which tracks the motion and growth of individual particles, is applied to a kinematic simulation of an extremely vertically elongated quasi-one-dimensional domain, after which the results are compared with those obtained from a spectral-bin model, which adopts the conventional Eulerian framework. The comparison results, which confirm good bulk statistical agreement between the Lagrangian and conventional spectral-bin simulations, also show that the Lagrangian simulation is free from the numerical diffusion found in the spectral-bin simulation. After analyzing the Lagrangian statistics of the surface raindrops that reach the ground surface, back-trajectory scrutiny reveals that the Lagrangian statistics of surface raindrops contains the information about the sky where the raindrops grow like the shape does for snow crystals.

1 Introduction

Because clouds play central roles in weather and climate, numerous cloud microphysics models have been developed to investigate their physics and predict their development. Conventional models are divided into either bulk or spectral-bin types based on their microphysical representations. In bulk models, all of the microphysical processes, such as mixing ratios or number concentrations of cloud hydrometers (cloud, rain, cloud ice, snow, graupel, etc.) are described in terms of grid-averaged parameters. In contrast, in spectral-bin models, hydrometer size or mass distributions are modeled directly. Although spectral-bin models are more complex and prognose more variables than bulk models, both types are the same in the sense that they prognose grid-averaged values. In other words, all conventional models are based on the Eulerian framework.

However, in recent years, a number of new cloud models that are based on the Lagrangian framework, in which the motion and growth of individual droplets are tracked, have been developed. These Lagrangian cloud models are also divided into two groups: super-droplet models (Dziekan and Pawlowska, 2017; Riechelmann et al., 2012; Shima et al., 2009) and direct tracking models (Chen et al., 2018; Grabowski and Wang, 2013; Kumar et al., 2014; Onishi et al., 2015; Saito and Gotoh, 2018). The former introduces the multiplicity concept, in which each droplet represents multiple droplets that share approximately the same attributes and positions, while the latter directly computes the motion and growth of each droplet and can consider the influence of microscale flow and scalar field on the droplet motion and growth, even though their computational costs are extremely high. For example, Onishi et al. (2015) developed the Lagrangian cloud simulator (LCS), which adopts the Eulerian–Lagrangian framework and can provide reference data for cloud microphysical models. Their study revealed the turbulence enhancement of collisional growth on the temporal evolution of droplet size distributions for a periodic box (cubic) domain. Saito and Gotoh (2018) reported on a direct tracking simulation for a periodic box domain that additionally considers condensational growth while ignoring the cloud condensation nuclei (CCN) activation. Here, it should be noted that other existing direct tracking models still lack the CCN activation process and also rely on periodic box domains, which are useful, but unphysical in the sense that large drops repeatedly reenter the same domain. However, no direct tracking simulations have ever succeeded in representing all of the warm-rain processes, which include CCN activation, condensation–evaporation, collision, and gravitational settling.

With the above background in mind, this study aims to establish a direct Lagrangian model that can compute all of the abovementioned warm-rain processes and obtain Lagrangian statistics on droplet growth in a vertically developing cloud. First, a simple stochastic CCN activation model for direct Lagrangian simulations was developed and implemented in the LCS. The integrated LCS was then applied to a kinematic simulation for a vertically developing warm cloud. The resulting computational model adopts an extremely vertically elongated quasi-one-dimensional domain that can allow gravitational settling of large raindrops in physical (rather than periodic) space at a feasible computational cost.

The rest of this paper is organized as follows. In the next section, we describe the numerical methods, including the newly developed CCN activation model, used for direct Lagrangian simulations. Computational settings, including the domain setting, are described in Sect. 3. Then, results and discussion for both Eulerian and Lagrangian simulations and statistics are presented in Sect. 4, and our conclusions are given in Sect. 5.

2 Numerical methods

2.1 Lagrangian cloud simulator (LCS) overview

The LCS (Onishi et al., 2015) adopts a hybrid Eulerian–Lagrangian framework in which flow motion and scalar transport are computed using a Eulerian method, and the particle motion and growth are obtained via a Lagrangian tracking method. Within that framework, cloud microphysics are computed by direct Lagrangian tracking, which follows the motion and growth of individual particles. Previously, the LCS was used primarily to focus on the collisional growth of droplets in a turbulent medium. In this study, in order to include the water droplet phase change, the humidity and temperature fields are calculated using the same Eulerian method that was used for the flow. In addition, to include the droplet activation (nucleation) process, this study presents a newly developed CCN activation model based on Twomey's modeling (Twomey, 1959). The resulting integrated LCS can track the key warm-rain processes of water droplets (CCN activation, condensational and collisional growth, and gravitational settling).

The following subsection describes the present kinematic simulation while Sect. 2.3 describes the present Eulerian methods used for the calculation of flow and scalar fields. Then, Sect. 2.4 describes the present Lagrangian method used for particle phase, which includes the newly developed CCN activation model designed for use with a Lagrangian framework.

2.2 Overview of quasi-one-dimensional kinematic simulation

2.2.1 Kinematic model

This study adopts the computational settings of the kinematic driver (KiD) model (Shipway and Hill, 2012), which was originally designed to provide an intercomparison framework for bulk and spectral-bin cloud microphysics models. The flow and temperature profiles are prescribed in a way that minimizes feedback between dynamics and microphysics and thus facilitate straightforward comparisons. Here, we adopt the simplest test, which is a shallow convection case (warm-1 case) in which a simple updraft is prescribed as

$$\begin{array}{}\text{(1)}& {\displaystyle }w\left(t\right)=\left\{\begin{array}{ll}{w}_{\mathrm{0}}\sin (\mathit{\pi }t/\mathrm{600})& \mathrm{for}t<\mathrm{600}\mathrm{s}\\ \mathrm{0}& \mathrm{otherwise}\end{array}\right.,\end{array}$$

with w₀=2 m s⁻¹. This prescribed updraft lifts all the air parcels by ($\int w\mathrm{d}t=$) 764 m. The duration and depth of the simulation are 3600 s and 3000 m, respectively. Table 1 shows the initial temperature and moisture profiles, which are set to be similar to those used in the Global Energy and Water Cycle Experiment (GEWEX) Cloud System Study (GCSS) Rain In Cumulus over the Ocean (RICO) composite intercomparison. Inside the surface layer below 764 m, the air is assumed to be well mixed and neutrally stratified. More specifically, the potential temperature Θ ($=T(p/p_{\mathrm{0}}{)}^{R/C_{\mathrm{p}}}$, where T is the temperature, p is the pressure, R is the gas constant of dry air (R=287 J kg⁻¹ K⁻¹), C_p is the specific heat at constant pressure (C_p=1004 J kg⁻¹ K⁻¹) and p₀ ($=\mathrm{1.00}\times {\mathrm{10}}^{\mathrm{5}}$ Pa) is the reference pressure), and the initial vapor mixing ratio Q_υ are set to the same values inside the layer.

Table 1 Initial profiles for the KiD warm-1 case.

2.2.2 MSSG-Bin simulation (a spectral-bin simulation)

The Multi-Scale Simulator for the Geoenvironment (MSSG; Matsuda et al., 2018; Takahashi et al., 2013) has a warm-bin–cold-bulk hybrid cloud microphysics model named MSSG-Bin (Onishi and Takahashi, 2012) in which the mass coordinate m was discretized as $m_k={\mathrm{2}}^{\mathrm{1}/s}{m}_{k-\mathrm{1}}$, and in which s was set to 16. The representative radius of the first bin was 2.7 µm and 528 classes were calculated, the largest class of which had a representative radius of 5.4 mm. The vertical grid spacing was set to Δ_z=25 m and the time interval was set to Δt=1 s. Following the KiD protocol, the initial CCN concentration was set to 5.0×10⁷ m⁻³ and kept constant for the entire simulation.

2.3 Flow and scalar phase in the Eulerian framework

In addition to solving the three-dimensional (3-D) continuity and Navier–Stokes equations for incompressible flows based on a finite difference method, the LCS solves the transport equations of scalars ϕ as

$$\begin{array}{}\text{(2)}& {\displaystyle }\left\{{\displaystyle \frac{\partial }{\partial t}}+U\cdot \mathrm{\nabla }\right\}\mathit{\varphi }={\mathit{\kappa }}_{\mathit{\varphi }}{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\varphi }+S_{\mathit{\varphi }},\end{array}$$

where U is the flow velocity, κ_ϕ is the diffusion coefficient and S_ϕ is the source term. The LCS considers two scalars; the ϕ scalar, which can be either the water vapor mixing ratio Q_υ or the potential temperature Θ.

The spatial derivatives were calculated using fourth-order central differences. The conservative scheme devised by Morinishi et al. (1998) was used for the advection terms and the second-order Runge–Kutta scheme was used for time integration. Since the temperature field for the KiD warm-1 simulation is fixed, only the transport equation for Q_υ was calculated explicitly in this study. The diffusion coefficient for the water vapor is ${\mathit{\kappa }}_q=\mathit{\nu }/\mathit{\text{Sc}}$, where ν is the kinematic viscosity and Sc is the Schmidt number (Sc = 0.675). The vapor field was coupled with the particle phase through the source term S_q, described in Eq. (12) in Sect. 2.5.

2.4 Particle phase in the Lagrangian framework

2.4.1 Motion of particles

Under the limit of a large ratio of the density of the particle material to that of the fluid (${\mathit{\rho }}_{\mathrm{p}}/\mathit{\rho }\gg \mathrm{1}$, where ρ_p and ρ are the densities of particle and air, respectively), the governing equation for the ith particle is given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{\mathrm{d}{V}_{\mathrm{p},i}}{\mathrm{d}t}}=-{\displaystyle \frac{{\mathit{\alpha }}_i}{{\mathit{\tau }}_{\mathrm{p},i}}}\left[V_{\mathrm{p},i}-\left(U(x_{\mathrm{p},i},t)+u(x_{\mathrm{p},i},t)\right)\right]\\ \text{(3)}& {\displaystyle }& {\displaystyle }+f_{\mathrm{coll},i}+g,\end{array}$$

where V_p is the particle velocity, U(x_p,t) is the air velocity at the particle position, u is the disturbance flow velocity caused by the surrounding particles, and τ_p is the particle relaxation time defined as ${\mathit{\tau }}_{\mathrm{p}}=(\mathrm{2}/\mathrm{9})({\mathit{\rho }}_{\mathrm{p}}/\mathit{\mu })r^{\mathrm{2}},$ where ρ_p is the particle density (ρ_p=1000 kg m⁻³), μ the air viscosity ($\mathit{\mu }=\mathrm{1.79}\times {\mathrm{10}}^{-\mathrm{5}}$ Pa⋅s at standard atmosphere), and r the particle radius. The impulsive acceleration f_coll represents the force resulting from collisions and g is the gravitational acceleration vector ($g=(\mathrm{0},\mathrm{0},-g)$ with g=9.81 m s⁻²). The nonlinear drag coefficient α (Rowe and Henwood, 1961) is obtained by $\mathit{\alpha }=\mathrm{1}+\mathrm{0.15}{\left({\mathit{\text{Re}}}_{\mathrm{p}}\right)}^{\mathrm{0.687}}$, where the particle Reynolds number Re_p is defined by ${\mathit{\text{Re}}}_{\mathrm{p}}=\left(\left|U-V_{\mathrm{p}}\right|\mathrm{2}{r}_{\mathrm{p}}\right)/\mathit{\nu }$.

One important physical process that is often neglected because of the high computational cost associated with its simulation is hydrodynamic interaction (HI) among moving particles. While moving in a flow medium, a particle induces a flow disturbance (denoted by u in Eq. 3) in its vicinity that may reduce collisions between approaching particle pairs. The significance of HI on the collisional growth of cloud droplets with O(10 µm) sizes is well known and has actually been confirmed recently by a Lagrangian tracking simulation (Onishi et al., 2015). This study considers HI using the binary-based superposition method (BiSM) (Onishi et al., 2013), which is one of the so-called superposition methods (Ayala et al., 2007), and which considers HI based on a pair-wise technique while assuming that interactions via three or more particles are negligible. This assumption dramatically reduces computational costs while maintaining reliability as long as the particle number concentration is small, as is found in atmospheric clouds. It should be noted that the superposition method, which assumes Stokes flows around moving particles, is valid for small particles whose Re_p is smaller than unity. This requirement typically corresponds to r<40 µm. For larger droplets, associated errors will grow but the influence of HI will become insignificant as the particle inertia increases. As a result, the significance of HI relative to particle inertia would level off at a certain particle size, the threshold of which would depend on the flow conditions. While a more precise discussion on such issues could be done with size-resolving simulations, they are not a central focus of this study. Furthermore, the lubrication effect is not included in the superposition method. This would cause a slight overestimation of the collisional growth rate in the present simulations. Again, while this issue could be solved with cutting-edge size-resolving simulations, such detailed discussions are out of the scope of this study.

The second-order Runge–Kutta method was used for the time integration. The flow velocity U at the droplet position was linearly interpolated from the adjacent grid values. Since the Δt time interval should be smaller than the relaxation time, it should be set to a very small value if a tiny particle is included in the domain. In order to avoid extremely small time intervals, we designate particles whose relaxation times are smaller than the time interval as tracer particles. In this study, we set the time interval to $\mathrm{1.25}\times {\mathrm{10}}^{-\mathrm{3}}$ s and designate particles with a radii smaller than 14 µm as tracers. This treatment does not significantly alter the growth of particles with radii smaller than the threshold because condensational growth is more dominant than collisional growth. Note that all the CCN (dry aerosol) particles, whose sizes were not treated explicitly, were also considered to be tracers.

The growth of the ith liquid droplet is calculated as

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}={\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{act}}+{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{cond}}+{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{coll}},\end{array}$$

where the subscripts “act”, “cond”, and “coll” represent the growth due to activation, condensation, and collision, respectively. It should be noted that cond represents the change due to phase change and includes evaporation shrinkage.

2.4.2 Growth of particles

CCN activation

Next, we explain our newly developed stochastic CCN activation method for direct Lagrangian tracking simulations. First, the number density of newly activated liquid droplets at the corresponding time step is diagnosed in each Euler grid cell (i.e., inside a ${\mathrm{\Delta }}_x\times {\mathrm{\Delta }}_y\times {\mathrm{\Delta }}_z$ volume, where Δ is the grid spacing and the subscript denotes the direction) using the bulk air saturation and bulk number liquid droplet density. Then, a stochastic judgment is made on whether or not to activate each CCN particle. If the decision is affirmative, another stochastic judgment is then made on which size is to be set.

The formulation of the liquid droplet activation process is based on the relationship between the number of activated CCN N_act and the supersaturation ratio $S_{\mathrm{w}}=(Q_{\mathit{\upsilon }}-{Q_{\mathit{\upsilon }}}_{\mathrm{sw}})/{Q_{\mathit{\upsilon }}}_{\mathrm{sw}}$, where ${Q_{\mathit{\upsilon }}}_{\mathrm{sw}}$ is the saturated mixing ratio with respect to water. The saturated mixing ratio is obtained as ${Q_{\mathit{\upsilon }}}_{\mathrm{sw}}=\mathit{\epsilon }{e}_{\mathrm{s}}/\left(p-e_{\mathrm{s}}\right)$, where ε is the ratio of the gas constants for dry air and water vapor (i.e., $\mathit{\epsilon }=R/R_{\mathit{\upsilon }}$=0.622) and e_s is the saturated vapor pressure given by the Tetens formula $e_{\mathrm{s}}=\mathrm{611.2}\exp \mathit{\left\{}\mathrm{17.67}\right(T-$ $\mathrm{273.15})/(T-\mathrm{29.65}\left)\mathit{\right\}}$ (Murray, 1967). In Twomey (1959), the relationship between N_act and S_w is written in the form $N_{\mathrm{act}}=C{S}_{\mathrm{w}}^k$, where C and k depend on the CCN type. If we define S_max as the supersaturation needed to activate the total particle count N_CCN+N_w, where N_CCN and N_w are the number concentrations of dry CCN and liquid droplets, then C can be represented as $C=(N_{\mathrm{CCN}}+N_{\mathrm{w}})S_{\max }^{-k}$. Thus, the number of activated CCN (tiny liquid droplets) can be expressed as

$$\begin{array}{}\text{(5)}& {\displaystyle }{N}_{\mathrm{act}}=\left(N_{\mathrm{CCN}}+N_{\mathrm{w}}\right){\left({\displaystyle \frac{S_{\mathrm{w}}}{S_{\max }}}\right)}^k.\end{array}$$

The number of newly activated droplets is calculated as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{N}_{\mathrm{act}}=\max \mathit{\{}\mathrm{0},\left(N_{\mathrm{CCN}}+N_{\mathrm{w}}\right)\min \left[\mathrm{1},{\left({\displaystyle \frac{S_{\mathrm{w}}}{S_{\max }}}\right)}^k\right]\\ \text{(6)}& {\displaystyle }& {\displaystyle }-N_{\mathrm{w}}\mathit{\}}.\end{array}$$

Assuming the maritime conditions given in Onishi and Takahashi (2012), the parameters k and S_max were set to 0.6 and 0.008, respectively. The conversion from a dry aerosol to a liquid droplet is stochastically determined using the probability N_act∕N_CCN for each dry aerosol particle. The activated (nucleated) liquid droplet size (r_act) is then determined stochastically so that its size distribution follows the exponential probability distribution given in Soong (1974) as

$$\begin{array}{}\text{(7)}& {\displaystyle }f\left(r_{\mathrm{act}}\right)={\displaystyle \frac{\mathrm{3}{r}_{\mathrm{act}}^{\mathrm{2}}}{{\stackrel{\mathrm{‾}}{r}}^{\mathrm{3}}}}\exp \left[-{\left({\displaystyle \frac{r_{\mathrm{act}}}{\stackrel{\mathrm{‾}}{r}}}\right)}^{\mathrm{3}}\right],\end{array}$$

where $\stackrel{\mathrm{‾}}{r}$ is the radius of an average mass droplet and it was set to 11 µm (Onishi and Takahashi, 2012). This stochastic procedure is introduced to avoid detail calculations of the CCN activation process, in which microscale supersaturation fluctuations and CCN density size fluctuations are to be properly represented. The present procedure reproduces realistic size distributions of activated droplets without those detail calculations.

The mass growth due to this activation process is then calculated as

$$\begin{array}{}\text{(8)}& {\displaystyle }{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{act}}={\displaystyle \frac{\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}{r}_{\mathrm{act},i}^{\mathrm{3}}/\mathrm{3}}{\mathrm{\Delta }t}}.\end{array}$$

Condensational growth

The phase change for the ith particle is written as (Houze, 1993)

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }{\left({\displaystyle \frac{\mathrm{d}{r}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{cond}}={\displaystyle \frac{\mathrm{1}}{r_{\mathrm{p},i}\left(F_{\mathrm{d}}+F_k\right)}}\left(S_{\mathrm{w}}-{\displaystyle \frac{\mathit{\alpha }/T}{r_{\mathrm{p},i}}}+{\displaystyle \frac{\mathit{\beta }}{r_{\mathrm{p},i}^{\mathrm{3}}}}\right),\text{(10)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{d}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{p}}}{\mathit{\rho }{\mathit{\kappa }}_q{Q_{\mathit{\upsilon }}}_{\mathrm{sw}}}},F_k=\left({\displaystyle \frac{L_{\mathit{\upsilon }}}{R_{\mathit{\upsilon }}T}}-\mathrm{1}\right){\displaystyle \frac{L_{\mathit{\upsilon }}{\mathit{\rho }}_{\mathrm{p}}}{KT}}.\end{array}$$

Here, F_d represents a thermodynamic term associated with vapor diffusion and F_k is associated with heat conduction. The terms with coefficients α and β represent the curvature effect and the reduction in vapor pressure due to CCN hydrophilicity, respectively. This study simply ignored the solute effect and adopted $\mathit{\alpha }=\mathrm{3.3}\times {\mathrm{10}}^{-\mathrm{7}}$ m K and β=0 m³. R_υ is the gas constant for water vapor (R_υ=461.7 J kg⁻¹ K⁻¹), κ_q is the diffusion coefficient for water vapor, and K is the coefficient of air thermal conductivity. It should be noted that Eq. (9) also covers particle evaporation. When undersaturated (i.e., S_w<0), a liquid droplet shrinks due to evaporation. When a particle becomes smaller than the threshold, it reverts to the CCN (dry aerosol) category. The threshold radius was set to 1 µm.

The mass growth rate is obtained from

$$\begin{array}{}\text{(11)}& {\displaystyle }{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{cond}}=\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{p}}{r}_{\mathrm{p},i}^{\mathrm{2}}{\left({\displaystyle \frac{\mathrm{d}{r}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{cond}}.\end{array}$$

Collisional growth

It was assumed that colliding particles are immediately united by conserving mass and momentum. In other words, the coalescence efficiency was unity, and subsequent breakups (collisional breakups) were not considered. This no-breakup assumption can be justified for shallow clouds like the present KiD warm-1 case, and none of the other currently used spectral-bin models actually consider breakups for such cases. A collision is judged from the trajectories of a droplet pair by assuming linear particle movement for the time interval Δt.

2.5 Phase coupling

This study adopts one-way momentum coupling, thereby neglecting the momentum feedback from the particle phase to the flow phase. Since the mass fraction of the particles to flow is O(10⁻³) in the present simulations, this is easily justified by the dilute condition. The vapor and particle phases are coupled in order to conserve the water content. The coupling is done via the source term S_q in Eq. (2).

$$\begin{array}{}\text{(12)}& {\displaystyle }{S}_q(x,t)=-\sum _{i\in V\left(x\right)}\left\{{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{act}}+{\left({\displaystyle \frac{\mathrm{d}{m}_{\mathrm{p},i}}{\mathrm{d}t}}\right)}_{\mathrm{cond}}\right\}\end{array}$$

3 Computational conditions and performance

3.1 Quasi-one-dimensional computational domain

Table 2 shows the computational settings for the present LCS simulations. Two differently sized domains were used. This study focuses on the smaller size simulation (NORM), which has the horizontal size of ($L_x=L_y=$) 0.01 m and a vertical size of 3000 m. Roughly speaking, the influential length scale of HI relative to the particle diameter is approximately 10 for small Re_p values (Ayala et al., 2007; Onishi et al., 2013), although it would be smaller for larger particles. The maximum raindrop diameter is around 10⁻³ m in the present simulations. Since the horizontal domain size is 10 times larger than the maximum diameter, the HI of a particle would not affect itself unphysically through the horizontal periodic boundary condition even for the largest drops.

The large size simulation (LARGE), the volume of which was 9 times larger than that of NORM, was performed in order to confirm the robustness of the NORM simulation as will be discussed in Sect. 4.1. The number of initial particles was set to 9 times larger than that for NORM in order to keep the particle number concentration the same.

The mean separation length $l_{\mathrm{sep}}\left(=n_{p\mathrm{0}}^{-\mathrm{1}/\mathrm{3}}\right)$ was $\mathrm{2.71}\times {\mathrm{10}}^{-\mathrm{3}}$ m. The horizontal grid spacing Δ_x ($=L_x/n_x$, where n_x is the number of grid points in the x direction) was set similar to l_sep, while the vertical grid spacing Δ_z ($=L_z/n_z$) was set longer than the maximum path of the largest drop within a single time interval (∼O(10) m s⁻¹ × O(10⁻³) s $\sim O\left({\mathrm{10}}^{-\mathrm{2}}\right)$ m).

Table 2 Computational conditions for the LCS simulations. The same settings are used for both horizontal axes: x and y directions.

3.2 Initial and boundary conditions

The air flow and the temperature field were prescribed as shown in Sect. 2.2.1. The pressure was determined by the hydrostatic equilibrium as

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{d}p}{\mathrm{d}z}}=-\mathit{\rho }g.\end{array}$$

The obtained pressure and temperature are also listed in Table 1. Air viscosity depends on temperature and decreases by about 5 % from 297.9 K (domain bottom) to 280.4 K (domain top). This study simply neglected this change and used a constant value: $\mathit{\mu }=\mathrm{1.79}\times {\mathrm{10}}^{-\mathrm{5}}$ Pa s at 298 K and 1 atm. Initially, dry aerosols (CCN) were randomly and uniformly distributed. The initial number density was $n_{p\mathrm{0}}=\mathrm{5.00}\times {\mathrm{10}}^{\mathrm{7}}$ m⁻³, which is the same value used in the MSSG-Bin simulation.

Figure 1 Quasi-one-dimensional domain for the direct Lagrangian tracking simulation. Liquid droplets at t=1300 s for a NORM simulation are drawn, while the CCN particles (dry aerosols) are not. The color of each droplet denotes its diameter. For more information, see the Supplement.

Periodic boundary conditions were applied in all three directions for the particle field, except for the particles that reached the ground surface (z=0). Those particles (hereafter, surface raindrops) are removed from the system immediately after reaching the ground. Due to the prescribed updraft (see Eq. 1) some particles move out from the top boundary and reenter the domain from the bottom (ground surface). Although this sounds unphysical, it does not alter the physical result since all the reentry particles are dry CCN (not activated liquid droplets). The prescribed updraft lifts all the air parcels by ($\int w\mathrm{d}t=$) 764 m, while there is an over 1000 m vertical gap between the domain top (z=3000 m as in Table 1) and cloud top (z∼2000 m) as will be seen in Fig. 3. This simple periodic treatment for the vertical direction precisely conserves the number of particles, thus keeping the particle number concentration near the surface, until the first raindrop reaches the surface and disappears.

Periodic boundary conditions were applied in horizontal directions for the vapor field, while the Neumann boundary condition with zero gradient was applied in the vertical direction. This restricts Q_υ near the surface to its initial value.

3.3 Sensitivity of computational settings and computational performance

We performed 30 production runs for NORM and one for LARGE. Each run was intense and required massively parallel high-performance computing. One simulation for LARGE required 11 times longer to complete than was required for NORM, while the domain size and number of particles for LARGE were 9 times larger than those for NORM. In NORM, the ratio of the number of particles to that of grid points was 21.7, which means the particle calculation was much heavier. The particle calculation component actually occupied 98 % of the total computational cost.

Next we checked the effect of the computational settings used for grid spacing and time interval on the results obtained by performing a finer-grid-resolution simulation for NORM with a half-size grid, i.e., number of grids 8 (=2³) times larger, and comparing the results to the reference setting in Table 2. We also performed an additional NORM simulation using time intervals that were finer by a factor of 2, i.e., with $\mathrm{\Delta }t=\mathrm{6.25}\times {\mathrm{10}}^{-\mathrm{4}}$ s. The results from those additional simulations were within the statistical fluctuations summarized in Table 3, thus indicating the validity of the present computational settings.

4 Results and discussion

4.1 Bulk statistics

Figure 2 shows the temporal evolution of water paths obtained from the present LCS together with those from the MSSG-Bin. The threshold radius between cloud and rain was set to 40 µm. All the results from the 30 LCS runs are drawn. However, it should be noted that even though the LCS results look like a single thick line, each LCS run is slightly different from the others as denoted by standard deviations, as shown in Table 3.

The total liquid water path increases due to the supersaturation caused by the prescribed updraft for t≤600 s, which remains constant after the updraft stops until the first raindrop reaches the ground surface and is removed from the system. Rainwater appears at around t∼600 s and increases rapidly until t∼1350 s when the raindrops start to reach the surface. These results are consistent between the LCS and MSSG-Bin results. However, there is a difference in the maximum rainwater path, which can be attributed to the difference in the CCN treatment. Following the KiD protocol, the MSSG-Bin simulation kept N_CCN constant while the LCS simulations did not. N_CCN in the LCS simulation decreased with time since CCN particles were consumed for activation. This led to larger raindrops, and consequently to larger rainwater amounts.

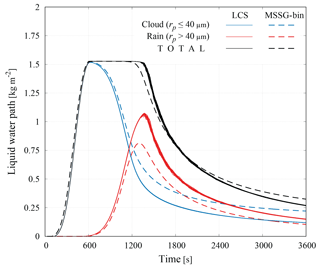
Figure 2 Temporal evolution of liquid water path. The solid lines show the LCS results (all 30 NORM runs are drawn independently while the deviation is small) while the dashed lines show the MSSG-Bin result.

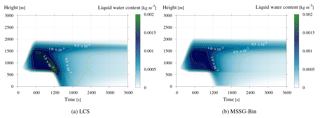
Figure 3 Temporal evolution of the vertical profile of liquid water content for (a) LCS and (b) MSSG-Bin. The yellow dashed lines are isolines at every $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{4}}$ kg m⁻³.

Table 3 shows a comparison of the bulk statistical values between the NORM and LARGE LCS runs. The values for LARGE range within the statistical variations in NORM. This suggests that the limited size of the NORM computational domain did not matter for bulk statistics.

Table 3 Comparison of bulk statistical values between NORM and LARGE runs. The values show (mean) ± (standard deviations).

Figure 3 shows the temporal evolution of the vertical profile of liquid water content. The vertical spacing of the LCS result for the plot was set to 25 m, which is the same vertical grid spacing used in the MSSG-Bin simulation. The results show that the cloud bottom exists at around z=600 m and that the cloud top is at z=2000 m. Raindrops appear from the bottom at around t=1100 s. These results are consistent for both the LCS and MSSG-Bin simulations. However, a remarkable difference is seen in the raindrop settling path for $\mathrm{600}<t<\mathrm{1100}$ s. The LCS result shows a sharp ridge, drawn by the contour line for $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{3}}$ kg m⁻³, inside the cloud layer, while the MSSG-Bin result does not. The MSSG-Bin somehow suffers from numerical diffusion because it adopts the Eulerian approach, while the LCS that uses a Lagrangian tracking approach does not. This clearly shows that the LCS can provide robust diffusionless numerical results.

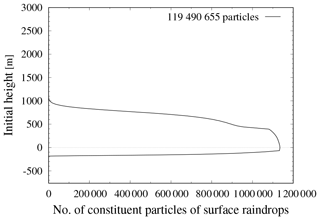
Figure 4 Initial locations of the particles that comprise the surface raindrops of the 30 NORM runs. The vertical distribution of the 119 490 655 particles that make up the 36 018 surface raindrops is drawn. The particles that are initially at negative height (near the top boundary) can be considered in the same manner as those that are transported into the domain along, or generated near, the surface.

Figure 5 Surface raindrop volume, V_sr, against the number of constituent particles, N_memb. The regression line shows $V_{\mathrm{sr}}=\mathrm{2.38}\times {\mathrm{10}}^{-\mathrm{14}}{N}_{\mathrm{memb}}$. The first 10 surface raindrops are denoted by red dots.

4.2 Lagrangian statistics

One of the strengths of direct Lagrangian simulations is that they can provide Lagrangian statistics on histories of individual Lagrangian particles. This study focuses on the Lagrangian statistics of surface raindrops, which are the raindrops that reach the ground surface (z=0 m). The 30 NORM simulations obtained a total of 36 018 surface raindrops, which means that each run obtained 1200 surface raindrops on average.

Figure 4 shows the initial locations of particles that comprise the 36 018 surface raindrops used in the 30 NORM runs. The total number of constituent particles was 119 490 655, which means that each surface raindrop contained an average of 3320 particles. The prescribed updraft lifted the air by 764 m. The air parcel was lifted by 764 m, while the cloud top was about 2000 m as in Fig. 3. The CCN initially located below about 1200 m (2000–764 m) in height participated in the cloud layer formation but those between 900 and 1200 m did not participate in the formation of the surface raindrops. The particles that were initially below 0 m can be considered in the same manner as those transported into the domain along, or generated near, the surface. This figure shows that surface raindrops consist of the CCN particles initially found below 900 m in height. This kind of information, which cannot be obtained from the conventional Eulerian-based bulk or spectral-bin simulations, can be used in other studies such as investigations into the chemical compositions of surface raindrops.

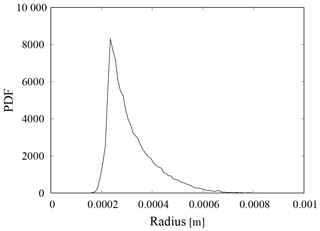
Figure 6 PDF of the sizes of the surface raindrops when they reach 600 m in height (nearly cloud bottom). Raindrops smaller than 200 µm in radius evaporated completely in the unsaturated air below the cloud bottom before reaching the ground surface and thus could not become surface raindrops.

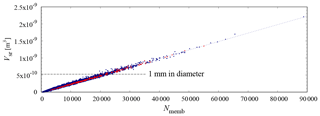
Figure 5 plots the surface raindrop volume, V_sr, against the number of constituent particles, N_memb. The regression line shows $V_{\mathrm{sr}}=\mathrm{2.38}\times {\mathrm{10}}^{-\mathrm{14}}{N}_{\mathrm{memb}}$, which means that the average diameter of each constituent is 36.1 µm. For example, a surface raindrop with a 1 mm diameter, whose volume is $\mathrm{5.24}\times {\mathrm{10}}^{-\mathrm{10}}$ m⁻³, consists of 22 000 constituent particles. Recalling that the mean diameter of the nucleated droplets was set to 22.0 µm (see Sect. 2.4.2), it can be surmised that condensation caused each constituent to grow from 22.0 to 36.1 µm, and then to grow further due to collisions. This is consistent with findings that show collisional growth is typically dominant for droplets with diameters larger than 40 µm.

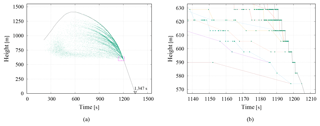
Figure 7 Collision events associated with a first surface raindrop. (a) All the associated collision events are plotted as dots, while the trajectory of the “mother” particle is shown as a line. (b) The enlarged view of the rectangular window shown in (a). The trajectories of raindrops (r_p>40 µm) on a vertical resolution with 7.81 m intervals. Each dot represents the individual collision events associated with the raindrops shown in colored lines.

Figure 6 shows the probability density function (PDF) of the surface raindrops when they reach 600 m height. Raindrops smaller than 200 µm in radius evaporated completely in the unsaturated air below the cloud bottom (z∼600 m) before reaching the ground surface, and thus could not become surface raindrops. That is, the unsaturated air near the surface acts as a barrier that prevents small raindrops from reaching the ground surface. This process cannot be represented in the parcel (zero-dimensional) concept and it is thus often neglected in theoretical works. For example, Kostinski and Shaw (2005) and Wilkinson (2016) discussed, neglecting that process, the stochastic aspect of the onset of surface precipitations and showed possible large deviations in the time required for droplets to grow, via collisions, from 10 to 50 µm in radius. The present result, however, suggests that the time required to grow from 10 to 200 µm, rather than to 50 µm, in radius should be measured for the discussion of the rapid onset of surface precipitations

Figure 7 shows the height against time collision history of the first surface raindrop, which reached the ground surface first in each run. The surface precipitation time T_surf was 1347 s. Here, we identify the “mother” particle from the tens of thousands of constituent particles making up the raindrop, each of which has its own ID number in the LCS simulation. When two particles collide and unite, the collector particle grows and the collected particle is removed, thereby conserving mass and momentum. In this process, the particle with the highest attained height of the raindrop constituents survives and its ID number is affixed to the raindrop. That particle is then designated as the mother of the surface raindrop. It should be noted that one particle attained its maximum height at t∼600 s when the updraft halted. In Fig. 7a, the trajectory of the mother particle is drawn as a line. The maximum height, H_max, attained by the mother particle can be used to characterize the surface raindrop. It should also be noted that the trajectory of a particle with constant settling velocity is drawn in a straight line, whereas the trajectory line of the mother particle appears to be parabolic. This result is attributed to the increasing settling velocity that results from collisional growth.

Figure 8 Maximum attained height of the mother particle for surface raindrops against surface precipitation time, T_surf. The circled points represent the first 10 raindrops. Only the plots for the first 10 raindrops are drawn in (b).

4.3 First 10 surface raindrops

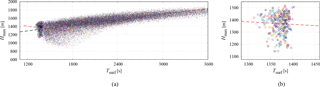
Figure 8 shows the relationship between the maximum attained height of the mother particle for each surface raindrop H_max against its surface precipitation time T_surf for all 30 NORM runs. In total, 36 018 dots are drawn in the figure. The black dashed line is obtained by least-squares regression for all the surface raindrops and is written as

$$\begin{array}{}\text{(14)}& {\displaystyle }{H}_{\max }=\mathrm{0.225}{T}_{\mathrm{surf}}+\mathrm{1020}.\end{array}$$

The positive correlation between H_max and T_surf means that larger H_max leads to larger T_surf because it takes longer for a droplet to fall far to the surface.

Interestingly enough, if restricted to the surface raindrops ranked as the first 10 with the earliest T_surf for each run, the correlation becomes negative as shown in Fig. 8b. Although the plots are very scattered, a statistical test has proven that a positive correlation is rejected with a 76 % confidence level, meaning that a negative correlation is very likely. We have also verified that the confidence level depends on computational conditions. If the evaporation rate is artificially strengthened by setting F_k=0 in Eq. (9), the confidence level becomes 99 % (virtually certain). This adds extra confidence to the supposition that this correlation reversal is possible under specific conditions.

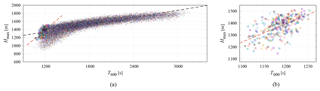
Figure 9 Attained maximum height against the time when the raindrop passes the height of 600 m (nearly cloud bottom), T₆₀₀. The black and red dashed lines show the least-squares regression line for all the surface raindrops and for the first 10 raindrops, respectively. In (b) only the plots for the first 10 raindrops are drawn.

In order to reveal the correlation reversal mechanism, we additionally collected T₆₀₀, the time when the raindrop passes z=600 m (i.e., near the cloud bottom). Figure 9 plots H_max against T₆₀₀. The black dashed line is obtained by least-squares regression for all the surface raindrops and is written as

$$\begin{array}{}\text{(15)}& {\displaystyle }{H}_{\max }=\mathrm{0.296}{T}_{\mathrm{600}}+\mathrm{987}.\end{array}$$

The sensitivity of H_max to T₆₀₀ is stronger, i.e., the slope is steeper than that for T_surf. Raindrops with higher H_max take longer to fall from H_max to the cloud bottom (z∼600 m). However, they can also collect more droplets during the longer fall and grow larger, and thus take less time to fall from 600 m to the surface. This weakens the correlation between T₆₀₀ and T_surf and consequently results in the stronger sensitivity (steeper slope in the linear form) of H_max to T₆₀₀ than to T_surf.

In contrast to Fig. 8, the correlation between H_max and T₆₀₀ for the first 10 is positive in Fig. 9. The sensitivity of H_max to T₆₀₀ for the first 10 raindrops is somewhat stronger than that for all the other surface raindrops. That is, the correlation reversal happens while the first 10 surface raindrops fall from the cloud bottom to the surface. These facts suggest the plausible scenario that larger drops among the first 10 surface raindrops, with higher H_max, pass the cloud bottom later and then overtake other raindrops before they can reach the surface. This kind of overtake would only occur if specific conditions are met.

This scenario can be confirmed in the Supplement (see Movie S1). The movie view consists of three windows; domain side view (left window), liquid water path (right top window) and look-up view from the ground (right bottom window). The look-up view shows that red spheres (raindrops about 500 µm in diameter) appear from the cloud bottom at around t=1100 s and that the blue spheres (raindrops about 1 mm in diameter) that appear just after tend to overtake the red spheres before they can reach the ground.

The Lagrangian statistics provide information about the surface raindrop growth history. They also show differences for the overall surface raindrops and differences for a fraction of the earliest raindrops. Another set of simulations shows that these differences are sensitive to the evaporation rate. These results suggest that the Lagrangian statistics of the surface raindrops have the potential to provide useful information for estimating atmospheric conditions aloft. They also remind us of the Nakaya diagram (Nakaya, 1954), which can translate the shapes of snow crystals into information on atmospheric conditions experienced by those crystals as they fell to the surface. The present Lagrangian simulation results clearly show that statistics of raindrops, as well as snow crystals, contain information about the sky that formed them.

5 Conclusions

The Lagrangian cloud simulator (LCS; Onishi et al., 2015) adopts a Eulerian–Lagrangian hybrid framework, in which the flow motion and scalar transport are computed using a Eulerian method, and the particle motion and growth are calculated using a Lagrangian tracking method. In that framework, cloud microphysics are based on direct Lagrangian tracking, which tracks the motion and growth of individual particles. In this study, we developed a CCN activation model for direct Lagrangian tracking simulations and implemented it in the LCS. This implementation enables complete tracking of particle growth from a CCN to surface raindrop, including the CCN activation, condensation–evaporation, collisions, and gravitational settling stages. It should also be noted that HI is considered for colliding droplet pairs in our newly developed LCS, which is currently the only model that can consider HI for tracking the simulation of droplet collisional growth at a reasonable computational cost.

The integrated 3-D LCS has previously been applied to a kinematic shallow convection cloud development in the case of the warm-1 KiD model (Shipway and Hill, 2012), which was originally designed to provide an intercomparison framework for bulk and bin cloud microphysics models. For the kinematic simulation used in this study, an extremely vertically elongated quasi-one-dimensional (quasi-1-D) computational domain has been adopted. Use of this domain enables the representation of vertical cloud development while keeping the computational domain volume (and consequently the total number of particles to track) small. The unique combination of the high-performance LCS and the extremely vertically elongated domain has allowed us, for the first time, to successfully complete a tracking simulation of droplet growth from CCN (dry aerosols) to raindrops in a reasonably realistic manner. For example, the process of droplet falling through unsaturated air below cloud layers, which is ignored in the parcel (zero-dimensional) modeling, can be represented. The air below the cloud layers is unsaturated (particularly for the onset time of surface precipitations) and the unsaturated air acts as a barrier that makes it difficult for raindrops to pass through via evaporation. A raindrop must grow large enough to overcome this evaporation barrier in order to become a surface raindrop. The present quasi-1-D approach can provide a practical platform for realistic discussion on the statistical deviations of the onset of surface precipitations, for example.

The results obtained from the LCS simulations are first compared to those from the MSSG-Bin model (Onishi and Takahashi, 2012), which is a spectral-bin cloud microphysics model based on the conventional Eulerian framework. The comparison results show good agreement, in terms of bulk statistics such as water mixing ratios, between the LCS and MSSG-Bin, except for slight variations due to CCN treatment differences. Furthermore, it has been confirmed that the LCS is free from particle-phase numerical diffusion.

One of the strengths of direct Lagrangian simulations is that they can provide Lagrangian statistics, on histories of individual Lagrangian particles. This study has focused on surface raindrops, which are the raindrops that reached the ground surface. For example, a surface raindrop with a 1 mm diameter consists of approximately 22 000 constituent particles. This means that each constituent particle grew to 36.1 µm in diameter due to condensation and then grew to 1 mm in diameter because of collisions. Additionally, by applying back-trajectory analysis to the surface raindrops, it was possible to identify the particle that attained the maximum height among all the constituent particles, which we define as the mother particle for a surface raindrop. These analysis results also show that the maximum attained height of mother particles has a positive correlation on their surface precipitation time. This can be easily explained by the fact that it takes more time for a particle to fall from higher altitudes. Interestingly, however, if restricted to the first 10 (the earliest 0.8 %) surface raindrops with the earliest surface precipitation time, the correlation was negative. As a plausible mechanism for this, it was suggested that larger drops among the first 10 surface raindrops, which are lifted up higher, pass the cloud bottom later but overtake the slower falling raindrops before they can reach the surface.

Based on the results obtained in this study, we can conclude that the use of Lagrangian statistics for evaluating surface raindrops can provide useful information for estimating atmospheric conditions aloft. These results also remind us of the Nakaya diagram (Nakaya, 1954), which can interpret the shapes of snow crystals into information on the atmospheric conditions experienced by the crystals. Since our present Lagrangian simulation clearly shows that the statistics of surface raindrops, as well as snow crystals, contain information about the conditions aloft, additional discussion becomes possible, thereby indicating that direct Lagrangian models can be powerful and promising meteorological tools.