The surface tension and cloud condensation nuclei (CCN) activation of sea spray aerosol particles

In marine environments, sea spray aerosol (SSA) particles have been found to contain surface-active substances (surfactants) originating from the sea surface microlayer. These surfactants can lower the surface tension of the SSA particles, facilitating their activation to cloud droplets. This effect is not considered in classical Köhler theory, which assumes droplets to be homogeneous with a surface tension of pure water. In this study the cloud condensation nuclei (CCN) activity of SSA particles calculated with classical Köhler theory is compared to a more complex calculation that considers bulk–surface partitioning, surface tension lowering, and liquid–liquid phase separation. The model approach presented here combines the multi-component Eberhart model for surface tension with the monolayer model and an activity model (Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients, AIOMFAC). This combination allows for calculating Köhler curves of surfactant-containing particles with a large number of compounds for the first time. In a sensitivity study we show that organic compounds can be categorized into weak, intermediate, and strong surfactants for CCN activation based on their separation factor in water S_1i and their pure component surface tension σ_i. For a quaternary model system of SSA particles, it is shown that high content of hydrophobic organic material (i.e. strong surfactants) in Aitken mode particles does not necessarily prevent good CCN activation but rather facilitates effective activation via surface tension lowering. Since common climate models use parameterizations that are based on classical Köhler theory, these results suggest that the CCN activity of small SSA particles might be underestimated in climate models.

1 Introduction

The oceans are covered to a large extent by an organic-rich layer, the so-called sea surface microlayer (SSM; Wurl et al., 2011). Since about 70 % of Earth's surface is covered by oceans, the SSM constitutes a large part of the interface between the condensed mass of the planet and its gaseous atmosphere. Its coverage is likely to even increase as climate change progresses and sea ice melts (Christiansen et al., 2020). The SSM contains surface-active organic substances such as lipids, fatty acids, polysaccharides, and proteins, as well as biota (e.g. bacteria and fish larvae) and substances of anthropogenic origin (e.g. plastics and tar lumps, Hardy, 1982; Wurl and Holmes, 2008). Aerosolization of the SSM by bubble bursting and wave breaking leads to sea spray aerosol (SSA) particles with high organic content (Facchini et al., 2008; O'Dowd et al., 2004). The presence of surface-active substances (surfactants) in aerosol particles can result in a surface tension lower than that of pure water or salt solutions, which reduces the Kelvin effect in the Köhler equation (Köhler, 1936). This raises the question of whether surface-active material facilitates cloud formation by enhancing cloud condensation nuclei (CCN) activation.

Classical Köhler theory, which is used as a basis for state-of-the-art climate modelling, does not take surface tension effects into account but assumes a surface tension of pure water for all aerosol particles. In order to analyse the potential error introduced by this assumption, a number of studies have investigated the potential influence that bulk–surface partitioning and surface tension lowering could have on CCN activation, yet no general agreement has been reached. While some studies suggest an enhanced CCN activation even for particles containing weakly surface-active substances (e.g. small dicarboxylic acids, Ruehl et al., 2016; Sareen et al., 2013), other studies find an effect only for strongly surface-active substances or droplets with high organic content (Ovadnevaite et al., 2017; Frosch et al., 2011; Kokkola et al., 2006; Lohmann and Leck, 2005) and further studies find no strong enhancement of CCN activity or cloud droplet number concentrations at all (Forestieri et al., 2018; Kristensen et al., 2014; Prisle et al., 2010; Lohmann et al., 2004).

The reason why these studies report seemingly contradictory results is that they greatly differ in the systems that were analysed (aerosol particle size and composition) as well as in their experimental methods or modelling approaches. On the experimental side, difficulties exist in determining the molecular composition of field samples. For laboratory-generated aerosol particles, challenges arise in producing particles with accurate surfactant content as well as minimizing impurities. On the modelling side, challenges include (i) modelling the surface tension of complex mixtures including non-ideality effects like salting out (El Haber et al., 2023), (ii) accounting for bulk depletion caused by the high surface-to-volume ratio in small droplets (Vepsäläinen et al., 2022, 2023), and (iii) determining the water activity of solutions containing surfactants. As a result, the relevance of surface effects on cloud formation is still uncertain despite considerable research efforts.

One of the first studies considering bulk depletion due to bulk–surface partitioning was that by Sorjamaa et al. (2004) using a model based on Gibbsian thermodynamics (“Gibbs model”). In the Gibbs model, the surface is described as an infinitely thin layer between the bulk phase and the gas phase – the so-called Gibbs dividing surface – and the Gibbs adsorption equation is used to relate the surface composition to the surface tension. Another partitioning model was suggested by Malila and Prisle (2018) based on the assumption that the surface phase consists of a one-molecule-thick layer (“monolayer model”). In this model, the surface tension is given by the average of the pure component surface tensions weighted by the substances' surface volume fractions. Besides these two models, various other approaches to modelling the bulk–surface partitioning in small droplets have been suggested in the past. In Vepsäläinen et al. (2022, 2023), six common model approaches are compared. For soluble organic acids (Vepsäläinen et al., 2022), it is concluded that the Gibbs model (Prisle et al., 2010) and the monolayer model (Malila and Prisle, 2018) are the current preferable options for modelling droplet growth and activation. For strongly surface-active substances (Vepsäläinen et al., 2023), no clear conclusion is presented as to which model can be recommended. Instead, it is shown that the models yield largely different surface tensions and critical supersaturations. Recently, Bzdek et al. (2020) and Bain et al. (2023) found good agreement when they compared the monolayer model to experimental results obtained from micrometre- and submicrometre-sized particles, suggesting the validity of this approach.

In this study, we address the challenges related to modelling surfactant-containing aerosol particles with a bottom-up-validated modelling approach. The model we present is able to take into account (i) non-ideality effects in surface tension, (ii) bulk depletion, and (iii) non-ideality in the bulk phase. Based on this model approach, we aim to provide an overview of which particle sizes and compositions necessitate the inclusion of surface effects for the calculation of the critical supersaturation and for what systems classical Köhler theory suffices. We focus on SSA due to its high abundance and since it is well known to contain strong surfactants (Bertram et al., 2018).

2 Modelling approach

The vapour pressure of a solution droplet was derived by Köhler (1936) as

$$\begin{array}{}\text{(1)}& \mathrm{SS}=\left(a_{\mathrm{w}}\exp \left({\displaystyle \frac{\mathrm{4}\mathit{\sigma }{v}_{\mathrm{w}}}{D_{\mathrm{wet}}RT}}\right)-\mathrm{1}\right)\cdot \mathrm{100}\mathit{\%},\end{array}$$

with the supersaturation SS in percent, the water activity a_w, the surface tension σ, the molar volume of water v_w, the wet diameter D_wet, the universal gas constant R=8.314 $\mathrm{J}{\mathrm{m}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$, and the temperature T. In this work, calculations are performed at room temperature, i.e. T=25 °C unless stated otherwise. The critical supersaturation SS_crit is given by the maximum of SS over D_wet. Since focus is laid on modelling the CCN activation, which requires supersaturated conditions, the particles are assumed to be in a liquid state at all considered levels of humidity.

In classical Köhler theory, solution ideality and the surface tension of water σ₁ are assumed. While these assumptions are justified for purely inorganic particles, the presence of organic substances can lead to non-ideal mixing and a lowering of the surface tension compared to that of water. To quantify the error that is introduced by assuming classical Köhler theory for surfactant-containing particles, we calculate SS_crit for SSA particles for both classical Köhler theory and a more complex model approach which accounts for solution non-ideality and surface tension lowering, as described in the following.

2.1 Composition-dependent surface tension

An atmospheric aerosol particle containing surfactants can experience lower surface tension than a particle without surfactants, and the extent of surface tension lowering depends on the size and dilution of the particle. At low relative humidity, a particle in a deliquesced state with a high concentration of surfactants is expected to have low surface tension. However, with increasing humidity, the particle dilutes, and, as a result, the surface tension increases and approaches the value of pure water, as illustrated in detail by Davies et al. (2019). Therefore, a surface tension model is required to quantify surface tension as a function of the solution composition.

For aqueous mixtures with one solute (binary solution), numerous surface tension models have been proposed in the past. A number of binary surface tension models were reviewed in Kleinheins et al. (2023) and tested for a broad range of compounds, showing that the experimental surface tension data at a fixed temperature (surface tension isotherm) closely follow a sigmoidal curve when plotted on an x axis with a logarithmic mole fraction. Based on the logistic function, the sigmoid model was derived as

$$\begin{array}{}\text{(2)}& \mathit{\sigma }={\mathit{\sigma }}_{\mathrm{1}}-\left({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_i\right)\left({\mathrm{10}}^{pd}+\mathrm{1}\right){\displaystyle \frac{x_i^d}{{\mathrm{10}}^{pd}+x_i^d}},\end{array}$$

where x_i is the mole fraction of the solute i and σ₁ and σ_i are the pure component surface tensions of water and a solute i, respectively. The parameters p and d can be obtained by fitting Eq. (2) to experimental data, and they characterize the inflection point (p) and the distance (d) of the inflection point from the critical micelle concentration (CMC). According to Kleinheins et al. (2023), with p, d, and σ_i, the surface tension isotherm of a substance is sufficiently characterized.

Among these parameters, d is of minor importance. El Haber et al. (2024) report binary aqueous surface tension data of over 130 organic compounds and provide fits with the sigmoid model for 56 of the compounds. From all fits, d has an average value of 1.3, and 80 % of all fits result in d between 0.6 and 1.7. In a simple sensitivity calculation, a variation in d in this range was found to have only a small influence on SS_crit, yielding a maximum deviation of ΔSS_crit≈0.05 % under extreme conditions (see Sect. S1 in the Supplement).

When choosing d=1, the sigmoid model simplifies to a function that is mathematically equivalent to the Eberhart model (Eberhart, 1966). Instead of a parameter p, the Eberhart model uses a separation factor S that describes the adsorption–desorption rate of the solute relative to the solvent. Using a subscript 1 for water and i for the solute, the model is written as

$$\begin{array}{}\text{(3)}& \mathit{\sigma }={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{1}}(\mathrm{1}-x_i)+{\mathit{\sigma }}_i{S}_{\mathrm{1}i}{x}_i}{(\mathrm{1}-x_i)+S_{\mathrm{1}i}{x}_i}}.\end{array}$$

Mathematically, S_1i is related to p via ${\mathrm{10}}^p=\mathrm{1}/(S_{\mathrm{1}i}-\mathrm{1})$. If S_1i=1, water and the solute i have the same adsorption–desorption rate to the surface such that no substance is enriched at the surface. If S_1i>1, the solute i has a preference to partition to the surface, while if S_1i<1, the solute i is expected to be depleted at the surface. Following the Eberhart model, we can fully characterize the surface tension behaviour of substances in a binary solution with water with only two parameters, i.e. S_1i and σ_i.

Atmospheric aerosol particles are complex mixtures with more than one solute. Therefore, to accurately calculate their surface tension, a multi-component surface tension model is required. Based on the binary Eberhart model and the multi-component Connors–Wright model by Shardt et al. (2021), a multi-component Eberhart model was derived by Kleinheins et al. (2024) as

$$\begin{array}{}\text{(4)}& \mathit{\sigma }=\sum _{i=\mathrm{1}}^n{\mathit{\sigma }}_i{x}_i+\sum _{i=\mathrm{1}}^n\left({\displaystyle \frac{x_i}{{\sum }_{j=\mathrm{1}}^n{x}_j/S_{ji}}}\sum _{j=\mathrm{1}}^n{\displaystyle \frac{x_j}{S_{ji}}}\left({\mathit{\sigma }}_j-{\mathit{\sigma }}_i\right)\right),\end{array}$$

where S_ij is the separation factor of a binary mixture of substances i and j. This model was found to accurately predict the surface tension of ternary ideal mixtures if all S_ij values are known from binary surface tension data. If a factor S_ij is unknown, it can be obtained by fitting it to ternary surface tension data.

Ternary solutions containing surfactants in a mixture with a salt were found to exhibit salting-out effects leading to an increased surface concentration of the surfactant (Kleinheins et al., 2024; El Haber et al., 2023). This non-ideal surface tension behaviour can be taken into account by additional parameters $A_{ij}^{\mathrm{SO}}$ and $B_{ij}^{\mathrm{SO}}$, for surface- and bulk-related non-ideality, respectively. When considering surface-related non-ideality ($A_{ij}^{\mathrm{SO}}\ne \mathrm{0}$), the surface tension of the surfactant σ_i is perturbed as a function of the mole fraction of the salt x_j as

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}_i^{\mathrm{non}-\mathrm{ideal}}={\mathit{\sigma }}_i\left(\mathrm{1}-x_j{A}_{ij}^{\mathrm{SO}}\right).\end{array}$$

For bulk-related non-ideality, the separation factor of the surfactant in water S_1i is perturbed as

$$\begin{array}{}\text{(6)}& S_{\mathrm{1}i}^{\mathrm{non}-\mathrm{ideal}}=S_{\mathrm{1}i}\left(\mathrm{1}+x_j{B}_{ij}^{\mathrm{SO}}\right).\end{array}$$

The salting-out factors $A_{ij}^{\mathrm{SO}}$ and $B_{ij}^{\mathrm{SO}}$ can be obtained by fitting the model (Eqs. 4–6) to ternary surface tension data as shown by Kleinheins et al. (2024).

2.2 Bulk–surface partitioning and bulk depletion

In large liquid volumes, the bulk composition $x_i^{\mathrm{bulk}}$ can be assumed to be equal to the total composition $x_i^{\mathrm{tot}}$ (i.e. $x_i=x_i^{\mathrm{bulk}}\approx x_i^{\mathrm{tot}}$) in surface tension isotherms (e.g. Eberhart model). Small droplets, however, have a large surface-to-volume ratio, and therefore the partitioning of substances to the surface of the droplet can lead to their depletion in the droplet bulk. To take this effect into account, a partitioning model is required that introduces mass conservation and allows for quantifying the bulk depletion based on physical and geometrical assumptions. Here, we choose the monolayer model (Malila and Prisle, 2018) for modelling bulk–surface partitioning, which has been validated with microscopic surface tension data in several studies (Bzdek et al., 2020; Bain et al., 2023, 2024).

Briefly, the monolayer model calculates the surface tension of a particle based on its surface composition and an experimentally constrained surface tension isotherm. To do so, the droplet is divided into a spherical bulk volume V^bulk and a surface volume V^surf, which has the shape of a spherical shell with a thickness of one molecular layer. The composition of the bulk and surface phases ($x_i^{\mathrm{bulk}}$ and $x_i^{\mathrm{surf}}$) and the surface tension σ of the droplet are determined using the total composition $x_i^{\mathrm{tot}}$ and the wet diameter D_wet of the droplet as input parameters. As a first constraint, mass conservation has to be fulfilled such that

$$\begin{array}{}\text{(7)}& n_i^{\mathrm{tot}}=n_i^{\mathrm{bulk}}+n_i^{\mathrm{surf}},\end{array}$$

where n_i is the number of molecules of substance i in the entire droplet (tot), the surface phase (surf), or the bulk phase (bulk). Note that $x_i^{\mathrm{tot}}\ne x_i^{\mathrm{bulk}}+x_i^{\mathrm{surf}}$. In the model suggested by Malila and Prisle (2018), composition-dependent density parameterizations are used. In contrast, for simplicity we assume volume additivity in all phases as $V={\sum }_i{n}_i{v}_i$, where v_i is the molecular volume of substance i, which is calculated as $v_i=M_i/\left({\mathit{\rho }}_i{N}_{\mathrm{A}}\right)$ from the substance's molar mass M_i, its density ρ_i, and Avogadro's number N_A. With these relationships, the number of molecules in each phase can be calculated from the volume and the composition of the phase.

For the calculation of V^surf, the monolayer thickness δ is required, which is assumed to depend on the monolayer composition as

$$\begin{array}{}\text{(8)}& \mathit{\delta }={\left({\displaystyle \frac{\mathrm{6}}{\mathit{\pi }}}\sum _i{v}_i{x}_i^{\mathrm{surf}}\right)}^{\mathrm{1}/\mathrm{3}}.\end{array}$$

Thus, δ is a number-weighted average of the equivalent diameter of the molecules in the surface phase, where the equivalent diameter of a molecule is given by the diameter of a sphere with the same volume as the molecular volume v_i.

In addition to these geometrical assumptions, the model requires information on (i) the strength of partitioning of a substance to the surface and (ii) how the surface composition relates to surface tension. The strength of partitioning of a substance is derived from the surface tension isotherm

$$\begin{array}{}\text{(9)}& \mathit{\sigma }=f\left(x_i^{\mathrm{bulk}}\right),\end{array}$$

which can be obtained from macroscopic surface tension measurements, where $x_i^{\mathrm{bulk}}=x_i^{\mathrm{tot}}$. Here, we use the multi-component Eberhart model (Kleinheins et al., 2024) in contrast to Malila and Prisle (2018) and Bain et al. (2023), who used a Szyszkowski–Langmuir-based equation, which is limited to ternary and quaternary solutions of specific systems. The surface tension σ is related to the surface composition via

$$\begin{array}{}\text{(10)}& \mathit{\sigma }={\displaystyle \frac{{\sum }_i{\mathit{\sigma }}_i{v}_i{x}_i^{\mathrm{surf}}}{{\sum }_i{v}_i{x}_i^{\mathrm{surf}}}},\end{array}$$

i.e. the surface tension is an average of the pure component surface tensions, weighted by the surface volume fractions, which is a key assumption of the monolayer model. Equations (7)–(10) provide a system of equations that can be solved iteratively for an infinite number of substances with a nested pseudo-binary approach. The procedure used in this study to solve the monolayer model for a quaternary system is shown in more detail in Sect. S2.

Monolayer model calculations can also be solved taking surface tension non-ideality, e.g. salting out, into account, but doing so requires an adaptation in the monolayer model equations. The enhanced partitioning and lowered surface tension due to salting out can be introduced via the surface tension isotherm, i.e. the multi-component Eberhart model using Eqs. (5) and (6). If $A_{ij}^{\mathrm{SO}}>\mathrm{0}$, the surface tension of the mixture σ can be lower than any of the pure component surface tensions ($\mathit{\sigma }<min\left({\mathit{\sigma }}_i\right)$). This is problematic when solving for the surface composition via Eq. (10). For consistency between the non-ideal Eberhart model and the monolayer model, Eq. (10) needs to be replaced with

$$\begin{array}{}\text{(11)}& \mathit{\sigma }={\displaystyle \frac{{\sum }_i{\mathit{\sigma }}_i^{\mathrm{non}-\mathrm{ideal}}{v}_i{x}_i^{\mathrm{surf}}}{{\sum }_i{v}_i{x}_i^{\mathrm{surf}}}}.\end{array}$$

To validate the presented model approach, the model was compared to surface tension measurements of 6–9 µm radius droplets containing a surfactant and 0.5 M NaCl, measured by Bain et al. (2023), as shown Sect. S3. Like the result by Bain et al. (2023), who used a combination of the monolayer model with a Szyszkowski–Langmuir-based surface tension isotherm, our combined Eberhart–monolayer model reproduces the general trends well, with a tendency to overestimate bulk–surface partitioning and underestimate the surface tension.

2.3 Water activity and solution non-ideality

Once $x_i^{\mathrm{surf}}$, $x_i^{\mathrm{bulk}}$, and σ are calculated with the monolayer model, the water activity a_w needs to be determined to finally calculate the critical supersaturation via Eq. (1). In classical Köhler theory, no bulk–surface partitioning is considered and solution ideality is assumed, i.e. $a_{\mathrm{w}}={\widehat{x}}_{\mathrm{w}}^{\mathrm{tot}}$, where ${\widehat{x}}_{\mathrm{w}}^{\mathrm{tot}}$ is calculated as

$$\begin{array}{}\text{(12)}& {\widehat{x}}_{\mathrm{w}}^{\mathrm{tot}}={\displaystyle \frac{x_{\mathrm{w}}^{\mathrm{tot}}}{{\sum }_i{x}_i^{\mathrm{tot}}{v}_{\mathrm{H},i}}},\end{array}$$

where v_H,i is the van 't Hoff factor of substance i. These assumptions are made in many studies. However, organic substances with a low oxygen-to-carbon (O:C) ratio can display non-ideal mixing behaviour in water. Therefore, for our best estimate of SS_crit, we add a calculation of a_w based on $x_{\mathrm{w}}^{\mathrm{bulk}}$ considering solution non-ideality.

To do so, an activity coefficient γ_w is introduced as $a_{\mathrm{w}}={\mathit{\gamma }}_{\mathrm{w}}{x}_{\mathrm{w}}^{\mathrm{bulk}}$. The group contribution model AIOMFAC (Aerosol Inorganic–Organic Mixtures Functional groups Activity Coefficients; Zuend et al., 2008, 2011) allows for calculating activity coefficients for organic–inorganic mixtures. Here, we use the web version (https://aiomfac.lab.mcgill.ca, last access: 20 January 2025) of AIOMFAC for the calculation of γ_w and a_w. In the calculations with the web version of AIOMFAC, all substances are assumed to be in a single homogeneous phase, and we therefore label this calculation “AIOMFAC-1ph”. When substances with a low oxygen-to-carbon (O:C) ratio are mixed with inorganic salts in the same particle, this can lead to unphysically high activity coefficients being predicted by AIOMFAC. In this case, the solution undergoes liquid–liquid phase separation (LLPS) (Zuend and Seinfeld, 2012; Ciobanu et al., 2009). When the organic substances are surfactants, micelles form at concentrations exceeding the CMC, which can be considered a type of phase separation. In both cases, the organic substance is strongly depleted in the aqueous phase and its contribution to the Raoult effect is diminished. To consider this effect, we calculate a_w assuming that the surfactant is totally hydrophobic and entirely present in a separate phase. In this case, the bulk mole fractions are converted to “surfactant-free” mole fractions ${\stackrel{\mathrm{̃}}{x}}_i^{\mathrm{bulk}}$ to calculate a_w with AIOMFAC. This approach gives the maximum limit of a_w at small wet diameters when micelles and/or LLPS are present. To obtain a best estimate of a_w, we combine the AIOMFAC-1ph result at large wet diameters with the hydrophobic approach at small wet diameters by always taking the lower value of the two. More details are given in Sect. S4. For the particles considered in this study, it is found that in most cases solution ideality can be assumed for the calculation of SS_crit. Only at high content of amphiphilic or hydrophobic organic substances and small dry diameters can LLPS lead to substantially higher SS_crit values as further discussed in Sect. 4 below.

Sodium dodecyl sulfate (SDS) – a substance that is used in this study – poses some additional difficulties for the calculation of the Raoult effect. First, it can dissociate in aqueous solution, and, second, its organic-sulfate group cannot be represented with the functional groups implemented in AIOMFAC. To address the second issue, we represent SDS with dodecanoic acid in AIOMFAC, which is a fatty acid with the same hydrocarbon chain length. We tested the influence of the degree of SDS dissociation and solution non-ideality when representing SDS with dodecanoic acid in Sect. S5. It was found that in classical Köhler theory, solution non-ideality and the degree of dissociation of SDS play an important role in the calculation of SS_crit. However, in calculations considering surface tension lowering, in most cases, solution ideality can be assumed and the degree of SDS dissociation has negligible influence on SS_crit, except for small dry diameters and high organic content. Since we use SDS in the following as a model compound to represent general organic, surface-active compounds, e.g. fatty acids, which do not dissociate, we proceed with representing SDS with dodecanoic acid and also use a van 't Hoff factor $v_{\mathrm{H},\mathrm{SDS}}=\mathrm{1}$ in classical Köhler theory unless stated otherwise.

3 Representation of sea spray aerosol particles

The marine aerosol can be divided into a primary aerosol produced by breaking waves (SSA) and a secondary aerosol produced by gas-to-particle conversion of volatile species (secondary marine aerosol) (Rinaldi et al., 2010). In this study, we focus on freshly emitted (nascent) SSA particles to investigate the influence of their high surfactant content on CCN activation. Note that atmospheric ageing of SSA leads to fragmentation reactions of organics with OH, resulting in organic mass loss (Trueblood et al., 2019), and uptake of sulfuric and nitric acid, methanesulfonic acid, and organic acids, resulting in chloride depletion (Su et al., 2022). These ageing processes are expected to increase the total fraction of soluble species and to potentially lower the fraction of large surface-active molecules. Therefore, by focusing on nascent SSA in this study, an upper estimate of the influence of surface effects on CCN activation is given.

In this study, we represent SSA by a quaternary model system as illustrated in Fig. 1a. Besides (1) water, the SSA is assumed to contain (2) surfactants, (3) water-soluble organic compounds (WSOCs), and (4) inorganic salts. For each of these categories, one model compound is chosen to represent the group of substances. For the inorganic salts, NaCl is chosen as the model compound because the inorganic fraction of nascent SSA was found to consist mostly of NaCl with only small amounts of calcium, magnesium and potassium chlorides, sulfates, and carbonates (Bertram et al., 2018). The mass fractions of the organic substances and their model compounds are discussed in the following sections. An illustrative depiction of bulk–surface partitioning in a droplet with a given total composition is shown in Fig. 1c.

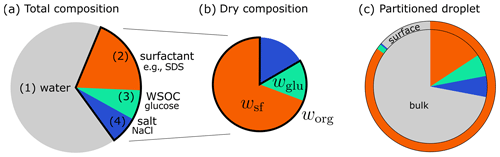
Figure 1 Schematic representation of the quaternary model SSA particle: (a) total composition with model compounds; (b) dry composition with organic fraction w_org, glucose fraction w_glu, and surfactant fraction w_sf; and (c) droplet with bulk–surface partitioning, where the surface is considered to comprise one molecular layer. Dimensions are not to scale.

3.1 Size-dependent organic content

The chemical composition of SSA has been reviewed thoroughly by Bertram et al. (2018), and we follow their recommendations in this study. Besides inorganic salts, SSA contains organic compounds originating from the SSM. It was found that the organic-to-inorganic ratio depends strongly on the size of the particles, with smaller particles having a higher organic content. Figure 2 summarizes measurements of the mass ratio of organic carbon to sodium ions $\mathrm{mC}/{\mathrm{mNa}}^{+}$ for a range of dry particle diameters, evidencing the increase in organic fraction with decreasing particle size (Bertram et al., 2018). To derive a simple relationship of the organic content in SSA particles as a function of size, a linear fit was made to the data resulting in

$$\begin{array}{}\text{(13)}& {\log }_{\mathrm{10}}\left(\mathrm{mC}/{\mathrm{mNa}}^{+}\right)=-\mathrm{0.448}-\mathrm{1.37}{\log }_{\mathrm{10}}\left(D_{\mathrm{dry}}/\mathrm{\mu }\mathrm{m}\right),\end{array}$$

where D_dry is the dry diameter in micrometres. Note that in real SSA particles, the presence of MgCl₂ and CaCl₂ may lead to the formation of hydrates upon efflorescence (Rasmussen et al., 2017). Calculation of the dry salt mass based on a measured dry diameter of such a particle can be erroneous if these hydrates are not accounted for correctly. In this study, the dry diameter refers to the equivalent diameter of a totally dry particle, i.e. containing no hydrates.

Besides experimental uncertainty, natural variability in the organic content contributes to some spread of the data around the fitted mean. To take this spread into account, 99 % confidence intervals of the linear fit were computed providing a lower (“low” case) and higher (“high” case) limit of the organic content in addition to the average value given by the linear fit (“med” case). Since no data are available for particles below 100 nm, the organic content of these particles is uncertain and can lie outside of the range covered by the low–high cases. Therefore, in Sect. 4.2, the organic content is varied in a broader range for sensitivity analysis.

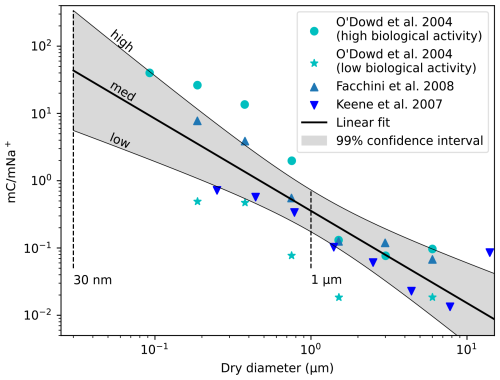
Figure 2 Mass ratio of organic carbon to sodium ions $\mathrm{mC}/{\mathrm{mNa}}^{+}$ of SSA particles as a function of their dry diameter. Symbols: measurements from field (O'Dowd et al., 2004) and laboratory studies (Facchini et al., 2008; Keene et al., 2007) reproduced from Bertram et al. (2018). Solid lines: linear fit (Eq. 13, med case) and 99 % confidence interval (low and high cases).

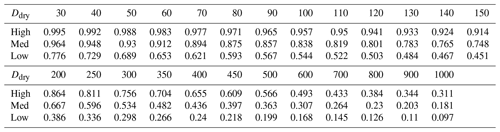
We converted $\mathrm{mC}/{\mathrm{mNa}}^{+}$ to an organic dry mass fraction w_org using O:C and H:C elemental ratios of 0.34 and 1.43, respectively, following the suggestion from Bertram et al. (2018) for sub-micrometre particles. The resulting w_org for the three cases of low, med, and high and dry diameters from 30 nm to 1 µm are shown in Table 1.

Table 1 Organic dry mass fraction w_org for a range of dry diameters D_dry (nm) derived from the linear fit in Fig. 2 (med case) and its 99 % confidence interval (low and high cases).

3.2 Composition of the organic fraction

The organic dry mass fraction given in Table 1 is subdivided into WSOCs and surfactants. A large fraction of WSOCs were identified as saccharides with glucose detected as the most abundant species (Bertram et al., 2018; Hasenecz et al., 2020; Jayarathne et al., 2016). Therefore, we represent WSOCs with glucose and define

$$\begin{array}{}\text{(14)}& w_{\mathrm{org}}=w_{\mathrm{glu}}+w_{\mathrm{sf}},\end{array}$$

where w_glu and w_sf are the dry mass fractions of glucose and the surfactant, respectively (see Fig. 1b). The percentage of WSOCs in the total organic mass was found to be very small (≈5 % for particles with D_dry=125–250 nm, Facchini et al., 2008). Hence, as our best estimate, we set the fraction of glucose in the total organic mass $w_{\mathrm{glu}}/w_{\mathrm{org}}$ to 0.05. In addition, $w_{\mathrm{glu}}/w_{\mathrm{org}}$ is also varied from 0 to 1 for the sensitivity analysis in Sect. 4.

The molecular identity of surfactants in SSA has been analysed by Cochran et al. (2016) with mass spectrometry. Their results suggest that the surfactants are mostly composed of saturated fatty acids, with palmitic (hexadecanoic) acid as the most abundant species. Besides saturated fatty acids, unsaturated fatty acids, hydroxyl-fatty acids, oxo-fatty acids, alkyl sulfates, and linear alkylbenzene sulfonates were also found.

Besides its functional groups, the surfactant model compound should be representative in its surface-active behaviour. As described in Sect. 2.1, surfactants can be characterized by their separation factor in water S_1i and their pure component surface tension σ_i. By fitting the binary Eberhart model (Eq. 3) to experimental surface tension data compiled by El Haber et al. (2024), S_1i and σ_i were determined for 76 organic substances, which are shown in Fig. 3. The fitting procedure is described in Sect. S6, and the data underlying Fig. 3 are provided in tabular form in Sect. S6 and as a CSV file (see “Code and data availability”). In addition to these 76 organic compounds, S_1i and σ_i of atmospheric samples taken at five different locations were considered. Ekström et al. (2010) and Gérard et al. (2016) measured surface tension isotherms of amphiphilic extracts from filter samples of atmospheric aerosol particles collected at coastal, marine, temperate forest, and tropical forest sites. These experimental surface tension data were fitted with the binary Eberhart model (see Sect. S7). The resulting S_1i and σ_i values are shown as blue squares in Fig. 3.

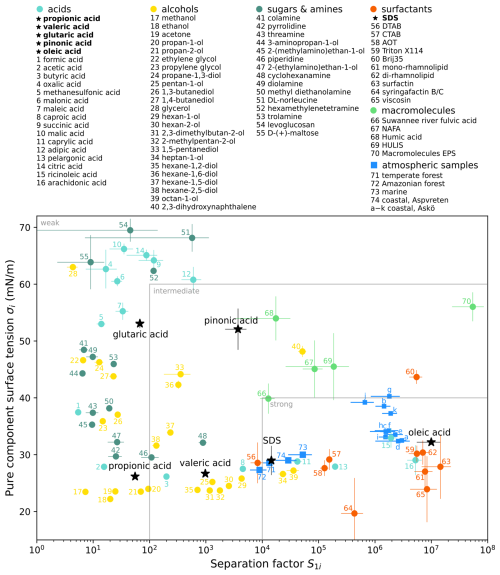
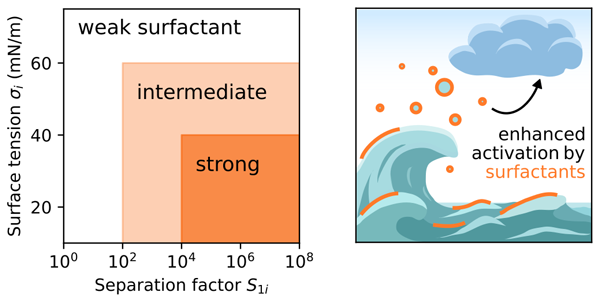
Figure 3 Separation factor in water S_1i and pure component surface tension σ_i of organic substances (stars and 1–70: based on data compiled by El Haber et al., 2024) and of atmospheric samples taken at five different locations (71–74: Ekström et al., 2010; a–k: Gérard et al., 2016; see also Sects. S6–S8). Substances with black stars as markers are used as model compounds in this study. S_1i was determined by fitting the binary Eberhart model (Eq. 3) to experimental surface tension data. If σ_i was not reported in El Haber et al. (2024), it was considered an additional fitting parameter. For the atmospheric samples, σ_i was taken as the lowest measured value. Uncertainty bars show the 95 % confidence intervals of the fit parameters. Substance names and categories are the same as in El Haber et al. (2024); i.e. the category of “alcohols” also contains ketones and aldehydes. Grey lines and labels of approximate regions of weak, intermediate, and strong surfactants show the suggested categorization following the results of this study.

Table 2 Physical properties and surface tension parameters used in this study: density ρ_i, molar mass M_i, molar volume v_iN_A, van 't Hoff factor v_H,i, pure component surface tension σ_i, and separation factor in water S_1i.

To show the sensitivity of the results to the choice of the surfactant model compound, we choose six different model surfactants that cover a broad range of S_1i values and two regimes of σ_i. First we choose SDS as a model surfactant having similar S_1i and σ_i values to that of the atmospheric samples from Ekström et al. (2010). Since surfactants in SSA have been largely identified as fatty acids (Cochran et al., 2016), we further choose three fatty acids among the model compounds, i.e. propionic acid (C₃H₆O₂), valeric acid (C₅H₁₀O₂), and oleic acid (C₁₈H₃₄O₂). From these, propionic acid has the lowest separation factor (S_1i=55.3) and can be considered a weakly surface-active substance. Valeric acid has a moderate separation factor (S_1i=974.6) that lies between that of propionic acid and SDS. Oleic acid marks the higher end of the separation factor range with $S_{\mathrm{1}i}=\mathrm{9.9}\times {\mathrm{10}}^{\mathrm{6}}$ and serves to represent the strong surfactants with numbers 59–65 in Fig. 3 as well as the atmospheric samples from Gérard et al. (2016). With these three fatty acids and SDS, four model compounds were found that cover a broad range of S_1i, while their σ_i value is in a small range of ±4 mN m⁻¹ around σ_i=30 mN m⁻¹. To show the influence of σ_i, two additional compounds with a higher σ_i of ${\mathit{\sigma }}_i=\mathrm{50}\pm \mathrm{3}$ mN m⁻¹ were chosen, namely glutaric acid and pinonic acid. Glutaric acid can be considered a weakly surface-active substance having a separation factor similar to that of propionic acid (S_1i=67.3). The separation factor of pinonic acid ($S_{\mathrm{1}i}=\mathrm{3.7}\times {\mathrm{10}}^{\mathrm{3}}$) lies between that of valeric acid and SDS. Both substances are atmospheric oxidation products and commonly found in secondary organic aerosol. The six model compounds are denoted by black stars in Fig. 3.

To model the atmospheric surfactants contained in SSA in the most representative manner, sodium dodecyl sulfate (SDS) is chosen as the reference surfactant for three reasons. First, SDS has a surface activity ($S_{\mathrm{1}i}=\mathrm{1.4}\times {\mathrm{10}}^{\mathrm{4}}$ and σ_i=29.0 mN m⁻¹) close to the atmospheric surfactants measured by Ekström et al. (2010). Second, its surface tension in mixtures with salts is well characterized (Kleinheins et al., 2023). Third, in agreement with the findings by Cochran et al. (2016), it has a molar mass (M=288 g mol⁻¹) similar to that of palmitic acid (M=256 g mol⁻¹), which is the most abundant species in SSA.

3.3 Surface tension parameters of the model compounds

The multi-component Eberhart model requires σ_i of all substances and separation factors S_ij between all substance pairs i–j in the mixture. To take surface tension non-ideality into account, additional parameters A_ij and B_ij are required. In the following, the substances are numbered as (1) water, (2) surfactant, (3) glucose, and (4) NaCl in the subscripts (Fig. 1).

The pure component surface tension σ_i and the binary separation factor in water S_1i of all substances used in this study are summarized in Table 2 (see Sect. S8 for underlying experimental data and model fits). For water, σ₁=72.0 mN m⁻¹ was used throughout the study. For the six model substances (propionic acid, glutaric acid, valeric acid, pinonic acid, SDS, and oleic acid) used in the surfactant category (2), σ₂ and S₁₂ are taken from the fits underlying Fig. 3. The pure-liquid surface tension of glucose at room temperature is not known, since glucose crystallizes at this temperature. The binary aqueous solution data from Aumann et al. (2010), Lee and Hildemann (2013), and Romero and Albis (2010) compiled by El Haber et al. (2024) are only available in a narrow concentration range. An extrapolation to supersaturated concentrations with the Eberhart model yields a very high value (σ₃>10 000 mN m⁻¹) with a large uncertainty (90 % confidence interval: ±10⁷). In contrast, for sucrose, an extrapolation of aqueous solution data with various models resulted in σ_sucrose between 80 and 120 mN m⁻¹ (Kleinheins et al., 2023), which seems more plausible. Because of the structural similarity between glucose and sucrose, we set the surface tension of glucose to σ₃=100 mN m⁻¹, i.e.  in the middle of the extrapolated range for sucrose. Fitting the Eberhart model with this value to the aqueous solution data for glucose leads to S₁₃=1.81, which means that glucose has a slight tendency to partition to the surface. For NaCl, σ₄=169.7 mN m⁻¹ and S₁₄=0.848 was used following Kleinheins et al. (2023). The separation factor S₁₄<1 describes a slight depletion of NaCl at the surface in binary aqueous solution.

Solute–solute separation factors (S₂₃, S₂₄, and S₃₄) only become important at a high solute concentration and are often poorly constrained by available ternary solution data (Kleinheins et al., 2024). In atmospheric aerosol particles, high solute concentrations and even supersaturated solutions can be reached at low relative humidity. However, at activation, the particles are dilute. Therefore, the choice of the solute–solute separation factors has only a minor influence on SS_crit. Here, we set S₂₃ and S₂₄ for all surfactants to a small value (10⁻¹⁵), assuming that the surfactant dominates the surface tension over the co-solute glucose or NaCl at low water content. The glucose–NaCl separation factor is set to S₃₄=1.

In a preliminary calculation, we tested the influence of salting out on the Köhler curve. For SDS–NaCl, $A_{\mathrm{24}}^{\mathrm{SO}}=\mathrm{22.63}$ and $B_{\mathrm{24}}^{\mathrm{SO}}=\mathrm{2.8}\times {\mathrm{10}}^{\mathrm{3}}$ were determined based on ternary solution data from Nakahara et al. (2011), which are rather high values compared to those found for other ternary solutions that have been examined by Kleinheins et al. (2024). Yet, the difference in SS_crit compared to a calculation assuming ideality ($A_{\mathrm{24}}^{\mathrm{SO}}=\mathrm{0}$ and $B_{\mathrm{24}}^{\mathrm{SO}}=\mathrm{0}$) was found to be very small (ΔSS_crit=0.015 %). Only when setting $B_{\mathrm{24}}^{\mathrm{SO}}$ to an artificially high value of 10⁵ could a considerable influence (ΔSS_crit>0.04 %) be found. This case is shown in Sect. S9. Since such a high salting-out factor does not appear realistic for any of the surfactants considered in this study; we conclude that the influence of salting out on SS_crit is negligible and proceed with the ideal Eberhart model (Eq. 4, A_ij=0, B_ij=0) in the following calculations.

In Table 2, additionally the parameters required by the monolayer model, namely the density ρ_i, the molar mass M_i, and the molar volume $v_i{N}_{\mathrm{A}}=M_i/{\mathit{\rho }}_i$ for the model compounds are given. Pure component densities for substances that are liquid at room temperature were taken from Yaws (1999) for propionic acid, valeric acid, and oleic acid and Lemmon et al. (2023) for water. For glutaric acid, pinonic acid, and glucose, the density of the liquid substance at 25 °C was estimated with the E-AIM model (Clegg and Wexler, 2024; Girolami, 1994). For NaCl, the density in a liquid state was estimated by an extrapolation from aqueous solution based on the data from Clegg and Wexler (2011). For SDS, the value of the pure solid specified by the manufacturer Merck KGaA has been used (Merck, 2023). Since the density of SDS in aqueous solution could deviate from the solid phase density, we tested the influence of a 10 % lower density on the results as shown in Sect. S10. It was found that the influence on SS_crit is small. In addition, Table 2 shows the van 't Hoff factors v_H,i that were used as default values for the calculation of the Raoult effect in classical Köhler theory.

4 Results

4.1 Köhler curve of a quaternary SSA particle

To determine the critical supersaturation of SSA particles, Köhler curves are constructed by solving bulk–surface partitioning and evaluating the Köhler equation (Eq. 1) for a range of wet diameters. In Fig. 4, Köhler curves based on three different model setups are shown for a D_dry=50 nm SSA particle. The main assumptions in the three model approaches are summarized in Table 3 and described in the following using Fig. 4 as an illustrative example of the main trends.

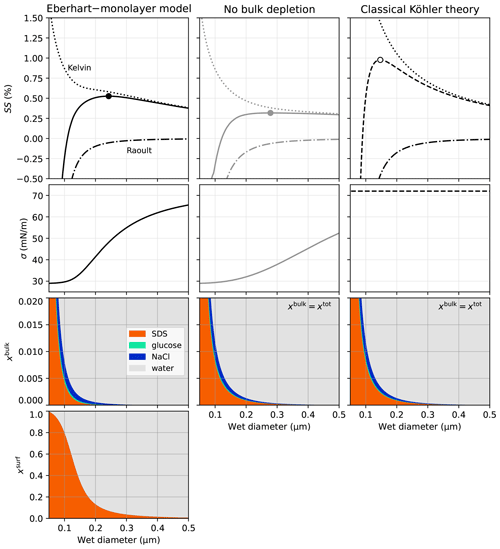
Figure 4 Köhler curves calculated with the Eberhart–monolayer model, assuming no bulk depletion, and with classical Köhler theory for an SSA model particle (SDS–glucose–NaCl) with D_dry=50 nm, w_org=0.93 (med), and $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.05}$. First row: Köhler curve (solid or dashed lines) with the Raoult (dash-dotted lines) and Kelvin effects (dotted lines) and critical supersaturation (circles). Second row: droplet surface tension. Third row: bulk composition (first column) and total composition (second and third columns). The y-axis range was limited to 0–0.02 for better visibility of the solute share. Fourth row: surface composition in the Eberhart–monolayer model. Since no partitioning is calculated in the second and third columns, the surface composition is not determined and hence not shown here.

In the first column, the multi-component Eberhart model (Sect. 2.1) is combined with the monolayer model (Sect. 2.2) to take bulk–surface partitioning and the surface tension of the partitioned droplet at the specific dilution into account. This model setup is labelled the “Eberhart–monolayer model” and represents our best estimate of the real SS of the SSA particles. The composition of the bulk and surface phases of the equilibrated, partitioned droplet are shown in the third and fourth row of Fig. 4, respectively. At small wet diameters the droplet has little total water content, leading to a highly concentrated bulk phase and a surface phase that is mostly composed of surface-active SDS. With further dilution at larger wet diameters, the solute concentration in the bulk phase decreases. This leads to a re-partitioning of SDS and a decrease in its surface coverage. As NaCl and glucose are not surface-active substances, they remain mainly in the bulk phase and cannot be seen in the surface composition. Only when the glucose fraction is high and no strong surfactant is present does some glucose partition to the surface, as shown in Fig. S13 in Sect. S11. The surface tension of the partitioned droplet (second row) is directly related to the bulk composition via the Eberhart model (Eqs. 4 and 9) and to the surface composition via Eq. (10). At low wet diameters where the surface is fully composed of SDS, the surface tension of the droplet is equal to that of pure SDS (σ=σ₂). As the droplet further dilutes with increasing wet diameter, the surface tension increases. Since SDS has a large separation factor, even for an increase in diameter by a factor of 10 (D_wet=0.5 µm), the surface tension of the droplet is still lower than that of pure water. If a compound with a smaller separation factor is used instead, e.g. propionic acid, the surface phase is less enriched in that compound for a given wet diameter, resulting in a higher surface tension such that at activation σ≈σ₁ (see Fig. S14 in Sect. S11). The surface tension directly affects the Kelvin curve (exponential function in Eq. 1), which is shown as a dotted line in the first row. The Raoult effect (a_w in Eq. 1, shown as a dash-dotted line in the first row) is calculated from $x_i^{\mathrm{bulk}}$ using AIOMFAC (Sect. 2.3). With the Kelvin and the Raoult effect, the Köhler curve can be calculated (Eq. 1, solid black line in the first row) and the critical supersaturation can be determined (SS_crit=0.53 %, black circle).

To illustrate the effect of bulk depletion, in the second column the Köhler curve is shown for the same model setup as in the first column but neglecting bulk depletion (labelled “no bulk depletion”). This means that bulk–surface partitioning is not calculated, but instead the total composition $x_i^{\mathrm{tot}}$ is used to calculate the surface tension with the Eberhart model and to calculate the water activity with AIOMFAC ($x_{\mathrm{2}}^{\mathrm{bulk}}=x_{\mathrm{2}}^{\mathrm{tot}}$). In the third row of Fig. 4, it can be seen that $x_{\mathrm{2}}^{\mathrm{bulk}}$ in the Eberhart–monolayer model is lower than in the case of no bulk depletion, which is due to the partitioning of the surfactant to the surface and its consequent depletion in the bulk phase. Due to the higher $x_{\mathrm{2}}^{\mathrm{bulk}}$ in the second column, the Eberhart model predicts a lower surface tension, as can be seen in the second row. Additionally, the higher $x_{\mathrm{2}}^{\mathrm{bulk}}$ leads to a slightly lower a_w. Together, the lowering of surface tension and a_w contribute to lower critical supersaturation (SS_crit=0.32 %) than that predicted with bulk depletion accounted for.

Table 3 Summary of the assumptions in the three model setups to calculate the bulk mole fraction $x_i^{\mathrm{bulk}}$, the surface tension σ, and the water activity a_w. For details about the calculation of $x_i^{\mathrm{bulk}}$, σ, and a_w, see Sect. 2.

In the third column of Fig. 4, for comparison, Köhler curves are constructed assuming classical Köhler theory. In this case, no bulk–surface partitioning is calculated such that $x_{\mathrm{2}}^{\mathrm{bulk}}$ is identical to that in the second column. In contrast to the case of no bulk depletion, the surface tension of the droplet is assumed to be that of pure water at all wet diameters (σ=σ₁) and solution ideality is assumed ($a_{\mathrm{w}}={\widehat{x}}_{\mathrm{w}}^{\mathrm{tot}}$). The consistently high surface tension increases the Kelvin effect, which leads to a higher SS_crit compared to the first two model setups (SS_crit=0.98 %). The difference in the Raoult effect, one using AIOMFAC (second column) and one assuming ideality (third column), is small. The reason is that in the case shown in Fig. 4, the droplet is rather dilute at activation such that the assumption of an ideal solution is valid. However, when the organic fraction is high, the droplet can still be concentrated at activation and present in a liquid–liquid phase separated state. In this case, the assumption of ideality leads to too low a Raoult effect compared to the case considering solution non-ideality and LLPS. Two such cases are shown in Sect. S4 (Fig. S5, SDS, high, 50 nm; Fig. S6, pinonic acid, high, 100 nm). Overall, it can be observed that surface tension lowering leads to a strong reduction in SS_crit in a 50 nm SSA particle.

4.2 Influence of the organic content

To analyse the sensitivity of SS_crit to the organic-to-inorganic ratio, in Fig. 5 SS_crit is shown for w_org ranging from 0–1 for 50 and 100 nm particles composed of SDS and NaCl. In classical Köhler theory (open circles), since the surface tension is not a function of composition (σ=σ₁), the Kelvin effect is independent of the composition, too. The strong increase in SS_crit with increasing w_org is therefore due to a change in the Raoult effect. Since SDS has a molar volume higher than NaCl (Table 2) and is assumed not to dissociate here (van 't Hoff factor of 1), an SDS particle of a given dry volume results in a smaller number of solute molecules than an NaCl particle of the same dry volume. This leads to a higher a_w and explains the strong increase in SS_crit with increasing w_org predicted using classical Köhler theory. Even with full dissociation of SDS (van 't Hoff factor of 2, cyan symbols and line), SS_crit increases with w_org due to the higher molar volume of SDS. Conversely, using the Eberhart model and neglecting bulk depletion (grey filled circles) strongly overestimates the surface tension lowering such that the critical supersaturation falls even below the one of pure NaCl for organic contents up to w_org≈0.8 for D_dry=50 nm.

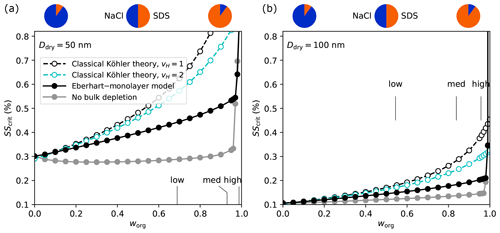
Figure 5 Influence of w_org on SS_crit for SDS–NaCl particles using three different model approaches. (a) D_dry=50 nm, (b) D_dry=100 nm. Pie charts above the plots show the composition of the dry particle (in mass fraction) at w_org=0.1, 0.5, and 0.9. The annotations of low, med, and high refer to the cases of the same name shown in Fig. 2. The curves in cyan are calculations with classical Köhler theory assuming full dissociation of SDS, i.e. $v_{\mathrm{H},\mathrm{SDS}}=\mathrm{2}$ for comparison to the black curves with $v_{\mathrm{H},\mathrm{SDS}}=\mathrm{1}$.

The Eberhart–monolayer model (black filled circles in Fig. 5) is in between these extreme cases. The increase in the Raoult effect with increasing w_org dominates over the decrease in the Kelvin effect such that pure NaCl activates at a supersaturation lower than any mixed SDS–NaCl particle. Yet, for w_org⪅0.3, a mixed SDS–NaCl particle still activates similarly to a pure NaCl particle. Between w_org=0.3 and 0.97, the higher the SDS content is, the larger the difference between SS_crit of pure NaCl and the mixed SDS–NaCl particles becomes. For w_org⪆0.97, a strong increase in SS_crit is observed. In this case, due to the hydrophobic nature of SDS and the small amount of NaCl, the hygroscopic growth of the particle is effectively insignificant, leading to the very high SS_crit values.

For 100 nm particles, the results are similar but SS_crit is generally shifted to lower values due to the lower Kelvin effect of larger particles. Because of the smaller relative importance of the Kelvin effect compared to the Raoult effect, surface tension lowering is also less important, leading to a smaller difference between SS_crit calculated with classical Köhler theory and with the Eberhart–monolayer model. Comparing SS_crit from classical Köhler theory with the one from the Eberhart–monolayer model, it can be seen that there is yet a significant influence of surface tension lowering for w_org>0.65 with differences in SS_crit⪆0.05 %.

4.3 Influence of the glucose content

The fraction of WSOCs in the total organic mass was found to be small (≈5 %) for small particles according to Facchini et al. (2008). However, atmospheric SSA may exhibit natural variability in its composition. Therefore, we investigate the sensitivity of SS_crit to $w_{\mathrm{glu}}/w_{\mathrm{org}}$ using the three models described in the previous section. In Fig. 6 the result is shown for a D_dry=50 nm SSA particle (left panel) and a D_dry=100 nm SSA particle (right panel), both with medium organic content.

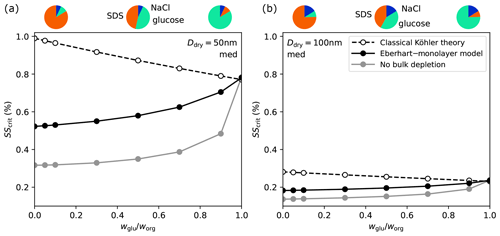
Figure 6 Influence of $w_{\mathrm{glu}}/w_{\mathrm{org}}$ on SS_crit for SSA model particles (SDS–glucose–NaCl) with three different model approaches. (a) D_dry=50 nm, w_org=0.93 (med); (b) D_dry=100 nm, w_org=0.838 (med). Pie charts above the plots show the composition of the dry particle (in mass fraction) at $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.1}$, 0.5, and 0.9.

In classical Köhler theory, the decrease in SS_crit with increasing $w_{\mathrm{glu}}/w_{\mathrm{org}}$ is due to a decrease in the Raoult effect due to the lower molar volume of glucose than SDS (see Table 2). When taking surface tension lowering into account, the presence of SDS leads to lowered surface tension which lowers the Kelvin effect. From the calculations of no bulk depletion, it can be seen that the lowered Kelvin effect outweighs the increase in the Raoult effect such that SS_crit increases here with increasing $w_{\mathrm{glu}}/w_{\mathrm{org}}$.

Considering bulk–surface partitioning in the Eberhart–monolayer model lowers the bulk concentration of SDS and increases the surface tension compared to the case of no bulk depletion (compare Fig. 4). As a consequence, the Raoult part of the Köhler equation increases due to a higher a_w and the Kelvin part increases due to the higher surface tension. Therefore, SS_crit calculated with the Eberhart–monolayer model is higher than suggested by the case of no bulk depletion at all $w_{\mathrm{glu}}/w_{\mathrm{org}}<\mathrm{1}$. Yet, similar to the case of no bulk depletion, the lowered Kelvin effect outweighs the increase in the Raoult effect, leading to an SS_crit that increases with increasing $w_{\mathrm{glu}}/w_{\mathrm{org}}$.

These trends are similar for the calculations with D_dry=100 nm, but all curves are shifted to lower supersaturations because of the strong dependence of the Kelvin effect on the diameter. Overall, in both panels the Eberhart–monolayer model predicts the lowest SS_crit to be reached at $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0}$. At $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{1}$ all models yield very similar SS_crit values because, in a glucose–NaCl–water droplet, bulk–surface partitioning is very weak at activation such that σ≈σ₁ in agreement with classical Köhler theory (see Fig. S15 in Sect. S11).

4.4 Influence of surfactant properties

To illustrate the influence of the surfactant properties, i.e. S₁₂ and σ₂, on the results, the calculations shown in the left panel of Fig. 6 were repeated with six different surfactant model compounds. The results are shown in Fig. 7 with a different surfactant model compound in each panel, sorted by S₁₂ and σ_i as in Fig. 3.

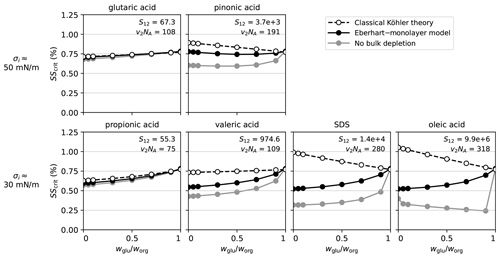
Figure 7 Influence of the surfactant type on SSA model particles (surfactant–glucose–NaCl): critical supersaturation as a function of the glucose content using six different surfactant model compounds and three different model approaches. In all panels, D_dry=50 nm and w_org=0.93 (med). The binary separation factor in water S₁₂ and the molar volume v₂N_A in cm³ mol⁻¹ for each surfactant are given in the respective panel. In the calculations with glutaric acid all curves overlap.

We start with analysing the lower row, which shows results of the substances with σ_i≈30 mN m⁻¹. The panel of SDS shows the same results as the left panel in Fig. 6 and has been discussed above. If SDS is replaced by a surfactant with a higher separation factor, i.e. oleic acid, the observed trends are similar and even more pronounced. Propionic acid and valeric acid are substances with a σ₂ similar to SDS and oleic acid but with a lower S₁₂. For these substances, the differences in SS_crit between the different model approaches decrease with a decreasing separation factor and decreasing molar volume. The primary reasons for this are the decrease in SS_crit calculated with classical Köhler theory and the increase in SS_crit for the model approach of no bulk depletion. In contrast, SS_crit from the Eberhart–monolayer calculations shows little change. In fact, SS_crit calculated with the Eberhart–monolayer model (black circles) is very similar between propionic acid, valeric acid, SDS, and oleic acid. Because propionic acid and valeric acid have a weaker tendency to partition to the surface, the surface tension at activation is closer to that of pure water, which increases the Kelvin effect. Conversely, the Raoult effect for propionic and valeric acids is stronger than for SDS and oleic acid and can compensate the increased Kelvin effect (detailed plots are shown in Fig. S16 in Sect. S12). Because the molar volumes of valeric acid and glucose are almost the same, SS_crit predicted by classical Köhler theory is almost independent of $w_{\mathrm{glu}}/w_{\mathrm{org}}$ for this model compound. The results obtained with classical Köhler theory depend strongly on the surfactant type because the stronger Raoult effect is not compensated by an increased Kelvin effect since σ=σ₁ for all compositions. For propionic acid, classical Köhler theory predictions of SS_crit are almost the same as the ones of the Eberhart–monolayer model, so we conclude that it should not be considered a surface-active compound with respect to CCN activation because of its low separation factor. In contrast, the SS_crit of valeric acid is decreased by surface tension lowering but less than for SDS, and thus it can be considered a moderately surface-active compound.

Now, we consider glutaric acid and pinonic acid, two substances with σ₂≈50 mN m⁻¹. For glutaric acid, classical Köhler theory is sufficient to describe SS_crit at all compositions. Due to its low S₁₂ and moderate σ₂, it should not be considered a surface-active compound for CCN activation. Pinonic acid, on the other hand, has a S₁₂ value that is much higher than the one of glutaric acid, lying between the one of valeric acid and SDS. As a result, for pinonic acid, a slightly lower SS_crit is predicted with the Eberhart–monolayer model compared to with classical Köhler theory, and, therefore, it can be considered a moderately surface-active compound, similar to valeric acid. The reduction in SS_crit, however, is less pronounced than for valeric acid, which can be attributed to its higher σ₂ value.

The combined influence of surfactant properties and the organic fraction (low, med, or high) is shown in Fig. S17 in Sect. S12. When the organic fraction is lowered, the particle contains more NaCl. Due to its low molar mass and its dissociation into two ions, NaCl strongly enhances the Raoult effect, and, as a result, all curves are shifted to lower SS_crit values. Vice versa, when the organic fraction is high, SS_crit is generally shifted to higher values. LLPS is observed at a high organic fraction and low glucose content ($w_{\mathrm{glu}}/w_{\mathrm{org}}\le \mathrm{0.05}$), for pinonic acid, SDS, and oleic acid. This causes SS_crit to be even higher than at $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.1}$ for the calculations with the Eberhart–monolayer model and in the case of no bulk depletion (details on the LLPS see Sect. S4). This effect is not present with classical Köhler theory since in that case solution ideality is assumed. For the cases, where the droplet exhibits LLPS at activation, the calculation of no bulk depletion yields the same result as the Eberhart–monolayer model because of the low dilution. In all other cases, bulk depletion can not be neglected, but the monolayer model must be used for an accurate calculation of SS_crit (except when w_sf=0).

Figure S17 in Sect. S12 also shows results for D_dry=100 nm. As observed in Fig. 6, SS_crit is shifted to lower values due to the smaller Kelvin effect for larger diameters, and the differences between the three approaches become smaller. Moreover, as a consequence of the stronger hygroscopic growth of the larger particles, no LLPS is observed.

From the results in Figs. 7 and S17 two main conclusions can be drawn. First, bulk depletion should generally be considered if surface-active compounds are present. Second, surface-active solutes in an aerosol particle can be characterized by three key properties determining their influence on the critical supersaturation: the binary separation factor in water S_1i, the pure component surface tension σ_i, and the molar volume v_iN_A. Based on the SS_crit results for 50 nm surfactant–NaCl particles at medium organic content in Fig. 7 (w_org=0.93, w_glu=0), we suggest categorizing organic compounds into weak, intermediate, and strong surfactants with respect to CCN activation as follows. Substances with S_1i<100 have negligible influence on SS_crit at any concentration and therefore should not be considered surface active for CCN activation (weak surfactants). For these, classical Köhler theory can be applied. Substances with S_1i between about 100 and 10⁴ influence SS_crit by surface tension lowering to a moderate degree (ΔSS_crit≈0.25 %) compared to classical Köhler theory (intermediate surfactants). Substances with S_1i>10⁴ and low σ_i can be considered strongly surface-active compounds that lower SS_crit substantially compared to classical Köhler theory (ΔSS_crit≈0.5 %). This categorization is also shown by the grey lines in Fig. 3.

4.5 CCN activity of sea spray aerosol

In order to analyse the potential of SSA to serve as CCN, we focus on our best-estimate representation of SSA using SDS as the surfactant and $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.05}$ in the following calculations. In Fig. 8, the critical supersaturation of SSA with medium organic content is given as a function of the dry diameter calculated either with the Eberhart–monolayer model or with classical Köhler theory. On a second y axis, the size-dependent organic mass fraction of the particle is shown in orange. It can be clearly seen that when considering bulk–surface partitioning and surface tension lowering using the Eberhart–monolayer model, an SSA particle of a given dry diameter activates at lower SS than predicted by classical Köhler theory. The difference in SS_crit between the two model approaches is larger, the smaller the dry diameter. There are two reasons for that. On the one hand, smaller particles have a higher organic content and therefore a higher surfactant content, and, on the other hand, smaller particles have a stronger Kelvin effect such that a change in the Kelvin effect has a larger effect on SS_crit.

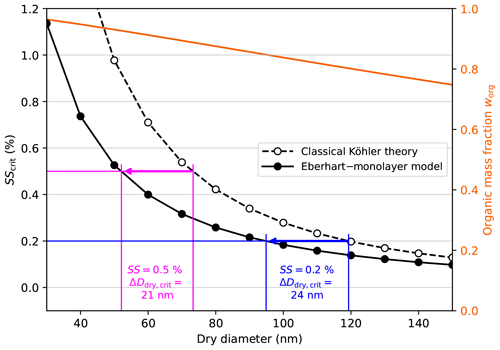
Figure 8 The critical supersaturation SS_crit of SSA model particles (surfactant–glucose–NaCl) with medium organic content calculated with two different model approaches. SSA particles are represented as a quaternary mixture of water, SDS, glucose, and NaCl. The organic mass fraction (med case) is given on the right y axis with an solid orange line. The fraction of glucose in the organic mass is $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.05}$. The difference in the critical dry diameter ΔD_dry,crit between the models for a supersaturation SS of 0.5 % and 0.2 % is annotated in magenta and blue, respectively.

The critical dry diameter D_dry,crit denotes the dry diameter of the smallest particles in a polydisperse aerosol of a uniform composition that can activate at a given supersaturation. Assuming equilibrium in an air parcel at all times, D_dry,crit is given by SS=SS_crit. In Fig. 8 it can be seen that for a supersaturation of SS=0.5 %, surface tension lowering yields a D_dry,crit that is 21 nm lower than that predicted by classical Köhler theory. Analogously, surface tension lowering leads to a change in D_dry,crit of 24 nm at a supersaturation of SS=0.2 %. For SSA with low organic content, the change in D_dry,crit is smaller ($\mathrm{\Delta }{D}_{\mathrm{dry},\mathrm{crit}}(\mathrm{SS}=\mathrm{0.5}$ %)=10 nm and $\mathrm{\Delta }{D}_{\mathrm{dry},\mathrm{crit}}(\mathrm{SS}=\mathrm{0.2}$ %)=11 nm), and, vice versa, for SSA with high organic content the change in D_dry,crit is higher ($\mathrm{\Delta }{D}_{\mathrm{dry},\mathrm{crit}}(\mathrm{SS}=\mathrm{0.5}$ %)=29 nm and $\mathrm{\Delta }{D}_{\mathrm{dry},\mathrm{crit}}(\mathrm{SS}=\mathrm{0.2}$ %)=41 nm). These cases are shown in Sect. S13.

In marine environments, supersaturations of SS=0.5 % can be reached (Gong et al., 2023; Svensmark et al., 2024). Based on the results in Fig. 8, this means that due to surface tension lowering, a large part of the Aitken mode particles can be activated ($D_{\mathrm{dry},\mathrm{crit}}(\mathrm{SS}=\mathrm{0.5}$ %) ≈50 nm) despite having high organic content.

The CCN activity of SSA particles and the importance of surface tension lowering can further be illustrated by comparing SS_crit of SSA particles to that of pure components. In panel (a) of Fig. 9, the SS_crit of SSA calculated with classical Köhler theory and with the Eberhart–monolayer model is shown together with the SS_crit of pure glutaric acid, ammonium sulfate ((NH₄)₂SO₄), and NaCl. In panel (b), the difference between SS_crit of the various cases and the one predicted with the Eberhart–monolayer model is shown. Compared to Fig. 8, the range of dry diameters is extended here up to 1 µm in both panels. For the pure components, AIOMFAC was used for the calculation of the water activity and a constant surface tension of σ₁ was used. The prediction of SS_crit of SSA particles with classical Köhler theory (dashed black line) changes from being higher than the one for glutaric acid (at D_dry<100 nm) to lower than that of ammonium sulfate (at D_dry>300 nm), which is related to the change in the organic content of SSA with size. If surface tension lowering is taken into account with the Eberhart–monolayer model, a CCN activity of SSA similar to the one of pure (NH₄)₂SO₄ is found at D_dry⪅300 nm. For D_dry>300 nm, the CCN activity approaches that of NaCl and classical Köhler theory is valid. For SSA particles with D_dry⪅60 nm and high organic content, LLPS causes SS_crit to be closer to that of glutaric acid than that of (NH₄)₂SO₄.

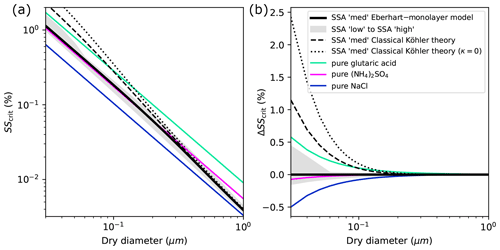
Figure 9 Comparison of the CCN activation potential of SSA model particles (surfactant–glucose–NaCl) with pure compounds. (a) Critical supersaturation as a function of dry diameter. (b) Difference to calculation with the Eberhart–monolayer model. The curves labelled “SSA `med' Classical Köhler theory” and “SSA `med' Eberhart–Monolayer model” are identical to those shown in Fig. 8 up to 150 nm. The grey-shaded area shows the range between the SS_crit of SSA with low and high organic content, as predicted with the Eberhart–monolayer model.

In climate models, parameterizations for CCN activation are usually used, which are based on κ-Köhler theory (Petters and Kreidenweis, 2007). In this theory, the water uptake and SS_crit of aerosol particles are calculated using classical Köhler theory and a hygroscopicity parameter κ which considers the molar volumes and the degree of dissociation of the solutes. For particles composed of various solutes, the overall κ value of the particle is calculated from the individual κ values of the solutes using the Zdanovskii–Stokes–Robinson (ZSR) rule (Petters and Kreidenweis, 2007). Organic substances are typically given low κ values (e.g. κ<0.06, Zhang et al., 2012) or assumed to be entirely hydrophobic (κ=0). The dashed black lines in Fig. 9 correspond to κ≈0.06 in κ-Köhler theory based on the molar volume of SDS. In addition, the dotted black lines show the calculation where the surfactant is assumed to be entirely hydrophobic (see also the underlying Köhler curves given by the dashed yellow lines in Figs. S5 and S6 in Sect. S4), which corresponds to choosing κ=0. In Fig. 9b it can be seen that both cases using classical Köhler theory lead to a strong underestimation of the activation potential of SSA particles and are less suited to represent their SS_crit than assuming pure NaCl.

5 Discussion

5.1 Uncertainties in the SSA representation

The results of this study showed that classical Köhler theory strongly underestimates the ability of surfactant-rich particles to form cloud droplets and that instead a more complex approach including concentration-dependent surface tension and bulk-depletion is required. It was furthermore shown that SSA particles in the Aitken mode with diameters down to ≈50 nm can serve as CCN particles in typical marine updraughts. These results are based on the assumptions of SSA composition, the choice of model compounds, and the modelling approach, which all influence the resulting SS_crit for CCN activation. The SSA particles have been represented with four model compounds (surfactant, glucose, NaCl, and water) and with a size-dependent composition based on SSA measurements. Despite the simplicity of this model system, we consider our results robust, even if the composition of atmospheric SSA has not been accurately represented. The reasons for that are discussed in the following.

The biggest uncertainty in the presented model approach might be the organic-to-inorganic ratio of SSA particles; in particular, the organic-to-inorganic ratio of particles with D_dry<100 nm is uncertain due to a lack of experimental data. To analyse the sensitivity to this parameter, we have shown results with low and high organic content in addition to the medium organic content. The resulting variation in SS_crit is shown in Fig. 9 with the grey-shaded area. It can be seen that even for a lower or higher inorganic content, SS_crit is still close to our best estimate (black line). A sensitivity analysis over the whole range of organic-to-inorganic ratios (Fig. 5) showed that only if the organic content of small particles is below approximately ≈40 % does the influence of surface tension lowering on SS_crit become insignificant and classical Köhler theory suffices. In this case, however, the particles would activate similar to pure NaCl, thus being good CCN anyhow. We therefore consider it robust enough to conclude that SSA particles in the Aitken mode can serve as CCN particles in marine updraughts, regardless of whether this is due to surface tension lowering at high organic content or due to strong hygroscopic growth at high inorganic content.

The WSOC content could depend on seasonal and spatial variability and ageing via the uptake of organic molecules from the gas phase or chemical breakdown of large surface-active organic molecules. Yet, in Figs. 6 and 7 it has been shown that the glucose content between 0 and 0.5 has only a small influence on SS_crit calculated with the Eberhart–monolayer model.

The surfactants in atmospheric SSA are composed of a complex mixture of different compounds, which we represented with pure SDS. The molecular identification of surfactants in SSA is still at an early stage and should clearly be investigated further. Nevertheless, there is increasing evidence that atmospheric surfactants are predominantly composed of fatty acids. Exchanging SDS with a fatty acid of a small, medium, or large chain length had little influence on SS_crit calculated with the Eberhart–monolayer model (compare results for propionic acid, valeric acid, SDS, and oleic acid in Fig. 7), possibly because these substances all have a similar σ_i of ≈30 mN m⁻¹. When a substance with a higher σ_i was chosen instead, the surface tension lowering was less pronounced and SS_crit was found to be higher compared to the cases with fatty acids (see glutaric acid and pinonic acid in Fig. 7). Therefore, if surfactants in atmospheric SSA were found to have σ_i>>30 mN m⁻¹, the conclusions of this study would need to be reconsidered. Since all fatty acids shown in Fig. 3 have σ_i≈30 mN m⁻¹, we consider our results based on SDS as a representative surfactant species to be robust.

Finally, all model calculations have been performed at 25 °C, a temperature that is hardly reached at typical liquid cloud base heights, which range from 200 m to 2 km above ground (Lu et al., 2021). Accordingly, CCN activation rather occurs at temperatures around or below 0 °C. To estimate the uncertainty introduced by assuming 25 °C throughout this study, we performed calculations similar to that shown in Fig. 8 at two different temperatures (−25 and +25 °C) but using oleic acid instead of SDS. Note that for SDS no temperature-dependent surface tension data could be found, which is why oleic acid was used for this sensitivity analysis. The direct effect of temperature on the Kelvin effect was considered as well as the indirect effect via the temperature dependence of the surface tension. Both effects lead to an increased Kelvin effect at lower temperatures, which results in a change in SS_crit to higher absolute values (see Appendix A). Furthermore, at a lower temperature, the relative difference between SS_crit calculated with classical Köhler theory and the Eberhart–monolayer model is slightly increased, suggesting that surface tension lowering could be even more relevant at lower temperatures.

5.2 Uncertainties in the modelling approach

Our results are based on a model approach that combines three pre-existing models: the Eberhart model for surface tension, the monolayer model for bulk–surface partitioning, and AIOMFAC for solution non-ideality. All three models have been validated separately by comparison to experimental data: the Eberhart model has been thoroughly validated for binary aqueous solutions and multi-component solutions (Kleinheins et al., 2023, 2024). The monolayer model in combination with Szyszkowski–Langmuir surface tension isotherms has been validated by direct comparison to the surface tension of small droplets (Bzdek et al., 2020; Bain et al., 2023). AIOMFAC has been validated against water activity measurements (Zuend et al., 2008, 2011). AIOMFAC has not been specifically trained for amphiphilic organic molecules like SDS and oleic acid; however, as discussed in Sect. 2.3, the exact representation of the organic molecule in AIOMFAC has a negligible influence on the prediction by the Eberhart–monolayer model, except for the prediction of LLPS at high organic content and small dry diameters.

In the literature, other partitioning models have been suggested besides the monolayer model, e.g. the Gibbs model (Sorjamaa et al., 2004; Prisle et al., 2010). Lin et al. (2018) compared these two models for various systems and found that the monolayer model generally predicts slightly lower SS_crit than the Gibbs model. Since only few experimental data from SS_crit measurements were available, no conclusion was drawn as to which model is more accurate. In this study the monolayer model was chosen, since it has been compared to experimental surface tension data of small droplets (Bzdek et al., 2020; Bain et al., 2023) with good agreement; however, whether the Gibbs model would yield higher accuracy by validation with the same data remains to be tested in future studies. Moreover, more measurements of the surface tension of small droplets, also using different experimental techniques, would help to elucidate which partitioning model is the most accurate. To conclude, a weaker or an even stronger bulk depletion effect cannot be excluded, which would shift the predicted critical supersaturation to either lower or higher values, respectively.

As an additional validation step, future work should be directed at comparing SS_crit predicted with the combined model to measurements of SS_crit of lab-generated surfactant-containing aerosol particles. A comparison to data from the literature was not included in this study for two reasons. First, such literature data are very limited, as can be seen from the study by Lin et al. (2018), where the experimental data were not sufficient to draw a conclusion about which of their two models was more accurate. Second, in previous studies, the exact composition of the aerosol particles was not confirmed by a measurement but taken as the composition of the solution filled into the atomizer. We suggest that a verification of the particle composition after atomization by e.g. an aerosol mass spectrometer is urgently needed for a reliable comparison to modelled SS_crit values. To our knowledge, no study has yet investigated potential composition changes when surfactant-containing particles are produced with atomizers.

5.3 Comparison to field and laboratory measurements of SSA

Our results suggest that despite high organic content, SSA particles can activate similarly to ammonium sulfate. Comparing this to CCN measurements of field and laboratory studies in the literature, our results lie within the range of what has been measured. Quinn et al. (2014) collected fresh SSA particles in the North Atlantic with an in situ particle generator (Sea Sweep). From CCN counter measurements, rather low CCN activity with κ values between 0.4 and 0.8 has been measured for SSA particles with D_dry=40–100 nm, which is thought to be due to high organic content. However, the organic content was not measured in that study and a later study of the same two first authors claims that the particles had not been dried enough in these measurements, which would lead to an overestimation of the size and a low bias for κ (Bates et al., 2020). Rasmussen et al. (2017) and Christiansen et al. (2020) measured the CCN activity of lab-generated SSA particles using seawater samples with and without algae cultures or sea surface microlayer samples. According to their measurements, the CCN activity of real seawater SSA resembled that of SSA generated from Sigma sea salt water in all cases very closely. Since the organic content of the SSA after aerosolization was not been quantified, it is not possible to directly compare their results to ours. Lastly, Bates et al. (2020) measured the CCN activity of SSA particles generated by Sea Sweep and in a tank and also quantified the organic content of the sub-180 nm fraction with FTIR measurements. Despite a high average organic content of 86 %, the particles showed a strong CCN activity in the range between that of pure ammonium sulfate and that of pure NaCl (Fig. 5 in Bates et al., 2020), which is close to the results in our study. For a better comparison of model results with measurements, it is crucial that future studies are undertaken to quantify the organic content of the aerosolized, dried aerosol that enters the CCN counter.

5.4 Representation of CCN activation in global models

In climate models, parameterizations based on classical Köhler theory are usually used to determine the CCN activation of aerosol particles. For example, in the global circulation model ECHAM-HAM (Stier et al., 2005; Neubauer et al., 2019), cloud droplet activation is calculated using κ-Köhler theory (Petters and Kreidenweis, 2007), which is based on classical Köhler theory. As such, the surface tension of water is generally assumed. The degree of under- or overestimation of CCN activation in climate models depends further on their representation of the composition. If the marine aerosol is assumed to be composed entirely of NaCl, the CCN activity for particles <100 nm would be overestimated, i.e. too low an SS_crit would be assumed (see blue line in Fig. 9b). If, on the other hand, an organic share is considered for example in the parameterization by Long et al. (2011), the magnitude of the error depends on the hygroscopicity of the organic mass that is assumed. If the organic mass is given a certain hygroscopicity, e.g. κ≈0.06 based on the molar volume of SDS, the predicted CCN activity would correspond to that predicted by our calculations with classical Köhler theory assuming solution ideality. As such, SS_crit would be strongly overestimated for all values of D_dry⪅300 nm as shown by the dashed black line in Fig. 9b. If the other extreme is considered, that is, the organic share is assumed to be entirely hydrophobic (κ=0), the predicted SS_crit is even higher (see dotted black line in Fig. 9b). Using the Eberhart–monolayer model as the ground truth, Fig. 9b suggests that, for the prediction of CCN activation, assuming the marine primary aerosol is composed entirely of pure NaCl is more accurate than considering an organic share with a low κ value.

In Sect. 4.5 it has been shown that Aitken mode particles can serve as CCN in marine updraughts. In ECHAM-HAM, however, sea salt aerosol is only included in the accumulation mode (D_dry=100 nm–1 µm, Stier et al., 2005). Given the high CCN activation potential of both surfactant-rich and NaCl-rich SSA particles found in this study, ECHAM-HAM seems to underestimate the CCN concentration in marine environments. This finding is in agreement with a study by Lohmann and Leck (2005), where in a parcel model simulation, a surface-active Aitken mode had to be included in order to bring the results into agreement with measured CCN concentrations from field campaigns in the Arctic.

6 Summary and conclusions

In this study we have presented an approach for modelling the critical supersaturation of surfactant-containing aerosol particles. The model is based on combining the multi-component Eberhart model (Kleinheins et al., 2024) for the surface tension of aqueous mixtures with the monolayer model (Malila and Prisle, 2018) for bulk–surface partitioning (Eberhart–monolayer model). To consider non-ideality and liquid–liquid phase separation, the group contribution model AIOMFAC was used. This novel model approach allows for calculating the CCN activity of surfactant-containing aerosol particles with more than one co-solute for the first time. For comparison, the CCN activity was calculated additionally using classical Köhler theory, which assumes a homogeneous droplet, solution ideality, and a surface tension of pure water.

The new model was applied on freshly emitted sea spray aerosol particles, which were represented by a quaternary system of water, a surfactant, glucose, and NaCl. Six different model compounds were chosen to represent the surfactant, covering a broad range of surface-active behaviour. The surface activity of the surfactant model compounds was characterized by the separation factor in water S_1i and the pure component surface tension σ_i. Based on this sensitivity analysis, it can be concluded that substances with a separation factor S_1i<100 should not be considered surfactants for CCN activation. For these substances, classical Köhler theory can be used. In contrast, substances with a separation factor between 10² and 10⁴ can be considered intermediate surfactants, leading to moderate reductions in SS_crit depending on their σ_i value, while substances with S_1i>10⁴ and a low σ_i value (e.g. σ_i=30 mN m⁻¹) should be considered substances with a strong surface activity. For the latter, strong reductions in SS_crit compared to classical Köhler theory were observed as a result of a strongly reduced Kelvin effect.

Additionally, the critical supersaturation as a function of the dry particle size was presented using either classical Köhler theory or the Eberhart–monolayer model. The results showed that the CCN activity of sea spray aerosol particles with a dry diameter below 300 nm is clearly underestimated when surface tension lowering is not considered. For example, in an updraught with a maximum supersaturation of 0.5 %, surface tension lowering allows for SSA particles down to D_dry≈50 nm to activate, while classical Köhler theory predicts CCN activation only for particles with D_dry⪆70 nm. From a comparison of sea spray aerosol with pure compounds this study suggests that the CCN activity is similar to that of ammonium sulfate for dry diameters below ≈300 nm. For larger sizes, their CCN activity approaches that of pure NaCl, due to their increasing NaCl content with size. The SS_crit of SSA is predicted to be closer to that of pure NaCl than to that predicted with κ-Köhler theory using κ≤0.06. Thus, accounting for an organic fraction in marine primary aerosol may worsen CCN number predictions in climate models compared to neglecting the organic fraction altogether. The low critical activation diameter for SSA particles furthermore emphasizes the need to consider the Aitken mode of SSA particles for cloud formation in climate models.

From this study it can further be concluded that bulk depletion must be considered when particles contain surfactants and that surface tension non-ideality (i.e. salting out) is only important at high salt concentrations and not relevant to CCN activation due to the high dilution of the particles at activation. It was further observed that small particles with high organic content can undergo LLPS due to solution non-ideality, which increases their critical supersaturation above the one obtained when assuming solution ideality. Lastly, a lower temperature was shown to increase the absolute value of SS_crit and slightly increase the relative difference between SS_crit calculated with classical Köhler theory and the one calculated with the Eberhart–monolayer model, highlighting the importance of surface tension lowering also at lower temperatures.

Overall, this study mapped out the impact of surface tension lowering on the CCN activity of primary sea spray aerosol. Future work could be directed at analysing the surface tension and CCN activity of secondary marine aerosol or continental aerosol, e.g. biomass burning aerosol.

Appendix A: Influence of temperature

Since surface tension is known to be a function of temperature, we test the influence of temperature on our results here. Critical supersaturation is a direct function of the temperature T via the Kelvin effect (exponential function in Eq. 1). Besides the direct influence, SS_crit is indirectly affected by T via a temperature dependence of activity coefficients, densities, and surface tension. We consider the direct influence of temperature in the Kelvin effect as well as the temperature dependence of the surface tension in the following and neglect the temperature dependence of activity coefficients and densities.

We introduce temperature-dependent surface tensions by replacing σ_i in the multi-component Eberhart model (Eq. 4) with σ_i(T) and assume the fit parameters S_ij to be temperature independent. Assuming temperature-independent fit parameters proved to be successful for the Connors–Wright and the Shereshefsky model (Shereshefsky, 1967) by Shardt and Elliott (2017). For the binary system 1–2, the Shereshefsky model is given by

$$\begin{array}{}\text{(A1)}& \mathit{\sigma }={\mathit{\sigma }}_{\mathrm{1}}-{\displaystyle \frac{\left({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{2}}\right)x_{\mathrm{2}}\exp \left(\mathrm{\Delta }{F}_{\mathrm{s}}/\left(RT\right)\right)}{\mathrm{1}+x_{\mathrm{2}}\left(\exp \left(\mathrm{\Delta }{F}_{\mathrm{s}}/\left(RT\right)\right)-\mathrm{1}\right)}},\end{array}$$

where ΔF₁₂ is a fit parameter. Tahery et al. (2005) showed that, while the fit parameter ΔF₁₂ depends on temperature, $\mathrm{\Delta }{F}_{\mathrm{12}}/\left(RT\right)$ is approximately temperature independent for many binary aqueous systems with organic solutes. Since the Eberhart model is mathematically equivalent to the Shereshefsky model with $S_{\mathrm{12}}=\exp \left(\mathrm{\Delta }{F}_{\mathrm{12}}/\left(RT\right)\right)$ (Kleinheins et al., 2023), it can be assumed that S₁₂ is also constant with temperature for these systems. Based on these previous studies on temperature dependence of surface tension, we consider S_ij temperature independent.

The temperature dependence of the pure components was modelled with a linear relationship (Shardt and Elliott, 2017) as

$$\begin{array}{}\text{(A2)}& {\mathit{\sigma }}_i\left(T\right)={\mathit{\theta }}_{\mathrm{0},i}+{\mathit{\theta }}_{\mathrm{1},i}T,\end{array}$$

where θ_0,i and θ_1,i are fit parameters specific for compound i. No temperature-dependent surface tension data could be found for SDS. However, we could find temperature-dependent experimental data for oleic acid; hence we continue this analysis using oleic acid as the surfactant. The parameters θ_0,i and θ_1,i were determined by fitting Eq. (A2) to experimental data reported by Wohlfarth and Wohlfarth (1997), which are shown in the left panel in Fig. A1.

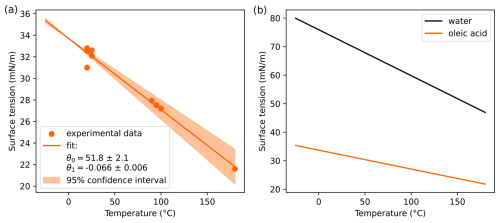
Figure A1 (a) Surface tension of pure oleic acid as a function of temperature. Markers show experimental data reported by Wohlfarth and Wohlfarth (1997). The solid line is a fit of Eq. (A2) to the experimental data resulting in the parameters reported in the legend (± 95 % confidence interval). The shaded area gives the 95 % confidence interval of the fit. (b) Comparison of the surface tension of pure oleic acid and pure water as a function of temperature using the parameters reported in Table A1.

For water, θ_0,i and θ_1,i were taken from Shardt and Elliott (2017). For glucose, no pure component surface tension data at any temperature could be found; therefore, its temperature dependence is neglected here. For NaCl, the temperature function by Janz (1980) was used. The parameters θ_0,i and θ_1,i of these four model compounds are reported in Table A1.

Shardt and Elliott (2017)Janz (1980)

Table A1 Temperature dependence parameters (θ_0,i, θ_1,i) with references and pure component surface tensions at −25 and 25 °C (calculated with θ_0,i, θ_1,i, and Eq. A2) for the model compounds.

The influence of temperature on SS_crit was analysed by running a calculation similar to the one behind Fig. 8 yet with oleic acid instead of SDS and for two temperatures, i.e. −25 and 25 °C. The comparison of SS_crit for these temperatures is given in Fig. A2, and the parameters for the four model compounds at −25 and 25 °C are reported in Table A1. Both the higher surface tension at lower temperature and the lower temperature itself contribute to a higher Kelvin effect. As a result, SS_crit is higher at a lower temperature for the same dry diameter. Moreover, the relative difference between SS_crit calculated with classical Köhler theory and with the Eberhart–monolayer model is slightly increased; i.e. ΔD_dry,crit values for SS =0.5 % and SS =0.2 % are larger at −25 °C because the temperature dependence of the surface tension of water is stronger than the one of oleic acid (see right panel of Fig. A1).

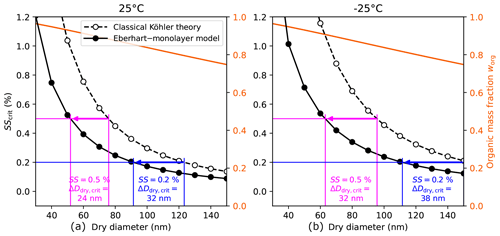
Figure A2 The critical supersaturation SS_crit of SSA particles with medium organic content calculated with two different model approaches and at two different temperatures. (a) Room temperature (25 °C), (b) −25 °C. SSA particles are represented as a quaternary mixture of water, oleic acid, glucose, and NaCl. The fraction of glucose in the organic mass is $w_{\mathrm{glu}}/w_{\mathrm{org}}=\mathrm{0.05}$. The difference in the critical dry diameter ΔD_dry,crit between the models for a supersaturation SS of 0.5 % and 0.2 % is annotated in magenta and blue, respectively.