On the impact of thunder on cloud ice crystals and droplets

Calculations are presented on the impact of thunder on cloud particles. The results show that the creation of a shock wave front near a lightning channel results in shattering of ice crystals, droplets, and dust aerosols, this being a yet unidentified mechanism for secondary ice production in clouds. At low altitudes shattering is more efficient. At the distance where the shock wave front decays to audio wave, another mechanism can cause agglomeration of particles. The cloud particles' characteristics appear to be not very suitable for extensive acoustic agglomeration if the sound pressure level (SPL) is below 120 dB. Nevertheless, even for SPL<120 dB, some agglomeration will occur. Agglomeration will occur readily if SPL > 135 dB at sound frequencies of 10 to 200 Hz. Agglomeration efficiency increases with height. More agglomeration will occur in pyroclouds, due to their large particle number densities. These results show that the electrical environment in clouds has, through thunder, effects on the size distribution and number density of ice particles and droplets, will hence influence thundercloud radiative properties, and may be a significant driver of secondary ice production. As global warming may influence the occurrence rate of lightning, a climate feedback may be induced by the mechanisms discussed here.

1 Introduction

Cloud droplet size distribution affects precipitation and the radiative effects of clouds. The effect of particulate matter on cloud droplet size distribution and precipitation rate has been investigated extensively in the last two decades (e.g., Stier et al., 2024).

Ice clouds are ubiquitous in the global atmosphere, making up to 70 % of clouds in the tropics. By absorbing longwave radiation and scattering shortwave radiation, they may warm or cool Earth's surface (Yang et al., 2015). The size distribution of ice particles is a crucial parameter not only with regard to longwave absorption and shortwave scattering efficiency (Liu et al., 2014) but also for precipitation rate. Reducing the uncertainty in ice particle size can result in large improvements in modeling climate sensitivity to increasing CO₂ concentrations in climate models (Wang et al., 2020). Observed ice crystal concentrations often exceed the concentration of ice nucleating particles (INPs) by orders of magnitude. Secondary ice production (SIP) may be very important in controlling the ice crystal concentrations (e.g., Field et al., 2017; Korolev and Leisner, 2020).

In the present work, we examine the effect that thunder can have on SIP and on the size distribution of cloud droplets.

Sonic flows have been in use for decades for the breakup of large droplets in many practical applications, such as combustion, gasification, emulsification, and medicine (e.g., Jain et al., 2015; Zhao et al., 2019, and references therein). Hanson et al. (1963) were among the first to investigate the breakup of droplets by air blasts. It is now well known that liquid droplets can undergo deformation and breakup if exposed to a gas stream of sufficient velocity (e.g., Wierzba, 1990; Guildenbecher et al., 2011). On the other hand, acoustic agglomeration of very small particles is also in practical use in air pollution control technologies. It has been studied for some decades now as an effective means for removing fine particles from industrial gaseous effluents (e.g., Scott, 1975; Hoffmann and Koopmann, 1996; Gallego-Juárez et al., 1999; Ng et al., 2017) or automotive exhaust (de Sarabia et al., 2003; Noorpoor et al., 2012) by coagulating them into coarser particles.

Very recently, interest has emerged, especially in China, for using artificial sounds to induce droplet coalescence in fog or clouds and hence disperse fog or induce rain. Liu et al. (2020) simulated numerically the condensation of fog under sound pressure levels (SPLs) of 140 to 160 dB and frequencies of 100–2000 Hz. Qiu et al. (2021), in a cloud chamber experiment with droplets of 10 µm diameter, observed effective agglomeration of water droplets for SPLs of 114 to 121 dB in the 50 to 65 Hz range. Unfortunately, they do not report the number concentrations of droplets used in the experiment. Jia et al. (2021) provided a theoretical examination of the effect of strong sound waves on cloud droplets. Wei et al. (2021) used artificially generated sounds in the field to induce droplet agglomeration in clouds. Bai et al. (2022) conducted laboratory experiments and simulations on the action of sound waves on microdroplets, using SPLs of 70 to 130 dB and frequencies of 30–280 Hz, while Shi et al. (2022) conducted extensive field tests with 10 kW speakers and output levels of 148.6 dB in order to study artificial rain production.

Very few people, however, have examined the effect of ambient sounds on droplets and aerosols. Recently, Kourtidis and Andrikopoulou (2022) examined whether bell sounds can have an impact on the size distribution of ambient aerosols. Some time ago, Temkin (1969) was the first to suggest, in a half-page paper, that thunder may induce collisions in cloud droplets and hence simulate droplet growth. Recently, Temkin (2021) presented calculations for droplet coalescence induced by the thunder sound, using a theoretically obtained value of 8 Hz as the dominant thunder clap frequency, and found that droplet agglomeration occurs.

Lightning occurs in cloud environments where not only large numbers of droplets but also ice nuclei are present. Thunder may induce mechanical effects on atmospheric particles, as the SPL can be quite high, and, additionally, thunder frequency spectra have peaks at low frequencies, where orthokinetic agglomeration is known to be very effective (e.g., Dong et al., 2006). Another mechanism that may influence the size distribution and number density of cloud particles, which has not been studied until now, is the supersonic shock wave front that results from the rapid heating of air to several tens of thousands degrees. The supersonic shock wave operates for some distance from the lightning channel, after which the shock wave decays to a sound wave.

In the present work we examine the effects of thunder on the size distribution of cloud droplets and ice nuclei. We will investigate not only droplet coalescence but also droplet and ice nuclei breakup in the thunder shock wave front. This is the first time the latter is studied.

2 Results and discussion

2.1 Particle breakup in the supersonic thunder shock wave front

Up to now, only Goyer et al. (1965) have studied effects of the thunder shock wave, investigating, in the laboratory, possible shock-induced freezing of supercooled water droplets. Here, we will examine a different effect of the thunder shock wave, namely the possibility for particle breakup by the rapid expansion of air in the lightning channel. During a lightning discharge, deposition of energy in the 4 to 100 J cm⁻¹ range (Stark et al., 1996; Borovsky, 1998; Lacroix et al., 2019) heats air within a few µs to 10⁴ to 10⁵ K plasma (e.g., Boggs et al., 2021, and references therein), resulting in very rapid expansion of air.

The non-dimensional Weber number is defined as $\mathit{\text{We}}={\mathit{\rho }}_{\mathrm{g}}{\mathit{\upsilon }}^{\mathrm{2}}d/\mathit{\sigma }$, where ρ_g is the air density in kg m⁻³, υ is the relative air velocity in m s⁻¹ between gas and particle, d is the particle diameter in m, and σ is the surface tension (surface energy, for solids) in N m⁻¹. Experiments show that droplets placed suddenly in a high-speed air flow will break up if the Weber number exceeds ≈12 (e.g., Krzeczkowski, 1980; Wierzba, 1990; Zilch et al., 2008). This number is the critical Weber number, We_cr. The modified Weber number ${\mathit{\text{We}}}^{*}=\mathit{\text{We}}/\mathrm{12}$, equals the ratio of the kinetic energy on impact to the surface tension (surface energy, for solid particles). Hence, when the Weber number exceeds We_cr, the kinetic energy on impact is higher than the surface tension (or energy). We will use the Weber number to examine if the conditions in the thunder shock wave lead to breakup of cloud particles (droplets, ice crystals, aerosols). To this end, the relative air velocity, which equals the shock wave front velocity, is a crucial parameter. So, we will first review the sparse literature on the matter, to obtain front velocities for the calculations that are as realistic as possible.

Navarro-González et al. (2001) simulated lightning in the laboratory by generating hot plasma with a pulsed Nd-YAG laser, and determined a shock wave front velocity of about 60 km s⁻¹ at 20 ns after the laser pulse. After about 3 µs, they observed decoupling of the resulting supersonic shock wave from the plasma, and the shock front cooled off to near ambient temperatures at around 5 µs, where it propagated at near sonic speed. In agreement with these results, Stark et al. (1996) also simulated lightning in the lab and found shock wave velocities of 2.2 km s⁻¹ at 1 µs after the discharge with a decreasing front velocity to below 1 km s⁻¹ after a few µs. Since the database on the shock waves of lightning discharges is rather limited, we quote here also some relevant results from explosions. Jenkins et al. (2013) derived experimentally, using a high-speed framing camera and particle image velocimetry, velocities of particles after explosions of 1.3 to 1.7 km s⁻¹. Lacroix et al. (2019) theoretically derived particle velocities after explosions of ≈0.3 km s⁻¹, while model results by Karch et al. (2018) show velocities 5 to > 10 times the speed of sound, i.e., 1.7 to > 3.4 km s⁻¹.

Liu and Zhang (2014), by generating spark discharges in the laboratory, found a linear relationship between electric discharge energy and shock wave energy. Since the shock wave energy will be related to its expansion speed, given the wide range of discharge energies observed in natural lightning, we will use shock wave front velocities of 60 and 1 km s⁻¹ in the following calculations, covering the range of observed front velocities, and will also cover a range of distances from the lightning channel.

For a 10 µm cloud droplet, and a shock wave front velocity of 60 km s⁻¹ in the immediate vicinity of the lightning channel, We equals several hundreds of thousands. Substituting in the Weber number equation for this particle size, of 10 µm, and the corresponding surface tension (or surface energy), even when the front velocity drops to 1 km s⁻¹, for a droplet We=167, for an ice particle We=63, and for a solid Al₂O₃ particle We=71.

In Table 1, calculations are presented for the minimum size of particles for which We=12 and We=120 will be exceeded. For Weber numbers near 12, the particles resulting from breakup have a bimodal distribution with a primary peak at $d/d_{\mathrm{0}}=$ 0.03 (where d is the diameter of the particles resulting from breakup of a particle with initial diameter d₀), a secondary peak at $d/d_{\mathrm{0}}=$ 0.06, and a Sauter mean diameter/d₀ around 0.09, whereas for Weber numbers near 120, the particles resulting from breakup have a unimodal lognormal distribution with a peak at $d/d_{\mathrm{0}}=\mathrm{0.023}$ and a Sauter mean diameter/d₀ around 0.03 (Jain et al., 2015). We note here that the Sauter mean diameter (Sauter, 1926) is the diameter of a drop having the same volume to surface area ratio as the entire spray.

Table 1 Minimum particle diameters (nm) in the thunder shock wave front (for front velocities of 60 and 1 km s⁻¹) where the Weber number (We) becomes equal to the critical Weber number We_cr=12 or We=120.

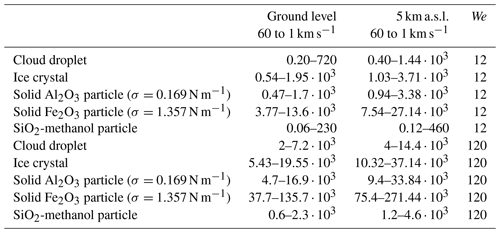
Calculations are for the following types of particles: cloud droplets (for which the surface tension of pure water, 0.072 N m⁻¹, is used), ice crystals (for which the surface energy of pure water ice, 0.19 N m⁻¹, is used, after Gundlach et al., 2011), solid Fe₂O₃ (σ=1.357 N m⁻¹) and Al₂O₃ particles (σ=0.169 N m⁻¹), and SiO₂-methanol particles (surface tension 0.023 N m⁻¹ from Bhuiyan et al., 2015). Solid Fe₂O₃ (iron(III) oxide, hematite) and Al₂O₃ particles are used as a proxy for dust, e.g., Saharan dust. SiO₂-methanol is used as a proxy for a dust particle covered with secondary organic aerosol (SOA). We note here, on the application of the critical Weber number to solid particles, the following. Although there are (to our knowledge) no experimental determinations of the critical Weber number for solids, the surface energy of solids and the surface tension of liquids both relate to the energy state of the surface molecules and can be both expressed in N m⁻¹; hence, it is possible to apply the same equation to solid particles. The modified Weber number, ${\mathit{\text{We}}}^{*}=\mathit{\text{We}}/\mathrm{12}$, equals the ratio of the kinetic energy on impact to the surface tension (surface energy, for solid particles). Hence, when the Weber number exceeds We_cr, the kinetic energy on impact is higher than the surface tension (or energy), resulting in breakup. Also, we note that ice crystals in clouds may or may not be entirely solid, i.e., snow crystals may also be present, for which the surface energy would be 0.03–0.72, depending on the liquid water content (e.g., Ketcham and Hobbs, 1969; Heil et al., 2020). Additionally, SiO₂-methanol particles are not entirely solid.

Above the minimum particle size depicted in Table 1, We will exceed 12 (or 120). The calculations for ground level and 5 km a.s.l. differ by the density of air, whereas possible changes in the surface energy of the particles due to the lower temperatures at 5 km a.s.l., have not been taken into account, since they are generally small. Since surface tension increases slightly with decreasing temperature, the results for 5 km a.s.l. presented in Table 1 underestimate the radii very slightly. Calculations are for front velocities ranging from 60 to 1 km s⁻¹.

We note that most SOA particles have a lower surface tension than water; hence, SOA will break up more easily than pure water droplets. Ice crystals and Al₂O₃ particles must have about 3 times the diameter of a water droplet to break, while Fe₂O₃ particles are the most difficult to break. This is not surprising as, setting We equal to 12 (critical Weber number) and solving the Weber equation for d (particle diameter), one gets $d=\mathrm{12}\mathit{\sigma }\mathit{\rho }g\mathit{\upsilon }/\mathrm{2}$; for higher σ, d will also be higher. As σ for water droplets is 0.072 N m⁻¹, while for water ice crystals it is 0.19 N m⁻¹ (2.64 times higher) and, e.g., for Al₂O₃ it is 0.169 N m⁻¹ (2.35 times higher), d is correspondingly higher for the latter two. At ground level, for sub-nanometer cloud particles and nanometer-sized Fe₂O₃ dust aerosols, We will reach the critical number 12, and hence the particles will break up in thunder shock wave fronts expanding at 60 km s⁻¹. Even at fronts expanding at 1 km s⁻¹, submicron cloud droplets and SiO₂-methanol particles, as well as small micrometer-sized ice crystals and Al₂O₃ particles, will break, while Fe₂O₃ particles must be larger than 13.6 µm to break. In thunder shock wave fronts expanding at 60 km s⁻¹, We=120 will be reached for nanometer-sized particles. At We=120, catastrophic breakup will occur and more secondary particles will be generated than for We=12. For a lower shock wave front velocity of 1 km s⁻¹, We=120 will be reached for all types of particles larger than around 20 µm, except Fe₂O₃ particles, which need to be larger than 136 µm to undergo catastrophic breakup.

At 5 km a.s.l., particles twice the size of the ones at ground level will break. So, for lightning channels extending vertically, a vertical gradient in the size distribution of cloud particles will be introduced near the lightning channel.

With the extreme scarcity of data on the possible extent of the shock wave, it is not possible to evaluate how large the parts of the cloud that are affected from the shock wave are. Goyer and Plooster (1968), using a numerical model of lightning discharge, calculated shock waves of the order of a few meters. Karch et al. (2018) simulated a 96.4 kA strike (i.e., 0.76×10⁴ J m⁻¹) and found the shock wave transitioning to acoustic velocities at around 6 cm. Takagi et al. (1998) observed return lightning strokes with a high-speed camera and found that the luminous region expands at about 100 km s⁻¹ during the initial stage and reaches a maximum diameter of several meters after about 100 µs.

If the Karch et al. (2018) 6 cm shock wave radius is used, then assuming a cylindrical geometry it is easy to calculate that the shock wave from a 500 m long intra-cloud (IC) discharge will affect a volume of 5.65 m³ within the cloud. Although this volume is small, multiple IC lightning discharges are common within thunderclouds and will increase it substantially. If we use the Goyer and Plooster (1968) calculations, or if the shock wave extends at the same distance as the luminous region, we can assume that the shock wave extends ≈3 m from the channel. Then a 500 m long IC discharge will affect a volume of the order of 14 × 10³ m³ within the cloud, which is substantial. Given also the fact that the total acoustical power of thunder was estimated by Bestard et al. (2023), from a study of 78 flashes, to span 4 orders of magnitude, from 10.6 kW to 165 MW, both of these calculations appear credible.

Given the importance of the ice phase in clouds in precipitation over the continents (Heymsfield et al., 2020), the importance of secondary ice production (SIP) in the formation of ice particles (Korolev and Leisner, 2020), and the need to properly describe SIP in climate and weather models, this mechanism may need to be taken into account in numerical descriptions.

2.2 Particle agglomeration in the thunder sonic field

After the supersonic wave front loses velocity, at some point, it decays to an expanding sonic field. There have been several subjective terms, such as clap, peal, roll, and rumble, to describe thunder sounds. Peals or claps are the sudden loud sounds that occur in a background of prolonged roll or rumble. The term roll is sometimes used to describe irregular sound variations whereas rumble is used to describe relatively weak sound of long duration (Depasse, 1994). Finite-amplitude propagation causes a doubling in the wavelength of the positive pulse within the first kilometer, but beyond this range the wavelength remains approximately constant (Few, 1995). As the SPL can be very high, thunder may induce mechanical effects on atmospheric particles (Few et al., 1967).

Sound is known to cause agglomeration at high SPLs, termed acoustic agglomeration or acoustic coagulation, due to particle resonance and the resulting relative motion of particles (e.g., Mednikov, 1965; Temkin, 1994). So, loud sound can impact atmospheric particles. We will examine here acoustic agglomeration due to the sound of thunder. The main identified mechanisms for agglomeration are orthokinetic collision and hydrodynamic collision. Orthokinetic collision is the main mechanism of sonic agglomeration for polydisperse particles at low sound frequencies and medium particle size ratios $d_{\mathrm{1}}/d_{\mathrm{2}}$. The orthokinetic mechanism refers to collisions between differently sized particles located within a distance that is approximately equal to the displacement amplitude of the acoustic field and with their relative motion parallel to the direction of vibration (Riera et al., 2015). It is based on the different resonance rates η of the particles due to their different sizes, with different displacement amplitudes for different sizes resulting in increased collisions. The resonance of particles in a sonic field can be characterized by the resonance rate (entrainment coefficient):

$$\begin{array}{}\text{(1)}& \mathit{\eta }=U_{\mathrm{p}}/U_{\mathrm{0}}=\mathrm{1}/\left[\mathrm{sqr}\right(\mathrm{1}+\left(\mathit{\omega }{\mathit{\tau }}_{\mathrm{p}}{)}^{\mathrm{2}}\right)]\end{array}$$

(Temkin and Leung, 1976; Hoffmann and Koopmann, 1996, 1997; González et al., 2000), where η is the resonance rate with values from 0 (no resonance) to 1 (complete resonance), U_p is the particle velocity amplitude, U₀ is the gas velocity amplitude, ω is the sound wave angular velocity, τ_p is the relaxation time (${\mathit{\tau }}_{\mathrm{p}}=\mathit{\rho }\cdot d^{\mathrm{2}}/\mathrm{0.00032886}$), ρ is the particle density, and d is the aerodynamic diameter of the particle. The sound wave angular velocity is given by ω=2πf, with f being the sound frequency. Equation (1) is the simplified Brandt–Freund–Hiedemann (BFH) equation (Brandt et al., 1936; González et al., 2000; Dong et al., 2006). The maximum inter-particle distance that, in the event of a collision, leads to agglomeration is the effective agglomeration length, L_eff, L_eff=εL, where ε is the collision efficiency (with values between 0 and 1) and L is the maximum inter-particle distance that can cause collision. The value of ε is controlled by the Stokes number S_t, ε= [$S_t/(S_t+A)]B$ where A and B are constants (Löffler, 1988). We note here that the validity of Eq. (1) has been demonstrated for spherical particles, single-frequency sound waves, small gas velocities, and relatively low frequencies and these assumptions may not hold throughout the cloud region. However, it can still give us an idea of the involved processes, as we apply here the equation to relatively low single frequencies and cloud droplets are spherical while cloud ice crystals may or may not be spherical. While in certain cloud regions ice crystal shapes may be dominated by spheroids (e.g., Lawson et al., 2001; Fleishauer et al., 2002), a variety of other shapes will dominate in other regions.

For the simulations presented here, we assumed liquid droplets with diameters d of 8 to 36 µm (e.g., Barthlott et al., 2022 and references therein) and density ρ= 1000 kg m⁻³. Saharan dust particles have diameters 0.01 to 20 µm, with mass peaks at around 0.4 and 3 µm (Gini et al., 2022), number concentration peaks at around 0.03 µm, and a surface area peak at around 10 µm (Weinzierl et al., 2009). So, in the calculations presented here, for Saharan dust we used diameters d in the 0.1 to 10 µm range, and density ρ=2500 kg m⁻³, which is very near the density of silica.

Few et al. (1967) determined dominant thunder frequencies in the 180 to 260 Hz range. Holmes et al. (1971), by analyzing 40 thunder events, determined peak power at frequencies from below 4 to 125 Hz. Intra-cloud (IC) discharges had a mean peak value of power at 28 Hz with mean total acoustic energy 1.9 × 10⁶ J, while cloud-to-ground (CG) discharges had a mean peak value of power at 50 Hz with a much higher mean total acoustic energy of 6.3 × 10⁶ J. Yuhua and Ping (2012) observed peak frequencies of 210 to 280 Hz, while the frequency spectrum went up to 1000 Hz. The same authors also calculated that the more powerful the lightning, the lower its peak frequency. Abegunawardana et al. (2016) determined a fundamental frequency of peals at 75 ± 22 Hz, of claps at 102 ± 36 Hz, and of rumbles at 63 ± 27 Hz. Bodhika et al. (2014) observed thunder frequency spectra with peaks for peals and claps at around 100 Hz, and around 50 Hz for thunder rumble sounds. Lacroix et al. (2018) reported spectra in the 1–200 Hz range, showing amplitudes of 88 to 90 dB in the 6 to 80 Hz range, for flash distances 2 to 4.3 km. The same authors also reported spectra from 14 events, exhibiting a frequency center of gravity spanning from 47 to 115 Hz for different events.

Hence, for the calculations presented here (Kourtidis et al., 2025), we use frequencies of 10 to 500 Hz.

In general, the resonance rate increases with decreasing frequency and decreasing particle size (Fig. 1). The results show complete or almost complete (> 0.8) resonance for cloud droplet diameters ≤24 µm for f≤70 Hz, while smallest 8 µm droplets remain completely resonant up to 200 Hz. Saharan dust particles with diameters up to 3 µm show complete resonance for f up to 500 Hz, while all dust particles up to 10 µm show complete or almost complete (> 0.8) resonance for frequencies of 100 Hz or lower.

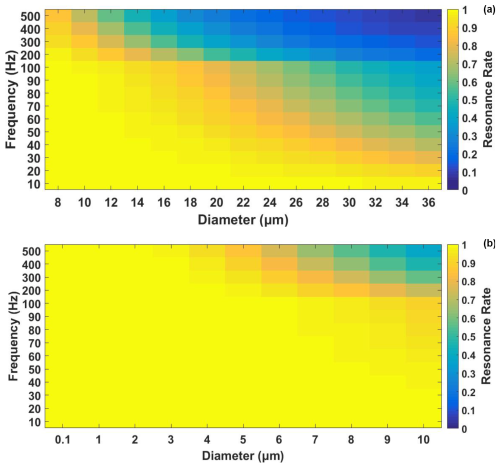
Figure 1 (a) Resonance rate η of cloud droplets with diameters 8–36 µm (calculation step 2 µm) for sound frequencies 10–500 Hz (calculation step 10 Hz up to 100 Hz and 100 Hz above that). (b) Resonance rate η of dust particles with diameters 0.1–10 µm (calculation step 1 µm) for sound frequencies 10–500 Hz (calculation step 10 Hz up to 100 Hz and 100 Hz above that).

To calculate L_eff, the SPL is needed. Not very many SPL measurements exist in the vicinity of thunder. Bodhika et al. (2018) observed peak SPLs above 110 dB for 30 % of recorded flashes at 3 km from the flash. Closer to the lightning, higher SPL values are to be expected. If only the geometrical spreading of a spherical wave in free space is considered, at half the distance the SPL would be increased by 6 dB. In a real atmosphere, the sound propagation deviates from a spherical shape, and ground reflection may increase the SPL; hence, the difference may be less than 6 dB. Farges et al. (2021) found decay of the thunder amplitude to scale with flash distance r as r^−0.717, while Shi et al. (2022) report SPL (dB) decay rates scaling with distance at r^−0.06339. Lacroix et al. (2019) calculated overpressures 2 m from the stroke that translate to SPLs of 134 to 151 dB (for deposited energy 4 to 60 J cm⁻¹). Lacroix et al. (2019) also noted near- and far-field behavior acoustic power scaling with r⁻¹ with distance (cylindrical wave decay) up to 3600 m and scaling with r⁻² (spherical wave decay) after that. So, it is reasonable to assume that the thunder SPL will exceed 120 dB at distances less than 800 m from the stroke and 130 dB at distances less than 200 m from the stroke. Hence, for the calculations presented hereafter, we will use SPL in the 90 to 135 dB range.

For two particles No. 1 and No. 2 (No. 1 being the larger particle and No. 2 the smaller one) with diameters d₁ and d₂, their relative resonance rate is given by ${\mathit{\eta }}_{\mathrm{12}}=\mathit{\omega }\cdot ({\mathit{\tau }}_{\mathrm{p}\mathrm{1}}-{\mathit{\tau }}_{\mathrm{p}\mathrm{2}})/\mathrm{sqr}\left[\right(\mathrm{1}+{\mathit{\omega }}^{\mathrm{2}}\cdot {\mathit{\tau }}_{\mathrm{p}\mathrm{1}}^{\mathrm{2}})\cdot (\mathrm{1}+{\mathit{\omega }}^{\mathrm{2}}\cdot {\mathit{\tau }}_{\mathrm{p}\mathrm{2}}^{\mathrm{2}}\left)\right]$, where ${\mathit{\tau }}_{\mathrm{p}\mathrm{1}}={\mathit{\rho }}_{\mathrm{1}}\cdot d_{\mathrm{1}}^{\mathrm{2}}/\mathrm{0.00032886}$ and ${\mathit{\tau }}_{\mathrm{p}\mathrm{2}}={\mathit{\rho }}_{\mathrm{2}}\cdot d_{\mathrm{2}}^{\mathrm{2}}/\mathrm{0.00032886}$ are the relaxation times of particle 1 and 2 and ω=2πf is the angular velocity of the sound wave. The effective agglomeration length for these two particles is calculated as L_eff= (${\mathit{\eta }}_{\mathrm{12}}\cdot U_{\mathrm{g}}/\mathit{\omega })\cdot [S_t/(S_t+\mathrm{0.65}){]}^{\mathrm{3.7}}$, where S_t is the Stokes number, $S_t={\mathit{\rho }}_{\mathrm{2}}\cdot {\mathit{\eta }}_{\mathrm{12}}\cdot U_{\mathrm{g}}\cdot d_{\mathrm{2}}^{\mathrm{2}}/(\mathrm{0.00032886}\cdot d_{\mathrm{1}})$, and $U_{\mathrm{g}}=\mathit{\left\{}{\mathrm{10}}^{\left[\right(\mathrm{SPL}-\mathrm{94})/\mathrm{20}]}\mathit{\right\}}/(c\cdot {\mathit{\rho }}_{\mathrm{g}})$, U_g being the gas velocity amplitude in the sound wave, c the velocity of sound in air, and ρ_g the density of air.

For two particles with d₁ in the 0.05 to 35 µm range and d₂ in the 0.02 to 30 µm range, for SPL = 100 dB and frequencies of 10, 50, and 200 Hz, the effective agglomeration length spans many orders of magnitude, and is larger for larger particle pairs (Fig. 2). For particles above around 25 µm, it ranges between 1 nm and 10 µm (Fig. 2). Increasing the SPL from 90 to 120 dB increases the agglomeration length by several (6–7) orders of magnitude (Figs. 3 and 4). Further increasing the SPL from 120 to 135 dB increases further the agglomeration length by 3 to 4 orders of magnitude. Hence, the agglomeration length ∼100 m from the strike will be 4 orders of magnitude longer than the agglomeration length ∼800 m thereof and 6 to 7 orders of magnitude longer than the agglomeration length ∼2 km thereof. Additionally, the agglomeration length is 10 to 50 times larger at 5 km a.s.l. than near ground level (Fig. 4); hence, in clouds with vertical extent, like cumulus congestus and cumulonimbus, the higher levels of the cloud will experience more coagulation than the lower ones.

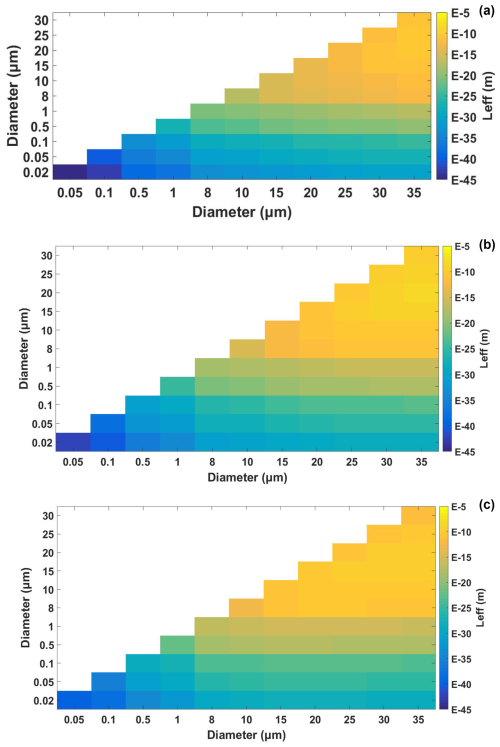
Figure 2 Effective agglomeration length near the surface for SPL=100 dB and sound frequencies of (a) 10, (b) 50, and (c) 200 Hz.

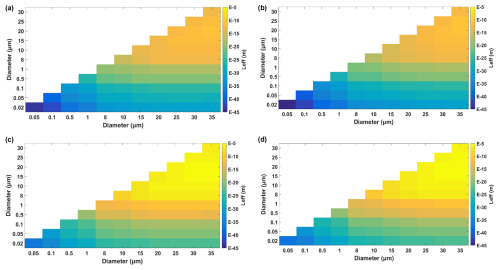
Figure 3 Effective agglomeration length for pairs of particles with diameters 20 nm–35 µm near ground level for sounds of (a, c) 100 Hz and (b, d) 50 Hz and SPL of (a, b) 90 dB and (c, d) 120 dB.

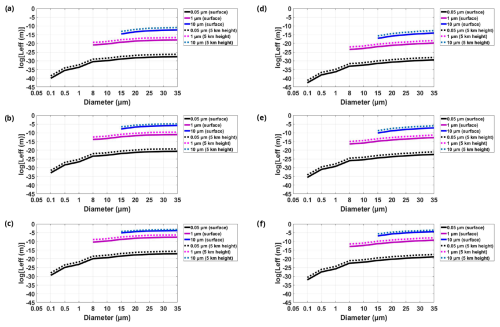
Figure 4 (a, b, c) Effective agglomeration length for large particles of diameter 0.1–35 µm and small particles of diameter 0.05, 1, and 10 µm, both at ground level and at 5 km height a.s.l., for f= 50 Hz and SPL of (a) 90 dB, (b) 120 dB, and (c) 135 dB. (d, e, f) Effective agglomeration length for large particles of diameter 0.1–35 µm and small particles of diameter 0.05, 1, and 10 µm, at both ground level and 5 km height a.s.l., for f= 10 Hz and SPL of (d) 90 dB, (e) 120 dB, and (f) 135 dB.

For number concentration of particles per unit volume N, the mean interparticle distance $<r>$ is proportional to the per particle volume $\mathrm{1}/N$. It can be defined as $<r>$ $=\mathrm{1}/N^{\mathrm{1}/\mathrm{3}}$, $<r>$ corresponding to the length of the edge of a cube of volume $\mathrm{1}/N$. For Saharan dust particles, for which N_dust∼1–100 particles cm⁻³, $<r>$ ∼2–10 mm. For cloud droplets N_{cloud_droplets} ∼ 200–1000 droplets cm⁻³, hence $<r>$ ∼1–1.7 mm; for ice particles N_{ice_particles} ∼ 0.1–50 particles cm⁻³ and $<r>$ ∼2.7 mm–2.15 cm. For pyroclouds, N_soot ∼ 200–10⁵ particles cm⁻³, $<r>$ ∼210 µm–1.7 mm.

The effective agglomeration length can be up to 10 µm for SPL 120 dB (Fig. 4); hence, interparticle distances appear much larger than L_eff for agglomeration to occur for SPL up to 120 dB. However, the use of mean inter-particle distance as $\mathrm{1}/N^{\mathrm{1}/\mathrm{3}}$ ignores the fact that interparticle distances will follow a probability density function $P\left(r\right)=(\mathrm{3}/a)(r/a{)}^{\mathrm{2}}{\mathrm{e}}^{[-(r/a{)}^{\mathrm{3}}]}$ and the substantial in-cloud turbulence of thunderclouds will further enhance the spread of P(r). So, a substantial number of cloud particles will be at interparticle distances ⋘$\mathrm{1}/N^{\mathrm{1}/\mathrm{3}}$ and thus even for SPL below 120 dB some agglomeration will occur.

For a SPL of 135 dB, the agglomeration length can be up to 10 µm for particles with d > 15 µm, and for very large particles (d= 35 µm) it can reach 1 mm. So, cloud droplets will agglomerate readily, and even more so in pyroclouds.

Ice, because its surface energy is higher than that of liquid water, will aggregate upon impact more easily than liquid water droplets (Gundlach and Blum, 2015). However, the aggregation process will be more complicated for ice collisions than for cloud droplets, since the event of ice–ice collision may cause, apart from agglomeration, rime splintering, and hence the formation of a larger particle may be accompanied by the ejection of many small splinters. The event of ice–liquid droplet collision, which is more likely, due to the higher abundance of cloud droplets, may lead to the formation of a larger ice crystal by freezing of the droplet water.

Qiu et al. (2021) observed effective agglomeration for SPLs of 114 to 121 dB in the 50 to 65 Hz range in cloud chamber experiments with droplets with diameters 4 to 20 µm; unfortunately, they do not report the number concentrations of droplets used in the experiment. Bai et al. (2022) determined critical SPLs of 110±15 dB for effective agglomeration of microdroplets in the 1 to 30 µm range. Bai et al. (2022) identified, in laboratory experiments, optimal orthokinetic agglomeration frequencies of 50 to 250 Hz for microdroplets. An optimal frequency, varying for different droplets, was identified in orthokinetic agglomeration within the 50 to 250 Hz range by Shi et al. (2023). Our results are consistent with these studies. However, we note here that in contrast to the present study, these studies were not concerned with naturally occurring sounds such as thunder, but with sounds deliberately produced for rain enhancement or fog dissipation.

Prior to the present study only Temkin (2021, 2023) presented calculations for the impact of thunder on cloud droplets. Temkin (2021), using 8 Hz as the dominant thunder clap frequency, calculated that droplet agglomeration will occur rapidly, while Temkin (2023) studied the combined effects of thunderclaps and gravity on rain production.

Reliable thunder SPL and frequency spectra measurements at very short distances (10 m to 1 km) from thunder will contribute to the refinement of the calculations, as also will studies that can help determine the shock wave extent. Field measurements within thunderclouds of cloud droplet and ice crystal concentrations before and after lightning will show the extent of the effect thunder has on the size distributions of cloud particles.

3 Conclusions

We present results that show that the occurrence of thunder has the potential to alter the number concentration and size distribution of ice particles and cloud droplets within thunderclouds via two mechanisms. As global warming may change the occurrence rate of lightning (e.g., Romps et al., 2014; Clark et al., 2017; Finney et al., 2018), a climate feedback may be introduced by the mechanisms discussed here.

The two mechanisms examined here have different impacts. The first, operating at the shock wave front in the vicinity of the lightning channel, results in extensive shattering of cloud particles, so it increases the number of particles and decreases their size. The mechanism may be important as a secondary ice production mechanism. The second mechanism, operating at larger distances from the lightning channel, causes coagulation, so it decreases the number of particles and increases their size.

The first mechanism operates at the shock wave front of the lightning and will cause extensive breakup of cloud particles larger than a given diameter, depending on their composition. SOA particles will break up more easily than pure water droplets. Ice crystals and Al₂O₃ particles must have about 3 times the diameter of a water droplet to break, while Fe₂O₃ particles are the most difficult to break. At ground level, sub-nanometer cloud particles and ice crystals, and nanometer-sized Fe₂O₃ dust aerosols will break up in thunder shock wave fronts expanding at 60 km s⁻¹. Even at fronts expanding at 1 km s⁻¹, submicron cloud droplets and SiO₂-methanol particles, ice crystals, and Al₂O₃ particles larger than ≈2 µm will break, while Fe₂O₃ particles must be larger than 13.6 µm to break. At 5 km a.s.l., particles twice the size of the ones at ground level will break. So, for lightning occurring at various cloud heights, a vertical gradient in the size distribution of cloud particles will be introduced. Data on the possible extent of the shock wave are extremely scarce and give ranges from a few centimeters to a few meters, so it is not possible to evaluate how large the parts of the cloud that will be affected from the shock wave are. Another uncertainty arises from the very limited data on the speed of the expansion of the shock wave front, which give ranges from 1 to 100 km s⁻¹ and result in uncertainties of 3 orders of magnitude as to the smallest size of the particles above which shattering occurs. However, even at the lower end of the expansion speed, all types of particles, except solid Fe₂O₃ ones, will break up if they are larger than ≈0.23 to 2 µm. As this is the first time this mechanism has been investigated, there are no previous results for comparison.

The second mechanism operates at larger distances from the lightning channel and results in acoustic agglomeration of cloud particles. Larger particles will agglomerate more readily than smaller ones, for SPLs above 120 dB and sound frequencies of 50 to 200 Hz. This mechanism's efficiency increases with height by about a factor of 10 to 50 every 5 km. Reliable thunder SPL and frequency spectra measurements at very short distances (10 m to 1 km) from lightning will contribute to the refinement of the calculations. The results presented here compare well with the emerging body of evidence from laboratory and field studies with artificial sounds. They are consistent with the only two previous studies investigating the coagulation impact of thunder (Temkin 2021, 2023), but substantially extend both the frequency range (as Temkin investigated frequencies of 5 and 8 Hz) and the size of particles (above around 20 µm for Temkin).

The two mechanisms described here are operating in tandem, and will also cause vertical changes in the size distribution of cloud particles, as they have different efficiencies at different heights. The results presented here demonstrate that thunder has the potential to alter the size distribution of cloud droplets and ice crystals in thunderclouds, and may be important in generating secondary ice particles. As the size distributions of droplets and ice crystals influence the rain generation process, on the one hand, and the radiative properties of clouds, on the other, the thunder impact is worth investigating further. The results are also relevant from an atmospheric electricity point of view. As the charge separation within thunderclouds is influenced by the size distribution of cloud particles and the collisions between them, it is interesting that this charge separation, causing lightning, also causes thunder that then results in collision enhancement and changes in the size distribution and hence might introduce a yet unquantified feedback in the electrification process. The extent of the changes these mechanisms introduce can be further quantified only with carefully designed field measurements. Field measurements within thunderclouds of cloud droplet and ice crystal concentrations before and after lightning, together with lightning location data and SPL measurements, may show the real extent of the effect thunder has on the size distributions of cloud particles.