Enhancing SO₃ hydrolysis and nucleation: the role of formic sulfuric anhydride

Although the nucleation route driven by sulfuric acid (H₂SO₄) and ammonia (NH₃) primarily dominates new particle formation (NPF) in the atmosphere, exploring the role of other trace species in the H₂SO₄–NH₃ system is crucial for a more comprehensive insight into NPF processes. Formic sulfuric anhydride (FSA) has been observed in the atmospheric environment and is found in abundance in atmospheric fine particles. Nevertheless, its effect on SO₃ hydrolysis and NPF remains poorly understood. Here, we studied the enhancing effect of FSA on gaseous and interfacial SO₃ hydrolysis as well as its impact on H₂SO₄–NH₃-driven NPF occurring through quantum chemical calculations, Atmospheric Cluster Dynamics Code (ACDC) kinetics combined with Born–Oppenheimer molecular dynamics (BOMD). Gaseous-phase findings indicate that FSA-catalyzed SO₃ hydrolysis is nearly barrierless. At an [FSA] = 10⁷ molecules cm⁻³, this reaction competes effectively with SO₃ hydrolysis in the presence of HNO₃ (10⁹ molecules cm⁻³), HCOOH (10⁸ molecules cm⁻³) and H₂SO₄ (10⁶ molecules cm⁻³) in the range of 280.0–320.0 K. At the gas–liquid nanodroplet interface, BOMD simulations reveal that FSA-mediated SO₃ hydrolysis follows a stepwise mechanism, completing within a few picoseconds. Notably, FSA enhances the formation rate of H₂SO₄–NH₃ clusters by over 10⁵ times in regions with relatively high [FSA] at elevated temperatures. Additionally, the interfacial FSA⁻ ion has the ability to appeal precursor species for particle formation from the gaseous phase to the water nanodroplet interface, thereby facilitating particle growth. These results present new insights into both the pathways of H₂SO₄ formation and aerosol particle growth in the polluted boundary layer.

1 Introduction

Sulfuric acid (SA) is an important atmospheric pollutant closely associated with new particle formation (NPF) events and is recognized as a vital precursor in the process of converting gases into particles. It facilitates the formation of sulfate aerosols and acid rain in diverse environments, influencing cloud formation, precipitation, and the Earth's radiation balance, ultimately contributing to climate change (Yao et al., 2018; Venkataraman et al., 2001; Kumar et al., 2024). Experimental (Couling et al., 2003; Reiner and Arnold, 1993; Bondybey and English, 1985) and theoretical studies (Feng and Wang, 2023; Kumar et al., 2024; Zhang et al., 2025) have shown that atmospheric gaseous SA primarily forms via SO₃ hydrolysis (Sarkar et al., 2019; Tao et al., 2018; Carmona-García et al., 2021). However, the likelihood of direct SO₃ hydrolysis in the atmosphere is low due to the high activation energy associated with the process (Chen and Plummer, 1985). Introducing a second water molecule has been shown to significantly lower the activation energy, making SO₃ hydrolysis more efficient (Morokuma and Muguruma, 1994). Further research indicates that, besides water molecules, other species such as formic acid (Kangas et al., 2020), oxalic acid (Yang et al., 2021), nitric acid (Long et al., 2022), SA (Wang et al., 2024), and ammonia (Sarkar et al., 2019) exhibit even greater catalytic efficiency in promoting SO₃ hydrolysis for SA formation. These findings provide valuable theoretical insights for understanding SA sources, particularly in regions where pollutant concentrations are notably elevated. Nevertheless, further investigation is necessary to fully understand the SO₃ hydrolysis mechanism in areas with high levels of specific pollutants, to better assess its behavior and effects under different atmospheric conditions.

Carboxylic sulfuric anhydrides (CSAs) are a recently identified class of atmospheric organosulfides, formed by the cycloaddition of SO₃ with organic carboxylic acids present (Fleig et al., 2012). These CSAs exhibit strong acidity and can act as proton transfer bridges, potentially influencing SO₃ hydrolysis and promoting the formation of SA in regions with high CSA concentrations. Research indicates that the gaseous CSA concentration can reach 10⁷ molecules cm⁻³ (Smith et al., 2020), creating conditions that may impact SO₃ hydrolysis. As the simplest CSA, formic sulfuric anhydride (FSA) has been characterized using microwave spectroscopic (Mackenzie et al., 2015). FSA is more acidic than formic acid and may facilitate proton transfer in the gaseous hydrolysis of SO₃. However, its role in this process has not yet been explored. Besides, it has been reported that the interfacial environment both initiates the organization and clustering of hydrophilic groups and acts as an effective medium for various atmospheric reactions (Ma et al., 2020; Zhong et al., 2019; Tan et al., 2022; Wan et al., 2023). Notably, proton transfer routes induced by interfacial water molecules accelerate numerous atmospheric reactions taking place on aerosol and droplet surfaces. These reactions typically proceed at accelerated rates and can differ from similar processes in the gas phase or bulk water (Tang et al., 2024; Fang et al., 2024; Martins-Costa and Ruiz-López, 2024). Thus, it is essential to investigate whether FSA accelerates SO₃ hydrolysis at the gas–liquid nanodroplet interface, as this could offer valuable insights into atmospheric chemistry and the mechanisms driving particle formation.

Additionally, new species generated from gas-phase reactions of SO₃ with trace substances (Li et al., 2018; Liu et al., 2019) can also significantly influence the NPF process. For example, Li et al. (2018) revealed that NH₂SO₃H, formed from the reaction of SO₃ with ammonia (A) not only contributes directly to SA–(CH₃)₂NH cluster formation but also enhances the maximum rate of NPF from SA and (CH₃)₂NH by approximately 2-fold in heavily polluted areas with high concentrations of basic substances. Similarly, Liu et al. (2019) predicted that methyl hydrogen sulfate (MHS), formed from the reaction of SO₃ with methanol, significantly impacts SA–(CH₃)₂NH nucleation, particularly in dry regions with high alcohol concentrations. FSA, produced from the reaction of SO₃ with HCOOH, contains the –OSO₃H functional group and exhibits a binding capability comparable to that of SA with nucleation precursors like A. The potential role of FSA in enhancing SA–A nucleation in the atmosphere requires further investigation to fully understand its contribution to NPF processes.

This work examined the catalytic effect of FSA on SO₃ hydrolysis and SA–A nucleation particle formation. Specifically, the catalytic effects of FSA on gaseous SO₃ hydrolysis were firstly explored. Following this, the differences between the gaseous and interfacial reactions of FSA-catalyzed SO₃ hydrolysis were evaluated using BOMD simulations. Subsequently, a qualitative evaluation of FSA's nucleation capability was conducted through molecular dynamics (MD) simulations. Finally, the atmospheric implications of FSA for particle formation were analyzed. This study not only deepens our understanding of the impact of FSA on SO₃ hydrolysis but also provides new molecular-level mechanisms for the contribution to SA–A particle formation.

2 Computational methods

2.1 Quantum chemical details

The M06-2X functional (Mardirossian and Head-Gordon, 2016; Pereira et al., 2017) is highly effective in describing noncovalent interactions and estimating the thermochemistry and equilibrium structures of atmospheric reactions. To investigate the impact of formic sulfuric anhydride (FSA) on gaseous SO₃ hydrolysis, the M06-2X/6-311$++$G(2df,2pd) computational method, as implemented in Gaussian 09 software (Frisch et al., 2009), was employed to analyze the geometric structures and vibrational frequencies of the relevant species. It is noted that the calculated bond distances and bond angles at the M06-2X/6-311$++$G(2df,2pd) level (Fig. S1 in the Supplement) are in good agreement with both experimental data and values obtained using the M06-2X/6-311$++$G(3df,3pd) method. Meanwhile, the calculations of the intrinsic reaction coordinate were carried out to conduct the connections between the transition states and their corresponding pre-reactive and post-reactive complexes. To enhance the reliability of the relative Gibbs free energies, single-point energies at the CCSD(T)-F12/cc-pVDZ-F12-CABS level were calculated using the ORCA software (Neese, 2012).

The most stable structure of the (FSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) clusters was obtained by the following three steps. Initially, the ABCluster program (Zhang and Dolg, 2015) was utilized to randomly produce n×1000 initial isomers ($\mathrm{1}\le n\le \mathrm{3}$), which were subsequently evaluated using the PM6 method via MOPAC 2016 (Partanen et al., 2016). Next, up to n×100 lowest-energy isomers were chosen and further refined using the method of M06-2X/6-31+G(d,p). Then, the top n×10 isomers were re-optimized at the M06-2X/6-311$++$G(2df,2pd) method level to ascertain their isomers with the lowest energy. Lastly, based on the optimized geometries of the stable clusters at the M06-2X/6-311$++$G(2df,2pd) level, the single-point energies were calculated at the DLPNO-CCSD(T)-F12/cc-pVDZ-F12-CABS level (Tsona Tchinda et al., 2022) using the ORCA. The optimized structures and their Gibbs free energies are detailed in Fig. S12 and Table S7 in the Supplement, respectively.

2.2 Rate coefficient computations

Rate coefficients for FSA-assisted SO₃ hydrolysis were calculated via two steps as follows. First, the VRC-VTST methodology (Zhang et al., 2023, 2024) was applied using the Polyrate program (Meana-Pañeda et al., 2024) to calculate the rate coefficients under high-pressure conditions. Next, the Master Equation Solver for Multi-Energy Well Reactions (Glowacki et al., 2012) was engaged in computing the rate coefficients for FSA-assisted SO₃ hydrolysis across a temperature range of 280.0 to 320.0 K. To estimate the rate coefficients for the barrier less formation of pre-reactive complexes from the separated reactants, we applied the inverse Laplace transform (ILT) method (Kumar et al., 2021). In parallel, RRKM theory (Bao et al., 2016) was utilized to estimate the rate coefficients for the transition from the pre-reactive complex to the post-reactive complex through a transition stat. Additionally, the MESMER calculations in this study applied an Eckart tunneling correction to the reaction rates. Details of the ILT methods and RRKM theory are provided in Part 1 and Part 2 in the Supplement, respectively.

2.3 BOMD simulations

BOMD simulations were conducted with the CP2K program (Hutter et al., 2014). The BLYP functional was applied to address exchange and correlation interactions (Becke, 1988; Lee et al., 1988). Grimme's dispersion-corrected method (Grimme et al., 2010) was employed to account for the dispersion interactions and effectively handle weak dispersion effects. The GTH norm-conserving pseudopotentials (Goedecker et al., 1996), along with the Gaussian DZVP basis set (Phillips et al., 2005) and the auxiliary plane wave basis set, were utilized to describe the core and valence electrons, respectively. The plane wave basis set was established with a 280 Ry energy cutoff, while the Gaussian basis set cutoff was set at 40 Ry. A supercell side length of 15 Å was used in gas-phase simulations to eliminate periodic boundary conditions with step of 0.5 fs. For interfacial reactions, a water droplet containing 191 water molecules was initially pre-optimized through BOMD simulation for approximately 5.0 ps at 300 K. Subsequently, SO₃ and FSA were positioned at the gas–liquid nanodroplet interface to perform the simulations over 10 ps. A supercell side length of 35 Å was set for gas–liquid nanodroplet interface simulations to prevent periodic interactions between neighboring water droplets, using a step of 1.0 fs. In all simulations under the NVT ensemble, a stable temperature of 300 K was maintained using the Nosé–Hoover thermostat.

2.4 Classical molecular dynamics simulation

MD simulations were conducted using the GROMACS 2024.3 software package (Abraham et al., 2024) with the general AMBER force field (GAFF). GAFF is a comprehensive force field that encompasses nearly all of organic chemical space, including elements such as C, N, O, S, P, H, F, Cl, Br, and I. This force field has been widely utilized in studies of the air–water interface, with the results confirming its suitability for predicting the properties of species at this interface (Li et al., 2024b; Cheng et al., 2025; Zhao et al., 2019). To get the force field parameters, geometry optimization at the M06-2X/6-311$++$G(2df,2pd) level was performed, following electrostatic potential (ESP) calculations at the same level. Geometry optimization and ESP calculations were carried out with the Gaussian 09 software. The restrained electrostatic potential (RESP) charges were calculated using Multiwfn 3.8 (dev) (Lu and Chen, 2012). Subsequently, the AMBER parameter and coordinate files were generated using Packmol (Martínez et al., 2009) and Sobtop (Lu, 2023), respectively.

2.4.1 Surface preference of SO₃, FSA and SO₃–FSA

A cubic box with a side length of 4 nm, containing 2165 water molecules, was initially constructed. The box was then extended along the z axis to a length of 9 nm. The water slab was positioned at the center of the box with the COM coordinates of 2.0, 2.0, and 4.5 nm, while the SO₃, FSA and SO₃–FSA complexes were placed at 2.0, 2.0, and 7.5 nm (Fig. S6c). Subsequently, a 150 ns NVT simulation was conducted.

2.4.2 Molecular dynamics simulation of nucleation

The simulation was performed within a cubic simulation box, each side measuring 200 Å in length. Following energy minimization, the system was further simulated under the NVT and NPT ensembles at 298 K for durations of 100 ps and 40 ns, respectively. The Berendsen pressure coupling method (Berendsen et al., 1984) and the velocity rescaling thermostat (Bussi et al., 2007) were used to regulate pressure and temperature, respectively. The system applied periodic boundary conditions to mimic an infinite environment, with a 1 fs time step. The electrostatic and van der Waals interactions were set with a 1.4 nm cutoff distance, and the Particle Mesh Ewald method (York et al., 1993) was implemented for long-range electrostatics. All the bond lengths were restricted by the LINCS algorithm (Hess et al., 1997) to preserve structural integrity during the simulation.

2.5 Atmospheric Cluster Dynamics Code (ACDC) model

The ACDC (McGrath et al., 2012) was employed to investigate cluster formation rates and growth mechanisms for (FSA)_x(SA)_y(A)_z clusters. The ACDC simulations were supplied with thermodynamic data, which were derived from quantum chemical calculations performed by M06-2X/6-311$++$G(2df,2pd). Accounting for all potential collision and evaporation processes, the following formulation represents the birth–death equations:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{c}_i}{\mathrm{d}t}}& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{j<i}{\mathit{\beta }}_{j,(i-j)}{C}_j{C}_{(i-j)}+\sum _j{\mathit{\gamma }}_{(i+j)\to i}\\ & C_{i+j}-\sum _j{\mathit{\beta }}_{i,j}{C}_i{C}_j-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{j<i}{\mathit{\gamma }}_{i\to j}{C}_i+Q_i-S_i.\end{array}\end{array}$$

In the above equation, c_i represents the concentration of i cluster, while β_i,j stands for the collision coefficient between i and j clusters. The term ${\mathit{\gamma }}_{(i+j)\to i}\to i$ refers to the coefficient at which the larger i+j cluster breaks down (or evaporates) into i and j clusters. Additionally, Q_i accounts for any possible external source of i cluster. To consider the external losses of i cluster, a coagulation sink coefficient of 2 × 10⁻² s⁻¹ was used, aligning with values typically found in polluted environments (Liu et al., 2021b). In ACDC, boundary clusters must be sufficiently stable, which allows them to continue growing. Therefore, the clusters of (SA)₄ ⋅ (A)₃, (SA)₄ ⋅ (A)₄, (FSA)₄ ⋅ (A)_3, (FSA)₄ ⋅ (A)₄, (FSA)₃ ⋅ SA ⋅ (A)_3, (FSA)₂ ⋅ (SA)₂ ⋅ (A)₃, and FSA ⋅ (SA)₃ ⋅ (A)₃ were selected as the boundary clusters in the SA–A–FSA system.

3 Results and discussion

3.1 The hydrolysis of SO₃ assisted by FSA

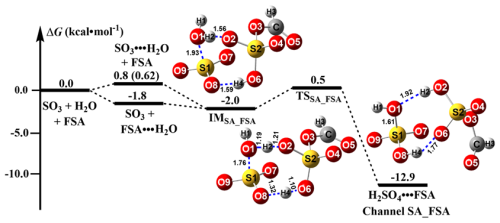
The SO₃ hydrolysis with HCOOSO₃H (FSA) can initially occur via the interaction between SO₃ (or FSA) and H₂O to form SO₃ ⋅  ⋅  ⋅ H₂O (or FSA ⋅  ⋅  ⋅ H₂O) dimer. Subsequently, the SO₃ ⋅  ⋅  ⋅ H₂O dimer collides with FSA, and the FSA ⋅  ⋅  ⋅ H₂O dimer interacts with SO₃. The predicted relative Gibbs free energy of SO₃ ⋅  ⋅  ⋅ H₂O is 0.8 kcal mol⁻¹ at the CCSD(T)-F12/cc-pVDZ-F12//M06-2X/6-311$++$G(2df,2pd) level, which is close to previously reported values (−0.2 to 1.0 kcal mol⁻¹) (Long et al., 2013, 2012; Lv et al., 2019; Bandyopadhyay et al., 2017). As compared with FSA ⋅  ⋅  ⋅ H₂O, the binding free energy of SO₃ ⋅  ⋅  ⋅ H₂O is less stable by 2.6 kcal mol⁻¹, which leads to the equilibrium coefficient of FSA ⋅  ⋅  ⋅ H₂O (2.63 × 10${}^{-\mathrm{18}}-\mathrm{2.49}\times$ 10⁻¹⁹ molecules cm⁻³) (Table S2), being at least 10 times larger than that of SO₃ ⋅  ⋅  ⋅ H₂O (2.45 × 10${}^{-\mathrm{20}}-\mathrm{5.10}\times {\mathrm{10}}^{-\mathrm{21}}$ molecules cm⁻³ within 280.0–320.0 K). Under the available concentrations ([FSA] $=\mathrm{1.0}\times$ 10⁷, [SO₃] $=\mathrm{1.0}\times$ 10³ molecules cm⁻³) (Liu et al., 2019), the concentration of FSA ⋅  ⋅  ⋅ H₂O is 1.36 × 10${}^{\mathrm{6}}-\mathrm{6.80}\times {\mathrm{10}}^{\mathrm{6}}$ molecules cm⁻³ within 280.0–320.0 K, which is 10⁶ times larger than that of SO₃ ⋅  ⋅  ⋅ H₂O (Table S3). Therefore, it is predicted that SO₃ hydrolysis with FSA predominantly take places via the collision between FSA ⋅  ⋅ H₂O and SO₃.

Starting from the FSA ⋅  ⋅  ⋅ H₂O + SO₃ reactants, an eight-membered ring pre-reactive complex SO₃ ⋅  ⋅  ⋅ H₂O ⋅  ⋅   ⋅ FSA (named as IM_{SA_FSA}) is found, and its Gibbs free energy relative to the isolated SO₃, H₂O, and FSA reactants is −2.0 kcal mol⁻¹. In comparison to the previously reported neutral (SO₃ ⋅  ⋅  ⋅ 2H₂O) and acidic complexes SO₃ ⋅  ⋅  ⋅ H₂O ⋅  ⋅  ⋅ X (X= HNO₃, HCOOH, (COOH)₂ and H₂SO₄) (Yang et al., 2021; Long et al., 2012, 2013; Torrent-Sucarrat et al., 2012), the stability of the SO₃ ⋅  ⋅  ⋅ H₂O ⋅  ⋅   ⋅ FSA complex is notably enhanced by 0.2–2.7 kcal mol⁻¹. This is because the positive electrostatic potential (ESP) of the hydrogen atom in the FSA molecule (Fig. S5) is stronger than that in H₂O and X molecules, resulting in stronger intermolecular interactions of SO₃ ⋅  ⋅  ⋅  H₂O ⋅  ⋅  ⋅ FSA. Following the IM_{SA_FSA} complex, the reaction proceeds via TS_{SA_FSA}, leading to the H₂SO₄ ⋅  ⋅  ⋅ FSA formation. For the FSA-catalyzed SO₃ hydrolysis, its Gibbs free energy barrier is 2.5 kcal mol⁻¹, representing a reduction of 22.1 kcal mol⁻¹ relative to the SO₃ hydrolysis without FSA (Table S1). Moreover, it is also 1.0–4.0 kcal mol⁻¹ lower in the free energy barrier than the SO₃ hydrolysis with H₂O, HNO₃, and H₂SO₄ (Table S1). Therefore, FSA is clearly more effective than H₂O, HNO₃, and H₂SO₄ in decreasing the energy barrier for SO₃ hydrolysis. H₂SO₄ ⋅  ⋅  ⋅ FSA is an eight-membered ring complex, similar to H₂SO₄ ⋅  ⋅  ⋅ X complexes in the SO₃ hydrolysis with X. The predicted free energy of H₂SO₄ ⋅  ⋅  ⋅ FSA (−12.9 kcal mol⁻¹) is lower by 10.9 kcal mol⁻¹ compared to that of the IM_{SA_FSA} complex. This indicates the thermodynamic favorability of FSA-assisted SO₃ hydrolysis.

Table 1 Rate constants (cm³ molecule⁻¹ s⁻¹) for SO₃ hydrolysis with and without FSA, H₂O, and X (X= HNO₃, HCOOH, (COOH)₂ and H₂SO₄) within the temperature range of 280–320 K.

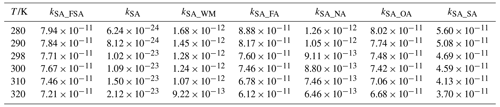
The computed rate coefficients for the hydrolysis of SO₃ with and without FSA, H₂O and X within 280.0–320.0 K are shown in Table 1. As observed at 298.0 K, the rate coefficient for the SO₃ hydrolysis with FSA (k_FSA) is 7.71 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹, surpassing that of the uncatalyzed SO₃ hydrolysis by a factor of 10¹². Additionally, the value of k_FSA at 298.0 K is larger by factors of 60.23 and 84.63 than for the SO₃ hydrolysis with H₂O (k_WM) and HNO₃ (k_NA), respectively. Similarly, within 280.0–320.0 K in Table 1, FSA can compete with HCOOH, (COOH)₂, and H₂SO₄, with the value of k_FSA being larger by factors of 1.02–1.64 than those of k_FA, k_OA, and k_SA. These findings indicate that the catalytic efficiency of FSA in SO₃ hydrolysis surpasses that of H₂O and HNO₃ and is comparable to HCOOH, (COOH)₂ and H₂SO₄.

To consider a contribution of FSA on SO₃ hydrolysis, the rate ratios between FSA- and X-catalyzed SO₃ hydrolysis reactions were calculated, as shown in Table S5. As observed, the SO₃ hydrolysis with H₂O is more favorable than with FSA because the [H₂O] (10¹⁶–10¹⁸ molecules cm⁻³) is significantly greater than [FSA] (10⁷ molecules cm⁻³). When the acid catalysts HNO₃ (10⁹ molecules cm⁻³), HCOOH (10⁸ cm⁻³) and SA (10⁶ molecules cm⁻³) are considered, FSA dominates over them within 280.0–320.0 K as the rate ratio $v_{\mathrm{WM}}/v_X$ is greater than 1. This reveals that the FSA-assisted reaction is indispensable in SO₃ hydrolysis within regions affected by FSA pollution and can significantly promote the hydrolysis of SO₃ within 280.0–320.0 K.

Figure 1 Energy diagrams for SO₃ hydrolysis with FSA at the CCSD(T)-F12/cc-pVDZ-F12//M06-2X/6-311$++$G(2df,2pd) level.

3.2 FSA-catalyzed SO₃ hydrolysis at the gas–liquid nanodroplet interface

Aqueous interfaces are widespread across Earth's atmosphere (Li et al., 2024a; Zhong et al., 2017; Sun et al., 2024; Gao et al., 2024; Dong et al., 2024). The gas–liquid nanodroplet interface serves as a significant site for adsorption and reactions, potentially enhancing atmospheric reaction rates and leading to the emergence of novel mechanisms. However, at the gas–liquid nanodroplet interface, comprehensive understanding of the mechanism for FSA-assisted SO₃ hydrolysis was lacking. Notably, during the 150 ns simulation, molecules of SO₃ and FSA and the SO₃–FSA complex were observed to reside at the interface for 35.8 %, 46.3 % and 40.5 % (Fig. S7), respectively, revealing that the presence of SO₃, the FSA molecule, and the SO₃–FSA complex cannot be ignored at the gas–liquid nanodroplet interface. To further investigate this prediction, we performed BOMD simulations to assess the FSA-assisted hydrolysis of SO₃ at the gas–liquid nanodroplet interface. Similar to the reactions of SO₃ with other acidic species at this interface, the interaction between SO₃ and FSA at the aqueous interface might take place via three pathways: (i) direct interaction of SO₃ with adsorbed FSA, (ii) interaction of adsorbed SO₃ with FSA, or (iii) reaction starting from the SO₃–FSA complex. Given the high reactivity and the brief residency time of SO₃ and FSA at the interface, as evidenced by their short lifetimes (Fig. S8) of only a few picoseconds and rapid formation of SA⁻ and FSA⁻ ion, the simulations have primarily considered the pathway of (iii). Notably, the contribution of pathway (iii) on the aqueous nanodroplet surface is slight due to the low concentration of SO₃–FSA complex (9.49 × 10⁻²³–1.80 × 10⁻²² molecules cm⁻³ within 280.0–320.0 K (Table S2)). However, this focus enabled a deeper understanding of the interfacial dynamics and the mechanisms underpinning these rapid transformations.

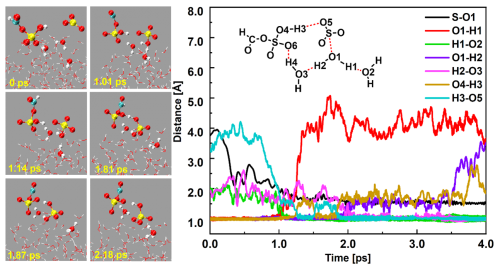
Figure 2 BOMD simulations of HSO${}_{\mathrm{4}}^{-}$ ⋅  ⋅  ⋅ FSA⁻ ⋅  ⋅  ⋅ H₃O⁺ ion pair formation from SO₃ hydrolysis with FSA at the air–water interface. (Top: snapshot structures from BOMD simulations, showing the ion pair formation. Bottom: time evolution of key bond distances S–O1, O5–H3, and O1–H2 during the induced mechanism.)

Unlike the gaseous hydrolysis mechanism of SO₃ with FSA, which occurs through the one-step mechanism, interfacial SO₃ hydrolysis mediated by FSA occurs via a stepwise mechanism (Fig. 2, Fig. S9, and Movie S1), consisting of three steps: (i) SO₃ hydrolysis along with proton transfer outside the ring, (ii) the deprotonation of FSA, and (iii) the deprotonation of H₂SO₄. Specifically, at 0 ps, a loop-structure complex, SO₃ ⋅  ⋅  ⋅ (H₂O)₂ ⋅  ⋅  ⋅ FSA, was initially found with the formations of three hydrogen bonds ($d_{({\mathrm{O}}_{\mathrm{6}}\cdot \cdot \cdot {\mathrm{H}}_{\mathrm{4}})}=\mathrm{1.75}$; $d_{({\mathrm{O}}_{\mathrm{3}}\cdot \cdot \cdot {\mathrm{H}}_{\mathrm{2}})}=\mathrm{1.92}$ and $d_{({\mathrm{O}}_{\mathrm{5}}\cdot \cdot \cdot {\mathrm{H}}_{\mathrm{3}})}=\mathrm{2.39}$ Å) and a van der Waals interaction ($d_{({\mathrm{O}}_{\mathrm{1}}\cdot \cdot \cdot \mathrm{S})}=\mathrm{2.31}$ Å). Then, the loop structure mechanism proceeded along with the simultaneous event of the proton transfer outside the ring. At 1.01 ps, an arrangement resembling a transition state was found for the interfacial SO₃ hydrolysis, characterized by shortening of the S–O1 and O2–H1 bonds and elongation of the O1–H1 bond. By 1.14 ps, the S–O1 and O2–H1 bond lengths had reduced to 1.45 and 0.97 Å, respectively, while the O1–H1 bond had elongated to 1.42 Å, indicating the formation of HSO${}_{\mathrm{4}}^{-}$ and H₃O⁺ ions. Due to the strong acidity of FSA, the H3 atom of FSA was moved to the O5 atom of the HSO${}_{\mathrm{4}}^{-}$ ion at 1.87 ps, leading to H₂SO₄ molecule and FSA⁻ ion. Finally, the deprotonation of H₂SO₄ was completed at 2.18 ps, with the H2 atom of H₂SO₄ moved to one interfacial water molecule inside the ring. In contrast to the SO₃ hydrolysis with FSA in the gas phase, which does not proceed within 100 ps, the reaction at the gas–liquid nanodroplet interface rapidly proceeds within just a few picoseconds. However, considering the harsh reaction conditions between SO₃ and FSA at the interface (i.e., the two molecules must be sufficiently close to form the SO₃–FSA complex) and the high concentration of water molecules at the aqueous interfaces, the direct hydrolysis of SO₃ at the aqueous interfaces is more advantageous than the SO₃–FSA complex reacting on the aqueous surface.

Table 2 Binding free energy (kcal mol⁻¹) for the formation of various clusters at 298 K.

Energies are given in kcal mol⁻¹ and calculated at the M06-2X/6-311$++$G(2df,2pd) level of theory. References are as follows: ^a Zhong et al. (2019). ^b Zhang et al. (2018). ^c Rong et al. (2020). ^d Gao et al. (2023). ^e Liu et al. (2021a). ^f Zhang et al. (2017).

Interestingly, the formation of FSA⁻ and HSO${}_{\mathrm{4}}^{-}$ is highly stable, and their dissociation did not occur within 10 ps. Species such as H₂SO₄ (SA), NH₃ (A), HNO₃, and (COOH)₂ are identified as candidates for particle formation, with the SA–A cluster serving as a significant precursor to atmospheric aerosols. Calculated binding free energies of the corresponding bimolecular clusters were shown in Table 2, where the computed binding free energies agree well with previous values (Zhong et al., 2019). As shown, the interactions of FSA⁻–SA (−21.2 kcal mol⁻¹) and FSA⁻–HNO₃ (−12.1 kcal mol⁻¹) are stronger than that of SA–A (−8.9 kcal mol⁻¹), illustrating that interfacial FSA⁻ and H₃O⁺ ions can attract precursor molecules from the gaseous phase to the aqueous nanodroplet surface, thus facilitating particle growth. Additionally, the enhancing potential of the FSA⁻ ion on the SA–A cluster was assessed by examining the binding free energies of the SA–A–FSA⁻ and SA–A-Y (Y= HOOCCH₂COOH, HOCCOOSO₃H, CH₃OSO₃H, HOOCCH₂CH(NH₂)COOH, and HOCH₂COOH) clusters. The binding free energies of SA–A–FSA⁻ and SA–A-Y clusters listed in Table 2 were consistent with previously reported values (Rong et al., 2020; Zhang et al., 2018, 2017; Gao et al., 2023; Liu et al., 2021a). Notably, compared to SA–A-Y, the binding free energy of SA–A–FSA⁻ (−25.6 kcal mol⁻¹) was larger than 5.2–12.8 kcal mol⁻¹, indicating that the FSA⁻ at the interface exhibits a greater nucleation capability than gaseous molecule Y. Consequently, FSA⁻ is expected to demonstrate enhanced nucleation potential at the gas–liquid interface. A further quantitative assessment of the aerosol nucleation potential of Y ions at the droplet interface could not be conducted, as data on the concentration of Y ions at the interface are not yet available.

Figure 3 ESP-mapped van der Waals surfaces of sulfuric acid (SA), ammonia (A), and formic sulfuric anhydride (FSA). Blue, red, yellow, cyan, and white spheres represent N, O, S, C, and H atoms, respectively, with ESP in kcal mol⁻¹.

3.3 FSA's role in nucleation and cluster formation

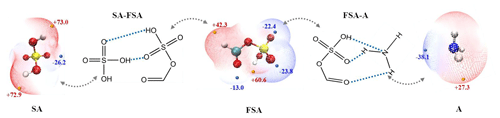
Electrostatic potential (ESP) analysis was conducted to predict the potential hydrogen bond binding sites among FSA, SA, and A. The –OH moiety in the FSA molecule contains a highly electrophilic hydrogen atom, making it a favorable donor site for hydrogen bonds (ESP value: +60.6 kcal mol⁻¹) (Fig. 3). Meanwhile, the terminal oxygen atoms of the –SO₃H and –COOH moieties in FSA can act as an effective hydrogen bond receptor site due to their stronger electronegativity (ESP values: −23.8, −22.4, and −13.0 kcal mol⁻¹). Thus, FSA can form stable clusters by forming hydrogen bonds with SA and A.

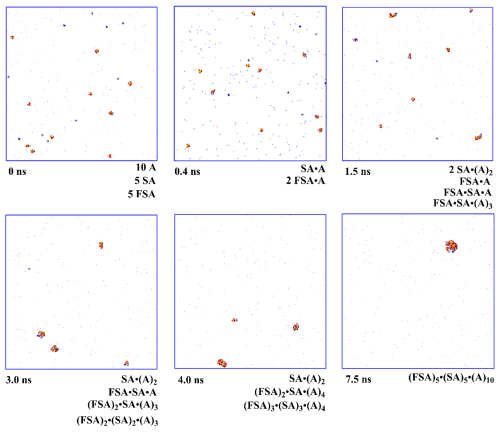
Figure 4 Snapshots of nucleation simulation at 258.15 K from FSA, SA and A using the van der Waals representation, with N₂ and O₂ shown using the line drawing method.

Using MD simulations, the aggregation behavior of FSA with SA and A molecules was investigated at various atmospheric temperatures (Figs. 4 and S10–S11). In these simulation systems, 5 FSA, 5 SA, 10 A, 20 H₂O, 41 O₂, and 154 N₂ molecules were included. Similar to previous studies (Ding et al., 2024; Wei et al., 2022; Li et al., 2023), the concentration of precursors was not considered, and only a qualitative assessment of FSA's involvement in SA–A nucleation was conducted. Notably, the complete stable (FSA)₅ ⋅ (SA)₅ ⋅ (A)₁₀ cluster was observed at all the three simulations temperatures. Figure 4 displayed the snapshots of the nucleation simulation at 258.15 K. The initial simulation at 0 ns shows that there is not effective nucleation, as all molecules in the system are scattered (Fig. 4). Subsequently, at 0.4 ns, various clusters such as SA ⋅ A and FSA ⋅ A clusters were formed. As molecular aggregation continued, the collision between FSA, SA, and A molecules results in the formation of SA ⋅ (A)₂, FSA ⋅ A, FSA ⋅ SA ⋅ A, and FSA ⋅ SA ⋅ (A)₃ clusters at 1.5 ns, and then the SA ⋅ (A)₂, FSA ⋅ SA ⋅ A_, (FSA)₂ ⋅ SA ⋅ (A)₃, and (FSA)₂ ⋅ (SA)₂ ⋅ (A)₃ clusters are formed at 3.0 ns. Next, with further aggregation of the molecules, SA ⋅ (A)₂, (FSA)₂ ⋅ SA ⋅ (A)₄, and (FSA)₃ ⋅ (SA)₃ ⋅ (A)₄ clusters are observed within 4.0 ns. Finally, the molecules fully aggregate to form (FSA)₅ ⋅ (SA)₅ ⋅ (A)₁₀ clusters at 7.5 ns, and this complete cluster stays stable throughout the entire simulation period. It is noteworthy that the number of FSA molecules can gradually interact with SA and A molecules to form relatively large clusters, where hydrogen bonds among SA, A, and FSA play a crucial role. It is also noteworthy that during the nucleation process, the proton transfer between acid and base molecules plays an important role in acid–base nucleation, which cannot be reflected in the classical MD simulation. However, it is initially predicted by classical MD simulation that FSA could act as a “participator” in NPF and could be directly involved in SA–A nucleation. Further predictions regarding the enhancement effect of FSA on SA–A molecular clustering should be conducted below by considering the cluster stability, the formation rate, and the growth pathways.

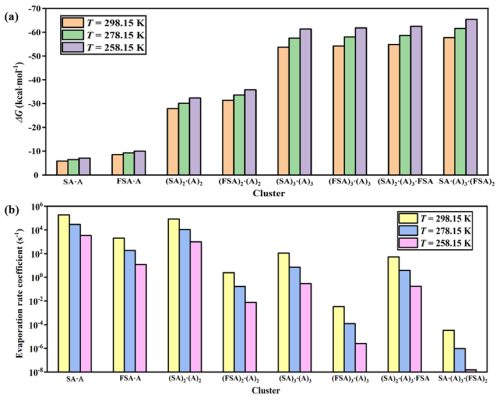
Figure 5 Histogram of (a) Gibbs free energy of formation (ΔG; kcal mol⁻¹) and (b) evaporation rate coefficient (γ; s⁻¹) for key pure SA–A clusters and FSA-containing stable clusters at 258.15, 278.15, and 298.15 K.

Figure 6 Cluster formation rate (J, cm⁻³ s⁻¹) with [SA] =10⁶ molecules cm⁻³ and [A] =10⁹ molecules cm⁻³ at three temperatures (black: 258.15 K, red: 278.15 K, blue: 298.15 K).

3.4 The impact of atmospheric conditions on the thermodynamic clusters stability

The Gibbs free energies of formation (ΔG; kcal mol⁻¹) and evaporation rate coefficients (γ; s⁻¹) of the (FSA)_x(SA)_y(A)_z clusters were analyzed to estimate the thermodynamic stability of the clusters involved in the SA–A–FSA system (Tables S7–S8). The ΔG and γ of the important pure SA ⋅ A clusters and FSA-containing stable clusters were primarily discussed at three temperatures. At 298.15 K, the ΔG value of the SA ⋅ A cluster was 2.69 kcal mol⁻¹ greater than that of the FSA ⋅ A cluster (Fig. 5). Meanwhile, its γ value was about 10² times greater than that of the FSA ⋅ A cluster, suggesting that the FSA ⋅ A cluster is more stable and likely to participate in subsequent growth as an initial cluster. For the (FSA)₂ ⋅ (A)₂ cluster, its ΔG (−31.41 kcal mol⁻¹) was smaller by 3.50 kcal mol⁻¹ than that of the (SA)₂ ⋅ (A)₂ cluster (−27.91 kcal mol⁻¹), with the γ value of the former one (2.48 s⁻¹) at least 10⁴ times lower than that of the latter one (8.35×10⁴ s⁻¹), indicating that the (FSA)₂ ⋅ (A)₂ cluster is more stable than clusters containing SA and A with the same acid–base number. For the (FSA)₃ ⋅ (A)₃ cluster, its γ (3.33 × 10⁻³ s⁻¹) was nearly 10⁵ times lower than that of the (SA)₃ ⋅ (A)₃ (1.11 × 10² s⁻¹) cluster, allowing (FSA)₃ ⋅ (A)₃ to serve as a critical nucleation cluster and participate in subsequent growth. Similarly, at 278.15 and 258.15 K, the FSA ⋅ A, (FSA)₂ ⋅ (A)₂, and (FSA)₃ ⋅ (A)₃ clusters were all more stable than the SA–A binary nucleation clusters with the same acid–base number. Regarding for the (FSA)₂ ⋅ SA ⋅ (A)₃⋅ and FSA ⋅ (SA)₂ ⋅ (A)₃ clusters at 298.15 K, the ΔG values (−57.73 and −54.83 kcal mol⁻¹) were lower than that of (SA)₃ ⋅ (A)₃ (−53.69 kcal mol⁻¹). Simultaneously, the γ values of the (FSA)₂ ⋅ SA ⋅ (A)₃ (3.38 × 10⁻⁵ s⁻¹) and FSA ⋅ (SA)₂ ⋅ (A)₃ (5.28×10¹ s⁻¹) clusters were 10⁶ lower and 2 times lower than that of (SA)₃ ⋅ (A)₃ (1.11×10² s⁻¹) respectively. Likewise, the (FSA)₂ ⋅ SA ⋅ (A)₃ and FSA ⋅ (SA)₂ ⋅ (A)₃ clusters were more stable than the (SA)₃ ⋅ (A)₃ cluster at low temperatures (278.15 and 258.15 K) due to their significantly lower evaporation rates. Therefore, compared to pure SA–A clusters, clusters containing FSA molecules exhibit higher stability and are more likely to engage in nucleation and subsequent cluster growth processes as stable clusters. The clusters of (SA)₃ ⋅ (A)₃, (FSA)₃ ⋅ (A)₃, (FSA)₂ ⋅ SA ⋅ (A)₃, and FSA ⋅ (SA)₂ ⋅ (A)₃⋅ have the potential to further grow into the boundary clusters ((SA)₄ ⋅ (A)₃, (SA)₄ ⋅ (A)₄, (FSA)₄ ⋅ (A)_3, (FSA)₄ ⋅ (A)₄, (FSA)₃ ⋅ SA ⋅ (A)_3, (FSA)₂ ⋅ (SA)₂ ⋅ (A)₃ and FSA ⋅ (SA)₃ ⋅ (A)₃), which have relative lower Gibbs free energy and evaporation rates.

3.5 Influence of particle formation rates under varying temperatures and nucleation precursor concentrations

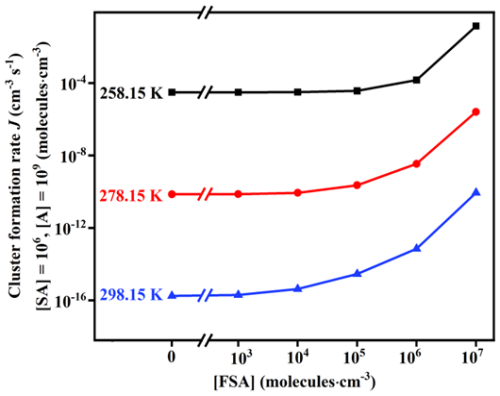
To investigate the cluster formation rate (J; cm⁻³ s⁻¹) of FSA-involved clusters, a range of ACDC simulations were performed using thermodynamic data of the SA–A–FSA clusters at varying temperatures and monomer concentrations ([SA] =10⁴–10⁸, [A] =10⁷–10¹¹ and [FSA] =10³–10⁷ molecules cm⁻³). The values of J for the SA–A–FSA system at varying temperatures (Fig. 6) showed that J increased as the temperature decreased, due to the smaller values of both ΔG and γ at lower temperatures. Specifically, when [FSA] ranges from 10³ to 10⁷ molecules cm⁻³, J can increase by up to 4 orders of magnitude at 258.15 K. At 298.15 K, J shows a significant increase, rising by 5 orders of magnitude. These findings suggest that the formation rate exhibits a substantial variation at high temperatures. Meanwhile, J increased with increasing [FSA], attributable to the formation of more SA–A–FSA clusters. For example, when [FSA] exceeds 10³ molecules cm⁻³ at the high temperature of 298.15 K, J exhibits a significant increase, rising by 5 orders of magnitude. This suggests that the involvement of FSA can strongly enhance the nucleation rate in SA–A-based NPF. In addition to temperature and [FSA], the varying concentrations of SA and A might have a significant impact on the nucleation rate. Figure 7 reveals a clear positive correlation between J and both [SA] and [A]. This can also be attributed to the fact that a higher concentration of nucleation precursors promotes an increase in J.

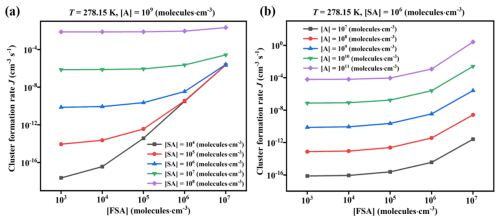
Figure 7 The cluster formation rate (J, cm⁻³ s⁻¹) as a function of (a) [SA] and (b) [A], with different concentrations of [FSA] =10³–10⁷ molecules cm⁻³ at 278.15 K.

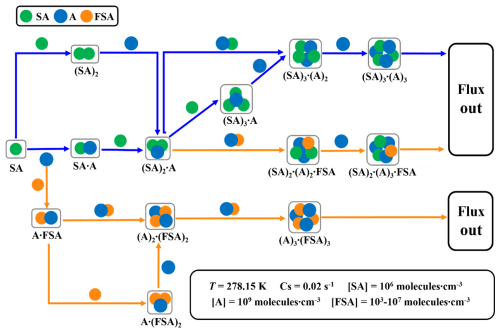
Figure 8 Primary growth pathways of clusters at T=278.15 K, [SA] =10⁶ molecules cm⁻³, [A] =10⁹ molecules cm⁻³, and [FSA] =10³–10⁷ molecules cm⁻³. Blue and orange arrows represent the SA–A-based and SA–A–FSA-based pathways, respectively.

Figure 9 Influence of (a) temperature, (b) [SA], (c) [A], and (d) [FSA] on the relative contribution of the pure SA–A pathway and the FSA-containing pathway to the flux out of the system.

3.6 FSA-driven nucleation enhancement mechanism

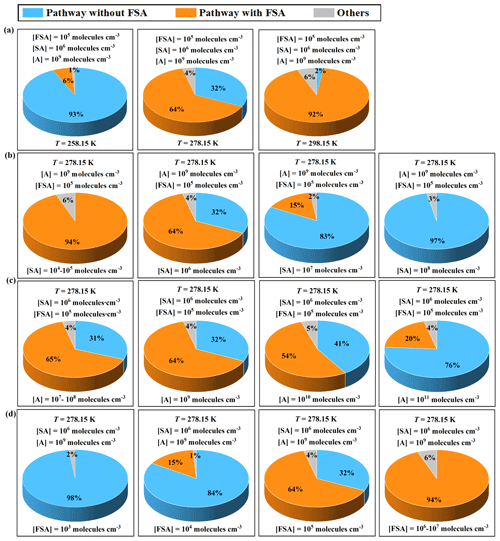
The clusters formed in the simulation system via two main pathways: the pure SA–A pathway and SA–A–FSA pathways (Fig. 8). The pure SA–A nucleation pathway primarily formed stable (SA)₃ ⋅ (A)₃ clusters through monomer addition and collision with SA ⋅ A cluster. The SA–A–FSA nucleation pathway can be categorized into two routes, with FSA acting as a “participator” in the SA–A–FSA-based nucleation process. This is in agreement with the results predicted by the molecular dynamics (MD) simulations. One route involved the initial formation of the stable cluster FSA ⋅ A, which then collided with one FSA molecule or another FSA ⋅ A cluster to form subsequent stable clusters and continue growing. The other route involved the initial formation of the stable (SA)₂ ⋅ A cluster, which then collided with one FSA ⋅ A cluster to form the stable (SA)₂ ⋅ (A)₂ ⋅ FSA, continuing to grow through the addition of an A molecule. Interestingly, at varying temperatures and concentrations of nucleating precursors, the FSA molecule exhibited distinct effects and contributions in the SA–A system. As the temperature increased, the contribution of the SA–A–FSA pathway rose from 6 % to 92 % (Fig. 9a). Therefore, the cluster growth pathway involving FSA appears to prevail at relatively higher temperatures, such as during summer or at lower altitudes. The involvement of FSA in the primary cluster formation pathway may also be influenced by the concentration of the precursors. Specifically, the contribution of the FSA participation pathway exhibited a negative correlation with [SA] or [A] at 278.15 K (Fig. 9b–c). Consequently, the contributions of the SA–A–FSA pathway may be more substantial in the clean atmospheric boundary layer with low [A] and [SA], such as in areas distant from heavy traffic and emission sources of SA. Additionally, the contribution of the SA–A–FSA pathway increases as [FSA] rises (Fig. 9d). At lower [FSA] (10⁴ molecules cm⁻³), the contribution of SA–A–FSA pathway was only 15 %, with cluster growth pathways predominantly governed by the formation of pure SA–A clusters. However, as [FSA] increased to 10⁵ molecules cm⁻³, the contribution of FSA-involved clusters rose to 64 %, making the pathway involving FSA dominant for cluster formation in the SA–A–FSA system. Moreover, the SA–A–FSA mechanism contributed more significantly (94 %) at higher [FSA] concentrations (10⁶–10⁷ molecules cm⁻³). In summary, the contribution of the pathway involving FSA is significantly prevalent in the NPF process with decreasing [SA] and [A] and increasing temperature and [FSA]. These results suggest that FSA could be a significant contributor to SA–A atmospheric NPF, and the SA–A–FSA pathway may prevail in regions with relatively higher temperatures and high FSA emissions, such as in Beijing, Shanghai, and Tangshan, where high concentrations of SO₃ and HCOOH are observed.

4 Summary and conclusions

The potential contribution of FSA to gaseous and interfacial SO₃ hydrolysis, as well as its enhancement of atmospheric particle formation, was investigated. Gaseous results indicated that SO₃ hydrolysis with FSA has a Gibbs free energy barrier as low as 1.5 kcal mol⁻¹ and can effectively compete with SO₃ hydrolysis by HNO₃ (10⁹ molecules cm⁻³), HCOOH (10⁸ molecules cm⁻³), and H₂SO₄ (10⁶ molecules cm⁻³) over a temperature range of 280.0–320.0 K. Interfacial BOMD simulations illustrated that FSA-mediated SO₃ hydrolysis at the gas–liquid interface occurs through a stepwise mechanism and can be completed within a few picoseconds. ACDC kinetic simulations indicated that FSA significantly enhances cluster formation rates in the H₂SO₄–NH₃ system during summer, increasing rates by more than 10⁷ times under conditions of high FSA concentrations and low H₂SO₄ and NH₃ levels. The H₂SO₄–NH₃–FSA nucleation mechanism exhibits a stronger nucleation ability than classical nucleation, making it a promising process for urban polluted environments rich in FSA sources. Meanwhile, the interfacial species formed, such as HSO${}_{\mathrm{4}}^{-}$, H₃O⁻, and FSA⁻, act to attract precursor species (e.g., H₂SO₄, NH₃, and HNO₃) from the gas phase to the nanodroplet interface, thereby facilitating further particle growth. This study broadens our understanding of a novel SO₃ hydrolysis pathway involving FSA in polluted regions, identifies previously overlooked new particle formation (NPF) sources in industrial areas, and deepens knowledge of the atmospheric organic–sulfur cycle.