How does the lifetime of detrained cirrus impact the high-cloud radiative effect in the tropics?

The lifetime of cirrus clouds from deep convection plays an important role in determining their overall cloud radiative effect (CRE). The net CRE of cirrus clouds from deep convection is close to zero over their whole lifetime. This CRE is the result of a near-cancellation of a large shortwave (SW) cooling and large longwave (LW) warming, such that small changes in cirrus properties have the potential to produce a significant net radiative effect. Changes in the atmospheric and sea surface temperature structure, along with changes in anthropogenic aerosol, have been hypothesised to impact the lifetime of detrained cirrus clouds, altering this radiative balance. Constraining the potential CRE response to changes in cirrus lifetime is therefore vital to understand the strength of these proposed climate forcings and feedbacks.

This paper tracks the evolution of detrained cirrus clouds along trajectories from deep convection. The total cirrus CRE in the tropics is found to be warming, at 11.2 ± 0.4 W m⁻². It is found that cirrus clouds along trajectories from oceanic origin convection have a warming CRE of 10.0 ± 0.4 W m⁻². In contrast, cirrus clouds along trajectories from land convection have a warming of 15.9 ± 0.7 W m⁻² throughout their lifetime. This contrast is predominantly due to differences in the diurnal cycle of the initial convection over land and ocean.

A proposed extension to the lifetime of the detrained cirrus leads to changes in the total cirrus CRE in the tropics. In all cases, doubling the lifetime of the detrained cirrus leads to an increase in the total cirrus CRE of 0.6 ± 0.1 W m⁻². Whilst there is uncertainty in the strength of mechanisms responsible for a change in cirrus lifetime, this work provides an important constraint on the impact that any potential lifetime extension may have.

1 Introduction

Deep convective clouds and their associated thin cirrus outflows occur predominantly in the tropical and subtropical regions. Deep convection is characterised by optically thick, high-altitude, and relatively short-lived convective cores. When these cores reach their maximum altitude, large anvil cirrus spread out from them around the areas of convection (Fan et al., 2013). The radiative effect of these convective cores and anvil cirrus clouds is strongly dependent on their optical thickness and ice water path (Berry and Mace, 2014; Hartmann and Berry, 2017), which change over time (Horner and Gryspeerdt, 2023). An important feature of the tropics is the cancellation between large longwave (LW) and shortwave (SW) components of the total cloud radiative effect (CRE) (Wielicki et al., 1996). This cancellation occurs due to the significant LW warming from high-altitude, thin cirrus clouds (typically defined as optical thickness below 0.3; Lee et al., 2009) and the high albedo of optically thick clouds occurring in the same region. This leads to a CRE in cloudy regions that is very similar to non-cloudy regions in the tropics (Ramanathan et al., 1989; Hartmann and Berry, 2017; Harrison et al., 1990). It is unclear whether this cancellation in the tropical CRE is a coincidence or due to feedbacks (Kiehl, 1994; Hartmann et al., 2001). Since the LW and SW CREs are so large, any small percentage change in the magnitudes of either of these components in a future climate could lead to significant changes in the overall CRE in the tropics. It is therefore vital to understand how changes in properties and the lifetime of cirrus clouds from convection affect the overall tropical CRE.

Cirrus clouds cover approximately 60 %–80 % of the tropics (Wylie and Menzel, 1999; Stubenrauch et al., 2006; Sassen et al., 2008; Nazaryan et al., 2008; Lee et al., 2009). Using observational data, Luo and Rossow (2004) found that 50 % of tropical cirrus were detrained cirrus; i.e. they originated out of deep convective cores. Using ground-based data and satellites, Mace et al. (2006) found that 47 % of cirrus observed over Manus Island in the western Pacific originated from deep convection occurring within the past 12 h. Many other modelling and observational studies also show that at least 50 % of tropical cirrus originate from convection (Massie et al., 2002; Gehlot and Quaas, 2012; Riihimaki et al., 2012). Given that detrained cirrus therefore cover approximately 30 %–40 % of the tropics, their radiative effects are an important contributor to the overall CRE balance in the tropics. Luo and Rossow (2004) found that detrained cirrus had longer average lifetimes than in situ cirrus, at around 30 h compared to 19 h for in situ.

In situ cirrus, whilst not formed directly from convective cores, do not exist independently from their detrained counterparts, given that the formation of in situ cirrus relies on water vapour in the upper troposphere, transported via convection. The lifetime and properties of detrained cirrus are affected by any factor that affects the distribution of deep convection (Gasparini et al., 2023). These large-scale factors range from variable sea surface temperatures (SSTs) to the Madden–Julian Oscillation (MJO) (Riley et al., 2011). Additionally, the existence of in situ cirrus will also affect the impact that convective air and moisture has on the free troposphere and lower stratosphere and therefore the development of detrained cirrus (Jensen et al., 2020). For these reasons, the total cirrus CRE in the tropics must be considered when investigating lifetime changes to detrained cirrus. Any change in the properties or amount of detrained cirrus will ultimately affect the average properties of all cirrus in the tropics.

Detrained cirrus and in situ cirrus have different radiative and microphysical properties. Of particular importance is the time dependence of the properties of detrained cirrus compared to in situ cirrus. The properties of detrained cirrus strongly depend on time since cirrus clouds are formed from deep convection (Horner and Gryspeerdt, 2023). Close to convection, the detrained anvil cirrus will be optically thick, with a SW cooling dominating the net CRE. As time since convection increases, the detrained cirrus have a tendency to thin and spread out, decreasing the SW cooling as the albedo decreases (Luo and Rossow, 2004; Hartmann et al., 2018; Gasparini et al., 2019, 2021). The albedo decreases faster than the LW emissivity, contributing to this switch from cooling to warming in the net CRE (Berry and Mace, 2014). The properties of in situ cirrus will vary, depending on the optical thickness and ice water path, as well as the altitude of the clouds (Hartmann and Berry, 2017). In contrast to in situ cirrus, where there is little time dependence on their radiative properties, the time dependence of detrained cirrus is an important factor in determining their CRE. Therefore when calculating the radiative balance in the tropics, any changes in the lifetime of detrained cirrus would have a significant, yet uncertain, impact on the delicate radiative balance in the tropics, given that their properties are such a strong function of time since convection.

In addition to the overall lifetime of the detrained cirrus, the timing of the initial convection plays an important role in determining the total cirrus cloud CRE over the detrained cirrus' lifetime. Jones et al. (2024) showed that the timing of the initial convection has a large effect on the total CRE across the detrained cirrus' lifetime. This is due to the dependence of SW cooling on incoming solar radiation. If convection occurs later in the day when solar insolation is lower, the SW cooling of the younger, thicker anvil cirrus will be less than if the convection occurs in the morning or middle of the day.

The diurnal dependence on the total lifetime CRE of detrained cirrus means that the location where the convection occurs has a large effect on the CRE across its lifetime. Many studies have investigated the diurnal cycle of regional convection (Chen and Houze, 1997; Lopez-Bravo et al., 2023; Krishna et al., 2021). Fewer studies have investigated large-scale differences in the diurnal cycle of deep convection (Ruppert and Hohenegger, 2018). The difference in the diurnal cycle from terrestrial and oceanic convection has been thoroughly studied (Dai et al., 1999; Dai, 2001; Albright et al., 1985; Zuidema, 2003). Of particular importance in this paper is not the mechanisms that govern the behaviour of terrestrial and oceanic convection but the effect that the difference in timing of this convection has on the subsequent radiative properties of the detrained cirrus.

The temperature of anvil clouds will remain the same in a warming climate for a given increase in altitude under the fixed anvil temperature (FAT) hypothesis (Hartmann and Larson, 2002). However, many modelling studies have predicted changes in the cloud fraction of detrained anvil clouds in a warming climate (Bony et al., 2016; Cronin and Wing, 2017; Su et al., 2017). Changes in cloud area can be thought of as changes in the lifetime from a Lagrangian viewpoint, assuming that the advection of the anvil cirrus remains the same (under the stability iris hypothesis, which states that the anvil area reduces as upper tropospheric stability increases, this may not be true), where “time since convection” is a function of distance from a convective core (Horner and Gryspeerdt, 2023). Raghuraman et al. (2024) used observational evidence to investigate these feedbacks, finding a near zero high-cloud amount feedback, providing evidence against an iris feedback.

Although there is some observational evidence for a decrease in cloud area/lifetime with warming SSTs, there is also a large spread in model responses to warming SSTs (Wing et al., 2020), with some models showing an increase in high-cloud amount with warming (Ohno and Satoh, 2018; Satoh et al., 2012; Tsushima et al., 2014). Gasparini et al. (2021) used Lagrangian trajectories and model studies to investigate the lifetime of anvil cirrus in present and future climate. They found the lifetime of the anvil cloud to be 15 h, significantly shorter than that of Luo and Rossow (2004), who found anvil lifetimes of 30 h. These studies are sensitive to the choice of methods and thresholds for cirrus detection used. For example, Luo and Rossow (2004) determine cirrus lifetime to be the point at which the cloud fraction along a trajectory first drops below 20 % of the maximum cloud fraction along the trajectory (nominally 100 %). There is no robust definition of when detrained cirrus have dissipated; therefore there is some spread in the given lifetimes of detrained cirrus in the literature.

Crucially, Gasparini et al. (2021) found no difference in the lifetime of anvil cirrus in the present climate compared to a 4K warming scenario. Beydoun et al. (2021) also found a similar negligible change in anvil lifetime using RCEMIP-style models. It should be noted that neither of these studies represents all the processes that would impact cirrus lifetime, particularly the lack of diurnal cycle. More observational studies are needed to assess the impact that these particular processes may have on the lifetime of detrained cirrus clouds. Overall, there is much uncertainty in the response of high-cloud area and lifetime to a warming climate.

Drivers of lifetime changes in detrained cirrus relate to the properties of the deep convection itself. Studies have investigated the aerosol invigoration hypothesis (Abbott and Cronin, 2021; Fan et al., 2013; Koren et al., 2010, 2005; Rosenfeld et al., 2008), which states that an increase in aerosol concentration should lead to increased updrafts in deep convection, leading to higher-altitude and, potentially, longer-lived anvil cirrus. Herbert and Stier (2023) provide an observational study investigating the impact of aerosol optical depth (AOD) on deep convection over the Amazon; however this is limited to short timescales, close to the convection. A much earlier study by Lin et al. (2006) also shows, using observations, a correlation between AOD and convective strength (via higher cloud tops). There is still more work needed to understand the full impact that aerosol invigoration may have on the life cycle of detrained cirrus as they evolve beyond the deep convection itself. A full critical evaluation of aerosol invigoration is given by Varble et al. (2023).

There are many factors that impact the decay, and therefore lifetime, of detrained cirrus clouds. Gasparini et al. (2022) used idealised cloud-resolving models to investigate the impact that the diurnal cycle has on the cirrus lifetime. They found that tropical anvil clouds forming in the day are more widespread and longer-lasting than those formed at night, due to the shortwave radiative heating during the day that lofts and spreads the anvil clouds. During the night there is an increase in ice nucleation; however this does not compensate for the entrainment of dry air that also acts to reduce anvil lifetime. Sokol and Hartmann (2020) also found that anvils thin more rapidly during the night due to the net radiative cooling eroding the cloud top. In both cases, it is found that the timing of convection is an important control on the lifetime of the detrained cirrus cloud.

This paper seeks to understand the extent to which changing the lifetime of detrained cirrus impacts the overall tropical CRE. If the effect is small, then many of the drivers of anvil development mentioned above may not be important when considering changes in total cirrus CRE in a warming tropics. This question is answered by first characterising the overall high-cloud CRE in the tropics as a combination of the CRE of the detrained cirrus and in situ cirrus distributions. The distribution of detrained cirrus is then modified by artificially altering its lifetime, and the impact that this has on the overall CRE is investigated. How the CRE of detrained cirrus from land convection differs from oceanic convection is also investigated and how their lifetime extensions change the overall tropical CRE. Answering these questions will allow us to investigate how sensitive the overall CRE in the tropics is to changes in the lifetime of the detrained cirrus clouds, enabling us to constrain future changes due to climate change or anthropogenic aerosol emissions.

2 Methods

2.1 Characterising cirrus evolution

The time since convection (TSC) algorithm (Horner and Gryspeerdt, 2023) assigns each grid box in the tropics a time in hours since that grid box last experienced a convective event, as defined by the presence of a deep convective core. The deep convective cores are identified from the 3-hourly International Satellite Cloud Climatology Project (ISCCP)-H dataset (Rossow et al., 2017) based on their cloud fraction, cloud optical thickness, and cloud top pressure data. This characterises each grid box as belonging to a distinct cloud regime, including a deep convective regime. The deep convective grid boxes are then advected forward in time following the ERA5 reanalysis wind field data (Hersbach et al., 2018) averaged between 200 and 300 hPa, with the associated TSC increasing as the air parcels are advected. As shown in Horner and Gryspeerdt (2023), these trajectories typically remain at this pressure level for the entirety of the detrained cirrus lifetime. Where new deep convection occurs (locations updated every 3 h), the TSC is reset to zero and advected as new convection. For a full description of the algorithm, see Horner and Gryspeerdt (2023). This method is used to characterise cirrus properties as a function of TSC to see how these cloud properties change as they move from deep convection through anvil cirrus to thin cirrus and eventually dissipate. The study period for this paper is between 2000–2016; however any results involving CERES data only go back to 2001.

2.2 Cirrus type flag: land/ocean and in situ/detrained

Air parcels along trajectories from deep convection contain detrained cirrus clouds, or they may contain in situ cirrus. Detrained cirrus, also known as liquid origin cirrus (Luebke et al., 2016), are defined as cirrus that have detrained directly from a deep convective core, such as thick anvil cirrus, with the air parcel remaining cloudy along the entire trajectory up to that point. In contrast, in situ cirrus were not directly detrained from a convective core but appear along the trajectories after the detrained cirrus have dissipated.

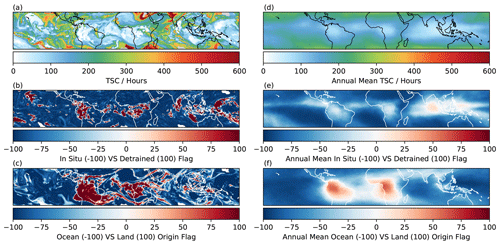
Figure 1 Sample TSC snapshot from 9 April 2008 at 00:30 UTC. (a) Time since convection (TSC). (b) In situ versus detrained cirrus flag values. (c) Land versus ocean convective origin flag. (d–f) 2008 annual mean for (a)–(c).

The TSC algorithm assigns a flag to each air parcel depending on properties at the origin of the convection. At TSC = 0, all air parcels are considered detrained, with the transition to an in situ state occurring when the ISCCP-H high-cloud fraction along a trajectory becomes less than 10 %. After this point, the air parcel is then considered in situ and remains as such until it is replaced by newer convection. These in situ air parcels may contain a cirrus cloud, which by definition would be an in situ cirrus cloud, or they may not contain any cirrus cloud at all. While the detrained air parcels by definition must be cloudy (and so contain a detrained cirrus cloud), the in situ air parcels could be cloud free and hence do not necessarily contain an in situ cirrus cloud. Instead, it indicates the origin of any potential cirrus cloud in a grid box.

When two trajectories enter the same grid box, the air that has more recently experienced convection (with a lower TSC) is deemed to be a more important indicator of cloud properties. As a result, the properties of the younger convection define that grid box.

When two trajectories diverge and a grid box is left empty, the value for that grid box is interpolated as the average of the surrounding eight grid boxes. In practice, the standard deviation of the flag values of the air parcels in the eight surrounding grid boxes is usually small. However, where there is a mixture of air parcel types in the surrounding boxes, this is represented in the flag value associated with the air parcel. The value of a detrained cirrus flag is 100, and an in situ flag is −100, with mixtures taking a value in between. For example, if six of the eight surrounding grid boxes contain detrained cirrus flags with a value of 100, and two contain in situ flags with a value of −100, the flag value of the divergent grid box will become 50; i.e. it is more likely to be a detrained cirrus air parcel but with decreased confidence due to the interpolation in the TSC algorithm. In all subsequent analyses, only air parcels with a high confidence (a magnitude larger than 50) are considered. This accounts for 88 % of all pixels, with 12 % being removed due to uncertainty.

This method is also adapted to store properties associated with the initial convection. The convective origin flag marks each air parcel with either a land-origin or an ocean-origin flag. This flag remains on the air parcel until it is replaced by a flag from newer convection. It is important to note that this flag does not just indicate whether a cirrus cloud is currently over land or ocean but rather whether the convection it originated from occurred over land or ocean. For this reason, it is often the case that land-origin convection exists over the ocean and vice versa (Fig. 1c).

Figure 1 shows (a) a snapshot TSC map from 00:30 UTC on the 9 April 2008, (b) a snapshot of the associated cirrus type flag, and (c) a convective origin flag. As values are interpolated during the advection algorithm generating the TSC and associated flags, the flag values are not a binary classification. Instead, the positive or negative sign indicates the flag value (i.e. positive cirrus type flag indicates detrained, negative in situ), and the magnitude can be considered an indication of the confidence in that flag following the merging of trajectories over time.

2.3 High-cloud radiative effect

The high-cloud CRE is calculated using the CERES SYN1deg L3 1-hourly dataset (NASA/LARC/SD/ASDC, 2017). It is necessary to isolate the CRE of the cirrus clouds from the effects of low clouds in order to investigate how the radiative properties of the high clouds alone change with TSC. To isolate the radiative effect of the high clouds, the monthly mean combined low-cloud and clear-sky albedo (hereafter referred to as the “background albedo”) are subtracted from the instantaneous all-sky albedo to give an estimated high-cloud albedo. To identify the background albedo, the ISCCP histograms are used to isolate grid boxes where the high-cloud fraction, as defined as the top three pressure bins in the ICCP-H joint histogram, is less than <1 %, thereby attributing the albedo to the low cloud and surface only. The monthly mean background is used in order to give sufficient coverage to co-locate regions of high cloud and background cloud. Equation (1) is used to isolate the albedo of the high clouds only:

$$\begin{array}{}\text{(1)}& {\mathit{\alpha }}_{\mathrm{high}}={\mathit{\alpha }}_{\mathrm{all}\mathrm{\_}\mathrm{sky}}-{\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\mathrm{bkg}},\end{array}$$

where α_high is the high-cloud albedo, α_{all_sky} is the all-sky albedo, and ${\stackrel{\mathrm{‾}}{\mathit{\alpha }}}_{\mathrm{bkg}}$ is the monthly mean background albedo. The background albedo is defined as the α_{all_sky} in regions with a <1 % high-cloud fraction. The SW high-cloud CRE can then be calculated using

$$\begin{array}{}\text{(2)}& \mathrm{SW}\mathrm{\_}{\mathrm{CRE}}_{\mathrm{high}}=F_{\downarrow }\times {\mathit{\alpha }}_{\mathrm{high}},\end{array}$$

where F_↓ is the incoming solar radiation. One shortcoming in using the monthly mean background albedo, and subtracting this from the instantaneous all-sky albedo, is that this introduces regions where there is a negative albedo and therefore an apparent positive instantaneous high-cloud SW CRE. This occurs in regions where the all-sky albedo is less than the monthly mean background albedo. Figure 2 shows (panel a) an instantaneous all-sky CRE, (panel b) the monthly mean background albedo (in this case the month of March), and (panel c) the instantaneous high-cloud CRE calculated from these.

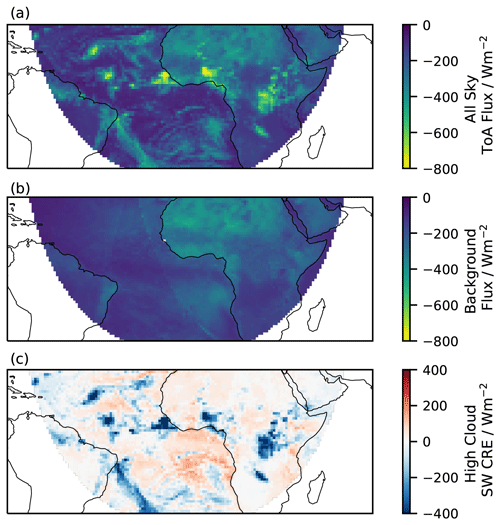
Figure 2 Snapshot of (a) all-sky SW CRE for 12:00 UTC on 6 July 2008, (b) monthly mean background SW CRE (March), and (c) high-cloud SW CRE for 12:00 UTC on 6 July 2008.

As seen in Fig. 2c, in regions with little to no high cloud, the SW CRE can be positive, since the all-sky instantaneous albedo is less than the annual mean background albedo. These non-physical regions disappear in the annual mean but are required to avoid biasing the mean high-cloud albedo. The LW CRE is calculated as the all-sky LW minus the clear-sky LW, due to the small LW CRE of low clouds.

3 Results

3.1 TSC distribution

Figure 1b shows the instantaneous detrained versus in situ flag map, and panel (e) shows the yearly mean flag values. The detrained cirrus in red are centred around regions of active convection. These extend beyond the original convective cores, much like anvil cirrus would extend beyond the active convection. All other regions contain in situ air parcels; i.e. if cirrus were to occur in these regions, they would be classed as in situ in origin.

Any region in Fig. 1e where the mean value is above zero is a region where detrained cirrus clouds are more often found. Compared to Fig. 1d, these occur at low TSC values, close to convection. The likelihood of finding detrained cirrus air parcels is highest over the Maritime Continent. This is because there is much more sustained convection over the ocean, which means convection here has a smaller diurnal variation. This allows for a constant supply of detrained air from convection over the course of 24 h. This compares to terrestrial regions over South America and central Africa, where the convective cycle is more diurnal. This means there are large periods in the day where there is little convection, and the detrained origin air parcels are advected away and replaced by in situ air parcels from the ocean.

Figure 3a shows the fraction of grid boxes containing detrained or in situ air parcels, as a function of TSC. Figure 3b shows the total counts of both origin types. Note that the scallop-like pattern along the lines in Fig. 3a is due to the temporal resolution of ISCCP data, meaning that convection is only initiated every 3 h. At low TSC values, most air parcels along trajectories contain detrained cirrus clouds. At ≈ 30 h, the number of grid boxes containing detrained cirrus or in situ air parcels is approximately equal. For example, at 30 h from convection, approximately 50 % of the detrained cirrus have dissipated. At higher TSC values than this, new cirrus clouds that occur along the trajectory are more likely to be in situ in origin.

The median lifetime, that is the TSC at the point a grid box switches from containing a detrained cirrus air parcel to an in situ air parcel, of a detrained cirrus cloud is 36 h. The modal lifetime is 25 h. These values are in agreement with Luo and Rossow (2004), who found the average detrained cirrus lifetime to be 30 ± 16 h.

The standard deviation of the lifetime is found to be 30 h. This is much larger than that found by Luo and Rossow (2004) since it does not track specific convective events but rather tracks all air from convection.

Figure 1d shows the instantaneous snapshot of the land- and ocean-origin air parcels. The majority of the tropics contain ocean-origin air parcels (blue), as the majority of convection that occurs in the tropics occurs over the ocean. Therefore for a given detrained cirrus cloud, it is more likely to be oceanic than terrestrial in origin.

The land-origin air parcels occur predominantly over land or near the coast. Figure 1f shows the mean land- and ocean-origin value. There are large regions over the South Atlantic Ocean that contain more frequent land-origin air parcels than average. This is due to wind fields that carry air from land-origin convection over the ocean, making it more likely to find land-origin detrained cirrus in this region compared to the rest of the global oceans.

The average air parcel origin map (Fig. 1f) shows which type of air parcel is most common for a particular region. For example, land air parcels are most likely seen over oceans in the SE Atlantic off the coast of Africa. Figure 1c shows that these instances of land-origin air parcels can occur in many regions over ocean and can travel long distances from any land source.

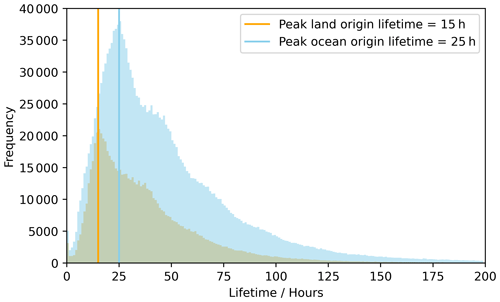
Figure 4 shows the distribution of the lifetime of the land- and ocean-origin detrained cirrus. The modal lifetime for land-origin detrained cirrus is 15 h, compared to 25 h for ocean-origin detrained cirrus. It should be noted that many of the very low lifetimes occur when convection replaces itself between time steps. However, these instances have a negligible impact on the median lifetime. Removing these very low lifetimes (lifetimes less than 5 h) increases the median lifetime by less than 1 h.

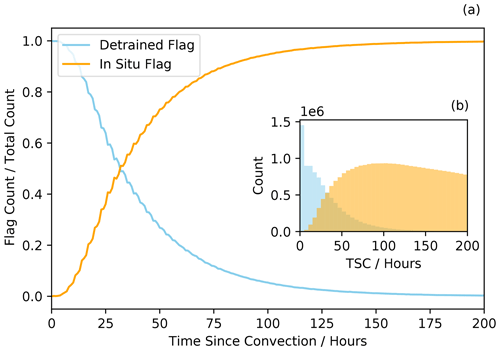
Figure 3 Distribution of detrained and in situ cirrus flags as a function of TSC. (a) The count of each flag as a fraction of the total TSC distribution. (b) The total distribution of each flag.

The difference in land- and ocean-origin detrained cirrus lifetime is significant. The land-origin lifetimes are much shorter than the ocean-origin lifetimes, likely due to the timing of the initial convection. Recalling that most land convection occurs closer to the evening, this means that the thicker anvil exists for most of its life during solar night. This is compared to the oceanic convection that sees a small morning peak, followed by a much greater proportion occurring during the day than at night. This means that for ocean, most of the thick anvil will spend its evolution in the solar day. Detrained cirrus is likely to dissipate much faster during the night due to, among other factors, the entrainment of dry air acting to reduce anvil lifetime (Gasparini et al., 2022). These lifetime differences also support findings by Sokol and Hartmann (2020), who found that anvils thin more rapidly during the night due to the net radiative cooling that erodes the cloud top. As well as the lifetimes being different between land-origin and ocean-origin detrained cirrus, the distribution shown in Fig. 4 shows an oscillation in the rate of decay for both origin cirrus.

Figure 4 Total distribution of the lifetimes of ocean-origin and land-origin detrained cirrus.

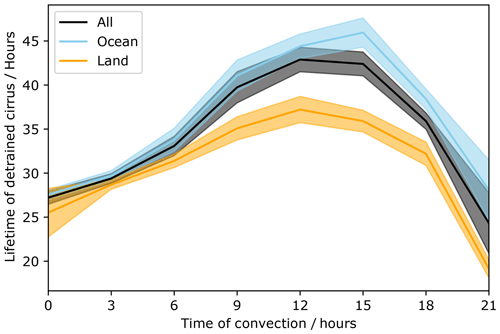
Figure 5 shows the median lifetime of detrained cirrus clouds as a function of the local solar time that the deep convection occurred at. This further shows a strong dependence of the lifetime of the detrained cirrus on the diurnal cycle of convection, with cirrus that originate from convection that occurs during the night having a shorter lifetime than cirrus that occur from convection during the day. For the all-origin case, cirrus that occur from convection occurring between 12:00–15:00 LST (local solar time) have a lifetime of 45 h on average. In contrast, cirrus that originate from convection occurring between 21:00 and midnight have an average lifetime of around 24 h, almost twice as short. This is the case for both land- and ocean-origin cirrus as well, with land-origin cirrus on average having a shorter lifetime, particularly for the longest-lived cirrus. This shows that the difference in the lifetimes as a function of time of initial convection is not simply showing a shift in the distribution of convection from ocean to land throughout the day. Whilst this figure does not control for other factors, such as the changing strength of convection throughout the day, it is further evidence for the hypothesis that cirrus decay quicker through the night than they do during the daytime.

Figure 5 Lifetime of detrained cirrus as a function of the timing of the initial convection for all-, land-, and ocean-origin cirrus. The error bars represent the interannual variability over the study period (2000–2014).

3.2 Cloud radiative effect – detrained versus in situ

Figure 6 shows the LW, SW, and net high-cloud CRE for detrained, in situ, and net of all air parcels as a function of TSC. They are weighted in each TSC bin by the relative occurrence of each bin. The total net CRE is negative (a cooling) at low TSC values, becoming a warming after ≈ 5 h, reflecting the shift from optically thick deep convective core and anvil cirrus to thinner cirrus. For the first 10 h, the mean high CRE is the same as the detrained cirrus CRE, as almost all air parcels at this point are considered detrained (Fig. 6).

The low occurrence of in situ air parcels at low TSC accounts for the erratic jumps in the weighted mean of the in situ CRE close to convection (Fig. 6). As these in situ air parcels become more common, the mean high-cloud CRE approaches the in situ CRE, although some differences remain even at several days from convection. This shift in the high-cloud CRE is most evident when considering the LW and SW CRE separately. The detrained clouds have a larger SW cooling, LW warming, and stronger net positive CRE than the in situ air parcels. There is still a small trend in the CRE of the in situ air parcels, even when their occurrence is low close to convection. This is likely due to shallower, mid-tropospheric convection that is not identified as deep convection but is still contributing to the CRE along trajectories.

After the initial cooling, the net high-cloud CRE peaks at ≈ 15 W m⁻² at 10 h since convection. There are some small oscillations in the CRE due to the diurnal cycle of convection formation (see Fig. 8). As the proportion of in situ air parcels increases as a function of TSC, the mean net CRE decreases, as the in situ air parcels have a smaller CRE than the detrained cirrus clouds. At low TSC values, the change in high-cloud CRE is dominated by the changing properties of the detrained cirrus clouds. As TSC increases, the change in total cirrus CRE reflects the change in distribution away from detrained cirrus clouds, towards in situ cirrus air parcels.

The total lifetime CRE of the high clouds for the entire tropics is calculated as the average the CRE along trajectories, weighted according to the distribution of TSC values in the tropics and the latitude that the values occur at (see Fig. 3b inset). The total lifetime radiative effect of high clouds in the tropics along trajectories from deep convection is 11.2 ± 0.4 W m⁻². The total radiative effect of the detrained cirrus is found to be 8.9 ± 0.8 W m⁻², whereas the total radiative effect from the in situ cirrus is found to be 11.5 ± 0.4 W m⁻². Although when summed over their whole lifetime detrained cirrus are more cooling than in situ, extending their lifetime still increases the overall warming because they have a greater instantaneous warming at longer TSC values than the in situ cirrus.

Figure 6 The cloud radiative effects (net, LW, SW) as a function of the TSC for both detrained, in situ air parcels and the weighted sum of both. The dotted line shows the modal lifetime of the detrained cirrus.

3.3 Cloud radiative effect – land versus ocean

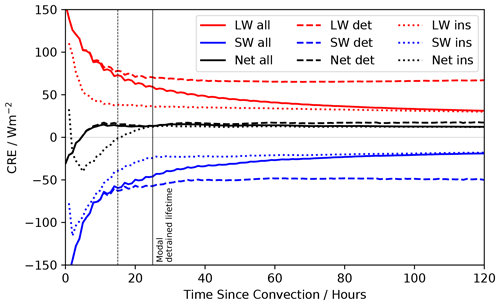
There are significant differences in the CRE of air parcels that originate from convection over land versus those that originate over the ocean. Figure 7 shows the LW, SW, and net CRE for ocean-origin air parcels and land-origin air parcels. It is found that 20 % of air parcels are of land origin, and 80 % are of ocean origin. The ocean-origin evolution is very similar to the all-origin evolution since the majority of the air parcels from convection are oceanic in origin. The largest differences in the land versus ocean CRE occur at low TSC values, driven predominantly by differences in the SW cooling in the early stages of the evolution. These differences arise due to the differences in timings of convection and the strong diurnal cycle in convection over land. Figure 8 shows the timing of convection from land-origin versus ocean-origin convection. There is a significant peak in convective activity over land in the late afternoon into the early evening. This is in contrast to oceanic convection which occurs comparatively uniformly throughout the day, with a smaller peak in the morning, which adds to the contrasting SW diurnal cycle between land and ocean.

Some of the difference is also due to the contrast in surface albedo between land and ocean. However, Fig. S3 in the Supplement shows that when controlling for the albedo, by only considering cirrus that exist over the ocean, there is still a significant difference in the SW CRE between land- and ocean-origin cirrus. This further suggests that differences in the net CRE are driven predominantly by differences in the timing of the initial convection. Further work is needed to quantify the contribution of both the albedo contrast and the diurnal cycle difference.

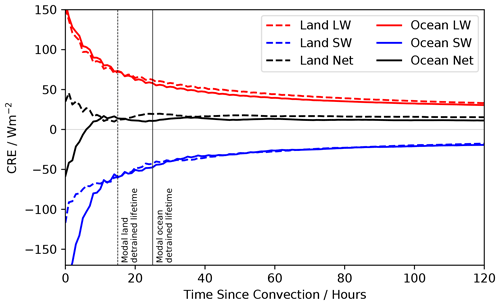
Figure 7 Total LW, SW, and net CRE as a function of TSC. Dotted lines show the land-origin CRE, and solid lines show the ocean-origin CRE. The vertical lines show the modal lifetimes of the ocean and land detrained cirrus.

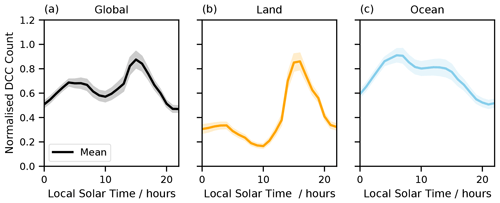
Figure 8 Diurnal cycle of tropical deep convection, normalised such that the maximum of each cycle is 1, for (a) the entire globe, (b) land-origin convection, and (c) ocean-origin convection. The error bars correspond to the standard deviation of the interannual variability between 2000 and 2016.

The timing of this convection over land means that the SW cooling from the optically thick cirrus is minimised compared to oceanic convection. Therefore the total net CRE is positive in the first hours from convection. By the time the incoming solar radiation is maximised, the cirrus have already thinned sufficiently that the SW cooling is significantly smaller than the LW warming. As a result, the land-origin air parcels have a positive CRE throughout its entire life cycle. The timing of terrestrial convection is shown to play a vital role in determining the total CRE of the detrained air parcels (Jones et al., 2024).

The differences in the LW warming between land- and ocean-origin air parcels are less clear. In the early stages of the convection, they are similar. After 20 h, the land-origin air parcels appears to have a slightly larger LW warming than the ocean-origin air parcels. This could be due to stronger convection occurring over land, leading to higher-altitude cirrus producing a larger LW warming (Takahashi et al., 2017).

Over the entire range of lifetimes, the weighted average of the land-origin CRE is 15.9 ± 0.6 W m⁻², and the ocean-origin has a total CRE of 10.0 ± 0.4 W m⁻². This difference in the lifetime CRE is almost entirely due to the differences in the timing of the initial convection and as such the lack of SW cooling that occurs in land-origin cirrus compared to ocean-origin cirrus.

3.4 Lifetime adjustments

Given that the CRE of detrained cirrus clouds is very different to the CRE of in situ cirrus air parcels (Fig. 6), the lifetime of the detrained cirrus clouds is very important when determining the total tropical CRE. As mentioned above, the median lifetime of the detrained cirrus is approximately 36 h, with a modal lifetime of 25 h. This is shown separately for land- and ocean-origin cirrus in Fig. 4. This is defined as the mean TSC when the air parcel changes from detrained to in situ.

The impact of extensions to detrained cirrus lifetime on the tropical CRE can be estimated through an artificial modification of the detrained cirrus distribution. The lifetime of the detrained cirrus can be artificially extended by modifying the fractional distribution of the detrained cirrus in Fig. 3, a novel method introduced in this work. The original distribution is stretched along the TSC axis by a given percentage, and this new distribution can be thought to represent the distribution of detrained cirrus in this new extended lifetime regime. This is shown in Fig. 9. By stretching the distribution along the x axis by some factor, the amount of detrained cirrus is artificially increased for a given TSC.

It is important to note that the TSC distribution is not changed when the lifetime of detrained cirrus is extended, just the radiative properties of the cirrus as a function of TSC. This decouples the cloud evolution from the convective occurrence and large-scale flow. This change, therefore, maintains the overall shape in the distribution of TSC whilst increasing the proportion of detrained cirrus air parcels for a given TSC. This increases the mean detrained cirrus lifetime by the prescribed factor.

Increasing the distribution is analogous to increasing the mean lifetime of each detrained cirrus by the same percentage. Figure 9 shows that for a 50 % increase in the detrained cirrus lifetime, this shifts the point at which the number of in situ and detrained parcels is equal from around 30 h to just under 50 h.

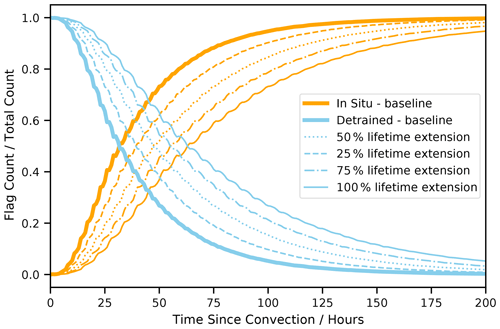
Figure 9 The fractional distribution of the detrained versus in situ air parcels. Dotted lines represent various distributions when the detrained cirrus are extended by a percentage.

As the all-cirrus LW, SW, and net CREs along trajectories from convection are a weighted average of the CRE contributions of detrained cirrus and in situ air parcels, changing the lifetime of the detrained cirrus changes the weighting and thus total CRE along the trajectories. With detrained cirrus having a stronger warming effect, extending their lifetime increases the overall warming of tropical cirrus clouds.

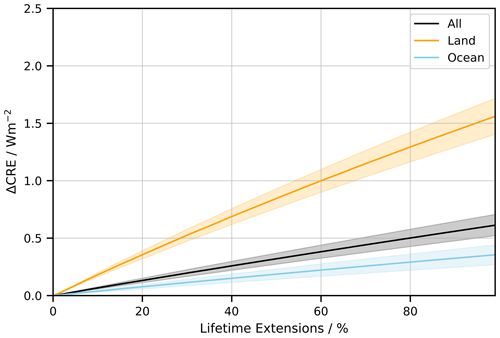
Figure 10 Change in CRE for all-, land-, and ocean-origin air parcels for a given percentage increase in the lifetime of the detrained cirrus clouds.

Figure 10 shows how the total tropical CRE changes when the lifetime of the detrained cirrus is increased. In all cases, the tropical CRE increases almost linearly for a given increase in the lifetime of the detrained cirrus. For a doubling in the lifetime of all-origin detrained cirrus, the tropical CRE increases from a baseline of 11.2 ± 0.4 to 11.8 ± 0.5 W m⁻². The uncertainties given represent the interannual variability in the increase in CRE for a given increase in detrained cirrus lifetime. In practice these uncertainties are likely larger due to the inherent uncertainties in the initial calculation of CRE; however these are normalised to a baseline. Therefore, there is no uncertainty in the lifetime extension when the lifetime extension is 0 h.

The increase in the high-cloud CRE is similar for an increase in the lifetime of ocean-origin detrained cirrus. This is to be expected given the greater proportion of convection originating over ocean versus land. A doubling in the ocean-origin detrained lifetime leads to an increase in the tropical CRE of 0.4 ± 0.1 W m⁻², from a baseline CRE of 10.0 ± 0.4, to 10.0 ± 0.4 W m⁻².

Interestingly the increase is not linear over time, with the first 50 % lifetime extension increasing the all-origin CRE by 0.02 W m⁻² more than the final 50 % increase. One reason for this is the decreasing difference between the in situ CRE and detrained CRE at longer TSC values. Therefore, any adjustment to the relative distributions at longer TSC will have a slightly smaller impact than initial adjustments to the shorter lifetimes.

For land-origin cirrus the increase in tropical CRE is much greater for a given increase in the detrained cirrus lifetime. A doubling in the land-origin detrained cirrus lifetime increases the tropical CRE from a baseline of 15.9 ± 0.7 to 17.5 ± 0.7 W m⁻². This is because land-origin detrained cirrus are much more warming than ocean-origin cirrus, particularly at low TSC values (Fig. 7). This is due in part to a smaller SW cooling in land-origin detrained cirrus because of differences in the timing of convection. This means that increasing the proportion of detrained cirrus for a given TSC increases the overall CRE by a larger amount than the same increase for ocean-origin detrained cirrus.

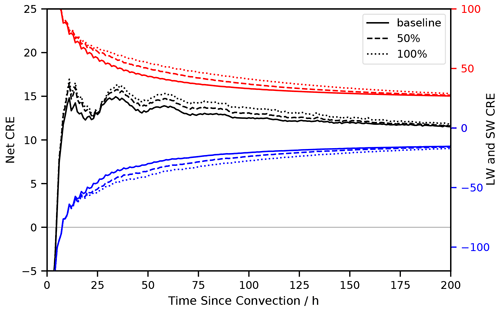
Figure 11 Total net (left axis) and LW and SW (right axis) CRE as a function of TSC. The dashed and dotted lines represent a 50 % and 100 % increase in the lifetime of detrained cirrus respectively. Note the separate axis for net, LW, and SW radiative effects, introduced here to show the changes in CRE for each lifetime extension more clearly.

Figure 11 shows the LW, SW, and net CRE as a function of TSC, for a baseline, as well as a 50 % and a 100 % increase in the lifetime of detrained cirrus. This shows an increase in the net CRE at all TSC values given an increase in the lifetime of detrained cirrus. At very low TSC values there is little change in the net CRE for an increase in lifetime. This is because at these low TSC values, detrained air parcels account for almost all the air parcels. Therefore there is no change in the relative distributions of detrained versus in situ air parcels (see Fig. 3) and no change in the overall CRE at low TSC values.

4 Discussion

In this work, the overall high-cloud CRE, including both detrained origin cirrus and in situ origin air parcels (which may contain in situ cirrus), was found to be 11.2 ± 0.4 W m⁻². However, there are still a number of uncertainties that need addressing. These uncertainties fall into three main categories: (a) isolating the radiative effects from high clouds, (b) the distinction between detrained and in situ air parcels, and (c) the method for extending the lifetime.

In order to isolate the radiative effects of high and low clouds, this paper attempts to consider the contributing radiative effect of the low clouds by calculating the monthly mean “background albedo”, which is then subtracted from the instantaneous all-sky albedo to give the “high-cloud” albedo. The background albedo is the all-sky albedo in regions with no high cloud. This method gives an approximate high-cloud SW CRE. However, it relies on the assumption that the monthly mean background albedo is approximately representative of the instantaneous background albedo, if it were possible to be calculated for everywhere in the tropics at each time step.

As the annual mean background albedo is subtracted from the instantaneous all-sky albedo, there are occasions where the annual background is greater than the all-sky albedo (Fig. 2). This produces a negative high-cloud albedo and thus a positive SW cooling value. It can be assumed in these regions that this occurs when the all-sky albedo is close to the clear-sky albedo value, with the total cloud fraction being lower than the average low-cloud fraction. This assumes that there is little correlation between the low- and high-cloud fraction. For a further discussion of cloud overlap statistics, see Tompkins and Giuseppe (2015). The impact of these cases averages to zero when calculating the annual mean SW high-cloud CRE and is less important for this work's analysis as they occur at large TSC values in regions where there is little high cloud. This situation occurs in regions where the average low-cloud cover is high and therefore the average background albedo is high. Therefore, if a trajectory is observed at this location that contains an optically thin high cloud, and little to no low cloud, the observed albedo will be lower than the average albedo, thus resulting in a “negative” high-cloud SW CRE. It is also known that the ISCCP cloud type histograms may over-attribute the top-of-atmosphere (TOA) cooling to low clouds (Stephens et al., 2018). This may lead to a positive (warming) bias in the results in this work; therefore it should be understood that these results represent an upper bound. However this bias is likely small in comparison to other uncertainties mentioned above.

The second area of uncertainty in this work surrounds the definition of detrained cirrus. This work defines the end of a detrained cirrus lifetime, and the beginning of the in situ air parcels, as the point at which a cloud along a trajectory from deep convection moves below 10 % cirrus cloud fraction for the first time. Any cirrus cloud that then appears along a trajectory after this point is defined as in situ in origin. This is similar to Luo and Rossow (2004), who define the end of their cirrus lifetime as the point at which the cirrus cloud reaches $\mathrm{1}/\mathrm{5}$ of the maximum cloud fraction along the trajectory. Changing the definition of detrained cirrus would not change the overall high-cloud CRE. However, it does change the calculated lifetime of detrained cirrus, which is shown in Fig. S1. There is no universal definition for “detrained” or “anvil” cirrus, and as such the lifetimes of these clouds vary depending on how they are defined. Nevertheless, the lifetimes in this work fall within the expected ranges given in the literature (Luo and Rossow, 2004), and as shown in Fig. S2, the final values for the change in CRE for a given lifetime extension are not particularly sensitive to the threshold used to define the convection.

The method used to extend the lifetime of the detrained cirrus is relatively idealised, insofar as it models a lifetime extension as a change in the distribution of detrained cirrus at the expense of in situ cirrus. Moreover, the extension in the distribution modifies the distribution mostly at the tail end of the detrained cirrus lifetimes, meaning that the oldest detrained cirrus are the ones that see the largest increase. The purpose of this work was not to assess the methods through which a lifetime extension would occur. Instead, the aim was to provide a bound on the impact that increasing the lifetime of the detrained cirrus would have on the tropical high-cloud CRE. By modifying the distribution to represent an increase in lifetime, particularly in a way that may impact the longer-lived detrained cirrus more than the short lived cirrus, we do provide such an upper bound. Any modification to the shorter lived cirrus would not increase the CRE by as much, as they are already more cooling. In reality, any physical routes through which the detrained cirrus lifetime is extended will likely increase the total CRE by less than the values we provide here. Further work is needed to assess the mechanisms through which lifetime extensions might occur and what the range of impacts this may have on the CRE is. For example, the lifetime could change due to a stronger clustering of convective cores (Jones et al., 2024) or increased updrafts via aerosol invigoration (Abbott and Cronin, 2021). Each of these mechanisms may impact the lifetime in a distinct way from the idealised setup in this work. Investigating these mechanisms and the specific impacts they had on the lifetime would make for an interesting comparison study to the idealised extension proposed in this work and would be a necessary addition to put these results into context, as well as developing a stronger constraint on the potential changes of the CRE.

As well as showing the difference in detrained cirrus CRE due to the origin of the convection, this work shows how extending the lifetime of the detrained cirrus changes the overall lifetime CRE. In this work, the lifetime is a simple distribution, and extending the lifetime is merely a case of extending the distribution at the expense of in situ air parcels. This assumes that every cirrus cloud in the tropics is either detrained or in situ, and these are distinct from each other; i.e. an increase in detrained air parcel amount should correlate with a decrease in in situ air parcel amount. The purpose of extending the lifetime is not to obtain a concrete value of the CRE for a given lifetime extension but instead to indicate the trend in CRE for an increase in lifetime. This helps to bound estimates of how much the lifetime of a detrained cirrus would need to change to significantly affect the tropical high-cloud CRE.

This work finds that increasing the lifetime of the detrained cirrus increases the overall high-cloud CRE in the tropics, resulting in an overall warming. This is because on average the detrained cirrus have a larger net CRE than the in situ air parcels. For a 50 % increase in the lifetime, the average CRE of tropical cirrus increases by 0.3 ± 0.1 W m⁻². Comparing this to aerosol invigoration studies which have shown lifetime extensions of detrained cirrus on the order of 30 % (Zang et al., 2023), it may be the case that aerosol invigoration may not have a large impact on the total tropical CRE; however more work is needed to constrain the lifetime extension from aerosol invigoration, which is currently highly uncertain.

The average lifetime of detrained cirrus clouds is found to be approximately 36 h, similar to that found by Luo and Rossow (2004). This implies that increasing the average lifetime of detrained cirrus clouds by 15 h would increase the overall high-cloud CRE by approx. 0.3 ± 0.1 W m⁻².

This increase is larger for land-origin convection, which increases by approx. 0.8 ± 0.1 W m⁻² for a 15 h increase in lifetime, and smaller for ocean-origin convection, which increases by approx. 0.2 ± 0.1 W m⁻².

5 Conclusions

The lifetime of detrained cirrus clouds from convection plays an important role in determining the overall detrained CRE in the tropics, and this may impact the total high-cloud CRE in the tropics. Small changes in the evolution of these clouds, driven either by their initial conditions or the meteorological environment, have been hypothesised to produce large responses in the high-cloud CRE, making understanding this evolution essential to constrain both climate forcings and feedbacks. By tracking the evolution of cirrus clouds throughout the tropics as they move away from convective events and isolating the high-cloud CRE from the background albedo variation caused by low clouds, this work characterises the life cycle of the cirrus CRE using satellite observations. Defining the lifetime of detrained cirrus based on the point along a trajectory following convection where the high-cloud fraction drops below 10 % (representing the time when the detrained cirrus has dissipated), the impact of cirrus formation mechanisms on CRE is isolated. By tracking the properties of the initial convection, this method also allows the impact of the initial convection on the CRE to be investigated. The tracking approach used in this work differs from previous studies, such as Jones et al. (2024), using ISCCP data with a much longer time record, as well as covering the entirety of the tropics, without explicitly tracking individual clouds at all. This allows for regional variations such as the land–ocean contrast to be thoroughly investigated.

Most detrained air parcels remain in the central tropical belt, close to active convection, while in situ air parcels exist throughout the tropics (Fig. 1b, e). The high-cloud radiative effect is calculated by subtracting the variability in the background albedo due to changes in low clouds from the overall CRE (Fig. 2). Calculating the total high-cloud CRE as the weighted mean CRE along trajectories from deep convection gives a total high-cloud topical CRE of 11.2 ± 0.4 W m⁻².

Air parcels along trajectories from oceanic convection are compared to those from detrained convection (Fig. 1c and f). It is found that air from land convection exists over large regions of the oceans, and air from oceanic convection often exists over land. The high-cloud CRE along trajectories from land-origin convection is 15.9 ± 0.7 W m⁻², compared to 10.0 ± 0.4 W m⁻² for cirrus along trajectories from ocean-origin convection. Strong differences in the timing of the initial convection over land and ocean (Fig. 8) lead to these differences in the net CRE of detrained cirrus clouds as a function of TSC. Detrained cirrus clouds from land are found to have a net warming across their entire lifetime, as land convection occurs much later in the day than oceanic convection (Fig. 8). This reduces the SW cooling from the thick anvils at low TSC values compared to oceanic convection, which detrained from convection much earlier in the day when the SW cooling is still significant. This is similar to the results of Jones et al. (2024), who showed the importance of the diurnal cycle in determining the lifetime CRE of detrained cirrus clouds.

The lifetime of detrained cirrus cloud differs depending on whether the cirrus originate from land convection or ocean convection. On average, detrained cirrus clouds originating from land convection have shorter lifetimes than detrained cirrus clouds that originate from ocean convection, at 15 and 25 h respectively (Fig. 4). It is also shown that the lifetime of detrained cirrus is strongly dependent on the timing of the initial convection, with cirrus that detrained in the night being shorter lived than those that originate from daytime convection (Fig. 5). This is true for both land- and ocean-origin detrained cirrus. This is further evidence that the timing of the initial convection impacts the lifetime of the detrained cirrus (Sokol and Hartmann, 2020; Gasparini et al., 2022).

The lifetime of detrained cirrus clouds is artificially increased by stretching the distribution of the detrained cirrus air parcels at the expense of the in situ air parcels (Fig. 9). These extended distributions are then used as the weights when calculating the total cirrus CRE in the tropics. It is found that increasing the lifetime of the detrained cirrus clouds increases the total CRE in the tropics almost linearly. For example, a 50 % increase in the detrained cirrus lifetime, from an average of 36 to 54 h, increases the total tropical CRE from 10.0 ± 0.4 to 10.4 ± 0.4 W m⁻² (Fig. 10).

The impacts of lifetime extension of detrained cirrus air parcels are calculated for both land-origin and ocean-origin cirrus. Increasing the land-origin detrained cirrus lifetime by 50 % increases the total land-origin CRE in the tropics by 0.8 ± 0.1 W m⁻². On the other hand, increasing the ocean-origin detrained cirrus lifetime by 50 % increases the total ocean-origin CRE in the tropics by only 0.2 ± 0.1 W m⁻². These contrasts arise because of the differences in the CRE of land-origin and ocean-origin detrained cirrus in the early stages of their development. Ocean-origin detrained cirrus have a negative (cooling) CRE at low TSC; therefore any increase in the lifetime of the detrained cirrus also increases the time spent cooling, thus dampening the warming impact they may also have at longer TSC. Land-origin detrained cirrus are warming at all stages of their development; therefore any increase in their lifetime will amplify their warming impact (see Fig. 7).

While this work shows the potential for cirrus lifetime changes to modify high-cloud CRE in the tropics, further work is required to assess and constrain these potential changes in detrained cirrus lifetime. In particular, work is needed to assess how specific mechanisms through which detrained cirrus lifetimes may be extended (such as aerosol invigoration) would impact the overall CRE. The impact of meteorological or anthropogenic drivers (such as aerosol invigoration) on the lifetime of anvil cirrus, and therefore the overall tropical cirrus CRE, must be bounded to fully constrain the magnitude of this effect.