Surface temperature dependence of stratospheric sulfate aerosol clear-sky forcing and feedback

Stratospheric sulfate aerosol originating from explosive volcanic eruptions can perturb the radiative budget for several years. However, the understanding of the state dependence of aerosol forcing and its effect on the radiative feedback is still incomplete. Using a one-dimensional radiative–convective equilibrium model of the tropical atmosphere, we quantify the contributions to clear-sky forcing and feedback from absorbing and re-emitting longwave radiation, stratospheric heating, and enhanced stratospheric water vapour. We show that aerosol forcing has a stronger surface temperature dependence than CO₂ forcing. At surface temperatures from 280 to 300 K, the aerosol forcing becomes less negative (weaker) with increasing surface temperature because its longwave component becomes more positive. Additionally, the radiative feedback is less negative in the presence of the aerosol. The dependence of the feedback parameter on the aerosol concentration and of the forcing magnitude on temperature arises from the same process: aerosol absorbs in the spectral range in which the atmosphere is optically thin and thus spectrally masks the temperature-dependent surface emissions. The study highlights the critical role played by the spectral nature of aerosol longwave absorption in determining the surface temperature dependence of the forcing and in reducing the feedback in comparison to an atmosphere without stratospheric aerosol.

1 Introduction

Strong volcanic eruptions can inject sulfur into the stratosphere, where it subsequently forms sulfate aerosol (Hansen et al., 1992; Robock, 2000). By scattering incoming shortwave (SW) radiation, the sulfate aerosol increases the planetary albedo, which cools the surface. To a lesser extent, sulfate aerosol also absorbs longwave radiation, which leads to a greenhouse effect and partly offsets the cooling (Andronova et al., 1999).

Understanding how aerosol forcing depends on the climate state is crucial for analysing the climatic effects of volcanic eruptions and the effectiveness of geoengineering attempts in different climate states and at different locations of the Earth. The effects of climate change on volcanic aerosol forcing (Aubry et al., 2022) in the light of changes to plume height (Aubry et al., 2021), anthropogenic pollution (Hopcroft et al., 2017), ocean stratification (Fasullo et al., 2017), and ocean and atmospheric circulation (Aubry et al., 2021; Zanchettin et al., 2013) have been studied, with contrasting predictions on the change in forcing magnitude. Andronova et al. (1999) showed that the longwave component of the stratospheric sulfate aerosol (“aerosol” hereafter) forcing increases with surface temperature but did not provide an explanation.

It has been shown that stratospheric sulfate aerosol forcing causes lower global-mean surface temperature change compared to CO₂ forcing of the same magnitude (Hansen et al., 2005; Boer et al., 2006; Marvel et al., 2016; Gregory et al., 2016; Günther et al., 2022). This disparity was attributed to the stronger feedback to aerosol forcing originating from differences in sea surface temperature (SST) response patterns (Günther et al., 2022) and hence tropospheric stability (Salvi et al., 2023). In addition to circulation and pattern effects, purely radiative effects, such as longwave absorption and re-emission by greenhouse gases, have been found to cause a state dependence of forcing and feedback to changes in CO₂ levels (Jeevanjee et al., 2021; Stevens and Kluft, 2023). In this work we explore if such a state dependence of radiative forcing and feedback also exists for aerosol and if the radiative effects from stratospheric aerosol loading may modify different radiative feedbacks in the atmosphere.

Insights into CO₂ forcing and radiative feedback provide a starting point to understanding the state dependence of aerosol forcing and the modulation of the feedback. CO₂ forcing originates from the increase in the emission height in the CO₂ absorption band and can be viewed as a swap of tropospheric or surface emissions with emissions from the stratosphere. Thus, the magnitude of CO₂ forcing depends primarily on the temperature contrast of the two layers and the quantity of water vapour (Huang et al., 2016; Jeevanjee et al., 2021; Stevens and Kluft, 2023). Drawing parallels to well-understood CO₂ forcing, the aerosol longwave absorption has a similar greenhouse effect. However, the forcing may show a different state dependence for three reasons. First, climate-relevant volcanic eruptions typically have an aerosol profile that peaks in the stratosphere in contrast to the well-mixed CO₂. Second, sulfate aerosol is a broadband absorber, while CO₂ absorbs in a relatively narrow and prominent spectral band. Third, stratospheric heating by the aerosol and the increase in water vapour concentration can also contribute to the forcing. In this paper we will disentangle and quantify these effects.

To summarize, we address the following questions in this work. How much do the individual aerosol radiative effects contribute to the aerosol forcing? How much does the presence of aerosol modulate the feedback? How does this contribution change with surface temperature? We use radiative transfer calculations and idealized climate simulations with the one-dimensional radiative–convective equilibrium (RCE) model konrad (Kluft et al., 2019; Dacie et al., 2019) to address these questions. The model's simple formulation allows for an analysis which is unhindered by complex interactions present in general circulation models (GCMs). We do not aim to provide strictly quantitative statements about the actual magnitude of clear-sky aerosol forcing and feedback in nature. Instead, we aim for a mechanistic understanding of the clear-sky radiative changes instigated by stratospheric sulfate aerosol and how they shape the forcing and feedback at climate states with different surface temperatures. Hence, the numbers we provide should not be mistaken for estimates of the real-world radiative feedback or climate sensitivity.

2 Methodology

2.1 Model setup

The study is performed with konrad (Kluft et al., 2019; Dacie et al., 2019), a one-dimensional radiative–convective equilibrium model. We choose this model as it offers high flexibility in controlling the atmospheric composition, vertical humidity profiles, surface attributes, and lapse rate, allowing us to isolate important processes and provide a mechanistic understanding. konrad also makes it possible to run simulations at a high vertical resolution to numerical equilibrium at low computational cost.

konrad accounts for convection by adjusting the temperature profile to a moist-adiabatic lapse rate. This convective adjustment results in a distinct convective top. Below the convective top, the atmosphere is in radiative–convective equilibrium and the surface temperature sets the temperature profile. Above the convective top, the atmosphere is in a radiative equilibrium.

We use 512 pressure levels in the atmosphere with a spacing that increases linearly in logarithmic pressure space ranging from 1000 to 0.1 hPa (Kluft et al., 2019). In the troposphere, the relative humidity (RH) is fixed at 80 % following Kluft et al. (2021). Above the cold point tropopause (i.e.  in the stratosphere), the water vapour volume mixing ratio is set to its value at the cold point. The pattern of surface warming and changes in circulation are not accounted for in the one-dimensional simplification.

konrad uses the Rapid Radiative Transfer Model for GCMs (RRTMG, Mlawer et al. (1997) to calculate radiation. RRTMG has been shown to produce results similar to line-by-line calculations for surface temperatures up to 305 K (Kluft et al., 2019, 2021). Following Wing et al. (2018), the solar constant is set to 551.58 W m⁻² at a zenith angle of 42.05°, resulting in a top-of-the-atmosphere solar insolation of 409.6 W m⁻², which is equal to the annual mean insolation of the tropics (0 to 20°). The surface albedo is set to 0.2 to account for the missing cloud albedo in our clear-sky setup. We use a fixed vertical distribution of ozone in pressure space following the RCEMIP protocol (Wing et al., 2018). Hence, the amount and distribution of ozone remains the same irrespective of the atmospheric state.

The Easy Volcanic Aerosol (EVA) forcing generator (Toohey et al., 2016) is employed to generate a vertical profile of aerosol optical properties (extinction, single scattering albedo, asymmetry parameter) for the RRTMG bands, which is then prescribed in the model. We utilize the aerosol optical profile, representing spatially averaged values between 23° N and 23° S, 6 months after equatorial eruptions with injection masses of 10 and 20 Tg sulfur. We name these cases “Tg10” and “Tg20” respectively. The largest extinction coefficients are found between 18 and 25 km altitude, as seen in Fig. 1a. While forcing due to a realistic volcanic eruption would first increase and then decrease within a time frame of only a few years, we study an idealized abrupt stratospheric sulfate aerosol forcing, which is static. The simplification allows us to examine how the radiative forcing and modulation of the radiative feedback emanating from sulfate aerosol injection in the stratosphere depend on surface temperature.

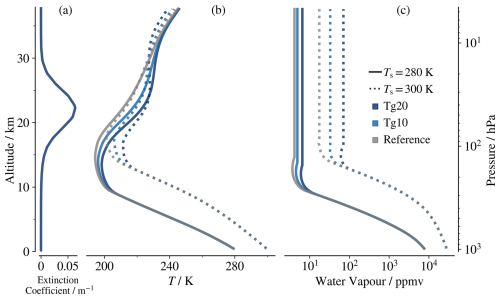
Figure 1 Vertical profiles of (a) aerosol extinction coefficient at 550 nm in the Tg20 experiment, (b) temperature, and (c) water vapour concentration at equilibrium for T_s= 280 K (solid) and T_s= 300 K (dotted). While shades of blue illustrate aerosol injection of different strengths, the grey lines show the reference state. The altitude represented in (a) is calculated from the atmospheric state with T_s= 300 K.

2.2 The forcing–feedback framework

We analyse the aerosol perturbation within the forcing–feedback framework (Gregory et al., 2004; Forster et al., 2021). If a climate state in equilibrium is perturbed, for example, by a change in CO₂ concentration or introduction of an aerosol layer, this will result in a radiative forcing F (positive downwards) and an imbalance in the top-of-atmosphere (TOA) net flux N. To regain equilibrium (i.e. ΔN=0), the climate system adapts via a radiative response R=λΔT_s (positive downwards) mediated through a change in surface temperature T_s. The energy balance of the evolving climate state can be represented by

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }N=F+\mathit{\lambda }\mathrm{\Delta }{T}_{\mathrm{s}}.\end{array}$$

F, also referred to as effective radiative forcing (Forster et al., 2016), includes rapid adjustments such as changes to the stratospheric temperature. The feedback parameter λ (Hansen et al., 1997; Rugenstein and Armour, 2021) quantifies the ability of the system to adjust to the imposed perturbation through a change in surface temperature. A negative λ drives the system to a new equilibrium state, thus representing a stable climate.

An estimate of the change in surface temperature at the new equilibrium ΔT_eq due to the imposed perturbation can be computed as

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{T}_{\mathrm{eq}}=-{\displaystyle \frac{F}{\mathit{\lambda }}}.\end{array}$$

2.3 Simulations

We consider two types of perturbation of the climate system over a temperature range of 280 to 300 K: (a) a halving of CO₂ concentrations and (b) the introduction of two different sulfate aerosol loadings formed from sulfur injections of 10 and 20 Tg. For the CO₂ forcing scenario, the CO₂ concentration is abruptly changed throughout the atmospheric column, and for the aerosol forcing scenario, the aerosol optical properties are prescribed abruptly.

To calculate the effective forcing, we run konrad with a fixed surface temperature and pre-industrial concentrations for greenhouse gases other than CO₂ until it reaches a radiative–convective equilibrium. A simulation with no aerosol injection and a vertically uniform CO₂ concentration of 348 ppmv serves as a reference state throughout the study. After perturbing the system, the new equilibrium state is compared to the initial equilibrium to evaluate the effective forcing (Shine et al., 2003; Hansen et al., 2002). For these perturbations, the TOA forcing is given by

$$\begin{array}{}\text{(3)}& F=N^{\mathrm{p}}-N^{\mathrm{o}},\end{array}$$

where N^p and N^o are the net TOA fluxes from the perturbed and the reference climate state for the given surface temperature.

To evaluate the feedback parameter, the surface temperature is changed by 2 K, and the system is allowed to equilibrate. The final equilibrium states corresponding to surface temperatures of T₁ and $T_{\mathrm{2}}=T_{\mathrm{1}}+\mathrm{2}\mathrm{K}$ are used to evaluate the feedback parameter at $(T_{\mathrm{1}}+T_{\mathrm{2}})/\mathrm{2}$ as (Seeley and Jeevanjee, 2021; Kluft et al., 2021)

$$\begin{array}{}\text{(4)}& \mathit{\lambda }={\displaystyle \frac{N_{T_{\mathrm{1}}}-N_{T_{\mathrm{2}}}}{T_{\mathrm{1}}-T_{\mathrm{2}}}}.\end{array}$$

In Eq. (4), the difference is calculated between the TOA fluxes at two different surface temperatures (“Cess sensitivity”,  Cess et al., 1989). We compute this either in the presence of the radiative perturbation or in the reference state.

Calculating climate sensitivity using Eq. (2) with F and λ from fixed surface temperature simulations can yield erroneous values as it does not account for the changes in F and λ when the system and its surface temperature evolve to a new equilibrium state. Thus, in addition to fixed surface temperature simulations, we perform simulations where the atmospheric column is coupled to a slab ocean with prognostic surface temperature. We run these simulations to equilibrium to diagnose the climate sensitivity to aerosol forcing more accurately (equivalent to the “Charney sensitivity” for CO₂ forcing). The slab ocean model used in this study is a simple heat sink in equilibrium with the atmosphere. The depth of the slab ocean only affects the time to reach equilibrium (Kluft et al., 2019) and is set to 10 m.

3 The aerosol radiative effects

In our analysis of forcing and feedback we will follow the nomenclature of Stevens and Kluft (2023). They define sensitive emitters as those whose emission temperature changes with surface temperature. The surface is the most trivial example of a sensitive emitter. Invariant emitters are emitters whose emission temperature is independent of surface temperature. According to Simpson's law (Simpson, 1928), the tropospheric water vapour at a fixed relative humidity is an example of an invariant emitter. Spectral masking happens when invariant emitters mask the response of sensitive emitters.

In our study, we elaborate on the three longwave radiative effects of stratospheric aerosol as follows.

1. Longwave absorption and re-emission: longwave absorption by the aerosol layer has a greenhouse effect. The resulting positive forcing is proportional to the difference in emission temperatures of the surface (or troposphere) and the aerosol layer. The temperature of the stratosphere (and aerosol layer) changes very little with the surface temperature, as seen in Fig. 1b, making the aerosol an almost invariant emitter. Thus, it partly masks the change in surface emissions with surface temperature.

2. Stratospheric heating: introducing a weak absorber in the stratosphere that absorbs in spectral regions where the atmosphere is optically thin results in radiative warming (Shine and Myhre, 2020). Figure 2 shows that sulfate aerosol absorbs in the spectral range of the optically thin atmospheric window, i.e. where the troposphere emits at high temperatures. Hence, temperatures increase in the lower stratosphere and upper troposphere (Fig. 1b). As a result, the atmosphere emits more longwave radiation at those heights than in the reference state not only because of a higher concentration of the absorber (included in our point 1) but also because all emitters in that altitude region emit at higher temperatures. This effect adds a negative contribution to the TOA radiation balance. Note that this aerosol effect is unlike the effect of an increase in CO₂, which absorbs strongly in a spectral region where the tropospheric emissions originate from relatively low temperatures and, therefore, cools the stratosphere.

3. Water vapour increase: due to the fixed relative humidity in the troposphere, the upper tropospheric warming increases the water vapour concentration in the upper troposphere and stratosphere (Joshi and Shine, 2003; Löffler et al., 2016; Kroll et al., 2023), as is also shown in Fig. 1c. Previous studies have shown that stratospheric water vapour plays an important role in modulating the rate of global warming (Solomon et al., 2010; Wunderlin et al., 2024). However, it has also been noted that the stratospheric water vapour increase caused by a warmer tropopause reduces the strong negative forcing from stratospheric aerosol only weakly (Kroll et al., 2021).

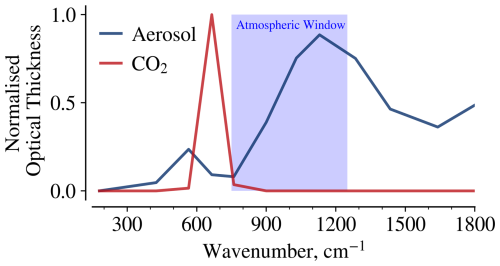
Figure 2 Spectral longwave absorption for aerosol and CO₂. The blue shaded region shows the atmospheric emission window between 750 and 1250 cm⁻¹ where water vapour is optically thin.

Using konrad we diagnose the contributions from each aerosol longwave effect individually. For example, the effect of the aerosol's longwave absorption and re-emission alone is determined by the change in the TOA radiative flux caused by introducing the aerosol layer while fixing the temperature and specific humidity profiles from the reference atmospheric state. Similarly, the change in the TOA radiative flux caused by prescribing the changed temperature profile without introducing the aerosol layer or the changed specific humidity profile provides the contribution from the stratospheric warming caused by the aerosol.

In the following sections, we analyse how these three effects come together to produce the differences in the forcing and feedback between aerosol injections and CO₂ concentration change. We also analyse their dependence on the surface temperature. The aerosol forcing and feedback are calculated from Eqs. (3) and (4), and examined by decomposing them into their longwave and shortwave components.

4 Forcing

Figure 3 shows the surface temperature dependence of the shortwave and longwave components of the forcing due to changes in CO₂ levels and aerosol. The net CO₂ forcing arises from the longwave component and is almost independent of temperature between 280 and 300 K. This behaviour is in agreement with previous studies (Jeevanjee et al., 2021; Kluft et al., 2021). The aerosol forcing is negative in the shortwave and positive in the longwave.

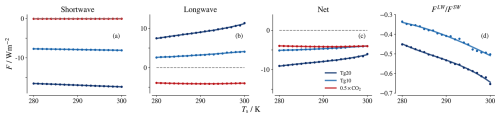
Figure 3 Surface temperature dependence of CO₂ and aerosol forcing F decomposed into shortwave (a) and longwave (b) contributions, as well as the total net (c) forcing. Panel (d) shows the ratio of the longwave and shortwave components. Cubic fits for each set are plotted as solid lines.

The net aerosol forcing (sum of longwave and shortwave components) is negative due to the stronger negative forcing in the shortwave bands. However, it becomes less negative with increasing temperature as the positive longwave component has a more pronounced temperature dependence. Between 280 and 300 K, the Tg20 aerosol forcing changes approximately from −9 to −6 W m⁻² (34 %) and the Tg10 aerosol forcing changes from −5 to −4 W m⁻² (20 %). The 0.5×CO₂ forcing changes only by 3 % in the same temperature range. The aerosol forcing shows a stronger temperature dependence than the forcing due to a change in CO₂ levels.

4.1 Forcing in the shortwave bands

As shown in Fig. 3a the shortwave aerosol forcing becomes slightly more negative at higher surface temperature. This can be explained by the fixed relative humidity, which leads to an increased quantity of water vapour in the atmosphere at higher surface temperatures. Introducing a reflective aerosol layer atop of a more absorbing background results in a more negative forcing, because reflection makes a bigger difference over a darker background. The water vapour increase due to the tropopause warming by the aerosol layer is also larger at higher surface temperatures, as shown in Fig. 1c, which further increases the atmospheric absorption. This is in agreement with the results from a multi-model study by Kashimura et al. (2017), who showed that the decrease in water vapour with surface cooling results in a weaker forcing.

4.2 Forcing in the longwave bands

The longwave component of the aerosol forcing (F^LW) becomes more positive with increasing surface temperature. This arises due to an interplay of the different aerosol effects on longwave radiation as described in Sect. 3. Below, we analyse the individual contributions of these effects decomposed using radiative transfer calculations. The corresponding results are shown in Fig. 4.

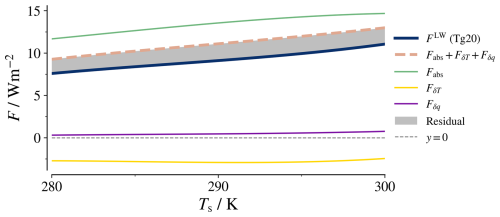
Figure 4 The components of aerosol longwave forcing F^LW from radiative transfer calculations for the Tg20 case. Only the cubic fits through the data points are shown.

Firstly, aerosol can absorb and emit longwave radiation. Hence, introducing an aerosol layer results in an increase in outgoing longwave radiation (OLR) emanating from atmospheric levels with much lower temperatures than the surface. This reduces the total outgoing longwave radiation and results in a positive forcing. We call this component F_abs. It represents the instantaneous forcing caused by the aerosol, i.e. the direct radiative effect in the absence of adjustments. The stratospheric heating and subsequent moistening, which we describe in the following, are stratospheric adjustments. Together, the instantaneous forcing and the adjustments constitute the effective forcing.

Secondly, warming the aerosol layer leads to more longwave emissions from other atmospheric species at these heights, resulting in a negative forcing F_δT relative to the reference state. As shown in Fig. 4, F_δT has a weak and non-monotonous temperature dependence due to the interplay between two effects. First, the radiation from the surface and lower atmospheric levels that the aerosol can absorb increases with surface temperature, resulting in more radiative heating. Additionally, at higher surface temperatures, the aerosol layer warming is limited to a smaller region due to the expansion of the tropopause, thus making radiative heating less effective.

Thirdly, the additional water vapour (i.e. change in specific humidity q) from the upper tropospheric warming results in a positive forcing F_δq. The magnitude of F_δq is much smaller than F_abs and F_δT but increases at higher surface temperatures. It constitutes around 4 % to 7 % of the total LW forcing. This is in agreement with the observation that humidity has a very weak influence on the aerosol longwave forcing by Andronova et al. (1999).

The residual ($F^{\mathrm{LW}}-(F_{\mathrm{abs}}+F_{\mathit{\delta }T}+F_{\mathit{\delta }q})$) is negative; it corresponds to the additional emission from the aerosol heated by its own absorption.

The major contribution to the longwave forcing and its temperature dependence comes from the longwave absorption and re-emission term F_abs. Although CO₂ forcing mainly originates from a similar effect, for aerosol, the effect depends strongly on the surface temperature but not for CO₂. It is worthwhile to analyse this component further to understand the different surface temperature dependencies.

In the atmospheric window (750 to 1250 cm⁻¹) where the atmosphere is optically thin, the longwave radiation at the TOA emanates mainly from the surface, which is a sensitive emitter. Outside the window, the surface emissions are replaced with RH-dependent atmospheric emissions from water vapour. Water vapour is an invariant emitter as its emission temperature remains fixed and uncoupled to the temperature of the surface (Simpson, 1928). A longwave absorber such as CO₂ or aerosol replaces the surface and atmospheric emissions in their spectral range with emissions from the colder stratosphere; thus the forcing magnitude strongly depends on the temperature contrast of the two emission layers (Huang et al., 2016; Jeevanjee et al., 2021).

Line-by-line calculations indicate that the CO₂ forcing originates primarily from the band between 550 and 800 cm⁻¹ (Pierrehumbert, 2011; Wilson and Gea-Banacloche, 2012; Kluft et al., 2021; Jeevanjee et al., 2021; Stevens and Kluft, 2023) (see also Fig. 2). In the surface temperature range of our study, the forcing primarily emanates from the band centre, whose emissions occur at stratospheric heights and are invariant with surface temperature. As this band lies outside and at the edge of the atmospheric emission window, the invariant emitter CO₂ absorbs and re-emits the emissions from the tropospheric water vapour, which is also an invariant emitter. Thus, the fixed emission temperature of the water vapour outside the atmospheric window and the fixed emission temperature of the CO₂ band centre in the stratosphere result in an almost unvarying temperature contrast between the two. Hence, the CO₂ forcing magnitude does not vary much between 280 and 300 K surface temperatures.

While the aerosol layer mainly resides in the lower stratosphere, whose temperature is also T_s-invariant, a significant contribution to the aerosol optical depth comes from within the atmospheric window (Fig. 2). Thus, the aerosol longwave forcing is primarily due to the replacement of emissions from the surface (sensitive emitter) by the emissions from the aerosol layer (invariant emitter). Hence, with an increase in surface temperature, the temperature contrast between the aerosol layer and surface increases and is responsible for the increasing magnitude of F_abs.

To summarize, the fact that aerosol forcing exhibits a pronounced surface temperature dependence while CO₂ forcing does not arises from two factors: (a) aerosol absorbs inside the atmospheric emission window whereas CO₂ does not and (b) aerosol is concentrated in the lower stratosphere whereas CO₂ is well-mixed throughout the atmosphere. The longwave forcing offsets around $\mathrm{1}/\mathrm{3}$ to $\mathrm{2}/\mathrm{3}$ of the SW forcing, and this ratio increases with surface temperature and aerosol load, as shown in Fig. 3d. Note that konrad does not represent tropospheric adjustments, which are therefore not included in this estimate.

5 Feedback

The flux change brought by a mere introduction of the perturbation is captured in the forcing. On the other hand, the feedback parameter λ represents how the climate response changes with surface temperature. The clear-sky longwave radiative feedback has been shown to weaken rapidly between surface temperatures of 280 and 300 K (Koll and Cronin, 2018; Kluft et al., 2021; Seeley and Jeevanjee, 2021). The weakening was attributed to the closing of the atmospheric emission windows, the spectral region where water vapour is optically thin (Kiehl and Trenberth, 1997), typically between 750 and 1250 cm⁻¹, due to an increase in atmospheric water vapour. We examine how the three longwave effects (longwave absorption and re-emission, temperature change, and water vapour increase) highlighted in Sect. 3 shape the feedback parameter in the presence of aerosol. The net feedback parameter calculated using Eq. (4) along with the shortwave and longwave components is shown in Fig. 5.

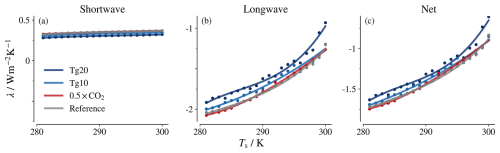
Figure 5 Temperature dependence of the feedback parameter λ decomposed into shortwave and longwave contributions. Cubic fits for each set are plotted as solid lines.

5.1 Feedback in the shortwave bands

The shortwave component of λ is positive and stems from the absorption of shortwave radiation by the water vapour. It becomes slightly more positive at higher surface temperatures. This can be attributed to the exponential increase in the water vapour amount following the Clausius–Clapeyron relationship at fixed relative humidity. However, the net feedback is dominated by the longwave component, both in absolute terms and with respect to the surface temperature dependence. Changes in surface albedo and clouds are not taken into account in our simulations.

5.2 Feedback in the longwave bands

The longwave component of λ is negative and depicts the ability of the system to equilibrate by counteracting the energy imbalance through a temperature change in the surface and the surface-coupled troposphere.

The decrease in the magnitude of the longwave feedback parameter between 280 and 300 K was elucidated using line-by-line radiation calculations in Seeley and Jeevanjee (2021) and Kluft et al. (2021). They showed that as the surface temperature increases, the atmosphere becomes progressively opaque due to the higher quantity of water vapour, and the atmospheric window narrows spectrally, resulting in more of the longwave emission to space emanating from higher up in the troposphere (i.e. lower emission temperatures). This reduces the capability of the system to maintain an energy balance through a change in surface temperature in response to the forcing, which transpires as a weaker negative feedback with an increase in surface temperature. Consistent with this explanation, Fig. 5b also shows that the temperature dependence of the longwave feedback for different atmospheric states, defined by different CO₂ concentrations and aerosol loadings, is similar to that of the reference state, as the increase in the water vapour amount with surface temperature is ubiquitous.

The feedback parameter does not change much with varying CO₂ levels (compare red and grey lines in Fig. 5). However, in the presence of aerosol the longwave feedback (and thus, the net feedback) becomes weaker with an increase in the aerosol loading. This is consistent with the temperature dependence of the forcing presented in Fig. 3. Although not obvious at first sight, the temperature dependence of the forcing ($\frac{\partial F}{\partial T}$) is equivalent to the dependence of the feedback on the forcing agent X ($\frac{\partial \mathit{\lambda }}{\partial X}$), which can be seen from the symmetry of the second derivatives (Clairaut's theorem; Bloch-Johnson et al., 2021; Xu and Koll, 2024):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\partial F}{\partial T}}={\displaystyle \frac{{\partial }^{\mathrm{2}}N}{\partial T\partial X}}={\displaystyle \frac{\partial \mathit{\lambda }}{\partial X}},\end{array}$$

using $F=\frac{\partial N}{\partial X}$ and $\mathit{\lambda }=\frac{\partial N}{\partial T}$. This has previously been shown for the case of CO₂ forcing (X=log₂CO₂; Bloch-Johnson et al., 2021; Xu and Koll, 2024). Our results confirm that this relationship also holds for aerosol. The positive slope of the temperature dependence of the longwave and total aerosol forcings in Fig. 3b and c requires that the respective feedbacks in Fig. 5b and c are less negative for higher aerosol loadings. The same arguments explain why we find no dependence of feedback on CO₂ concentration ($\frac{\partial \mathit{\lambda }}{\partial {\log }_{\mathrm{2}}{\mathrm{CO}}_{\mathrm{2}}}\approx \mathrm{0}$, Fig. 5), since CO₂ forcing does not strongly depend on temperature in the temperature range that we study ($\frac{\partial F}{\partial T}\approx \mathrm{0}$, Fig. 3).

However, the weakened feedback in the presence of stratospheric aerosol is in contrast to results from GCMs (Günther et al., 2022), where the pattern effect dominates the purely radiative effects and causes aerosol to produce more negative feedback than CO₂ forcing. The pattern effect describes the dependence of radiative feedback on patterns of sea surface temperature change, which our 1D column model cannot represent.

As a next step, we identify the source of the weaker feedback in the presence of aerosol using radiative transfer calculations. The feedback to aerosol forcing λ^p can be expressed as the feedback in the reference state λ^o modulated by the changes introduced due to aerosol Δλ:

$$\begin{array}{}\text{(6)}& {\mathit{\lambda }}^{\mathrm{p}}={\mathit{\lambda }}^{\mathrm{o}}+\mathrm{\Delta }\mathit{\lambda }.\end{array}$$

The net change in feedback due to aerosol Δλ is, up to the first order, the sum of the changes due to each of the effects listed in Sect. 3. That is,

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }\mathit{\lambda }=\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{abs}}+\mathrm{\Delta }{\mathit{\lambda }}_{\mathit{\delta }T}+\mathrm{\Delta }{\mathit{\lambda }}_{\mathit{\delta }q},\end{array}$$

where Δλ_abs represents the direct effect of the longwave absorption and re-emission by the aerosol layer, Δλ_δT represents the effect due to the warming by the aerosol layer, and Δλ_δq represents the effect of specific humidity change.

They are calculated as the difference with respect to the reference state in the longwave component of λ, calculated using radiative transfer calculations with only the associated change present. That is,

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{i}}={\mathit{\lambda }}^{\mathrm{o},\mathrm{i}}-{\mathit{\lambda }}^{\mathrm{o}}.\end{array}$$

For example, λ^o,abs is the longwave feedback parameter in the presence of the aerosol layer but with the temperature and specific humidity profile of the reference state (i.e. no stratospheric heating or water vapour increase). Analogously, λ^o,δT(λ^o,δq) is the feedback parameter calculated with only the modified temperature profile (specific humidity profile) introduced to the reference state.

The feedback in the Tg20 case is around 0.15 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ more positive (weaker) than the reference across the temperature range, i.e. such a quantity of aerosol reduces the net feedback by about 10 %–20 %. While the difference remains relatively constant under surface temperature change, the contribution from the different effects of the aerosol changes. At low temperatures, the aerosol absorption and re-emission effect dominates; at higher temperatures, the contribution from stratospheric warming becomes the leading term (see green and yellow lines in Fig. 6).

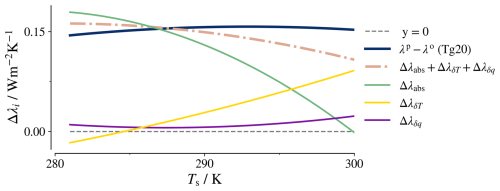
Figure 6 The components of modulation of longwave feedback by aerosol from radiative transfer calculations for the Tg20 case. Only the cubic fits through the data points are shown.

The positive (weakening) longwave absorption effect from the aerosol on the feedback (Δλ_abs) originates from spectral masking and is more effective at lower surface temperatures. The spectral regions in which the aerosol absorbs cannot contribute to the feedback because aerosol is an invariant emitter, decreasing Earth's capability to increase outgoing longwave radiation with temperature. As emissions from the surface (sensitive emitter) are replaced by emissions from water vapour (invariant emitter) at higher temperatures due to the closing of the atmospheric window, the spectral masking effect of the aerosol decreases.

Stratospheric warming (Δλ_δT) contributes positively to the feedback, especially at higher surface temperatures. This effect is in part artificial and originates from the fact that the height of the aerosol layer is fixed in konrad. With higher surface temperatures, the tropopause shifts upward, which results in the aerosol heating more strongly affecting tropospheric levels. The upper troposphere subsequently does not contribute to the feedback, because its temperature is not set by the surface temperature any longer but instead by the aerosol heating. This is a positive contribution to the net feedback. However, Aubry et al. (2021) argue that the injection height of volcanic eruptions of the magnitude we study would increase in a warmer climate so that the aerosol layer would remain in approximately the same distance to the tropopause. Even if injection heights would not increase, it is an unrealistic assumption that an aerosol layer could be sustained well below the tropopause. Therefore, the Δλ_δT contribution is somewhat artificial, and we expect that in reality the difference between feedback to aerosol and CO₂ forcing to be less pronounced at higher temperatures.

Changes in specific humidity have little influence on λ. Additionally, there is a small residual from the non-linear terms that we neglected in our linear decomposition (difference between dash-dotted and blue line in Fig. 6).

To summarize, the 10 %–20 % weaker radiative feedback in the presence of aerosol is mostly due to the masking effect of surface emissions, which dominates at lower temperatures, and stratospheric heating, which dominates at higher temperatures.

6 Summary and conclusions

We use the 1D-RCE model konrad and radiative transfer calculations to provide a mechanistic understanding of the clear-sky radiative forcing and feedback mechanisms due to the introduction of aerosol in the stratosphere. Comparing the aerosol injections to well-studied CO₂ level perturbations, we analyse to what extent the differences can be attributed to three effects of the aerosol layer, i.e. (1) longwave absorption and re-emission, (2) stratospheric heating, and (3) water vapour increase. Among the three effects, longwave absorption and re-emission by aerosol primarily determine the magnitude and state dependence of longwave aerosol forcing and modulates the radiative feedback. Stratospheric heating weakens longwave aerosol forcing but does not alter the state dependence. The water vapour increase has a negligible impact on both forcing and feedback.

We show that the net forcing due to aerosol injection has a stronger temperature dependence than forcing due to changing CO₂ levels. While the scattering of shortwave radiation results in a negative forcing, the longwave absorption and re-emission from the aerosol layer produces a smaller but more strongly temperature-dependent positive forcing. The longwave forcing increases with temperature because stratospheric temperatures are not closely linked to surface temperatures, so that the aerosol spectrally masks larger emissions resulting from larger surface temperatures. This implies that a larger aerosol injection would be required at higher surface temperatures to obtain the same forcing magnitude. When compared to CO₂ forcing, the temperature dependence of aerosol longwave forcing is far more pronounced because aerosol, unlike CO₂, absorbs in the atmospheric window. Outside the window, emissions mainly come from water vapour, which already masks surface temperature changes.

We also show that the clear-sky radiative feedback in the presence of aerosol follows a similar surface temperature dependence as the reference state or a state with a changed CO₂ level. However, the longwave feedback is consistently weaker at all temperatures than that of the CO₂ level perturbations by ≈ 0.15 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (≈ 10 %–20 %) and thus depends on the nature of the forcing. At relatively low surface temperatures, the weaker feedback is dominated by the masking of emissions from a sensitive emitter (dominantly the surface) by emissions from a largely invariant emitter, the aerosol layer. At higher surface temperatures, the aerosol heating more strongly affects the tropopause layer due to the higher tropopause, which leads to larger parts of the troposphere being independent of the surface temperature. This constitutes a positive feedback contribution that we expect to be largely an artefact of our model setup because in warmer climates the injection height is projected to increase with tropopause height (Aubry et al., 2021), while it is kept fixed in our simulations. Furthermore, according to GCM studies, the Brewer–Dobson circulation would accelerate, which would reduce the warming of the tropical stratosphere (Pitari and Rizi, 1993; Garcia et al., 2011; Aquila et al., 2013) and influence its emissions.

As Bloch-Johnson et al. (2021) and Xu and Koll (2024) point out for the case of CO₂, the temperature dependence of the forcing of stratospheric aerosol is equivalent to the dependence of the feedback on the aerosol loading. Hence, the weaker feedback for higher aerosol loading has to be accompanied by the positive temperature dependence of the forcing. We identify the same dominant mechanism for both dependencies: the surface temperature dependence of emissions is masked by the aerosol, which emits largely independent of surface temperature.

The weaker feedback for aerosol injections than for perturbations of the atmospheric CO₂ concentration stands in contrast with the opposite difference simulated in GCMs (Hansen et al., 2005; Boer et al., 2006; Marvel et al., 2016; Gregory et al., 2016; Günther et al., 2022). The stronger feedback in GCM simulations with stratospheric aerosol was attributed to different tropospheric stability and surface warming patterns, which cannot be represented in our one-dimensional column model. Our interpretation is that the feedback strengthening due to the pattern effect in GCMs overcompensates for the weakening from radiative causes that we find in our single column study.

In Appendix A, the climate sensitivity is examined using surface-coupled slab ocean simulations. The temperature change in equilibrium is less temperature-dependent for the aerosol injections than for CO₂ forcing as the decrease in the feedback parameter is partly compensated for by the decrease in forcing. Further, in Appendix B, we analyse how the forcing and feedback would behave at different surface temperatures driven by a change in CO₂ concentration and show that our results on the surface temperature dependence of forcing and modulation of feedback do not change substantially. This is expected as CO₂ and aerosol have little to no interaction and act in different spectral regions with minimal overlap.

The simulations used in the study represent a 1D-RCE of the atmosphere. Even though the studied surface temperature range (280–300 K) is too wide for global-mean surface temperatures under CO₂ forcing, it is not extreme in terms of regional temperature differences on Earth. Thus, the temperature dependence of the forcing and feedback might be useful to understand the impacts of volcanic eruptions or solar geoengineering at different latitudes. However, other effects such as circulation or eruption characteristics might be more important than pure radiative effects (Zanchettin et al., 2013; Aubry et al., 2022).

The simple conceptual model used for our study enables an understanding of the physics behind the temperature dependence of aerosol forcing and feedback and their quantification in such an idealized setting. However, the realism of the setting is limited in particular by (a) the assumption of tropical atmospheric conditions and (b) neglecting cloud effects. Despite the simplicity of the 1D-RCE approach, forcing and feedback estimates obtained with konrad and similar tools are in general very similar to estimates using general circulation models. For example, 1D-RCE estimates of the clear-sky feedback are robustly close to −2.2 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (Manabe and Wetherald, 1967; Kluft et al., 2019; Koll and Cronin, 2018; Koll et al., 2023), while estimates from CMIP models lie between about −1.9 and −2.2 $\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}}$ (Held and Shell, 2012; Zelinka et al., 2020; Vial et al., 2013; Koll et al., 2023). The usefulness of studying averaged atmospheric conditions for Earth is partly related to Earth’s OLR being an approximately linear function of surface temperature. This characteristic implies that the impact of radiative forcing is very similar for warm and cold climates (Koll and Cronin, 2018). Furthermore, our arguments are purely radiative and barely depend on the vertical structure of the atmosphere. Thus, although konrad simulates the tropical atmosphere, we expect that our results for forcing and feedback apply to global-mean conditions, as well as for different regions and seasons. Changing the location or season would merely cause a shift along the temperature axis but not lead to a qualitative change. The only exception to this is that the quantity of water vapour in the atmospheric column determines how much radiation originates from the atmosphere vs. from the surface, which is important for spectral masking. Thus, regions that are drier than the assumed 80 % fixed relative humidity are expected to behave more similar to colder regions.

This study addresses longwave forcing and feedback, and adding clouds would likely change the results quantitatively. We expect that the idealized study presented here provides a useful background for potential future attempts to assess the temperature dependence of stratospheric aerosol forcing on Earth. In Appendix C, we add a brief discussion about cloud effects, and estimate that the aerosol longwave forcing (and its temperature dependence) and the feedback difference between an atmosphere with and without aerosol scale with (1−f_hc). The shortwave forcing would be reduced by a factor of (1−f_c). f_hc and f_c are the high and total cloud fraction respectively.

While we have studied the particular case of stratospheric sulfate aerosol, the qualitative behaviour of the forcing and feedback at different surface temperatures and the underlying reasoning should be applicable in general to any stratospheric species that weakly absorbs in the atmospheric emission window, such as halocarbons (Shine and Myhre, 2020). Conversely, this also means that the same reasoning or temperature dependence might not be applicable for other aerosols in the stratosphere that do not absorb in the atmospheric window.

The radiative perspective on stratospheric sulfate aerosol forcing highlights the critical role played by longwave absorption and spectral masking by aerosol in determining the magnitude and temperature dependence of the forcing–feedback mechanisms.

Appendix A: Implications for climate sensitivity

Having analysed forcing and feedback at different surface temperatures, we investigate how their combination, i.e. the surface temperature change at equilibrium as provided by Eq. (2), varies with surface temperature. As the surface temperature change is large (e.g. for Tg20, ΔT_eq≈6 K at T_s=300 K), one also has to account for the change in forcing and feedback magnitudes as the surface temperature evolves. Using the values of F and λ calculated from fixed-SST simulations would lead to erroneous values of surface temperature change. Simulations with a coupled slab ocean surface with a variable surface temperature incorporate the changes in F and λ. We determine forcing, feedback, and equilibrium temperature change as N intercept, slope, and T intercept of N(T) (Gregory et al., 2004). This method gives a representative average of the forcing and feedback in the temperature range. Thus, minor differences in the values of F and λ may be expected compared to results from fixed-SST simulations.

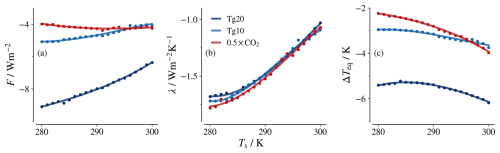
Figure A1 Temperature dependence of F, λ, and ΔT_eq derived using the Gregory method using slab ocean simulations. The x axis represents the surface temperature at the time of introducing the perturbation. Cubic fits for each set are plotted as solid lines.

Figure A1 shows F, λ, and ΔT_eq calculated using the Gregory method. The forcing and feedback parameter show similar qualitative behaviours when compared to the values obtained from the fixed-SST simulations (Figs. 3c and 5c). The feedback parameters for the different cases become almost indistinguishable at higher surface temperatures. The efficacy of stratospheric aerosol forcing, i.e. the effectiveness of a unit forcing to cause temperature changes in comparison to CO₂ forcing (Hansen et al., 2005), is greater than 1 at low surface temperatures but approximately 1 above 295 K.

The temperature change in equilibrium shows a weaker surface temperature dependence for aerosol forcing than CO₂ forcing because the decrease in the absolute value of the forcing at higher surface temperatures partly compensates for the weakening of the feedback parameter. For the Tg20 case, the decrease in absolute values of the forcing with temperature initially dominates over the weakening of the feedback, resulting in a decrease in absolute ΔT_eq at lower surface temperatures.

Appendix B: Dependence on climate state

In Sects. 4 and 5 and in Appendix A, we studied how the forcing, feedback, and climate sensitivity respectively depend on surface temperature and pointed out the differences to forcing from CO₂. However, it is worth noting that the different surface temperatures studied up to this point are artificial as they do not have a physical driver but are prescribed to the model. This leads to configurations where the CO₂ concentration is physically inconsistent with the surface temperature. To generalize the understanding from surface temperature dependence to climate state dependence, we follow the strategy to adjust CO₂ concentrations to the surface temperatures put forward in Romps (2020). We analyse how the forcing and feedback would behave at different surface temperatures driven by a change in CO₂ concentration.

For a fixed surface temperature, the CO₂ concentration is adjusted to reach a closed TOA radiation budget. This represents a CO₂-induced warming, thus allowing us to analyse the forcing–feedback dependence on the representative climate state. The aerosol injections, or the 0.5×CO₂ perturbation, are performed relative to these reference states to diagnose the forcing and feedback due to each perturbation.

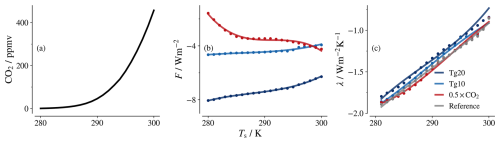
Figure B1 Temperature dependence of the CO₂ concentration, F, and λ in interactive CO₂ simulations. Cubic fits for each set are plotted as solid lines.

The CO₂ concentrations at equilibrium at different surface temperatures are shown in Fig. B1a. It is worth noting that the resultant concentration of CO₂ at low surface temperatures is unrealistic compared to the CO₂ concentrations on Earth. The F and λ calculated from these simulations, shown in Fig. B1b and c, can be compared to Figs. 3c and 5c when trying to understand which difference comes from the CO₂ concentration.

Figure B1b shows that the 0.5×CO₂ forcing is weaker for lower temperatures than what is seen in Fig. 3c. This is due to the significantly lower quantity of CO₂ at these temperatures (He et al., 2023). At higher temperatures, the 0.5×CO₂ forcing shows similar behaviour as depicted in Figs. 3c and A1a. While slightly weaker in magnitude, the aerosol forcing shows the same qualitative behaviour as noted in earlier sections.

The feedback parameter shown in Fig. B1c shows a rapid weakening with increasing surface temperature, similar to that of Fig. 5c and as noted in earlier studies (Kluft et al., 2021; Seeley and Jeevanjee, 2021). The weakening of the feedback parameter in the presence of aerosol is also clearly visible.

Thus, the surface temperature dependence we find for forcing and feedback is also valid as a more general climate state dependence. This can be expected as CO₂ and aerosol act on different spectral regions with minimal overlap. The fact that our results do not change substantially even under the unrealistically low background CO₂ concentrations at cold temperatures seen in Fig. B1a corroborates that there is little interaction between aerosol and CO₂.

Appendix C: Cloud effects

This study uses the konrad model under clear-sky conditions. In this section, we discuss how our findings on the aerosol's forcing and feedback may change in the presence of clouds. Stevens and Kluft (2023) discuss how clouds affect forcing and feedback to CO₂ forcing, and we apply these ideas to stratospheric aerosol forcing.

Our main finding is that the temperature dependence of the aerosol longwave forcing ($\partial F/\partial T$), as well as the dependence of the longwave feedback parameter on aerosol load ($\partial \mathit{\lambda }/\partial X$), arise from the spectral masking of emissions in the atmospheric window. Clouds also mask emissions from the atmospheric window when the cloud top temperatures do not change with surface temperature, which is a reasonable approximation for high clouds but not for low clouds (McKim et al., 2021). Spectral masking applies only once; so if emissions are already masked by clouds, aerosols cause no additional masking. In other words, in the presence of high clouds, the aerosol longwave forcing would be less temperature dependent and the feedback would be less different from the feedback in an aerosol-free atmosphere. Since cloud top temperatures of low clouds generally vary with surface temperature, the spectral masking due to the aerosol still applies in the presence of low clouds. Thus, similar to the estimate in Stevens and Kluft (2023) for CO₂, we expect the temperature dependence of aerosol longwave forcing and the dependence of the longwave feedback parameter on aerosol concentration to scale with (1−f_hc), where f_hc is the high cloud fraction.

However, clouds not only affect the temperature dependence of LW forcing but also the forcing itself. Also, the forcing is related to masking, namely of surface or atmospheric emissions by the aerosol layer, and is determined by the temperature difference between the emission layers. Assuming that high clouds emit at temperatures similar to that of the aerosol layer and low clouds at temperatures similar to the surface, one can estimate that, again, only high clouds affect the aerosol forcing and would scale it by the same factor (1−f_hc). This would mean that the relative temperature dependence of the aerosol forcing would remain nearly unaffected by clouds.

Clouds (both high and low) also reduce aerosol SW forcing as additional SW reflection by aerosol has less impact over bright surfaces than dark ones. This leads to a reduction in the SW forcing that scales with (1−f_c), where f_c is the total cloud fraction. However, the clouds do not affect the SW forcing's temperature dependence, which is already minimal under clear-sky conditions. The same is true for the dependence of the SW feedback on the aerosol load.