Snow particle fragmentation enhances snow sublimation

Fragmentation of snow particles – wherein freshly deposited dendritic crystals are rapidly transformed into smaller, rounded grains through collisions with the surface and other particles during drifting and blowing snow – plays a critical role in governing snowpack evolution and transport dynamics. However, existing models of drifting and blowing snow often neglect the effects of snow particle fragmentation, introducing uncertainties in the prediction of flow dynamics and sublimation rates. In this study, we incorporate a snow particle fragmentation model into a well-developed blowing snow model to quantitatively investigate the influence of fragmentation under varying wind conditions. Our results reveal that fragmentation within the saltation layer generates smaller particles, leading to an increase in mass flux and subsequently enhancing sublimation rates in drifting and blowing snow. The effects of fragmentation on sublimation are more pronounced for suspension particles than for saltation particles, particularly when the friction velocity is less than 0.3 m s⁻¹. This work highlights the critical role of collision-induced fragmentation, wherein dendritic crystals are shattered into smaller particles during transportation. This quantitative assessment of fragmentation impact on snow sublimation underscores its importance for improving the physical representation of drifting and blowing snow in snow transport models and for potential applications in snow hydrology and climate modeling.

1 Introduction

Snow plays an important role in Earth's climate system because of its wide coverage and seasonal variation, leading to variable surface conditions. Sublimation is a significant process for snow surface to exchange heat, mass, and energy with the atmosphere. Snow sublimation includes static surface sublimation and dynamic airborne particle sublimation. The latter process usually happens in drifting and blowing snow (DBS), in which snow particles follow the air flow, driven by the wind. Water vapor transport created by snow sublimation has a significant influence on the local hydrological cycle and distribution, especially in polar and high alpine regions. For example, in the coastal area of Antarctica, ice sheet mass loss caused by DBS reaches 18.3 % of the whole snowfall amount each year (Pomeroy and Jones, 1996). In Antarctica, snow sublimation depletes approximately 17 %–20 % of its annual precipitation (Déry and Yau, 2001). In Mongolia, snow sublimation depletes 20.3 %–21.6 % of annual snowfall (Zhang et al., 2008). On the Tibetan Plateau, due to its extremely dry, cold, and windy environmental conditions, the sublimation amount is very high, up to about 50 % of the amount of snow cover every year (Ueno et al., 2007).

Typical DBS sublimation fluxes (40–60 W m⁻²) are more than twice as high as surface sublimation fluxes (20–30 W m⁻²) (Pomeroy and Essery, 1999). DBS sublimation is larger than surface snow sublimation for several reasons: (1) the turbulence is stronger during DBS events, (2) aerodynamically entrained particles from the surface enlarge the contact surface with air, and (3) the relative humidity decreases during DBS at a greater height level, which promotes a faster sublimation process. Therefore, investigating the role of sublimation in DBS is a requirement to accurately assess the water equivalent and understand the interaction between land surface and atmosphere in cold areas, especially for polar regions.

In DBS, mass, momentum, and energy are transferred between the surface and atmosphere accompanied by snow particle movement. Snowfall is the initial source of snow particles on the ground. Once the snow particles deposit on the surface, they may undergo surface creep, be entrained into saltation by wind, and, under sufficiently strong wind conditions, transition from saltation into the suspension layer. During particle saltation, they bounce on the ground surface and may release more particles starting to move, which is called splash. The above processes are described in detail in the current numerical models of DBS (Pomeroy and Male, 1992; Taylor, 1998; Lehning et al., 2008; Vionnet et al., 2014; Sigmund et al., 2021; Yu et al., 2022; Melo et al., 2022). Early saltation models are usually empirical mass transport equations, which are functions related to surface shear stress (Pomeroy et al., 1993; Déry and Yau, 2001). These models are susceptible to the empirical parameters. Doorschot et al. (2004) developed a numerical model for steady-state saltation by considering the aerodynamic entrainment and rebound processes, showing a more physical picture. Nemoto and Nishimura (2004) developed a new numerical model for saltation and suspension that considers aerodynamic entrainment, grain–bed collision, and wind modification processes with a distribution of grain sizes. Based on their model, a few subsequent studies by Zhang and Huang (2008), Wang and Huang (2017), Yu et al. (2022), Hames et al. (2022), and Melo et al. (2022) were carried out. However, the role of sublimation in drifting snow has not been demonstrated in these models.

For a single snow particle sublimation process, the sublimation rate is described in detail in the model proposed by Thorpe and Mason (1966), in which the sublimation rate is related to the particle size and environmental conditions. This T&M model has been implemented in the present snow models to estimate the sublimation in DBS, to assess the amount of sublimation caused during DBS on a small scale (m) (Groot Zwaaftink et al., 2011; Huang and Shi, 2017; Dai and Huang, 2014; Vionnet et al., 2014; Sharma et al., 2018) and on an intermediate scale (km) (Sharma et al., 2023; Gadde and Berg, 2024). The numerical simulation results from the above models all show that snow sublimation is an important snow physical process that cannot be ignored in DBS. In these small-scale snow models, each single snow particle's trajectory is tracked, while the particle diameter is unchanged. Also, the parameterization of sublimation in those kilometer-scale snow models is from these small-scale snow models, based on the same assumption.

Snow particles are fragile granular systems that can undergo fragmentation – a process that occurs during saltation, where particle–particle and particle–surface collision cause snow crystals to break apart and transform into smaller particles. This fragmentation not only alters their dynamic behavior by changing particle size (Sato et al., 2008; Walter et al., 2024) but also significantly impacts the sublimation rate, as the sublimation of snow particles is closely linked to their size, shape, and specific surface area (Domine et al., 2009). The sublimation rate is mainly driven by the pressure gradient between the surface saturation vapor and the ambient air, and the surface saturation vapor is influenced not only by air temperature, but also by particle curvature (Neumann et al., 2009). For a particle moving in the air, the reduction in size is a joint effect of breakage and sublimation. In turn, the dynamically varying size of snow particles will govern their motion, such as changing their trajectories, which further influences the mass flux and sublimation rate. However, this mutual physical feedback caused by fragmentation in DBS has not been reported in detail, and the relevant model is still missing.

To date, there is only one model (Comola et al., 2017) considering the fragmentation of snow particles during drifting snow. That study, using a statistical mechanics model, calculates the number of fragmented particles from the perspective of energy and mass balance and analyzes the effect of fragmentation on the particle size distribution. However, it does not explore the impact of fragmentation on drifting snow flux or the subsequent sublimation of snow particles.

In this work, we introduce a snow fragmentation model into the drifting snow model of Huang and Shi (2017), enabling a more realistic representation of the movement and dynamic size changes of individual particles in the air. This advancement allows a more accurate representation of snow particle sublimation rates, offering critical insights into the micro-scale processes that govern snow–atmosphere interactions.

2 Model description

The model by Huang and Shi (2017) is a simulation framework for DBS that is able to simultaneously describe the behavior of both saltation and suspension particles. In our model, the saltation particles are described using a two-dimensional Euler–Lagrangian tracking method, which captures the saltating motion of particles. For suspension particles, which are typically smaller in size, we employ a dispersion function to characterize their movement dynamics. A threshold grain size was used to separate the saltating and suspended particles, depending on the Rouse number (Scott, 1995). The T&M model is used to calculate the sublimation of DBS. The feedback of particle motion and particle sublimation to the wind field, air temperature, and air humidity is also considered.

The Comola et al. (2017) model, the only drifting snow model considering snow particle fragmentation, is a one-dimensional, non-computational fluid dynamics (CFD) statistical approach. While it incorporates particle fragmentation, it does not couple the particles with the wind field. As a result, the effects of fragmentation on the wind field cannot be evaluated in this framework.

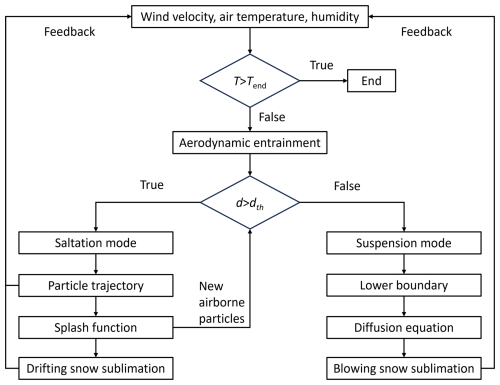
Building on the Huang and Shi (2017) model, we incorporated the fragmentation model of Comola et al. (2017) and set up a comprehensive DBS model. This new model addresses the limitations of Comola's model and provides a more comprehensive description of the interactions between particle fragmentation and the wind field. The particle fragmentation is now taken into consideration in the saltation splash process as follows.

2.1 Air flow

Considering the steady state of saltation, the horizontal wind field satisfies the following equations (Nemoto and Nishimura, 2004):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle \frac{\partial }{\partial z}}\left({\mathit{\rho }}_f{\mathit{\kappa }}^{\mathrm{2}}{z}^{\mathrm{2}}\left|{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}z}}\right|{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}z}}\right)+f_{\mathrm{p}}=\mathrm{0},\end{array}$$

where z is the height above surface, ρ_f is the air density, κ is the von Karman constant, u is the wind speed, and f_p is the feedback force of the airborne snow particles.

The air temperature and humidity equations, Eqs. (2) and (3), respectively, satisfying the horizontal uniformity condition are formulated according to Bintanja (2000):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle \frac{\partial \mathit{\theta }}{\partial t}}={\displaystyle \frac{\partial }{\partial z}}\left(K_{\mathit{\theta }}{\displaystyle \frac{\partial \mathit{\theta }}{\partial z}}\right)+S_{\mathit{\theta }},\end{array}$$

where θ is the air potential temperature, $K_{\mathit{\theta }}=\mathit{\kappa }{u}_{*}z+K_T$ is the turbulent heat exchange coefficient, K_T is the molecular diffusion coefficient of heat, S_θ is the sublimation heat feedback of the airborne snow particles, and u_* is the friction velocity.

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle \frac{\partial q_{\mathrm{v}}}{\partial t}}={\displaystyle \frac{\partial }{\partial z}}\left(K_q{\displaystyle \frac{\partial q_{\mathrm{v}}}{\mathrm{d}z}}\right)+S_q,\end{array}$$

where q_v is the water vapor mixing ratio, $K_q=\mathit{\kappa }{u}_{*}z+K_v$ is the water vapor turbulent exchange coefficient, K_v is the molecular diffusion coefficient of water vapor, and S_q is the sublimation humidity feedback of the airborne snow particles.

2.2 Snow saltation

The motion of saltating snow particles can be described as five sub-processes, namely aerodynamic entrainment, particle trajectory, splash function, sublimation, and feedback to air.

• 1.

  Aerodynamic entrainment

  The snow particles start to move when the wind speed reaches a critical value (namely fluid threshold, usually represented by friction velocity) for a given snow surface; this is called aerodynamic entrainment. The rate of aerodynamic entrainment N_a is known as a linear function of the surface shear stress τ (Anderson and Haff, 1991):

  $$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{N}_{\mathrm{a}}=A(\mathit{\tau }-{\mathit{\tau }}_{\mathrm{t}}),\end{array}$$

  in which A (${\mathrm{N}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$) is an empirical coefficient and τ_t is the threshold surface shear stress. The particle size distribution f(d) follows a gamma distribution (Schmidt, 1982):

  $$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }f\left(d\right)={\displaystyle \frac{d^{\mathit{\alpha }-\mathrm{1}}}{{\mathit{\beta }}^{\mathit{\alpha }}\mathrm{\Gamma }\left(\mathit{\alpha }\right)}}{\mathrm{e}}^{-d/\mathit{\beta }},\end{array}$$

  where α and β are the shape and inverse scale parameters and d is the particle diameter.

  There are two ways to describe the motion pattern of snow particles. The most common way is to define a threshold height to divide the saltation and suspension layers, which is easy to apply. However, the threshold value is empirical and varies significantly in the existing literature. The other way is related to the particle size, which is based on the traceability. The lifting velocity of aerodynamic entrainment particles is set to $\sqrt{\mathrm{2}gd}$ (Dai and Huang, 2014), where g is gravitational acceleration, which is not sensitive to the steady state of saltation.

• 2.

  Particle trajectory

  After the snow particles are lifted into the air, their ballistic trajectories can be described by Newton's second law:

  $$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }m{\displaystyle \frac{\mathrm{d}\mathit{r}}{\mathrm{d}t}}={\mathit{f}}_{\mathrm{d}}-m\mathit{g},\end{array}$$

  where m is the mass of the snow particle, r(x,z) is the location of the particle, f_d is the drag force by fluid, g is the gravitational acceleration, and t is the time.

• 3.

  Splash function

  In this model, we use probability functions to describe particle movement after they impacted the surface (Sugiura and Maeno, 2000). The probability distribution function of the restitution coefficient in the vertical direction S_v(e_v), the restitution coefficient in the horizontal direction S_h(e_h), and the number of particles ejected from a surface n_e are defined as follows:

  $$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }{S}_{\mathrm{v}}\left(e_{\mathrm{v}}\right)={\displaystyle \frac{e_{\mathrm{v}}^{a-\mathrm{1}}}{b^a\mathrm{\Gamma }\left(a\right)}}{\mathrm{e}}^{-\frac{e_{\mathrm{v}}}{b}},\text{(8)}& {\displaystyle }& {\displaystyle }{S}_{\mathrm{h}}\left(e_{\mathrm{h}}\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}\mathit{\pi }{\mathit{\sigma }}^{\mathrm{2}}}}}{\mathrm{e}}^{-\frac{(e_{\mathrm{h}}-\mathit{\mu }{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}},\text{(9)}& {\displaystyle }& {\displaystyle }{n}_{\mathrm{e}}=C_m^{n_{\mathrm{e}}}{p}^{n_{\mathrm{e}}}(\mathrm{1}-p{)}^{m-n_{\mathrm{e}}},\end{array}$$

  where $e_{\mathrm{v}}=v_{\mathrm{e}y}/v_{\mathrm{i}y}$ is the vertical recovery coefficient, $e_{\mathrm{h}}=v_{\mathrm{e}x}/v_{\mathrm{i}x}$ is the horizontal recovery coefficient, v_ix is the horizontal velocity component of the impacting grain, v_iy is the vertical velocity component of the impacting grain, v_ex is the horizontal velocity component of the ejected grain, and v_ey is the vertical velocity component of the ejected grain. n_e is the number of ejected snow grains. Γ(a) is the gamma function, $C_m^{n_{\mathrm{e}}}=m\mathrm{!}/\left[n_{\mathrm{e}}\mathrm{!}\right(m-n_{\mathrm{e}}\left)\mathrm{!}\right]$ is the combination number.

  Particle fragmentation was not considered in Sugiura and Maeno's splash function. We add it when a particle–bed collision happens. The probability that a particle will fragment upon impact is calculated following the approach of Comola et al. (2017):

  $$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle }p\left(f\right)=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+\frac{{\mathit{\sigma }}^{\mathrm{2}}}{w_{\mathrm{s}}}}}},\end{array}$$

  where ${\mathit{\sigma }}^{\mathrm{2}}=\mathrm{2.5}{u}_{*}^{\mathrm{2}}$ is the turbulence velocity variance, representing fluctuations in velocity caused by turbulent eddies (Stull, 1988). w_s is the terminal velocity of snow particles. When a snow particle falls back to the ground (initial velocity v_i≥0.5 m s⁻¹), Eq. (10) is used to determine whether it breaks. Then, the number of snow particles N is calculated according to Eq. (11), and the ratio of particle size before and after fragmentation λ is calculated according to Eq. (12), again following Comola et al. (2017):

  $$\begin{array}{}\text{(11)}& {\displaystyle }& {\displaystyle }\left\{\begin{array}{ll}N=\mathrm{15}{v}_{\mathrm{i}}-\mathrm{2.5},& \mathrm{0.5}<v_{\mathrm{i}}<\mathrm{1.5}\\ N=\frac{\mathrm{5}}{\mathrm{7}}(\mathrm{6}{v}_{\mathrm{i}}+\mathrm{19}),& v_{\mathrm{i}}>\mathrm{1.5}\end{array}\right.,\text{(12)}& {\displaystyle }& {\displaystyle }\left\{\begin{array}{ll}\mathit{\lambda }=-\mathrm{0.4}{v}_{\mathrm{i}}+\mathrm{0.7},& \mathrm{0.5}<v_{\mathrm{i}}<\mathrm{1.0}\\ \mathit{\lambda }=-\mathrm{0.1}{v}_{\mathrm{i}}+\mathrm{0.4},& \mathrm{1.0}<v_{\mathrm{i}}<\mathrm{1.5}\\ \mathit{\lambda }=\mathrm{0.25},& v_{\mathrm{i}}>\mathrm{1.5}.\end{array}\right.\end{array}$$

  The velocity and the direction angle of the newly produced snow particles are kept the same as those of the original snow particles.

• 4.

  Sublimation

  The drifting snow sublimation is calculated using the T&M model (Thorpe and Mason, 1966):

  $$\begin{array}{}\text{(13)}& {\displaystyle }{\displaystyle \frac{\mathrm{d}m}{\mathrm{d}t}}={\displaystyle \frac{\mathit{\pi }d(\mathrm{RH}-\mathrm{1})-\frac{Q_{\mathrm{r}}}{K\mathit{\text{Nu}}T}\left(\frac{L_{\mathrm{s}}}{R_{\mathrm{v}}T}-\mathrm{1}\right)}{\frac{L_{\mathrm{s}}}{K\mathit{\text{Nu}}T}\left(\frac{L_{\mathrm{s}}}{R_{\mathrm{v}}T}-\mathrm{1}\right)+\frac{R_{\mathrm{v}}T}{\mathit{\text{Sh}}D{e}_{\mathrm{s}}}}},\end{array}$$

  where m is the particle mass, d is the particle diameter, T is the air temperature, RH is the air relative humidity, Q_r is the solar radiation which snow particles absorb, K is the heat conductivity, R_v is the specific gas constant of water vapor (461.5 J kg⁻¹ K), D is the molecular diffusivity of water vapor, e_s is the saturated vapor pressure relative to the ice surface, Nu is the Nusselt number, and Sh is the Sherwood number.

• 5.

  Feedback to air

  The airborne particles have a significant effect on airflow. To consider this effect, we use an equivalent body force in those grids containing particles, which can be calculated as

  $$\begin{array}{}\text{(14)}& {\displaystyle }{\displaystyle }{\mathit{f}}_{\mathrm{p}}=-{\displaystyle \frac{\mathrm{1}}{V}}\sum _{i=\mathrm{1}}^N{\mathit{f}}_{\mathrm{d}\mathit{i}},\end{array}$$

  where V is the volume of the grid, N is the total number of airborne particles in the grid, and f_di is the drag force of the ith particle in the grid.

  The volume sublimation rate in each control volume mesh can be calculated as

  $$\begin{array}{}\text{(15)}& {\displaystyle }{\displaystyle }S=-{\displaystyle \frac{\mathrm{1}}{V}}\sum _{i=\mathrm{1}}^N{\displaystyle \frac{\mathrm{d}{m}_i}{\mathrm{d}t}},\end{array}$$

  where m_i is the mass of the ith particle in the grid.

  Then, the sublimation feedbacks to air temperature and humidity are, respectively,

  $$\begin{array}{}\text{(16)}& {\displaystyle }& {\displaystyle }{S}_{\mathit{\theta }}=-{\displaystyle \frac{L_{\mathrm{s}}S}{{\mathit{\rho }}_{f}C}},\text{(17)}& {\displaystyle }& {\displaystyle }{S}_q={\displaystyle \frac{S}{{\mathit{\rho }}_f}},\end{array}$$

  where $L_{\mathrm{s}}=\mathrm{2.84}\times {\mathrm{10}}^{\mathrm{6}}$ J kg⁻¹ is the latent heat of sublimation and $C=\mathrm{1.01}\times {\mathrm{10}}^{\mathrm{3}}$ J kg⁻¹ K is the specific heat of air.

2.3 Snow suspension

In the simulation, we define a diameter threshold for distinguishing suspension and saltation particles (Huang and Shi, 2017), which is calculated based on the Rouse number:

$$\begin{array}{}\text{(18)}& {\displaystyle }{\displaystyle }{R}_N={\displaystyle \frac{w_{\mathrm{s}}}{\mathit{\kappa }{u}_{*}}}.\end{array}$$

Therefore, the conditions for determining the saltation and suspension snow particles are (Scott, 1995)

$${\displaystyle }{\displaystyle }\left\{\begin{array}{ll}{R}_N>\mathrm{1},& \text{saltation}\\ R_N\le \mathrm{1},& \text{suspension}.\end{array}\right.$$

The suspended snow follows the vertical diffusion equation (Déry and Yau, 2002):

$$\begin{array}{}\text{(19)}& {\displaystyle }{\displaystyle \frac{\partial q_{\mathrm{s}}}{\partial t}}={\displaystyle \frac{\partial }{\partial z}}\left(K_{\mathrm{s}}{\displaystyle \frac{\partial q_{\mathrm{s}}}{\mathrm{d}z}}+w_{\mathrm{s}}{q}_{\mathrm{s}}\right)+S,\end{array}$$

where q_s is the suspended snow particle mixing ratio; $K_{\mathrm{s}}=\mathit{\delta }\mathit{\kappa }{u}_{*}z$ is the diffusion coefficient of suspended particles; and δ is the decreasing factor of the asymptotic diffusivity of heavy particles in the vertical direction referring to gaseous materials, which can be expressed as (Csanady, 1963)

$$\begin{array}{}\text{(20)}& {\displaystyle }{\displaystyle }\mathit{\delta }={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+\frac{{\mathit{\beta }}^{\mathrm{2}}{f}^{\mathrm{2}}}{\stackrel{\mathrm{‾}}{{w^{\prime }}^{\mathrm{2}}}}}}},\end{array}$$

where β=1 is the proportionality constant, w^′ is the vertical turbulent fluid velocity, and $\stackrel{\mathrm{‾}}{{w^{\prime }}^{\mathrm{2}}}=u_{*}^{\mathrm{2}}$. A flowchart of the model is shown in Fig. 1 to illustrate the new splash function.

Figure 1 Flowchart of the drifting and blowing snow model.

2.4 Model verification

To verify the model, we compared simulated particle size distribution, sublimation rate, and mass concentration to observational data. We firstly compared the particle size distribution at all heights above ground with the field observation data of Gordon and Taylor (2009) (Manitoba, Canada) and Nishimura and Nemoto (2005) (Mizuho Station, Antarctica), shown in Fig. 2. The simulation results for the range and trend of the size distribution agree with these field observations. Overall, the size distribution variation with height deviates more significantly close to the surface (0.02–0.1 m) than further up (0.12–1.13 m). The proportion of smaller-sized particles increases when considering the fragmentation (blue columns in Fig. 2), which is closer to the observation results (white columns in Fig. 2). For particles at levels between 0.12–1.13 m, particle size is in a narrow range of 0–90 µm. In contrast, within the saltation layer (up to 0.1 m in height), particle sizes display a broader distribution, ranging from 50–450 µm, and the simulated average particle size decreases with increasing height. However, this trend is not evident in the field observations, which might be due to measurement challenges in the field compared to ideal simulation and due to limitations in the accuracy of the sensors.

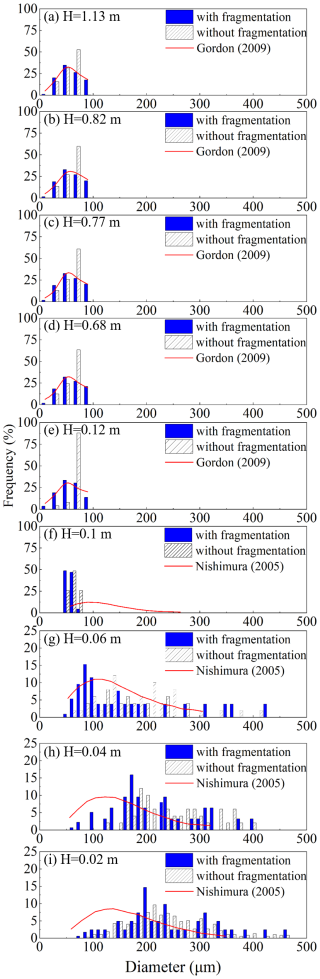
Figure 2 Particle size distributions at nine different heights above the surface: 1.13, 0.82, 0.77, 0.69, 0.12, 0.10, 0.06, 0.04, and 0.02 m. Blue bars represent simulation results with fragmentation considered, and gray bars denote results without fragmentation. The red solid line represents field measurements. For heights below 0.1 m, simulated results are compared with observations from Nishimura and Nemoto (2005) at Mizuho Station, Antarctica; for heights above 0.1 m, comparisons are made with data from Gordon and Taylor (2009) in Manitoba, Canada.

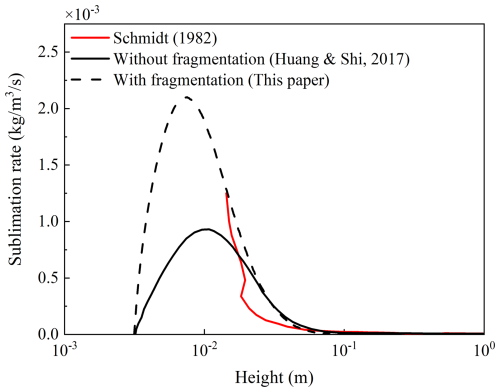
Here we defined the total sublimation rate as the sum of the sublimation rates of both the saltation layer and the suspension layer. Figure 3 compares the total sublimation rate profiles obtained from the numerical simulation with field observation data (measured by Schmidt, 1982, near Wyoming, USA). The sublimation rates in both profiles are of the same order of magnitude, demonstrating that the model can reasonably predict the sublimation rate of blowing snow. While Huang and Shi (2017) show good agreement with observations at higher elevations, their results underestimated the sublimation rate near the surface. By incorporating fragmentation, the model not only performs well near the surface but also shows better agreement with the observed sublimation rates. This indicates that the modified model can more accurately capture the near-surface snow particle dynamics, especially the particle–surface interaction.

Figure 3 Comparison of the total sublimation rate profile for this paper and field observations (Schmidt, 1982) for $u_{*}=\mathrm{1.1}$ m s⁻¹, $z_{\mathrm{0}}=\mathrm{3.2}\times {\mathrm{10}}^{-\mathrm{4}}$ m, and T=265.65 K.

The mass concentrations from the simulation (with fitting curve) and from field observations under the same friction velocity and temperature are compared in Fig. 4. The field data were measured by Pomeroy and Male (1992) near Saskatoon, Canada. The simulated and observed values show good agreement, and the mass concentration can be described by the function $c_m=\mathrm{58}/z-\mathrm{8}$ (unit: µg m⁻³).

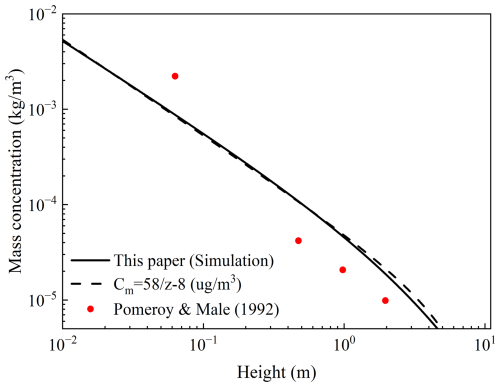
Figure 4 Comparison of simulated mass concentration (this paper, with fitting curve) and field observations (Pomeroy and Male, 1992) for $u_{*}=\mathrm{0.31}$ m s⁻¹ and T=265 K.

In the field observations of Schmidt (1982) in Wyoming, they tested 10 min data, in which SPC (snow-particle counter) was used for measuring vertical profiles of blowing snow concentration, number flux, particle size, and particle speed at six heights of 0.05, 0.10, 0.20, 0.35, 0.50, and 1.00 m above the surface; anemometers were used for measuring wind speed at five heights of 0.16, 0.5, 1.0, 1.6, and 2.4 m above the surface; and a thermocouple psychrometer was used for measuring air humidity. In the field observations of Pomeroy and Male (1992) in Saskatoon, they tested 7.5 min data, in which wind speed was measured with anemometers at six levels, logarithmically spaced from 0.35 to 3.0 m above the snow surface; air temperature was measured by thermistors at five levels from 0.1 to 2 m above the snow surface; humidity was measured by lithium chloride electrochemical hygrometers at five levels in tandem with the thermistors; and the flux of blowing snow particles was measured with optoelectronic snow particle detectors located at five levels, spaced logarithmically from 0.01 to 2 m above the snow surface, with the particle flux converted to a mass flux.

Suspension sublimation rates predicted by different blowing snow models are intercompared, as shown in Fig. 5. The models generally have similar laws, but the value of the predictions by the bulk model PIEKTUK-B (Déry and Yau, 1999) is smaller than those of the spectral models, WINDBLAST (Mann, 1998), SNOWSTORM (Bintanja, 2000), and PIEKTUK-T (Déry et al., 1998), which resolve particle size distributions across different bins. This discrepancy arises because the bulk model averages particle properties by integrating across sizes, thereby filtering out certain turbulence characteristics. Moreover, all the above models treat the saltation layer as a lower boundary, neglecting sublimation within this layer by assuming the RH of 100 %. In contrast, Huang and Shi (2017) considered the moisture transport within the saltation layer and calculated suspension sublimation initiating from the surface. This consideration of moisture transport results in continuous sublimation in both the saltation and suspension layers, enhancing the sublimation rate due to a higher lapse rate of water vapor. In our model, particle fragmentation further strengthens sublimation by modifying the particle size distribution. Notably, the peak of the black curve occurs at a lower position (0.05 m) compared to other curves (0.1 m), indicating that accounting for fragmentation significantly alters the transport structure. Overall, these findings suggest that particle size distribution plays a crucial role in DBS sublimation.

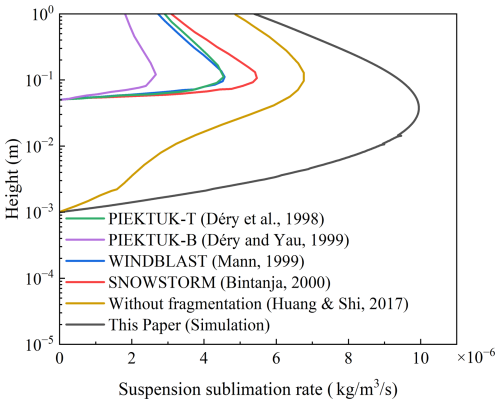
Figure 5 Comparison of suspension sublimation rates predicted by different blowing snow models. The black line shows the sublimation rate of suspension when snow particle fragmentation is considered (this study), while the remaining curves represent simulation results without fragmentation from several existing models: PIEKTUK-T (Déry et al., 1998), PIEKTUK-B (Déry and Yau, 1999), WINDBLAST (Mann, 1998), and SNOWSTORM (Bintanja, 2000), without fragmentation (Huang and Shi, 2017) and with fragmentation (this paper). $u_{*}=\mathrm{0.87}$ m s⁻¹, z₀=0.001 m, and T₀=253.16 K.

3 Results

3.1 Fragmentation effects on particle size distribution

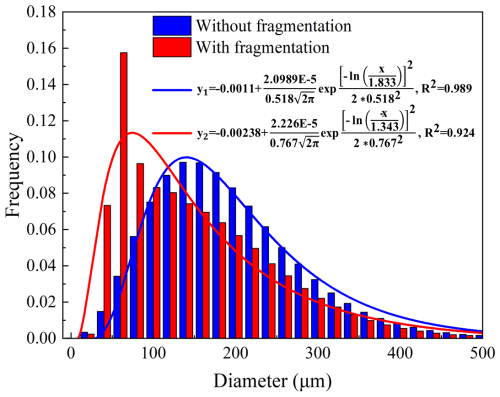
The fragmentation of snow particles firstly leads to changes in their size distribution, releasing numerous smaller particles. Simulations were conducted to analyze the effect of fragmentation on particle size distribution.

Simulations are conducted with the same friction velocity of $u_{*}=\mathrm{0.45}$ m s⁻¹ and the same initial mean particle size of $\overline{d}=\mathrm{200}$ µm. As shown in Fig. 6, the size distribution pattern for particles, without considering fragmentation, follows the log-normal distribution function. When considering fragmentation, the proportion of smaller-sized particles (<100 µm) increases, while the overall proportion of larger-sized particles decreases. This results in a decrease in the average particle size.

Figure 6 Particle size distribution with and without considering the particle fragmentation in the simulation.

3.2 Fragmentation effects on snow particle number

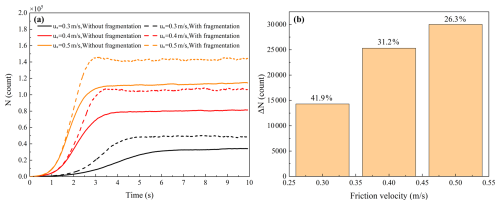
Figure 7 presents the temporal evolution of the concentration of snow particles suspended in the air. It is observed that the number of saltation particles increases over time until reaching a steady state, regardless of the presence of fragmentation. It is noted that, when fragmentation processes are taken into consideration, the steady-state concentration of snow particles is consistently higher at all friction velocities. Under low friction velocity ($u_{*}=\mathrm{0.3}$ m s⁻¹), the particle number increases by 42 %. Under high friction velocity ($u_{*}=\mathrm{0.5}$ m s⁻¹), the particle number increases by 26 %. The increase in particle number resulting from fragmentation is notably more pronounced at lower friction velocities. This is because, at lower friction velocities, the baseline number of particles is relatively small; therefore, even a modest absolute increase due to fragmentation leads to a larger relative increase ratio.

Figure 7 (a) Saltating particle number variation with time under wind conditions of $u_{*}=\mathrm{0.3}$, 0.4, and 0.5 m s⁻¹. (b) Increment number and ratios of saltation snow particles in the air.

3.3 Fragmentation effects on mass concentration and mass flux

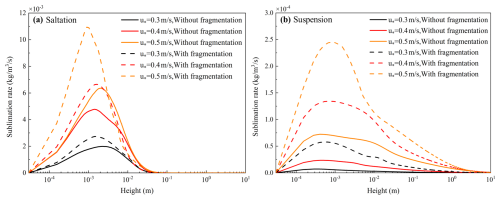
For near-surface particle transport, Fig. 8 illustrates the variation in the mass concentration of saltating and suspended particles with height. The fragmentation of snow particles enhances the concentration of both saltating and suspended particles, at levels close to the surface. Figure 8a depicts the mass flux vs. height above the surface, showing that fragmentation enhances the transport of saltating particles near the ground. This is because the fragmentation of snow particles increases the number of airborne saltation particles, and more saltation particles take part in the splash process, further increasing the air saltation particle number. When the friction velocity is 0.3 m s⁻¹, the relative increment proportion of fragmentation mass concentration is 19 %; when the friction velocity is 0.5 m s⁻¹, it is 3 %, which means the fragmentation has stronger effects on the mass concentration under weak wind conditions.

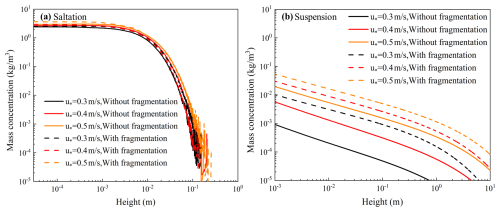
Figure 8 Simulated mass concentration of (a) saltation and (b) suspension particles with/without considering fragmentation, under wind conditions of $u_{*}=\mathrm{0.3}$, 0.4, and 0.5 m s⁻¹.

For particles suspended further aloft, it is shown in Fig. 8b that the mass concentration of the suspended snow particles at the same height is higher and that the overall suspension height is higher when considering snow particle fragmentation. This is because of smaller and lighter particles created by snow fragmentation, which have a higher possibility of being entrained and suspended to higher levels.

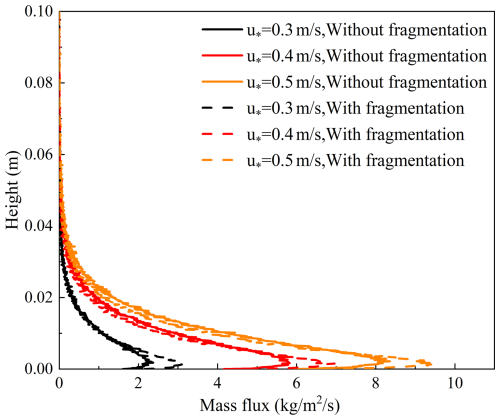
For the same friction velocity, the mass flux of near-surface (<0.01 m) snow particles is larger with snow fragmentation than without, as shown in Fig. 9. It is concluded that fragmentation increases snow particle transport.

Figure 9 Simulated horizontal mass flux profile of snow particles with/without considering fragmentation, under wind conditions of $u_{*}=\mathrm{0.3}$, 0.4, and 0.5 m s⁻¹.

3.4 Fragmentation effects on sublimation rate

The sublimation rates of saltating and suspended snow particles increase with fragmentation implemented in the model, as shown in Fig. 10. This enhancement is more significant at lower friction velocities, indicating that snow particle fragmentation has a more profound effect on sublimation under such conditions.

Figure 10 Simulated sublimation rate vs. height. (a) Saltation particles. (b) Suspension particles.

To evaluate the overall effect, we calculate the height-integrated sublimation rate of saltation particles and find that, for a friction velocity of 0.3 m s⁻¹, the average sublimation rate of saltation particles increases by 20 % due to fragmentation, from $\mathrm{1.56}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{1.87}\times {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻² s. However, for a friction velocity of 0.5 m s⁻¹, this increase drops to 3 %, from $\mathrm{4.37}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{4.49}\times {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻² s, indicating that the impact of fragmentation on the sublimation rate diminishes under stronger wind conditions. This trend can be attributed to the fact that higher friction velocities enhance particle transport and mixing, which reduces the relative contribution of fragmentation to the overall sublimation process.

A similar behavior is observed for suspension particles at higher altitudes. For a friction velocity of 0.3 m s⁻¹, the average sublimation rate of suspension particles increases by 8×, from $\mathrm{1.09}\times {\mathrm{10}}^{-\mathrm{6}}$ to $\mathrm{9.83}\times {\mathrm{10}}^{-\mathrm{6}}$ kg m⁻² s, when fragmentation is considered. For a friction velocity of 0.5 m s⁻¹, this growth decreases to 54 %, from $\mathrm{3.70}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{5.69}\times {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻² s. While the effect of fragmentation on sublimation remains significant at higher friction velocities, the reduction in growth indicates that other factors, such as increased turbulence and particle dispersion, may play a more prominent role in driving sublimation under these conditions.

Overall, snow fragmentation has a more pronounced effect on the sublimation rate of suspension particles than for saltation particles. This difference can be attributed to the longer residence time and greater exposure of suspension particles to the airflow, which amplifies the impact of fragmentation on their sublimation rates. In contrast, saltation particles, which are closer to the surface and are subject to more frequent impact and splash processes, experience a relatively weaker influence from fragmentation as wind speed increases.

3.5 Effects of size distribution on fragmentation

Size distribution of particles obeys the Gamma distribution function, characterized by the parameters α (shape factor) and β (scale factor), as defined in Eq. (5). The averaged size is defined as $\stackrel{\mathrm{‾}}{d}=\mathit{\alpha }\times \mathit{\beta }$. The shape factor α determines the peak position of size distribution, while the scale factor β controls the width of the distribution – the larger the value of β, the broader the size distribution.

To investigate the effects of average particle diameter and size proportion on the results, we have set up nine cases, whose parameters are shown in Table 1.

Table 1 Parameters of α and β settings for all simulation cases.

3.5.1 Average particle diameter

The effect of shape parameter α at a constant scale parameter β=40 is tested in cases 1–3. The variation in the number of particles N with time is shown in Fig. 11a. The results show that, as α increases from 5 to 10, the average article diameter becomes larger (as shown in the insets), leading to a significant increase in the total number of fragmentation-produced particles N over time. This indicates that distributions with a larger average particle diameter result in greater particle production through fragmentation.

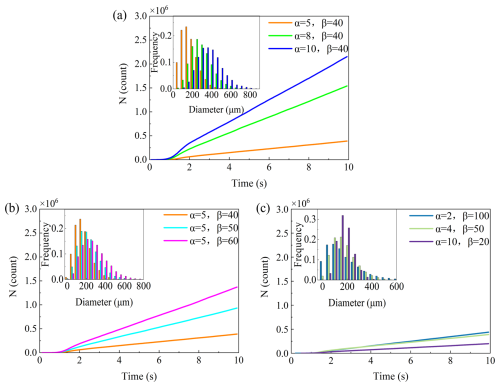
Figure 11 Number of snow particles as a function of time. (a) Variation in shape parameter α, scale parameter β=40, const. (b) Variation in scale parameter β, shape parameter α=5, const. (c) α×β = average diameter $\overline{d}=\mathrm{200}$ µm.

In contrast, cases 4–6 investigate the influence of increasing the scale parameter β from 40 to 60 while keeping the shape parameter α=5 constant. With larger β, the distribution becomes broader and contains more larger particles, as shown in the insets. As a result, the total particle count N produced by fragmentation also increases with β. This suggests that not only the average particle size but also the width of the initial size distribution (characterized by β) has a significant impact on fragmentation outcomes.

Overall, both a higher average particle diameter (increasing α) and a broader size distribution (increasing β) enhance the extent of fragmentation and increase the production rate of small particles during drifting snow.

3.5.2 Size proportion

We configured cases 7–9 with the same mean diameter $\overline{d}=\mathrm{200}$ µm but different α and β parameters. These differences in α and β result in particle systems with varying size distributions. In these three cases, the proportion of particles with diameter larger than the threshold diameter is 73 % (blue), 85 % (green), and 96 % (purple), respectively.

As shown in Fig. 11c, the fragmentation is significant under the same mean averaged diameter when the large particles take a higher proportion in a granular system. The fragmentation number of snow particles with different particle size distribution increases almost linearly with time. This is because, if there are only snow particles with a larger size than the threshold diameter, more snow particles will join the fragmentation.

4 Discussion

In this study, we investigated how particle fragmentation affects snow transport and sublimation processes. We found that, when fragmentation is considered, the particle size distribution is modified, leading to an expected increase in snow sublimation during DBS. This occurs because fragmentation generates a higher number of smaller-sized particles, increasing the average specific surface area of transported snow. Since the sublimation rate is directly proportional to the specific surface area, the presence of smaller particles enhances sublimation. Additionally, the smaller particles produced by fragmentation reduce the averaged diameter of surface snow particles, leading to a lower threshold velocity of aerodynamic entrainment. As a result, more particles are lifted from the surface and transported by wind, further increasing the number and decreasing the surface roughness available for sublimation during transport. Moreover, the sublimation rate is directly proportional to the mass concentration of drifting snow particles, amplifying the overall sublimation effect.

However, fragmentation has a limited impact on the overall mass flux profile, with notable changes primarily observed in the near-surface layer. Specifically, when fragmentation is considered, the mass flux below 0.01 m increases. This increase is mainly attributed to changes in the mass concentration of suspension particles, as the mass concentration of saltation particles remains largely unchanged. This indicates that fragmentation predominantly occurs within the saltation layer and primarily contributes to an increased concentration of suspended particles within this near-surface region. This is because smaller fragmented particles are more easily entrained and maintained in the airflow within the near-surface layer.

Moreover, the fragmentation of the snow particles produces smaller-sized fragments that remain in saltation and suspension, while those deposited on the surface alter its size distribution of the surface. These changes in particle size distribution influence snow surface properties, such as albedo (Manninen et al., 2021), snow microstructure, static snow cover sublimation rate (Albert and Mcgilvary, 1992), and surface roughness. Larger snow particles reduce multiple scattering because light travels longer paths within larger particles, leading to increased absorption, particularly in the near-infrared spectrum. Thus, larger snow particles have a lower snow albedo. Smaller snow particles, with their higher specific surface area, increase multiple scattering within the snowpack and reduce the absorption of solar radiation, leading to a higher albedo, especially in the visible spectrum. The variation in snow surface size distribution due to fragmentation in DBS influences the surface energy balance by changing the snow surface albedo. Additionally, smaller grains affect the snow thermal conductivity, the mechanical stability, and the retention of impurities, which can reduce albedo and accelerate snowmelt. Therefore, this variation in snow surface properties plays a critical role in determining the energy exchange between the snowpack and the atmosphere.

These findings highlight the importance of incorporating particle fragmentation processes into spatially distributed surface energy balance models. This can improve the accuracy of snowpack mass balance assessments, enhance predictions of seasonal snow dynamics, and better represent snow transport and sublimation processes in atmospheric and climate models.

5 Conclusions

In this study, we carried out a numerical simulation to investigate the snow particle fragmentation and sublimation in drifting and blowing snow (DBS). The model is based on an Euler–Lagrangian method to track the trajectories of individual snow particles. To account for sublimation processes, we implemented the Thorpe and Mason (1966) model, which calculates the sublimation rate of snow particles based on their size, their temperature, and the surrounding environmental conditions.

The simulation incorporates key physical processes in DBS, including particle–particle interactions and fragmentation due to collisions. The model was validated with experimental data from previous studies. This integrated method provides a detailed understanding of the dynamics of snow particles and their sublimation during snow particle transport.

In this study, we developed a drifting snow model that incorporates the snow particle fragmentation process. This model simultaneously accounts for both the dynamic processes, including the movement of saltation and suspension particles, and the thermodynamic processes, such as snow sublimation. The model was validated using experimental data from previous studies, assessing their performance and reliability. This integrated approach offers a comprehensive understanding of snow particle dynamics and sublimation during transport in DBS events.

Based on this model, this work investigates the significant role of snow particle fragmentation in DBS. We find that fragmentation not only alters the particle size distribution but also increases the number, concentration, and mass flux of particles in DBS. Subsequently, these processes affect the sublimation rate of airborne snow particles. Specifically, fragmentation reduces the average particle size, creating smaller particles that are more prone to sublimation. The effects of fragmentation on sublimation are more pronounced for suspension particles than for saltation particles, particularly under low wind conditions.

We analyzed the impact of particle size distribution on the results and found that, when the average particle size is larger or when the proportion of large particles is higher, fragmentation in the air becomes more significant, generating more small particles. Consequently, the overall sublimation rate increases. These results underscore the importance of accurately representing fragmentation and size distributions in snow transport models.

Our simulation results are consistent with previous observational data, suggesting the validity of the model. Furthermore, a comparison of simulation results considering or ignoring fragmentation of snow particles shows that our sublimation rates are 2–4 times higher than other previous model results. This is because fragmentation reduces the snow particle's size and increases the number of airborne particles that are more susceptible to sublimation. By integrating fragmentation into the numerical model, this study marks a significant step forward in understanding and quantifying the effects of particle dynamics on snow sublimation.

Our work provides insights into the complex dynamics of DBS. It provides a deeper understanding of the physical process of snow particle fragmentation during saltating/suspending in the air. This indicates the importance of fragmentation in the numerical models of DBS. However, the model used is a two-dimensional numerical model, which could not be applied to larger regions, especially for complex terrains. Therefore, the expansion of this model into a three-dimensional drifting snow model in the future is necessary. Moreover, crystal shape/habitus is another important factor in influencing the sublimation rate of snow particles, such as density, size, and specific surface area. Future numerical simulation should be carried out regarding crystal habitus factors. Besides, there is a lack of observational data on the evolution of particle size distributions during drifting and blowing snow processes. Furthermore, the influence of crystal mechanical properties on the fragmentation process is still unclear. To further improve the model, detailed observations exploring how the habitus of various crystals affects fragmentation and subsequent particle size distributions are needed.

The simulation results provide detailed insights into the physical processes of particle–atmosphere momentum transfer and heat and mass transfer from a single-particle perspective. This work provides the theoretical foundation and prediction method for accurately assessing the amount of snow sublimation during DBS. These findings have important implications for improving the representation of snow transport and sublimation processes in atmospheric and climate models, which can enhance predictions of snow mass balance and its broader environmental impacts.