Evaluating NO_x fate and organic nitrate chemistry from α-pinene oxidation using stable oxygen and nitrogen isotopes

The oxidation of biogenic volatile organic compounds (BVOCs) such as α-pinene in the presence of nitrogen oxides (NO_x= NO + NO₂) initiates complex photochemical processes that produce organic nitrates (RONO₂) and influence atmospheric oxidation capacity, air quality, and the fate of reactive nitrogen. However, tracking the chemical fate of RONO₂ remains challenging as it includes pathways such as renoxification, aerosol partitioning, deposition, and/or hydrolysis to nitric acid (HNO₃). Stable oxygen (Δ¹⁷O, δ¹⁸O) and nitrogen (δ¹⁵N) isotope measurements can provide a unique tool to probe these processes, as NO_y species can exhibit distinct isotopic signatures due to characteristic oxygen-transfer dynamics and isotope fractionation. Here, we present chamber experiments of α-pinene oxidation in the presence of NO_x under a range of oxidant and photochemical conditions, reporting the Δ¹⁷O, δ¹⁸O, and δ¹⁵N values of simultaneously collected NO₂, HNO₃, and particulate nitrate (pNO₃), the latter of which derived predominantly from RONO₂ in the conducted experiments. A strong linear relationship between δ¹⁸O and Δ¹⁷O across all NO_y species (r=0.992; p<0.01) supports a two-endmember mixing model, in which oxygen atoms are transferred from isotopically distinct sources that include ozone (O₃) with high δ¹⁸O and Δ¹⁷O as well as peroxy and hydroxyl radicals (RO₂, HO₂, OH) with lower values. Nitrogen isotope fractionation, quantified as the difference in δ¹⁵N values (Δδ¹⁵N), revealed consistently positive Δδ¹⁵N(HNO₃–NO₂) values (+28.9 ± 13.4 ‰ in daytime experiments; +22.2 ± 1.4 ‰ at night) and negative Δδ¹⁵N(pNO₃–NO₂) values (−13.6 ± 5.8 ‰ in daytime experiments). This reflected distinct formation pathways and isotope effects including NO_x photochemical cycling, thermal dinitrogen pentoxide (N₂O₅)–nitrate radical (NO₃)–NO₂ equilibrium, and HNO₃ production mechanisms. Box-model simulations based on Δ¹⁷O values as a constraint were conducted using a newly developed gas-phase mechanism, which reproduced Δ¹⁷O(NO₂) and Δ¹⁷O(pNO₃) (compared to simulated Δ¹⁷O(RONO₂)) accurately, with an average model bias of 0.9 ± 2.4 ‰ (R²=0.98) and −1.4 ± 2.4 ‰ (R²= 0.55 and R²= 0.97 when excluding one outlier), respectively. We further empirically derived important isotopic parameters such as the Δ¹⁷O value transferred from O₃ through comparison of model-simulated oxygen atom source contributions with observed Δ¹⁷O values for NO₂ and pNO₃ across experiments. This yielded best-fit slopes of 39.4 ± 0.6 ‰ for NO_x photochemical cycling and 41.7 ± 1.2 ‰ for RONO₂ formation, consistent with near-surface observations of Δ¹⁷O in the terminal oxygen atom of O₃. Despite the agreement with NO₂ and RONO₂, accurately simulating Δ¹⁷O(HNO₃) proved challenging. Sensitivity tests revealed that model biases likely stemmed from a combination of factors including background HNO₃ chamber blanks affecting low-NO_x experiments, missing N₂O₅ heterogeneous hydrolysis under nighttime conditions, and an overestimation in the Δ¹⁷O(HNO₃) mass balance resulting from the NO₂+ OH reaction, which was improved by adjusting the contribution from ($\mathrm{2}/\mathrm{3}$)Δ¹⁷O(NO₂) to ($\mathrm{1}/\mathrm{2}$)Δ¹⁷O(NO₂). These adjustments reduced the average model bias in Δ¹⁷O(HNO₃) from 6.7 ± 3.3 ‰ (R²= 0.39) in the base mechanism to 1.6 ± 1.3 ‰ (R²= 0.48) in the modified mechanism. These findings demonstrate the utility of Δ¹⁷O and δ¹⁵N for disentangling nitrate formation mechanisms, while also highlighting critical gaps in our understanding of the isotope dynamics involving HNO₃ formation. Future experimental work targeting isolated HNO₃ pathways is essential to refine isotopic mass balance assumptions and nitrogen isotope fractionation.

1 Introduction

The oxidation of biogenic volatile organic compounds (BVOCs) in the presence of nitrogen oxides (NO_x= NO + NO₂) plays a central role in atmospheric chemistry, linking anthropogenic emissions to the formation of ozone (O₃), secondary organic aerosol (SOA), and the cycling of reactive nitrogen (Hoyle et al., 2011; Ng et al., 2017; Romer et al., 2016; Sato et al., 2022; Takeuchi and Ng, 2019; Xu et al., 2015b, 2020; Zare et al., 2018). A key product of this interaction is organic nitrate (RONO₂), which can be produced during both daytime and nighttime oxidation reactions involving monoterpenes (Ng et al., 2017). The RONO₂ product can act either as a temporary NO_x reservoir or a permanent sink, depending on its atmospheric fate (Fisher et al., 2016). Once formed, gas-phase RONO₂ can photolyze or oxidize, leading to the release of NO_x (“renoxification”); partition into the particle phase, resulting in particulate RONO₂(pRONO₂) (Beaver et al., 2012; Browne et al., 2014; Browne and Cohen, 2012; Fisher et al., 2016; Wang et al., 2023); and/or undergo dry and wet deposition, leading to the removal of reactive nitrogen from the atmosphere. Hydrolysis has emerged as an important pathway that directly converts RONO₂ into HNO₃, which acts as a permanent sink of NO_x, but the efficiency of this process remains challenging to constrain. Model investigations have suggested a lifetime of RONO₂ with respect to hydrolysis on the order of a few hours (Fisher et al., 2016; Zare et al., 2018). Experimental measurements have indicated a complex picture, in which not all monoterpene-derived RONO₂ hydrolyzes, and the lifetime of α-pinene-derived RONO₂ due to hydrolysis ranges on the order of minutes to hours and even days (Rindelaub et al., 2015; Takeuchi and Ng, 2019; Wang et al., 2021). Due to these complexities, the contributions of RONO₂ to HNO₃ and particulate nitrate (pNO₃) budgets remain poorly constrained. These uncertainties hinder our ability to predict NO_x lifetime and oxidant budgets, particularly in regions where high BVOC emissions coincide with anthropogenic NO_x such as forested areas near urban locations. Here, we develop new tools aimed at tracking RONO₂ contributions to HNO₃ and pNO₃ budgets using stable isotope measurements (Δ¹⁷O, δ¹⁸O, δ¹⁵N) in controlled α-pinene + NO_x chamber experiments, providing mechanistic insights into RONO₂ formation and loss pathways.

The natural variations of stable oxygen and nitrogen isotopes in various reactive nitrogen (NO_y= NO_x+ HNO₃+ RONO₂+ peroxy nitrate (RO₂NO₂)+ etc.) molecules offer a powerful diagnostic tool to investigate NO_x and oxidation chemistry (Michalski et al., 2012; Walters et al., 2018). Stable isotope constraints may also serve as quantitative tracers to distinguish daytime (e.g., RO₂+ NO) versus nighttime (e.g., NO₃ + BVOC) RONO₂ production, quantify the extent of RONO₂ hydrolysis to HNO₃, and constrain the relative contributions of organic versus inorganic pathways to the pNO₃ budget. Variations in oxygen (O) isotope ratios (i.e., ¹⁸O $/$ ¹⁶O and ¹⁷O $/$ ¹⁶O), commonly quantified using isotope delta notation (Δ¹⁷O and δ¹⁸O), offer a powerful proxy for assessing oxidation pathways involving NO_x photochemical cycling and nitrate formation (Albertin et al., 2021; Alexander et al., 2020; Michalski et al., 2003; Morin et al., 2011; Walters et al., 2024b). This is owing to distinct Δ¹⁷O and δ¹⁸O values exhibited by key atmospheric oxidants, which are proportionally transferred to NO_x during oxidation in the atmosphere (Hastings et al., 2003; Michalski et al., 2003). For instance, tropospheric O₃ has an elevated Δ¹⁷O with a mean value near 26 ‰ and the transferable terminal oxygen atom of O₃ (O${}_{\mathrm{3}}^{\mathrm{term}}$) exhibiting a Δ¹⁷O of 39 ± 2 ‰ and elevated δ¹⁸O near 126 ± 12 ‰ based on recent near-surface observations (Ishino et al., 2017; Vicars and Savarino, 2014). In contrast, other atmospheric oxidants such as RO₂ $/$ HO₂ and OH have Δ¹⁷O values assumed to be near 0 ‰ (Lyons, 2001; Walters et al., 2024a). The δ¹⁸O values of RO₂, HO₂, and OH have not been directly determined but are anticipated to be lower than the δ¹⁸O(O${}_{\mathrm{3}}^{\mathrm{term}}$) (Michalski et al., 2012).

The Δ¹⁷O isotopic composition provides a quantitative framework to evaluate NO_x photochemical cycling and the formation pathways of nitrate-containing species. This tracer has been widely used to assess NO_x oxidation and secondary product formation, as different atmospheric reactions impart distinct Δ¹⁷O signatures based on mass balance relationships (Alexander et al., 2020; Michalski et al., 2003; Morin et al., 2011; Walters et al., 2024b) (Table 1). For instance, mass balance calculations predict that Δ¹⁷O should differ between HNO₃ produced via the daytime NO₂+ OH reaction and that derived from the hydrolysis of daytime-formed RONO₂, where the Δ¹⁷O of the nitrooxy (−NO₃) functional group reflects a combination of NO + RO₂ oxidation. These differences make Δ¹⁷O a potentially powerful diagnostic tool for quantifying RONO₂ contributions to HNO₃ formation. Moreover, substantial Δ¹⁷O differences are expected between RONO₂ formed through daytime RO₂+ NO reactions and those formed via nighttime NO₃+ BVOC reactions. Thus, Δ¹⁷O could also be a useful tool for distinguishing between daytime and nighttime formation pathways of RONO₂, potentially aiding our ability to accurately predict the atmospheric burden of RONO₂. Despite major advances in applying Δ¹⁷O to constrain atmospheric nitrogen oxidation chemistry, a significant limitation remains: most Δ¹⁷O pathway estimates rely on theoretical mass balance assumptions that have only been empirically validated for a limited number of reactions (e.g., NO + O₃ and NO₂+ O₃) (Berhanu et al., 2012; Savarino et al., 2008). Further, we have yet to measure the Δ¹⁷O of RONO₂ directly. Expanding direct Δ¹⁷O measurements of key NO_y compounds under various oxidant conditions is critical for testing these assumptions.

Table 1 Expected Δ¹⁷O values for reactive nitrogen species formed via different oxidation pathways based on oxygen isotope mass balance. Each pathway is expressed as a weighted average of the Δ¹⁷O values of precursor oxidants based on the proposed reaction mechanism. Species include NO₂, HNO₃, and RONO₂.

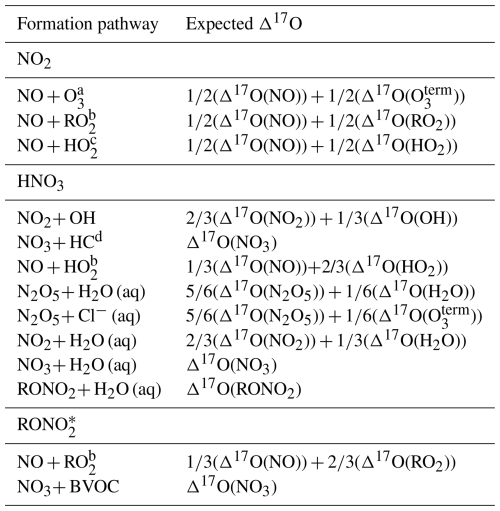
^a O${}_{\mathrm{3}}^{\mathrm{term}}=$ terminal oxygen in ozone. ^b RO₂= organic peroxy radical. ^c HO₂= hydroperoxyl radical. ^d HC = hydrocarbon. ^* Δ¹⁷O calculated from the nitrooxy (−NO₃) functional group.

The stable nitrogen (N) isotope ratio variations (δ¹⁵N) of NO_x and atmospheric nitrate have long served as a valuable proxy for evaluating precursor emission sources because of the preserved N mass between the precursor and oxidized end products (Elliott et al., 2019; Hastings et al., 2013). However, it is essential to consider that NO_x photochemical cycling and atmospheric nitrate formation processes can also induce significant mass-dependent fractionation effects (Freyer et al., 1993; Li et al., 2020; Walters et al., 2016; Walters and Michalski, 2015, 2016a). Field δ¹⁵N observations of NO₂ and nitrate have demonstrated the potential of these fractionation effects to offer additional valuable information concerning NO_x photochemical cycling and atmospheric nitrate formation (Albertin et al., 2021; Bekker et al., 2023; Li et al., 2021; Walters et al., 2018). Recently, a novel chemical mechanism was devised to model the nitrogen isotope fractionation associated with NO_x chemistry, called incorporating ¹⁵N into the Regional Atmospheric Chemistry Mechanism (i_NRACM) (Fang et al., 2021). Leveraging these advancements, we may utilize δ¹⁵N to gather supplementary quantitative insights into BVOC and NO_x interactions and their impact on RONO₂ and contributions to HNO₃ formation. Importantly, nitrogen isotope fractionation may lead to distinct δ¹⁵N values in HNO₃ and RONO₂ due to differences in their formation pathways. If characterized, these δ¹⁵N signatures could offer an additional tracer for quantifying RONO₂ contributions to the overall HNO₃ budget. While strides have been made in understanding δ¹⁵N fractionation during NO_x oxidation and equilibrium partitioning (Freyer et al., 1993; Li et al., 2020; Walters et al., 2016; Walters and Michalski, 2015), the specific nitrogen fractionation factors associated with HNO₃ and RONO₂ formation remain poorly constrained. Targeted laboratory and field studies are needed to directly measure these values and validate their use as diagnostic tools in atmospheric reactive nitrogen chemistry.

This study presents the first simultaneous measurements of Δ¹⁷O, δ¹⁸O, and δ¹⁵N in key NO_y species that included NO₂, HNO₃, and RONO₂ generated under controlled laboratory conditions involving α-pinene oxidation. By varying oxidant regimes to probe distinct RO₂ fates, we aimed to (1) determine the Δ¹⁷O and δ¹⁵N values of simultaneously collected HNO₃, NO₂, and RONO₂ under a range of atmospheric oxidation conditions; (2) evaluate the validity of oxygen isotope mass balance assumptions used in the formation of NO₂, HNO₃, and RONO₂; (3) characterize nitrogen isotope fractionation patterns across NO_y species; and (4) assess whether stable isotope measurements can provide meaningful constraints on the fate of RONO₂ in the atmosphere. Further, by incorporating recent isotope modeling frameworks (Walters et al., 2024a) we simulated the Δ¹⁷O values of various NO_y components and compared them against observations, yielding insights into the oxidative formation and Δ¹⁷O transfer dynamics during NO_x oxidation.

2 Methods

2.1 Chamber experiments

Photochemical and nighttime oxidation chamber experiments were conducted involving α-pinene, NO_x, and oxidant precursors at the Georgia Institute of Technology Environmental Chamber Facility that houses two 12 m³ Teflon reactors (Boyd et al., 2015). A total of six different initial experimental conditions were targeted, including five photochemical and one nighttime condition as previously reported (Blum et al., 2023) (Table 2). The experiments varied in their precursor concentrations and oxidant types, which were utilized to probe different α-pinene oxidation reactions involving OH, O₃, and NO₃ and RO₂ fates. Replicates were conducted in two of the targeted experimental conditions. The conducted chamber experiments follow previous laboratory protocols (Boyd et al., 2015; Nah et al., 2016; Takeuchi and Ng, 2019; Tuet et al., 2017). Briefly, photochemical experiments were conducted by injecting dry ammonium sulfate seed aerosol and precursor (i.e., α-pinene (99 % Sigma-Aldrich)), NO (Matheson), hydrogen peroxide (H₂O₂), or nitrous acid (HONO)) into the chamber, where either H₂O₂ or HONO was used as an OH precursor to simulate different extents of the RO₂+ NO pathway. Once the levels of precursors stabilized, the chamber lights were turned on, signifying the start of the photochemical experiments. The procedure used to generate HONO (e.g., the reaction of sodium nitrite with sulfuric acid) also leads to the generation of significant NO and NO₂ as a reaction by-product (Kroll et al., 2005; Tuet et al., 2017). For simulated nighttime conditions, dry ammonium sulfate seed aerosol and α-pinene were injected into the chamber, followed by flowing dinitrogen pentoxide (N₂O₅) for 15 min (Boyd et al., 2015; Takeuchi and Ng, 2019). The N₂O₅ injection corresponded to the start of the nighttime experiments. The N₂O₅ was generated by reacting NO₂ from a gas cylinder (Matheson) with O₃ in a flow tube prior to the introduction to the chamber at a ratio of 2:1 to minimize O₃ concentrations in the chamber to avoid ozonolysis. All experiments were conducted at a relative humidity (RH) and temperature of 30 % and 22 °C, respectively. Before each experiment, the chamber was flushed with zero air and irradiated for at least 24 h.

Table 2 Summary of measured NO_y precursor concentrations and targeted H₂O₂ concentrations for the chamber experiments. All experiments were conducted using dry ammonium sulfate seed at a fixed temperature (22 °C) and relative humidity (30 %).

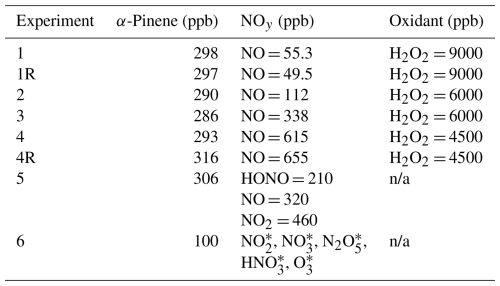
^* The emission rates of NO₂, NO₃, N₂O₅, HNO₃, and O₃ into the chamber for a 20 min injection period were modeled based on a flow tube simulation of the reaction of NO₂ with O₃ with a residence time of 70 s.
n/a: not applicable.

Continuous online measurements of NO, NO₂, and O₃ were conducted using chemiluminescence (Teledyne 200EU), cavity-attenuated phase shift (CAPS), and an O₃ monitor (Teledyne T400). A chemical ionization mass spectrometer (CIMS) was used for various NO_y measurements including HONO and HNO₃ (Huey et al., 1998). The α-pinene decay was monitored using a gas chromatography flame ionization detector (GC-FID; Agilent 7890A). Gaseous organic nitrate was monitored using a filter inlet for gases and aerosols (FIGAERO) coupled to a high-resolution time-of-flight iodide chemical ionization mass spectrometer (HR-ToF-I-CIMS) with particles collected on a Teflon filter (Lopez-Hilfiker et al., 2014; Nah et al., 2016; Takeuchi et al., 2022; Takeuchi and Ng, 2019; Wang et al., 2023). Aerosol composition was measured using a high-resolution time-of-flight aerosol mass spectrometer (HR-ToF-AMS) that included measurement of non-refractory organics (Org), sulfate (SO₄), nitrate (NO₃), and ammonium (NH₄) (DeCarlo et al., 2006; Farmer et al., 2010). Water-soluble aerosol components were also measured using a particle-into-liquid sampler (PILS) coupled to ion chromatography (IC) (Orsini et al., 2003). This method differs from the HR-ToF-AMS measurements, which quantify total aerosol composition, including both water-soluble and water-insoluble components. For example, nitrate measured by the AMS represents total pNO₃, whereas nitrate measured by the PILS-IC system corresponds only to the water-soluble fraction of pNO₃.

Collections of various NO_y gaseous and aerosol components, including HNO₃, NO₂, and pNO₃, were conducted using a modified version of the ChemComb Speciation Cartridge (CCSC) with an extended denuder body for offline concentration and isotope composition analysis (Blum et al., 2020, 2023). Briefly, the CCSC collections began when the aerosol mass spectrometer data indicated the nitrate and secondary organic aerosol mass concentrations had peaked. The CCSC samples were collected at 8 L min⁻¹ for up to 4 h. To maintain the chamber integrity, zero air was used to dilute at 25 L min⁻¹ once the aerosol peak was reached and CCSC sample collection initiated. The CCSC denuder bodies were replaced one to four times depending on the concentration of NO_x in the chamber. For each experiment, a single filter was used in the CCSC. In addition to the chamber experiments, samples were collected directly from the NO₂ tank (Matheson), which was used in the generation of N₂O₅ for the nighttime oxidation experiments.

Honeycomb denuders were coated for the selective collection of HNO₃ (captured as nitrate (NO${}_{\mathrm{3}}^{-}$)) and NO₂ (captured as nitrite (NO${}_{\mathrm{2}}^{-}$)). A detailed description of the coating solutions, denuder preparation, and denuder extraction was previously described, and the pooled isotope reproducibility for both HNO₃ and NO₂ was ± 1.7 ‰, ± 1.8 ‰, and ± 0.7 ‰ for δ¹⁵N, δ¹⁸O, and Δ¹⁷O for these chamber experiments (Blum et al., 2023). The collection of PM_2.5 was conducted using a quartz filter (Cytiva Whatman, Grade QM-A; 47 mm diameter) that was housed in the ChemComb filter cartridge positioned downstream of the denuders. Prior to use, filters were pre-combusted at 550 °C overnight and stored in an airtight container. Quartz filters were selected because they facilitate efficient water-based extraction of collected material and tolerate high-temperature pre-cleaning to remove organic contaminants. The filter samples were extracted in 20 mL of Milli-Q water (> 18.2 MΩ) and allowed to leach for at least 1 week at room temperature. This method was conducted to enable hydrolysis of collected organic nitrate particles as previous studies have shown organic nitrate derived from α-pinene oxidation to hydrolyze to NO${}_{\mathrm{3}}^{-}$ in water with a lifetime of 8.8 h at pH = 6.9 (Rindelaub et al., 2016) and 2.5 h at pH = 7.44 (Wang et al., 2021). Other types of organic nitrate, such as secondary nitrates, have been reported to be stable in water, especially at a neutral pH (Wang et al., 2021). The efficiency of our filter extraction technique for facilitating organic nitrate hydrolysis was evaluated using the online AMS and PILS data. After the filters were leached, the filters were removed, and the samples were shipped to Brown University where they were placed in a freezer until subsequent concentration and isotope analysis. For all sample media types, including denuders and filters, lab blanks were frequently taken. These blanks were prepared, handled, and analyzed the same way as all samples.

2.2 Concentration and isotope analysis

The denuder and filter extracts were analyzed for their NO${}_{\mathrm{2}}^{-}$ and NO${}_{\mathrm{3}}^{-}$ content using a standardized colorimetric technique (e.g., EPA Methods 353.2) or ion chromatography, as previously described (Blum et al., 2020, 2023). The limits of detection (LOD) were approximately 0.1 µmol L⁻¹ and 0.3 µmol L⁻¹ for NO${}_{\mathrm{2}}^{-}$ and NO${}_{\mathrm{3}}^{-}$ via colorimetric analysis and 3.0 µmol L⁻¹ for NO${}_{\mathrm{2}}^{-}$ via ion chromatography. For all analyses, the average percent relative standard deviation was below 5 %. The NO${}_{\mathrm{2}}^{-}$ and NO${}_{\mathrm{3}}^{-}$ concentrations from denuder blank extractions used for NO₂ (n= 5) and HNO₃ (n= 5) collection were below the detection limits. Significant blanks were observed in the quartz filter extracts (1.5 ± 0.2 µmol L⁻¹; n= 5), which we refer to hereinafter as a method blank.

The δ¹⁵N, δ¹⁸O, and Δ¹⁷O isotope compositions were analyzed using the denitrifier method for NO${}_{\mathrm{3}}^{-}$ samples (e.g., from HNO₃ denuder and aerosol filter extracts) following Casciotti et al. (2002), Kaiser et al. (2007), and Sigman et al. (2001) and the sodium azide and acetic acid buffer method for NO${}_{\mathrm{2}}^{-}$ samples (from NO₂ denuder extracts), following McIlvin and Altabet (2005) and Walters and Hastings (2023). Briefly, 20 nmol of NO${}_{\mathrm{3}}^{-}$ or NO${}_{\mathrm{2}}^{-}$ samples was converted to N₂O, which is extracted, purified, concentrated, and injected into a continuous-flow isotope ratio mass spectrometer (IRMS) for δ¹⁵N and δ¹⁸O determination from $m/z$ measurement at 44, 45, and 46. In a separate batch analysis, 50 nmol of NO${}_{\mathrm{3}}^{-}$ or NO${}_{\mathrm{2}}^{-}$ was converted to N₂O, decomposed to O₂ using a gold tube heated at 770 °C, and analyzed at $m/z$ 32, 33, and 34 for Δ¹⁷O determination (Kaiser et al., 2007; Walters and Hastings, 2023). To minimize potential memory effects from residual O₂ in the gold tube and headspace trapping system, samples were grouped and analyzed in separate batches based on their expected Δ¹⁷O values. Specifically, NO₂ samples (high Δ¹⁷O), HNO₃ (moderate Δ¹⁷O), and pNO₃ (low Δ¹⁷O) were each analyzed in separate batches. Analytical blanks associated with the conversion of NO${}_{\mathrm{3}}^{-}$ and/or NO${}_{\mathrm{2}}^{-}$ to N₂O or O₂ for subsequent IRMS analysis were assessed for each batch and were always below the detection limit (∼ 0.2 nmol). These blanks are not anticipated to affect the analytical precision of the reported isotope values. The samples were calibrated with respect to internationally recognized NO${}_{\mathrm{3}}^{-}$ standards (IAEA-NO-3, USGS35, USGS34) or NO${}_{\mathrm{2}}^{-}$ reference materials (RSIL-N7373 and RSIL-10219) (Böhlke et al., 2003, 2007). In line with the identical treatment principle, the reference materials are treated the same as samples, including matching concentrations, sample amounts, and reagent additions, to ensure analytical consistency. The pooled standard deviations of the reference materials were ± 0.1 ‰ and ± 0.6 ‰ for δ¹⁵N and δ¹⁸O of the NO${}_{\mathrm{3}}^{-}$ standards (n = 78) and ± 0.3 ‰ and ± 0.3 ‰ for δ¹⁵N and δ¹⁸O of the NO${}_{\mathrm{2}}^{-}$ reference materials (n= 15), respectively. The Δ¹⁷O had a pooled standard deviation of ± 0.6 ‰ (n= 53).

All isotope measurements are reported relative to reference standards using delta (δ) notation (Eq. 1):

$$\begin{array}{}\text{(1)}& \mathit{\delta }=\left({\displaystyle \frac{R_x}{R_{\mathrm{SD}}}}-\mathrm{1}\right).\end{array}$$

where R is the ratio of the abundance of the heavy to the light isotope (i.e., ¹⁵N $/$ ¹⁴N, ¹⁸O $/$ ¹⁶O, or ¹⁷O $/$ ¹⁶O), x denotes the sample, and SD is an abbreviation for standard (Sharp, 2017). The nitrogen and oxygen reference material includes atmospheric air and Vienna Standard Mean Ocean Water (VSMOW), respectively. Oxygen isotope mass independence (Δ¹⁷O) was quantified using the linear definition with a mass-dependent coefficient of 0.52, which is approximately representative of oxygen mass-dependent coefficients expected and observed in nature (Young et al., 2002) (Eq. 2):

$$\begin{array}{}\text{(2)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}={\mathit{\delta }}^{\mathrm{17}}\mathrm{O}-\mathrm{0.52}\times {\mathit{\delta }}^{\mathrm{18}}\mathrm{O}.\end{array}$$

The linear Δ¹⁷O approximation is commonly used to describe large mass-independent fractionation such as those related to O₃ reactions, and this definition is commonly used in the atmospheric chemistry community to track the influence of O₃ oxidation and Δ¹⁷O propagation into reactive components (Alexander et al., 2020; Kim et al., 2023; Michalski et al., 2003; Savarino et al., 2013).

2.3 Data reduction and corrections

Due to significant NO${}_{\mathrm{3}}^{-}$ blanks found in the pNO₃ filter extracts (i.e., method blank), the measured nitrate isotope values (δ¹⁵N, δ¹⁸O, and Δ¹⁷O) were corrected using a mass balance approach to isolate the isotopic composition of NO${}_{\mathrm{3}}^{-}$ generated within the chamber experiments (Eqs. 3–4):

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathit{\delta }\left(\mathrm{corrected},{\mathrm{pNO}}_{\mathrm{3}}\right)={\displaystyle \frac{\mathit{\delta }\left(\mathrm{measure}\right)-\left(f\left(\mathrm{blank}\right)\times \mathit{\delta }\left(\mathrm{blank}\right)\right)}{\mathrm{1}-f\left(\mathrm{blank}\right)}},\text{(4)}& {\displaystyle }f\left(\mathrm{blank},{\mathrm{pNO}}_{\mathrm{3}}\right)={\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{3}}^{-}\left(\mathrm{blank}\right)\right]}{\left(\left[{\mathrm{NO}}_{\mathrm{3}}^{-}\left(\mathrm{blank}\right)\right]+\left[{\mathrm{NO}}_{\mathrm{3}}^{-}\left(\mathrm{sample}\right)\right]\right)}},\end{array}$$

where [NO${}_{\mathrm{3}}^{-}$] corresponds to the concentration of NO${}_{\mathrm{3}}^{-}$ in either the blank or sample, and f(blank) corresponds to the NO${}_{\mathrm{3}}^{-}$ method blank fraction. The quartz filter method blanks had measured δ¹⁵N, δ¹⁸O, and Δ¹⁷O values of 1.6 ± 1.1 ‰, 16.6 ± 1.4 ‰, and 3.4 ± 0.5 ‰, respectively (n= 3). Blank corrections were made for all samples when f(blank) was less than 30 %. Samples with an f(blank) that exceeded 30 % were not reported for their isotope compositions, which included one out of eight quartz filter extracts. The uncertainty in the blank-corrected isotope deltas was calculated using a Monte Carlo simulation for 10 000 iterations and assuming a normal distribution using MATLAB. For the quality assurance criterion of an f(blank) < 30 %, the uncertainties were calculated to be less than 4.1 ‰, 1.4 ‰, and 0.9 ‰ for δ¹⁵N, δ¹⁸O, and Δ¹⁷O, respectively. These values are small compared to the observed ranges for pNO₃, which spanned 67.8 ‰ for δ¹⁵N, 29.3 ‰ for δ¹⁸O, and 10.4 ‰ for Δ¹⁷O and thus do not significantly affect the interpretation of isotope patterns. These uncertainties reflect the standard deviation of the 10 000 Monte Carlo iterations for each pNO₃ sample, which account for uncertainty in both the sample and method blank concentrations and isotope values. These reported uncertainties for chamber-derived pNO₃ isotope values represent total propagated error after blank correction, not the raw instrumental precision.

2.4 Aerosol nitrate composition

The relative contribution of organic aerosol nitrate (pNO₃(Org)) to the total pNO₃ was determined from two approaches. First, the relative proportion of pNO₃(Org), was calculated based on NO⁺ and NO${}_{\mathrm{2}}^{+}$ HR-ToF-AMS fragmentation as previously described (Farmer et al., 2010; Fry et al., 2009; Kiendler-Scharr et al., 2016; Xu et al., 2015a) (Eq. 5):

$$\begin{array}{}\text{(5)}& f\left({\mathrm{pNO}}_{\mathrm{3}},\mathrm{Org}\right)={\displaystyle \frac{\left(R_{\mathrm{obs}}-R_{\mathrm{AN}}\right)\left(\mathrm{1}+R_{\mathrm{ON}}\right)}{\left(R_{\mathrm{ON}}-R_{\mathrm{AN}}\right)(\mathrm{1}+R_{\mathrm{obs}})}},\end{array}$$

where f(pNO₃, Org) refers to the fraction of pNO₃(Org) to the total pNO₃, R refers to NO⁺ $/$ NO${}_{\mathrm{2}}^{+}$ fragments, and obs, AN, and ON refer to the observations, ammonium nitrate, and organic nitrate, respectively. The R_AN was obtained from routine ionization efficiency calibration of the HR-ToF-AMS using 300 nm ammonium nitrate aerosols and was 1.37. The R_ON was calculated based on the measured R_AN and the ratio of $R_{\mathrm{ON}}/R_{\mathrm{AN}}$ previously reported for similar conducted experiments (Takeuchi and Ng, 2019), resulting in an R_ON of 2.70 ± 0.29 and 3.86 ± 0.34 for photochemical and nighttime oxidation experiments, respectively. The second method for qualitatively determining f(pNO₃, Org) involved evaluating the relative change in the molar ratio of NH₄ $/$ SO₄, as an increase in NH₄ $/$ SO₄ has been observed to be associated with inorganic pNO₃ formation (Takeuchi and Ng, 2019).

2.5 Box-model simulations

The chamber experiments were simulated using the Framework for 0-D Atmospheric Modeling (F0AM) box model (Wolfe et al., 2016). The conducted model simulations primarily focus on accurately representing initial precursor oxidation (i.e., NO, α-pinene) and simulation of Δ¹⁷O observations. We chose not to include δ¹⁵N model simulations in this study due to several key uncertainties. These include incomplete knowledge of the δ¹⁵N values of all initial NO_y sources, limited constraints on isotope effects during NO_y oxidation and photolysis reactions, the potential for unquantified, species-specific fractionation due to chamber wall interactions, and potential for chamber blanks with unknown δ¹⁵N values. Given these limitations, δ¹⁵N modeling will be deferred to future work focused specifically on nitrogen isotope dynamics.

The model was initiated for each experiment using the measured precursor concentrations for NO, NO₂, HONO, and α-pinene before chamber lights were turned on or N₂O₅ was injected and using the targeted H₂O₂ concentrations. The pressure, temperature, and relative humidity were fixed at 1013 mbar, 295 K, and 30 %, respectively. The measured chamber light flux data were used. The model was run in two parts for the photochemical reactions, including from “lights on” to peak SOA mass concentration (part 1) and from aerosol decay and chamber dilution to the end of NO_y collections (part 2). For the nighttime experiments, the model simulations were conducted in three parts, including from the start of N₂O₅ injection to the end of N₂O₅ injection (part  1), from the end of N₂O₅ injection to peak SOA mass concentrations (part 2), and from the decay of organic aerosol and chamber dilution to the end of NO_y collection (part 3). The N₂O₅ injection was simulated by first modeling the NO₂ reaction with O₃ in the flow tube, considering a flow tube residence time of 70 s. The nighttime experiment was then simulated by allowing the flow tube products (i.e., NO₂, O₃, NO₃, HNO₃, and N₂O₅) to emit into the chamber for 20 min (part 1). Next, the experiment was modeled without the flow tube emission to the start of aerosol decay and chamber dilution (part 2) and from aerosol decay and chamber dilution to the end of NO_y collections (part 3). For both photochemical and nighttime experiments, the model simulations from the decay of organic aerosol to the end of NO_y collection included a chamber dilution rate constant (k_dil) of $\mathrm{3.47}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹, which was calculated based on the dilution flow rate (25 LPM) and chamber volume (12 m³). Sensitivity tests were performed to assess the impact of the selected k_dil on model results by evaluating a range of k_dil values.

A new chemical mechanism was developed, termed NO_x-α-pinene (NO_x-API), to accurately model the oxidation of NO_x and α-pinene (Tables S1–6). This mechanism was developed due to difficulties in simulating the initial decay of the aerosol precursors including α-pinene, NO, NO₂, and HONO for the various experimental conditions using either the Regional Atmospheric Chemical Mechanism, v2 (RACM2) (Goliff et al., 2013) or the Master Chemical Mechanism v3.3.1 (Jenkin et al., 1997; Saunders et al., 2003). The NO_x-API mechanism focuses on simulating α-pinene and NO decay along with NO_x oxidation but does not intend to accurately simulate SOA production and later-generation chemistry. The mechanism has the inorganic reactions in RACM2, including 16 species and 45 reactions. It also incorporates 29 organic species and 61 reactions to detail organic chemistry up to one generation past pinonaldehyde formation as well as the formation of pinonaldehyde-derived peroxyacetyl nitrate formation, with subsequent chemistry represented by a lumped approach. The α-pinene oxidation pathways involving OH, O₃, and NO₃, along with specific reactions of the resulting RO₂ with HO₂, NO, NO₃, and other RO₂ radicals, are also included. The photochemical oxidation of α-pinene largely follows the MCMv3.3.1 (Master Chemical Mechanism) (Saunders et al., 2003), incorporating two hydroxyl-nitrate isomers from OH/O₂/NO, including one tertiary (ONITa) and one secondary (ONITb) and the formation of a tertiary pinene carbonyl nitrate (ONITc). Nighttime oxidation chemistry integrates a recent mechanism for organic nitrate formation, producing pinene nitrate hydroperoxide, including one tertiary (ONITOOHa) and one secondary (ONITOOHb) via HO₂ reactions and dimer/pinene dinitrate (PDN) through RO₂ interactions (Bates et al., 2022). The box-model simulation is a gas-phase mechanism that does not explicitly model heterogeneous reactions or aerosol chemistry, such as organic nitrate hydrolysis. The impact of heterogenous reactions is considered in the evaluation of the Δ¹⁷O model simulation results compared to observations.

The Δ¹⁷O values of NO_y compounds were simulated using the newly developed NO_x-API mechanism modified using the InCorporating Oxygen Isotopes of oxidized reactive Nitrogen in the Regional Atmospheric Chemistry Mechanism, Version 2 (ICOIN-RACM2) model framework (Walters et al., 2024a). Briefly, the model framework tracks the transfer and propagation of Δ¹⁷O from O₃ into NO_y and O_x species. This mechanism tags the oxygen atoms transferred from O₃ into NO_y and O_x considering mass balance and reaction stoichiometry and enables the offline calculation of Δ¹⁷O based on the output of concentrations of various NO_y and HO_x isotopologues (Eq. 6):

$$\begin{array}{}\text{(6)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left(X\right)=f\left(Q\right)\times {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{O}}_{\mathrm{3}}^{\mathrm{term}}\right),\end{array}$$

where X refers to the various NO_y and O_x molecules and f(Q) is the fraction of oxygen atoms deriving from O${}_{\mathrm{3}}^{\mathrm{term}}$ for a particular molecule. The Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) represents the Δ¹⁷O value of the terminal and transferrable O atom of O₃, which was assumed to be 39 ± 2 ‰ based on recent near-surface collections of O₃ (Ishino et al., 2017; Vicars and Savarino, 2014) and O₃ generated from O₂ $/$ NO_x photochemical experiments conducted under normal temperature and pressure conditions (Michalski et al., 2014).

All Δ¹⁷O model simulations were conducted without considering chamber wall losses. The potential impact of wall loss was evaluated through sensitivity tests that involved comparing simulated Δ¹⁷O values. The sensitivity tests included a no-wall-loss case, wall loss involving O₃, NO, NO₂, HNO₃, N₂O₅, and organic nitrate based on previous reports from chamber experiments (Morales et al., 2021; Wang et al., 2014), and an elevated wall loss scenario, in which the wall loss rate constants were increased by 10 times to account for uncertainty since wall loss rates were not determined in this work (Table S7).

3 Results and discussion

3.1 Isotope observations

The Δ¹⁷O, δ¹⁸O, and δ¹⁵N measurements of NO_y species offer insight into the oxidation pathways and sources contributing to their formation. In this study, we focus on interpreting the Δ¹⁷O, δ¹⁸O, and δ¹⁵N of NO₂, HNO₃, and pNO₃ collected under a range of controlled experiments involving NO${}_x/\mathit{\alpha }$-pinene oxidation. These observations provide constraints on the relative importance of different oxidants (e.g., O₃, OH, RO₂) and reaction mechanisms, and they also allow us to test our understanding of oxygen isotope mass balance assumptions, O isotope transfer dynamics, and nitrogen isotope fractionation associated with NO_x oxidation. Below, we first discuss the observed patterns in oxygen isotopes (Δ¹⁷O and δ¹⁸O), followed by an examination of nitrogen isotope (δ¹⁵N) trends and their implications.

3.1.1 Δ¹⁷O and δ¹⁸O of NO_y

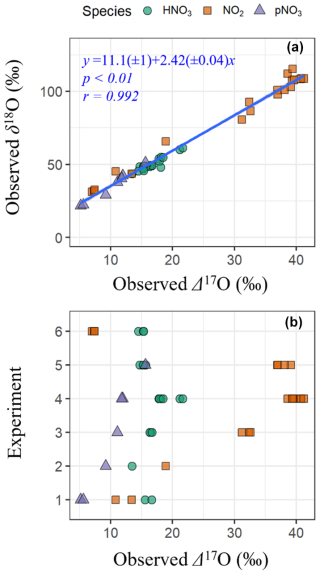
The observations indicate a significant relationship between δ¹⁸O and Δ¹⁷O across NO_y species (δ¹⁸O = 11.1(± 1.0) + 2.42(± 0.04) × Δ¹⁷O; r= 0.992 ; p<0.01) (Fig. 1a). The strong linear relationship between δ¹⁸O and Δ¹⁷O indicates that the oxygen isotopes of the various collected NO_y compounds derived from two dominant pools of O sources, with high and low δ¹⁸O and Δ¹⁷O values that were consistent across all experimental conditions. The observed Δ¹⁷O and δ¹⁸O values of NO_y species are anticipated to reflect a balance between oxygen atom transfer from O₃, which has high Δ¹⁷O and δ¹⁸O values, and oxygen atom transfer from RO₂, HO₂, OH, and H₂O, which have lower Δ¹⁷O and δ¹⁸O values. Assuming a Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) value of 39 ± 2 ‰ (Ishino et al., 2017; Vicars and Savarino, 2014) would indicate a δ¹⁸O transferred from O${}_{\mathrm{3}}^{\mathrm{term}}$ to the NO_y products of 106 ± 5.0 ‰. Conversely, the low-Δ¹⁷O oxidant endmember at a Δ¹⁷O ≈ 0 ‰ implies an associated δ¹⁸O value of approximately 11.1 ± 1.0 ‰. This value likely reflects oxygen transfer from oxidants such as RO₂, HO₂, and OH.

The derived low-end δ¹⁸O oxidant value is consistent with a scenario in which these radicals are sourced from atmospheric O₂ (δ¹⁸O ≈ 23 ‰; Craig, 1957) but undergo isotopic fractionation during their formation and subsequent oxygen atom transfer to NO_y. Although the exact δ¹⁸O enrichment factors for RO₂, HO₂, or OH formation and reaction are not well-constrained, a net isotope enrichment factor ∼ −12 ‰ is plausible, particularly for unidirectional reactions involving ¹⁸O fractionation (Walters and Michalski, 2016a). Additionally, contributions from OH could further influence the low-δ¹⁸O endmember, especially if oxygen atom exchange with ambient water vapor occurs (Dubey et al., 1997). Altogether, the inferred δ¹⁸O of 11.1 ‰ for the low-Δ¹⁷O oxidant endmember likely represents a composite signal from multiple oxidants (RO₂, HO₂, OH) originating from O₂ and/or H₂O, modified by kinetic and equilibrium isotope effects. Despite these uncertainties, the consistent δ¹⁸O–Δ¹⁷O trend across NO_y products supports a two-endmember mixing model governed by oxidants with distinct isotopic values.

The Δ¹⁷O and δ¹⁸O values increased in the order pNO₃ ($\stackrel{\mathrm{‾}}{x}$ ± σ; Δ¹⁷O = 10.0 ± 3.4 ‰; δ¹⁸O = 35.0 ± 10.1 ‰; n= 7) < HNO₃ (Δ¹⁷O = 16.7 ± 2.0 ‰; δ¹⁸O = 50.2 ± 4.5 ‰; n= 20) < NO₂ (Δ¹⁷O = 29.6 ± 12.8 ‰; δ¹⁸O = 84.1 ± 29.6 ‰; n= 20). The Δ¹⁷O values and δ¹⁸O of NO₂, HNO₃, and pNO₃ were sensitive to the types of experiments and thus oxidant conditions (Fig. 1b). For example, NO₂ samples collected during the photochemical experiments (i.e., Exps. 1–5) indicated that δ¹⁸O(NO₂) and Δ¹⁷O(NO₂) increased with the initial [NO_y], the ratio of initial [NO_y] : [BVOC], and with decreasing initial [H₂O₂]. These sensitivities of δ¹⁸O(NO₂) and Δ¹⁷O(NO₂) reflect the balance between NO branching ratios involving O₃ versus RO₂ $/$ HO₂ (Albertin et al., 2021; Walters et al., 2018). Thus, the relative branching ratios of NO + O₃ and NO + RO₂ $/$ HO₂ changed with experimental photochemical conditions, favoring a greater proportion of NO + O₃ reactions for higher initial NO_y and lower [H₂O₂] conditions. For the nighttime oxidation experiment (Exp. 6), the Δ¹⁷O and δ¹⁸O reflected the initial production of N₂O₅ from the oxidation of NO₂ (from a gas cylinder) with O₃. The expected Δ¹⁷O and δ¹⁸O values can be calculated assuming N₂O₅ equilibrium between NO₃ and NO₂ (i.e., N₂O₅ NO₂+ NO₃) and using O isotope mass balance (Eq. 7):

$$\begin{array}{}\text{(7)}& \mathit{\delta }\left({\mathrm{NO}}_{\mathrm{2}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}\left(\mathit{\delta }\left({{\mathrm{O}}_{\mathrm{3}}}^{\mathrm{term}}\right)\right)+{\displaystyle \frac{\mathrm{4}}{\mathrm{5}}}\left(\mathit{\delta }\left({\mathrm{NO}}_{\mathrm{2}}^{\mathrm{tank}}\right)\right),\end{array}$$

where δ refers to either Δ¹⁷O or δ¹⁸O, O${}_{\mathrm{3}}^{\mathrm{term}}$ refers to the O atom at the terminal end of O₃, and NO${}_{\mathrm{2}}^{\mathrm{tank}}$ refers to the NO₂ from the tank source with measured Δ¹⁷O and δ¹⁸O values of −0.1 ± 0.1 ‰ (n= 3) and 13.1 ± 0.2 ‰ (n= 3), respectively. Using the assumed Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) of 39 ± 2 ‰ and the calculated δ¹⁸O(O${}_{\mathrm{3}}^{\mathrm{term}}$) incorporated into NO_y (106 ± 5.0 ‰) we estimate the Δ¹⁷O and δ¹⁸O of NO₂ for the nighttime oxidation experiment to be 7.7 ± 0.4 ‰ and 31.7 ± 1.0 ‰, respectively, which was near their measured values from the nighttime chamber experiments of (7.2 ± 0.2 ‰) and (31.9 ± 0.7 ‰) (n= 3), respectively.

Figure 1 The observed oxygen isotope delta values of various NO_y species (i.e., HNO₃, NO₂, and pNO₃) from the α-pinene $/$ NO_y oxidation experiments including (a) linear regression between δ¹⁸O and Δ¹⁷O and (b) Δ¹⁷O values of NO_y species sorted by experiment.

3.1.2 δ¹⁵N of NO_y

The observed δ¹⁵N of all NO_y species exhibited a large range from −90.3 ‰ to −4.0 ‰ (n = 47) (Fig. 2a). This large range of δ¹⁵N values was significantly influenced by the δ¹⁵N values of the various initial NO_y sources that included tank NO (Exps. 1–4), HONO (Exp. 5), and tank NO₂ (Exps. 6). The experiments using tank NO had the lowest δ¹⁵N ($\stackrel{\mathrm{‾}}{x}$ ± σ) of (−56.1 ± 21.3 ‰; n = 32), followed by tank NO₂ of (−34.7 ± 12.2 ‰; n = 6), and the highest average was for the HONO experiments of (−7.8 ± 5.7 ‰; n = 9). The differences in the observed δ¹⁵N values by NO_y source likely reflect the isotopic composition of the initial NO_y used in each experiment. The trend in observed δ¹⁵N across experiments is consistent with either measured or literature-based reports of the δ¹⁵N values of the initial NO_y species. For example, the δ¹⁵N of laboratory-generated HONO, prepared using a similar methodology as in this study, has been reported to be −5.9 ± 0.5 ‰ (Chai and Hastings, 2018). This value is relatively high compared to the δ¹⁵N(NO₂) from tank NO₂ used in these experiments that was measured to be −40.9 ± 0.2 ‰, which is higher than the δ¹⁵N(NO) of tank NO previously reported at −70.0 ± 1.4 ‰ (Fibiger et al., 2014). In addition to the source δ¹⁵N effects, the experiments also indicate large δ¹⁵N fractionation between the various NO_y species. Overall, δ¹⁵N(HNO₃) averaged −25.9 ± 13.0 ‰ (n = 20), which was significantly higher than both δ¹⁵N(NO₂) (−52.5 ± 25.2 ‰; n = 20) and δ¹⁵N(pNO₃) (−72.6 ± 22.9 ‰; n = 7) based on a two-sample t test (p < 0.01). While δ¹⁵N(NO₂) values were higher than those of δ¹⁵N(pNO₃), this difference was not statistically significant based on a two-sample t test (p > 0.05). This trend suggests that the produced HNO₃ was generally associated with a positive nitrogen isotope enrichment factor (¹⁵ε) favoring preferential incorporation of ¹⁵N relative to NO₂, whereas pNO₃ formation involved a negative ε, favoring incorporation of ¹⁴N.

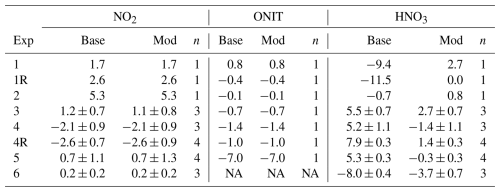
We quantified the δ¹⁵N enrichment of HNO₃ and pNO₃ relative to NO₂ as Δδ¹⁵N (defined as δ¹⁵N(product) – δ¹⁵N(NO₂)) (Fig. 2b). Among the photochemical experiments initiated with NO and H₂O₂ (Exps. 1–4), the average Δδ¹⁵N(HNO₃–NO₂) was consistently high, averaging 33.7 ± 7.1 ‰, while the HONO experiment (Exp. 5) had a much smaller enrichment value of 0.4 ± 1.7 ‰. This difference is somewhat surprising, given that both systems are expected to involve NO₂ + OH as a major pathway for HNO₃ production. The ¹⁵ε associated with NO₂+ OH has yet to be directly measured but has been predicted in the literature with large differences in the suggested value. For example, the ¹⁵ε for NO₂+ OH has been suggested to be −3 ‰ based on the reduced masses of the transition complex (Freyer et al., 1993), while it has been predicted to be +40 ‰ in the i_NRACM based on the assumption that NO₂ and the excited HNO₃ intermediate formed during the NO₂+ OH reaction achieve isotopic equilibrium prior to collisional deactivation (Fang et al., 2021). The relatively low Δδ¹⁵N(HNO₃–NO₂) observed in the HONO experiment is more consistent with the former, while the higher Δδ¹⁵N(HNO₃–NO₂) values in the NO $/$ H₂O₂ experiments support the latter interpretation. The cause of this discrepancy remains unclear but may reflect differences in reaction kinetics and environmental conditions. For example, in the HONO experiment, the aerosol formation peak (Fig. 3) and HNO₃ production (Fig. S1) occurred relatively rapidly compared to the NO $/$ H₂O₂ experiments. This timing shift may potentially alter the influence of nitrogen isotope fractionation effects such as NO_x photochemical equilibrium. Additional isotope effects may also contribute, such as fractionation during HONO photolysis, unknown mass-dependent processes, or experimental artifacts including wall loss or residual background levels. Further investigation is needed to isolate and quantify the influence of these factors.

In the nighttime experiment (Exp. 6), Δδ¹⁵N(HNO₃–NO₂) was also elevated with an average value of 22.2 ± 1.4 ‰ . The cause of the nighttime ¹⁵N enrichment in the generated HNO₃ relative to NO₂ is likely due to isotopic effects associated with the NO₂+ NO₃ N₂O₅ equilibrium, which has been predicted to have ¹⁵ε of 25.5 ‰ at 300 K (Walters and Michalski, 2016b) falling near the observed value for the nighttime experiments (Fig. 2b). The Δδ¹⁵N(pNO₃–NO₂) values were consistently negative, averaging −13.6 ± 5.8 ‰ across the photochemical experiments. This value suggests that pNO₃ formation involved reactions that preferentially favored ¹⁴N. Before speculating on the cause of the low observed Δδ¹⁵N(pNO₃–NO₂), it is essential to first determine the chemical composition of the produced pNO₃ and whether it originates primarily from inorganic or organic nitrate.

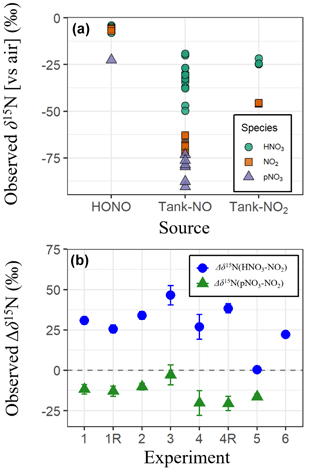
Figure 2 (a) The observed δ¹⁵N of various NO_y species (i.e., HNO₃, NO₂, and pNO₃) collected during the various conducted α-pinene and NO_y oxidation experiments. The measured δ¹⁵N values were sorted by the various starting NO_y sources, including HONO, tank NO, and tank NO₂. (b) Calculated Δδ¹⁵N values for each experiment, defined as the δ¹⁵N difference between HNO₃ and NO₂ and between pNO₃ and NO₂. Data represent experiment-specific averages, with error bars reflecting the propagated standard deviation.

3.2 Particle nitrate composition

The generated pNO₃ could have both inorganic (i.e., HNO₃ condensation) and organic (i.e., organic nitrate condensation) contributions. The δ¹⁵N data qualitatively indicate that the pNO₃ was derived from a source separate from HNO₃ due to their large δ¹⁵N differences, which would suggest that pNO₃ was derived primarily from organic nitrate. For example, the observed δ¹⁵N difference between HNO₃ and pNO₃ that averaged 46.7 ‰ suggests that these species may originate from distinct sources. Given that inorganic nitrate would typically equilibrate isotopically between HNO₃ and NO${}_{\mathrm{3}}^{-}$ with an expected offset of only ∼ 1 ‰–3 ‰, and often slightly enriched in pNO₃ (Bekker et al., 2023), the substantially lower δ¹⁵N values observed in pNO₃ imply that the collected nitrate may originate from organic nitrate species or unique NO_y formation pathways from HNO₃ production.

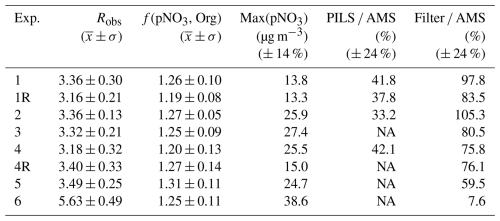
We utilized the HR-ToF-AMS NO⁺ and NO${}_{\mathrm{2}}^{+}$ data to evaluate the contributions of pNO₃ for the experiments. The f(pNO₃, Org) was calculated according to Eq. (5) for each of the conducted experiments (Table 3). Overall, f(pNO₃, Org) was calculated to have a mean of (1.25 ± 0.04; n=8), indicating that the generated pNO₃ derived from organic nitrate. The calculated f(pNO₃, Org) was higher than 1 even when considering uncertainty estimates. This could be due to calculating R_ON values from reported $R_{\mathrm{ON}}/R_{\mathrm{AN}}$ ratios from previously conducted α-pinene oxidation experimental conditions utilizing substantially lower (∼ ×10) initial precursor concentrations (Takeuchi and Ng, 2019). Thus, due to the potential uncertainty in our approach in estimating f(pNO₃, Org), the composition of the generated pNO₃ was also investigated using a qualitative approach involving evaluating the relative change in the molar ratio of NH₄ $/$ SO₄ from the HR-ToF-AMS (Fig. S2). For each type of experiment, we found the NH₄ $/$ SO₄ molar ratio to be consistently near 1.5. This type of NH₄ $/$ SO₄ profile is consistent with the generated pNO₃ deriving from organic nitrate, as the dissolution of HNO₃ into aqueous aerosol followed by neutralization with available NH₃ would be expected to lead to an abrupt increase in the molar ratio of NH₄ $/$ SO₄ (Takeuchi and Ng, 2019). Furthermore, the acidic nature of the particles and limited availability of NH${}_{\mathrm{4}}^{+}$ likely inhibited HNO₃ uptake, suppressing condensation pathways and reinforcing the interpretation that pNO₃ originated predominantly from organic nitrate formation. Overall, both the quantitative and qualitative analysis of pNO₃ composition utilizing the AMS data as well as our δ¹⁵N data indicates that pNO₃ was mainly derived from organic nitrate. Hereafter, we assume that the NO${}_{\mathrm{3}}^{-}$ extracted from the filter collections derived from organic nitrate.

Table 3 Summary of the HR-ToF-AMS data including NO⁺ $/$ NO${}_{\mathrm{2}}^{+}$ fragmentation data (R_obs), calculated f(pNO₃, Org), and maximum pNO₃ (Max(pNO₃)). Additionally, we quantified the amount of pNO₃ from the PILS (PILS $/$ AMS) and the filter collection relative to the HR-ToF-AMS (filter $/$ AMS). Uncertainties for pNO₃ quantification and intercomparison ratios are reported in parentheses.

NA: not available.

The pNO₃ measured by the HR-ToF-AMS indicated similar profiles for the various types of conducted experiments, in which pNO₃ concentrations peaked and subsequently decayed due to wall loss and chamber dilution (Fig. 3). Overall, the maximum pNO₃ concentrations ranged from 13.3 to 38.6 µg m⁻³, depending on the experiment (Table 3). The typical measurement uncertainty for pNO₃ quantification using the HR-ToF-AMS is approximately ± 14 % (Bahreini et al., 2009; Takeuchi et al., 2024). Given that we assume 100 % of the particulate nitrate is organic nitrate (i.e., f(pNO₃, Org) = 1), the uncertainty in pNO₃ concentration is based solely on the AMS nitrate measurement error, estimated at ± 14 %. The lowest maximum pNO₃ corresponded to experimental conditions with low initial NO_x relative to H₂O₂ and BVOC conditions (i.e., Exp. 1). In contrast, the highest maximum pNO₃ occurred during the nighttime oxidation experiments (i.e., Exp. 6). The pNO₃ concentrations determined from the HR-ToF-AMS were compared with additional measurement techniques, including the PILS and the filter collections for offline analysis (Fig. 3; Table 2). The PILS pNO₃ measurements were available for four out of the eight conducted experiments and indicated a similar time profile as the HR-ToF-AMS; however, the PILS pNO₃ observations were always lower than the HR-ToF-AMS with the amount of pNO₃ determined from PILS relative to the HR-ToF-AMS (PILS $/$ AMS) ranging between 33.2 %–53.8 %. The uncertainty associated with pNO₃ quantification by the PILS system is approximately ± 20 % (Guo et al., 2016). Accordingly, the propagated uncertainty for the PILS $/$ AMS ratio is approximately 24 %.

The pNO₃ quantified using the filter collection and extraction technique was higher than the PILS and in closer agreement with the HR-ToF-AMS. For the photochemical experiments (Exps. 1–5), the pNO₃ determined using the filter collection relative to the HR-ToF-AMS (filter $/$ AMS) for the photochemical experiments ranged between 59.5 % and 105.3 % and averaged 86.5 ± 12.4 % (n=7). The filter collection technique has an estimated uncertainty for pNO₃ quantification of approximately ± 20 % based on the average percent difference from side-by-side ChemComb filter pack measurements of ambient air using nylon filters (Blum et al., 2020). Although different filters were used in this study, the same collection system and mass flow controllers were employed, and we therefore expect a comparable difference between system replicates. Accordingly, the propagated uncertainty for the filter $/$ AMS ratio is ± 24 %. However, the filter collection resulted in nearly negligible pNO₃ for the nighttime oxidation experiments (i.e., Exp. 6).

The pNO₃ concentrations determined using the PILS were always lower than that determined by the HR-ToF-AMS and the offline filter collection technique, which would indicate that not all collected pNO₃, which was shown to mainly derive from organic nitrate, was hydrolyzed to NO${}_{\mathrm{3}}^{-}\left(\mathrm{aq}\right)$ within the PILS chamber before quantification via ion chromatography. The filter collection and extraction method (i.e., leach in MQ water for 1 week) enabled the successful hydrolysis of the collected pNO₃ to NO${}_{\mathrm{3}}^{-}\left(\mathrm{aq}\right)$ from the photochemical experiments, an important pre-requisite for subsequent isotope analysis. The filter collection technique, however, resulted in near-negligible pNO₃ for the nighttime oxidation experiments, limiting our ability to measure the isotope composition of pNO₃ from this experiment. This difference in the efficacy of the offline filter collection technique for pNO₃ characterization between the photochemical and nighttime oxidation experiments could be related to the type of organic nitrate formed during the conducted experiments. The photochemical α-pinene oxidation experiments have been suggested to result in higher relative production of tertiary organic nitrate, while nighttime oxidation leads to a relatively lower fraction of tertiary organic nitrate with estimated values of 62 % and 15 %, respectively (Zare et al., 2018). Recent work has suggested a hydrolysis lifetime of no more than 30 min and a hydrolyzable portion of particulate organic nitrate from α-pinene oxidation experiments between 23 %–32 % and 9 %–17 % for α-pinene + OH and α-pinene + NO₃ reactions, respectively (Takeuchi and Ng, 2019).

The offline filter collection and extraction technique follows the observed trend of a greater proportion of pNO₃ hydrolyzed to NO${}_{\mathrm{3}}^{-}\left(\mathrm{aq}\right)$ in photochemical experiments (82.6 ± 14 %; n= 7) compared to nighttime conditions (7.6 %; n= 1). This is inferred based on the relative amount of quantified NO${}_{\mathrm{3}}^{-}\left(\mathrm{aq}\right)$ from the filter extraction solution to the total pNO₃ measured by HR-ToF-AMS. However, the filter-based method suggested a higher proportion of potentially hydrolyzable pNO₃ in the photochemical experiments than previously reported estimates. From these results and comparisons, we conclude that the pNO₃ offline filter measurements encompass the hydrolyzable portion of pNO₃ within 1 week, while the HR-ToF-AMS measurements represent the total pNO₃, and the PILS measurements correspond to the readily hydrolyzable portion of pNO₃. Further, the box-model simulations (see below) of organic nitrate speciation indicate that the nighttime organic nitrate had a high fraction of dimer and pinene dinitrate (Fig. S3). If this assignment is correct, the results imply that these organic nitrate compounds are effectively non-hydrolyzable under aqueous conditions.

Our results demonstrated that organic nitrate aerosols (pRONO₂) can hydrolyze and contribute to the NO${}_{\mathrm{3}}^{-}$ measured in aerosol extracts. While our chamber experiments were conducted under controlled conditions with low relative humidity (∼ 30 %) and dry aerosol seeds, they highlight the need to consider the fact that NO${}_{\mathrm{3}}^{-}$ collected on filters may originate from both inorganic nitrate (derived from HNO₃ uptake) and hydrolyzed organic nitrate. However, we caution that these findings do not imply that all pNO₃ observed in ambient field measurements is organic in origin. The extent to which organic nitrate contributes to pNO₃ in field settings will depend on regional BVOC emissions, which govern precursor availability, as well as environmental factors such as aerosol pH and relative humidity, which influence the lifetime and hydrolysis rates of pRONO₂ prior to filter collection. Further, while gas-phase organic nitrates (e.g., RONO₂, RO₂NO₂) can be present and were detected by CIMS measurements during the experiments, the strong agreement between filter-based and AMS-based pNO₃ measurements supports the idea that the nitrate extracted from aerosol filters was primarily derived from particle-phase organic nitrate rather than from gas-phase organic nitrate contributions. Finally, given that the collected pNO₃ was predominantly derived from RONO₂, the negative Δδ¹⁵N(pNO₃–NO₂) values (Fig. 2b) suggest a preferential incorporation of ¹⁴N into the RONO₂ product. This is consistent with NO_x photochemical equilibrium in which ¹⁵N is enriched in NO₂, leaving NO relatively depleted in ¹⁵N (Li et al., 2020; Walters et al., 2016). Subsequent reaction of this ¹⁵N-depleted NO with RO₂ forms RONO₂, thereby transferring the isotopically lighter nitrogen signature into RONO₂ that then condenses to the particle phase and is hydrolyzed to NO${}_{\mathrm{3}}^{-}$.

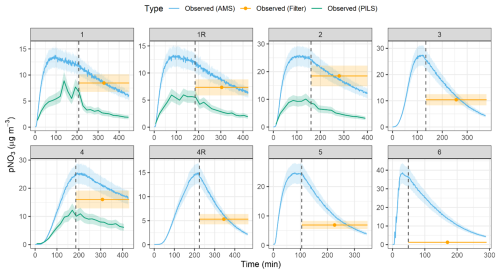
Figure 3 The observed pNO₃ concentration data are shown for each of the conducted experiments. Concentrations were determined using a high-resolution time-of-flight aerosol mass spectrometer (HR-ToF-AMS), a particle-into-liquid sampler (PILS), and filter collection (filter). The start of chamber dilution is indicated by the dashed vertical lines, corresponding to the abrupt decrease in pNO₃. The lighter shaded regions correspond to the measurement uncertainty for the various analytical techniques.

3.3 Model simulations

To further interpret the experimental results, we employed a box model to simulate the formation and evolution of NO_y species and their Δ¹⁷O values. We begin by examining the developed gas-phase chemical mechanism (NO_x-API) simulation of the initial aerosol precursor decay including α-pinene and NO. For comparison, simulations were also conducted using established gas-phase chemical mechanisms that included RACM2 and the MCM to evaluate the treatment of α-pinene oxidation and oxidation chemistry across different chemical frameworks for a range of experimental conditions. Model sensitivity tests were then conducted to assess the impact of key physical parameters that included chamber dilution rate and wall loss rates on simulated Δ¹⁷O values. Finally, we compare the modeled Δ¹⁷O values of NO_y species with experimental observations to evaluate the model's ability to reproduce isotopic values under different photochemical and nighttime oxidation conditions.

3.3.1 Precursor decay

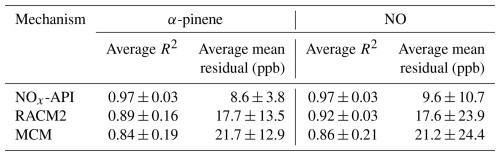
Box-model simulations were conducted to evaluate the oxidation and decay of precursors used in the experiments, ensuring that the correct amount of oxidant was accurately simulated. The MCM, RACM2, and NO_x-API were used to simulate the decay of α-pinene and NO, with results compared against experimental observations (Figs. 4–5). Model performance was evaluated by comparing measured and modeled concentrations of NO and α-pinene using one-to-one plots, with corresponding R² values and quantification of model biases (Figs. S4–5), and Table 4 summarizes these results. Overall, the NO_x-API mechanism provided improved model performance, as evidenced by consistently higher R² values (averaging 0.97 ± 0.03) and lower absolute residuals for both α-pinene and NO decay compared to the other mechanisms. We attribute this enhanced model performance to the simplified treatment of higher-generation products in the NO_x-API mechanism. Unlike MCM and RACM2, which allow continued gas-phase reactions of all products through extensive reaction propagation, the NO_x-API mechanism terminates the chemistry of these products after a limited number of steps. Given that the box-model simulations do not include an explicit aerosol-phase treatment, continued gas-phase reactivity of condensable species (as implemented in MCM and RACM2) may unrealistically disrupt the oxidant budget. Therefore, the NO_x-API mechanism as employed in the box model is better aligned with the experimental design and will be used for subsequent Δ¹⁷O simulations of the chamber experiments.

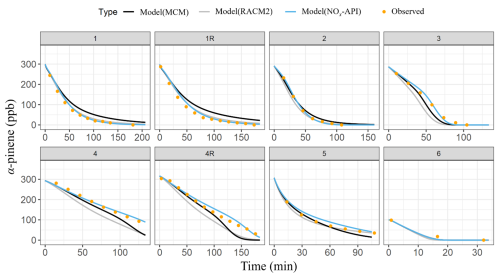
Figure 4 The observed (orange data points) and the modeled (lines) α-pinene decay for the various conducted experiments. The modeled results are based on three chemical mechanisms: MCM (black), RACM2 (gray), and NO_x-API (light blue).

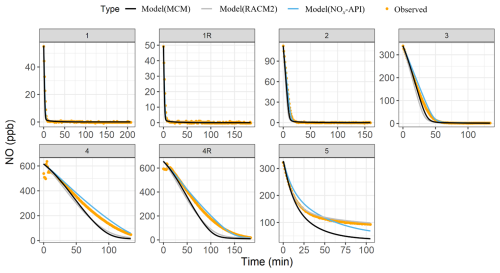
Figure 5 The observed (orange data points) and the modeled (lines) NO decay for the various conducted photochemical experiments. The modeled results are based on three chemical mechanisms: MCM (black), RACM2 (gray), and NO_x-API (light blue). Experiment 6 (nighttime oxidation) was omitted from the analysis as NO was not among the initial reactants.

Table 4 Summary of model performance for α-pinene and NO using the NO_x-API, RACM2, and MCM. Values represent the average coefficient of determination (R²) and average mean residuals (in ppb) across all experiments, with associated standard deviations.

3.3.2 Δ¹⁷O model sensitivity to dilution and wall loss

Before comparing modeled Δ¹⁷O values to observations, we first evaluated the model's sensitivity to our treatment of key physical parameters, including chamber dilution and wall loss, and their potential impact on the simulated Δ¹⁷O (Fig. 6). These sensitivity tests focused on Experiment 1, one of the longest-duration experiments, where dilution and wall loss would be expected to exert the strongest influence on gas-phase chemistry and Δ¹⁷O values.

The impact of chamber dilution was assessed using four scenarios: no dilution and first-order dilution rate constants (k_dil) of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$, and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ (Fig. 6a). Dilution was initiated at t= 208 min in the model to match the experimental protocol. Across all scenarios, simulated Δ¹⁷O values of total organic nitrate (ONIT = ONITa + ONITb + ONITc + ONITOOHa + ONITOOHb + DIMER + PDN) were minimally impacted by dilution. For instance, Δ¹⁷O(ONIT) varied by only 0.06 ‰ between the no-dilution and highest dilution rate constant scenario (k_dil= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹), corresponding to a relative difference of −1.1 %. This insensitivity reflects the fact that organic nitrate chemistry was largely completed by the time dilution began. In contrast, simulated Δ¹⁷O values for HNO₃ and NO₂ were more sensitive to the dilution rate. Between the no-dilution and lowest dilution rate constant scenario (k_dil= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹), Δ¹⁷O(HNO₃) and Δ¹⁷O(NO₂) changed by only −0.01 ‰ (corresponding to a relative difference of −0.2 %) and −0.11 ‰ (−0.7 %), respectively. However, increasing the dilution rate constant from $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ led to additional decreases of 0.32 ‰ (−5.0 %) for HNO₃ and 0.88 ‰ (−5.6 %) for NO₂. The most extreme dilution rate constant scenario (k_dil= $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹) reduced Δ¹⁷O by a total of 0.50 ‰ (−7.9 %) for HNO₃ and 1.62 ‰ (−10.3 %) for NO₂ relative to the no-dilution case. For the main box-model simulations, we adopted a dilution rate constant of $\mathrm{3.47}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹, corresponding to a measured flow rate of 25 LPM in a 12 m³ chamber. Assuming no more than ± 20 % uncertainty in the actual flow rate, we estimate that the resulting uncertainty in simulated Δ¹⁷O values due to dilution would be approximately ± 2.5 % for HNO₃, ± 3 % for NO₂, and less than ± 1 % for ONIT. These estimates are based on the observed Δ¹⁷O variation between the $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ scenarios.

Next, we evaluated the potential influence of chamber wall loss on the simulated Δ¹⁷O values (Fig. 6b). Three scenarios were tested: (1) no wall loss, (2) a wall loss scenario incorporating NO_y and O₃ loss rates from previous studies (Morales et al., 2021; Wang et al., 2014), and (3) an extreme case in which wall loss rate constants were increased by a factor of 10 (Table S7). In the base comparison between the no-wall-loss and reported wall loss scenario, the effect on modeled Δ¹⁷O values was minimal. Specifically, Δ¹⁷O changed by −0.02 ‰ for HNO₃ (−0.3 %), −0.37 ‰ for NO₂ (−2.3 %), and +0.03 ‰ for ONIT (+0.5 %). These small differences suggest that moderate wall loss rates, consistent with literature values, would not substantially alter the Δ¹⁷O simulations. However, the extreme wall loss scenario revealed a much stronger impact. In this case, Δ¹⁷O decreased by 2.5 ‰ for NO₂ (−15.8 %) and increased by 0.50 ‰ for HNO₃ (+7.8 %) and 0.69 ‰ for ONIT (+11.4 %) relative to the no-wall-loss case. The drop in Δ¹⁷O(NO₂) arises from the altered oxidant concentrations and rapid photochemical cycling of NO_x, which can reset its Δ¹⁷O values on short timescales. Conversely, the rise in Δ¹⁷O for HNO₃ and ONIT reflects preferential removal of early-formed products with lower Δ¹⁷O, allowing later-formed products with higher Δ¹⁷O values to dominate. Because we lacked experimental constraints on wall loss during the chamber experiments, the box-model simulations presented in this study did not include wall loss. Based on our sensitivity analysis, omitting wall loss introduces an estimated uncertainty of ± 0.3 % for HNO₃, ± 2.3 % for NO₂, and ± 0.5 % for ONIT assuming a moderate wall loss scenario. If actual wall loss rates in the chamber were significantly higher than those reported in the literature, the model is anticipated to overestimate Δ¹⁷O in NO₂ and underestimate it in HNO₃ and ONIT.

Overall, based on the results of the model sensitivity tests, we estimate that the propagated uncertainty in the simulated Δ¹⁷O values due to chamber dilution and wall loss is approximately ± 2.5 % for HNO₃, ± 3.8 % for NO₂, and ± 1.1 % for ONIT. These values reflect the combined effects of plausible variation in dilution rate (± 20 %) and the difference in simulated Δ¹⁷O values from literature-based estimates of NO_y and O₃ wall loss compared to a case of no wall loss. Further, considering that the uncertainty in the measured Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) is approximately ± 5 % (Vicars and Savarino, 2014), we calculate an overall model uncertainty for Δ¹⁷O of ± 5.6 %, ± 6.3 %, and ± 5.1 % for HNO₃, NO₂, and ONIT, respectively. Clearly, the uncertainty in Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) is expected to be the largest source of uncertainty in the modeled Δ¹⁷O values as opposed to our treatment of dilution and chamber wall loss. Still, we conservatively apply these propagated uncertainty estimates when presenting and interpreting the model results.

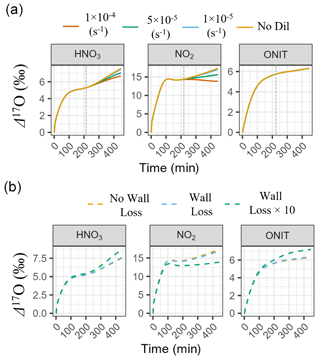
Figure 6 Modeled Δ¹⁷O sensitivity to physical chamber parameters. (a) Model simulations testing the sensitivity of Δ¹⁷O in NO₂, HNO₃, and ONIT to chamber dilution rates, including scenarios with no dilution and with first-order dilution constants of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$, and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹. (b) Model simulations testing the impact of wall loss, comparing a no-wall-loss case, a wall loss scenario using reaction rates from Wang et al. (2014) and Morales et al. (2021), and a high-loss case in which wall loss rates were increased by a factor of 10. All simulations were performed under the conditions of Experiment 1. The gray dashed line in panel (a) corresponds to the start of chamber dilution.

3.3.3 Δ¹⁷O base model simulations

Building on the results of the sensitivity analyses, we next evaluate the performance of the base box model in simulating the Δ¹⁷O values of key NO_y species, including NO₂, HNO₃, and ONIT under the various experimental conditions. These simulations incorporate the best-estimate physical parameters (e.g., dilution rate) and chemical mechanism inputs, including a representative Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) value of 39 ± 2 ‰ (Fig. 7). Overall, the model simulations for the photochemical experiments indicate a substantial temporal change in Δ¹⁷O for all considered NO_y compounds. The Δ¹⁷O(NO₂) initially starts at 0 ‰ and begins to increase due to the production of O₃ that elevates Δ¹⁷O(NO₂) as NO is oxidized by O₃. For the nighttime experiment, the box model predicts Δ¹⁷O(NO₂) to remain steady with a value near 7.6 ‰ due to N₂O₅ thermal equilibrium with NO₂ and NO₃, resulting in the Δ¹⁷O(NO₂)≈Δ¹⁷O(N₂O₅). Generally, the Δ¹⁷O simulations of NO₂ were in excellent agreement with the observations, as indicated by an average model bias of 0.9 ± 2.4 ‰ (n= 8; Table 5) and a strong correlation indicated by a regression R² value of 0.98. This strong agreement indicates that the box model and employed chemical mechanism accurately simulated NO_x photochemical cycling and NO₂ $/$ NO₃ $/$ N₂O₅ thermal equilibrium. The simulation of Δ¹⁷O(NO₂) is inherently sensitive to the assumed value of Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$), which represents the isotopic signature transferred from the terminal O atom of O₃ to NO₂ during oxidation. The relationship between measured Δ¹⁷O(NO₂) and the modeled fraction of O atoms in NO₂ deriving from O₃ (denoted as f(Q)) indicates that Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) is 39.4 ± 0.6 ‰ (Fig. S6), which is in excellent agreement with recent independent measurements of tropospheric O₃ reporting values of 39 ± 2 ‰ (Ishino et al., 2017; Vicars and Savarino, 2014).

The measured Δ¹⁷O(pNO₃) was compared with the simulated Δ¹⁷O of (ONIT) based on our understanding that pNO₃ was apparently dominated by RONO₂ contributions. The temporal evolution of the simulated Δ¹⁷O(ONIT) closely followed that of Δ¹⁷O(NO₂) but remained lower due to dilution effects associated with the dominant formation pathway of organic nitrates via NO + RO₂ reactions during the photochemical experiments, resulting in ONIT dominated by ONITa, ONITb, and ONITc compounds (Fig. S3). During nighttime oxidation experiments, ONIT formation primarily proceeded via α-pinene + NO₃ reactions, leading to ONIT with a higher contribution of DIMER and PDN compounds. Due to NO₂ $/$ NO₃ $/$ N₂O₅ thermal equilibrium that resulted in Δ¹⁷O(NO₂)≈Δ¹⁷O(NO₃) ≈Δ¹⁷O(N₂O₅), the simulated nighttime Δ¹⁷O(ONIT) values were approximately equal to the simulated Δ¹⁷O(NO₂). The simulated Δ¹⁷O(ONIT) closely matched the Δ¹⁷O(pNO₃) observations with an average bias of −1.4 ± 2.4 ‰ (n=7), indicating that the relative production routes of organic nitrate (RO₂+ NO vs. BVOC + NO₃; Table 1) were correctly simulated for the various experimental conditions. The overall correlation was moderate, with R²= 0.55.

The bias for simulated Δ¹⁷O(ONIT) compared to the Δ¹⁷O(pNO₃) observations was within 1.4 ‰ for all experiments except Exp. 5, where a substantially higher bias of −7.0 ‰ was observed. Excluding this outlier increased the correlation to R²= 0.97. Based on Cook's distance and the Studentized residual, Experiment 5 was identified as an outlier in the linear regression analysis. The larger model–data difference for Exp. 5 may reflect different oxidation dynamics or, more likely, uncertainty in the extraction of pNO₃. Specifically, Experiment 5 yielded the lowest filter $/$ AMS ratio among the photochemical experiments, with the ratio falling below the quantitative range when accounting for propagated uncertainty. This suggests potential under-recovery or sampling artifacts, indicating that the measured Δ¹⁷O(pNO₃) in this experiment may not accurately represent the pNO₃ formed during the chamber experiment (Table 3). Thus, the larger model–measurement Δ¹⁷O(ONIT) disagreement for Exp. 5 likely reflects uncertainty in the extracted NO${}_{\mathrm{3}}^{-}$ rather than model misrepresentation of ONIT formation pathways. The measured Δ¹⁷O(pNO₃) was also evaluated relative to the modeled f(Q) for ONIT formation. A linear regression constrained through the origin, excluding Exp. 5, yielded a slope of 41.7 ± 1.2 ‰ (R² = 0.996; Fig. S7). This derived Δ¹⁷O(Q) value is in close agreement with the assumed Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) value of 39 ± 2 ‰ and is consistent with the value determined from the measured Δ¹⁷O(NO₂) comparison with the modeled f(Q) of NO₂.

The simulated dynamics of Δ¹⁷O(HNO₃) closely follow the temporal evolution of Δ¹⁷O(NO₂), initially starting at 0 ‰ and increasing as O₃ production occurs in the chamber during the photochemical experiments (i.e., Exps. 1–5) (Fig. 7). The simulated Δ¹⁷O(HNO₃) for the photochemical experiments was always lower than Δ¹⁷O(NO₂) for the photochemical experiments, as the model simulation predicts HNO₃ is predominantly produced through the NO₂+ OH pathway (Fig. S8). Based on the conventional oxygen isotope mass balance calculations, this pathway results in a dilution factor of $\mathrm{2}/\mathrm{3}$ relative to Δ¹⁷O(NO₂) (Table 1). For the nighttime experiment (Exp. 6), Δ¹⁷O(HNO₃) is predicted to be slightly lower than Δ¹⁷O(NO₂), primarily due to the contributions from two formation pathways: NO₃+ pinonaldehyde and N₂O₅+ H₂O(g), representing approximately 60 % and 40 % of nighttime HNO₃ production, respectively. Since Δ¹⁷O(NO₃)≈Δ¹⁷O(NO₂) under nighttime conditions due to rapid thermal equilibrium, NO₃+ pinonaldehyde should result in Δ¹⁷O(HNO₃) ≈ Δ¹⁷O(NO₂). However, the N₂O₅ hydrolysis pathway incorporates one oxygen atom from water, which has Δ¹⁷O ≈ 0 ‰, resulting in an effective dilution of the product Δ¹⁷O(HNO₃) relative to Δ¹⁷O(NO₂). Overall, the model exhibits poor agreement with observed Δ¹⁷O(HNO₃) values with a model bias that ranged from −11.5 ‰ to 7.9 ‰ (Table 4) and a weak correlation (R²= 0.39). The model underpredicts Δ¹⁷O(HNO₃) for the low-NO_x photochemical experiments (Exps. 1 and 2) and the nighttime oxidation experiment (Exp. 6) but overpredicts Δ¹⁷O(HNO₃) for the high-NO_x photochemical experiments (Exps. 3, 4, and 5). If the isotope mass balance assumptions are correct, this pattern suggests that a missing or underrepresented source of high-Δ¹⁷O HNO₃ may exist under low NO_x conditions, and a missing low Δ¹⁷O HNO₃ source may exist under high-NO_x conditions.

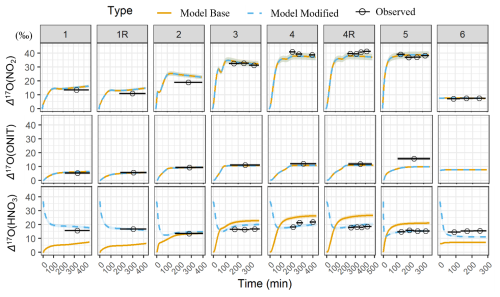
Figure 7 Comparison between the modeled (base and modified) and observed Δ¹⁷O(NO₂), Δ¹⁷O(ONIT), and Δ¹⁷O(HNO₃) values sorted by the various conducted experiments. The data points represent the average time of each sample collection, and the black line spans the duration of the collection period. The measurement uncertainty (± σ) is included as the shaded region. The modeled Δ¹⁷O(ONIT) is compared to the observed Δ¹⁷O(pNO₃).

Table 5 Summary of the calculated average bias (Δ¹⁷O(Model) – Δ¹⁷O(Observed)) for the Δ¹⁷O model simulations using the NO_x-API base and modified (Mod) mechanisms. For experiments with multiple observations, the bias is reported as the mean ± standard deviation.

NA: not available.

3.3.4 Δ¹⁷O(HNO₃) model sensitivity tests

To investigate the causes of the observed discrepancies between modeled and measured Δ¹⁷O(HNO₃) values, we conducted a series of model sensitivity tests focused on modifying HNO₃ formation pathways. These tests aimed to assess whether adjustments to reaction pathways or rate constants could reconcile the overprediction of Δ¹⁷O(HNO₃) during the high-NO_x photochemical experiments (Exps. 3, 4, and 5) and the underprediction during low-NO_x and nighttime experiments. The following sections describe these targeted evaluations and their implications for understanding the Δ¹⁷O(HNO₃) produced under different chemical regimes.

We first investigated the potential causes of the model overprediction in Δ¹⁷O(HNO₃) during the high-NO_x photochemical experiments (Exps. 3, 4, and 5). Two alternative HNO₃ production pathways were identified that could yield lower Δ¹⁷O(HNO₃) values than the assumed predominant daytime production pathway involving NO₂+ OH reactions based on oxygen isotope mass balance assumptions (Table 1). One such pathway is the reaction of NO with HO₂, which can form HNO₃ with a Δ¹⁷O transfer factor of ($\mathrm{1}/\mathrm{3}$)Δ¹⁷O(NO) (Alexander et al., 2020; Table 1). However, an underestimation of this pathway in the model is unlikely to account for the observed model–measurement discrepancy across all experiments. For instance, HO₂ concentrations in Exp. 5 are expected to be low due to the absence of a significant quantity of HO₂ precursors, unlike Exps. 3 and 4, which had elevated HO₂ precursors from the initial injected H₂O₂. Moreover, Exps. 1 and 2, which had the highest initial H₂O₂ concentrations and thus the greatest potential for HO₂ formation, exhibited model Δ¹⁷O(HNO₃) values that were too low, further suggesting that this pathway cannot explain the observed discrepancies. Still, as a sensitivity test, we increased the rate constant for the NO + HO₂→ HNO₃ reaction (R027 in the NO_x-API mechanism; Table S3) by an order of magnitude (Fig. S9). Despite this adjustment in the NO + HO₂→ HNO₃ reaction rate constant, the impact on modeled Δ¹⁷O(HNO₃) remained small with a change in Δ¹⁷O(HNO₃) of less than 1.6 ‰ and as little as 0.3 ‰ for Exp. 5. This change in model Δ¹⁷O(HNO₃) is too small to account for the observed model bias of 5.2 ‰ to 7.9 ‰ across Exps. 3 to 5 (Table 4).

Next, the hydrolysis of organic nitrates to HNO₃ was evaluated as a potential low-Δ¹⁷O(HNO₃) source, since hydrolysis of photochemically produced RONO₂ (R + OH $/$ O₂ $/$ NO) could produce HNO₃ with a Δ¹⁷O transfer factor of ($\mathrm{1}/\mathrm{3}$)(Δ¹⁷O(NO)) (Table 1) considering that Δ¹⁷O(RO₂) is presumably 0 ‰. Based on simulation results (Fig. S10), 21.8 %, 14.8 %, and 13.4 % of the total NO_y was present as HNO₃ for Exps. 3, 4, and 5, respectively, compared to only 11.0 %, 6.8 %, and 4.0 % as RONO₂ (defined as ONIT in our model simulations; ONIT = ONITa + ONITb + ONITc + ONITOOHa + ONITOOHb + PDN + DIMER). Nonetheless, as a sensitivity test, we added ONIT hydrolysis with an assumed lifetime of 30 min (Table S8), consistent with recent experimental determinations (Takeuchi and Ng, 2019); however, this study showed that only 23 %–32 % of organic nitrates derived from α-pinene + OH and 9 %–17 % from α-pinene + NO₃ are susceptible to hydrolysis (Takeuchi and Ng, 2019), suggesting that this sensitivity test should overestimate the impact of ONIT hydrolysis as a production route for HNO₃. The inclusion of ONIT hydrolysis in the model reduced Δ¹⁷O(HNO₃) by 1.4 ‰–3.4 ‰ relative to the base model, partially improving agreement with observations (Fig. S11). However, even under the unrealistic assumption of complete organic nitrate hydrolysis, the bias between the model and observed Δ¹⁷O(HNO₃) values remained between 1.7 ‰ and 4.6 ‰ across experiments, indicating that hydrolysis alone cannot fully explain the model–observation discrepancy. Furthermore, while organic nitrate hydrolysis modestly improved the Δ¹⁷O(HNO₃) comparison, it worsened the agreement for Δ¹⁷O(ONIT) (Fig. S12). The bias for the simulated Δ¹⁷O(ONIT) relative to the observed Δ¹⁷O(pNO₃) increased substantially, ranging from 5.1 ‰–15.0 ‰. These results suggest that organic nitrate hydrolysis is unlikely to be the primary cause of the observed lower Δ¹⁷O(HNO₃) values relative to model simulations.

Overall, we were unable to identify a missing or underrepresented HNO₃ production pathway that could reconcile the observed Δ¹⁷O(HNO₃) values within the bounds of the assumed Δ¹⁷O mass balance framework (Table 1). This suggests that current assumptions regarding oxygen atom transfer during HNO₃ formation may need to be revisited. For the high-NO_x photochemical experiments (Exps. 3–5), plotting measured Δ¹⁷O(HNO₃) against the modeled fraction of O₃-derived oxygen atoms (f(Q)(HNO₃)) gave a slope of 28.9 ± 0.5 ‰, representing the Δ¹⁷O of the O${}_{\mathrm{3}}^{\mathrm{term}}$ (Fig. S13). This slope is lower than the ∼ 39 ‰–41 ‰ slope obtained from similar analyses of Δ¹⁷O(NO₂) and Δ¹⁷O(pNO₃) (Fig. S6–7), which are more consistent with recent near-surface observations of Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) (Ishino et al., 2017; Vicars and Savarino, 2014). The lower slope in the f(Q) versus Δ¹⁷O(HNO₃) relationship potentially implies that not all oxygen atoms from NO₂ are retained during HNO₃ formation in the dominant NO₂+ OH reaction under high-NO_x photochemical conditions. Traditionally, it is assumed that two-thirds of the oxygen atoms in HNO₃ are inherited from NO₂ and one-third from OH (with Δ¹⁷O ∼ 0 ‰) (Table 1), but this oxygen mass balance may need adjustment. Adjusting the slope for Δ¹⁷O(HNO₃) versus f(Q) to match that for NO₂ would require adjustment of the oxygen mass balance in the NO₂+ OH reaction. Specifically, scaling the NO₂ contribution by ∼ 0.74 lowers its O atom fractional contribution in HNO₃ from 66.7 % to ∼ 49 %, resulting in an effective relationship of Δ¹⁷O(HNO₃) $\approx \mathrm{1}/\mathrm{2}$ Δ¹⁷O(NO₂). This deviation from the expected $\mathrm{2}/\mathrm{3}$ to an effective $\mathrm{1}/\mathrm{2}$ contribution of Δ¹⁷O(NO₂) may reflect partial oxygen atom exchange or isotopic scrambling during the formation of an excited HNO₃ intermediate prior to collisional stabilization. Such processes could result in the effective loss or redistribution of the oxygen atoms originally inherited from NO₂ in the HNO₃ product. Indeed, previous experimental studies using isotopically labeled ¹⁸OH in reactions with NO₂ have demonstrated that the O atoms in the HNO₃ reactive intermediate product can undergo rapid intramolecular scrambling (Donahue et al., 2001). While this specific mechanism alone cannot easily explain the observed loss of approximately one-sixth of the original NO₂-derived oxygen atoms in the final HNO₃ product, it does suggest that interesting O isotope dynamics occur during the NO₂+ OH reaction. While the exact mechanism that could explain the redistribution of ∼ $\mathrm{1}/\mathrm{6}$ of O atoms derived from NO₂ in the HNO₃ product remains uncertain and warrants further investigation, we conducted a sensitivity test by updating the NO_x-API mechanism to reflect the potential modified mass balance for the NO₂ + OH reaction, assuming Δ¹⁷O(HNO₃)= $\mathrm{1}/\mathrm{2}{\mathrm{\Delta }}^{\mathrm{17}}$O(NO₂) (Fig. S14). This adjustment substantially improved the model performance for Exps. 3–5, yielding biases that ranged from −2.6 ‰ to +1.0 ‰ relative to the observations.

Next, we examine the cause of the low model bias in Δ¹⁷O(HNO₃) relative to observations during the nighttime oxidation experiment. In this experiment, the measured Δ¹⁷O(HNO₃) exceeded that of Δ¹⁷O(NO₂), implying greater O₃ incorporation into HNO₃ than is represented in the model. The dominant modeled pathway for HNO₃ formation at night was the reaction of NO₃ with pinaldehyde (Fig. S8). However, this route yields Δ¹⁷O(HNO₃) ≈ Δ¹⁷O(NO₃) because NO₂, NO₃, and N₂O₅ rapidly equilibrate thermally overnight, leading to Δ¹⁷O(NO₂) ≈ Δ¹⁷O(NO₃) ≈ Δ¹⁷O(N₂O₅). Therefore, this pathway alone cannot account for the elevated observed Δ¹⁷O(HNO₃) relative to the model simulation. To explain this discrepancy, an additional source of high-Δ¹⁷O external to the NO_y reservoir must be involved. One possibility is that the heterogeneous uptake of N₂O₅ on aerosol surfaces could involve incorporation of an oxygen atom from O₃ rather than liquid water. In this case, based on our mass balance framework (Table 1), the Δ¹⁷O of HNO₃ formed via this pathway can be represented as

$$\begin{array}{}\text{(8)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{HNO}}_{\mathrm{3}}\right)=(\mathrm{5}/\mathrm{6}){\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}\right)+(\mathrm{1}/\mathrm{6}){\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{O}}_{\mathrm{3}}^{\mathrm{term}}\right).\end{array}$$

Since Δ¹⁷O(NO₂) ≈ Δ¹⁷O(N₂O₅) for our nighttime oxidation experiment conditions, this expression simplifies to

$$\begin{array}{}\text{(9)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{HNO}}_{\mathrm{3}}\right)=(\mathrm{5}/\mathrm{6}){\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{NO}}_{\mathrm{2}}\right)+(\mathrm{1}/\mathrm{6}){\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{O}}_{\mathrm{3}}^{\mathrm{term}}\right).\end{array}$$

This mass balance equation is similar to that assumed for N₂O₅ heterogenous reaction involving particulate Cl⁻ (Table 1). While we did not initiate our experiment with a Cl⁻ source, we must have a source of Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$) external to NO_x to explain the underestimate of simulated Δ¹⁷O(HNO₃) relative to observations.

To test the potential impact of this mechanism, we incorporated N₂O₅ heterogeneous uptake into the model (Table S9). The uptake rate coefficient (k_het) was estimated assuming an aerosol seed number and volume concentration upon atomization of 2×10⁴ cm⁻³ and 2×10¹⁰ nm³ cm⁻³, respectively, which was taken from previously reported values from similarly conducted α-pinene + NO₃ nighttime experiments (Takeuchi and Ng, 2019), and an N₂O₅ uptake coefficient (γ) of $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ for organic carbon with RH ≥ 30 % (Escorcia et al., 2010). Due to uncertainty in these parameters, we performed a sensitivity analysis across a range of k_het values from $\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, corresponding to N₂O₅ lifetimes between approximately 0.46 and 4.6 h. Model results show that increasing the N₂O₅ heterogeneous reaction rate systematically reduces the Δ¹⁷O(HNO₃) model bias. Specifically, the bias decreased from 8.1 ‰ in the base case (no heterogeneous uptake) to 3.5 ‰ for the highest assumed k_het (Fig. S15). This supports the hypothesis that N₂O₅ heterogeneous reactions incorporating O₃-derived oxygen significantly influence the isotopic composition of HNO₃ produced under nighttime conditions. However, the highest assumed k_het rate led to an increase in the overall model bias for Δ¹⁷O(HNO₃) simulations the high-NO_x photochemical experiments (Exps. 3–5), shifting from −0.8 ± 1.5 ‰ in the modified mass balance simulation to +1.8 ± 2.5 ‰ (Fig. S16). To avoid overcorrection, we selected a k_het rate of $\mathrm{9.11}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹, which improved agreement in the nighttime oxidation experiments without negatively impacting the Δ¹⁷O(HNO₃) predictions under high-NO_x photochemical conditions.

Lastly, we sought to diagnose the potential underprediction of Δ¹⁷O(HNO₃) in the model relative to observations from the low-NO_x photochemical experiments (Exps. 1–2). We observed a relatively large amount of HNO₃ present before the experiments began, ranging from 3.2 to 5.1 ppb, which represented 20.1 %, 18.0 %, and 7.9 % of the maximum HNO₃ concentrations measured during Exps. 1, 1R, and 2, respectively (Table S10; Fig. S1). This suggested the possibility of a substantial chamber blank influencing the Δ¹⁷O(HNO₃) measurements. Unfortunately, we did not directly quantify chamber blanks during these experiments. Thus, to evaluate the potential impact, we conducted a sensitivity analysis by introducing a new model tracer, HNO${}_{\mathrm{3}}^{\mathrm{blank}}$, which was initialized using pre-experiment CIMS measurements. This tracer was treated identically to HNO₃ in the model, undergoing the same reactions and loss processes as HNO₃ (Table S11). We then used an isotope mass balance framework to infer the Δ¹⁷O of the blank component required to reproduce the observed Δ¹⁷O(HNO₃) (Eq. 10):

$$\begin{array}{}\text{(10)}& {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{blank}}\right)={\displaystyle \frac{\begin{array}{c}{\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{obs}}\right)-\left(\mathrm{1}-f_{\mathrm{blank}}\right)\\ {\mathrm{\Delta }}^{\mathrm{17}}\mathrm{O}\left({\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{prod}}\right)\end{array}}{f_{\mathrm{blank}}}},\end{array}$$

where Δ¹⁷O(HNO${}_{\mathrm{3}}^{\mathrm{obs}}$) is the observed value, Δ¹⁷O(HNO${}_{\mathrm{3}}^{\mathrm{prod}}$) is the value for photochemically produced HNO₃ in the model, and f_blank is the fractional contribution of the chamber blank from the model simulation:

$$\begin{array}{}\text{(11)}& f_{\mathrm{blank}}={\displaystyle \frac{\left[{\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{blank}}\right]}{\left[{\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{blank}}\right]+\left[{\mathrm{HNO}}_{\mathrm{3}}^{\mathrm{prod}}\right]}}.\end{array}$$

Using this approach, we calculated an average Δ¹⁷O(HNO${}_{\mathrm{3}}^{\mathrm{blank}}$) of 36.1 ± 4.0 ‰ (n= 3). While elevated, this value is plausible if HNO₃ formation occurred predominantly through nighttime N₂O₅ heterogeneous uptake under dark chamber conditions prior to the start of the experiment and if the precursor NO₂ had a high Δ¹⁷O value. Such conditions could arise from residual NO₂ in the chamber either from previous experiments or background air that underwent oxidation while the chamber remained dark and inactive before the conducted experiments were initiated. It is also important to note that the CIMS HNO₃ measurements are subject to a relatively large uncertainty of approximately ± 20 ‰, which may further influence the inferred blank correction.

Overall, to improve the accuracy of simulated Δ¹⁷O(HNO₃), we implemented a series of modifications to the NO_x-API mechanism based on the conducted sensitivity tests, termed NO_x-API (modified). First, we revised the oxygen mass balance for Δ¹⁷O(HNO₃) formation via the NO₂+ OH reaction to ($\mathrm{1}/\mathrm{2}$)Δ¹⁷O(NO₂). Second, we included a chamber-derived HNO₃ background using a fixed Δ¹⁷O value of 36.1 ‰. This background was initialized in all simulations based on CIMS-derived HNO₃ concentrations prior to photolysis onset (Table S10). Finally, we added a heterogeneous N₂O₅ hydrolysis pathway with a first-order loss rate of $\mathrm{9.11}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹, using a Δ¹⁷O(HNO₃) formation mass balance of ($\mathrm{5}/\mathrm{6}$) ×Δ¹⁷O(N₂O₅) + ($\mathrm{1}/\mathrm{6}$) ×Δ¹⁷O(O${}_{\mathrm{3}}^{\mathrm{term}}$). As shown in Fig. 7, while these modifications had a minor effect on Δ¹⁷O(NO₂) and Δ¹⁷O(ONIT), in which the base NO_x-API mechanism were already in strong agreement with the observations, they substantially improved the model's performance for Δ¹⁷O(HNO₃). The average absolute bias across all experiments decreased from 6.7 ± 3.3 ‰ in the base mechanism to 1.6 ± 1.3 ‰ in the modified mechanism (Table 5) with an improved correlation (R²= 0.48). These results demonstrate the difficulty of accurately simulating Δ¹⁷O(HNO₃) across diverse experimental conditions, highlighting the need for future experiments that more directly constrain oxygen isotope mass balance assumptions in HNO₃ formation pathways. At the same time, careful attention to HNO₃ collection methods and blank corrections is essential to ensure meaningful comparisons between models and observations.

4 Conclusions

This study presents the first chamber experiments combining comprehensive NO_y and α-pinene oxidation chemistry with stable isotope constraints. Using a suite of observations and box-model simulations, we demonstrate how multi-isotope analyses of Δ¹⁷O, δ¹⁸O, and δ¹⁵N can yield novel insights into atmospheric oxidation pathways, including the formation and transformation of gas-phase and pNO₃ species. We observed a strong linear relationship between Δ¹⁷O and δ¹⁸O values across all collected NO_y species. We derived a δ¹⁸O value of 106 ± 5 ‰ for oxygen atoms transferred into NO_y from O${}_{\mathrm{3}}^{\mathrm{term}}$ and a value of 11.1 ± 1.0 ‰ for oxygen atoms transferred from other oxidants with an assumed Δ¹⁷O ∼ 0 ‰, such as RO₂, HO₂, and OH. These results provide a new isotopic constraint for disentangling multi-oxidant systems in both chamber and ambient settings. Nitrogen isotope fractionation was evaluated from the observations, which indicated Δδ¹⁵N(HNO₃–NO₂) values were generally enriched, while Δδ¹⁵N(pNO₃–NO₂) values were negative, reflecting preferential ¹⁵N incorporation into HNO₃ and ¹⁴N incorporation into pNO₃. However, large differences in the observed Δδ¹⁵N(HNO₃–NO₂) between H₂O₂ $/$ NO (33.7 ± 7.1 ‰) and HONO (0.4 ± 1.7 ‰) photochemical experiments remain unresolved, particularly since these experiments should have produced HNO₃ from a similar pathway, namely the NO₂+ OH reaction. These discrepancies make it challenging for us to recommend a fractionation value associated with the NO₂+ OH reaction and indicate the need for future targeted studies of the isotope effects during the NO₂+ OH reaction. Importantly, isotope observations revealed stark differences between HNO₃ (medium to high Δ¹⁷O and high δ¹⁵N) and pNO₃ (low Δ¹⁷O and low δ¹⁵N), with the later predominately derived from organic nitrate. These isotope differences between HNO₃ and organic nitrate could serve as a useful qualitative constraint to evaluate inorganic and organic nitrate contributions to HNO₃ and pNO₃ budgets.

Model simulations of Δ¹⁷O were conducted and indicated that our model captured Δ¹⁷O(NO₂) and Δ¹⁷O(ONIT) (compared with observed Δ¹⁷O(pNO₃) values) well. Simulating Δ¹⁷O(HNO₃), however, proved more challenging. The model tended to overestimate Δ¹⁷O under high NO_x conditions, underestimate it in low NO_x experiments, and underpredict nighttime values. A series of sensitivity tests suggests that this mismatch likely arises from multiple contributing factors, including potential HNO₃ measurement biases (e.g., chamber blank), missing heterogeneous pathways (e.g., N₂O₅ hydrolysis), and the need to revisit assumptions in the isotopic mass balance of the NO₂+ OH reaction. From these experiments, it is evident that we have a solid understanding of oxygen isotope transfer associated with NO_x photochemical cycling and the formation of organic nitrates. However, our understanding of the oxygen and nitrogen isotope dynamics of HNO₃ remains more uncertain. Our findings indicate the need for future experiments specifically designed to probe the formation pathways of HNO₃ and their associated isotope dynamics. This includes chamber studies that isolate individual pathways as well as targeted flow tube experiments. Such efforts are essential to refine oxygen isotope mass balance assumptions and are critical if Δ¹⁷O and δ¹⁵N are to be used quantitatively to track HNO₃ chemistry in both laboratory and ambient environments.