Drivers of droplet formation in east Mediterranean orographic clouds

The purpose of this study is to understand the drivers of cloud droplet formation in orographic clouds. We used a combination of modeling, in situ, and remote sensing measurements at the high-altitude Helmos Hellenic Atmospheric Aerosol and Climate Change ((HAC)²) station, which is located at the top of Mt. Helmos (1314 m above sea level), Greece, during the Cloud–AerosoL InteractionS in the Helmos Background TropOsphere (CALISHTO) campaign in fall 2021 (https://calishto.panacea-ri.gr/, last access: 1 August 2024) to examine the origins of the aerosols (i.e., local aerosol from the planetary boundary layer (PBL) or long-range-transported aerosol from the free-tropospheric layer (FTL) contributing to the cloud condensation nuclei (CCN)), their characteristics (hygroscopicity, size distribution, and mixing state), and the vertical velocity distributions and resulting supersaturations.

We found that the characteristics of the PBL aerosol were considerably different from FTL aerosol and use the aerosol particle number and equivalent mass concentration of the black carbon (eBC) in order to determine when (HAC)² was within the FTL or PBL based on time series of the height of the PBL. During the (HAC)² cloud events we sample a mixture of interstitial aerosol and droplet residues, which we characterize using a new approach that utilizes the in situ droplet measurements to determine time periods when the aerosol sample is purely interstitial. From the dataset we determine the properties (size distribution and hygroscopicity) of the pre-cloud, activated, and interstitial aerosol. The hygroscopicity of activated aerosol is found to be higher than that of the interstitial or pre-cloud aerosol. A series of closure studies with the droplet parameterization shows that cloud droplet concentration (N_d) and supersaturation can be predicted to within 25 % of observations when the aerosol size distributions correspond to pre-cloud conditions. The analysis of the characteristic supersaturation of each aerosol population indicates that droplet formation in clouds is aerosol-limited when formed in FTL air masses – hence droplet formation is driven by aerosol variations, while clouds formed in the PBL tend to be velocity-limited and droplet variations are driven by fluctuations in vertical velocity. Given that the cloud dynamics do not vary significantly between air masses, the variation in aerosol concentration and type is mostly responsible for these shifts in cloud microphysical state and sensitivity to aerosol. With these insights, the remote sensing of cloud droplets in such clouds can be used to infer either CCN spectra (when in the FTL) or vertical velocity (when in the PBL). In conclusion, we show that a coordinated measurement of aerosol and cloud properties, together with the novel analysis approaches presented here, allows for the determination of the drivers of droplet formation in orographic clouds and their sensitivity to aerosol and vertical velocity variations.

1 Introduction

Aerosol–cloud interactions hold the largest source of uncertainty in predictions of anthropogenic climate change (IPCC, 2023). A large fraction of this uncertainty arises from impacts of aerosols on cloud droplet formation in liquid- and mixed-phase clouds (IPCC, 2013; Lohmann, 2017). High aerosol levels generally lead to increased cloud droplet number and cloud albedo (Twomey, 1974, 1991), but the exact relationship depends on many factors, including cloud dynamics (cloud-scale vertical velocity distributions), aerosol size distribution, and hygroscopicity, while the description of these dependencies in a realistic way in models poses a challenge that the development of large observation datasets can help resolve.

Not all clouds are equally sensitive to changes in the cloud condensation nuclei (CCN), i.e., the subset of aerosol that activates into cloud droplets. For clouds to be sensitive to aerosol variations, there needs to be sufficient supersaturation during the stages of cloud droplet formation (Nenes et al., 2001) so that droplet formation can take place. At a relatively low concentration of aerosols, water vapor availability (i.e., supersaturation) is large, so variations in pre-cloud aerosol readily translate to droplet variations. These conditions correspond to aerosol-limited clouds, and the cloud droplet concentration (N_d) is very sensitive to aerosol changes. When CCN concentrations become large, the competition for water vapor required to activate them to cloud droplets becomes so significant that supersaturation is low and N_d becomes insensitive to aerosol load changes. Under such conditions, clouds are said to be “velocity-limited” (Reutter et al., 2009; Georgakaki et al., 2021) because vertical velocity is the driver of the expansion cooling that generates supersaturation. In cases of extreme competition for water vapor, the droplet number tends to reach a “limiting” value that is solely a function of vertical velocity (e.g., Georgakaki et al., 2021).

The differences between the aerosols that are involved in cloud droplet formation (i.e., the CCN) and those that are not, called “interstitial”, are important to understand. Studies focusing on both the activated and the interstitial particles have been carried out on airborne platforms (e.g., Ditas et al., 2012; Kleinman et al., 2012) and at high-altitude stations (Collaud Coen et al., 2018) that can reside in clouds formed on mountain tops, such as Puy de Dôme (Venzac et al., 2009; Asmi et al., 2012), Jungfraujoch (Hammer et al., 2014; Bukowiecki et al., 2016), Storm Peak (Obrist et al., 2008), Mont Sonnblick (Schauer et al., 2016), Monte Cimone (Marinoni et al., 2008; Cristofanelli et al., 2016), and Zeppelin Station (Tunved et al., 2013).

The established way to separate interstitial aerosols from cloud droplets is to use a “twin inlet system”, one of which is used for sampling the interstitial aerosols (“interstitial inlet”) and the other for sampling the interstitial and the evaporated cloud droplets (“total” or “whole air inlet”). This sampling strategy is based on the large size difference between droplets and interstitial aerosol, so an appropriate selection of inlet cut-off size for the interstitial inlet allows for the separate collection of interstitial aerosols. The challenge is therefore to correctly select the cut-off diameter/size to avoid mixing droplets with interstitial aerosols in the interstitial inlet, given that droplet size varies considerably between clouds. Hammer et al. (2014) and Krüger et al. (2014) used an interstitial inlet consisting of a cyclone with a 2.5 µm cut-off diameter (PM_2.5) to remove droplets, while Portin et al. (2014) and Väisänen et al. (2016) used a PM₁ (1 µm cut-off diameter) impactor nozzle plate to prevent the cloud droplets from entering the sample line. Other studies, such as that of Mertes et al. (2005), Drewnick et al. (2006), and Asmi et al. (2012), have used a 5 µm cut-off diameter inlet system. Given the large variability in droplet and aerosol sizes, the use of a fixed cut-off size in the interstitial inlet may not always sufficiently separate interstitial aerosols from some evaporated cloud droplets. This can be a problem in velocity-limited clouds with low supersaturation, where interstitial aerosol may have a comparable size to the activated droplets (Charlson et al., 2001).

It may also be possible to separate interstitial aerosols from evaporated cloud droplets with a single-inlet (total) system if there are concurrent in situ measurements of droplet size that allow for the application of a temporal filter on the time series (e.g., consider only parts of the time series for which droplets do not pass through the inlet). We explore this technique at the high-altitude Helmos Hellenic Atmospheric Aerosol and Climate Change (HAC)² station at Mt. Helmos, Greece, during the CALISHTO campaign and study the factors driving cloud formation at an orographic site. We specifically examine the origins and sources of aerosols contributing to the CCN (e.g., local aerosol in the PBL or long-range-transported aerosol from the FTL), their characteristics (hygroscopicity, size distribution, and mixing state), and the vertical velocity distributions and resulting supersaturations. Several closure studies are carried out to test the ability to predict the droplet number and supersaturation.

2 Methodology

2.1 Measurement sites

Mt. Helmos is the second highest mountain in the Peloponnese (southern Greece), peaking at 2355 m above sea level (a.s.l.), while the (HAC)² station is located at the mountain top (coordinates 37.984076° N, 22.196115° E), generally isolated from local human activities and surrounded, at lower altitudes, by lush forests and pristine alpine landscapes (Fig. 1). A second temporary site during CALISHTO, called “Vathia Lakka” (VL), was located at the lee side of the mountain approximately 1.7 km away (coordinates 37.999473° N, 22.193391° E) and 500 m below (HAC)². In situ measurements are available at both (HAC)² and VL, the latter being used as a pre- or post-cloud proxy.

Figure 1 The study area (left) and the sub-domain over Greece (middle) and the regional area around HELMOS (right) shown in the red color on the altimeter map given by the NASA Digital Elevation Model (NASA JPL, 2020). The symbols represent the location of the two sites, (HAC)² and VL, while Kalavrita is the closest village to the site.​​​​​​​

Given that (HAC)² can be either within the FTL or within the PBL (Foskinis et al., 2024a), a major parameter controlling the aerosol sampled at any given time is the height of the PBL (PBLH); here we used the PBLH data that were derived according to Foskinis et al. (2024a) based on the turbulence threshold technique applied to the wind Doppler lidar measurements. When the PBLH exceeds the (HAC)² altitude, the site resides within the PBL, which may be rich in biogenic particles originating from the nearby forest and anthropogenic emissions originating from the greater region. When the PBLH is below (HAC)², the station is in the FTL and receives air masses and aerosol from long-range transport: continental aerosols originating from Europe and the Balkans, marine aerosols from the Mediterranean Sea, and dust from the Sahara (Papayannis et al., 2005, 2008; Kallos et al., 2007; Kaskaoutis et al., 2012; Soupiona et al., 2018). (HAC)² frequently resides in the clouds, about ∼ 25 % in September to ∼ 65 % in October, and in November and December the (HAC)² cloud coverage is 45 % (Fig. S5 in the Supplement). During the whole period (HAC)² resides about half of the time within the FTL (Foskinis et al., 2024a).

2.2 Dataset and study period

The dataset analyzed was collected during the CALISHTO campaign, which was designed to study the cloud microphysical properties using in situ and remote sensing techniques. We focus on October and November 2021, dividing the study period into PBL-influenced and FTL-influenced regimes based on the PBLH time series by Foskinis et al. (2024a). Furthermore, we divide each regime into “cloudy” when the cloud liquid water content (LWC) exceeded 0.02 g m⁻³ (Prabhakar et al., 2014; Braun et al., 2018; Dadashazar et al., 2018) and “cloud free” otherwise.

2.3 Instrumentation

2.3.1 Inlets

The aerosol inlets at (HAC)² are designed to maintain laminar flow and minimize particle losses (vertical orientation, stainless steel tubing) over a wide range of aerosol sizes (< 10 µm), in line with Aerosol, Clouds and Trace gases Research Infrastructure (ACTRIS) recommendations for aerosol inlets and sampling tubes. For this setup, the diffusion losses are negligible (< 1 % for particle sizes greater than 100 nm) for scanning mobility particle sizer (MPSS), Aethalometer (AE31), and time-of-flight aerosol chemical speciation monitor (ToF-ACSM) measurements.

2.3.2 TROPOS scanning mobility particle sizer (MPSS)

A TROPOS (Leibniz Institute for Tropospheric Research) scanning mobility particle sizer (MPSS) was used to measure submicron aerosol size distributions at (HAC)² every 5 min. The MPSS employs a Vienna-type differential mobility analyzer (DMA; electrode length 28 cm) with a condensation particle counter (CPC model 3772, TSI Inc.) to measure particles ranging from 10 to 800 nm. The MPSS operated at a sheath flow rate of 5 L min⁻¹ and an aerosol flow rate of 1 L min⁻¹. Before detection, the ambient aerosol enters the DMA and passes through an Kr-85 neutralizer to achieve an equilibrium charge distribution. Both the aerosol sample flow and the sheath airflow were dried below 40 % relative humidity (RH) using Nafion dryers. The temperature, relative humidity, and pressure inside the instrument are continuously monitored during the sampling process. Additionally, there was a second MPSS (DMA model 3081 and CPC model 3775, TSI Inc.) located at VL, and it was operated at a sheath flow rate of 3 L min⁻¹ and an aerosol flow rate of 0.3 L min⁻¹, and it was equipped with a Nafion dryer to dry the sheath airflow below 40 % relative humidity. The second MPSS was used to provide the pre-cloud proxy in the cases where (HAC)² was in clouds. In both cases, the number size distribution data are corrected for diffusion losses within the aerosol inlet and the instrument's internal tubing (TROPOS MPSS inversion software) using the method of “equivalent length” (Wiedensohler et al., 2012, 2018).

2.3.3 Time-of-flight aerosol chemical speciation monitor (ToF-ACSM)

The ToF-ACSM (Aerodyne Research Inc., Billerica, MA, USA) measures the non-refractory submicron aerosol mass and chemical composition (ammonium, sulfate, nitrate, chloride, and organics) every 10 min (Fröhlich et al., 2013). The sampling air enters through a PM_2.5 virtual impactor, which is followed by a Nafion drier. A 120 µm orifice (for high-altitude measurements) was used for sampling the PM₁ fraction. An aerodynamic particle focusing lens converts the sample into an air beam under high-vacuum conditions. The non-refractory material is then flash vaporized on a tungsten plate surface at 600 °C and is subsequently ionized by electron impact ionization at 70 eV. The resulting ions are detected by a TOFWERK time-of-flight mass analyzer. The instrument allows the detection of aerosols of ∼ 40–1000 nm vacuum aerodynamic diameters. A collection efficiency (CE) of 0.3 (Zografou et al., 2024) was chosen based on a comparison of the PM₁ mass as the sum of the ACSM and eBC concentrations versus the total PM₁ mass by the MPSS (Fröhlich et al., 2015) using densities of 1.8 g cm⁻³ for sulfates and 1.3 g cm⁻³ for organics. The CE accounts for the fraction of the non-refractory particles that bounce off the vaporizer and are not detected. The relative ionization efficiencies for sulfate and ammonium were determined after the calibration of the instrument with ammonium sulfate and ammonium nitrate to be 1.19 and 3.11, respectively.

2.3.4 Aethalometer (AE31)

A seven-wavelength (370, 470, 520, 590, 660, 880, and 950 nm) Aethalometer (AE31 model, Magee Scientific) measures absorption by light-transmission measurements through a filter tape and was used to determine the eBC concentration following Hansen et al. (1982) and Petzold et al. (2013). We used the 880 nm channel to constrain the equivalent black carbon concentration. eBC is used in this study as an FTL/PBL proxy, since black carbon mostly originates from anthropogenic activities and is expected to be much higher in the PBL than in the FTL; thus when eBC is high, (HAC)² is expected to be within the PBL, while as eBC reduces, (HAC)² is influenced less from the PBL and tends to be within the FTL (Lund et al., 2018; Motos et al., 2020).

2.3.5 Particulate volume monitor (PVM-100)

A particulate volume monitor (Gerber Scientific Inc, PVM-100) was used to obtain the liquid water content (LWC), the particle surface area (PSA), and the effective droplet radius (R_eff) and diameter (D_eff) of clouds by measuring the forward scatter of droplets encountered by a diode laser beam along a 40 cm path (Gerber, 1984) in an open-path geometry. The signals are then converted to droplet size and number concentration as follows: $N_{\mathrm{d}}=\mathrm{1.07}\frac{\mathrm{LWC}}{{\mathit{\rho }}_{\mathrm{w}}{R}_{\mathrm{eff}}^{\mathrm{3}}}$ (Rezacova et al., 2007).

2.3.6 Cloud condensation nuclei counter (DMT CCN-100)

CCN concentrations as a function of supersaturation (“CCN spectra”) were measured with a Droplet Measurement Technologies (DMT) CCN-100 counter, which is based on the continuous-flow streamwise thermal-gradient chamber design of Roberts and Nenes (2005). The instrument generates supersaturation through the principle of relative diffusion of heat and water vapor. An aerosol sample, surrounded by filtered sheath air, flows through a cylindrical, metallic tube in the axial direction with wetted inner walls and a positive streamwise temperature gradient. The relative diffusion of water and heat from the tube walls towards the centerline generates a supersaturation (s) that peaks at the centerline. The value of this maximum supersaturation depends on the flow rate, streamwise temperature gradient, and pressure (Roberts and Nenes, 2005; Lance et al., 2006). Part of the aerosol sample, which is mostly located around the centerline, becomes activated and grows to sizes (0.75–10 µm diameter) large enough to be detected at the exit of the flow tube by an optical particle counter (OPC). The CCN concentration then at the centerline s is equal to the number concentration of droplets measured in the OPC. By changing the streamwise temperature gradient every 6 min (and ignoring data collected during the instrument transients), we cycle through 0.1 % up to 1 % with a supersaturation step of 0.1 % to obtain a CCN spectrum every hour.

2.3.7 Wind Doppler lidar

The vertical velocity of the air was derived by using a wind Doppler lidar (StreamLine XR, HALO Photonics) operating in stare mode (Pearson et al., 2009). It was installed at the VL site in order to obtain the updraft currents towards (HAC)² and the surrounding area. Excluding precipitation, the HALO lidar provides vertical velocity (w) at 30 m range resolution. The range of the HALO StreamLine XR lidar is 12 km, but during the campaign the maximum range of useful signal varies from 2 to 3 km depending on the atmospheric aerosol load. Vertical stare was configured at 5 s integration time, alternating between co- and cross-polar receiver. In addition to the vertical stare, velocity azimuth display (VAD) scans were included but are not utilized here. The HALO lidar is a pulsed Doppler lidar that operates at 1.5 µm wavelength (Pearson et al., 2009). The backscattered frequency of each pulse shifts due to the “Doppler effect”, which depends on the relative motion of the scatterer and HALO lidar (Newsom and Krishnamurthy, 2020). The backscattered fraction of the initial pulse is collected back from the HALO lidar and analyzed as a time- and frequency-resolved signal. The time delay between each outgoing and backscattered pulse indicates the distance of the scatterers, while the Doppler shift reveals the radial velocity of the scatterer, which corresponds to the aerosol velocity at the given height.

Following Barlow et al. (2011) and Newsom and Krishnamurthy (2020), we excluded the data with a signal-to-noise ratio (SNR) lower than −20 dB, which limits instrumental uncertainty in w to 0.1 m s⁻¹ at maximum (Pearson et al., 2009). Then, we generated segments containing datasets with a 30 min moving window (Schween et al., 2014) of the noise-filtered dataset for every 5 min (Lenschow et al., 2012), and we calculated the standard deviation of w(σ_w) for every height. Considering that a convective plume within the PBL has on average an ascent speed of 1 m s⁻¹ and that the typical mixing layer height at our site is about 1 km, then the average interval is about twice the lifetime of the plume. This is typical of the derivation of turbulent fluxes from eddy covariance stations (Schween et al., 2014). The 30 min window is comparable to the average mixing time in the boundary layer.

2.4 Modeling

2.4.1 Aerosol hygroscopicity and critical supersaturation

Two approaches are used to constrain the aerosol hygroscopicity. First, we determine the bulk hygroscopicity parameter (κ) of the submicron aerosol (Petters and Kreidenweis, 2007) using the measured chemical composition and the approach outlined in Padró et al. (2010). This involves applying the ISORROPIA II thermodynamic equilibrium model (Fountoukis and Nenes, 2007) using as inputs the observed inorganic components measured by ToF-ACSM to calculate the composition (e.g., NH₄HSO₄, NH₄Cl, NH₄NO₃, (NH₄)₂SO₄, H₂SO₄) of the inorganic aerosol fraction. The Zdanovskii, Stokes, and Robinson (ZSR) mixing rule was then applied to the volume fraction of the inorganic salts, including the volume fraction of eBC and hygroscopicity parameters from Table 2 of Padró et al. (2010), while the hygroscopicity value of eBC was considered equal to 0.2 based on Ding et al. (2021). Second, we determined the characteristic hygroscopicity parameter (κ^∗) which was explicitly obtained from the combination of the CCN-100 and MPSS data based on the CCN spectrum cycles. For each supersaturation cycle we calculated the characteristic critical supersaturation (s^∗) (Cerully et al., 2011), which is defined as the supersaturation at which half of the CCN population is activated to droplets and is determined using the procedure of Cerully et al. (2011), and the characteristic size ($D_{\mathrm{cr}}^{\ast }$), which is defined as the corresponding MPSS distribution integrated from the largest resolved size (800 nm) until the $D_{\mathrm{cr}}^{\ast }$ to give an aerosol number equal to the observed CCN concentration. Then, the κ^∗ of each CCN cycle was determined from κ-Köhler theory (Petters and Kreidenweis, 2007) as ${\mathit{\kappa }}^{\ast }=\left(\frac{\mathrm{4}{A}^{\mathrm{3}}}{\mathrm{27}{D_{\mathrm{cr}}^{\ast }}^{\mathrm{3}}{s^{\ast }}^{\mathrm{2}}}\right)$, where $A=\frac{\mathrm{4}{M}_{\mathrm{w}}\mathit{\sigma }}{RT{\mathit{\rho }}_{\mathrm{w}}}$ is the Kelvin parameter, M_w (kg mol⁻¹) is the molar mass of water, σ (J m⁻²) is the surface tension of the activated droplets (here assumed to be equal to pure water), R (J mol⁻¹ K⁻¹) is the universal gas constant, T (K) is the ambient temperature, ρ_w is the density of liquid water, and $D_{\mathrm{cr}}^{\ast }$ is the characteristic dry size of the particle that activates at supersaturation $s^{\ast }.$

Both approaches give similar results (not shown here) but occasionally diverge. For instance, the bulk hygroscopicity assumes that particles are internally mixed, which for periods of sampling in the FTL is an excellent assumption (e.g., Bougiatioti et al., 2016); for PBL-dominated periods it is also a reasonable assumption due to the remote location of the station, while the characteristic hygroscopicity strictly corresponded to the average hygroscopicity for particles of size $D_{\mathrm{cr}}^{\ast }$ and was used to characterize the hygroscopicity of the resolved CCN spectrum. During periods when particles at the station will originate from both PBL and FTL, it is expected that they have an intermediate mixing state that will introduce some uncertainty in subsequent calculations.

2.4.2 Droplet activation parameterization

We use a physically based aerosol activation parameterization developed by Nenes and Seinfeld (2003) and further expanded by Fountoukis and Nenes (2005), Barahona et al. (2010), and Morales Betancourt and Nenes (2014) to calculate the droplet number formed in clouds using the wind vertical velocity and the aerosol characteristics. The droplet activation parameterization solves the equations of motion of an ascending air parcel which contains aerosols and water vapor and calculates the point where the supersaturation is maximum (s_max) as well as the corresponding droplet number, N_d.

The parameterization inputs include pressure, temperature, aerosol size distribution measured by the MPSS, the bulk hygroscopicity parameter κ, and the updraft velocity obtained by the HALO lidar. Given that the latter varies considerably over time and within each cloud event, we consider a probabilistic approach by first computing the hourly probability density function (PDF) of vertical velocity. We then apply the parameterization to calculate the PDF-integrated N_d, which is assumed to describe the average droplet number in clouds that form in the vicinity of the sampling site. This PDF-averaging approach has been shown to successfully reproduce cloud-scale values of N_d in numerous field studies in the case of cumulus and stratocumulus clouds (Conant et al., 2004; Meskhidze et al., 2005; Fountoukis and Nenes, 2007; Kacarab et al., 2020; Georgakaki et al., 2021; Foskinis et al., 2022).

The PDF-integrated N_d is computed using the characteristic velocity (w^∗) approach of Morales and Nenes (2010), in which the parameterization is applied once using w^∗ in its input but provides directly the PDF-averaged droplet number. w^∗ is given by (Foskinis et al., 2022)

$$\begin{array}{}\text{(1)}& w^{\ast }=\mathit{\epsilon }\stackrel{\mathrm{̃}}{\mathit{\lambda }}{\mathit{\sigma }}_w,\end{array}$$

where σ_w is the standard deviation of the vertical velocity PDF (assumed to be a Gaussian with zero mean), ε is the entrainment parameter, and $\stackrel{\mathrm{̃}}{\mathit{\lambda }}$ is the characteristic nondimensional velocity. The entrainment parameter (ε) accounts for lateral diabatic mixing of entrained air in the updraft zones – which effectively reduces s_max, hence w^∗. ε=1 corresponds to adiabatic updrafts, but the parameter can be lower in the case of cumulus and convective clouds, affecting the vertical distribution of liquid water and the number of droplets (Morales et al., 2011). Based on numerous in situ sampling campaigns of boundary layer clouds, ε has been found to be on average 0.68. According to Morales and Nenes (2010), $\stackrel{\mathrm{̃}}{\mathit{\lambda }}$ is affected by the total aerosol concentration (N_Total), and it is assigned values equal to 0.70, 0.79, 0.84, and 0.98, when N_Total ranges between 0–340, 340–500, 500–6400, and 6400–106 000 cm⁻³, respectively.

3 Experimental results

3.1 Dataset overview

Figure 2a shows when (HAC)² is in the FTL and when it is in the PBL based on the relative position of the PBLH (given by Foskinis et al., 2024a) against the altitude of the (HAC)² station (shown with the horizontal black line). When the station is in the FTL, the PBLH is below the (HAC)² line and vice versa when it is in the PBL. The air mass typing is consistent with the observed moisture content, since under cloud-free conditions, the FTL air masses are markedly dryer (RH = 34 ± 26 %) than the PBL air masses (RH = 65 ± 16 %) (Fig. 2c). Also, when (HAC)² is in the FTL, we observed two dominant wind directions, one at 30° N and one at 80° N, where for both N_Total approaches the lowest values are observed (∼ 45 cm⁻³) (Fig. S2d), and eBC levels approach its detection limit (∼ 0.01 µg m⁻³). These wind directions are directly related to the long-range-transported air mass; when arriving from the north, it usually originates from eastern Europe and the Balkans and is rich in sulfur (Stavroulas et al., 2021). When the air mass arrives from the east or southeast, it often carries dust aerosols (Gao et al., 2024). Additionally, we identified three prevailing wind directions that correspond to the local transport patterns (Fig. S2f) from 90, 180, and 320° N. We also found that the N_Total tends to maximize (> 1000 cm⁻³) when the wind blew from 225–270° N and air masses originated from the PBL. For the remaining wind directions, N_Total varied between 300–1000 cm⁻³ (Fig. S2f), and the eBC values increase up to ∼ 0.4 µg m⁻³ when the wind speed exceeds 6 m s⁻¹ and becomes maximum when the wind blows from 160–220° N (Fig. S2c).

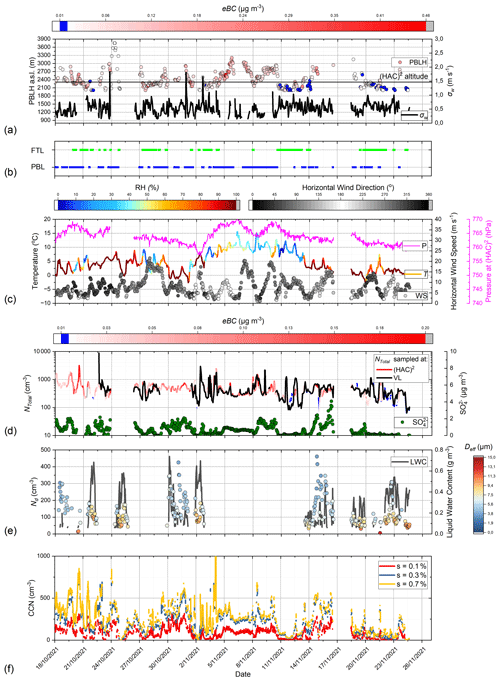
Figure 2 Time series of characteristic parameters for the CALISHTO campaign. (a) PBLH (circles) and filled colors correspond to the eBC. If PBLH is below (HAC)² (horizontal black line), (HAC)² is within the FTL (eBC < 0.01 µg m⁻³ – blue color), and vice versa if in the PBL (eBC > 0.01 µg m⁻³, red color). On the right-hand-side axis, the σ_w drives the PBLH. (b) The moments when (HAC)² is within FTL (blue color) and within PBL (green color). (c) The ambient air temperature trace is colored by the RH (in the FTL when < 40 %, and vice versa when inside the PBL). The horizontal wind speed is given by the circles colored by the horizontal wind direction in gray scale, and the ambient pressure is presented by the magenta line. (d) N_Total measured at (HAC)² (colored by the eBC amount) and the N_Total measured at VL (black line). N_Total measured at (HAC)² comparable to the one of VL implies both sites reside in the same atmospheric layer – also indicated by a high concentration of eBC. SO${}_{\mathrm{4}}^{\mathrm{2}-}$ concentration is presented by the green symbols and is also used as a proxy for (HAC)² being in the PBL. (e) N_d colored by the D_eff, while on the right axis is the LWC. (f) The CCN time series at different supersaturation values (s = 0.1, 0.3, and 0.7).

Additionally, we found a dependence of the PBLH on the wind direction, since when the wind passes over mountain tops before reaching the site, the PBLH tends to be higher (Fig. S2a) and the σ_w tends to be lower (Fig. S2b). We observed that the increase in N_Total (from ∼ 250 to ∼ 750 cm⁻³) (Fig. S3a) leads to an increase in N_d (from ∼ 100 to ∼ 300 cm⁻³) (Fig. S3b) and decrease in the cloud droplet size (D_eff) (from ∼ 17.5 to ∼ 10 µm) (Fig. S3c), consistent with the Twomey effect (Twomey, 1977) of aerosols on clouds (IPCC, 2023).

3.2 Separating interstitial aerosol from cloud droplet residuals at (HAC)²

Aerosol particles that act as CCN have a dry diameter on the order of 100 nm and grow at least 10-fold when they activate into cloud droplets (Fig. 3) (Rogers and Yau, 1996; Pierce et al., 2015). Indeed, when the (HAC)² station was in clouds, the droplet effective diameter, D_eff, varied between 2 and 15 µm (Fig. 2). When the clouds are formed with FTL aerosol, the D_eff was on average 17.0 ± 2.7 and 10.3 ± 1.9 µm when formed with PBL aerosol. The average size differences between the two types of air masses can be explained by the different CCN concentrations in them. The FTL has fewer CCN, and hence droplets are generally larger than in PBL air masses (Fig. 2f). In both cases, the aerosol inlet (which is a PM₁₀ inlet – 10 µm cut-off diameter) would sample inactivated (known as “interstitial”) aerosol together with some of the droplets. These droplets subsequently evaporate in the heated inlet and contribute to the size distribution and other aerosol characteristics measured by the online in situ aerosol instrumentation. This means that when the station is in-cloud, the aerosol sampled from the PM₁₀ inlet corresponds to a mixture of interstitial aerosol and evaporated cloud droplet residuals. However, D_eff varies considerably during a cloud event (Fig. 2e) and often exceeds 10 µm. This implies that considering subsets of the in-cloud time series when the D_eff is large enough can ensure that during these periods the PM₁₀ inlet samples only interstitial aerosol, as droplets would be too large to pass through the inlet.

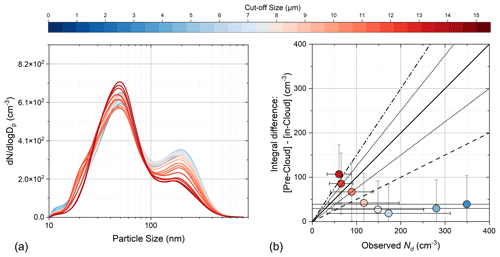
Figure 3 (a) The averaged $\mathrm{d}N/\mathrm{d}\log D_{\mathrm{p}}$​​​​​​​ size distribution of the captured cloud transition moments when using different cut-off threshold values, the so-called “sensitivity analysis”, and the cut-off threshold (D_eff as measured in situ with the PVM-100) that was applied is represented by the color scale. (b) The integrated difference between pre-cloud and in-cloud aerosol size distributions from ∼ 70 nm to the largest sizes when compared to the droplet number measured in situ concurrently by the PVM-100. Each symbol corresponds to the application of a different D_eff threshold (as indicated by the symbol color, using the same scheme as in a), while the error bars correspond to the standard deviation.

We therefore consider the above concept and develop a “virtual filter” technique to define the D_eff threshold (measured in situ and continuously by the PVM-100) that ensures that the aerosol sampled by the PM₁₀ inlet does not contain aerosol from evaporated droplets but only interstitial aerosols. In applying this filter, we ignore periods of the respective measurements during which the in situ D_eff of the droplets is less than the threshold. We select the periods during which we were sampling at least 30 min continuously in cloud-free conditions followed by (or proceeded by) at least 30 min of cloudy conditions to allow multiple size distribution measurements during the pre-/post-cloud and the in-cloud phases. Additionally, the 30 min sampling time was found to be a “best choice” to obtain a large number of samples that at the same time are subject to the least statistical noise from the natural variability occurring in each cloud event. Hence, the distributions under cloud-free conditions are then averaged to give the “total aerosol distribution”. The in-cloud distributions are averaged for periods when the droplet D_eff exceeds a predefined threshold (starting from 0 µm). The in-cloud distributions are averaged for different values of the D_eff threshold until 16 µm.

We select as the optimum D_eff the minimum value above which the measured aerosol size distribution becomes insensitive to the chosen threshold value. Figure 3 displays an example of this process applied to a segment of data from CALISHTO. We find in this case that a D_eff threshold of 13.5 µm is the minimum for which the observed size distribution stopped to be sensitive to further increases in the cut-off size (Fig. 3a). Additionally, we compare the difference between the aerosol size distribution pre-cloud and the interstitial aerosol distribution (i.e., with the application of the 13.5 µm threshold) with the observed droplet number, and we found that indeed the integrated difference between these distributions (from ∼ 70 nm to the largest sizes measured by the MPSS) matches with the droplet number obtained in situ with the PVM-100 to within ±25 % (Fig. 3b). Thus, we confirm that this threshold is consistent with allowing only the interstitial aerosol to pass through the inlet. Given that in situ closure studies often involve this degree of uncertainty (e.g., see relevant discussion by Foskinis et al., 2024a, and relevant references cited therein) in addition to any other uncertainties that may exist at this particular site (e.g., variations in aerosol entering the cloud, sampling efficiency of the inlet, and uncertainties in the droplet number determination with the PVM-100), we conclude that the latter distribution is indeed representative of the interstitial aerosol. Additional support for this conclusion is provided later by the ability to predict cloud droplet number (Sect. 3.4) as it requires the correct parameters of hygroscopicity, size distribution, and vertical velocity.

3.3 Differences among the properties of total, activated, and interstitial aerosol

We identified more than 20 periods of cloud-free and cloudy transitions during the CALISHTO campaign. We applied the methodology of Sect. 3.2 to estimate the corresponding cloud-free, interstitial-only, and mixed-aerosol (cloud residues and interstitial combined) size distributions. We then determined s^∗ and κ^∗ (Sect. 2.4.1​​​​​​​) of the cloud-free (κ_cf), interstitial (κ_i), and interstitial and droplet residue aerosol mixture (Fig. 4a). Assuming that the pre-/post-cloud hygroscopicity is the volume-average hygroscopicity of the interstitial and activated aerosol, we estimate the hygroscopicity of the activated aerosol, κ_a, using the mixing rules of Petters and Kreidenweis (2007) as ${\mathit{\kappa }}_{\mathrm{a}}=\frac{{\mathit{\kappa }}_{\mathrm{cf}}{V}_{\mathrm{cf}}-{\mathit{\kappa }}_{\mathrm{i}}{V}_{\mathrm{i}}}{V_{\mathrm{cf}}-V_{\mathrm{i}}}$, where V_cf is the total volume of pre-/post-cloud aerosols and V_i is the total volume of interstitial aerosols. The estimation of κ_a assumes that all populations are internally mixed, and the activated cloud aerosol plus the interstitial aerosol is equal to the pre-/post-cloud aerosol volume. This is a reasonable assumption given that Brownian losses affect the smallest particle sizes, which have a minor contribution to the aerosol volume.

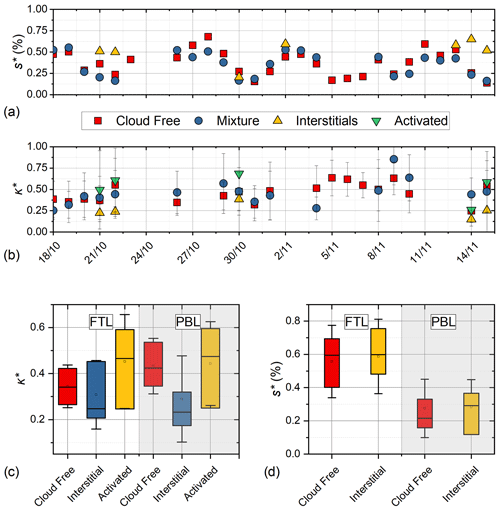
Figure 4 Daily averaged (a) s^∗ and (b) κ^∗ of the aerosol in cloud-free regimes, of the mixture of interstitial aerosols and some droplets residues, and of the activated aerosols; (c, d) the distributions of κ^∗ and s^∗ when the air mass originates from the FTL or the PBL, respectively.

Figure 4 presents the results of our analysis. Figure 4a shows the characteristic supersaturation, s^∗, for each aerosol population. Typically, s^∗ is higher for interstitial aerosol and lower for the mixed aerosol. This is consistent with the expectation that particles that activate to form droplets tend to be more hygroscopic than the interstitial aerosol (e.g., Cerully et al., 2011). Indeed, during periods when cloud formation is influenced by FTL air masses, the average κ^∗ was 0.34 ± 0.09 % for pre-/post-cloud, 0.31 ± 0.15 % for interstitial, and 0.45 ± 0.20 % for activated aerosol. During periods that clouds were forming on PBL aerosol, the average κ^∗ was 0.43 ± 0.12 % for pre-cloud, 0.29 ± 0.19 % for interstitial, and 0.44 ± 0.18 % for activated aerosol (Fig. 4b).

The average s^∗ (Fig. 4c) during periods where cloud formation is influenced by FTL air masses was equal to 0.56 ± 0.21 % and 0.59 ± 0.22 %, while during PBL-influenced periods, it was found to be 0.27 ± 0.18 % and 0.28 ± 0.16 % for the pre-/post-cloud and interstitial aerosols, respectively. These results showed little sensitivity to air mass origins, i.e., FTL or PBL. Clearly, the interstitial aerosol is less hygroscopic on average, and the activated aerosol can be up to twice as hygroscopic. This is important for understanding the role of cloud processing in the aging of particles and transferring hygroscopic material to evaporated cloud residuals.

Analysis of s^∗ of the activated aerosol can provide important insights about cloud formation when FTL or PBL air masses are involved. The critical supersaturation of most of the activated cloud droplet residuals should be close to the maximum supersaturation in the cloud. Indeed, when cloud s_max is high, droplet formation is aerosol-limited and vice versa when droplet formation is velocity-limited. According to Georgakaki et al. (2021) and Motos et al. (2023), clouds are velocity-limited when the s_max is ∼ 0.15 % or lower and aerosol-limited otherwise. Indeed, using s^∗ of the activated aerosol population as a proxy for s_max (which is supported by the analysis of Sect. 3.4), we see that clouds formed from FTL air masses have s^∗ > 0.5 %; hence the corresponding clouds are highly aerosol-sensitive. In contrast, clouds formed in PBL air masses have a much lower s^∗, reaching even 0.15 % (Fig. 4d); hence their formation tends to be velocity-sensitive. Given that the σ_w does not change significantly when clouds form upon FTL or PBL air masses (σ_w = 0.58 ± 0.25 m s⁻¹) and given that the N_Total in PBL air masses was roughly 3 times higher than the N_Total in FTL air masses (approximately 750 and 250 cm⁻³, respectively) (Fig. S3a), much of this distinction between aerosol- and velocity-limited conditions is driven by variations in aerosol rather than variations in cloud dynamics (i.e., σ_w).

Figure 5 shows what is measured on average during the cloud sampling through PM₁₀ in respect of the aerosols and the droplet residues. The pre-/post-cloud and in-cloud datasets here are the same that were used in Sect. 3.2 (the periods during which we sampled at least 30 min continuously in cloud-free conditions followed – or proceeded – by at least 30 min of cloudy conditions) and the interstitial aerosol dataset derived after removing from the in-cloud dataset the data where the D_eff was not exceeding the threshold of 13.5 µm. Thus, we calculated the average size distributions of the pre-/post-cloud and the in-cloud phases as well as the interstitial aerosols. The average size distribution of aerosols that activated to droplets is then the difference between the average distribution of the pre-/post-cloud aerosols and the interstitial aerosol, while the average size distribution of the droplet residuals was derived by the difference in the in-cloud and interstitial aerosols. Finally, we calculated the size-resolved “activation fraction” as the ratio of the interstitial aerosols to the pre-/post-cloud aerosols (from 70 nm and above, given that smaller particles are not expected to activate) and the size-resolved “penetration fraction” as the ratio of droplet residues to the in-cloud aerosols. Hence, we found that when we sampled within the clouds through a PM₁₀ inlet, the penetration fraction on average can reach up to 80 %. This means that a comparison of pre-/post-cloud and in-cloud aerosol distributions may provide qualitatively consistent microphysical insights that are however subject to an uncertainty of around 40 %. In the end, we calculated the size distribution of the aerosols that activated droplets by the difference between the in-cloud and the interstitial averaged size distributions and the size-resolved activation fraction as the ratio of the activated aerosols to droplets against the pre-/post-cloud aerosols. We found that the activation fraction is roughly 60 % for most of the activated aerosol sizes (Fig. 5), while about 50 % of them constitutes the droplet residues that penetrated the PM₁₀ inlet.

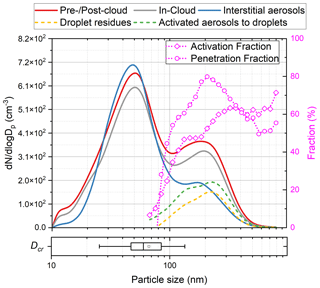
Figure 5 Averaged $\mathrm{d}N/\mathrm{d}\log D_{\mathrm{p}}$ particle size distributions for pre-/post-cloud, in-cloud, and interstitial moments (using the D_eff threshold of 13.5 µm). Shown also are two estimations of the activated aerosol distribution and the droplet residues or “dried droplets” distribution (dashed yellow line), estimated from the difference between the measured in-cloud and the interstitial aerosols, and the “activated droplets” distribution (green line), estimated by the difference between the pre-cloud and the interstitial aerosol distribution. The latter gives an estimate of the aerosol that gives droplets that are too large to be sampled at any size threshold by the inlet, while the former provides the activated aerosol from droplets that are sampled by the inlet when in cloud. The activation and the penetration fraction were estimated similarly by counting the ratio between the “activated droplets” and “pre-/post-cloud aerosols” and between “dried droplets” and “pre-/post-cloud aerosols”.

3.4 Closure study of N_d and s^∗

We applied the droplet activation parameterization of Morales Betancourt and Nenes (2014), using the size distributions measured at (HAC)² and VL and the σ_w and bulk hygroscopicity parameter κ measured at (HAC)², to predict the N_d and s^∗ of the clouds formed at (HAC)². It is important to mention here that the droplet activation parameterization of Morales Betancourt and Nenes (2014) is designed to calculate the s_max and the N_d when it is initialized by the ambient aerosols, and that is why we used the size distributions that were measured at VL. On the other hand, when we use the in-cloud aerosol size distributions measured at (HAC)², given that this is a combination of both interstitial aerosols and droplet residues, these distributions which we have already shown in Sect. 3.3 differ from each other, which results in an underestimations of the N_d. Here we examine under which conditions the use of the in-cloud aerosol can give reliable results compared to the in situ observations of N_d and s^∗ and to evaluate the internal consistency of the dataset and analysis carried out in the previous section, as well as to evaluate the ability of the parameterization to predict microphysical quantities for clouds influenced by the types of air masses (FTL, PBL) considered.

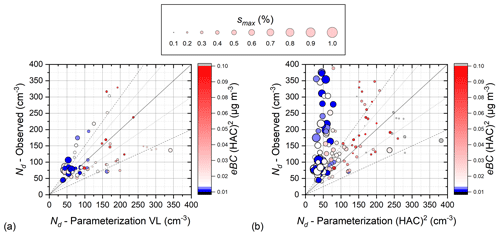
Figure 6 N_d from PVM-100 observations at (HAC)² (vertical axis) against parameterization predictions (horizontal axis) using observed aerosol distributions from (a) VL and (b) (HAC)². The symbol color corresponds to the eBC amount, and symbol size corresponds to the parameterization-predicted s_max, while the dot and the dashed lines indicate regions of ±25 % and ±50 % deviation from the 1 : 1 line, respectively.

We found that we can obtain N_d closure to within 25 % when using the aerosol distributions from VL (Fig. 6a) – even when the eBC levels are low. This may imply that VL may at times also reside in the FTL or at the catabatic region of the cloud during these specific periods, and hence its aerosol distributions may be representative of the total aerosol, including that which activated into cloud droplets. On the other hand, by using the aerosol from (HAC)² we obtained a reasonable closure only when eBC is high and the s_max is low – in other words when (HAC)² cloud droplets were formed upon aerosol from the PBL. However, when aerosol at (HAC)² is influenced by the PBL (eBC is high, more than > 0.01 µg m⁻³), N_d is predicted to within 25 % (Fig. 6b). That means that, when the in-cloud aerosol distributions from (HAC)² are used as input for the parameterization and clouds form in FTL air masses (i.e., eBC is very low, less than < 0.01 µg m⁻³), the parameterization highly underestimates N_d (Fig. 6b) because activated droplets were not sampled by the PM₁₀ inlet. We conclude that the usage of the (HAC)² distributions leads to an underprediction of droplet number (50 % or more) especially when the measured eBC levels are low, consistent with the view that VL aerosol is less representative of FTL.

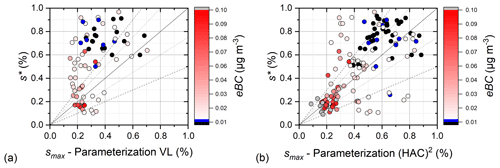
Figure 7 s^∗ of the total aerosol distribution (vertical axis) against parameterization predictions (horizontal axis) using observed aerosol distributions from (a) VL and (b) (HAC)². The symbol color corresponds to the eBC amount, while the dot and dashed lines indicate regions of ±25 % and ±50 % deviation from the 1 : 1 line, respectively.

Additionally, we found that when we used the aerosol from VL, s^∗ agrees with s_max to within ±25 % when eBC was high (∼ 0.1 µg m⁻³) (Fig. 7a). When we used the aerosol from (HAC)², the s^∗ matches with s_max to within ±25 % most of the time (Fig. 7b); this is because when in cloud, aerosols exposed at lower supersaturation values than the s_max have already been activated to droplets. Thus, the residuals give s^∗ values close to s_max.

When applying the parameterization to size distributions observed at VL, we expect that the predicted N_d (and s_max) will be close to observations when the cloud at (HAC)² is dominated by PBL aerosol and deviate largely when FTL air masses are at (HAC)². Similarly, (HAC)² pre-cloud aerosol distributions should provide good predictions of N_d when the air mass at the site is from the FTL. The use of in-cloud aerosol distributions is expected to result in deviations of the predicted from the observed N_d given that nucleation scavenging will lead to cloud droplets that are not sampled by the aerosol inlet and hence will not be measured. The magnitude of this deviation depends on the size of the droplets sampled, which in turn depends also on the amount of aerosol that is available for activation because cloud droplet sizes are expected to become progressively smaller as CCN concentrations increase.

4 Conclusions

We study the drivers of cloud droplet formation in orographic clouds using a combination of modeling, in situ, and remote sensing measurements at the (HAC)² station during the CALISHTO campaign in fall 2021. We study the origins of the aerosols (e.g., local aerosol from the PBL or from long-range transport from the FTL), which can be used to understand their characteristics (hygroscopicity, size distribution, and mixing state), contribution to CCN, N_d, and resulting supersaturations.

We found that the N_Total and the eBC within the FTL get low values (∼ 45 cm⁻³ and ∼ 0.01 µg m⁻³), while within the PBL they both get considerably larger values (∼ 3300 cm⁻³ and ∼ 0.4 µg m⁻³). That means that the PBL has more CCN, which results in more (from ∼ 100 to ∼ 300 cm⁻³) and smaller droplets (from ∼ 17.5 to ∼ 10 µm).

We also study the characteristics of aerosols involved in cloud droplet formation and those that do not activate (i.e., interstitial aerosols). To accomplish this, we develop a new algorithm applied to the aerosol time series measured with the PM₁₀ single-inlet system, which can sample interstitial aerosol and droplets with sizes up to the inlet's cut-off size (thus the droplet residues get dried and mixed with the interstitial aerosols) when in cloud. This separation algorithm involves applying a “virtual filter” to the aerosol time series from the PM₁₀ inlet based on a droplet size threshold (13.5 µm) derived from in situ observations (PVM-100) that determines when the aerosol sampled does not contain droplet residuals. Thus, when the in situ average droplet size exceeds the threshold, droplets would be too large to pass through the inlet so that the aerosol sampled by the PM₁₀ inlet is interstitial aerosol. Not considering this filter can considerably bias the results, as up to ∼ 80 % of aerosol can be dried droplet residuals.

Based on the above, we separated the dataset to pre-/post-cloud and interstitial regimes, and we studied the characteristics of the pre-/post-cloud, interstitial, and activated aerosol to droplets. We found that when air masses originated from the FTL, the κ^∗ was on average 0.34 ± 0.09 % for pre-/post-cloud, 0.31 ± 0.15 % for interstitial, and 0.45 ± 0.20 % for activated aerosol. When the air masses originated from the PBL, the κ^∗ was on average 0.43 ± 0.12 % for pre-cloud, 0.29 ± 0.19 % for interstitial, and 0.44 ± 0.18 % for activated aerosols. That means that the interstitial aerosols are the least hygroscopic of aerosol types, and the activated aerosols can be up to twice as hygroscopic than interstitial aerosol. This is important for understanding the role of cloud processing in the aging of particles and the accumulation of hygroscopic material on evaporated cloud residuals.

The average s^∗ during periods when cloud formation is influenced by the FTL was found to equal to 0.56 ± 0.21 % and 0.59 ± 0.22 %, while during PBL-influenced periods it was 0.27 ± 0.18 % and 0.28 ± 0.16 % for the pre-/post-cloud and interstitial aerosols, respectively. These results exhibited little sensitivity to air mass origins, i.e., FTL or PBL. When a cloud is formed in FTL air masses, the droplet formation is more sensitive to changes in the aerosol load, while it tends to be more sensitive in changes on vertical velocity when a cloud is formed in the PBL. Given that the cloud dynamics do not vary significantly between air masses, the variation in aerosol concentration is mostly responsible for these shifts in cloud microphysical state and sensitivity to aerosol.

Finally, a series of closure studies with the droplet parameterization is carried out to determine its ability to predict droplet number and supersaturation and constrain the cloud microphysical state (i.e., whether it is velocity- or aerosol-limited). We show that N_d can be predicted to be within 25 % of observations when the aerosol size distributions best approximate the pre-cloud distributions. The high degree of droplet and supersaturation closure ensures that the model–data fusion and novel approaches for determining the aerosol populations (interstitial and activated cloud droplets) are consistent, provide a realistic assessment of cloud state, and can be applied in future studies.

In conclusion, we present a coordinated, innovative approach that allows the determination of the drivers of droplet formation in orographic clouds and their sensitivity to aerosol and vertical velocity variations.