Bacteria in clouds biodegrade atmospheric formic and acetic acids

Formic and acetic acids are major organic species in cloud water and affect precipitation acidity. In atmospheric models, their losses are limited to chemical oxidation in the gas and aqueous phases and deposition processes. Previous lab studies suggest that these acids can be efficiently biodegraded in water by atmospherically relevant bacteria. However, the importance of biodegradation as a loss process in the atmospheric multiphase system has not been fully assessed. We implemented biodegradation as a sink of formic and acetic acids in a detailed atmospheric multiphase chemistry model. In our model, biodegradation is considered in 0.1 % of cloud droplets according to atmospheric bacteria concentrations of 0.1 cm⁻³. We predict that up to 20 ppt h⁻¹ formic acid and 5 ppt h⁻¹ acetic acid are biodegraded. This translates into a concentration change of 20 % and 3 % in addition to that caused by chemical losses. Our sensitivity studies suggest that acetic acid is most efficiently biodegraded at pH > 5, whereas biodegradation is least efficient for formic acid under such conditions. This trend can be explained by the fact that formic acid partitions more efficiently into the aqueous phase due to its higher Henry's law constant ($K_{\mathrm{H},\mathrm{eff}}\left(\mathrm{HCOOH}\right)=\mathrm{2}\times {\mathrm{10}}^{\mathrm{5}}$ M atm⁻¹ vs. $K_{\mathrm{H},\mathrm{eff}}\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{COOH}\right)=\mathrm{3}\times {\mathrm{10}}^{\mathrm{4}}$ M atm⁻¹ at pH = 5). Therefore, under such conditions, formic acid evaporates less efficiently from bacteria-free droplets, resulting in less formic acid in the gas phase for dissolution bacteria-containing droplets to replenish biodegraded acid. Our analysis demonstrates that previous estimates of the importance of atmospheric biodegradation were often biased high as they did not correctly account for such uptake limitation in bacteria-containing droplets. The results suggest that, under specific conditions, biological processes can significantly affect atmospheric composition and concentrations in particular volatile, moderately soluble organics.

1 Introduction

Small monocarboxylic acids have been of particular interest for several decades as they control, to a large extent, the acidity of cloud water, fog, dew and rainwater in regions that are not heavily anthropogenically impacted (Pye et al., 2020). They contribute up to 60 % to the free acidity in remote areas and up to ∼ 30 % in polluted regions (Millet et al., 2015). Recently, it was proposed that the increase in organic particulate matter in continental areas leads to a new chemical regime, in which acid deposition is largely controlled by organic acids, as opposed to the previous dominance by secondary inorganic pollutants (sulfate, nitrate) (Lawrence et al., 2023). Formic and acetic acids, which are the smallest organic acids, are commonly found to be major contributors to the global organic acid budget (Khare et al., 1999; Paulot et al., 2011). Typical mixing ratios range from 0.015 to 40 ppb for formic acid and 0.05 to 16 ppb for acetic acid (Chebbi and Carlier, 1996; Millet et al., 2015). Their direct emission sources include biomass burning, fossil fuel combustion, biogenic sources and land use activities (Khare et al., 1999; Paulot et al., 2011; Gong et al., 2020). Their abundance in regions far from direct emission sources, e.g., in the Arctic, implies their formation in the atmosphere (Mungall et al., 2018). Their chemical sources include the oxidation of isoprene-derived products by ozone or OH in the gas phase (Paulot et al., 2011) and the oxidation of formaldehyde and acetaldehyde by the OH radical in the aqueous phase (Jacob, 1986; Chebbi and Carlier, 1996). Significant fractions (∼ 20 %–90 %) of formic and acetic acids are dissolved in the aqueous phase of clouds, comprising a major fraction of the total dissolved organic carbon (Herckes et al., 2013). Therefore, major losses of atmospheric formic and acetic acids include wet deposition and aqueous phase oxidation. Such source and sink processes are included in atmospheric models of various scales (Paulot et al., 2011). The comparisons of chemical models to observations show generally good agreement on a global scale; however, they often reveal discrepancies on regional scales, possibly pointing to inaccurate emission inventories and/or incomplete chemical mechanisms (Franco et al., 2020).

Recent lab studies suggest that formic and acetic acids are biodegraded by bacteria under atmospherically relevant conditions (Herlihy et al., 1987; Vaïtilingom et al., 2011; Liu et al., 2023). Bacteria comprise a small number fraction of total atmospheric aerosol particles (≪ 1 %), with concentrations on the order of ∼ 10³ to 10⁵ cells m${}_{\mathrm{air}}^{-\mathrm{3}}$; this corresponds to 10³ to 10⁵ cells mL${}_{\mathrm{aq}}^{-\mathrm{1}}$ at typical cloud liquid water contents (∼ 0.1–1 g m${}_{\mathrm{air}}^{-\mathrm{3}}$) (Amato et al., 2007). However, to date, biological processes and functions, such as biodegradation, are not included in atmospheric models to describe their potential effects on atmospheric composition or, in turn, the influence of the atmosphere on the aeromicrobiome (Amato et al., 2023). The consideration of bacteria in models is usually limited to their role as ice nuclei (Fröhlich-Nowoisky et al., 2016, and references therein). However, ice nucleation does not necessarily require living, biologically active cells. The atmosphere is considered to be a harsh environment for microorganisms due to extreme and rapidly changing conditions in terms of temperature, pH, water and nutrient availability (Amato et al., 2007). Yet, living bacteria cells are commonly found far from emission sources and have been isolated from cloud and fog water, which suggests that clouds may be “atmospheric oases” for bacteria (Fuzzi et al., 1997; Sattler et al., 2001; Amato et al., 2017; Šantl-Temkiv et al., 2022). Biodegradation is a well-known efficient aerobic loss process for organics in soil where bacteria cell concentrations are on the order of 10⁹ cell cm⁻³ (Adeleke et al., 2017). Cell concentrations in the atmosphere are much lower (∼ 0.01 cm⁻³) than in the denser soil that typically has an aerobic layer of ∼ 10 cm. Therefore the atmospheric volume is much larger as compared to the biotic terrestrial and aquatic environments which may result in comparable rates (cell concentration × volume) if one compares losses in different environments (atmosphere vs. soil vs. surface waters).

A first comparison of biodegradation rates to those of chemical processes in clouds was performed based on atmospherically relevant cell concentrations and lab-derived biodegradation rates of organic acids. This comparison suggests that biodegradation might be similarly efficient as OH or NO₃ reactions in cloud water (Vaïtilingom et al., 2013; Jaber et al., 2021). However, such processes are not widely included in atmospheric models, mainly due to the lack of comprehensive data sets and appropriate model approaches. Comparing typical number concentrations of cloud droplets (∼ 50–500 cm⁻³) to those of bacteria cells, it is evident that only a small subset of cloud droplets (∼ 0.01 %–0.1 %) contain a bacteria cell (or possibly a few cells). In the current study, we use a multiphase chemistry model complemented by biodegradation processes to systematically explore the conditions under which biodegradation of formic and acetic acids by bacteria may be a significant sink in addition to chemical losses in the gas and aqueous phases. We investigate the sensitivities to wide ranges of cloud droplet diameters and pH values.

2 Description of the multiphase model

2.1 Model equations

We use a multiphase chemistry box model with detailed gas- and aqueous-phase chemistry, including 58 reactions in the gas phase and 34 in the aqueous phase (Ervens et al., 2014; Khaled et al., 2021). In total, 15 of the 31 chemical species are transferred between the gas and aqueous phases. All parameters for the aqueous-phase reactions and phase transfer processes are listed in Tables S1–S4 in the Supplement. We use the standard equations to describe the multiphase chemistry system:

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{aq},\mathrm{g}}}{\mathrm{d}t}}=& \underset{\mathrm{phase}\mathrm{transfer}}{\underbrace{k_{\mathrm{mt}}\mathrm{LWC}\left(C_{\mathrm{g}}-{\displaystyle \frac{C_{\mathrm{aq},\mathrm{g}}}{\mathrm{LWC}{K}_{\mathrm{H}\left(\mathrm{eff}\right)}RT}}\right)}}\\ & +\underset{\mathrm{chemical}\mathrm{processes}}{\underbrace{S_{\mathrm{aq}}-L_{\mathrm{aq}}}}-L_{\mathrm{bact}},\end{array}\text{(2)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\mathrm{d}{C}_{\mathrm{g}}}{\mathrm{d}t}}=& -\underset{\mathrm{phase}\mathrm{transfer}}{\underbrace{k_{\mathrm{mt}}\mathrm{LWC}\left(C_{\mathrm{g}}-{\displaystyle \frac{C_{\mathrm{aq},\mathrm{g}}}{\mathrm{LWC}{K}_{\mathrm{H}\left(\mathrm{eff}\right)}RT}}\right)}}\\ & +\underset{\mathrm{chemical}\mathrm{processes}}{\underbrace{S_{\mathrm{g}}-L_{\mathrm{g}}}},\end{array}\end{array}$$

where LWC is the liquid water content (vol vol⁻¹), K_H(eff) is the (effective) Henry's law constant (M atm⁻¹), and R is the constant for ideal gases (0.082 L atm (mol K)⁻¹). All concentrations are expressed in units related to the gas-phase volume (mol g${}_{\mathrm{air}}^{-\mathrm{1}}$). The terms S_aq, L_aq, S_g and L_g denote the chemical sources and losses in the aqueous (aq) and gas (g) phases. L_bact refers to the loss rates of formic and acetic acids by the biodegradation that occurs in a subset of droplets. We derived rate constants for biodegradation by converting lab-derived biodegradation rates (mol cell⁻¹ s⁻¹) into k_bact (L cell⁻¹ s⁻¹) (Reactions R33 and R34 in Table S1) (Khaled et al., 2021). We use data measured at a temperature of 17 °C for Pseudomonas sp., being a representative genus for commonly abundant atmospheric bacteria (Vaïtilingom et al., 2011). Unlike for chemical reactions, we did not account for temperature-dependent biodegradation rates. The reasoning for this assumption is explored in Sect. 4.2. k_bact is multiplied with the (constant) cell concentration of 2 × 10⁸ cells g${}_{\mathrm{air}}^{-\mathrm{1}}$ and the modeled organic acid concentrations to obtain L_bact (mol L⁻¹ s⁻¹). The phase transfer of soluble gases is described by means of the kinetic mass transfer coefficient k_mt (Schwartz, 1986; Nathanson et al., 1996):

$$\begin{array}{}\text{(3)}& k_{\mathrm{mt}}={\left({\displaystyle \frac{r_{\mathrm{d}}^{\mathrm{2}}}{\mathrm{3}{D}_{\mathrm{g}}}}+{\displaystyle \frac{r_{\mathrm{d}}}{\mathrm{3}\mathit{\alpha }}}\sqrt{{\displaystyle \frac{\mathrm{2}\mathit{\pi }{M}_{\mathrm{g}}}{RT}}}\right)}^{-\mathrm{1}},\end{array}$$

where r_d is the drop radius (cm), D_g is the gas-phase diffusion coefficient (cm² s⁻¹), α is the dimensionless mass accommodation coefficient, and M_g is the molecular weight (g mol⁻¹).

2.2 Model initialization and simulations

The box model includes a monodisperse drop population with a constant liquid water content of 0.42 g m⁻³. Simulations are performed at constant temperature (286 K) and air density (1.032 × 10⁻³ g cm⁻³). Drop diameter D_d, number concentration N_d and pH value are kept constant throughout each simulation. The model is initialized with the mixing ratios summarized in Table S5. All simulations are performed for 1 h. This period reflects multiple cloud cycles for a single particle (e.g., bacteria cell) given the lifetime of droplets on the order of ∼ 10–30 min (Ervens et al., 2008). Simulations are performed for 30 pH values (3 ≤ pH ≤ 6) and 30 drop diameters (1 µm ≤ D_d ≤ 30 µm). Given the constant LWC, the total drop number concentration N_d increases with decreasing D_d:

$$\begin{array}{}\text{(4)}& N_{\mathrm{d}}\propto {\displaystyle \frac{\mathrm{6}\mathrm{LWC}}{\mathit{\pi }{D}_{\mathrm{d}}^{\mathrm{3}}}}.\end{array}$$

In the reference set of 900 simulations, no bacteria are considered (L_bact = 0); i.e., all droplets have the same composition. The results are compared to a second set of simulations, in which it is assumed that a small number fraction of the droplets contains bacteria cells (N_d2 = N_cell = 0.1 cm${}_{\mathrm{air}}^{-\mathrm{3}}$). This concentration is at the upper end of atmospheric bacteria cell concentrations. To quantify the importance of biodegradation for each D_d–pH combination, we define the differences between the total acid concentrations (gas + aqueous) predicted in the two simulation sets as follows:

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }C=|C_{\mathrm{t},\mathrm{nocell}}-C_{\mathrm{t},\mathrm{cell}}|.\end{array}$$

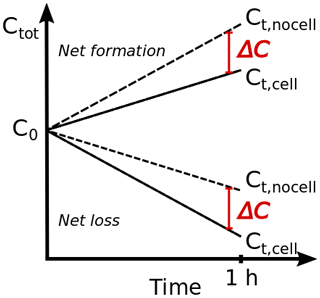
ΔC represents the absolute difference in predicted total acid concentration (expressed as mixing ratios [ppt]) at the end of the simulation (Fig. 1). Thus, it quantifies the extent to which the total acid concentration is overestimated if biodegradation is not included. Accordingly, the relative difference is

$$\begin{array}{}\text{(6)}& \mathrm{\Delta }{C}_{\mathrm{rel}}=\left|{\displaystyle \frac{\mathrm{\Delta }C}{C_{\mathrm{0}}-C_{\mathrm{t},\mathrm{nocell}}}}\right|\cdot \mathrm{100}\mathit{\%}.\end{array}$$

Depending on model conditions (D_d, pH), the two acids show either a net increase or a loss, as schematically shown in Fig. 1. All model parameters are defined in Table A1. Therefore, ΔC_rel expresses either the relative extent to which the net increase is reduced or the relative extent to which the net loss is enhanced due to biodegradation under the model conditions.

Figure 1 Schematic to illustrate the predicted absolute (ΔC) and relative (ΔC_rel) differences in predicted total (gas + aqueous) acid concentrations in the absence (C_t,nocell) and presence (C_t,cell) of bacteria cells after 1 h simulation time.

3 Model results

3.1 Absolute and relative differences in predicted acid concentrations – ΔC and ΔC_rel

Figure 2 shows the predicted absolute concentration difference ΔC from 900 1 h model simulations as a function of pH value and D_d for formic and acetic acids. The maximum values are ΔC_max ∼ 20 ppt for formic acid (pH = 4.7, D_d = 30 µm) and ΔC_max ∼ 8.5 ppt for acetic acid (pH = 6, D_d = 27 µm). These values correspond to ∼ 4 % of the initial acid mixing ratios of 500 and 200 ppt (Table S5). Both maxima appear at high D_d values but at different pH.

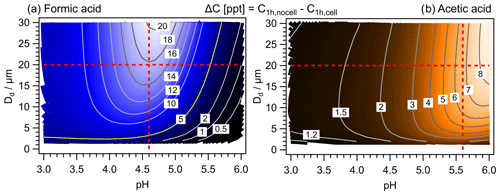
Figure 2 Predicted concentration differences (ΔC; Eq. 5) of 900 model simulations for all combinations of 30 pH and 30 D_d values. (a) Formic acid. (b) Acetic acid. The red lines denote conditions that are discussed in detail in Sect. 3.2 and 3.3. The numbers on the contour lines indicate ΔC (in ppt h⁻¹).

The comparison of the mixing ratios (ppt) of the two acids reveals that they show different trends as a function of pH: whereas formic acid is predicted to be highest at the highest pH value (Fig. S1a, b), the opposite trend is seen for acetic acid (Fig. S2a, b). There is a net loss in formic acid at pH ≳ 3.5 (Fig. S1c, d) and a net formation of acetic acid at pH = 6 (Fig. S2c, d), nearly doubling its initial mixing ratio. The resulting relative differences ΔC_rel (Eq. 6) are shown in Figs. S1e and S2e. For formic acid, ΔC_rel exceeds 100 % at pH ∼ 3.5; however, these values do not seem to be meaningful since the absolute change in acid concentration is very small (< 1 ppt). In less acidic droplets, ΔC_rel for formic acid decreases from ∼ 50 % (pH ∼ 4) to < 1 % at pH > 5.5. The corresponding values for acetic acid show a continuous increase with increasing pH, resulting in $\left|\mathrm{\Delta }{C}_{\mathrm{rel}}\right|$ = 2.8 % at pH ∼ 6 (Fig. S2e).

For both acids, biodegradation might lead to decreases in total concentrations on the order of ∼ 4 % h⁻¹. This corresponds to an enhancement of the formic acid loss rate by up to 20 % as compared to chemical losses alone. The net formation rate of acetic acid is reduced by up to 8 % under the model conditions. In other words, the formic acid loss by chemical processes of ∼ 300 ppt (pH = 5.5) is enhanced to 360 ppt due to biodegradation. Acetic acid is predicted to increase by ∼ 80 ppt h⁻¹ due to chemical processes (at pH = 5.5); this net increase is reduced to 66 ppt h⁻¹ in the presence of bacteria cells. These numbers or trends may increase or decrease in different chemical regimes or may possibly depend on the details of the chemical mechanism; however, the dependence on D_d and pH is likely to be robust. In the following, it will be explored why the two acids show differences in the dependency of their biodegradation efficiency on pH and D_d.

3.2 Dependence of ΔC on D_d

Both ΔC and ΔC_rel show the highest values at the largest D_d. To more clearly illustrate this trend, Fig. 3a repeats ΔC as a function of D_d, as seen along the vertical red lines in Fig. 2, at a single pH (pH = 4.6 for formic acid, pH = 5.6 for acetic acid). The drop size dependence of chemical reactions with organics in the atmospheric multiphase system has been discussed previously. It was demonstrated that organic oxidation tends to be more efficient in small droplets due to higher OH uptake rates (k_mt ∝ $D_{\mathrm{d}}^{\mathrm{2}}$) and resulting enhanced OH(aq) concentrations (Ervens et al., 2014; Chakraborty et al., 2016). Biodegradation apparently shows the opposite trend, i.e., higher efficiency in large droplets (Fig. 3a). If OH(aq) were significantly smaller in large droplets, less acid may be oxidized there, leaving higher acid concentrations for biodegradation. However, neither the acid concentration nor the OH(aq) concentration shows any clear trend with drop size (Fig. 3b). Therefore, we conclude that uptake limitation of the reactants into the droplets and competition effects between chemical and biodegradation processes cannot be the main reason for the ΔC dependence on D_d.

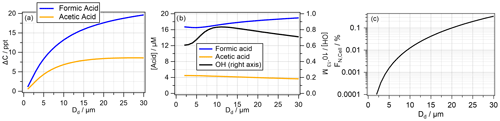
Figure 3 Dependence of (a) ΔC of formic acid (pH = 4.6) and acetic acid (pH = 5.6) on the droplet diameter D_d; (b) aqueous-phase concentrations of formic acid (pH = 4.6) and acetic acid (pH = 5.6) (left scale) and the OH radical (right scale) as a function of D_d; and (c) the percentage of bacteria-containing droplets F_NCell for LWC = 0.42 g m⁻³, with N_Cell = 0.1 cm⁻³ as a function of D_d. All values were derived from simulations after 1 h simulation time.

A change in D_d leads to a change in the total droplet number concentration N_d since we assume a constant LWC. The number concentration of bacteria cells (N_cell = 0.1 cm⁻³) does not change in our simulations. This implies that the fraction of bacteria-containing droplets (F_NCell) to the total drop number concentration N_d changes with D_d according to

$$\begin{array}{}\text{(7)}& F_{\mathrm{NCell}}={\displaystyle \frac{N_{\mathrm{cell}}}{N_{\mathrm{tot}}}}=N_{\mathrm{cell}}{\displaystyle \frac{\frac{\mathit{\pi }{D}_{\mathrm{d}}^{\mathrm{3}}}{\mathrm{6}}}{\mathrm{LWC}}}\cdot \mathrm{100}\mathit{\%}.\end{array}$$

F_NCell can vary largely depending on conditions and on the aerosol size range that is considered. It may be as high as several percent if N_tot is assumed to constitute only super-micron particles in dust storms (Hu et al., 2020) or in the upper troposphere (DeLeon-Rodriguez et al., 2013). If the total particle size range is taken into account (D > 10 nm), the fraction can be calculated as being < 0.001 %, e.g., for conditions that are typical at the Puy de Dôme station (N_tot,average ∼ 2000 cm⁻³ for D_particle > 10 nm and 10⁴ ≤ N_cell ≤ 10⁵; Baray et al., 2020). In a coniferous forest, the fraction of bioaerosol particles (including bacteria but also other microbes) to total particles in ambient aerosol populations has been found to be in the range of 0.1 %–0.5 % for super-micron particles (Petersson Sjögren et al., 2023).

Accordingly, Fig. 3c shows that F_NCell spans several orders of magnitude from ∼ 10⁻⁴ % to ∼ 0.3 %. Thus, when droplets are large, biodegradation occurs in a relatively larger fraction of the aqueous phase, with more acid being directly accessible for the bacteria. This relationship can explain the trend of an increase in ΔC by a factor of ∼ 7 (3 ppt ≤ ΔC ≤ 20 ppt) for formic acid and by a factor of ∼ 3 (2 ppt ≤ ΔC ≤ 6 ppt) for acetic acid (Fig. 3a). It is not expected that the increase in ΔC is as strong as that for F_NCell since the complex interactions of chemical and phase transfer processes within the multiphase system do not necessarily translate into linear relationships between loss rates and reaction volume (Sect. 3.5). A similar increase with D_d as for ΔC is also seen for ΔC_rel (Figs. S1e and S2e), in particular for relatively small D_d (≲ 10 µm). Based on the ΔC_rel values, it may be concluded that a fraction of ∼ 0.01 % bacteria-containing cloud droplets may be sufficient to impact the total acid concentrations by several percentage points. The assumptions of a constant bacteria concentration and varying drop number concentration may represent very specific conditions. Often, the drop number concentration is a function of the total particle concentration. Under highly polluted conditions, the bacteria concentration scales with the particle number concentration of PM_2.5 or PM₁₀ (Gao et al., 2016; Zhai et al., 2018), which may ultimately lead to similar F_NCell, but the specific trend will depend on the air mass composition. An increase in N_cell may lead to a nearly linear increase in biodegraded mass (Khaled et al., 2021).

3.3 Dependence of ΔC on pH value

Similarly to the analysis in the previous section, Fig. 4a shows the ΔC values, as seen along the red horizontal lines in Fig. 2, i.e., the pH dependence at D_d = 20 µm. Most strikingly, the ΔC trends with pH for the two acids are different, with a maximum at pH ∼ 4.6 for formic acid and a continuous increase over the full pH range for acetic acid. ΔC of formic acid spans a range of ∼ 1 to ∼ 17 ppt, while this is smaller for acetic acid with 1 ppt < ΔC < 7 ppt. The biodegradation rates themselves are assumed to be pH-independent due to intracellular buffering, in agreement with lab studies that showed only small variations in biodegradation rates for cloud-relevant pH ranges (Liu et al., 2023; Vaïtilingom et al., 2011). The biodegradation rate constants of the two acids differ by less than a factor of 2 (Table S1); therefore, it seems unlikely that they cause a significant difference in the general trends of ΔC_rel with any parameter. Thus, differences in the (physico)chemical properties of the carboxylic acids may be rather responsible for the trends. Rate constants of OH reactions with undissociated acids k_RCOOH are usually smaller than those of the corresponding carboxylates k_RCOO due to a shift in the mechanism from H abstraction to electron transfer (Herrmann, 2003). The overall rate constant is a combination of the two rate constants and the proportions of the undissociated acid χ_RCOOH and the carboxylate (1−χ_RCOOH) as a function of pH:

$$\begin{array}{}\text{(8)}& k_{\mathrm{OH},\mathrm{tot}}={\mathit{\chi }}_{\mathrm{RCOOH}}\cdot k_{\mathrm{RCOOH}}+(\mathrm{1}-{\mathit{\chi }}_{\mathrm{RCOOH}})\cdot k_{\mathrm{RCOO}},\end{array}$$

where k_ROO refers to the rate constants of Reactions (R21) and (R30), k_ROOH refers to those of Reactions (R22) and (R29) (Table S1), and χ_RCOOH is dependent on the acid dissociation constant K_a.

$$\begin{array}{}\text{(9)}& {\mathit{\chi }}_{\mathrm{RCOOH}}={\left(\mathrm{1}+{\displaystyle \frac{K_{\mathrm{a}}}{{\mathrm{10}}^{-\mathrm{pH}}}}\right)}^{-\mathrm{1}}\end{array}$$

As seen in the above, k_OH,tot is shown for both acids as a function of pH in Fig. 4b. The dotted lines in the figure (right axis) illustrate the relative increase normalized to the smallest k_OH,tot at pH = 3. This comparison demonstrates that both rate constants increase by a factor of ∼ 5.5 over the pH range between 3 and 6. A high k_OH,tot at high pH implies that more acid is chemically degraded, reducing the acid concentration available for biodegradation. This would be opposite to the predicted ΔC trend with pH for acetic acid and could only explain ΔC values above pH ∼ 4.6 for formic acid. Thus, the competition between the pH-dependent chemical rate and the biodegradation cannot be the main reason for the apparent pH dependence of ΔC.

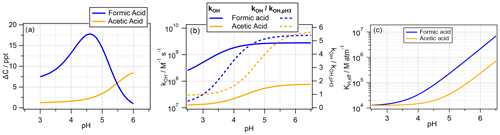
Figure 4 The pH dependencies of (a) the predicted concentration difference in the absence and presence of bacteria cells (ΔC). (b) The total rate constant for the oxidation of formic and acetic acids according to Eq. (8). (c) Effective Henry's law constant.

The second pH-dependent parameter that may affect conversion rates in the aqueous phase is the effective Henry's law constant K_H,eff, the ratio between the total aqueous-phase concentration (undissociated acid and carboxylate) and its gas-phase partial pressure at thermodynamic equilibrium:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{K}_{\mathrm{H},\mathrm{eff}}& ={\displaystyle \frac{[\mathrm{RCOOH}{]}_{\mathrm{aq}}+[\mathrm{RCOO}{]}_{\mathrm{aq}}}{[\mathrm{RCOOH}{]}_{\mathrm{gas}}}}\\ & =K_{\mathrm{H}}\cdot \left(\mathrm{1}+{\displaystyle \frac{K_{\mathrm{a}}}{\left[{\mathrm{H}}^{+}\right]}}\right).\end{array}\end{array}$$

K_H is the physical Henry's law constant (M atm⁻¹). The increase in K_H,eff with pH is approximately 1 order of magnitude higher for formic acid than for acetic acid (Fig. 4c). Therefore, it can be expected that, under equilibrium conditions, more formic acid is available for biodegradation, leading to a higher ΔC with increasing pH. The fact that either pH-dependent parameter k_OH,tot or K_H,eff can explain some range of the Δ values in Sect. 3.3 suggests that a combination of the aqueous-phase partitioning and reactivity leads to the differences in the trends shown in Fig. 2.

3.4 Dependence of ΔC on the gas–aqueous-phase partitioning

The fraction of a compound in the aqueous phase can be defined as

$$\begin{array}{}\text{(11)}& {\mathit{ϵ}}_{\mathrm{aq}}={\displaystyle \frac{C_{\mathrm{aq},\mathrm{g}}}{C_{\mathrm{aq},\mathrm{g}}+C_{\mathrm{g}}}}\end{array}$$

when aqueous- and gas-phase concentrations (C_aq,g and C_g) are given in identical units (e.g., mol g${}_{\mathrm{air}}^{-\mathrm{1}}$). Aqueous-phase concentrations of C_aq (typically given in units of mol L${}_{\mathrm{aq}}^{-\mathrm{1}}$) can be converted by

$$\begin{array}{}\text{(12)}& C_{\mathrm{aq},\mathrm{g}}={\mathrm{10}}^{-\mathrm{3}}{C}_{\mathrm{aq}}\mathrm{LWC}{\mathit{\rho }}_{\mathrm{air}}.\end{array}$$

At equilibrium conditions (eq), the aqueous-phase concentration $C_{\mathrm{aq},\mathrm{g}}^{\mathrm{eq}}$ is

$$\begin{array}{}\text{(13)}& C_{\mathrm{aq},\mathrm{g}}^{\mathrm{eq}}=K_{\mathrm{H},\mathrm{eff}}{C}_{\mathrm{g}}\mathrm{LWC}RT.\end{array}$$

The values for ϵ_aq at thermodynamic equilibrium (${\mathit{ϵ}}_{\mathrm{aq}}^{\mathrm{eq}}$) are shown in Fig. 5a, overlaid with the ΔC values from Fig. 4a (dotted lines). It is evident that the decrease in ΔC for formic acid occurs when more than 50 % of formic acid is predicted to be in the aqueous phase under equilibrium conditions. The threshold of ${\mathit{ϵ}}_{\mathrm{aq}}^{\mathrm{eq}}$ = 0.5 is not reached for acetic acid due to its significantly smaller effective Henry's law constant (smaller K_a, Table S2), and ΔC continues to increase with pH.

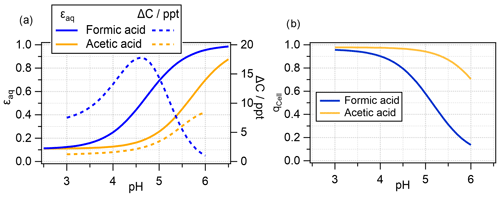
Figure 5 (a) Aqueous-phase fraction of total formic and acetic acids (undissociated and dissociated) at thermodynamic equilibrium; (b) deviation from thermodynamic equilibrium in the bacteria-containing droplets (D_d = 20 µm; 1 h simulation) (Eq. 14); the corresponding q values for bacteria-free droplets are not shown as they are at unity, i.e., indicating thermodynamic equilibrium.

The assumption of equilibrium conditions may not be always valid. Species that are very reactive in the aqueous phase are more efficiently consumed than they may be replenished by uptake. To quantify deviations from thermodynamic equilibrium, a parameter q can be used to represent the ratio of the equilibrium concentration to measured or modeled aqueous-phase concentrations (Ervens, 2015; Barth et al., 2021):

$$\begin{array}{}\text{(14)}& q={\displaystyle \frac{C_{\mathrm{aq}}}{p_{\mathrm{g}}{K}_{\mathrm{H},\mathrm{eff}}}}={\displaystyle \frac{{\mathit{ϵ}}_{\mathrm{aq}}}{\mathrm{1}-{\mathit{ϵ}}_{\mathrm{aq}}}}{\displaystyle \frac{\mathrm{1}-{\mathit{ϵ}}_{\mathrm{aq}}^{\mathrm{eq}}}{{\mathit{ϵ}}_{\mathrm{aq}}^{\mathrm{eq}}}},\end{array}$$

where p_g corresponds to the gas-phase partial pressure (atm). The resulting values for the bacteria-containing drop class q_Cell are shown in Fig. 5b. It is evident that the acids in the bacteria-containing droplets are in equilibrium at pH = 3 but are increasingly subsaturated at higher pH. At pH = 5.6, the formic acid concentration is only about 30 % of the equilibrium concentration (q_Cell = 0.3), whereas it is nearly 90 % for acetic acid. This suggests that, at high pH, relatively little formic acid is available for biodegradation, resulting in low ΔC values. The higher q_Cell value for acetic acid implies that it is closer to equilibrium; therefore, ΔC values correlate approximately with K_H,eff.

These q_Cell trends apparently contradict findings from previous measurements or model studies that have often shown that not only formic and acetic acids are in thermodynamic equilibrium in clouds or fog – this is also the case for other small organics (Winiwarter et al., 1994; Voisin et al., 2000; Facchini et al., 1992; Ervens, 2015). However, it should be kept in mind that the bacteria-containing droplets only comprise 0.1 % of all droplets (if D_d = 20 µm, Fig. 3c). Such a small deviation would not be detected in measurements of bulk cloud water or in models that treat the aqueous volume as a homogeneously composed aqueous phase. In fact, the corresponding predicted q values for the bacteria-free droplets are all at unity over the full pH range (not shown).

3.5 Redistribution of acids between the gas phase and droplets

The previous sections point to the competition of the biodegradation with chemical loss processes but also with the phase transfer to replenish biodegraded acids. To quantify these effects, we compare in the following the individual process rates for the two acids at different pH values. Figure 6a shows a schematic of all processes considered in the model (Eqs. 1 and 2). In Fig. 6b–d, the relative rates for all processes are shown (at pH values of 3, 4.6 and 5.6), normalized to the biodegradation rate L_bact (in units of mol g${}_{\mathrm{air}}^{-\mathrm{1}}$ s⁻¹). Accordingly, the biodegradation rate is indicated as being at unity. The units are used as they reflect the differences of the liquid water contents of the two drop classes (999 : 1). The absolute values for L_bact are shown in the last column at the bottom of each panel, together with the aqueous-phase concentrations (in mol L${}_{\mathrm{aq}}^{-\mathrm{1}}$) of the acids and the OH radical. The rates for all processes are summarized in Table S6 (in units of mol g${}_{\mathrm{air}}^{-\mathrm{1}}$ s⁻¹ and mol L${}_{\mathrm{aq}}^{-\mathrm{1}}$ s⁻¹).

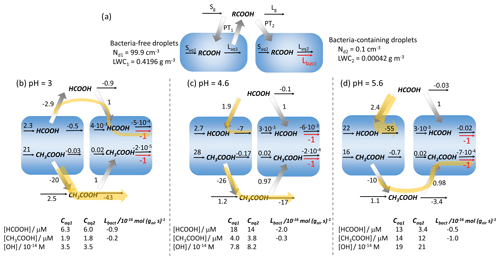
Figure 6 (a) Schematic of the chemical sources (S) and losses (L), biodegradation (L_bact), and phase transfers (PT) of acids in the gas (g) and aqueous (aq) phases. (b–d) Numbers next to the arrows denote the relative rates, normalized to the biodegradation rate L_bact (mol g${}_{\mathrm{air}}^{-\mathrm{1}}$ s⁻¹); (b) pH = 3; (c) pH = 4.6; (d) pH = 5.6. Yellow arrows indicate the series of processes that explain the pH dependencies of ΔC and ΔC_rel for formic and acetic acids. The tables at the bottom show the aqueous-phase concentrations of the acids and the OH radical, together with the absolute value of L_bact (10⁻¹⁶ mol g${}_{\mathrm{air}}^{-\mathrm{1}}$ s⁻¹). All results are for 1 h model simulations – D_d = 20 µm.

At pH = 3, both acids evaporate from the bacteria-free droplets and are taken up by the bacteria-containing droplets. All chemical loss rates for formic acid are less than unity; i.e., the biodegradation represents the strongest sink in the full multiphase system even though it only occurs in 0.1 % of the aqueous-phase volume. The lack of efficient chemical sinks for formic explains the high ΔC_rel at low pH (Fig. S1e). However, at this pH, the chemical loss of formic acid is negligible since the oxidation in the gas phase (Rg3, Table S4) is relatively slow; in addition, the oxidation in the aqueous phase is not efficient due to low K_H,eff and k_OH,tot. The aqueous-phase concentrations in the two drop classes do not differ, which suggests that the biodegradation – though relatively efficient – does not significantly affect the absolute concentration. This explains the small ΔC values at low pH (Fig. 2a). This is also reflected in the identical rates within the aqueous phase if expressed in units of mol L${}_{\mathrm{aq}}^{-\mathrm{1}}$ s⁻¹ (bottom part of Table S6), which would be expected in a system where all droplets are considered to be identical.

The rate constant of the gas-phase loss of acetic acid is 1 order of magnitude higher than that of formic acid (Rg4, Table S4). This leads to efficient acetic acid loss in the gas phase, exceeding by far (factor 43) the rates of the uptake into the bacteria-containing droplets and the subsequent biodegradation. This results in low values of ΔC_rel (Fig. S2e). Similarly to formic acid, the chemical rates in the bacteria-containing droplets are not affected by biodegradation; i.e., the total amount of biodegraded acetic acid is very small (low ΔC). The yellow arrows in Fig. 6b illustrate the major pathways of the two acids that explain the similarities in ΔC due to the sequence of evaporation, uptake and biodegradation and the differences in terms of loss processes resulting in differences in ΔC_rel.

At pH = 4.6, the effective Henry's law constants for formic and acetic acid are higher by factors of ∼ 10 and ∼ 2 as compared to pH = 3 (Fig. 4c). The increased aqueous-phase partitioning leads to higher phase transfer rates into the droplets. Also, the rate constants for the aqueous-phase loss k_OH,tot are higher by factors of 5 and 3 for formic and acetic acids, respectively (Fig. 4b). This increased aqueous-phase loss leads to a fast consumption and phase transfer of formic acid in all droplets. Most formic acid is taken up by the bacteria-free droplets and consumed there (yellow arrow). However, only about two-thirds of formic acid (PT1 $/$ PT2 = 1.9 $/$ 1) is taken up into bacteria-free droplets, whereas one-third is transferred into the bacteria-containing droplets even though they only comprise 0.1 % of the total aqueous phase. The chemical loss rate of formic acid is only 7 times higher than the loss by biodegradation ($L_{\mathrm{aq}\mathrm{1}}/L_{\mathrm{bact}}$ = 7) despite the much smaller drop volume. The higher partitioning allows more formic acid to be biodegraded (high ΔC), but its contribution relative to the chemical losses is smaller than at low pH (low ΔC_rel). For acetic acid, the increases in k_OH,tot and K_H,eff are not sufficient to compete with its strong gas-phase sink and to shift the direction of the major pathways towards predominating uptake into bacteria-free droplets. Thus, the rate pattern does not change significantly as compared to the lower pH and only results in small increases in both ΔC and ΔC_rel.

At pH = 5.6, ∼ 90 % of formic acid is expected to partition to the aqueous phase under equilibrium conditions (Fig. 5a). However, the concentration in bacteria-containing droplets is only ∼ 30 % of this value (Fig. 5b). The efficient uptake into the bacteria-free droplets and the consumption there dominate the sinks ($L_{\mathrm{aq}\mathrm{1}}/L_{\mathrm{bact}}$ = 55). This leads to even less efficient replenishment of biodegraded acid in the bacteria-containing droplets so that the formic acid concentrations between the droplet classes differ by a factor of ∼ 4 (C_aq1 = 13 µM, C_aq2 = 3.4 µM). In a previous model study, even higher concentration differences in bacteria-free and bacteria-containing droplets were predicted (Khaled et al., 2021). This led to the conclusion that biodegradation for highly soluble compounds may be inefficient. However, this latter study did not include aqueous-phase formation processes (S_aq) to provide a continuous acid source (e.g., for formic acid: Reactions R7 and R9 in Table S1). For acetic acid, gas-phase loss becomes relatively less important with increasing K_H,eff and k_OH,tot. Instead, the fraction of acetic acid being taken up into the bacteria-containing droplets increases, increasing both ΔC and ΔC_rel. Unlike formic acid that is only formed in the aqueous phase, formation of acetic acid also takes place in the gas phase (Rg1, Rg2, Table S4) in addition to its aqueous-phase sources (Reactions R17–R19, Table S1). The efficient net production of acetic acid leads to significantly higher total acetic acid concentrations as compared to those for formic acid, resulting in more acetic acid being degraded at high pH (higher ΔC, Fig. 2).

4 Discussion

4.1 Comparison to previous estimates of the importance of biodegradation in the atmosphere: F_bact,aq and F_bact

4.1.1 Estimates based on the comparison of measured chemical and biodegradation rates

The importance of biodegradation has been compared to chemical loss processes in the atmospheric multiphase system in several previous studies. Most of these comparisons limited the comparison to losses in the aqueous phase:

$$\begin{array}{}\text{(15)}& F_{\mathrm{bact},\mathrm{aq}}={\displaystyle \frac{L_{\mathrm{bact}}}{L_{\mathrm{bact}}+\underset{L_{\mathrm{aq},\mathrm{tot}}}{\underbrace{L_{\mathrm{aq}\mathrm{1}}+L_{\mathrm{aq}\mathrm{2}}}}}}\cdot \mathrm{100}\mathit{\%}.\end{array}$$

Only a few studies extended the comparison to gas-phase losses to consider the full atmospheric multiphase system:

$$\begin{array}{}\text{(16)}& F_{\mathrm{bact}}={\displaystyle \frac{L_{\mathrm{bact}}}{L_{\mathrm{bact}}+\underset{L_{\mathrm{aq},\mathrm{tot}}}{\underbrace{L_{\mathrm{aq}\mathrm{1}}+L_{\mathrm{aq}\mathrm{2}}}}+L_{\mathrm{g}}}}\cdot \mathrm{100}\mathit{\%}.\end{array}$$

Table 1 summarizes F_bact,aq and F_bact values based on literature data for formic and acetic acids and other organics, together with the assumptions made in these comparisons. Most values are based on comparisons of lab-derived biodegradation rates L_bact and chemical rates with the OH radical in aqueous solution (“bulk L_aq,tot”) (Vaïtilingom et al., 2010, 2011, 2013; Ariya et al., 2002; Liu et al., 2023). Herlihy et al. (1987) reported biodegradation rates of formic and acetic acid observed in incubated rainwater. To derive F_bact,aq, we calculated L_aq assuming [OH(aq)] = 10⁻¹³ M and k_OH at pH = 4.6. Similarly, Ariya et al. (2002) compared L_aq to biodegradation rates that were estimated after exposing solutions of carboxylic acids to atmospheric fungi in ambient air. Predicted values of F_bact,aq for formic acid differ between < 0.004 % and 66 %. According to our discussion in Sect. 3.5, the lowest value (≤ 2 %) is expected at pH < 5.6. Only the study by Pailler et al. (2023) was performed at such high pH and resulted in a much higher value (F_bact,aq ∼ 28 %). Their bulk model (where biodegradation occurs in all cloud droplets) cannot represent the redistribution of acids that leads to a reduced L_bact at high L_aq and K_H,eff (Fig. 6d and Sect. 4.1.2). Therefore, their model overestimates losses by biodegradation for highly soluble species (e.g., formic acid at high pH), as also discussed previously by Khaled et al. (2021). Instead of drop classes with significant differences in acid concentration due to biodegradation, as shown in Fig. 6d, such a bulk model predicts relatively high acid concentrations in all droplets (similarly to those as predicted for bacteria-free droplets in the current simulations). In such a bulk approach, substrate-limited conditions may not even be reached where biodegradation efficiency becomes negligible below some threshold of substrate (acid) concentration.

Table 1 Literature data on the relative importance of biodegradation as compared to chemical processes of organic compounds in the atmospheric aqueous-phase F_bact,aq (Eq. 15) and F_bact (Eq. 16).

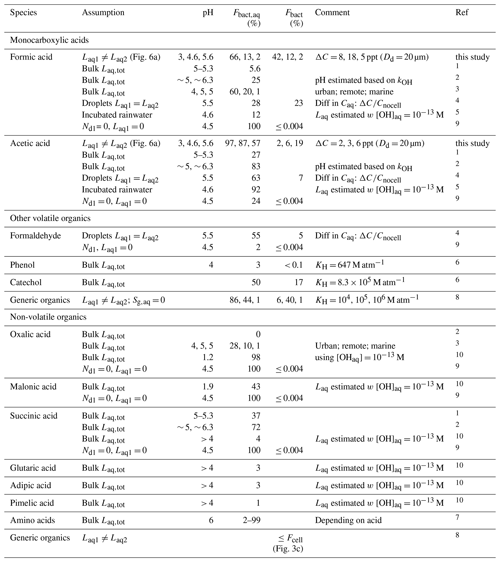
¹ Vaïtilingom et al. (2010) – P. graminis; ² Vaïtilingom et al. (2011); ³ Liu et al. (2023); ⁴ we compare to the conditions as defined by “summer” in Pailler et al. (2023) since our [OH]_aq in Fig. 6d is most similar to these conditions; ⁵ Herlihy et al. (1987); ⁶ Jaber et al. (2020); ⁷ Jaber et al. (2021); ⁸ Khaled et al. (2021) – $R_{\mathrm{g}}={\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, R_bact = 10⁻³ s⁻¹, R_aq= 10⁻³ s⁻¹; ⁹ Fankhauser et al. (2019); ¹⁰ Ariya et al. (2002).

Liu et al. (2023) predict decreasing F_bact,aq with pH for formic acid. However, the agreement of this trend with our results in Fig. 6 seems fortuitous. In their study, the pH value is considered to be a proxy for pollution level (urban, remote, marine); thus, not only the pH value changed between scenarios – this is also the case for oxidant levels and bacteria concentrations. All other values for F_bact,aq in Table 1 that were determined for pH ≤ 5 agree approximately with those found in the current study. As discussed in Sect. 3.5, under such conditions, the composition of the aqueous phase is not largely affected by biodegradation; therefore, the assumption of a bulk aqueous phase is applicable for species with chemical reactivity comparable to that of formic acid. Similarly, literature values of F_bact,aq for acetic acid are in agreement with those found in the current study. Small differences between the values are expected since different bacteria species and strains were used in the various experiments. The K_H of phenol is even smaller than that of formic acid and acetic acid at pH = 3. Therefore, its F_bact,aq estimated by Jaber et al. (2020) is likely a good approximation. However, given the much higher K_H of catechol (comparable to K_H,eff of formic acid at pH = 5.6), we conclude that their estimate of F_bact(aq) may be too high. Only a few studies provided values of F_bact. The F_bact values predicted by Fankhauser et al. (2019) (≤ 0.004 %) are orders of magnitude lower than our results (2 %–42 % for formic acid, 2 %–19 % for acetic acid). Their value is based on the assumption that only organics present in bacteria-containing droplets are biodegraded, and they estimate that 0.004 % of the atmospheric aqueous volume contains bacteria (D_d = 10 µm). However, these considerations neglect the sequence of processes as discussed in Sect. 3.5.

4.1.2 Implementation of organic acid biodegradation into multiphase chemistry models

The few studies that implemented biodegradation of organic acids into multiphase chemistry models applied different assumptions:

1. The model approach by Khaled et al. (2021) is similar to the current model. The only difference is that they focused on the comparison of loss processes of generic organics over wide ranges of chemical and biodegradation rates and solubility but without any chemical sources.

2. Fankhauser et al. (2019) considered only bacteria-containing droplets, i.e., a total LWC that is several orders of magnitude smaller than in real clouds (N_d1 = 0). Thus, the reactor volume for aqueous-phase chemical reactions is small.

3. Pailler et al. (2023) used a multiphase box model with similar LWC and drop sizes as in the current model. They assumed that biodegradation occurs in all droplets in an analogy to chemical reactions. They used the same lab data for biodegradation rates by Vaïtilingom et al. (2010) as we do in the current study. However, their model approach implied that the biodegradation rate in each droplet is smaller by a factor $\mathrm{1}/F_{\mathrm{NCell}}$ as compared to our approach, where no biodegradation occurs in > 99 % of the droplets.

The commonalities and differences between these approaches are summarized in Table 2.

Table 2 Comparison of model features between our model study¹ and the ones by Fankhauser et al. (2019)² and Pailler et al. (2023)³.

All three models included a (I) multiphase chemistry mechanism and explored the potential importance of biodegradation in the atmosphere by means of (II) sensitivity studies in the absence and presence of bacteria cells, respectively. However, there are distinct differences between the three model approaches that allow us to address the different aspects of the importance of biodegradation. They are briefly discussed in the following.

Realistic cloud liquid water content (III). We show in Fig. 6 that, at pH = 3, the bacteria-free droplets act as efficient reactors of formic acid and acetic acid production. In the absence of bacteria, all droplets would produce these acids at pH = 3 and, thus, increase the total acid concentration in the atmosphere. This acid production is not fully represented in the model by Fankhauser et al. (2019) because of the limited “reactor size”, comprised of the very small aqueous-phase volume. Thus, in their study, the importance of biodegradation may have been generally underestimated because of an incomplete multiphase system that did not comprehensively represent the full organic acid budget.

When acids are chemically formed in bacteria-free droplets, evaporate and then are taken up into bacteria-containing droplets (Fig. 6), contributions by biodegradation can exceed, by far, the fraction of the aqueous volume where biodegradation occurs. This may ultimately result in biodegradation rates being comparable to chemical loss rates in the total aqueous phase (Table S6). Considering bacteria-containing droplets to be isolated systems is only appropriate for non-volatile organics, including (di)carboxylic and amino acids, that are not replenished by phase transfer into bacteria-containing droplets. For such compounds, the upper limit of F_bact is indeed constrained by the aqueous-phase volume that contains bacteria. This limit may be as high as 0.3 %, depending on LWC, N_d and D_d (Fig. 3c).

Uptake limitation (IV). As discussed in Sect. 3.4 and shown in Fig. 6, the loss by biodegradation in the bacteria-containing droplets is very efficient; neither chemical reactions in the aqueous phase nor the uptake from the gas phase are sufficient to compensate for this rapid acid consumption, resulting in q ≤ 1 (Fig. 5c). Even though Fankhauser et al. (2019) did not explicitly discuss it in their study, similar trends can be deduced from their results since the formic acid concentration in the aqueous phase is basically zero in the presence of bacteria cells, whereas, in the absence of cells, the aqueous-phase concentration corresponds to its equilibrium value (Sect. S1). Pailler et al. (2023) did not observe that uptake limitation affected the formic acid aqueous-phase concentration. In their model, biodegradation occurred in all droplets but at moderate rates which could be always compensated for by acid sources (either uptake or chemical production in the aqueous phase). Even in the presence of bacteria cells, formic acid was apparently (approximately) in thermodynamic equilibrium, which may explain their findings that the net phase transfer was negligible. Thus, their predictions of biodegraded formic acid might represent overestimates since the acid concentration available for biodegradation may have been to high. Although they implemented an expression to account for a non-linear decrease of biodegradation at low substrate (acid) concentrations, such conditions may not have even been reached. In our model study, the biodegradation rate depends linearly on the substrate concentration (k_bact × [Acid]_aq) and was, thus, significantly suppressed under uptake-limited conditions.

Biodegradation of species with K_H(eff) ≥ ∼ 10⁵ M atm⁻¹ (VI). Uptake limitations are most prominent for species that are predicted to partition to a significant fraction in the aqueous phase, such as formic acid at pH ≥ 5 (K_H,eff ≥ 10⁵ M atm⁻¹). Our model study is the first one to systematically explore the sensitivity of biodegradation (as quantified by ΔC and ΔC_rel) to the solubility (K_H(eff) of specific substrates. The finding that biodegradation of species with K_H(eff) ≥ 10⁵ is likely unimportant in the atmosphere gives important guidance for future research, e.g., for lab experiments dedicated to the investigation of biodegradation rates of additional compounds.

Consideration of multiple drop classes with and without bacteria (V and VII). We conclude that it is essential in models to distinguish the small number concentration of bacteria-containing droplets from those without cells to properly account for uptake limitations. The implementation of biodegradation in models of larger (regional, global) scales may, thus, not be straightforward since such models usually do not distinguish drop classes but rather assume homogeneous monodisperse drop populations.

4.2 Potential effects of additional microphysical chemical and biological parameters on ΔC, ΔC_rel and F_bact

The results discussed in the previous section cover a limited set of cloud (micro)physical, chemical and biological parameters. However, based on our sensitivity studies, we can predict trends of the absolute (ΔC) and relative (ΔC_rel, F_bact) importance of biodegradation as a function of various parameters, as schematically shown in Fig. 7.

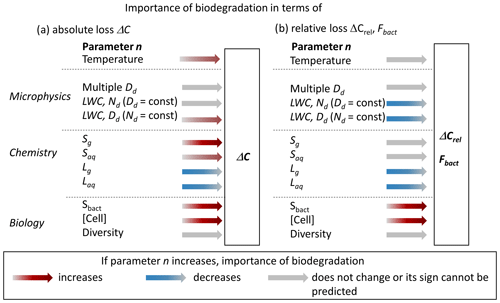
Figure 7 Predicted change of absolute (ΔC) or relative (ΔC_rel, F_bact) importance of biodegradation as a function of cloud microphysical, chemical and biological parameters. Red (blue) arrows indicate increased (decreased) importance with an increase in model parameter n; color intensity scales with the expected strength of the effect. Gray arrows denote either an insignificant change or an unpredictable sign of the change depending on n. These estimates are based on the assumption that one parameter at a time is varied.

One simplified assumption regarding the biodegradation rates is the use of values derived in lab studies at 17 °C. Similarly to chemical rates, biodegradation rates also show a temperature dependence. Based on the measurements by Vaïtilingom et al. (2010) at 5 and 17 °C, we estimated activation energies E_a of 90 and 27 kJ mol⁻¹ for the biodegradation of formic and acetic acid, respectively (Sect. S2). To describe the temperature dependence of biological processes, often the Q₁₀ factor is used to quantify the change in a rate within a temperature interval of 10 K. The resulting Q₁₀ factors are 3.9 and 1.5 for biodegradation of formic and acetic acids by Pseudomonas sp.; these are in general agreement for other biological processes that often show values between 2 and 3. The overview of E_a and Q₁₀ values in Tables S7 and S8 suggests that differences between bacteria species may be larger than those due to temperature variation for a single species. However, these trends should cautiously interpreted due to the very limited data base they were derived on. It should be also noted that the rates of biological processes often follow Arrhenius' law over limited temperature intervals only as they decrease beyond an optimum temperature (Schipper et al., 2014). Based on the current very limited data set, it may be concluded that, overall, the temperature dependence of biodegradation rates may not have a large impact on ΔC. Given that the trend with temperature is similar for chemical reactions and biodegradation (both follow the Arrhenius law), ΔC_rel may be even less affected.

A monodisperse droplet population is a simplified representation of realistic cloud microphysical properties. The assumption of a polydisperse population with the same LWC and cell concentration distributed randomly across the population will not change F_NCell; therefore, ΔC is not expected to change. Rates of OH(aq) reactions haven been shown to be enhanced in small droplets and correspondingly decreased in large droplets (Ervens et al., 2014; Chakraborty et al., 2016). These effects might (partially) cancel each other, resulting in a similar total L_aq, which implies that neither ΔC_rel nor F_bact will change. An increase in LWC (typically in the range of 0.1–1 g m⁻³ for warm clouds) might be caused by a higher droplet number concentration (N_d) or larger droplets (D_d) (or a combination of both; Eq. 4). An increase in D_d results in an increase in the fraction of bacteria-containing droplets F_NCell (Fig. 3c), leading to somewhat higher ΔC and ΔC_rel. Accordingly, an increase in N_d leads to a decrease in F_NCell and to lower ΔC and ΔC_rel since the reaction volume for chemical aqueous-phase reactions and therefore L_aq increase. The absolute amount of acid that is biodegraded ΔC is a function of the number of available cells; thus, it is not expected to significantly change as a function of available liquid water. So far, the microphysical parameters LWC, N_d and D_d referred to properties of clouds. Given that aerosol particles outside clouds also contain liquid water, similar considerations may apply to such scenarios. Studies of gas–particle partitioning of acids have shown that significant acid fractions are partitioned into particles despite very low LWC (∼ 10 s µg m⁻³) (Yuan et al., 2015; Nah et al., 2018). If metabolic activity under such water-limited conditions were comparable to that in clouds, ΔC may be comparable if it scales by cell concentration only. There are indications that bacteria are metabolically active outside clouds (Krumins et al., 2014; Péguilhan et al., 2023). The relative importance of biodegradation (ΔC_rel, F_bact(aq)) might be even higher than under cloud conditions due to the smaller role of aqueous-phase chemical reactions. However, due to the lack of systematic data for biodegradation under such conditions, to date, such comparisons cannot be reliably performed.

Chemical models often underpredict observed formic acid and acetic acid concentrations (Millet et al., 2015). In addition to missing emission sources, recent studies suggested that chemical mechanisms are not complete in terms of gas-phase sources (Paulot et al., 2011; Yuan et al., 2015; Chen et al., 2021; Gao et al., 2022; Luo et al., 2023). The addition of such formation processes would enhance S_g, leading to higher atmospheric acid concentrations and higher ΔC. However, the higher concentrations would enhance loss rates in both phases so that, overall, ΔC_rel might remain constant. In the aqueous phase, the direct oxidation processes of aldehydes (Reactions R7 and R19, Table S1) are likely to be the main sources of formic and acetic acids. However, additional multiphase pathways, as suggested by Franco et al. (2021), may occur. Such sources increase S_aq in all cloud droplets. Given that most additional acid would be produced in or on bacteria-free droplets, the additional acid directly accessible to the bacteria may be very small, leading to a small increase in ΔC. Consequently, ΔC_rel may decrease since the increased acid concentration will enhance L_aq in the total aqueous volume. Additional acid loss processes of acids in either phase (L_g, L_aq) lead to a decreased role of biodegradation, both in absolute and relative numbers. Such losses may include not only chemical reactions but also acid removal by deposition, which is considered to be a major loss for small acids (Chebbi and Carlier, 1996).

In addition to gaps in chemical mechanisms, current models are even more incomplete with regards to biological processes. Formic and acetic acids may not only be biodegraded but also formed by metabolic processes (Vyas and Gulati, 2009). Such a process could be added as S_bact in Fig. 6a. Formaldehyde is a likely substrate that may be metabolized and converted into formic acid, in parallel to the chemical pathway (Reaction R7, Table S1). The biodegradation rate of formaldehyde is comparable to that of the aqueous-phase oxidation (Pailler et al., 2023); as a consequence, S_bact could be comparable to L_bact. An additional formic acid source in bacteria-containing droplets would enhance ΔC, ΔC_rel and F_bact. Depending on the biotransformation efficiency, this process may affect the formaldehyde concentration not only in the bacteria-containing droplets but possibly even in the full multiphase system. However, due to the lack of data describing such bioformation processes (rates, yields) under atmospherically relevant conditions, they are neglected in our model.

The cell concentration assumed in the current study (0.1 cm⁻³) is at the upper end of the range of in-cloud observations. Such high concentrations may be particularly relevant in fog close to the ground and/or near strong emission sources of bacteria. All three parameters – ΔC, ΔC_rel and F_bact – are expected to linearly scale with the concentration of (living, metabolically active) cells (Khaled et al., 2021). For simplicity, we assumed that the total bacteria population is composed of metabolically active Pseudomonas sp. since they usually represent a major fraction of atmospheric bacteria. However, this assumption underestimates the bacteria diversity in the atmosphere since, usually, a mixture of different bacteria types and strains are present (Gandolfi et al., 2013). The biodegradation rates of formic and acetic acids span a range of more than 1 order of magnitude (Vaïtilingom et al., 2010, 2011). Thus, both the proportions of individual bacteria strains and their different metabolic activities vary depending on the location. It may be speculated that, on average, the consideration of a greater bacteria diversity may not change our results and conclusions for formic and acetic acids significantly. However, more detailed studies are warranted to confirm the validity of this assumption for different locations and atmospheric conditions.

5 Summary and conclusions

Bacteria comprise a ubiquitous, small number fraction of atmospheric aerosol particles. The potential of their metabolic process to affect atmospheric composition has not been widely explored yet. We extended a multiphase box model including detailed gas- and aqueous-phase chemistry by implementing biodegradation of formic and acetic acids in cloud droplets. Biodegradation is considered in a small subset of the droplets reflecting a typical atmospheric bacteria concentration of 0.1 cm${}_{\mathrm{air}}^{-\mathrm{3}}$. Model studies were performed for a cloud liquid water content (LWC) of 0.42 g m⁻³ with a monodisperse droplet population. To identify scenarios where biodegradation significantly affects formic acid and acetic acid concentrations, wide ranges of cloud droplet diameters (1 µm ≤ D_d ≤ 30 µm) and cloud water acidity (3 ≤ pH ≤ 6) were explored.

We predict losses of ΔC ≤ 20 and ≤ 5 ppt h⁻¹ for formic and acetic acids, respectively, corresponding to loss rates of 4 % h⁻¹ for both acids. This enhances the chemical net loss of formic acid by ΔC_rel ≤ 20 % and reduces the net formation of acetic acid by ΔC_rel ≤ 3 %. ΔC and ΔC_rel are highest in the presence of large droplets, i.e., when the total droplet number concentration is small and, consequently, the fraction of bacteria-containing droplets is largest. The loss by biodegradation increases with pH for acetic acid; however, it reaches its maximum at pH ∼ 4.6 for formic acid and decreases at higher pH. The inefficient biodegradation of formic acid at high pH is explained by its strong aqueous-phase partitioning (K_H,eff = 8 × 10⁵ M atm⁻¹) and high aqueous-phase reactivity (k_OH = 3 × 10⁹ M⁻¹ s⁻¹) at pH = 5.6. These factors lead to the predominant consumption of formic acid in the bacteria-free droplets that comprise > 99 % of all cloud droplets. As both the solubility and reactivity of acetic acid are lower at the same pH (K_H,eff = 8 × 10⁴ M atm⁻¹, k_OH = 7 × 10⁷​​​​​​​ M⁻¹ s⁻¹), sufficient gas-phase acetic acid is available to replenish biodegraded acetic acid in the bacteria-containing droplets.

We compared our results to previous estimates of the importance of biodegradation as a loss process in the atmospheric aqueous phase (F_bact,aq) and in the complete atmospheric multiphase system (F_bact) based on the simplistic comparison of chemical vs. biodegradation rates. The analysis of our model results revealed that the assumption of an averaged biodegradation rate in the full aqueous volume is only appropriate for volatile compounds with low or moderate solubility and aqueous-phase reactivity. A detailed comparison of our model results to those of the previous model studies by Pailler et al. (2023) and Fankhauser et al. (2019) highlighted important differences between the three model approaches. Based on this, we conclude that the role of biodegradation of compounds with K_H(eff) ≥ ∼ 10⁵ M atm⁻¹ will be overestimated by a bulk approach, in which biodegradation is assumed to occur in the full aqueous volume, since uptake-limited phase transfer processes between bacteria-containing and bacteria-free droplets cannot be properly described. For the same reasons, bulk models overestimate the biodegradation of non-volatile species that, in the real atmosphere, only takes in the small subset of bacteria-containing droplets. For such species, the upper limit of the biodegradable mass of non-volatile species (e.g., dicarboxylic acids) is constrained by the number fraction of bacteria-containing droplets. Our conclusions based on the comparison of the three model approaches show the need for the developments of parameterizations to describe biodegradation in larger-scale models since such models usually do not distinguish individual drop classes with different chemical compositions (e.g., with and without bacteria cells).

We also highlight the need for more refined data on the abundance and diversity of (living) bacteria in the atmosphere. Additional biological processes may lead not only to the consumption but also to the formation of organic compounds in clouds and possibly also aqueous aerosol particles outside clouds. We conclude that, despite a very small number concentration in the atmosphere (≤ 0.1 % of all aerosol particles and cloud droplets), metabolically active microorganisms (bacteria, fungi, yeast) may be efficient drivers to significantly affect atmospheric concentrations of organic compounds. Our model can be considered a starting point for future studies to further constrain the role of biological processes in the atmosphere to affect biogeochemical cycles in the Earth system.

Appendix A

Table A1 Definition of model parameters.