Sensitivity of global direct aerosol shortwave radiative forcing to uncertainties in aerosol optical properties

New satellite missions promise global reductions in the uncertainties in aerosol optical properties, but it is unclear how those reductions will propagate to uncertainties in the shortwave (SW) direct aerosol radiative effect (DARE) and direct aerosol radiative forcing (DARF), which are currently large, on the order of at least 20 %. In this work, we build a Monte Carlo framework to calculate the impact of uncertainties in aerosol optical depth (AOD), single scattering albedo (SSA), and the asymmetry parameter on the uncertainty in shortwave DARE and DARF. This framework uses the results of over 2.3 million radiative transfer simulations to calculate global clear-sky DARE and DARF based on a range of uncertainties in present-day and pre-industrial aerosol optical properties, representative of existing and future global observing systems. We find the 1σ uncertainty varies between ±0.23 and ±1.91 W m⁻² (5 % and 42 %) for the top-of-atmosphere (TOA) clear-sky DARE and between ±0.08 and ±0.47 W m⁻² (9 % and 52 %) for the TOA DARF. At the TOA, AOD uncertainty is the main contributor to overall uncertainty except over bright surfaces where SSA uncertainty contributes most. We apply regionally varying uncertainties to represent current measurement uncertainties and find that aerosol optical property uncertainties represent 24 % of TOA DARE and DARF. Reducing regionally varying optical property uncertainties by a factor of 2 would reduce their contributions to TOA DARE and DARF uncertainty proportionally. Applying a simple scaling to all-sky conditions, aerosol optical property uncertainty contributes to about 25 % total uncertainty in TOA, all-sky SW DARE, and DARF. Compared to previous studies which considered uncertainties in non-aerosol variables, our results suggest that the aerosol optical property uncertainty accounts for one-third to half of the total direct SW uncertainty. Recent and future progress in constraining aerosol optical properties using ground-based or satellite retrievals could be translated into DARE and DARF uncertainty using our freely available framework.

1 Introduction

Aerosols are one of the major contributors to the radiative forcing of Earth's climate via changes in its radiation budget. In addition to their indirect effects on climate due to their influence on cloud microphysical properties, aerosols also interact with radiation directly via absorption and scattering. The effect on the radiation budget due to these aerosol–radiation interactions is referred to as the “direct aerosol radiative effect” (DARE, also called radiative effect of aerosol–radiation interactions in the Intergovernmental Panel on Climate Change, or IPCC, assessment reports), while the effect of the change in aerosol distributions from pre-industrial times due to only anthropogenic aerosols is termed the “direct aerosol radiative forcing” (DARF, also called radiative forcing of aerosol–radiation interactions). These quantities are typically considered at the surface and at the top of atmosphere (TOA).

Quantification of the magnitude of the aerosol radiative forcing is a major challenge that has motivated a significant body of research over the last 30 years (Bellouin et al., 2020). Although uncertainties in effective radiative forcing are dominated by aerosol–cloud interactions and have been the focus of much recent work, uncertainties due to direct radiative effects are still large (i.e. on the order of 100 %) (Forster et al., 2021). Aerosol–radiation and aerosol–cloud interactions depend on different aerosol properties and atmospheric processes. In this study, we focus on direct aerosol–radiation interactions and the aerosol properties relevant to them.

Table 1 Top-of-atmosphere (TOA) and surface clear-sky direct aerosol radiative effect (DARE) and direct aerosol radiative forcing (DARF), both in W m⁻², for previous studies and this work, along with their uncertainties (where applicable). Thorsen et al. (2021) refer to the uncertainties in their “enhanced” methodology (see Sect. 2). The numbers for this work are reflective of the AERONET v1-like uncertainties (see Sect. 3) or the upper and lower limits of our sampled uncertainty range (Table 3). “Forc. eff.” refers to forcing efficiency in W m⁻² per unit AOD. Note: NA – not available.​​​​​​​​​​​​​​

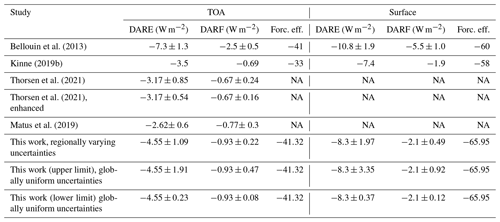
There have been recent attempts to constrain the value of DARE and DARF using a variety of methodologies. Bellouin et al. (2013) used satellite data from MODIS assimilated into the Monitoring Atmospheric Composition and Climate (MACC) aerosol reanalysis to estimate clear-sky (cloud-free) and all-sky TOA/surface DARF and DARE. Kinne (2019a) used a two-stream radiative transfer code with eight shortwave (SW) bands in conjunction with the Max Planck Aerosol Climatology version 2 (MACv2, Kinne, 2019b; see also Sect. 2.1) to obtain estimates of clear- and all-sky TOA and surface DARE and DARF, separated into SW and longwave (LW) components, as well as by aerosol type. An uncertainty estimate was obtained for the total aerosol radiative forcing but was not separated into uncertainties for the direct and indirect effects separately. Matus et al. (2019) obtained vertical profiles of clouds and aerosols from CloudSat and Cloud-Aerosol lidar and Infrared Pathfinder Satellite Observation (CALIPSO) observations and used radiative kernels to estimate clear- and all-sky DARE and DARF at the TOA. Thorsen et al. (2020, 2021) applied radiative kernels derived using MERRA-2 data to estimate TOA DARE and its uncertainties (Thorsen et al., 2020) and then obtain similar kernels for TOA DARF (Thorsen et al., 2021). This approach allows for systematic estimation of the uncertainties, particularly due to aerosol optical properties. These optical properties are based on those obtained via the Aerosol Robotic Network (AERONET; Holben et al., 1998) using a matching algorithm to pair AERONET sites with similar aerosol characteristics to gridded MERRA-2 reanalysis data. This gives a “best estimate” uncertainty based on a hypothetical global observation system with AERONET-like accuracy. They also provide a hypothetical “enhanced” estimate of this uncertainty by assuming that the single scattering albedo of highly scattering aerosols is known perfectly (equal to 1 in the visible spectrum) and that it is only directly retrieved for absorbing aerosols, in addition to assumed improvements in vertical profiles via lidar measurements. The results of those studies are summarised in Table 1 for clear-sky conditions, which are the primary focus of the present work. They suggest that these different approaches generally agree on the central value of DARE and DARF. There remains, however, a large uncertainty in DARE and DARF across different studies, typically on the order of at least ∼ 20 % or greater.

There are many factors which control uncertainties in DARE and DARF. These include uncertainties in aerosol loading, optical properties, and the anthropogenic fraction, as well as biases inherent to the aerosol environment, such as cloud properties, surface albedo, and gaseous absorption (Stier et al., 2013). Radiative transfer considerations, such as the spectral resolution used in the calculations, also play a role (Randles et al., 2013). Parameters relating to aerosol distribution and optical properties are typically measured and provided to the community via observations from satellites such as the Moderate Resolution Imaging Spectroradiometer (MODIS) or via ground-based remote-sensing observation networks, notably AERONET. The ongoing Metrology for aerosol optical properties (MAPP) project aims to make significant reductions in the uncertainties in retrievals of aerosol optical properties, in particular, using the Generalized Retrieval of Aerosol and Surface Properties (GRASP) algorithm (Dubovik et al., 2021; Herrera et al., 2022). Next-generation satellite retrievals of aerosol optical properties are also expected, such as those from the EarthCARE (Wehr et al., 2023) and Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) satellite missions (Werdell et al., 2019). It is well known that aerosol optical depth (AOD) and aerosol single scattering albedo (SSA) are primary drivers of observation-based DARF uncertainties (e.g. Loeb and Su, 2010).

The impact of increased accuracy and precision of measurements and retrievals of the aerosol optical properties on DARE and DARF uncertainties likely to result from these upcoming satellite missions has been less studied. In this work, we build a Monte Carlo framework to calculate the impact of variable uncertainties in aerosol optical depth (AOD), single scattering albedo (SSA), and asymmetry parameter on the uncertainty in shortwave DARE and DARF. This framework uses the results of over 2.3 million radiative transfer simulations to quantify the range in global clear-sky DARE and DARF based on a range of aerosol optical property uncertainties, representative of existing and future global observing systems. Thus, we are able to estimate the likely possible reduction in the total clear-sky SW DARE and DARF given measurement improvements in quantifying aerosol property uncertainties and the remaining uncertainty to be tackled due to non-aerosol properties and processes. We explore the impacts of assuming both uniform global aerosol optical property uncertainties and also regionally varying uncertainties. This also provides a tool to identify which regions and variables may provide the largest reduction in the global mean forcings. We also give particular attention to the role of uncertainties in the aerosol optical properties of the pre-industrial reference state.

2 Methodology

2.1 Radiative transfer model setup

Radiative transfer calculations are performed with the UK Met Office's “Suite of Community RAdiative Transfer Codes based on Edwards and Slingo” (SOCRATES) in its two-stream, six-band shortwave configuration as used in the GA9 configuration of the UK Met Office Unified Model (denoted in SOCRATES as sp_sw_ga9, updated from the GA7 configuration of Walters et al., 2019). This configuration uses solar spectral irradiance from Lean et al. (2005), with gaseous absorption computed using the correlated k-distribution method with HITRAN 2012 spectroscopic data (Rothman et al., 2013) and what is referred to within SOCRATES as the Elsey–Shine water vapour continuum (see Elsey et al., 2020; Anisman et al., 2022).

Aerosols are prescribed using the MACv2 aerosol climatology (Kinne, 2019b). MACv2 provides AOD, SSA (denoted ω₀), and g for each month of the year for both present-day and pre-industrial cases for different aerosol types. MACv2 obtains these distributions with a combination of observations from the ground-based sun photometer network AERONET and global aerosol modelling derived mostly from AeroCom Phase 1 simulations (Kinne et al., 2006). We interpolate these properties to a 5° × 5° latitude–longitude grid from the native 1° × 1°, with 20 vertical levels. Calculations are done here on a seasonal average to reduce the number of radiative transfer calculations by a factor of 3 with a limited impact on the calculated DARE and DARF. Aerosols are separated into anthropogenic fine-mode, natural fine-mode, and coarse-mode aerosols. MACv2 provides gridded vertical profile information for AOD at 550 nm for fine-mode and coarse-mode aerosols, as well as spectral AOD, asymmetry factor, and SSA for each type. These vertical profiles are combined with the spectral information and applied to the relevant aerosol types to obtain the vertically resolved AOD at each wavelength, scaling them proportionally to the AOD at 550 nm. To include the MACv2 aerosol optical properties in SOCRATES, it is necessary to transform the original AOD and SSA distributions into absorption and scattering coefficients at each grid point and vertical level. This is done by multiplying the vertically resolved AOD by the thickness of each vertical layer, as defined by MACv2, to obtain an extinction coefficient, and then multiplying this by ω₀ or 1−ω₀ to get scattering and absorption coefficients, respectively. This is done for each of the points in our 5° × 5° latitude–longitude grid for each aerosol type. The original MACv2 vertical profiles do not contain information about single scattering albedo or asymmetry factor. These are therefore kept constant throughout the whole vertical profile for each aerosol type. Doing so leads to a vertical variation in the total optical properties of the combined aerosols since the relative proportion of fine and coarse aerosol types varies with height. These resulting optical properties for the 16 SW spectral bands of MACv2 are then interpolated to the 6 bands used here in SOCRATES. These profiles are then perturbed depending on the relevant uncertainties and combined to create a single aerosol column.

Surface albedo is taken from the SOCRATES ocean albedo scheme (over ocean), which accounts for the effect of changes in solar zenith angle, and satellite data from the SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY version 2.6 (SCIAMACHY; Tilstra et al., 2017) over land, interpolated from the native 33 nm spectral resolution to the six SW bands used in SOCRATES and regridded to a 5° × 5° latitude–longitude grid. More details on the surface albedo used can be found in Sect. 2 and the Supporting Information from Byrom and Shine (2022).

Standard atmospheric profiles (McClatchey, 1972) corresponding to latitude and time of year are used as the underlying climatology in 30° latitude bands. All simulations were performed in clear skies only. For each simulation, the radiative transfer code is called three times with different solar zenith angles computed according to the latitude, time of year, and the outputs combined using Gaussian quadrature to obtain the diurnally averaged irradiances.

2.2 Benchmark estimates of DARE and DARF

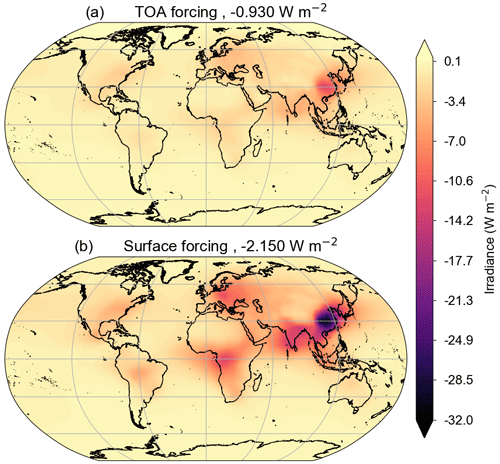
The unperturbed aerosol optical properties from MACv2 are used to calculate SW radiative fluxes at the top of the atmosphere and surface. The difference with a no-aerosol calculation provides DARE, while the difference with the pre-industrial calculation provides the DARF. Figure 1 shows the annual-mean reference TOA (top panel) and surface (lower panel) DARE, while Fig. 2 shows the same for DARF.

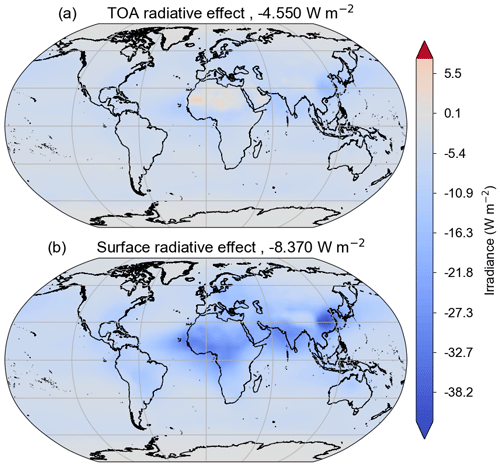
Figure 1 The direct aerosol radiative effect (DARE), in W m⁻² at the top of the atmosphere (TOA, a) and surface (b), as estimated using the SOCRATES radiative transfer code applied to the MACv2 aerosol climatology. Global average values are given above each panel.

Figure 2 Same as Fig. 1, but for the direct aerosol radiative forcing (DARF), in W m⁻².

Since the aerosol properties used here are derived from MACv2, also used in Kinne (2019a), these results can be directly compared since the only differences are the methodological and modelling approaches. Both the upper and lower panels of Fig. 2 show spatial distributions similar to the anthropogenic annual-mean clear-sky DARF shown in Fig. 7 of Kinne (2019a), although the estimate from this work is about 0.2 W m⁻² larger in both cases. This may be due to a combination of the various host model uncertainties detailed in Stier et al. (2013) and Randles et al. (2013).

The most significant differences are likely due to different assumptions about the surface albedo, the lower-resolution latitude–longitude grid, and the coarser spectral resolution used in this work. To investigate the latter, an additional reference calculation was performed using the 260-band version of SOCRATES (referred to within the code as sp_sw_260_jm3), with the corresponding interpolation of surface and aerosol properties. The differences between the 6- and 260-band versions of the DARF calculation are shown in Fig. 3. While there are biases of up to 5 % locally, these almost entirely cancel out when averaging over the globe for both the TOA and surface. This results in a more negative DARF by 1 % to 2 % at both the TOA and surface for the 260-band case, further increasing the differences between this work and Kinne (2019a), which used 8 solar wavebands. While the spatial differences will likely result in biases when calculating uncertainties (see Sect. 3), these are also likely to average out on a global mean-scale and therefore the decreased spectral resolution should not significantly impact those results.

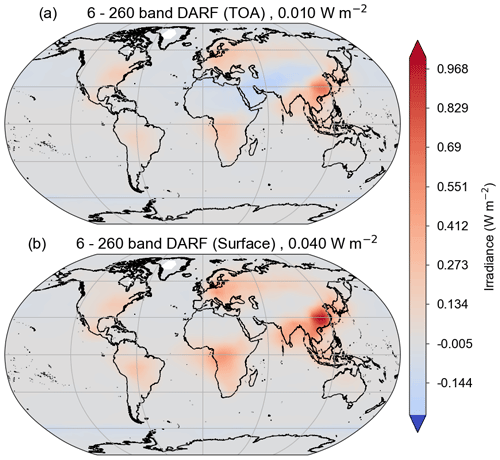
Figure 3 Differences in top-of-atmosphere (TOA, a) and surface (b) direct aerosol radiative forcing (DARF), in W m⁻², between radiative transfer calculations using a 260-band version of SOCRATES, with corresponding higher-resolution aerosol optical properties, and the 6-band version used as reference in this work. The numbers in the panel labels are the globally averaged differences.

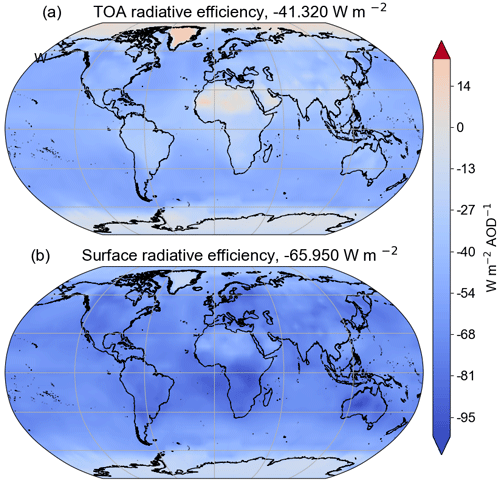
The results of this work and previous observation-based estimates are shown in Table 1. A large amount of the spread between estimates can be attributed to different global mean AOD, in particular those derived using MACC (Bellouin et al., 2013), which had a significantly larger global mean AOD at 0.18 compared to 0.12 for this work. To compare like with like, it is therefore useful to compare the radiative forcing efficiency, defined as the radiative forcing per unit optical depth. This is also shown in Table 1 where given in the cited literature and suggests a much better agreement between studies. There is good agreement between the radiative efficiency estimates derived in this work and various estimates in the literature, including Bellouin et al. (2013). This confirms that differences with previous work are in great part due to differences in AOD and gives confidence in our methodology and the representativity of the uncertainty estimates in the following sections. Figure 4 shows the forcing efficiency at the TOA and surface derived in this work.

Figure 4 TOA (a) and surface (b) annual-mean direct aerosol radiative forcing (DARF) efficiency, in W m⁻² per unit AOD, as derived from MACv2 and SOCRATES. Global mean values are shown above each panel.

2.3 Uncertainties

MACv2 does not contain direct information about uncertainties in aerosol optical properties. To obtain a realistic estimate of the uncertainty in DARE and DARF due to those uncertainties, we assume a range of uncertainties in the columnar optical properties, which are reflective of column-averaged upper and lower limits that are attainable from measurements, with a balance struck between encapsulating the plausible range and allowing for a large enough statistical sampling to obtain a robust uncertainty estimate. The range and application of the uncertainties used are shown in Table 2. The uncertainties described in Table 2 all refer to 1σ systematic (i.e. affecting every grid point equally) uncertainties. AOD uncertainties are reflective of the spread in global satellite-derived uncertainty – the range chosen has a larger upper limit than the spread in Fig. 5 of Kinne et al. (2006). SSA and asymmetry factor uncertainties were selected to span the range of uncertainties from Table 1 of Dubovik et al. (2002). The uncertainties in the optical properties are defined at 550 nm, and the fractional uncertainty at 550 nm is then assumed for all other wavelengths. This will result in biases relative to an approach which has a more sophisticated spectral treatment but is necessary for computational tractability. While the true uncertainty in DARE and DARF is a function of many variables other than the aerosol optical properties, as discussed previously, here we only account for the uncertainty attributable to the aerosol optical properties themselves. This choice matches our objective to quantify the reduction in uncertainty that could come from improved retrievals of AOD, SSA, and asymmetry parameter.

Table 2 Uncertainty ranges and statistical distribution shapes used for aerosol optical properties in the Monte Carlo experiments.

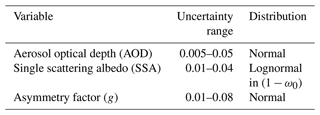
For each given combination of the systematic uncertainties listed in Table 2, 500 sets of perturbations to the optical properties are performed in a Monte Carlo framework. First, we draw global offsets to MACv2 AOD, SSA, and g using probability distribution functions that cover the ranges specified in the second column of Table 2 with the shapes specified in the third column. Perturbed distributions are then used in radiative transfer calculations. Finally, these calculations are aggregated to obtain the uncertainty in DARE and DARF. This process also effectively produces lookup tables consisting of a variety of optical property uncertainties and their associated DARE and DARF uncertainties.

Given the size of the parameter space to be sampled, the results given in this paper are made of over 2.3 million gridded radiative transfer simulations, resulting in over 6 billion calls to the radiative transfer solver. Each Monte Carlo perturbation is made with vertically resolved optical properties at each point of the 5×5 lat–long grid, which are perturbed by the same relative amount. The same perturbation is applied to each of the calculations that make up the calculation of the annual mean in order to simulate a systematic uncertainty or bias that applies throughout the whole year. This ensures that any resulting uncertainties in the TOA or surface DARE or DARF are not masked by compensating biases. The same perturbations are applied to both present-day and pre-industrial aerosols. This ensures that the anthropogenic fraction remains constant, meaning that any resulting uncertainty can be attributed solely to the aerosol optical properties. This methodology therefore explicitly accounts for amplification or masking of the anthropogenic DARE by perturbations to the natural aerosol optical properties, in contrast to other estimates (e.g. Thorsen et al., 2021), and accounts for the combined impacts of uncertainties in different optical properties (e.g. the impact of an uncertainty in ω₀ on DARE and DARF will depend on the degree of uncertainty in g and vice versa).

The uncertainty in the AOD in this work is taken to be representative of an uncertainty in the global mean AOD as measured by satellites, because past observationally based estimates used AOD derived by satellites rather than ground-based photometers for the sake of achieving global coverage. A draw is taken from a Gaussian distribution centred on the global mean AOD and covering the AOD uncertainty range shown in Table 2. The ratio $\frac{{\mathrm{AOD}}_{\mathrm{global}}^{\mathrm{perturbed}}}{{\mathrm{AOD}}_{\mathrm{global}}^{\mathrm{orig}}}$ is used to perturb each grid point by the same fractional amount for a given sample so that the relative distribution of AOD remains constant. A grid-point-wise (i.e. random) uncertainty is also applied depending on surface type, similarly to Bellouin et al. (2013):

$${\mathit{\sigma }}_{\mathrm{AOD},\mathrm{random}}=\left\{\begin{array}{l}\mathrm{0.03}+\mathrm{0.05}\cdot \mathrm{AOD}\left(\mathrm{over}\mathrm{ocean}\right)\\ \mathrm{0.03}+\mathrm{0.15}\cdot \mathrm{AOD}\left(\mathrm{over}\mathrm{land}\right)\end{array}\right..$$

The SSA uncertainty ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ is taken to be representative of the uncertainty in an inversion from a ground-based sun photometer, e.g. from AERONET version 3 (Sinyuk et al., 2020) or GRASP (Dubovik et al., 2021). This is because SSA uncertainties remain better characterised in ground-based inversions than in the relatively recent satellite-based SSA products. SSA perturbations are applied separately to the coarse-mode, pre-industrial fine-mode, and anthropogenic fine-mode aerosols. These perturbations are again spatially and temporally consistent.

An absolute change in SSA has more of an effect at large values (close to 1), since such a change will result in a larger proportional increase in the absorption coefficient. Additionally, SSA is constrained by the range $\mathrm{0}\le {\mathit{\omega }}_{\mathrm{0}}\le \mathrm{1}$. Since typical values of ω₀ are around 0.9 or above, a normal distribution in log (1−ω₀) is used. This transformation ensures that any perturbed values of ω₀ remain within the physical bounds of 0 and 1. Perturbations drawn from this lognormal distribution in (1−ω₀) are then converted back into perturbations in ω₀, and new absorption and scattering coefficients are calculated. This approach is not without its limitations; at large values of ω₀, such a lognormal distribution will result in significantly more extreme values than at lower SSA. Therefore, we assume that for regions where the SSA is large (ω₀>0.98) for a given aerosol type, such as regions with high concentrations of sea salt and sulfate aerosols, there is no SSA uncertainty in that aerosol type and the SSA is not perturbed. This approach is similar to the hypothetical enhanced approach of Thorsen et al. (2021) and will result in reduced SSA uncertainties but ensures that outliers drawn from such a distribution do not artificially increase the DARF uncertainty. The choice of probability distribution is somewhat subjective; this approach was chosen since it best retained the link between the input uncertainty and the width of the resulting probability distribution without the need for any tuned parameters.

A similar treatment is applied to the uncertainty in the asymmetry factor g. The uncertainty is assumed to be normally distributed and systematic globally. Like in the SSA case, a different draw from the probability distribution is made for each aerosol type and sample and applied globally to ensure that the present-day natural and pre-industrial aerosols share the same perturbation.

Using this approach, it is possible to determine the relative importance of uncertainties in each of these three optical properties and also the uncertainty in DARE and DARF obtainable by advances in measurements and retrievals of these optical properties. In addition, while in each of these scenarios the optical properties are perturbed within the same uncertainty limits globally, which is not necessarily realistic for measurements that may have different regional biases, the DARF uncertainty for each grid point is independent of its neighbours. Therefore, the output DARE and DARF uncertainties in each single column can be combined by mixing results from different sets of simulations to determine a more realistic assessment of the global DARE/DARF uncertainties, as demonstrated in Sect. 4.3. A stand-alone software tool is provided (see Sect. 6), which uses the simulations performed in this work to determine the resulting forcing uncertainty for a given set of optical property uncertainties.

3 Uncertainties in DARE and DARF

As with the reference case, for each perturbed set of aerosol parameters, the four radiative transfer calculations comprising the seasonal averages are compared with either a no-aerosol case to compute DARE at the TOA and surface or a corresponding perturbed pre-industrial case to obtain DARF at the TOA and surface. The resulting values of DARE and DARF, either globally averaged or for a single column, are combined in a histogram with the standard deviation giving the 1σ uncertainty. Figure 5 shows an example of the global annual mean TOA DARF for one set of input uncertainties (σ_AOD=0.03, ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}=\mathrm{0.02}$, σ_g=0.02), with Fig. 6 showing the evolution of the standard deviation with respect to the number of samples. These figures show a clear Gaussian distribution (despite the distribution of ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ not being so) with little skewness and few outliers and with statistical stability to a precision of two decimal places at the TOA in the derived σ_DARF after about 250 samples, which is a similar number to that found in Bellouin et al. (2013).

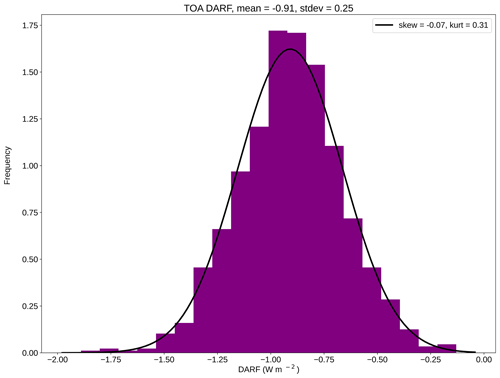
Figure 5 Example histogram generated by 500 samples of global annual mean direct aerosol radiative forcing (DARF) at the top of the atmosphere (TOA), in W m⁻², for σ_AOD=0.03, ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}=\mathrm{0.02}$, and σ_g=0.02.

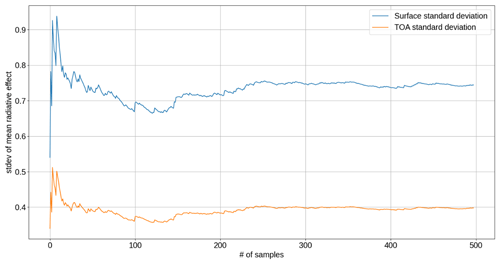
Figure 6 Standard deviation of the histogram shown in Fig. 5 as a function of the number of samples that make up the perturbed parameter ensemble for a given set of optical property uncertainties.

Figure 7 shows several maps of TOA DARF uncertainty with respect to different choices of input uncertainties; in this case, σ_AOD=0.02 and σ_g=0.03, with varying values of ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$. The gridded uncertainties show the same spatial distribution as the forcing values shown in Fig. 2, as would be expected, with σ_DARF monotonic in ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$.

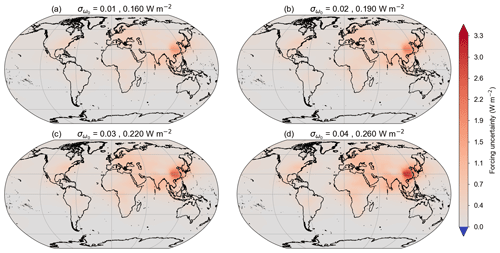
Figure 7 Example maps of uncertainty in top-of-atmosphere direct aerosol radiative forcing (DARF), calculated as the standard deviation in W m⁻², generated using 500 Monte Carlo samples for four combinations of optical property uncertainties. Each panel has the same uncertainty in aerosol optical depth and asymmetry factor of σ_AOD=0.02 and σ_g=0.03, respectively, with increasing uncertainty in single scattering albedo ${\mathit{\sigma }}_{{\mathit{\varpi }}_{\mathrm{0}}}$ as indicated in the panel titles.

3.1 Uncertainty ranges

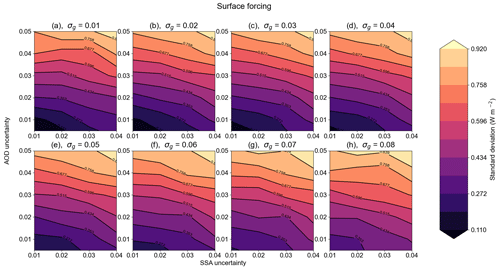
Figures 8 and 9 show the global annual mean TOA and surface DARF uncertainty derived using the uncertainty ranges in Table 1 with respect to ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ and σ_AOD. Each panel represents a step change in σ_g from 0.01 to 0.08. There are several features of note in these figures. At the TOA, the radiative forcing uncertainty appears to be roughly equivalently dependent on the uncertainties in AOD and SSA with a smaller dependence on the uncertainty in asymmetry parameter. At the surface, the change in the DARF uncertainty is more clearly dominated by changes in the AOD uncertainty, as is the case when looking at DARE (see the Supplement). In each of these cases, there appears to be roughly equal weighting to increases in ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ and σ_g.

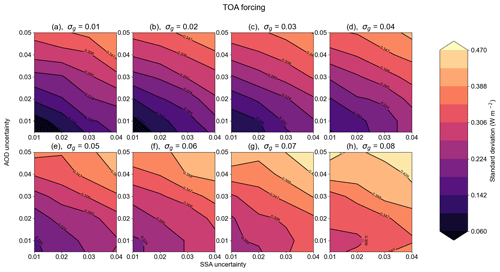
Figure 8 Contour of top-of-atmosphere (TOA) direct aerosol radiative forcing uncertainty, in W m⁻², with respect to SSA (x axis) and AOD (y axis) uncertainty. Each panel represents a change in asymmetry factor uncertainty of 0.01, within the 0.01 to 0.08 range.

Figure 9 Same as Fig. 8, but for surface direct aerosol radiative forcing.

Several studies (Loeb and Su, 2010; Thorsen et al., 2021; Samset et al., 2018) demonstrated that ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ is a dominant source of uncertainty in TOA DARF; this may be due to their smaller global mean AOD uncertainty than used in the ranges in Table 2, which are taken to be reflective of the spread in observed global mean AOD from satellites rather than the uncertainty in AERONET retrievals (Thorsen et al., 2021; Dubovik et al., 2000). Figure 8 indicates that the uncertainty in TOA DARF is instead more sensitive to an uncertainty in the AOD, which is intuitive. The shape of the contours may be indicative of some covariance or non-linearity between the different optical property uncertainties in some cases, e.g. in panel (h) of Fig. 8. This may also be due to statistical anomalies as a result of insufficient sampling; however, as demonstrated in Figs. 5 and 6, this is unlikely to be a significant effect, since the derived σ_DARF at both the TOA and surface appear to be stable after only 250 of the 500 samples ran in each case.

The uncertainties in Fig. 8 range from 0.08–0.47 W m⁻², i.e. ∼ 9 %–52 % relative uncertainty. This represents the upper and lower limits of what is feasibly attainable by hypothetical measuring systems capable of measuring globally with the uncertainties shown in Table 1. However, this is not necessarily representative of the real uncertainty for two reasons. Firstly, this only accounts for uncertainties in aerosol optical properties. Host model uncertainties and uncertainties in variables not accounted for explicitly (such as anthropogenic fraction) will still be present. In addition, Figs. 8 and 9 assume that the absolute uncertainty is the same everywhere globally, which is not the case because uncertainties in AOD and SSA, for example, are anti-correlated (Dubovik et al., 2000); i.e. regions with low AOD (and correspondingly low absolute uncertainty in the AOD) will have large uncertainties in SSA. A more realistic assessment of uncertainty in DARE and DARF is given in Sect. 3.3.

3.2 Attribution of DARE and DARF uncertainty to uncertainties in optical properties

The results in Sect. 3.1 are idealised and provide a broad range in which σ_DARF and σ_DARE are likely to sit as a function of only uncertainties in the optical properties. It is instructive to determine the sensitivity of σ_DARF to each of the input uncertainties in turn. Assuming linearity and no covariance, the sensitivity coefficient c_x is simply given as follows:

$$c_x={\displaystyle \frac{\partial {\mathit{\sigma }}_{\mathrm{DARF}}}{\partial {\mathit{\sigma }}_x}},$$

where x is either AOD, ω₀, or g. It is worth bearing in mind that this is done for heuristic purposes. As shown in Figs. 8 and 9, even on the global mean scale, significant non-linearities/covariances exist which may be stronger locally. Nevertheless, this gives an indication of which uncertainties are strongest in which regions and therefore where the most value can be obtained by increasing precision in a given variable.

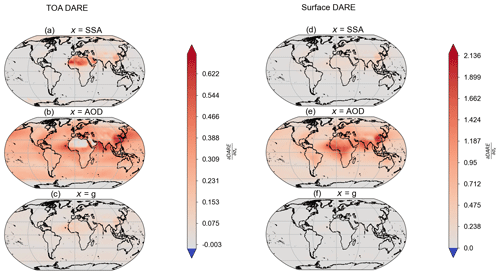
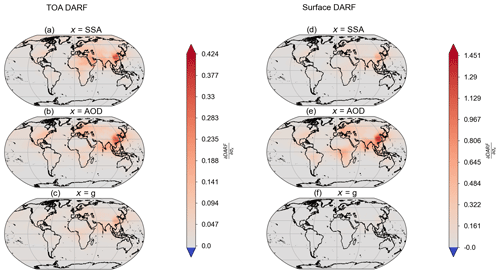
Figure 10 Sensitivity of direct aerosol radiative effect (DARE) at top-of-atmosphere (TOA) (a, b, c) and surface (d, e, f) to uncertainties in aerosol optical depth (AOD), single scattering albedo (ω₀), and asymmetry parameter (g). Units are W m⁻² per unit optical property uncertainty.

Figure 11 Same as Fig. 10, but for direct aerosol radiative forcing (DARF).

The results for TOA and surface DARE are shown in Fig. 10, and Fig. 11 shows the corresponding results for TOA and surface DARF. These two figures show a number of interesting features. Figure 10 shows that the DARE for both the TOA and surface is much more sensitive to σ_AOD than ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ and σ_g. However, the uncertainty in SSA dominates at the TOA (Fig. 10a) over desert (and to a lesser extent polar) regions. This is due to the combination of a more strongly absorbing aerosol over a highly reflective surface. It may also be due to limitations in the modelling framework, as coarse dust aerosols tend to have a lower Ångström exponent, i.e. have a larger AOD at longer wavelengths, and the fractional uncertainty is assumed to be equal at all wavelengths. It may also be due to other effects (e.g. increased scattering from a larger SSA amplified by increased backscatter from a smaller asymmetry).

Figure 11a and b show that the sensitivities of DARF uncertainty to AOD and SSA are very similar for most regions, and this is particularly apparent over East Asia where there is a strong anthropogenic forcing. There are stronger effects from SSA over desert regions and stronger sensitivity to AOD over regions with significant anthropogenic aerosol, such as southern Africa and North America, as shown by the contours in Fig. 8. There is a slightly larger effect globally from AOD, with the contribution from SSA coming next. Panel (c) of Fig. 11 shows that the asymmetry factor uncertainty is also important but less so than SSA and AOD. At the surface, the uncertainty in surface DARF is almost entirely insensitive to σ_g, aside from the region of strong anthropogenic emissions over East Asia, and much more sensitive to σ_AOD than ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$, as shown in Fig. 9. In both the surface and TOA cases, one expects a first-order cancellation of the radiative effects of the present-day natural and pre-industrial aerosols, which are the same in our framework, so their uncertainties do not matter much for DARF in contrast to DARE.

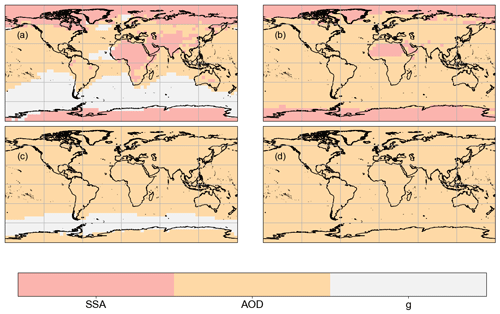
Figure 12 The largest contributor to the uncertainty in each of the three single scattering properties for four different cases: top-of-atmosphere (TOA) direct aerosol radiative forcing (DARF, a), TOA direct aerosol radiative effect (DARE, b), surface DARF (c), and surface DARE (d).

Figure 12 shows the largest contributor to the uncertainty among AOD, ω₀, and g for TOA and surface DARF and DARE. At the surface, the main contributor to uncertainty is AOD almost everywhere on the globe, for both DARE and DARF. At the TOA, a more complex picture develops. For DARE (Fig. 12b), the uncertainty in SSA is dominant in regions with high surface albedo such as deserts and at the poles, with AOD being most important elsewhere. For DARF (Fig. 12a), the main contributor varies regionally, but AOD generally dominates, except again over bright surfaces. SSA dominates uncertainty over a wider area than in the case of DARE, including the dust belt covering northern Africa, the Middle East, Central Asia, and the Chinese deserts, as well as central Australia. SSA also dominates DARF uncertainty over central Africa and India – regions known to be regularly dominated by absorbing anthropogenic aerosol with higher SSA uncertainty. Asymmetry parameter g dominates over remote, low-AOD regions over the Southern Ocean, where scattering dominates due to high SSA sea-salt aerosol, and also within the Saharan dust plume in the tropical Atlantic, where the mineral dust DARE also enhances the importance of anthropogenic scattering. Previous studies (Loeb and Su, 2010; Samset et al., 2018; Thorsen et al., 2021) found that SSA uncertainties were more dominant but used smaller AOD uncertainties based on the abilities of ground-based sun photometers rather than those of satellite retrievals.

3.3 Regionally based estimates

The analysis has so far assumed that uncertainties are globally uniform. But the lookup tables derived in Sect. 3.1 can also be used to obtain regionally based estimates of the DARE and DARF uncertainty using regionally varying estimates of σ_AOD, ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$, and σ_g. As stated in Sect. 3.1, Figs. 8 and 9 are global mean representations of thousands of similar plots corresponding to each grid point. We can therefore get a more realistic estimate of the uncertainty in DARE or DARF by selecting the point in each of these individual contour maps that correspond to a user-defined uncertainty in the aerosol optical properties in each grid box from a lookup table and recombining them to generate a new global annual mean. By attributing to each grid point a specific σ_AOD, ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$, and σ_g, it is possible to obtain a more realistic estimate of σ_DARE and σ_DARF. This section outlines an example of this approach, using optical property uncertainties similar to Bellouin et al. (2013) (henceforth referred to as B13), which are based on AERONET v1 uncertainties (Dubovik et al., 2002). The software and data used to obtain this estimate, and to generate such estimates for other sets of input uncertainties (Elsey et al., 2023), are available for download (see the “Code and data availability” section). B13 define regional uncertainties for anthropogenic aerosols only (their Table 1), so for consistency the uncertainty in ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}$ and σ_g in each grid point is only applied to the anthropogenic part of the total AOD by scaling by the anthropogenic AOD fraction at 550 nm. σ_AOD is fixed to 0.03 everywhere as in B13; i.e. we similarly assume that all the uncertainty is due to anthropogenic aerosol for this case.

B13 and this work differ significantly in their methodological frameworks despite both having DARF uncertainties derived via Monte Carlo sampling of the input uncertainties. Particularly relevant to this comparison is that B13 include several uncertainties not factored in here, such as uncertainties in anthropogenic fraction (Table 1 of B13). Additionally, B13 and this work use significantly different methods to determine aerosol type, with B13 using a bespoke algorithm on MACC reanalysis data compared to the prescribed aerosol optical depth used in MACv2. Nevertheless, the use of similar optical properties allows for a direct comparison.

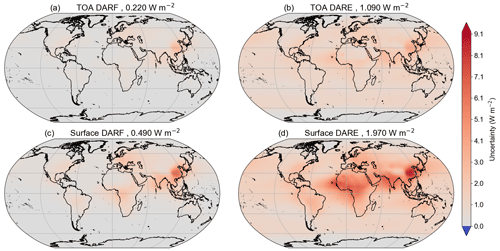
Figure 13 Top-of-atmosphere (TOA, a, b) and surface (c, d) direct aerosol radiative forcing (DARF, a, c) and direct aerosol radiative effect (DARE, b, d), in W m⁻², as derived using regional optical property uncertainties from AERONET v1. Global average values are shown in the panel titles.

The DARE and DARF uncertainties obtained via this approach are shown in Fig. 13. Global averages can be compared with those given in Table 2 of B13. At the TOA, the uncertainty in this work (±0.22 W m⁻²) is significantly smaller for DARF (“anthropogenic DRE” in B13, ±0.5 W m⁻²), even when scaling the values and their associated uncertainties by the global mean AOD (i.e. simply scaling the B13 values by a factor of 0.66, assuming a linear dependence between AOD and its contribution to uncertainty, giving ±0.33 W m⁻²). Similarly, the surface DARF uncertainty is significantly lower in this work (±0.49 W m⁻²) than B13 (±1.1, ±0.73 W m⁻² when scaled). Taking both sets of uncertainties at face value, this would suggest that the optical properties account for around 40 %–60 % of the total uncertainty in the aerosol radiative forcing at both the TOA and surface, with the remainder being the result of other uncertainties (i.e. anthropogenic fraction) considered in B13. For DARE, the results of this work and B13 are much more similar (±1.09 vs. ±1.3/±0.86 W m⁻² at the TOA, ±1.97 vs. ±1.9/1.26 W m⁻² at the surface), likely due to the anthropogenic fraction being a second-order contributor to the uncertainty in DARE, as would be expected.

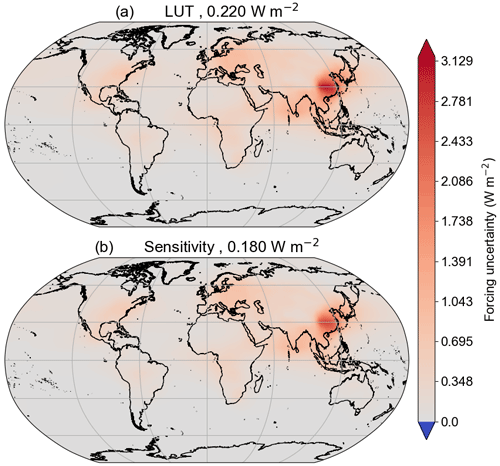
Figure 14 Top-of-atmosphere direct aerosol radiative forcing, in W m⁻², derived using (a) the lookup table approach (Sect. 3.1) against that derived using (b) the sensitivity coefficients derived in Sect. 3.2 for the AERONET v1 example described in Sect. 3.3. Global mean values are shown in the panel headings.

It is also possible to use the sensitivity coefficients derived in Sect. 3.2 to obtain a similar estimate of the uncertainty to that obtained using the lookup table approach (Sect. 3.1). This allows us to look at the degree of additivity to the uncertainty in DARE and DARF that arises from combinations of uncertainties, as opposed to the uncertainty that arises when applying an uncertainty to AOD, SSA, or g individually. Figure 14 shows this method applied to the TOA forcing uncertainty derived using the input uncertainties described earlier in Sect. 3.3. The two approaches differ by 0.04 W m⁻², indicating that in this case, this additive effect increases the uncertainty by a factor of ∼ 20 %.

4 Scaling to all-sky conditions

The central estimate and uncertainty limits obtained in Sects. 2 and 3 are applicable only to clear (cloud-free) skies. It is, however, possible to scale these uncertainties to all (clear and cloudy) skies at the TOA using a cloud fraction distribution to scale the grid-box-level DARE or DARF for each of the four seasonal-mean calculations that make up an estimate of the global annual mean. To do this, we use the monthly mean cloud fraction and cloud optical depth, τ_cloud, from the International Satellite Cloud Climatology Project (ISCCP) H series product (Young et al., 2018) over the period 1983–2017. They are combined to obtain a present-day seasonal average cloud fraction and optical thickness, interpolating to the 5° × 5° latitude–longitude grid used in the radiative transfer simulations. We assume that the DARE is entirely masked by clouds when optically thick (τ_cloud>1) clouds are present but that optically thin clouds (τ_cloud<1) do not mask the DARE and leave it unchanged. The TOA DARE and DARF (and the calculation of the associated uncertainties) are then scaled by the cloud fraction in grid cells where the cloud is optically thick. These assumptions are not entirely correct, as it is known that above-cloud aerosol–radiation interactions occur from biomass-burning aerosols in cloudy regions. However, the corresponding cloudy-sky DARE is likely small globally, with Myhre et al. (2020) estimating a global average of only 0.01 ± 0.1 W m⁻². Additionally, optically thin clouds will serve to mask some of the aerosol effect, further constraining both our central estimate and the uncertainty. We do not consider any uncertainties due to the clouds themselves here; this analysis is purely to scale the global mean uncertainty in the aerosol optical properties. Other estimates that use a more sophisticated cloud representation have an increased uncertainty in all-sky conditions to reflect uncertainties in cloud properties but also have an increased uncertainty associated with aerosol retrievals in cloudy conditions (Kacenelenbogen et al., 2019). It would be possible to account for these effects using our framework by considering that the optical property uncertainties in cloudy regions are larger than those in clear-sky regions.

Table 3 Top-of-atmosphere, all-sky direct aerosol radiative effect (DARE) and direct aerosol radiative forcing (DARF), in W m⁻², for this work and selected comparable previous studies, along with their uncertainties where available. Uncertainty estimates for this work are obtained using the optical property uncertainties from Bellouin et al. (2013). The numbers in brackets for Thorsen et al. (2021) are the uncertainties in their “enhanced” methodology (see Sect. 1). Uncertainties from Kinne (2019b) are asymmetric, with −0.35 being the central value. Note: NA – not available.​​​​​​​

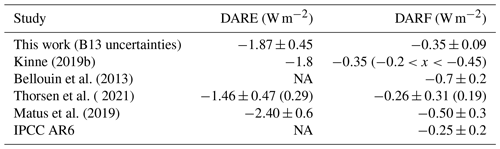
The results of the scaling described above are shown in Table 3, alongside the latest estimate from the Intergovernmental Panel on Climate Change AR6 report (Forster et al., 2021) and other recent studies that provide all-sky DARE and DARF estimates. The central estimate obtained with our approach is in very good agreement with the other estimates, with results almost identical to those of Kinne (2019a) and sitting in the range of plausible values implied by the various studies. However, our uncertainties are significantly lower than all other cases, since we only account for uncertainty in clear-sky aerosol optical properties. Taken together, Table 3 suggests that aerosol optical property uncertainty accounts for one-third to half of total uncertainty.

5 Conclusions

Despite several decades of research, uncertainties in DARE and DARF remain large (Forster et al., 2021). Based on plausible measurement uncertainties in AOD, SSA, and asymmetry parameter, we quantified shortwave, clear-sky, TOA, and surface DARE and DARF uncertainties. We used a new Monte Carlo framework (available for download) applied to over 2 million radiative transfer simulations using the radiative transfer code SOCRATES. We first assume uniform uncertainties globally and then use regionally varying uncertainties. Results are summarised in Table 1. When using globally uniform uncertainties, aerosol optical property uncertainties represent between 5 % and 42 % of DARE and 9 % and 52 % of DARF uncertainty at the TOA. At the TOA, AOD uncertainty is the main contributor to overall uncertainty, except over bright surfaces where SSA uncertainty contributes most. When using regionally varying uncertainties, aerosol optical property uncertainties represent 24 % of TOA DARE and DARF. Clear-sky results are then scaled to all-sky conditions by scaling by ISCCP cloud fraction and assuming that clouds with an optical depth larger than 1 totally mask the DARE. Under these assumptions, aerosol optical property uncertainty contributes to about 25 % uncertainty in TOA, all-sky DARE, and DARF. Comparing our uncertainties (which only include the contribution of AOD, SSA, and asymmetry parameter uncertainties) to uncertainties obtained in previous studies that also considered uncertainties in non-aerosol variables suggests that the aerosol optical property uncertainty accounts for one-third to half of total uncertainty. This result suggests that reducing aerosol retrieval uncertainties, for both ground-based sun photometers and satellite instruments, needs to be done in combination with reductions in non-aerosol uncertainties such as surface and cloud properties.

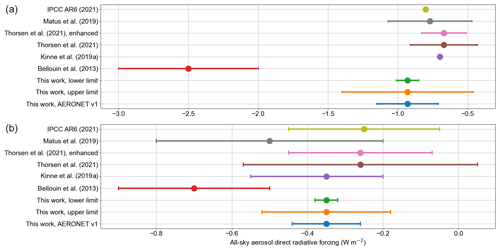
Figure 15 Clear-sky (a) and all-sky (b) TOA forcing estimates, in W m⁻², and their 1σ uncertainties (where available) from this work compared with previous studies.

Figure 15 shows estimates of the TOA DARF and its uncertainties in clear- and all-sky conditions for the studies presented in Tables 1 and 3. The estimates for the present work correspond to the lower and upper limits of our globally uniform aerosol optical property uncertainties and the regionally varying uncertainties from Sect. 3.3. Using the ranges of uncertainty tested in this work, the smallest reasonable uncertainties in the optical properties (σ_AOD=0.005, ${\mathit{\sigma }}_{{\mathit{\omega }}_{\mathrm{0}}}=\mathrm{0.01}$, and σ_g=0.01) result in a clear-sky TOA DARF uncertainty of ±0.08 W m⁻². This value is significantly smaller than the range of uncertainties estimated from existing studies shown in Fig. 15 and Table 1, which spans ±0.16 to ±0.50 W m⁻². This again suggests that reducing aerosol optical property uncertainty would only reduce overall DARF uncertainty by up to a half. Using our regionally varying aerosol optical property uncertainties based on AERONET v1, the TOA DARF uncertainty of ±0.22 W m⁻² is 2.75 times larger than our minimum value and is broadly consistent with the values derived in the radiative kernel study of Thorsen et al. (2021), which range from 0.22 to 0.31 W m⁻². A benefit of our framework is that it allows for a quick assessment of the impacts of reduced uncertainties in AOD, SSA, and asymmetry parameter in specific regions, which can help inform which regions and variables go furthest to reduce the global mean uncertainty. For example, if we divide the regionally varying uncertainties used in Sect. 3.3 by 2, the uncertainty in TOA DARF would be reduced from 0.22 (25 % of DARF) to 0.12 W m⁻² (13 % of DARF), a factor of just under 2.

There are several caveats that need to be considered when using the results from this work. While we can sample the parameter space of the aerosol optical properties to a reasonable degree, there are some components of the uncertainty which we do not represent. Most notably, we assume that AOD and SSA uncertainties are independent of AOD. The strength of that assumption is difficult to assess for AOD because uncertainties in individual AERONET AOD measurements depend on errors due to cloud masking, viewing geometry, and assumptions regarding aerosol shape that are AOD-independent. It is unclear how those uncertainties average into an AOD-dependent behaviour. The situation is much clearer with SSA uncertainties, and Sinyuk et al. (2020) suggest that SSA uncertainties decrease in a power law with increasing AOD, suggesting the high tail of our DARE uncertainty distribution is overestimated. We also assume that the aerosol property uncertainty is proportionally equal at all wavelengths. This is primarily for reasons relating to computational tractability, as applying different perturbations to different wavelengths would significantly increase the number of radiative transfer calculations required. A future experiment might include some uncertainty in the extinction and/or absorption Ångström exponents. Additionally, we do not represent the longwave component of DARE or DARF here. This is most relevant for coarse-mode aerosols such as mineral dust and sea salt and therefore for estimating DARE. Due to the net positive longwave DARE of coarse aerosols at the TOA (e.g. Ryder, 2021), the total (i.e. shortwave plus longwave) DARE would be less negative than values given here overall when incorporating longwave effects, although it is unclear whether longwave uncertainties would partly compensate for uncertainties in the shortwave. DARF, in contrast, is dominantly determined by changes in fine- to accumulation-mode aerosols (making up the anthropogenic component of aerosol species), which mostly impact the shortwave spectrum, as represented here. Finally, we focus solely on the direct radiative effect and forcing and neglect the effects of aerosol–cloud interactions, all of which need to be captured to fully represent the effects of aerosols on climate. Nevertheless, the relative uncertainties in the DARF are as large as those due to aerosol–cloud interactions (Forster et al., 2021), rendering it important to understand the contributors to these uncertainties. Finally, our estimation of the all-sky DARE and DARF is based on a simple scaling based on cloud optical depth and cloud fraction, as described in Sect. 4. More complex methods could be applied and could form the basis of further work. However, the simple method used here provides a first-order estimate of the contribution of clear-sky DARF uncertainty to all-sky DARF.

Recent progress in constraining optical properties, i.e. from AERONET v3 (Sinyuk et al., 2020) and GRASP (Herrera et al., 2022), could further reduce the TOA DARF uncertainty, although non-aerosol uncertainties contribute substantially to total uncertainty, as noted above. Our results provide a framework within which future measurement uncertainties can be evaluated globally to estimate their impact on global DARE and DARF uncertainty, such as those from missions such as EarthCARE (Wehr et al., 2023) and Plankton, Aerosol, Cloud, Ocean Ecosystem (PACE; Werdell et al., 2019).