Reaction of SO₃ with H₂SO₄ and its implications for aerosol particle formation in the gas phase and at the air–water interface

The reactions between SO₃ and atmospheric acids are indispensable in improving the formation of aerosol particles. However, relative to those of SO₃ with organic acids, the reaction of SO₃ with inorganic acids has not received much attention. Here, we explore the atmospheric reaction between SO₃ and H₂SO₄, a typical inorganic acid, in the gas phase and at the air–water interface using quantum chemical (QC) calculations and Born–Oppenheimer molecular dynamics simulations. We also report the effect of H₂S₂O₇, the product of the reaction between SO₃ and H₂SO₄, on new particle formation (NPF) in various environments using the Atmospheric Cluster Dynamics Code (ACDC) kinetic model and QC calculations. The present findings show that the gas-phase reactions of SO₃ + H₂SO₄ without and with water molecules are both low-energy-barrier processes. With the involvement of interfacial water molecules, H₂O induced the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, ${\mathrm{HSO}}_{\mathrm{4}}^{-}$ mediated the formation of the ${\mathrm{HSO}}_{\mathrm{4}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, and the deprotonation of H₂S₂O₇ was observed and proceeded on the picosecond timescale. The present findings suggest the potential contribution of the SO₃–H₂SO₄ reaction to NPF and aerosol particle growth, showing that (i) although H₂S₂O₇ is easily hydrolyzed with water to form H₂SO₄, it can directly participate in H₂SO₄–NH₃-based cluster formation and can present a more obvious enhancement effect on SA–A-based cluster formation, and (ii) the formed interfacial ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ can attract candidate species from the gas phase to the water surface and, thus, accelerate particle growth.

1 Introduction

Sulfur trioxide (SO₃) is a major air pollutant (Zhuang and Pavlish, 2012; Chen and Bhattacharya, 2013; Cao et al., 2010; Kikuchi, 2001; Mitsui et al., 2011) and can be considered the most important oxidation product of SO₂ (Starik et al., 2004). As an active atmospheric species, SO₃ can lead to the formations of acid rain and atmospheric aerosol (Sipilä et al., 2010; Mackenzie et al., 2015; England et al., 2000; Li et al., 2016; Renard et al., 2004) and thus plays a well-documented role in regional climate and human health (Zhang et al., 2012, 2015; Pöschl, 2005; Pöschl and Shiraiwa, 2015; Haywood and Boucher, 2000; Lohmann and Feichter, 2005). In the atmosphere, the hydrolysis of SO₃ to the H₂SO₄ product (SA) is a major loss route of SO₃ (Morokuma and Muguruma, 1994; Akhmatskaya et al., 1997; Larson et al., 2000; Hazra and Sinha, 2011; Long et al., 2013a; Torrent-Sucarrat et al., 2012; Ma et al., 2020). As a complement to the loss of SO₃, the ammonolysis reaction of SO₃ in polluted areas of NH₃ can form H₂NSO₃H, which not only can be competitive with the formation of SA from the hydrolysis reaction of SO₃ but also can enhance the formation rates of sulfuric acid (SA)–dimethylamine (NH(CH₃)₂; DMA) clusters by about 2 times. Similarity, the reactions of SO₃ with CH₃OH and organic acids (such as HCOOH) were reported (Liu et al., 2019; Hazra and Sinha, 2011; Long et al., 2012; Mackenzie et al., 2015; Huff et al., 2017; Smith et al., 2017; H. Li et al., 2018), and both processes can provide a mechanism for incorporating organic matter into aerosol particles. However, the reaction mechanisms between SO₃ and inorganic species are still unclear.

As a major inorganic acidic air pollutant (Tilgner et al., 2021), SA can play an important role in new particle formation (Weber et al., 1995, 1996, 2001; Sihto et al., 2006; Riipinen et al., 2007; Sipilä et al., 2010; Zhang et al., 2012) and acid rain (Calvert et al., 1985; Finlayson-Pitts and Pitts, 1986; Wayne, 2000). The source of gas-phase SA is mainly the gas-phase hydrolysis reaction of SO₃. The direct reaction between SO₃ and H₂O hardly takes place in the atmosphere due to a high energy barrier (Chen and Plummer, 1985; Hofmann and Schleyer, 1994; Morokuma and Muguruma, 1994; Steudel, 1995). However the addition of a second water molecule (Morokuma and Muguruma, 1994; Larson et al., 2000; Loerting and Liedl, 2000), the hydroperoxyl radical (Gonzalez et al., 2010), formic acid (Hazra and Sinha, 2011; Long et al., 2012), sulfuric acid (Torrent-Sucarrat et al., 2012), nitric acid (Long et al., 2013a), oxalic acid (Lv et al., 2019), and ammonia (Bandyopadhyay et al., 2017) has been reported to catalyze the formation of SA from the hydrolysis reaction of SO₃ as these compounds can promote atmospheric proton transfer reactions. Similarly, as SA can give out protons more readily than H₂O, which in turn is more conducive to the proton transfer, we predict that the addition reaction involving the proton transfer between SO₃ and SA is much easier under atmospheric conditions than that between SO₃ and H₂O. However, this gas-phase reaction has not been investigated as far as we know. Previous studies have shown that the concentration of water vapor decreases significantly with increasing altitude (Anglada et al., 2013), leading to longer atmospheric lifetimes of SO₃. The gas-phase reaction of SO₃ with H₂SO₄ may contribute significantly to the loss of SO₃ in dry areas where [H₂SO₄] is relatively high (especially at lower temperatures) and at a higher altitude. So, it is important to study the reaction mechanism of SO₃ with H₂SO₄ and its competition with H₂O-assisted hydrolysis of SO₃. Meanwhile, in many gas-phase reactions, a single water molecule can play a catalyst role by increasing the stability of pre-reactive complexes and reducing the activation energy of transition states (Kanno et al., 2006; Stone and Rowley, 2005; Chen et al., 2014; Viegas and Varandas, 2012, 2016). For example, a single water molecule in the H₂O⋯HO₂ + SO₃ reaction can catalyze the formation of HSO₅ (Gonzalez et al., 2010). Thus, it is equally important to study the SO₃ + SA reaction without and with H₂O. In addition to the gas-phase reactions, many new atmospheric processes and new reaction pathways have been observed at the air–water interface (Zhong et al., 2017a, b; Kumar et al., 2017, 2018; Zhu et al., 2016; Li et al., 2016; Zhu et al., 2017). For example, the organic acids reacting with SO₃ can form the ion pair of carboxylic sulfuric anhydride and hydronium at the air–water interface (Zhong et al., 2019). This mechanism is different from the gas-phase reaction in which the organic acid either serves as a catalyst for the hydrolysis of SO₃ or acts as a reactant reacting with SO₃ directly. So, water droplets may play important roles in atmospheric behaviors between SO₃ and SA. Thus, it is also important to study the interfacial mechanism between SO₃ and SA and to compare its difference with the corresponding gas-phase reaction.

Previous experimental studies (Otto and Steudel, 2001; Abedi and Farrokhpour, 2013) found that disulfuric acid (H₂S₂O₇, DSA) is the product of the reaction between SO₃ and SA. From the perspective of structure, DSA possesses two HO functional groups. Both HO groups can act as hydrogen donors and acceptors to interact with atmospheric particle precursors. It has been shown that the reaction between SO₃ and some important atmospheric species (H. Li et al., 2018; Yang et al., 2021; Liu et al., 2019; Rong et al., 2020) not only can cause appreciable consumption of SO₃ and thus reduce the abundance of SA from the hydrolysis of SO₃ in the atmosphere but also can promote the new particle formation (NPF) process by their products. For example, the products of NH₂SO₃H, HOOCOOSO₃H, CH₃OSO₃H, and HOCCOOSO₃H from the reactions of SO₃ with NH₃ (H. Li et al., 2018), H₂C₂O₄ (Yang et al., 2021), CH₃OH (Liu et al., 2019) and HOOCCHO (Rong et al., 2020) all have a catalytic effect on the formation of new particles in aerosols. However, whether DSA produced by the reaction between SO₃ and SA contributes to aerosol formation or not is still unclear. Thus, another main question that we intend to address here is the role of DSA in atmospheric SA–NH₃ (A) nucleation. These chemicals have been recognized as dominant precursors in highly polluted areas, especially in some megacities in Asia.

In this work, using quantum chemical calculations and the master equation, we first studied the gas-phase reaction between SO₃ and SA to produce DSA, with H₂O acting as a catalyst. Then, we use the Born–Oppenheimer molecular dynamics (BOMD) simulations to evaluate the reaction mechanism of SO₃ with SA at the air–water interface. Finally, we used the Atmospheric Clusters Dynamic Code (ACDC) kinetic model and quantum chemical calculations to investigate atmospheric implications of the SO₃–SA reaction for the atmospheric particle formation. Particular attention in this work is given to the study of (i) the mechanism difference of the SO₃ + SA reaction in the gas phase and at the air–water interface and (ii) the fate of DSA in atmospheric NPF and its influence in various environmental conditions.

2 Computational details

2.1 Quantum chemical calculation

The M06-2X functional has been proved to be one of the best functionals to describe the noncovalent interactions and estimate the thermochemistry and equilibrium structures for atmospheric reactions (Elm et al., 2012; Mardirossian and Head-Gordon, 2016). So, for the SO₃ + SA reaction without and with water molecules in the gas phase, the optimized geometries and vibrational frequencies of reactants, pre-reactive complexes, transition states (TSs), post-reactive complexes, and products were calculated using the M06-2X method (Zhao and Truhlar, 2008; Elm et al., 2012) with the 6-311$++$G(2df,2pd) basis set by Gaussian 09 packages (Hratchian et al., 2009). It is noted that the calculated bond distances and bond angles at the M06-2X/6-311$++$G(3df,2pd) level (Fig. S1 in the Supplement) agree well with the available experimental values (Kuczkowski et al., 1981). At the same level, the connectivity between the TSs and the suitable pre- and post-reactant complexes was performed by intrinsic reaction coordinate (IRC) calculations. Then, single-point energy calculations were calculated at the CCSD(T)-F12/cc-pVDZ-F12 level (Adler et al., 2007; Knizia et al., 2009) using ORCA (Neese, 2012).

A multistep global minimum sampling technique was used to search for the global minima of the (DSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) molecular clusters. Specifically, a multistep global minimum sampling technique was used to search for the global minima of the (SA)_x(A)_y(DSA)_z ($\mathrm{0}y\le x+z\le \mathrm{3}$) clusters. Specifically, the initial n × 1000 (1 < n < 5) configurations for each cluster were systematically generated by the ABCluster program (Zhang and Dolg, 2015, 2016) and were optimized at the semi-empirical PM6 (Stewart, 2013) methods using MOPAC 2016 (Stewart, 2016, 2013, 2007). Then, up to n × 100 structures with relatively lowest energy among the n × 1000 (1 < n < 5) structures were selected and re-optimized at the M06-2X/6-31+G(d,p) level. Finally, n × 10 lowest-lying structures were optimized by the M06-2X/6-311$++$G(2df,2pd) level to determine the global minimum. To obtain the reliable energies, single-point energy calculations were refined at the DLPNO-CCSD(T)/aug-cc-pVTZ level based on the optimized geometries at the M06-2X/6-311$++$G(2df,2pd) level. The optimized structures and the formation Gibbs free energy of the stable clusters are summarized in Fig. S9 and Table S8 in the Supplement, respectively.

2.2 Rate constant calculations

Using the Rice–Ramsperger–Kassel–Marcus-based master equation (ME/RRKM) (Miller and Klippenstein, 2006), the kinetics for the SO₃ + SA reaction without and with water molecule were calculated by adopting a Master Equation Solver for Multi Energy-well Reactions (MESMER) code (Glowacki et al., 2012). In the MESMER calculation, the rate coefficients for the bimolecular barrier-less association step (from reactants to pre-reactive complexes) were evaluated by the inverse Laplace transform (ILT) method (Horváth et al., 2020); meanwhile the unimolecular step was performed by the RRKM theory combined with the asymmetric Eckart model. The ILT method and RRKM theory can be represented in Eqs. (1) and (2), respectively.

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{k}^{\mathrm{\infty }}\left(\mathit{\beta }\right)={\displaystyle \frac{\mathrm{1}}{Q\left(\mathit{\beta }\right)}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}k\left(E\right)\mathit{\rho }\left(E\right)\exp (-\mathit{\beta }E)\mathrm{d}E\text{(2)}& {\displaystyle }& {\displaystyle }k\left(E\right)={\displaystyle \frac{W(E-E_{\mathrm{0}})}{h\mathit{\rho }\left(E\right)}},\end{array}$$

where h is denoted as Planck's constant, ρ(E) is denoted as the active density of state of the reactant at energy level E, E₀ is denoted as the reaction threshold energy, and W(E−E₀) is denoted as the sum of the rovibrational states of the transition state (TS) geometry (excluding the degree of freedom related to passing the transition state). The input parameters for electronic geometries, vibrational frequencies, and rotational constants were calculated at the M06-2X/6-311$++$G(2df,2pd) level, and single-point energy calculations were refined at the CCSD(T)-F12/cc-pVDZ-F12 level for the modeling.

2.3 Born–Oppenheimer molecular dynamics (BOMD) simulation

The CP2K code (Hutter et al., 2014) was used in the BOMD simulations. The Becke–Lee–Yang–Parr (BLYP) functional (Becke, 1988; Lee et al., 1988) was chosen to look at the exchange and correlation interactions, and Grimme's dispersion was carried out to account for the weak dispersion interaction (Grimme et al., 2010). The Goedecker–Teter–Hutter (GTH) conservation pseudopotential (Goedecker et al., 1996; Hartwigsen et al., 1998) with the Gaussian DZVP basis set (VandeVondele and Hutter, 2007) and the auxiliary plane wave basis set was applied to correct the system valence electrons and the core electrons, respectively. For the plane wave basis set and Gaussian basis set, the energy cutoff levels (Zhong et al., 2017a, b, 2018, 2019) were set to 280 and 40 Ry, respectively. For each simulation in the gas phase, a 15 × 15 × 15 ų supercell with periodic boundary condition was adopted with a time step of 0.5 fs. As the droplet system with 191 water molecules is sufficient to describe the interfacial mechanism (Zhong et al., 2017a), the air–water interfacial system here included 191 water molecules, SO₃, and SA in the BOMD simulation. It is pointed out that the droplet system with 191 water molecules had been equilibrated before SO₃ and H₂SO₄ were added at the water surface. The details of the equilibrium process for the droplet system with 191 water molecules are shown in the Supplement Sect. S4. To avoid periodic interactions between adjacent water droplets, the size of the simulation box (Kumar et al., 2017, 2018; Ma et al., 2020) was set as 35 × 35 × 35 ų with a time step of 1.0 fs. Notably, the time step of 1.0 fs has been proved to achieve sufficient energy conservation for the water system (Zhong et al., 2015; Li et al., 2016; Zhu et al., 2016; Kumar et al., 2017). For all the simulations in the gas phase and at the air–water interface, the Nosé–Hoover thermostat (Zhong et al., 2017a, b, 2018, 2019; Kumar et al., 2017, 2018; Ma et al., 2020) was selected in the NVT ensemble to control the temperature around 300 K. To eliminate the influence of the initial configuration on the simulation results of interfacial reaction, 40 BOMD simulations for the air–water interface reactions were carried out.

2.4 Atmospheric Clusters Dynamic Code (ACDC) model

The Atmospheric Cluster Dynamics Code (ACDC) (McGrath et al., 2012) model was used to simulate the cluster formation rates and mechanisms of (DSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) clusters at different temperatures and monomer concentrations. The thermodynamic data of quantum chemical calculation at the DLPNO-CCSD(T)/aug-cc-pVTZ//M06-2X/6-311$++$G(2df,2pd) level of theory can be used as the input of the ACDC. The birth–death equation (Eq. 3) for clusters solves the time development of cluster concentrations by numerical integration using the ode15s solver in MATLAB (Shampine and Reichelt, 1997).

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{c}_i}{\mathrm{d}t}}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{j<i}{\mathit{\beta }}_{j,(i-j)}{C}_j{C}_{(i-j)}+\sum _j{\mathit{\gamma }}_{(i+j)\to i}{C}_{i+j}\\ & -\sum _j{\mathit{\beta }}_{i,j}{C}_i{C}_j-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sum _{j<i}{\mathit{\gamma }}_{i\to j}{C}_i+Q_i-S_i,\end{array}\end{array}$$

where c_i is the concentration of cluster i, β_i,j is the collision coefficient between clusters i and j, ${\mathit{\gamma }}_{(i+j)\to i}$ is the evaporation coefficient of cluster i+j evaporating into clusters i and j, and Q_i is all other source term of cluster i (see more details of β and γ in SI Appendix Part 4). In addition, a constant coagulation sink coefficient 2 × 10⁻² s⁻¹ (corresponding to the median observed in contaminated areas) was used for taking into account external losses (Yao et al., 2018; Zhang et al., 2022; L. Liu et al., 2021). The boundary conditions in the ACDC require that the smallest clusters outside of the simulated system should be very stable so that they do not evaporate back immediately (McGrath et al., 2012). Based on cluster volatilization rate (shown in Table S10 in the Supplement) and the formation Gibbs free energy of the clusters (shown in Table S8), the cluster boundary conditions simulated in this study were set as (SA)₄⋅(A)₃, (SA)₄⋅(A)₄, $\mathrm{SA}\cdot (\mathrm{A}{)}_{\mathrm{3}}\cdot (\mathrm{DSA}{)}_{\mathrm{3}}$, $(\mathrm{SA}{)}_{\mathrm{3}}\cdot (\mathrm{A}{)}_{\mathrm{4}}\cdot (\mathrm{DSA}{)}_{\mathrm{1}}$, and $(\mathrm{SA}{)}_{\mathrm{2}}\cdot (\mathrm{A}{)}_{\mathrm{3}}\cdot (\mathrm{DSA}{)}_{\mathrm{2}}$. According to field observations, the concentration of SA and A was, respectively, set in a range of 10⁶–10⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ and 10⁷–10¹¹ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ (Almeida et al., 2013; Kuang et al., 2008; Bouo et al., 2011; Zhang et al., 2018). As the prediction in Table S7 in the Supplement shows, the concentration of DSA is set to 10⁴–10⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$. However, DSA is easily hydrolyzed with abundant water in the troposphere to form H₂SO₄; the concentration of DSA listed in Fig. S9 was overestimated. So, the maximum concentration of DSA (10⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$) was not included in the effects of H₂S₂O₇ on new particle formation (NPF) in various environments. In addition, the temperature was set to be in the range 218.15–298.15 K, which spans most regions of the troposphere and the polluted atmospheric boundary layer.

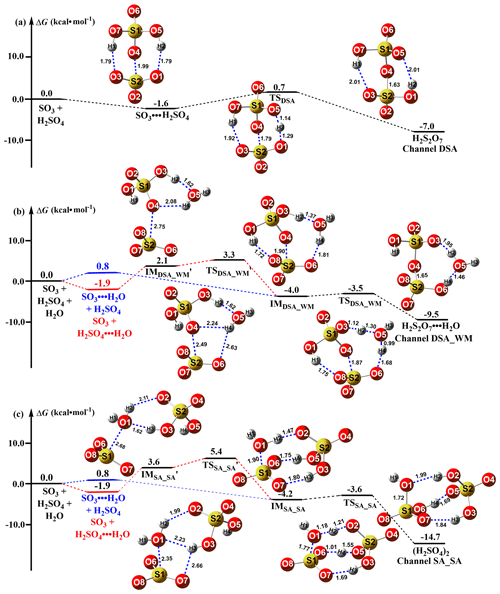
Figure 1 Schematic potential energy surface for the SO₃ + H₂SO₄ → H₂S₂O₇ reaction. Distances are given in units of Ångström at the M06-2X/6-311$++$G(2df,2pd) level, while the energy values correspond to the calculations at the CCSD(T)-F12/cc-pVDZ-F12//M06-2X/6-311$++$G(2df,2pd) level. The pre-reactive complex and TS for the route of DSA formation from the SO₃ + H₂SO₄ reaction with H₂O were denoted by “IM_{DSA_WM}” and “TS_{DSA_WM}”, respectively, while the corresponding pre-reactive complex and TS for the process of SA formation from the hydrolysis of SO₃ with H₂SO₄ were respectively labeled as “IM_{SA_SA}” and “TS_{SA_SA}”.

Table 1 The rate constant (${\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$) for the SO₃ + H₂SO₄ reaction and the effective rate constant (${\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$) for the SO₃ + H₂SO₄ reaction with H₂O (100  % RH) within the temperature range of 280–320 K.

k_DSA is the rate constant for the SO₃ + H₂SO₄ reaction. $k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{o}}^{\prime }$ and $k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}^{\prime }$ are, respectively, the effective rate constants for the H₂O-assisted SO₃ + H₂SO₄ reaction occurring through one-step and stepwise routes.

3 Results and discussion

3.1 Reactions in the gas phase

The addition reaction involving the proton transfer between SO₃ and SA (Channel DSA) proceeded through the formation of the SO₃⋯H₂SO₄ complex followed by unimolecular transformation through the transition state TS_DSA to form H₂S₂O₇ (Fig. 1a). The reactant complex SO₃⋯H₂SO₄ was a double six-membered ring complex with a relative Gibbs free energy of −1.6 kcal mol⁻¹. After the formation of the SO₃⋯H₂SO₄ complex, Channel DSA overcame a Gibbs free energy barrier of 2.3 kcal mol⁻¹, which was lower than that of H₂O-catalyzed hydrolysis of SO₃ by 4.2 kcal mol⁻¹ (Fig. S1). The rate constant for the SO₃ + SA reaction was calculated at various temperatures (Table 1). Within the temperature range of 280–320 K, the rate constants for the SO₃ + SA reaction were calculated to be 2.57 × 10⁻¹²–5.52 × 10⁻¹² ${\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$, which were larger than the corresponding values of H₂O-catalyzed hydrolysis of SO₃ by 3.43–4.03 times. Therefore, it can be said that the direct reaction between SO₃ and SA occurs easily under atmospheric conditions.

The SO₃ + H₂SO₄ reaction with H₂O produced two distinct products, labeled (i) H₂S₂O₇ (DSA; Channel DSA_WM) and (ii) H₂SO₄ (SA; Channel SA_SA). A single water molecule in (i) acted as a catalyst, while it played the role of a reactant in (ii). The schematic potential energy surface for the SO₃ + H₂SO₄ reaction with H₂O was shown in Fig. 1. As the probability of simultaneous collision (Pérez-Ríos et al., 2014; Elm et al., 2013) of three molecules of SO₃, SA, and H₂O was quite low under realistic conditions, both Channel DSA_WM and Channel SA_SA can be considered sequential bimolecular processes. In other words, both Channel DSA_WM and Channel SA_SA occurred via the collision between SO₃ (or H₂SO₄) and H₂O to form the dimer (SO₃⋯H₂O and H₂SO₄⋯H₂O) first and then the dimer encountered with the third reactant H₂SO₄ or SO₃. The computed Gibbs free energies of dimer complexes SO₃⋯H₂O and H₂SO₄⋯H₂O were, respectively, 0.8 and −1.9 kcal mol⁻¹, which were, respectively, consistent with the previous values (the range from −0.2 to 0.62 kcal mol⁻¹ for the SO₃⋯H₂O complex (Bandyopadhyay et al., 2017; Long et al., 2012) and the range from −1.82 to −2.63 kcal mol⁻¹ for the H₂SO₄⋯H₂O complex (Long et al., 2013b; Tan et al., 2018)). The Gibbs free energy of H₂SO₄⋯H₂O was lower than that of SO₃⋯H₂O by 2.7 kcal mol⁻¹, thus leading to the equilibrium constant of the former complex being larger than that of the latter one in Table S2 in the Supplement by 1–2 orders of magnitude. Additionally, the larger equilibrium constant of the H₂SO₄⋯H₂O complex led to its higher concentration in the atmosphere. For example, when the concentrations of SO₃ (Yao et al., 2020), H₂SO₄ (Liu et al., 2015), and H₂O (Anglada et al., 2013) were 10⁶, 10⁸, and 10¹⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$, respectively, the concentrations of SO₃⋯H₂O and H₂SO₄⋯H₂O were 2.41 × 10³–2.01 × 10⁴ and 5.01 × 10⁵–3.01 × 10⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ within the temperature range of 280–320 K (see Table S3 in the Supplement), respectively. So, we predict that Channel DSA_WM and Channel SA_SA mainly take place via the collision of H₂SO₄⋯H₂O with SO₃. In order to check this prediction, the effective rate constants for two bimolecular reactions of H₂SO₄⋯H₂O + SO₃ and SO₃⋯H₂O + H₂SO₄ were calculated, and the details are shown in SI Appendix, Part 3 and Table 1. As seen in Table 1, the SO₃⋯H₂O + H₂SO₄ reaction in both Channel DSA_WM and Channel SA_SA can be neglected as their effective rate constants were smaller than the corresponding values in the H₂SO₄⋯H₂O + SO₃ reaction by 16.7–48.5 and 1.02–3.05 times within the temperature range of 280–320 K, respectively. Therefore, we only considered the H₂SO₄⋯H₂O + SO₃ bimolecular reaction in both Channel DSA_WM and Channel SA_SA.

As for Channel DSA_WM, the H₂SO₄⋯H₂O + SO₃ reaction occurred in a stepwise process as displayed in Fig. 1b, which was similar to the favorable routes in the hydrolysis of COS, HCHO, and CH₃CHO catalyzed by sulfuric acid (Long et al., 2013b; K. Li et al., 2018; Tan et al., 2018). When the H₂SO₄⋯H₂O complex and SO₃ served as reactants, the reaction was initiated by the complex ${\mathrm{IM}}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}^{\prime }$, where a van der Waals interaction (S2⋯O4, 2.75 Å) was found between the O₄ atom of SA moiety in H₂SO₄⋯H₂O and the S atom of SO₃. After the complex ${\mathrm{IM}}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}^{\prime }$, the ring enlargement from ${\mathrm{IM}}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}^{\prime }$ to the SO₃⋯H₂SO₄⋯H₂O complex occurred through the transition state ${\mathrm{TS}}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}^{\prime }$ with a Gibbs free energy barrier of 1.2 kcal mol⁻¹. The IM_{DSA_WM} complex was 6.1 kcal mol⁻¹ lower in energy than ${\mathrm{IM}}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}^{\prime }$. In IM_{DSA_WM}, SO₃ acted as a double donor of the hydrogen bond to form a cage-like hydrogen bonding network with H₂SO₄⋯H₂O. Then, starting with the IM_{DSA_WM} complex, the H₂SO₄⋯H₂O + SO₃ reaction occurred through the transition state TS_{DSA_WM} with a Gibbs free barrier energy of 0.5 kcal mol⁻¹ to form a quasi-planar network complex, H₂S₂O₇⋯H₂O. TS_{DSA_WM} was in the middle of a double proton transfer, where H₂O played the role of a bridge for proton transfer, along with the simultaneous formation of the O4⋯S2 bond. In order to estimate the catalytic ability of H₂O in the SO₃ + SA reaction, the effective rate constant ($k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}^{\prime }$) of the H₂SO₄⋯H₂O + SO₃ reaction was compared with the rate constant (k_DSA) of the SO₃ + H₂SO₄ reaction. As seen in Table 1, under the experimental concentration (Anglada et al., 2013) ([H₂O] = 5.20 × 10¹⁶–2.30 × 10¹⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$) within the temperature range of 280–320 K, the calculated $k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}^{\prime }$ was 1.03 × 10⁻¹¹–4.60 × 10⁻¹² ${\mathrm{cm}}^{\mathrm{3}}\mathrm{molec}{.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$, which was larger than that of k_DSA by 1.79–1.86 times. This result shows that H₂O exerts a catalytic role in promoting the rate of the SO₃ + H₂SO₄ reaction.

Regarding Channel SA_SA, the stepwise reaction occurred firstly via the ring enlargement from the six-membered ring complex ${\mathrm{IM}}_{\mathrm{SA}\mathrm{\_}\mathrm{SA}}^{\prime }$ to a cage-like hydrogen bonding network IM_{SA_SA} and then took place by going through a transition state, TS_{SA_SA}, to form the product complex (H₂SO₄)₂. TS_{DSA_WM} was in the middle of a double-hydrogen transfer, where H₂SO₄ acted as a bridge of the hydrogen atom from the H₂O to SO₃ along with the O1 atom of the H₂O addition to the S atom of SO₃. It is worth noting that the energy barriers of two elementary reactions involved in the stepwise route of Channel SA_SA were only 1.8 and 0.6 kcal mol⁻¹, respectively, showing that the occurrence of the stepwise route of Channel SA_SA is feasible from an energetic point of view. To check whether Channel DSA_WM is more favorable than Channel SA_SA or not, their rate ratios listed in Eq. (4) have been calculated and are shown in Table 1. The calculated rate ratio $v_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}/v_{\mathrm{SA}\mathrm{\_}\mathrm{SA}}$ shows that Channel DSA_WM is more important than Channel SA_SA because the rate ratio $v_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}/v_{\mathrm{SA}\mathrm{\_}\mathrm{SA}}$ is 1.53–3.04 within the temperature range of 280–320 K. So, we predicted that the SO₃ + H₂SO₄ reaction with H₂O producing H₂S₂O₇ is more favorable than that forming H₂SO₄.

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\displaystyle \frac{v_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}}}{v_{\mathrm{SA}\mathrm{\_}\mathrm{SA}}}}& ={\displaystyle \frac{v_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}+v_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{o}}}{v_{\mathrm{SA}\mathit{\_}SA\mathit{\_}s}+v_{\mathrm{SA}\mathrm{\_}\mathrm{SA}\mathrm{\_}\mathrm{o}}}}\\ & ={\displaystyle \frac{\begin{array}{c}{k}_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}\times K_{\text{eq}\left({\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}\\ +k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{o}}\times K_{\text{eq}\left({\mathrm{SO}}_{\mathrm{3}}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}\end{array}}{\begin{array}{c}{k}_{\mathrm{SA}\mathrm{\_}\mathrm{SA}\mathrm{\_}\mathrm{s}}\times K_{\text{eq}\left({\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}\\ +k_{\mathrm{SA}\mathrm{\_}\mathrm{SA}\mathrm{\_}\mathrm{o}}\times K_{\text{eq}\left({\mathrm{SO}}_{\mathrm{3}}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}\end{array}}}\end{array}\end{array}$$

3.2 Reactions at the air–water interface

The mechanism for the SO₃ + SA reaction at the air–water interface was lacking. Notably, SO₃, SA, and DSA molecules can stay at the interface for 35.8 %, 30.1 %, and 39.2 % of the time in the 150 ns simulation (Fig. S2 in the Supplement), respectively, revealing that the existence of SO₃, SA, and DSA at the air–water interface cannot be negligible. So, the BOMD simulations were used to evaluate the reaction mechanism of SO₃ with SA at the aqueous interfaces. Similar to the interfacial reaction of SO₃ with organic and inorganic acids (Cheng et al., 2023; Zhong et al., 2019), the reaction between SO₃ and SA at the aqueous interface may occur in three ways: (i) SO₃ colliding with adsorbed SA at the air–water interface, (ii) SA colliding with adsorbed SO₃ at the aqueous interface, or (iii) the SO₃–SA complex reacting at the aqueous interface. However, due to the high reactivity of both SO₃ and SA at the air–water interface, the lifetimes of SO₃ (Zhong et al., 2019) and SA (Fig. S3) (on the order of a few picoseconds) on the water droplet were extremely short, and the SA⁻ ion can be formed quickly. In addition, as shown by the result calculated above, the SO₃⋯H₂SO₄ complex can generate DSA easily before it approaches the air–water interface. So, two possible models were mainly considered for the SO₃ + SA reaction on the water surface: (i) gaseous SO₃ colliding with SA⁻ at the air–water interface and (ii) the DSA (the gas-phase product of SO₃ and SA) dissociating on the water droplet.

3.2.1 Gaseous SO₃ colliding with SA⁻ at the air–water interface

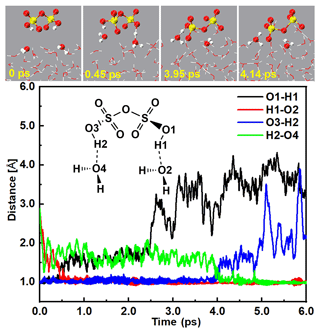
At the water droplet's surface, the interaction between SO₃ and SA⁻ included two main channels: (i) H₂O induced the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair (Fig. 2 and Fig. S4 and Movie S1 in the Supplement), and (ii) SA⁻ mediated the formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair (Fig. 3 and Figs. S5 and S6 and Movies S2 and S3 in the Supplement). The BOMD simulations for the H₂O-induced formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair are illustrated in Fig. 2; the H1 atom of the SA⁻ ion can combine with a nearby interfacial water molecule at 8.18 ps via a hydrogen bond (d_(O3–H1) = 1.17 Å) interaction, thus forming the hydrated hydrogen sulfate ion (SA⁻⋯H₂O). Then, the H1 atom of the SA⁻ ion was moved to the O3 atom of the interfacial water molecule at 8.28 ps, revealing the formation of the ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair. Additionally, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ gradually approached the SO₃ molecule, with a shortening of the S1–O1 bond. At 9.26 ps, the S1–O1 bond length was 1.84 Å, which was close to the length of the S–O1 (1.65 Å) bond in the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ ion (Fig. S8), revealing the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair.

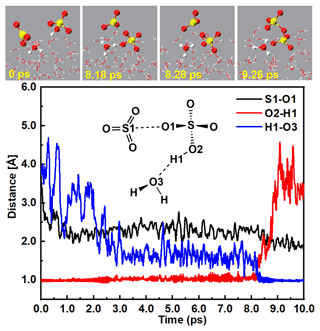
Figure 2 Top panel: snapshot structures taken from the BOMD simulations, which illustrate that H₂O induced the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair as a result of the reaction of SO₃ with ${\mathrm{HSO}}_{\mathrm{4}}^{-}$ at the air–water interface. Lower panel: time evolution of key bond distances (S–O1, O2–H1, and O3–H1) involved in the induced mechanism.

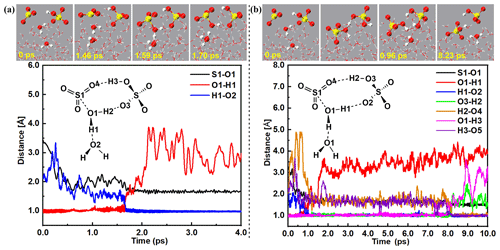
Figure 3 The top parts of (a) and (b) show snapshot structures taken from the BOMD simulations, which illustrate the hydration reaction mechanism of SO₃ mediated by ${\mathrm{HSO}}_{\mathrm{4}}^{-}$ at the air water interface. The bottom parts of (a) and (b) show the time evolution of key bond distances (S–O1, O1–H2, O5–H2, O2–H1, O3–H4, and O4–H3) involved in the hydration mechanism.

Both direct (Figs. 3a and S5 and Movie S2) and indirect (Figs. 3b and S6 and Movie S3) forming mechanisms were observed in SA⁻-mediated formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair. The direct SA⁻-mediated formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair was a loop structure mechanism, which was consistent with gas-phase hydrolysis of SO₃ assisted by acidic catalysts of HCOOH, HNO₃, H₂C₂O₄, and SA in previous works (Long et al., 2012, 2013a; Torrent-Sucarrat et al., 2012; Lv et al., 2019) and the interfacial reactions of HNO₃-mediated Criegee hydration (Kumar et al., 2018) and the hydration of SO₃ via the loop-structure formation (Lv and Sun, 2020). As for the direct formation mechanism of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair seen in Fig. 3a and Movie S2, an eight-membered loop complex, SO₃⋯H₂O(1)⋯SA⁻, was found at 1.46 ps, with the formation of two hydrogen bonds (d_(O3⋯H2) = 2.13 Å; d_(O4⋯H3) = 2.18 Å) and a van der Waals interaction (d_(S1⋯O1) = 2.14 Å). Subsequently, SO₃ and interfacial H₂O(1) were close to each other. At 1.59 ps, a transition-state-like loop structure was observed, and proton transfer from interfacial H₂O(1) to another suspended H₂O(2) was found, where the bond lengths of S1–O1, O1–H1, and H1–O2 were 1.94, 1.19, and 1.32 Å, respectively. At 1.70 ps, the bond lengths of S–O1 and H1–O2 were reduced to 1.73 and 1.01 Å, while the bond length of H1–O2 was extended to 1.61 Å, showing the formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair. During the direct formation route of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, SA⁻ played the role of a spectator, while interfacial water molecules acted as both a reactant and a proton acceptor. As compared with the hydration reaction mechanism of SO₃ at the air–water interface reported by Lv et al. (Lv and Sun, 2020), the loop-structure formation with proton transferred in the loop was not observed in the direct mechanism of SA⁻-mediated formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair. This was probably because the SA⁻ ion was more difficult to give the proton.

As seen in Fig. 3b and Movie S3, the indirect forming process of ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair contained two steps: (i) SO₃ hydration along with SA formation and (ii) SA deprotonation. Specifically, as for step (i), at 0.70 ps, a transition-state-like structure of SO₃ hydration was observed with SO₃, SA⁻, and an interfacial water molecule involved. Note that at this time the H1 atom in the interfacial H₂O molecule migrated to the O2 atom of the SA⁻ ion instead of the surrounding water molecule. At 0.96 ps, the O1–H1 bond of H₂O was broken with the length of 1.56 Å, while the S1–O1 bond was formed with the length of 1.75 Å, demonstrating the completion of the hydrolysis reaction of SO₃ and the formation of the SA molecule. Then, at 8.08 ps, the H2 proton transferred from SA to the O4 atom of SA⁻ ion and to the O5 atom of the nearby water molecule was occurred, where the O3–H2 and O1–H3 bonds extended to 1.13 and 1.22 Å, and the length of O4–H2 and O5–H3 bonds shortened to 1.45 and 1.20 Å. Finally, SA deprotonation was completed at 8.23 ps with the formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair. During the whole indirect formation process of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, SA⁻ played the role of protons' donor and acceptor, and water molecules acted as hydration reactants and proton acceptors. Compared with the direct mechanism of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, the indirect formation process of the ${\mathrm{HSO}}_{\mathrm{4}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair required more time. This was consistent with the interfacial reactions of CH₂OO + HNO₃ (Kumar et al., 2018) and the hydration of SO₃ (Lv and Sun, 2020), where the direct forming mechanism needed less time than indirect forming mechanism.

Figure 4 Top panel: snapshot structures taken from the BOMD simulations, which illustrate the deprotonation of H₂S₂O₇ at the air water interface. Lower panel: time evolution of key bond distances (O1–HI, O1–H2, O3–H2, and H2–O4) involved in the hydration mechanism.

3.2.2 H₂S₂O₇ dissociating on the water droplet

In addition to the gaseous SO₃ colliding with SA⁻ at the air–water interface, DSA, the product of the barrier-less reaction between SO₃ and SA can further quickly react with the interfacial water molecule at the air–water interface. As seen in Figs. 4 and S7 and Movie S4, DSA was highly reactive at the air–water interface and can undergo two levels of deprotonation to form the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ ion. Specifically, the DSA can firstly form a H bond with the interfacial water molecule at 0.45 ps. After that, the H1 atom of DSA transferred to interfacial water and produced ${\mathrm{HS}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{-}$ and H₃O⁺ ions. The formed ${\mathrm{HS}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{-}$ ion can survive for ∼ 3 ps on water droplet. At 4.14 ps, the H2 atom of the ${\mathrm{HS}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{-}$ ion moved to the O4 atom of a nearby interfacial water molecule and formed the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, which was stable at the air–water interface over a simulated timescale of 10 ps. Note that the second deprotonation of DSA indeed needs more time than its first deprotonation as the pK_a1 (pK_a1 = −16.05) of DSA is much smaller than its pK_a2 (pK_a2 = −4.81) (Abedi and Farrokhpour, 2013). In brief, at the air–water interface, both of these routes of the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair occurred on the picosecond timescale.

3.3 Atmospheric implications

3.3.1 Application of the SO₃ + SA reaction in atmospheric chemistry

In the gas phase, the main sink route of SO₃ was H₂O-assisted hydrolysis of SO₃ (Morokuma and Muguruma, 1994; Akhmatskaya et al., 1997; Larson et al., 2000; Hazra and Sinha, 2011; Long et al., 2013a; Torrent-Sucarrat et al., 2012; Ma et al., 2020). To study the atmospheric importance of the SO₃ + SA reaction without and with H₂O, the rate ratio ($v_{\mathrm{DSA}}/v_{\mathrm{SA}}$) between the SO₃ + SA reaction and H₂O-assisted hydrolysis of SO₃ was compared, which is expressed in Eq. (5).

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{v_{\mathrm{DSA}}}{v_{\mathrm{SA}}}}={\displaystyle \frac{\begin{array}{c}{k}_{\mathrm{DSA}}\times \left[{\mathrm{SO}}_{\mathrm{3}}\right]\times \left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]+k_{\mathrm{DSA}\mathrm{\_}\mathrm{WM}\mathrm{\_}\mathrm{s}}\\ \times K_{\text{eq1}}\times \left[{\mathrm{SO}}_{\mathrm{3}}\right]\times \left[{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\right]\times [{\mathrm{H}}_{\mathrm{2}}\mathrm{O}]\end{array}}{\begin{array}{c}{k}_{\mathrm{SA}\mathrm{\_}\mathrm{WM}}\times K_{\text{eq2}}\times \left[{\mathrm{SO}}_{\mathrm{3}}\right]\\ \times \left[{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]\times \left[{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]\end{array}}}\end{array}$$

Table 2 The rate ratio between the SO₃ + H₂SO₄ reaction and the hydrolysis of SO₃ at different altitudes in the atmosphere of Venus.

k_DSA, k_{DSA_WM_s}, and k_{SA_SA} are, respectively, the rate constants for the SO₃ + H₂SO₄ reaction, the H₂O-assisted SO₃ + H₂SO₄ reaction occurring through the stepwise route, and the hydrolysis reaction of SO₃ + (H₂O)₂.

In Eq. (5), K_eq1 and K_eq2 are the equilibrium constants for the formation of H₂SO₄⋯H₂O and SO₃⋯H₂O complexes shown in Table S2, respectively; k_DSA, k_{DSA_WM_s}, and k_{SA_WM} respectively denote the bimolecular rate coefficient for the H₂SO₄ + SO₃, H₂SO₄⋯H₂O + SO₃, and SO₃⋯H₂O + H₂O reactions; and [H₂O] and [H₂SO₄] respectively represent the concentration of H₂O and SA taken from references (Anglada et al., 2013; Liu et al., 2015). The value of $v_{\mathrm{DSA}}/v_{\mathrm{SA}}$ was listed in Table S7 (0 km altitude) and Table S8 (5–30 km altitude). As seen in Table S7, the hydrolysis reaction of SO₃ with (H₂O)₂ dominates over the SO₃ + H₂SO₄ reaction at 0 km altitude as the [H₂O] (10¹⁶–10¹⁸ molec. cm³) was much larger than that of [H₂SO₄] (10⁴–10⁸ molec. cm³). Although the concentration of water molecules decreases with the increase in altitude in Table S8, the concentration of [H₂O] is still much greater than that of [H₂SO₄], resulting in the SO₃ + H₂SO₄ reaction not being able to compete with the H₂O-assisted hydrolysis of SO₃ within the altitude range of 5–30 km. Even considering the high H₂SO₄ concentration at the end and outside the aircraft engine and at a flight altitude of 10 km (Curtius et al., 2002), the SO₃ + H₂SO₄ reaction was not the major sink route of SO₃. Notably, as the concentration of sulfuric acid was even greater than that of water vapor in the atmosphere of Venus, the SO₃ + SA reaction was probably more favorable than the H₂O-assisted hydrolysis of SO₃ in Venus' atmosphere. To check whether the SO₃ + H₂SO₄ reaction was more favorable than H₂O-assisted hydrolysis of SO₃ or not in Venus' atmosphere, the rate ratio of $v_{\mathrm{DSA}}/v_{\mathrm{SA}}$ listed in Eq. (4) has been calculated in Table 2. It can be seen from Table 2 that the rate ratio of $v_{\mathrm{DSA}}/v_{\mathrm{SA}}$ was 3.24 × 10⁸–5.23 × 10¹⁰ within the altitude range of 40–70 km in Venus' atmosphere, which indicates that the SO₃ + H₂SO₄ reaction is significantly more favorable than the hydrolysis reaction of SO₃ + (H₂O)₂ within the altitude range of 40–70 km in Venus' atmosphere.

Figure 5 The Gibbs free energy (kcal mol⁻¹) diagram of (DSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) clusters at 278.15 K and 1 atm. “A” refers to sulfuric acid, “D” refers to disulfuric acid, and “N” refers to ammonia.

3.3.2 Enhancement effect of DSA on NPF

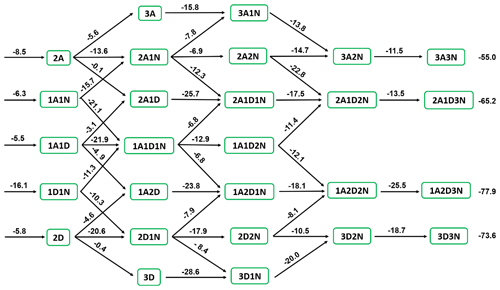
From the multistep global minimum sampling technique, for (DSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) molecular clusters, the 27 most stable structures in the present system have been found (Fig. S11 in the Supplement). To evaluate the thermodynamic stability of these clusters, Gibbs formation free energies (ΔG) at 278.15 K and evaporation rate coefficient (γ, s⁻¹) for (DSA)_x(SA)_y(A)_z ($z\le x+y\le \mathrm{3}$) molecular clusters were calculated in Fig. 5 and Tables S11 and S12 in the Supplement, respectively. As for dimers formed by SA, A, and DSA, the ΔG of (A)₁⋅(DSA)₁ was −16.1 kcal mol⁻¹, which was lowest in all dimers followed by (SA)₂ (−8.5 kcal mol⁻¹) and then (SA)₁⋅(A)₁ (−6.3 kcal mol⁻¹), meanwhile, the γ of (A)₁⋅(DSA)₁ (1.17 × 10⁻³ s⁻¹) was lower than that of (SA)₂ (3.81 × 10² s⁻¹) and (SA)₁⋅(A)₁ (4.19 × 10⁴ s⁻¹). Regarding the SA–A–DSA-based clusters, the values of ΔG and γ of SA–A–DSA-based clusters containing more DSA molecules were relatively lower than the corresponding values of other SA–A–DSA-based clusters with the same number of acid and base molecules. In the free-energy diagram for cluster formation steps of the SA–A–DSA system (Fig. 5), thermodynamic barriers were weakened mainly by the subsequential addition of the A or DSA monomer. Also, the SA–A–DSA-based growth pathway was thermodynamically favorable, with decreasing ΔG. These results indicate that DSA not only can promote the stability of SA–A–DSA-based clusters but also may synergistically participate in the nucleation process.

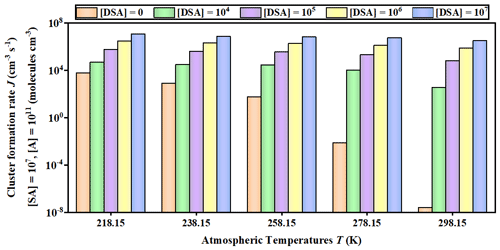
Figure 6 Cluster formation rates J (${\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) against the of DSA monomer concentration (unit: $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$) under different temperatures (218.15, 238.15, 258.15, 278.15, and 298.15 K), where [SA] = 10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ and [A] = 10⁹ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$.

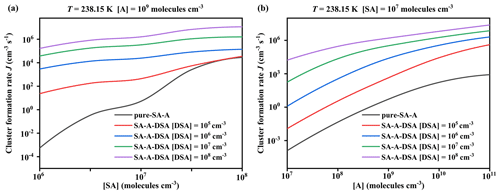
Figure 7 Simulated cluster formation rates J (${\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) as a function of (a) [SA] and (b) [A], with different concentrations of disulfuric acid [DSA] of 10⁴ (red), 10⁵ (blue), 10⁶ (green), 10⁷ (purple), and 0 $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$ (black; pure SA–A), at T = 238.15 K.

The potential enhancement influence of DSA on the SA–A-based particle formation was shown in Fig. 6. The formation rate (J; ${\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) of the SA–A–DSA-based system illustrated in Fig. 6 was negatively dependent on temperature, demonstrating that the low temperature is a key factor to accelerate cluster formation. It is noted that, at low temperatures of 218.15 K (Fig. S12 in the Supplement) and 238.15 K (Fig. S13 in the Supplement), the actual ΔG of clusters has been calculated to ensure meaningful cluster dynamics of the 3 × 3 systems, where the actual ΔG surface represented that the simulated set of clusters always included the critical cluster. In addition to temperature, the J of the SA–A–DSA-based system shown in Fig. 6 rises with the increase in [DSA]. More notably, the participation of DSA can promote J to a higher level, indicating its enhancement in SA–A nucleation. In addition, there was significantly positive dependence of the J of the SA–A–DSA-based system on both [SA] and [A] in Fig. 7 (238.15 K) and Figs. S15–S18 in the Supplement (218.15, 258.15, 278.15, and 298.15 K). This was because the higher concentration of nucleation precursors could lead to higher J. In addition, Fig. S19 in the Supplement showed the nucleation rate when the sum ([SA] + [DSA]) was kept constant. $J_{\mathrm{DSA}/\mathrm{SA}}$ under substituted conditions was higher than that under unsubstituted conditions. These results indicated that DSA can greatly enhance the SA–A particle nucleation in the atmospheric boundary layer heavily polluted by sulfur oxide, especially at an average flight altitude of 10 km with high [DSA].

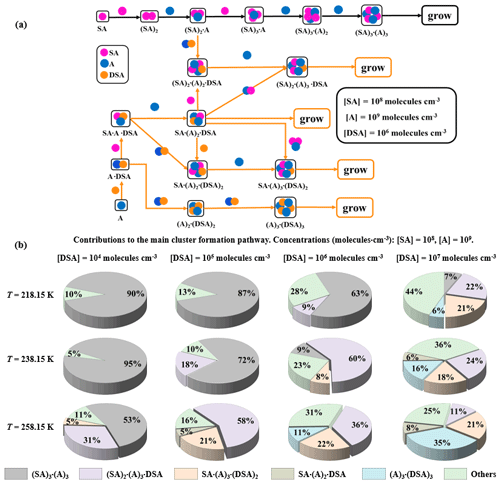
Figure 8 (a) The main pathways of clusters growing out of the research system under conditions with 218.15, 238.15, and 258.15 K where [SA] = 10⁸ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$, [A] = 10⁹ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$, and [DSA] = 10⁶ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$. (b) The contribution of different concentrations of DSA to the main cluster formation pathway at 218.15, 238.15, and 258.15 K is shown in the pie charts.

Two main cluster formation pathways, the pure SA–A-based cluster (i) and the DSA-containing cluster (ii), at different [DSA] and different temperatures (218.15, 238.15, and 258.15 K), are shown in Fig. 8a. As seen, the DSA molecule exhibited an ability to directly participate in cluster formation under high [SA] and [DSA] and median [A]. Interestingly, at different temperatures and different [DSA], the DSA molecule showed a different effect mechanism and contribution in the SA–A system. As seen in Fig. 8b and Fig. S20b in the Supplement, the cluster growth pathways were dominated by DSA-containing cluster formation under the conditions of 238.15 K ([DSA] is 10⁶–10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$), 258.15 K ([DSA] is 10⁵–10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$), 278.15 K ([DSA] is 10⁴–10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$), and 298.15 K ([DSA] is 10⁴–10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$). The cluster growth pathways were completely dominated by the DSA-containing cluster at 298.15 K, where [DSA] = 10⁵–10⁷ $\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}$, and its contribution for growth flux out of the system reached 100 % (Fig. S22 in the Supplement). In short, on the one hand, the contribution of the DSA participation pathway has been increased with increasing temperature. On the other hand, the contribution of the pathway with participation of DSA increased with increasing [DSA], while the number of DSA molecules contained in clusters [$(\mathrm{SA}{)}_{\mathrm{2}}\cdot (\mathrm{A}{)}_{\mathrm{3}}\cdot \mathrm{DSA}$, $\mathrm{SA}\cdot (\mathrm{A}{)}_{\mathrm{2}}\cdot \mathrm{DSA}$, $\mathrm{SA}\cdot (\mathrm{A}{)}_{\mathrm{3}}\cdot (\mathrm{DSA}{)}_{\mathrm{2}}$, and (A)₃⋅(DSA)₃] that can contribute to cluster growth had a positive correlation with [DSA]. These results suggested that DSA has the ability to act as a potential contributor to SA–A-based NPF in the atmosphere at low T, low [SA], high [A], and high [DSA], and the DSA participation pathway can be dominant in the atmospheric boundary layer that is heavily polluted by sulfur oxide in the seasons of late autumn and early winter.

Table 3 Gibbs free energy (ΔG, kcal mol⁻¹) for the formation of ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}$, ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{HNO}}_{\mathrm{3}}$, ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }(\mathrm{COOH}{)}_{\mathrm{2}}$, H₃O⁺⋯NH₃, H₃O⁺⋯H₂SO₄, ${\mathrm{HSO}}_{\mathrm{4}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}$, ${\mathrm{HSO}}_{\mathrm{4}}^{-}\mathrm{\cdots }(\mathrm{COOH}{)}_{\mathrm{2}}$, ${\mathrm{HSO}}_{\mathrm{4}}^{-}\mathrm{\cdots }{\mathrm{HNO}}_{\mathrm{3}}$, H₂SO₄⋯NH₃, ${\mathrm{SO}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}\mathrm{\cdots }{\mathrm{NH}}_{\mathrm{3}}$, HOOCCH₂COOH⋯H₂SO₄⋯NH₃, HOCCOOSO₃H⋯H₂SO₄⋯NH₃, CH₃OSO₃H⋯H₂SO₄⋯NH₃, and HOOCCH₂CH(NH₂)COOH⋯H₂SO₄⋯NH₃ at 298 K.

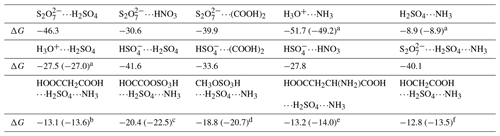
Energies are given in kcal mol⁻¹ and calculated at the M06-2X/6-311$++$G(2df,2pd) theoretical level. References are as follows: ^a Zhong et al. (2019). ^b Zhang et al. (2018). ^c Rong et al. (2020). ^d Gao et al. (2023). ^e J. Liu et al. (2021). ^f Zhang et al. (2017).

At the air–water interface, an important implication of the BOMD simulations was that the reaction between SO₃ and SA at the air–water interface can be accomplished within a few picoseconds, whereby the interfacial water molecules played a significant role in promoting the formation of ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ and ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pairs. Furthermore, the adsorption capacity of ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$, H₃O⁺, and SA⁻ to gaseous precursors in the atmosphere was further investigated by the calculated interaction free energies. Herein, the species of SA, NH₃, HNO₃, and (COOH)₂ have been regarded as the candidate species (Kulmala et al., 2004; Kirkby et al., 2011). Our calculated Gibbs free energies in Table 3 show that the interactions of ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}$, ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{HNO}}_{\mathrm{3}}$, ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }(\mathrm{COOH}{)}_{\mathrm{2}}$, H₃O⁺⋯NH₃, H₃O⁺⋯H₂SO₄, SA⁻⋯H₂SO₄, SA⁻⋯(COOH)₂, and SA⁻⋯HNO₃ were stronger than those of H₂SO₄⋯NH₃ (major precursor of atmospheric aerosols), with their binding free energies enhanced by 18.6–42.8 kcal mol⁻¹. These results reveal that interfacial ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$, SA⁻, and H₃O⁺ can attract candidate species from the gas phase to the water surface. Moreover, we evaluated whether ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ could lead to increased particle growth in the SA–A cluster by considering geometrical structure and the formation free energies of the $\left(\mathrm{SA}{)}_{\mathrm{1}}\right(\mathrm{A}{)}_{\mathrm{1}}({\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}{)}_{\mathrm{1}}$ clusters. Compared with (SA)₁(A)₁(X)₁ (X = HOOCCH₂COOH, HOCCOOSO₃H, CH₃OSO₃H, HOOCCH₂CH(NH₂)COOH and HOCH₂COOH) clusters (Zhong et al., 2019; Zhang et al., 2018; Rong et al., 2020; Gao et al., 2023; J. Liu et al., 2021; Zhang et al., 2017), the number of hydrogen bonds in the $\left(\mathrm{SA}{)}_{\mathrm{1}}\right(\mathrm{A}{)}_{\mathrm{1}}({\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}{)}_{\mathrm{1}}$ cluster presented in Fig. S8 increased, and the ring of the complex was enlarged. It was demonstrated that ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ has the highest potential to stabilize SA–A clusters and promote SA–A nucleation in these clusters due to its acidity and structural factors, such as more intermolecular hydrogen bond binding sites. Subsequently, compared to (SA)₁(A)₁(X)₁ clusters (Table 2), the Gibbs formation free energy ΔG of $\left(\mathrm{SA}{)}_{\mathrm{1}}\right(\mathrm{A}{)}_{\mathrm{1}}({\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}{)}_{\mathrm{1}}$ cluster was lower, showing that the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ ion at the air–water interface has stronger nucleation ability than X in the gas phase. Therefore, we predict that ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ at the air–water interface would lead to increased particle growth.

4 Summary and conclusions

In this work, we employed QC calculations, BOMD simulations, and the ACDC kinetic model to characterize the SO₃–H₂SO₄ interaction in the gas phase and at the air–water interface to study the effect of H₂S₂O₇ on H₂SO₄–NH₃-based clusters. Results revealed that the energy barrier of the gas-phase SO₃ + H₂SO₄ reaction without and with H₂O was less than 2.3 kcal mol⁻¹. Rate constants indicated that though the SO₃ + H₂SO₄ reaction cannot compete with the H₂O-assisted hydrolysis of SO₃ within the temperature range of 280–320 K, its rate constant was close to the upper limits for bimolecular reactions, and H₂O exerted an obvious catalytic role in promoting the reaction rate. Moreover, ACDC kinetic simulations showed that DSA has unexpected facilitate effects on the NPF process and can present a more obvious enhancement effect on SA–A-based cluster formation in the polluted atmospheric boundary layer. Of particular note is that DSA can directly participate in the SA–A-based cluster formation pathway and that the contribution of the pathway with participation of DSA increases with increasing [DSA] in regions with atmospheric pollution boundary layer of high concentrations of SO₃, especially in late autumn and early winter.

At the air–water interface, H₂O induced the formation of the ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, SA⁻ mediated the formation of the ${\mathrm{SA}}^{-}\mathrm{\cdots }{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ ion pair, and the deprotonation of H₂S₂O₇ was observed; these can occur within a few picoseconds. The formed interfacial ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$, SA⁻, and H₃O⁺ can attract candidate species (such as H₂SO₄, NH₃, and HNO₃) for particle formation from the gas phase to the water surface and thus accelerate the growth of particle. Moreover, the potential of X (X = ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$, HOOCCH₂COOH, HOCCOOSO₃H, CH₃OSO₃H, HOOCCH₂CH(NH₂)COOH and HOCH₂COOH) in the ternary SA–A–X cluster formation indicated that ${\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{7}}^{\mathrm{2}-}$ has the highest potential to stabilize SA–A clusters and promote SA–A nucleation in X.

The present work will expand our understanding of new pathways for the loss of SO₃ in acidic polluted areas. Moreover, this work will also help to reveal some missing sources of NPF in metropolitan industrial regions and to understand the atmospheric organic–sulfur cycle more comprehensively.