Measurement report: Water diffusion in single suspended phase-separated aerosols

Water diffusion is a typical thermodynamic process in ambient aerosols that plays pivotal roles in their physicochemical properties and atmospheric lifetime and influences the climate and human health. A fair amount of aerosols become phase-separated after experiencing atmospheric aging processes such as efflorescence, amorphization, and liquid–liquid phase separation. However, detecting the hygroscopicity of heterogeneous aerosols is quite intractable. Here, for the first time, we directly characterized the water diffusion in single suspended phase-separated aerosols via a self-constructed laser tweezer Raman spectroscopy (LTRS) system. The H₂O–D₂O isotope exchange was harnessed to trace the water diffusion in single laser-levitated homogenous/heterogeneous microdroplets. The time-resolved cavity-enhanced Raman spectra of the microdroplets were used to detect the diffusion process in real time. Two archetypes of phase-separated aerosols, i.e., partially engulfed and core–shell, were studied. Moreover, we quantified the dynamic water diffusion process by experimentally measuring the diffusion coefficients. The results showed that compared with the homogenous aerosols, water diffusion limitations existed in the phase-separated aerosols. The incomplete diffusion may stem from the formation of certain hydrated molecule clusters. This work provides possible implications for the evolutions, especially the gas–particle partition, of the actual phase-separated atmospheric aerosols.

1 Introduction

Gas–particle partitioning is one of the most significant atmospheric processes of aerosols and plays a crucial role in impacting air quality and the atmospheric environment. As water is often the most mobile component in troposphere aerosols, a clear picture of water diffusion within aerosols is essential. Under various meteorological conditions, the size and refractive index of aerosols change via hydration and dehydration, which then influence the optical properties and ice-nucleating ability of aerosols and the atmospheric energy distribution (Hallquist et al., 2009; Mellouki et al., 2015; Titos et al., 2016). Moreover, water diffusion dictates the moisture content in aerosols and then impacts their component concentrations and phase states. Some previous works have shown that a substantial fraction of secondary organic aerosols (SOAs) have glassy or gel states which present slow heterogeneous reaction rates and nonequilibrium gas–particle partition (Bones et al., 2012; Fowler et al., 2020; Shiraiwa and Pöschl, 2021). It then may lead to significant kinetic constraints on aerosol processing, heterogeneous chemistry, and component lifetimes (Renbaum-Wolff et al., 2013a; Shiraiwa et al., 2011; Vaden et al., 2011).

Numerous techniques have been developed to study the hygroscopicity of aerosols, including electrodynamic balance, a humidified tandem differential mobility analyzer, micro-Fourier transform infrared (FTIR) spectroscopy, atomic force microscopy, X-ray elemental microanalysis, and attenuated total reflection FTIR spectroscopy (Kreidenweis and Asa-Awuku, 2014; Tang et al., 2019; Kuang et al., 2020). In these techniques, four main methods are used to detect the water diffusion process. (i) The differential step isothermal method developed by (Aristov et al., 2006; Cai et al., 2015; Lv et al., 2020; Tong et al., 2022a, b) circumvents the non-linear boundary value problem in analyzing the water diffusion process and can readily retrieve the water diffusion coefficient by fitting the response of a single droplet to a changing relative humidity (RH) during sorption/desorption experiments. However, it can only be used to simulate the hygroscopic process of high-viscosity droplets where water diffusion is quite slow and cannot apply to constant-RH conditions. (ii) The Stokes–Einstein (S–E) equation relates the water diffusion coefficient to the particle viscosity. Many experimental and theoretic evaluation methods have been developed to measure the viscosity of aerosol particles both in the laboratory and in the field (Sastri and Rao, 1992; Cao et al., 1993; Rothfuss and Petters, 2017; Booth et al., 2014; Maclean et al., 2021; Smith et al., 2021; Fitzgerald et al., 2016; Renbaum-Wolff et al., 2013b; Bishop et al., 2004). However, application of the S–E equation in tandem with viscosity measurements may also miscalculate the diffusion coefficient because the S–E equation has been shown to break drown at high viscosities (Power et al., 2013; Molinero and Goddard, 2005). (iii) Another method leverages the response of aerosols to the oscillating RH to retrieve the diffusion coefficient. The exploited RH is regulated to oscillate in pulse form (Leng et al., 2015; Shi et al., 2017) or sinusoidal form (Preston et al., 2017) . For a sinusoidal RH oscillation, the amplitude and frequency of the aerosol size fluctuation are dictated by the RH frequency and the diffusion coefficient of water molecules. Nonetheless, this method demands a highly sensitive and precise RH control system, which increases the complexity of the experiments. (iv) The isotopic tracer method can directly unveil the water diffusion process of aerosol droplets, where the deuterium oxide (D₂O) molecules are leveraged to trace the diffusion of water within hydrogen oxide (H₂O) microdroplets (Price et al., 2014; Davies and Wilson, 2016; Moridnejad and Preston, 2016; Nadler et al., 2019). One prominent advantage of this method is that it is able to study the water diffusion process under constant-RH conditions, where the chief driving force of diffusion is the concentration gradient rather than RH changes, while the aforementioned methods can only study the hygroscopic response of aerosols to RH changes.

Previous works have mainly focused on the hydration/dehydration of homogenous aerosols. However, a plethora of studies have shown that phase separation is prevalent in ambient aerosols (You et al., 2014; Freedman, 2017, 2020; Pöhlker et al., 2012; You et al., 2012; Lee et al., 2020). Modeling works show that ignoring phase separation by forcing a single non-ideal phase can lead to vastly incorrect gas–particle partitioning predictions (Pye et al., 2017; Zuend and Seinfeld, 2012). Indeed, it is now widely recognized that the existence of heterogeneous states (e.g., phase-separated and amorphous states) could have significant consequences for the composition of the condensed aerosol phase. For example, the isoprene-derived SOAs are typical phase-separated aerosols which are formed by heterogeneous reactive uptake of epoxydiols onto sulfate aerosol particles. Some works reported that the growth of SOA coatings may impede the reactive uptake of epoxydiols, rendering a self-limiting effect in isoprene-derived SOA formation (Zhang et al., 2018, 2019; Riva et al., 2019). A similar diffusion limitation was also observed in the uptake of α-pinene oxide onto acidic aerosols (Drozd et al., 2013) and in the ozonolysis of polycyclic aromatic hydrocarbons within SOAs (Zhou et al., 2019). For water diffusion, the reported results were inconsistent. Davies et al. (2013) found that organic coatings (long-chain alcohols) may reduce the evaporation of the aerosol liquid water and enhance the condensation of water on the droplets. Other works found that the water condensation was hampered by organic shells and that the hygroscopic growth of phase-separated aerosols was dependent on the thickness of the shells (Ruehl and Wilson, 2014; Li et al., 2021; Mikhailov et al., 2021). However, some other works reported that phase separation had no profound effect on water diffusion under normal ambient conditions (Chan et al., 2006; Zawadowicz et al., 2015; Lienhard et al., 2015).

Notwithstanding, nearly all previous works used the substrate-deposited samples to study mass transfer in phase-separated aerosols. Contrastingly, contactless single particle techniques are appealing because the impacts of surface perturbations on component concentrations and aerosol morphology can be excluded (Zhou et al., 2014). In addition, single particle measurements are preferred over ensemble-averaged experiments because composition and local chemical environments vary from particle to particle. In this work, we utilized isotope tracing to characterize the water diffusion process in single suspended phase-separated aerosols at constant RH and room temperature via a self-constructed laser tweezer Raman spectroscopy (LTRS) system. The time-resolved cavity-enhanced Raman spectra of the microdroplets were recorded to both detect the phase state and reveal the diffusion of water. Three types of aerosols are studied herein, including homogenous aerosols (D₂O + citric acid (CA)), partially engulfed aerosols (H₂O + ammonium sulfate (AS) + oleic acid (OA)), and core–shell aerosols (H₂O + AS + diethyl-L-tartrate (DLT) and H₂O + AS + 1,2,6-hexanetriol (HEX)). Moreover, the influence of acid on water diffusion in aerosols are also discussed.

2 Experiments and methods

2.1 Laser tweezer Raman spectroscopy system

A schematic of the LTRS system is shown in Fig. 1. A laser beam with a wavelength of 532 nm (Excelsior-532-200, Spectra-Physics) was used as both a Raman-trapping and a Raman-exciting light. The backscattering Raman light was conducted into a spectrograph (SpectaPro 2300i, Acton) equipped with a liquid-nitrogen-cooled CCD (Spec-10, Princeton Instruments) working at a temperature of −120 °C. The spectrograph grating used herein was 1200 grooves mm⁻¹, and the spectrometer resolution was ∼4 cm⁻¹.

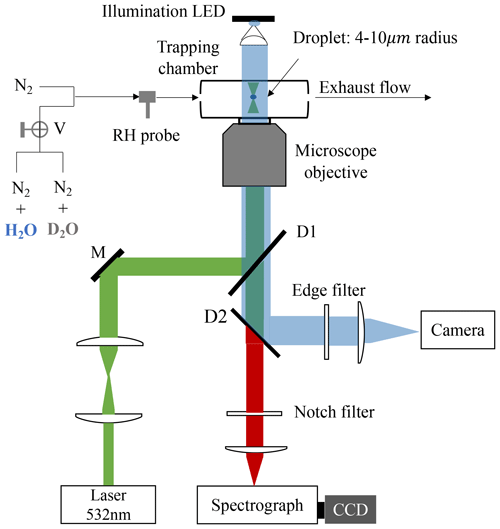
Figure 1 Schematic of the laser tweezer Raman spectroscopy system. A 532 nm laser beam was used to trap the aerosol droplet and excite its Raman signal. The droplet was imaged using a 470 nm illumination LED and a high-frame-rate camera. The Raman spectra of the trapped droplets were recorded using a spectrograph and a CCD. The RH in the aerosol trapping chamber was regulated by a flow of mixing N₂ $/$ N₂ + H₂O or N₂ $/$ N₂ + D₂O. V is three-way valves. M is a mirror. D1 and D2 are dichroic mirrors.

Bulk solutions with desired chemical compositions were used to generate the aerosol droplets through a medical nebulizer (Mint PN100). In a tailored aerosol trapping chamber (Fig. S1), individual droplets (4–10 µm) from an incoming droplet train were trapped and levitated by the laser tweezers. More details of the LTRS system can be found in our previous works (Tong et al., 2022a, b, c). For D₂O with solute aerosols, a D₂O bubbler was first used to provide moisture in the trapping chamber; after the droplet equilibrated with the surrounding water vapor, the flow path was turned into a H₂O bubbler by three-way valves to observe the substitution of H₂O for D₂O within the droplet. For H₂O with solute aerosols, the moisture was first provided by the H₂O bubbler and then by the D₂O bubbler, and the substitution process of D₂O for H₂O was studied. The volume of the aerosol chamber was <24.7 cm³ (Fig. S1). The gas-washing bottle used as a bubbler herein had a volume of 100 mL and contained 30 mL of D₂O. The total flux of dry and wet N₂ used herein was 100 sccm. Thus, at an RH of 60 %, the maximum time required for the chamber vapor to switch between H₂O and D₂O was 1.58 min, which can be identified as the response time of the chamber (formally τ_cell).

2.2 Detection of phase separation

The phase separation in substrate-deposited aerosols can be directly observed through bright-field imaging, transmission electron microscopy, or transmission X-ray microscopy (Pöhlker et al., 2012; You et al., 2012; Lee et al., 2020; Ma et al., 2021). However, for levitated droplets, the defocusing of the trapped droplets blurs the direct imaging. Instead, previous studies have shown that the time-resolved Raman spectra of the trapped droplets can be used to efficiently detect phase separation (Tong et al., 2022c; Gorkowski et al., 2016, 2018, 2020; Sullivan et al., 2020).

The trapped droplet works as an enhancing cavity and will overlap stimulated sharp peaks at wavelengths commensurate with whispering gallery modes (WGMs) on the spontaneous Raman spectra. The Raman spectra of aerosols with three different morphology archetypes are shown in Fig. S2. (i) The spectra containing high-quality WGMs indicate the isotropy within the particle and yield a homogenous morphology. (ii) The spectra containing weak but noticeable WGMs indicate the symmetry of the particle remains and yield a core–shell morphology. The shell thickness has appreciable influences on the aerosol spectrum. The weak WGMs may be caused by bad sphericity of the droplet, such as non-uniform shell thickness. A droplet with good spherical symmetry and deep WGM penetration induces well-resolved WGM peaks, while a droplet with a nonstatic core leads to non-uniform shell thickness and induces unstable WGMs. (iii) The spectra without any WGMs indicate the destruction of both isotropy and symmetry in the particle and yield a partly engulfed morphology. Alternatively, Stewart et al. (2015) put forward another two signatures to detect phase separation in aerosol. One is that if the droplet radius and refractive index calculated by the Mie scattering model present an abrupt change that is not realistic, the phase separation may have occurred. The other is that if we fit the Raman spectra with the Mie scattering model for a homogenous droplet and the fitting errors between the measured and simulated WGM peaks increase by orders of magnitude, the droplet can be determined as inhomogeneous. Herein, we deploy the signatures of WGMs and fitting errors to detect the phase separation. The homogenous Mie scattering fitting model used in this work was developed by Preston and Reid (2015).

3 Results

Here, we first detected the water diffusion in homogenous droplets to validate the performance of the isotope trace method. Then, the water diffusions in H₂O + AS + OA, H₂O + AS + DLT, and H₂O + AS + HEX droplets were studied. The diffusion differences in these aerosols with different morphologies are discussed. Moreover, we added sulfuric acid to H₂O + AS + DLT droplets and also discuss the influence of protons on water diffusion in aerosols.

3.1 Raman spectrum snapshots during water diffusion

Although H₂O and D₂O have nearly identical physical properties, O–D and O–H have different energy levels, which are therefore characterized with disparate Raman shifts (see the spectra of bulk H₂O and D₂O solutions in Fig. S3). Thus, the rise and fall of O–D $/$ O–H peaks in Raman spectra can be used to trace water diffusion.

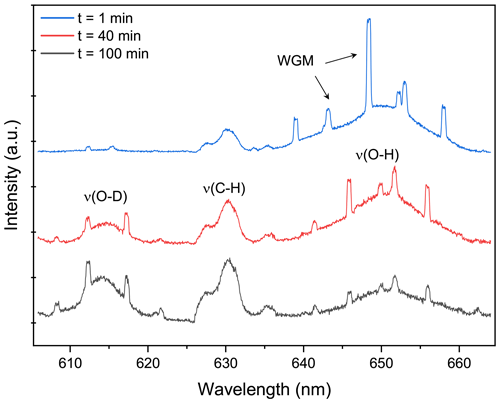
Figure 2 Raman spectrum snapshots of H₂O + AS + DLT aerosol at different times during the water diffusion process. The set RH in the trapping chamber remained at 60 %. The blue, red, and black curves indicate the Raman spectrum extracted from Fig. 5a at 1, 40, and 100 min, which correspond to the initial, middle, and end stages of the water diffusion process, respectively. The WGMs and Raman feature bands are pointed out. When t = 0, it signifies the onset of switching H₂O moisture vapor to D₂O vapor.

Figure 2 presents the representative stills of the Raman spectra of the H₂O + AS + DLT droplet at different water diffusion progressions. The Raman peak assignment of representative atmospheric species has already been summarized in previous review papers (Liang et al., 2022; Estefany et al., 2023). The band range of 640–660 nm corresponded to the bending and stretching modes of O–H of water, the band in the range of 605–625 nm corresponded to the modes of O–D, and the range of 627–635 nm corresponded to the bending mode of C–H in organics (DLT here). It can be seen that at the early stage (t = 1 min) of water diffusion, the ν(O–H) was vastly predominant and the ν(O–D) was quite trivial. As water diffusion progresses (t = 40 min), the intensity of the ν(O–D) mode rose, while the intensity of the ν(O–H) mode fell. It indicated that with the surrounding moisture vapor being switched from H₂O to D₂O, the H₂O molecules within the droplet were being replaced by D₂O molecules, albeit under a constant-RH condition. For t = 100 min, ν(O–D) became predominant compared with ν(O–H), indicating that the droplet had changed from a H₂O droplet to a D₂O-dominating droplet. Compared with Fig. S3, it can be seen that both ν(O–H) and ν(O–D) modes in suspended aerosols were weaker than those in corresponding bulk solutions, which means the total water content in aerosols was far lower than that in their mother solutions. It underscores the advantage of this contactless single technique that without the surface perturbations, the component concentration in the aerosol can exceed its solubility limit.

Under a constant-RH condition, the total amount of water (D₂O plus H₂O) in the aerosol can be assumed to remain constant. Thus, the time-resolved fractional concentration of D₂O (denoted by ϕ_OD) can be calculated from the ν(O–H) and ν(O–D) modes at each spectral time:

$$\begin{array}{}\text{(1)}& {\mathit{\varphi }}_{\mathrm{OD}}={\displaystyle \frac{{\mathrm{A}}_{\mathrm{OD}}}{{\mathrm{A}}_{\mathrm{OD}}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{\mathrm{A}}_{\mathrm{OH}}}},\end{array}$$

where A_OD and A_OH are the integrated intensities of the ν(O–D) and ν(O–H) modes, respectively. The factor of $\mathrm{1}/\sqrt{\mathrm{2}}$ before A_OH is to compensate for the difference in reduced mass between hydrogen and deuterium (Price et al., 2014; Nadler et al., 2019). Therefore, temporal variations in ϕ_OD retrieved from the aerosol Raman spectra can be used to quantify the water diffusion process. A caveat is that Fig. S4 shows the calculated ϕ_OD after effacing WGMs in the spectra, indicating that the contribution of WGMs to the peak areas is inconsequential. The O–H and O–D bands were quite broad, while the WGM peaks were somewhat narrow (Fig. 2). The fractional concentration of D₂O was retrieved from the Raman band area rather than the peak intensity; thus the interference of WGMs with ϕ_OD was trivial. The presented ϕ_OD was hereafter calculated by ignoring the WGM influences.

3.2 Water diffusion in homogenous aerosols

The water diffusion of a single D₂O + CA aerosol exposed to H₂O moisture vapor is shown in Fig. 3. The droplet was first trapped and equilibrated in D₂O vapor. At t = 0, the manifold gas valves were rotated to switch from D₂O to H₂O. In Fig. 3a, it can be seen that, over time, the intensity of ν(O–D) deteriorated rapidly and that of ν(O–H) increased. Meanwhile, the intensity of ν(C–H) remained stable, indicating that the component concentration in the aerosol was roughly constant throughout the experiment. The existing WGMs in each spectrum mean that the droplet was spherically symmetric.

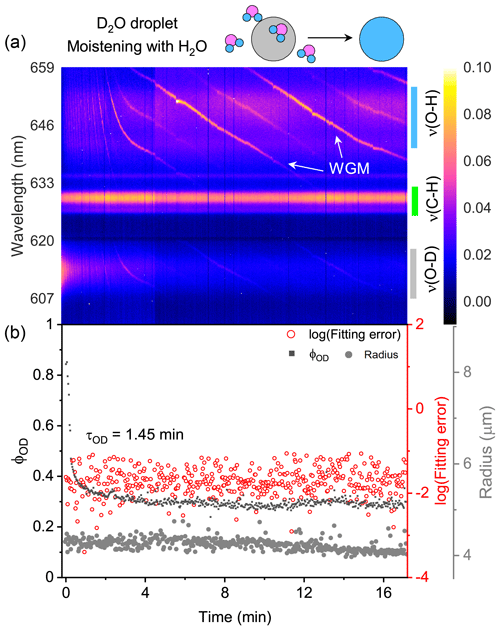
Figure 3 Water diffusion in a single homogenous D₂O + CA aerosol at RH = 60 %. (a) The time-resolved cavity-enhanced Raman spectra of the droplet. The abscissa is the time, and the ordinate indicates the wavelength. The spectral intensity at each wavelength and time is illustrated with color. The WGMs are pointed out with white arrows. The top diagram depicts the water diffusion process, where light gray represents the D₂O phase, and blue represents the H₂O phase. The modes of ν(O–H), ν(C–H), and ν(O–D) are pointed out with different color bars on the right. (b) Black, the temporal variation in the fractional concentration of D₂O within the droplet; red, the fitting errors of the WGMs based on the homogenous Mie scattering model; gray, the fitted aerosol radius. τ_OD is the e-folding time of the ϕ_OD curve. When t = 0, it signifies the onset of switching from D₂O moisture vapor to H₂O vapor. The experiment was conducted at room temperature.

Of note, the WGMs shown in Fig. 3a (0–2 min) changed rapidly. It may have been induced by the change in the true RH experienced by the droplet. While the moisture was switched from D₂O to H₂O, the H₂O needed ∼1.6 min (τ_cell) to fill the chamber. However, during this period, dry nitrogen entered the chamber sustainedly, while H₂O molecules delayed in the bubbler bottle and gas tubes. The true RH experienced by the droplet may hence decrease, inducing the WGM shift. Furthermore, some spontaneous surface fluctuations, e.g., thermally induced capillary waves, existed in the optically trapped droplet (Endo et al., 2018; Pigot and Hibara, 2012; Chung et al., 2017). Surface fluctuations disturbed the standing wave at the interface between droplet and air, which may also contribute to the unstable spectral WGMs.

The temporal variation in ϕ_OD in Fig. 3b shows the substitution of H₂O for D₂O. The calculated e-folding time of the ϕ_OD curve (formally τ_OD) was 1.45 min, indicating that the homogenous aerosol can promptly respond to the variation in the surrounding atmosphere. However, τ_OD<τ_cell implies that H₂O had started to diffuse into the droplet before the gas exchange from D₂O to H₂O was completed. Hence, water diffusion in a homogenous CA droplet may be even faster than Fig. 3 shows. Figure 3b shows that the fitting errors of the measured WGMs calculated by the homogenous Mie scattering model were of the order of 10⁻², which is quite small (compared with Fig. 7). It means that the droplet was well mixed and isotropic. CA is a water-soluble organic compound; thus the suspended D₂O + CA aerosol was homogenous and had a spherical shape. It was validated by both the WGMs in the spectra and the fitting errors. The water diffusion of the CA droplet at lower RH (20 %) is shown in Fig. S6. The retrieved τ_OD was 13.67 min, which was longer than that at RH = 60 %, indicating that water diffusion was retarded under very-low-RH conditions. This result agreed well with previous works (Table S1), validating the performance of our system.

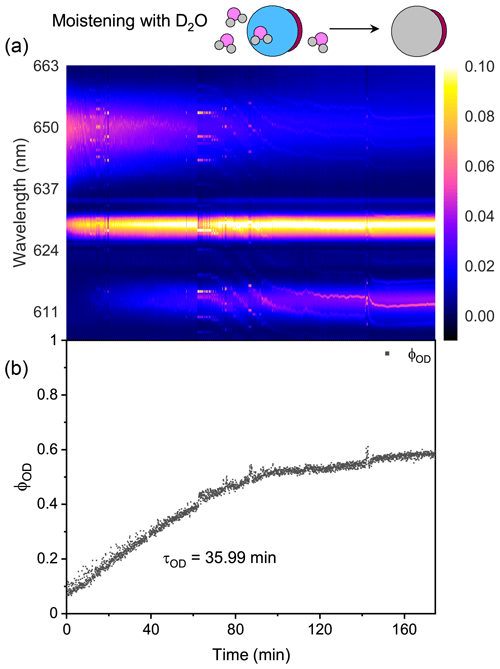
Figure 4 Water diffusion in a single phase-separated H₂O + AS + OA aerosol at RH = 60 %. (a) The time-resolved Raman spectra of the droplet. The top diagram depicts the water diffusion process in the partly engulfed aerosol, where light gray represents the D₂O phase, blue represents the H₂O phase, and dark red represents the hydrophobic organic phase. (b) The temporal variation in the fractional concentration of D₂O within the droplet. When t = 0, it signifies the onset of the switch from H₂O moisture vapor to D₂O vapor. The experiment was conducted at room temperature.

3.3 Water diffusion in partly engulfed aerosols

The oleic acid is a preferential proxy of water-insoluble organics in ambient aerosols. Herein, the H₂O + AS + OA droplet was generated by nebulizing a mixed solution containing AS, OA, and water. The volume ratio of the OA + AS mother solution was $\mathrm{4}/\mathrm{1}$ (aqueous AS $/$ OA). The mixture was fully shaken to form an aqueous OA emulsion before nebulization. Thus, a number of OA inclusions would be contained in the nascent droplet. The OA content in the droplet herein was random. If the droplet spectra could not support a partly engulfed morphology, the droplet was released until one spectra-confirmed partly engulfed droplet was captured. The droplet was trapped and equilibrated in H₂O vapor. Then the vapor was switched from H₂O to D₂O.

Figure 4 shows the water diffusion in a single H₂O + AS + OA aerosol. Figure 4a shows no evident WGMs in the aerosol spectrum, indicating the destruction of both isotropy and symmetry in the particle. Thus, the droplet should have a partly engulfed morphology after reaching a thermodynamic equilibrium with the surrounding moisture, where a hydrophobic cap of OA encases an aqueous phase. Ishizaka et al. (2021) reported that the hydrophobic phase was not always at the bottom of the droplet; thus the herein observed spectral variation at t = ∼60 min may stem from the drift of the hydrophobic cap. The volume ratio of the aqueous phase and hydrophobic phase in the trapped droplet cannot be preset because of the stochastic mixing of OA emulsions and water during nebulizing. If an approximately spherical cavity occurs for the aqueous volume, the WGM fingerprint of the droplet may be of low quality and complexity. Moreover, the band of C–H here was stronger than that in Fig. 3a, which may result from the fact that the OA molecule has more C–H bonds than CA.

The ϕ_OD shown in Fig. 4b changed more slowly than that in Fig. 3b. The calculated τ_OD of the H₂O + AS + OA aerosol was ∼35.99 min, which was 25 times longer than that of D₂O + CA. It means that an inhibition of gas–particle partitioning occurred in such a phase-separated droplet. The OA phase in the droplet had a considerably strong hydrophobicity, which may prevent the moisture from diffusing through the organic cap. The effective interface between the aqueous phase and the air reduced because of the phase separation, leading to a slower water diffusion compared with the homogenous aerosol.

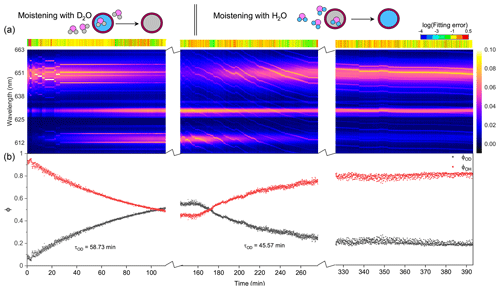
Figure 5 Water diffusion in a single phase-separated H₂O + AS + DLT aerosol at RH = 60 %. (a) The time-resolved cavity-enhanced Raman spectra of the droplet. The top color bars indicate the log (fitting errors) of the WGMs based on the homogenous Mie scattering model. The running of the spectrograph needed a break to avoid overloading the shutter, which caused the hiatuses in the spectra. (b) Black, the temporal variation in the fractional concentration of D₂O within the droplet; red, the temporal variation in the fractional concentration of H₂O within the droplet; ϕ_OH = 1−ϕ_OD. The droplet was first trapped and equilibrated in H₂O vapor. When t = 0, it signifies the onset of the switch from H₂O moisture vapor to D₂O vapor. At t = 160 min, the moisture vapor was switched back from D₂O to H₂O. The experiment was conducted at room temperature.

3.4 Water diffusion in core–shell aerosols

The core–shell morphology is another prevailing phase-separated morphology of ambient aerosols. Here, we generated aerosol droplets from mother solutions containing H₂O + AS + DLT and H₂O + AS + HEX and induced phase separation in them by presetting the surrounding RH below their separation relative humidity (SRH; the RH level at which phase separation occurs). The droplets were trapped and equilibrated in H₂O vapor before switching the moisture vapor from H₂O to D₂O.

Figure 5 presents the diffusion of D₂O and H₂O in a single H₂O + AS + DLT droplet during a 7 h observation at RH = 60 %. As shown in Fig. 5a, the log (fitting errors) throughout the observation was roughly higher than −1, which was 1 order higher than the homogenous aerosol errors, indicating that the droplet was not homogenous. Furthermore, the WGMs persisted in the whole observation; thus the droplet should be core–shell.

To provide detailed insights into the phase-separated structure, we used a core–shell Mie model developed by Vennes and Preston (2019) to calculate the core and shell radii of the droplet (see more details in Sect. S7). In Fig. 6, it can be seen that for the spectra shown in Fig. 5a (t = 0–110 min), the calculated particle radius was around 5 µm, and the fluctuation was quite trivial. Meanwhile, the calculated radius ratio (i.e., the ratio of the core radius to the whole particle radius) was around 0.8, which yielded a core radius of 4 µm and a shell thickness of 1 µm. The results validated that at RH = 60 %, the liquid–liquid phase separation occurred in the H₂O + AS + DLT aerosol, and the separated morphology was core–shell.

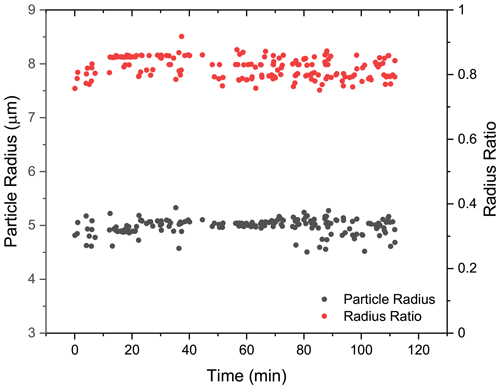
Figure 6 Radius of the phase-separated H₂O + AS + DLT aerosol at RH = 60 %. Black, the aerosol radius; red, the ratio of the core radius to the whole particle radius. The results were obtained by fitting the spectra in Fig. 5a (t = 0–110 min) with a core–shell model developed by Vennes and Preston (2019) .

For t = 0–160 min (denoted by Stage I), the droplet was moistened by D₂O vapor, and D₂O molecules started to diffuse into the droplet. The intensity of the O–H band in Fig. 5a decreased, while the intensity of the O–D band increased; this variation is crystal clear in Fig. 5b, where ϕ_OD grew and ϕ_OH fell over time. However, in this stage where D₂O diffused into the droplet, the ϕ_OD plateaued to a constant value of 0.55 after more than 150 min diffusion, indicating that the H₂O molecules in the initial droplet could not be replaced completely by the surrounding gas-phase D₂O molecules. The intensity of the O–H band could not diminish to zero in the exchange process. Similar results can also be seen in the partly engulfed aerosol and even in the homogenous aerosol, where the final values of ϕ_OD were 0.6 and 0.3, respectively. Previous works have reported such kinetic limitations of diffusion in ultra-viscous or amorphous-state aerosols: significant radial gradients in pH (Wei et al., 2018), solute concentrations (Zobrist et al., 2008), and reactant uptake (Virtanen et al., 2010; Davies and Wilson, 2015; Gaston and Thornton, 2016) solidly existed in ambient aerosols. A possible explanation is that certain molecule clusters composed of hydroxyls, electrolytes, and organics formed in the aerosols because of supersaturation, which protected a handful of H₂O molecules in the aerosols from being replaced by D₂O molecules. Moreover, as water diffusion progressed, the diffusion-driving forces attenuated because of the reducing deviation of vapor pressures between the gas and particle phase, which might both decrease the success of surface accommodation of gas molecules and make the solvation through the particle bulk more difficult, rendering an incomplete molecule substitution.

For t>160 min (denoted by Stage II), the moisture vapor was switched back from D₂O to H₂O. In Fig. 5a, it can be seen that the Raman band of O–H rebounded and that of O–D declined over time. After molecules diffused for 4 h, ϕ_OD did not diminish to 0, and ϕ_OH did not return to 1, yielding a similar incomplete substitution. Noteworthily, in Fig. 5b, throughout Stages I and II, the maximum of ϕ_OH was 0.8, which was higher than that of ϕ_OD. This indicates that, at the later stage of diffusion, D₂O was harder to partition into the particle phase compared with H₂O. Considering the virtually identical chemistry of these two molecules, the difference in molecular mass may give rise to the different final diffusion extent. From another perspective, during the process of aerosol trapping, the generated aerosol train may condense some droplets on the walls of the chamber and tubes. The H₂O molecules within these droplets may then interfere with the subsequent water diffusion.

As shown in Fig. 5b, the τ_OD of Stages I and II was 58.7 and 45.6 min, respectively, which were both higher than that of partly engulfed aerosol and homogenous aerosol. The average τ_OD was 52.2 min, which was 1.5 times that of the partly engulfed aerosol and 36 times that of the homogenous aerosol, implying a more profound diffusion inhibition in core–shell aerosols. With the organic shell totally encasing the aqueous core, the moisture molecules had to penetrate through the shell during diffusion, which vastly retarded the molecule exchange.

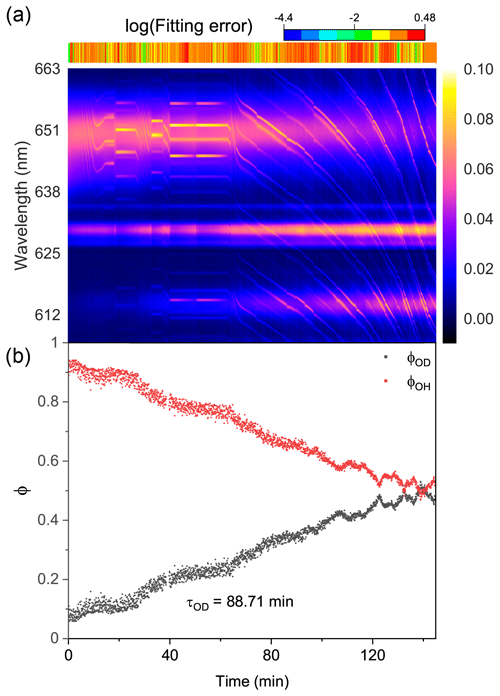
Figure 7 Water diffusion in a single phase-separated H₂O + AS + HEX aerosol at RH = 60 %. (a) The time-resolved cavity-enhanced Raman spectra of the droplet. The top color bars indicate the log (fitting errors) of the WGMs based on the homogenous Mie scattering model. (b) The temporal variations in the fractional concentration of water molecules within the droplet. The droplet was first trapped and equilibrated in H₂O vapor. When t = 0, it signifies the onset of the switch from H₂O moisture vapor to D₂O vapor. The experiment was conducted at room temperature.

We then observed the water diffusion in a single H₂O + AS + HEX aerosol. Figure 7 shows the recorded Raman spectra and variations in fractional concentrations. At t = 0, D₂O vapor started to moisten the H₂O droplet. The results of the log (fitting errors) and spectral WGMs indicated that the droplet was phase-separated with a core–shell morphology throughout the observation. With the droplet being exposed to the D₂O vapor, the Raman O–H band diminished and the O–D band rose. However, as shown in Fig. 7b, the calculated τ_OD was 88.7 min, implying a more severe diffusion inhibition compared with the H₂O + AS + DLT aerosol. Ma et al. (2021) reported that the structure of the phase-separated AS + HEX droplet was considerably complex at RH = 60 %, where a HEX-rich shell, an AS-rich core, and more concentrated AS inclusions in the core coexisted. The force between AS and water molecules, particularly in the concentrated AS inclusions, was much stronger than that between HEX and water. Bound water may form in this circumstance. The substitution of D₂O for H₂O needed to overcome the bound water force, which might be quite difficult because the solute concentration in the AS inclusions was far beyond its solubility limit. This may contribute to the slow water diffusion in the AS + HEX droplet. Moreover, Richards et al. (2020) reported that supramolecular ion–organic interactions may exist when aerosols contain organics (specifically those containing vicinal hydroxyl groups) and inorganic divalent ions, which produces internal cross-linking molecular networks. Such ion–organic networks might have formed in the shell of the H₂O + AS + HEX aerosol and thus blocked the passage of water molecules.

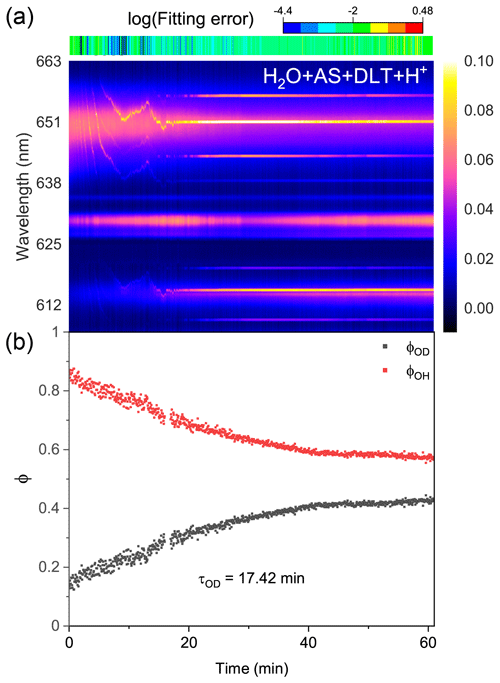
Figure 8 Water diffusion in single acidified H₂O + AS + DLT aerosol at RH = 60 %. (a) The time-resolved cavity-enhanced Raman spectra of the droplet. The top color bars indicate the log (fitting errors) of the WGMs based on the homogenous Mie scattering model. (b) The temporal variations in the fractional concentration of water molecules within the droplet. The droplet was first trapped and equilibrated in H₂O vapor. When t = 0, it signifies the onset of the switch from H₂O moisture vapor to D₂O vapor. The experiment was conducted at room temperature.

Protons are considered to have appreciable impacts on the phase separation in ambient aerosols (Tong et al., 2022c; Dallemagne et al., 2016; Losey et al., 2016). Here, we added sulfuric acid to H₂O + AS + DLT droplets and observed the water diffusion process in the resultant acidified aerosols. The pH of the mother solution to generate aerosols was preset to 1.17. Figure 8 shows the recorded Raman spectra and variations in the fractional concentrations of a single acidified H₂O + AS + DLT droplet. The results of the log (fitting errors) and spectral WGMs indicated that the droplet was homogenous. After being moistened by D₂O vapor at t = 0, the Raman O–H band faded and the O–D band increased. The τ_OD shown in Fig. 8b was 17.4 min, which was less than the value of the two types of phase-separated aerosols. It shows that the surplus protons improved water diffusion in H₂O + AS + DLT aerosols, which indicated that the added sulfuric acid may impede the occurrence of phase separation. The aerosol pH was reported to have significant impacts on liquid–liquid phase separation. However, the impacts were different and related to the organic component. Previous works have found that the SRH of some organic acids (e.g., 3-methylglutaric acid) increased as the aerosol pH decreased (Losey et al., 2016), while the SRH of other organics (e.g., polyols) decreased as the pH decreased (Losey et al., 2018). From a fundamental physical chemistry perspective, the fluctuations in the local solute concentration will lead to thermodynamic instability in the droplet structure and subsequently induce phase separation. Herein, the added sulfuric acid increased droplet viscosity and reduced its liquidity, which may limit concentration fluctuations and promote homogeneity.

4 Discussion

The isotope exchange during the water diffusion process in single aerosols can be well elucidated by the solution to Fick’s second law for a sphere (Price et al., 2014; Moridnejad and Preston, 2016; Nadler et al., 2019) :

$$\begin{array}{}\text{(2)}& {\mathit{\varphi }}_{\mathrm{OD}}=\mathrm{1}-\left({\displaystyle \frac{\mathrm{6}}{{\mathit{\pi }}^{\mathrm{2}}}}\right)\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}}{n^{\mathrm{2}}}}\exp \left(-{\displaystyle \frac{n^{\mathrm{2}}{\mathit{\pi }}^{\mathrm{2}}{D}_{\mathrm{w}}t}{a^{\mathrm{2}}}}\right),\end{array}$$

where a is the particle radius and D_w is the diffusion coefficient of water. A prerequisite of applying the Fickian diffusion model is that the particle achieves a homogenous mixture after sufficient equilibration time, which is however not available for the aerosols studied here. Thus, a modified Fickian diffusion model (Eq. 3) is used to analyze the observed incomplete isotope exchange, where a correction factor χ is introduced to reveal the diffusion limitation and indicate the diffusing extent,

$$\begin{array}{}\text{(3)}& {\mathit{\varphi }}_{\mathrm{OD}}=\mathit{\chi }\left[\mathrm{1}-\left({\displaystyle \frac{\mathrm{6}}{{\mathit{\pi }}^{\mathrm{2}}}}\right)\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}}{n^{\mathrm{2}}}}\exp \left(-{\displaystyle \frac{n^{\mathrm{2}}{\mathit{\pi }}^{\mathrm{2}}{D}_{\mathrm{w}}t}{a^{\mathrm{2}}}}\right)\right].\end{array}$$

The radii of the aerosols can be determined by bright-field imaging and the core–shell Mie model. Then, D_w can be expediently derived by using a three-term expansion of the modified Fickian diffusion model to fit the temporal variations of ϕ_OD retrieved from the Raman spectra. An application of the diffusion model to the isotope exchange data is shown in Fig. S5. The water diffusion coefficients of the aforementioned aerosols are summarized in Table 1. The comparison between the measured water diffusion coefficients in this work and those of literature works can be seen in Sect. S6. The measured D_w of phase-separated droplets was considerably lower than the values of homogenous droplets studied in literature works, indicating the occurrence of the water diffusion limitations.

Table 1 Water diffusion coefficients of aerosols with various morphologies at RH = 60 %.

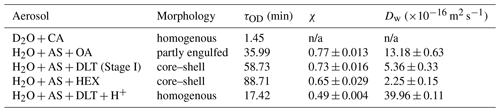
n/a: not applicable.

The isotope exchange method has some experimental limitations. For example, the spectral acquisition costs time; after switching H₂O to D₂O, it also takes time to fully replace the composition of the atmosphere in the trapping chamber. Due to these inevitable time limitations, the isotope exchange method does not adapt to quantifying the rapid diffusion circumstance, leading to an upper limit of diffusion coefficient measuring of $\sim {\mathrm{10}}^{-\mathrm{13}}$ m² s⁻¹ (Davies and Wilson, 2016; Nadler et al., 2019). The water diffusion in the D₂O + CA droplet was quite fast; hence the onset of water diffusion could not be exactly determined. As shown in Sect. 3.2, the observed τ_OD did not closely mirror the rate of water diffusion. Thus, the D_w of the D₂O + CA aerosol was not calculated in Table 1. The H₂O + AS + OA aerosol was treated as an approximate sphere. The measured D_w decreased in the order of homogenous, partly engulfed, and core–shell aerosols, which was in line with the diffusion rate presented in Sect. 3.

The parameter of the first exponential term in Eq. (2) (i.e., ${\mathit{\pi }}^{\mathrm{2}}{D}_{\mathrm{w}}/a^{\mathrm{2}}$) indicates the rate of diffusion for a homogenous aerosol, the reciprocal of which means the equilibrium mixing time (denoted by τ_mixing) of volatile molecules within the homogenous aerosol. According to the modified Fickian diffusion model, the fitted τ_mixing of H₂O + AS + DLT was 182 min (see Fig. S5). However, in Fig. 5b, it can be seen that when t = 130 min, the ϕ_OD leveled off, which means the diffusion of D₂O had reached a balance. The observed equilibrium diffusion time was less than the calculated τ_mixing. It implies that the water molecules within these aerosols did not diffuse to an isotropically stable state; thus concentration gradients existed in the aerosols. It revalidated the deductions from the final value of ϕ_OD. If considering the correction factor χ, the χτ_mixing of H₂O + AS + DLT was 132 min, which agreed well with the experimental observation. It means the modified Fickian diffusion model works well to simulate the water diffusion presented here.

The χ of H₂O + AS + DLT was 0.7, which means that 70 % of the total H₂O molecules in the droplet were substituted by D₂O molecules. The χ of H₂O + AS + HEX was 0.65, indicating that its more complex phase-separated structure led to a lower diffusion extent of D₂O than H₂O + AS + DLT. Contrastingly, the χ of the H₂O + AS + OA aerosol was 0.77, which indicated that the partly uncovered gas–particle interface allowed for a higher diffusion extent of D₂O than the core–shell aerosols. Of note, the χ of the H₂O + AS + DLT + H⁺ aerosol was 0.5, which was lower than the partly engulfed and core–shell aerosols. A fair number of studies have reported the existence of hydrated proton clusters with diverse structures in acid solutions (Headrick et al., 2005; Biswas et al., 2017; Knight and Voth, 2012; Agmon et al., 2016). Therefore, the hydrated proton clusters in the acidified H₂O + AS + DLT aerosol may preclude the substitution of D₂O for H₂O and give rise to a low diffusion extent. Moreover, the existence of bound water may limit water molecule evaporation and reduce the equilibrium water vapor pressure at the surface of acidified homogenous droplets (solute effect). While the surrounding moisture was switched from H₂O to D₂O, H₂O molecules within the droplet began to evaporate into the gas to keep its vapor pressure equal to the equilibrium pressure. Lower equilibrium vapor pressure means a weaker driven force of diffusion; thus the water molecule substitution in the droplet with low pH was not as fast as in the neutral homogenous droplet. Such a diffusion limitation may provide a possible explanation for the long lifetime of certain ambient aerosols of which the unreacted core species were protected from potential surface-sensitive phenomena such as cloud condensation nucleation and ice nucleation activities (Zhang et al., 2019; Adachi and Buseck, 2008; Kanji et al., 2019; Yu et al., 2019).

5 Conclusions

In this work, we characterized the water diffusion process in single suspended phase-separated aerosols via a self-constructed laser tweezer Raman spectroscopy system. The recorded Raman spectra of the aerosols were used to detect their morphology and observe the exchange of D₂O $/$ H₂O molecules. The results of the core–shell aerosols show that water molecules can pass through the organic shell and diffuse into the particle bulk, and the diffusion rate depended on the type of the organic compound. The partly engulfed and homogenous aerosols had higher diffusion rates compared with core–shell aerosols. The results of the acidified H₂O + AS + DLT aerosol show that protons can improve water diffusion in the aerosol, indicating that acid inhibited phase separation. Moreover, incomplete diffusion was observed in all three types of aerosols with different morphologies. By measuring the water diffusion coefficients and diffusion extents with a modified Fickian diffusion model, we found that 65 %–75 % of the total H₂O molecules in the phase-separated aerosols were substituted by D₂O molecules, which implies that certain molecule clusters formed in the aerosols.

More work on the reactive uptake of gas molecules into phase-separated aerosols should be done in the future. Additionally, considering that the sizes of the droplets studied here were 4–10 µm, it is imperative to develop techniques for detecting water diffusion in smaller phase-separated droplets in the future.