Ice-nucleating particle concentration impacts cloud properties over Dronning Maud Land, East Antarctica, in COSMO-CLM²

Ice-nucleating particles (INPs) have an important function in the freezing of clouds but are rare in East Antarctica. At the Belgian Princess Elisabeth Antarctica station, immersion freezing INP concentrations between $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{6}}$ and $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹ have been observed with an activation temperature of −20 °C. These low concentrations offer a possible explanation for the occurrence of supercooled liquid water in clouds observed using the station's micro rain radar and ceilometer. We used the model of the Consortium for Small-scale Modeling (COSMO) in climate mode (CLM) coupled to the Community Land Model (CLM) (COSMO-CLM²) with an added aerosol-cycle module to test the cloud phase's sensitivity in response to varying prescribed INP concentrations. We tested two cases, one in austral summer and one in austral winter, and analysed the differences resulting from INP concentration changes for an area around the station and over the Southern Ocean within the selected domain. Our results show a strong influence of the INP concentration on the liquid water path in both regions, with higher concentrations reducing the amount of liquid water. Over the Southern Ocean, this effect is stronger during winter: during summer, a significant portion of water remains in liquid state regardless of INP concentration. Over the continent, this effect is stronger during summer: temperatures in winter frequently fall below −37 °C, allowing homogeneous freezing. The largest increase in the liquid water fraction of total cloud hydrometeor mass is simulated over the Southern Ocean in winter, from 9.8 % in the highest tested INP concentration to 50.3 % in the lowest. The radiative effects caused by the INP concentration changes are small, with less than 3 W m⁻² difference in the averages between different concentrations.

1 Introduction

Microphysical properties of mixed-phase clouds are heavily influenced by ice-nucleating particles (INPs; Kanji et al., 2017), which grow efficiently via depositional growth (Korolev, 2007; Morrison et al., 2012). In Antarctica, where INPs are very sparse compared to mid-latitude regions, the number of cloud droplets freezing at temperatures above about −37 °C, the temperature at which water freezes homogeneously (Murray et al., 2010), is therefore limited. This leads to the presence of liquid cloud droplets in a supercooled state alongside ice crystals. Over the Southern Ocean, liquid-containing clouds including these mixed-phase clouds (MPCs) make up the majority of clouds below a height of 4 to 7 km (Dietel et al., 2024). Over Antarctica, liquid-containing clouds were observed during 20 % of overcast periods (Gorodetskaya et al., 2015). MPCs can often be identified by their characteristic two-layer structure, with a liquid layer above an ice layer, which is generated by faster growth and larger sedimentation velocities of the relatively few ice crystals near the cloud top (Bromwich et al., 2012).

The cloud phase is known to have impacts on the radiative forcings exerted by the cloud (Van Tricht et al., 2016; Matus and L'Ecuyer, 2017; Hogan et al., 2003). In general, cloud radiative effects (CREs) can be summarised using Eq. (1), where ${\text{SW}}_{\text{all-sky}}^{\mathrm{net}}$ denotes the total net downward shortwave (SW) radiation at the surface (i.e. ${\text{SW}}_{\mathrm{surface}}^{\downarrow }-{\text{SW}}_{\mathrm{surface}}^{\uparrow }$ so that a higher ${\text{SW}}_{\text{all-sky}}^{\mathrm{net}}$ means more downwelling shortwave radiation reaching the surface without being reflected), and ${\text{SW}}_{\text{clear-sky}}^{\mathrm{net}}$ denotes the net SW downward radiation without clouds, with their longwave (LW) equivalents being ${\text{LW}}_{\text{all-sky}}^{\mathrm{net}}$ and ${\text{LW}}_{\text{clear-sky}}^{\mathrm{net}}$:

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}\text{CRE}& ={\text{CRE}}_{\text{SW}}+{\text{CRE}}_{\text{LW}}\\ & ={\text{SW}}_{\text{all-sky}}^{\mathrm{net}}-{\text{SW}}_{\text{clear-sky}}^{\mathrm{net}}+{\text{LW}}_{\text{all-sky}}^{\mathrm{net}}-{\text{LW}}_{\text{clear-sky}}^{\mathrm{net}}.\end{array}\end{array}$$

At equal total water content, clouds containing supercooled liquid water have a larger CRE as liquid droplets reflect more sunlight, decreasing ${\text{SW}}_{\text{all-sky}}^{\mathrm{net}}$, but they also are more opaque to longwave radiation, increasing ${\text{LW}}_{\text{all-sky}}^{\mathrm{net}}$ (Matus and L'Ecuyer, 2017). This implies that changes in cloud phase caused by a change in INP concentration can have a significant secondary effect on the change in radiative forcing and, therefore, the surface energy balance. This in turn can have other effects; for example, the cloud phase has a significant impact on the rate of surface melt (Gilbert et al., 2020).

In most weather and climate models, there is a positive bias in the net SW radiation (${\text{SW}}_{\text{all-sky}}^{\mathrm{net}}$) over the Southern Ocean (Kay et al., 2016) compared to observations derived from the Cloud–Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO, Winker et al., 2009) missions. This has been attributed to an underestimation of supercooled liquid water in clouds in those models. This problem also affects future scenarios, as with rising temperatures, the liquid water content of clouds is expected to rise more quickly than the ice content (Chyhareva and Krakovska, 2022). In models that resolve this bias, it is often at the expense of other modelling errors, such as an overall increase in total cloud water content (i.e. both liquid and ice) in the Met Office Unified Model (UM; Brown et al., 2012; Van Weverberg et al., 2023). The model of the Consortium for Small-scale Modeling (COSMO) in climate mode (CLM), coupled to the Community Land Model (CLM), COSMO-CLM², simulates radiation in Antarctica with a mean absolute error between 7 and 20 W m⁻² for different radiation components (SW^↓, SW^↑, LW^↓, and LW^↑) and no significant biases, except for a bias in LW^↓ during winter, which is on average 20 W m⁻² too low, once again linked to an underrepresentation of liquid water in clouds (Souverijns et al., 2019). The aforementioned SW bias over the Southern Ocean does not affect continental Antarctica very much, thanks to the ice sheet's high albedo. Overall, this is comparable to other models: the Community Earth System Model (CESM) has a 30 W m⁻² (warm) bias in CRE_SW and a −10 W m⁻² (cold) bias in CRE_LW over the Southern Ocean in version 1 (Kay et al., 2012). This has since been reduced in CESM2 with the Community Atmosphere Model (CAM) version 6 (Gettelman et al., 2020). In an ensemble mean of Coupled Model Intercomparison Project (CMIP) version 5 models, the SW bias over the Southern Ocean was found to be 20 W m⁻² (Hwang and Frierson, 2013). In West Antarctica, the ERA5 and Antarctic WRF Mesoscae Prediction System (AMPS) reanalyses were found to have a 14 and 21 W m⁻² LW bias respectively, with spikes of up to 50 W m⁻² when liquid or mixed-phase clouds were present (Silber et al., 2019). These biases are not exclusive to Antarctica either, as in the northern polar region, a wide range of reanalyses (ERA5, ERA-Interim, CFSv2, MERRA-2, JRA-55, and ASRv2; Graham et al., 2019) show a negative bias in LW balance of 3 to 19 W m⁻².

There have been attempts to reduce the radiation biases through correcting the liquid water content: supercooled liquid water clouds that were observed using the station's instruments at Dome C (75.10° S, 123.35° E) were modelled in two case studies using the regional climate model (RCM) Action de Recherche Petite Echelle Grande Echelle – Southern Hemisphere (ARPEGE-SH; Ricaud et al., 2020). Using a new liquid water partition function, Ricaud et al. (2020) managed to remove the LW bias in one of their two case studies under stable atmospheric conditions, whereas in their second case study, which featured a capping inversion and was generally warmer, liquid water amounts were still too low, and the radiation bias persisted. In the Icosahedral Nonhydrostatic (ICON) weather and climate model, a bias in SW radiation balance was found to be caused by an underestimation of the cloud layer's thickness, liquid water content, and hydrometeor number concentration (Kretzschmar et al., 2020). Changing the cloud condensation nuclei (CCN) activation scheme reduced the bias in ICON but did not fully resolve it. Another approach has been the implementation of macrophysical schemes for the Met Office UM (Van Weverberg et al., 2023), aimed at improving the representation of subgrid cloud structures, and while it was shown that these schemes have an influence, they cannot fully resolve the issue, with liquid water contents remaining underestimated. Very few studies exist in which the influence of INPs as a potential source of liquid water is tested in a model. One notable exception to this is a study by Vignon et al. (2021), where different INP parameterisations are used in the Weather Research and Forecasting (WRF) model for a short case study in austral summer, with results indicating a strong link between INP concentration and liquid cloud water content.

Even though most RCMs are optimised for mid-latitude performance, some adaptations aiming to model the climate in Antarctica, as well as in the Arctic, already exist. For COSMO-CLM², such adaptations have been done in a study by Souverijns et al. (2019), in which the atmospheric part of the model was modified by reducing the modelled turbulence and thermal circulation, and the surface part was modified by changing the snow properties. These changes lead to good agreement of the modelled temperature, wind, and surface mass balance with the observations, although, as previously noted, biases in LW radiation remain. This model is now also part of the polar Coordinated Regional Climate Downscaling Experiment (CORDEX; Giorgi et al., 2009) suite. A different modification was added to the model to investigate the impact of ship exhausts on clouds in the Arctic (Possner et al., 2017). This modification added an aerosol scheme, which resolves CCN and INP concentrations explicitly and uses a two-moment hydrometeor scheme (Seifert and Beheng, 2006). Another notable development is that of PARASO, which adds an ocean model, Nucleus for European Modelling of the Ocean (NEMO); a sea ice model, the Louvain-la-Neuve sea ice model (LIM); and a continental ice model, the fast Elementary Thermomechanical Ice Sheet (f.ETISh) model, to COSMO-CLM² (Pelletier et al., 2022).

It seems likely that the underestimation of liquid water in Antarctica at least partially originates from the optimisation of climate models for mid-latitude regions. As such, this also concerns their freezing schemes. These often implicitly assume that INPs are distributed homogeneously around the world, even though it is known that their concentration is much lower over Antarctica. As a result, models may underestimate the liquid water fraction in this region at temperatures below 0 °C. With most models not resolving INPs explicitly, there is also little knowledge as to what impact a change in their concentration would have.

In the study presented here, we do not aim to explain the current radiation biases in climate models, as that would also involve much tuning and error compensation in other parts of COSMO-CLM². We rather aim to improve the understanding of the role of INPs by testing the sensitivity of the cloud phase with respect to the INP concentration by prescribing different concentrations in an RCM capable of simulating INPs explicitly. Contrary to Vignon et al. (2021), who use different INP parameterisations, a module is available where INP and CCN concentrations are treated as prognostic variables. In this paper, we test if there is significant variations between INP concentrations that are relevant for Antarctica today, using unique INP measurements from the Belgian Princess Elisabeth Antarctica (PEA) station. Such a sensitivity to Antarctic-range INPs would indicate a need for a detailed simulation of INPs in climate and weather models. Furthermore, we test if there is a significant impact to be expected when using INP concentrations measured in mid-latitude regions, which is relevant for evaluating climate and weather models. These models are most frequently applied to mid-latitude regions, and therefore parameterisations for ice nucleation are generally optimised to match the effects of higher INP concentrations found there. It might also become relevant should INP concentrations in Antarctica change in the future: Twohy et al. (2021) suggest that a decrease in Antarctic sea ice and an increase in water temperatures in the Southern Ocean could result in an increase in INP concentrations in Antarctica.

2 Observations

The Belgian Princess Elisabeth Antarctica (PEA) station is a zero-emission research base, located in Dronning Maud Land, close to the Sør Rondane Mountains, at 70°57^′ S, 23°20^′ E and 1390 m above mean sea level. It is inhabited during the Antarctic summer between November and February and is operated via remote access during the other months. It is close to the Antarctic plateau (50 km) and the Ragnhild coast (200 km) and is located in a relatively mild microclimate. The site is dominated by an easterly wind year-round (>90 %), and air temperatures vary between −36 and −5 °C (Gorodetskaya et al., 2013; Pattyn et al., 2010). At PEA, an extensive weather and cloud observatory was installed in 2009 (Gorodetskaya et al., 2015). This observatory consists of an automated weather station (AWS), a micro rain radar (MRR), and a ceilometer. While the AWS and MRR enable the detection of snowfall rates and properties, like fall speed and temperature, the ceilometer detects cloud properties, such as cloud height, and also facilitates cloud phase estimation (Guyot et al., 2022). Radio soundings by weather balloons delivered vertical profiles of temperature, humidity, pressure, and wind. These soundings have been performed since 2014/15 during each austral summer up to now, except in 2016/17.

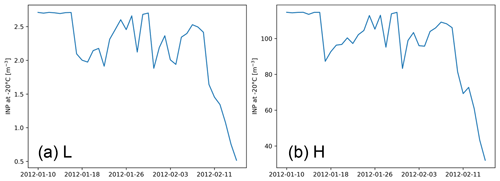
In addition to the weather and cloud observations, ground-based INP measurements were taken in the 2020/21 and 2021/22 austral summers. These INP measurements were taken using 47 mm polytetrafluorethylene filters with a pore size of 800 nm (Whatman Nuclepore no. 10417312), which were set up in a shelter around 500 m north of PEA station. The 47 mm filters were placed inside a hard plastic filter holder. This had a metal cap (inversed funnel type) with an inlet opening of 0.25 in. diameter. On it, a 15 cm piece of black conductive silicon tubing with a 0.25 in. outer diameter and 0.19 in. inner diameter was fitted. The filter holder was situated outside, located 50 cm above the shelter's roof. The end of the 15 cm conductive tubing pointed downward and was oriented perpendicular to the main wind direction (NE). The sampling losses within the 15 cm tube are negligible at the given flow rate, and particles larger than 1 µm are very rare in the PEA area (Herenz et al., 2019). The sample duration was around 10 d per filter, and each season, blank samples were taken. Subsequent measurements were done in the same way as in Sze et al. (2023), using two well-established offline techniques, the Leipzig Ice Nucleation Array (LINA) and the Ice Nucleation Droplet Array (INDA; Lacher et al., 2024). The INP profiles of the blank samples were subtracted from the measurement results, although the difference compared to the results derived from the samples directly was very small. Our observations at PEA are compared here with observations taken from the literature in order to identify suitable INP concentrations to use for the sensitivity experiments performed with COSMO-CLM².

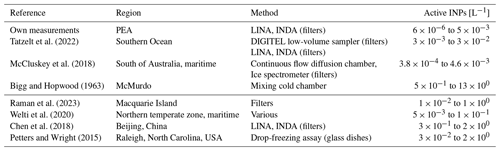
The observations at PEA indicate substantial temporal variability in the concentrations, with concentrations varying from $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{6}}$ to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ active INPs per litre at an activation temperature of −20 °C. To simplify comparisons, we compared all measured concentrations at a −20 °C reference temperature and converted measurements only available at other temperatures using the parameterisation of DeMott et al. (2010) (see also Eq. 2). Other recent INP measurements taken over the Southern Ocean are slightly higher: Tatzelt et al. (2022) and McCluskey et al. (2018) measured similar concentrations over the Southern Ocean to those over Antarctica at $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{3}}$ to $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹ and $\mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{4.6}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹ respectively but do not reach the extreme low values we observed at PEA. Older observations, such as the ones by Bigg and Hopwood (1963) and Saxena and Weintraub (1988), sometimes report much higher numbers with peaks of up to 13 L⁻¹ (Bigg and Hopwood, 1963). Given the large number of more recent observations with much lower results, the validity of this exceptionally high result may be questioned. It is especially remarkable when compared to recent measurements in other regions that are known to experience higher aerosol concentrations: Chen et al. (2018) measured INP concentrations of up to 2 L⁻¹ in Beijing; Petters and Wright (2015) reported a similar amount in North Carolina, with lower bounds of $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹ in Beijing and $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹ in North Carolina. Peak concentrations might be higher than the observations presented here, as filter measurements typically collect INPs over the course of several hours. Compared to the newer Antarctic measurements, both the observations by Bigg and Hopwood (1963) and the more recent observations elsewhere in the world deliver high results nonetheless. Even though slightly lower values are observed in mid-latitude oceans (e.g. Welti et al., 2020, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; Raman et al., 2023, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{2}}$ to 1×10⁰ L⁻¹) compared to those in Chen et al. (2018) and Petters and Wright (2015), it can be concluded that INP number concentrations in Antarctica are overall exceptionally low. This is in line with Raman et al. (2023), who found that high INP concentrations on Macquarie Island are correlated with organic matter and dust emission events occurring in nearby New Zealand and favourable conditions for phytoplankton growth, both of which seem unlikely to frequently happen in such close proximity to PEA that they would have a significant impact on INP concentrations. However, Twohy et al. (2021) suggest that at least phytoplankton activity might increase in future climate scenarios. Table 1 provides an overview of the INP measurements taken into account when selecting the prescribed concentrations.

Tatzelt et al. (2022)McCluskey et al. (2018)Bigg and Hopwood (1963)Raman et al. (2023)Welti et al. (2020)Chen et al. (2018)Petters and Wright (2015)

Table 1 Overview of different INP measurements taken into account for scenario selection. All measured concentrations were converted into a −20 °C activation temperature using the parameterisation of DeMott et al. (2010). The second horizontal line separates Antarctic and Southern Ocean measurements from measurements in other regions.

The combination of these measurements makes PEA an ideal site for investigating aerosol–cloud interactions, as simultaneous ground-based radar, lidar, and INP measurements are not available anywhere else on the continent. In addition to this, the zero-emission approach of the station allows us to investigate the atmosphere and clouds without disturbances by emissions from the station. We assume that the concentration of INPs will have a significant impact on the cloud phase, with a lower concentration limiting the amount of ice production, and, in turn, we expect a stronger CRE, for both SW radiation, decreasing ${\text{SW}}_{\text{all-sky}}^{\mathrm{net}}$, and LW radiation, increasing ${\text{LW}}_{\text{all-sky}}^{\mathrm{net}}$.

3 Methodology

3.1 Model description

In this study, we deploy COSMO-CLM² version 5.0, using the combined modifications done by Souverijns et al. (2019) and Possner et al. (2017). COSMO-CLM² consists of two main components: the COSMO regional atmosphere model in climate mode (COSMO-CLM; Steger and Bucchignani, 2020), which is maintained by the Climate limited-area Modelling Community (CLM-Community), and the Community Land Model (CLM; Oleson et al., 2013), which is the land component of the Community Earth System Model (CESM). These two models are coupled using the OASIS Model Coupling Toolkit (OASIS3-MCT; Will et al., 2017; Craig et al., 2017). The changes made by Souverijns et al. (2019) improve the representation of the Antarctic climate in the model through optimisations and reimplementations of surface snow and ice sheet parameterisations, changing the roughness length of snow for a correct representation of katabatic winds and modifying the settings of the turbulent kinetic energy scheme to account for the more stable atmosphere over the Antarctic ice sheet.

The aerosol and ice nucleation module (Possner et al., 2017) improves the parameterisation of cloud microphysics by resolving CCN and INPs explicitly, based on the parameterisation described by Solomon et al. (2015). Hydrometeors are simulated according to the two-moment scheme by Seifert and Beheng (2006). This module adds 16 different INP concentration variables corresponding to different activation temperatures. The first variable stores the concentration of available INPs that activate at or above 258.15 K (−15 °C). The remaining 15 variables store the INPs activating at lower temperatures, with each activation temperature being 1.3 K colder than the previous; i.e. the second bin contains the concentration of INPs activating between 258.15 and 256.85 K. This places the lowest temperature at 238.65 K (−34.5 °C), close to the temperature at which homogeneous freezing starts to occur. For each of the 16 concentration bins, half of the INPs activate per simulation time step if the temperature is below the bin's temperature, converting an equal amount of supercooled liquid water particles (if available) into ice particles. The INPs used are then depleted, reducing their concentration, but can be reintroduced by sublimation of snow or ice particles. The module also accounts for secondary ice production (SIP) but only in the mode of rime splintering (Hallett and Mossop, 1974).

For the initial and boundary conditions, we prescribe one INP concentration per simulation, given as the concentration of INPs activating at or above 253.15 K (−20 °C). The individual number concentrations N_INP(T) for the different activation temperatures T in kelvin are then derived using Eq. (2) (DeMott et al., 2010; Solomon et al., 2015), where F is a scaling factor, chosen so that N_INP(253.15) results in the prescribed concentration.

$$\begin{array}{}\text{(2)}& N_{\text{INP}}\left(T\right)=F^{\mathrm{1.25}}\exp \left(\mathrm{0.46}\right(\mathrm{273.16}-T)-\mathrm{11.6})\end{array}$$

In Eq. (2), N_INP(T) describes the total number of INPs activating at or above a given temperature T in kelvin. For each activation temperature bin, except the first one with the highest temperature, the concentrations should however correspond to the INPs activating between the bin's activation temperature and the activation temperature of the previous bin. Therefore, the actual prescribed initial concentration will be the difference between the results of Eq. (2) for the two temperatures; i.e. for the second bin, the prescribed concentration would be N_INP(256.85)−N_INP(258.15).

As the amount of aerosol particles is subject to significant spatial and temporal variability (Raman et al., 2023; McFarquhar et al., 2020), the prescription of the same concentrations on all pressure levels at all times on the model boundaries is not a realistic assumption, even when allowing variation within the domain. However, prescribing different concentrations allows us to examine the potential effects that those different concentrations may have.

3.2 Model setup

Our simulation domain has a size of 400 by 400 grid points with a resolution of 0.025° and is centred around PEA. Vertically, the grid consists of 40 levels, 18 of which are within 3 km of the surface at sea level. For our boundary and initial conditions, we use 3-hourly ERA5 data and produce hourly output for the analysed variables, while the simulation time step is 20 s. We also did preliminary tests using a smaller domain with a size of 192 by 175 grid points in a nested configuration with the model output of Souverijns et al. (2019) as boundary conditions but found that the clouds are much better represented in terms of height, timing, and structure when using the larger domain.

Based on the observations, we selected the following five INP concentration settings: first, we prescribe INP concentrations close to the lower end of the observed range in Antarctica at $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹ (at −20 °C), named “very low” (VL; see Table 2). Second, we use a concentration close to the upper end of recently observed concentrations in Antarctica at $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹, named “low” (L). Third, we prescribe $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹, which we consider a realistic value for continental INP concentrations at more remote locations, excluding Antarctica and maritime conditions, named “medium” (M). This medium concentration also serves as an augmentation for the SIP modes not captured by our setup (except rime splintering, which is included), as it was found that these modes can increase ice crystal number concentrations (ICNCs) by a factor of 10 (Sotiropoulou et al., 2020) in Antarctica. It is noted that this assumption is not very accurate: SIP is only active very locally with great spatial variance (Georgakaki et al., 2022), and simulating additional SIP modes is necessary for a realistic simulation of the vertical structure of MPCs (Schäfer et al., 2024). However, due to the scale of the model, we expect the overall error in our results caused by this to be small. Fourth, we prescribe $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹ as the first control run with continental concentrations, named “high” (H). Fifth, 2 L⁻¹ is used as the maximum prescribed concentration, named “very high” (VH), which corresponds to the maximum observed concentrations. It should also be noted that this is in the range observed by Bigg and Hopwood (1963), which, while we do not consider it to be an accurate measurement anymore, showcases the large variability of possible concentrations. Table 2 gives a summary of the settings used. In addition to INP concentrations, concentrations of CCN can also be prescribed in the aerosol module. However, we performed initial tests, varying the prescribed CCN concentrations from 10 to 1300 cm⁻³, corresponding to the measured range at PEA (Herenz et al., 2019). These tests were performed for the time period from 3 to 12 January 2016, which featured similar weather conditions to the austral summer period presented here. The results showed, agreeing with previous findings (Solomon et al., 2018), a negligible impact of CCN concentrations on cloud phase, which is why the impact of CCN concentrations was not investigated further. Thus, in all of our simulations, we used the low-end CCN concentration of 10 cm⁻³.

Table 2 Overview of prescribed INP settings. All concentrations refer to the −20 °C temperature bin. L and H settings were not used for the winter period.

We selected the periods to simulate based on two important factors: first, observations of both the MRR and the ceilometer should be available to be able to control the accuracy of the model output. Second, there should be a variety of observed cloud features to test the model under different conditions. Furthermore, one of the runs should be in the summer and the other during the winter to see if the differences in temperature and radiation between the seasons have an impact on the results.

The first simulated period spans 40 d in the summer from 10 January 2012 to 19 February 2012. This period was selected because it is the period with the most variation in cloud types in a given amount of time recorded by the ceilometer and because there is already a study identifying the different cloud types (Gorodetskaya et al., 2015): from 6 to 7 February, the ceilometer registered a very optically thick layer, leading to quick extinction of the lidar signal, indicating the occurrence of a liquid-containing cloud. Shortly after that, a frontal system passed over the station from 8 to 11 February, shown in Fig. 1, bringing snowfall to the station, as registered by the MRR, and causing the ceilometer signal to extinguish at a low level. There was, however, a short gap in the precipitation, where low-level mixed-phase clouds become visible (see Fig. 2a and b). This frontal system was quickly followed by a second, weaker one, passing the station from 12 to 14 February, consisting of mostly ice clouds.

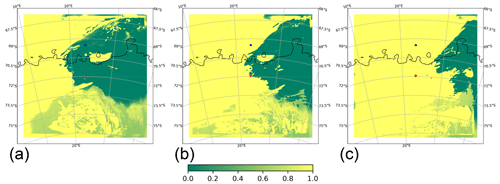
Figure 1 Low cloud cover fraction over the domain on (a) 8 February 2012, 18:00 UTC; (b) 9 February 2012, 00:00 UTC; and (c) 9 February 2012, 06:00 UTC. The red diamond denotes the location of the Princess Elisabeth Antarctica (PEA) station, and the blue dot marks the location over the Southern Ocean, which is analysed in more detail later.

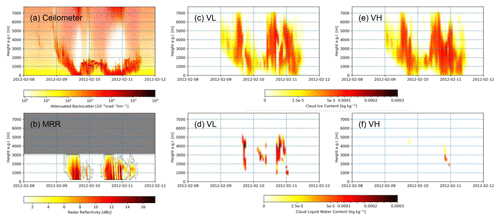
Figure 2 Cloud liquid water (b, f) and ice (c, e) for the VL (very low INP concentration, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; c, d) and VH (very high INP concentration, 2 L⁻¹; e, f) settings compared to the ceilometer (a) and MRR (b) measurements in the time period of 8 to 12 August 2012.

In the second period that was simulated, we looked at the Antarctic winter between 20 July and 15 August 2022. Data availability for the cloud observatory is limited in winter periods, as the lack of sunlight and low temperatures limit power supply and the operation ability of the instruments, so we have only recently been able to observe a full winter with all instruments. In the given time period, the observatory registered three major events. First, between 25 and 27 July, intense snowfall can be seen on both the ceilometer and the MRR. Second, a series of non-precipitating clouds passed over the station between 3 and 7 August, with no clear indications of liquid water. Third, a similar cloud series passed over the station between 10 and 15 August. An overview of the MRR and ceilometer measurements for the relevant periods can be found in Fig. A2.

4 Results

By comparing the results of a simulation where we prescribe an INP concentration on the low end of the observed range in Antarctica to those of a simulation where we prescribe a concentration on the high end, we tested the model sensitivity of clouds and radiation to different INP concentrations. Furthermore, the results achieved with Antarctic INP concentrations are compared to those with mid-latitude concentrations, which are unrealistically high for the region. Finally, all of this output is compared to cloud observations taken at PEA to verify that cloud properties are well represented and to gain insight into which INP concentrations give the most realistic results. Overall, the results show a strong connection between INP concentration and cloud liquid water contents.

In the summer period, the temperatures are sufficiently high such that a limited amount of INPs results in supercooled liquid water persisting in some of the clouds, although the total amount of liquid water remains limited to a few spots. This behaviour can be seen in Fig. 2, where a significant portion of hydrometeors in the cloud remains in a liquid state when using the VL setting, as opposed to the VH setting. Furthermore, the simulated cloud matches the observations in timing and cloud height well. However, most of the liquid water simulated under VL conditions does not form a thin, consistent layer, as expected and observed by the ceilometer around midnight on 10 February between 1 and 2 km height. Instead, the liquid water reaches much higher altitudes of up to 5 km in the area that could not be observed by the ceilometer due to signal extinction. This does not change significantly when looking at other areas over the continent within the domain. Consistent with the inability of the model to simulate a persistent layer of supercooled liquid water, the stratocumulus cloud observed by the ceilometer between 6 and 8 February, consisting of mostly liquid water, is not present in the model output at all (not shown).

In the winter period, the influence of the INP concentration has a much smaller effect, as shown in Fig. 3. The ceilometer data show a cloud similar to the one seen in Fig. 3 but without the interruption in precipitation and without a clear liquid layer. The MRR observations show that there is near-constant light precipitation during the depicted period. Again, all concentration variants capture the observed clouds well, with ice crystals reaching down to the surface between the early morning of 25 July and the late evening of 26 July 2022. Liquid water is, however, almost completely absent, except for a few patches in the VL setting at a height between 1000 and 2000 m. With the modelled temperature being at or slightly above 250 K at the surface (Fig. A1) during the period and decreasing with height, homogeneous nucleation offers a likely explanation for this reduced sensitivity.

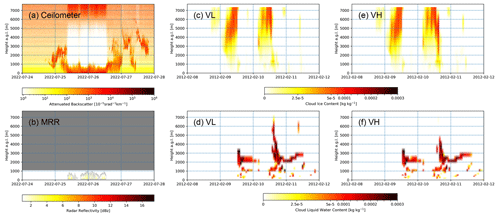
Figure 3 Cloud liquid water (d, f) and ice (c, e) for the VL (very low INP concentration, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹ at −20 °C; c, d) and VH (very high INP concentration, 2 L⁻¹ at −20 °C; e, f) settings compared to the ceilometer (a) and MRR (b) measurements in the time period of 24 to 28 July 2022. The MRR was set to only measure up to a height of 1 km at an increased resolution for this time period.

The average amount of cloud liquid water varies significantly between the different concentrations, from 0.4 g m⁻² at the VH setting to 3.9 g m⁻² at the VL setting in summer. Meanwhile, the change in cloud ice content at PEA across the different concentrations is small. Figure 4a shows that the absolute change in cloud ice content has a similar order of magnitude in absolute numbers, but in relation to the total content, this difference is much smaller (26.9 g m⁻² in VL and 28.8 g m⁻² in VH). In other words, the liquid mass fraction of hydrometeors (i.e. $\frac{\text{TQC}}{\text{TQI}+\text{TQC}}$, with TQC being the vertically integrated liquid water content and TQI being the vertically integrated ice water content) at PEA in the summer period increased to 12.6 % in VL, from 1.3 % in VH. When looking at the winter period (Fig. 4b), the influence of INP concentrations on cloud properties at the station is drastically reduced (for VL, the liquid mass fraction of hydrometeors is 4.0 % and 0.1 % for VH), which is in line with our expectation that extremely low temperatures allow widespread homogeneous freezing and the behaviour seen in Fig. 3. All of these values are averaged over a 21 by 21 grid cell area centred at PEA.

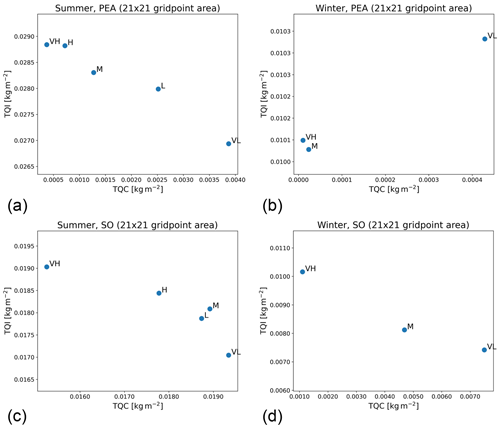
Figure 4 Average amounts of vertically integrated liquid water and ice under different INP concentrations over the summer period (10 January to 18 February 2012, a, c) and the winter period (20 July to 15 August 2022, b, d) at a 21 by 21 grid point box around the Princess Elisabeth Antarctica (PEA; a, b) station and around 69.5° S, 23.35° E in the Southern Ocean (SO; c, d). TQI is vertically integrated cloud ice, and TQC is vertically integrated cloud water. VL – very low INP concentration setting, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; L – low INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹; M – medium INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹; H – high INP setting, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; VH – very high INP setting, 2 L⁻¹. All INP concentration settings are at −20 °C.

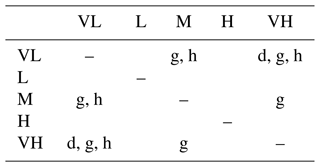
The radiative effects caused by these changes in cloud phase are small. Figure 5a shows that the median and mean cloud radiative effects generally stay between 50 and 60 W m⁻² for the summer period, with the extremes being slightly lower in the VH setting and with no clear trends connected to INP concentrations. Only the M setting compared to the VH setting shows a statistically significant difference in the paired t test (Table 3). When the total CRE is split up into a shortwave and longwave part (Fig. 5b and c), the means of the shortwave CRE decrease toward a lower INP concentration, indicating that the higher liquid share is more optically thick and therefore reflects a higher portion of sunlight back to space. This is offset by the trend of the longwave CRE, which increases toward a lower INP concentration, indicating that the higher liquid portion also reflects more radiation back to the ground. However, if we only look at the time steps with significant liquid water present (Fig. 5d), we can see that in the VL and L settings, the mean CRE is significantly lower than in the cases with higher INP concentrations (VL: 65.4 W m⁻², L: 67.2 W m⁻²; M: 68.8 W m⁻², H: 69.4 W m⁻², VH: 69.7 W m⁻²), indicating that for these thicker clouds, the increased shortwave reflection outweighs the longwave reflection. The sample size, however, becomes rather small as there are only 11 time steps with sufficient liquid water available to meet our criteria when averaging over the 21 by 21 grid point area.

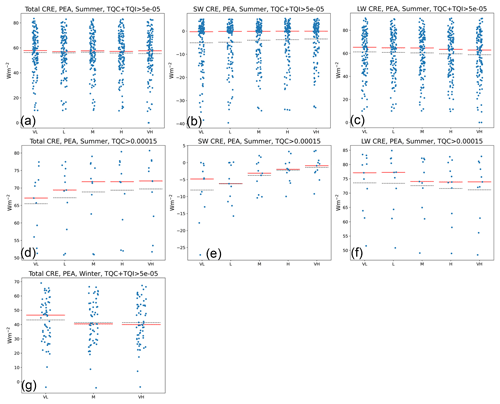
Figure 5 Different cloud radiative effect (CRE) statistics for the summer (a–f) and winter (g) period, averaged over a 21×21 area around the grid cell of PEA. TQI is vertically integrated cloud ice, and TQC is vertically integrated cloud water. The blue markers indicate individual time steps, the solid red line indicates the median, and the dashed black line indicates the mean. Sample sizes for the subfigures are (a–c) 131, (d–f) 11, and (g) 61. VL – very low INP concentration setting, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; L – low INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹; M – medium INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹; H – high INP setting, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; VH – very high INP setting, 2 L⁻¹. All INP concentration settings are at −20 °C.

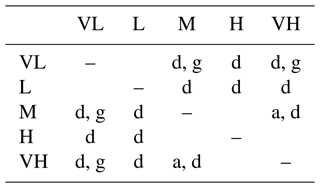
Table 3 Samples with a significant (p<0.05) difference in total cloud radiative effects (CREs) between two INP settings averaged over a 21×21 grid cell area around the grid cell of the Princess Elisabeth Antarctica station, tested by the paired t test. Letters a, d, and g refer to the selection criteria and periods as shown in the subfigures of Fig. 5 (a – summer period, only time steps with $\text{TQI}+\text{TQC}>\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻² in at least one of the INP concentrations; d – summer period, only time steps with $\text{TQC}>\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ g m⁻²; g – winter period, only time steps with $\text{TQI}+\text{TQC}>\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻²). TQI is vertically integrated cloud ice, and TQC is vertically integrated cloud water. VL – very low INP concentration setting, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; L – low INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹; M – medium INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹; H – high INP setting, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; VH – very high INP setting, 2 L⁻¹. All INP concentration settings are at −20 °C.

We also analysed the phase of hydrometeors found further north over the Southern Ocean at the grid cells around 69.5° S, 23.35° E. Over the ocean, the average air temperature is warmer, and as such, liquid water is more common, even when prescribing a higher amount of INPs. Changing the INP concentration still has an impact on the cloud phase (see Fig. 4c), with the average amount of liquid water – averaged over a 21 by 21 grid cell area around the central point – increasing from 15.2 g m⁻² in the VH to 19.3 g m⁻² in the VL setting for the summer period, while the cloud ice content decreases from 19.0 to 17.0 g m⁻². However, while this change is noticeable, it does not have an impact on the general structure of the cloud like it has on the clouds at PEA in Fig. 2, and the liquid mass fraction of hydrometeors changes only from 44.5 % in VH to 53.2 % in VL. During the winter period in the Southern Ocean, the INP concentration has a much larger impact, compared to both the summer period at the same location and the winter period at PEA, with the amount of cloud liquid water ranging from 1 g m⁻² at VH to 7.5 g m⁻² at the VL setting for liquid water mass fractions of 9.8 % (VH) and 50.3 % (VL; see Fig. 4d).

Overall, the radiative effects of clouds are stronger over the Southern Ocean than over the continent. As shown in Fig. 6a, when analysing the summer period's time steps with liquid or ice hydrometeors above 0.05 g m⁻² available, the median CREs are all around the 0 W m⁻² mark, with a maximum of 5.4 W m⁻² for the M concentration, but with the total CRE going down to extremes of −500 W m⁻² in some time steps. When applying the constraint to only count time steps with at least 0.15 g m⁻² of liquid water available, it can be seen that the radiative effects of these clouds are much stronger, placing the medians between −45 and −50 W m⁻² (VL: −46.3 W m⁻², L: −45.5 W m⁻², M: −47.9 W m⁻², H: −45.9 W m⁻², VH: −48.0 W m⁻²). This also highlights how liquid cloud water causes stronger cloud radiative effects. However, during the entire summer period, there is no clear difference between the different concentrations. Only when comparing the VL with the VH INP concentration for the stricter condition of 0.15 g m⁻² of liquid water is the difference per time step statistically significant (Table 4).

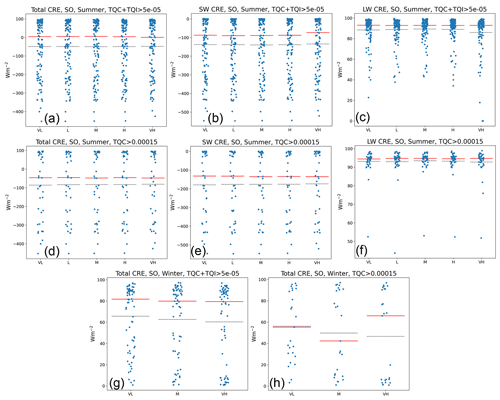
Figure 6 Different cloud radiative effect (CRE) statistics for the summer (a–f) and winter (g, h) period, averaged over a 21×21 area around 69.5° S, 23.35° E in the Southern Ocean. TQI is vertically integrated cloud ice, and TQC is vertically integrated cloud water. The blue markers indicate individual time steps, the solid red line indicates the median, and the dashed black line indicates the mean. Sample sizes for the subfigures are (a–c) 121, (d–f) 41, (g) 71, and (h) 25. VL – very low INP concentration setting, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; L – low INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹; M – medium INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹; H – high INP setting, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; VH – very high INP setting, 2 L⁻¹. All INP concentration settings are at −20 °C.

Table 4 Samples with a significant (p<0.05) difference in total cloud radiative effects (CREs) between two INP settings averaged over a 21×21 grid cell area around 69.5° S, 23.35° E in the Southern Ocean, tested by the paired t test. Letters a, d, g, and h refer to the selection criteria and periods as shown in the subfigures of Fig. 6 (d – summer period, only time steps with $\text{TQC}>\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ g m⁻²; g – winter period, only time steps with $\text{TQI}+\text{TQC}>\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}$; h – winter period, only time steps with $\text{TQC}>\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ g m⁻²). TQI is vertically integrated cloud ice, and TQC is vertically integrated cloud water. VL – very low INP concentration setting, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹; L – low INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹; M – medium INP setting, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ L⁻¹; H – high INP setting, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹; VH – very high INP setting, 2 L⁻¹. All INP concentration settings are at −20 °C.

During winter, the median CRE is increased in the VL setting compared to the M and VH settings (Fig. 6g; VL: 81.6 W m⁻², M: 79.8 W m⁻², VH: 79.4 W m⁻²) over the Southern Ocean, using the more relaxed condition of at least 0.05 g m⁻² of water and ice. This is in line with our findings from Fig. 5c and f, where we found an increase in the longwave part of CREs for liquid-containing clouds: during the polar winter, the clouds cannot reflect any sunlight, thus resulting in a shortwave CRE of 0 (this is also why only total CREs are shown for the winter period). As shown by Fig. 6g, the increase in CREs in the VL setting is especially pronounced during time steps with a smaller CRE. In the VH setting, there are a lot of samples clustered at or slightly above a CRE of 0 W m⁻², while that cluster spreads out to 20 to 40 W m⁻² for the M and VL settings. This indicates that it is the less optically dense clouds whose CRE is enhanced the most when limiting available INPs. When limiting the time steps to 0.15 g m⁻² of liquid cloud water (Fig. 6h), this effect gets even stronger: there is no longer a clear signal in the median, likely because it falls in a region with very few samples, but, while the area above the median line has a similar distribution, the area closer to 0 W m⁻² is very spread out in VL and very clustered close to 0 W m⁻² in VH, with M being in between. This is also reflected by the mean. With only 25 time steps available when applying this limitation, the sample size is very small but still sufficient to find a significant (p<0.5) difference of the VL from the other concentrations (Table 4).

5 Discussion

In summer, a clear relation was found between the simulated concentration of INPs and the presence of liquid water in the clouds at PEA. The higher amounts of liquid water in the simulations with a limited INP concentration (VL and L) agree better with the ceilometer and MRR observations. While this improves the representation of the cloud phase overall, the model still fails to accurately represent the long-lived, dense liquid and mixed-phase layers observed at the station. This effect is not caused by restricting our view to a single grid cell, as it can also be seen when averaging the liquid water content over an area of 10 grid cells to all sides of PEA (not shown). The radiative effects caused by the added liquid are noticeable but in general do not affect the overall radiative balance of the model significantly. It should be noted, for both the PEA case and the Southern Ocean case, that stratocumulus clouds, which the model was unable to represent, are very likely to contain supercooled liquid water (Gorodetskaya et al., 2015; Twohy et al., 2021), which might result in an underestimation of cloud liquid water content and therefore the radiative effects. The differences that we found generally support the findings of Ricaud et al. (2024), who estimate that over the Antarctic Plateau, supercooled liquid water only has a weak radiative effect of up to 7 W m⁻², as opposed to up to 40 W m⁻² over the Antarctic Peninsula, and who found a clear correlation between cloud liquid water content and temperature.

Over the Southern Ocean, a relation between INP concentrations and liquid water presence was also found, but even in the highest INP setting, a significant amount of liquid water remains. This may be explained by the higher overall temperature, as even with temperatures below 0 °C, not all INPs activate immediately. In fact, the first INP temperature bin of our model activates at −15 °C, so at higher temperatures, ice production is limited to secondary processes. However, the cloud top temperatures we observed in the model during that time period were around or below −15 °C (not shown). As the variability of the liquid mass fraction of hydrometeors is relatively small, unlike at PEA, it seems unlikely that in the summer months INP concentrations have noticeable impacts on the cloud phase over the Southern Ocean in our model.

During the winter period, the relationship between INP concentrations and liquid water concentration changes. On the one hand, at PEA, only small amounts of liquid water remain in the clouds. As temperatures over the inland regions of Antarctica commonly reach below the threshold of −37 °C required for homogeneous nucleation in our model, even at the surface level, this is not particularly surprising. Hence, changing the INP concentration only has a much smaller effect on the cloud properties at the station. Over the Southern Ocean, on the other hand, temperatures are still high enough for liquid water to persist under lower INP concentrations. The behaviour now resembles the summer period at PEA, indicating that it is mostly influenced by temperature rather than location. This also means that, in winter, the change in INP concentration has more significant impacts on the cloud phase for the Southern Ocean, as with sufficient INPs, almost all liquid water will freeze. The response of liquid cloud water mass to a change in INP concentration is about the same in both the summer and the winter periods over the Southern Ocean, but the percentage change and the change in the liquid mass fraction of hydrometeors are much larger during the winter. Thus, over the Southern Ocean, INP concentrations have a much more significant impact during the winter than during the summer, which is in contrast to the behaviour over land at PEA. This can also be seen in the CRE: the largest influence of INP concentration on total CRE is seen during the winter period, over the Southern Ocean, and while there is no influence of INP concentrations on total CRE during the summer at PEA, such an influence can be seen on the individual components (LW and SW).

The spin-up time is expected to be low due to the frequent and fast exchange of air masses in relation to the domain size. As can be seen in Fig. A3, INP concentrations drop slightly initially but stay close below their prescribed concentration. There is a significant drop at the end of the simulation period, but this drop is likely not related to spin-up, as after 2 months of simulation, all initial air masses should have been exchanged. The L and H settings are very similar in their INP timeline too, indicating that the deviations in concentrations are caused by synoptic-scale weather systems and not spin-up errors. The drop in concentration toward the end of the shown period can be explained by upstream scavenging of available INPs (not shown).

Finally, it should be noted that our model, while representing a wide range of INP concentrations, is limited to the parameterisations it uses. There is evidence that secondary ice processes not represented in the model are temporally and spatially variable (Georgakaki et al., 2022) and that the ratio of the ice crystal number concentration to the concentration of active INPs is temperature dependent (Järvinen et al., 2022), so increasing the INP concentration by a constant factor to account for missing SIP modes inevitably leads to errors in the distribution of ice. The distribution of activation temperatures, as prescribed in Eq. (2), might also be a source of inaccuracy, as we have only tested one distribution based on the parameterisation by DeMott et al. (2010) and used a scaling factor for different INP concentrations. Other distributions often have a lower increase in the INP concentration at lower temperatures, such as the Measurements of Aerosols, Radiation, and Clouds over the Southern Ocean (MARCUS) fit presented in Vignon et al. (2021), which does not have any additional INPs activating in the lower temperature range below about −30 °C, while having a steeper increase in activated INPs between −15 and −30 °C.

Nevertheless, our findings with respect to the temperature sensitivity of the cloud response to INP concentration changes should still hold, as the steeper increase in the activation temperature profile measured in campaigns such as MARCUS (Vignon et al., 2021) would only cause an even stronger temperature sensitivity than the gradual increase we used here. In addition to this, the reduced sensitivity seen at PEA during the winter period can be explained by homogeneous nucleation. With air temperatures falling below the −37 °C (236.15 K) threshold required for homogeneous nucleation at altitudes as low as 2000 m a.g.l. (Fig. A1), the occurrence of INPs is no longer necessary for primary ice production, effectively reducing the sensitivity of cloud phase to INP concentration. Only the low sensitivity we found over the Southern Ocean in summer would potentially be affected, as the temperature range found for this situation would mostly fall in the region with a higher increase, but even keeping that in mind, the INP settings we tested covered a wide enough range for any increase from realistic values to fall into the tested range.

On the higher temperature end, having the highest INP activation temperature at −15 °C is a simplification as well. The concentration of INPs activating at such higher temperatures is extremely small and would likely have no significant effect. However, not having any INPs means that rime splintering, which is active in the temperature range between −3 and −8 °C, has to rely on small amounts of ice already existing, as there is no primary ice nucleation active in this temperature range that could initiate secondary ice production. This would possibly increase the effects of INP concentration over the ocean in summer, which we found to be very low, as such higher temperatures are mostly found there.

All in all, it is conceivable that the lack of representation of stratocumulus clouds with supercooled liquid water, which were observed at the station, and the possible overestimation of INPs at lower temperatures lead to an overall underrepresentation of liquid water in the model. This implies that the actual effects caused by changing INP concentrations are stronger than presented here, as the liquid water amounts in the lowest INP concentration would likely be enhanced the most by the inclusion of additional clouds.

6 Conclusions

Our results highlight the importance of ice-nucleating particles (INPs) for the cloud phase in Antarctica. While the simulated clouds do not perfectly match the observations at the station in terms of cloud phase, limiting the amount of available INPs does result in an increase in liquid water in clouds and is more closely in alignment with the ceilometer, MRR, and INP observations at the station. This effect is shown to be particularly relevant during the austral summer for continental Antarctica, whereas during austral winter, the colder temperatures facilitate homogeneous freezing, and INP concentrations therefore become less important. Over the Southern Ocean, the opposite is the case: during austral summer, temperatures are high enough to allow liquid water to persist in the clouds at any INP concentration, whereas during the winter, a higher INP concentration leads to the complete freezing of clouds. The change in cloud phase also has radiative effects, but in the given model setup, an improved representation of INPs would not alleviate biases in the near-surface radiation. Further research is needed to improve the simulation, in particular the cloud phase, with respect to microphysical processes that are not yet (well) represented in the model, such as secondary ice processes beyond rime splintering. The current version of the INP simulation module is computationally expensive due to the 16 added variables, and a simplified and more optimised parameterisation might be sufficient. An increased vertical resolution might then help reduce the remaining model errors in the representation of clouds. When restricting the CRE statistics to optically denser clouds, the radiative effects of the cloud were stronger in the cases where the concentration of INPs had relevant impacts (i.e. during summer over the continent and during winter over the ice sheet).

Appendix A

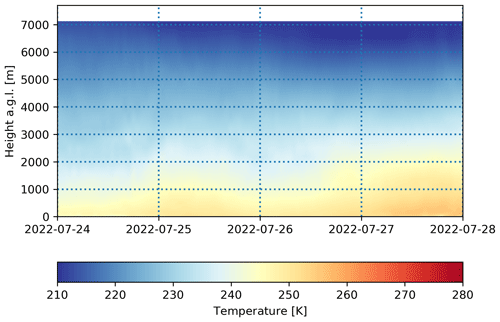
Figure A1 Temperature modelled at the Princess Elisabeth Antarctica (PEA) station in the time period from 24 to 28 July 2022 for the VL (very low INP concentration, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ L⁻¹ at −20 °C) setting.

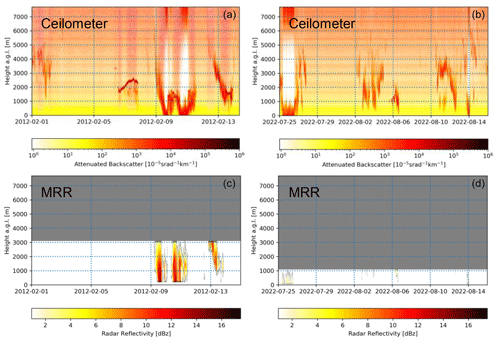
Figure A2 Ceilometer (a, b) and MRR (c, d) measurements for the time periods of 1 to 15 February 2012 (a, c) and 25 July to 16 August 2022 (b, d). The MRR was set to only measure up to a height of 1 km at an increased resolution during the winter period (b, d).

Figure A3 Average INP concentration at −20 °C in the L (low INP concentration, $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ L⁻¹) setting (a) and H (high INP concentration, $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹) setting (b) for a 21×21 area around PEA at a height of 2250 m.