Can general circulation models (GCMs) represent cloud liquid water path adjustments to aerosol–cloud interactions?

General circulation models (GCMs), unlike other lines of evidence, indicate that anthropogenic aerosols cause a global-mean increase in cloud liquid water path (ℒ) and thus a negative adjustment to radiative forcing of the climate by aerosol–cloud interactions. In part 1 of this series of papers, we showed that this is true even in models that reproduce the negative correlation observed in present-day internal variability in ℒ and cloud droplet number concentration (N_d). We studied several possible confounding mechanisms that could explain the noncausal cloud–aerosol correlations in GCMs and that possibly contaminate observational estimates of radiative adjustments. Here, we perform single-column and full-atmosphere GCM experiments to investigate the causal model-physics mechanisms underlying the model radiative adjustment estimate. We find that both aerosol–cloud interaction mechanisms thought to be operating in real clouds – precipitation suppression and entrainment evaporation enhancement – are active in GCMs and behave qualitatively in agreement with physical process understanding. However, the modeled entrainment enhancement has a negligible global-mean effect. This raises the question of whether the GCM estimate is incorrect due to parametric or base-state representation errors or whether the process understanding gleaned from a limited set of canonical cloud cases is insufficiently representative of the diversity of clouds in the real climate. Regardless, even at limited resolution, the GCM physics appears able to parameterize the small-scale microphysics–turbulence interplay responsible for the entrainment enhancement mechanism. We suggest ways to resolve tension between current and future (storm-resolving) global modeling systems and other lines of evidence in synthesis climate projections.

1 Introduction

Increased aerosol concentration modifies cloud properties by increasing cloud droplet number, which initially makes clouds more reflective. When the aerosol concentration increase is due to an agent external to the climate system such as anthropogenic emissions, this cloud-brightening aerosol–cloud interaction (ACI) exerts a negative radiative forcing (RFaci) on the climate. However, clouds then adjust to the cloud droplet number (N_d) perturbation by changing their liquid water path (ℒ) and cloud coverage; this enhancement or weakening of the instantaneous RFaci is called the radiative adjustment due to ℒ (RA_ℒ) or cloud fraction (RA_f).

General circulation models (GCMs) have long disagreed with other lines of evidence on the sign of RA_ℒ, predicting that anthropogenic aerosols increase ℒ when observational and large-eddy simulation (LES) estimates predict that ℒ decreases (Bellouin et al., 2020). Recently, Christensen et al. (2023), Varble et al. (2023), and Mülmenstädt et al. (2024b) showed that several Coupled Model Intercomparison sixth-generation GCMs from the Coupled Model Intercomparison Project 6 (CMIP6) generation (Eyring et al., 2016) produce negative correlations between cloud droplet number concentration, N_d, and ℒ in present-day internal variability. This is welcome news because the inability of GCMs to match observations was interpreted as GCMs' inability to represent enhanced cloud-top entrainment of dry air at high N_d values. Enhanced entrainment is the dominant RA_ℒ mechanism according to assessments based on multiple lines of evidence.

However, even GCMs that produce negative N_d–ℒ correlations in the present day still predict an ℒ increase in response to anthropogenic aerosol emissions. In other words, the causal response of the model climate to secular changes in aerosols has the opposite sign to the correlation in present-day internal variability. This is concerning for the negative correlation in observations is one pillar on which the sign of RA_ℒ rests in assessments based on multiple lines of evidence. Part 1 of this series of papers (Mülmenstädt et al., 2024b) offered several hypotheses for confounders that could produce a noncausal negative correlation between N_d and ℒ.

In this paper, we return to entrainment-mediated evaporation of clouds as an adjustment mechanism and the question of whether this mechanism is represented in GCMs. If so, then GCMs would also agree with the second pillar on which our multiline assessment of RA_ℒ rests: LES of cloud turbulence–microphysics interactions that shows a causal mechanism by which an increased droplet number results in increased entrainment drying of stratocumulus (Sc) clouds (Ackerman et al., 2004; Bretherton et al., 2007). We show that a broadly similar causal mechanism appears to exist in GCMs. This is also concerning because the GCM results suggest that the well-understood and exhaustively LES-modeled RA_ℒ in subtropical stratocumulus clouds may not be representative of the global-mean RA_ℒ.

The results of Mülmenstädt et al. (2024b) and this paper, taken together, complicate the Bellouin et al. (2020) picture of reduced ℒ in response to anthropogenic aerosol. It is possible that the known weaknesses of the tools at our disposal (observations, process modeling, and global modeling) are causing us to misunderstand the sign of RA_ℒ. We conclude with recommendations for using the complementary strengths of our toolset to increase the robustness of multiline assessments of ACI adjustments.

2 Data and methods

The hypothesis that our methods are designed to test is that a causal connection exists between N_d and ℒ in GCM physics that proceeds via enhanced cloud-top entrainment. Thus, we focus on causal and mechanism-denial experiments in single-column and three-dimensional (3D) atmosphere runs to elucidate the causal link between N_d and ℒ and on diagnostics of cloud-top entrainment to ascertain that enhanced entrainment is involved in RA_ℒ.

2.1 Models

We use two of the three CMIP6-era models analyzed by Mülmenstädt et al. (2024b) that produce an inverted-V-shaped N_d–ℒ correlation: the US Department of Energy Exascale Earth System Model (E3SM) and NASA Goddard Institute for Space Studies (GISS) ModelE3. These models have different turbulence schemes; as entrainment-mediated ACI mechanisms must involve at least the turbulence and microphysics parameterizations, it was desirable to include model diversity in this study. ModelE3 and E3SM are used in single-column mode (Sects. 2.3 and 3.2). E3SM is also used in 3D atmosphere runs (Sects. 2.4, 3.1, and 3.3).

In part 1, we used E3SMv1; here, we use E3SMv2 (Golaz et al., 2022) instead because it is significantly more efficient at archiving the large, high-frequency fields required for the entrainment diagnostics. E3SMv2 differs from v1 largely in the parametric tuning (Ma et al., 2022) rather than in changes to the physics formulation. The N_d–ℒ relationship documented in E3SMv1 persists in E3SMv2 for Sc clouds (Fig. S1).

In part 1, we used a ModelE3 parameter tuning derived from machine learning; here, we use the default tuning from the ModelE3 development team, which produces a very similar N_d–ℒ relationship but does not produce the oscillations in surface precipitation at the lowest N_d values that result from an assertive subgrid-scale multiplier tuning of autoconversion in nonturbulent layers.

2.2 Cloud selection

As the process understanding of entrainment-mediated RA_ℒ is based chiefly on a small number of canonical subsidence Sc cases, our main focus is on understanding this cloud type in the GCMs as well. Thus, while the eventual goal is to understand the full spectrum of clouds that occur in the real atmosphere, for now we apply a restrictive set of criteria to maximize the similarity between model clouds and Sc:

• warm (cloud-top temperature warmer than freezing and zero ice water path) and overcast (cloud fraction of f>0.9) columns,

• in locations where the dynamic–thermodynamic criteria of Medeiros and Stevens (2011) – with pressure vertical velocity, ω, at 700 and 500 hPa (${\mathit{\omega }}_{\mathrm{700}\mathrm{hPa}}>\mathrm{10}{\mathrm{hPa}\mathrm{d}}^{-\mathrm{1}}$ and ${\mathit{\omega }}_{\mathrm{500}\mathrm{hPa}}>\mathrm{10}{\mathrm{hPa}\mathrm{d}}^{-\mathrm{1}}$) and lower tropospheric stability (potential temperature difference of ${\mathit{\theta }}_{\mathrm{700}\mathrm{hPa}}-{\mathit{\theta }}_{\mathrm{1000}\mathrm{hPa}}>\mathrm{18.55}$ K) – are met at least 30 % of the time in the annual mean (see part 1),

• during Sc season (northeastern Pacific: Jun–Aug; southeastern Pacific and southeastern Atlantic: Oct–Feb), and

• with an inversion between model levels 10 and 15 from the surface (approximately 750–1400 m).

We also remove cases where the parameterized convection is triggered as this introduces transport through the planetary boundary-layer (PBL) top that is not considered in the entrainment diagnostics (Sect. 2.5). In the single-column experiments (Sect. 2.3), the convection scheme does not trigger in either ModelE3 or E3SM. In E3SM, the “shallow” convection parameterization is part of the Cloud Layers Unified By Binormals (CLUBB; Golaz et al., 2002; Larson, 2022) cloud macrophysics and turbulence scheme, which does not produce nonlocal (i.e., across multiple vertical levels in one time step) transport through the PBL top. The “deep” convection scheme in E3SM (Zhang and Mcfarlane, 1995; Xie et al., 2019) occasionally triggers in the 3D atmosphere run even in the stratocumulus-like conditions we select for; these columns make up 2.0 % of the total and are removed from the analysis. The occurrence of deep convection is rare enough that we do not attempt to analyze its effect on time steps after the removed deep-convective time step.

These cloud requirements reduce the complication that the cloud sample may comprise different cloud regimes governed by different ACI mechanisms (Mülmenstädt and Feingold, 2018), ensure validity of the cloud-top entrainment diagnostics, and avoid difficulties in the interpretation of cloud-top entrainment in partly cloudy model columns.

2.3 Single-column model experiments

We use an extensively studied, idealized subsidence Sc-like case specification to construct single-column experiments that are designed to investigate the mechanisms underlying the response of entrainment and ℒ to N_d in GCM physics.

2.3.1 DYCOMS-II RF02 case description

The initial conditions and forcings for the single-column models (SCMs) follow the specifications of Ackerman et al. (2009) for an intercomparison of lightly drizzling Sc. This setup is based on measurements during research flight 2 (RF02) of the second Dynamics and Chemistry of Marine Stratocumulus (DYCOMS-II) field study off the California coast (Stevens et al., 2003; vanZanten et al., 2005) obtained by horizontally averaging a notably heterogeneous field of somewhat heavily drizzling open cells within barely drizzling closed cells. With regard to the sensitivity of cloud thickness to entrainment in this case, the inversion is sufficiently strong and the overlying air sufficiently dry that the cloud is not close to the regime of cloud deepening through entrainment from Randall (1984), and thus entrainment is expected to thin the cloud layer as found in the LES intercomparison. (As a side note, we note that there is a sign error in Eq. 3 of Ackerman et al., 2009, specifying the total moisture profile above the inversion: the difference in the innermost brackets should be z_i−z rather than z−z_i as written.)

The Wyant et al. (2007) SCM intercomparison study used nearly the same setup as Ackerman et al. (2009), and both studies found that including drizzle and cloud droplet sedimentation generally slowed entrainment and enhanced domain-mean liquid water path among a variety of models. Like the previous LES intercomparison of nocturnal Sc by Stevens (2005), the idealized setup ignored horizontal advective tendencies of cooling and drying associated with the large-scale flow for subtropical Sc decks as well as any solar radiation, consistent with the approximately 5 h of aircraft sampling nocturnal boundary-layer air along an approximately Lagrangian trajectory. These and other simplifications, such as constant subsidence and turbulent surface fluxes, are consistent with the 6 h simulation duration for the DYCOMS-II RF02 intercomparisons.

2.3.2 GISS ModelE3 SCM description

The GISS ModelE3 SCM is a single-column version of the ModelE3 GCM that includes a number of updates to the column moist physics as summarized in Cesana et al. (2021) and described in more detail by Cesana et al. (2019); unpublished manuscripts will document the model-physics parameterizations more completely and also discuss the machine learning approach to tuning the atmospheric model. In SCM mode, the resolved advection is neglected, and vertical advection is treated by multiplying the vertical wind by the local gradient of all prognostic variables as done for LES with periodic lateral boundary conditions (e.g., Stevens, 2005; Ackerman et al., 2009) to avoid complications associated with representing a divergent flow in a 1D framework. The ModelE3 SCM allows for a number of specified forcings to override the native model parameterizations, which for this case consists of the following: (1) the radiative transfer uses a Beer's law treatment that computes cloud-top cooling and cloud-base warming from the respective cumulative water paths downward from above and upward from below, (2) geostrophic wind forcing is computed as in the LES framework using a fixed profile of geostrophic wind and the prescribed latitude, and (3) surface drag is computed using a fixed friction speed.

For the ModelE3 SCM simulations here, we depart from the DYCOMS-II RF02 LES intercomparison specification in two ways. For the sake of simplicity, instead of a bimodal cloud condensation nuclei (CCN) distribution, we specify a single lognormal mode of ammonium bisulfate with a geometric mean radius of 60 nm and a geometric standard deviation of 1.7. We also extend the duration of the simulations to 24 h to check whether the clouds reach a steady state in each model; the latter half (hours 12.5–24) is not further analyzed.

Appendix A compares the SCM behavior against LES and assesses variations in the SCM setup that differ from those used for the E3SM SCM.

2.3.3 E3SM SCM description

The E3SM SCM is described in Bogenschutz et al. (2020). DYCOMS-II RF02 is part of the standard E3SM SCM case library. The main differences compared with the ModelE3 SCM are as follows. Since E3SMv2, the SCM has used the same vertical advection scheme as the 3D model. The idealizations active in the baseline experiment are prescribed surface heat fluxes, prescribed geostrophic wind, prescribed profile of divergence, and prescribed bimodal aerosol profile as in the ModelE3 setup. Prescribing the surface wind stress or friction velocity, u_*, is not supported in the E3SM SCM; during spin-up, the SCM stabilizes to $u_{*}\approx \mathrm{0.4}$ m s⁻¹, which is substantially higher than the DYCOMS-II RF02 case specification ($u_{*}=\mathrm{0.25}$ m s⁻¹).

Differences in model configuration in sensitivity experiments and N_d susceptibility scans are described in the discussion of those experiments.

2.4 3D GCM configuration

The models analyzed in part 1 produced RA_ℒ<0 in the default model configuration, presumably because of precipitation suppression. To disentangle the opposing RA_ℒ of precipitation suppression and a potential entrainment mechanism (RA_ℒ>0), we turn off the precipitation suppression in E3SM by setting the exponent on N_d in the autoconversion parameterization to zero, removing the explicit N_d dependence of the autoconversion process. To maintain a climate state similar to the default model, we increase the autoconversion scale factor (Mahfouz et al., 2024). This is equivalent to presenting autoconversion with a globally constant N_d≈50 cm⁻³ and results in present-day top-of-atmosphere radiative flux and cloud radiative effect changes of <1 W m⁻² compared with the default configuration. The warm-cloud over-ocean mean, calculated using present-day (PI) and preindustrial (PD) values, is log ℒ_PD−log ℒ_PI $=\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{3}}$ in this configuration compared with $\mathrm{3.2}\times {\mathrm{10}}^{-\mathrm{2}}$ in the default configuration. This indicates that switching off the precipitation suppression mechanism eliminates the strong negative RA_ℒ of the default model configuration but does not expose a strong positive RA_ℒ in its stead. The N_d–ℒ correlation becomes more negative in Sc clouds when precipitation suppression is turned off (Fig. S2) compared with when precipitation suppression is active.

2.5 Entrainment diagnostics

As the causal ACI mechanism hypothesized to lead to RA_ℒ>0 is enhanced entrainment with increasing N_d, we make it a focus of this paper to understand how entrainment behaves in the models. To this end, we use an entrainment diagnostic that calculates the mixing between the free troposphere (FT) and well-mixed boundary layer as a residual term in the mixed-layer budgets of water and temperature. Note that we do not include budget terms for nonlocal transport through the PBL top by parameterized convection schemes. This limits the applicability of the diagnostics to strictly stratocumulus-topped boundary layers (excluding, e.g., the stratocumulus-to-cumulus transition), which the subsidence-based and stability-based regional selection (Sect. 2.2) is intended to enforce.

Let q_v and q_l be water vapor and liquid mixing ratio and θ and T potential temperature and temperature. In adiabatic expansion and condensation, the total water mixing ratio of

$$\begin{array}{}\text{(1)}& q_{\text{t}}=q_{\text{v}}+q_{\text{l}}\end{array}$$

and liquid water potential temperature, θ_l, are conserved; we approximate

$$\begin{array}{}\text{(2)}& {\mathit{\theta }}_{\text{l}}=\mathit{\theta }-{\displaystyle \frac{L_{\text{v}}}{c_{\mathrm{p}}}}{\displaystyle \frac{\mathit{\theta }}{T}}{q}_{\text{l}},\end{array}$$

with L_v being the latent heat of the evaporation of water (which, for simplicity, we take as temperature-independent using its value at 273 K) and c_p the isobaric specific heat of dry air. Budget equations for θ_l, q_t, and total mass, vertically integrated over the PBL, involve fluxes of water, dry air, and heat across the boundaries of the PBL (Lilly, 1968; Stevens, 2002; Caldwell et al., 2005; Kalmus et al., 2014; Mellado, 2017). Crucially for our purposes, this includes the entrainment flux into the boundary layer. We express the budget equations following Kalmus et al. (2014) but modify the notation to highlight the similarity with source and sink terms in a prognostic equation in Lagrangian form:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }h{\displaystyle \frac{\widehat{D}\left(\mathit{\rho }{\mathit{\theta }}_{\text{l}}\right)}{\widehat{D}t}}=-{\displaystyle \frac{\mathrm{\Delta }F}{c_{\mathrm{p}}}}+{\displaystyle \frac{L_{\text{v}}R}{c_{\mathrm{p}}}}+{\displaystyle \frac{\text{SH}}{c_{\mathrm{p}}}}+E_{\mathit{\theta }}({\mathit{\theta }}_{\text{l}}^{+}-\langle {\mathit{\theta }}_{\text{l}}\rangle ),\text{(4)}& {\displaystyle }& {\displaystyle }h{\displaystyle \frac{\widehat{D}\left(\mathit{\rho }{q}_{\text{t}}\right)}{\widehat{D}t}}=-R+{\displaystyle \frac{\text{LH}}{L_{\text{v}}}}+E_q(q_{\text{t}}^{+}-\langle q_{\text{t}}\rangle ),\text{(5)}& {\displaystyle }& {\displaystyle }\mathit{\rho }{|}_{z=h}\left({\displaystyle \frac{\partial h}{\partial t}}+\mathit{v}\cdot {\mathrm{\nabla }}_{H}h\right)=E_h-\mathit{\omega }/g,\end{array}$$

where ρ is the density, ΔF the radiative cooling, R the precipitation mass flux at the surface, LH and SH the latent and sensible heat fluxes at the surface, h the PBL geometric depth, v the wind vector, $\mathit{\omega }=Dp/Dt$ the large-scale pressure velocity, and g the gravitational acceleration. The operator ∇_H is the horizontal gradient. Quantities with a superscript plus (i.e., $q_{\text{t}}^{+}$ and ${\mathit{\theta }}_{\text{l}}^{+}$ in Eqs. 3–4) are evaluated just above the inversion. Quantities in angular brackets (〈A〉) are mass-weighted vertical averages of a quantity (A), evaluated at a model-level midpoint k between the lowermost atmosphere level, k_sfc, and the uppermost level below the inversion, k_pbl:

$$\begin{array}{}\text{(6)}& \langle A\rangle ={\displaystyle \frac{\mathrm{1}}{\langle \mathit{\rho }\rangle h}}\sum _{k=k_{\text{sfc}}}^{k_{\text{pbl}}}{\mathit{\rho }}_k\mathrm{\Delta }{z}_k{A}_k.\end{array}$$

The PBL-averaged material derivative of a 3D quantity A is defined as

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\displaystyle \frac{\widehat{D}\left(\mathit{\rho }A\right)}{\widehat{D}t}}& =\langle \mathit{\rho }\rangle {\displaystyle \frac{\partial \langle A\rangle }{\partial t}}+\langle \mathit{\rho }\mathit{v}\cdot {\mathrm{\nabla }}_{\mathrm{H}}A\rangle +\langle \mathit{\rho }\rangle (A{|}_{z=h^{-}}\\ & -\langle A\rangle )\mathit{v}\cdot {\mathrm{\nabla }}_{\mathrm{H}}h.\end{array}\end{array}$$

The PBL-averaged material derivative differs from the conventional material derivative in two ways. First, vertical advection is absent as the motion of the boundary between PBL and free troposphere does not affect the within-PBL average. Second, the final term in Eq. (7) accounts for the horizontal advection of the PBL top; the $A{|}_{z=h^{-}}$ notation indicates the field is to be evaluated just below the inversion.

Each of the budgets of θ_l, q_t, and h (Eqs. 3–5) can be solved for an entrainment mass flux to get E_θ, E_q, and E_h, respectively. Physically, the following applies:

$$\begin{array}{}\text{(8)}& E_{\mathit{\theta }}=E_q=E_h.\end{array}$$

However, models do not necessarily respect this equality. Therefore, we retain the freedom to diagnose E_θ, E_q, and E_h separately; in the following, we use the degree of equality between these fluxes as a criterion for model fidelity to the physical system.

3 Results

In Sect. 3.1, we describe the effective entrainment in the Sc regime in E3SM according to the entrainment diagnostics introduced in Sect. 2.5. We analyze which properties of the atmospheric column influence the entrainment. To perform an unambiguous demonstration of a causal effect of increased aerosol on entrainment and PBL drying, we then turn to SCM analysis in ModelE3 and E3SM in Sect. 3.2. We return to the 3D atmosphere in a model configuration without precipitation suppression in Sect. 3.3 to search for evidence of a causal mechanism leading to reduced ℒ in response to anthropogenic aerosols.

3.1 GCM effective entrainment

In a numerical model, the spatial discretization can potentially alter the behavior of the PBL in a qualitative way. The physical Sc-topped PBL entrains free-tropospheric air by O(1 m)-scale turbulent exchange through a sharp buoyancy barrier (Wood, 2012, and references therein). In the model, the static stability due to thermodynamic jumps across the inversion at PBL top is less localized and weaker due to the finite vertical resolution. Depending on the model resolution, the resolved-scale advection scheme, and the turbulence parameterization, vertical mixing across the poorly resolved inversion may be too strong. This can occur because the stability reported to the turbulence scheme is underestimated or because fluctuations in the resolved-scale vertical velocity mix the air masses instead of moving the boundary between them. Collectively, we term these behaviors model artifacts. The problem with model artifacts in mixing is that the effect of such mixing on the PBL temperature and humidity need not have the correct susceptibility to the multitude of anthropogenic perturbations – forcing by and adjustments to both aerosol and greenhouse-gas forcings as well as feedback mechanisms in response to anthropogenic global warming – that are hypothesized to influence cloud-top entrainment by changing the atmospheric state (N_d, temperature, and humidity in the PBL and FT and FT emissivity).

Therefore, our task is to determine whether the mixing in the model behaves more like physical entrainment or more like artificial mixing. If we calculate E_θ, E_q, and E_h in Eqs. (3)–(5) as residuals, then they describe the mixing between PBL and FT, including both entrainment and model artifacts. We then apply three criteria that help us make that determination:

1. In the real atmosphere, $E_{\mathit{\theta }}=E_q=E_h$ all describe the same entrainment mass flux that comes about due to turbulent processes at the boundary-layer top. In a numerical model, however, the equality of the entrainment fluxes is not a given. For one, models treat θ_l and q_t differently, for example, to ensure nonnegative definite q_t. For another, the length scales at which entrainment occurs reach below 1 m, far beyond the resolved dynamics of most types of models. Mixing between the boundary layer and FT in a model, therefore, results from a combination of resolved advection and parameterizations. Having multiple independent measures of the entrainment mass flux affords us the ability to ask both whether the model-diagnosed entrainment estimates are consistent and whether they are physical. Consistent fluxes are highly correlated, with E_q, E_θ, and E_h close to a 1:1 regression slope. (In an Eulerian model, E_h is difficult to diagnose when the advective tendency of h over a model time step is small compared to the vertical resolution, which is the case in GCMs. We restrict our analysis to E_q and E_θ.)

2. Even if the diagnosed entrainment fluxes are consistent, however, they can still be unphysical. That is, the mass flux could be detraining air out of the boundary layer instead of entraining it into the boundary layer.

3. Finally, the dependence of the entrainment flux on atmospheric conditions can indicate that the wrong mechanisms are at work in the model. For example, a strong dependence of entrainment on the FT vertical velocity would indicate overly strong vertical advection through the capping inversion.

Thus, we propose three measures of the realism of the entrainment representation in a model: the joint distribution of E_θ and E_q, the sign of the mass flux, and the dependence of the entrainment flux on the atmospheric state.

Under Sc conditions (as defined in Sect. 2.2), E3SM produces vertical profiles of q_t and θ_l consistent with a fairly well-mixed PBL capped by a fairly sharp thermodynamic jump. Figure 1 shows composite vertical profiles stratified by PBL depth.

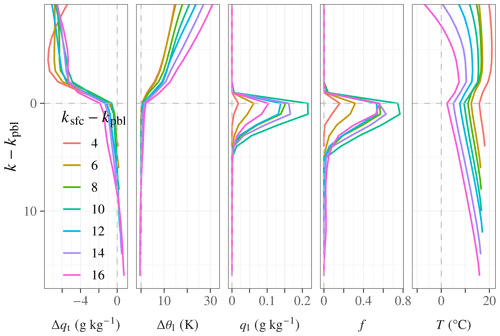
Figure 1 Composite vertical profiles in E3SM Sc conditions as defined in Sect. 2.2. To enable the plotting of a cloud cover profile, the f>0.9 requirement is not applied. Model-level differences are used as the vertical coordinate to avoid artificially smearing the vertical gradients through remapping to a pressure or geometric height coordinate; model thickness varies with height and surface pressure but averages approximately 80 m in the profiles shown. The lowest level in the column at which the temperature increases with altitude is identified as the PBL top, with the corresponding level number, k_pbl. The vertical coordinate is the model level referenced to the PBL top, k−k_pbl (positive downward). Profiles are stratified by the PBL depth, measured as the difference between the PBL-top model level and the lowermost model level k_sfc. (In E3SMv2, k_sfc=72.) Profiles of q_t and θ_l are shown as differences Δq_t and Δθ_l with respect to the mass-weighted vertical mean over the PBL.

The effective entrainment qualitatively agrees very well with physical understanding of the Sc-topped PBL. The fluxes derived from the separate budgets agree well with each other, yielding a close relationship with a slope of near 1 (see joint probability in Fig. 2). Furthermore, the sign of the fluxes is consistent with physical entrainment from the FT into the PBL (E>0; see the marginal cumulative distribution functions in Fig. 2) rather than showing a distribution including both positive and negative values, which would be consistent with numerical diffusion. The instantaneous entrainment also qualitatively responds in the expected way to instantaneous variability (as opposed to climatological spatial variability, seasonal temporal variability, etc.) in properties of the atmospheric column (Fig. 3). Entrainment increases with surface heat fluxes and cloud-top radiative cooling, consistent with increased turbulence production leading to increased entrainment; decreases with the magnitude of the θ_l jump at the inversion, consistent with a stronger buoyancy barrier suppressing entrainment (the negative q_t jump, which reduces the buoyancy barrier, is strongly correlated with the positive θ_l jump); and is independent of the instantaneous grid-scale vertical velocity, consistent with large-scale subsidence moving the boundary between air masses (i.e., the FT and the PBL) rather than mixing them.

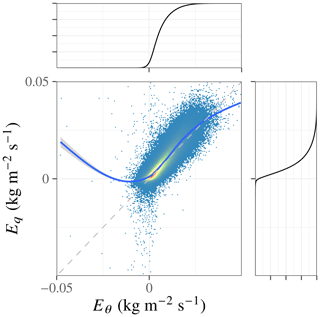
Figure 2 Physical consistency checks on E_q and E_θ. The central panel shows the joint probability density, P(E_q,E_θ), along with a mean E_q smoothed by locally estimated scatterplot smoothing (LOESS) as a function of E_θ (blue line) and dashed gray 1:1 line. The outer panels show the marginal cumulative distributions of E_q and E_θ.

In summary, the entrainment behavior of the GCM, according to the criteria tested for, appears free of numerical artifacts that are due to coarse model resolution. While not exhaustive (e.g., the effect of mixing on the model levels above the inversion is not examined), these entrainment diagnostics allow us to compare the GCM physics to the foundational LES modeling studies on Sc entrainment (e.g., Ackerman et al., 2004; Bretherton et al., 2007; Ackerman et al., 2009), which diagnose entrainment from the entrainment velocity, i.e., the PBL mass budget. We next focus on the effects of anthropogenic perturbations on the modeled entrainment and on how the parameterized model physics affects those entrainment responses.

3.2 Entrainment ACI mechanism in single-column runs

Figure 3 shows that entrainment depends on numerous properties of the atmospheric column. This creates a bewildering web of possible causal and covariability effects by which entrainment internal variability could be correlated with aerosol internal variability in 3D atmosphere runs. SCM runs, in contrast, provide a clean way to diagnose cause and effect in GCM column physics, which is a reason they are widely used during model development. First, the SCM allows us to hold any combination of boundary conditions on a single column fixed. Thus, we can switch off any effects mediated by the grid-scale horizontal circulation. These effects include synoptic-scale confounders of the type discussed by Mülmenstädt et al. (2024b). Second, and relatedly, we are free to explore the effects of model physics on ACI without having to retune the model to the global-mean energy balance. Thus, we avoid the difficult problem of whether to attribute changes in model behavior to the physics changes under investigation versus the nuisance changes required to restore the energy balance that might also affect the ACI behavior (e.g., Golaz et al., 2011; Mülmenstädt et al., 2020, 2021).

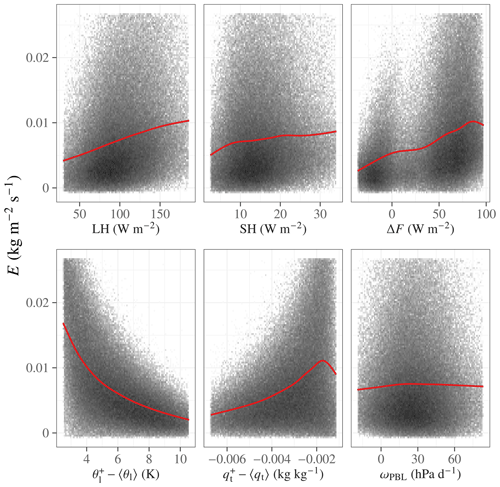
Figure 3 Dependence of entrainment on column properties: surface latent and sensible heat flux, LH and SH; radiative cooling, ΔF (cooling is positive); thermodynamic jumps across the inversion, Δθ_l and Δq_t; and pressure vertical velocity at the PBL top, ω_PBL.

A welcome side effect (and a raison d'être) of SCM use is that the experiment setup closely matches the LES runs that inform so much of our process understanding. Like Ackerman et al. (2004), Bretherton et al. (2007), and Hoffmann et al. (2020), we can focus on well-understood subtropical-subsidence-region Sc and vary one boundary condition – the aerosol concentration – at a time (and, if desired, one model-physics mechanism at a time). This does not address the question of whether the model results are representative of the global-mean effective radiative forcing, which is best addressed with global runs, but it answers the question of whether LES and GCM column physics respond similarly to perturbations around an as-near-as-possible identical base state.

The E3SM SCM uses the two-mode prescribed aerosol concentration profile specified for RF02 (Wyant et al., 2007), while the ModelE3 SCM uses a single accumulation mode aerosol size distribution as described above. We then modify the amplitude of this profile to elucidate the causal effect of N_d change on ℒ. In the ModelE3 SCM, we scan the aerosol number concentration $N_{\text{a}}=\mathit{\{}\mathrm{20},\mathrm{30},\mathrm{40},\mathrm{60},\mathrm{80},\mathrm{120},\mathrm{160},\mathrm{320},\mathrm{640}\mathit{\}}$ cm⁻³. In the E3SM SCM, we scale the prescribed aerosol concentration up and down by a factor of 8: $N_{\text{a}}=N_{{\text{a}}_{\mathrm{0}}}\times \mathit{\{}\mathrm{1}/\mathrm{8},\mathrm{1}/\mathrm{4},\mathrm{1}/\mathrm{2},\mathrm{1},\mathrm{2},\mathrm{4},\mathrm{8}\mathit{\}}$. Prescribing aerosol eliminates ACI mechanisms in which clouds affect the aerosol state, such as potential effects of aerosol scavenging on the N_d–ℒ relationship (McCoy et al., 2020). This simplifies the attribution of ℒ responses to N_d perturbations by removing one class of processes from consideration.

Figures 4 and 5 show the ModelE3 and E3SM SCM time series. In both models, the PBL deepens, indicating entrainment in excess of the subsidence rate; the PBL in both models also deepens by a similar amount when native longwave radiative transfer is used (see Appendix). With the exception of a short duration before and after steps in the discretized PBL depth in E3SM, both models maintain an overcast cloud; the loss of cloud cover in E3SM's SCM when the PBL top jumps by a model level is clearly a model artifact, so these periods are excluded from further analysis by requiring f>0.9 as in the 3D model analysis both here and in part 1. Furthermore, the discrete PBL depth increases are associated with discontinuities in the entrainment diagnostics: a dependence of E on how long the top model level of the PBL has been subject to entrainment in E3SM and a reversion to a constant E once the PBL has deepened in ModelE3. We may be mitigating the E3SM artifact by averaging over two full deepening cycles, effectively averaging over the dependence of E on position in the deepening cycle. We attempt to mitigate the ModelE3 artifact by only averaging E until the first PBL deepening occurs. This choice is subjective, and we note that the other obvious choice, which is to average the entrainment over the same time period (hours 2–12) as the other variables, produces no clear relationship between E and N_d. However, the problem with this averaging method is that earlier deepening in the more entraining cases means that these cases spend more time in the apparent low-entrainment state that characterizes the entrainment-diagnostics artifact, which most strongly lowers the average apparent entrainment in the highest-entrainment cases. On balance, it appears to us that the averaging method we choose better summarizes the behavior of ModelE3 – namely, that the greater magnitude of the entrainment flux with increasing N_d is consistent with the earlier deepening.

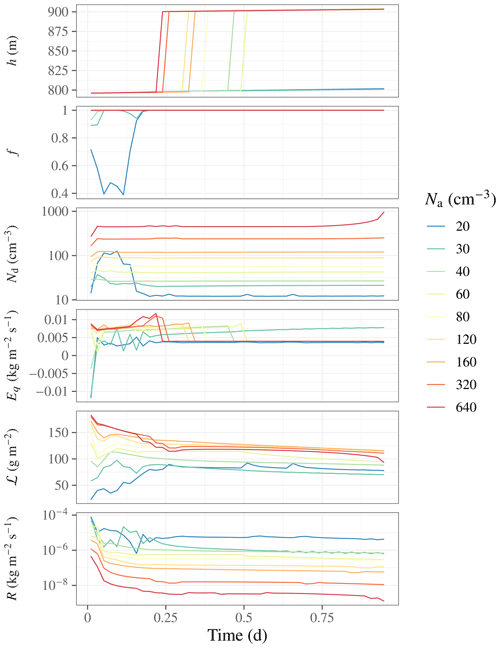
Figure 4 GISS ModelE3 SCM time series of PBL height (height of lowest model level with inverted temperature lapse), h; cloud cover, f; mean droplet number, N_d; entrainment, E; liquid water path, ℒ; and surface precipitation rate, R, for the DYCOMS-II RF02 experiment. Prescribed aerosol concentration varies between N_a=20 and 640 cm⁻³.

As expected, varying the aerosol concentration strongly affects the droplet concentration. From this response, the two SCMs then diverge in the details of their behavior, but they reach the same behavioral endpoint at sufficiently large N_d: enhanced entrainment leading to a loss of ℒ as N_d increases. In ModelE3, ℒ after spin-up starts out with a monotonically increasing N_d dependence; after spin-up, the low-N_d runs experience an increase in ℒ, while the high-N_d runs experience a decrease, leading to a time-average ℒ that first increases with N_d and then decreases (Figs. 4 and 6). The increasingly negative ℒ tendency as a function of N_d accompanies an increasingly strong entrainment warming and drying (Fig. 6). The increase in entrainment with increasing N_d competes with a decrease in precipitation (Fig. 4). ModelE3 with native longwave radiation, however, maintains a 3 times greater ℒ after 24 h duration (see Appendix).

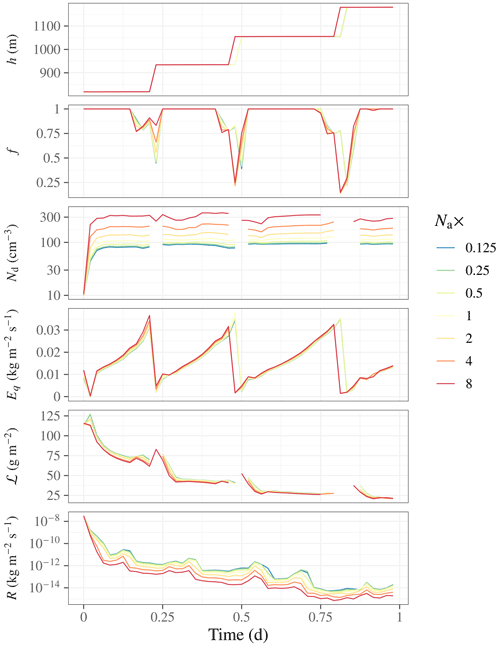
Figure 5 E3SM SCM time series for the DYCOMS-II RF02 setup as in Fig. 4. Prescribed aerosol concentration is varied by a factor of 8 above and below its default value.

In E3SM, ℒ after spin-up has a monotonically decreasing relationship with N_d, which remains true at each point in time throughout the runs. As all runs experience fairly rapid ℒ loss with time, time averages only show weak dependence on N_d (Fig. S3). We can instead quantify susceptibilities by scanning across the different aerosol experiments at each time step; this is shown for ℒ in Fig. 7 and for E in Fig. 8. Precipitation in E3SM largely ceases after the first time step even though drizzle was measured in the DYCOMS-II RF02 observations. In ModelE3 with native LW radiation, precipitation experiences sharp peaks with a periodicity similar to PBL depth increases.

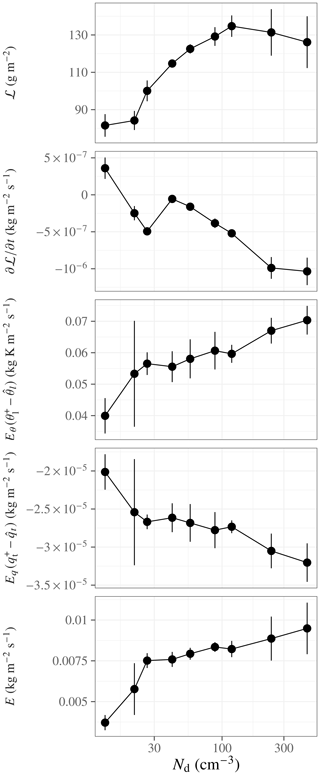
Figure 6 GISS SCM N_d relationships. State variables are averaged over the time period from 2–12 h; error bars indicate the standard deviation. The tendency, $\partial \mathcal{L}/\partial t$, is calculated by linear regression over overcast conditions (f>0.9) between the end of spin-up (hour 2) and hour 12; error bars indicate the standard error in the regression slope. In the thermodynamic jumps, we use the shorthand ${\widehat{\mathit{\theta }}}_{\text{l}}=\langle {\mathit{\theta }}_{\text{l}}\rangle$ and ${\widehat{q}}_{\text{t}}=\langle q_{\text{t}}\rangle$.

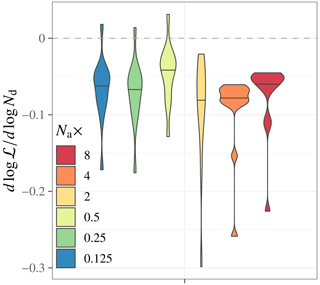
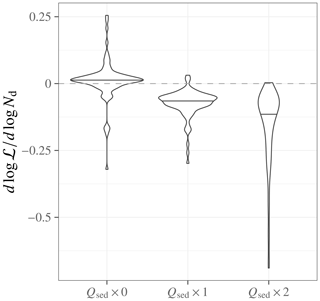
Figure 7 E3SM SCM $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$. Susceptibilities are calculated at every time step from the δlog ℒ and δlog N_d in the perturbed-aerosol experiment relative to the default-aerosol experiment. The plot shows the density distribution of $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$ over all time steps from the end of the spin-up period (2 h) to 12 h, excluding periods when the cloud fraction drops below 0.9. Horizontal black lines across the density plots indicate the median.

Figure 8 E3SM SCM $\partial \log E/\partial \log N_{\text{d}}$ as in Fig. 7 but showing the susceptibility of cloud-top entrainment.

Whether the effect of varying the aerosol concentration on ℒ is expected depends on our Bayesian prior. The agreement on RA_ℒ<0 across CMIP5-era GCMs (Gryspeerdt et al., 2020), which persists in the newer-generation models examined in part 1, and the absence of enhanced entrainment physics in some GCMs (e.g., Salzmann et al., 2010) have led to the notion that GCMs may be structurally incapable of representing the enhanced entrainment mechanism known from LES (e.g., Zhou and Penner, 2017). This thinking is in tension with a long line of parameterization work (e.g., Randall et al., 1985; Lock et al., 2000; Bretherton and Park, 2008; Guo et al., 2011; Karset et al., 2020), indicating that it may well be possible to represent this mechanism in GCMs either through direct parameterization or as emergent behavior. If our expectation is based on the LES-based process understanding, then we would predict the causal effect of N_d to be a decrease in ℒ. The surprising result is that the SCM sides with the LES (see Appendix) rather than the 3D GCM with which the SCM shares its model physics. Recall that the E3SM 3D GCM run, in contrast to the E3SM SCM run, showed negligible response of climatological ℒ to the anthropogenic N_d increase (Sect. 2.4).

While the SCM behavior is consistent with our mechanistic understanding of entrainment-mediated drying, we need to point out several caveats. First, the details of what entrainment-mediated drying entails are different in the two models as discussed above, and we find in Sect. 3.3 that the behavior in the 3D E3SM run is more consistent with the ModelE3 SCM than with the E3SM SCM. Second, the E3SM SCM entrainment fluxes reach the equivalent of several centimeters per second in entrainment velocity, which is significantly stronger than the fluxes that LES or the ModelE3 SCM produces for this case and stronger than the fluxes that the E3SM 3D run produces for Sc on average. Third, if the E3SM physics had not serendipitously produced very low precipitation rates, the decrease in ℒ with increasing N_d would probably have been overwhelmed by the precipitation suppression signal. None of these caveats negate the finding that the GCM physics appears capable of producing entrainment-mediated ℒ loss qualitatively consistent with LES findings, and significant intermodel diversity is to be expected in SCM studies (Zhu et al., 2005; Wyant et al., 2007). They do, however, indicate that there is ample further process investigation to be performed in future work.

We conduct several additional E3SM SCM experiments with perturbed physics. These experiments further test that the causal effect of aerosols on ℒ in SCM mode not only has the same sign as in LES but also proceeds via the same physical mechanisms and show that the entrainment-mediated drying can be tuned to agree quantitatively with LES.

• Sedimentation–entrainment feedback is the source of entrainment enhancement. Size-dependent sedimentation is one of the processes by which higher-N_d clouds lose liquid relative to lower-N_d clouds in LES (Bretherton et al., 2007) under sufficiently dry overlying air (Ackerman et al., 2004). The Gettelman et al. (2015) microphysics parameterizes size-dependent sedimentation. Guo et al. (2011) showed through process denial experiments that ℒ loss only occurs when this process is included in the SCM version of the Geophysical Fluid Dynamics Laboratory (GFDL) AM3 model. This is true in the E3SM SCM as well; Fig. 9 shows that $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$, which is negative when the size-dependent sedimentation is active, becomes ≈0 when we switch off the sedimentation flux and thus its size dependence.

• Parameter tuning can move the GCMs toward quantitative agreement with LES on susceptibility. The ModelE3 SCM closely replicates LES of the RF02 case (Appendix A). While the E3SM SCM behaves significantly differently than LES in that it is non-precipitating for most of the run, it does appear that its entrainment-mediated ℒ susceptibility can be moved closer to LES estimates by appropriate parameter choices. Figure 9 also shows that increasing the size-dependent sedimentation by a factor of 2 makes $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$ more negative. Quantitatively, this brings the E3SM SCM closer to quantitative agreement with LES ($-\mathrm{0.35}\le \partial \log \mathcal{L}/\partial \log N_{\text{d}}\le -\mathrm{0.22}$; Ackerman et al., 2004, Table S1 in the Supplement). It may be possible to achieve quantitative agreement by combining the sedimentation tuning factor with similar tuning factors in the turbulence parameterization. This would not be an outlandish model tuning, considering that it may be taking the role of an enhancement factor (Covert et al., 2022) compensating for the coarse vertical discretization, O(100 m), compared to the process scale, O(1 m).

• The liquid water path reduction could also have an important shortwave absorption component. The DYCOMS-II RF02 SCM specification calls for a nocturnal simulation, i.e., without shortwave radiative effects. In the E3SM SCM, we perform a sensitivity test with shortwave radiative effects in which the sun rises at 12 h (not shown); this simulation is less entraining overall, deepening only once, and is only able to sustain its cloud cover for ≈18 h. During the daytime portion (hours 12–18), this configuration's $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$ is more negative than that of the LW-only simulation. The absorption of shortwave radiation at cloud top exerts a warming effect that increases with N_d (Stephens, 1978; Hoffmann et al., 2020). The behavior of the SCM run with shortwave radiation is consistent with this N_d-dependent cloud-top heating. Cloud-top heating counteracts longwave cloud-top cooling, reducing the entrainment. Shortwave heating increases with increasing N_d and decreasing ℒ.

Figure 9 E3SM SCM $\partial \log \mathcal{L}/\partial \log N_{\text{d}}$ variation with size-dependent sedimentation as in Fig. 7 but with a varying scale factor applied to the sedimentation flux, Q_sed.

3.3 Entrainment ACI mechanism in 3D model runs

If the entrainment-mediated adjustment of ℒ is evident in the SCMs, what becomes of it in the full 3D model atmosphere? From Mülmenstädt et al. (2024b), we know that RA_ℒ<0; that is, ℒ under PD emissions is greater than ℒ under PI emissions, opposite in sign to what is expected from the entrainment-mediated mechanisms and from the SCM. To understand why this happens, we use diagnostics targeted at entrainment mechanisms and perform model experiments designed to isolate entrainment mechanisms.

3.3.1 Indications of entrainment mechanisms in PD correlations

Figure 10a shows cloud-top entrainment into the Sc PBL as a function of N_d and ℒ. Two things are readily apparent in this figure. First, entrainment has a strong dependence on ℒ. Entrainment is expected to increase with ℒ based on the ability of the cloud to generate turbulence, which depends on the availability of liquid water for evaporation and cloud-top radiative cooling. The ℒ values at which entrainment turns on are in reasonable agreement with recent LES (Hoffmann et al., 2020) and observational (Zhang and Feingold, 2023) results. Zhang and Feingold (2023), reporting on MODIS retrievals, state that 50 g m⁻² is the threshold for efficient radiative cooling. Hoffmann et al. (2020), reporting on LES experiments, are less explicit, but, depending on the choice of entrainment parameterization and for their LWP_∞=60 g m⁻² simulation, their Fig. 4 shows a sharp turn-on that saturates between approximately 20 and 40 g m⁻².

Second, at a given ℒ, entrainment increases with N_d. This is shown quantitatively in Fig. 11: in all three Sc regions (see Sect. 2.2), the entrainment susceptibility, $\partial \log E/\partial \log N_{\text{d}}{|}_{\mathcal{L}}$, is higher than 0 except at low ℒ, and the cloud water loss increases (the Eulerian tendency, $\partial \mathcal{L}/\partial t$, becomes more negative) with increasing N_d.

The main conclusion from these plots is that the model produces greater entrainment in response to higher N_d in Sc clouds with high-enough ℒ to support strong entrainment. In other words, there appears to be mechanistic agreement between the model physics and process understanding of RA_ℒ via entrainment enhanced by increased droplet number. Further support for this conclusion comes from the instantaneous ℒ tendency, $\partial \mathcal{L}/\partial t$. The regression slope, ${\partial }^{\mathrm{2}}\mathcal{L}/\partial$ $N_{\text{d}}\partial t{|}_{\mathcal{L}}$, is predominantly negative except at low ℒ. In other words, clouds with a positive entrainment susceptibility also exhibit a negative liquid water tendency, the magnitude of which increases with N_d, confirming that there is a relationship between entrainment susceptibility and cloud water loss (presumably to drying).

There is reason to be cautious, however. We have tested whether the known negative N_d–ℒ correlation occurs in conjunction with positive N_d–E and negative N_d–$\partial \mathcal{L}/\partial t$ correlations, consistent with an entrainment drying adjustment to an N_d increase. This peels away one layer of confounding between N_d and ℒ, increasing our confidence that there is a mechanistic link between N_d, E, and ℒ. However, it is possible that the relationships of E and $\partial \mathcal{L}/\partial t$ with N_d are themselves confounded, just as the regression between N_d and ℒ was found to be a result of covariability by Mülmenstädt et al. (2024b).

3.3.2 Absence of entrainment-mediated adjustment in PI and PD emissions experiments

In the Sc regime, there are hints of behavior in accordance with process understanding (e.g., Randall, 1984; Ackerman et al., 2004): ℒ decreases in response to the anthropogenic N_d increase when the relative humidity (RH) in the FT (diagnosed from the first model level above the inversion) is the lowest, as shown in Fig. 12. However, there are multiple reasons these results should be treated with caution until they can be confirmed in longer model runs. First, the dependence on FT RH is not robust across Sc regions. While northeast Pacific (NEP) and southeast Pacific (SEP) Sc regions show negative ℒ susceptibility to anthropogenic N_d at low FT RH and positive ℒ susceptibility at high FT RH (with ℒ decrease overall), the southeast Atlantic (SEA) Sc region shows no clear pattern. Furthermore, the NEP and SEP behavior requires us to select only the completely overcast condition (cloud fraction of f=1 rather than the default f>0.9 requirement we use elsewhere; this reduces the data sample from approximately 3.7×10⁵ to 1.2×10⁵ columns). Otherwise, the ℒ susceptibility has no clear sign or FT RH dependence across regions. A final puzzling observation is that the entrainment mass flux, entrainment temperature flux, and entrainment moisture flux are all virtually unchanged between PD and PI emissions. On balance, the conservative interpretation of these results is that any potential ℒ reduction signal in response to anthropogenic aerosol is small enough to require far longer model runs to detect.

In the global mean, ℒ is virtually unchanged when emissions are changed from PI to PD in our E3SM configuration with deactivated precipitation suppression. (The reader may recall from Sect. 2.4 that the global-mean warm, overcast cloud is $\mathrm{\Delta }\log \mathcal{L}=\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{3}}$.) Thus, even if an entrainment-drying ACI mechanism is represented in the model (as the evidence from the SCM experiments in Sect. 3.2 and the PD statistics in Sect. 3.3.1 suggests), the model considers that mechanism's global effect to be negligible.

One possible explanation as to why the positive susceptibility of E to N_d seen in PD internal variability does not lead to a decrease in ℒ is that entrainment susceptibility may beget its own demise (Zhu et al., 2005; Wood, 2012). (We reiterate, as throughout, that another possible explanation for relationships seen in internal variability is confounding.) It is true that E appears to increase with N_d at given ℒ (Fig. 10a). However, ℒ is not fixed during the temporal evolution of a cloud; as long as the cloud remains surface-coupled, closed-cell Sc, increased entrainment leads to loss of ℒ. But at lower ℒ, entrainment is weaker. Eventually, entrainment may even decrease ℒ to a low-enough value that the cloud is protected from further entrainment drying (Hoffmann et al., 2020; Zhang et al., 2022). Cloud aggregate statistics are consistent with this interpretation, where the E susceptibility to N_d at fixed ℒ is positive (Fig. 10a), but the overall susceptibility of E on N_d still becomes negative at sufficiently high N_d (Fig. 10b) due to the strong negative correlation between ℒ and N_d. If such a negative feedback mechanism is at play, it would be an example of buffering in the cloud system (Stevens and Feingold, 2009): an initial cloud loss process being shut off by the change in cloud state due to that process.

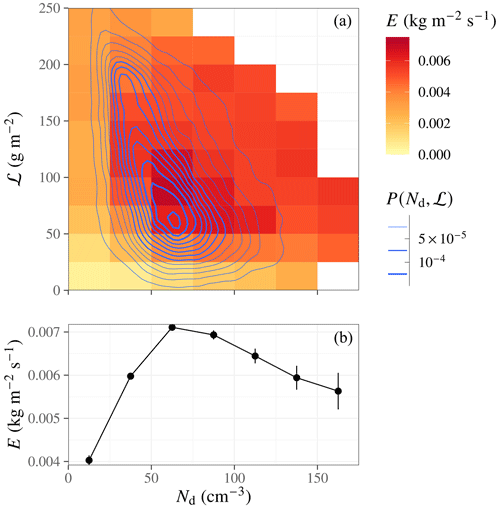
Figure 10 E3SM 3D atmosphere entrainment, E. Panel (a) shows the dependence on ℒ and N_d; only boxes with n>25 points are included. Contours of the density, P (N_d, ℒ), are overlaid. Panel (b) shows the dependence of E on N_d when the ℒ-dependent entrainment, E (N_d, ℒ), is integrated over the ℒ distribution; error bars indicate the standard error.

4 Discussion, conclusions, and recommendations

We have documented two surprising behaviors from GCMs. The first is that GCMs can produce negative N_d–ℒ PD correlations that do not predict RA_ℒ (Mülmenstädt et al., 2024b). In terms of mechanistic understanding, the simplest explanation is that the correlation is due to confounding rather than a causal relationship involving the entrainment-mediated mechanisms suggested by process scale modeling.

This is where models had a second surprise in store: there is actually a causal negative relationship between aerosol and ℒ. The evidence for this causal relationship comes from SCM studies, where, like Guo et al. (2011), we find that increased aerosol, while holding all other boundary conditions fixed, leads to liquid water loss at sufficiently high N_d. Furthermore, this loss appears to be due to increased entrainment, or at least it occurs in conjunction with increased entrainment when the aerosol boundary condition is increased. At face value, this would seem to indicate excellent mechanistic agreement with LES-based process understanding that enhanced entrainment drying reduces ℒ. Also, 3D atmosphere runs show evidence for entrainment-mediated liquid water loss in correlations between entrainment and N_d.

However, like Karset et al. (2020), we find that a secular N_d increase caused by anthropogenic emissions leads, at best, to a very weak decrease in ℒ unlike what would be expected from the SCM idealized case study or the relationships found in PD internal variability (increased E and increasingly negative $\partial \mathcal{L}/\partial t$ when N_d increases). This may be a manifestation of buffering of the cloud system against perturbations; a candidate for the buffering mechanism is that enhanced entrainment leads to sufficient liquid water loss to shut off entrainment driven by cloud-top radiative cooling, protecting the clouds from further liquid loss.

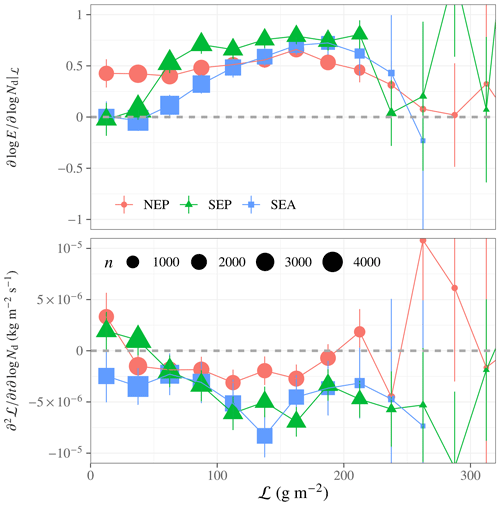
Figure 11 Susceptibility of entrainment and $\partial \mathcal{L}/\partial t$ to N_d. Susceptibility to N_d is calculated as linear regression slope of log E and $\partial \mathcal{L}/\partial t$ against log N_d over instantaneous PD statistics within each ℒ bin.

Summarizing the findings from parts 1 and 2 of this series of papers, we come to the following conclusions. First, negative relationships between N_d and ℒ observed in PD internal variability are not necessarily indicative of a causal reduction in ℒ and thus not necessarily predictive of decreased ℒ when N_d increases due to anthropogenic emissions in GCMs. Second, causal negative relationships between N_d and ℒ in LES are not necessarily representative of the more diverse ensemble of clouds in the global-mean RA_ℒ. Thus, the disagreement on the sign of RA_ℒ between global models and other lines of evidence (Bellouin et al., 2020) may not be solely due to a deficiency in the GCM physics; it could also be due to known deficiencies in the other lines of evidence.

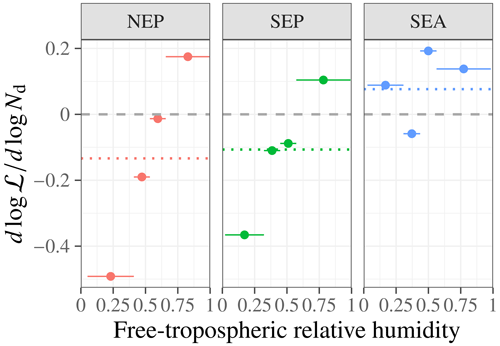
Figure 12 E3SM 3D atmosphere, $d\log \mathcal{L}/d\log N_{\text{d}}$, stratified by free-tropospheric relative humidity quartiles. The susceptibility is calculated from the differences, Δlog ℒ and Δlog N_d, between PD and PI emission runs averaged over each RH bin in each Sc region. Dashed lines indicate the regional Sc $d\log \mathcal{L}/d\log N_{\text{d}}$ mean integrated over free-tropospheric relative humidity.

Casting doubt on whether we even know the sign of RA_ℒ is a highly unsatisfactory state of affairs. Answering the following six questions would provide a potential remedy:

• What complexity is required? Many different processes are at play, and it is not clear which ones are represented in the models studied here through either parameterization or emerging from the interplay of physics and dynamics. There is certainly value in (and models are suited to) studying how the climate response depends on the processes included in the model. But trying to include all known or hypothesized processes could fall into the trap of amassing a zoo of nth indirect effects (Stevens and Feingold, 2009; Mülmenstädt and Feingold, 2018). Instead of making the model overly elaborate with redundant and competing parameterizations (Proske et al., 2023), the approach leading to the lowest climate projection uncertainty may lie in finding the minimal set of parameterizations that allow for the model to reproduce physical process understanding of the sensitivities that matter for the climate problem: sensitivities to those boundary conditions that change with aerosol and greenhouse-gas effective radiative forcing (ERF) or with global warming. Evident qualitative differences in the E3SM and ModelE3 SCM behaviors compared with one LES and the challenges of well-constraining LES with observations are reminders that the representation of basic microphysical and turbulent processes still afford ample opportunity for tighter constraints.

• What resolution is required? GCM resolution can offer, at best, a cartoon version of the mechanisms at play in real clouds. But cartoon does not have to be a pejorative; it is the simplest representation of reality that can convey the author's intent (wit; satire; heuristic simplification; or, when applied metaphorically to models, predictive skill for a different climate state). As noted in the previous paragraph, there is value in simplicity. There is a trade-off between resolution and simplicity, however; the coarser the resolution, the greater the reliance on the parameterized physics and the longer the list of phenomena that need to be parameterized. Can the climate effect of entrainment be adequately captured by bulk entrainment throughout the GCM grid box, or is the mesoscale variability, in the form of the cloud-top circulation engulfing free-tropospheric air (e.g., Yamaguchi and Randall, 2012; Zhou and Bretherton, 2019), essential for a correct projection of the entrainment response to anthropogenic perturbations? (And, in that case, are kilometer-scale storm-resolving global models able to represent these features by beginning to resolve the mesoscale dynamics of large Sc cells?) How far this trade-off between resolution and parameterization can be pushed determines the minimal resolution required for reliable climate projections. Terai et al. (2020) and other studies already provide hints at the answer. An important additional piece of information that can be obtained from the entrainment diagnostics presented here is how entrainment behavior changes, qualitatively and quantitatively, as model resolution is coarsened from LES (or, ideally, direct numerical simulation of the cloud-top turbulence; Mellado et al., 2018) to global storm-resolving models to 10–100 km scale GCMs.

• How do base-state and process errors affect modeled climate responses? Our results show that entrainment and its susceptibility are strong functions of ℒ and N_d. The climate response may also be a function of the model's FT RH, which appears biased high in E3SMv2. Dependence on base state (Christensen et al., 2023; Varble et al., 2023) and competing processes (Mülmenstädt et al., 2020, 2021) in models necessitates careful evaluation of the base-state N_d and ℒ, paying close attention to issues of definition and aggregation (Elsaesser et al., 2017; Feingold et al., 2022; Varble et al., 2023). Better constraints on the base state alone can run into equifinality problems (von Bertalanffy, 1950; Beven and Freer, 2001; Lee et al., 2016; Regayre et al., 2018; Mülmenstädt and Feingold, 2018) that negate a direct reduction in climate projection uncertainty (Lee et al., 2016; Regayre et al., 2018; Mülmenstädt et al., 2020, 2021; Zelinka et al., 2022). In the case of entrainment, however, the apparent strong dependence of the process representation on base-state errors may yield a significant payoff in tighter constraints on climate projections when the base state is improved.

• What observational constraints on the entrainment process are available? Along with vital advances in teasing causality out of observations of cloud N_d and ℒ (Fons et al., 2023), the biggest step forward along the observational track would be better constraints on the entrainment process itself. One possibility may be to diagnose subadiabaticity (Merk et al., 2016; Varble et al., 2023) as an indicator of the cloud liquid loss. This would only provide a time-integrated measure of the loss processes and, as such, would require disentangling entrainment drying from precipitation.

• How representative are susceptibilities derived in small ensembles of individual cases? Given the difficulty of placing observational constraints on entrainment, the most convincing evidence for entrainment-mediated RA_ℒ continues to come from LES studies. Large ensembles of LES cases (e.g., Gustafson Jr. et al., 2020; Glassmeier et al., 2019) are vital to provide resilience against the possibility that the well-studied, often idealized canonical subsidence Sc conditions may not be representative of the global-mean role that cloud-top entrainment plays in effective radiative forcing of the climate by aerosol–cloud interactions (ERFaci). These LES ensembles will be particularly valuable if they span the initial-value and boundary-value problem aspects of the climate response (i.e., sample the vast variability in meteorology encountered by Sc clouds in the climate) and if they provide cloud life cycle evolution (Kazil et al., 2021) that can be validated against cloud life cycle observations (Christensen et al., 2020) sufficiently to ensure LES adequacy for purpose, given differing results in multi-LES studies (e.g., Ackerman et al., 2009). The same point on the importance of large ensembles holds for SCM studies: the differences between E3SM and ModelE3 SCM of the DYCOMS-II RF02 case, as well as the differences between the high-entrainment E3SM SCM and moderate-entrainment E3SM 3D runs, illustrate the need for a set of SCM test cases that better approximate the diversity of meteorological conditions encountered in the climate. A way forward would be to perform the suite of SCM causal aerosol perturbation experiments and mechanism denial experiments from Sect. 3.2 on an ensemble of single-column cloud cases from a 3D run using the SCM ability to replay the forcing of the column by the 3D atmosphere (Bogenschutz et al., 2020).

• Was precipitation suppression the bigger problem all along? According to our results, and consistent with Karset et al. (2020), cloud-top entrainment, even when represented in the model physics, only appears to play a small role in the global-mean RA_ℒ. If this GCM finding reflects reality, focusing on the precipitation-mediated component of RA_ℒ takes on renewed importance.

Recognizing that the ACI climate problem is, at its core, a multiscale physics problem is crucial, as is recognizing that no single line of evidence is capable of putting our knowledge of RA_ℒ on solid footing (Mülmenstädt and Feingold, 2018). The above research questions are a sketch of a multiscale modeling and observations roadmap. Simultaneously, by accounting for the multiscale nature of the problem, they would put us on a path of reliable climate projections beyond the global energy budget (e.g., projecting regional hydrologic extremes due to the spatial heterogeneity of ERFaci) by ensuring that global modeling systems correctly represent both the spatial pattern of ERF and the response of the circulation at all scales to this forcing (Mülmenstädt and Wilcox, 2021).

Appendix A: Tracing DYCOMS-II RF02 model behavior from LES to SCM

The SCM setup here is based on the Ackerman et al. (2009) intercomparison of LESs, which is in turn based on airborne observations of a nocturnal marine Sc deck during the DYCOMS-II project (Stevens et al., 2003; vanZanten et al., 2005) following an approximate Lagrangian trajectory over 5 h (to paraphrase the description of Wyant et al., 2007). The purpose of this appendix is to connect LES of the case to the SCM setups and results in this study.

A representative LES in that study was the Distributed Hydrodynamic Aerosol and Radiative Modeling Application (DHARMA) model, run here with two-moment cloud microphysics (Tornow et al., 2021) and with a vertical grid spacing of δz=5 to 200 m above the original inversion to avoid a positive feedback between entrainment and grid spacing that arises on the grid specified by Ackerman et al. (2009), which was designed to accommodate simulations of 6 h in duration instead of the 24 h used here.

The ModelE3 SCM is run here following the specifications of Ackerman et al. (2009), with one departure being that aerosols are treated as a monomodal lognormal distribution with a fixed-number mixing ratio (corresponding to 60 cm⁻³ at 900 hPa and 10 °C) instead of the bimodal size distribution specified by Ackerman et al. (2009), which produces comparable N_d values to the LES, as seen in Fig. A1.

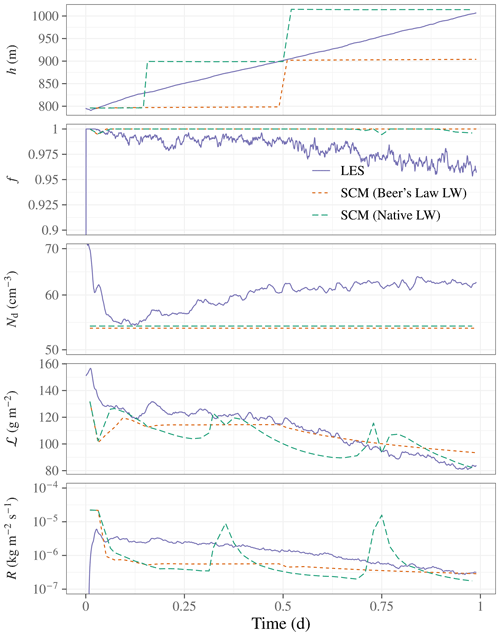
Figure A1 Evolution of domain-mean scalar diagnostics during 24 h simulations from DHARMA LES (solid blue line) and ModelE3 SCM using Beer's law parameterization of longwave radiative cooling per Ackerman et al. (2009) (short-dashed red line) and the ModelE3 native LW radiative transfer (long-dashed green line). The panels at the top depict domain-mean inversion height (location of maximum gradient in potential temperature below 5 km in altitude), stratiform cloud cover (fraction of columns with an opacity of at least 2.5 in the LES), cloud droplet concentration (average weighted by cloud water mixing ratio), liquid water path, and surface precipitation rate.

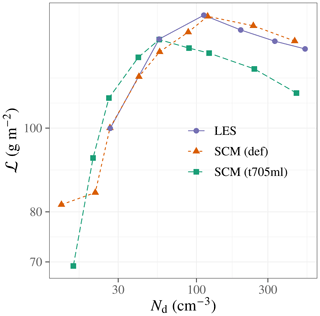
Figure A2 Domain-mean ℒ versus N_d (vertical average weighted by the cloud water mixing ratio) for the DHARMA LES (solid blue line) and two ModelE3 SCM configurations: the default tuning (short-dashed red line) analyzed in this study and the machine learning tuning, Tun1 (long-dashed green line), used in part 1. The outputs are averaged over hours 2–12, and Beer's law parameterization of longwave flux divergence is used for the LES and SCM.

The LES and ModelE3 SCM model setups also both depart from the Ackerman et al. (2009) specification of cloud water sedimentation and instead use the treatment in their (similar) native microphysics schemes of cloud water sedimentation (assuming a gamma distribution with a relative dispersion of 0.3, per Geoffroy et al., 2010, in the SCM and with a relative dispersion of 0.2 in the LES).

Given that this case was used for the development and default tuning of the ModelE3 SCM, it is not a surprise that the SCM results match the LES reasonably well, with the greatest differences being (1) modestly slower entrainment and, thus, deepening of the marine boundary layer (MBL) in the SCM and (2) about a factor of 2 less drizzle reaching the surface for most of the duration. While the formulations of the SCM and LES are different and such differences are to be expected, we note that a narrowing of the assumed droplet size distribution to match that in the LES has little impact and does not deepen the MBL more over the 24 h duration (not shown). We also note that the stronger drizzle for the LES is not explained by its assumption of a narrower raindrop size distribution, which on its own would instead be expected to result in weaker drizzle at the surface.

As briefly noted in the main text, the SCM setup used for the E3SM further departs from the Ackerman et al. (2009) specification and the ModelE3 SCM setup here in a number of ways, among them by (1) not using the specified surface stress, (2) not adopting the specified Beer's law parameterization of longwave flux divergence, and (3) not applying the local subsidence rate to vertical gradients using first-order upwinding to avoid complications with divergent flow but instead treating the specified divergence using the dynamic core. While we are unable to even begin to match departure (3), we are able to consider departures (1) and (2) with the ModelE3 SCM. For (1), we adopted the equilibrated surface stress from the E3SM results, which has had very little impact on the results (not shown). For (2), we used the ModelE3 native longwave radiation scheme employing the ModelE3 SCM standard machinery to patch in the McClatchey et al. (1972) standard atmosphere above the 1.5 km top of the initial sounding provided by Ackerman et al. (2009). As seen in Fig. A1, doing so results in appreciably faster entrainment, which better matches the E3SM SCM results (Fig. 2) that also deepens by about 350 m over the 24 h duration.

The inverted-V relationship between ℒ and N_d is evident in the LES and ModelE3 SCM results (Fig. A2). The match to the LES results is not a surprise for the default tuning as such a comparison was considered in the ModelE3 model development phase. However, the decent match of Tun1, a product of the machine learning tuning of the parent GCM, results partly from skill in limiting the range of parameters that the machine learning explored and partly from luck as some parameter combinations devised by the machine learning did not result in such a good match to the LES result in these terms (not shown).