Improved calculation of single-scattering properties of frozen droplets and frozen-droplet aggregates observed in deep convective clouds

During multiple field campaigns, small quasi-spherical ice crystals, commonly referred to as frozen droplets (FDs), and their aggregates (frozen-droplet aggregates, FDAs) have been identified as the predominant habits in the upper regions of deep convective clouds (DCCs) and their associated anvils. These findings highlight the significance of FDs and FDAs for understanding the microphysics and radiative properties of DCCs. Despite the prevalence of FDs and FDAs at the tops of DCCs where they directly contribute to cloud radiative effect, the detailed single-scattering properties (e.g., scattering-phase function P₁₁ and asymmetry parameter g) of FDs and FDAs remain highly uncertain. This uncertainty is mainly due to insufficient in situ measurements and the resolution of cloud probes, which hinder the development of idealized shape models for FDs and FDAs. In this study, two shape models, the Gaussian random sphere (GS) and droxtal (DX), are proposed as possible representations for the shapes of FDs and FDAs measured in situ. A total of 120 individual models of GSs and 129 models of DXs were generated by varying their shapes. Furthermore, by attaching these individual models in both a homogeneous and heterogeneous manner, three different types and a total of 404 models of FDAs were created: (1) aggregates of GSs; (2) aggregates of DXs; and (3) combinations of GSs and DXs, which are called habit mixtures (HMs). The P₁₁ and g values of the developed models were calculated using a geometric optics method at a wavelength of 0.80 µm and then compared with those obtained using a polar nephelometer (PN) during the CIRCLE-2 field campaign to assess the models. Both individual-component ice crystals (i.e., either GS or DX) and homogeneous-component aggregates (i.e., either aggregates of GSs or aggregates of DXs) showed substantial differences compared with the PN measurements, whereas the P₁₁ of the HMs was found to most accurately match the P₁₁ measured in situ, reducing the differences to +0.87 %, +0.88 %, and −5.37 % in the forward-, lateral-, and backward-scattering regions, respectively. The g value of the HMs was found to be 0.80, which falls within the range of the PN measurement (0.78 ± 0.04). The root-mean-square error for the HM was minimized to a value of 0.0427. It was shown that the novel HMs developed in this study demonstrated better performance than in previous research where HMs were developed indirectly by weighting the calculated P₁₁ of shape models to interpret in situ measurement. The results of this study suggest potential implications for enhancing the calculation of single-scattering properties of ice crystals in DCCs.

1 Introduction

Deep convective clouds significantly influence the Earth's energy budget, hydrological cycle, and climate system (Jensen et al., 1996; de Reus et al., 2009; Frey et al., 2011; Gayet et al., 2012; Raymond and Blyth, 2016). Characterized by intense updrafts and towering vertical structures, these clouds play a crucial role in transporting heat, moisture, and momentum throughout the troposphere (Houze, 2014; Lee et al., 2019), as well as injecting water vapor into the stratosphere (Dauhut and Hohenegger, 2022). Vertical motions lift moist air, resulting in the formation of ice crystals and subsequent precipitation (Andreae et al., 2004). Their radiative properties are crucial, affecting the Earth's radiative balance, through solar and terrestrial radiation interactions. Understanding these properties is vital for climate models and feedback mechanisms. Furthermore, deep convective clouds contribute to severe weather events, like thunderstorms, heavy rainfall, and lightning, impacting weather prediction and societal concerns (Williams, 2018). Therefore, investigating their radiative properties advances our comprehension of their atmospheric and climatic role, enhancing climate projections and weather forecasting.

Limited in situ observations have been made to characterize the microphysical and radiative properties of deep convective clouds, especially in convective cores, due to safety concerns related to the vigorous updrafts (> 15 m s⁻¹), which prevent penetrations of research aircraft into the cores. During the Cirrus Cloud Experiment (CIRCLE-2, Gayet et al., 2012), the Deep Convective Clouds and Chemistry (DC3, Barth et al., 2015), and the CapeEx19 (Nairy, 2022) field campaigns, the microphysical properties (e.g., size and habit distributions) of ice crystals at the upper levels of deep convective clouds were measured. These upper regions of deep convective clouds were characterized by abundant quasi-spherical ice crystals, with maximum dimensions (D_max) smaller than ∼ 50 µm (Heymsfield and Sabin, 1983; Phillips et al., 2007; Lawson et al., 2010; Järvinen et al., 2016) and their aggregates (Gayet et al., 2012; Baran et al., 2012; Stith et al., 2014; Järvinen et al., 2016; Um et al., 2018). The presence of small quasi-spherical frozen droplets (FDs) has been attributed to homogeneous freezing of supercooled droplets rapidly ascending in the updraft (Rosenfeld and Woodley, 2000; Gayet et al., 2012), whereas linear “chain-like” frozen-droplet aggregates (FDAs) have been observed in environments with enhanced electric fields (e.g., electrified thunderstorms) (Saunders and Wahab, 1975; Stith et al., 2002, 2004; Lawson et al., 2003; Connolly et al., 2005; Um and McFarquhar, 2009; Pedernera and Ávila, 2018; Um et al., 2018).

Gayet et al. (2012) observed FDs and FDAs in the overshooting tops of a continental deep convective cloud at a temperature of approximately −58 °C during CIRCLE-2 with unusually high concentrations of ice crystals up to 70 cm⁻³. A dense cloud top exhibited a mean effective diameter of ∼ 43 µm and a maximum particle size of approximately 300 µm, whereas the average asymmetry parameter (g) was determined to be approximately 0.776 using a polar nephelometer (PN) (Crépel et al., 1997; Gayet et al., 1997). Um et al. (2018) further investigated the morphological characteristics of FDs and FDAs using cloud particle imager (CPI) data obtained during the DC3 field campaign. The CPI data were collected from the upper anvils of two storms at altitudes between 12.0 and 12.4 km at temperatures (T) ranging from −61 to −55 °C. It was revealed that FDs and FDAs were the predominant habits, comprising 93.9 % (by number) and 86.3 % (by projected area) of the observed particles, respectively. The average number (4.7 ± 5.0), size (31.79 ± 7.12 µm), and relative position of element FDs comprising the FDAs were also determined (Um et al., 2018).

To quantify the radiative impacts of deep convective clouds, calculations of single-scattering properties of constituent ice crystals are required, and idealized models representing realistic shapes of these constituent ice crystals should be developed. The assumption of spherical shapes for the element FDs within FDAs was made to quantify the morphological characteristics of FDs and FDAs by Um et al. (2018). This assumption is valid for determining the size (i.e., D_max) and the relative position between FDs within FDAs, but it is not suitable for calculating the single-scattering properties (e.g., scattering-phase function P₁₁ and g) of non-spherically shaped FDs (Um and McFarquhar, 2011).

Even though a high-resolution (i.e., 2.3 µm) CPI was used during the CIRCLE-2 (Gayet et al., 2012) and DC3 (Stith et al., 2014) campaigns to image FDs, its resolution was not sufficiently high to fully resolve the three-dimensional morphological features (e.g., non-sphericity and surface roughness) of FDs. This limitation introduces uncertainties in the calculations of single-scattering properties (Um and McFarquhar, 2011). In contrast, the FDs and FDAs imaged by the particle habit imaging and polar scattering (PHIPS, Abdelmonem et al., 2016) probe during the CapeEx19 campaign showed distinct non-spherical, plate-like shapes (Nairy, 2022). On the other hand, FDs captured in the vicinity of the convective core using the Ice Cryo-Encapsulation by Balloon (ICE-Ball) system showed quasi-spherical shapes with pronounced surface roughness (Magee et al., 2021). Laboratory-grown FDs and FDAs have also shown both quasi-spherical and non-spherical shapes of FDs (Pedernera and Ávila, 2018).

Given the uncertainties surrounding the shapes of observed FDs and small ice crystals, several idealized shape models have been proposed to better represent the quasi-spherical nature of FDs and small ice crystals (Jang et al., 2022). These models include the Gaussian random sphere (Muinonen et al., 1996), droxtal (Yang et al., 2003), budding Bucky ball (Um and McFarquhar, 2011), and Chebyshev particle (Mugnai and Wiscombe, 1980; McFarquhar et al., 2002; Um and McFarquhar, 2011; Baran et al., 2012). In particular, two methods, the Gaussian random sphere and droxtal, produce shapes that closely resemble those observed in field campaigns and experiments (Thuman and Robinson, 1954; Ohtake, 1970; Yamazaki and Gonda, 1984; Pedernera and Ávila, 2018; Magee et al., 2021). The Gaussian random sphere is well suited to describe FDs composed of roughened facets, while experiments conducted in a cold cloud chamber at temperatures below −40 °C suggest that the shapes of FDs more closely resemble those of droxtals (see Figs. 2 and 3 of Pedernera and Ávila, 2018). Although Baran et al. (2012) applied a weighted habit mixture model of Chebyshev particles and hexagonal ice aggregates to calculate the single-scattering properties of FDAs, the development of idealized models specifically for FDAs and direct calculations of their single-scattering properties has yet to be thoroughly explored.

In this study, idealized shape models were developed using Gaussian random spheres and droxtals to represent the shapes of FDs and FDAs, and the corresponding single-scattering properties were computed using a geometric optics method. The results of these theoretical calculations are then compared with in situ measurements obtained during CIRCLE-2 to evaluate the developed models. The remainder of this paper is organized into the following sections: Sect. 2 outlines the development of shape models for FDs and FDAs based on in situ measurements. Section 3 details the theoretical methodology used to calculate the single-scattering properties of FDs and FDAs. Section 4 discusses the results, and Sect. 5 provides a summary and conclusion of this study.

2 Idealized models representing the shapes of frozen droplets and frozen-droplet aggregates

To compute the single-scattering properties of FDs and FDAs, it is essential to have idealized shape models that closely replicate their natural form. In this study, these models were developed using Gaussian random spheres and droxtals, based on the shapes observed during field campaigns and laboratory experiments. This section presents the geometrical description of the Gaussian random sphere and droxtal. Additionally, it outlines the procedure used to construct shape models of FDAs.

2.1 Gaussian random sphere

The Gaussian random sphere is widely used to depict natural particles characterized by uneven surfaces, such as asteroids (Muinonen and Lagerros, 1998), desert dust particles (Nousiainen et al., 2003), and small ice crystals (Nousiainen and McFarquhar, 2004; Nousiainen et al., 2011). Magee et al. (2021) recently revealed previously undiscovered uneven and rough surfaces due to the limited resolution of imaging probes. Therefore, the Gaussian random sphere is well suited for generating models to represent FDs because it is designed to represent uneven and rough surfaces. Here, idealized models of FDs, represented by Gaussian random spheres, were developed using the SIRIS software (Muinonen et al., 1996; Nousiainen et al., 2003). This software enables the generation of quasi-spherical shapes with randomly deformed surfaces through the utilization of Gaussian random sphere geometry along with several statistical parameters.

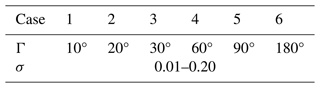
Two statistical parameters, the relative standard deviation of radius (σ) and correlation angle (Γ), were varied to generate a total of 120 Gaussian random spheres. A total of 20 different Γ (i.e., from 0.01 to 0.20) values were used to develop each case of Gaussian random spheres. Adjusting σ affects the radius vector (Υ) of the Gaussian random sphere and the radius vector is defined in spherical coordinates as

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathbf{{\rm Y}}(\mathit{\vartheta },\mathit{\phi })={\displaystyle \frac{a}{\sqrt{\mathrm{1}+{\mathit{\sigma }}^{\mathrm{2}}}}}\exp \left[s\left(\mathit{\vartheta },\mathit{\phi }\right)\right]\widehat{{\mathit{e}}_{\mathit{r}}}\text{and}\text{(2)}& {\displaystyle }s(\mathit{\vartheta },\mathit{\phi })={\sum }_{l=\mathrm{0}}^{\mathrm{\infty }}{\sum }_{m=-l}^l{s}_{\mathrm{lm}}{Y}_{\mathrm{lm}}(\mathit{\vartheta },\mathit{\phi }),\end{array}$$

where a denotes the mean radius, Y_lm is the orthonormal spherical harmonics, and s_lm is a Gaussian random variable generated with zero means (Muinonen et al., 2007). Here,  s and $\widehat{{\mathit{e}}_{\mathit{r}}}$ are log radius and a unit vector pointing outward in the direction (ϑ,φ) in spherical coordinates, respectively, while Γ is the correlation angle, which is defined by

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathrm{\Gamma }=\mathrm{2}\text{arcsin}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}l\right)\text{ and}\text{(4)}& {\displaystyle }{C}_{\mathrm{s}}\left(r\right)=\exp (-{\displaystyle \frac{\mathrm{2}}{l^{\mathrm{2}}}}{\sin }^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}r),\end{array}$$

where C_s is the correlation function and l is the correlation length (Nousiainen, 2002). Table 1 lists the values of these statistical parameters used to generate the Gaussian random spheres. Figure 1 shows example realizations of the geometric shapes of Gaussian random spheres with D_max = 30 µm. As Γ decreases while σ remains constant (i.e., from Fig. 1f to Fig. 1a), the shapes of Gaussian random spheres progressively deviate from a spherical form, assuming an increasingly spiky appearance not like those of observed ice crystals. More detailed information on the SIRIS software and Gaussian random sphere geometry can be found in Muinonen et al. (1996) and Nousiainen et al. (2003).

Table 1 Statistical parameters, Γ and σ, used to develop six cases of FDs represented by Gaussian random spheres.

Figure 1 Example realizations of the Gaussian random spheres based on six different Γ values. The σ is 0.15 for all the cases presented here and the values of Γ for each model are embedded at the bottom of each panel. The D_max of Gaussian random spheres is identical (i.e., 30 µm) for all the cases.

2.2 Droxtal

Thuman and Robinson (1954) researched Alaskan ice fog, collecting ice crystals using glass slides. They discovered unusual, small ice particles that exhibited characteristics of both droplets and crystals at temperatures less than −35 °C. These particles were more prevalent than the well-formed hexagonal columns and plates typically expected. The researchers named these unique ice particles droxtals. Later, Ohtake (1970) identified droxtals as 14- or 20-faced polyhedral crystals, noting that such particles are no longer considered unusual in ice fog conditions. Yamazaki and Gonda (1984) advanced this understanding by demonstrating the growth of a 20-faceted ice crystal from a frozen droplet through their experiments (see their Fig. 1). The droxtals were used to calculate single-scattering properties of small quasi-ice crystals observed in cirrus clouds using the finite-difference time domain method (Yang et al., 2003) and the improved geometric optics method (Zhang et al., 2004).

For T < −40 °C, cloud droplets freeze so rapidly that they do not have sufficient time to develop into typical shapes, such as hexagonal columns (Ohtake, 1970). Recent laboratory results reported that FDs observed at temperatures less than −40 °C bear a resemblance to the shape of droxtals (Pedernera and Ávila, 2018). Considering the aforementioned observations and experiments, it is plausible to assume the droxtal geometry as a possible candidate representing the shape of small and quasi-spherical ice crystals that are observed in the upper anvil of deep convective clouds (DCCs).

Figure 2 shows the geometrical configuration of a droxtal. Two angular parameters θ₁ and θ₂, in conjunction with the radius (R) of a circumscribing sphere, determine the geometry of the droxtal. The relationships of these parameters are given by

$$\begin{array}{}\text{(5)}& {\displaystyle }{a}_{\mathrm{1}}=R\sin {\mathit{\theta }}_{\mathrm{1}}\text{ and }{a}_{\mathrm{2}}=R\sin {\mathit{\theta }}_{\mathrm{2}},\text{(6)}& {\displaystyle }{L}_{\mathrm{1}}=R\cos {\mathit{\theta }}_{\mathrm{1}}\text{ and }{L}_{\mathrm{2}}=R\cos {\mathit{\theta }}_{\mathrm{2}},\end{array}$$

where a₁ and a₂ are connected with the area of hexagonal faces of the droxtal. In Eq. (6), L₁ and L₂ are related to the area of rectangular and trapezoidal faces, respectively. With a total of 20 faces, a single droxtal features 12 trapezoidal faces (e.g., EFF^′E^′ in Fig. 2a), 6 rectangular faces (e.g., E^′F^′F^′′E^′′ in Fig. 2a), and 2 hexagonal faces (e.g., ABCDEF in Fig. 2a). The single droxtal, specified by θ₁ = 32.35° and θ₂ = 71.81°, exhibits maximum sphericity. Based on this model representing maximum sphericity, modifications were made to generate the idealized droxtal models. By adjusting either θ₁ or θ₂ at one-degree intervals, a total of 129 idealized droxtal models with D_max = 30 µm were developed. Four example realizations of the droxtal are illustrated in Fig. 3. Figure 3a and b correspond to the case where θ₁ varies, while θ₂ is fixed at 71.81°. Conversely, Fig. 3c and d show the cases where θ₂ is varied, while θ₁ is held constant at 32.35°. The corresponding values of θ₁ and θ₂ are shown at the bottom of each panel. Table 2 gives the values and ranges of the angular parameters for each droxtal case developed in this study.

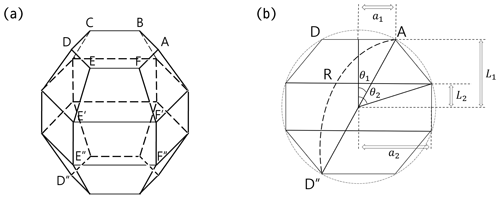
Figure 2 Geometrical configuration of a droxtal. The $\stackrel{\mathrm{‾}}{A{D}^{\prime \prime }}$ in (b) corresponds to the maximum dimension (D_max). Adjusting the two angles, θ₁ and θ₂, influences the area of hexagonal, rectangular, and trapezoidal faces of droxtal.

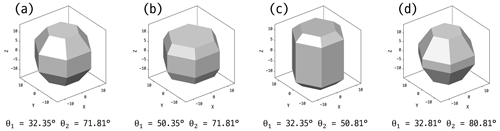
Figure 3 Example realizations of droxtal models based on the four cases shape statistics. The D_max for each droxtal model is 30 µm. Corresponding statistical parameters, θ₁ and θ₂, are shown at the bottom of each panel.

Table 2 Statistical parameters, θ₁ and θ₂, used to develop four cases of FDs represented by droxtals.

2.3 Frozen-droplet aggregates

Linearly chained FDAs are one of the distinct characteristics of continental DCCs, which may be produced by high electric fields that exist within the clouds (Saunders and Wahab, 1975; Stith et al., 2002, 2004, 2014; Connolly et al., 2005; Gayet et al., 2012; Järvinen et al., 2016; Um et al., 2018). According to an analysis on the morphological properties of FDAs by Um et al. (2018), on average FDAs consisted of 4.7 ± 5.0 individual FDs, with approximately 90 % of the measured FDAs being composed of 2 to 10 individual FDs.

In this section, idealized models representing the linearly chained and complex shapes of FDAs are developed. To this end, individual models of FDs (i.e., either Gaussian random spheres or droxtals) were distributed in three-dimensional space with random orientations, reflecting the natural tendency of ice crystals in the atmosphere to have no preferred orientations. Additionally, the following assumptions were made to develop the idealized models of FDAs.

• No overlap exists between the constituents of FDA models.

• The maximum number of contact points between the constituents of an FDA model is two.

The aggregation index (AI) is used to describe the shape of FDAs in three-dimensional (3D) space. The AI has been used for analyzing the impacts of 3D shapes of aggregates of ice crystals, such as bullet rosettes and plates, on their corresponding scattering properties (Um and McFarquhar, 2009; Um et al., 2018). The AI is defined as

$$\begin{array}{}\text{(7)}& \text{AI}={\displaystyle \frac{{\sum }_i^n{\sum }_j^n{D}_{ij}}{\text{MAX}\left({\sum }_i^n{\sum }_j^n{D}_{ij}\right)}},\end{array}$$

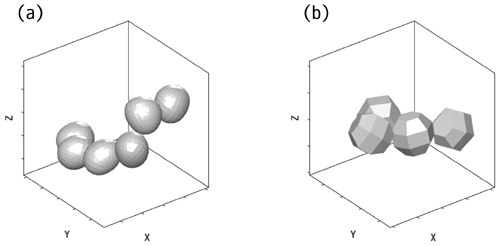
where D_ij is the distance between the center of the circumscribing circle of frozen droplet i and that of frozen droplet j. The AI is calculated only for the cases where n ≥ 3 (Um and McFarquhar, 2009; Um et al., 2018). As the AI value increases, the shape of FDAs becomes more similar to that of a linearly chained structure. A total of 404 idealized FDAs models were generated, varying the number of constituent FDs (i.e., n ranging 2 to 10). Figure 4 shows examples of aggregates of six Gaussian random spheres and aggregates of four droxtals.

Figure 4 Examples of newly developed models for FDAs. (a) FDAs represented by aggregates of six Gaussian random spheres and (b) FDAs represented by aggregates of four droxtals.

3 Geometric optic method for calculating single-scattering properties

Here, P₁₁ and g are single-scattering properties of great interest in both remote sensing and climate models studies. In this case, P₁₁ is the first element of the phase matrix (P) that describes the scattering intensity of radiation when the incident light is unpolarized (Bohren and Huffman, 1983). Here, g, which is defined as the cosine-weighted normalized P₁₁, provides a measure for assessing asymmetry in the forward-scattering region of the phase function. Thus, g takes on values between −1 and 1 depending on the direction of scattered energy;  g equals 1 when all radiation is scattered into the forward hemisphere and −1 when all radiation is scattered in the backward hemisphere. When g equals 0, this indicates isotropic or hemispherically symmetric scattering. The normalized P₁₁ and g are defined as

$$\begin{array}{}\text{(8)}& {\displaystyle }{P}_{\mathrm{11}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}}{\int }_{\mathrm{4}\mathit{\pi }}{P}_{\mathrm{11}}\mathrm{d}\mathrm{\Omega },\text{(9)}& {\displaystyle }g={\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}}{\int }_{\mathrm{4}\mathit{\pi }}{P}_{\mathrm{11}}\cos \mathit{\theta }\mathrm{d}\mathrm{\Omega },\end{array}$$

where Ω and θ are the solid angle and scattering angle, respectively (Bohren and Huffman, 1983).

The geometric optics method (GOM), also known as ray optics or the ray-tracing method, is a widely used approximation technique that calculates single-scattering properties (e.g., P₁₁ and g) of atmospheric ice crystals (e.g., Yang and Liou, 1995; Macke et al., 1996; Konoshonkin et al., 2015). Furthermore, various methods derived from the GOM, such as the improved geometric optics method (IGOM, Yang and Liou, 1998; Havemann et al., 2003), ray tracing with diffraction on facets (RTDF, Hesse, 2008; Hesse et al., 2009), and geometrical-optics–integral-equation method (GOIE, Ishimoto et al., 2012) have been developed and are in use. The GOM is applicable when the size parameter (χ = $\frac{\mathrm{2}\mathit{\pi }r}{\mathit{\lambda }}$) of scatterers is significantly larger than the wavelength (λ) of incident light (i.e., χ ≫ 1), but the lower size limit of the applicability of conventional GOM is not well defined, and it depends on the morphology of scatterer (Um and McFarquhar, 2015). For the calculation of single-scattering properties of FDs and FDAs, the modified version of the geometric ray-tracing code (Macke et al., 1996), which includes parallelized computation, was used (Um and McFarquhar, 2009).

For the simulations presented here, 72 000 randomly chosen orientations and 1000 incoming rays per orientation were used to calculate single-scattering properties at λ = 0.80 µm. The refractive index of ice at this λ is 1.3049 + 1.34 × 10⁻⁷ (Warren and Brandt, 2008), where i is the imaginary part, and a scattering angle resolution of 0.25° was employed. The results of simulations are compared with the single-scattering properties measured by a PN during CIRCLE-2 to determine the best-fit model that most accurately matches the observations. To this end, two criteria were used to select the best-fit model: the root-mean-square error (RMSE) and number of angles (ω) falling within the ±20 % uncertainty range of PN. Essentially, the best-fit model is the one that minimizes RMSE while maximizing ω. The models were sorted by their RMSE values in ascending order, and the model with the largest ω value was selected. In this study, RMSE is defined as

$$\begin{array}{}\text{(10)}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\left\{{\sum }_{i=\mathrm{1}}^{i=\mathrm{32}}{X}_i^{\mathrm{2}}\right\}},\end{array}$$

where X_i represents the log difference between the measured average P₁₁ and computed P₁₁. The i (i = $\mathrm{1},\mathrm{2},\mathrm{\dots },\mathrm{32}$) is the number of scattering angles measured by the PN instrument.

4 Calculation results and comparison with in situ measurements

The PN, as detailed by Gayet et al. (1997), is an airborne instrument designed to measure the angular scattering pattern or scattering-phase function of an ensemble of cloud particles ranging from a few micrometers to about 1 mm in diameter. Operating at a wavelength of 0.8 µm, the PN captures scattering angles between ±15 and ±162° with a resolution of 3.5°, typically providing data at 32 distinct angles from among 56 photodiodes (Jourdan et al., 2010). Measurements at near-forward and backward angles (θ < 15° and θ > 162°) are less reliable due to diffraction effects caused by the edges of holes drilled in the paraboloidal mirror (Gayet et al., 1997). To ensure continuous sampling, the PN integrates the signals from each photodiode over periods selectable by the operator, commonly around 100 ms. The average measurement errors for the angular scattering coefficients range from 3 % to 5 % for angles between 15 and 162°, with a maximum error reaching 20 % at the outermost angles (Shcherbakov et al., 2006). The instrument's ability to directly measure the scattering-phase function allows for differentiation of particle types and calculation of essential optical parameters, such as the extinction coefficient and g. Gayet et al. (2002) reported an uncertainty of 25 % for the PN-derived extinction coefficient, while the estimated absolute error for the g value ranges from ±0.04 to ±0.05, depending on the prevalence of large ice crystals within the cloud (Jourdan et al., 2010).

To determine the ice crystal model that best matches the P₁₁ and g of FDAs observed by the PN during CIRCLE-2, the single-scattering properties of individual crystals (i.e., either Gaussian random spheres or droxtals) with varying shapes and those of their aggregates (i.e., either aggregates of Gaussian random spheres or aggregates of droxtals) with varying 3D morphologies (e.g., AI) were calculated. Initially, the single-scattering properties of the individual component ice crystals were calculated and then compared with the PN measurements in Sect. 4.1. A total of 120 Gaussian random spheres (discussed in Sect. 4.1.1) and 129 droxtals (discussed in Sect. 4.1.2) were used for this purpose. This step is crucial to verify whether a constituent crystal can represent the single-scattering properties of their aggregates, as previous studies (Um and McFarquhar, 2007, 2009) have demonstrated similarities between the single-scattering properties of aggregate crystals and their component crystals. Subsequently, the calculated single-scattering properties of homogeneous component aggregates (i.e., either aggregates of Gaussian random spheres or aggregates of droxtals) were compared with those observed by the PN (Sect. 4.2 and the Supplement). Finally, models for heterogeneous component aggregates, which are mixtures of Gaussian random spheres and droxtals, were developed in Sect. 4.3.

4.1 Single frozen droplets

4.1.1 Gaussian random spheres

Figure 5a illustrates the comparison between the P₁₁ of 120 single FD models, represented by Gaussian random spheres, and the PN-measured average P₁₁ reported in previous studies (Baran et al., 2012; Gayet et al., 2012) obtained in the developed overshooting convective cell at 11 080 m altitude (T = −58 °C) at 13:08:15–13:08:40 UTC on 26 May 2007 during CIRCLE-2 (i.e., filled black circles). The P₁₁ was divided into three different scattering regions, i.e., forward-scattering (0 to 60°), lateral-scattering (60 to 120°), and backward-scattering (120 to 180°) angles, to analyze the relative contribution to each region. Single models of Gaussian random spheres showed average differences of 10.63 ± 5.19 %, 47.28 ± 27.67 %, and 32.19 ± 12.21 % in the forward-, lateral-, and backward-scattering regions, respectively, compared with the PN measurements. In particular, the energy scattered into the lateral and backward directions exhibited notable differences compared to that scattered into the forward region. This discrepancy is attributed to the typical characteristic of quasi-spherical ice crystals, low lateral-scattering, as identified by Mishchenko and Travis (1998). Additionally, unlike other non-spherical ice crystals (e.g., hexagonal columns and droxtals), the P₁₁ of the Gaussian random sphere did not show sharp peaks in the forward-scattering region. The average g was 0.83 ± 0.05, which falls outside the measurement range of the PN (i.e., 0.78 ± 0.04). However, it was shown that the Gaussian random spheres representing spiky forms, as illustrated in Fig. 1a, b, and c, have g values with uncertainty ranges of 0.77 ± 0.04, 0.80 ± 0.04, and 0.81 ± 0.04, respectively, which are close to those of the PN (indicated by dashed blue lines in Fig. 5b). These results, as clearly depicted in Fig. 5b, show that the spherical shape models scatter with more intensity into the forward-scattering region, consequently leading to an increased g.

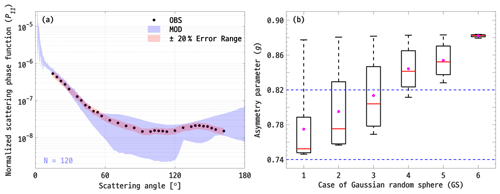
Figure 5 (a) A comparison of the computed P₁₁ for single Gaussian random sphere models (shaded blue area) against P₁₁ obtained during CIRCLE-2 (filled black circles). A shaded red area represents the 20 % uncertainty range of P₁₁ measurements obtained during CIRCLE-2. (b) The computed g for each case of individual Gaussian random spheres. The dashed blue lines indicate the uncertainty range for g of PN measurement (i.e., 0.78 ± 0.04). The median and mean for each case of the single Gaussian random sphere model are plotted as solid red lines and filled magenta circles in the box plot, respectively.

To address the discrepancy in the lateral scattering observed in spherical cases of Gaussian random spheres (i.e., Fig. 1d–f), additional simulations using the distortion parameter (t) were conducted. Using t is a statistical method reflecting the influence of distorted faces of ice crystals on the single-scattering properties. It involves tilting the path of the reflected and refracted ray randomly during the simulation around its original direction. The zenith and azimuth tilt angles are randomly selected with an equal distribution between 0 and ${\mathit{\theta }}_t^{\text{max}}$ and between 0 and 2π, respectively. The degree of distortion is defined by the following relation: t = ${\mathit{\theta }}_t^{\text{max}}/\mathrm{90}\mathit{°}$ (Macke et al., 1996).

Figure 6 shows box plots analyzing ω, RMSE, and g for single Gaussian random sphere models as a function of t, ranging from 0.0 to 0.95 in 0.05 intervals. The ω slightly increased with t, reaching a maximum of 23 at t = 0.45 as it reduced discrepancy in lateral scattering, resulting in more observation angles in the lateral-scattering region falling within the PN uncertainty range. However, ω decreases, particularly when t exceeds 0.70, which corresponds to unrealistic, highly distorted surfaces. In contrast to ω, RMSE decreases as t increases, reaching a minimum of 0.0813 at t = 0.55, but it also rises when t exceeds 0.70. For g, the average ± standard deviation of the computed values at t = 0.65 was 0.77 ± 0.04, which closely matches the PN measurements (0.78 ± 0.04). However, the smallest difference in g was −0.01 % at t = 0.55 and not at t = 0.65. This is because the ω in the forward-scattering region at t = 0.55 (i.e., 6.39 ± 1.45 out of 12) was greater than at t = 0.65 (i.e., 3.91 ± 1.17 out of 12).

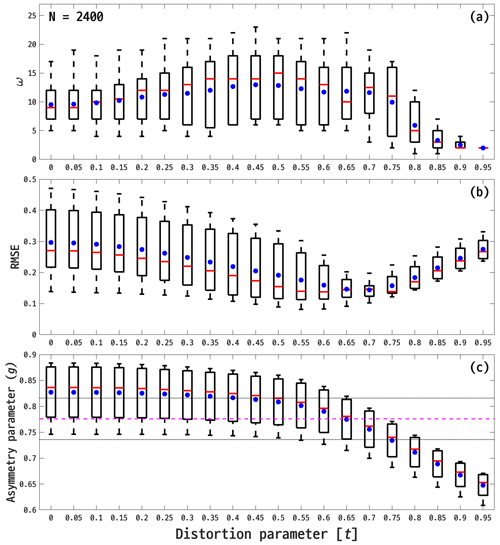
Figure 6 Results for single Gaussian random sphere models with t values ranging from 0.0 to 0.95 in 0.05 intervals, focusing on (a) ω, (b) RMSE, and (c) g. The solid red lines and filled blue circles represent the median and mean, respectively. The dotted black lines and dashed magenta line in panel (c) indicate the boundaries of the PN uncertainty range and the mean of PN measurements (i.e., 0.78 ± 0.04), respectively. The total number of simulated Gaussian random sphere models (N) is shown in panel (a).

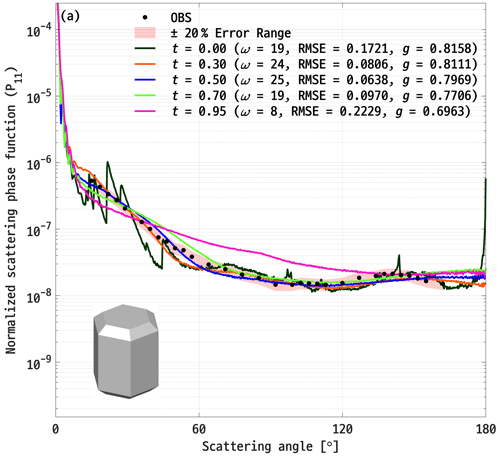
Figure 7 shows the P₁₁ of Gaussian random spheres when assuming varying t values from 0.0 (indicating no distortion) to 0.95 (indicating high distortion). Each colored solid line (not all lines are shown for brevity) corresponds to the P₁₁ with different values of t, exhibiting the smallest RMSE when compared with the P₁₁ measured by the PN (indicated by filled black circles in Fig. 7). A single Gaussian random sphere (i.e., the bottom-left side of Fig. 7) with t = 0.55 was the best-fit model, minimizing the RMSE to a value of 0.0813. The differences in the forward-, lateral-, and backward-scattering regions for the best-fit model were +1.64 %, −0.16 %, and −9.37 %, respectively. The g value was calculated to be 0.79, which falls within the measurement range of the PN.

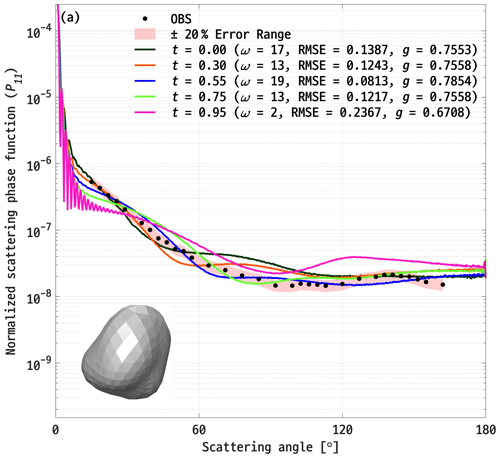
Figure 7 A comparison of the average P₁₁ measured in situ (represented by filled black circles) with the calculated P₁₁ of single Gaussian random sphere models. A shaded red area indicates the ±20 % uncertainty range of the PN measurements, and each solid line corresponds to the best-fit model at t values ranging from 0.0 to 0.95 (not all lines are shown here for brevity). The t values for each best-fit line, along with the corresponding ω, RMSE, and g are shown on the upper-right side of the panel. The shape of the single Gaussian random sphere with the minimum RMSE out of 120 models is shown on the bottom-left side of the panel.

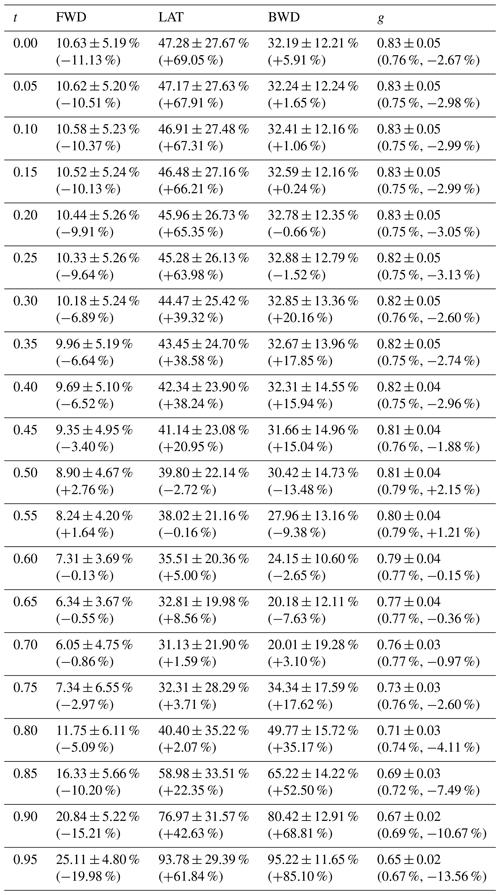
The t was applied for the purpose of reducing the difference in the lateral-scattering region caused by general features of quasi-spherical ice crystals (i.e., low lateral scattering) and to improve overall agreement with the PN measurements. This approach effectively minimized the RMSE and increased ω to certain extent (see Fig. 6). The differences in the P₁₁ and g between the Gaussian random sphere models and in situ measurements, across distortion parameter values, are summarized in Table 3.

Table 3 The calculated average ± standard deviation of the difference (relative difference of the best-fit model) in P₁₁, compared to the PN measurements, for 120 single-particle models represented by Gaussian random spheres across the forward- (FWD), lateral- (LAT), and backward-scattering (BWD) regions. For g, the average ± standard deviation is shown, with the relative difference indicated in parentheses. The t values, ranging from 0.0 to 0.95 in 0.05 intervals, were applied.

4.1.2 Droxtals

Figure 8a shows a comparison of the P₁₁ of 129 droxtals with the P₁₁ measured in situ. Due to their faceted structure, the droxtals have P₁₁ characterized by several sharp peaks in the forward-scattering directions (Zhang et al., 2004; Um and McFarquhar, 2011; Yang et al., 2013). The strong peaks are distinctly visible in the P₁₁ of droxtals in Fig. 8a, and the most pronounced peak was found at 6.5°. These peaks indicate angles of minimal deviation, caused by the refraction of rays passing through two facets of a particle.

Figure 8 The same as Fig. 5 but for the single-droxtal models.

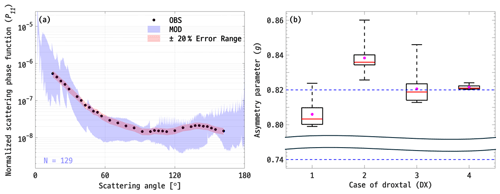
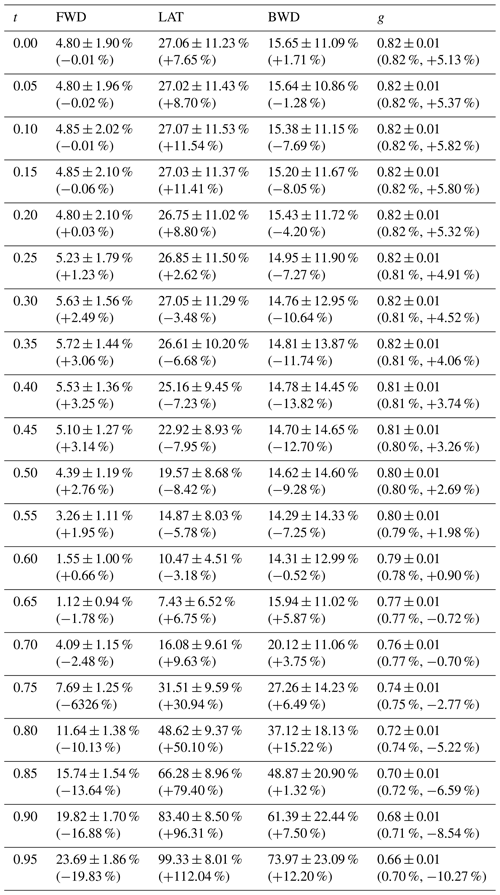
For the droxtals, the average differences between the droxtal models and in situ measurements in the forward-, lateral-, and backward-scattering regions were 4.80 ± 1.90 %, 27.06 ± 11.23 %, and 15.66 ± 11.09 %, respectively. The droxtals showed a smaller difference in both the lateral- and backward-scattering directions compared to the Gaussian random sphere. The overall shape of the P₁₁ in the forward-scattering region appears to deviate significantly from observations. As a result, the average ω in the forward-scattering region was 2.00 ± 1.40 out of 12, which is notably smaller than that of Gaussian random sphere (i.e., 5.65 ± 1.19). However, in the lateral- and backward-scattering regions, ω was 4.51 ± 2.05 out of 11 and 3.99 ± 1.53 out of 9, respectively, indicating that these models effectively simulate the total intensity scattered in the lateral- and backward-scattering regions compared to the single Gaussian random spheres (i.e., 1.90 ± 1.80 out of 11 and 1.97 ± 1.68 out of 9). With an average RMSE of 0.2462 ± 0.0427 and ω of 10.50 ± 2.85 across four cases, the droxtals demonstrated better performance than the single Gaussian random sphere. Figure 8b illustrates the comparison of g values of droxtals with the measurement range of the in-situ measurements (indicated by dashed blue lines in Fig. 8b) using box plots. Droxtals representing the typical shapes (i.e., a in Fig. 3) and the shape most closely resembling columns (i.e., in Fig. 3c) have average g of 0.81 ± 0.01 and 0.82 ± 0.01, respectively. These results fall within the upper measurement range of the PN measurements (i.e., 0.78 ± 0.04).

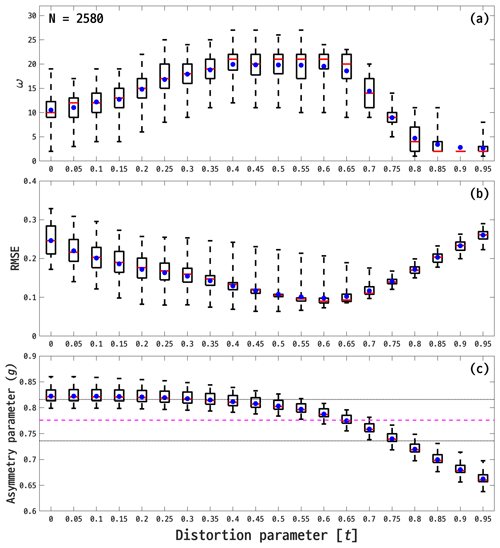
Box plots in Fig. 9 show the analysis of ω, RMSE, and g for single-droxtal models with varying t, ranging from 0.0 to 0.95 in 0.05 intervals. Increasing t smooths the forward-scattering region of P₁₁, resulting in more observation angles falling within the PN uncertainty range and reducing the differences between the models and PN measurements (see Fig. 9a and Table 4). Overall, ω initially rises with t, peaking at 27 when t = 0.40, 0.45, and 0.55, which is higher than for single Gaussian random sphere, and then starts to decrease when t exceeds 0.60. RMSE decreases with t, reaching a minimum value of 0.0637 at t = 0.50, but it then rises when t exceeds 0.60. At t = 0.65, g had an average of 0.78 ± 0.01, which is a close match to the PN measurements (0.78 ± 0.04).

Figure 9 The same as Fig. 6 but for the single-droxtal models.

Table 4 The same as Table 3 but for 129 single-droxtal models.

Figure 10 shows the selected P₁₁ of droxtals with the smallest RMSE for t ranging from 0.0 to 0.95. Each P₁₁ of the droxtal is depicted using the colored solid lines, whereas the in situ measurements and their ±20 % uncertainty range are represented by the filled black circles and shaded red area, respectively. One distinct finding is the expected disappearance of strong peaks in the forward-scattering region as t increases, leading to improved agreement in that region. A single droxtal model using t = 0.50 minimized the RMSE to 0.0638 and achieved an ω of 25, both outperforming the single Gaussian random sphere (0.0813 and 17, respectively). The calculated differences between the P₁₁ of the droxtal at t = 0.50 and the PN measurements were +2.76 %, −8.42 %, and −9.28 % in the forward-, lateral-, and backward-scattering regions, respectively. The g value was found to be 0.80, slightly higher than the average g of PN measurements. A more detailed summary of the statistics for the differences in P₁₁ and g between the developed droxtal models and the PN measurements at different t values is provided with Table 4.

Figure 10 The same as Fig. 7 but for the single-droxtal models.

4.2 Aggregates of single frozen droplets

Based on the results of the single-particle models discussed in Sect. 4.1, models of FDAs were constructed using the Gaussian random sphere and droxtal, which provided the smallest RMSE in comparison to the in situ measurements. These developed FDAs featured homogeneous components, with the component shapes of the FDAs varying and the number of components in each model ranging from 2 to 10. For each particle count, 18 different FDAs models were generated (e.g., creating 18 models for two-particle aggregates, 18 for three-particle aggregates). This approach was applied to both the Gaussian random spheres and droxtals, meaning that the total number of developed models amounts to 324.

As the observed FDAs have a myriad range of morphologies including “linearly chained” or “compact” shapes (Gayet et al., 2012; Stith et al., 2014; Um et al., 2018), diverse 3D morphological characteristics should be considered. The AI (discussed in Sect. 2.3) was introduced for this purpose. Analysis regarding the AI of the constructed FDAs reveals that for models composed of homogeneous Gaussian random spheres, the AI values range from a minimum of 0.5305 to a maximum of 0.9480, with a mean value of 0.8352. For those composed of homogeneous droxtal components, the minimum, maximum, and mean AI values are 0.4224, 0.9738, and 0.7575, respectively.

Previous research (Um and McFarquhar, 2007, 2009) has shown that the single-scattering properties of aggregates are similar to those of the individual components. In this study, it was also found that the single-scattering properties of FDAs constructed with homogeneous components did not significantly differ from those of the individual components, indicating that the impact of aggregation on the single-scattering properties is not significant. Consequently, the comparison results showed similar trends. To avoid redundancy, a more detailed explanation is provided in Sects. S1 and S2.

4.3 Habit mixture model

Different morphological features of FDAs were reported by Stith et al. (2014), with the FDAs comprised of mixtures of quasi-spherical FDs and faceted ice crystals (see Fig. 14 in Stith et al., 2014). The faceted ice crystals within these aggregates often manifested as hexagonal plates or column crystals. However, the CPI instrument used for capturing images of ice crystals is limited in its ability to fully describe the three-dimensional structures of ice crystals. When imaged by the CPI, ice crystals are presented at specific angles, suggesting that what were identified as hexagonal plates in FDAs may actually be hexagonal facets of droxtals. This interpretation is supported by the experimental findings of Yamazaki and Gonda (1984) and Pedernera and Ávila (2018), which showed that FDs can evolve into hexagonal column-like structures over time.

In previous research, habit mixture models were used to interpret the single-scattering properties of FDAs observed in DCCs during CIRCLE-2. However, the computations of these properties were made indirectly through the weighted habit mixture model (Baran et al., 2012). Baran et al. (2012) introduced four different shape models: Chebyshev particles, spheroids (e.g., prolate and oblate), ice spheres, and highly randomized 10-element hexagonal column aggregates. In that paper, weighting applied to each P₁₁ of these models and the sum of weighting is equal to 1. A combination of two different types of Chebyshev particles and a highly irregular 10-element column aggregate with t = 0.8, called model 4 in that paper, provided the best fit to the in situ measurements obtained during CIRCLE-2 (see Fig. 8 of Baran et al., 2012).

In this study, the theoretical method from the previous work is advanced by implementing a direct computation using habit mixture models. First, the three models with the lowest RMSE and the three models with the highest ω for both individual Gaussian random spheres and droxtals, as determined in Sect. 4.1, were selected. This resulted in a total of 12 different individual models, which were then randomly combined to develop the habit mixture models. These habit mixture models were developed by varying their 3D morphologies (i.e., AI) as discussed in Sect. 2.3. The AI values range from a minimum of 0.4808 to a maximum of 0.9787, with a mean value of 0.7540. The single-scattering properties of both the habit mixture models developed in this study and the weighted habit mixture models from previous work were computed under conditions identical to those used for the FDs and FDAs models.

Figure 11a–c present the shapes and P₁₁ of the three best-matching models (represented by solid blue lines) selected from 80 different habit mixtures developed in this study. A total of 1120 simulations were conducted using these habit mixture models, and the models that best match the PN measurements are shown. The corresponding t, ω, RMSE, and g with relative difference are provided at the bottom of each panel. The average and ±20 % uncertainty range of the PN measurements (represented by the filled black circles and shaded red area, respectively) are also shown, along with model 4 (dashed red lines) developed by Baran et al. (2012), denoted as AB12. It should be noted that AB12 was normalized to the PN measurements using the same method as the other models for this comparison.

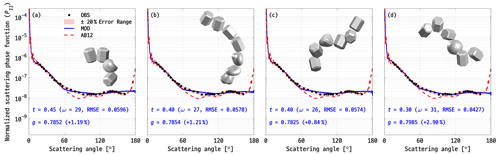
Figure 11 Shapes and P₁₁ of the best-fit habit mixture models, along with the corresponding t, ω, RMSE, and g with relative difference. The P₁₁ of the weighted habit mixture model developed by Baran et al. (2012) (AB12, dashed red lines) and the PN measurements (filled black circles) with their uncertainty range (shaded red area) are also shown.

The first habit mixture model (i.e., Fig. 11a), hereafter referred to as model A, consists of 1 Gaussian random sphere and 3 droxtals. For the P₁₁ of model A, when compared to the PN measurements the scattered energy in the forward-, lateral-, and backward-scattering regions differed by +1.03 %, +1.69 %, and +0.12 %, respectively. Model A simulated the energy scattered into the backward-scattering region with high accuracy. It led to ω of 29 out of 32 observation angles falling within the PN uncertainty range, comprising 12 out of 12 in the forward-scattering region, 10 out of 11 in the lateral-scattering region, and 7 out of 9 in the backward-scattering region. The RMSE was minimized to 0.0596 with t = 0.45, and g was 0.7852, which is slightly higher than the average of PN measurements.

Figure 11b shows model B, which is a mixture of three Gaussian random spheres and four droxtals, and the corresponding P₁₁. Compared to model A, model B with t = 0.40 exhibited a smaller RMSE of 0.0578 but a slightly decreased ω of 27. Although model B reduced the relative difference in the forward-scattering region to −0.18 %, the differences in the lateral- and backward-scattering regions increased to +6.40 % and −0.69 %, respectively. Consequently, this led to a couple of angles falling outside the PN uncertainty range compared to model A. The increased differences in both the lateral- and backward-scattering regions, caused by the increase in component number from 4 to 7, allowed for multiple scattering events between the components, leading to more light being scattered in the lateral- and backward-scattering regions, which induces greater discrepancy in those regions.

Next, model C, which is comprised of one Gaussian random sphere and five droxtals, is depicted in Fig. 11c, which shows its shape and P₁₁. Model C had a smaller RMSE value of 0.0574 compared to the previous two models, with a t value of 0.40. The relative differences from the PN measurements in the forward-, lateral-, and backward-scattering regions were −0.44 %, +7.08 %, and +1.78 %, respectively. This result is comparable to model B despite the difference in the number and fraction of their components. The g value was calculated to be 0.7825, which was similar to the previous two models but showed a reduced difference to some extent. Despite the increased relative differences in three different scattering regions and one less ω (i.e., 26 out of 32), when model C compared to model B, RMSE was slightly decreased. To investigate this, the differences in scattered energy were analyzed at specific discrete observation angles, which were divided into three different scattering regions. The average differences at discrete observation angles in the forward-, lateral-, and backward-scattering regions for model C were 8.61 ± 6.78 %, 13.01 ± 7.18 %, and 12.94 ± 9.75 %, respectively. For model B, these were 8.34 ± 6.43 %, 13.16 ± 7.66 %, and 13.56 ± 8.47 %. Model C showed smaller average differences in the lateral- and backward-scattering regions, which is reflected in its lower RMSE. This comparison supports the above result, as the RMSE was calculated across the 32 observation angles common to both the in situ measurements and the model (see Eq. 10 in Sect. 3).

To reduce the difference in lateral-scattering region, model C, which exhibited the smallest RMSE, was intentionally modified, and additional simulations were conducted. A component represented by a Gaussian random sphere in model C was replaced with a more spherically shaped one. The shape and the P₁₁ of modified model C, hereafter referred to as model D, are shown in Fig. 11d. Model D, with +1.30 % difference, demonstrated better performance in simulating lateral scattering than models A, B, and C (as intended). Although the differences in the forward- and backward-scattering regions were +1.30 % and −5.33 %, respectively, which were comparable to the others, the RMSE was minimized to 0.0427 at t = 0.3, which is an improved result. The ω was 31 out of 32, with only one angle in the lateral-scattering region falling outside the PN uncertainty range. As for g, the replaced spherical component in model D caused a slight increase in scattered energy in the forward-scattering region, which led to a deviation from the average g of PN measurements. With a g value of 0.7985 and a +2.90 % relative difference, model D falls within the uncertainty range of PN measurements. Additional simulations were conducted with habit mixture models consisting of different component shapes; however, none performed better than model D.

Following this, AB12 was compared to the PN measurements. The relative differences in P₁₁ between AB12 and the PN measurements were +2.08 %, −9.45 %, and −12.09 % in the forward-, lateral-, and backward-scattering regions, respectively. As clearly depicted in Fig. 11, there is disagreement in the lateral-scattering region. Although AB12 captured the distinct features in the lateral- and backward-scattering regions, the simulated intensities were much weaker than the observations. These discrepancies in the lateral- and backward-scattering region led to an RMSE of 0.0663, which is higher than that of model D developed in this study. The ω was 23 out of a total 32 observation angles. For g, it is comparable to the four habit mixture models developed in this study, with a value of 0.79.

Lastly, a weighted habit mixture model (i.e., indirect method) was tested to determine whether similar results to those obtained from model D could be obtained. The P₁₁ and g of the components of model D were weighted following the method of Baran et al. (2012). The results showed that directly constructed habit mixture models more accurately simulate the in situ measurements than those developed using the indirect method or single-particle models and aggregate models consisting of homogeneous components. A more detailed explanation is provided in Sect. S3.

5 Summary and conclusions

In this study, idealized models representing the shapes of FDs and FDAs observed in deep convective clouds were developed based on in situ aircraft measurements and laboratory experiments, and the corresponding single-scattering properties (i.e., scattering-phase function P₁₁ and the asymmetry parameter g) were calculated. These computed values of P₁₁ and g were subsequently compared with those obtained during the CIRCLE-2 field campaign. Gaussian random spheres and droxtals were proposed as possible candidates for representing the forms of observed FDs and FDAs. A total of 120 individual models of Gaussian random spheres and 129 models of droxtals were generated by varying their shapes. Additionally, by attaching the individual models in both a homogeneous or heterogeneous manner and considering 3D morphologies with varying AI, three different types and a total of 404 models of FDAs were created: (1) aggregates of Gaussian random spheres; (2) aggregates of droxtals; and (3) mixtures of Gaussian random spheres and droxtals, which are referred to as habit mixtures.

The P₁₁ and g values of the newly developed models were calculated using a parallelized version of geometric optics method at λ = 0.80 µm for the comparison with the PN measurements from CIRCLE-2. The distortion parameter (t), an indirect method to represent the distorted faces of natural ice crystals, was also considered in the calculations. The computed P₁₁ was divided into three different scattering regions, i.e., a forward-scattering region (0–60°), a lateral-scattering region (60–120°), and a backward-scattering region (120–180°), with differences between the calculations and PN measurements analyzed across these regions. The variation in the g value from the calculations, RMSE, and ω compared to the PN measurements was also evaluated. The most important findings of this research are summarized below.

• 1.

  For individual models, although the calculated g for both droxtals and Gaussian random spheres falling within the measurement range of the PN, the droxtal exhibited better agreement with the P₁₁ measured in situ than the Gaussian random sphere. This finding suggests that faceted ice crystals (e.g., on the droxtal) may be responsible for scattered energy into the lateral-scattering region of the observations from CIRCLE-2. However, it may be particularly true for the specific cases from CIRCLE-2. Therefore, it is necessary to carefully examine whether faceted ice crystals are a common occurrence in the upper parts of anvil clouds associated with continental DCCs.

• 2.

  The application of the distortion parameter (t) in the calculations of single-scattering properties facilitates the production of smoother P₁₁, reduces g, and increases ω, thereby enhancing the agreement with the PN measurements to certain extent (e.g., up to t = ∼ 0.3). However, larger t values diminished the agreement beyond this threshold.

• 3.

  Constructing FDAs from a heterogeneous mixture of quasi-spherical (i.e., Gaussian random spheres) and faceted crystals (i.e., droxtals) resulted in significantly improved alignment with the PN measurements compared to homogeneous mixtures (i.e., aggregates of solely Gaussian random spheres or droxtals) or individual models (i.e., Gaussian random spheres or droxtals). The heterogeneous mixture model (i.e., model D), which consists of one Gaussian random sphere and five droxtals, demonstrated the closest match to PN measurements. This model effectively replicated P₁₁ and g, minimized the RMSE to 0.0427, and achieved a high level of agreement with an ω value of 31 out of 32.

• 4.

  Calculations of single-scattering properties for FDAs using a direct computational approach, in which FDAs were generated by aggregating heterogeneous components, yielded more accurate results compared to the indirect method, where single-scattering properties were computed by weighting the calculated P₁₁ of individual shape models. This finding underscores the critical importance of employing realistic shape models and highlights the significant impact of the aggregation process on the calculations of single-scattering properties of aggregate ice crystals.

The findings of this study suggest potential implications for improving the accuracy of simulations regarding the radiative impacts of deep convective clouds and associated anvils on the Earth's climate system. A comprehensive understanding of the single-scattering properties of the constituent particles of deep convective clouds is essential to effectively interpret and represent the role of these clouds in large-scale climate models. To this end, in situ measurements of single-scattering properties obtained during the field campaign were analyzed using shape models that represent the observed habits, along with methods for calculating these properties. In this research, interpreting single-scattering properties measured in situ using models of aggregates with heterogeneous components has proven to be more accurate than aggregate models with homogeneous components or individual shape models. This result agrees with the interpretations with weighted habit mixture models proposed by Baran et al. (2012). Nonetheless, it is important to note that these conclusions may be particularly relevant to the specific cases analyzed in this study, highlighting the need to investigate whether FDAs with heterogeneous components are a common feature of deep convective clouds (Stith et al., 2014). Furthermore, the in situ measurements used to assess the developed models did not sufficiently resolve the backward-scattering region and are sensitive to variations in the orientation, shape, and heterogeneities (e.g., distorted surfaces, surface roughness, or inclusions) of ice crystals. In this respect, it should be emphasized that the measurements of the intensities of scattered light across the full range of scattering angles, coupled with images of ice crystals, are required. The use of an advanced cloud probe, such as a particle habit imaging and polar scattering probe (Abdelmonem et al., 2016; Schnaiter et al., 2018; Waitz et al., 2021), capable of capturing the detailed 3D morphologies of FDs or FDAs, is essential to further this understanding. Additionally, cloud chamber experiments, where the atmospheric conditions of deep convective clouds can be accurately replicated and studied repeatedly, could offer a viable solution for obtaining more accurate single-scattering measurements or exploring the mechanisms of producing FDAs which is not covered in this study.