Diurnal evolution of non-precipitating marine stratocumuli in a large-eddy simulation ensemble

We explore the cloud system evolution of non-precipitating marine stratocumuli with a focus on the impacts of the diurnal cycle and free-tropospheric (FT) humidity based on an ensemble of 244 large-eddy simulations generated by perturbing initial thermodynamic profiles and aerosol conditions. Cases are categorized based on their degree of decoupling and the cloud liquid water path (LWP_c, based on model columns with cloud optical depths greater than one). A budget analysis method is proposed to analyze the evolution of cloud water in both coupled and decoupled boundary layers. More coupled clouds start with a relatively low LWP_c and cloud fraction (f_c) but experience the least decrease in LWP_c and f_c during the daytime. More decoupled clouds undergo greater daytime reduction in LWP_c and f_c, especially those with higher LWP_c at sunrise because they suffer from faster weakening of net radiative cooling. During the nighttime, a positive correlation between FT humidity and the LWP_c emerges, consistent with higher FT humidity reducing both radiative cooling and the humidity jump, both of which reduce entrainment and increase LWP_c. The LWP_c is more likely to decrease during the nighttime for a larger LWP_c and greater inversion base height (z_i), conditions under which entrainment dominates as turbulence develops. In the morning, the rate of the LWP_c reduction depends on the LWP_c at sunrise, z_i, and the degree of decoupling, with distinct contributions from subsidence and radiation.

1 Introduction

Subtropical marine stratocumuli cover vast areas of Earth's surface and play an important role in Earth's energy balance by reflecting solar radiation back to space. A cloud reflects more solar radiation when its liquid water is distributed among a larger number of aerosol particles to form more numerous and smaller cloud droplets (Twomey, 1974, 1977). This initial effect propagates to other cloud properties through a series of complex processes, e.g., suppression of precipitation formation (Albrecht, 1989; Pincus and Baker, 1994), enhancement of cloud-top entrainment (Bretherton et al., 2007; Wang et al., 2003), and an increase in solar absorption (Boers and Mitchell, 1994). These processes, all considered part of aerosol–cloud interactions (ACIs), may offset one another, and their importance depends on the cloud's properties, its environment, and the timescale of interest (Stevens and Feingold, 2009).

From observations alone, it is difficult to identify and quantify the details of the aforementioned processes (e.g., Gryspeerdt et al., 2019; Wall et al., 2023), given the incomplete information of observed clouds and their environments, including co-varying meteorology and aerosols, which is often in the form of snapshots rather than the temporal evolution of the same cloud field (Stevens and Feingold, 2009; Mülmenstädt and Feingold, 2018). Despite recent efforts to infer processes after constraining such co-variations (e.g., Zhang et al., 2022; Zhang and Feingold, 2023) and to quantify the temporal evolution in the cloud responses to aerosol perturbations (e.g., Qiu et al., 2024; Smalley et al., 2024; Gryspeerdt et al., 2022), causality or process attribution remains a challenge. While opportunistic experiments, such as ship tracks, provide a way to observe the adjustment of cloud properties to additional aerosol, they are often limited in their ability to represent the wide range of conditions that the marine stratocumuli reside in (e.g., Manshausen et al., 2022; Yuan et al., 2023; Toll et al., 2019).

Meanwhile, fine-scale numerical modeling has been used to provide a process level understanding of ACIs. Many previous works focused on case studies with aerosol perturbation experiments (Sandu et al., 2008; Caldwell and Bretherton, 2009; Wang and Feingold, 2009b; Wang et al., 2010; Chen et al., 2011; Yamaguchi et al., 2015; Possner et al., 2018; Kazil et al., 2021; Prabhakaran et al., 2023; Chun et al., 2023). Although much has been learned from these studies, they do not cover the wide range of real-world conditions.

Recent work by Feingold et al. (2016) and Glassmeier et al. (2019) took a different approach, namely exploring ACIs in large-eddy simulation (LES) ensembles of marine stratocumuli. Instead of performing aerosol perturbation experiments for each combination of meteorological factors, they used experiment design techniques to optimize the sampling of the initial condition space and later distilled the information regarding ACIs from both the individual and collective behaviors of ensemble members. The methodology is as follows: LESs of large numbers of idealized cases are each set up with different initial profiles of thermodynamic variables and aerosol that are generated by perturbing six parameters. These parameters, which we will introduce in detail in Sect. 2, were drawn independently from ranges of reasonable values, although the co-variability between parameters was not constrained to match the co-variability in nature. Other configurations are more idealized. For example, all cases share the same fixed sea surface temperature (SST), subsidence profile, and prescribed surface fluxes, but all are based on an observed case (DYCOMS-II RF02; Ackerman et al., 2009). The resulting clouds are realistic in terms of the range of liquid water path (LWP).

This approach has proved to be fruitful. Based on an LES ensemble of more than 150 nocturnal marine stratocumulus simulations, Glassmeier et al. (2019) found that several cloud properties (cloud fraction, cloud albedo, and relative cloud radiative effect) of ensemble members can be well described in the state space of the liquid water path (LWP) and cloud droplet number concentration (N_d). Using the same LES ensemble, Hoffmann et al. (2020) showed that all non-precipitating cases in this ensemble approach a steady-state LWP band from different parts of the state space: clouds starting with high LWP thin over time, and clouds starting with low LWP, and possibly partial cloudiness, thicken over time. The authors further performed a budget analysis based on mixed-layer theory (MLT; Lilly, 1968) and demonstrated how the balance between radiative cooling, cloud-top entrainment warming and drying, and other processes shaped the N_d-dependence of steady state LWP. Glassmeier et al. (2021) estimated the magnitude and timescale of the LWP adjustment to an N_d perturbation from the collective behavior of the ensemble members and used them to infer biases in using ship-track to estimate the climatological forcing of anthropogenic aerosol. Hoffmann et al. (2023) explored the evolution of precipitating and non-precipitating stratocumuli in the space of albedo and cloud fraction with another LES ensemble of 127 cases that used ERA5 climatology to constrain the initial thermodynamic profiles and employed interactive surface fluxes to improve the realism of the simulations.

The environmental conditions covered in the LES ensembles used by these works can be expanded. For instance, the free-troposphere (FT) in these simulations was fairly dry, while in reality a moister FT reduces cloud-top radiative cooling and modulates cloud-top entrainment warming and drying (Ackerman et al., 2004; Eastman and Wood, 2018). The ERA5 climatology used in Hoffmann et al. (2023) is based on all months, while the conditions during the months when the stratocumuli prevail are more relevant (Wood, 2012). In addition, the surface fluxes in those simulations were either constants prescribed following DYCOMS-II RF02 (Ackerman et al., 2009) or were interactive but only responded to local wind fluctuations with calm mean winds, leading to relatively weak (but not unrealistic) surface fluxes (Hoffmann et al., 2023). Last, despite the insights gained from nocturnal simulations, the daytime behavior of marine stratocumulus population needs to be explored to understand the shortwave radiative effects of these clouds, which are more relevant to aerosol–cloud climate forcing and issues like marine cloud brightening (Latham, 1990; Feingold et al., 2024).

In this study, we explore the cloud system evolution within an LES ensemble that includes more realistic interactive surface fluxes, with a focus on the impacts of the diurnal cycle and FT humidity. The rest of this paper is organized as follows. We first introduce the model and simulation configurations in Sect. 2 and then provide an overview of the LES ensemble in Sect. 3. Next, we introduce a budget analysis method and present results in Sect. 4. With this method, we examine the nighttime and daytime evolution of individual cases in Sect. 5. A few specific issues will be discussed in Sect. 6, after which we end the paper with a summary in Sect. 7.

2 Model and simulations

All LESs for this study are performed using the System for Atmospheric Modeling (SAM; Khairoutdinov and Randall, 2003), version 6.10.10. SAM solves the anelastic Navier–Stokes equations in finite difference representation for the atmosphere on the Arakawa C grid. Similar to recent work by Yamaguchi et al. (2017) and Glassmeier et al. (2019), SAM is configured with a fifth-order advection scheme by Yamaguchi et al. (2011) and Euler time integration scheme for scalars; a second-order center advection scheme and with the third-order Adams–Bashforth time integration scheme for momentum; a 1.5-order turbulent kinetic energy (TKE)-based subgrid-scale (SGS) model (Khairoutdinov and Randall, 2003; Deardorff, 1980); a bin-emulating bulk two-moment microphysics parameterization (Feingold et al., 1998), assuming a log-normal aerosol size distribution with fixed size and width parameters; and the rapid radiative transfer model for GCMs (RRTMG; Mlawer et al., 1997; Iacono et al., 2008) that is modified to take into account background profiles of temperature and moisture above the model domain top (Yamaguchi et al., 2015), which is critical for radiative transfer in shallow domain simulations.

Different from Yamaguchi et al. (2017) and Glassmeier et al. (2019), the SAM used for this work uses the total water mixing ratio (sum of vapor and hydrometeors) and the total number concentration (sum of aerosol and drop number concentrations) as prognostic variables to ensure better closure of the budgets associated with these two quantities for advection and several other physical processes (Morrison et al., 2016; Ovtchinnikov and Easter, 2009). As a result, the water vapor mixing ratio is diagnosed from the total water and hydrometeor mixing ratios and the aerosol number concentration is diagnosed from the total, cloud droplet, and rain drop number concentrations. See the last paragraph of Sect. 2 in Yamaguchi et al. (2019) for a comprehensive summary of the advantages and disadvantages of this method.

As in Feingold et al. (2016) and Glassmeier et al. (2019), the LES ensemble members are generated from perturbed initial profiles. The initial profiles of liquid water potential temperature (θ_l) and total water mixing ratio (q_t) are each constructed from two parts: a well-mixed boundary layer (BL) profile including a sharp jump at the top of the BL and a FT profile based on ERA5 climatology (Hersbach et al., 2020) and the Marine ARM GPCI Investigation of Clouds (MAGIC) campaign (Lewis et al., 2012; Zhou et al., 2015) observations. The initial BL θ_l and q_t profiles are controlled by five parameters: θ_l and q_t in the BL and their jumps, Δθ_l and Δq_t, across the inversion base at the height of h_mix. See Appendix A for details on the FT profiles and the construction of the complete profiles. The initial aerosol number mixing ratio, specified by a sixth parameter, N_a, is uniform throughout the domain. The initial horizontal wind speed is 0 m s⁻¹ everywhere. With this simplified configuration, there is no shear in the mean wind profile in our simulations to produce TKE, making the turbulence closer to a free convection.

Hundreds of initial profiles are set up from sets of these six parameters randomly and independently drawn from their ranges. BL θ_l is drawn from 284 to 294 K, BL q_t from 6.5 to 10.5 g kg⁻¹, Δθ_l from 6 to 10 K, Δq_t from −10 to 0 g kg⁻¹, h_mix from 500 to 1300 m, and N_a from 30 to 500 mg⁻¹. Compared with the parameter ranges used in Glassmeier et al. (2019), the range for Δq_t now covers −6 to 0 g kg⁻¹ to include conditions with a more humid FT. All initial profiles with (1) the height of lifted condensation level (z_LCL) between around 225 m and 1075 m; (2) a saturated layer (i.e., h_mix>z_LCL); and (3) FT θ_l and q_t profiles falling between the minimum and maximum of the ERA5 climatological profiles are simulated with the lower-boundary conditions and large-scale forcings described below, which are the same for all simulations.

First, the surface fluxes of sensible heat, latent heat, and momentum are computed based on Monin–Obukhov similarity. The sea surface temperature (SST) is fixed for all simulations at 292.4 K. Since the mean horizontal wind speed is close to 0 m s⁻¹ in the lowest model level as a result of the simulation setup, a constant horizontal wind speed of 7 m s⁻¹ is added to the surface local wind fluctuation when calculating sensible and latent heat fluxes to obtain realistic flux values. Both this wind speed and the aforementioned SST are based on the ERA5 climatology from the same region and time period as described in Appendix A. This wind speed is also comparable to that in Kazil et al. (2016), which is produced by specifying the geostrophic wind velocity following DYCOMS-II RF01 (Stevens et al., 2005). Second, a constant surface aerosol flux of 70 cm⁻² s⁻¹, based on estimates by Kazil et al. (2011), is prescribed to offset the loss of aerosol through coalescence scavenging (Wang et al., 2010). Last, a time-invariant subsidence profile is imposed as

$$\begin{array}{}\text{(1)}& w_{\mathrm{s}}=\left\{\begin{array}{l}-Dz,z<\mathrm{2000}\mathrm{m}\\ -\mathrm{0.0075}\mathrm{m}{\mathrm{s}}^{-\mathrm{1}},z\ge \mathrm{2000}\mathrm{m},\end{array}\right.\end{array}$$

where the divergence $D=\mathrm{3.75}\times {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹. No other large-scale forcing is applied in the simulations.

The simulation domain is 48 × 48 × 2.5 km³ in the x, y, and z dimensions with 200 m horizontal and 10 m vertical grid spacings. The horizontal grid spacing is relatively coarse, while the simulations for typical marine stratocumuli do not converge until a much finer resolution (Stevens et al., 2000; Mellado et al., 2018; Matheou and Teixeira, 2019); it leaves a significant fraction of small-scale turbulence to be parameterized by the SGS model. However, there is empirical evidence that simulations with such a coarse resolution could be useful. Wang and Feingold (2009a) showed that the differences between closed- and open-cell stratocumuli captured by simulations using a 300 m horizontal grid spacing are similar to those using a 100 m horizontal grid spacing. Also, Pedersen et al. (2016) found that anisotropic grids may perform better in simulating the anisotropic turbulence in the inversion layer. Their findings are consistent with Mellado et al. (2018), who reported that the LES of the DYCOMS-II RF01 case (Stevens et al., 2005) with a coarser vertical resolution requires a larger aspect ratio to match observations. The capability of the coarse resolution and large aspect ratio to reproduce a single case certainly does not guarantee good performance for a range of environmental conditions, which essentially requires a correct representation of the sensitivity of clouds to environmental conditions. However, considering all these factors, we choose to use a 200 m horizontal grid spacing to pair with the 10 m vertical grid spacing. With this choice, we are able to afford a larger number of ensemble members.

The simulation domain uses periodic lateral boundary conditions and has a damping layer from 2 km to the domain top. The domain resides at 25° N, 235° W. All simulations are initialized at 18:40 local time (LT; 03:00Z) and then advanced for 24 h with a 1 s time step. Sunrise occurs between 05:23 and 05:24 LT and sunset occurs between 18:36 and 18:37 LT, following the diurnal cycle on 16 May at the location of the domain. The location of the domain and the day of year of the simulation are selected based on the centers of the region and the time period during which the ERA5 climatology is used to configure the simulations (see Appendix A).

For this study, we focus on non-precipitating cases, defined by a cloud base precipitation rate of less than 0.5 mm d⁻¹ (Wood, 2012). We further exclude simulations with multi-layer clouds, including surface fog. Finally, we discard simulations where the cloud top ever reaches 1.9 km, 100 m below the lower bound of the damping layer, where the damping could potentially interfere with the dynamics in the hydrometeor-free entrainment interfacial layer (Moeng et al., 2005; Haman et al., 2007; Kurowski et al., 2009). This leaves 244 cases for further investigation. The first 2 h of each simulation is excluded as the spin-up.

3 Overview of LES ensemble behavior

In this section, we present an overview of the evolution of the 244 non-precipitating cases in our LES ensemble. Following Glassmeier et al. (2019), we start with the trajectories in the plane of the cloud droplet number concentration (N_d) and cloud liquid water path (LWP_c) (Fig. 1). Both variables are based on cloudy columns, which are defined as columns with cloud optical depths greater than one. During the nighttime, the cases that start with low LWP_c experience an increase in LWP_c, while the behavior of the high LWP_c cases is not immediately clear. The nighttime cloud fractions (f_c) are usually high. At sunrise, 67 % of cases have f_c > 0.99, and 86 % of cases have f_c > 0.95. During the daytime, all cases start to lose LWP_c and f_c right after sunrise or in the early morning. Between noon and 15:00 LT, about 89 % of cases reach their lowest daytime LWP_c. In the last hour of the simulation, 95 % of cases are gaining LWP_c. Very low f_c occurs for many cases in the afternoon. The variation in N_d is rather weak for most cases.

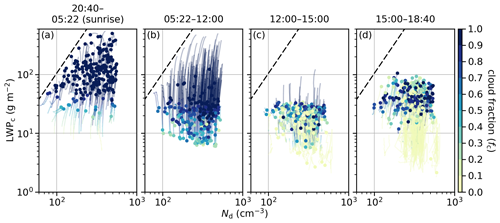
Figure 1 Evolution of the simulations in the plane of cloud droplet number concentration (N_d) and cloud LWP (LWP_c) split in to four time periods, as shown in the panel titles. Curves indicate the trajectories over the time period, and dots indicate the states at the end of the time period. The dashed black lines correspond to a characteristic mean drop radius of 12 µm, below which precipitation is inhibited.

3.1 Categorization of cases

To provide a more consolidated view of the evolution, we categorize the cases by their degree of decoupling in the morning because the diurnal decoupling (Nicholls, 1984; Turton and Nicholls, 1987) is a common feature of the cloud-topped marine BL diurnal cycle, and we expect different diurnal cycles between more coupled and more decoupled cases. We compute the relative decoupling index (denoted with 𝒟) defined by Kazil et al. (2017),

$$\begin{array}{}\text{(2)}& \mathcal{D}={\displaystyle \frac{\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}-\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}}{\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}}},\end{array}$$

where $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$ and $\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}$ are the mean cloud base height and mean lifting condensation level (LCL; determined from conditions in the lowest model level), both averaged for cloudy columns. This index is a variant of the subcloud decoupling index, $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}-\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}$, originally proposed by Jones et al. (2011). A cloudy BL with a small value of 𝒟 is more likely to be coupled while a large value of 𝒟 is more decoupled.

Figure 2a shows 𝒟 at 09:40 LT in the plane of the LWP_c and domain mean inversion base height (z_i, based on levels with the greatest vertical gradient of liquid water static energy in individual columns) at sunrise. Clouds with greater 𝒟 tend to occur in deeper BLs; many of these clouds experience very low daytime f_c minima (Fig. 2b), unless they start with very high LWP_c at sunrise, although most cases have daytime f_c maxima that are close to overcast (not shown). Based on this finding, we divide the cases into three categories based on 𝒟 at 09:40 LT and LWP_c at sunrise (05:22 LT): (1) lo𝒟loL (𝒟 ≤ 1), (2) hi𝒟loL (𝒟 > 1 and LWP_c ≤ 180 g m⁻², which is the highest LWP_c for the lo𝒟loL category), and (3) hi𝒟hiL (𝒟 > 1 and LWP_c > 180 g m⁻²) for further analysis (Fig. 2c). Figure 2d shows the time series of 𝒟 by category. During the nighttime, the medians of 𝒟 for all three categories are relatively small, suggesting more coupled conditions. Some cases in the hi𝒟loL and hi𝒟hiL categories always exhibit a higher degree of decoupling during the night. During the daytime, 𝒟 for all three categories increases into the afternoon. Overall, cases in the lo𝒟loL category experience weaker decoupling with their 𝒟 start to increase at a slower rate from a later time, compared with other two categories. Figure 2e shows the time series of median $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$ and median $\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}$ by category. During the daytime, the median $\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}$ decreases for both hi𝒟loL and hi𝒟hiL, consistent with a strengthening decoupling limiting the surface-based mixed layer. This does not happen to lo𝒟loL. Also, both hi𝒟loL and hi𝒟hiL categories experience dramatic diurnal changes in the median $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$ and the cloud depth, approximated with $z_{\mathrm{i}}-\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$. Even though the categorization is based on 𝒟 at 09:40 LT, it nicely separates the lo𝒟loL category from the other two categories through the daytime (Fig. 2e).

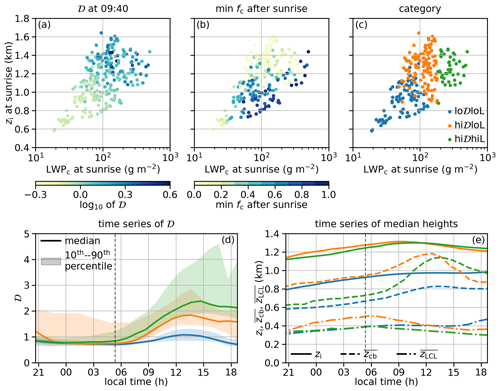
Figure 2 (a) Relative decoupling index (𝒟) at 09:40 LT and (b) minimum cloud fraction (min f_c) after sunrise in the plane of inversion base height (z_i) and cloud LWP (LWP_c) at sunrise. (c) Categories based on 𝒟 at 09:40 LT and LWP_c at sunrise include (1) lo𝒟loL (𝒟≤1), (2) hi𝒟loL (𝒟>1 and LWP_c≤180 g m⁻²), and (3) hi𝒟hiL (𝒟>1 and LWP_c>180 g m⁻²). Time series of the (d) median and quantiles of 𝒟 and the (e) medians of z_i, $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$, and $\stackrel{\mathrm{‾}}{z_{\mathrm{LCL}}}$ by category. The vertical dashed black lines in panels (d) and (e) indicate sunrise.

We include the profiles at sunrise and 13:30 LT from two example cases from lo𝒟loL and hi𝒟loL in the Supplement (Fig. S1). They show many features consistent with the observed profiles for coupled and decoupled marine-stratocumulus-topped BLs (e.g., Nowak et al., 2021), especially the decoupled conditions at 13:30 LT for the case from the hi𝒟loL category, namely the stratified layer between the relatively well-mixed cloud layer and surface-based mixed layer, the pronounced stratification in the q_t profile (Fig. S1f), and the weak fluxes above the surface-based mixed layer through cloud top (Fig. S1g).

3.2 Cloud evolution by category

Figure 3a and b display the average time series of LWP_c and f_c for three categories. Among the three categories, the lo𝒟loL category shows the lowest nighttime LWP_c and f_c. However, this category also has the smallest decrease in LWP_c and f_c during the day. By contrast, the hi𝒟loL category has greater LWP_c and nearly overcast conditions (f_c > 0.99) at sunrise but experiences a much more dramatic decrease in both LWP_c and f_c. The hi𝒟hiL category has the highest LWP_c and f_c at sunrise among all three categories. This category also shows diurnal fluctuations in large amplitude in both LWP_c and f_c with the daytime minimum between the lo𝒟loL and hi𝒟loL categories for both variables. It reaches its lowest LWP_c and lowest f_c latest in the day among all three categories. At the end of the simulation, all three categories experience a recovery of both LWP_c and f_c. At this stage, they all have similar LWP_c, indicating that the diurnal cycle imposes a strong constraint to narrow the range of LWP_c, consistent with previous findings (e.g., van der Dussen et al., 2013). In contrast, f_c differs significantly: the lo𝒟loL category has the highest f_c and the hi𝒟loL category the lowest f_c.

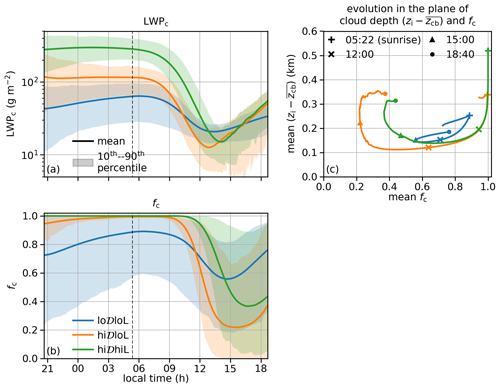
Figure 3 Time series of (a) cloud LWP (LWP_c) and (b) cloud fraction (f_c). (c) Evolution by category in the plane of cloud depth ($z_{\mathrm{i}}-\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$). The vertical dashed black lines in panels (a) and (b) indicate sunrise.

When plotted in the plane of f_c and the cloud depth ($z_{\mathrm{i}}-\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$) (Fig. 3c), the mean trajectories of the three categories produce loops of different sizes. The trajectory of the lo𝒟loL category makes the smallest loop, which can be interpreted as the least diurnal variation in cloud aspect ratio (the ratio between the cloud depth and f_c). Clouds in the hi𝒟loL and hi𝒟hiL categories experience greater variation in the aspect ratio, more so for the hi𝒟loL categories. We examine the 3-D cloud fields for selected cases from these two categories and find that clouds in both categories evolve into a cumulus-rising-into-stratocumulus structure by noon (not shown). The cloud bases of the cumuli lower slightly, while the stratocumuli continue to thin and lose f_c. This transition lowers $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$ and leads to the segments in the trajectories where f_c decreases but cloud depth starts to recover. As the clouds develop towards sunset, they regain f_c to become stratiform again.

These behaviors agree with observed diurnal cycles of marine stratocumuli. As summarized in Sect. 2.b.5 in Wood (2012), the marine stratocumuli near the coast show weaker diurnal variability in LWP and cloud fraction and are more coupled to the sea surface in shallower BLs, while the clouds observed downwind of the subtropical maxima show stronger diurnal variability in deeper and more decoupled BLs. The similar range of evolution between our LES ensemble and the observations are not necessarily driven by the same mechanisms because our ensemble is limited by the experiment design, especially the simplified treatment of the wind profile and the lack of realistic co-variability between the environmental conditions in simulation configurations, e.g., between SST and BL depth, between subsidence and inversion strength (Wood and Bretherton, 2006), and between FT θ_l and FT q_t (Eastman and Wood, 2018). Still, the capability of our LES ensemble to capture a variety of features in observed diurnal cycles of marine stratocumuli suggests that analysis of the statistical behavior of this data set is valuable.

3.3 Surface fluxes

To end this overview, we summarize the surface fluxes in the simulations (Figs. S2a and S1b). At the end of the first 2 h of the simulations, both the ranges of surface sensible heat flux (SHF) and latent heat flux (LHF) from all simulations encompass the values prescribed in the DYCOMS-II RF02 case (i.e., 16 and 93 W m⁻², respectively). Afterwards, the SHF decreases over time until late afternoon as the SHF effectively brings the BL air temperature towards the SST. The SHF is the strongest in the lo𝒟loL category, followed by the hi𝒟hiL and then the hi𝒟loL categories. This is because the shallower BLs in our ensemble also tend to be colder due to the criteria applied in the initial profiles. (For example, for a shallow BL to be initially saturated, its z_LCL needs to be lower, which is more likely when the initial BL θ_l is low. See more in Sect. 2.) LHF shows a smaller relative change throughout the day. During the nighttime, the LHF for the lo𝒟loL category remains quite steady and that for the hi𝒟loL category even increases as the turbulence spins up. The LHF is also the strongest in the lo𝒟loL category, while the LHF from the other two categories are comparable at all times.

Following Eq. (1) in Lilly (1968), the domain mean SHF and LHF can be written as

$$\begin{array}{}\text{(3)}& \mathrm{\text{SHF}}=C_{\mathrm{T}}U\left({\mathit{\theta }}_{\mathrm{SST}}-{\mathit{\theta }}_{\mathrm{air}}\right),\text{LHF}=C_{q}U\left(q_{\mathrm{sat}}\left(\text{SST}\right)-q_{\mathrm{v},\mathrm{air}}\right),\end{array}$$

where the wind speed used for surface flux calculations (U), lowest model level air temperature, and water vapor mixing ratio (θ_air and q_v,air) are also the domain means. Recall that in our simulations, the SST is 292.4 K and equivalent to a potential temperature, θ_SST, of 290.9 K, given the surface pressure used in the simulations (see Appendix A). The saturation mixing ratio at SST (q_sat(SST)) is approximately constant due to the negligible drift of surface pressure. Comparing Fig. S2c–f with Fig. S2a–b, it is clear that the evolutions of the SHF and LHF in our simulations are driven primarily by (θ_SST−θ_air) and $\left(q_{\mathrm{sat}}\right(\text{SST})-q_{\mathrm{v},\mathrm{air}})$, respectively. On average, the transfer coefficients for SHF (C_T) and for LHF (C_q) that are diagnosed from Eq. (3) decrease slightly over time, although cases with θ_air very close to θ_SST see larger fluctuations in C_T. U mostly ranges between 7 and 7.3 m s⁻¹ throughout the day (Fig. S3) because they result from the summation of relatively weak local wind velocities and a large constant wind speed (7 m s⁻¹; see Sect. 2). Our results are consistent with the findings reported by Kazil et al. (2014) for a closed-cell stratocumulus case.

4 Budget analysis for evolution of LWP_c

We perform a detailed budget analysis to understand the simulated LWP_c evolution. Previous studies used mixed-layer theory (MLT) to calculate the LWP_c tendency from the tendencies of BL mean liquid water potential temperature (θ_l) and total water mixing ratio (q_t), as well as the motion of z_i (Wood, 2007; Caldwell and Bretherton, 2009; Ghonima et al., 2015; Hoffmann et al., 2020). In particular, van der Dussen et al. (2014) derived the LWP budget equations focusing only on the adiabatic cloud layer by replacing the surface flux term with a cloud-base term. Many clouds in our simulations occur in decoupled BLs with partial cloudiness, especially during the daytime. Therefore, we apply the MLT-based approach to the cloud volume (CV), which we define for a given time t as the volume consisting of all cloudy columns between z_i(t) and the first grid box interface below $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}\left(t\right)$ (Fig. S4). The choice of this volume is inspired by previous work showing success in assuming that the cloud layer is well-mixed in decoupled BLs (Turton and Nicholls, 1987; Bretherton and Wyant, 1997). It is also based on our observation that in our simulations, the entrainment velocity, diagnosed as

$$\begin{array}{}\text{(4)}& w_{\mathrm{e}}={\displaystyle \frac{\mathrm{d}{z}_{\mathrm{i}}}{\mathrm{d}t}}-w_{\mathrm{s}}\left(z_{\mathrm{i}}\right),\end{array}$$

is rarely negative, even at its weakest point in the late afternoon, meaning that there is always some turbulent motion near the cloud top that mixes the air between the cloud layer and the FT. Different from these two previously mentioned papers and van der Dussen et al. (2014), we only assume that the cloudy region of the cloud layer is well mixed to deal with partial cloudiness. This is an alternative method to Chun et al. (2023), where the authors diagnosed the LWP budget by first assuming an overcast cloud in a well-mixed BL and then attributed the difference between the actual LWP tendency and the sum of diagnosed terms to partial cloudiness and deviation from adiabaticity clouds. The specific definition of the CV base takes full advantage of quantities reported by SAM at the grid box interface to reduce the impacts of vertical interpolation. The CV depth defined this way is within a few percent of the actual cloud depth. We first show the derivation of CV budgets and then show results from both the BL and CV budgets.

4.1 Derivation

Consider a scalar quantity ϕ (in our case θ_l or q_t) at time t in a volume consisting of a set of model columns covering a fraction of the domain area (f(t), which is one for the BL budget and f_c for the CV budget) between the volume base height z₀(t) (which is zero for the BL budget and CV base height for the CV budget) and z_i(t). Inspired by the BL total water budget in Appendix B in Kazil et al. (2016), we build a budget for the mean scalar quantity in this volume, 〈ϕ〉, from the budgets of the total amount of this scalar quantity, Φ, and total air mass, M, in this volume. Since SAM solves the anelastic equations of motion, where the air density ρ₀ only changes with height,

$$\begin{array}{}\text{(5)}& \mathrm{\Phi }\left(t\right)=f\left(t\right)\underset{z_{\mathrm{0}}\left(t\right)}{\overset{z_{\mathrm{i}}\left(t\right)}{\int }}{\mathit{\rho }}_{\mathrm{0}}\left(z\right)\mathit{\varphi }(z,t)\mathrm{d}z,\end{array}$$

and

$$\begin{array}{}\text{(6)}& M\left(t\right)=f\left(t\right)\underset{z_{\mathrm{0}}\left(t\right)}{\overset{z_{\mathrm{i}}\left(t\right)}{\int }}{\mathit{\rho }}_{\mathrm{0}}\left(z\right)\mathrm{d}z=\langle {\mathit{\rho }}_{\mathrm{0}}\rangle \left(t\right)f\left(t\right)h\left(t\right),\end{array}$$

where 〈ρ₀〉(t) is the mean air density of the volume, ϕ(z,t) is the time-dependent mean ϕ profile of the volume, and $h\left(t\right)=z_{\mathrm{i}}\left(t\right)-z_{\mathrm{0}}\left(t\right)$ is the volume thickness. Then,

$$\begin{array}{}\text{(7)}& \langle \mathit{\varphi }\rangle =\mathrm{\Phi }/M,\end{array}$$

$$\begin{array}{}\text{(8)}& \Rightarrow {\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{M}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}-{\displaystyle \frac{\mathrm{\Phi }}{M^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{M}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}-{\displaystyle \frac{\langle \mathit{\varphi }\rangle }{M}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}.\end{array}$$

(Starting from Eq. 7, we omit (t) for most time-dependent variables to simplify the notation.) The 〈ϕ〉 tendency can also be decomposed into the contributions from various processes,

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}=\sum _P{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}{\mathrm{|}}_P=\sum _P\left({\displaystyle \frac{\mathrm{1}}{M}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_P-{\displaystyle \frac{\langle \mathit{\varphi }\rangle }{M}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}{\mathrm{|}}_P\right),\end{array}$$

where the processes P include volume-top entrainment (ENTR); processes at volume sides (LAT for lateral); radiation (RAD); subsidence (SUBS); and processes at the volume base, namely transport flux at volume base (BASE), precipitation flux at volume base (PRCP), and a term tracking the impacts of the rising or lowering of the volume base (BM, which stands for base motion). The $\mathrm{d}\langle \mathit{\varphi }\rangle /\mathrm{d}t$ due to each of these seven processes can be calculated from $\mathrm{d}\mathrm{\Phi }/\mathrm{d}t$ and $\mathrm{d}M/\mathrm{d}t$ due to the same process via Eq. (9).

When we apply this approach to the budget of 〈ϕ〉 in a CV, f is equivalent to cloud fraction f_c, and several terms are quite straightforward to estimate accurately. The RAD and BASE terms for Φ are directly computed from the 3-D modeled fields of radiative heating rate, vertical velocity, and ϕ, and neither process modifies M. Although we are dealing with non-precipitating cases, we retain the PRCP terms to minimize the residual. The BM term is calculated as follows:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{BM}}& ={\displaystyle \frac{\mathrm{1}}{M}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{BM}}-{\displaystyle \frac{\langle \mathit{\varphi }\rangle }{M}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{BM}}\\ & =-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{0}}\right)\mathit{\varphi }(z_{\mathrm{0}},t)f_{\mathrm{c}}}{M}}{\displaystyle \frac{\mathrm{d}{z}_{\mathrm{0}}}{\mathrm{d}t}}+{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{0}}\right)\langle \mathit{\varphi }\rangle f_{\mathrm{c}}}{M}}{\displaystyle \frac{\mathrm{d}{z}_{\mathrm{0}}}{\mathrm{d}t}}.\end{array}\end{array}$$

The SUBS term for Φ is diagnosed by applying the Reynolds transport theorem (RTT),

$$\begin{array}{}\text{(11)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}\\ & =f_{\mathrm{c}}\underset{z_{\mathrm{0}}}{\overset{z_{\mathrm{i}}}{\int }}{\mathit{\rho }}_{\mathrm{0}}\left(z\right){\displaystyle \frac{\mathrm{d}\mathit{\varphi }(z,t)}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}\mathrm{d}z+{\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{i}}\right)\mathit{\varphi }(z_{\mathrm{i}},t)f_{\mathrm{c}}{\displaystyle \frac{\mathrm{d}{z}_{\mathrm{i}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}\\ & =f_{\mathrm{c}}\underset{z_{\mathrm{0}}}{\overset{z_{\mathrm{i}}}{\int }}{\mathit{\rho }}_{\mathrm{0}}\left(z\right){\displaystyle \frac{\mathrm{d}\mathit{\varphi }(z,t)}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}\mathrm{d}z+{\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{i}}\right)\mathit{\varphi }(z_{\mathrm{i}},t)f_{\mathrm{c}}{w}_{\mathrm{s}}\left(z_{\mathrm{i}}\right),\end{array}\end{array}$$

where $\mathrm{d}\mathit{\varphi }(z,t)/\mathrm{d}t{\mathrm{|}}_{\mathrm{SUBS}}$ is calculated by applying the SAM subsidence subroutine to the ϕ(z,t) profile. Note that although the CV base is defined to be close to $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$, which evolves due to many processes, this choice of CV base is to avoid applying MLT later to deeper stratified layers. In other words, as long as the CV base sits in a well-mixed layer, there is no need to update its height based on the cloud base height, and our choice to move it following the cloud base height is arbitrary. So, physical processes do not directly move the CV base, and there is no $\mathrm{d}{z}_{\mathrm{0}}/\mathrm{d}t$ in the terms for any processes but the BM term. The SUBS term for M is

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}={\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{i}}\right)f_{\mathrm{c}}{w}_{\mathrm{s}}\left(z_{\mathrm{i}}\right).\end{array}$$

The ENTR flux of Φ can be parameterized as

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}={\mathit{\rho }}_{\mathrm{0},\mathrm{e}}{\mathit{\varphi }}_{\mathrm{e}}{f}_{\mathrm{c}}{w}_{\mathrm{e}},\end{array}$$

where w_e is the entrainment velocity estimated from Eq. (4), and ρ_0,e and ϕ_e are an air density and a ϕ value that are relevant to the entrainment flux of ϕ. (Subscript “e” stands for entrainment, as in w_e.) Combined with the ENTR term for M, the contribution of entrainment to the 〈ϕ〉 tendency is

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}& ={\displaystyle \frac{\mathrm{1}}{M}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}-{\displaystyle \frac{\langle \mathit{\varphi }\rangle }{M}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}\\ & ={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0},\mathrm{e}}{\mathit{\varphi }}_{\mathrm{e}}{f}_{\mathrm{c}}{w}_{\mathrm{e}}}{M}}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{i}}\right)\langle \mathit{\varphi }\rangle f_{\mathrm{c}}{w}_{\mathrm{e}}}{M}}.\end{array}\end{array}$$

Assuming constant ρ₀ and overcast conditions (f_c = 1), Eq. (14) reduces to

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}={\displaystyle \frac{\mathrm{1}}{h}}{w}_{\mathrm{e}}\mathrm{\Delta }\mathit{\varphi },\end{array}$$

where Δϕ is the ϕ jump at the volume top. Previous work used ϕ values at certain levels above and below z_i (usually denoted as z₊ and z₋) to calculate the jump (Yamaguchi et al., 2011; Bretherton et al., 2013). Comparing Eqs. (14) and (15), it seems that we can follow a similar method to find a level above z_i and use the ϕ and ρ₀ at this level in place of ϕ_e and ρ_0,e. However, it is unclear what formula can be used to reliably find this level for all coupled and decoupled conditions in our simulations. With Eq. (14), the challenging part is the entrainment flux term, $\mathrm{d}\mathrm{\Phi }/\mathrm{d}t{\mathrm{|}}_{\mathrm{ENTR}}$. For now, we approximate it with the entrainment flux term for the BL. We first apply Eq. (9) to the whole BL. In this case, the BM and LAT terms vanish, and the BASE term is calculated from the surface fluxes reported by SAM (denoted with the SURF term). Because all terms other than the ENTR term are relatively easy to estimate directly and accurately, we do not keep a residual term, essentially lumping any residual into the ENTR term. So,

$$\begin{array}{}\text{(16)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}& ={\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}-({\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{RAD}}+{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SUBS}}\\ & +{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{SURF}}+{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{PRCP}}).\end{array}\end{array}$$

Then,

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{\mathrm{\Phi }}_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}& =\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}{\displaystyle \frac{\mathrm{d}{M}_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}+M_{\mathrm{BL}}{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}\\ & ={\mathit{\rho }}_{\mathrm{0}}\left(z_{\mathrm{i}}\right)\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}{w}_{\mathrm{e}}+M_{\mathrm{BL}}{\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{BL}}}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}.\end{array}\end{array}$$

We use this term in place of $\mathrm{d}\mathrm{\Phi }/\mathrm{d}t{\mathrm{|}}_{\mathrm{ENTR}}$ in the CV budget.

Regarding the LAT term, we can write

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{\langle \mathit{\varphi }\rangle }{M}}{\displaystyle \frac{\mathrm{d}M}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{LAT}}={\displaystyle \frac{\langle \mathit{\varphi }\rangle h\langle {\mathit{\rho }}_{\mathrm{0}}\rangle }{M}}{\displaystyle \frac{\mathrm{d}{f}_{\mathrm{c}}}{\mathrm{d}t}}={\displaystyle \frac{\langle \mathit{\varphi }\rangle }{f}}{\displaystyle \frac{\mathrm{d}{f}_{\mathrm{c}}}{\mathrm{d}t}}.\end{array}$$

Finally, we attribute all the remaining 〈ϕ〉 tendency to $\mathrm{d}\mathrm{\Phi }/\mathrm{d}t{\mathrm{|}}_{\mathrm{LAT}}$ to close the budget without the need for a residual term.

Thus far, we have been tracking the budget of 〈θ_l〉 and 〈q_t〉 and have not invoked MLT. Next, we apply the following equation for the LWP_c tendency, derived based on MLT, to the CV,

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}{\text{LWP}}_{\mathrm{c}}}{\mathrm{d}t}}\\ & ={\mathrm{\Gamma }}_{\mathrm{l}}\langle {\mathit{\rho }}_{\mathrm{0}}\rangle \left(z_{\mathrm{i}}-z_{\mathrm{cb}}\right)\left[{\displaystyle \frac{\mathrm{d}{z}_{\mathrm{i}}}{\mathrm{d}t}}-\left({\displaystyle \frac{\partial z_{\mathrm{cb}}}{\partial \langle q_{\mathrm{t}}\rangle }}{\displaystyle \frac{\mathrm{d}\langle q_{\mathrm{t}}\rangle }{\mathrm{d}t}}+{\displaystyle \frac{\partial z_{\mathrm{cb}}}{\partial \langle {\mathit{\theta }}_{\mathrm{l}}\rangle }}{\displaystyle \frac{\mathrm{d}\langle {\mathit{\theta }}_{\mathrm{l}}\rangle }{\mathrm{d}t}}\right)\right],\end{array}\end{array}$$

where z_cb is the mean cloud base height, Γ_l is the liquid water adiabatic lapse rate, and $\partial {\mathrm{z}}_{\mathrm{cb}}/\partial \langle {\mathit{\theta }}_{\mathrm{l}}\rangle$ and $\partial z_{\mathrm{cb}}/\partial \langle q_{\mathrm{t}}\rangle$ are based on the derivation in Ghonima et al. (2015) and follow similar notations in Hoffmann et al. (2020). In the calculation of Γ_l, $\partial z_{\mathrm{cb}}/\partial \langle {\mathit{\theta }}_{\mathrm{l}}\rangle$, and $\partial z_{\mathrm{cb}}/\partial \langle q_{\mathrm{t}}\rangle$, the actual cloud base air temperature and pressure are used. We decompose $\mathrm{d}{z}_{\mathrm{i}}/\mathrm{d}t$ into the sum of w_e and w_s; substitute $\mathrm{d}\langle q_{\mathrm{t}}\rangle /\mathrm{d}t$ and $\mathrm{d}\langle {\mathit{\theta }}_{\mathrm{l}}\rangle /\mathrm{d}t$ with the sum of individual budget terms diagnosed earlier; and finally group the $\mathrm{d}{z}_{\mathrm{i}}/\mathrm{d}t$, $\mathrm{d}\langle q_{\mathrm{t}}\rangle /\mathrm{d}t$, and $\mathrm{d}\langle {\mathit{\theta }}_{\mathrm{l}}\rangle /\mathrm{d}t$ terms on the right-hand side of Eq. (19) by processes. Budget terms are diagnosed at the end of each simulation hour (local time at 40 min past each hour). A residual (RES) term is required to close the LWP_c budget.

4.2 BL budgets

Before presenting results for the CV budgets, we briefly introduce the diurnal cycles of the BL budgets, including the BL 〈θ_l〉 and 〈q_t〉 budgets and the LWP_c budget when they are used in Eq. (19). These results serve as a reference for the CV budgets in the next section.

The BL 〈θ_l〉 and 〈q_t〉 budgets share similarity between the three categories, i.e., lo𝒟loL, hi𝒟loL, and hi𝒟hiL (Fig. 4). For the BL 〈θ_l〉 budget (left column in Fig. 4), RAD and ENTR are the leading terms during the nighttime. After sunrise, RAD quickly changes from cooling to warming, while ENTR warming weakens at a slower rate, leading to a peak in positive net BL 〈θ_l〉 tendency in the morning. For the BL 〈q_t〉 budget (right column in Fig. 4), ENTR and SURF are the leading terms throughout the day. After sunrise, ENTR drying weakens faster than SURF moistening, leading to a peak in positive net BL 〈q_t〉 tendency between noon and 15:00 LT. Recall that in MLT, the subsidence has zero contributions to the tendencies of both the mixed-layer 〈θ_l〉 and mean 〈q_t〉. In our case, the contributions are not zero but still small compared with leading terms.

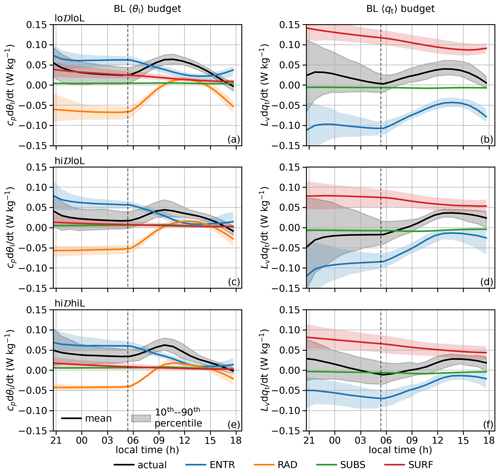
Figure 4 Time series of actual BL 〈θ_l〉 and 〈q_t〉 tendencies and budget terms due to individual processes by category. The vertical dashed black lines indicate sunrise.

Figure 5 shows the LWP_c budgets when the BL 〈θ_l〉 and 〈q_t〉 budgets are used in Eq. (19). Comparing the actual LWP_c tendency diagnosed from the time series of LWP_c; the sum of the ENTR, RAD, SUBS, and SURF terms; and the RES term in the right column of Fig. 5, applying MLT to the BL achieves fairly good closure during the nighttime for the lo𝒟loL category and between 02:00 LT and sunrise for the hi𝒟loL category but not during the daytime when the BLs are more decoupled.

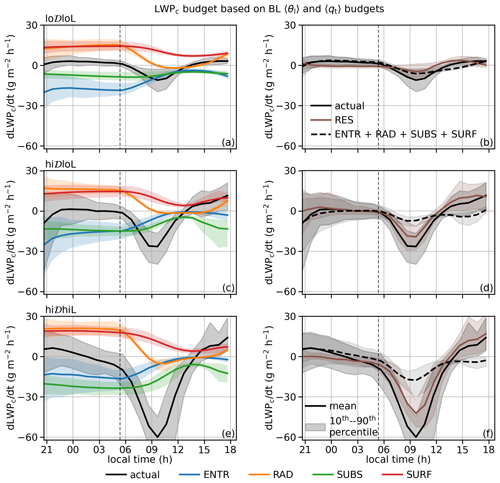
Figure 5 Time series of LWP_c tendencies and budget terms due to individual processes by category, based on BL 〈θ_l〉 and 〈q_t〉 budgets. The actual LWP_c tendencies are shown in both the left and right columns for easier comparison with individual budget terms. The vertical dashed black lines indicate sunrise.

The left column in Fig. 5 shows the actual LWP_c tendency, as well as the contributions from the RAD, ENTR, SUBS, and SURF terms. During the nighttime, the most distinct feature is that the SUBS term is much more important relative to other terms in the LWP_c budget than in the BL 〈θ_l〉 and 〈q_t〉 budgets. This is due to the strong negative contribution by the subsidence to the $\mathrm{d}{z}_{\mathrm{i}}/\mathrm{d}t$ term in Eq. (19). It is more negative for the hi𝒟loL and hi𝒟hiL categories because cases in these two categories have a higher z_i and thus a stronger subsidence due to the subsidence profile we impose. The ENTR term is comparable to other terms because its strong warming and drying effect (Fig. 4) is offset by its positive contribution to the $\mathrm{d}{z}_{\mathrm{i}}/\mathrm{d}t$ term (see Fig. S5). We do not discuss the results for the daytime due to the large residual.

4.3 CV 〈θ_l〉 and 〈q_t〉 budgets

We first present the diurnal cycles of CV 〈θ_l〉 and 〈q_t〉 budgets averaged by category (Fig. 6). Similar to the BL budgets, the ENTR and RAD terms are the leading terms for the CV 〈θ_l〉 budget during the nighttime. Both weaken after sunrise, with RAD cooling weakening faster. The ENTR warming decreases steadily towards late afternoon and becomes stronger before sunset. The main difference from the BL budgets in the left column of Fig. 4 is that RAD is mostly cooling during the daytime because much of the warming effect by RAD occurs in the subcloud layer and is excluded in the CV 〈θ_l〉 budget. This warming strengthens the stratification of the subcloud layer, weakens the turbulent motion, and limits its impacts on the CV. The remaining effects of this subcloud warming on the CV are accounted as transport in BASE and LAT terms (see Fig. S6 for an example). The RAD cooling becomes stronger after around 09:00 or 10:00 LT. It continues to strengthen through the rest of the day for the lo𝒟loL and hi𝒟hiL categories, even though the LWP_c does not recover until afternoon (Fig. 3a). This trend is dominated by the trend in CV-integrated radiative heating rates (not shown). For the hi𝒟loL category, there is a second weakening–strengthening cycle. This is a signature of the rapid lowering of $\stackrel{\mathrm{‾}}{z_{\mathrm{cb}}}$ in this category, as the stratiform parts of the clouds shrink and cumulus parts dominate (see Sect. 3 and Fig. 2e), and as a result, the total radiative divergence for the CV is distributed over a deeper layer. Note that due to subsidence and the growing of z_i, the FT in all our simulations becomes drier over time. (FT q_t values at the end of the simulations are between 64 % and 85 % of those at sunrise.) This effect likely also modulates the balance between longwave cooling and shortwave absorption.

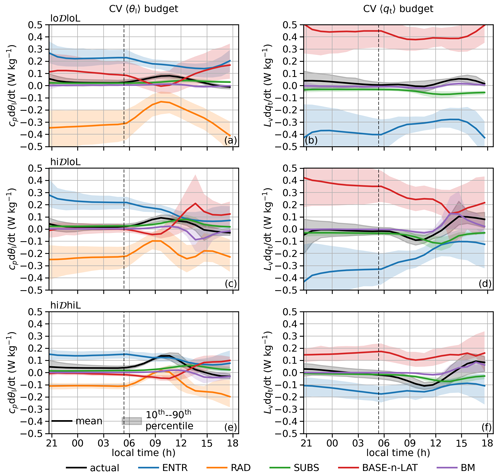
Figure 6 Time series of actual CV 〈θ_l〉 and 〈q_t〉 tendencies and budget terms due to individual processes by category. The vertical dashed black lines indicate sunrise.

As the ENTR term for the CV 〈θ_l〉 continues to decrease after the radiation passes its morning weakest point, the BASE-n-LAT term starts to play a more significant role (left column in Fig. 6). This term is defined as the sum of the BASE and LAT terms. It represents the processes associated with the interface between the CV and the rest of the BL (i.e., CV base and lateral sides). It shows an opposite trend from the RAD term and becomes the main term balancing the radiation in the afternoon. This can be interpreted as follows: while there is not enough kinetic energy for mixing across the inversion base, the radiative cooling in the CV still couples with the dynamics inside the BL.

For 〈q_t〉, the ENTR and BASE-n-LAT terms are the leading terms (right column of Fig. 6). Unlike the BASE-n-LAT term for the 〈θ_l〉 budget, which can warm or cool the CV at different times, the BASE-n-LAT term mostly moistens the CV.

As mentioned before, the base motion (BM) term comes from the arbitrary choice of the CV base height, although it is related to the actual cloud base height evolution. When the BL is stratified, a rising CV base means the air mass near the cloud base, which has lower θ_l than the CV mean, is excluded from the CV. This results in an increase in 〈θ_l〉 in the CV. Similarly, we can infer the sign of this term for 〈θ_l〉 and 〈q_t〉 budgets under other conditions. This BM term is near-zero during the nighttime when the BL is close to being well mixed. Its relative importance peaks between 13:00 and 15:00 LT for both 〈θ_l〉 and 〈q_t〉 when the cloud base averaged for all cases starts to lower, accompanying the recovery of LWP_c. The magnitudes of cooling and moistening during this time are greater than the magnitudes of warming and drying between 09:00 LT and noon, primarily because the layer near the cloud base is more stratified in the afternoon.

The SUBS term always warms and dries the CV. Its effect peaks in the early afternoon around the time when the clouds are the thinnest.

4.4 LWP_c budget based on CV 〈θ_l〉 and 〈q_t〉 budgets

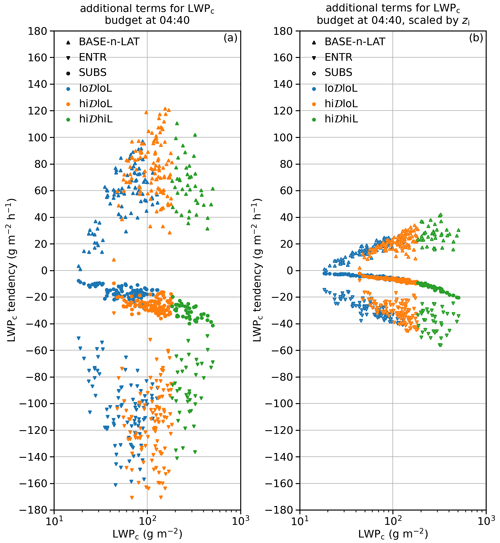
Figure 7 shows the LWP_c budget by category, with the actual LWP_c tendency and ENTR, RAD, SUBS, and BASE-n-LAT terms in the left column and the BM and RES terms in the right column. The PRCP terms are negligible and omitted.

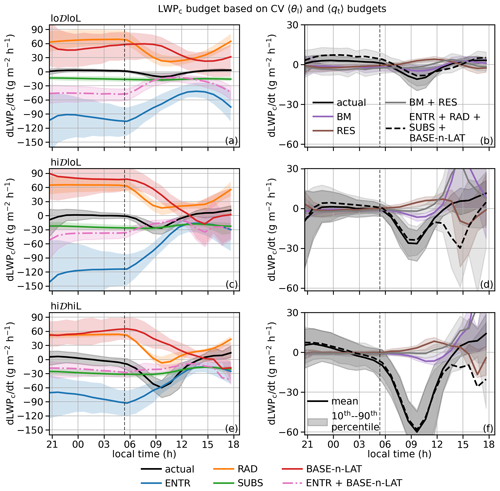
Figure 7 Time series of LWP_c tendencies and budget terms due to individual processes by category, based on CV 〈θ_l〉 and 〈q_t〉 budgets. The actual LWP_c tendencies are shown in both the left and right columns for easier comparison with individual budget terms. The vertical dashed black lines indicate sunrise.

We start with the terms in the right column. For all three categories, it is encouraging that the RES term in the LWP_c budget is fairly small. The improvement over the results based on the BL budgets (Fig. 5) is dramatic for all three categories between sunrise and early afternoon; it is also evident for the hi𝒟hiL category during the nighttime. Although the BM term is overall not important until early afternoon, quantifying it for CV 〈θ_l〉 and 〈q_t〉 budgets makes the LAT term (and thus the BASE-n-LAT term) slightly more accurate. Interestingly, the sum of the BM and RES term is even closer to zero. Qualitatively, the correlation between the BM term and the RES is expected, considering that more stratified conditions simultaneously lead to a larger BM term and less applicability of MLT.

Moving to the terms in the left column of Fig. 7, we know based on the small sum of the BM and RES term that the ENTR, RAD, SUBS, and BASE-n-LAT terms collectively explain the actual evolution of the LWP_c very well until early afternoon. In particular, we can infer from the small sum of the BM and RES term that the sum of these four terms captures the reduction in LWP_c, most rapid for the hi𝒟hiL category and least for the lo𝒟loL category, in the morning, as is evident in the time series of the actual LWP_c tendency.

The ENTR, RAD, and BASE-n-LAT terms are expected to be the leading terms simply based on their roles in the CV 〈θ_l〉 and 〈q_t〉 budgets. By contrast with the results in Fig. 5, the SUBS terms are less important relative to the ENTR term. This is because the $\mathrm{d}{z}_{\mathrm{i}}/\mathrm{d}t$ term in Eq. (19) is constant in the two versions of LWP_c budget, but the $\mathrm{d}\langle {\mathit{\theta }}_{\mathrm{l}}\rangle /\mathrm{d}t$ and $\mathrm{d}\langle q_{\mathrm{t}}\rangle /\mathrm{d}t$ terms are strongly affected by the depth over which the volume-integrated forcing is distributed.

The SUBS term has the smallest diurnal fluctuation among the four terms. As a result, one can infer that the net effect of the ENTR, RAD, and BASE-n-LAT terms would approximately follow the trend of the actual LWP_c tendency for each category. Among these three terms, the ENTR and RAD terms always begin to weaken right after sunrise. The BASE-n-LAT term remains near its maximum strength until 09:00 LT for the lo𝒟loL category, but it starts to weaken right after sunrise for the other two categories. This delay is likely the signature of better coupling with the surface. Due to this delay, although the rate of ENTR weakening for the lo𝒟loL category is slower than for the hi𝒟loL category, the combined negative effect from ENTR and BASE-n-LAT terms (dash-dotted pink lines) diminishes faster between sunrise and 09:40 LT for lo𝒟loL. Since the change in the RAD term from sunrise to between 09:00 and 10:00 LT is about the same between these two categories, the delayed decrease in the BASE-n-LAT term explains the slower LWP_c reduction for the lo𝒟loL category. The weakening of the BASE-n-LAT term balances that of the ENTR term closely for the hi𝒟hiL category, and the net effect (the pick dash-dotted lines) only weakens very slowly. As a result, the line for the RAD term is nearly parallel to the line for the actual LWP_c tendency. Interestingly, when the actual LWP_c tendency becomes the most negative in the morning for the lo𝒟loL and hi𝒟loL categories, its value is very close to the SUBS term, meaning the ENTR, RAD, and BASE-n-LAT terms sum to about zero. It is unclear whether this is by accident, but this is different for the hi𝒟hiL category, where the actual LWP_c tendency can be much more negative than the SUBS term, which is driven by the dramatic change in the RAD term.

To summarize, applying the MLT to the CV achieves satisfactory closure for the LWP_c budget from nighttime to early afternoon. In the morning, the coupling to the surface, evident in the BASE-n-LAT term, explains the relatively smaller loss of LWP_c for the lo𝒟loL category. The strong reduction in the RAD cooling causes the rapid reduction in LWP_c for the hi𝒟hiL category. In the next section, we will use the budget analysis to understand the evolution of individual LES ensemble members, not just the mean evolution by category.

5 Nighttime and daytime evolution of LES ensemble members

With the categorization of cases and the budget analysis presented, we can now examine the nighttime and daytime evolution of simulations in detail.

5.1 Nighttime evolution of individual cases

Figure 8 highlights several aspects of the nighttime evolution. Overall, the nighttime evolution is characterized by the establishment of a positive correlation between LWP_c and a characteristic FT q_t. (Since subsidence is the only process that modifies the FT q_t profile in our simulations, the characteristic FT q_t is determined as follows. For a given time, we track the air mass at 20 m above z_i back in time using the subsidence profile, Eq. (1), to calculate its height at the beginning of the simulation and represent the current FT q_t with the initial q_t at that height.) This can be seen by comparing the trajectories, colored by FT q_t, during the first 3 h after the start of the simulations (Fig. 8a) and during the 3 h before sunrise (Fig. 8b). It is also evident in the time series of the correlation coefficient between LWP_c and FT q_t (Fig. 8c). At the beginning of each simulation, LWP_c is determined by three of the six prescribed parameters: BL θ_l, BL q_t, and h_mix. As a result of the random sampling of the initial conditions, it is largely uncorrelated with the FT q_t, even after we exclude cases based on criteria described in Sect. 2. FT q_t acts as a boundary condition for the simulated clouds. It affects LWP_c by modulating entrainment drying and the downward longwave radiation reaching the cloud top, two effects that compete with each other (Eastman and Wood, 2018). Based on the way we specify FT q_t profiles, the FT humidity controlling the longwave radiation positively correlates with the FT humidity that is relevant to the entrainment. For example, a case with a dry FT in our ensemble would experience greater entrainment drying; at the same time, it experiences strong radiative cooling because the FT is more transparent to longwave radiation. Although this strong radiative cooling favors high LWP_c, it also drives the clouds to entrain more, potentially reducing LWP_c. The positive correlation between LWP_c and FT q_t in our simulations suggests that the entrainment effect dominates.

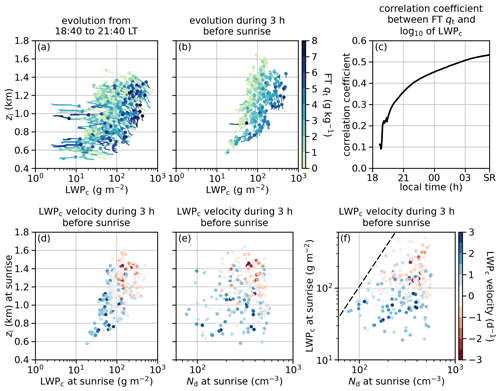
Figure 8 Evolution of LES ensemble members during nighttime. In panels (a) and (b), curves indicate the trajectories over the time period, and dots indicate the states at the end of the time period shown in the panel titles. SR indicates sunrise.

Figure 8d–f show the LWP_c velocity, defined as the ratio between LWP_c change and mean LWP_c over a period of time for the 3 h before sunrise in the LWP_c–z_i, N_d–z_i, and N_d–LWP_c planes, where the locations of dots are based on states at sunrise. Most cases with the LWP_c less than 60 g m⁻² at sunrise gain LWP_c during the 3 h before sunrise (Fig. 8d and f). This qualitatively agrees with Hoffmann et al. (2020) and Glassmeier et al. (2021). However, the sign of the LWP_c velocity is mixed for cases with greater LWP_c, where only 56 % of cases are gaining LWP_c. Among these cases, there is a weak negative correlation between z_i and LWP_c velocity, i.e., shallower/deeper BLs tend to see increasing/decreasing LWP_c, possibly because deeper BLs are more likely to be decoupled from the surface. When projected onto the N_d–LWP_c plane (Fig. 8f), cases with low LWP_c and low N_d mostly gain LWP_c, while cases losing LWP_c only occur under high LWP_c and high N_d conditions. To some extent, this is consistent with the findings in Hoffmann et al. (2020) and Glassmeier et al. (2021).

However, due to some potentially realistic yet complicated correlations among LWP_c, N_d, z_i, and FT q_t, we cannot simply attribute the correlation between LWP_c velocity and N_d to N_d. First, there is a positive correlation between LWP_c and N_d because we focus on the non-precipitating conditions, and high LWP_c cases are only possible if N_d is sufficiently high to suppress the cloud base precipitation (Fig. 8f). Second, due to the positive correlation between LWP_c and z_i (deeper z_i supporting higher LWP_c; Fig. 8d), there is also a positive correlation between z_i and N_d (notice very few cases in the upper-left corner of Fig. 8e). Similarly, because of the positive correlation between LWP_c and FT q_t (Fig. 8b and c), there is a positive correlation between FT q_t and N_d (not shown).

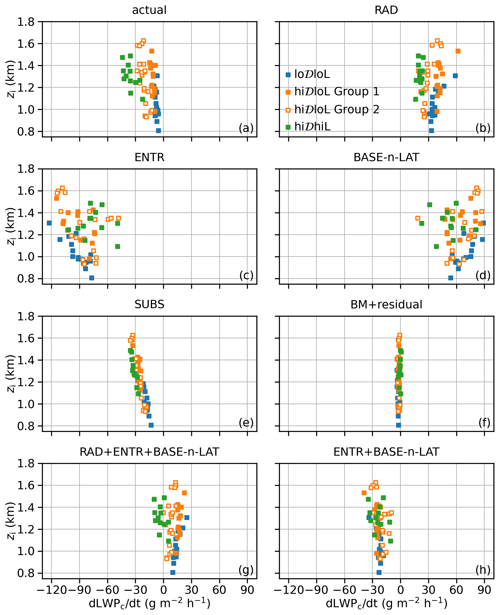
We examine the correlation between radiative cooling and LWP_c to assess the impacts of the positive correlation between FT q_t and LWP_c on the LWP_c tendency (Fig. 9). Recall that to calculate the RAD term for the LWP_c budgets, we first calculate the CV-integrated radiative heating rate, then assume that it evenly distributes in the CV to calculate the RAD term for the CV 〈θ_l〉 budget, and then use Eq. (19) to calculate the RAD term for the LWP_c. The CV-integrated radiative heating rate strongly depends on FT q_t, while the cloud-top temperature (approximated using the lowest temperature in the mean temperature profile for the CV) explains a small portion of its variance (i.e., lower cloud-top temperature associates with less integrated radiative cooling; Fig. 9a). The sensitivity of the CV-integrated radiative heating rate to FT q_t increases for FT q_t below 3 g kg⁻¹. More than 90 % of cases have LWP_c greater than 40 g m⁻² at this time, and the emissivity of these clouds should have saturated (Garrett et al., 2002; Petters et al., 2012). (Our integrated radiative heating rate with FT q_t of 4.5 g kg⁻¹, the FT q_t estimated from Fig. 2 in Petters et al., 2012, is very close to the saturated cloud-integrated radiative heating for longwave radiation in their Fig. 1.) However, the RAD contribution to the CV 〈θ_l〉 budget strongly and positively correlates with LWP_c (filled circles in Fig. 9b) due to correlation between LWP_c and 〈q_t〉, as well as the scaling by CV depth. Earlier, we showed that the MLT-based budget works well for the lo𝒟loL and hi𝒟loL categories during the nighttime (Fig. 5). One might argue that it is more appropriate to assume the CV-integrated radiative heating rate is distributed from the surface to z_i. This scaling reduces the slope but not the sign of the correlation between the scaled RAD term and LWP_c (hollow circles in Fig. 9b). It is only when we use the CV-integrated radiative cooling rate scaled with z_i in Eq. (19) that we find a positive correlation between the scaled RAD term for the LWP_c tendency and LWP_c (hollow circles in Fig. 9c; compare with hollow circles in Fig. 9b).

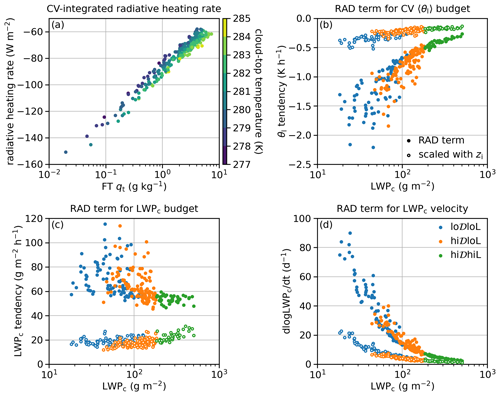
Figure 9 Radiative cooling at 04:40 LT. (a) CV-integrated radiative heating rate, (b) RAD term for CV 〈θ_l〉 budget, (c) RAD term for LWP_c budget, and (d) radiative contribution to LWP_c velocity. Hollow circles in panels (b) and (c) represent the tendencies when the CV-integrated radiative heating rate is hypothetically uniformly distributed over the entire BL depth.

The ratio between the scaled RAD term for the LWP_c tendency and for the CV 〈θ_l〉 tendency depends on Γ_l, 〈ρ₀〉, cloud depth, and $\partial z_{\mathrm{cb}}/\partial \langle {\mathit{\theta }}_{\mathrm{l}}\rangle$. Both the positive correlations between the cloud depth and LWP_c, as discussed in Hoffmann et al. (2020), and between other prefactors and LWP_c (not shown) contribute to this change in the sign of the correlation. For the LWP_c velocity, the division by LWP_c itself further modifies the correlation and the slope between a budget term and LWP_c (Fig. 9d). In summary, not only the FT q_t but also the z_i, the coupling state, and other factors (e.g., the prefactors in Eq. 19) shape the correlation between the radiative contribution to LWP_c tendency or velocity and the LWP_c.

We show the behavior of other terms for the LWP_c tendency in Fig. 10a. The BASE-n-LAT term positively contributes to the LWP_c tendency. It negatively correlates with LWP_c for greater LWP_c but positively correlates with it for lower LWP_c, probably because cases with lower LWP_c at sunrise, mostly in the lo𝒟loL category, have weaker boundary layer circulation. The ENTR term negatively contributes to the LWP_c tendency. It positively correlates with LWP_c for greater LWP_c but negatively correlates with it for lower LWP_c. Compared with the RAD and BASE-n-LAT terms, this correlation suggests that, in the first order, the entrainment is determined by the driving force for the turbulence, e.g., the radiative cooling and the boundary layer circulation. The SUBS term negatively contributes to the LWP_c velocity and positively correlates with LWP_c. After scaling by z_i, the BASE-n-LAT, ENTR, and SUBS terms show a much tighter positive, negative, and negative correlation with LWP_c (Fig. 10b).

Figure 10 Co-variability between ENTR, BASE-n-LAT, and SUBS terms for LWP_c budget and LWP_c at 04:40 LT.

5.2 Daytime evolution of individual cases

Figure 11a and b show the most distinct feature of the daytime evolution of the individual cases. More decoupled cases tend to lose LWP_c more rapidly between sunrise and 12:00 LT. For cases with z_i greater than about 0.9 km, the positive correlation between LWP_c and z_i at sunrise (dots in Fig. 8b) becomes negative by 12:00 LT (dots in Fig. 11a). In the afternoon, the LWP_c recovers for most cases, and a positive correlation between LWP_c and z_i is restored by the end of the simulation.

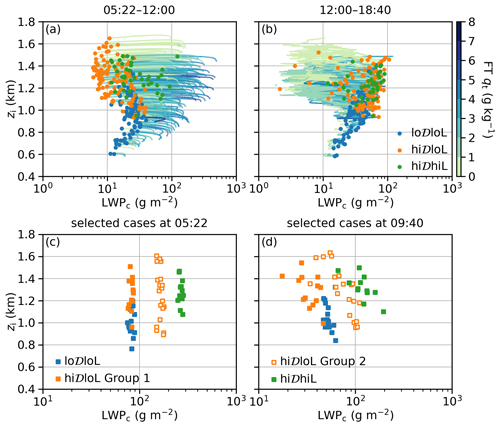
Figure 11 Evolution of LES ensemble members during daytime. In panels (a) and (b), curves indicate the trajectories over the time period, and dots indicate the states at the end of the time period, as shown in the panel titles. Symbols in panels (c) and (d) indicate groups of cases that are selected for further examination: (1) lo𝒟loL cases with LWP_c at sunrise between 75 and 90 g m⁻², (2) hi𝒟loL cases with LWP_c at sunrise in the same range (hi𝒟loL; group 1), (3) hi𝒟loL cases with LWP_c at sunrise between 150 and 180 g m⁻² (hi𝒟loL; group 2), and (4) hi𝒟hiL cases with LWP_c at sunrise between 240 and 300 g m⁻².

To understand the factors controlling the evolution of LWP_c in the LWP_c–z_i plane, we investigate the behavior of four groups of cases with different properties: (1) lo𝒟loL cases with LWP_c at sunrise between 75 and 90 g m⁻², (2) hi𝒟loL cases with LWP_c at sunrise in the same range (hi𝒟loL; group 1), (3) hi𝒟loL cases with LWP_c at sunrise between 150 and 180 g m⁻² (hi𝒟loL; group 2), and (4) hi𝒟hiL cases with LWP_c at sunrise between 240 and 300 g m⁻². Comparing Fig. 11c and Fig. 11d, all four groups develop negative slopes between LWP_c and z_i between sunrise and 09:40 LT, with the least negative slopes for the lo𝒟loL group and the most negative slopes for the hi𝒟hiL group. Figure 12a shows the LWP_c tendencies and budget terms for each case in these four groups. The mean LWP_c tendency between sunrise and 09:40 LT differs between groups by z_i and by degree of coupling. For example, the loss of the LWP_c is faster/slower for groups with higher/lower LWP_c at sunrise; within each group, cases with greater z_i tend to lose LWP_c faster, and the hi𝒟loL group 1 loses LWP_c faster than the lo𝒟loL group. Across different z_i, the RAD term positively correlates with the actual LWP_c tendency and shows a similar spread (Fig. 12b). The variation in the RAD term between groups is consistent with both the nighttime behavior of the RAD term (i.e., more positive RAD term for low LWP_c and low FT q_t, e.g., cases with higher z_i in the lo𝒟loL group and hi𝒟loL group 1; also see Figs. 8b and 9c) and the anticipated greater absorption of shortwave radiation for cases with higher LWP_c (e.g., the hi𝒟hiL group). Unfortunately, we do not have separate longwave and shortwave radiative output to quantify the relative importance of longwave cooling and shortwave warming at this point. The ENTR and BASE-n-LAT terms are larger in magnitude than the RAD term (Fig. 12c and d). The SUBS term shows negative z_i dependence, with small differences between groups (Fig. 12e). The sum of the BM and RES terms is very small when compared with other terms and the actual LWP_c tendency (Fig. 12f). Based on these results, it is reasonable to take the sum of the SUBS, the BM, the PRCP, and the RES terms as a baseline and investigate how much the RAD, the ENTR, and the BASE-n-LAT terms drive the actual LWP_c tendency to deviate from this baseline. Figure 12g and h show the sum of the RAD, the ENTR, and the BASE-n-LAT terms, as well as the sum of the ENTR and the BASE-n-LAT terms. Combined with the RAD term in Fig. 12b, we conclude that the differences in LWP_c tendency between groups with different LWP_c at sunrise are more associated with the RAD term, and the other details derive from a subtle balance between the RAD, ENTR, and BASE-n-LAT terms.

Figure 12 Mean LWP_c tendencies and budget terms due to individual processes for selected cases between sunrise and 09:40 LT.

6 Discussion

In this section, we discuss an uncertainty in our budget analysis method and then address the sensitivity of cloud evolution to SST.

6.1 Uncertainty in ENTR term for 〈θ_l〉 and 〈q_t〉 budgets

As described earlier, we use the entrainment fluxes (i.e., $\mathrm{d}\mathrm{\Phi }/\mathrm{d}t{\mathrm{|}}_{\mathrm{ENTR}}$) from the BL 〈θ_l〉 and 〈q_t〉 budgets to calculate the ENTR term for the CV. However, because the cloudy region of a domain is more turbulent than the clear-sky region, one would expect a higher entrainment flux in the cloudy region than the domain mean for partially cloudy scenes. Underestimating the magnitude of entrainment fluxes for the CV budget will cause a compensating error in the BASE-n-LAT term because the latter holds the residual between the actual CV 〈θ_l〉 and 〈q_t〉 tendencies and the sum of the other terms.

In this subsection, we resort to the jump-based method (Eq. 15) to assess the potential bias in our ENTR term. We first repeat the budget analysis for all clear-sky columns between the same base and top as the CV (denoted with nCV, meaning not CV) and then partition the total entrainment warming and drying in the CV and the nCV with the cloudy-region jump Δϕ_CV and clear-sky jump Δϕ_nCV. This alternative estimate of the entrainment tendency for the CV is

$$\begin{array}{}\text{(20)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\langle \mathit{\varphi }\rangle }{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR},\mathrm{alt}}\\ & ={\displaystyle \frac{f_{\mathrm{c}}\left(\mathrm{d}\langle \mathit{\varphi }\rangle /\mathrm{d}t{\mathrm{|}}_{\mathrm{ENTR}}\right)+(\mathrm{1}-f_{\mathrm{c}})\left(\mathrm{d}\langle \mathit{\varphi }{\rangle }_{\mathrm{nCV}}/\mathrm{d}t{\mathrm{|}}_{\mathrm{ENTR}}\right)}{f_{\mathrm{c}}+(\mathrm{1}-f_{\mathrm{c}})\mathrm{\Delta }{\mathit{\varphi }}_{\mathrm{nCV}}/\mathrm{\Delta }{\mathit{\varphi }}_{\mathrm{CV}}}},\end{array}\end{array}$$

where alt stands for alternative, and again, ϕ represents either θ_l or q_t. The question becomes how to define z₊ and z₋ separately for ϕ profiles averaged in the cloudy- and clear-sky regions to calculate the jumps. We follow Yamaguchi et al. (2011), where the authors check the domain-wide liquid water static energy (s_l) variance profile and define z₊ and z₋ as the levels with s_l variance falling to 5 % of the peak value. This method works reasonably well for DYCOMS-II RF02, which is the case simulated in Yamaguchi et al. (2011) (see Appendix C in that work). We apply a constant absolute s_l variance threshold of 0.235 K² (5 % of 4.7 K²; the peak s_l variance in Yamaguchi et al., 2011) to search for z₊ and z₋ to qualitatively capture the idea that the jump is smaller when turbulence mixing is weaker (lower peak s_l variance).

We take a few extra steps to handle potential outliers. We exclude all time steps with f_c < 0.01 (1.9 % of all time steps) and keep the entrainment tendencies with f_c > 0.99 unchanged. Sometimes, the peak s_l variance of a profile (usually the clear-sky ones) is below 0.235 K², and no z₊ or z₋ are identified. For this situation, we keep a data point if only Δϕ_CV can be calculated (about 6.4 % of all time steps) and set its Δϕ_nCV to 0, which actually exaggerates the difference between the cloudy- and clear-sky regions. We exclude a data point if neither Δϕ_CV nor Δϕ_nCV can be calculated, which rarely occurs.

For all three categories, we find no significant difference between the current and the alternative ENTR terms until the afternoon (Fig. 13). These results certainly depend on details of our method, e.g., the value of the s_l variance threshold. However, without a more solid foundation for an alternative choice of the threshold, sensitivity tests would not provide a more reliable quantification of the bias.

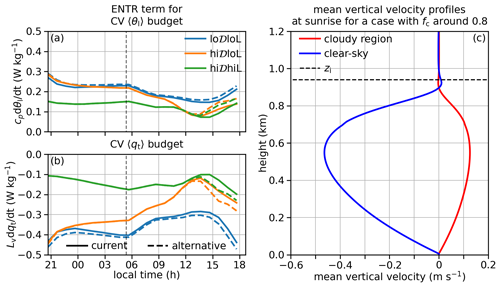
Figure 13 Time series of current and alternative estimates of the entrainment contribution to CV (a) 〈θ_l〉 and (b) 〈q_t〉 budgets. The vertical dashed black lines indicate sunrise. Panel (c) shows an example to facilitate the discussions near the end of Sect. 6.1.

One other method is to partition the entrainment flux using Eq. (13), such that

$$\begin{array}{}\text{(21)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR},\mathrm{alt}}\\ & ={\displaystyle \frac{\mathrm{1}}{f_{\mathrm{c}}+(\mathrm{1}-f_{\mathrm{c}}){\left({\mathit{\rho }}_{\mathrm{0},\mathrm{e}}{\mathit{\varphi }}_{\mathrm{e}}\right)}_{\mathrm{nCV}}/{\left({\mathit{\rho }}_{\mathrm{0},\mathrm{e}}{\mathit{\varphi }}_{\mathrm{e}}\right)}_{\mathrm{CV}}}}{\displaystyle \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}}{\mathrm{|}}_{\mathrm{ENTR}}.\end{array}\end{array}$$

If we use ρ₀ϕ at z₊, identified earlier as an estimate of ρ_0,eϕ_e, the resulting ENTR terms are even closer to our current estimates.

These results do not necessarily mean that our current ENTR term is accurate. They simply suggest that the two alternative methods we test to introduce contrast between cloudy-region and clear-sky entrainment produce limited correction to current ENTR estimates. While these results provide some confidence in the robustness of current ENTR estimates, it seems to be inconsistent with the argument that the cloudy region is more turbulent and thus should entrain more. We argue that this inconsistency is partially rooted in the assumption that the movement of z_i is the result of the entrainment and the subsidence (Eq. 4). We find that the air is on average descending/ascending at speeds around a few millimeters per second near the mean z_i in the cloudy-/clear-sky region, which are indeed at very similar heights, despite the mean updraft/downdraft for the bulk of BL in the cloudy-/clear-sky region (Fig. 13c). This is probably the signature of a mesoscale (instead of large scale, e.g., the prescribed subsidence, which is horizontally uniform in the domain) mean circulation in the FT, similar to the one shown in Zhou and Bretherton (2019) (see their Fig. 9). In other words, the cloudy-/clear-sky region is more/less turbulent, but there may be a mesoscale downdraft/updraft limiting/promoting the growth of z_i. With Eq. (4), the effect of this mesoscale mean air motion is lumped into the entrainment. This finding suggests that our current ENTR term should be interpreted as a collective effect of processes, except the prescribed subsidence that move the z_i.

6.2 Sensitivity of cloud evolution to SST

As mentioned earlier, our LES ensemble covers a wide range of conditions by perturbing initial profiles. However, all simulations are configured with the same fixed SST and subsidence profile. As a result, the initial BL θ_l could be more than 6.8 K colder than θ_SST, which is not very realistic for marine stratocumuli. Also, the correlation that the initially shallower BLs in our ensemble tend to be colder and drier (see Sect. 3.3) means that shallower BLs tend to be colder than the SST and experience greater surface fluxes. To capture more realistic co-variability between environment conditions, one may consider simulating marine stratocumuli as they are advected towards warmer SST (e.g., Sandu and Stevens, 2011; Teixeira et al., 2011; Bretherton and Blossey, 2014; Yamaguchi et al., 2015; de Roode et al., 2016; Kazil et al., 2021) or as they reach equilibrium with different environmental conditions along this transition (Chung et al., 2012).

For now, we assess the impacts of this correlation on our results by re-running all simulations with the SST set to 0.5 K warmer than the initial lowest model level air temperature for each case. (Hereafter, we refer to this LES ensemble as the SST0.5K+ set and the original LES ensemble as the fSST set, where f stands for fixed.) Compared with the fSST set, the surface fluxes in the SST0.5K+ set are much weaker (Fig. S9a and b), which are consistent with the overall more decoupled conditions, especially in the afternoon (cf. Figs. S8d and 2d). The LWP_c values at sunrise increase in the SST0.5K+ set; they are less correlated with z_i but more positively correlated with FT q_t (Fig. S14b and c). This behavior broadly agrees with De Roode et al. (2014), where warmer SST causes thinning of stratocumuli when the response in entrainment is strong. Other results are similar between SST0.5K+ and fSST. In particular, in the morning, clouds in deeper BLs still experience dramatic loss in LWP_c, such that a negative correlation develops between LWP_c and z_i (compare Fig. S17a and Fig. 11a). We present other figures based on the SST0.5K+ set from in the Supplement.

7 Summary

In this work, we explore the cloud system evolution of non-precipitating marine stratocumuli with a focus on the impacts of the diurnal cycle and free-tropospheric (FT) humidity by analyzing 244 cases in an LES ensemble generated by perturbing initial profiles and aerosol conditions.

We separate the cases into three categories with distinct behavior based on their relative decoupling index (𝒟) at 09:40 LT and cloud liquid water paths (LWP_c) at sunrise: a lo𝒟loL category (𝒟 ≤ 1), a hi𝒟loL category (𝒟 > 1 and LWP_c ≤ 180 g m⁻², which is the highest LWP_c for the lo𝒟loL category), and a hi𝒟hiL category (𝒟 > 1 and LWP_c > 180 g m⁻²). Cases in the lo𝒟loL category are commonly associated with lower z_i. They start with the lowest LWP_c and cloud fraction (f_c) among the three categories and may not ever become overcast. However, on average, they also experience the least reduction in LWP_c and f_c during the daytime. Clouds in the hi𝒟loL category occur in deeper BLs, start with more LWP_c, and tend to be overcast during the nighttime. On average, they experience dramatic LWP_c and f_c reductions during the day. These clouds tend to evolve into a cumulus-rising-into-stratocumulus structure in the afternoon. Clouds in the hi𝒟hiL category share many features with those in the hi𝒟loL category but show different timing and amplitude of daytime LWP_c and f_c fluctuations. The diurnal cycles of LWP_c and f_c for three categories are closely related to the diurnal cycles of their coupling states.

We perform a budget analysis to understand the diurnal cycle of LWP_c by tracking the mean θ_l and q_t budgets for the cloud volume (CV), which is a volume consisting of all cloudy columns between the first grid box base below the mean cloud base and z_i, and then applying the LWP budget equation (Eq. 19) to the CV, assuming it is well mixed. By focusing on the cloudy region of the cloud layer, this method closes the budget with a very small residual (RES) until early afternoon. In particular, it adequately captures the rapid LWP_c reduction in the morning for all categories. A delayed decrease in the positive contribution to LWP_c from the BASE-n-LAT term, a term that tracks the impacts of the processes associated with the interface between the CV and the rest of the BL (i.e., CV base and lateral sides), after sunrise explains the slower LWP_c reduction in the lo𝒟loL category than in the hi𝒟loL category. For the hi𝒟hiL category, the strong decrease in the radiative (RAD) cooling results in the most rapid LWP_c reduction in this category.

The impact of a humid FT on the evolution of simulations during the nighttime is distinct. A positive correlation between FT q_t and LWP_c emerges and strengthens towards sunrise. Because the longwave emissivity of clouds is saturated in most cases, the FT q_t strongly affects the CV-integrated radiative heating rate. As a result, there is stronger radiative cooling for cases with lower LWP_c through the correlation between the FT q_t and LWP_c. This illustrates how the co-variability among state variables and cloud controlling factors modifies the distribution of LWP_c tendency in state variable spaces. During the daytime, clouds in deeper BLs lose LWP_c faster in the morning, again suggesting that state variables beyond LWP_c and N_d are necessary to understand the LWP_c tendency. A closer analysis reveals that the LWP_c tendency in the morning varies with the LWP_c at sunrise, z_i, and the degree of decoupling. A budget analysis for LWP_c shows that the subsidence term (SUBS) causes a more negative LWP_c tendency at deeper z_i, and this effect is similar for cases with different LWP_c at sunrise and at the degree of decoupling. The entrainment (ENTR) and BASE-n-LAT terms closely balance each other, and there is a weak dependence of the net effect on z_i. It is the RAD term that differentiates cases with similar z_i in terms of the LWP_c tendency.

In the design of the current LES ensemble, SST and subsidence profiles are not perturbed. Also, the natural co-variability between different environmental conditions is not captured. To partially address these limitations, we perform additional runs for all cases with the SST set to 0.5 K warmer than the initial lowest model level air temperature for each case. The statistical behavior of the clouds with this configuration is similar to the LES ensemble with fixed SST, although the correlation between LWP_c and z_i at sunrise becomes weaker. Future simulations should use more realistic forcings and naturally co-varying thermodynamic and aerosol conditions to improve the realism of the LES ensemble. A related issue is that the 24 h length of current simulations, although covering one diurnal cycle, is insufficient for the mesoscale organization of clouds to fully develop (Kazil et al., 2017). This limitation should be addressed in future work.

We demonstrate the emergence of the correlations among environmental conditions and state variables as the clouds evolve. All these correlations project onto the correlations with N_d and need to be carefully considered when we distill the causality between N_d and variables like the LWP_c tendency or the LWP_c velocity. We pursue this task in Zhang et al. (2024).

Appendix A: Constructing initial thermodynamic profiles

In this section, we describe the method for (1) creating the upper-air θ_l and q_t profiles and (2) connecting them with the initial BL θ_l and q_t profiles (described in Sect. 2) to construct the initial θ_l and q_t profiles.

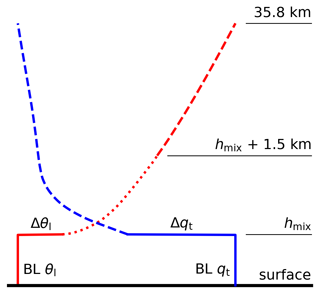
To prepare for the upper-air profiles, we generate ERA5-based climatological profiles in a few steps. First, we produce mean profiles from all ERA5 profiles in the Californian stratocumulus region (i.e., the 10° × 10° box between 20° N, 30° N, 120° W, and 130° W, as defined in Klein and Hartmann, 1993) during April, May, and June (the months with highest stratocumulus cover in the region; Wood, 2012) from 2000 to 2011. Then, we search for the height with the maximum θ_l gradient below 2 km and keep the mean profile segments between this height and 35.8 km, which is the top of the mean profiles.

When we connect the θ_l climatological profile produced this way to the initial BL profiles, some simulations experience very rapid growth in the inversion base height (z_i) in the first few hours, suggesting that the θ_l gradient across the inversion is too weak. To solve this issue, we prepare a transitional profile for θ_l. We average the observed θ_l profiles during the warm-season legs of the MAGIC campaign after translating them vertically to line up at inversion bases and having their BL values subtracted at all heights. We keep the first 1.5 km of this mean profile above the inversion base.

To construct an initial θ_l profile, we first translate the transitional profile so that its lowest point attaches to point right above the inversion base. Next, we scale the ERA5-based θ_l climatological profile so that its lowest point attaches to the highest point of the transitional profile (now sitting at 1.5 km above h_mix), while its highest point stays fixed at 35.8 km. For an initial q_t profile, we scale the ERA5-based q_t climatological profile so that its lowest point directly attaches to the point right above the inversion base, while its highest point stays fixed at 35.8 km. A constant surface pressure of 1018.52 hPa, based on ERA5 climatology, is used for all initial profiles. See Fig. A1 for an illustration.

Figure A1 A sketch showing the construction of the initial θ_l and q_t profiles (in red and blue, respectively) from the initial BL profiles (solid segments), ERA5-based climatological profiles (dashed segments), and the MAGIC-based transitional θ_l profile (dotted segment).