A global re-analysis of regionally resolved emissions and atmospheric mole fractions of SF₆ for the period 2005–2021

We determine the global emission distribution of the potent greenhouse gas sulfur hexafluoride (SF₆) for the period 2005–2021 using inverse modelling. The inversion is based on 50 d backward simulations with the Lagrangian particle dispersion model (LPDM) FLEXPART and on a comprehensive observation data set of SF₆ mole fractions in which we combine continuous with flask measurements sampled at fixed surface locations and observations from aircraft and ship campaigns. We use a global-distribution-based (GDB) approach to determine baseline mole fractions directly from global SF₆ mole fraction fields at the termination points of the backward trajectories. We compute these fields by performing an atmospheric SF₆ re-analysis, assimilating global SF₆ observations into modelled global three-dimensional mole fraction fields. Our inversion results are in excellent agreement with several regional inversion studies in the USA, Europe, and China. We find that (1) annual US SF₆ emissions strongly decreased from 1.25 Gg in 2005 to 0.48 Gg in 2021; however, they were on average twice as high as the reported emissions to the United Nations. (2) SF₆ emissions from EU countries show an average decreasing trend of −0.006 Gg yr⁻¹ during the period 2005 to 2021, including a substantial drop in 2018. This drop is likely a direct result of the EU's F-gas regulation 517/2014, which bans the use of SF₆ for recycling magnesium die-casting alloys as of 2018 and requires leak detection systems for electrical switch gear. (3) Chinese annual emissions grew from 1.28 Gg in 2005 to 5.16 Gg in 2021, with a trend of 0.21 Gg yr⁻¹, which is even higher than the average global total emission trend of 0.20 Gg yr⁻¹. (4) National reports for the USA, Europe, and China all underestimated their SF₆ emissions. (5) Our results indicate increasing emissions in poorly monitored areas (e.g. India, Africa, and South America); however, these results are uncertain due to weak observational constraints, highlighting the need for enhanced monitoring in these areas. (6) Global total SF₆ emissions are comparable to estimates in previous studies but are sensitive to a priori estimates due to the low network sensitivity in poorly monitored regions. (7) Monthly inversions indicate that SF₆ emissions in the Northern Hemisphere were on average higher in summer than in winter throughout the study period.

1 Introduction

Sulfur hexafluoride (SF₆) is the greenhouse gas (GHG) with the highest known global warming potential (GWP), 24 300, over a 100-year time horizon (Smith et al., 2021). Once emitted, SF₆ accumulates in the atmosphere, as it is only slowly degraded via photolysis and electron attachment (Ravishankara et al., 1993), resulting in a very long atmospheric lifetime, with estimates ranging from 580 to 3200 years (Kovács et al., 2017; Patra et al., 1997; Ravishankara et al., 1993; Ray et al., 2017). The ocean also acts as a sink for atmospheric SF₆; however, its magnitude is debated, with estimates ranging up to 7 % of the global annual emissions (Ni et al., 2023). Regardless of its exact lifetime and possible ocean sink, SF₆ emissions will cause a positive radiative forcing for hundreds of years.

Since the early 2000s, global mole fractions of SF₆ have undergone a rapid increase, more than doubling from roughly 4.5 ppt (parts per trillion) in 2000 to 10 ppt in 2020 (Lan et al., 2024). In 2020, the radiative forcing of SF₆ was 5.9 mW m⁻² (Laube et al., 2023). This value could surge 10-fold by the end of the 21st century if the upward trend in global SF₆ emissions persists, as pointed out by Hu et al. (2023).

SF₆ plays a crucial role in various industrial applications due to its remarkable insulating properties and chemical stability (e.g. Cui et al., 2024). It is primarily used in high-voltage electrical equipment in the power industry, such as gas-insulated switch gears (IEEE, 2012), transmission lines (Koch, 2008), and transformers (Gouda et al., 2012), where it acts as a dielectric and insulator. Here, emissions occur primarily during leakage, maintenance, and decommissioning of equipment (Zhou et al., 2018). Furthermore, SF₆ finds applications in semiconductor manufacturing, facilitating precise etching processes (Lee et al., 2004), and serves as blanketing gas or for degassing in the magnesium or aluminium metal industry (Maiss and Brenninkmeijer, 1998). Moreover, it is used in medicine (Lee et al., 2017; Brinton and Wilkinson, 2009); photovoltaic manufacturing (Andersen et al., 2014); military applications (Koch, 2004); particle accelerators (Lichter et al., 2023); soundproof glazing (Schwarz, 2005); sport shoes (Pedersen, 2000); car tyres (Schwaab, 2000); wind turbines (EPA, 2023); and as a tracer gas in the atmosphere (Martin et al., 2011), in groundwater (Okofo et al., 2022), in rivers (Ho et al., 2002), and in oceans (Tanhua et al., 2004).

SF₆ is regulated under the Kyoto Protocol. Thus, countries classified as Annex I nations must submit reports detailing their SF₆ emissions to the United Nations Framework Convention on Climate Change (UNFCCC). These national inventories are almost exclusively created by bottom-up methods, wherein statistical data of industrial production and consumption are used, along with source-specific emission factors to estimate the emissions. However, SF₆ emissions have been shown to be strongly underestimated by the bottom-up reports, underlining the need for independent verification methods (Levin et al., 2010). Therefore, top-down approaches such as inverse modelling on the basis of atmospheric measurements have been used in several studies to estimate SF₆ emissions (e.g. Brunner et al., 2017; Fang et al., 2014; Ganesan et al., 2014; Hu et al., 2023; Rigby et al., 2011; Simmonds et al., 2020; Vojta et al., 2022).

Around the year 2000, there was a notable shift in the global SF₆ emission pattern from a declining to an increasing trend, which has continued since then (Simmonds et al., 2020). This rising trend was primarily attributed to the increasing emissions from non-Annex-I Asian countries (Rigby et al., 2010). An inversion study by Fang et al. (2014) confirmed a strong increase in East Asian SF₆ emissions between 2006 and 2009 and found its contribution to the global total emissions to be 45 %–49 % between 2009 and 2012, with China being the largest contributor. Several other inversion studies identified China as the major contributor to global SF₆ emissions (e.g. Ganesan et al., 2014; Rigby et al., 2011; Vojta et al., 2022). From 2007 to 2018, China's annual emissions increased from 1.4 to 3.2 Gg yr⁻¹, accounting for 36 % of the global total emissions in 2018, according to Simmonds et al. (2020). A recent inversion study by An et al. (2024) had access to data from a relatively dense monitoring network inside China and estimated even higher Chinese emissions, with an increase from 2.6 Gg yr⁻¹ in 2011 to 5.1 Gg yr⁻¹ in 2021. Simmonds et al. (2020) also constrained western European SF₆ emissions for the years 2013–2018, using three different regional inversion systems. Two of these inversion systems closely matched the emissions reported to the UNFCCC, while the third indicated substantially higher emissions. Brunner et al. (2017) found that western European SF₆ emissions were 47 % higher than reported to the UNFCCC for the year 2011. As part of the UK annual report to the UNFCCC, Manning et al. (2022) reported inversion results for SF₆ emissions in northwestern Europe and found a decreasing trend, dropping from 0.37 Gg yr⁻¹ in 2004 to 0.18 Gg yr⁻¹ in 2021. An atmospheric inversion study by Hu et al. (2023) found that annual US SF₆ emissions decreased between 2007 and 2018 but were, on an annual basis, 40 %–250 % higher than calculated by the U.S. Environmental Protection Agency's national inventory submitted to UNFCCC. They also suggested that US SF₆ emissions were substantially higher in the winter than in the summer.

Global total SF₆ emissions can be well constrained by global box models, such as the AGAGE 12-box model (e.g. Rigby et al., 2013). While Rigby et al. (2010, 2011) presented global SF₆ inversion studies, and recent regional studies have estimated SF₆ emissions in specific regions (e.g. Hu et al., 2023; An et al., 2024), an updated, comprehensive, and top-down perspective of the global SF₆ emission distribution is needed. Moreover, existing inversion studies often only use data from continuous surface station measurements or from specific observation networks, potentially missing valuable information from other available observations. In the absence of accurate global SF₆ mole fraction fields, many studies use statistical observation-based methods to determine initial conditions for their inversions, which are suspected of introducing systematic errors in the inversion results (Vojta et al., 2022). Last, the seasonality of SF₆ emissions has not been considered by inversion studies so far, with the exception of the recent study by Hu et al. (2023).

Our study offers a comprehensive global and regionally resolved top-down perspective of SF₆ emissions, using inverse modelling to determine the global emission distribution for the period between 2005 and 2021. We use all available SF₆ observations that we could track down by merging continuous surface station measurements, flask measurements, and observations from aircraft and ship campaigns. We consider multiple a priori emission fields for our inversion. For the initial conditions (Vojta et al., 2022), we assimilate global SF₆ observations into modelled global three-dimensional SF₆ concentration fields, resulting in an atmospheric SF₆ re-analysis for the period 2005–2021. We investigate regional and national SF₆ emission trends with annual and also monthly resolutions and compare our results to various existing regional studies. Finally, we discuss our global total emission trend and compare it to results from the AGAGE 12-box model and to global emissions directly calculated from annual increases in globally averaged atmospheric SF₆ mole fractions provided by NOAA (Lan et al., 2024).

2 Methods

2.1 Measurement data

The SF₆ re-analysis (Sect. 2.3) and the atmospheric inversion (Sect. 2.5) are based on globally distributed atmospheric observations of SF₆ dry-air mole fractions collected during the period 2005 to 2021. Our data set combines both continuous online and instantaneous flask sample measurements from surface stations, with observations from moving platforms. Figure 1 shows all surface station sites included in the inversion and the re-analysis. Figure A1 gives an overview of all the measurements from moving platforms, highlighting the measurement date and altitude with different colours. In addition, Sect. S3, as well as Tables S1 (continuous surface stations), S2, S3 (flask measurement stations), and S4 (moving platforms) in the Supplement, lists all the data sets used and gives further details. The measurements were provided by several independent organisations and by international observation networks such as AGAGE and NOAA. Table S5 lists all the individual providers and their acronyms. Most of the data can be found in databases like WDCGG (di Sarra et al., 2022), EBAS (Tørseth et al., 2012), and CEDA (CEDA, 2023). We standardise all observations to the Scripps Institution of Oceanography's SIO-2005 calibration scale, as described in Sect. S4.

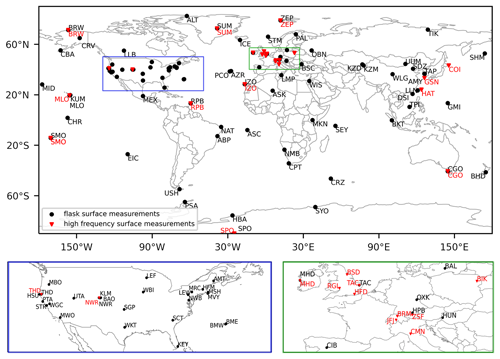
Figure 1 Locations of stations with continuous surface measurements (red triangles) and surface flask measurements (black dots) used in the inversion.

For the inversion, continuous surface measurements were averaged over 3 h intervals. Observations from moving platforms were averaged on a spatiotemporal grid with a temporal resolution of 3 h and a spatial resolution of 0.5° in latitude, 0.5° in longitude, and 300 m in height. No observation averaging was performed for the re-analysis. In addition, we adopted a method by Stohl et al. (2009) to identify observations that cannot be brought into agreement with modelled mole fractions by the inversion, which we removed entirely (in contrast to Stohl et al., 2009, who assigned larger uncertainties to these observations). We utilised the kurtosis of the a posteriori error frequency distribution and iteratively excluded observations causing the largest absolute errors until the kurtosis of the remaining error values fell below 5, approximating a Gaussian distribution. Our complete data set consists of around 2.7 million observations, while the averaged data set comprises roughly 800 000 observations. Figure S1 in the Supplement shows the total number of annual observations available for (a) the entire data set and (b) the averaged data set.

2.2 Atmospheric transport

We use the Lagrangian particle dispersion model (LPDM) FLEXPART 10.4 (Pisso et al., 2019a) to simulate the atmospheric transport of SF₆ between the emission sources and the measurement locations. The model does not account for removal processes, as SF₆ is almost inert in the troposphere to middle stratosphere. We run FLEXPART in backward mode, releasing 50 000 particles continuously over 3 h intervals from the measurement locations and tracking them backward in time for 50 d. The choice of the 50 d simulation period was motivated by the findings of Vojta et al. (2022), who tested the effect of different simulation periods (1–50 d) and found that 50 d simulations resulted in an improved model–measurement agreement and in more robust inversion results in comparison to shorter periods (e.g. 1, 5, 10, or 20 d). For the continuous and moving platform observations, the 3 h intervals are identical to the 3 h averaging windows mentioned above (Sect. 2.1). For the flask measurements, the 3 h intervals are centred around the measurement time. FLEXPART determines emission sensitivities shown as the linear operator H_e, which allows us to relate mole fraction values at the measurement location and time y with the corresponding emissions e occurring during the 50 d simulation period. The emissions prior to the simulation cannot be directly related but still contribute to the measured mole fraction value and thus must be accounted for in the model as well (Sect. 2.2.2). Therefore, FLEXPART also determines sensitivities to the initial conditions, which are shown as the linear operator H_i, which is multiplied by a three-dimensional SF₆ mole fraction field y_i (Sect. 2.3) 50 d before the respective measurement to obtain the baseline H_iy_i. The relationship between receptor mole fractions y, initial conditions y_i and emissions e is given by

$$\begin{array}{}\text{(1)}& \mathit{y}={\mathbf{H}}_{\mathrm{e}}\mathit{e}+{\mathbf{H}}_{\mathrm{i}}{\mathit{y}}_{\mathrm{i}}=\mathbf{H}\mathit{x},\end{array}$$

where H is the complete atmospheric transport operator combining H_e and H_i, and x is the state vector combining e and y_i. Note at this point that for the optimisation, we aggregate grid cells of the emission grid (see Sect. 2.5) and that the just-defined variables (H_e, e, H_i, and y_i) refer to aggregated groups of grid cells. For a detailed description, please see Thompson and Stohl (2014).

We run FLEXPART with hourly ECMWF ERA5 wind fields (Hersbach et al., 2018) with 0.5°×0.5° resolution and 137 vertical levels. The global output grid has a resolution of 1°×1° and 18 vertical layers with interface heights at 0.1, 0.5, 1, 2, 3, 4, 5, 7, 9, 11, 13, 15, 17, 20, 25, 30, 40, and 50 km above ground level (a.g.l.). The emission sensitivities were calculated only for the lowest layer from 0 to 100 m a.g.l., where most emissions occur.

2.2.1 Emission sensitivities

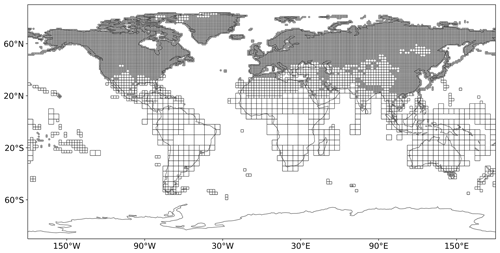
Figure 2 shows the annual averaged emission sensitivities for all observations made in the example year 2019. Areas of high sensitivity are well covered by the measurement data set, so that emissions can be well constrained by the inversion. Emission sensitivities in the Northern Hemisphere are much higher than in the Southern Hemisphere, and the high-SF₆-emitting countries of China and the USA are reasonably well covered. The largest values are observed in northwestern Europe, which is very well monitored by the dense British observation network. However, large land areas in the Southern Hemisphere, including South America, southern Africa, and northern Australia, are poorly sampled due to a lack of continuous measurements. India, which is considered to have high SF₆ emissions, is also poorly covered. In these areas, the emissions may not be determined well by the inversion.

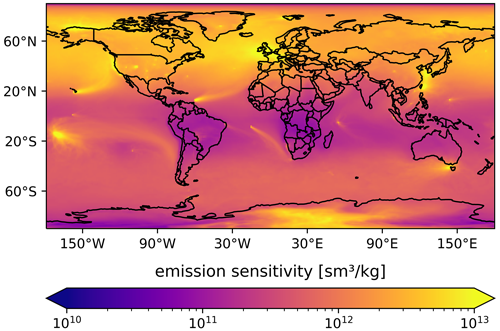
Figure 2 Annually averaged emission sensitivities for the example year 2019 obtained from FLEXPART 50 d backward simulations. Notice that values represent averages over all cases for which FLEXPART calculations were made. Thus, sites with high-frequency online observations are weighted more strongly than sites where only flask measurements are made or where observations are made from moving platforms.

2.2.2 Initial conditions

Using a LPDM to calculate emission sensitivities for atmospheric inversions, we release virtual particles directly from the measurement location and benefit from almost infinite resolution at the receptor. The disadvantage of using a LPDM is that we have to deal with the initial conditions, as virtual particles can be followed backward only for a limited period due to the computational costs. Only emissions that occur within this LPDM simulation period can be directly related to observed mole fraction values and are accessible to the inversion. We, therefore, need to define a baseline that accounts for all the emission contributions prior to the simulation period that contribute to the observed mole fraction. In this study, we use the global-distribution-based (GDB) method (Vojta et al., 2022) to determine the baseline. We couple the mole fraction sensitivity at the endpoints of the FLEXPART back trajectories to a global field of SF₆ mole fractions (for more details, see Thompson and Stohl, 2014). In essence, this propagates the time-resolved three-dimensional mole fractions in space and time along the 50 d trajectories to the receptor location and time. As pointed out by Vojta et al. (2022), the GDB method has many advantages over observation-based filtering methods. GDB baselines are consistent with the LPDM backward simulation length, account for meteorological variability, and allow the inclusion of low-frequency measurements and measurements from moving platforms in the inversion. However, the method requires unbiased global time-resolved three-dimensional fields of SF₆.

2.3 Global SF₆ fields

In this study, we generate global fields of SF₆ mole fractions for the period between 2005 and 2021, using the LPDM FLEXPART 8-CTM-1.1 (Henne et al., 2018). The model is described by Groot Zwaaftink et al. (2018), who tested its performance for CH₄, while Vojta et al. (2022) applied it to SF₆. We operate FLEXPART-CTM in a domain-filling mode, where 80 million virtual particles are dispersed globally in proportion to air density. The initialisation is based on a latitudinal SF₆ profile determined by interpolation of surface measurements and accounts for the “age of air” (Stiller et al., 2021) at higher altitudes (for more details, see Sect. S5). Released particles are tracked forward in time and carry both an air tracer and the chemical species SF₆. When they reside in the atmospheric boundary layer, the model accounts for SF₆ emissions by increasing the SF₆ masses of the respective particles. The emission uptake of the particles is driven by the “UP” a priori emission data set (see Sect. 2.4).

As model errors and inaccurate emission fields lead to errors and biases in the global SF₆ fields, a nudging routine is used to push the simulated mole fractions towards the observations within predefined kernels centred around the measurement locations. We include the entire observation data set in the nudging routine, comprising continuous surface station measurements, flask measurements, and observations from aircraft and ship campaigns. Furthermore, we assign different kernel sizes to individual observations, according to the observed variability in a selected time window for stationary sites and according to the measurement height for moving platforms. Small kernels are attributed to observations with higher variability and observations close to the surface to preserve the spatial variability in SF₆ mole fractions over land masses. Detailed kernel configurations can be found in Table S6. We run the model with the 0.5°×0.5° ERA5 data set and produce daily average output with a resolution of 3°×2°. The daily-resolved global SF₆ mole fraction fields between 2005 and 2021 can be freely downloaded from https://doi.org/10.25365/phaidra.489 (Vojta, 2024).

2.4 A priori emissions

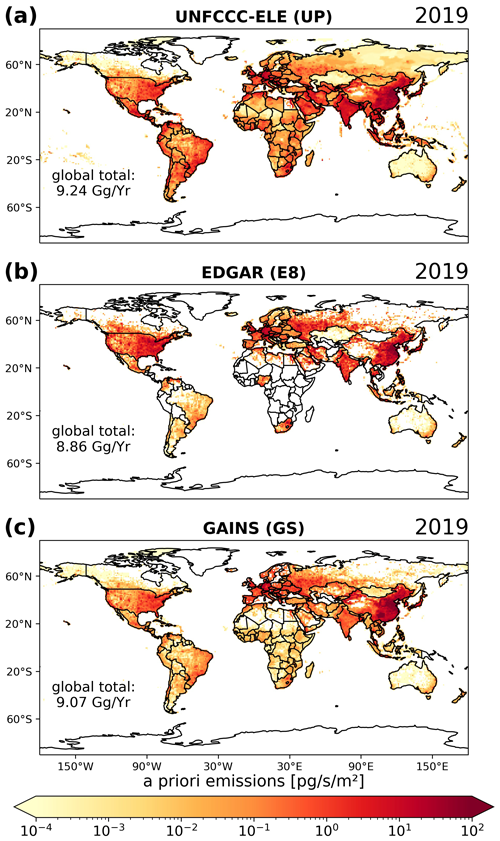
We generate six different annually resolved global SF₆ emission fields for the period 2005 to 2021 that are used as a priori emissions in the inversions (Sect. 2.5). One of these fields is also used to drive FLEXPART-CTM (Sect. 2.3). Our six a priori emissions are based on three different inventories (see Table 1) and globally gridded based on different proxy information at a resolution of 1°×1°.

Table 1 Overview of global SF₆ a priori emission fields used in this study.

2.4.1 UNFCCC-ELE

For every year, we gather total national SF₆ emissions reported to the UNFCCC (UNFCCC, 2021) and add total Chinese emissions estimated by Fang et al. (2014). We then subtract the total emissions of these countries from the total global SF₆ emissions calculated by Simmonds et al. (2020). The residual emissions are then distributed among all other countries proportionally to their national electricity generation. Gaps in the SF₆ emissions or electricity generation data are filled by linear interpolation. Last, the attributed total national SF₆ emissions are further distributed within the respective borders of each country according to two different proxy data sets, (1) the gridded population density (CIESIN, 2018) (UP) and (2) night light remote sensing data (Elvidge et al., 2021) (UN), thus resulting in two different UNFCCC-ELE a priori emission versions.

2.4.2 EDGAR

We use the gridded annual global SF₆ emission inventory provided by the Emissions Database for Global Atmospheric Research (EDGAR, 2023; Crippa et al., 2023), part of the recently updated data set EDGARv8.0 (E8). In addition, we also utilise the national annual totals of SF₆ emissions provided by EDGARv7.0 (EDGAR, 2022; Crippa et al., 2021), which are not gridded. As for the UNFCCC-ELE emissions, we distribute those national totals according to the gridded population density (CIESIN, 2018) (E7P) or night light remote sensing (Elvidge et al., 2021) (E7N).

2.4.3 GAINS

Furthermore, we use the GAINS gridded global emission inventory. This inventory is based on the study by Purohit and Höglund-Isaksson (2017) and was updated until 2020 as described in Sect. S6. The provided data set was extended to 2021 by linear extrapolation (GS).

Figure 3 A priori emissions from the different sources (a) UNFCCC-ELE (UP), (b) EDGAR (E8), and (c) GAINS (GS) for the year 2019.

2.4.4 Comparison

Emission fields from the three inventories (UNFCCC-ELE, EDGAR, and GAINS) show much stronger differences than the two variations in UNFCCC-ELE and EDGAR generated using different proxy information for spatial distribution. In Fig. 3, we therefore only compare three a priori emissions (UP, E8, and GS) for 2019, as an example, while UN, E7N, and E7P are shown in the Supplement (Fig. S25). It is noteworthy that all a priori emission fields show similar global total SF₆ emissions in 2019. Figure 3 shows significantly higher emissions in the Northern Hemisphere than in the Southern Hemisphere for all three fields, with China being the biggest emitter. Other high-emitting areas are Europe, the USA, and India. While emissions in Europe are comparable across all data sets, notable differences can be seen in other regions: (1) UNFCCC-ELE (electricity generation distributed data for non-reporting countries) shows relatively high emissions in India and the Southern Hemisphere compared to EDGAR and GAINS, (2) EDGAR shows higher emissions in the USA than the other two a priori fields, and (3) GAINS exhibits higher emissions in China than UNFCCC-ELE and EDGAR.

Figure 4 Global inversion grid with variable grid cell sizes for the example year 2019.

2.5 Inversion method

We employ the inversion framework FLEXINVERT+ (Thompson and Stohl, 2014) to calculate optimised emissions (a posteriori emissions). FLEXINVERT+ uses Eq. (1), the atmospheric transport operator H, a priori emissions x_p, initial conditions y_i, and observed mole fractions y to minimise the cost function J (Eq. 2), which represents the negative exponent of the a posteriori emission probability distribution, derived by the Bayes' theorem (e.g. Tarantola, 2005). The a posteriori emissions defined by the maximum of the distribution are found by minimising the mismatch between modelled and observed mole fractions weighted by the observation error covariance matrix R and the difference between emissions x and their a priori values x_p weighted by the a priori emission error covariance matrix B.

$$\begin{array}{}\text{(2)}& J\left(\mathit{x}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathit{x}-{\mathit{x}}_{\mathrm{p}}\right)}^T{\mathbf{B}}^{-\mathrm{1}}\left(\mathit{x}-{\mathit{x}}_{\mathrm{p}}\right)+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathbf{H}\mathit{x}-\mathit{y}{)}^T{\mathbf{R}}^{-\mathrm{1}}(\mathbf{H}\mathit{x}-\mathit{y}).\end{array}$$

We use the analytic solution to minimise J, which reads

$$\begin{array}{}\text{(3)}& \widehat{\mathit{x}}={\mathit{x}}_{\mathrm{p}}+\mathbf{G}\left(\mathit{y}-\mathbf{H}{\mathit{x}}_{\mathrm{p}}\right),\end{array}$$

with the defined gain matrix G,

$$\begin{array}{}\text{(4)}& \mathbf{G}={\mathbf{BH}}^T{\left({\mathbf{HBH}}^T+\mathbf{R}\right)}^{-\mathrm{1}}.\end{array}$$

We optimise emissions on a 6-monthly basis and average the results for each year to obtain annual emissions between 2005 and 2021. In addition to the emissions, we also optimise the baseline (H_iy_i) in the inversion, where the whole field is adjusted on a monthly basis. The uncertainty in the baseline is set to 0.15 ppt. The a priori emission uncertainty is estimated to be 70 % of the a priori value in each grid cell with a minimum value of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{13}}$ kg m⁻² h⁻¹. Correlations between emission uncertainties are accounted for using an exponential decay model with a spatial scale length of 250 km and a temporal scale length of 90 d. FLEXINVERT+ assumes a diagonal observation error covariance matrix R and, therefore, does not account for possible error correlations between different observations. The diagonal elements represent the sum of measurement and model error, where we assume the latter to be dominant. Our error estimates are based on a number of initial inversion runs, where we assessed the model error according to the a posteriori model residuals (difference between observed and a posteriori simulated mole fractions) and such that the reduced chi-square value (the value of the cost function at minimum divided by the number of observations and divided by 2) is close to 1. The a posteriori emission error covariance matrix $\widehat{\mathbf{B}}$ is calculated as

$$\begin{array}{}\text{(5)}& \widehat{\mathbf{B}}=\mathbf{B}-\mathbf{GHB}.\end{array}$$

The relative uncertainty reduction was calculated for every grid cell, based on the a priori and a posteriori emission uncertainties in the respective cell as $\mathrm{1}-\frac{\mathrm{a}\mathrm{posteriori}\mathrm{uncertainty}}{\mathrm{a}\mathrm{priori}\mathrm{uncertainty}}$.

For the inversion, we use emission grids with different cell sizes (Figs. 4, S2, and S3), defined by the aggregation of grid cells with low-emission contributions based on emission sensitivities and a priori emissions. Emissions in the fine grid are thereby weighted according to the ratio of the area of the fine grid to the variable-resolution coarse grid into which it is aggregated. After the inversion, optimised emissions in the variable grid were redistributed onto the fine grid according to the relative distribution of the a priori emissions (see Thompson and Stohl, 2014, for a detailed description). We also exclude grid cells over the oceans from the inversion. The global inversion grid has a resolution of 1 to 16°, and the total number of grid cells varies between years, ranging from a minimum of 5841 (2005) to a maximum of 11 901 (2016), which is related to the number of available observations in each year (see Fig. S1). To study the seasonal emission patterns, we also perform monthly inversions, using a coarser global inversion grid of 953 grid cells for all years and a timescale length of 30 d for the correlation between a priori emission uncertainties.

For SF₆, we only expect positive fluxes over land. However, the inversion algorithm may create negative a posteriori fluxes. To address this issue, we apply an inequality constraint on the a posteriori emissions, using the truncated Gaussian approach by Thacker (2007). A posteriori emissions $\widehat{x}$ are corrected to positive values by applying inequality constraints as error-free observations as follows:

$$\begin{array}{}\text{(6)}& \widehat{\mathit{x}}=\mathit{x}+{\mathbf{AP}}^T{\left({\mathbf{PAP}}^T\right)}^{-\mathrm{1}}(\mathit{c}-\mathbf{P}\mathit{x}),\end{array}$$

where P represents a matrix operator selecting the fluxes violating the inequality constraint, and c is a vector of the inequality constraint. x and A represent the a posteriori emissions and error covariance matrix, respectively.

2.6 Sensitivity tests and setup

Before deciding on our final inversion setup, we performed several sensitivity tests. We tested different (1) a priori emission uncertainties between 50 % and 100 % of the respective a priori values and minimal absolute uncertainties between $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{14}}$ and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{12}}$ kg m⁻² h⁻¹; (2) spatial and temporal correlation scale lengths of the a priori uncertainties of 100 to 300 km and 30 to 180 d, respectively; and (3) baseline uncertainties from 0.05 to 0.25 ppt. We found that inversion results were relatively stable for these different settings (see Sect. S7) and that the choice of the a priori emission inventory (UNFCCC-ELE, EDGAR, or GAINS) showed the biggest influence on the inversion results. While the inversion results were similar when using different variations in the UNFCCC-ELE (UP and UN) or EDGAR (E8, E7P, and E7N) a priori emissions (see Sect. 2.4), we found substantial differences when switching between UNFCCC-ELE, EDGAR, and GAINS. Therefore, we ran inversions with all six variations listed in Table 1 individually and averaged the results of UP and UN, as well as E8, E7P, and E7N, to compile one inversion result for each a priori emission inventory (UNFCCC-ELE, EDGAR, and GAINS). Since it is challenging to identify the most accurate inventory, we also provide an average of these three inversion results. In order to reflect the sensitivity of the results to the a priori emissions, we define the uncertainty intervals of aggregated emissions as the minimum and maximum 1σ uncertainty limits across the inversion results, using the different a priori emissions.

3 Results and discussion

3.1 Observed and modelled mole fractions

To illustrate the inversion optimisation process, we compare observed and modelled mole fractions (before and after the inversion) at the Gosan observation station (Fig. 5a), at the Ragged Point station (Fig. 5b), and all other continuous surface measurement sites (Figs. A2, A3, and S4–S23), using the E7P emissions field as the a priori in the inversion. The Gosan station is situated on the southwestern tip of the South Korean island of Jeju, monitoring pollution events from East Asia. However, during the Asian summer monsoon, typically from June to September, clean air from the Southern Hemisphere, low in SF₆, is episodically passing over the station (e.g. Li et al., 2018), making it challenging to accurately define the baseline during this period. The background station, Ragged Point, located on Barbados' eastern edge, primarily receives clean air masses from the Atlantic. It also exhibits intrusions of southern air masses that are low in SF₆ during the summer, resulting in distinct minima in the mole fraction time series and a complex baseline. With the GDB method, we can address these challenges of complex baselines. As illustrated in Fig. 5, the calculated baselines capture the low summer observations, representing a significant advantage over statistical baseline methods. This advantage also becomes apparent for other stations with complex baselines such as Hateruma (Japan; Fig. A2) or Izaña (Tenerife; Fig. A3). Additionally, the optimisation of the baseline shows relatively little impact at all stations, implying that the GDB method and the utilised global SF₆ mole fraction fields already lead to a well-fitting baseline that cannot be improved substantially by the inversion. Figure 5a also illustrates the emission improvement achieved by the inversion. The optimised a posteriori emissions result in mole fractions that are much closer to the observations than the a priori modelled values. For Gosan, the correlation (r²) between (detrended, i.e. removing the 2005–2021 trend from the time series) observed and modelled values improves from 65% to 81% and the mean squared error (MSE) halves from 0.4 to 0.2 ppt². Table S7 and Fig. S24 demonstrate the statistical improvements at all continuous surface stations, emphasising the proper functioning of the inversion.

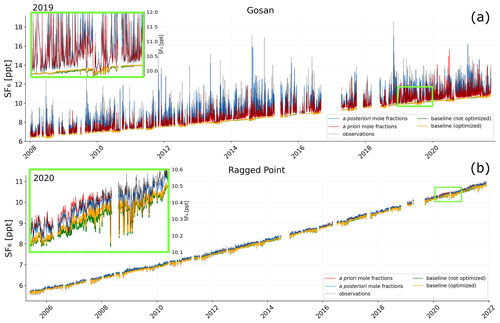
Figure 5 Mole fraction time series at the (a) Gosan and (b) Ragged Point measurement stations. Red lines represent the modelled a priori mole fractions calculated with the E7P a priori emissions and blue lines represent the modelled a posteriori mole fractions. The green line illustrates the baseline derived by the GDB method, and the orange line shows the optimised baseline. The grey line represents the observed mole fractions. The insets zoom into the year (a) 2019 (Gosan) and (b) 2020 (Ragged Point), as illustrated by the light green rectangles.

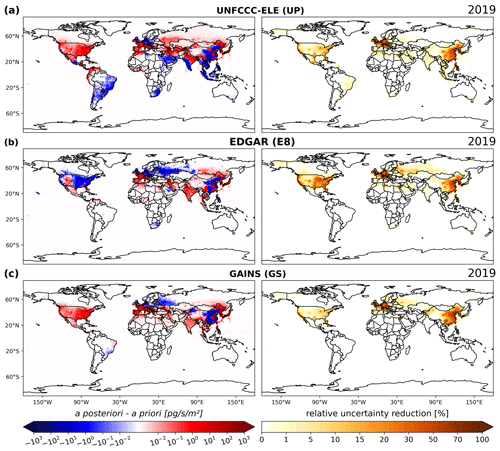
3.2 Inversion increments and relative error reduction

Figure 6 shows the inversion increments (a posteriori minus a priori emissions) and the relative uncertainty reductions achieved by the inversion for the example year 2019 when using the a priori emission fields UP (UNFCCC-ELE), E8 (EDGAR), and GS (GAINS), while the results for UN, E7N, and E7P are shown in the Supplement (Fig. S26). Across all cases, the emission optimisation predominantly occurs in the Northern Hemisphere, characterised by non-zero inversion increments and large error reductions. The limited number of observations in the Southern Hemisphere results in small emission sensitivities there (see Fig. 2), limiting the effects of the inversion primarily to Northern Hemisphere emissions. Only in the case of the UNFCCC-ELE inventory, does Fig. 6a show (negative) inversion increments and a notable error reduction in southern regions like South America and southern Africa. This might indicate that the UNFCCC-ELE a priori emissions are significantly overestimated in these areas. All three data sets show the biggest error reduction and inversion increments in the USA, Europe, and China, where the a priori emissions are high, and many observations are available. While the increments look similar for the three a priori emissions for Europe and China, they are very different for the USA, where the inversion produces predominantly negative increments when using the EDGAR inventory, while only positive increments are obtained using UNFCCC-ELE and GAINS. These differences suggest that the true 2019 US emissions lie between the high EDGAR and the lower UNFCCC-ELE/GAINS estimates.

Figure 6 Inversion increments (a posteriori minus a priori emissions; left panels) and the relative uncertainty reductions (right panels) shown when using the priors (a) UNFCCC-ELE (UP), (b) EDGAR (E8), and (c) GAINS (GS) for the example year of 2019.

3.3 National and regional emissions

Figure 7 illustrates the global SF₆ a posteriori emissions for the example year of 2019, averaged over all emission fields as described in Sect. 2.6. The individual a posteriori emission fields using the different a priori emissions are shown in the Supplement (Fig. S27). The highest SF₆ emissions can be seen in the USA, Europe, China, and India, while emissions are smaller in South America, Africa, and Australia. SF₆ emissions of these countries and regions are discussed in more detail in the following subsections, showing their national/regional emission time series between 2005 and 2021. National and regional emissions are calculated by aggregating the emissions within the respective grid cells of the corresponding country or region, employing a national identifier grid (CIESIN, 2018).

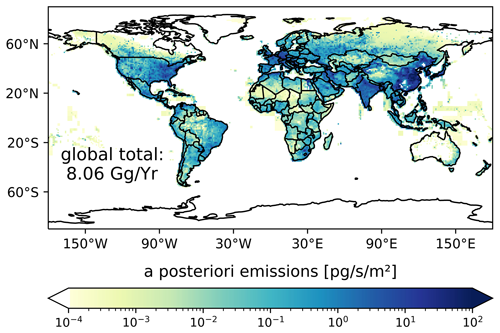
Figure 7 Global a posteriori emissions for the example year of 2019 averaged over the inversion results, using the six different a priori emissions.

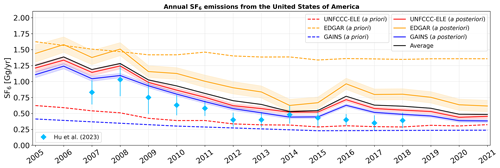
Figure 8 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions in the US shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line. The results of Hu et al. (2023) are shown with blue diamonds, together with their respective 2σ uncertainties.

3.3.1 Emissions from the United States of America

Figure 8 shows the annual a priori and a posteriori US SF₆ emissions for the different priors for the period between 2005 and 2021. The inversion results show a clearly declining annual emission trend of −0.054 Gg yr⁻¹, dropping from 1.25 [1.06–1.58] Gg in 2005 to 0.48 [0.36–0.71] Gg in 2021 (Fig. 8; a posteriori average). The uncertainty intervals represent the minimum and maximum 1-σ uncertainty limits across the inversion results, using the different a priori inventories. The a posteriori emissions are larger (by a factor of 2 on average) than the emissions reported to UNFCCC (Fig. 8; a priori UNFCCC-ELE) throughout the entire study period. While the different a priori emissions show big differences, a posteriori emissions agree much better. At the beginning of the study period, all three a posteriori emissions are substantially higher than the UNFCCC-reported a priori emissions and closer to the EDGAR a priori estimates. Between 2005 and 2012, the a posteriori emissions show a substantial decrease, after which they approach the UNFCCC-reported values but still remain higher. It also seems that the GAINS a priori emissions are far too low at the beginning of our study period, while the EDGAR a priori emissions are far too high at the end of our study period. Our results are a bit higher compared to the regional inversion study by Hu et al. (2023); however, they show a remarkably similar declining trend in US SF₆ emissions between 2007 and 2018.

3.3.2 Total emissions from EU countries

Figure 9 illustrates the total annual a priori and a posteriori SF₆ emissions from all EU countries¹. Here, the three a priori data sets show almost no trend and are very similar to each other throughout the study period, indicating a consistent framework for bottom-up reporting of EU emissions. The annual a posteriori emissions show a decreasing trend of −0.006 Gg yr⁻¹, dropping from 0.41 [0.35–0.46] Gg in 2005 to 0.25 [0.22–0.29] Gg in 2021 (Fig. 9; a posteriori average). While a posteriori emissions are relatively stable and exceed the a priori emissions until 2017, there is a significant drop in 2018, after which they are closer to the a priori emissions. It seems plausible that this drop in SF₆ emissions in 2018 was a result of the EU's F-gas regulation 517/2014 (European Parliament and Council of the European Union, 2014), which requires new electrical switch gear put into service from 2017 onwards to be equipped with a leak detection system and bans the use of SF₆ for recycling magnesium die-casting alloys as of 2018. Our results suggest that in their reports to the UNFCCC, EU countries underestimated their SF₆ emissions prior to 2018 but at the same time underestimated the positive effect of the F-gas regulation 517/2014 in cutting SF₆ emissions.

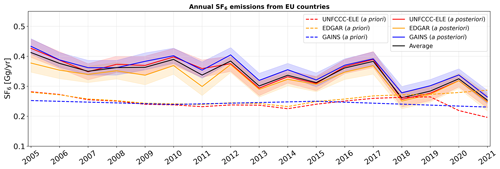
Figure 9 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions aggregated for all EU countries, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line.

As one of only three countries, the United Kingdom also includes top-down inversion results in its annual UNFCCC reports (Manning et al., 2022). As part of this top-down approach, Manning et al. (2022) also reported emissions of northwestern Europe² to which we compare our inversion results (Fig. A4). The a posteriori emissions from northwestern Europe are generally similar to EU emissions shown in Fig. 9; however, they show an even clearer negative trend of −0.009 Gg yr⁻¹. Our results agree well, on average within 16 %, and they agree better after 2012 with those reported by Manning et al. (2022). Furthermore, Simmonds et al. (2020) presented inversion-derived emissions for western Europe³ for four different inversion setups. Our a posteriori emissions agree very well with three of these four inversions (Fig. A5). The fourth inversion shows consistently lower emissions; however, this inversion setup used fewer observation stations than the other three and is likely less accurate. It is likewise noteworthy that the first three inversions of Simmonds et al. (2020) show an emission drop in 2018, which we also find.

3.3.3 Emissions from China

Chinese a priori and a posteriori SF₆ emissions are illustrated in Fig. 10. The inversion-derived a posteriori emissions reveal a distinct positive trend of 0.21 Gg yr⁻¹ (Fig. 10; a posteriori average without GAINS), with a particularly rapid increase between 2006 and 2014 (0.35 Gg yr⁻¹), followed by a stabilisation thereafter. The UNFCCC-ELE a priori Chinese emissions slightly exceed the EDGAR a priori emissions between 2007 and 2011, after which they align well. UNFCCC-ELE and EDGAR a posteriori emissions show almost identical Chinese emissions that are also close to their a priori values. The GAINS a priori Chinese emissions differ significantly from the other two inventories. After 2005, the GAINS a priori emissions show a very strong upward trend, increasingly diverging from the other two priors until the end of the study period, at which point the GAINS Chinese emissions are almost twice as high as the other priors. In the GAINS inventory, China's 2021 emissions alone would account for almost all of the known total global SF₆ emissions (see Sect. 3.3.5), which seems unrealistic. The GAINS a posteriori emissions for China show lower values compared to the a priori emissions; however, they still exceed the UNFCCC-ELE- and EDGAR-derived results. It seems likely that the inversion improves the overestimated Chinese GAINS emissions, yet it may not entirely correct them, given the considerably overestimated a priori estimates. Due to these concerns about the Chinese GAINS a priori emissions, we provide both a Chinese a posteriori emission average including (see Table A3) and excluding GAINS inversions (solid black line in Fig. 10).

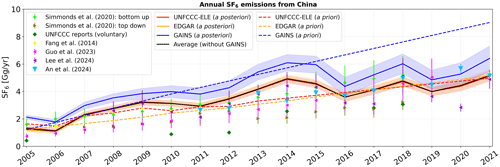
Figure 10 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from China, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using EDGAR and UNFCCC-ELE, are shown with a solid black line.

China is not obliged to report its national emissions, but it voluntarily reported bottom-up SF₆ estimates in their national communications and biennial updates to the UNFCCC for 2005 (China, 2012), 2010 (China, 2018a), 2012 (China, 2016), 2014 (China, 2018b), 2017 (China, 2023a), and 2018 (China, 2023b). These reported values are much smaller than our a posteriori emissions, especially in 2010, 2012, and 2014. The values from the more recent reports in 2017 and 2018 are, however, closer to our inversion results, indicating an improvement in Chinese reports. We also compare our results to various other studies of Chinese emissions, using bottom-up or top-down approaches. Our results agree within 15 % with the inversion study by Fang et al. (2014), who used a similar inversion setup, based on the continuous measurements in Gosan (South Korea), Hateruma (Japan), and Cape Ochiishi (Japan), and FLEXPART atmospheric transport modelling. Furthermore, our results align closely with a recent inversion study by An et al. (2024) (agreeing within 12 %), who had access to data from a relatively dense monitoring network over China. Our results also agree well (within 15 %) with the findings of Gawon Lee (personal communication, 2024), whose regional inversion study (in preparation) utilises observations from Gosan to estimate emissions in Southeast Asia. Note that the patterns of our time series are very similar to the ones of Gawon Lee (personal communication, 2024), suggesting that our Chinese a posteriori emissions are highly influenced by the Gosan observation station. Our derived emissions also agree well (within 8 %) with bottom-up estimates by Guo et al. (2023) after 2015 and (within 18 %) with the bottom-up estimates by Simmonds et al. (2020). Our results are, however, higher than the bottom-up estimates by Guo et al. (2023) between 2008 and 2015 and the inversion-derived emissions by Simmonds et al. (2020). However, Simmonds et al. (2020) based their inversion results on only one station (Gosan), coarser meteorology, and an inversion domain representing only 34 % of China's population, which could have resulted in a substantial underestimation of the emissions.

3.3.4 Other regions

In this section, we present the a priori and a posteriori SF₆ emissions from Africa, South America, Australia, and India. It is important to note that there are no emission reports to the UNFCCC for Africa, South America, and India. In these regions, the UNFCCC-ELE a priori emissions are derived by distributing the emissions residuals from the global total emissions (Simmonds et al., 2020) when subtracting the cumulative reported emissions from Annex I countries, according to the national electricity generation (Sect. 2.4).

Africa

Figure 11 shows African a priori and a posteriori SF₆ emissions. One can see that the GAINS inventory is very low and the UNFCCC-ELE inventory is very high in comparison to the EDGAR inventory. Before 2018, the UNFCCC-ELE a posteriori emissions are lower than the a priori values and align with them afterwards. EDGAR a posteriori emissions are overall higher than the respective a priori emissions. It seems likely that the inversion improves the UNFCCC-ELE overestimation and the EDGAR underestimation but cannot, however, entirely correct them, as large parts of Africa are poorly covered by the observation network (see Fig. 2). The GAINS a posteriori emissions are consistently higher than the GAINS a priori emissions, but the increases are very small. It seems that the GAINS a priori emissions are too small, and the inversion tries to increase them but is bound by the low uncertainties assumed, resulting only in minor corrections. Thus, even the GAINS a posteriori likely underestimate the true emissions. Note that both UNFCCC-ELE and EDGAR a posteriori emissions show a larger positive trend than the a priori emissions. This is also true for the GAINS prior; however, the differences are very small. The averaged a posteriori emissions are close to the EDGAR inventory and show a slowly increasing trend of 0.006 Gg yr⁻¹, growing from 0.13 [0.02–0.31] Gg in 2005 to 0.25 [0.02–0.47] Gg in 2021.

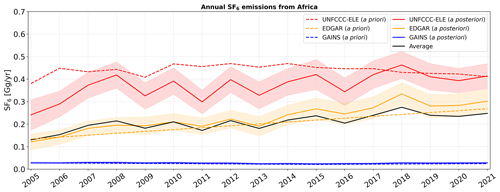
Figure 11 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from Africa, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line.

South America

For South America (see Fig. A6), the UNFCCC-ELE inventory is more than 10 times higher than the EDGAR and GAINS inventory, and GAINS is on average 38 % higher than EDGAR. Due to the narrow uncertainty bands and the poor observational coverage of South America, the inversion results stay close to the a priori emissions for EDGAR and GAINS. For UNFCCC-ELE a posteriori emissions are smaller than the a priori values, especially at the beginning of the study period. We therefore suspect a substantial overestimation by the UNFCCC-ELE a priori inventory, given that the UNFCCC-ELE a posteriori emissions are partly lowered considerably, despite the poor coverage. Note also that UNFCCC-ELE inversion results show a positive trend of 0.007 Gg yr⁻¹, in contrast to the a priori inventory.

Australia

Figure A7 shows Australian a priori and a posteriori SF₆ emissions. All a priori emission inventories show similar values throughout the whole study period which are well below 0.01 Gg yr⁻¹. The inversion results stay close to the a priori values. Note that our results are lower than the top-down estimates from Rigby et al. (2010), who estimated Oceanian (Australia plus Aotearoa / New Zealand) emissions of roughly 0.02 Gg yr⁻¹ between 2004 and 2008.

India

India can be identified as the most challenging region for SF₆ inverse modelling, where a priori emission inventories show substantial differences but where emissions could be of global significance (UNFCCC-ELE emissions are about 8 % of global emissions in 2021) (Fig. A8). For the UNFCCC-ELE inventory, Indian inversion increments are much higher compared to EDGAR or GAINS (see Fig. 6), resulting in large discrepancies across the a posteriori emissions of the different inventories (Fig. A8). This can be related to the poor observational coverage (see Fig. 2) in combination with the relatively high UNFCCC-ELE a priori uncertainties, which might allow the algorithm to excessively relate the distant high East Asian measurements to Indian emissions. The GAINS inventory shows by far the lowest Indian a priori emission, while inversion results stay very close to the prior values, due to the small a priori uncertainty bands. However, all inversions show a much stronger trend in a posteriori SF₆ emissions than in the a priori emissions. A strong upward trend in SF₆ emissions may indeed be expected given that the installed electric power generation capacity in India has almost quadrupled between 2002 and 2022 (Government of India, 2023).

3.3.5 The global perspective

Our study aimed to incorporate all globally accessible SF₆ observations in the inversion in combination with long backward trajectories of 50 d to make the best use of the observation network (Vojta et al., 2022). These are optimal conditions for constraining both regional and global SF₆ emissions. To judge the quality of our a posteriori global emission, we compare our results with the global emissions calculated by Simmonds et al. (2020) for the years 2005 to 2018 and updated until 2021 (An et al., 2024; Laube et al., 2023) using the AGAGE 12-box model (e.g. Rigby et al., 2013). Such box models are considered to be capable of constraining the global total SF₆ emissions to within a few percent because the average atmospheric growth rate can be measured accurately, and the very long atmospheric lifetime of SF₆ leads to small uncertainties in global total emissions. In addition, we compare our results with global emissions directly calculated from annual increases in globally averaged atmospheric SF₆ mole fractions provided by NOAA (Lan et al., 2024), which we multiply by the factor $\frac{M_{{\mathrm{SF}}_{\mathrm{6}}}}{M_{\mathrm{air}}}\cdot m_{\mathrm{atm}}$, where $M_{{\mathrm{SF}}_{\mathrm{6}}}$ and M_air represent the molecular weights of SF₆ and air, and m_atm is the mass of the atmosphere. We refer to these emissions as “NOAA growth rate emissions”.

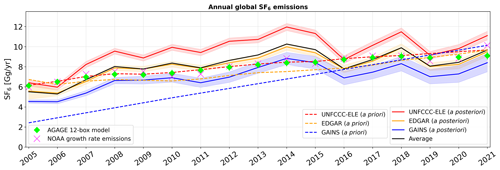
Figure 12 Annual total global a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions, shown for the period between 2005 and 2021, when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line. Reference values of the AGAGE 12-box model and NOAA growth rate emissions are shown with green diamonds and purple crosses, respectively.

Figure 12 illustrates the a priori and a posteriori total global SF₆ emissions, compared to the reference values of the AGAGE 12-box model and the NOAA growth rate emissions. In general, the NOAA growth rate emissions agree well with the box model; however, they show more temporal variability. The UNFCCC-ELE a priori global emissions coincide per definition with the AGAGE 12-box model (Sect. 2.4), while the UNFCCC-ELE a posteriori global emissions are on average 18 % higher. The uncertainties stated for the AGAGE 12-box model are only about 3 %, with an additional 1 % that may be attributed to SF₆ lifetime uncertainties (Simmonds et al., 2020). Overall, our UNFCCC-ELE a posteriori global emissions seem to be systematically too high. One possibility for explaining this discrepancy is a potential ocean sink of SF₆ that is not accounted for in the AGAGE 12-box model, leading to a potential underestimation of global emissions in the box model. Ni et al. (2023) recently suggested that such an ocean sink may account for about 7 % of the global SF₆ emissions. They estimated this global oceanic sink by scaling up calculations of sea–air fluxes based on simultaneous measurements of SF₆ concentrations in the atmosphere and surface seawater of the western Pacific and eastern Indian Ocean. However, since the ocean fluxes are highly inhomogeneous (strong oceanic sources might exist in other regions), we suspect the upscaled estimate to be very uncertain. Nevertheless, we tested the hypothesis by allowing for an oceanic sink in our inversion. However, the inversion-derived oceanic a posteriori emissions showed either a lot of noise or no fluxes at all (in the case of optimising ocean fluxes in one aggregated oceanic grid cell). Therefore, we were unable to confirm the presence of oceanic SF₆ sinks with our inversion. Yet, another possible explanation for the increase in the global UNFCCC-ELE emissions by the inversion is the positivity constraint employed on the emissions over land, which might lead to a positive bias of the a posteriori global emissions. However, tests showed that the positivity constraint on the a posteriori emissions had very little effect (<1 %) on the total global emissions. There is a better explanation for our a posteriori UNFCCC-ELE emissions that are too high. As discussed in Sect. 3.2, the measurement data put relatively strong constraints on the high-emitting regions of China, Europe, and the USA that are responsible for the largest share of the global SF₆ emissions. National inversion results showed that reported UNFCCC emissions in these regions are predominantly underestimated. Consequently, to match the global total emission, our UNFCCC-ELE inventory attributed excessive emissions to countries not reporting their emissions to the UNFCCC (e.g. in South America, Africa, or India). Unfortunately, the emissions in these regions are very poorly constrained by the existing observation network (see Fig. 2). As shown in Sect. 3.3.4, the inversion can reduce large biases in these regions, but we cannot expect it to remove them completely, and this leads to a positive bias in a posteriori global emissions.

The global GAINS a priori emissions are lower than all other inventories at the beginning of the study period, and its positive trend is larger than, and inconsistent with, the global atmospheric SF₆ growth derived by the box model and the NOAA measurements. Due to this rapid increase, the GAINS a priori emissions converge with the other emission inventories by the end of the study period. The global GAINS a posteriori emissions are much closer to the AGAGE box model results and NOAA growth rate emissions than the a priori emissions and align well with their trends. However, a posteriori emissions are 15 % lower on average, indicating that aggregated emissions are underestimated in poorly monitored areas. This claim can be supported by comparing the global GAINS and Chinese GAINS a priori emissions (Fig. 10). At the beginning of the study period, GAINS seems to produce realistic Chinese emissions, while at the same time global GAINS emissions are significantly underestimated. After rapid growth, global GAINS emissions are close to the reference box model value, while Chinese GAINS emissions are significantly overestimated at the end of the study period. In both cases, this suggests an underestimation of the emission residuals between the global and the Chinese emissions. Consequently, GAINS also provides the lowest a posteriori emission estimates in almost all shown regions, except China, resulting in an underestimation of the global emissions.

In the case of EDGAR, both the a priori and a posteriori emissions agree with the reference values of the AGAGE 12-box model and NOAA growth rate emissions within 8 %–9 %. While the a priori emissions are on average biased low by 6 %, the a posteriori emissions show on average almost no bias (<1 %) compared to the reference values. We, therefore, conclude that EDGAR provides a good estimate for the accumulated SF₆ emissions, also from poorly monitored areas, which is well suited for global inversions.

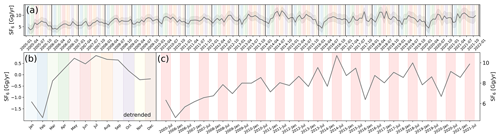
Figure 13 Inversion results from monthly SF₆ inversions for the Northern Hemisphere. (a) Monthly a posteriori emissions for the period 2005–2021, (b) detrended a posteriori emissions averaged for each month across all years, and (c) semi-annual a posteriori emissions. Distinct months are highlighted with different colours. In panel (c), the specified summer (April–September) and winter periods (October–March) are shown in red and white, respectively.

The average of the total global emissions of the different discussed cases provides a very good estimate for the global SF₆ emissions, showing average biases of +2.2 % and 1.4 % compared to the AGAGE box model and the NOAA growth rate emissions, with an agreement within 10 %. Its trend shows an increase until 2014, followed by a stabilisation thereafter (similar to the Chinese emission trend). This is a pattern that can be also observed for the annual increases in the globally averaged NOAA atmospheric SF₆ mole fractions and derived emissions. Note also that the average global trend (0.20 Gg yr⁻¹) is similar to the Chinese emission trend (0.21 Gg yr⁻¹).

Despite some potential problems with our inversion setup that can lead to biased a posteriori global emissions (as could be clearly seen and explained with the UNFCCC-ELE and GAINS a priori emissions in poorly observed regions), overall our a posteriori global emissions seem to be quite accurate, with average biases to the box model and NOAA growth rate emissions of +18 %, −15 %, and <1 % for UNFCCC-ELE, GAINS, and EDGAR, respectively. Even strongly biased global a priori emissions, as for GAINS until 2015, could be brought relatively close to these previous estimates. This is beneficial, since our regional estimates combined are then consistent with the global emissions. However, the uncertainties in the inversion-derived emissions remain large in India and the Southern Hemisphere. While the aggregated emission in these regions is also quite well known as the residual between global emissions and emissions in well-monitored areas, the distribution of the emissions between and within these regions is less well known.

3.3.6 Seasonality of SF₆ emissions

Our a priori emission data sets contain no seasonal information and are assumed to be constant throughout the year. Figure 13 shows the monthly resolved a posteriori total SF₆ emissions in the Northern Hemisphere, using the E7P a priori emission inventory. Figure  13a shows the whole time series, and Fig. 13b presents monthly averages over this time period, after detrending the time series. While different years have unique seasonal patterns, a notable emission minimum can be observed at the beginning of every year (January/February), and emissions tend to be highest in the summer. This is most clearly seen in the averaged seasonal cycle (Fig. 13b), which shows a minimum in February and a broad maximum from May to September. To better demonstrate the consistency of this seasonal cycle throughout the entire period of our study, Fig. 13c shows semi-annual SF₆ emissions in the Northern Hemisphere, derived by averaging seasonal emissions for winter (October–March) and summer (April–September). In line with Fig. 13a and b, Fig. 13c shows higher emissions in summer than in winter, and this pattern is found in almost every individual year. However, the seasonal SF₆ emission patterns vary by region (shown for China, the USA, and the EU in Fig. A9). For the EU emissions, no clear seasonal cycle can be seen. Note at this point that SF₆ emissions from northwestern Europe were found to maximise in the winter (Redington et al., 2019); however, this was observed without showing a very systematic seasonal cycle. For Chinese SF₆ emissions, the seasonality is similar to the one in the Northern Hemisphere (Fig. 13b). For the USA, we find an even stronger seasonal variation with a May/June peak of SF₆ emissions. This result is in contradiction to Hu et al. (2023), who suggested US SF₆ emissions to peak in winter. Hu et al. (2023) argued that many US companies maintain electrical equipment in the winter rather than in the summer and that cold temperatures can cause sealing materials in electrical equipment to become brittle, resulting in more leaks. We suspect that the contradictions between our two studies are mainly due to the different baseline treatments. As discussed in Sect. 3.1, our baseline lowers in the summer for several stations, a feature which we argued is realistic and reflects the transport of different, cleaner air masses over the respective stations. Neglecting such a lowered baseline would lead to underestimated summer emissions. In addition, high-frequency measurements from Trinidad Head (THD) and Niwot Ridge (NWR) have not been used by Hu et al. (2023). A possible explanation for the summer emission maximum might be the seasonal variability in electricity generation, which peaks in summer for most of the Northern Hemisphere (see, e.g., https://www.eia.gov/electricity/, last access: 1 July 2024). In addition, the increasing SF₆ pressure at high summer temperatures and heat stress of the electrical equipment could lead to more leakage. However, further research on the seasonal cycle of SF₆ emissions is needed to provide a more conclusive answer as to the cause(s).

4 Conclusions

Our inversion study provides observation-based, regionally resolved global SF₆ emission estimates for the period 2005–2021, using initial conditions based on an atmospheric SF₆ re-analysis. We further consider different a priori emission inventories and use a newly compiled, extensive observation data set, along with 50 d LPDM backward simulations to provide accurate estimates of the global spatially distributed SF₆ emissions. Our main findings are the following:

• The GDB approach is a robust method for estimating boundary conditions, especially at challenging measurement stations. We demonstrate that it successfully accounts for meteorological variability (e.g. the Asian summer monsoon) in the baseline, reducing the need for baseline optimisation by the inversion.

• Our inversion produces regional a posteriori emissions that, taken together, are consistent within 10 % with the well-known global emissions based on observed atmospheric growth rates.

• The global inversion shows the largest emission improvements in the high-emitting regions of China, the USA, and Europe, where the observation networks used have good coverage. Our annual inversion results are in excellent agreement with several existing regional inversion studies focusing on these three regions.

• Annual US SF₆ emissions strongly decreased from 1.25 [1.06–1.58] Gg in 2005 to 0.48 [0.36–0.71] Gg in 2021, showing a trend of −0.054 Gg yr⁻¹. However, these inversion-derived emissions are on average twice as high as the emissions reported to the UNFCCC. Thus, we find that the US is systematically underreporting its SF₆ emissions.

• Annual total SF₆ emissions from EU countries show a decreasing trend of −0.006 Gg yr⁻¹ from 0.41 [0.35–0.46] Gg in 2005 to 0.25 [0.22–0.29] Gg in 2021. However, Europe also systematically underreports its SF₆ emissions to UNFCCC.

• The European emissions show a substantial drop in 2018, resulting most likely from the EU's F-gas regulation 517/2014 (European Parliament and Council of the European Union, 2014), which requires the new electrical switch gear put into service from 2017 onwards to be equipped with a leak detection system and bans the use of SF₆ for recycling magnesium die-casting alloys as of 2018. This might suggest that the EU's new F-gas regulation was almost immediately successful in reducing SF₆ emissions.

• Chinese SF₆ emissions show an increasing trend of 0.21 Gg yr⁻¹, growing from 1.28 [1.03–1.57] Gg in 2005 to 5.16 [4.75–5.60] Gg in 2021, with a particularly steep trend until 2014 and a flattening afterwards. China's official voluntary reports substantially underestimate their SF₆ emissions (by more than 50 %); however, the latest reports in 2017 and 2018 seem to have improved.

• SF₆ emissions in the Southern Hemisphere and some other parts of the world (e.g. India) are hard to constrain due to insufficient coverage by observations. While the inversion most likely reduces large biases of a priori estimated emissions in Africa and South America, substantial uncertainties about these emissions remain. The EDGAR bottom-up inventory seems to provide a relatively good estimate for the total emissions aggregated over all the poorly monitored regions (residual between global emissions and emissions in well-monitored areas) as, otherwise, the global a posteriori emissions would be more strongly biased against the relatively well-known global emissions based on atmospheric growth rates. Nevertheless, more observations are needed to investigate if also regional emission patterns in those areas are accurate.

• Our inversions suggest globally significant and strongly increasing emissions in India since 2005. However, the results for this region are very uncertain because of a weak observational constraint. Adding monitoring capacity in this region should have a high future priority.

• Our monthly inversion results show overall higher SF₆ emissions in the summer (April–September) than in winter (October–March) in the Northern Hemisphere, with a distinct minimum at the beginning of the year. While America's SF₆ emissions show a clear peak in May and June, and China's emission pattern is similar to the Northern Hemisphere, no clear seasonal pattern is identified for Europe. As our findings for the US contradict Hu et al. (2023), we suggest that more research on the seasonality of SF₆ emissions is needed.

• On the basis of the inversion results, we can neither confirm nor refute the hypothesis that the ocean sink of SF₆ is a substantial part (up to 7 %, according to Ni et al., 2023) of the anthropogenic emission fluxes.

• Since we find that national reports for the US, Europe, and China all underreport their SF₆ emissions, while other countries with potentially high emissions (e.g. India) do not report their emissions at all, we suggest that bottom-up methods to determine the emissions need to be refined. This should include a better quantification of the processes causing the emissions that could explain the emission seasonality found here.

Appendix A

Table A1 Inversion results for the annual SF₆ emissions from the United States of America for the period 2005–2021. Annual emissions are shown, together with their uncertainties, for different a priori emission inventories. We also provide an average of the inversion results, while respective uncertainties represent the minimum and maximum uncertainty limits across the results.

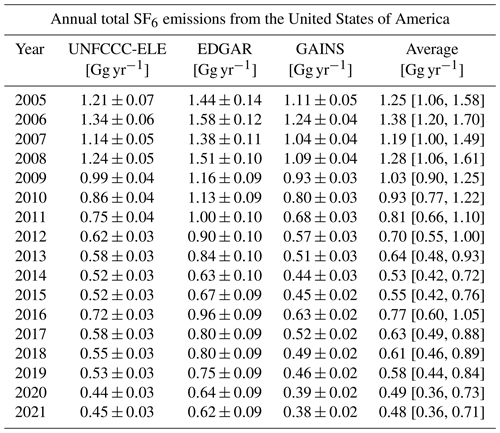
Table A2 Inversion results for the annual total SF₆ emissions from EU countries for the period 2005–2021. Annual emissions are shown, together with their uncertainties, for different a priori emission inventories. We also provide an average of the inversion results, while respective uncertainties represent the minimum and maximum uncertainty limits across the results.

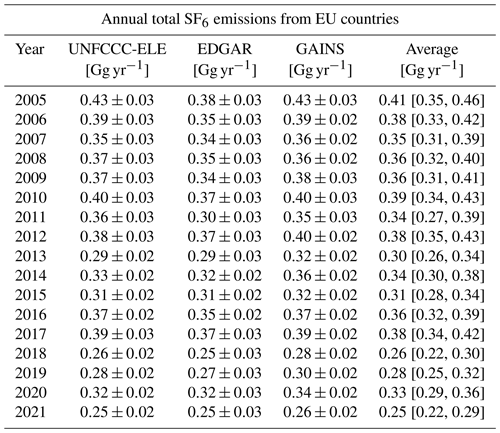
Table A3 Inversion results for the annual Chinese SF₆ emissions for the period 2005–2021. Annual emissions are shown, together with their uncertainties, for different a priori emission inventories. We also provide an average of the inversion results and an average excluding the GAINS-derived inversion, while uncertainties represent the minimum and maximum uncertainty limits across the results.

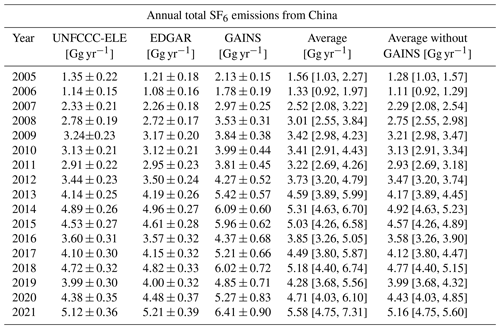
Table A4 Inversion results for the annual global total SF₆ emissions for the period 2005–2021. Annual emissions are shown, together with their uncertainties, for different a priori emission inventories. We also provide an average of the inversion results, while respective uncertainties represent the minimum and maximum uncertainty limits across the results.

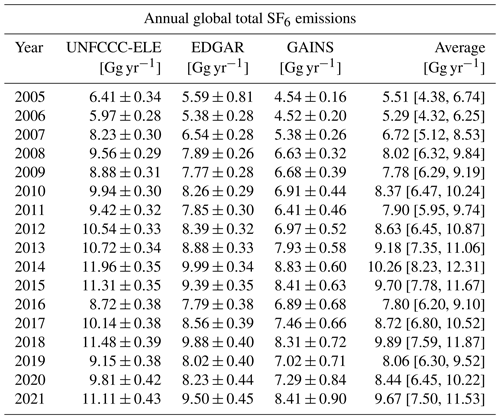
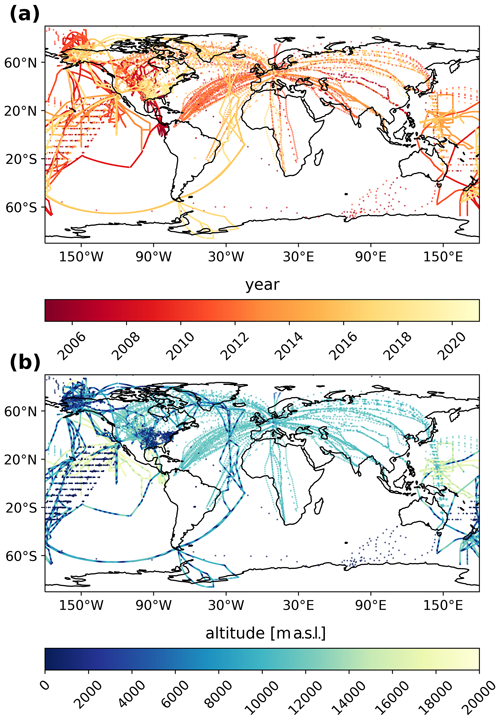
Figure A1 Observations from aircraft and ship campaigns from 2005–2021. The colour bars indicate (a) the measurement date and (b) the altitude of the respective observations.

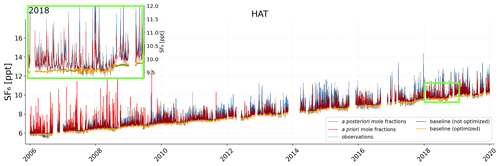
Figure A2 Mole fraction time series at the Hateruma (Japan) measurement station. Red lines represent the modelled a priori mole fractions calculated with the UP a priori emissions and blue lines represent the modelled a posteriori mole fractions. The green line illustrates the baseline derived by the GDB method, and the orange line shows the optimised baseline. The grey line represents the observed mole fractions. The inset panel zooms into the year 2018, as illustrated by the light green rectangle.

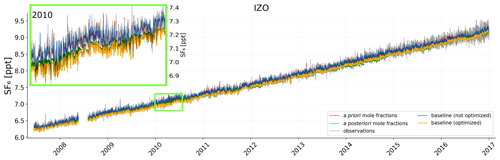
Figure A3 Mole fraction time series at the Izaña (Tenerife) measurement station. Red lines represent the modelled a priori mole fractions calculated with the UP a priori emissions and blue lines represent the modelled a posteriori mole fractions. The green line illustrates the baseline derived by the GDB method, and the orange line shows the optimised baseline. The grey line represents the observed mole fractions. The inset panel zooms into the year 2010, as illustrated by the light green rectangle.

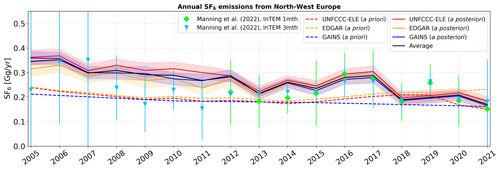
Figure A4 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from northwestern Europe, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line. The blue rectangles and the green diamonds represent the results from Manning et al. (2022), using the InTEM (Inversion Technique for Emissions Modelling) model, with inversion time frames set to 3 and 1 months, respectively.

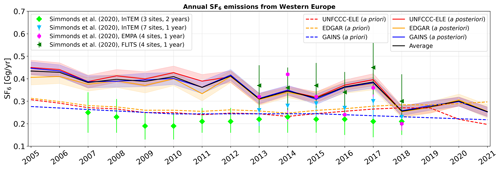
Figure A5 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from western Europe shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line. Furthermore, the results from Simmonds et al. (2020) are shown, using four different inversion setups.

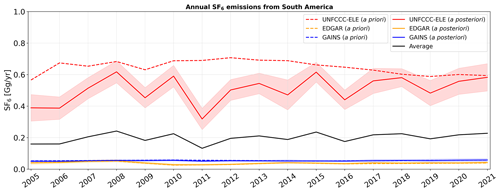
Figure A6 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from South America, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line.

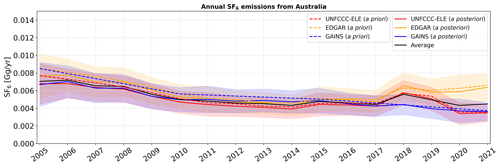
Figure A7 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from Australia are shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated, together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results using the different inventories are shown with a solid black line.

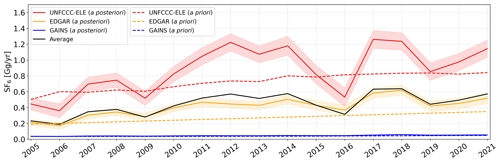
Figure A8 Annual a priori (dashed lines) and a posteriori (solid lines) SF₆ emissions from India, shown for the period between 2005 and 2021 when using different a priori emission inventories (UNFCCC-ELE in red, EDGAR in orange, and GAINS in blue). A posteriori emissions are illustrated together with their respective uncertainties (coloured shadings are defined as the minimum and maximum 1σ uncertainty limits across the inversion results for different a priori variations). The a posteriori emissions averaged over the inversion results, using the different inventories, are shown with a solid black line.

Figure A9 Seasonal variation in SF₆ emissions in China, the United States of America, and EU countries. The figure shows the detrended monthly inversion results averaged for each month across all years for the period 2005–2021.