Technical note: Nighttime OH and HO₂ chemical equilibria in the mesosphere–lower thermosphere

​​​​​​​At the altitudes of the mesosphere–lower thermosphere, OH and HO₂ play a significant role in many physicochemical processes. Thus, monitoring their spatiotemporal evolution, together with other chemically active trace gases, is one of the most important problems for this atmosphere region, in which direct measurements are difficult. This paper studies the nighttime OH and HO₂ chemical equilibria using the 3D chemical transport modeling within the general approach, which includes the identification of the main sources and sinks in the equilibrium space–time areas and the derivation of analytical criteria for equilibrium validity. The presented analysis shows that there are extended areas where nighttime HO₂ and OH are close to their local equilibrium concentrations, determined mainly by the reaction between HO_x and O_x components among themselves and with H₂O₂, N, NO, NO₂, and CO. In the upper mesosphere–lower thermosphere, the equilibrium expressions can be shortened so that they include the HO_x–O_x chemistry only. These expressions describe the HO₂ and OH equilibria from the top down to some boundaries, the altitude positions of which vary in the interval between 72–73 and 85 km and depend essentially on season and latitude. The developed analytical criteria reproduce the main features of these boundaries well almost everywhere. Due to weak sensitivity to uncertainties of reaction rates and other parameters, the criteria can be regarded as a robust instrument for HO₂ and OH equilibrium validation. The obtained results allow us to extend previously proposed methods for the retrieval of poorly measured components from measurement data and to develop new approaches.

1 Introduction

Monitoring the spatiotemporal evolution of chemically active trace gases is one of the most important problems in atmospheric research. Despite the increase in the experimental data volume nowadays, primarily due to the development of remote-sensing methods, many important trace gases continue to be unavailable for direct and regular measurements. A well-known way to increase the information content of experimental campaigns is to use the available experimental data in conjunction with a certain chemical or physicochemical model to derive unmeasured characteristics indirectly. Within the framework of this approach, the model acts as an a priori relationship between directly measured and retrieved characteristics. The simplest model, which makes it possible to implement this approach, is based on the condition of local (in both time and space) photochemical/chemical balance (local equilibrium) between sources and sinks of the so-called “fast” components: trace gases with short lifetimes relative, in particular, to the characteristic transport times. Mathematically this condition does not mean that the fast variables are at equilibrium, but, when it is fulfilled, the corresponding concentrations are close to their instantaneous equilibrium values. At the same time, due to the strong dissipation in most cases (except the special cases where the ensemble of fast components includes the slow family of these components), there is no need to follow the law of matter conservation. It is possible to disregard insignificant sinks and sources, including those caused by transport, in the corresponding balance equations without the loss of accuracy. The resulting algebraic equations are the simplest a priori local relations between measurable and retrieved trace gases. These relationships can be used to derive information about hard-to-measure atmospheric species, determine key atmospheric characteristics (for example, temperature; Marchand et al., 2007), validate the data quality of simultaneous measurements of several atmospheric components (Kulikov et al., 2018a), estimate reaction rate constants (Stedman et al., 1975; Avallone and Toohey, 2001), evaluate sources/sinks (Cantrell et al., 2003), etc.

For several decades, the photochemical/chemical equilibrium approximation has been used to solve many atmospheric tasks. It is applied (see, e.g., the short review in Kulikov et al., 2018a, and references therein) in investigations of the surface layer and free troposphere chemistry in different regions (over megapolises, in rural areas, in the mountains, over the seas); in stratospheric chemistry studies, including derivation of critical parameters in the ozone destruction catalytic cycles; and in studies of the HO_x–O_x chemistry and airglows (O(¹S) green-line, O₂ A-band, and OH Meinel-band emissions) at the heights of the mesosphere–lower thermosphere. In the latter case, the distributions of unmeasured characteristics are determined from the data of daytime and nighttime rocket and satellite measurements (e.g., Evans and Llewellyn, 1973; Good, 1976; Pendleton et al., 1983; McDade et al., 1985; McDade and Llewellyn, 1988; Evans et al., 1988; Thomas, 1990; Llewellyn et al., 1993; Llewellyn and McDade, 1996; Russell and Lowe, 2003; Russell et al., 2005; Kulikov et al., 2006, 2009, 2017, 2022a, b; Mlynczak et al., 2007, 2013a, b, 2014, 2018; Smith et al., 2010; Xu et al., 2012; Siskind et al., 2008, 2015; Fytterer et al., 2019) with the use of equilibrium assumptions for ozone and excited states of OH, O, and O₂. For example, such an approach is applied to the data of the Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) instrument on board the Thermosphere–Ionosphere–Mesosphere Energetics and Dynamics (TIMED) satellite, which, since 2002, has continued to measure simultaneous profiles of temperature, ozone, and volume emission rates of OH* transitions in wide ranges of altitude, local time, and latitude with a rather high space–time resolution.

Note a number of general aspects of the application of equilibrium conditions in the above examples. First of all, there are no clear criteria indicating the conditions under which the use of equilibrium approximation is justified. Usually, a certain component is taken to be a fast variable if its lifetime is much shorter than the lifetimes of other components of studied photochemical/chemical systems or than the duration of a day, daytime, nighttime, etc. For example, in the papers on SABER data processing (Mlynczak et al., 2013a, b, 2014, 2018), it is assumed that the nighttime ozone chemical equilibrium in the mesopause is well fulfilled at altitudes of 80–100 km, since the nighttime ozone lifetime at these altitudes varies in the range from several minutes to several tens of minutes. Note that this assumption is quite popular and is used in different tasks (e.g., Swenson and Gardner, 1998; Marsh et al., 2006; Smith et al., 2009; Nikoukar et al., 2007; Xu et al., 2010, 2012; Kowalewski et al., 2014; Grygalashvyly et al., 2014; Grygalashvyly, 2015; Sonnemann et al., 2015; Kulikov et al., 2021). Belikovich et al. (2018) and Kulikov et al. (2018b, 2019, 2023a) analyzed the nighttime ozone chemical equilibrium numerically, analytically, and with the use of SABER/TIMED data. It was revealed that the short lifetime is not a sufficient condition, so this equilibrium may be significantly disturbed above 80 km. The local ratio between true and equilibrium concentrations may vary widely and reach up to several orders of magnitude (e.g., Fig. 5 in Kulikov et al., 2018b). Thus, without special restrictions, the error in retrieved characteristics due to the use of equilibrium approximation is uncontrollable and may significantly exceed all other errors in the retrieval procedure due to, for example, uncertainties in the measurement data and rate constants.

Since the papers of Belikovich et al. (2018) and Kulikov et al. (2018b, 2019, 2023a), we developed the general approach to correctly identify fast components, employing the data from a global 3D chemical transport model. It includes the following:

• 1.

  Plotting of the equilibrium space–time maps of the components of interest.

• 2.

  Identification of the main sources and sinks in the equilibrium areas found.

• 3.

  Derivation and subsequent use of analytical criteria that make it possible to determine the fulfillment of the equilibrium condition locally (in time and space) with the use of the measurement data only.

The latter point is based on the theory of chemical equilibrium of a certain trace gas, acquired from estimations of its lifetime and equilibrium concentration, and time dependences of these characteristics (Kulikov et al., 2023a). Note that, when an equilibrium condition is applied to measurement data in the retrieval of unmeasured characteristics, the criterion allows us to control and limit the possible error caused by the equilibrium approximation.

The main goal of the paper is to apply this approach to the analysis of nighttime OH and HO₂ chemical equilibria in the mesosphere–lower thermosphere. Along with O and H, OH and HO₂ are important components of HO_x–O_x chemistry, participating (a) in chemical heating through, in particular, $\mathrm{O}+\mathrm{OH}\to {\mathrm{O}}_{\mathrm{2}}+\mathrm{H}$ and $\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}$ exothermic reactions; (b) in the formation of airglows; and (c) in catalytic cycles of the ozone destruction. Moreover, the equilibrium conditions of OH and HO₂ are additional a priori relationships that can be used to retrieve these components or other characteristics from measured data. In particular, Panka et al. (2021) proposed the method for nighttime total OH retrieval from SABER/TIMED data at 80–100 km, which does not use the ozone chemical equilibrium. However, the method applies the equilibrium between sources and sinks not only to excited states of OH with ultrashort lifetimes but also to the ground state. Therefore, this point is verified in our paper.

In the next section we present the model and methods used. In Sect. 3 the model data are used to plot HO₂ and OH equilibrium maps. In Sects. 4–5 we identify the main reactions, determining equilibria of these gases, and present their shortened equilibrium conditions at the upper-mesosphere and lower-thermosphere altitudes. In Sect. 6 the criteria for HO₂ and OH equilibrium validity are developed. In Sect. 7 we discuss the obtained results and their possible applications.

2 3D model and approaches used

The analysis of OH and HO₂ nighttime chemical equilibria was carried out, using the data obtained with the calculation of a 3D chemical transport model of the middle atmosphere, developed at the Leibniz Institute of Atmospheric Physics (e.g., Sonnemann et al., 1998; Körner and Sonnemann, 2001; Grygalashvyly et al., 2009; Hartogh et al., 2004, 2011), to investigate the mesosphere–lower thermosphere chemistry, in particular, in the extended mesopause region. A number of papers (e.g., Hartogh et al., 2004, 2011; Sonnemann, et al., 2006, 2008) validated the model with measurements, in particular, of ozone and water vapor.

The space–time distribution of temperature and winds was taken from the model of the dynamics of the middle atmosphere, COMMA-IAP (e.g., Kremp et al., 1999; Berger and von Zahn, 1999), with an updated frequency of 1 d and linear smoothing between subsequent updates to avoid unrealistic jumps in the calculated concentrations of trace gases. 3D advective transport is taken into account with the use of the Walcek scheme (Walcek, 2000). The vertical diffusive transport (turbulent and molecular) is calculated with the use of the implicit Thomas algorithm (Morton and Mayers, 2005). The model grid has 118 pressure-height levels (0–135 km), 16 latitudinal levels, and 32 longitudinal levels. The chemical module (see Table 1) comprises 25 constituents (O, O(¹D), O₃, H, OH, HO₂, H₂O₂, H₂O, H₂, N, NO, NO₂, NO₃, N₂O, CH₄, CH₂, CH₃, CH₃O₂, CH₃O, CH₂O, CHO, CO, CO₂, O₂, N₂), with 54 chemical reactions between them and 15 photodissociation reactions. The model utilizes the pre-calculated dissociation rates (Kremp et al., 1999) and their dependence on the altitude and solar zenith angle.

Table 1 List of reactions included in the 3D chemical transport model, with the corresponding reaction rates taken from Burkholder et al. (2020).​​​​​​​

The model was used to calculate a 1-year global evolution of the abovementioned trace gases. To remove the transition regions corresponding to sunset and sunrise, we use only local times when the solar zenith angle χ > 105°. As a result, we find the spatiotemporal series of the $\mathrm{OH}/\mathrm{OH}$^eq and ${\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ ratios. Here, OH and HO₂ are the local nighttime values of hydroxyl and hydroperoxyl radicals calculated by the model, with OH^eq and $\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ as their local equilibrium values, corresponding to the instantaneous balance between production and loss terms, respectively. To determine each local value of OH^eq and $\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$, we used the local values of the parameters (temperature, O₂, and N₂) and the concentrations of other trace gases, determining local chemical sources and sinks of OH and HO₂. Then, the $\mathrm{OH}/\mathrm{OH}$^eq and ${\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ series were averaged over the zonal coordinate and time during each month and were presented as height–latitude maps, depending on the month. Each map contains lines, marking the boundaries of the equilibrium areas, where the following conditions are satisfied:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& \left\{\begin{array}{c}\left|<{\mathrm{OH}/\mathrm{OH}}^{\mathrm{eq}}>-\mathrm{1}\right|\le \mathrm{0.1}\\ {\mathit{\sigma }}_{{\mathrm{OH}/\mathrm{OH}}^{\mathrm{eq}}}\le \mathrm{0.1}\end{array}\right.,\\ & \left\{\begin{array}{c}\left|<{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}>-\mathrm{1}\right|\le \mathrm{0.1}\\ {\mathit{\sigma }}_{{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}}\le \mathrm{0.1}\end{array}\right.,\end{array}\end{array}$$

where the angle brackets are used to denote the values averaged in time and space and ${\mathit{\sigma }}_{{\mathrm{OH}/\mathrm{OH}}^{\mathrm{eq}}}$ and ${\mathit{\sigma }}_{{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}}$ are standard deviations of the $\mathrm{OH}/\mathrm{OH}$^eq and ${\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ ratios from 1, respectively.

Then, we plotted spatiotemporal maps showing the relative contribution of each reaction to a summarized source or sink at all altitudes and latitudes. These maps helped us to identify the main sources and sinks, describing the chemical equilibrium of nighttime OH and HO₂ in the equilibrium areas to an accuracy of better than a few percent.

Finally, we obtained and verified the analytical criteria of OH and HO₂ nighttime chemical equilibria according to Kulikov et al. (2023a). The paper considered the pure chemical evolution of a certain trace gas n:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}n}{\mathrm{d}t}}=I_n-S_n=-{\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_n}}\left(n-n^{\mathrm{eq}}\right),\\ & {\mathit{\tau }}_n={\displaystyle \frac{n}{S_n}},n^{\mathrm{eq}}={\displaystyle \frac{n\cdot I_n}{S_n}},\end{array}\end{array}$$

where t is time; I_n and S_n are total photochemical/chemical sources and sinks of n, respectively; τ_n is the n lifetime; and n^eq is its equilibrium concentration, corresponding to the condition I_n=S_n. The lifetime determines the characteristic timescale for which n approaches n^eq when n^eq = const. In general, τ_n and n^eq are functions of time. Kulikov et al. (2023a) showed, in a strict mathematical sense, that the local values of n and n^eq are close to each other (n(t)≈n^eq(t)) when ${\mathit{\tau }}_n\ll {\mathit{\tau }}_{n^{\mathrm{eq}}}$, where ${\mathit{\tau }}_{n^{\mathrm{eq}}}$ is the local timescale of n^eq:

$$\begin{array}{}\text{(3)}& {\mathit{\tau }}_{n^{\mathrm{eq}}}\equiv {\displaystyle \frac{n^{\mathrm{eq}}}{\left|\mathrm{d}{n}^{\mathrm{eq}}/\mathrm{d}t\right|}}.\end{array}$$

The expression for τ_n is found from the total sink of n. The expression for ${\mathit{\tau }}_{n^{\mathrm{eq}}}$ is derived from Eq. (3) with the use of differential equations, describing the chemical evolution of other reacting components, which determine the expression for n^eq. Kulikov et al. (2023a) also showed that, when ${\mathit{\tau }}_n\ll {\mathit{\tau }}_{n^{\mathrm{eq}}}$, $n\cong n^{\mathrm{eq}}\left(\mathrm{1}-\text{sign}\left(\frac{\mathrm{d}{n}^{\mathrm{eq}}}{\mathrm{d}t}\right)\cdot \frac{{\mathit{\tau }}_n}{{\mathit{\tau }}_{n^{\mathrm{eq}}}}\right)$ in the first-order approximation. Thus, the criterion

$$\begin{array}{}\text{(4)}& {\mathit{\tau }}_n/{\mathit{\tau }}_{n^{\mathrm{eq}}}\le \mathrm{0.1}\end{array}$$

is sufficient in order for the possible relative difference between n and n^eq to be no more than 0.1.

3 Nighttime HO₂ and OH chemical equilibria

According to Table 1, nighttime HO₂ chemical sources are determined by the following reactions:

$$\begin{array}{}\text{(R20)}& {\displaystyle }\mathrm{H}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{M}\to {\mathrm{HO}}_{\mathrm{2}}+\mathrm{M},\text{(R22)}& {\displaystyle }\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}},\text{(R29)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}},\text{(R19)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}},\text{(R40)}& {\displaystyle }\mathrm{CHO}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{HO}}_{\mathrm{2}}+\mathrm{CO},\text{(R37)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}},\end{array}$$

whereas chemical sinks of this component are as follows:

$$\begin{array}{}\text{(R18)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}},\text{(R23)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}},\text{(R28)}& {\displaystyle }\mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}},\text{(R14)}& {\displaystyle }\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to \mathrm{2}\mathrm{OH},\text{(R15)}& {\displaystyle }\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{O},\text{(R16)}& {\displaystyle }\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}},\text{(R50)}& {\displaystyle }\mathrm{NO}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH},\text{(R30)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}},\text{(R31)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}+\mathrm{M}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{M}.\end{array}$$

Thus, the HO₂ local equilibrium concentration is described by the following equation:

$$\begin{array}{}\text{(5)}& {{\mathrm{HO}}_{\mathrm{2}}}^{\mathrm{eq}}={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}+k_{\mathrm{22}}\cdot \mathrm{OH}\cdot {\mathrm{O}}_{\mathrm{3}}\\ +k_{\mathrm{29}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{OH}+k_{\mathrm{19}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}\\ +k_{\mathrm{40}}\cdot \mathrm{CHO}\cdot {\mathrm{O}}_{\mathrm{2}}+k_{\mathrm{37}}\cdot {\mathrm{CH}}_{\mathrm{3}}\mathrm{O}\cdot {\mathrm{O}}_{\mathrm{2}}\end{array}}{\begin{array}{l}{k}_{\mathrm{18}}\cdot \mathrm{O}+k_{\mathrm{23}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{28}}\cdot \mathrm{OH}\\ +\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}+k_{\mathrm{50}}\cdot \mathrm{NO}\\ +\mathrm{2}\cdot \left(k_{\mathrm{30}}+k_{\mathrm{31}}\cdot \mathrm{M}\right)\cdot {\mathrm{HO}}_{\mathrm{2}}\end{array}}}.\end{array}$$

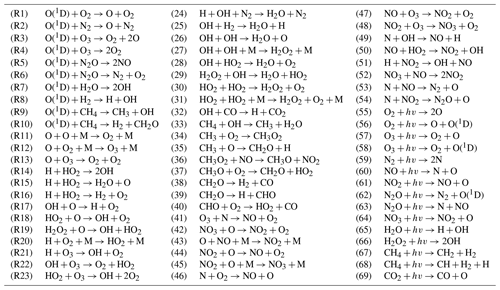
Figure 1 plots height–latitude cross-sections for the $<{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}>$ ratio for each month. The solid black lines mark the boundaries of equilibrium areas where, according to condition (1), local values of HO₂ are close to their equilibrium values, with a possible bias of less than 10 %. At low and middle latitudes one can see the presence of the main equilibrium area, which extends from the top of the analyzed altitude range to the lower boundary. The height of this equilibrium boundary, $z_{\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}}$, depends on the season and latitude and varies in the interval between 73 and 85 km. It is at its highest and lowest during summer and winter, respectively, at the middle latitudes. Near the Equator, $z_{\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}}$ demonstrates the weakest annual variations and varies in the 81–83 km range. There are local areas below the uppermost and longest black line, but they are small and irregular and can be omitted from our consideration. Note that the maps show the existence of equilibrium near 50 km, which can be assumed to be the beginning of the main equilibrium area in the stratosphere. At high latitudes there is also a main equilibrium area, as at low and middle latitudes, but this area above 70–75° of latitude can extend down to 50 km.

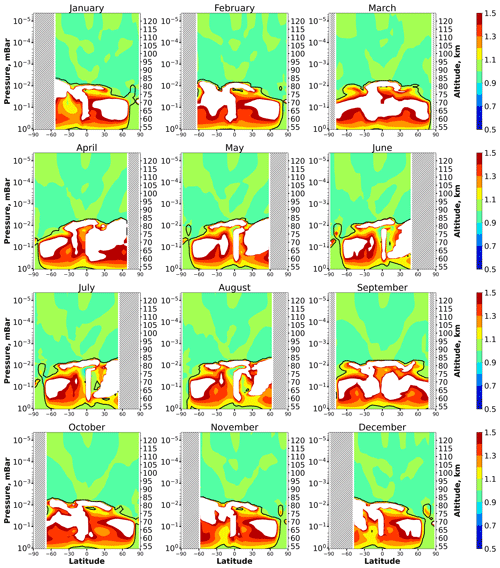
Figure 1 Nighttime mean and monthly averaged ${\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$, where $\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ is the equilibrium concentration determined by Eq. (5). The black line shows the boundary of HO₂ equilibrium according to condition (1). The stippling corresponds to χ < 105°. The white area represents the $<{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ > ratio outside the [0.5,1.5] interval.

In accordance with Table 1, OH chemical sources are determined by the following reactions:

$$\begin{array}{}\text{(R21)}& {\displaystyle }\mathrm{H}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}},\text{(R18)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}},\text{(R23)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}},\text{(R14)}& {\displaystyle }\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to \mathrm{2}\mathrm{OH},\text{(R50)}& {\displaystyle }\mathrm{NO}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH},\text{(R19)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}},\text{(R51)}& {\displaystyle }\mathrm{H}+{\mathrm{NO}}_{\mathrm{2}}\to \mathrm{OH}+\mathrm{NO},\text{(R7)}& {\displaystyle }\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}\mathrm{OH},\text{(R8)}& {\displaystyle }\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\to \mathrm{H}+\mathrm{OH},\text{(R9)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{4}}+\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\to {\mathrm{CH}}_{\mathrm{3}}+\mathrm{OH},\end{array}$$

whereas chemical sinks of this component are as follows:

$$\begin{array}{}\text{(R17)}& {\displaystyle }\mathrm{OH}+\mathrm{O}\to \mathrm{H}+{\mathrm{O}}_{\mathrm{2}},\text{(R22)}& {\displaystyle }\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}},\text{(R28)}& {\displaystyle }\mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}},\text{(R26)}& {\displaystyle }\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{O},\text{(R27)}& {\displaystyle }\mathrm{OH}+\mathrm{OH}+\mathrm{M}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{M},\text{(R24)}& {\displaystyle }\mathrm{H}+\mathrm{OH}+{\mathrm{N}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{N}}_{\mathrm{2}},\text{(R29)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}},\text{(R32)}& {\displaystyle }\mathrm{OH}+\mathrm{CO}\to \mathrm{H}+{\mathrm{CO}}_{\mathrm{2}},\text{(R33)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{4}}+\mathrm{OH}\to {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O},\text{(R25)}& {\displaystyle }\mathrm{OH}+{\mathrm{H}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{H},\text{(R49)}& {\displaystyle }\mathrm{N}+\mathrm{OH}\to \mathrm{NO}+\mathrm{H}.\end{array}$$

Thus, the OH local equilibrium concentration is described by the following equation:

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\mathrm{OH}}^{\mathrm{eq}}=(& k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{18}}\cdot \mathrm{O}\cdot {\mathrm{HO}}_{\mathrm{2}}+k_{\mathrm{23}}\cdot {\mathrm{HO}}_{\mathrm{2}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ & +\mathrm{2}\cdot k_{\mathrm{14}}\cdot \mathrm{H}\cdot {\mathrm{HO}}_{\mathrm{2}}+k_{\mathrm{50}}\cdot {\mathrm{HO}}_{\mathrm{2}}\cdot \mathrm{NO}\\ & +k_{\mathrm{19}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}+k_{\mathrm{24}}\cdot \mathrm{H}\cdot {\mathrm{N}}_{\mathrm{2}}+k_{\mathrm{51}}\cdot {\mathrm{NO}}_{\mathrm{2}}\cdot \mathrm{H}\\ & +\mathrm{2}\cdot k_{\mathrm{7}}\cdot \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+k_{\mathrm{8}}\cdot \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\cdot {\mathrm{H}}_{\mathrm{2}}\\ & +k_{\mathrm{9}}\cdot \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\cdot {\mathrm{CH}}_{\mathrm{4}})/(k_{\mathrm{17}}\cdot \mathrm{O}+k_{\mathrm{22}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ & +k_{\mathrm{28}}\cdot {\mathrm{HO}}_{\mathrm{2}}+\mathrm{2}\cdot (k_{\mathrm{26}}+k_{\mathrm{27}}\cdot \mathrm{M})\cdot \mathrm{OH}\\ & +k_{\mathrm{29}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+k_{\mathrm{32}}\cdot \mathrm{CO}+k_{\mathrm{33}}\cdot {\mathrm{CH}}_{\mathrm{4}}+k_{\mathrm{25}}\cdot {\mathrm{H}}_{\mathrm{2}}\\ & +k_{\mathrm{25}}\cdot \mathrm{N}).\end{array}\end{array}$$

Figure 2 shows height–latitude cross-sections for the < $\mathrm{OH}/\mathrm{OH}$^eq > ratio for each month. In this case, the equilibrium covers up to 70 %–80 % of the presented ranges of heights and latitudes so that the solid black lines mark the external boundaries of non-equilibrium areas. In March and September this area is almost symmetrical to the Equator. In April–August it is shifted towards the Northern Hemisphere. In October–February this area is higher in the Southern Hemisphere. In all months it is below 85–86 km. In the polar regions there are latitudinal ranges where OH is close to equilibrium throughout the entire height range.

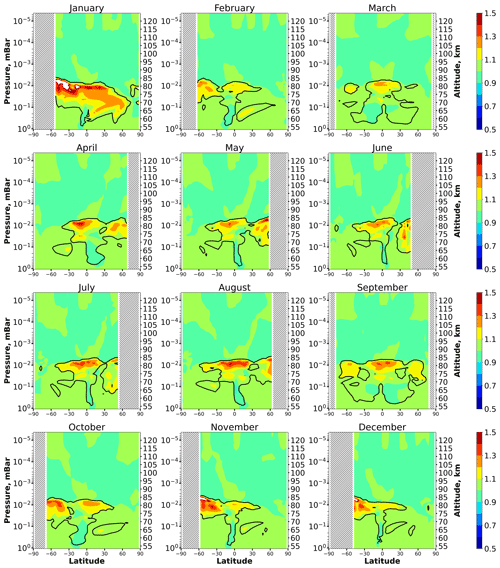
Figure 2 Nighttime mean and monthly averaged $\mathrm{OH}/\mathrm{OH}$^eq, where OH^eq is the equilibrium concentration determined by Eq. (6). The black line shows the boundary of OH equilibrium according to condition (1). The stippling corresponds to χ < 105°. The white area represents the < $\mathrm{OH}/\mathrm{OH}$^eq > ratio outside the [0.5,1.5] interval.

4 The main reactions, determining HO₂ and OH equilibria

Figure 3 presents height–latitude contour maps showing the relative contribution of a certain reaction to the total source and sink of HO₂ in January, taken as an example. To increase the information content of the panels, the altitude range is cut off everywhere to 10⁻³ hPa, since there are no significant changes above. Note, firstly, that reaction $\mathrm{H}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{M}\to {\mathrm{HO}}_{\mathrm{2}}+\mathrm{M}$ determines a major (up to 95 % and more) contribution in the main equilibrium area almost everywhere, except for the polar regions above 70–75° of latitude and below 75–80 km, where the reactions $\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}$ and ${\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}$ become important and should be taken into account. Other reactions (${\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}$, $\mathrm{CHO}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{HO}}_{\mathrm{2}}+\mathrm{CO}$, and ${\mathrm{CH}}_{\mathrm{3}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{CH}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}$) together contribute less than 2 %–3 % to the total source of HO₂ in the main equilibrium area and may be omitted. Secondly, the reaction ${\mathrm{HO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}}$ determines a major (up to 95 % and more) contribution to the total sink in the main equilibrium area almost everywhere, except for the same small polar areas, as in the considered case with the sources, where the reactions ${\mathrm{HO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}}$ and $\mathrm{NO}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH}$ are important and should be taken into account. The reactions $\mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}$, $\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to \mathrm{2}\mathrm{OH}$, $\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{O}$, and $\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}$ cumulatively contribute up to 10 %–15 % of the total sink near the boundary of the main equilibrium area. The remaining reactions (${\mathrm{HO}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}$ and ${\mathrm{HO}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}+\mathrm{M}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{M}$) are not important in the main equilibrium area and can be omitted. The complete figures for HO₂ sources and sinks for every month (all 12 panels) are given in the Supplement (Figs. S3–S11).

Figure 3 Nighttime mean and monthly averaged relative contribution of a certain reaction to the total source or sink of HO₂ in equilibrium areas. The stippling corresponds to χ < 105°. White indicates non-equilibrium areas of HO₂.

Therefore, the expression for HO₂ local equilibrium concentration can be simplified as follows:

$$\begin{array}{}\text{(7)}& \mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}+k_{\mathrm{22}}\cdot \mathrm{OH}\cdot {\mathrm{O}}_{\mathrm{3}}\\ +k_{\mathrm{29}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{OH}\end{array}}{\begin{array}{l}{k}_{\mathrm{18}}\cdot \mathrm{O}+k_{\mathrm{23}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{28}}\cdot \mathrm{OH}\\ +\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}+k_{\mathrm{50}}\cdot \mathrm{NO}\end{array}}}.\end{array}$$

Figure 4 presents height–latitude contour maps showing the relative contribution of a certain reaction to the total source and sink of OH in January, taken as an example in Fig. 3. As in the previous case, the altitude range is cut off at 10⁻³ hPa because only the panels for the reactions $\mathrm{H}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}}$ and ${\mathrm{HO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}}$ consist of interesting variations above. Note, firstly, that these reactions are the main OH sources in the upper part of the presented distributions down to 70–75 km, where they jointly provide up to a 95 % contribution to the equilibrium concentration. Also, the reaction ${\mathrm{HO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}}$ is major source in the lower part of the presented distribution from 50 to 60–70 km. The reaction $\mathrm{NO}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{OH}$ is important around non-equilibrium areas of OH and should be taken into account, whereas the reaction $\mathrm{H}+{\mathrm{NO}}_{\mathrm{2}}\to \mathrm{OH}+\mathrm{NO}$ is important in compact altitude–latitude areas near the poles. The reaction $\mathrm{H}+{\mathrm{HO}}_{\mathrm{2}}\to \mathrm{2}\mathrm{OH}$ gives up to 10 %–15 % contribution in small areas near the equilibrium boundary. Other reactions ($\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}\mathrm{OH}$, $\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\to \mathrm{H}+\mathrm{OH}$, ${\mathrm{CH}}_{\mathrm{4}}+\mathrm{O}{(}^{\mathrm{1}}\mathrm{D})\to {\mathrm{CH}}_{\mathrm{3}}+\mathrm{OH}$, and ${\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}$) together contribute less than 2 %–3 % of the total source of OH in the main equilibrium area and can be omitted. Secondly, the reaction $\mathrm{OH}+\mathrm{O}\to \mathrm{H}+{\mathrm{O}}_{\mathrm{2}}$ is the main OH sink in the upper part of the presented distributions down to 70–80 km, where it provides up to 95 % of the equilibrium concentration. The reactions $\mathrm{OH}+\mathrm{CO}\to \mathrm{H}+{\mathrm{CO}}_{\mathrm{2}}$ and $\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}$ are major in the lower part of the presented distributions from 50 to 70–80 km. The reaction $\mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}$ is significant enough around non-equilibrium areas of OH, whereas the reaction ${\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{HO}}_{\mathrm{2}}$ is important in the compact altitude–latitude area near the poles. Other reactions ($\mathrm{OH}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{O}$, $\mathrm{OH}+{\mathrm{H}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{H}$, $\mathrm{N}+\mathrm{OH}\to \mathrm{NO}+\mathrm{H}$, ${\mathrm{CH}}_{\mathrm{4}}+\mathrm{OH}\to {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, $\mathrm{H}+\mathrm{OH}+{\mathrm{N}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{N}}_{\mathrm{2}}$, and $\mathrm{OH}+\mathrm{OH}+\mathrm{M}\to {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{M}$) together contribute less than 2 %–3 % to the total sink of OH in the main equilibrium area and can be omitted. The complete figures for OH sources and sinks for every month (all 12 panels) are given in the Supplement (Figs. S12–S24).

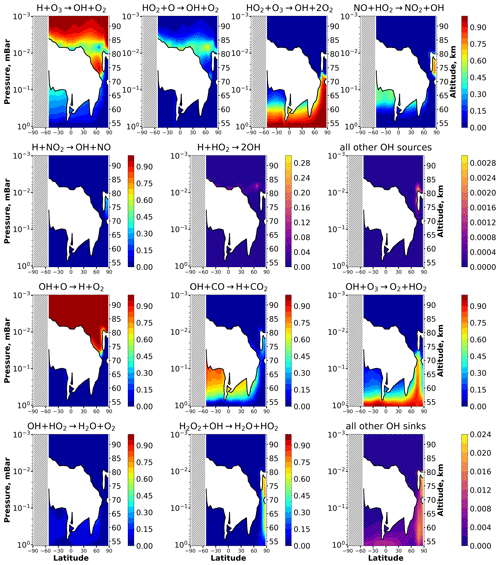
Figure 4 Nighttime mean and monthly averaged relative contribution of a certain reaction to the total source or sink of OH in equilibrium areas. The stippling corresponds to χ < 105°. White indicates non-equilibrium areas of OH.

Therefore, the expression for OH local equilibrium concentration can be simplified as follows:

$$\begin{array}{}\text{(8)}& {\mathrm{OH}}^{\mathrm{eq}}={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{18}}\cdot \mathrm{O}\cdot {\mathrm{HO}}_{\mathrm{2}}+k_{\mathrm{23}}\cdot {\mathrm{HO}}_{\mathrm{2}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ +\mathrm{2}\cdot k_{\mathrm{14}}\cdot \mathrm{H}\cdot {\mathrm{HO}}_{\mathrm{2}}+k_{\mathrm{24}}\cdot \mathrm{H}\cdot {\mathrm{N}}_{\mathrm{2}}\\ +k_{\mathrm{50}}\cdot {\mathrm{HO}}_{\mathrm{2}}\cdot \mathrm{NO}+k_{\mathrm{51}}\cdot {\mathrm{NO}}_{\mathrm{2}}\cdot \mathrm{H}\end{array}}{\begin{array}{l}{k}_{\mathrm{17}}\cdot \mathrm{O}+k_{\mathrm{22}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{28}}\cdot {\mathrm{HO}}_{\mathrm{2}}\\ +k_{\mathrm{29}}\cdot {\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+k_{\mathrm{32}}\cdot \mathrm{CO}\end{array}}}.\end{array}$$

5 Shortened equilibrium conditions of HO₂ and OH in the upper mesosphere and lower thermosphere

The above analysis revealed that the reactions describing equilibrium conditions (7)–(8) in the lower and middle mesosphere are different from those in the upper mesosphere and lower thermosphere. This means that the task of applying these conditions can be divided into two parts depending on the selected altitude range. At the upper-mesosphere and lower-thermosphere altitudes, we can only consider the HO_x–O_x chemistry, excluding reactions with the participation of H₂O₂, N, NO, NO₂, and CO. In addition, we can omit the reactions ${\mathrm{HO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{3}}\to \mathrm{OH}+\mathrm{2}{\mathrm{O}}_{\mathrm{2}}$, $\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\to {\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}$, and $\mathrm{OH}+{\mathrm{HO}}_{\mathrm{2}}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}$ due to their insignificance here. As a result, the shortened equilibrium conditions of HO₂ and OH for this altitude range are as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}={\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}}},\text{(10)}& {\displaystyle }{\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}={\displaystyle \frac{k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{18}}\cdot \mathrm{O}\cdot {\mathrm{HO}}_{\mathrm{2}}+\mathrm{2}\cdot k_{\mathrm{14}}\cdot \mathrm{H}\cdot {\mathrm{HO}}_{\mathrm{2}}}{k_{\mathrm{17}}\cdot \mathrm{O}}}.\end{array}$$

Figure 5 shows height–latitude cross-sections for the $<{\mathrm{HO}}_{\mathrm{2}}/{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}>$ ratio for each month. In each panel the uppermost and longest black line marks the lower boundary of the main equilibrium area, where, according to condition (1), ${\mathrm{HO}}_{\mathrm{2}}\approx {\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ with possible bias of less than 10 %. As in the case of Fig. 1, this area extends from the top of the analyzed altitude range. There are also very small equilibrium areas below, which can be omitted from our consideration. The height of the lower boundary of the main equilibrium area, $z_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}$, depends essentially on the season and latitude. In comparison with Fig. 1, one can see that it reproduces many features of $z_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}$ at low and middle latitudes. In particular, $z_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}$ varies in the interval between 73 and 85 km, as in the case of $z_{\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}}$. In the middle latitudes, $z_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}$ in summer is several kilometers higher than in winter. Near the Equator, $z_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}$ demonstrates the weakest annual variations and varies in the range of 81–83 km. One can therefore conclude that the exclusion of a number of reactions does not lead to significant changes in the space–time distributions of the HO₂ equilibrium.

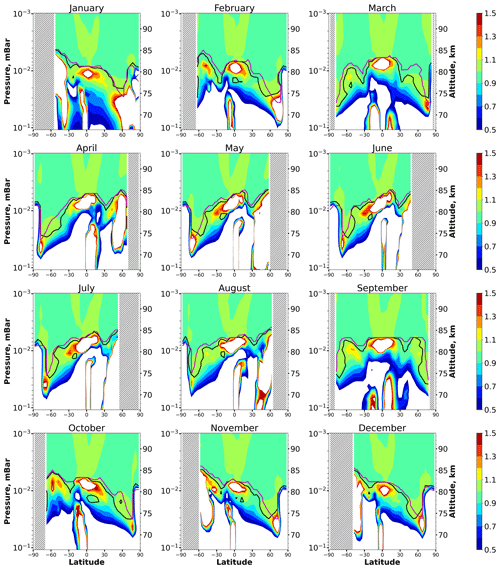
Figure 5 Nighttime mean and monthly averaged ${{\mathrm{HO}}_{\mathrm{2}}/{\mathrm{HO}}_{\mathrm{2}}}_{\mathrm{sh}}^{\mathrm{eq}}$, where ${{\mathrm{HO}}_{\mathrm{2}}}_{\mathrm{sh}}^{\mathrm{eq}}$ is the shortened equilibrium concentration determined by Eq. (9). The black line shows the boundary of HO₂ equilibrium according to condition (1). The magenta line shows < Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ > = 0.1. The stippling corresponds to χ < 105°. The white area represents the $<{\mathrm{HO}}_{\mathrm{2}}/\mathrm{HO}{}_{\mathrm{2}}^{\mathrm{eq}}$ > ratio outside the [0.5,1.5] interval.

Figure 6 plots height–latitude cross-sections for the $<\mathrm{OH}/\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}>$ ratio for each month. As in the previous case, this is the lower boundary of the equilibrium area, where, according to condition (1), $\mathrm{OH}\approx \mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}$ with good precision. The dependence of the boundary height, $z_{\mathrm{OH}}{}_{\mathrm{sh}}^{\mathrm{eq}}$, on the season and latitude mainly repeats the behavior of $z_{{\mathrm{HO}}_{\mathrm{2}}}{}_{\mathrm{sh}}^{\mathrm{eq}}$. In particular, $z_{\mathrm{OH}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ varies in the interval between 73 and 85 km. At middle latitudes, $z_{\mathrm{OH}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ is several kilometers higher in summer than in winter. Near the Equator, $z_{\mathrm{OH}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ also demonstrates the weakest annual variations and varies in the range of 81–83 km. Nevertheless, in some cases, the OH equilibrium boundary lies slightly higher than the HO₂ boundary. In particular, it can be seen in April–August above 50° S, which can be explained by the difference between HO₂ and OH lifetimes (${\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}<{\mathit{\tau }}_{\mathrm{OH}}$), mainly due to k₁₈ > k₁₇. In comparison with Fig. 2, one can see the exclusion of the abovementioned reactions from consideration results in the absence of the OH equilibrium areas at low- and middle-mesosphere altitudes, as expected.

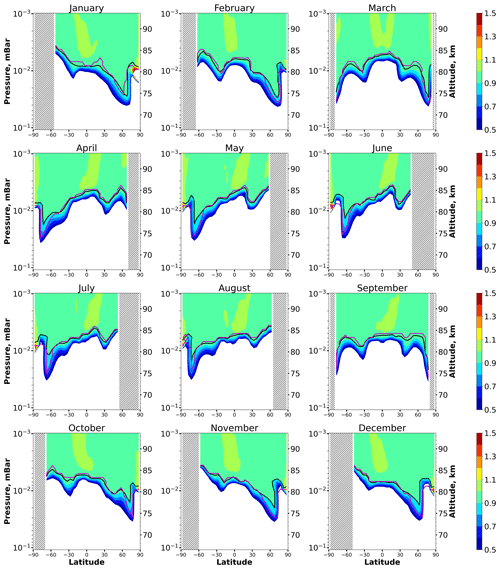
Figure 6 Nighttime mean and monthly averaged ${\mathrm{OH}/\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}$, where ${\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}$ is the shortened equilibrium concentration determined by Eq. (10). The black line shows the boundary of OH equilibrium according to condition (1). The magenta line shows < Crit_OH > =0.1. The stippling corresponds to χ < 105°. The white area represents the < $\mathrm{OH}/\mathrm{OH}$^eq > ratio outside the [0.5,1.5] interval.

6 The criteria for HO₂ and OH equilibrium validity in the upper mesosphere and lower thermosphere

Firstly, we determine HO₂ and OH lifetimes and the local timescales of ${\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ and ${\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}$, according to Sect. 2.

From Eqs. (2)–(3) and (9), the HO₂ lifetime and local timescales of ${\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}$ are as follows:

$$\begin{array}{}\text{(11)}& {\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}={\displaystyle \frac{\mathrm{1}}{k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}}},\end{array}$$

$$\begin{array}{}\text{(12)}& {\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}={\displaystyle \frac{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\left|\mathrm{d}{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}/\mathrm{d}t\right|}}.\end{array}$$

Then we find the expression for $\mathrm{d}{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}/\mathrm{d}t$:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\mathrm{d}t}}& ={\displaystyle \frac{k_{\mathrm{18}}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{H}}{\mathrm{O}}\right)\cdot {\mathrm{O}}^{\mathrm{2}}}{{\left(k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}\right)}^{\mathrm{2}}}}\\ & =-{\displaystyle \frac{k_{\mathrm{18}}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{O}}{\mathrm{H}}\right)\cdot {\mathrm{H}}^{\mathrm{2}}}{{\left(k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}\right)}^{\mathrm{2}}}}.\end{array}\end{array}$$

Kulikov et al. (2023a) analyzed the local nighttime evolution of O and H within the framework of pure HO_x–O_x chemistry and found the expression for $\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{O}}{\mathrm{H}}\right)$:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\mathrm{O}}{\mathrm{H}}}\right)& =-\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-{\displaystyle \frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}}\right)-k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ & -k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot {\displaystyle \frac{\mathrm{O}}{\mathrm{H}}}.\end{array}\end{array}$$

Thus, Eq. (13) can be rewritten in the following form:

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{d}{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\mathrm{d}t}}={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{18}}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot H^{\mathrm{2}}\cdot (\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\\ \cdot \left(\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ +k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{O}}{\mathrm{H}})\end{array}}{{\left(k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}\right)}^{\mathrm{2}}}}.\end{array}$$

By combining Eqs. (9), (12), and (15), we obtain the expression for the local timescales of ${\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}$:

$$\begin{array}{}\text{(16)}& {\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}={\displaystyle \frac{\begin{array}{l}(k_{\mathrm{18}}\cdot \mathrm{O}+(k_{\mathrm{14}}+k_{\mathrm{15}}\\ +k_{\mathrm{16}})\cdot \mathrm{H})\end{array}}{\begin{array}{l}{k}_{\mathrm{18}}\cdot \mathrm{H}\cdot (\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}\right)\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{O}}{\mathrm{H}})\end{array}}}.\end{array}$$

Thus, taking into account Eqs. (4), (11), and (16), the criterion for HO₂ equilibrium validity is written in the form:

$$\begin{array}{}\text{(17)}& \begin{array}{rl}& {\text{Crit}}_{{\mathrm{HO}}_{\mathrm{2}}}={\displaystyle \frac{{\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}}{{\mathit{\tau }}_{{\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}}}}}\\ & ={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{18}}\cdot H\cdot (\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot (\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}})\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{O}}{\mathrm{H}})\end{array}}{{\left(k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}\right)}^{\mathrm{2}}}}\le \mathrm{0.1}.\end{array}\end{array}$$

We calculated Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ using the global 3D chemical transport model and included the zonally and monthly averaged lines < Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ > = 0.1 in Fig. 5 (see magenta lines). One can see that, depending on the month, each magenta line reproduces the lower boundary of the main HO₂ equilibrium area well and follows almost all its features and variations. Note that, in the zeroth-order approximation, criterion (17) can be simplified as

$$\begin{array}{}\text{(18)}& \begin{array}{rl}& {\text{Crit}}_{{\mathrm{HO}}_{\mathrm{2}}}\\ & \approx (\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-{\displaystyle \frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ & +k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot {\displaystyle \frac{\mathrm{O}}{\mathrm{H}}})\cdot {\displaystyle \frac{\mathrm{H}}{k_{\mathrm{18}}\cdot {\mathrm{O}}^{\mathrm{2}}}}\le \mathrm{0.1}.\end{array}\end{array}$$

From Eqs. (2)–(3) and (10), the OH lifetime and local timescales of ${\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}$ are as follows:

$$\begin{array}{}\text{(19)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{OH}}={\displaystyle \frac{\mathrm{1}}{k_{\mathrm{17}}\cdot \mathrm{O}}},\text{(20)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}}={\displaystyle \frac{\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\left|\mathrm{d}\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}/\mathrm{d}t\right|}}.\end{array}$$

Before determining the expression for $\mathrm{d}\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}/\mathrm{d}t$, one should keep in mind that Eq. (10) depends on the HO₂ concentration. As previously mentioned, near and above the OH equilibrium boundary, HO₂ is in equilibrium (${\mathrm{HO}}_{\mathrm{2}}\approx {\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}$), and we can use Eq. (9). In view of $k_{\mathrm{18}}\cdot \mathrm{O}\gg \left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}$,

$$\begin{array}{}\text{(21)}& {\mathrm{HO}}_{\mathrm{2}}{}_{\mathrm{sh}}^{\mathrm{eq}}\approx {\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\left(\mathrm{1}-{\displaystyle \frac{\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right).\end{array}$$

The substitution of Eq. (21) into Eq. (10) yields

$$\begin{array}{}\text{(22)}& \begin{array}{rl}& \mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}=k_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\\ & \cdot {\displaystyle \frac{\left(\mathrm{1}+\frac{\mathrm{2}\cdot k_{\mathrm{14}}\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)\cdot \left(\mathrm{1}-\frac{\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)}{k_{\mathrm{17}}\cdot \mathrm{O}}}+{\displaystyle \frac{k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}}{k_{\mathrm{17}}\cdot \mathrm{O}}}\\ & \approx {\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{17}}\cdot \mathrm{O}}}\cdot \left(\mathrm{1}+{\displaystyle \frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right)\\ & +{\displaystyle \frac{k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}}{k_{\mathrm{17}}\cdot \mathrm{O}}}.\end{array}\end{array}$$

Thus, the expression for $\mathrm{d}\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}/\mathrm{d}t$ is

$$\begin{array}{}\text{(23)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\mathrm{H}}{\mathrm{O}}}\right)\cdot ({\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{17}}}}\\ & \cdot \left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}\cdot \left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right)+{\displaystyle \frac{k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}}{k_{\mathrm{17}}}})\\ & +{\displaystyle \frac{k_{\mathrm{21}}\cdot \mathrm{H}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}}{k_{\mathrm{17}}\cdot \mathrm{O}}}{\displaystyle \frac{\mathrm{d}{\mathrm{O}}_{\mathrm{3}}}{\mathrm{d}t}}.\end{array}\end{array}$$

Taking into account Eq. (14) and the differential equation for O₃ time evolution,

$${\displaystyle \frac{\mathrm{d}{\mathrm{O}}_{\mathrm{3}}}{\mathrm{d}t}}=k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}-k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}},$$

Eq. (23) can be rewritten in following form:

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}}{\mathrm{d}t}}\\ & ={\displaystyle \frac{(\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{O}}{\mathrm{H}})\cdot {\mathrm{H}}^{\mathrm{2}}}{{\mathrm{O}}^{\mathrm{2}}}}\\ & \cdot \left({\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{17}}}}\cdot \left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}\cdot \left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right)+{\displaystyle \frac{k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}}{k_{\mathrm{17}}}}\right)\\ & +{\displaystyle \frac{k_{\mathrm{21}}\cdot \mathrm{H}\cdot \left(k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}-k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}\right)}{k_{\mathrm{17}}\cdot \mathrm{O}}}.\end{array}\end{array}$$

Thus, by combining Eqs. (4), (19), (20), (22), and (24), we obtain the expression for the criterion for OH equilibrium validity:

$$\begin{array}{}\text{(25)}& \begin{array}{rl}& {\text{Crit}}_{\mathrm{OH}}={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{OH}}}{{\mathit{\tau }}_{{\mathit{\tau }}_{\mathrm{OH}{}_{\mathrm{sh}}^{\mathrm{eq}}}}}}\\ & ={\displaystyle \frac{\left(\begin{array}{l}(\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}\right)\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\cdot \frac{\mathrm{H}}{\mathrm{O}}+k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}})\\ \cdot (k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+\frac{\mathrm{2}\cdot \left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}})\\ +k_{\mathrm{21}}\cdot \left(k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}-k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}\right)\end{array}\right)}{\begin{array}{l}{k}_{\mathrm{17}}\cdot \mathrm{O}\cdot (k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+\frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}})\end{array}}}\\ & \le \mathrm{0.1}.\end{array}\end{array}$$

We calculated Crit_OH using the global 3D chemical transport model and included the zonally and monthly averaged lines < Crit_OH > = 0.1 in Fig. 6 (see magenta lines). One can see that, depending on the month, the magenta line reproduces the lower boundary of the OH equilibrium area almost everywhere and repeats mainly its features and variations. Nevertheless, there are a few (by latitude) narrow areas (in April–August near 70° S and in October–December near 70° N) where the criterion gives a position of the OH equilibrium boundary that is few kilometers lower. Our analysis revealed that the main reason for that is the lack of $\mathrm{OH}+\mathrm{CO}\to \mathrm{H}+{\mathrm{CO}}_{\mathrm{2}}$ reaction among the sources of H in the corresponding differential equation of its chemical balance. In order to improve the criterion, we revised the derivation of Eq. (14) for $\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\mathrm{O}}{\mathrm{H}}\right)$ following Kulikov et al. (2023a):

$$\begin{array}{}\text{(26)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}\left({\displaystyle \frac{\mathrm{O}}{\mathrm{H}}}\right)& =-\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-{\displaystyle \frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}}\right)\\ & -k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}-k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot {\displaystyle \frac{\mathrm{O}}{\mathrm{H}}}-{\displaystyle \frac{k_{\mathrm{32}}\cdot \mathrm{CO}}{k_{\mathrm{17}}\cdot \mathrm{H}}}\\ & \cdot (k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+{\displaystyle \frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right)\\ & +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}).\end{array}\end{array}$$

As a result, the corrected criterion for OH equilibrium validity is as follows:

$$\begin{array}{}\text{(27)}& \begin{array}{rl}& {\text{Crit}}_{\mathrm{OH}}^m\\ & ={\displaystyle \frac{\begin{array}{l}\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-\frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\\ +k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \frac{\mathrm{O}}{\mathrm{H}}+\frac{k_{\mathrm{32}}\cdot \mathrm{CO}}{k_{\mathrm{17}}\cdot \mathrm{H}}\\ \cdot \left(k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+\frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\right)\end{array}}{\begin{array}{l}{k}_{\mathrm{17}}\cdot \mathrm{O}\cdot (k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+\frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)\\ +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}})\end{array}}}\\ & \cdot {\displaystyle \frac{\mathrm{H}}{\mathrm{O}}}\cdot (k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+{\displaystyle \frac{\mathrm{2}\cdot \left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}})\\ & +{\displaystyle \frac{k_{\mathrm{21}}\cdot \left(k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \mathrm{O}-k_{\mathrm{21}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}\right)}{k_{\mathrm{17}}\cdot \mathrm{O}\cdot \left(k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}+\frac{\left(k_{\mathrm{14}}-k_{\mathrm{15}}-k_{\mathrm{16}}\right)\cdot \mathrm{H}}{k_{\mathrm{18}}\cdot \mathrm{O}}\right)+k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}\right)}}\\ & \le \mathrm{0.1}.\end{array}\end{array}$$

We calculated this criterion using the global 3D chemical transport model and included the zonally and monthly averaged lines < Crit${}_{\mathrm{OH}}^m$ > = 0.1 on the OH equilibrium maps (see Fig. 7). One can see that the inclusion of this additional term actually eliminates the noted discrepancy between OH boundary and criterion. However, the application of this criterion requires CO data.

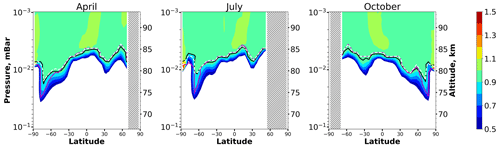
Figure 7 Nighttime mean and monthly averaged $\mathrm{OH}/{\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}$. The black line shows the boundary of OH equilibrium according to condition (1). The magenta line shows < Crit_OH > = 0.1, and the dotted white line shows < Crit${}_{\mathrm{OH}}^m$ > = 0.1.

Note, also, that our numerical analysis shows that, in the zeroth-order approximation, criterion (25) can be simplified as

$$\begin{array}{}\text{(28)}& \begin{array}{rl}{\text{Crit}}_{\mathrm{OH}}& \approx (\mathrm{2}\cdot k_{\mathrm{20}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot \left(\mathrm{1}-{\displaystyle \frac{k_{\mathrm{15}}+k_{\mathrm{16}}}{k_{\mathrm{18}}}}\right)\\ & +k_{\mathrm{21}}\cdot {\mathrm{O}}_{\mathrm{3}}+k_{\mathrm{12}}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}\cdot {\displaystyle \frac{\mathrm{O}}{\mathrm{H}}})\cdot {\displaystyle \frac{\mathrm{H}}{k_{\mathrm{17}}\cdot {\mathrm{O}}^{\mathrm{2}}}}\le \mathrm{0.1}.\end{array}\end{array}$$

7 Discussion

We now discuss obtained results and their possible applications.

Pay attention to the fact that the presented results were plotted using the lower threshold at 105° for the nighttime solar zenith angle (χ) to exclude the twilight transition processes. Nevertheless, our additional analysis revealed that OH and HO₂ equilibrium conditions are fulfilled at χ > 95° (see Figs. S1–S2 and S25–S26). Evidently, during the processing of the measurement data, taking the twilight χ (95°, 105°) range into account extends the latitude range of OH and HO₂ equilibrium application and allows us to take a noticeable part of the data into consideration. However, in this case, one should check for an additional condition (Kulikov et al., 2023a),

$$\begin{array}{}\text{(29)}& e^{{\int }_{{\mathrm{lt}}_{\mathrm{bn}}}^{\mathrm{lt}}{\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}^{-\mathrm{1}}\mathrm{d}t}\gg \mathrm{1},e^{{\int }_{{\mathrm{lt}}_{\mathrm{bn}}}^{\mathrm{lt}}{\mathit{\tau }}_{\mathrm{OH}}^{-\mathrm{1}}\mathrm{d}t}\gg \mathrm{1},\end{array}$$

where ${\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}$ and τ_OH are the HO₂ and OH lifetimes determined by Eqs. (11) and (19), lt is the local time of the data, and lt_bn is the local time at the beginning of the night. Note that, at night, O and H tend to decrease due to the shutdown of the O_x and HO_x family photochemical sources, so ${\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}$ and τ_OH increase. Thus, analyzing the measurement data, one can apply more stringent conditions:

$$\begin{array}{}\text{(30)}& e^{\frac{\text{lt}-{\text{lt}}_{\mathrm{bn}}}{{\mathit{\tau }}_{{\mathrm{HO}}_{\mathrm{2}}}}}\gg \mathrm{1},e^{\frac{\text{lt}-{\text{lt}}_{\mathrm{bn}}}{{\mathit{\tau }}_{\mathrm{OH}}}}\gg \mathrm{1}.\end{array}$$

The main results were obtained using a 3D model, where temperature and wind distributions are updated every 24 h. This excluded the influence of the atmospheric wave motion, in particular, associated with tides, which is one of the main dynamical drivers in the tropical mesopause. We carried out additional modeling with the distributions of the main characteristics, calculated by the Canadian Middle Atmosphere Model for the year 2009 (Scinocca et al., 2008), with a 6-hourly frequency for updating. The analysis of the time–height evolution of OH and HO₂, especially at low latitudes, showed that our criteria reproduce the local variations in the OH and HO₂ equilibrium boundaries quite well in such conditions (see Fig. S27).

We evaluated the sensitivity of the presented HO₂ and OH criteria (Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ and Crit_OH) to the uncertainties of characteristics involved in expressions (17) and (25). The local heights of the OH and HO₂ equilibrium boundaries ($z_{{\mathrm{HO}}_{\mathrm{2}}}^{\mathrm{crit}}$ and $z_{\mathrm{OH}}^{\mathrm{crit}}$) according to the criteria are determined as the altitudes at which Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ = 0.1 and Crit_OH = 0.1, respectively. We considered the whole dataset of nighttime profiles, obtained by the numerical simulation of a 1-year global evolution of the mesosphere–lower thermosphere, and estimated total uncertainties in the determination of $z_{{\mathrm{HO}}_{\mathrm{2}}}^{\mathrm{crit}}$ and $z_{\mathrm{OH}}^{\mathrm{crit}}$ from each local (in time and space) dataset (profiles of O, H, O₃, M, O₂, and temperature). Following the typical analysis presented, for example, in Mlynczak et al. (2013a, 2014), each uncertainty was calculated as a root-sum-square of the sensitivities to the individual perturbations of certain variables or parameters in expressions (17) and (25). The following uncertainties in the variables were used: 5 K in the temperature and 30 % in O₃, O, and H. The uncertainties in reaction rates and their temperature dependencies were taken from Burkholder et al. (2020). As a result (see Fig. 8), the monthly and longitudinal means of total uncertainties in the determination of $z_{{\mathrm{HO}}_{\mathrm{2}}}^{\mathrm{crit}}$ and $z_{\mathrm{OH}}^{\mathrm{crit}}$ were found to vary in the range of 0.02–1 km, depending on altitude and season. Note that these values are comparable with the typical height resolution of satellite data. The latter allows us to regard our criteria as a robust instrument for equilibrium condition validation. The main reason for the relatively low sensitivity of $z_{{\mathrm{HO}}_{\mathrm{2}}}^{\mathrm{crit}}$ and $z_{\mathrm{OH}}^{\mathrm{crit}}$ is the strong height dependence of Crit${}_{{\mathrm{HO}}_{\mathrm{2}}}$ and Crit_OH near the value of 0.1 (see Fig. S28).

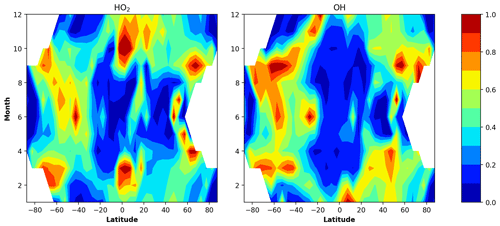
Figure 8 Monthly and longitudinal means of total uncertainties (in km) in determination of the local heights of the OH and HO₂ equilibrium boundaries according to criteria (17) and (25). White indicates the absence of data due to polar day.

As noted, Figs. 5–6 represent an interesting peculiarity. At the middle latitudes, summer $z_{{{\mathrm{HO}}_{\mathrm{2}}}_{\mathrm{sh}}^{\mathrm{eq}}}$ and $z_{{\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}}$ are remarkably higher than winter ones. For example, in February, the $z_{{{\mathrm{HO}}_{\mathrm{2}}}_{\mathrm{sh}}^{\mathrm{eq}}}$ at 60° N is ∼ 84 km, whereas the one at 60° S is ∼ 74 km. Recently, Kulikov et al. (2023b) found such a feature in the evolution of the nighttime ozone chemical equilibrium boundary (Fig. 5 there), derived from SABER/TIMED data. The study showed that the boundary closely follows the transition zone that separates strong and weak diurnal oscillations of O and H (see Figs. 1–3 and 13 in Kulikov et al., 2023b). Above the zone, the behavior of components is dynamically driven and seasonality is the result of change in global-scale circulation, with vertical advection being the primary factor according to Wang et al. (2023). In the transition zone and below, O and H concentrations change by orders of magnitude during the night driven by photochemical processes. Kulikov et al. (2023b) studied the photochemistry at these altitudes and its seasonal dependence. It was shown analytically that nighttime O decreases with the characteristic timescale ${\mathit{\tau }}_{\mathrm{O}}=\mathrm{O}/\left|\mathrm{d}\mathrm{O}/\mathrm{d}t\right|$ proportional to the $\mathrm{O}/\mathrm{H}$ value at the beginning of the night (see ​​​​​​​Eq. 13 there). At the same time, according to the distributions derived from SABER measurements, $\mathrm{O}/\mathrm{H}$ during summer daytime (and thus also at the beginning of the night) at the middle latitudes is remarkably less than during winter daytime (see Fig. 14 there). Consequently, summer values of nighttime τ_O below ∼ 84 km are significantly shorter than winter ones, so summer O during the night decreases much faster than in winter. In our case, lifetimes of HO₂ and OH are proportional mainly to $\frac{\mathrm{1}}{\mathrm{O}}$ (see Eqs. 11 and 19), so, following the approach described in Sect. 2, the summer rise in $z_{{{\mathrm{HO}}_{\mathrm{2}}}_{\mathrm{sh}}^{\mathrm{eq}}}$ and $z_{{\mathrm{OH}}_{\mathrm{sh}}^{\mathrm{eq}}}$ at the middle latitudes can be explained by the seasonal difference in O diurnal photochemical evolution at these altitudes.

As noted in the Introduction, the conditions of nighttime OH and HO₂ equilibria, together with those of O₃ equilibrium and their analytical criteria, constitute a useful tool for the retrieval of these components or other characteristics (for example, O and H) from measured data. At the altitudes of the upper mesosphere–lower thermosphere, these conditions can be applied, for example, to the MLS/Aura database (measured characteristics: OH, HO₂, O₃, and CO), SMILES (HO₂ and O₃), SCIAMACHY (O(¹S) green-line, O₂ A-band, and OH Meinel-band emissions), SABER/TIMED (O₃ and OH Meinel-band emissions at 2.0 µm (9 → 7 and 8 → 6 bands) and at 1.6 µm (5 → 3 and 4 → 2 bands)), and others, including the improvement of existing retrieval approaches. In particular, Panka et al. (2021) proposed the method of simultaneous derivation of O and OH at the levels v = 0–9 from SABER data (volume emission rates at 2.0 and 1.6 µm, VER_2 µm and VER_1.6 µm) at 80–100 km, taking into account the equilibrium condition for all states of OH. Such an approach is valid for excited states due to their very short lifetimes determined by radiative transitions and quenching with O₂, N₂, and O. In the case of the OH ground state, its lifetime is determined only by the reaction $\mathrm{OH}+\mathrm{O}\to \mathrm{H}+{\mathrm{O}}_{\mathrm{2}}$. This means that Panka et al. (2021) used an equilibrium condition for total OH, which, as one can see in Fig. 6, may be significantly disrupted above 80 km. On the other hand, there are latitude ranges and months when the OH equilibrium boundary drops remarkably below 80 km. Moreover, the Panka et al. (2021) method requires external data about HO₂, since the reaction ${\mathrm{HO}}_{\mathrm{2}}+\mathrm{O}\to \mathrm{OH}+{\mathrm{O}}_{\mathrm{2}}$ becomes the important source for OH below 87 km (Panka et al., 2021; see also Fig. 4 in our paper).

The results of our paper allow us to modify the Panka et al. (2021) method to extend its capabilities. The simplest development of this method seems to be the following. First of all, note that the HO₂ equilibrium condition (9) depends on H and O only and can be used within the self-consistent retrieval procedure, considering the following system of equations:

$$\begin{array}{rl}& \mathrm{OH}\left(v=\mathrm{1}-\mathrm{9}\right)\\ & ={\displaystyle \frac{\begin{array}{l}{k}_{\mathrm{12}}\cdot \mathrm{H}\cdot {\mathrm{O}}_{\mathrm{3}}\cdot \mathrm{M}\cdot f\left(v\right)+{\sum }_{v^{\prime }>v}(a_{\mathrm{1}}\left(v^{\prime },v\right)\\ +a_{\mathrm{2}}\left(v^{\prime },v\right)\cdot {\mathrm{O}}_{\mathrm{2}}+a_{\mathrm{3}}\left(v^{\prime },v\right)\cdot {\mathrm{N}}_{\mathrm{2}}\\ +\left(a_{\mathrm{4}}\left(v^{\prime },v\right)+a_{\mathrm{5}}\left(v^{\prime },v\right)\right)\cdot \mathrm{O})\cdot \mathrm{OH}\left(v^{\prime }\right)\end{array}}{\begin{array}{l}{a}_{\mathrm{6}}\left(v\right)\cdot \mathrm{O}+{\sum }_{v>v^{\prime }}(a_{\mathrm{1}}\left(v,v^{\prime }\right)+a_{\mathrm{2}}\left(v,v^{\prime }\right)\cdot {\mathrm{O}}_{\mathrm{2}}\\ +a_{\mathrm{3}}\left(v,v^{\prime }\right)\cdot {\mathrm{N}}_{\mathrm{2}}+\left(a_{\mathrm{4}}\left(v,v^{\prime }\right)+a_{\mathrm{5}}\left(v,v^{\prime }\right)\right)\cdot \mathrm{O})\end{array}}},\end{array}$$

$$\mathrm{OH}\left(\mathrm{0}\right)={\displaystyle \frac{\begin{array}{l}{\sum }_{v^{\prime }>\mathrm{0}}(a_{\mathrm{1}}\left(v^{\prime },\mathrm{0}\right)+a_{\mathrm{2}}\left(v^{\prime },\mathrm{0}\right)\cdot {\mathrm{O}}_{\mathrm{2}}\\ +a_{\mathrm{3}}\left(v^{\prime },\mathrm{0}\right)\cdot {\mathrm{N}}_{\mathrm{2}}+(a_{\mathrm{4}}\left(v^{\prime },\mathrm{0}\right)\\ +a_{\mathrm{5}}\left(v^{\prime },\mathrm{0}\right))\cdot \mathrm{O})\cdot \mathrm{OH}\left(v^{\prime }\right)\\ +k_{\mathrm{18}}\cdot \mathrm{O}\cdot {\mathrm{HO}}_{\mathrm{2}}+\mathrm{2}\cdot k_{\mathrm{14}}\cdot \mathrm{H}\cdot {\mathrm{HO}}_{\mathrm{2}}\end{array}}{k_{\mathrm{17}}\cdot \mathrm{O}}},$$

$${\mathrm{HO}}_{\mathrm{2}}={\displaystyle \frac{k_{\mathrm{20}}\cdot \mathrm{H}\cdot \mathrm{M}\cdot {\mathrm{O}}_{\mathrm{2}}}{k_{\mathrm{18}}\cdot \mathrm{O}+\left(k_{\mathrm{14}}+k_{\mathrm{15}}+k_{\mathrm{16}}\right)\cdot \mathrm{H}}},$$

$${\text{VER}}_{\mathrm{2}\mathrm{\mu }\mathrm{m}}=a_{\mathrm{1}}(\mathrm{9},\mathrm{7})\cdot \mathrm{OH}\left(\mathrm{9}\right)+a_{\mathrm{1}}(\mathrm{8},\mathrm{9})\cdot \mathrm{OH}\left(\mathrm{8}\right),$$

$${\text{VER}}_{\mathrm{1.6}\mathrm{\mu }\mathrm{m}}=a_{\mathrm{1}}(\mathrm{5},\mathrm{3})\cdot \mathrm{OH}\left(\mathrm{5}\right)+a_{\mathrm{1}}(\mathrm{4},\mathrm{2})\cdot \mathrm{OH}\left(\mathrm{4}\right),$$

where a₁₋₆ are the constant rates of the processes $\mathrm{OH}\left(v\right)\to \mathrm{OH}\left(v^{\prime }<v\right)+hv,\mathrm{OH}\left(v\right)+{\mathrm{O}}_{\mathrm{2}}\to \mathrm{OH}\left(v<v^{\prime }\right)+{\mathrm{O}}_{\mathrm{2}},\mathrm{OH}\left(v\right)+{\mathrm{N}}_{\mathrm{2}}\to \mathrm{OH}\left(v<v^{\prime }\right)+{\mathrm{N}}_{\mathrm{2}},\mathrm{OH}\left(v\right)+\mathrm{O}{(}^{\mathrm{3}}\mathrm{P})\to \mathrm{OH}\left(v^{\prime }\le v-\mathrm{5}\right)+\mathrm{O}{(}^{\mathrm{1}}\mathrm{D}),\mathrm{OH}\left(v\right)+\mathrm{O}{(}^{\mathrm{3}}\mathrm{P})\to \mathrm{OH}(v^{\prime }<v)+\mathrm{O}{(}^{\mathrm{3}}\mathrm{P})$, and $\mathrm{OH}\left(\mathit{\nu }\right)+\mathrm{O}{(}^{\mathrm{3}}\mathrm{P})\to \mathrm{H}+{\mathrm{O}}_{\mathrm{2}}$, respectively. Take into consideration that this system includes 13 equations with 13 unknown variables. Therefore, the solution to the system for a single set of SABER measurements (simultaneously measured profiles of O₃, temperature​​​​​​​, pressure, VER_2 µm, and VER_1.6 µm) gives one simultaneously retrieved profile of O, H, OH(v = 0–9), and HO₂. By applying criteria (17) and (25) to obtained O and H profiles, we verify the fulfillment of OH and HO₂ equilibrium conditions and determine the height below which the resulting profiles should be cut. More advanced retrieval procedure would be statistical, based on Bayes' theorem, taking into account the uncertainties in measurement data and rate constants. For example, similarly to Kulikov et al. (2018a), it should include a derivation of the posterior conditional probability density function of retrieved characteristics and a numerical analysis of this function. Detailed development of this retrieval method is outside the scope of this paper and should be carried out in a separate work.

8 Conclusions

The presented analysis shows that there are extended areas in the mesosphere and lower thermosphere where nighttime HO₂ and OH are close to their local equilibrium concentrations, determined mainly by the reactions between HO_x and O_x components amongst themselves and with H₂O₂, N, NO, NO₂, and CO. In the upper mesosphere–lower thermosphere, the shortened expressions for their local equilibrium concentrations are valid, including the HO_x–O_x chemistry only. These conditions describe the HO₂ and OH equilibrium from the top to some lower boundaries, the altitude position of which varies in the interval between 73 and 85 km and depends essentially on the season and latitude. We proposed analytical criteria which reproduce the main features of these boundaries quite well almost everywhere. Due to the weak sensitivity to uncertainties in reaction rates and variables, these criteria can be regarded as a robust instrument for HO₂ and OH equilibrium validation. The obtained results allow us to extend the abilities of the method created by Panka et al. (2021) to retrieve unmeasured components from SABER data. The simultaneous application of OH and HO₂ equilibrium conditions to the SABER data, together with the OH and HO₂ criteria to control this equilibrium validity, allows us to retrieve all unknown HO_x–O_x components (O, H, OH, and HO₂) and to extend the altitude range of downward retrieval below 80 km and without external information.