Measurement of the collision rate coefficients between atmospheric ions and multiply charged aerosol particles in the CERN CLOUD chamber

Aerosol particles have an important role in Earth's radiation balance and climate, both directly and indirectly through aerosol–cloud interactions. Most aerosol particles in the atmosphere are weakly charged, affecting both their collision rates with ions and neutral molecules, as well as the rates by which they are scavenged by other aerosol particles and cloud droplets. The rate coefficients between ions and aerosol particles are important since they determine the growth rates and lifetimes of ions and charged aerosol particles, and so they may influence cloud microphysics, dynamics, and aerosol processing. However, despite their importance, very few experimental measurements exist of charged aerosol collision rates under atmospheric conditions, where galactic cosmic rays in the lower troposphere give rise to ion pair concentrations of around 1000 cm⁻³. Here we present measurements in the CERN CLOUD chamber of the rate coefficients between ions and small (<10 nm) aerosol particles containing up to 9 elementary charges, e. We find the rate coefficient of a singly charged ion with an oppositely charged particle increases from 2.0 (0.4–4.4) × 10⁻⁶ cm³ s⁻¹ to 30.6 (24.9–45.1) × 10⁻⁶ cm³ s⁻¹ for particles with charges of 1 to 9 e, respectively, where the parentheses indicate the ±1σ uncertainty interval. Our measurements are compatible with theoretical predictions and show excellent agreement with the model of Gatti and Kortshagen (2008).

1 Introduction

Atmospheric aerosols play an important, yet uncertain, role in Earth's radiative balance. The largest source of uncertainty in current climate projections is due to aerosols and their interactions with clouds (Intergovernmental Panel on Climate Change, 2014a). For new atmospheric particles to be climatically relevant, they must grow to sizes above approximately 50 nm where they can constitute cloud condensation cloud nuclei, CCN (Intergovernmental Panel on Climate Change, 2014b). During this growth – and especially in the size range below 10 nm where they are highly mobile – new particles are highly susceptible to loss from scavenging by pre-existing larger particles. Consequently, the balance between growth rates due to collisions with condensable vapours and the loss rates to pre-existing particles plays a central role in determining the fraction of new particles that reach CCN sizes and influence climate (Marten et al., 2022; Mahfouz and Donahue, 2021a; Kulmala et al., 2017).

Electric charge plays an important role in new particle formation by stabilising the embryonic molecular clusters against evaporation (Kirkby et al., 2016, 2011; Turco et al., 1998). The presence of charges also enhances the growth rate of molecular clusters (He et al., 2021) and newly formed particles (Stolzenburg et al., 2020). However, charge can also enhance particle losses to pre-existing particles of opposite polarity (Mahfouz and Donahue, 2021a, b) or even neutral particles via van der Waals enhancement. To understand the role of charge in the formation of CCN requires a quantitative understanding of the charge state of the atmospheric aerosol. This, in turn, requires knowledge of particle–particle and ion–particle rate coefficients under atmospheric conditions. Previous studies have for the most part considered collisions between particles or molecules where only one is charged (e.g. Dépée et al., 2021; He et al., 2021). Yet, particles with larger numbers of charges are found in the atmosphere (e.g. Tinsley et al., 2000) and in many laboratory experiments, especially in generation of calibration aerosols.

In the atmosphere, high charges exist not only on aerosol particles and hydro-meteors in thunderclouds, but also on aerosol particles during fair weather resulting from the evaporation of charged cloud droplets (Tinsley et al., 2000). The excess charge on aerosol particles in cloud systems is expected to enhance “electro-scavenging” whereby charged particles are lost to bigger droplets of opposite sign (Tinsley et al., 2000; Guo and Xue, 2021). Simulations by Guo and Xue (2021) show that multiply charged particles can have a significant influence on cloud lifetime. Charge is transferred from smaller particles to larger droplets when they collide, which increases the growth rate of multiply charged CCN compared with their neutral counterparts (Guo and Xue, 2021). Moreover, there exists a charge gradient on droplets in a cloud, where droplets have positive charges atop of the cloud and negative charges at the bottom of it (Zhou and Tinsley, 2007). Quantifying the rate coefficients between available atmospheric ions and charged particles can thus inform models and understanding of cloud systems.

In this study, we report measurements of the rate coefficients between ions and charged small (<10 nm) aerosol particles containing up to 9 elementary charges, e, of opposite charge. Such highly overcharged particles below 10 nm are extremely rare in the atmosphere, but they provide an important and sensitive constraint for theory. Knowledge of ion–aerosol rate coefficients is important to infer the particle steady-state charge distribution and to model the dynamics of aerosol populations. In particular, the particle steady-state charge distribution is essential for mobility-based size distribution measurements, for example when using differential mobility analysers (Kangasluoma and Kontkanen, 2017; Zeleny, 1900; Winklmayr et al., 1991; Flagan, 1998). To estimate the rate coefficients under atmospheric conditions, theoretical models based on first principles are often used. Chief amongst the current paradigms to estimate the charge-enhanced collisions are models based on the limiting-sphere model as detailed (and extended) by López-Yglesias and Flagan (2013) and references therein (e.g. Fuchs, 1963; Hoppel and Frick, 1986). In the limiting-sphere model, the motion between particles that are far from each is described by continuum mechanics, but within a limiting-sphere radius, their motion is described by free molecular mechanics; at the limiting-sphere radius, both motion fluxes are set to be equal.

An alternative approach to limiting-sphere models includes calculations based on mean first-time passage and dimensional analysis as discussed by Gopalakrishnan and Hogan (2012) and subsequent studies (e.g. Ouyang et al., 2012; Gopalakrishnan et al., 2013; Chahl and Gopalakrishnan, 2019; Suresh et al., 2021). Gopalakrishnan and Hogan (2012) question the validity of limiting-sphere models in the presence of potential interactions and argue their long-standing success is due to the fact that it “can be fit” to experimental data, but they do not necessarily “agree” with said data (Gopalakrishnan and Hogan, 2012). In their recent studies, Tamadate et al. (2020a, b) show that a hybrid modelling approach connecting the continuum regime (outside the limiting sphere) with molecular dynamics (MD; inside the limiting sphere) simulations can achieve good agreement with some laboratory experiments. Compared with limiting sphere simulations, continuum–MD simulations contain more detailed processes; chemical structures of the colliding entities are considered, as well as changes in translational, rotational, and vibrational degrees of freedom (Tamadate et al., 2020a, b).

Gatti and Kortshagen (2008) propose a linear combination of three regimes (continuum, molecular, and transition) to construct a simple analytical model of rate coefficients. By conducting MD simulations between particles of diameters 10–1000 nm and gas pressures 10⁻⁵–10⁵ Pa, Gatti and Kortshagen (2008) show that in the low- and high-pressure limits, results converge onto the limiting-sphere model and hydrodynamic (molecular) limit, respectively. In the transition regime, they find the limit-sphere model underpredicts the collision rates by up to 500 %. As such, the authors propose a weighted linear combination of the three regimes, accounting for three-body trapping in the transition regime. When using the proposed analytical model by Gatti and Kortshagen (2008), as reformulated by Gopalakrishnan and Hogan (2012), we find that it shows the best agreement with our experimental results presented in this study.

We measure the rate coefficients of singly charged ions with multiply charged aerosol particles under atmospheric conditions in the CERN CLOUD chamber. We use an electrospray aerosol generator to generate multiply charged particles of around 10 nm diameter carrying positive charges. The particles are exposed with an X-ray source for control experiments with singly charged and neutral particles. The evolution of most relevant properties of the particles are monitored with a comprehensive suite of instruments that continuously sample air from the CLOUD chamber. The positive charge on the particles gradually decays due to collisions with negative ions produced by galactic cosmic rays traversing the chamber. From our measurements, we derive the ion–aerosol rate coefficients for particles carrying up to nine positive charges.

Previously, experimentally determined ion–aerosol rate coefficients for multiply charged particles have been reported only for aerosol particles larger than 100 nm (e.g. Dépée et al., 2021). For particles smaller than 10 nm, only singly charged ion–ion recombination coefficients have been experimentally reported (Franchin et al., 2015). The collision rate of uncharged monomers with singly charged aerosol particles below 2 nm size has been measured by He et al. (2021). Owing to the dearth of experimental measurements for multiply charged particles, Tamadate et al. (2020a) compared their modelled coefficients with measured multiply charged PEG particles from an electrospray. To our knowledge, our study represents the first experimental measurement of ion–aerosol rate coefficients for multiply charged, small (< 10 nm) aerosol particles under atmospheric conditions. We compare our results to several theoretical predictions and find they are generally compatible while identifying some models that show excellent agreement.

Table 1 Parameter list.

2 Methods

The overall goal of the experiments herein is to infer the rate coefficients between negative atmospheric ions and positively overcharged small atmospheric aerosols. To achieve this, particles were produced using the CHARGE instrument (Sect. 2.1.2) and injected into the CERN CLOUD chamber (Sect. 2.1.1). A comprehensive suite of instruments (Sect. 2.1.4) is used to monitor particles and charge states through the experiment to constrain and infer (Sect. 2.2) the ion–charged aerosol rate coefficients.

2.1 Experimental approach

Our experimental approach follows the one documented by Dada et al. (2020). Below, we summarise key aspects of the overall experimental approach that are most relevant to the subject of this study. The reader is invited to find more details about the experimental setup in Dada et al. (2020).

2.1.1 CLOUD chamber

The Cosmic Leaving Outdoor Droplets (CLOUD) chamber at CERN is a 26.1 m³ stainless-steel container that enables aerosol experiments to be performed under atmospheric conditions with very low contaminant levels (Kirkby et al., 2011; Pfeifer et al., 2020). The chamber uses synthetic air from cryogenic nitrogen and oxygen (dilution flow rate during the experiments: 250 L min⁻¹). All parameters of the air in the chamber – such as temperature, relative humidity, UV light intensities, and trace vapours – can be controlled with high precision (Dias et al., 2017; Kupc et al., 2011). For experiments under neutral (uncharged) conditions, an electric field of around 20 kV m⁻¹ can be established with two electrodes, which sweeps ions from the chamber within 1 s. All experiments described here were carried out in dark conditions; that is, no UV lamps were switched on. The relative humidity was maintained at 80 % and ozone at 40 ppbv. The electrospray generator used a dilute sulfuric acid solution in water. No other trace gases were added during the experiments.

2.1.2 CHARGE instrument

We developed the CHarged AeRosol GEnerator (CHARGE) electrospray instrument to obtain multiply charged particles under atmospheric conditions. Electrospray is used in various research fields to enable the generation of singly and multiply charged particles (Sterling et al., 2011; Hogan and de la Mora, 2011; Marginean et al., 2008). By applying a strong voltage gradient at the tip of a capillary, a liquid solution emerging from the capillary is drawn into a so-called Taylor cone. Highly charged droplets stream from the tip of the Taylor cone. Once exposed to sub-saturated air, the charged droplets evaporate and shrink until the repulsive electrostatic force causes them to break up into several multiply charged smaller droplets (Rayleigh, 1882; Smith et al., 2002). Following López-Herrera et al. (2004), we used electrospray solutions consisting of sulfuric acid (0.02 wt. %) and purified water (0.98 wt. %) to generate positively charged particles using a positive voltage of 5200 V (Myhre et al., 1998; Kebarle and Verkerk, 2009). CHARGE incorporated an X-ray ion generator along the path of the charged particles. When switched on, this generated a highly concentrated bipolar ion distribution, thereby forcing the particles to their particle charge steady state. This way, multiply charged particles in one experiment could be directly compared to an otherwise identical experiment performed with a particle distribution in charge steady state, presumably containing neutral and singly charged particles.

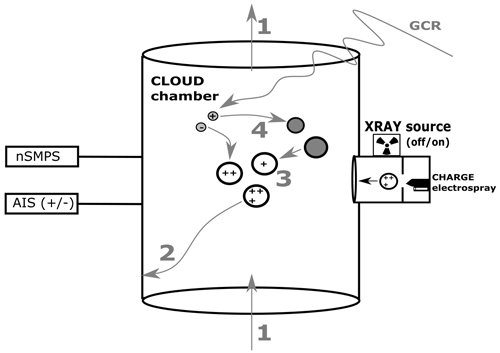
Figure 1 Schematic representation of the experimental measurements. Charged particles are produced by the CHARGE electrospray instrument (right). With the X-ray source switched off, charged particles enter the CLOUD chamber. With the X-ray source switched on, the particles are neutralised, i.e. have a steady-state charge distribution, before entering the CLOUD chamber. After an injection period of around 30 min, particle injection from CHARGE is switched off and the evolution of the particle charges during the “decay stage” is monitored by sampling instruments such as the nSMPS and AIS (left). The evolution of particle and ion charges in the chamber is analysed as a function of the production and loss terms: (1) dilution loss, (2) wall loss, (3) coagulation loss, and (4) collisions of aerosols with ions produced by galactic cosmic rays.

2.1.3 Experimental overview

Figure 1 shows a schematic representation of the experiments reported in this study. We performed two distinct experiments: with and without X-ray. All experiments started with the injection of particles to the chamber from CHARGE; the number of particles and their charge then decayed inside the chamber. During injection, we injected particles through a large-diameter tube (100 mm in diameter) at a high carrier flow rate of approximately 200 L min⁻¹. During the decay stage, we turned off all voltages and flows in CHARGE and observed the decay of the particle and ion distributions in the chamber. Since no more particles were added during this stage, the decay could be described by the production and loss terms shown in Fig. 1 and described in Sect. 2.2.3. Between experiments, we removed particles and ions by increasing the flow rate of the chamber and the fan speed as well as turning on the high-voltage electrode grids to remove any remaining charged particles and ions.

2.1.4 Instrumentation and measurements

Relative humidity was measured with a tunable diode laser system, TDL (Skrotzki, 2012). In addition, a chilled dew point mirror (Edgetech Instruments) was used to derive the relative humidity utilising water vapour pressure calculations (Murphy and Koop, 2005). An ozone monitor (Thermo Electron Corporation Model 49C) was used to measure the ozone concentrations. Sulfuric acid and gaseous compounds were measured with a nitrate chemical ionisation–atmospheric pressure interface–time-of-flight mass spectrometer, CI-APi-TOF (Kürten et al., 2014). The instrument was operated and calibrated following Kürten et al. (2012).

The total particle concentration (all charge states) was measured with a NanoScan Mobility Particle Sizer, nSMPS, TSI, Model 3936 (Lehtipalo et al., 2014; Tritscher et al., 2013; Wiedensohler et al., 2012). The concentrations were compared to the Scanning Mobility Particle Sizer (SMPS) results (Birmili et al., 1997; Wiedensohler, 1988). Total particle concentrations for diameters larger than 2.5 nm (i.e. integrated over sizes above 2.5 nm) were obtained with a particle size magnifier, PSM, and a condensation particle counter, CPC (Vanhanen et al., 2011; Liu et al., 2006).

Ion concentrations and the concentrations of charged particles with both polarities were measured with a Neutral cluster and Air Ion Spectrometer (NAIS). To increase time resolution during the experiments, the NAIS was only used to measure ions, that is, in “ion mode” (Manninen et al., 2009, 2016; Mirme and Mirme, 2013); as such, we refer to it as AIS (Air Ion Spectrometer) for the rest of this study. Measurements from AIS were also compared with measurements from a nano-radial differential mobility analyser (DMA) (Amanatidis et al., 2021).

To analyse the experiments, we primarily use data from the AIS (charged distribution) and from the nSMPS (total distribution). All data have been converted from the measured mobility diameter to mass diameter (Ku and de la Mora, 2009; Larriba et al., 2011). A comparable setup for chamber measurements of particle and ion distributions is described in more detail by Dada et al. (2020).

2.2 Data analysis

2.2.1 AIS inversion

The AIS instrument is based on the design of electrical aerosol spectrometers (e.g. Flagan, 1998; Mirme et al., 2007). The mobility analyser consists of multiple electrode rings to measure a differential ion distribution. Two analysers are arranged in parallel with different polarities, where the sample flow (54 L min⁻¹) is split. This allows measuring particle distributions of positive and negative polarity in parallel. While the instrument can also measure neutral particles by first filtering natural ions (using an electric field) and afterwards charging the remaining neutral particles (with a corona needle), only charged particles were measured in our experiments; as such, the ion filter and the corona needle were switched off. The AIS version used in our experiments has 25 electrode channels. It is capable of measuring charged particles, cluster ions, and small ions in the mobility range from 3.2 to 0.0013 cm² V⁻¹ s⁻¹ (Mirme and Mirme, 2013; Manninen et al., 2016).

We follow the inversion function presented by Mirme and Mirme (2013) in analysing the AIS measurements. However, we find that we need to adjust the approach in the case of multiply charged particles. First, we observed that the established (Mirme and Mirme, 2013) AIS inversion jumps suddenly during our experiments. However, we did not see this jump in the measured current of the differential AIS channels. Furthermore, as shown in the next paragraphs, we want to describe the AIS measurement as a linear combination of several lognormal distributions with charge number j. The original inversion function used squares of cosine functions as basis functions to obtain a mobility distribution from the measured current. Accordingly, the measured current of the AIS channels would ultimately be described by several squares of cosine distributions, which afterwards would be fitted using several lognormal distributions. It thus seems more natural for our measurements to use lognormal distributions to describe transfer functions instead, and it seems to be a more natural choice for log-normally distributed aerosol distributions. We additionally skip the Tikhonov regularisation previously employed (Tikhonov, 1963; Mirme and Mirme, 2013) as our updated inversion seems not to benefit from it.

The calculated current, I_calc, can be expressed as a product of the instrument apparatus matrix H and the lognormal distribution coefficients vector ϕ as I_calc=Hϕ (Mirme and Mirme, 2013; Manninen et al., 2016). The matrix H is determined through instrument calibration (Mirme and Mirme, 2013). In our case, ϕ is a vector of the coefficients of 25 individual lognormal distributions; that is, it is a vector of the total number concentrations of each one of them. These 25 distributions correspond to 25 AIS channels; the mean and standard deviation of each of the 25 distributions are calculated by fitting the matrix H to lognormal distributions but not supplanting it.

If we let the lognormal probability distribution function be ${\widehat{\mathrm{\Omega }}}_i$, then the full calculated distribution is $\mathrm{\Omega }={\sum }_{i=\mathrm{1}}^{\mathrm{25}}{\mathit{\varphi }}_i{\widehat{\mathrm{\Omega }}}_i$, where ϕ_i are the elements of ϕ, and Ω is the calculated total charged (negative or positive, Ω_±) distribution. We minimise the residuals between the calculated current (I_calc) and the measured current (I_meas) from AIS using nonlinear least squares, with 25 concentration coefficients as free parameters. We solve the nonlinear least squares computationally, and we do not supplement it with any regularisation technique. The procedure is repeated for each polarity separately; hence the resulting distributions are Ω_±. (More details are provided in Sect. 4 by Mirme and Mirme (2013) on the theoretical basis for H.)

A known limitation of the AIS is its inability to detect ions whose mobility diameter is lower than 0.82 nm (Manninen et al., 2016). To this end, we extrapolate the missing measurements by assuming the ion distribution follows a lognormal distribution even below 0.82 nm. This extension allows us to account for a wider distribution of available ions, especially where the expected value of collisions is higher (smaller ions collide at a higher rate with the same reference oppositely charged particle).

While we find our approach to be more useful with multiply charged particles than the standard procedure, it does not deviate significantly from the standard procedure by Mirme and Mirme (2013) under normal operating conditions. Compared to five randomly selected nucleation experiments conducted throughout the same CLOUD campaign, where no significant multiply charged particles are expected, we find a median of about 12 % deviation (over all mobilities) between our modified method and the original method.

2.2.2 Multi-charge inference

When operated in “ion mode” like in our case, the typical AIS inversion provides information directly only about singly charged particles (Manninen et al., 2016). However, we are interested in multiply charged particles which are briefly present away from steady state. To deduce information about multiply charged particles present in our experiments from the total charged distributions from Sect. 2.2.1 (Ω_±), we identify a time when the steady-state assumptions are expected to hold: we postulate this happens at the end of the decay stage when the ratio of the positive and negative concentrations tends to be unity. Once in steady state after interacting with ions produced from galactic cosmic rays (GCRs), it is reasonable to assume that all multiply charged particles have been neutralised due to collisions with ions of opposite polarity.

At the end of the decay stage, t=t_end, we set the concentration of singly charged positive particles to be the same as the inferred concentration from the AIS in Sect. 2.2.1; that is, as ${\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t=t_{\mathrm{end}}\right)={\mathrm{\Omega }}_{-}\left(d_{\mathrm{p}};t=t_{\mathrm{end}}\right)$, we assume all of particles in ${\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t=t_{\mathrm{end}}\right)$ are singly (positively) charged. Our goal is to then estimate ${\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t<t_{\mathrm{end}}\right)$ as a combination of multiply charged distributions as in Eq. (1), where γ_j are free parameters that determine the total number of particles of a given charge state j and $\widehat{\mathit{\omega }}$ is the density function for each charging state. We further assume the dynamic evolution of ${\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t\right)$ can be described as a first-order loss process (to walls and dilution) as the charges themselves are simply redistributed among charging states. For ease of presentation, we set ${\mathit{\omega }}_j={\mathit{\gamma }}_j{\widehat{\mathit{\omega }}}_j$ after this section.

$$\begin{array}{}\text{(1)}& {\mathrm{\Omega }}_{+}\left(t\right)={\sum }_{j=\mathrm{1}}^{\mathrm{9}}{\mathit{\gamma }}_j{\widehat{\mathit{\omega }}}_j={\sum }_{j=\mathrm{1}}^{\mathrm{9}}{\mathit{\omega }}_j\end{array}$$

We assume the probability density function ${\widehat{\mathit{\omega }}}_{\mathrm{1}}$ has the same shape as ${\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t=t_{\mathrm{end}}\right)$ as in Eq. (2) after accounting for wall, dilution, and coagulation losses. While coagulation can play a role in the shape of the distribution ${\widehat{\mathit{\omega }}}_{\mathrm{1}}$, wall loss and dilution loss are clearly dominant in our experiments (see Fig. 2).

$$\begin{array}{}\text{(2)}& {\widehat{\mathit{\omega }}}_{\mathrm{1}}={\displaystyle \frac{{\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t_{\mathrm{end}}\right)}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t_{\mathrm{end}}\right)\mathrm{d}\ln d_{\mathrm{p}}}}\end{array}$$

At the end of the decay stage, ${\mathit{\gamma }}_{\mathrm{1}}={\int }_{\mathrm{0}}^{\mathrm{\infty }}{\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t_{\mathrm{end}}\right)\mathrm{d}\ln d_{\mathrm{p}}$ and ${\mathit{\gamma }}_{j\ne \mathrm{1}}=\mathrm{0}$ by definition. Since ${\widehat{\mathit{\omega }}}_{\mathrm{1}}$ is now known, we can estimate ${\widehat{\mathit{\omega }}}_j$ using the Millikan equation relating electric mobility, charge number, and particle diameter (Lehtinen and Kulmala, 2003; Mirme and Mirme, 2013; Manninen et al., 2016). For the same electric mobility Z_p, different pairs of charge number j and particle diameter d_p are linked through Eq. (3) assuming constant viscosity η and elementary charge constant q (C_c is the Cunningham's slip correction factor which depends on size). We use Eq. (3) to estimate ${\widehat{\mathit{\omega }}}_j$ by shifting ${\widehat{\mathit{\omega }}}_{\mathrm{1}}$ in diameter, holding everything else constant.

$$\begin{array}{}\text{(3)}& Z_{\mathrm{p}}={\displaystyle \frac{jq{C}_{\mathrm{c}}\left(d_{\mathrm{p}}\right)}{\mathrm{3}\mathit{\pi }\mathit{\eta }{d}_{\mathrm{p}}}}\end{array}$$

We finally add one correction to ω_j. As the AIS uses the electric mobility diameter, multiply charged particles will be detected at higher mobilities than their singly charged counterparts. And since they carry more charges, the measured current will be higher. Thus, we divide each ω_j by its charge state j and we use the mobility diameter throughout our calculations as retrieved by Eq. (3). All in all, ω_j can be expressed as in Eq. (4) as a size- and time-dependent function of γ_j, the positive charge concentration Ω₊, and a loss constant k_loss related to particle losses wall, dilution, and coagulation.

$$\begin{array}{}\text{(4)}& {\mathit{\omega }}_j\left(t\right)={\displaystyle \frac{{\mathit{\gamma }}_j}{{\sum }_{j=\mathrm{1}}^{\mathrm{11}}{\mathit{\gamma }}_j}}{\mathrm{\Omega }}_{+}\left(d_{\mathrm{p}};t\right)e^{-k_{\mathrm{loss}}t}\end{array}$$

We note that in estimating ω_j in Eq. (4), we assume measurements below 2 nm electric mobility diameter are singly charged or neutral as most entities present below 2 nm can be safely considered ions whose concentration is accounted for in Ω_± from, Sect. 2.2.1. Moreover, we simplify our calculation by assuming all measurements above 10 nm electric mobility diameter to be at most singly charged as well. We are able to make these two assumptions because the CHARGE instrument produces particles of sizes around 6 nm electric mobility diameter. Consequently, the total number concentration decreases significantly above 10 nm and below 2 nm, and so does the ratio of multiply charged particles in it as well, and the timescale of neutralisation (i.e. timescale to reaching particle charge steady state) for particles bigger than 10 nm is significantly faster than for smaller ones. While the limits of this interval are arbitrary, their values are allowed to vary within a range of ±50 % in the error estimation calculation as discussed in the Supplement.

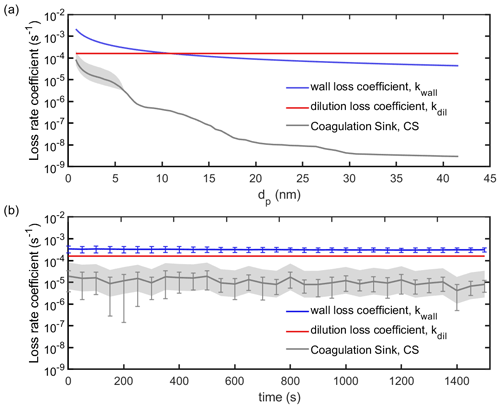
Figure 2 Summary of the particle loss rates during the decay stage. (a) Size dependency of the loss rates for a distribution (ω_j) during a decay stage (averaged over an entire decay period). (b) The loss rates due to different processes for a given distribution ω_j as a function of time during a decay stage. The grey bands indicate uncertainty ranges resulting from errors on measurements of the total particle number concentrations below 6 nm. We assume generous (±400 %) errors since instruments can vary widely at small particle sizes (Kangasluoma et al., 2020).

2.2.3 Population balance

We derive the ion–aerosol rate coefficients from data collected during the decay stage. Since the CHARGE instrument produces and injects particles at high flow rate (200 L min⁻¹), the flow rates in the CLOUD chamber are not balanced immediately after an injection stage. Thus, the decay stage starts as soon as the flow inside the chamber is in steady state, which can be estimated from the flow rates exiting the chamber and from the overpressure inside the CLOUD chamber. We account for the production and loss terms of all the particles and ions inside the chamber as a function of time. After injection, particles and ions in the chamber dynamically evolve in time due to several processes, related to chamber dilution, wall processes, aerosol–aerosol collisions, and ion–aerosol collisions. The individual loss rates and their time dependence during our experiments are summarised in Fig. 2.

In the CLOUD chamber during these experiments, the dilution rate coefficient, k_dil, was constant at $\mathrm{1.60}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, which is the result from dividing the volume flow rate (250 L min⁻¹) by the total volume (26.1 m³) (e.g. Simon et al., 2016; Pfeifer et al., 2020). The chamber wall loss rate coefficient is calculated using $k_{\mathrm{wall}}=C_{\mathrm{wall}}\sqrt{D_{\mathrm{p}}}$, where D_p is the particle diffusion coefficient and C_wall is a proportionality constant whose value has been measured as $\mathrm{7.70}\times {\mathrm{10}}^{-\mathrm{3}}$ cm⁻¹ s${}^{-\mathrm{1}/\mathrm{2}}$ based on wall loss of sulfuric acid vapour (Metzger et al., 2010; Ehrhart et al., 2016; Stolzenburg et al., 2020; He et al., 2021). For the collisions involving at least one neutral aerosol particle, we follow Seinfeld and Pandis (2016) to estimate the coagulation rate coefficient, K, between neutral particles and thus the coagulation sink, CS. We account for the effects of charges on coagulation in the calculation of β in the following paragraphs.

The main goal of our experiment is to quantify the ion–charged aerosol rate coefficients, which play a role in the dynamic evolution of the particle size distribution and particle charge distribution. More precisely, we estimate the rate coefficients, ${\mathit{\beta }}_j={\mathit{\beta }}_{-,j}$, between the negative ion distribution (<2 nm) and the particle distribution (2–10 nm) with j positive charges. By setting up the balance equations, we track the number and charge evolution over time and thus constrain β_j(d_p).

Beyond these terms, we assume sources and sinks related to evaporation, condensation, and nucleation are negligible in our experiments. At 80 % relative humidity and 278 K, the evaporation of sulfuric acid is negligible (Stolzenburg et al., 2020). We assume the growth rates of particles in our experiment are on the order of 1.8 nm h⁻¹ as those reported for sulfuric acid–water systems (Nieminen et al., 2010). These growth rates are too small to influence the dynamics herein, especially compared with the duration of the experiments (at most 1500 s). Using parameterisations for the sulfuric acid–water system from Vehkamäki et al. (2002), we calculate nucleation rates of about $\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{8}}$ cm⁻³ s⁻¹ for the measured sulfuric acid concentrations (about 5×10⁷ cm⁻³ in the beginning of a decay and during injection), which is negligible (Vehkamäki et al., 2002; Dunne et al., 2016). We assume particles produced inside the chamber during the experiments consist of sulfuric acid and water with a uniform density of 1600 kg m⁻³ (Myhre et al., 1998). (The robustness of these assumptions is verified in the Supplement, where we randomly vary all parameters. For example, the density is varied between that of pure water (997 kg m⁻³) and that of pure sulfuric acid (1830 kg m⁻³), finding negligible sensitivity of the assumption herein.)

From Sect. 2.2.2, using AIS measurements, we obtain Ω_± as a distribution over sizes 0.2–40 nm of diameters and ω_j as a distribution over sizes 2–40 nm of diameters. We also infer Ω₀, which is the distribution of neutral entities over sizes 2–40 nm of diameters by combining AIS and nSMPS measurements. We can thus write the balance equations for the positively charged particles compactly in Eq. (6), which is valid for $\mathrm{1}<j<\mathrm{9}$. However, because of the size dependence of Ω and ω, we introduce a coefficient σ to account for the size dependency normalised by its value at the lowest size (ion size). That is, σ is unity at the ion size (1 nm diameter) and it is less than unity for bigger sizes. This formulation yields β for the ion–aerosol coefficients while still accounting for events including charged particles and ions in the rest of distribution that are ignored earlier in using K. We use the coulombic enhancement coefficient to calculate σ following Seinfeld and Pandis (2016; p. 564, Eq. 13A.16), with d_p1 and d_p2 referring to the sizes of coagulating particles in nm in Eq. (5).

$$\begin{array}{}\text{(5)}& {\displaystyle }\begin{array}{rl}& {\stackrel{\mathrm{ˇ}}{\mathit{\sigma }}}_j\left(d_{\mathrm{p}\mathrm{1}},d_{\mathrm{p}\mathrm{2}}\right)=-{\displaystyle \frac{j}{d_{\mathrm{p}\mathrm{1}}+d_{\mathrm{p}\mathrm{2}}}}{\displaystyle \frac{\mathrm{1}}{\exp \left(-\frac{j}{d_{\mathrm{p}\mathrm{1}}+d_{\mathrm{p}\mathrm{2}}}\right)-\mathrm{1}}};\\ & {\mathit{\sigma }}_j={\displaystyle \frac{{\stackrel{\mathrm{ˇ}}{\mathit{\sigma }}}_j\left(d_{\mathrm{p}\mathrm{1}},d_{\mathrm{p}\mathrm{2}}\right)}{{\stackrel{\mathrm{ˇ}}{\mathit{\sigma }}}_j\left(d_{\mathrm{p}\mathrm{1}}=\mathrm{1}\mathrm{nm},d_{\mathrm{p}\mathrm{2}}\right)}}\end{array}\text{(6)}& {\displaystyle \frac{d{\mathit{\omega }}_j}{\mathrm{d}t}}={\mathit{\sigma }}_{j+\mathrm{1}}{\mathit{\beta }}_{j+\mathrm{1}}{\mathrm{\Omega }}_{-}{\mathit{\omega }}_{j+\mathrm{1}}-{\mathit{\sigma }}_j{\mathit{\beta }}_j{\mathrm{\Omega }}_{-}{\mathit{\omega }}_j-L_j\end{array}$$

In Eq. (6), the positively charged size distribution ω at each charge state j evolves in time due to production and loss. On the right-hand side, the first term denotes the gain of a particle of charge j as a result of a coagulation event between a particle of charge j+1 of concentration ω_j+1 and a negative ion of concentration Ω₋. The second term denotes the loss of a particle of charge j and of concentration ω_j as it collides with a negative ion of concentration Ω₋. The third term lumps all other losses, which are to the wall, dilution, and coagulation sink (CS; including in-distribution losses, that is, coagulation within the distribution of particles of diameters 2–10 nm) as shown in Eq. (7).

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{L}_j& ={\mathit{\omega }}_j\left(k_{\mathrm{wall}}+k_{\mathrm{dil}}+\mathrm{CS}\right)\\ & ={\mathit{\omega }}_j\left(k_{\mathrm{wall}}+k_{\mathrm{dil}}\right)+{\mathit{\omega }}_j{\sum }_l{K}_l{\mathit{\omega }}_l\end{array}\end{array}$$

To complete the description in Eq. (6), we use Eqs. (8) and (9) for the cases j=1 and j=9, respectively. In Eq. (8), we use β₀ to denote collision coefficient between positive small ions Ω₊ (d_p<2 nm) and neutral particles Ω₀ inferred from the NAIS and nSMPS measurements. As such, β₀ is calculated in the same way K_l in Eq. (7) is calculated, following Seinfeld and Pandis (2016).

$$\begin{array}{}\text{(8)}& {\displaystyle }\begin{array}{rl}j=\mathrm{1};& {\displaystyle \frac{\mathrm{d}{\mathit{\omega }}_j}{\mathrm{d}t}}={\mathit{\beta }}_{\mathrm{0}}{\mathrm{\Omega }}_{+}{\mathrm{\Omega }}_{\mathrm{0}}+{\mathit{\sigma }}_{j+\mathrm{1}}{\mathit{\beta }}_{j+\mathrm{1}}{\mathrm{\Omega }}_{-}{\mathit{\omega }}_{j+\mathrm{1}}\\ & -{\mathit{\sigma }}_j{\mathit{\beta }}_j{\mathrm{\Omega }}_{-}{\mathit{\omega }}_j-L_j=K{\mathrm{\Omega }}_{+}{\mathrm{\Omega }}_{\mathrm{0}}\\ & +{\mathit{\sigma }}_{j+\mathrm{1}}{\mathit{\beta }}_{j+\mathrm{1}}{\mathrm{\Omega }}_{-}{\mathit{\omega }}_{j+\mathrm{1}}-{\mathit{\sigma }}_j{\mathit{\beta }}_j{\mathrm{\Omega }}_{-}{\mathit{\omega }}_j-L_j\end{array}\text{(9)}& {\displaystyle }j=\mathrm{9};{\displaystyle \frac{\mathrm{d}{\mathit{\omega }}_j}{\mathrm{d}t}}=-{\mathit{\beta }}_j{\mathrm{\Omega }}_{-}{\mathit{\omega }}_j-L_j\end{array}$$

The system of equations (Eqs. 6, 7, and 8) is solved numerically for each time step during the decay stage. One time step corresponds to the duty cycle of the AIS (50 s), and the nSMPS measurement is synchronised to this time step using linear interpolation. Accordingly, for each charge number j, there exists one solution for each cycle of 50 s, where the calculation is only solved within the respective lifetime of each ω_i. The lifetime is determined using an exponential fit through the time evolution of each ω_i. For example, j=9 with an estimated lifetime of 200 s yields four measurements (one each 50 s) and thus four coefficients are calculated for this charge number in this specific experiment. For smaller j, the lifetime increases and, thus, more coefficients are calculated per experiment.

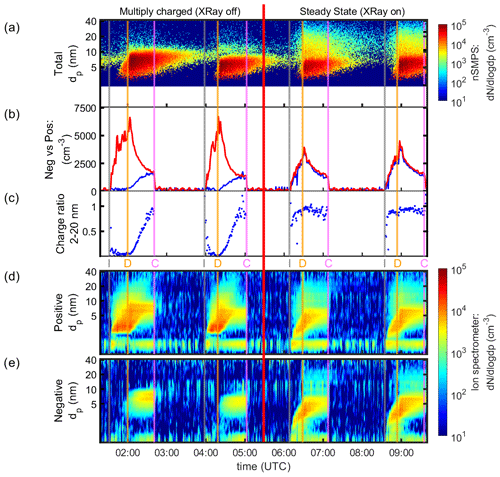
Figure 3 Example experiments performed without and with charge neutralisation by X-rays. Time series showing two experiments with X-ray off followed by two experiments with X-ray on (separated by the red vertical line). The grey vertical line marks the beginning of an injection stage (I), the orange line a decay stage (D), and the pink line a cleaning stage (C). The panels show the time series of (a) particle size distributions measured with a nSMPS, (b) number concentrations of positive (red) and negative (blue) charged particles, (c) negative : positive charged particle ratio, and (d) positive and (e) negative charged particle apparent size distributions measured with an AIS. Here the apparent size incorrectly assumes singly charged particles.

3 Results

In Fig. 3, we show a time series of two experiments with X-ray off and two with X-ray on. A total of four experiments without X-ray and two with X-ray were conducted to ensure reproducible results. As detailed in Sect. 2.1, particle measurements were carried out with an NAIS (Manninen et al., 2016, 2009) and an SMPS (Tritscher et al., 2013) for the total particle concentration. Gas phase concentrations were measured using several mass spectrometers (Kürten et al., 2011, 2012; Breitenlechner et al., 2017; Wang et al., 2021). We calculate the ion–aerosol rate coefficients during the decay stage starting as soon as the chamber flow is in steady state after injection. We note that the negative and position ion distributions in panel (b) approach are similar to the canonical value of 1500 cm⁻³ often reported for ion concentrations in the atmosphere. More precisely, the concentration of positive ions averages around 1500 cm⁻³, while the negative ions average around 1350 cm⁻³, agreeing with previous studies showing the concentration of negative ions is often lower (Franchin et al., 2015).

With the X-ray off, we observe almost no negative ions during injection. Negative ions are entirely consumed by ion–ion recombination and ion–aerosol attachment as there is a significant amount of positive charge available during injection via the positively charged particles formed. However, we observe an increase in the number of negative ions during the decay stage, which can only come from ion–aerosol attachment of (singly charged) negative ions with (neutral) particles.

With the X-ray on, we observe that the ratio between positively to negatively charged particles is almost unity. This indicates that the X-ray source effectively pushes a large fraction of particles to its steady-state particle charge distribution. Thus, it seems natural that we can assume that all particles carry at most j=1 charges during experiments with the X-ray on. However, when assuming steady-state charge distribution with a maximum of one charge (j=1), our calculations result in systematically smaller coefficients during the experiments with the X-ray on compared to the experiments with the X-ray off. This implies that there is an additional source term in the case of experiments with the X-ray on. Since the particles from the CHARGE electrospray generator pass the X-ray source at a flow rate of 200 L min⁻¹, it is plausible to assume that a few particles are still doubly charged in the beginning of the decay stages. For these experiments, we therefore calculate rate coefficients twice: once assuming charge steady state (maximum j=1 charges) and once including a small fraction of doubly charged particles, that is, assuming singly : doubly charged ratio of 5:1 at the beginning of the decay stage. The latter assumption is further justified by the presence of the seemingly larger particles in the steady-state cases; the nSMPS inversion algorithm assumes at most singly charged particles after passing the particles through the nSMPS's neutraliser and compensates for this seemingly erroneous assumption by counting multiply charged particles as larger particles. We show the charge fraction of positively charged particles in the first experiment in Figs. 3 and S4.

The total distribution is similar in both experiments in Fig. 3, and observed deviations in the size distributions between NAIS and nSMPS are within the expected range from other measurements (Kangasluoma et al., 2020). During both experiments, as expected, a significant fraction of the particle distribution is neutral (approximately 98 %). SMPS measurements are subject to measurement errors especially below 6 nm (Kangasluoma et al., 2020); however, during our experiments, the influence of the measured total particle concentration on the calculation of the rate coefficients is relatively small, since wall loss and dilution loss dominate (see Fig. 2). Further, the influence of varying the concentrations measured by the SMPS within the estimated error range is also discussed in the Supplement and shown in Fig. S3.

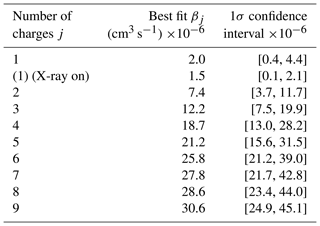
Figure 4 summarises the calculated rate coefficients from our experiments. The error bars indicate the 1σ confidence interval of numerical solutions from all experiments (for all time steps) for the respective charge number j. The calculations are carried out for maximum j=11 charges, with the assumptions summarised in Sect. 2. To calculate the “best fit” values from all our data, we use an exponential fit through the respective experiments, which is solved using nonlinear least squares. It is based on the same production and loss rates as in case of the numerical solution in Sect. 2.2.3. In contrast to the numerical solution, steady-state conditions are assumed in the case of this fit, except for ion–aerosol collisions. As such, we take time-averaged values for various coefficients in Eq. (10). As an example, for j=1 charge, the approximation by the fit is described following Eq. (8) by Eq. (10) below.

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\mathit{\omega }}_j\left(t\right)& ={\mathit{\omega }}_{j,t=\mathrm{0}}\exp \left(-\left(\stackrel{\mathrm{‾}}{k_{\mathrm{wall}}+k_{\mathrm{dil}}+\text{CS}}-{\displaystyle \frac{\stackrel{\mathrm{‾}}{{\mathit{\beta }}_{\mathrm{0}}{\mathrm{\Omega }}_{+}{\mathrm{\Omega }}_{\mathrm{0}}}}{\stackrel{\mathrm{‾}}{{\mathrm{\Omega }}_{+}}}}\right.\right.\\ & \left.\left.+{\mathit{\beta }}_j{\mathit{\sigma }}_i{\mathrm{\Omega }}_{-}-{\displaystyle \frac{{\mathit{\beta }}_{j+\mathrm{1}}{\mathit{\sigma }}_{j+\mathrm{1}}{\mathrm{\Omega }}_{-}{\mathit{\omega }}_{j+\mathrm{1}}}{{\mathit{\omega }}_j}}\right)t\right)+{\mathit{\omega }}_{j,\mathrm{\infty }}\end{array}\end{array}$$

In Eq. (10), ω_j, ∞ denotes instrumental background at the end of the decay stage and ${\mathit{\omega }}_{j,t=\mathrm{0}}$ is the concentration at the beginning of the decay stage. The best fit of the numerical solution and the 1σ confidence interval are summarised in Table 1. In Fig. 4, we compare our measurements with leading representative models and with the MD simulations from Tamadate et al. (2020a). Our results confirm the robustness of the selected models calculating the ion–aerosol rate coefficient (López-Yglesias and Flagan, 2013; Gopalakrishnan and Hogan, 2012; Gatti and Kortshagen, 2008; D'yachkov et al., 2007), which we calculate using the Particula software package, version 0.0.10 (Mahfouz et al., 2022). In particular, we find the results by Gatti and Kortshagen (2008) and López-Yglesias and Flagan (2013) to be most compatible with our experimental estimation.

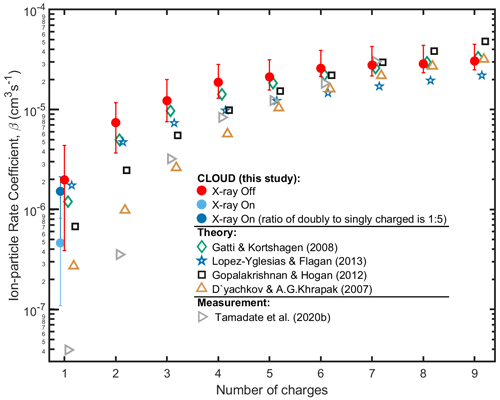
Figure 4 Ion–particle rate coefficients versus number of charges on the particle. The CLOUD measurements are indicated by filled circles that are coloured red for X-ray off experiments, blue for X-ray on experiments assuming full steady-state ion distributions, and cyan for X-ray on and assuming incomplete steady-state ion distributions. Theoretical predictions based on the limiting-sphere paradigm and Langevin dynamics are shown in open symbols for 1 nm negative ions colliding with positively charged particles of 6 nm diameter. Recent results for multiply charged PEG₄₆₀₀ particles with ions are shown in grey triangles (Tamadate et al., 2020a). The symbols are offset from integer charges to improve their visibility.

Table 2 Experimentally inferred ion–aerosol rate coefficients.

4 Discussion

In general, we find the limiting-sphere model by López-Yglesias and Flagan (2013) and linear combination of models by Gatti and Kortshagen (2008) to best represent our experimentally determined rate coefficients. It is imperative to note that while the approach based on the limiting sphere is fine-tuned to atmospheric applications (meaning parameterised for atmospheric ions and conditions), the approaches based on mean first-time passage and dimensional analysis (e.g. ones by Gopalakrishnan and Hogan, 2012, and others following it) are more general. This could explain the discrepancy – in other words, adjusting the input parameters of the latter approach could lead to a better fit with our data. Notwithstanding this discrepancy, the results from all theoretical models point to similar trajectory. Our results most resemble the analytical model by Gatti and Kortshagen (2008) as reformulated by Gopalakrishnan and Hogan (2012). In their model, a linear combination of continuum, free molecular, and transition regimes is used to describe collisions of nanoparticles in plasmas.

We compare our results to recent results based on continuum–MD simulations (Tamadate et al., 2020a), which are for multiply charged PEG₄₆₀₀ particles with ions. Our results align well with previous models (López-Yglesias and Flagan, 2013; Gopalakrishnan and Hogan, 2012; Gatti and Kortshagen, 2008; D'yachkov et al., 2007). Additionally, our results align with all models, including the additional one by Tamadate et al. (2020a), for >5 charges where the effect of charge likely outweigh the effects of geometry. Nonetheless, we find our results deviate from those by Tamadate et al. (2020a) especially for a low number of charges (<5). This could be explained by the geometry (and thus size) of the simulated PEG₄₆₀₀ particles. Moreover, the flexible nature of the ions and particles in their study likely plays a central role and cannot be compared directly to our results herein.

The primary implication of our results here is providing an experimental basis for model calculations of the ion–aerosol rate coefficient. In so doing, this enables researchers to implement and tune model calculations more readily like those based on the limiting sphere or Langevin dynamics approaches cited earlier. This eventually provides further evidence in constraining the cosmic galactic rays' role in climate change. While availability of ions generated by cosmic rays can influence new-particle formation and growth to an extent, their influence is dampened by the fact that charged particles are more readily scavenged by existing bigger particles (Mahfouz and Donahue, 2021a). In the limit, this scavenging rate is doubled, and the probability of survival is thus squared (Mahfouz and Donahue, 2021a, b). However, questions remain open regarding ion–aerosol interactions in scenarios close to aerosol–cloud interactions and the subsequent interactions between ions and climate variability (e.g. Guo and Xue, 2021; Tinsley, 2022). Furthermore, the comparison with the results by Tamadate et al. (2020a) shows that future studies will need to focus on the dependency of parameters kept constant in this study, for example, relative humidity, chemical composition, and turbulence. This experimental procedure will enable further exploration and experimental evidence in resolving these questions, e.g. in designing and building experiments in cloud chambers.

5 Summary

In this study, we present novel experiments to calculate ion–aerosol rate coefficients under atmospherically relevant conditions in the CERN CLOUD chamber. After assessing the robustness of our calculations, we test our experimentally inferred results against those predicted by leading models. We find overall agreement with the selected models, but especially with one employing a linear combination of limiting behaviours across regimes (Gatti and Kortshagen, 2008). This study, and follow-up experiments, will help constrain charge-related dynamics affecting atmospheric particles, which can play an important role in the formation and growth of particles as well as the subsequent dynamics in thunderstorm and non-thunderstorm clouds.