the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Size-dependent hygroscopicity of levoglucosan and D-glucose aerosol nanoparticles
Ting Lei
Nan Ma
Ulrich Pöschl
Alfred Wiedensohler
The interaction between water vapor and aerosol nanoparticles is important in atmospheric processes. Hygroscopicity of sub-10 nm organic nanoparticles and their concentration-dependent thermodynamic properties (e.g., water activity) in the highly supersaturated concentration range are, however, scarcely available. Here we investigate the size dependence of hygroscopicity of organics (i.e., levoglucosan, D-glucose) in dry particle diameter down to 6 nm using a nano-hygroscopicity tandem differential mobility analyzer (nano-HTDMA). Our results show that there is only weak size-dependent hygroscopic growth of both levoglucosan and D-glucose nanoparticles with diameters down to 20 nm. In the diameter range smaller than 20 nm (down to 6 nm), we observed strong size-dependent hygroscopic growth for D-glucose nanoparticles. The hygroscopic growth factors cannot be determined for levoglucosan below 20 nm due to its evaporation. In addition, we compare hygroscopicity measurements for levoglucosan and D-glucose nanoparticles with E-AIM (standard UNIFAC – functional group activity coefficients), the ideal solution theory, and differential Köhler analysis (DKA) predictions. The ideal solution theory describes the measured hygroscopic growth factors of levoglucosan with diameters down to 20 nm and D-glucose nanoparticles with diameters larger than 60 nm, while E-AIM (standard UNIFAC) can successfully predict the growth factors of D-glucose nanoparticles with diameters from 100 down to 6 nm at RH above 88 %–40 % (e.g., at RH above 88 % for 100 nm D-glucose, at RH above 40 % for 6 nm D-glucose). The use of the DKA method leads to good agreement with measured hygroscopic growth factors of D-glucose aerosol nanoparticles with diameters from 100 down to 6 nm. Predicted water activity for these aqueous organic solutions (i.e., levoglucosan, D-glucose) from different parameterization methods agrees well with observations in the low solute concentration range (< 20 mol kg−1) and starts to deviate from observations in the high solute concentration (> 20 mol kg−1).
- Article
(2519 KB) - Full-text XML
-
Supplement
(609 KB) - BibTeX
- EndNote
Organic aerosol nanoparticles play an important role in new particle formation, subsequent condensation and coagulation growth, cloud condensation nuclei (CCN), and thus in affecting visibility degradation, radiative forcing, and climate (Chylek and Coakley, 1974; Charlson et al., 1992; Dusek et al., 2010; Cheng et al., 2012; Zhang et al., 2012; Kulmala et al., 2013). Both growth of nanoparticles and their ability to act as CCN are directly related to the hygroscopicity that describes the interaction between organic nanoparticles and water vapor (Köhler, 1936; Kreidenweis et al., 2005; Su et al., 2010; Cheng et al., 2015; Wang et al., 2015). However, current knowledge of the hygroscopicity of sub-10 nm organic nanoparticles and their concentration-dependent thermodynamic properties (e.g., water activity) in the highly supersaturated concentration range is scarcely available.
Levoglucosan aerosol nanoparticles have attracted increasing interest in recent years (Simoneit et al., 1999; Mochida and Kawamura, 2004; Mikhailov et al., 2009; Elias et al., 2010; Lei et al., 2014, 2018; Bhattarai et al., 2019) and are considered an ideal tracer for characterization and quantification of biomass burning (Fraser and Lakshmanan, 2000). Also, levoglucosan is typically the most abundant species in wood-burning aerosols, which substantially contributes (16.6 %–30.9 % by mass) to the total organics in PM2.5 (Mochida and Kawamura, 2004; Bhattarai et al., 2019). D-glucose, a hydrolysis product of cellulose and levoglucosan, is a major pyrolysis product of wood (Mochida and Kawamura, 2004; Bhattarai et al., 2019; Mikhailov and Vlasenko, 2020). Hygroscopicity of levoglucosan and D-glucose substances is thus important in reproducing the overall hygroscopic behavior of the real biomass burning aerosol particles (Bhandari and Bareyre, 2003; Mochida and Kawamura, 2004; Chan et al., 2005; Koehler et al., 2006; Peng et al., 2010; Mikhailov and Vlasenko, 2020). For example, a small difference in the hygroscopicity parameter (κ) is observed between measured data for model mixtures including levoglucosan and ammonium sulfate in the laboratory using the hygroscopicity tandem differential mobility analyzer (HTDMA) and biomass burning aerosol particles in the field using CCN activity measurement due to the similar O : C ratios of levoglucosan and ammonium sulfate mass fractions used in model mixtures when experimental κ data from sub- and supersaturated water vapor conditions are compared (Bhandari and Bareyre, 2003; Mochida and Kawamura, 2004; Chan et al., 2005; Koehler et al., 2006; Peng et al., 2010; Pöhlker et al., 2016; Lei et al., 2018; Mikhailov and Vlasenko, 2020). Most previous lab studies have focused on investigation of the hygroscopic behavior of 100 nm levoglucosan and D-glucose aerosol nanoparticles, which mainly utilized humidified tandem differential mobility analyzers (DMAs) (Mikhailov et al., 2004; Mochida and Kawamura, 2004; Koehler et al., 2006; Lei et al., 2014, 2018). For example, Mochida and Kawamura (2004) observed that 100 nm levoglucosan and D-glucose aerosol nanoparticles uptake and release water continuously in both deliquescence and efflorescence modes, respectively. To our knowledge, there are no phase transitions for these organic aerosol nanoparticles in deliquescence or efflorescence processes.
Early studies showed that the hygroscopicity and solubility of inorganic aerosols, such as ammonium sulfate (AS) and sodium chloride (NaCl), exhibited a strong size dependence (Cheng et al., 2015). Firstly, hygroscopic diameter growth factors of AS, NaCl, and Na2SO4 nanoparticles are found to decrease with size decreases in both deliquescence and efflorescence modes (Biskos et al., 2006a, b, c; Lei et al., 2020). Secondly, there is no significant difference in the deliquescence relative humidity (DRH) or the efflorescence relative humidity (ERH) between AS nanoparticles with dry diameters of 6 and 60 nm (Biskos et al., 2006b; Lei et al., 2020), while a pronounced size dependence of the DRH of NaCl is up to 10 % RH between dry diameters of 6 and 60 nm (Biskos et al., 2006a). The behaviors of change of phase transition RH and concentrations of Na2SO4 are between NaCl and AS (Lei et al., 2020). However, there are very few lab studies investigating hygroscopicity (Gf, DRH, ERH) of organic aerosol nanoparticles in the sub-10 nm size range (Wang et al., 2017). It is not clear how the size effect influences the hygroscopic growth of organics, especially those without DRH and ERH. Besides technique limitation (Lei et al., 2020; Wang et al., 2017), another reason is the high diffusion of sub-100 nm organic nanoparticles, especially in the sub-10 nm size range, which results in nanoparticle losses in the HTDMA system (Seinfeld and Pandis, 2006).
Thermodynamic models are widely used to predict the hygroscopic growth factor of organic aerosol particles as a function of RH (Bhandari and Bareyre, 2003; Chan et al., 2005; Koehler et al., 2006; Peng et al., 2010). The current thermodynamic models mainly rely on concentration-dependent thermodynamic data (such as water activity, liquid–vapor interfacial energy), which are often derived from the measurements of large droplets and/or bulk solution (Tang and Munkelwitz, 1994; Tang 1996; Pruppacher and Klett, 1997; Clegg et al., 1998). Nanodroplets can become more highly supersaturated, thus reaching higher solute concentration compared to bulk solution, which makes it difficult for models to predict hygroscopicity. Cheng et al. (2015) pointed out that the size effect might be taken into account by models. By measuring the hygroscopic growth factor of organic nanoparticles (e.g., levoglucosan and D-glucose) of different sizes, we may be able to retrieve these thermodynamic data using a differential Köhler analysis (DKA) method (Cheng et al., 2015). This will further help us to understand new particle formation, transportation, and their interactions with water molecules.
In this study, we investigate the hygroscopic growth factors of levoglucosan and D-glucose nanoparticles down to 6 nm in size using a nano-hygroscopic tandem differential mobility analyzer (nano-HTDMA, Lei et al., 2020). Moreover, we compare our measurement data with model prediction from the Extended Aerosol Inorganic Model (E-AIM, standard UNIFAC) (Clegg et al., 2001; Clegg and Seinfeld, 2006; http://www.aim.env.uea.ac.uk/aim/aim.php, last access: 19 April 2023), the ideal solution theory, and DKA. In addition, the DKA method is used to calculate thermodynamic properties (e.g., water activity) of D-glucose nanodroplets in the highly supersaturated concentration range and then to compare with KD-derived data (KD: Kreidenweis), thermodynamic property data from Köhler (Kreidenweis et al., 2005), E-AIM (standard UNIFAC), and references.
2.1 Experimental methods
2.1.1 Nanoparticle generation
An electrospray is employed to generate levoglucosan and D-glucose aerosol nanoparticles of 6, 8, 10, and 15 nm using 2, 3, 5, and 10 mM aqueous solutions with 50 % volume fraction of a 20 mM ammonium acetate buffer solution (Chen et al., 2005; Wang et al., 2015), respectively. The generated nanoparticles are diluted by mixing with dry and filtered N2 (1 L min−1) and CO2 (0.1 l min−1), bringing aerosol nanoparticles to a dry RH state (≤ 2 % RH). Subsequently, aerosol nanoparticles pass through a Po210 neutralizer to reach the equilibrium charge distribution (Wiedensohler, 1986). In order to avoid blocking the 25 µm capillary tube in the electrospray with high-concentration solution, the aerosol nanoparticles with diameters of 60–100 and 20 nm are generated by an atomizer with a 0.05 wt % and 0.01 wt % organic solution (i.e., levoglucosan and D-glucose), respectively. The chemical substances and their physical properties are characterized in Table S1. These solutions are prepared with distilled and de-ionized Milli-Q water (resistivity of 18.2 MΩ cm at 298.15 K). Note that the size selected by the nano-DMA1 should be the right part of peak diameter of the number size distribution of the generated nanoparticles, which minimizes the influence of the multiple charged nanoparticles in hygroscopicity measurements. This is to ensure that we could have as many particles as possible to compensate for the strong loss of very small particles in the whole humidification system.
2.1.2 Nano-HTDMA setup
Figure 1 shows a schematic of the nano-HTDMA system for investigating the hygroscopic behavior of aerosol nanoparticles, especially in the sub-10 nm size range. The detailed description, calibration, and validation of the nano-HTDMA setup have been reported in a previous paper (Lei et al., 2020). In brief, the polydisperse aerosol nanoparticles pass through a silica gel diffusion dryer and a Nafion gas dryer (TROPOS model ND.070, length 60 cm). The dry aerosol nanoparticles at RH below 10 % are charged by a Kr85 bipolar charger and then enter the first nano-differential mobility analyzer (nano-DMA1, TROPOS model Vienna-type short DMA), where a monodisperse distribution of nanoparticles with the desired dry diameter is selected. The monodispersed nanoparticles are subsequently exposed to different RH conditions, which can be set to deliquescence mode (from low RH to high RH for measuring deliquescence) or efflorescence mode (from high RH to low RH for measuring efflorescence). In the deliquescence mode, the dry aerosol nanoparticles are gradually humidified to a target RH through a Nafion humidifier (NH-1, TROPOS model ND.070, length 60 cm). In the efflorescence mode, after deliquescence of aerosol nanoparticles with RH above 97 % in a Nafion humidifier (NH-2: Perma Pure model MH-110, length 30 cm), the deliquesced aerosol nanoparticles are stepwise dried to a target RH in NH-1. The number size distribution of the humidified nanoparticles is then measured by a nano-differential mobility analyzer (nano-DMA2) at a target RH through a Nafion humidifier (NH-3, Perma Pure model PD-100) coupled with an ultrafine condensation particle counter (CPC, TSI, model no. 3776). To have uniform RH within the nano-DMA2 for the accurate determination of hygroscopicity (Gf, DRH, ERH) of aerosol nanoparticles, the difference between the sheath flow RH (RHs) and the aerosol flow RH (RHa) upstream of the nano-DMA2 is kept < 1 %. Most importantly, the temperature difference between the inlet and outlet of the nano-DMA2 is maintained below 0.2 ∘C during the measurements. In addition, the residence time (e.g., 5.4 s: between the humidifier and the nano-DMA2; 0.07 s: deliquescence for aerosol nanoparticles) is sufficient for water-soluble aerosol nanoparticles to equilibrate with water vapor at a given RH and for solid–liquid phase transition to occur (Kerminen, 1997; Duplissy et al., 2005; Raoux et al., 2007).
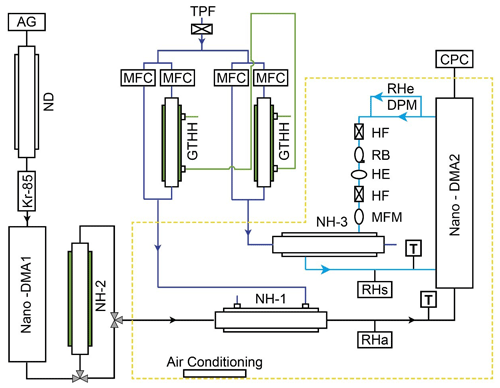
Figure 1Experimental setup of the nano-HTDMA. AG: aerosol generator (aerosol atomizer or electrospray); ND: Nafion dryer; Kr-85: krypton source aerosol neutralizer; Nano-DMA: nano-differential mobility analyzer; TPF: total particle filter; HF: hydrophobic filter; MFC: mass flow controller; MFM: mass flow meter; RB: recirculation blower; DPM: dew point mirror; GTHH: Gore-Tex humidifier and heater; NH: Nafion humidifier; HE: heat exchanger; CPC: condensation particle counter. Black line: aerosol line; blue line: sheath line; royal blue line: humidified air; green line: Milli-Q water (resistivity of 18.2 MΩ cm at 298.15 K). RHa and RHs (measured by RH sensors) represent the RH of aerosol and sheath flow in the inlet of nano-DMA2, respectively. RHe (measured by dew point) represents the RH of excess air. T represents the temperature of aerosol and sheath flow in the inlet of nano-DMA2.
2.2 Theory and modeling methods
2.2.1 Köhler theory
The fractional ambient relative humidity () over a spherical droplet in equilibrium with the environment is described by the Köhler equation (Köhler, 1936):
where aw is the water activity of the solution droplet, σsol is the liquid–vapor interfacial energy of solution droplet (also called surface tension), vw is the partial molar volume of water, R is the universal gas constant, T is the temperature, Gf is the diameter growth factor of aerosol particles, and Ds is the dry diameter of spherical aerosol particles. The hygroscopic growth curve (Gf vs. RH) is estimated based on the assumptions in models or theories described in the following sections (Sect. 2.2.2–2.2.3).
2.2.2 Water activity
The expression for water activity used in the simplified Köhler theory (SKT) assumes that the droplet contains nw moles of water and ns moles of non-volatile solute.
v is the number of ions of solute present in solution (v=1 for organic composition). This expression has been applied to the diluted solution (Kreidenweis et al., 2005; Koehler et al., 2006).
The following KD expression proposed by Kreidenweis et al. (2005) (KD: Kreidenweis) is to present the relationship between aw and Gf determined in hygroscopic growth measurements.
The coefficients a, b, and c for organic solution droplets in this study are from Lei et al. (2014, 2018) and Estillore et al. (2017) as shown in Table S2.
Differential Köhler analysis (DKA) proposed by Cheng et al. (2015) is theoretically based on the Köhler equation (Köhler, 1936) to determine water activity by measuring hygroscopic growth factors of aerosol nanoparticles in different sizes.
Here, sw1 and sw2 are water saturation ratios measured at the same Gf but at different initial dry diameters (Ds1, Ds2, respectively). Using the DKA method can calculate the water activity in the highly supersaturated concentration range.
2.2.3 Growth factor
For an ideal solution, the hygroscopic curve can be estimated assuming that the water activity aw of the solution containing the non-volatile and non-electrolyte solute component is equal to the molar ratio of water in the solution. Here, the partial molar volume of pure water in the solution is equal to the molar volume of pure water. Since the hygroscopic diameter growth factor measurements are on a volume basis using the nano-HTDMA system, the expression of Gf as a function of molar ratio (xj), molar mass (Mj), and mass density (ρj) of components j is as follows.
The hygroscopic growth curve of aerosol particles is commonly evaluated from the Extend Aerosol Inorganic Model (E-AIM). It is a thermodynamic equilibrium model used for calculating phase partitioning (gas–liquid–solid). Most importantly, E-AIM can model thermodynamic properties (e.g., water activity, liquid–vapor interfacial energy, and solution density) in the highly supersaturated concentration solution (Dutcher et al., 2013). Also, the standard universal quasi-chemical functional group activity coefficients (UNIFAC) within E-AIM can be used to predict aw, σsol, and ρsol of organic aqueous solution (Fredenslund et al., 1975; Hansen et al., 1991). Note that the E-AIM calculations based on the standard UNIFAC group contribution method predict hygroscopic growth factors of the organic aerosol particle (i.e., E-AIM, standard UNIFAC) growth curve as a function of RH based on Eqs. (1) and (6).
ρs and ρsol are the density of solute and solution, respectively, and xs is the solute mass fraction.
3.1 Levoglucosan
3.1.1 Concentration-dependent water activity of levoglucosan solution
By applying a water activity parameterization model (KD, Eq. 3) to measured growth factors of levoglucosan aerosol nanoparticles with diameters from 20 to 100 nm using a nano-HTDMA, as shown in Fig. 2, we obtain water activity of aqueous levoglucosan nanoparticles with molality up to 140 mol kg−1. Chan et al. (2005) levitated single particles of ∼ 10 µm levoglucosan at different RHs in an electrodynamic balance for mass measurements and reported water activity data for aqueous droplets with molality up to 14 mol kg−1. These water activity data are compared with predictions from Köhler (Kreidenweis et al., 2005, Eq. 2) and E-AIM, respectively. Good agreement between KD-derived water activity and Köhler indicates that these aerosol particles are aqueous droplets with molality less than 20 mol kg−1. However, a derivation of SKT from the KD-derived water activity is observed as the molality increases from 20 to 120 mol kg−1, indicating that levoglucosan nanoparticles become highly supersaturated. Also, a discrepancy exists between KD-derived data and E-AIM prediction. For DKA-derived water activity calculations, a strong size dependence of the hygroscopic growth factors is needed for aerosol nanoparticles in the different sizes, which is not the case for the hygroscopic measurements of levoglucosan nanoparticles.
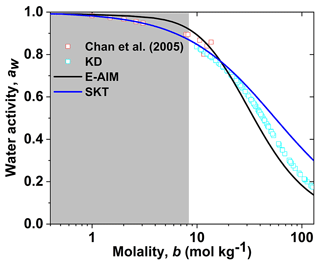
Figure 2Concentration-dependent water activity (aw) of levoglucosan solution. The KD-derived aw (KD: Kreidenweis, cyan open square) is compared with observations (red open square), E-AIM (Extend Aerosol Inorganic Model, black line), and the aw model (SKT, blue line). The light grey shaded areas mark the subsaturated concentration with respect to bulk solution.
3.1.2 Size-dependent hygroscopicity of levoglucosan nanoparticles
Black solid squares in Fig. 3 show the measured humidogram of 100 nm levoglucosan nanoparticles in both deliquescence and efflorescence modes. Levoglucosan nanoparticles water take up continuously from 5 % RH to 90 % RH. Also, they gradually release water as RH decreases down to 5 %. The hygroscopic growth factors of levoglucosan nanoparticles in deliquescence and efflorescence modes overlap. For example, the hygroscopic growth factors of levoglucosan nanoparticles at 80 % RH and 87 % RH are 1.16 and 1.23, respectively, in the deliquescence mode, which is very close to the corresponding values in the efflorescence mode at the same RH (shown in Fig. S1), suggesting that growing and shrinking of particles are in equilibrium. No prompt phase transitions of levoglucosan nanoparticles are observed in deliquescence or efflorescence modes. A similar non-prompt phase transition of levoglucosan nanoparticles was observed in previous studies (Mochida and Kawamura, 2004; Chan et al., 2005; Svenningsson et al., 2006; Mikhailov et al., 2008; Lei et al., 2014, 2018). This study is in good agreement with most of the referenced results, but there is a difference in the hygroscopic growth factor of levoglucosan nanoparticles between Mikhailov et al. (2008) and this study. The reason is that Mikhailov et al. (2008) used minimum mobility diameter measured in the deliquescence and efflorescence modes instead of the initial dry mobility diameter measured in the deliquescence or efflorescence modes to calculate the hygroscopic growth factor of levoglucosan nanoparticles, which could lead to higher hygroscopic growth factors of levoglucosan nanoparticles than those of this study.
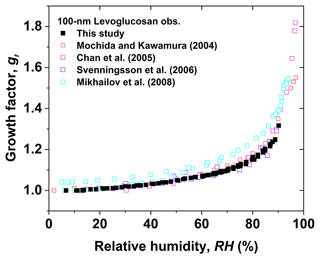
Figure 3Hygroscopic diameter growth factor (Gf) of levoglucosan particles with a dry diameter of 100 nm in both deliquescence and efflorescence mode processes (black solid square). The measured data compared with literature data from Mochida and Kawmura (2004) in both deliquescence and efflorescence modes (red open square), Chan et al. (2005) in the deliquescence mode (magenta open square), Svenningsson et al. (2006) in the deliquescence mode (violet open square), and Mikhailov et al. (2008) in both deliquescence and efflorescence modes (cyan open square).
Figure 4 shows measured size-resolved hygroscopic growth factors of levoglucosan nanoparticles against RH up to 90 %. There is a weak size dependence of hygroscopic growth factors of levoglucosan nanoparticles with diameters down to 20 nm in both deliquescence and efflorescence modes. For example, the slight difference in the hygroscopic growth factor between 100 and 20 nm levoglucosan nanoparticles is ∼ 0.02 at 88 % RH. In addition, E-AIM (standard UNIFAC) and ideal solution theory are used to predict our measurement results as shown in Fig. 4a and b, respectively. E-AIM (standard UNIFAC) is applied to estimate the hygroscopic growth of organic aerosol nanoparticles according to the UNIFAC group contribution method. Ideal solution theory is used to describe water absorption of the ideal and diluted aqueous solution nanodroplets. Due to consideration of the Kelvin effect in the model and theory, these model predictions are expected to present a size dependence of growth factors of nanoparticles in size from 100 down to 20 nm. For example, as shown in Fig. 4a, for levoglucosan nanoparticles with diameters of 100, 60, and 20 nm, the thermodynamic equilibrium model (E-AIM, standard UNIFAC) shows a weak size dependence of the growth factors at low RH but a strong size dependence of growth factors at RH above 70 %. However, the calculated growth factors of nanoparticles down to 20 nm in size deviate from the measured growth factors of levoglucosan nanoparticles at RH below 80 %, which is similar to the 100 nm levoglucosan hygroscopicity prediction from previous studies (Lei et al., 2014, 2018). Lei et al. (2014, 2018) explained that the possible reason for this discrepancy is that the E-AIM (standard UNIFAC) predictions are not suitable for organic compounds with the strongly polar functional groups in series (Fredenslund et al., 1975; Hansen et al., 1991). Since levoglucosan contains three OH groups in series, thermodynamic properties (e.g., water activity, surface tension) in E-AIM (standard UNIFAC) are more likely to be invalid for the levoglucosan system. However, good agreement of growth factors of levoglucosan with diameters 100, 60, and 20 nm is observed between measurements and predictions by ideal solution theory as shown in Fig. 4b.
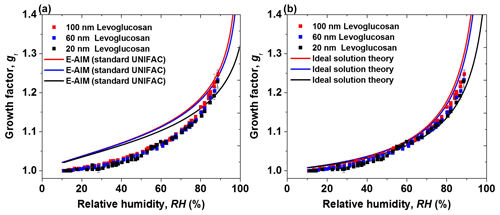
Figure 4Hygroscopic diameter growth factor (Gf) of levoglucosan particles with dry diameters of 100 nm (red square), 60 nm (blue square), and 20 nm (green square). Köhler model curves are based on (a) E-AIM (standard UNIFAC) (100 nm: red, 60 nm: blue, 20 nm: green line) and (b) ideal solution theory (100 nm: red, 60 nm: blue, 20 nm: green line).
The hygroscopic growth for sub-20 nm levoglucosan nanoparticles cannot be determined with the nano-HTDMA system because we observed significant evaporation of the dry particles in the measurement system. Figure 5a–b show the measured peak diameter of a normalized size distribution scanned by the nano-DMA2 and nano-DMA1 for sub-20 nm levoglucosan nanoparticles. It is obvious that the size of nanoparticles in DMA2 is smaller than that in DMA1, corresponding to a decrease of 22 % to 50 % of 15 and 10 nm levoglucosan nanoparticles, respectively, indicating significant evaporation of these small levoglucosan nanoparticles in the system. To test this hypothesis, we estimate the ratio of gas-phase concentration to the total concentration of the generated levoglucosan nanoparticles in the different sizes. Firstly, the calculated gas-phase concentration of levoglucosan is based on the Kelvin equation and ideal gas equation (Eqs. S1, S2, Supplement S1). Figure 5c shows the vapor saturation ratio of levoglucosan as nanodroplet diameter increases from 1 to 100 nm. The inset in Fig. 5c is an enlarged view (black open square) of the vapor saturation ratio of levoglucosan as a function of nanodroplet diameters below 20 nm. Levoglucosan is semi-volatile at ambient conditions (Hennigan et al., 2010). Due to the Kelvin effect, sub-20 nm levoglucosan aerosol particles become more volatile. Secondly, the total concentration of levoglucosan particles is estimated by Eq. (S3). The results of the ratio of gas-phase concentration (mg) to the total concentration (mt) are shown in Fig. 5d and Table S3 for levoglucosan nanoparticles in the diameter range from 10 to 100 nm. It shows a slight increase in the calculated ratio () for levoglucosan aerosol nanoparticles with diameters from 100 down to 20 nm. However, the ratio of gas-phase concentration to the total concentration is dramatically enhanced for sub-20 nm levoglucosan aerosol nanoparticles, which is consistent with measurement observations, indicating the larger impact of evaporation of sub-20 nm levoglucosan nanoparticles on the measurement results. Therefore, there is obvious partial levoglucosan evaporation from DMA1 to DMA2 within several seconds.
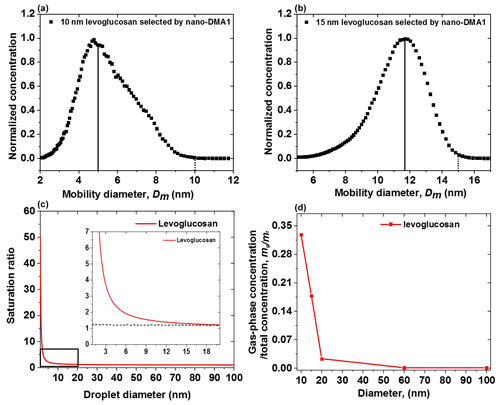
Figure 5The normalized size distributions scanned by nano-DMA2 for (a) 10 and (b) 15 nm levoglucosan at 10 % at 298 K. The dotted lines mark the diameters of the monodispersed nanoparticles selected by the nano-DMA1. The back solid lines mark the peak diameters from the normalized size distributions scanned by the nano-DMA2. (c) Vapor saturation ratio of levoglucosan as a function of nanodroplet diameter according to the Kelvin equation. The diameter range 1–20 nm for the saturation ratio of levoglucosan particles is shown as an inset. The value of surface tension of pure levoglucosan is 0.0227104 [J m−2]. (d) The ratio of gas-phase concentration (mg) to the total concentration (mt) of levoglucosan nanoparticles against diameter.
3.2 D-glucose
3.2.1 Concentration-dependent water activity of D-glucose solution
Figure 6 shows the DKA-derived water activity of aqueous D-glucose nanodroplets with diameters from 6 to 100 nm with molality up to 1000 mol kg−1 (Cheng et al., 2015, Eq. 4). Here, by comparing with KD-derived water activity, Köhler, E-AIM, and observations from the literature (Comesaña et al., 2001; Peng et al., 2001; Bhandari and Bareyre, 2003; Ferreira et al., 2003), good agreement among them is observed in the solute concentration below 20 mol kg−1. However, there is disagreement between water activity results in the highly supersaturated concentration range (> 20 mol kg−1).
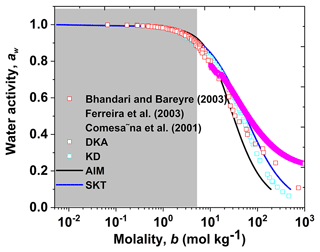
Figure 6Concentration-dependent water activity (aw) of D-glucose solution. The DKA-derived aw (differential Köhler analysis, magenta open square) is compared with observations (red open square), E-AIM (Extend Aerosol Inorganic Model, black line), aw model (SKT, blue line), and the parameterization model for aw (KD: Kreidenweis, cyan open square). The light grey shaded areas mark the subsaturated concentration with respect to bulk solution.
3.2.2 Size-dependent hygroscopicity of D-glucose nanoparticles
Figure 7 shows the measured hygroscopic growth factors of 100 nm D-glucose nanoparticles as a function of RH. No significant difference in the hygroscopic growth factor of 100 nm D-glucose nanoparticles is found between deliquescence and efflorescence measurement modes (Fig. S2). For example, the measured growth factors of D-glucose nanoparticles at 81 % RH and 88 % RH are 1.16 and 1.25 in the deliquescence mode, respectively, in good agreement with results in the efflorescence mode (Gf=1.17 at 81 % RH, Gf=1.26 at 88 % RH shown in Fig. S2). Also, measured hygroscopic growth factors of 100 nm D-glucose are consistent with results from previous studies (Mochida and Kawamura. 2004; Chan and Chan, 2005; Suda and Petters, 2013; Estillore et al., 2017; Mikhailov and Vlasenko, 2020). For example, Mikhailov and Vlasenko (2020) investigated the hygroscopic behavior of 100 nm D-glucose aerosol particles using an H-HTDMA in deliquescence, efflorescence, and restructuring modes of operation. A clear morphology effect on the hygroscopicity of D-glucose aerosol particles is observed in the RH range from 2 % RH to 96 % RH. No prompt phase transitions are observed in deliquescence or efflorescence measurement modes. Estillore et al. (2017) observed a slightly amorphous structure of D-glucose particles under ambient conditions using atomic force microscopy, and D-glucose particles grow through gradual water uptake. Thus, continuous growth and shrinking of diameter in both deliquescence and efflorescence modes is explained by the lack of crystallization of D-glucose nanoparticles upon drying to low RH below 10 %.
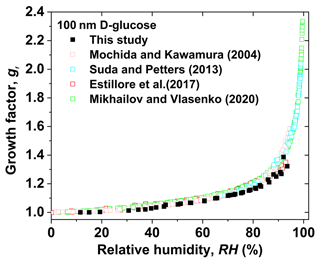
Figure 7Hygroscopic diameter growth factor (Gf) of D-glucose particles with a dry diameter of 100 nm in both deliquescence and efflorescence modes (black solid square). The measured data compared with reference data from Mochida and Kawmura (2004) in both deliquescence and efflorescence modes (pink open square), Suda and Petters (20017) in deliquescence mode (violet open square), Estillore et al. (2017) in both deliquescence and efflorescence modes (red open square), and Mikhailov and Vlasenko (2020) in both deliquescence and efflorescence modes (green open square).
Figure 8a shows the size dependence of measured hygroscopic growth factors of D-glucose nanoparticles in the size range from 6 to 100 nm, with differences in growth factor up to 0.14 between 100 and 6 nm nanoparticles at 90 % RH (Fig. S2). A weak size dependence on the hygroscopic growth factors of D-glucose nanoparticles is observed in the size range from 20 to 100 nm, which is similar to observation for levoglucosan nanoparticles with diameters down to 20 nm. However, there is a strong size-dependent growth factor of D-glucose nanoparticles with diameters from 6 to 20 nm, especially at high RH, i.e., RH ⩾ 80%. There is no evident difference in hygroscopic growth factors of D-glucose nanoparticles at RH below 80 % in the size range from 6 to 100 nm. The reason that the growth factor shows size dependence only in the regime of hygroscopic growth (RH ⩾ 80 %), and not in the regime of water adsorption (RH ⩾ 80 %), has not been explained before. Our hypothesis is that the distinct behaviors between high RH and low RH regions can be attributed to the distinct size effect on the hygroscopic growth and adsorption; i.e., the growth factor shows size dependence only in the regime of hygroscopic growth (RH ⩾ 80 %), and not in the regime of water adsorption (RH ⩾ 80 %). Figure 8b further shows the clear change in the hygroscopic growth factor of D-glucose aerosol nanoparticles with diameters from 100 down to 6 nm at 87 % RH. The hygroscopic growth factor of D-glucose nanoparticles is almost unchanged with diameters from 20 to 100 nm. However, a marked increase in the hygroscopic growth factor of D-glucose aerosol nanoparticles is observed as size increases from 6 to 20 nm. E-AIM predicts the measured hygroscopic growth factors of D-glucose with diameters smaller than 15 nm at 87 % RH well, while ideal solution theory agrees with hygroscopic measurement results of D-glucose with diameters larger than 60 nm at the same RH. The use of DKA methods leads to good agreement between measurements and model predictions.
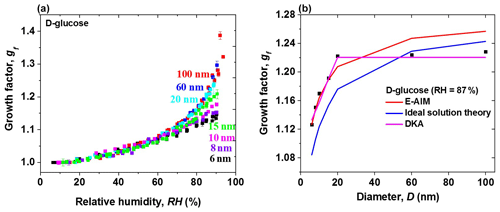
Figure 8(a) Hygroscopic diameter growth factor (Gf) of D-glucose nanoparticles with dry diameters of 100 nm (red square), 60 nm (blue square), 20 nm (cyan square), 15 nm (green square), 10 nm (pink square), 8 nm (royal square), and 6 nm (black square). (b) Hygroscopic diameter growth factor (Gf, black square) of D-glucose nanoparticles with dry diameters from 6 to 100 nm at 87 % RH. The measured hygroscopic growth factors of D-glucose nanoparticles with diameters from 100 down to are compared with E-AIM (red line), ideal solution theory (blue line), and DKA prediction (pink line).
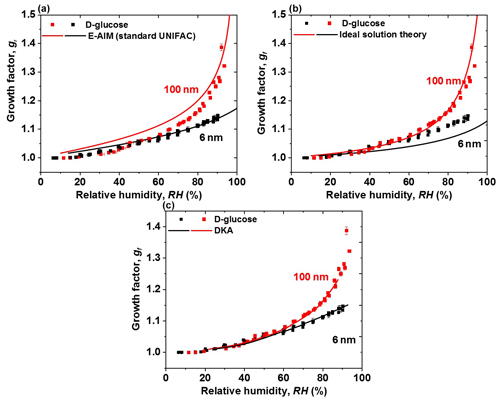
Figure 9Hygroscopic diameter growth factor (Gf) of D-glucose nanoparticles with dry diameters of 100 nm (red square) and 6 nm (black square). Köhler model curves are based on (a) AIM (standard UNIFAC), (100 nm: red, 6 nm: black line), (b) ideal solution theory (100 nm: red, 6 nm: black line), and (c) DKA mode (100 nm: red, 6 nm: black line).
The measured hygroscopic growth factors of D-glucose nanoparticles with diameters of 6 and 100 nm are compared with the model and theory shown in Figs. 9, S3, and S4, respectively. Ideal solution theory is applied to predict the hygroscopic growth factor of organics in the ideal solution. Figures 9a and S3 show that the measured growth factors of 100 nm D-glucose nanoparticles are lower than predicted growth factors from E-AIM (standard UNIFAC), especially at RH below 85 %. Also, E-AIM (standard UNIFAC) could predict the measured hygroscopic growth factor of 6 nm D-glucose aerosol nanoparticles at RH above 40 % well, as shown in Figs. 9a and S3. The possible reason for discrepancies between E-AIM (standard UNIFAC) and measurements is inaccurate thermodynamic parameters (e.g., water activity, surface tension) estimated by E-AIM (standard UNIFAC) without consideration of intramolecular interaction (Fredenslund et al., 1975; Hansen et al., 1991; Fredenslund and Sørensen, 1994; Mochida and Kawamura, 2004). D-glucose contains five OH groups in series, and the hydrogen bond could potentially exist and affect the E-AIM (standard UNIFAC) model–measurement agreement for D-glucose aerosol nanoparticle systems (Mochida and Kawamura, 2004; Lei et al., 2014, 2018). The ideal solution theory is used to predict the hygroscopic curve of D-glucose nanoparticles with diameters of 6–100 nm, shown in Figs. 9b and S3. There is good agreement between measured growth factors of 100 nm D-glucose and ideal theory predictions. This suggests that thermodynamic parameters (e.g., water activity, surface tension, and solution density) assumed by the ideal solution theory are accurate to use in Eqs. (1) and (2) for predicting the hygroscopic curve of D-glucose nanoparticles with large sizes (e.g., 60, 100 nm). However, an underestimation of growth factors of 6 nm D-glucose nanoparticles is shown in Figs. 9b and S3 by ideal solution theory prediction at RH above 30 %. For an ideal solution, water activity of liquid droplets can be simply estimated from the mole fraction of water. With from 20 down to 6 nm, D-glucose nanodroplets can be highly supersaturated, and the water activity is not equal to the mole fraction of water. Thus, with the assumption of an idea solution, the model failed to predict the observed growth factors of 6 nm D-glucose nanoparticles at RH above 30 %. However, the current thermodynamic models (e.g., E-AIM) mostly rely on the concentration-dependent thermodynamic properties (such as water activity) derived from the measurements of large aerosol particles or even bulk samples (Tang and Munkelwitz, 1994; Tang, 1996; Pruppacher and Klett, 1997; Clegg et al., 1998). They are thus difficult or impossible to apply to describe the hygroscopic behavior of sub-10 nm nanoparticles, which can often be supersaturated in concentration compared to bulk solutions (Cheng et al., 2015). Thus, the nanosize effect on these thermodynamic properties has been taken into account in models and theories (Cheng et al., 2015). The combination of DKA methods and hygroscopic measurements of aerosol nanoparticles in different sizes can be used to determine the thermodynamic properties (e.g., water activity) in the highly supersaturated concentration range (Cheng et al., 2015). Therefore, as shown in Figs. 9c and S4, the use of the DKA method leads good agreement with the measured hygroscopic growth factors of glucose nanoparticles with diameters from 100 down to 6 nm.
In this study, we investigate the hygroscopic behavior of levoglucosan and D-glucose nanoparticles with diameters down to 6 nm using a nano-HTDMA. Due to the larger impact of evaporation of sub-20 nm levoglucosan nanoparticles in the nano-HTDMA system, we measure the hygroscopic growth factor of levoglucosan with diameters down to 20 nm. There is a weak size dependence of the hygroscopic growth factor of levoglucosan and D-glucose with diameters down to 20 nm, while a strong size dependence of the hygroscopic growth factor of D-glucose has been clearly observed in the size range from 6 to 20 nm. No prompt phase transitions occur in deliquescence or efflorescence modes for both levoglucosan and D-glucose nanoparticles. By comparing with the KD-derived water activity, Köhler, E-AIM, and DKA-derived data, the predicted water activity of an aqueous organic solution (levoglucosan and D-glucose) is consistent with observation data from references in the low solute concentration (< 20 mol kg−1) but failed in the solute concentration (> 20 mol kg−1). In addition, ideal solution theory predicts the hygroscopic behavior of two specific organics with diameters larger than 60 nm (levoglucosan and D-glucose) well, while the hygroscopic growth factor of D-glucose down to 6 nm in size is in good agreement with E-AIM (standard UNIFAC) prediction at high RH. The use of the DKA method leads to good agreement with the measured hygroscopic growth factor of glucose nanoparticles with diameters from 100 down to 6 nm.
Readers who are interested in the data should contact Yafang Cheng (yafang.cheng@mpic.de).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-23-4763-2023-supplement.
YC and HS designed and led the study. TL performed the experiments. All co-authors discussed the results and commented on the paper. TL wrote the paper with input from all co-authors.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Chemistry and Physics. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was supported by the Max Planck Society (MPG) and Leibniz Society. Ting Lei acknowledges support from the China Scholarship Council (CSC). Yafang Cheng would like to acknowledge the Minerva Program of MPG.
The article processing charges for this open-access publication were covered by the Max Planck Society.
This paper was edited by Dara Salcedo and reviewed by two anonymous referees.
Bhandari, B. and Bareyre, I.: Estimation of crystalline phase present in the glucose crystal–solution mixture by water activity measurement, LWT, Food Sci. Technol., 36, 729–733, 2003.
Bhattarai, H., Saikawa, E., Wan, X., Zhu, H., Ram, K., Gao, S., Kang, S., Zhang, Q., Zhang, Y., Wu, G., Wang, X., Kawamura, K., Fu, P., and Cong, Z.: Levoglucosan as a tracer of biomass burning: Recent progress and perspectives, Atmos. Res., 220, 20–33, 2019.
Biskos, G., Malinowski, A., Russell, L. M., Buseck, P. R., and Martin, S. T.: Nanosize effect on the deliquescence and the efflorescence of sodium chloride particles, Aerosol Sci. Technol., 40, 97–106, 2006a.
Biskos, G., Paulsen, D., Russell, L. M., Buseck, P. R., and Martin, S. T.: Prompt deliquescence and efflorescence of aerosol nanoparticles, Atmos. Chem. Phys., 6, 4633–4642, https://doi.org/10.5194/acp-6-4633-2006, 2006b.
Biskos, G., Russell, L. M., Buseck, P. R., and Martin, S. T.: Nanosize effect on the hygroscopic growth factor of aerosol particles, Geophys. Res. Lett., 33, L07801, https://doi.org/10.1029/2005GL025199, 2007.
Chan, M. N. and Chan, C. K.: Mass transfer effects in hygroscopic measurements of aerosol particles, Atmos. Chem. Phys., 5, 2703–2712, https://doi.org/10.5194/acp-5-2703-2005, 2005.
Chan, M. N., Choi, M. Y., Ng, N. L., and Chan, C. K.: Hygroscopicity of water-soluble organic compounds in atmospheric aerosols: Amino acids and biomass burning derived organic species, Environ. Sci. Technol., 39, 1555–1562, 2005.
Charlson, R. J., Schwartz, S. E., Hales, J. M., Cess, R. D., Coakley, J. A., Hansen, J. E., and Hoffmann, D. J.: Climate forcing by anthropogenic aerosols, Science, 255, 423–430, 1992.
Chen, D.-R., Pui, D. Y. H., and Kaufman, S. L.: Electrospraying of conducting liquids for monodisperse aerosol generation in the 4 nm to 1.8 nm diameter range, J. Aerosol Sci., 26, 963–977, 2005.
Cheng, Y. F., Su, H., Rose, D., Gunthe, S. S., Berghof, M., Wehner, B., Achtert, P., Nowak, A., Takegawa, N., Kondo, Y., Shiraiwa, M., Gong, Y. G., Shao, M., Hu, M., Zhu, T., Zhang, Y. H., Carmichael, G. R., Wiedensohler, A., Andreae, M. O., and Pöschl, U.: Size-resolved measurement of the mixing state of soot in the megacity Beijing, China: diurnal cycle, aging and parameterization, Atmos. Chem. Phys., 12, 4477–4491, https://doi.org/10.5194/acp-12-4477-2012, 2012.
Cheng, Y. F., Su, H., Koop, T., Mikhailov, E., and Pöschl, U.: Size dependence of phase transitions in aerosol nanoparticles, Nat. Commun., 6, 5923, https://doi.org/10.1038/ncomms6923, 2015.
Chýlek, P. and Coakley, J. A.: Aerosols and climate, Science, 183, 75–77, 1974.
Clegg, S. L. and Seinfeld, J. H.: Thermodynamic models of aqueous solutions containing in-organic electrolytes and dicarboxylic acids at 298.15 K, 2. Systems including dissociation equilibria, J. Phys. Chem. A, 110, 5718–5734, https://doi.org/10.1021/jp056150j, 2006.
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic model of the system H+-NH-SO-NO3–H2O at tropospheric temperatures, J. Phys. Chem. A, 102, 2137–2154, https://doi.org/10.1021/Jp973042r, 1998.
Clegg, S. L., Seinfeld, J. H., and Brimblecombe, P.: Thermody-namic modelling of aqueous aerosols containing electrolytes and dissolved organic compounds, J. Aerosol Sci., 32, 713–738, https://doi.org/10.1016/s0021-8502(00)00105-1, 2001.
Comesaña, J. F., Correa, A., and Sereno, A. M.: Water activity at 35 ∘C in “sugar” + water and “sugar” + sodium chloride + water systems, Int. J. Food Sci. Tech., 36, 655–661, 2001.
Duplissy, J., Gysel, M., Sjogren, S., Meyer, N., Good, N., Kammermann, L., Michaud, V., Weigel, R., Martins dos Santos, S., Gruening, C., Villani, P., Laj, P., Sellegri, K., Metzger, A., McFiggans, G. B., Wehrle, G., Richter, R., Dommen, J., Ristovski, Z., Baltensperger, U., and Weingartner, E.: Intercomparison study of six HTDMAs: results and recommendations, Atmos. Meas. Tech., 2, 363–378, https://doi.org/10.5194/amt-2-363-2009, 2009.
Dusek, U., Frank, G. P., Curtius, J., Drewnick, F., Schneider, J., Kürten, A., Rose, D., Andreae, M. O., Borrmann, S., and Pöschl, U.: Enhanced organic mass fraction and decreased hygroscopicity of cloud condensation nuclei (CCN) during new particle formation events, Geophys. Res. Lett., 37, L03804, https://doi.org/10.1029/2009GL040930, 2010.
Dutcher, C. S., Ge, X., Wexler, A. S., and Clegg, S. L.: An Isotherm-Based Thermodynamic Model of Multicomponent Aqueous Solutions, Applicable Over the Entire Concentration Range, J. Phys. Chem. A, 117, 3198–3213, 2013.
Elias, V. O., Simoneit, B. R. T., Cordeiro, R. C., and Turcq, B.: Evaluating levoglucosan as an indicator of biomass burning in Carajás, amazônia: a comparison to the charcoal record, Geochim. Cosmochim. Ac., 65, 267–272, 2001.
Estillore, A. D., Morris, H. S., Or, V. W., Lee, H. D., Alves, M. R., Marciano, M. A., Laskina, O., Qin, Z., Tivanski, A. V., and Grassian, V. H.: Linking hygroscopicity and the surface microstructure of model inorganic salts, simple and complex carbohydrates, and authentic sea spray aerosol particles, Phys. Chem. Chem. Phys., 19, 21101–21111, 2017.
Ferreira, O., Brignole, E. A., and Macedo, E. A.: Phase equilibria in sugar solutions using the A-UNIFAC model, Ind. Eng. Chem. Res., 42, 6212–6222, 2003.
Fraser, M. P. and Lakshmanan, K.: Using Levoglucosan as a Molecular Marker for the Long-Range Transport of Biomass Combustion Aerosols, Environ. Sci. Technol., 34, 4560–4564, 2000.
Fredenslund, A., Jones, R. L., and Prausnitz, J. M.: Group-contribution estimation of activity-coefficients in nonideal liquid-mixtures, Aiche J., 21, 1086–1099, https://doi.org/10.1002/aic.690210607, 1975.
Hansen, H. K., Rasmussen, P., Fredenslund, A., Schiller, M., and Gmehling, J.: Vapor–liquid equilibria by UNIFAC group contribution, 5. Revision and extension, Ind. Eng. Chem. Res., 30, 2352–2355, https://doi.org/10.1021/ie00058a017, 1991.
Hennigan, C. J., Sullivan, A. P., Collett, J. L., and Robinson, A. L.: Levoglucosan stability in biomass burning particles exposed to hydroxyl radicals, Geophys. Res. Lett., 37, L09806, https://doi.org/10.1029/2010gl043088, 2010.
Kerminen, V.-M.: The effects of particle chemical character and atmospheric processes on particle hygroscopic properties, J. Aerosol Sci., 28, 121–132, 1997.
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, Trans. Farad. Soc., 32, 1152–1161, 1936.
Köhler, K. A., Kreidenweis, S. M., DeMott, P. J., Prenni, A. J., Carrico, C. M., Ervens, B., and Feingold, G.: Water activity and activation diameters from hygroscopicity data – Part II: Application to organic species, Atmos. Chem. Phys., 6, 795–809, https://doi.org/10.5194/acp-6-795-2006, 2006.
Kreidenweis, S. M., Koehler, K., DeMott, P. J., Prenni, A. J., Carrico, C., and Ervens, B.: Water activity and activation diameters from hygroscopicity data – Part I: Theory and application to inorganic salts, Atmos. Chem. Phys., 5, 1357–1370, https://doi.org/10.5194/acp-5-1357-2005, 2005.
Kulmala, M., Kontkanen, J., Junninen, H., Lehtipalo, K., Manninen, H. E., Nieminen, T., Petäjä, T., Sipilä, M., Schobesberger, S., Rantala, P., Franchin, A., Jokinen, T., Järvinen, E., Äijälä, M., Kangasluoma, J., Hakala, J., Aalto, P. P., Paasonen, P., Mikkilä, J., Vanhanen, J., Aalto, J., Hakola, H., Makkonen, U., Ruuskanen, T., Mauldin, R. L., Duplissy, J., Vehkamäki, H., Bäck, J., Kortelainen, A., Riipinen, I., Kurtén, T., Johnston, M. V., Smith, J. N., Ehn, M., Mentel, T. F., Lehtinen, K. E. J., Laaksonen, A., Kerminen, V.-M., and Worsnop, D. R.: Direct Observations of Atmospheric Aerosol Nucleation, Science, 339, 943–946, 2013.
Lei, T., Zuend, A., Wang, W. G., Zhang, Y. H., and Ge, M. F.: Hygroscopicity of organic compounds from biomass burning and their influence on the water uptake of mixed organic ammonium sulfate aerosols, Atmos. Chem. Phys., 14, 11165–11183, https://doi.org/10.5194/acp-14-11165-2014, 2014.
Lei, T., Zuend, A., Cheng, Y., Su, H., Wang, W., and Ge, M.: Hygroscopicity of organic surrogate compounds from biomass burning and their effect on the efflorescence of ammonium sulfate in mixed aerosol particles, Atmos. Chem. Phys., 18, 1045–1064, https://doi.org/10.5194/acp-18-1045-2018, 2018.
Lei, T., Ma, N., Hong, J., Tuch, T., Wang, X., Wang, Z., Pöhlker, M., Ge, M., Wang, W., Mikhailov, E., Hoffmann, T., Pöschl, U., Su, H., Wiedensohler, A., and Cheng, Y.: Nano-hygroscopicity tandem differential mobility analyzer (nano-HTDMA) for investigating hygroscopic properties of sub-10 nm aerosol nanoparticles, Atmos. Meas. Tech., 13, 5551–5567, https://doi.org/10.5194/amt-13-5551-2020, 2020.
Mikhailov, E., Vlasenko, S., Martin, S. T., Koop, T., and Pöschl, U.: Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 9, 9491–9522, https://doi.org/10.5194/acp-9-9491-2009, 2009.
Mikhailov, E. F. and Vlasenko, S. S.: High humidity tandem differential mobility analyzer for accurate determination of aerosol hygroscopic growth, microstructure and activity coefficients over a wide range of relative humidity, Atmos. Meas. Tech., 13, 2035–2056, https://doi.org/10.5194/amt-13-2035-2020, 2020.
Mikhailov, E. F., Vlasenko, S. S., and Ryshkevich, T. I.: Influence of chemical composition and microstructure on the hygroscopic growth of pyrogenic aerosol, Izv, Atmos. Ocean. Phys., 44, 416–431, 2008.
Mochida, M. and Kawamura, K.: Hygroscopic properties of levoglucosan and related organic compounds characteristic to biomass burning aerosol particles, J. Geophys. Res.-Atmos., 109, D21202, https://doi.org/10.1029/2004jd004962, 2004.
Peng, C., Chow, A. H. L., and Chan, C. K.: Hygroscopic study of glucose, citric acid, and sorbitol using an electrodynamic balance: comparison with UNIFAC Predictions, Aerosol Sci. Technol., 35, 753–758, 2001.
Pruppacher, H. R. and Klett, J. D: Microphysics of clouds and precipitation, Kluwer Academic Publishers, Dordrecht, the Netherlands, 1997.
Pöhlker, M. L., Pöhlker, C., Ditas, F., Klimach, T., Hrabe de Angelis, I., Araújo, A., Brito, J., Carbone, S., Cheng, Y., Chi, X., Ditz, R., Gunthe, S. S., Kesselmeier, J., Könemann, T., Lavrič, J. V., Martin, S. T., Mikhailov, E., Moran-Zuloaga, D., Rose, D., Saturno, J., Su, H., Thalman, R., Walter, D., Wang, J., Wolff, S., Barbosa, H. M. J., Artaxo, P., Andreae, M. O., and Pöschl, U.: Long-term observations of cloud condensation nuclei in the Amazon rain forest – Part 1: Aerosol size distribution, hygroscopicity, and new model parametrizations for CCN prediction, Atmos. Chem. Phys., 16, 15709–15740, https://doi.org/10.5194/acp-16-15709-2016, 2016.
Raoux, S., Rettner, C. T., Jordan-Sweet, J. L., Kellock, A. J., Topuria, T., Rice, P. M., and Miller, D. C.: Direct observation of amorphous to crystalline phase transitions in nanoparticle arrays of phase change materials, J. Appl. Phys., 102, 094305, https://doi.org/10.1063/1.2801000, 2007.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd Edn., Wiley Interscience, New York, 2006.
Simoneit, B. R. T., Schauer, J. J., Nolte, C. G., Oros, D. R., Elias, V. O., Fraser, M. P., Rogge, W. F., and Cass, G. R.: Levoglucosan, a tracer for cellulose in biomass burning and atmospheric particles, Atmos. Environ., 33, 173–182, 1999.
Su, H., Rose, D., Cheng, Y. F., Gunthe, S. S., Massling, A., Stock, M., Wiedensohler, A., Andreae, M. O., and Pöschl, U.: Hygroscopicity distribution concept for measurement data analysis and modeling of aerosol particle mixing state with regard to hygroscopic growth and CCN activation, Atmos. Chem. Phys., 10, 7489–7503, https://doi.org/10.5194/acp-10-7489-2010, 2010.
Suda, S. R. and Petters, M. D.: Accurate determination of aerosol activity coefficients at relative humidities up to 99 % using the hygroscopicity tandem differential mobility analyzer technique, Aerosol Sci. Technol., 47, 991–1000, https://doi.org/10.1080/02786826.2013.807906, 2013.
Svenningsson, B., Rissler, J., Swietlicki, E., Mircea, M., Bilde, M., Facchini, M. C., Decesari, S., Fuzzi, S., Zhou, J., Mønster, J., and Rosenørn, T.: Hygroscopic growth and critical supersaturations for mixed aerosol particles of inorganic and organic compounds of atmospheric relevance, Atmos. Chem. Phys., 6, 1937–1952, https://doi.org/10.5194/acp-6-1937-2006, 2006.
Tang, I. N.: Chemical and size effects of hygroscopic aerosols on light scattering coefficients, J. Geophys. Res., 101, 19245–19250, 1996.
Tang, I. N., Fung, K. H., Imre, D. G., and Munkelwitz, H. R.: Phase Transformation and Metastability of Hygroscopic Microparticles, J. Geophys. Res.-Atmos, 99, 18801–18808, 1994.
Wang, Z., Su, H., Wang, X., Ma, N., Wiedensohler, A., Pöschl, U., and Cheng, Y.: Scanning supersaturation condensation particle counter applied as a nano-CCN counter for size-resolved analysis of the hygroscopicity and chemical composition of nanoparticles, Atmos. Meas. Tech., 8, 2161–2172, https://doi.org/10.5194/amt-8-2161-2015, 2015.
Wang, Z., Cheng, Y., Ma, N., Mikhailov, E., Pöschl, U., and Su, H.: Dependence of the hygroscopicity parameter κ on particle size, humidity and solute concentration: implications for laboratory experiments, field measurements and model studies, Atmos. Chem. Phys. Discuss. [preprint], https://doi.org/10.5194/acp-2017-253, in review, 2017.
Wiedensohler, A., Lütkemeier, E., Feldpausch, M., and Helsper, C.: Investigation of the bipolar charge distribution at various gas conditions, J. Aerosol Sci., 17, 413–416, https://doi.org/10.1016/0021-8502(86)90118-7, 1986.
Zhang, R.: Getting to the Critical Nucleus of Aerosol Formation, Science, 328, 1366–1367, 2010.
Zhang, R., Suh, I., Zhao, J., Zhang, D., Fortner, E. C., Tie, X., Molina, L. T., and Molina, M. J.: Atmospheric New Particle Formation Enhanced by Organic Acids, Science, 304, 1487–1490, 2004.
Zhang, R., Khalizov, A., Wang, L., Hu, M., and Xu, W.: Nucleation and Growth of Nanoparticles in the Atmosphere, Chem. Res., 112, 1957–2011, 2012.





