Quantifying particle-to-particle heterogeneity in aerosol hygroscopicity

The particle-to-particle heterogeneity in aerosol hygroscopicity is crucial for understanding aerosol climatic and environmental effects. The hygroscopic parameter κ, widely applied to describe the hygroscopicity for aerosols both in models and observations, is a probability distribution highly related to aerosol heterogeneity due to the complex sources and aging processes. However, the heterogeneity in aerosol hygroscopicity is not adequately represented in observations and model simulations, leading to challenges in accurately estimating aerosol climatic and environmental effects. Here, we propose an algorithm for quantifying the particle-to-particle heterogeneity in aerosol hygroscopicity, based on information-theoretic entropy measures, by using the data that come only from the in situ measurement of the hygroscopicity tandem differential mobility analyzer (H-TDMA). Aerosols in this algorithm are assumed to be simple binary systems consisting of the less hygroscopic and more hygroscopic components, which are commonly used in H-TDMA measurement. Three indices, including the average per-particle species diversity D_α, the bulk population species diversity D_γ, and their affine ratio χ are calculated from the probability distribution of κ to describe aerosol heterogeneity. This algorithm can efficiently characterize the evolution of aerosol heterogeneity with time in the real atmosphere. Our results show that the heterogeneity varies much with aerosol particle size, and large discrepancies exist in the width and peak value of particle number size distribution (PNSD) with varied heterogeneity after hygroscopic growth, especially for conditions with high relative humidity. This reveals a vital role of the heterogeneity in ambient PNSD and significant uncertainties in calculating the climate-relevant properties if the population-averaged hygroscopicity is applied by neglecting its heterogeneity. This work points the way toward a better understanding of the role of hygroscopicity in evaluating aerosol climatic and environmental impacts.

1 Introduction

Aerosol hygroscopicity describes the interaction of aerosol particles and water vapor and severely influences aerosol climatic and environmental effects (Wang and Chen, 2019; Swietlicki et al., 2008; Liu et al., 2013; Tie et al., 2017). It is highly related to the particle-to-particle heterogeneity in aerosol hygroscopicity, which is crucial but not adequately considered in observations and models, posing a challenge in accurately estimating aerosol effects on climate and environment.

Köhler theory (Köhler, 1936) is the basis of the studies on aerosol hygroscopicity. Nowadays, the most widely used parameter to describe aerosol hygroscopicity in observations and models is the hygroscopicity parameter, κ, proposed in κ-Köhler theory (Petters and Kreidenweis, 2007). κ extends and facilitates the application of Köhler theory (Zieger et al., 2013; Bian et al., 2014; Chen et al., 2014; Tao et al., 2014; Brock et al., 2016) and can be expediently observed under both subsaturated (Liu et al., 1978; Kuang et al., 2017) and supersaturated conditions (Petters and Kreidenweis, 2007; Cai et al., 2018). It can also be derived from the observed chemical composition (Liu et al., 2014). Considering that ambient aerosol particles in an aerosol differ dramatically in chemical composition due to the complex sources and aging processes (Li et al., 2021; Zheng et al., 2021; Pang et al., 2022), in terms of aerosol hygroscopicity, the distribution of the nearly hydrophobic (NH), the less hygroscopic (LH), and the more hygroscopic (MH) components (Liu et al., 2011; Tan et al., 2013b; Yuan et al., 2020) vary between and within particles; such particle-to-particle heterogeneity in aerosol hygroscopicity results in a probability distribution of κ (κ-PDF) for an aerosol (Su et al., 2010). Among the three abovementioned observing techniques, although the hygroscopicity tandem differential mobility analyzer (H-TDMA) can directly achieve κ-PDF under subsaturated condition, which is essential to investigate the hygroscopicity and activation property of aerosols, most studies focus on the analysis and application of the population-averaged κ (κ_mean) by neglecting the heterogeneity (Chen et al., 2014; Tao et al., 2014; Brock et al., 2016; Kuang et al., 2017; Liu et al., 1978, 2014; Cai et al., 2018; Yuan et al., 2020; Wang et al., 2018), leading to uncertainties in the estimation of aerosol impacts on climate and the environment.

Many research fields face the problem of heterogeneity involving the diversity of variables or issues. The diversity was first quantified in Whittaker (1972) by introducing the information-theoretic entropy in ecology and then in many other fields, including economics (Drucker, 2013), immunology (Tsimring et al., 1996), neuroscience (Strong et al., 1998), and genetics (Falush et al., 2007). Riemer and West (2013) applied it in atmospheric science for the research of aerosol mixing states. By referring to Whittaker (1972) and Riemer and West (2013), the impact of the mixing state of black-carbon-containing (BC-containing) particles on light absorption enhancement was investigated, which showed that absorption is strongly affected by the heterogeneity of BC-containing aerosol and explained that the discrepancy between simulated and observed absorption enhancement accounts for the particle-to-particle heterogeneity in composition (Fierce et al., 2016, 2020; Zhao et al., 2021). How crucial is the heterogeneity in aerosol hygroscopicity for the highly climate-relevant aerosol size distribution and optical and activation properties? However, to the best of the authors’ knowledge, most studies are not focused on quantitatively evaluating the heterogeneity concerning aerosol hygroscopicity for in situ measurements.

Given these considerations, we proposed an algorithm for quantifying the particle-to-particle heterogeneity in aerosol hygroscopicity in the real atmosphere. This algorithm is based on information-theoretic entropy measures, employing observed data from the in situ measurement of the H-TDMA. In the following, Sect. 2 describes the algorithm in detail, and the interpretation of the results from the algorithm is presented in Sect. 3. The importance of the heterogeneity and the application of the algorithm are discussed and also included in Sect. 3. The last section comes to the conclusions.

2 Data and methods

2.1 Measurement site

The campaign was implemented for two periods from 23 January to 25 February and 19 July to 8 September 2019, respectively, at the meteorological station (30.58^∘ N, 103.98^∘ E) inside the campus of Chengdu University of Information and Technology (CUIT) located in the district of Shuangliu, southwest of the main urban area of Chengdu, China. The elevation of the observation site is approximately 500 m. Figure S1 in the Supplement shows the map of the site. It is surrounded by residential neighborhoods with no nearby sources of significant industrial pollution. Aerosol particles here are representative of the urban environments. More details can be found in Yuan et al. (2020).

2.2 Data of H-TDMA measurement

A custom-built H-TDMA designed by Tan et al. (2013a) was employed to obtain the hygroscopic properties for aerosol particles with dry diameters D_p(Dry) of 40, 80, 110, 150, and 200 nm. The schematic structure of the H-TDMA is shown in Fig. S2. This H-TDMA was placed in a temperature-controlled (25^∘ C) container. The aerosol inlet equipped with a PM_2.5 impactor was set on top of the container (approximately 3 m aboveground). It mainly consists of two differential mobility analyzers (DMA) (Model 3081A, TSI Inc., USA), a humidification system, and a condensation particle counter (CPC) (Model 3787, TSI Inc., USA). Aerosol samples with a flow of 0.6 L ⋅ min⁻¹ are first introduced into a Nafion dryer (Model MD-700-24S-3, Perma Pure Inc., USA) by an external vacuum pump to maintain the relative humidity (RH) below 10 %. These aerosol particles flow through an advanced aerosol X-ray neutralizer (Model 3088, TSI Inc., USA) to be single-charged and are then screened by the first DMA (DMA-1) with set voltages. Subsequently, the selected quasi-monodisperse dry particles feed into a Nafion humidifier (Model PD-07018T-24MSS, Perma Pure Inc., USA) with a RH of 90 % (±0.3 %). Finally, the PNSDs of humidified particles out of the humidifier are measured by the second DMA (DMA-2) coupled with the CPC. The details of the H-TDMA refer to Yuan et al. (2020).

The growth factor g of the quasi-monodisperse aerosol particles g[D_p(Dry)] selected by DMA-1 equipped in the H-TDMA can be then calculated by

$$\begin{array}{}\text{(1)}& g\left[D_{\text{p}}\right(\text{Dry}\left)\right]={\displaystyle \frac{D_{\text{p}}\left(\text{RH}\right)}{D_{\text{p}}\left(\text{Dry}\right)}},\end{array}$$

where D_p(RH) represents the particle diameter screened by DMA-2 at a specific relative humidity (RH), e.g., 90 % in this study. The measured distribution function of g (g-MDF) is calculated from aerosol particle number size distribution (PNSD) counted by the CPC installed downstream of DMA-2. The TDMA_fit algorithm (Stolzenburg and McMurry, 2008) is employed to convert the g-MDF to the actual probability distribution function (g-PDF) in the campaign (Gysel et al., 2009). For each measured dry diameter, the g-PDFs are thereafter normalized as

$$\begin{array}{}\text{(2)}& \underset{\mathrm{1}}{\overset{\mathrm{\infty }}{\int }}c\left(g\right)\text{d}g=\mathrm{1},\end{array}$$

where c(g) represents the normalized g-PDF. For each g, κ can be converted using κ-Köhler theory (Petters and Kreidenweis, 2007):

$$\begin{array}{}\text{(3)}& \mathit{\kappa }=(g^{\mathrm{3}}-\mathrm{1})\times [{\displaystyle \frac{\mathrm{1}}{\text{RH}}}\times \exp ({\displaystyle \frac{\mathrm{4}{\mathit{\sigma }}_{s/a}{M}_{\text{w}}}{RT{\mathit{\rho }}_{\text{w}}{D}_{\text{p}}\left(\text{Dry}\right)g}})-\mathrm{1}],\end{array}$$

where σ_s/a of 0.072 J ⋅ m⁻² is the surface tension of the solution–air interface, M_w of 18.015 g ⋅ mol⁻¹ is the molecular weight of water, ρ_w of 1.0 g ⋅ cm⁻³ is the density of water, R of 8.315 J ⋅ K⁻¹ ⋅ mol⁻¹ is the universal gas constant, and T of 298.15 K is the temperature in Kelvin. Then, the κ-PDF can be obtained and normalized as

$$\begin{array}{}\text{(4)}& \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}c\left(\mathit{\kappa }\right)\text{d}\mathit{\kappa }=\mathrm{1},\end{array}$$

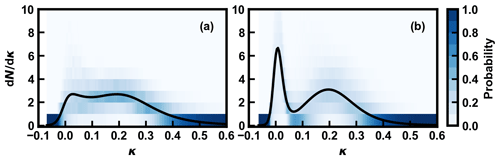
where c(κ) is the normalized κ-PDF as the examples shown in Fig. 1.

Figure 1 Typical κ-PDF for 100 nm aerosols in winter (a) and summer (b) measured by the H-TDMA over Chengdu. The shaded area is the frequency distribution of κ-PDF, and the solid lines show the campaign average of κ-PDF.

2.3 Calculation of the heterogeneity in aerosol hygroscopicity

The particle-to-particle heterogeneity in aerosol hygroscopicity is calculated by using the H-TDMA-measured κ-PDF (e.g., the examples in Fig. 1). The key assumption is that an aerosol containing N aerosol particles is a binary system consisting of the LH and MH components with respective κ of 0.01 (κ_LH) (typical for organics) and 0.6 (κ_MH) (typical for sulfate and nitrate). Each aerosol particle in the population contains one or two of the LH and MH components, and thus their κ varied between 0.01 and 0.6. κ-PDF of the aerosol can be considered the normalized aerosol number fractions varied with κ between 0.01 and 0.6 (Fig. 1). The volume fraction of these two components in each aerosol particle can be calculated based on κ according to the Zdanovskii–Stokes–Robinson (ZSR) mixing rule (Zdanovskii, 1948; Stokes and Robinson, 1966).

By referring to information-theoretic entropy measures (Whittaker, 1972; Riemer and West, 2013; Zhao et al., 2021), three indices, including the average per-particle species diversity D_α, the bulk population species diversity D_γ, and their affine ratio χ, are calculated to together describe the heterogeneity. The details are described as follows.

Firstly, for the aerosol with a given dry diameter and a known κ-PDF with X bins, the volume fraction of the LH and MH components at bin i ($i=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots },X$), i.e., P_i,LH and P_i,MH, can be calculated by the combination of

$$\begin{array}{}\text{(5)}& P_{i,\text{LH}}+P_{i,\text{MH}}=\mathrm{1}\end{array}$$

and

$$\begin{array}{}\text{(6)}& P_{i,\text{LH}}\times {\mathit{\kappa }}_{\text{LH}}+P_{i,\text{MH}}\times {\mathit{\kappa }}_{\text{MH}}={\mathit{\kappa }}_i,\end{array}$$

where κ_i is the κ at bin i.

Secondly, the mixing entropy for particles at bin i (H_i) can be calculated by

$$\begin{array}{}\text{(7)}& H_i=-P_{i,\text{LH}}\times \text{ln}{P}_{i,\text{LH}}-P_{i,\text{MH}}\times \text{ln}{P}_{i,\text{MH}}.\end{array}$$

Then the average particle mixing entropy for the aerosol (H_α) is calculated by

$$\begin{array}{}\text{(8)}& H_{\mathit{\alpha }}=\sum _{j=\mathrm{1}}^N{P}_j\times H_j,\end{array}$$

where H_j is the mixing entropy for particle j ($j=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{\dots },N$) in the aerosol. P_j is the volume proportion of particle j to the total volume of the aerosol, which is calculated by

$$\begin{array}{}\text{(9)}& P_j={\displaystyle \frac{V_j}{V_{\text{total}}}}={\displaystyle \frac{\mathrm{1}}{N}},\end{array}$$

because all particles have the same diameters. Considering that particles in the same κ bin have the same physical and chemical properties, they have the same mixing entropy. Equations (8) and (9) can be simplified as

$$\begin{array}{}\text{(10)}& H_{\mathit{\alpha }}=\sum _{i=\mathrm{1}}^X{H}_i\times c(\mathit{\kappa }{)}_i\times \mathrm{\Delta }\mathit{\kappa },\end{array}$$

where, c(κ)_i is the probability density value of the normalized κ-PDF at bin i, and Δκ is the bin width.

Additionally, the population-level mixing entropy (Hγ) is calculated by

$$\begin{array}{}\text{(11)}& H_{\mathit{\gamma }}=-P_{\text{LH}}\times \text{ln}{P}_{\text{LH}}-P_{\text{MH}}\times \text{ln}{P}_{\text{MH}},\end{array}$$

where P_LH and P_MH are the respective volume fraction of the LH and MH components in the population, and they can be calculated by

$$\begin{array}{}\text{(12)}& P_{\text{LH}}=\sum _{i=\mathrm{1}}^X{P}_{i,\text{LH}}\times c(\mathit{\kappa }{)}_i\times \mathrm{\Delta }\mathit{\kappa }\end{array}$$

and

$$\begin{array}{}\text{(13)}& P_{\text{MH}}=\sum _{i=\mathrm{1}}^X{P}_{i,\text{MH}}\times c(\mathit{\kappa }{)}_i\times \mathrm{\Delta }\mathit{\kappa }.\end{array}$$

Thirdly, the per-particle species diversity (D_i), the average per-particle species diversity (D_α), and the population species diversity (D_γ) can be calculated as

$$\begin{array}{}\text{(14)}& {\displaystyle }{D}_i=e^{H_i},\text{(15)}& {\displaystyle }{D}_{\mathit{\alpha }}=e^{H_{\mathit{\alpha }}},\end{array}$$

and

$$\begin{array}{}\text{(16)}& D_{\mathit{\gamma }}=e^{H_{\mathit{\gamma }}}.\end{array}$$

Finally, a hygroscopic heterogeneity parameter χ can be calculated as

$$\begin{array}{}\text{(17)}& \mathit{\chi }={\displaystyle \frac{D_{\mathit{\alpha }}-\mathrm{1}}{D_{\mathit{\gamma }}-\mathrm{1}}},\end{array}$$

which varied from 0 % that all particles in the population purely consist of the LH or MH component to 100 % that the LH and MH components are homogeneously distributed across all particles in the population with identical volume fractions.

2.4 Calculation of the size-resolved heterogeneity

A typical four-mode (i.e., a nucleation mode, an Aitken mode, an accumulation mode, and a coarse mode) PNSD with a wide size range of 3 nm–10 µm obtained by Ma (2013) is used for the calculation and presentation of the size-resolved heterogeneity. According to the assumption that aerosol particles in a specific mode have common sources or have experienced similar aging processes, the corresponding κ_mean and κ-PDF of one mode should be the same. The campaign average κ_mean and κ-PDF for particles with diameters of 40, 80, and 200 nm measured by the H-TDMA are used to deduce the respective κ_mean and κ-PDF for the nucleation mode, Aitken mode, and accumulation mode of the fitted PNSDs. Although the primary chemical compositions in the coarse-mode aerosol are nearly hydrophobic, some studies showed that this aerosol is slightly hygroscopic due to the coating in atmospheric aging processes (Hegg et al., 2006; Massling et al., 2009; Liu et al., 2014). However, κ for the coarse-mode aerosol is hard to be observed by the H-TDMA technique so far, due to the technical bottleneck. Considering that this aerosol has limited influence on radiative forcing and cloud because of its short lifetime and low number concentration, κ for this aerosol is assumed to be 0 as Chen et al. (2012) set. According to the contribution of each mode to the κ_mean of specific particle size, the size-resolved κ_mean for aerosol particles ranging from 3 nm–10 µm can be estimated from the known κ_mean of each mode (κ_mean,i) as

$$\begin{array}{}\text{(18)}& {\mathit{\kappa }}_{\text{mean}}\left(D_{\text{p}}\right)={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{\mathrm{4}}{\mathit{\kappa }}_{\text{mean},i}\times N_i\left(D_{\text{p}}\right)}{{\sum }_{i=\mathrm{1}}^{\mathrm{4}}{N}_i\left(D_{\text{p}}\right)}}.\end{array}$$

The size-resolved κ-PDF c(κ, D_p) can be calculated using the similar method with Eq. (19):

$$\begin{array}{}\text{(19)}& c(\mathit{\kappa },D_{\text{p}})={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{\mathrm{4}}{N}_i\left(D_{\text{p}}\right)\times c(\mathit{\kappa }{)}_i\times \mathrm{\Delta }\mathit{\kappa }}{{\sum }_{i=\mathrm{1}}^{\mathrm{4}}{N}_i\left(D_{\text{p}}\right)\times \mathrm{\Delta }\mathit{\kappa }\times \mathrm{\Delta }\text{log}{D}_{\text{p}}}}.\end{array}$$

Then, the size-resolved heterogeneity D_α(D_p), Dγ(D_p), and χ(D_p) for the wide range of 3 nm–10 µm can be obtained by using Eqs. (5)–(17).

3 Results

3.1 Diagram for particle-to-particle heterogeneity in aerosol hygroscopicity

From the calculation of Eqs. (15)–(17), D_α can represent the average of the effective number of species existing in each particle, and Dγ can represent the effective number of species in the population. Note that 1 $\le D_{\mathit{\alpha }}\le D\mathit{\gamma }$. D_α=1 when all particles are pure, while D_α=Dγ when all aerosol particles have identical components. The value of Dγ ranges from 1 to 2 according to the volume ratio of the LH and MH components in the population. Specifically, it is 1 when the population purely consists of the LH or MH component, while it is 2 when the population has the equivalent volume of the LH and MH components. A triangular region is thus presented in Fig. 2, in which χ is represented by contours.

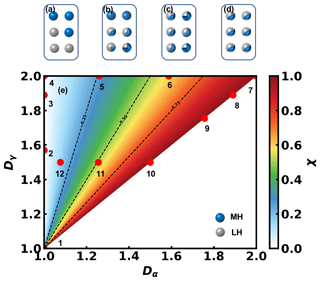
Figure 2 Example of the evolution of the heterogeneity in aerosol hygroscopicity (a–d) and diagram for the relationship among D_α, D_γ, and χ (e). Twelve different aerosols, each of which consists of six particles as shown in Table 1, are represented by the red points.

Table 1 The sketch map of the components and the corresponding indices for the 12 different aerosols in Fig. 2. The LH and MH components are represented by the colors gray and blue, respectively; V_LH and V_MH represent their volumes.

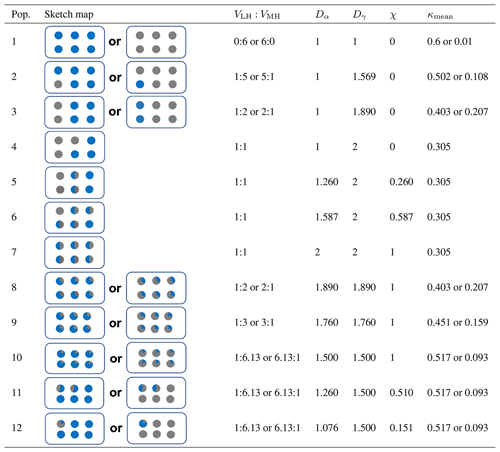
Figure 2a–d show an example of the evolution of the heterogeneity in aerosol hygroscopicity. The distributions of the NH and MH components vary between and within populations, causing different heterogeneities for these aerosols. Twelve red dots in Fig. 2e represent aerosols, each consisting of six aerosol particles with varied fractions of the LH and MH components. Their respective sketch maps and heterogeneity indices are summarized in Table 1, and the corresponding κ-PDFs are listed in Fig. S3.

For aerosols with particles purely consisting of the LH component or MH component (e.g., populations 1–4 in Fig. 2e and Table 1), D_α equals 1 and χ equals 0, although Dγ varies from 1 to 2 due to the change of the bulk volume ratio of the LH and MH components. Their κ-PDFs show that κ distributes only at 0.01 for the LH component or 0.6 for the MH component due to the pure component in each particle.

For aerosols with equal bulk volume fractions of the LH and MH components (e.g., populations 4–7 and populations 10–12 in Fig. 2e and Table 1), Dγ have constant values of 2 and 1.5, respectively. However, the different distributions of the LH and MH components in each particle of an aerosol contribute to different D_α and χ. Specifically, the heterogeneous distribution (e.g., populations 4–6 and populations 11–12 in Fig. 2e and Table 1) leads to relatively small values of D_α and χ and the dispersed κ-PDF. On the contrary, the homogeneous distribution (e.g., populations 7 and 10 in Fig. 2e and Table 1) generates a narrow κ-PDF and thus relatively high D_α and χ.

For aerosols consisting of particles with identical volume fractions of the LH and MH components (e.g., populations 7–10 in Fig. 2e and Table 1), equal values of D_α and Dγ for each population result in χ of 1, although the bulk ratio of the LH to MH components changes between populations. Accordingly, their κ-PDFs are concentrated at a single value of κ_mean.

From the populations, it can be concluded that the particle-to-particle heterogeneity in hygroscopicity resulting from the distribution discrepancy of the LH and MH components within particles can be quantified according to the κ-PDF using the proposed algorithm of this work, which is of importance to the further analysis of the existing κ-PDF and can help the heterogeneity to be considered in the calculation of aerosol climate-relevant properties.

3.2 Evolution of the heterogeneity in the real atmosphere

In this section, we apply the proposed algorithm to the in situ measurement of the H-TDMA that was implemented for two periods in 2019, located in Chengdu, China. In the following, the expression of the κ-PDF is equivalent to the g-PDF due to their one-to-one corresponding relationship. In order to show the variation characteristics and the significance of D_α, Dγ, and χ in the real atmosphere, especially for the condition that the total hygroscopicity of aerosol remained constant, two episodes with a tiny change of κ_mean during the observation periods are presented. The 110 nm aerosol is chosen as an example to show the typical evolution processes for aerosol heterogeneity, because it has a large number concentration and lies in the transition zone between the diameters that show the processes of gas-to-particle (<100 nm) and aging (>100 nm) in the atmosphere. The variation of the heterogeneity in a 110 nm aerosol can better reflect the evolution of aerosol particles in the real atmosphere and may have a great impact on the direct radiative forcing. The first episode appeared from 22:00 (LST) 23 January 2019 to 08:00 (LST) 24 January 2019, and the other one occurred from 00:00 27 January 2019 to 12:00 27 January 2019. The variations of D_α, Dγ, χ, and κ_mean during these two episodes are shown in Fig. 3. The tiny change of κ_mean indicates the slight variation of the bulk fraction of the LH and MH components in the aerosol. The decreasing trends of D_α and χ reveal that the existing aged aerosols with uniformly distributed LH and MH components among particles at night, indicated by the unimodal distributions of κ-PDF and relatively high χ (0.831 for episode 1 at 22:00 and 0.832 for episode 2 at 00:00), were intruded upon by the fresh emissions during midnight as reflected by the bimodal and wider distribution of κ-PDF (Yuan et al., 2020). This process led to component discrepancies among particles in populations and thus the decrease of D_α and χ during midnight.

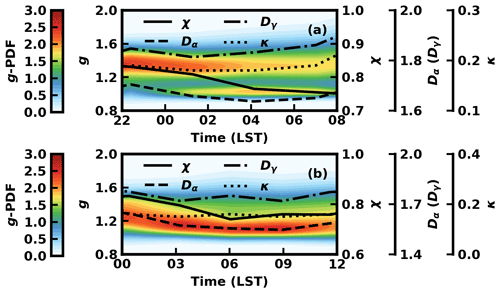
Figure 3 The variation of κ-PDF, D_α, D_γ, and χ during two typical evolution processes for 110 nm aerosols with tiny changes of κ_mean on 23 January 2019 (a) and 27 January 2019 (b).

The statistics of D_α, D_γ, and χ for aerosols with five measured diameters are shown in Fig. 4. The patterns of the distributions for D_α and D_γ move to larger values with increasing diameter, indicating that the effective number of species increases in aerosols with larger diameters due to the longer aging time in the atmosphere. This trend is more obvious in the summer campaign. Taking the aerosol of 110 nm for example, D_α varies between 1.386 and 1.850, and D_γ varies between 1.470 and 2.000 during the winter field measurements. The ranges of D_α and D_γ in summer are 1.280–1.928 and 1.371–2.000, respectively, contributing to a wider distribution of χ. This indicates that the fraction of the LH and MH components varied more pronouncedly due to the more complex aging processes in summer compared to that in winter. χ ranging from 0.6 to 0.9 reveals the large variation of heterogeneity in aerosol hygroscopicity in the real atmosphere.

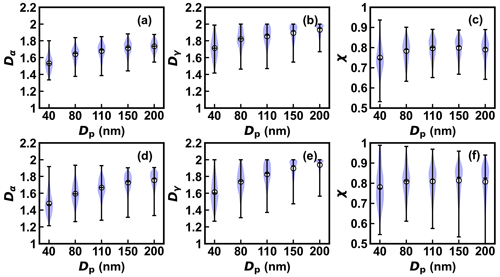
Figure 4 The statistics of D_α, D_γ, and χ for aerosols of five measured diameters in winter (a), (b), (c) and summer (d), (e), (f). The shaded area is the frequency distribution of the indices. The three bars on the whisker for each diameter from the bottom to the top are the minimum, median, and maximum, and the circles represent the average of the indices.

The details in the variation characteristics of the heterogeneity and the difference among the aerosols of five measured diameters will be further discussed in our future studies. It can be concluded from the discussion above that aerosols with a tiny variation of κ_mean can have ever-changing heterogeneity in aerosol hygroscopicity in the atmosphere. The algorithm proposed in this work can efficiently characterize this heterogeneity with time and provide detailed information about the evolution of aerosols in the air. More importantly, this algorithm offers an unexplored understanding of the H-TDMA measurement.

3.3 Importance of the heterogeneity in aerosol hygroscopicity

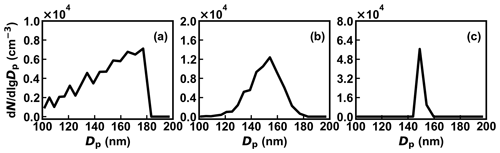
The same bulk volume fraction of the LH and MH components indicates the same κ_mean for populations (e.g., populations 4–7 and populations 10–12). This reveals the identical diameter for all particles in each population after hygroscopic growth at high RH. Actually, due to the particle-to-particle heterogeneity in one population, different ratios of the LH and MH components in each particle result in different κ (e.g., particles in each of populations 4–7), which can lead to different ambient number size distributions, especially for the condition with high RH. Figure 5 depicts a sample of the hygroscopic size distribution, where RH is 90 %, for three aerosols with the same κ_mean of 0.305 but different χ of 0.653, 0.884, and 0.999, respectively. Each of these three populations contains 1000 aerosol particles with dry diameters of 100 nm. Significant discrepancies can be seen in the number size distribution that the width decreases, while the peak value increases with increasing χ after hygroscopic growth. Thus, the heterogeneity in aerosol hygroscopicity plays a significant role in the evolution of aerosol ambient number size distributions, which is a key factor for evaluating aerosol radiative forcing.

Figure 5 Aerosol particle size distributions after hygroscopic growth at a RH of 90 % for three aerosols with χ of 0.653 (a), 0.884 (b), and 1 (c). Each of these three populations has the same κ_mean of 0.305 and contains 1000 aerosol particles with dry diameters of 100 nm.

3.4 Size-resolved heterogeneity in aerosol hygroscopicity

The heterogeneity for only one size can contribute to dramatically different ambient size distributions, especially for the condition under high RH. Thus, it is urgently needed to figure out how the heterogeneity varies with aerosol size in the real atmosphere. This section discusses the characteristic of the size-resolved heterogeneity in aerosol hygroscopicity.

The PNSD within the range of 3 nm–10 µm is commonly observed by commercial instruments, including the scanning mobility particle sizer (SMPS) and the Wide-range Particle Spectrometer (WPS) around the world (Wu and Boor, 2021). However, the widely used H-TDMA technic can only observe the growth factor of aerosols with limited sizes (generally smaller than 350 nm in the dry condition), e.g., 40, 80, 110, 150, and 200 nm in this study. Recently, Shen et al. (2021) extended the H-TDMA measurement of aerosol hygroscopic properties to 600 nm in the urban environment. Although κ for larger particles (>1 µm) can be derived from the size-resolved chemical composition (Gysel et al., 2007; Liu et al., 2014), the size-resolved κ with high size and time resolution is scarce and is needed to be observed or reversed by more advanced technology and new algorithms. Fortunately, Chen et al. (2012) provided an approach to derive the size-resolved κ for aerosols within the range of 3 nm–10 µm based on the measured PNSDs and H-TDMA-determined κ. They used the κ_mean for each measured size by neglecting aerosol heterogeneity. Here, the heterogeneity in aerosol hygroscopicity is considered based on the method provided by Chen et al. (2012).

The typical four-mode PNSD mentioned above is used and shown in Fig. 6a and d. The κ_mean and the corresponding κ-PDFs for the nucleation mode, Aitken mode, and accumulation mode are represented by those measured at sizes of 40, 80, and 200 nm, respectively, during the winter (Fig. 6b) and summer (Fig. 6e) campaigns. The calculated size-resolved κ_mean are shown in Fig. 6c (winter) and Fig. 6f (summer), in which κ-PDF for each size contributed by the heterogeneity in aerosol hygroscopicity is represented by the contour. The variation of both the size-resolved κ_mean and the corresponding κ-PDF is influenced by the contribution of each mode to the total number concentration. The corresponding χ for the size range of 3 nm–10 µm can therefore be calculated by using the framework proposed by this work.

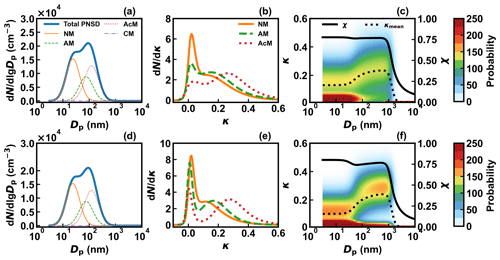
Figure 6 The typical PNSD (a), (d) and the κ-PDF during the winter (b) and summer campaigns (e) used for calculating the size-resolved κ_mean, the size-resolved κ-PDF, and the corresponding size-resolved χ (c), (f). The solid lines (blue) in (a) and (d) are the measured PNSD that can be fitted by a four-mode (a nucleation mode (NM), an Aitken mode (AM), an accumulation mode (AcM), and a coarse mode (CM)) lognormal distribution, which is represented by the thin solid line (orange), the dashed line (green), the dotted line (red), and the dash-dotted line (purple), respectively. The corresponding type and color lines represent the measured campaign average κ-PDF for each mode in (b) and (e). The dotted line in (c) and (f) is the calculated size-resolved κ_mean, and the shaded color is the corresponding size-resolved κ-PDF. The solid lines in (c) and (f) are the calculated size-resolved χ.

As shown in Fig. 6, the consideration of the heterogeneity provides the size-resolved κ-PDF, which can further show the region where κ is mostly distributed for aerosols of any size and how aerosol particles evolve with size in the population. For example, although the κ_mean for aerosols smaller than 40 nm is 0.131 during the winter campaign, the κ-PDF shows most κ locate at a narrow area lower than 0.05. The continuous evolution of the κ-PDF with sizes smaller than 1 µm indicates that on the one hand, a part of the aerosol particles in the population has increasing hygroscopicity during the aging process of growing up, which is the main reason for the increase of κ_mean, and on the other hand, NH-dominated particles exist across all sizes. This corresponds to the slight decreasing trend of χ accompanied by a wider area of κ ranging from 0.01 to larger than 0.4, which reflects the heterogeneous distribution of the LH and MH components between aerosol particles within a population during the aging progress.

Additionally, the phenomenon that a sharp decrease of χ close to 0.1 for aerosols larger than 1 µm and the κ-PDFs for this size range shows a very narrow band lying at κ of 0 responds to the assumption that the coarse-mode particle is mainly composed of the NH component.

Overall, this newly developed aerosol heterogeneity provides more insight into the evolution of aerosols during the aging processes. The hygroscopicity of an aerosol is complicated and diverse due to the particle-to-particle heterogeneity in aerosol hygroscopicity; if only the κ_mean is applied without considering aerosol heterogeneity, significant uncertainty will occur.

4 Conclusions

The particle-to-particle heterogeneity in aerosol hygroscopicity is of great importance for a better understanding of the impact of hygroscopicity on estimating aerosol climatic and environmental effects. Unfortunately, the heterogeneity has not been paid attention to in previous studies, of which only the population-averaged hygroscopicity parameter, κ_mean, is considered, mainly because the heterogeneity is difficult to be quantified in both observations and models.

In this work, we proposed an algorithm to quantify the particle-to-particle heterogeneity in aerosol hygroscopicity from the in situ measurement for the first time. This algorithm is an innovation on the basis of the mature theory in information-theoretic entropy and the widely used assumption that aerosols are binary systems consisting of the commonly defined LH and MH components from H-TDMA measurement.

Three indices, including the average per-particle species diversity D_α, the bulk population species diversity D_χ, and their affine ratio χ, are calculated from the probability distribution of κ to together describe aerosol heterogeneity. They can efficiently characterize and provide more insight into the evolution of aerosol heterogeneity with time in the real atmosphere during the aging processes.

The heterogeneity varies much with aerosol particle size, and large discrepancies can be seen in aerosol particle number size distribution (PNSD) that the width decreases, while the peak value of the PNSD increases with increasing χ after hygroscopic growth, especially for conditions with high relative humidity, indicating the vital role of the heterogeneity in the evolution of ambient PNSD.

Considering that PNSD is a key factor for the evaluation of aerosol impacts on radiative forcing, significant uncertainties will occur in calculating the climate-relevant properties if κ_mean is applied by neglecting its heterogeneity. Thus, the particle-to-particle heterogeneity in aerosol hygroscopicity is urgently needed to be represented in models. The algorithm proposed by this work, which has the intuitive and quantitative interpretation of aerosol heterogeneity, sheds light on the reanalysis of the existing H-TDMA datasets and could have a large impact on how we use and think about these datasets. It can also provide a bridge for using observations to constrain numerical models to deeply investigate how heterogeneity in aerosol hygroscopicity influences aerosol effects on climate and the environment.