the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Parameterizing the aerodynamic effect of trees in street canyons for the street network model MUNICH using the CFD model Code_Saturne
Cédric Flageul
Bertrand Carissimo
Yunyi Wang
Andrée Tuzet
Trees provide many ecosystem services in cities such as urban heat island reduction, water runoff limitation, and carbon storage. However, the presence of trees in street canyons reduces the wind velocity in the street and limits pollutant dispersion. Thus, to obtain accurate simulations of pollutant concentrations, the aerodynamic effect of trees should be taken into account in air quality models at the street level.
The Model of Urban Network of Intersecting Canyons and Highways (MUNICH) simulates the pollutant concentrations in a street network, considering dispersion and physico-chemical processes. It can be coupled to a regional-scale chemical transport model to simulate air quality over districts or cities. The aerodynamic effect of the tree crown is parameterized here through its impact on the average wind velocity in the street direction and the vertical transfer coefficient associated with the dispersion of a tracer. The parameterization is built using local-scale simulations performed with the computational fluid dynamics (CFDs) code Code_Saturne. The two-dimensional CFD simulations in an infinite street canyon are used to quantify the effect of trees, depending on the tree characteristics (leaf area index, crown volume fraction, and tree height to street height ratio) using a drag porosity approach. The tree crown slows down the flow and produces turbulent kinetic energy in the street, thus impacting the tracer dispersion. This effect increases with the leaf area index and the crown volume fraction of the trees, and the average horizontal velocity in the street is reduced by up to 68 %, while the vertical transfer coefficient by up to 23 % in the simulations performed here.
A parameterization of these effects on horizontal and vertical transfers for the street model MUNICH is proposed. Existing parameterizations in MUNICH are modified based on Code_Saturne simulations to account for both building and tree effects on vertical and horizontal transfers. The parameterization is built to obtain similar tree effects (quantified by a relative deviation between the cases without and with trees) between Code_Saturne and MUNICH. The vertical wind profile and mixing length depend on leaf area index, crown radius, and tree height to street height ratio. The interaction between the trees and the street aspect ratio is also considered.
- Article
(3104 KB) - Full-text XML
- BibTeX
- EndNote
Cities are, by definition, areas with high densities of people, infrastructure, and activities, and this urbanization causes many issues. First, air quality is poor because of the numerous air pollutants emitted by anthropic activities such as traffic, industries, or residential activities, and the reduction in air flow by high buildings limits the dispersion of these pollutants (Faiz, 1993; Akimoto, 2003; Yuan et al., 2014; Zhang et al., 2020). In addition to air pollution issues, radiative and water budgets are strongly modified in cities compared to the countryside (Bozonnet et al., 2015). Temperatures are, on average, higher than in the countryside because of the urban heat island created by additional anthropogenic energy released, storage of radiative energy in dark materials, radiation multi-reflection, and lack of vegetation and associated evapotranspiration (Oke, 1982; Pigeon et al., 2007; Stewart, 2011; Hebbert and Jankovic, 2013). Impervious soils also decrease water infiltration and intensify runoff (Leopold, 1968). In addition, growing urbanization and increasing extreme events (due to climate change) such as pollution peaks, heat waves, and floods have negative consequences on the environment and human health (Robine et al., 2007; Angel et al., 2011; Pascal et al., 2013; West et al., 2016; IPCC, 2021).
One nature-based solution is to green the city by planting vegetation as lawns, planting trees in streets or in parks, and growing green walls and roofs (Livesley et al., 2016; Revelli and Porporato, 2018). Vegetation and especially trees contribute to improve human thermal comfort by creating a favorable micro-climate with lower air temperature (through solar radiation interception and creation of shade) and higher evaporation (through ground and vegetation evapotranspiration; Taha et al., 1991; Bowler et al., 2010; Gillner et al., 2015; Klemm et al., 2015; Lobaccaro and Acero, 2015; Gunawardena et al., 2017). This positive effect of trees is significant in particular during heat wave episodes, which will be more frequent in the future due to climate change (IPCC, 2021). Trees and vegetated areas also favor infiltration in soils that contributes to offset water runoff induced by soil artificialization (Armson et al., 2013; Berland et al., 2017). Besides, vegetation is known to store carbon (Nowak and Crane, 2002; Svirejeva-Hopkins et al., 2004) and to enhance human well-being (van Dillen et al., 2012; Bertram and Rehdanz, 2015; Krekel et al., 2015). For all these ecosystem services in urban areas, city greening is often promoted and, for example, the city of Paris has about 205 000 trees of which 52 % are roadside trees (Direction des Espaces Verts et de l'Environnement – Mairie de Paris, 2021).
Many studies have tried to figure out the impact of trees on air pollution in a street canyon, and they have shown that trees are an important parameter to take into account if we want to understand and accurately simulate the pollutant concentrations in the streets (Beckett et al., 1998; Nowak et al., 1998; Jayasooriya et al., 2017). Vegetation, and especially trees, represent surfaces available for pollutant dry deposition and, hence, can contribute to reducing air pollutant concentrations. However, pollutant removal and its impact on air quality vary greatly, depending on tree characteristics, tree species, and pollutant type (Nowak et al., 2006; Hwang et al., 2011; Selmi et al., 2016; Xue and Li, 2017; Ozdemir, 2019). Trees may also affect atmospheric chemistry by emitting biogenic volatile organic compounds (BVOCs), which may lead to the formation of ozone and secondary organic aerosols (Calfapietra et al., 2013; Préndez et al., 2019; Gu et al., 2021). Furthermore, trees may alter air quality by influencing aerodynamic processes and limiting the pollutant dispersion (Buccolieri et al., 2011; Wania et al., 2012; Vos et al., 2013; Gromke and Ruck, 2007, 2009, 2012; Gromke and Blocken, 2015). The aerodynamic effect of trees is defined as the drag force resulting from the friction between the air and the leaves. Since the tree crown can be seen as a porous medium as air passes through it but is slowed down, and the drag force increases with the leaf surface.
For wind perpendicular to a street, the air recirculates inside the street canyon (Harman et al., 2004). Pollutants emitted at the bottom of the street (by traffic) accumulate on the leeward side of the street, inducing higher local concentrations (Vardoulakis et al., 2003; Cai et al., 2008; Huang et al., 2019). Obstacles in the street, such as trees, can strongly impact the air flow and intensify the pollutant accumulation (Vos et al., 2013). This effect has been studied using computational fluid dynamics (CFD) models where the aerodynamic influence of trees on the flow is represented by a porosity model (Buccolieri et al., 2009; Zaïdi et al., 2013; Wei et al., 2016; Jeanjean et al., 2017; Santiago et al., 2017). Vos et al. (2013) showed that pollutant concentrations may increase by 20 % in a street because of the presence of two rows of trees in the street. The effects of vegetation depend on the height, width, and density (leaf area index) of trees (Vos et al., 2013; Janhäll, 2015), as well as the height to width ratio of streets (Wania et al., 2012). Finally, it is necessary to accurately assess the effect of trees on pollutant dispersion in order to find what configurations are more effective in reducing air pollution in street canyon and to guide urban development policy (Janhäll, 2015).
The effect of trees on aerodynamic processes should also be considered at the street level in air quality models. As discussed previously, CFD models including trees are used to study wind fields and pollutant transport in street canyons (Li et al., 2006). However, as the street is discretized with a fine mesh, the computational cost is high, and simulations at the city scale are too expensive today. Fast-running codes, such as simplified street network or street-in-grid models, are developed to simulate street pollutant concentrations over neighborhoods or cities, but they do not take into account the effect of trees in the streets. The objective of this study is to parameterize the effect of trees on air flow in the Model of Urban Network of Intersecting Canyons and Highways (MUNICH; Kim et al., 2018; Lugon et al., 2020, http://cerea.enpc.fr/munich/, last access: 17 December 2021). To build this parameterization, simulations in street canyons are performed with Code_Saturne (Archambeau et al., 2004, https://www.code-saturne.org/, last access: 17 December 2021), a CFD code, which can represent the tree aerodynamic effect with a drag porosity approach (Katul et al., 2004) and has previously been compared with field measurements (Zaïdi et al., 2013). MUNICH parameterizations have already been compared with Code_Saturne results in a treeless canyon, and a new parameterization for horizontal and vertical transfers has been developed in MUNICH based on Wang (2012, 2014) and Code_Saturne simulations (Maison et al., 2022). In the present study, the tree aerodynamic effect is added to this parameterization, and Code_Saturne (version 6.0) is used as a reference to parameterize the aerodynamic effect of trees in the street network model MUNICH. CFD simulations are performed in three streets of aspect ratios varying from 0.3 to 1.0, and a large range of tree leaf area index, crown radius, and heights is tested. The tree aerodynamic effect quantified with Code_Saturne is analyzed depending on these street and tree characteristics.
The approach to modeling the dispersion of pollutants in MUNICH and Code_Saturne is fundamentally different due to their physical modeling and discretization in space and time. MUNICH is a street network model that simulates air pollutant concentration in an urban canopy. Street dimensions and pollutant concentrations are assumed to be homogeneous in each street segment. Air flow is divided into a horizontal flux from one street to another and a vertical flux between the street and the background (Maison et al., 2022). Background concentrations above the street can be computed by 3D chemistry transport models (CTMs), such as Polair3D (Sartelet et al., 2018; Lugon et al., 2020, 2021). To build the tree parameterization, the CFD simulation setup is adapted for the comparison with MUNICH, and several simulations are performed with Code_Saturne, considering a range of street and tree characteristics.
The structure of the paper is as follows. The MUNICH and Code_Saturne models are presented in Sect. 2. Then, the tree effect on horizontal wind speed and vertical transfer coefficient is quantified with Code_Saturne simulations in Sect. 3 and parameterized in MUNICH in Sect. 4. Conclusions are presented in Sect. 5.
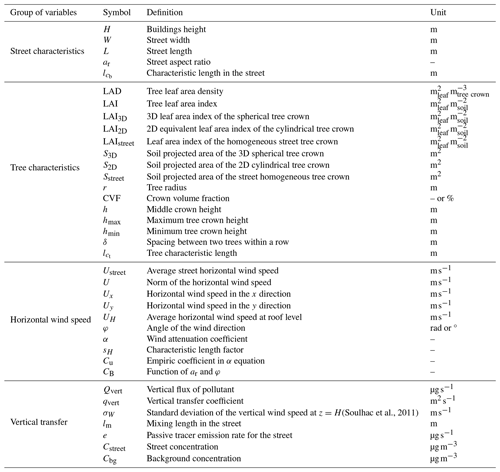
2.1 Description of MUNICH
In MUNICH, each street segment is assumed to be homogeneous, i.e., with uniform building height H and street width W and of length L (m). The street is characterized by its height-to-width ratio called the aspect ratio, (–). Only the average pollutant concentrations over the street are considered. Pollutants are transported by the horizontal wind speed (advection) in the street network and by a vertical transfer coefficient between the streets and the background. Several parameterizations of the horizontal wind speed and of the vertical transfer coefficient exist in MUNICH. The ones recently developed in Maison et al. (2022) and based on Code_Saturne simulations are used and detailed here. The vertical profile of the wind speed in the street direction is calculated as an attenuation of the wind speed in the street direction and at the roof level, UH,φ (m s−1), as follows (Maison et al., 2022):
where C1 and C2 are integration coefficients, and I0 and K0 are the first and second type modified Bessel functions of order 0. Besides, the wind speed at the roof level UH has to be multiplied by to select the component of the wind speed in the street direction, where φ is the angle between the wind direction and the street orientation (∘). This vertical wind profile is then integrated between the soil roughness (m) and H to compute the average horizontal wind speed in the street direction. The function g is calculated as follows (Wang, 2012, 2014):
and
where α is a dimensionless coefficient expressing the effects of wind angle on wind attenuation in the street. It is computed as follows:
where is a dimensionless factor describing the effect of canopy on the mixing length lm (Wang, 2012, 2014). The mixing length is calculated as follows:
where κz corresponds to the mixing length over a rough bare soil (without canopy), and is the characteristic length (m) in the street canyon, corresponding to the mixing length of the urban canopy alone ( W).
The vertical transfer coefficient that drives pollutant exchange between the street and the background zone is calculated at z=H as follows:
where σW (in m s−1) is a velocity scale equal to the standard deviation of the vertical wind speed. It depends on both the friction velocity above the urban canopy, u*, and on atmospheric stability (Soulhac et al., 2011).
In Sect. 4, the tree effect is parameterized by taking into account the characteristic length of the trees in the mixing length lm (Eq. 19, which leads to modifications in the coefficient α Eq. 23).
2.2 Description of Code_Saturne
2.2.1 Street and tree modeling setup
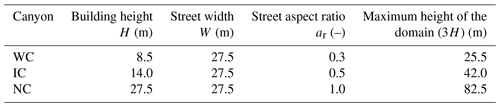
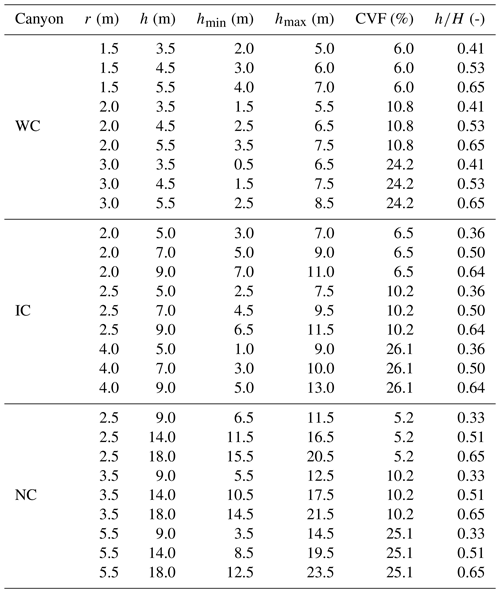
In the present study, the tree effect is studied in three street canyons of the following different street aspect ratios: a wide street canyon (WC), an intermediate canyon (IC), and a narrow canyon (NC). Their characteristics are presented in Table 1.
A color code is introduced to simplify the reading of the figures, with red symbols for the wide canyon (WC), purple ones for the intermediate canyon (IC), and blue ones for the narrow canyon (NC). Abbreviations, parameters, and variables used are listed in Appendix A.
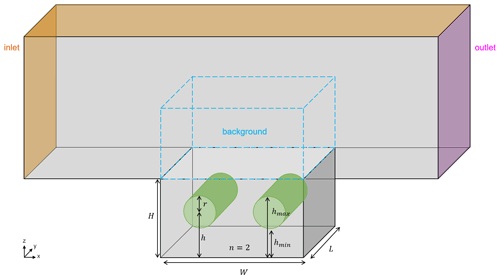
The k−ε linear production turbulence model is used in Code_Saturne. Stationary simulations are performed with a thermally neutral atmosphere. A 2D infinite street canyon is modeled with periodic condition on the y axis, but the flow and the wind speed vector are 3D. The mesh is composed of hexahedral cells of 1 m in the y-axis direction and 0.5 m on the x and z axes. The vertical profiles of U, k, and ε are set in the inlet (top left border of the domain). The complete description of Code_Saturne simulation setup in treeless canyons can be found in Maison et al. (2022).
The tree geometry and its representation in Code_Saturne are shown in Fig. 1. Here, two rows of trees (n=2) are considered, with one on each side of the street, and whose positions on the x axis are x=34.5 m and x=48.0 m (the wall positions are x=27.5 and x=55.0 m). The tree crown centers are located in a position on the x axis so that the largest crowns (CVF≈25 %) do not reach the street walls for the three street canyons studied. r is the tree radius (m), h, hmin, and hmax correspond, respectively, to the middle, minimum, and maximum heights of the tree crown (m). Note that all the simulations verify hmax≤H, i.e., the top of the trees do not exceed the top of the street.
In the cells containing the trees, an additional drag term is added to the Navier–Stokes equations as follows (Katul et al., 2004; Zaïdi et al., 2013):
where |U| is the modulus of U, Ui is the velocity in the i-direction, LAD is the leaf area density in square meters of leaf surface per cubic meter of crown volume (), ρ is the air density, and is the tree drag coefficient set to 0.2, which is a representative value for trees (Katul and Albertson, 1998). The leaf area index (LAI) is the one-sided green leaf area per unit ground surface area, and the leaf area density (LAD) is the one-sided green leaf area per unit volume. They are calculated as follows:
The source terms for trees are also implemented in the k−ε equations as follows:
where , βp=1.0, and βd=5.03 are constants of the model (Zaïdi et al., 2013). Note that this type of tree aerodynamic effect modeling is commonly used and evaluated by comparison with experimental results (Buccolieri et al., 2018).
Only the impact of the tree leaves is considered, and the impact of the tree trunk and branches on the flow is not modeled. As the streets are modeled in 2D and an infinite length in the y direction is assumed (see Sect. 2), the LAI considered here is the equivalent cylindrical LAI2D. Usually, studies consider the tree LAI, which is well defined for a 3D tree. The relation between the tree LAI3D and the equivalent cylindrical LAI2D is given in Appendix B. To check that this effect of trees is well modeled using this simplified 2D setup, 3D simulations were performed and compared to some of the 2D simulations presented here, showing very good agreement between the 2D and 3D simulations in terms of the influence of the trees on the flow (Appendix B).
To gain a complete vision of the effect of trees, 45 simulations are performed per canyon, and the impact of three independent tree parameters are studied, including the following:
-
The 2D-equivalent LAI, i.e., LAI2D=0.5, 1, 2, 3, and 4 (see Appendix B, for the conversion between LAI3D and equivalent LAI2D).
-
The crown volume fraction (CVF), calculated as the tree (2D cylindrical) crown volume divided by the street volume, i.e., . This ratio is already used in studies quantifying the effect of trees on street pollution such as Gromke and Blocken (2015). The relation between 2D and 3D CVF is shown in Appendix B. Note that, apart from Appendix B, all CVF mentioned in the figures and in the text refer to the 2D CVF. In total, the following three CVF ranges are simulated: CVF≈5, 10, and 25 %.
-
The tree-to-street height ratio calculated as the crown middle height divided by the building height (). In total, the following three ranges are simulated: , , and .
Note that these three tree characteristics are normalized by street characteristics, and similar values are chosen in the three canyons to be able to compare them and to quantify if the street aspect ratio influences the tree effect (i.e., if there is an interaction between tree and building effects). However, the normalized tree characteristics are not exactly equal in the three canyons due to the street sizes and the 0.5 m mesh cells that limit the possible range of tree sizes. The detailed list of the tree characteristics and the different values used for the tree parameters are presented in Table A4.
2.2.2 Calculation of vertical and horizontal transfers in Code_Saturne for comparison to MUNICH
To evaluate the vertical transfer between the street and the background zone in Code_Saturne, a passive tracer is emitted in each mesh cell of the street, with an arbitrary stationary emission rate e=1000 µg s−1 for a street canyon of length L=1 m. For the tracer to be dispersed only by vertical transfers and not by horizontal winds within the street, simulations are performed with the wind perpendicular to the street at the inlet (φ=90∘). The initial street and background tracer concentrations are zero. At the end of the simulation (stationary state reached), the tracer concentration is averaged in the street and in the background zone (denoted as Cstreet and Cbg in µg m−3) to reproduce a MUNICH homogeneous street assumption. The background zone corresponds to the area of the same volume as the street but located just above the street (see Maison et al., 2022, for more details). In the absence of other processes (horizontal transport, deposition, and chemical reactions), the tracer mass balance in the street yields the following:
where Qvert is the vertical flux of pollutant at the roof level for the whole street (µg s−1), qvert is the vertical transfer coefficient (m2 s−1), and WL is the exchange surface (m2). Thus, the vertical transfer coefficient can be compared between both models. In Code_Saturne, qvert is calculated from the emission rate e and the concentration gradient , following Eq. (14), and in MUNICH, it is calculated from Eq. (7).
In MUNICH, the horizontal transfer velocity is equal to the street average horizontal wind speed in the street direction Ustreet, which is calculated by integrating Eq. (1) between and z=H. In Code_Saturne, Ustreet is estimated from the wind speed in the y direction averaged over the street mesh cells. In addition to Ustreet, the MUNICH vertical profile of the wind speed (Eq. 1) can also be compared to Code_Saturne by averaging the wind speed in the y direction over the street width (x axis).
As the objective of the study is to parameterize the aerodynamic effect of trees, the chemistry and deposition on built and vegetated surfaces are not considered here. Further details on the simulation setup of MUNICH and Code_Saturne and on the comparison of vertical and horizontal transfers in a treeless canyon are presented in Maison et al. (2022).
To quantify tree effect on the horizontal wind speed along the street and on the vertical transfer coefficient, Code_Saturne simulations are performed for a large range of tree characteristics (LAI2D, CVF, and height ratio ), as summarized in Table A4. The tree effect is expressed as a relative deviation between the simulations without and with trees.
3.1 Tree effect on horizontal transfer
To quantify and compare the effect of tree crowns in Code_Saturne and MUNICH, and thus to overcome eventual differences between the two models observed in a treeless canyon for the horizontal velocity Ustreet, a relative deviation (RD) of Ustreet, between the simulations with and without trees (%), is computed as follows:
where stands for the average wind velocity in a treeless street, and Ustreet is the average wind velocity in a street with trees, as computed with Code_Saturne. This RD between the Code_Saturne simulations with and without trees is shown in Fig. 2a for WC, 2b for IC, and 2c for NC. It shows that becomes increasingly negative, meaning that Ustreet decreases as the LAI2D and the CVF increase. On the opposite, the tree height has either no impact or a small impact compared to LAI2D and CVF. When the effect of tree height is noticeable, an increase in the tree height induces a decrease in RD.
In the range of the tree characteristics studied, Ustreet is attenuated from 7.3 % to 62.3 %. The tree effect on Ustreet can be compared between the three canyons. The tree effect on Ustreet increases as the canyon is deeper, highlighting the complex interaction between the street dimensions and the tree effect on the velocity. This observation is consistent with the study of Wania et al. (2012).
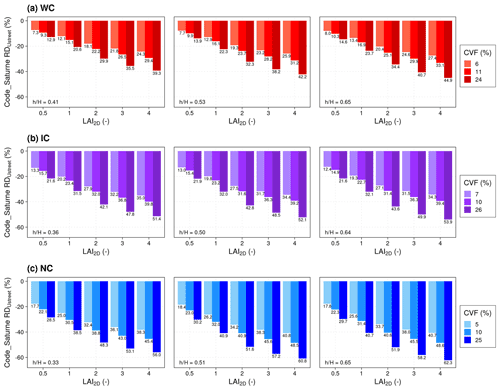
Figure 2Relative deviation (RD) of Ustreet computed from Code_Saturne simulations for different tree LAI2D, CVF, and height ratio for WC (a), IC (b), and NC (c). The graphic is divided into three columns corresponding to the three height ratios, and higher CVF correspond to darker colors. values are specified with data labels.
3.2 Tree effect on vertical transfer
The relative deviation of the vertical transfer coefficient () between simulations with and without trees is introduced to quantify the tree effect on the vertical transfer coefficient. Similar to the relative deviation of Ustreet (Eq. 15), the relative deviation (%) is expressed as follows:
where stands for the vertical transfer coefficient in a treeless street, and qvert is the vertical transfer coefficient in a street with trees. Code_Saturne is plotted for different tree parameters LAI2D, CVF, and height ratio in Fig. 3a for WC, 3b for IC, and 3c for NC.
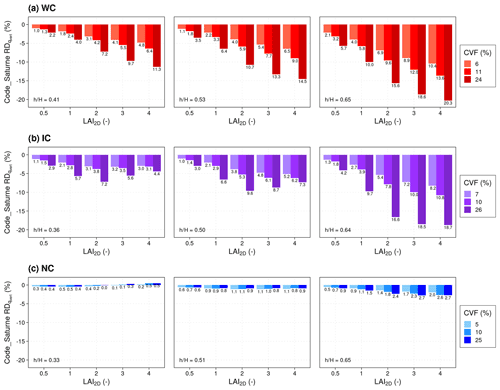
Figure 3Relative deviation (RD) of qvert computed from Code_Saturne simulations for different tree LAI2D, CVF, and height ratio for WC (a), IC (b), and NC (c). The graphic is divided into three columns corresponding to the three height ratios, and higher CVF correspond to darker colors. values are specified with data labels.
For WC, increases with tree LAI2D, CVF, and height ratio (Fig. 3a). For IC, also increases with CVF and height ratio, but tends to slightly decrease as the LAI increase when the LAI is high and the ratio is small (differences between LAI=3 and 4 for and 0.50; Fig. 3b). For NC, a small increase in with LAI2D and CVF is observed for . However, for the two other smaller height ratios, the tree effect is very low (; Fig. 3c).
This reduction in the tree effect on qvert when LAI or CVF increases for small ratios in IC and NC can be explained by micro-scale effects (modified air flow path and turbulent viscosity) and is left out of the scope of the present study due to the corresponding low amplitude. Besides, investigation of such micro-scale effects would probably require more advanced turbulence models, for example, switching from a first-order model, k−ε, to a second-order one (Rij-SSG; Speziale et al., 1991) or a 3D large eddy simulation (LES).
Note that, unlike Ustreet (Sect. 3.1), the tree effect on qvert decreases when the canyon becomes deeper. For example, the tree effect, as quantified by , ranges between −1.0 % and −20.3 % for WC, −1.0 % and −18.7 % for IC, and 0.5 % and −2.7 % for NC. The averaged tree effect is relatively less strong when the canyon is deeper. In other words, regarding vertical transfers, the street effect dominates over the tree effect.
For vertical transfer, a wind perpendicular to the street (φ=90∘) is used to focus on the effects on vertical transfers only. In this case of perpendicular wind, the air flow occurring in street canyons is complex and leads to heterogeneous tracer concentration in the street. In general, for the three canyons, the presence of the two tree crowns tends to increase the tracer concentration on the leeward side of the street and to decrease it on the windward side (Buccolieri et al., 2009; Gromke and Ruck, 2012). Depending on the street aspect ratio and, therefore, on the air flow regime (Oke, 1988; Harman et al., 2004) and on the tree characteristics, the tree crown effect on local tracer concentration (leeward versus windward side) is more or less important. For example, for NC, the flow regime is skimming, and on average, the variation in Cstreet due to the presence of trees compensates between the two sides of the street, explaining why is very low for NC.
This section demonstrated that the tree effect parameterizations should depend on tree characteristics and also on building characteristics to account for the building–tree interactions. The next section aims to parameterize in MUNICH the tree effect on Ustreet and qvert observed in Code_Saturne simulations.
4.1 Model description
The MUNICH parameterizations of horizontal and vertical transfers detailed in Maison et al. (2022) are modified to take into account the tree effects. These parameterizations are based on Wang (2012, 2014) equations, which were originally developed for homogeneous vegetated cover. To remain consistent with this hypothesis, the parameterization will depend on the homogeneous leaf area index in the street, denoted as LAIstreet. As for the conversion from LAI3D to LAI2D, LAIstreet is estimated from LAI2D conserving the leaf surface. LAIstreet is calculated by spreading the tree crown cylindrical LAI2D over the whole street width as follows:
where Sstreet is the soil-projected area of the street homogeneous tree crown, and S2D is the soil-projected area of the Code_Saturne 2D cylindrical tree crown (in m2). Note that, regardless of the tree crown geometry, LAIstreet is always equal to the street total leaf surface divided by the street ground area (WL).
To account for the tree effect on the mixing length, the characteristic length of the trees ( in m) is added into the equation describing the mixing length lm as follows:
where corresponds to the leaf frontal area density, assuming a random leaf orientation distribution, Et is a proportionality constant taken equal to 0.054 for vegetated cover, as suggested by Wang (2014), and fb×t is a function parameterized based on Code_Saturne simulations in Sect. 4.2 and representing the interaction between buildings, trees, and the tree crown height.
The dimensionless factor sH expressing the effects of the tree canopy on the mixing length lm is calculated using its definition in Eq. (6) and the expression of lm in Eq. (19) as follows:
The simulations with and without trees have to be distinguished to avoid any convergence issue since tends to +∞ when LAIstreet tends to 0. This sH factor now includes rough soil, buildings, and tree effects on the mixing length and is then used in the calculation of the attenuation coefficient α (Eq. 4). In the numerator, the expressions for buildings and trees are added as follows:
where is the tree drag coefficient (dimensionless) taken equal to the one, as used in Code_Saturne (). Wang (2014) presents Cu as a dimensionless coefficient homogeneous on the vertical axis, but that can depend on canopy features. This coefficient has to be determined based on experimental or simulated observation data and will be parameterized in Sect. 4.2 with CFD simulations.
4.2 Parameter determination based on Code_Saturne simulations
There are two parameters introduced in lm and α equations, i.e., fb×t and Cu (Eqs. 19 and 23), that have to be determined based on Code_Saturne and . The function fb×t depends on ar to account for the interaction between trees and buildings observed in Fig. 3 and also on hmax to account for the effect of the tree height. Note that, since tree crowns are assumed to be homogeneous within the canopy in the original Wang formulation, the tree crown height hmax is not taken into account (see Eq. 20), and therefore, it needs to be included in the function fb×t. The fb×t expression is determined by maximizing the fit between Code_Saturne and MUNICH as follows:
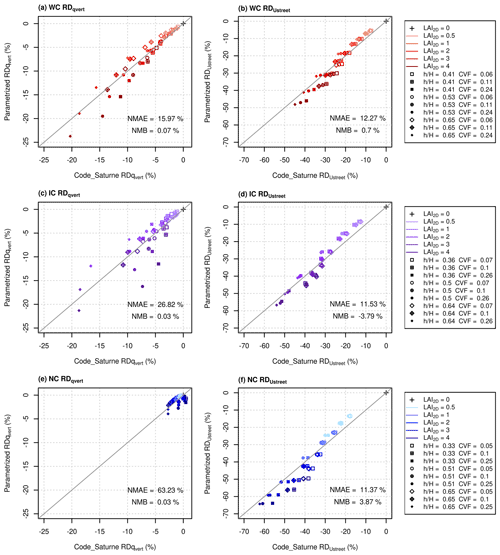
A comparison of Code_Saturne and the parameterized with Eqs. (7), (19), (20), and (24) is presented for the three canyons in Fig. 4a, c, e. The normalized mean absolute error (NMAE) and bias (NMB) are calculated to compare Code_Saturne and MUNICH results (see Appendix C for the definition of the statistical indicators). Figure 4a, c, e show a good agreement between Code_Saturne and the parameterized because the fb×t function was determined to minimize bias. The NMAE can be high for (up to 63 % in NC) because the parameterization does not reproduce the slight decrease in when LAI2D increases from LAI2D=3 to 4 when and (see Sect. 3.2 and Fig. 3b and c). But this is not an issue for NC since the qvert values are low.
For Ustreet, the parameter Cu also needs to be determined. A constant value of Cu=6.7 is sufficient to obtain a good fit between Code_Saturne and MUNICH . No dependency of Cu on building or tree features is needed, as shown in Fig. 4b, d, f, which compares Code_Saturne and the parameterized . Note that the parameterizations of and fb×t impact not only the vertical transfers but also the horizontal wind speed because they are involved in the calculation of the sH factor and, hence, of the α coefficient. The good comparisons between Code_Saturne and MUNICH also show that the parameterized sH reproduces the horizontal wind speed well and, therefore, also the interactions between trees and building effects and the influence of hmax.
4.3 Comparison of qvert, Ustreet, and wind profiles
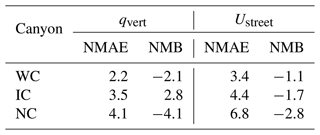
Figure 5a and b present, respectively, a comparison of Code_Saturne and parameterized qvert and Ustreet. The statistical indicators are presented in Table 2. As MUNICH was parameterized to reproduce the tree effect observed in Code_Saturne well, and as the two models agree well in a treeless canyon (Maison et al., 2022), the vertical transfer coefficient and wind speed with trees are close between the two models, as expected (Fig. 5 and Table 2). The parameterized vertical transfer coefficients with trees agree well with the Code_Saturne ones, with normalized mean absolute errors ranging from 2.2 % to 4.1 % and bias from −4.1 % to 2.8 %. The parameterized average wind speed with trees agree well with Code_Saturne ones, with normalized mean absolute errors ranging from 3.4 % to 6.8 % and a normalized mean bias from −2.8 % to −1.1 %.
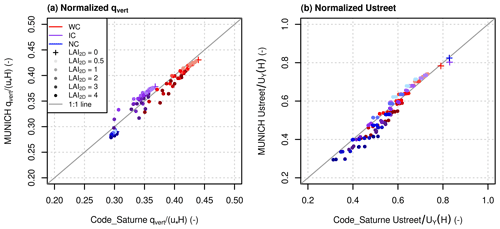
Figure 5Normalized Ustreet and qvert computed from Code_Saturne simulations for different tree LAI2D, CVF, and height ratios.
Table 2Statistical indicators (normalized mean absolute error, NMAE, and bias, NMB, in percent) for the comparison of Code_Saturne and MUNICH qvert and Ustreet.
For each street canyon, Fig. 6 compares the Code_Saturne and parameterized vertical wind profiles for fixed CVF and ratio but for five different LAI2D.
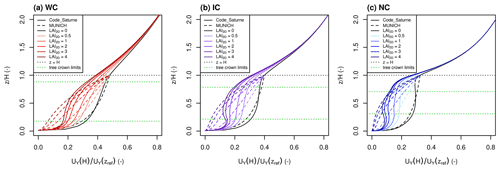
Figure 6Comparison of Code_Saturne (solid lines) and parameterized (dotted lines) vertical wind profiles. The profiles in a treeless canyon are in black and darker colors correspond to increasing LAI2D. For the three canyons, and CVF≈25 %.
Figure 6 shows that an increase in the LAI2D induces a decrease in the wind velocity. Concerning the vertical profile shape, trees induce a lower wind velocity on the entire street and not only in the tree crown. They even slightly impact the velocity just above the street. The maximum of attenuation of the wind is located in the middle of the tree crown and the wind velocity is re-accelerated under the tree crown. In the middle of the tree crown, the parameterized wind speed is close to the one of Code_Saturne. In the lower part and under the tree crown, the parameterized wind speed is underestimated. In fact, the re-acceleration under the tree crown is complex to consider in parameterized models. Besides, in real streets the tree height is not homogeneous, so this re-acceleration under the tree crown might be unrealistic in Code_Saturne simulations. In the parameterized wind profile with trees, the reduction in the wind speed just above the street due to the presence of trees was neglected. So the parameterized wind speed above and in the upper part of the tree crown is overestimated compared to Code_Saturne. Note that Kent et al. (2017) proposed a method to include the vegetation effect in aerodynamic roughness parameters and so to account for vegetation in the above-urban canopy wind profile of Macdonald et al. (1998). This method considers vegetation at the city scale and is not applicable here, since we work at the street scale. For now, as MUNICH assumes a homogeneous street canyon, the profile is averaged to compute Ustreet, and the shape of the profile is not used.
Moreover, to illustrate the impact of the developed parametrization on pollutant concentrations, MUNICH simulations are performed with carbon monoxide emissions in IC without and with trees of various characteristics. The results are presented in Appendix D.
Although the discretizations and the physical modeling used in MUNICH and Code_Saturne are fundamentally different, the setup of the CFD simulations was adapted to compare the two models through the average horizontal wind speed along the street and the calculation of the vertical transfer coefficient at the roof level by averaging a passive tracer concentration in the street and the background (above the streets). To build a parameterization suited to the street network model MUNICH, the CFD simulations were simplified with several hypothesis such as an infinite street canyon with 2D CFD simulations and homogeneous emissions over the street. Furthermore, quantities of interest were averaged over the street in the CFD simulations.
The aerodynamic effect of trees in street canyons is quantified with Code_Saturne simulations. Simulations were performed with two rows of trees and a large range of tree leaf area index, crown radius, and heights. In the range of the simulations performed, the average horizontal velocity in the street is reduced by −7.3 % to −62.3 % and the vertical transfer coefficient by +0.5 % to −20.3 %. This highlights the necessity of adding the tree aerodynamic effects into street models such as MUNICH.
Maison et al. (2022) proposed a parameterization of horizontal and vertical transfers in a treeless canyon, and the present study adds the tree effect to the building effect in this parameterization. The differences in wind speed and vertical transfer coefficient in a treeless canyon are very low between the two models (Maison et al., 2022). However, to overcome any model-specific difference and to build a parameterization for MUNICH of the tree effect on the aerodynamic parameters, relative deviation ratios between cases without and with trees are defined.
First, the Maison et al. (2022) vertical transfer coefficient parameterization is modified by adding a term representing the tree effect and the interaction between the trees and the buildings in the mixing-length expression. This term is a function of two dimensionless parameters to characterize the trees, street leaf area index (LAIstreet) and tree-to-street height ratio (), and also of street characteristics, building height (H), and street width (W). A parameterization of the tree mixing length was defined from Code_Saturne simulations to obtain a tree effect as close as possible in the two models. The parameterized vertical transfer coefficients with trees agree well with those of Code_Saturne, with the normalized mean absolute error ranging from 2.2 % to 4.1 % and bias from −4.1 % to 2.8 %.
Second, this new mixing length expression is also used to compute the vertical wind profile and average wind speed along the street. Only one constant is fixed in the wind attenuation coefficient to maximize the fit between Code_Saturne and MUNICH tree effect on average wind speed. The comparison of the average wind speed gives a normalized mean absolute error ranging from 3.4 % to 6.8 % and a normalized mean bias from −2.8 % to −1.1 %.
MUNICH now includes a relatively simple parameterization of the tree effect on both horizontal and vertical aerodynamic processes, based on commonly used tree parameters that can be easily computed from urban databases and can reproduce the main effects obtained in much more detailed and costly CFD simulations. This parameterization can also be used in urban climate models to compute water and heat transfer in tree-lined streets. The perspectives of this study are to quantify the effect of street trees on air quality from the street level to the scale of the city of Paris. Dry deposition of gaseous pollutants and aerosols on tree leaves and emission of biogenic organic volatile compounds related to tree water stress will be considered in MUNICH. The contribution of biogenic and anthropic precursors to the formation of organic aerosols over an entire city will be compared.
Each line of the Table A4 corresponds to the parameters of a simulation. For each case, simulations with different LAI2D were performed as follows: 0.5, 1, 2, 3, and 4.
Wang (2014)(Katul and Albertson, 1998)(Soulhac et al., 2011)Code_Saturne simulations were performed in a periodic 2D canyon of length L=1 m, and the street was therefore considered infinite due to this periodicity. In this case, the tree crown is represented as an infinite cylinder of radius r. To take into account the fact that, in reality, most of the tree crowns are spherical and are spaced from each other, an equivalent cylindrical LAI2D is calculated in the 2D simulations. For the tree effect to be similar, the surface of the leaves is kept constant between the 2D and 3D simulations, as follows:
where δ is the spacing between two tree crowns within the row, and 2r+δ is the length of the street section for one spherical tree (m). S3D and S2D are, respectively, the soil-projected area of the 3D and 2D tree crowns (m2). In addition to the leaf surface and tree height, the tree radius is also conserved between 2D and 3D simulations; however, the value of the crown volume fraction (CVF) varies, as follows:
Vstreet is the street volume (m3), and V3D and V2D are, respectively, the 3D and 2D tree crown volumes (m3). The relation between 2D and 3D CVF is therefore as follows:
2D and 3D simulations with different LAI are performed to check the validity of the 2D infinite street canyon hypothesis. 3D simulations are realized with a periodic street with a 10 m length and cell meshes of m in the x, y, and z directions. In both 2D and 3D simulations, Cstreet and Cbg are computed with a normal wind to the street (φ=90∘) and Ustreet with φ=45∘. The results are presented in Figs. B1a–d for WC, B1e–h for IC, and B1i–l for NC.
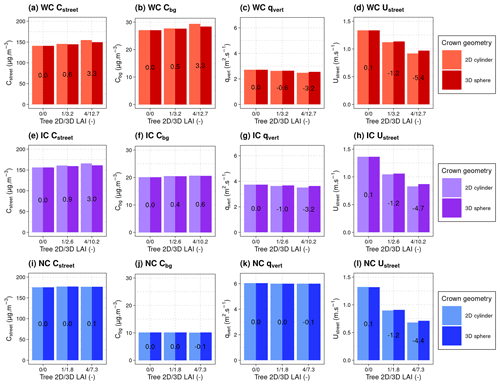
Figure B1Comparison of Cstreet (a, e, i), Cbg (b, f, j), qvert (c, g, k), and Ustreet (d, h, l) for 2D and 3D simulations in the three canyons without and with trees of LAI2D=1 and 4. CVF2D≈10 % and are fixed. The percentages written in the middle of the histogram bars correspond to the RD between the 2D and 3D cases.
For each canyon, the cases without tree (LAI=0) are equivalent. Cstreet, Cbg, qvert, and Ustreet are similar between the 2D and 3D cases, with a maximum relative difference of 0.1 % for Ustreet. For the cases with trees, concerning Cstreet, Cbg, and qvert, the differences between the 2D and 3D cases are relatively low over the range of simulations performed with a maximum of 3.3 % for Cstreet and Cbg in WC. For Ustreet, slightly larger differences are observed (up to −5.4 % in WC for ). These differences can be explained by the distribution of the turbulence around the crown. For each variable and canyon, the relative deviation between the 2D and 3D cases increases with the tree LAI. Given the low differences observed between the 2D and 3D simulations, the hypothesis of a 2D canyon with a cylindrical tree crown associated with an equivalent LAI2D to represent a spherical tree crown spaced of δ m in a street of length L is reasonable.
Code_Saturne and MUNICH simulations are denoted csi and mi, respectively. In this section, n is the total number of simulations, which is equal to 45 per street canyon.
-
Normalized mean absolute error (%):
-
Normalized mean bias (%):
To illustrate the impact of the developed parameterization on pollutant concentrations, MUNICH simulations are performed in the Intermediate Canyon (IC) with carbon monoxide (CO) emissions in the street. The input parameters are detailed in Table D1.
In the simulations, only the tree aerodynamic effect is considered, and there is no chemistry, no deposition of pollutants on urban or tree surfaces, and no biogenic volatile organic compound (BVOC) emission. One street is modeled without any inflow of pollutant from nearby streets. The following three processes are taken into account: pollutant emission in the street, pollutant outflow by horizontal transfer, Qoutflow (function of the parameterized Ustreet), and vertical transfer between the street and the background, Qvert (function of the parameterized qvert).
The street average CO concentrations (Cstreet) are compared in Fig. D1 for a canyon without trees (Fig. D1a) and for a canyon with trees of various LAI, CVF, and height ratios (Fig. D1b, c).
Figure D1 shows that the increase in tree LAI and CVF induces higher average street CO concentrations. The effect of the tree height ratio is negligible for low LAI and increases when the LAI increases. The variations in the concentrations are due to both the effect of trees on the horizontal transfer velocity, Ustreet, and on the vertical transfer coefficient, qvert.
In this example, the aerodynamical effect of trees leads to a large increase in the CO concentration from 4 % to 45 %. However, to simulate the global effect of trees on air quality at street level, other processes such as dry deposition on leaves and BVOC emissions need to be considered.
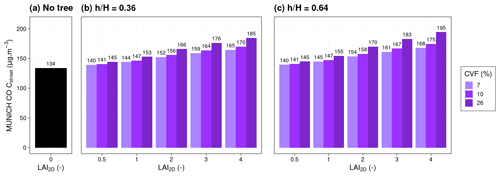
Figure D1Comparison of CO concentration (Cstreet) simulated with MUNICH in IC for different tree LAI2D, CVF, and tree height ratios . The graphic is divided into three columns corresponding to the treeless canyon (a) and to canyons with trees of height ratios (b) and 0.64 (c). The concentrations Cstreet (in µg m−3) are specified with data labels.
The last version of the MUNICH source code is available online at https://doi.org/10.5281/zenodo.4168984 (Kim et al., 2022) and https://github.com/cerea-lab/munich (last access: 5 January 2022).
For the three 2D canyons considered in the present study, the mesh, the source code, and the XML setup file allowing the reproduction of the CFD results using Code_Saturne version 6.0 are available online at https://gitlab.enpc.fr/alice.maison/tree_parametrization (last access: 3 December 2021) and at https://doi.org/10.17632/fzfrjsz3mv.2 (Maison and Flageul, 2021) under the GNU GPL2.0 license.
KS, CF, BC, and AM were responsible for the conceptualization. AM developed the MUNICH model code and performed the Code_Saturne simulations. AM, KS, CF, and BC performed the formal analysis. AM conducted the visualization. AM, KS, and CF were responsible for writing the original draft, and BC and AT reviewed it. CF, BC, and YW provided support for the Code_Saturne computing resources. KS and AT were responsible for the funding acquisition.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Air quality research at street level (ACP/GMD inter-journal SI)”. It is not associated with a conference.
The authors thank Youngseob Kim and Lya Lugon, for their support in the development of the MUNICH model, and Martin Ferrand, for his support in the understanding of the Code_Saturne model.
This work has partially been funded by the sTREEt ANR project (grant no. ANR-19-CE22-0012),the DIM Qi2 (Air Quality Research Network on air quality in the Île-de-France region), and Paris Île-de-France Region.
This paper was edited by Yang Zhang and reviewed by two anonymous referees.
Akimoto, H.: Global Air Quality and Pollution, Science, 302, 1716–1719, https://doi.org/10.1126/science.1092666, 2003. a
Angel, S., Parent, J., Civco, D. L., Blei, A., and Potere, D.: The dimensions of global urban expansion: Estimates and projections for all countries, 2000–2050, Prog. Plann., 75, 53–107, https://doi.org/10.1016/j.progress.2011.04.001, 2011. a
Archambeau, F., Méchitoua, N., and Sakiz, M.: Code Saturne: A finite volume code for the computation of turbulent incompressible flows-Industrial applications, International Journal on Finite Volumes, 1, 1–62, https://hal.archives-ouvertes.fr/hal-01115371 (last access: 18 July 2022), 2004. a
Armson, D., Stringer, P., and Ennos, A.: The effect of street trees and amenity grass on urban surface water runoff in Manchester, UK, Urban For. Urban Gree., 12, 282–286, https://doi.org/10.1016/j.ufug.2013.04.001, 2013. a
Beckett, K., Freer-Smith, P., and Taylor, G.: Urban woodlands: their role in reducing the effects of particulate pollution, Environ. Pollut., 99, 347–360, https://doi.org/10.1016/S0269-7491(98)00016-5, 1998. a
Berland, A., Shiflett, S. A., Shuster, W. D., Garmestani, A. S., Goddard, H. C., Herrmann, D. L., and Hopton, M. E.: The role of trees in urban stormwater management, Landscape Urban Plan., 162, 167–177, https://doi.org/10.1016/j.landurbplan.2017.02.017, 2017. a
Bertram, C. and Rehdanz, K.: The role of urban green space for human well-being, Ecol. Econ., 120, 139–152, https://doi.org/10.1016/j.ecolecon.2015.10.013, 2015. a
Bowler, D. E., Buyung-Ali, L., Knight, T. M., and Pullin, A. S.: Urban greening to cool towns and cities: A systematic review of the empirical evidence, Landscape Urban Plan., 97, 147–155, https://doi.org/10.1016/j.landurbplan.2010.05.006, 2010. a
Bozonnet, E., Musy, M., Calmet, I., and Rodriguez, F.: Modeling methods to assess urban fluxes and heat island mitigation measures from street to city scale, International Journal of Low-Carbon Technologies, 10, 62–77, https://doi.org/10.1093/ijlct/ctt049, 2015. a
Buccolieri, R., Gromke, C., Di Sabatino, S., and Ruck, B.: Aerodynamic effects of trees on pollutant concentration in street canyons, Sci. Total Environ., 407, 5247–5256, https://doi.org/10.1016/j.scitotenv.2009.06.016, 2009. a, b
Buccolieri, R., Salim, M., Leo, L. S., Di Sabatino, S., Chan, A., Ielpo, P., de Gennaro, G., and Gromke, C.: Analysis of local scale tree–atmosphere interaction on pollutant concentration in idealized street canyons and application to a real urban junction, Atmos. Environ., 45, 1702–1713, https://doi.org/10.1016/j.atmosenv.2010.12.058, 2011. a
Buccolieri, R., Santiago, J.-L., Rivas, E., and Sanchez, B.: Review on urban tree modelling in CFD simulations: Aerodynamic, deposition and thermal effects, Urban For. Urban Gree., 31, 212–220, https://doi.org/10.1016/j.ufug.2018.03.003, 2018. a
Cai, X.-M., Barlow, J., and Belcher, S.: Dispersion and transfer of passive scalars in and above street canyons – Large-eddy simulations, Atmos. Environ., 42, 5885–5895, https://doi.org/10.1016/j.atmosenv.2008.03.040, 2008. a
Calfapietra, C., Fares, S., Manes, F., Morani, A., Sgrigna, G., and Loreto, F.: Role of Biogenic Volatile Organic Compounds (BVOC) emitted by urban trees on ozone concentration in cities: A review, Environ. Pollut., 183, 71–80, https://doi.org/10.1016/j.envpol.2013.03.012, 2013. a
Faiz, A.: Automotive emissions in developing countries-relative implications for global warming, acidification and urban air quality, Transportation Res. A-Pol., 27, 167–186, https://doi.org/10.1016/0965-8564(93)90057-R, 1993. a
Gillner, S., Vogt, J., Tharang, A., Dettmann, S., and Roloff, A.: Role of street trees in mitigating effects of heat and drought at highly sealed urban sites, Landscape Urban Plan., 143, 33–42, https://doi.org/10.1016/j.landurbplan.2015.06.005, 2015. a
Gromke, C. and Blocken, B.: Influence of avenue-trees on air quality at the urban neighborhood scale. Part II: Traffic pollutant concentrations at pedestrian level, Environ. Pollut., 196, 176–184, https://doi.org/10.1016/j.envpol.2014.10.015, 2015. a, b
Gromke, C. and Ruck, B.: Influence of trees on the dispersion of pollutants in an urban street canyon – Experimental investigation of the flow and concentration field., Atmos. Environ., 41, 3287–3302, https://doi.org/10.1016/j.atmosenv.2006.12.043, 2007. a
Gromke, C. and Ruck, B.: On the Impact of Trees on Dispersion Processes of Traffic Emissions in Street Canyons, Bound.-Lay. Meteorol., 131, 19–34, https://doi.org/10.1007/s10546-008-9301-2, 2009. a
Gromke, C. and Ruck, B.: Pollutant Concentrations in Street Canyons of Different Aspect Ratio with Avenues of Trees for Various Wind Directions, Bound.-Lay. Meteorol., 144, 41–64, https://doi.org/10.1007/s10546-012-9703-z, 2012. a, b
Gu, S., Guenther, A., and Faiola, C.: Effects of Anthropogenic and Biogenic Volatile Organic Compounds on Los Angeles Air Quality, Environ. Sci. Technol., 55, 12191–12201, https://doi.org/10.1021/acs.est.1c01481, 2021. a
Gunawardena, K., Wells, M., and Kershaw, T.: Utilising green and bluespace to mitigate urban heat island intensity, Sci. Total Environ., 584–585, 1040–1055, https://doi.org/10.1016/j.scitotenv.2017.01.158, 2017. a
Harman, I. N., Barlow, J. F., and Belcher, S. E.: Scalar fluxes from urban street canyons. Part II Model, Bound.-Lay. Meteorol., 113, 387–409, https://doi.org/10.1007/s10546-004-6205-7, 2004. a, b
Hebbert, M. and Jankovic, V.: Cities and Climate Change: The Precedents and Why They Matter, Urban Stud., 50, 1332–1347, https://doi.org/10.1177/0042098013480970, 2013. a
Huang, Y.-D., Hou, R.-W., Liu, Z.-Y., Song, Y., Cui, P.-Y., and Kim, C.-N.: Effects of Wind Direction on the Airflow and Pollutant Dispersion inside a Long Street Canyon, Aerosol Air Qual. Res., 19, 1152–1171, https://doi.org/10.4209/aaqr.2018.09.0344, 2019. a
Hwang, H.-J., Yook, S.-J., and Ahn, K.-H.: Experimental investigation of submicron and ultrafine soot particle removal by tree leaves, Atmos. Environ., 45, 6987–6994, https://doi.org/10.1016/j.atmosenv.2011.09.019, 2011. a
IPCC: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Report, Intergovernmental Panel on Climate Change, United Nations, edited by: Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S. L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M. I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J. B. R., Maycock, T. K., Waterfield, T., Yelekçi, O., Yu, R., and Zhou, B., Cambridge University Press, https://www.ipcc.ch/report/ar6/wg1/ (last access: 18 July 2022), 2021. a, b
Janhäll, S.: Review on urban vegetation and particle air pollution – Deposition and dispersion, Atmos. Environ., 105, 130–137, https://doi.org/10.1016/j.atmosenv.2015.01.052, 2015. a, b
Jayasooriya, V., Ng, A., Muthukumaran, S., and Perera, B.: Green infrastructure practices for improvement of urban air quality, Urban For. Urban Gree., 21, 34–47, https://doi.org/10.1016/j.ufug.2016.11.007, 2017. a
Jeanjean, A., Buccolierib, R., Eddy, J., Monks, P., and Leigh, R.: Air quality affected by trees in real street canyons: The case of Marylebone neighbourhood in central London., Urban For. Urban Gree., 22, 41–43, https://doi.org/10.1016/j.ufug.2017.01.009, 2017. a
Katul, G. and Albertson, J.: An Investigation of Higher-Order Closure Models for a Forested Canopy, Bound.-Lay. Meteorol., 89, 47–74, https://doi.org/10.1023/A:1001509106381, 1998. a, b
Katul, G. G., Mahrt, L., Poggi, D., and Sanz, C.: ONE- and TWO-Equation Models for Canopy Turbulence, Bound.-Lay. Meteorol., 113, 81–109, https://doi.org/10.1023/B:BOUN.0000037333.48760.e5, 2004. a, b
Kent, C. W., Grimmond, S., and Gatey, D.: Aerodynamic roughness parameters in cities: Inclusion of vegetation, J. Wind Eng. Ind. Aerod., 169, 168–176, https://doi.org/10.1016/j.jweia.2017.07.016, 2017. a
Kim, Y., Wu, Y., Seigneur, C., and Roustan, Y.: Multi-scale modeling of urban air pollution: development and application of a Street-in-Grid model (v1.0) by coupling MUNICH (v1.0) and Polair3D (v1.8.1), Geosci. Model Dev., 11, 611–629, https://doi.org/10.5194/gmd-11-611-2018, 2018. a
Kim, Y., Sartelet, K., Lugon, L., Roustan, Y., Sarica, T., Maison, A., Valari, M., Zhang, Y., and André, M.: The Model of Urban Network of Intersecting Canyons and Highways (MUNICH), Zenodo [code], https://doi.org/10.5281/zenodo.6167477, 2022. a
Klemm, W., Heusinkveld, B. G., Lenzholzer, S., and van Hove, B.: Street greenery and its physical and psychological impact on thermal comfort, Landscape Urban Plan., 138, 87–98, https://doi.org/10.1016/j.landurbplan.2015.02.009, 2015. a
Krekel, C., Kolbe, J., and Wüstemann, H.: The Greener, The Happier? The Effects of Urban Green and Abandoned Areas on Residential Well-Being, The German Socio-Economic Panel study at DIW Berlin, 728, 65, https://doi.org/10.2139/ssrn.2554477, 2015. a
Leopold, L. B.: Hydrology for urban land planning – A guidebook on the hydrologic effects of urban land use, US. Geological Survey, 554, 18, https://doi.org/10.3133/cir554, 1968. a
Li, X., Liu, C., Leung, D., and Lam, K.: Recent progress in CFD modelling of wind field and pollutant transport in street canyons, Atmos. Environ., 40, 5640–5658, https://doi.org/10.1016/j.atmosenv.2006.04.055, 2006. a
Livesley, S. J., McPherson, E. G., and Calfapietra, C.: The Urban Forest and Ecosystem Services: Impacts on Urban Water, Heat, and Pollution Cycles at the Tree, Street, and City Scale, J. Environ. Qual., 45, 119–124, https://doi.org/10.2134/jeq2015.11.0567, 2016. a
Lobaccaro, G. and Acero, J.: Comparative analysis of green actions to improve outdoor thermal comfort inside typical urban street canyons, Urban Climate, 14, 251–267, https://doi.org/10.1016/j.uclim.2015.10.002, 2015. a
Lugon, L., Sartelet, K., Kim, Y., Vigneron, J., and Chrétien, O.: Nonstationary modeling of NO2, NO and NOx in Paris using the Street-in-Grid model: coupling local and regional scales with a two-way dynamic approach, Atmos. Chem. Phys., 20, 7717–7740, https://doi.org/10.5194/acp-20-7717-2020, 2020. a, b
Lugon, L., Sartelet, K., Kim, Y., Vigneron, J., and Chrétien, O.: Simulation of primary and secondary particles in the streets of Paris using MUNICH, Faraday Discuss., https://doi.org/10.1039/D0FD00092B, 2021. a
Macdonald, R., Griffiths, R., and Hall, D.: An improved method for the estimation of surface roughness of obstacle arrays, Atmos. Environ., 32, 1857–1864, https://doi.org/10.1016/S1352-2310(97)00403-2, 1998. a
Maison, A. and Flageul, C.: Parameterizing the aerodynamic effect of trees in street canyons for the street-network model MUNICH using the CFD model Code_Saturne – Code_Saturne simulation dataset, V2, Mendeley Data [code], https://doi.org/10.17632/fzfrjsz3mv.2, 2021. a
Maison, A., Flageul, C., Carissimo, B., Tuzet, A., and Sartelet, K.: Parametrization of Horizontal and Vertical Transfers for the Street-Network Model MUNICH Using the CFD Model Code_Saturne, Atmosphere, 13, 527, https://doi.org/10.3390/atmos13040527, 2022. a, b, c, d, e, f, g, h, i, j, k, l
Direction des Espaces Verts et de l'Environnement – Mairie de Paris: Les arbres – OpenDataParis, https://opendata.paris.fr/explore/dataset/les-arbres/, last access: 17 December 2021. a
Nowak, D. J., McHale, P. J., Ibarra, M., Crane, D., Stevens, J. C., and Luley, C. J.: Modeling the Effects of Urban Vegetation on Air Pollution, in: Air Pollution Modeling and Its Application XII, edited by: Gryning, S. E. and Chaumerliac, N., NATO, Challenges of Modern Society, vol 22., Springer, Boston, MA, 1998. a
Nowak, D. J. and Crane, D. E.: Carbon storage and sequestration by urban trees in the USA, Environ. Pollut., 116, 381–389, https://doi.org/10.1016/S0269-7491(01)00214-7, 2002. a
Nowak, D. J., Crane, D. E., and Stevens, J. C.: Air pollution removal by urban trees and shrubs in the United States, Urban For. Urban Gree., 4, 115–123, https://doi.org/10.1016/j.ufug.2006.01.007, 2006. a
Oke, T.: Street design and urban canopy layer climate, Energ. Buildings, 11, 103–113, https://doi.org/10.1016/0378-7788(88)90026-6, 1988. a
Oke, T. R.: The energetic basis of the urban heat island, Q. J. Roy. Meteor. Soc., 108, 1–24, https://doi.org/10.1002/qj.49710845502, 1982. a
Ozdemir, H.: Mitigation impact of roadside trees on fine particle pollution, Sci. Total Environ., 659, 1176–1185, https://doi.org/10.1016/j.scitotenv.2018.12.262, 2019. a
Pascal, M., Corso, M., Chanel, O., Declercq, C., Badaloni, C., Cesaroni, G., Henschel, S., Meister, K., Haluza, D., Martin-Olmedo, P., and Medina, S.: Assessing the public health impacts of urban air pollution in 25 European cities: Results of the Aphekom project, Sci. Total Environ., 449, 390–400, https://doi.org/10.1016/j.scitotenv.2013.01.077, 2013. a
Pigeon, G., Legain, D., Durand, P., and Masson, V.: Anthropogenic heat release in an old European agglomeration (Toulouse, France), Int. J. Climatol., 27, 1969–1981, https://doi.org/10.1002/joc.1530, 2007. a
Préndez, M., Araya, M., Criollo, C., Egas, C., Farías, I., Fuentealba, R., and González, E.: Urban Trees and Their Relationship with Air Pollution by Particulate Matter and Ozone in Santiago, Chile, in: Urban Climates in Latin America, edited by: Henríquez, C. and Romero, H., Springer International Publishing, pp. 167–206, https://doi.org/10.1007/978-3-319-97013-4_8, 2019. a
Revelli, R. and Porporato, A.: Ecohydrological model for the quantification of ecosystem services provided by urban street trees, Urban Ecosyst., 21, 489–504, https://doi.org/10.1007/s11252-018-0741-2, 2018. a
Robine, J., Cheung, S., and Roy, S. L.: Report on excess mortality in Europe during summer 2003, Tech. Rep., EU Community Action Programme for Public Health, http://ec.europa.eu/health/ph_projects/2005/action1/docs/action1_2005_a2_15_en.pdf (last access: 18 July 2022), 2007. a
Santiago, J.-L., Rivas, E., Sanchez, B., Buccolieri, R., and Martin, F.: The Impact of Planting Trees on NOx Concentrations: The Case of the Plaza de la Cruz Neighborhood in Pamplona (Spain), Atmosphere, 8, 131, https://doi.org/10.3390/atmos8070131, 2017. a
Sartelet, K., Zhu, S., Moukhtar, S., André, M., André, J., Gros, V., Favez, O., Brasseur, A., and Redaelli, M.: Emission of intermediate, semi and low volatile organic compounds from traffic and their impact on secondary organic aerosol concentrations over Greater Paris, Atmos. Environ., 180, 126–137, 2018. a
Selmi, W., Weber, C., Rivière, E., Blond, N., Mehdi, L., and Nowak, D.: Air pollution removal by trees in public green spaces in Strasbourg city, France, Urban For. Urban Gree., 17, 192–201, https://doi.org/10.1016/j.ufug.2016.04.010, 2016. a
Soulhac, L., Salizzoni, P., Cierco, F.-X., and Perkins, R.: The model SIRANE for atmospheric urban pollutant dispersion; part I, presentation of the model, Atmos. Environ., 45, 7379–7395, https://doi.org/10.1016/j.atmosenv.2011.07.008, 2011. a, b
Speziale, C., Sarkar, S., and Gatski, T.: Modelling the pressure-strain correlation of turbulence – An invariant dynamical systems approach, J. Fluid Mech., 227, 245–272, https://doi.org/10.1017/S0022112091000101, 1991. a
Stewart, I.: A systematic review and scientific critique of methodology in modern urban heat island literature, Int. J. Climatol., 31, 200–217, https://doi.org/10.1002/joc.2141, 2011. a
Svirejeva-Hopkins, A., Schellnhuber, H., and Pomaz, V.: Urbanised territories as a specific component of the Global Carbon Cycle, Ecol. Model., 173, 295–312, https://doi.org/10.1016/j.ecolmodel.2003.09.022, 2004. a
Taha, H., Akbari, H., and Rosenfeld, A.: Heat island and oasis effects of vegetative canopies: Micro-meteorological field-measurements, Theor. Appl. Climatol., 44, 123–138, https://doi.org/10.1007/BF00867999, 1991. a
van Dillen, S. M. E., de Vries, S., Groenewegen, P. P., and Spreeuwenberg, P.: Greenspace in urban neighbourhoods and residents' health: adding quality to quantity, J. Epidemiol. Commun. H., 66, e8, https://doi.org/10.1136/jech.2009.104695, 2012. a
Vardoulakis, S., Fisher, B. E., Pericleous, K., and Gonzalez-Flesca, N.: Modelling air quality in street canyons: a review, Atmos. Environ., 37, 155–182, https://doi.org/10.1016/S1352-2310(02)00857-9, 2003. a
Vos, P. E., Maiheu, B., Vankerkom, J., and Janssen, S.: Improving local air quality in cities: To tree or not to tree?, Environ. Pollut., 183, 113–122, https://doi.org/10.1016/j.envpol.2012.10.021, 2013. a, b, c, d
Wang, W.: An Analytical Model for Mean Wind Profiles in Sparse Canopies, Bound.-Lay. Meteorol., 142, 383–399, https://doi.org/10.1007/s10546-011-9687-0, 2012. a, b, c, d
Wang, W.: Analytically Modelling Mean Wind and Stress Profiles in Canopies, Bound.-Lay. Meteorol., 151, 239–256, https://doi.org/10.1007/s10546-013-9899-6, 2014. a, b, c, d, e, f, g
Wania, A., Bruse, M., Blond, N., and Weber, C.: Analysing the influence of different street vegetation on traffic-induced particle dispersion using microscale simulations., J. Env. Manag., 94, 91–101, https://doi.org/10.1016/j.jenvman.2011.06.036, 2012. a, b, c
Wei, X., Dupont, E., Gilbert, E., Musson-Genon, L., and Carissimo, B.: Experimental and Numerical Study of Wind and Turbulence in a Near-Field Dispersion Campaign at an Inhomogeneous Site, Bound.-Lay. Meteorol., 160, 475–499, https://doi.org/10.1007/s10546-016-0148-7, 2016. a
West, J. J., Cohen, A., Dentener, F., Brunekreef, B., Zhu, T., Armstrong, B., Bell, M. L., Brauer, M., Carmichael, G., Costa, D. L., Dockery, D. W., Kleeman, M., Krzyzanowski, M., Künzli, N., Liousse, C., Lung, S.-C. C., Martin, R. V., Pöschl, U., Pope, C. A., Roberts, J. M., Russell, A. G., and Wiedinmyer, C.: What We Breathe Impacts Our Health: Improving Understanding of the Link between Air Pollution and Health, Environ. Sci. Technol., 50, 4895–4904, https://doi.org/10.1021/acs.est.5b03827, 2016. a
Xue, F. and Li, X.: The impact of roadside trees on traffic released PM10 in urban street canyon: Aerodynamic and deposition effects, Sustain. Cities Soc., 30, 195–204, https://doi.org/10.1016/j.scs.2017.02.001, 2017. a
Yuan, C., Ng, E., and Norford, L. K.: Improving air quality in high-density cities by understanding the relationship between air pollutant dispersion and urban morphologies, Build. Environ., 71, 245–258, https://doi.org/10.1016/j.buildenv.2013.10.008, 2014. a
Zaïdi, H., Dupont, E., Milliez, M., Musson-Genon, L., and Carissimo, B.: Numerical Simulations of the Microscale Heterogeneities of Turbulence Observed on a Complex Site, Bound.-Lay. Meteorol., 147, 237–259, https://doi.org/10.1007/s10546-012-9783-9, 2013. a, b, c, d
Zhang, Y., Gu, Z., and Yu, C. W.: Impact Factors on Airflow and Pollutant Dispersion in Urban Street Canyons and Comprehensive Simulations: a Review, Current Pollution Report, 6, 425–439, https://doi.org/10.1007/s40726-020-00166-0, 2020. a
- Abstract
- Introduction
- Materials and methods
- Quantification of the tree crown effect on horizontal and vertical transfers by Code_Saturne simulations
- Parameterization of the aerodynamic effect of tree crowns in MUNICH
- Conclusions
- Appendix A: Lists of abbreviations, variable parameters, and tree dimensions
- Appendix B: Comparison of 2D and 3D Code_Saturne simulations with trees
- Appendix C: Definition of the statistical indicators
- Appendix D: Aerodynamic tree effect on concentration
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Materials and methods
- Quantification of the tree crown effect on horizontal and vertical transfers by Code_Saturne simulations
- Parameterization of the aerodynamic effect of tree crowns in MUNICH
- Conclusions
- Appendix A: Lists of abbreviations, variable parameters, and tree dimensions
- Appendix B: Comparison of 2D and 3D Code_Saturne simulations with trees
- Appendix C: Definition of the statistical indicators
- Appendix D: Aerodynamic tree effect on concentration
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References