the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Updraft dynamics and microphysics: on the added value of the cumulus thermal reference frame in simulations of aerosol–deep convection interactions
Daniel Hernandez-Deckers
Toshihisa Matsui
Ann M. Fridlind
One fundamental question about atmospheric moist convection processes that remains debated is whether, or under which conditions, a relevant variability in background aerosol concentrations may have a significant dynamical impact on convective clouds and their associated precipitation. Furthermore, current climate models must parameterize both the microphysical and the cumulus convection processes, but this is usually implemented separately, whereas in nature there is a strong coupling between them. As a first step to improve our understanding of these two problems, we investigate how aerosol concentrations modify key properties of updrafts in eight large-eddy-permitting regional simulations of a case study of scattered convection over Houston, Texas, in which convection is explicitly simulated and microphysical processes are parameterized. Dynamical and liquid-phase microphysical responses are investigated using the following two different reference frames: static cloudy updraft grid cells versus tracked cumulus thermals. In both frameworks, we observe the expected microphysical responses to higher aerosol concentrations, such as higher cloud number concentrations and lower rain number concentrations. In terms of the dynamical responses, both frameworks indicate weak impacts of varying aerosol concentrations relative to the noise between simulations over the observationally derived range of aerosol variability for this case study. On the other hand, results suggest that thermals are more selective than cloudy updraft grid cells in terms of sampling the most active convective air masses. For instance, vertical velocity from thermals is significantly higher at upper levels than when sampled from cloudy updraft grid points, and several microphysical variables have higher average values in the cumulus thermal framework than in the cloudy updraft framework. In addition, the thermal analysis is seen to add rich quantitative information about the rates and covariability of microphysical processes spatially and throughout tracked thermal lifecycles, which can serve as a stronger foundation for improving subgrid-scale parameterizations.
- Article
(3628 KB) - Full-text XML
-
Supplement
(748 KB) - BibTeX
- EndNote
The net impacts of atmospheric aerosol concentration on deep convective cloud systems and their environment remain highly uncertain, with mixed results that do not generally yield conclusive answers yet (e.g., Khain et al., 2008; Tao et al., 2012). All else being equal, a higher aerosol concentration generally corresponds to more condensation nuclei at any given supersaturation, which, in turn, is expected to produce more but smaller cloud droplets within a convective updraft. This may delay the occurrence of initial warm precipitation formation due to a less efficient collision–coalescence process, enhancing latent heat release above the freezing level (Rosenfeld et al., 2008). However, when or if this has a substantial impact on the amount or intensity of cold precipitation is not clear due to the uncertainties of subsequent ice and mixed-phase microphysics (e.g., Korolev et al., 2020) and the complex morphology and feedback of deep convective clouds under various environmental conditions (e.g., Tao et al., 2012; Fan et al., 2016; Abbott and Cronin, 2021). One approach, to reduce such complexities to some degree, is to focus on aerosol–cloud interactions in relatively isolated convective cells (e.g., Fridlind et al., 2019), where the various mechanisms by which aerosol may impact updraft properties remain operative.
The recent Aerosol, Cloud, Precipitation and Climate (ACPC) working group model intercomparison project (MIP) compared regional model simulations of such scattered convection in response to a realistic dynamic range of ambient aerosol concentration profiles with similar large-scale forcing. Although participating models exhibited similar updraft invigoration at low levels, differences between the models are larger than each model's response to ambient aerosol loading (Marinescu et al., 2021), offering little clear guidance for larger-scale models. Indeed, it is even more challenging to represent such processes in a climate model because updraft microphysics and dynamics are often simplified by cumulus parameterization at a much coarser spatiotemporal resolution (McFarlane, 2011). To better represent such processes in climate models, it is imperative to disentangle aerosol-deep convection interactions from the wider spectrum of microphysics and dynamical processes.
One foundational step in order to tackle this problem is to investigate the possible links between the updraft and microphysical processes in moist convection. Characterizing dynamical and microphysical properties in response to the ambient aerosols is very difficult from existing observations, but current high-resolution numerical models in which cumulus convection does not require being parameterized, such as those analyzed by Marinescu et al. (2021) or Abbott and Cronin (2021), offer a useful alternative. In order to study convective cloud properties in such simulations, the active cloudy regions must be identified first, which is traditionally done by sampling grid points with specific thresholds of vertical velocity and liquid water content; we call these cloudy updraft grid points. Such active cloud sampling criteria have been widely used since large-eddy simulations (LESs) have been available (e.g., Siebesma and Cuijpers, 1995; de Roode and Bretherton, 2003). However, with notable exceptions, as in supercells, moist convection commonly constitutes a series of many short-lived thermals within each cumulus cloud (Scorer and Ludlam, 1953; Woodward, 1959; Blyth et al., 2005; Damiani et al., 2006; Sherwood et al., 2013; Yano, 2014; Hernandez-Deckers and Sherwood, 2016; Morrison and Peters, 2018; Yeung et al., 2021), raising the question of whether the traditional grid point selection criteria are the most appropriate. For instance, cumulus thermals themselves can be very heterogeneous due to their own internal circulation structure (Hernandez-Deckers and Sherwood, 2016), so traditional grid point sampling may miss relevant air masses. In addition, traditional grid point sampling may include rising or cloudy points that are unrelated to the relevant convective air masses (e.g., Mrowiec et al., 2015). This can be avoided with even more selective criteria, such as that by Marinescu et al. (2021), who only include grid points within 6 km deep (or more) cloudy updraft columns, thus considering only well-developed deep convective cores. However, important microphysical activity may also occur outside of such cores, and their initial lifetime stages remain unaccounted for. For instance, recent observations by Yeung et al. (2021) indicate that most updrafts are less than 2 km deep, suggesting that a large fraction of mass flux may be left out by such selection criteria. All this suggests the possibility of exploring an alternative, more objective-based definition of the active cloudy regions arising from cumulus thermals.
The identification and tracking of cumulus thermals in numerical simulations have been used to investigate their intrinsic dynamical properties in studies such as those by Sherwood et al. (2013), Romps and Charn (2015), Hernandez-Deckers and Sherwood (2016), Hernandez-Deckers and Sherwood (2018), Moser and Lasher-Trapp (2017), Lecoanet and Jeevanjee (2019), or Peters et al. (2020). Their results have contributed to improving the understanding of the dynamical properties and the role of thermals in cumulus convection, which is necessary for the development of new convection parameterization schemes. However, to our knowledge, cumulus thermal identification has not been used as a sampling approach similar to the traditional cloudy updraft grid points or convective core identification. Here, we apply the thermal identification and tracking method of Hernandez-Deckers and Sherwood (2016), using it as a novel sampling approach, and compare it to the traditional cloudy updraft grid point method in the context of dynamical and microphysical impacts on deep convection due to changes in aerosol concentrations.
The more complex cumulus thermal framework enables a direct, three-dimensional, structure-based analysis of how the internal updraft dynamical structure is coupled to the microphysical processes, which is something that is difficult to obtain from the grid point framework. Both frameworks are expected to provide important information about the impact of aerosol concentrations on the dynamical and microphysical properties of deep convection, and here we compare the approaches in a systematic fashion. Although the ultimate aerosol impact on precipitation amount and intensity may depend on details of the particular microphysical parameterizations used, the first step we carry out here is to use both reference frames to investigate the basic impacts on the initial warm-phase microphysics and dynamics within scattered isolated convection. Through a series of relatively high-resolution, large-eddy-permitting regional model experiments, this study investigates the impact of a sequential increase in aerosol concentrations on the simulated dynamics and microphysics of deep convection. From the microphysical point of view, we focus on warm-phase microphysics because of larger uncertainties in ice nucleation and subsequent ice and mixed-phase microphysics. Here we investigate the dynamics–microphysics coupling using a single model and case study with two analysis approaches because differences between both models and case studies are expected (e.g., Tao et al., 2012; Marinescu et al., 2021); however, it will not be possible to establish the generality of our results to other models and scenarios without future work, and its potential merit may, nonetheless, be partly guided by our initial findings here.
Following this introduction, Sect. 2 describes the simulations analyzed here and a summary of the thermal identification and tracking method. Section 3 presents the main results, first in terms of composites of thermals, next in terms of vertical profiles of various quantities, and finally comparing the cloudy updraft grid point and thermal frameworks. Section 4 presents the summary and conclusions of this study.
2.1 Case study and model setup
The case study is based on scattered, isolated convective clouds that developed over Houston, Texas, on 19–20 June 2013, following the ACPC MIP simulations (Marinescu et al., 2021). During the daytime, the heating over the land develops a pressure gradient between the land and ocean. The associated afternoon sea breeze front triggers scattered convection by disturbing conditionally unstable layers. This study uses the NASA-Unified Weather Research and Forecasting (NU-WRF) model (Peters-Lidard et al., 2015) configuration that was also used in the ACPC MIP study as a basis (Marinescu et al., 2021); however, the domains, grid spacing, and aerosol concentrations are revised in order to investigate cumulus thermals.
This case study utilizes a single large domain (998×998 horizontal grid cells) with 250 m horizontal grid spacing and without nesting (Fig. 1). This type of domain setting exceeds the traditional downscaling ratio (1:3 1:5), resulting in reduced precipitation forecasting skill compared to multi-nested domains. However, it successfully generates thermal bubbles of isolated convection driven by sea breeze circulation for a given computational resource. The analysis is focused on the scattered convection that occurs due to mesoscale circulations within the domain. Vertical grid spacing stretches from approximately 50 m near the surface to 300 m near the 4 km level, with 96 vertical levels. The model top is approximately 22 km (50 hPa). The planetary boundary layer (PBL) parameterization was turned off, and only the turbulent kinetic energy (TKE) scheme is used; we found that the TKE scheme with the PBL scheme at this resolution unphysically suppresses the number of cumulus thermals within the middle of boundary layer (not shown). Other physics options include the new Goddard radiation scheme (Matsui et al., 2020), Noah-MP land surface model, and Predicted Particle Properties (P3) scheme with a single ice species.
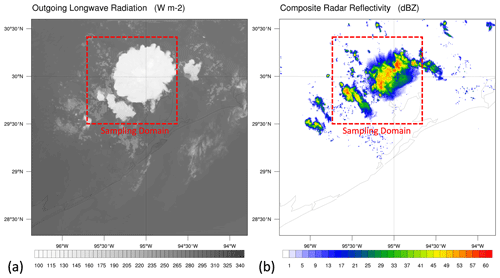
Figure 1NU-WRF domain and sampling domain showing (a) outgoing longwave radiation (OLR) and (b) composite radar reflectivity, on 19 June 2013 at 23:25 UTC, for the simulation with an aerosol number concentration of 500 cm−3.
The P3 scheme predicts the mass and number concentrations of cloud droplets, raindrops, and ice particles, and additional tracers (rime mass and volume) are also predicted to better characterize ice properties (Morrison and Milbrandt, 2015). Aerosol activation follows Abdul-Razzak and Ghan (2000), using the minimum supersaturation from Morrison and Grabowski (2008) (their Eq. A10). Based on regional observations (Marinescu et al., 2021), aerosol profiles spanning the boundary layer (up to 2500 m a.g.l. – above ground level) are stratified in the eight sensitivity experiments from relatively clean continental (500 cm−3) up to polluted conditions (4000 cm−3), increasing by 500 cm−3 for each sensitivity experiment. Aerosol is specified as a single-mode lognormal distribution with a fixed mean diameter (100 nm), lognormal distribution width (1.8), and hygroscopicity parameter (0.2). As in Marinescu et al. (2021), aerosol transport (resolved and subgrid), activation, removal by droplet coalescence, and regeneration from droplet evaporation follows the method in Fridlind et al. (2017), while the aerosol impact on ice nuclei is not considered. The polluted and clean aerosol size distributions and vertical profiles were based on the data from Deriving Information on Surface conditions from Column and Vertically Resolved Observations Relevant to Air Quality (DISCOVER-AQ) in September 2013 and satellite-based estimates (Rosenfeld et al., 2012) near Houston on 19 June 2013. The timing of the satellite cloud condensation nuclei (CCN) observations is identical to the simulation dates. The profiles feature constant values in the boundary layer up to 2.5 km and in the free troposphere over 5 km, with a linear transition between these heights. Aerosol removal/replenishment processes are based on the semi-diagnostic methods in Fridlind et al. (2017). This method activates cloud droplets for a given supersaturation rate and aerosol characteristics and tracks the sum of activated and unactivated aerosol through advection and mixing. Additional cloud droplets can be activated when the newly activated cloud droplets number exceeds the present number of cloud droplets. Aerosol number concentrations will be reduced only when cloud droplets are reduced by a coalescence process (i.e., autoconversion to precipitation class). The advantage of this approach is to account for activation and regeneration of aerosols without explicitly accounting for aerosols within cloud droplets (see details in Fridlind et al., 2017).
NCEP Final Analysis (FNL) was used to initialize NU-WRF on 19 June 2013 at 12:00 UTC, and it continued updating lateral boundary conditions until 20 June 2013 at 15:00 UTC. The 6 h lateral boundary conditions from GFS are spatially and temporally interpolated to update the model lateral boundary conditions at every model time step, while sea breeze dynamics are explicitly simulated by model physics and dynamics within the domain. Since thermal tracking requires 1 min temporal resolution of NU-WRF output, we focused on the 3 h time window from 19 June 21:00 UTC for thermal and cloudy updraft grid point analysis during the active convection period. Figure 1 shows the actual sampling domain used (a 100×100 km area), where most active convection occurs during this time window.
2.2 Thermal identification and tracking
Sufficiently high-resolution simulations can generally reproduce the expected thermal-like structures that are characteristic of cumulus clouds (e.g., Sherwood et al., 2013; Varble et al., 2014; Romps and Charn, 2015). This provides a numerical tool to investigate the dynamics of these thermals, which, in turn, leads to a better understanding of many aspects of convection (Morrison, 2016; Moser and Lasher-Trapp, 2017; Hernandez-Deckers and Sherwood, 2018; Peters et al., 2020). Here we identify, track, and analyze cumulus thermals in the NU-WRF simulations described in the previous section, using the methodology of Hernandez-Deckers and Sherwood (2016). In the following, we describe the main features of this method; for further details, please refer to their study.
To identify thermals, an automated algorithm identifies peaks in vertical velocity throughout a particular volume of the simulation at each output time step and assumes that these indicate the instantaneous locations of the thermals' centers. By comparing these locations in consecutive output time steps, the algorithm can estimate each thermal's trajectory, which also yields an estimate of their ascent rates at each time step. Assuming spherical shapes, a thermal's size can be estimated by choosing the radius that makes the average vertical velocity of the enclosed volume match the corresponding ascent rate. Notice that each thermal's ascent rate can vary between time steps, and hence, the estimated size of a thermal may also vary in time. The smallest radius permitted for a thermal is twice the model grid spacing, which is 500 m in this case. Smaller thermals are discarded. This ensures that each identified thermal corresponds to a coherent rising volume of air. Hernandez-Deckers and Sherwood (2016) showed that, indeed, thermal shapes do not deviate much from sphericity, making this a good approximation. Finally, it is worth noting that the algorithm only takes into account thermals with average ascent rates of at least 1 m s−1 and with centers that have at least 0.01 g kg−1 of cloud condensate. Furthermore, it computes each thermal's vertical momentum budget and discards any cases in which the tracked trajectory is inconsistent with it. From the sample of tracked thermals, different statistical measures can be obtained for both microphysical and dynamical properties. These can be then compared to results based on the cloudy updraft sampling framework. For consistency, our threshold criteria for selecting cloudy updraft grid points is a vertical velocity of 1 m s−1 and a cloud condensate of 0.01 g kg−1.
The mass flux captured by the tracked thermals is typically 15 %–20 % of the estimated total mass flux, as will be shown below. Despite this being a relatively small fraction, Hernandez-Deckers and Sherwood (2016) showed that the convective evolution is well represented by the thermals, suggesting that their dynamics are representative of the entire convective activity (discussed later). Untracked updrafts are typically too small or too slow to be tracked with this algorithm. Furthermore, the total mass flux is not uniquely defined and may contain spurious non-convective contributions (e.g., Mrowiec et al., 2015). Finally, it is worth noting that we find very similar properties of thermals in this study compared to what Hernandez-Deckers and Sherwood (2016) found with their higher-resolution simulations (65 m horizontal grid spacing). The only prominent difference is that our thermals are larger (R∼1.2 km, compared to R∼0.3 km), which may be expected given our coarser spatial resolution setting, but this could also be partially attributable to differences in the case study conditions. Owing to the similarity of results to those of Hernandez-Deckers and Sherwood (2016), we expect that finer-resolution results would be more converged but similar in nature.
3.1 Thermal composites
Figure 2 shows statistical composites of microphysics properties within tracked thermals from the selected background aerosol cases of 500, 1000, 2000, and 4000 cm−3 (i.e., for each subsequent doubling of aerosol concentrations). For these composites, only the time step of the maximum ascent rate of each thermal is considered. The results demonstrate that an increase in background aerosol concentrations tends to (a) increase cloud droplet nucleation rates, (b) reduce supersaturation values, (c) increase cloud droplet number concentrations, and (d) decrease rain number concentrations (Fig. 2a–d). Plots of average values of these quantities within thermals as a function of aerosol number concentration (not shown here) reveal that nucleation rates, supersaturation values, and cloud drop number concentration behave roughly linearly with aerosol number concentration, whereas rain number concentration decreases exponentially, which is consistent with raindrop generation by coalescence of cloud droplets. On the other hand, although number concentrations of both cloud droplets and raindrops are strongly affected by aerosol number concentration, their mixing ratios respond less strongly (Fig. 2e and f) and in such a way that the total liquid water mixing ratio remains more weakly impacted (not shown here).
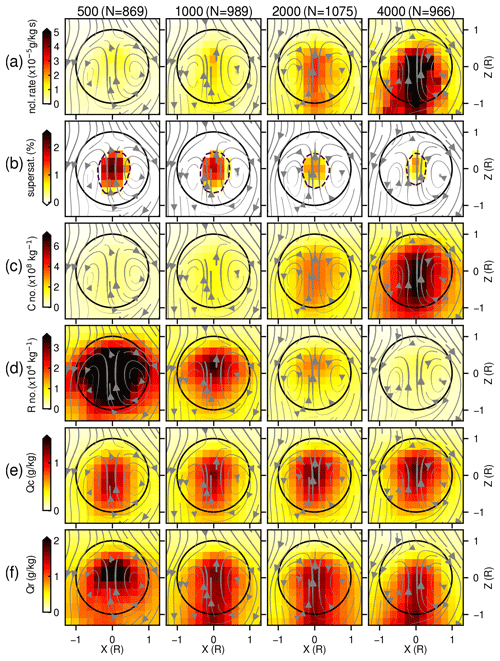
Figure 2Cross sections along the xz plane of mean values of (a) cloud nucleation rate, (b) supersaturation values, (c) cloud drop number concentration (C no.), (d) rain number concentration (R no.), (e) cloud liquid water mixing ratio (Qc), and (f) rain mixing ratio (Qr), for composites of all tracked thermals scaled by their radius (horizontal and vertical coordinates are in units of mean thermal radii). Each column corresponds to a simulation with initial aerosol number concentration (indicated above in counts per cubic centimeter; hereafter cm−3). N corresponds to the number of tracked thermals used for the composites. Arrows indicate the streamlines of the average flow in the reference frame of the rising thermal. The dashed contour in supersaturation values corresponds to 100 % relative humidity.
Microphysical quantities are found to peak at thermal centers nearly universally, which reinforces the important role of thermals as the building blocks of convection from both a dynamical and microphysical point of view. For example, supersaturation values are only reached inside thermals, generating numerous cloud droplets around their cores. Streamlines of the averaged flow also indicate a more turbulent mixing around the thermal frame, whereas upstream currents are present in the core of thermals.
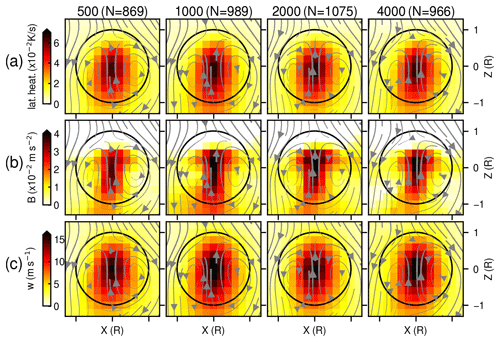
Figure 3Composites for all tracked thermals, as in Fig. 2, but for (a) latent heating rates, (b) buoyancy, and (c) vertical velocity.
The microphysical response to aerosol number concentration could cause a prominent dynamical response in thermals via changes in the rate at which latent heat is released due to condensation. For example, following the reasoning by Fan et al. (2018), a reduction in supersaturation rates could result from the larger number of smaller droplets (and, hence, more available surface area for condensation) as aerosol concentrations increase. All else being equal, this could imply a faster latent heat release due to condensation. However, Fig. 3a indicates no prominent mean response in latent heating rates within the tracked thermals (summed over all source terms), while cloud nucleation rates increase and supersaturation rates decrease with increasing aerosol concentrations (Fig. 2a and b). This implies that there is no prominent change in latent heating per unit of time available for the dynamics of the thermals, which indicates similar total condensation rates despite changes in driving supersaturations. A possible explanation is that supersaturation differences are sustained within the context of negligibly different total condensate production rates within the thermal core, but that hypothesis cannot be definitively supported without additional diagnostics that separate the sources of latent heat in future work. Figure 3b and c also show no notable changes in their composite buoyancy (B) or vertical velocity (w). We do not find any prominent trends in terms of the thermals' composite lifetime, vertical distance traveled (DZ), or radius (R). For R and DZ, this can be inferred from the vertical profiles shown in Fig. 6b and d. Furthermore, the histograms of these quantities are negligibly changed (not shown).
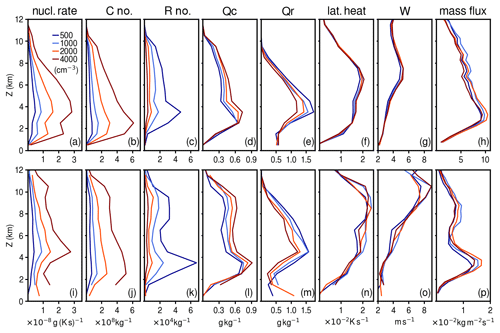
Figure 4Vertical profiles of the cloud nucleation rate (a, i), cloud number concentration (b, j), rain number concentration (c, k), cloud water mixing ratio (d, l), rain water mixing ratio (e, m), latent heating rates (f, n), vertical velocity (g, o), and mass flux (h, p) for experiments with different aerosol number concentrations (see the legend in panel a). Top panels (a–h) are computed from cloudy updraft grid points and lower panels (i–p) from tracked thermals. Note the different scales used for mass flux in panels (h) and (p).
3.2 Vertical profiles
Since many of these variables have strong vertical dependencies, we next investigate these responses in terms of vertical profiles of microphysical quantities, latent heating rates, vertical velocity, and mass flux, as estimated from cloudy updraft grid points (Fig. 4a–h) and from the tracked thermals (Fig. 4i–p). To begin with, notice that the vertical profiles in both frameworks show qualitatively consistent features at most elevations. Perhaps the most prominent difference between these two frameworks is that thermals indicate a larger contribution than cloudy updraft grid points to several quantities at levels above 6–7 This is very clear in terms of vertical velocity (Fig. 4g and o), where both frameworks yield very similar profiles up to ∼6–7 but significantly different values aloft. According to cloudy updraft grid points, vertical velocity reaches its maximum near 7 , whereas, according to thermals, it continues to increase, reaching its maximum near 10 This suggests that the thermal sampling criteria is more selective of vigorous updrafts aloft. This also results in a slightly more top-heaviness of the profiles of other quantities, which reflects how strongly coupled microphysical processes are with updraft dynamics. In terms of mass flux, both frameworks yield a maximum near 3 , but thermals indicate a secondary maximum between 7 and 9 Notice that this corresponds to the contribution of relatively few thermals (Fig. 6a), suggesting that, unlike near the cloud base where convection results from small contributions of many updrafts, convection at mid and high levels near the cloud top is more tightly linked to the contribution of relatively few but vigorous updrafts, a feature that may be better captured by the cumulus thermal framework.
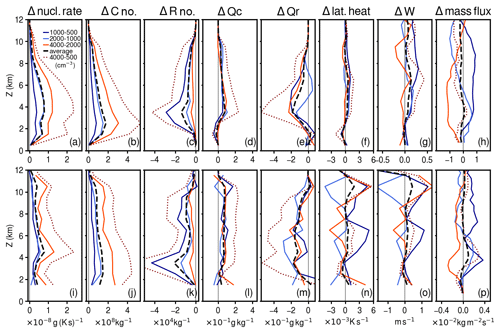
Figure 5Differences between vertical profiles in Fig. 4, corresponding to each doubling of aerosol number concentrations (continuous colored lines), their average change (dashed black line), and the change between the two extreme cases, i.e., 4000 and 500 cm−3 (dotted line). Top panels (a–h) correspond to cloudy updraft grid points and lower panels (i–p) to tracked thermals. Note the different scales used for vertical velocity and for mass flux.
It is important to point out that, throughout the 3 h period analyzed here, convection evolves and may behave differently at different stages. To assess this, Figs. S1–S3 in the Supplement show profiles, as in Fig. 4, where the 3 h period has been divided into three stages. These profiles reflect the fact that convection deepens with time but, otherwise, show consistency with Fig. 4. Furthermore, considering the entire 3 h period provides a larger sample of updrafts, which, in turn, aids in reducing the noise.
Regarding the responses to increases in aerosol concentrations, both frameworks show overall agreement. To visualize these responses more clearly, Fig. 5 shows the differences between profiles for each successive doubling of aerosol concentrations, their average change, and the difference between the most and least polluted cases. This figure also helps to identify in which quantities there is a consistent response to increases in aerosol concentrations. Notice how linear the response is for cloud nucleation rate and cloud droplet number concentration (Fig. 5a, b and i, j) and how the decrease in rain number concentration behaves exponentially, with the largest changes for lower aerosol number concentrations (Fig. 5c and k). On the other hand, the increase in the cloud water mixing ratio is slightly offset by the decrease in the rain water mixing ratio (Fig. 5d–e and l–m), so that there is a slight net decrease in total liquid water mixing ratio (not shown here). However, the variability in the decrease in rain water mixing ratio between pairs of experiments is significantly higher than in the increase in the cloud water mixing ratio, which also makes the net decrease in total water mass highly variable between simulations.
In contrast to the microphysical quantities, latent heating rates, vertical velocity and mass flux do not reveal such prominent and consistent responses to aerosol concentrations (Fig. 5f–h and n–p), and this is true in both frameworks. As expected, changes in vertical velocity closely follow changes in latent heating rates, but both are small on average, with a high level of noise between different pairs of experiments and more so in the cumulus thermal framework. For example, in the comparison between 4000 and 500 cm−3, we find an increase of ∼10 % in the vertical velocity near heights of 6 and 11 (consistent with findings by Marinescu et al., 2021). The average response for a doubling of aerosol concentrations at these altitudes also suggests an increase, but it is much weaker (∼2 %); however, not all individual pairs of cases show such an increase, and the amplitude of the individual responses is usually larger than the average one.
Regarding mass flux, notice that its estimate based on tracked thermals is ∼15 % of the cloudy updraft estimate (Fig. 4h and p). As shown by Hernandez-Deckers and Sherwood (2016), the relatively low fraction captured by thermals results from mainly small and slow thermals that are harder to identify and track with our method; however, it is representative of the entire convective activity. In fact, notice that the changes in mass flux for each doubling are consistent between the thermal estimate and the cloudy updraft grid point estimate (Fig. 5h and p). Here, too, the average response for doubling aerosol concentrations is weaker than the individual responses. In fact, it is nearly zero everywhere, except for a slight increase around 4 in the thermals' framework, which can be linked to an increase in the number of tracked thermals (Fig. 6e).
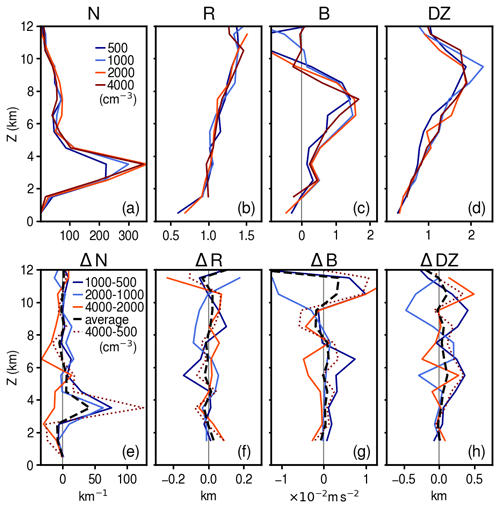
Figure 6Vertical profiles of the (a) number of thermals (per vertical kilometer), (b) average thermal radius, (c) average buoyancy, and (d) average vertical distance traveled by thermals for the different aerosol number concentrations (see the legend). Panels (e) through (h) show the differences in the quantities of panels (a) through (d) between successive pairs of profiles (continuous colored lines), their average change (dashed black line), and the change between the two extreme cases, i.e., 4000 and 500 cm−3 (dotted color line).
Similar results are seen for other quantities relevant for cumulus thermals (Fig. 6). A certain degree of correspondence can be seen between buoyancy changes (Fig. 6g) and vertical velocity changes (Fig. 5o), with hardly any average response when doubling the aerosol concentrations, despite significant (but not consistent) changes between individual pairs of simulations. Changes in the average vertical distance traveled by thermals (DZ; Fig. 6h) is also similar to changes in the vertical velocity of thermals, especially its average response for a doubling of aerosol concentrations (Fig. 5o). This indicates that the average thermal lifetime (not shown here) is also invariant to aerosol number concentrations.
All these quantities related to the thermals' dynamics seem to respond only very weakly to changes in aerosol number concentrations, compared to the natural variability between each pair of simulations. This is a known limitation when investigating the aerosol invigoration of convection. Several studies have emphasized the difficulty of rising above the noise level when trying to identify aerosol indirect effects (e.g., Morrison and Grabowski, 2011; Grabowski, 2014). For a given microphysics and dynamics framework, our results support this view from both the cloudy updraft and the thermal frameworks regarding fundamental dynamical properties, since results vary widely, depending on which pair of experiments is taken into account. However, we also see some indication of a change in the sign of the trend across the full dynamic range of aerosol variability. For instance, the doubling aerosol initially increases buoyancy near 6 but ultimately decreases buoyancy at that elevation by a similar amount when reaching the highest aerosol concentration. Similar responses can be seen in terms of w, DZ, and mass flux, which is consistent with an aerosol-limited regime (e.g., Koren et al., 2014).
Average thermal size, which we estimate here with its radius R, shows no systematic change related to aerosol number concentrations (Fig. 6b and f). However, we do find a response in the number of tracked thermals, particularly between 2–4 , where most thermals develop. This response also seems to depend on the particular range of aerosol variability, with more thermals being tracked as aerosol concentrations increase in the cleaner regime (500–2000 cm−3) and fewer thermals being tracked when aerosol concentrations are doubled in the more polluted regime (2000–4000 cm−3).
3.3 Thermals vs. cloudy updraft grid points
We have shown how our two sampling criteria provide a general agreement in terms of the microphysical and dynamical responses to increases in aerosol number concentrations. However, we have also noted differences which reveal important features of thermal and grid point analyses. The scatterplots in Fig. 7 show how relevant quantities averaged within thermals compare to the same quantities averaged over cloudy updraft grid points, both for different vertical layers (circle dots) and for the entire columns (crosses) in the different aerosol number concentration experiments. In general, these plots confirm that both thermal and cloudy grid points analyses are close to each other, but interesting features emerge from their comparison.
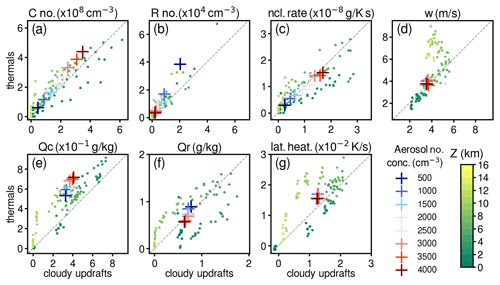
Figure 7Scatterplots of (a) cloud drop number concentrations (C no.), (b) rain number concentrations (R no.), (c) cloud nucleation rates, (d) vertical velocity (w), (e) cloud water mixing ratio (Qc), (f) rain water mixing ratio (Qr), and (g) latent heating rates, as obtained from averaging over thermals (vertical axis) and over cloudy updraft grid points (horizontal axis). Averages over thermals are computed by first obtaining an average value for each thermal and then averaging over all thermals at a certain altitude range (colored dots) or averaging over all thermals (crosses; colors according to aerosol number concentration of each experiment). Values for cloudy updraft grid points are obtained by averaging these per altitude range (colored dots) or per experiment (crosses).
Cloud and rain number concentration, as well as cloud mass mixing ratio (Fig. 7a and e), appear to be similar between thermal and cloudy grid points but have slightly higher values within thermals than for cloudy updraft grid points. This is more prominent at higher altitudes, where thermals tend to be larger and vigorous, and the same applies for rain number concentrations. In other words, at higher elevations, thermals differ more from the average cloudy conditions than at lower elevations, which emphasizes their important role in the deepening of the convective cloud. At the near-surface level (∼1 ), the cloud number and mass concentrations are lower than the cloudy updraft grid points, most likely due to the thermal's internal circulations that may include downdrafts and/or condensate-free volumes of air, but, nevertheless, are dynamically connected to the rising thermals and their internal microphysical processes.
Rain mass mixing ratios also appear to be higher in thermals than in cloudy updraft grid points but have, on average, similar values in both cases (Fig. 7f). When separated by height, thermals at higher altitudes tend to have higher rain mass mixing ratios than cloudy updraft grid points, but the opposite is true at lower altitudes. This can be explained if one thinks of thermals at upper levels as the regions where rain is starting to form and, hence, have more rain mass than the average cloudy updraft grid points, whereas rain at lower levels tends to be concentrated at downdraft regions where rising thermals are limited. An interesting feature here is that the average values per experiment cross the 1:1 line in such a way that thermals have higher rain mixing ratios than the average cloudy updraft grid points in the cleaner cases but lower rain mixing ratios in the polluted cases. This would be in line with raindrops being larger (and fewer) in the polluted cases, making them fall faster and less likely to be inside a rising thermal.
Averaged over the entire vertical column, thermals and cloudy updraft grid points respond almost equally in terms of nucleation rates to varying aerosol number concentrations (Fig. 7c). However, thermals tend to have slightly higher nucleation rates in the upper levels and lower nucleation rates in the lower levels compared to cloudy updraft grid points. This small difference may be because thermals in the upper levels tend to sample the larger, faster, and, hence, less diluted updrafts, while the cloudy updraft grid points may also sample weaker, shorter-lived updrafts where nucleation rates are lower. On the other hand, at lower altitudes, thermals tend to be smaller and more numerous, likely sampling similar updrafts as cloudy updraft grid points, but thermals include a larger volume of air surrounding the updrafts, slightly reducing their average nucleation rates.
In terms of overall column averages, we see that, for both thermals and cloudy updraft grid points, latent heating rates, and vertical velocity appears to be similar (Fig. 7d and g). Regarding the relation between thermal averages and cloudy updraft grid points, there are important differences with altitude. For example, the average vertical velocity of cloudy updraft grid points and thermals follows the 1:1 line closely up to about 6 m s−1. Average vertical velocity for thermals, in particular above an altitude of about 6 , does exceed this value, while the average for cloudy updraft grid points does not. To understand this, notice that the mass flux captured by thermals (Fig. 4e) has a first maximum just below 4 and a second maximum around 8–9 The first maximum coincides with the layer where most smaller and short-lived thermals are found within the boundary layer; the second maximum has about half the mass flux of the first but only about a sixth of the number of thermals (Fig. 6a). Thus, the thermals above 6–7 are not as numerous, but larger ones individually contribute much more to the total mass flux than those in the boundary layer. Increasing the vertical velocity threshold for the cloudy updraft grid point definition, while it does not modify the aerosol sensitivities found here, yields closer values between frameworks for several quantities at upper levels but at the expense of larger differences at middle and lower levels that result in less overall consistency (Figs. S4 and S5). Further investigation of the detailed differences between the two frameworks at upper levels is left for a future study, with a focus extended to ice microphysical processes.
Finally, the fact that latent heating rates tend to be higher for thermals than for cloudy updraft grid points at a higher altitude (Fig. 7g) suggests that thermals are capturing the most relevant regions where condensation occurs and, thus, the most relevant convective regions of the cloud. Latent heating rates of thermals largely exceed those of cloudy updraft grid points at higher altitude but underestimate at near-surface level. These are very similar patterns of those combined from cloud and rain mass mixing ratio (Fig. 7e–g). Overall, these results highlight how both frameworks are generally consistent, while subtle differences between them can provide additional useful information.
In order to investigate the coupling between updraft dynamics and microphysics, we study the impact of ambient aerosol concentration on deep convection in a series of eight simulations at 250 m horizontal grid spacing of a case study over Houston, Texas, where initial background aerosol concentrations are systematically varied from 500 to 4000 cm−3 in intervals of 500 cm−3. Apart from the traditional cloudy updraft grid point analysis (e.g., summarized in Tao et al., 2012; Fan et al., 2016), we also identify and track cumulus thermals and use these as an alternative sampling criteria to study the deep convective response to the imposed aerosol concentrations, based on the idea that thermals are the building blocks of cumulus clouds (e.g., Sherwood et al., 2013; Varble et al., 2014; Romps and Charn, 2015). A comparative analysis between cloudy updraft grid points and cumulus thermals provide new insights into the coupling between updraft dynamics and microphysics.
As a first step, and given the uncertainties in the current representation of convective microphysical processes, this study focuses only on the warm-phase microphysics. We find similar microphysical responses to an increase in aerosol concentrations for thermals and for cloudy updraft grid point analyses because nucleation rates and cloud drop number concentrations increase, while supersaturation values and rain number concentrations decrease. That is, more – but smaller – cloud droplets form, leading to fewer – but larger – raindrops. These responses are very consistent throughout the entire sets of experiments, indicating a clear connection to aerosol number concentrations in rising thermals, and cloudy updraft grid points. However, average latent heating rates are not impacted by changing aerosol concentrations, except in the middle troposphere (4 and 6 ), where average ∼2 % increases of latent heating rates, ascent rate, and vertical velocity occur for every doubling of aerosol number concentrations (similarly between thermal and cloudy updraft grid point analyses).
Nevertheless, these responses for thermals and cloudy updraft grid points are not entirely consistent between individual pairs of doubling experiments. Thus, very different conclusions could be drawn from each pair of experiments due to natural variability (e.g., Morrison and Grabowski, 2011; Grabowski, 2014) and several other factors, such as the synoptic forcing, ambient relative humidity, the actual range of aerosol concentrations, and specific microphysics schemes (Fan et al., 2007; White et al., 2017; Barthlott and Hoose, 2018; Iguchi et al., 2020; Abbott and Cronin, 2021; Marinescu et al., 2021). Therefore, results of this type are usually case and model dependent, and conclusions from a single model configuration or a single – or few – cases should be interpreted with caution. Our simulations, which intend to replicate a real continental case where only aerosol number concentrations are varied over an observationally established range, suggest that the natural variability largely surpasses the impact of aerosols on the dynamical features of convection. It is, therefore, not surprising that intermodel variability has also been found to be larger than aerosol-related variability in terms of its impact on convection (e.g., Marinescu et al., 2021).
Despite the uncertainties of the model response to background aerosol concentrations, the comparison between cloudy updraft grid points and thermals indicates a general agreement between both frameworks, while subtle differences between them allow us to identify important features. Thermals, especially in the middle and upper troposphere, are larger, more vigorous, and undiluted so that they nucleate higher droplet and raindrop concentrations and higher cloud water mixing ratios than the average cloudy updraft grid points and acting as rain incubators too. On the other hand, at the lower troposphere (below 4 ), where smaller, short-lived thermals are predominant, the updraft velocity, cloud nucleation, and latent heating rates of thermals tend to be equivalent to or smaller than cloudy updraft grid points, likely due to the thermals' internal heterogeneity, which may also be important to consider. Consequently, microphysics quantities tend to also be equivalent or lower in thermals than in cloudy updraft grid points at such altitudes. This suggests that thermals and cloudy updraft grid points are similar sampling criteria in the lower troposphere, but from the middle troposphere upward, large and vigorous thermals may offer a more selective sampling criteria that captures the most relevant convective air masses where microphysical processes are indeed most active. This increases the level of noise in the thermal framework compared to the cloudy updraft grid point framework, but that may also represent information content regarding the scarcity of what have sometimes been referred to as lucky updrafts.
On the other hand, the thermal tracking approach yields an abundance of additional information on the spatiotemporal evolution and life cycle of the structures that largely drive hydrometeor production processes within convective clouds; indeed, this is the key information needed for subgrid-scale parameterizations in climate models and is the gray zone in which convective processes remain poorly resolved. For instance, efforts to extend climate model convection schemes that parameterize updraft velocities and use these to inform microphysical process rates (e.g., Wu et al., 2009) can draw upon the three-dimensionally colocated properties and process statistics directly identified within the structures that they seek to represent. The thermal approach is also likely to naturally avoid the inclusion of oscillatory gravity wave motions, which may contribute substantially to mass flux especially in stable regions of the atmosphere, such as the upper troposphere (Mrowiec et al., 2015). Overall, this further motivates the use of thermals as the basic elements to develop a parameterization of coupled convective dynamics and microphysics for a climate model to better represent aerosol–deep convection interactions in the future.
The NASA-Unified WRF (NU-WRF) is maintained at NASA GSFC, and available for public use upon request (https://nuwrf.gsfc.nasa.gov/, NUWRF, 2022). NU-WRF outputs are available upon request from the NASA GSFC Cloud Library (https://portal.nccs.nasa.gov/cloudlibrary/, GSFC, 2022). All other processing code used for this study is available upon request to the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-22-711-2022-supplement.
All authors conceived and designed the research. TM carried out the model simulations and performed the cloudy updraft grid point analyses. DHD performed the thermal tracking and its analysis and led the writing of the paper, with input from all authors.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the NASA Advanced Supercomputing (NAS) Division, for providing the computational resources to conduct and analyze the NU-WRF simulations. We also thank the three anonymous reviewers, for their constructive comments which greatly improved the paper. Toshihisa Matsui has been funded by the U.S. Department of Energy ASR program (grant no. DE-SC0021247) and NASA PMM program (grant no. 80NSSC19K0724). Ann M. Fridlind has been supported by the Office of Science (BER) and U.S. Department of Energy (grant nos. DE-SC0006988 and DE-SC0016237), and Daniel Hernandez-Deckers has been funded by Universidad Nacional de Colombia.
This research has been supported by the U.S. Department of Energy ASR program (grant nos. DE-SC0021247 and DE-SC0016237), NASA PMM program (grant no. 80NSSC19K0724), and Office of Science (BER; grant no. DE-SC0006988).
This paper was edited by Farahnaz Khosrawi and reviewed by three anonymous referees.
Abbott, T. H. and Cronin, T. W.: Aerosol invigoration of atmospheric convection through increases in humidity, Science, 371, 83–85, https://doi.org/10.1126/science.abc5181, 2021. a, b, c
Abdul-Razzak, H. and Ghan, S. J.: A parameterization of aerosol activation: 2. Multiple aerosol types, J. Geophys. Res.-Atmos., 105, 6837–6844, https://doi.org/10.1029/1999JD901161, 2000. a
Barthlott, C. and Hoose, C.: Aerosol Effects on Clouds and Precipitation over Central Europe in Different Weather Regimes, J. Atmos. Sci., 75, 4247–4264, https://doi.org/10.1175/JAS-D-18-0110.1, 2018. a
Blyth, A. M., Lasher-Trapp, S. G., and Cooper, W. A.: A study of thermals in cumulus clouds, Q. J. Roy. Meteor. Soc., 131, 1171–1190, https://doi.org/10.1256/qj.03.180, 2005. a
Damiani, R., Vali, G., and Haimov, S.: The Structure of Thermals in Cumulus from Airborne Dual-Doppler Radar Observations, J. Atmos. Sci., 63, 1432–1450, https://doi.org/10.1175/JAS3701.1, 2006. a
de Roode, S. R. and Bretherton, C. S.: Mass-Flux Budgets of Shallow Cumulus Clouds, J. Atmos. Sci., 60, 137–151, https://doi.org/10.1175/1520-0469(2003)060<0137:MFBOSC>2.0.CO;2, 2003. a
Fan, J., Zhang, R., Li, G., and Tao, W.-K.: Effects of aerosols and relative humidity on cumulus clouds, J. Geophys. Res.-Atmos., 112, D14204, https://doi.org/10.1029/2006JD008136, 2007. a
Fan, J., Wang, Y., Rosenfeld, D., and Liu, X.: Review of Aerosol–Cloud Interactions: Mechanisms, Significance, and Challenges, J. Atmos. Sci., 73, 4221–4252, https://doi.org/10.1175/JAS-D-16-0037.1, 2016. a, b
Fan, J., Rosenfeld, D., Zhang, Y., Giangrande, S. E., Li, Z., Machado, L. A. T., Martin, S. T., Yang, Y., Wang, J., Artaxo, P., Barbosa, H. M. J., Braga, R. C., Comstock, J. M., Feng, Z., Gao, W., Gomes, H. B., Mei, F., Pöhlker, C., Pöhlker, M. L., Pöschl, U., and de Souza, R. A. F.: Substantial convection and precipitation enhancements by ultrafine aerosol particles, Science, 359, 411–418, https://doi.org/10.1126/science.aan8461, 2018. a
Fridlind, A. M., Li, X., Wu, D., van Lier-Walqui, M., Ackerman, A. S., Tao, W.-K., McFarquhar, G. M., Wu, W., Dong, X., Wang, J., Ryzhkov, A., Zhang, P., Poellot, M. R., Neumann, A., and Tomlinson, J. M.: Derivation of aerosol profiles for MC3E convection studies and use in simulations of the 20 May squall line case, Atmos. Chem. Phys., 17, 5947–5972, https://doi.org/10.5194/acp-17-5947-2017, 2017. a, b, c
Fridlind, A. M., van Lier-Walqui, M., Collis, S., Giangrande, S. E., Jackson, R. C., Li, X., Matsui, T., Orville, R., Picel, M. H., Rosenfeld, D., Ryzhkov, A., Weitz, R., and Zhang, P.: Use of polarimetric radar measurements to constrain simulated convective cell evolution: a pilot study with Lagrangian tracking, Atmos. Meas. Tech., 12, 2979–3000, https://doi.org/10.5194/amt-12-2979-2019, 2019. a
Grabowski, W. W.: Extracting Microphysical Impacts in Large-Eddy Simulations of Shallow Convection, J. Atmos. Sci., 71, 4493–4499, https://doi.org/10.1175/JAS-D-14-0231.1, 2014. a, b
GSFC: Goddard Space Flight Center Data Portal – Cloud Library, available at: https://portal.nccs.nasa.gov/cloudlibrary/, last access: 11 January 2022. a
Hernandez-Deckers, D. and Sherwood, S. C.: A numerical study of cumulus thermals, J. Atmos. Sci., 73, 4117–4136, https://doi.org/10.1175/JAS-D-15-0385.1, 2016. a, b, c, d, e, f, g, h, i, j
Hernandez-Deckers, D. and Sherwood, S. C.: On the Role of Entrainment in the Fate of Cumulus Thermals, J. Atmos. Sci., 75, 3911–3924, https://doi.org/10.1175/JAS-D-18-0077.1, 2018. a, b
Iguchi, T., Rutledge, S. A., Tao, W.-K., Matsui, T., Dolan, B., Lang, S. E., and Barnum, J.: Impacts of Aerosol and Environmental Conditions on Maritime and Continental Deep Convective Systems Using a Bin Microphysical Model, J. Geophys. Res.-Atmos., 125, e2019JD030952, https://doi.org/10.1029/2019JD030952, 2020. a
Khain, A. P., BenMoshe, N., and Pokrovsky, A.: Factors Determining the Impact of Aerosols on Surface Precipitation from Clouds: An Attempt at Classification, J. Atmos. Sci., 65, 1721–1748, https://doi.org/10.1175/2007JAS2515.1, 2008. a
Koren, I., Dagan, G., and Altaratz, O.: From aerosol-limited to invigoration of warm convective clouds, Science, 344, 1143–1146, https://doi.org/10.1126/science.1252595, 2014. a
Korolev, A., Heckman, I., Wolde, M., Ackerman, A. S., Fridlind, A. M., Ladino, L. A., Lawson, R. P., Milbrandt, J., and Williams, E.: A new look at the environmental conditions favorable to secondary ice production, Atmos. Chem. Phys., 20, 1391–1429, https://doi.org/10.5194/acp-20-1391-2020, 2020. a
Lecoanet, D. and Jeevanjee, N.: Entrainment in Resolved, Dry Thermals, J. Atmos. Sci., 76, 3785–3801, https://doi.org/10.1175/JAS-D-18-0320.1, 2019. a
Marinescu, P. J., van den Heever, S. C., Heikenfeld, M., Barrett, A. I., Barthlott, C., Hoose, C., Fan, J., Fridlind, A. M., Matsui, T., Miltenberger, A. K., Stier, P., Vie, B., White, B. A., and Zhang, Y.: Impacts of Varying Concentrations of Cloud Condensation Nuclei on Deep Convective Cloud Updrafts–A Multimodel Assessment, J. Atmos. Sci., 78, 1147–1172, https://doi.org/10.1175/JAS-D-20-0200.1, 2021. a, b, c, d, e, f, g, h, i, j, k
Matsui, T., Zhang, S. Q., Lang, S. E., Tao, W.-K., Ichoku, C., and Peters-Lidard, C. D.: Impact of radiation frequency, precipitation radiative forcing, and radiation column aggregation on convection-permitting West African monsoon simulations, Clim. Dynam., 55, 193–213, https://doi.org/10.1007/s00382-018-4187-2, 2020. a
McFarlane, N.: Parameterizations: representing key processes in climate models without resolving them, WIREs Clim. Change, 2, 482–497, https://doi.org/10.1002/wcc.122, 2011. a
Morrison, H.: Impacts of Updraft Size and Dimensionality on the Perturbation Pressure and Vertical Velocity in Cumulus Convection. Part II: Comparison of Theoretical and Numerical Solutions and Fully Dynamical Simulations, J. Atmos. Sci., 73, 1455–1480, https://doi.org/10.1175/jas-d-15-0041.1, 2016. a
Morrison, H. and Grabowski, W. W.: Modeling Supersaturation and Subgrid-Scale Mixing with Two-Moment Bulk Warm Microphysics, J. Atmos. Sci., 65, 792–812, https://doi.org/10.1175/2007JAS2374.1, 2008. a
Morrison, H. and Grabowski, W. W.: Cloud-system resolving model simulations of aerosol indirect effects on tropical deep convection and its thermodynamic environment, Atmos. Chem. Phys., 11, 10503–10523, https://doi.org/10.5194/acp-11-10503-2011, 2011. a, b
Morrison, H. and Milbrandt, J. A.: Parameterization of Cloud Microphysics Based on the Prediction of Bulk Ice Particle Properties. Part I: Scheme Description and Idealized Tests, J. Atmos. Sci., 72, 287–311, https://doi.org/10.1175/JAS-D-14-0065.1, 2015. a
Morrison, H. and Peters, J. M.: Theoretical Expressions for the Ascent Rate of Moist Deep Convective Thermals, J. Atmos. Sci., 75, 1699–1719, https://doi.org/10.1175/jas-d-17-0295.1, 2018. a
Moser, D. H. and Lasher-Trapp, S.: The Influence of Successive Thermals on Entrainment and Dilution in a Simulated Cumulus Congestus, J. Atmos. Sci., 74, 375–392, https://doi.org/10.1175/jas-d-16-0144.1, 2017. a, b
Mrowiec, A. A., Pauluis, O. M., Fridlind, A. M., and Ackerman, A. S.: Properties of a Mesoscale Convective System in the Context of an Isentropic Analysis, J. Atmos. Sci., 72, 1945–1962, https://doi.org/10.1175/JAS-D-14-0139.1, 2015. a, b, c
NUWRF: NASA-Unified Weather Research and Forecasting, available at: https://nuwrf.gsfc.nasa.gov/, last access: 11 January 2022. a
Peters, J. M., Morrison, H., Varble, A. C., Hannah, W. M., and Giangrande, S. E.: Thermal Chains and Entrainment in Cumulus Updrafts. Part II: Analysis of Idealized Simulations, J. Atmos. Sci., 77, 3661–3681, https://doi.org/10.1175/JAS-D-19-0244.1, 2020. a, b
Peters-Lidard, C. D., Kemp, E. M., Matsui, T., Santanello, J. A., Kumar, S. V., Jacob, J. P., Clune, T., Tao, W.-K., Chin, M., Hou, A., Case, J. L., Kim, D., Kim, K.-M., Lau, W., Liu, Y., Shi, J., Starr, D., Tan, Q., Tao, Z., Zaitchik, B. F., Zavodsky, B., Zhang, S. Q., and Zupanski, M.: Integrated modeling of aerosol, cloud, precipitation and land processes at satellite-resolved scales, Environ. Modell. Softw., 67, 149–159, https://doi.org/10.1016/j.envsoft.2015.01.007, 2015. a
Romps, D. M. and Charn, A. B.: Sticky Thermals: Evidence for a Dominant Balance between Buoyancy and Drag in Cloud Updrafts, J. Atmos. Sci., 72, 2890–2901, https://doi.org/10.1175/JAS-D-15-0042.1, 2015. a, b, c
Rosenfeld, D., Lohmann, U., Raga, G. B., O'Dowd, C. D., Kulmala, M., Fuzzi, S., Reissell, A., and Andreae, M. O.: Flood or Drought: How Do Aerosols Affect Precipitation?, Science, 321, 1309–1313, https://doi.org/10.1126/science.1160606, 2008. a
Rosenfeld, D., Williams, E., Andreae, M. O., Freud, E., Pöschl, U., and Rennó, N. O.: The scientific basis for a satellite mission to retrieve CCN concentrations and their impacts on convective clouds, Atmos. Meas. Tech., 5, 2039–2055, https://doi.org/10.5194/amt-5-2039-2012, 2012. a
Scorer, R. S. and Ludlam, F. H.: Bubble theory of penetrative convection, Q. J. Roy. Meteor. Soc., 79, 94–103, https://doi.org/10.1002/qj.49707933908, 1953. a
Sherwood, S. C., Hernandez-Deckers, D., Colin, M., and Robinson, F.: Slippery Thermals and the Cumulus Entrainment Paradox, J. Atmos. Sci., 70, 2426–2442, https://doi.org/10.1175/JAS-D-12-0220.1, 2013. a, b, c, d
Siebesma, A. P. and Cuijpers, J. W. M.: Evaluation of Parametric Assumptions for Shallow Cumulus Convection, J. Atmos. Sci., 52, 650–666, https://doi.org/10.1175/1520-0469(1995)052<0650:EOPAFS>2.0.CO;2, 1995. a
Tao, W.-K., Chen, J.-P., Li, Z., Wang, C., and Zhang, C.: Impact of aerosols on convective clouds and precipitation, Rev. Geophys., 50, RG2001, https://doi.org/10.1029/2011RG000369, 2012. a, b, c, d
Varble, A., Zipser, E. J., Fridlind, A. M., Zhu, P., Ackerman, A. S., Chaboureau, J.-P., Collis, S., Fan, J., Hill, A., and Shipway, B.: Evaluation of cloud-resolving and limited area model intercomparison simulations using TWP-ICE observations: 1. Deep convective updraft properties, J. Geophys. Res.-Atmos., 119, 13891–13918, https://doi.org/10.1002/2013jd021371, 2014. a, b
White, B., Gryspeerdt, E., Stier, P., Morrison, H., Thompson, G., and Kipling, Z.: Uncertainty from the choice of microphysics scheme in convection-permitting models significantly exceeds aerosol effects, Atmos. Chem. Phys., 17, 12145–12175, https://doi.org/10.5194/acp-17-12145-2017, 2017. a
Woodward, B.: The motion in and around isolated thermals, Q. J. Roy. Meteor. Soc., 85, 144–151, https://doi.org/10.1002/qj.49708536407, 1959. a
Wu, J., Del Genio, A. D., Yao, M.-S., and Wolf, A. B.: WRF and GISS SCM simulations of convective updraft properties during TWP-ICE, J. Geophys. Res.-Atmos., 114, D04206, https://doi.org/10.1029/2008JD010851, 2009. a
Yano, J.-I.: Basic convective element: bubble or plume? A historical review, Atmos. Chem. Phys., 14, 7019–7030, https://doi.org/10.5194/acp-14-7019-2014, 2014. a
Yeung, N. K. H., Sherwood, S. C., Protat, A., Lane, T. P., and Williams, C.: A Doppler Radar Study of Convective Draft Lengths over Darwin, Australia, Mon. Weather Rev., 149, 2965–2974, https://doi.org/10.1175/MWR-D-20-0390.1, 2021. a, b





