Observational constraints on methane emissions from Polish coal mines using a ground-based remote sensing network

Given its abundant coal mining activities, the Upper Silesian Coal Basin (USCB) in southern Poland is one of the largest sources of anthropogenic methane (CH₄) emissions in Europe. Here, we report on CH₄ emission estimates for coal mine ventilation facilities in the USCB. Our estimates are driven by pairwise upwind–downwind observations of the column-average dry-air mole fractions of CH₄ (XCH₄) by a network of four portable, ground-based, sun-viewing Fourier transform spectrometers of the type EM27/SUN operated during the CoMet campaign in May–June 2018. The EM27/SUN instruments were deployed in the four cardinal directions around the USCB approximately 50 km from the center of the basin. We report on six case studies for which we inferred emissions by evaluating the mismatch between the observed downwind enhancements and simulations based on trajectory calculations releasing particles out of the ventilation shafts using the Lagrangian particle dispersion model FLEXPART. The latter was driven by wind fields calculated by WRF (Weather Research and Forecasting model) under assimilation of vertical wind profile measurements of three co-deployed wind lidars. For emission estimation, we use a Phillips–Tikhonov regularization scheme with the L-curve criterion. Diagnosed by the emissions averaging kernels, we find that, depending on the catchment area of the downwind measurements, our ad hoc network can resolve individual facilities or groups of ventilation facilities but that inspecting the emissions averaging kernels is essential to detect correlated estimates. Generally, our instantaneous emission estimates range between 80 and 133 kt CH₄ a⁻¹ for the southeastern part of the USCB and between 414 and 790 kt CH₄ a⁻¹ for various larger parts of the basin, suggesting higher emissions than expected from the annual emissions reported by the E-PRTR (European Pollutant Release and Transfer Register). Uncertainties range between 23 % and 36 %, dominated by the error contribution from uncertain wind fields.

1 Introduction

The atmospheric abundance of methane (CH₄) has increased by a factor of 2.6 since pre-industrial times from roughly 720 ppb (parts per billion) to about 1879 ppb in 2020 (Dlugokencky, 2021), mainly driven by anthropogenic influences (e.g., Bousquet et al., 2006; Loulergue et al., 2008; Kirschke et al., 2013; IPCC, 2013; Nisbet et al., 2014; Conley et al., 2016; Schwietzke et al., 2016; Worden et al., 2017; Alvarez et al., 2018; Saunois et al., 2020; Hmiel et al., 2020). Roughly 20 % of the total global anthropogenic CH₄ emissions are caused by the fossil fuel industry (Bousquet et al., 2006; Schwietzke et al., 2016; Saunois et al., 2020) and an extensive source of CH₄ is hard coal mining. Poland is the largest hard coal producer in the European Union with the Upper Silesian Coal Basin (USCB) as one of the largest hard coal producing regions in Europe. Several bottom-up inventories report on the total CH₄ emissions for the USCB: according to the GESAPU database, the USCB emitted a total of 405 kt CH₄ in 2010 (Bun et al., 2019). The E-PRTR (http://prtr.ec.europa.eu/, European Pollutant Release and Transfer Register, 2018) collects emission reports of every individual mine, yielding an aggregated total of 507 kt CH₄ a⁻¹ for the USCB. Dreger (2021) reports hard coal mining emissions of 530 kt CH₄ for the USCB in 2018, and the Copernicus Atmosphere Monitoring Service regional emission inventory (CAMS-REG-GHG/AP) lists 632 kt CH₄ a⁻¹ (Granier et al., 2019; Fiehn et al., 2020). EDGAR v4.3.2 (Emission Database for Global Atmospheric Research) gives emissions of 675 kt CH₄ a⁻¹ (Janssens-Maenhout et al., 2017) for fuel exploitation emissions (EDGAR abbreviation PRO) for the USCB in the year 2012. EDGAR v6.0 (Crippa et al., 2020) states 454 kt CH₄ a⁻¹ for the sector abbreviation PRO COAL for the USCB in 2018. The extrapolated seasonal breakdown provided by EDGAR for the relevant months May and June 2018 matches the total 2018 EDGAR emission estimate for the USCB.

In addition to the bottom-up inventories, top-down approaches have examined USCB emissions. During the CoMet mission (Carbon dioxide and Methane mission 2018, from 23 May to 12 June 2018), several ground-based instruments and aircraft measured the atmospheric CH₄ abundance in the USCB. In our precursor study (Luther et al., 2019), we used stop-and-go measurements of the column-average dry-air mole fractions of CH₄ (XCH₄) by a mobile, ground-based Fourier transform spectrometer (FTS) to evaluate the mining emissions of individual ventilation facilities and found similar emissions as suggested by the E-PRTR inventory. The total USCB emission estimates of Fiehn et al. (2020) and Kostinek et al. (2021), based on airborne in situ measurements, are in broad agreement with the E-PRTR data for single flights. Using airborne imager data, Krautwurst et al. (2021) found some discrepancies between their estimates and the E-PRTR inventory for small groups of ventilation facilities. The isotopic CH₄ composition was measured by Menoud et al. (2021) with ground-based in situ instruments. Swolkień (2020) discusses the short-term, shaft-wise CH₄ release in the USCB.

Given the magnitude of emissions and the range of estimates, CH₄ in the USCB warrants further investigation. Here, we report on CH₄ emission estimates derived from measurements of four stationary, sun-viewing FTSs of the type EM27/SUN arranged in a network-like pattern enclosing the USCB during the CoMet campaign activities. The setup largely mimics previous network deployments for quantifying urban greenhouse gas emissions in Berlin (Hase et al., 2015), Paris (Vogel et al., 2019), St. Petersburg (Makarova et al., 2021), Munich (Dietrich et al., 2021), Indianapolis (Jones et al., 2021), and other places. Our four EM27/SUN instruments were positioned in the four cardinal directions at a distance of a few tens of kilometers to the center of the USCB. We calculate differences between pairs of upwind and downwind observations to determine enhancements (ΔXCH₄) in our XCH₄ records attributable to sources within the USCB. Further developing the model setup of Kostinek et al. (2021), we use the flexible Lagrangian particle dispersion model (FLEXPART) together with wind fields from the Weather Research and Forecasting model (WRF) constrained by three wind lidars to translate the observed XCH₄ enhancements into emission estimates for groups of coal mine ventilation shafts. To this end, we set up an inverse estimation scheme based on Phillips–Tikhonov regularization. This setup enables careful information content analysis while not relying on estimates of a priori emission uncertainties, which are often inaccessible. This work demonstrates emission estimation of a methane-emitting hotspot based on an FTS network combined with a Phillips–Tikhonov regularized inversion approach.

Our paper first summarizes the campaign setup (Sect. 2). Then, Sects. 3 and 4 detail the modeling and regularization methods. Section 5 reports on emission estimates for six case studies, and Sect. 6 discusses our results in terms of compatibility with other emission estimates and methodological strengths and weaknesses.

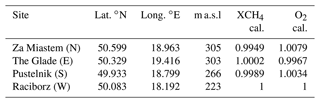
Figure 1 The USCB in southwest Poland. The small inset on the left illustrates the region of Silesia in black and the map excerpt of the USCB in red. Ventilation shafts are marked as grey triangles. Stationary EM27/SUN FTS locations are marked as red triangles; the three wind lidars DLR85, DLR86, and DLR89 are marked as red stars. Eastern and southern wind lidars are placed at the same locations as the respective EM27/SUN instruments. The western wind lidar is located about 30 km to the east of the western EM27/SUN. Background map from ESRI (2019).

2 Campaign deployment and XCH₄ measurements

As part of the CoMet activities in May and June 2018, our campaign deployment of the EM27/SUN focused on the USCB, extending roughly 80 × 80 km² in the southwest of Poland. Figure 1, adopted from our precursor study on mobile measurements (Luther et al., 2019), illustrates the network pattern together with the locations of the most important coal mine ventilation shafts and the wind lidars. The four stationary EM27/SUN spectrometers are positioned roughly in the four cardinal directions around the center of the basin, ensuring that at least one instrument measures upwind and one downwind of the USCB for most wind situations. Due to mainly easterly wind conditions prevailing during our deployment, the eastern station (The Glade) functions as the upwind station for all case studies discussed here. The respective downwind stations are located in the south (Pustelnik) and west (Raciborz) of the USCB. The northern station (Za Miastem) was identified as neither an upwind nor downwind station for any of the cases.

The functioning of the EM27/SUN FTS and the data reduction techniques are described in detail by Gisi et al. (2012), Hase et al. (2015, 2016), and with a particular focus on our setup by Luther et al. (2019). Generally, the EM27/SUN instruments observe spectra of direct sunlight in the shortwave infrared spectral range from which the total column concentrations of CH₄, carbon dioxide (CO₂), water vapor (H₂O), molecular oxygen (O₂), carbon monoxide (CO), and other substances (Butz et al., 2017) can be retrieved. CH₄ and O₂ are of relevance here. All EM27/SUN spectrometers participating in the campaign successfully underwent the instrumental quality assurance tests required by the Collaborative Carbon Column Observing Network (COCCON) and presented in Frey et al. (2019) before field deployment.

We run the software package PROFFIT (Hase et al., 2004) to retrieve the column concentrations [O₂] and [CH₄] from the 7765 to 8005 and 5897 to 6145 cm⁻¹ spectral windows, respectively, using absorption line parameters by Toon (2017) and Rothman et al. (2009). The respective column-average dry-air mole fractions of methane, XCH₄, are calculated via normalization through $\frac{\left[{\mathrm{CH}}_{\mathrm{4}}\right]}{\left[{\mathrm{O}}_{\mathrm{2}}\right]}\times \mathrm{0.2094}$, where the atmospheric O₂ mole fraction is assumed to be 0.2094. The normalization is generally recommended to lessen spurious artifacts due to pressure and solar zenith angle (SZA) dependencies. The SZAs during our measurements did not exceed 56^∘, which is within the range that does not require air-mass-dependent bias correction (Frey et al., 2015). Slightly deviating from the processing recipe (Frey et al., 2019) and in line with our precursor study (Luther et al., 2019), our CH₄ retrievals only scale the CH₄ concentrations in the layers below 1700 m a.g.l. where we expect elevated methane due to the localized sources at the ground. Further, we extract the a priori CH₄ profiles from a dedicated ECHAM/MESSy Atmospheric Chemistry simulation described by Jöckel et al. (2016) and Nickl et al. (2020).

For network deployments such as undertaken here, it is common practice to cross-calibrate the network nodes by side-by-side measurements (Frey et al., 2015, 2019; Chen et al., 2016; Jones et al., 2021; Dietrich et al., 2021) in order to exclude spurious gradients when conducting upwind–downwind analyses. We calibrated the four instruments through side-by-side measurements on 23 and 26 May 2018 at the southern location Pustelnik. Figure 2 shows the raw and calibrated XCH₄ records, and Table 1 lists the respective calibration factors. These instrument-specific empirical calibration factors have been applied to the XCH₄ campaign data discussed in the following. After calibration, the mean absolute instrument-to-instrument difference is roughly 1 ppb, which is compatible with Frey et al. (2019), who state the instrument-to-instrument difference for an EM27/SUN ensemble as 0.8 ppb for XCH₄. We estimate the precision for XCH₄ as 0.6 ppb for 1 min integration time from measurements sampled during the campaign in the rather variable methane field of the USCB, which is consistent with the precision stated by Chen et al. (2016). Based on measurements of the eastern and northern instruments (The Glade – E and Za Miastem – N) observed from 07:00 to 10:00 UTC on 28 May 2018 (upper panel Fig. 7), we calculated the precision as the standard deviation of the observations averaged between the two instruments during this period. We chose this period, since the two timelines are not affected by any strong methane sources in the vicinity.

In addition to the EM27/SUN network, we also operated three Leosphere Windcube 200S Doppler wind lidars (Vasiljević et al., 2016; Wildmann et al., 2018, 2020) marked as red stars in Fig. 1 and as detailed in Luther et al. (2019) and Kostinek et al. (2021). The measured wind profiles (10 min time interval) reach up to 4 km a.g.l. and are assimilated into the WRF simulations to improve the modeled wind fields as discussed in Sect. 3.

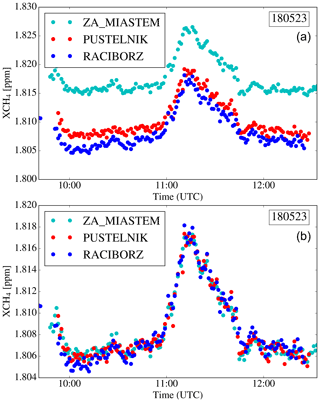
Figure 2 Side-by-side measurements at station Pustelnik (S) on 23 May 2018 on the first day of the deployment. (a) Unscaled data with an average instrument-to-instrument difference of 5 ppb. (b) Measured XCH₄ after scaling with about 1 ppb of instrument-to-instrument difference. Note that the instruments detected a plume-like structure at the beginning of the measurements and around 11:20 UTC. The instrument for The Glade (E) measured side-by-side on 26 May with the Pustelnik (S) instrument (data in Fig. A1).

Table 1 Calibration factors towards the western station Raciborz for each instrument and species, along with the nominal geolocation in the network.

3 Dispersion modeling of methane

Our simulations of methane dispersion in the USCB are partitioned into two steps, largely adopting the basic setup reported by Kostinek et al. (2021): first (Sect. 3.1), the wind fields are modeled by a two-domain WRF setup including assimilation of the wind lidar observations. Second, the WRF wind fields drive the particle dispersion in the Lagrangian particle dispersion model FLEXPART (Sect.  3.2).

3.1 WRF wind fields

The WRF V4 (Skamarock et al., 2019) setup is driven by 3-hourly GFS data (NCEP, 2017) in two domains (Fig. 3) focusing on central Europe and the USCB. The outer domain has a spatial resolution of roughly 15 km, and the inner domain has a spatial resolution of roughly 3 km. The simulations start at 00:00 UTC on the day of interest to allow for several hours of spin-up. Details are explained in Kostinek et al. (2021).

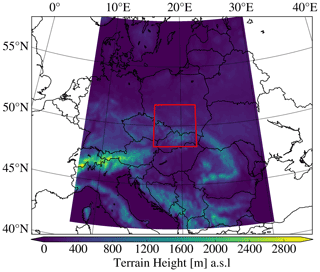
Figure 3 Overview of the two WRF domains over central Europe. The first larger domain (colored shape) has a spatial resolution of ∼15 km. The inner domain (red rectangle) has a spatial resolution of ∼3 km and is focused on the USCB. The Tatra mountain ridge (with elevations >2000 m a.s.l.) in the southern part of the second domain along the border towards Slovakia is fully enclosed by the inner domain.

WRF has the possibility to assimilate observational data via four-dimensional data assimilation (FDDA), which we use for our wind lidar measurements. At a 10 min time interval, the wind profile observations are fed into the WRF calculations to constrain the simulated wind fields. The assimilation process is adjustable via several parameters, e.g., radius of influence r_xy, time window Δt, and horizontal wind coefficient c_uv, in the WRF input file directly. Kostinek et al. (2021) have identified a selection of parameter settings to obtain the best-guess parameter combinations for the same region, WRF domains, and time periods discussed here. Therefore, we adopt the same setup here and report on the overall WRF performance by comparing the simulations with the wind lidar observations.

Figure 4 displays a comparison between modeled and observed wind speed (upper panel) and wind direction (lower panel) for altitude levels in the planetary boundary layer (PBL). PBL height is estimated by means of eddy dissipation rate gradients calculated from the wind lidar observations directly. The observation levels of the wind lidar do not match the WRF grid levels exactly. Thus, the comparison includes modeled and observed data if the WRF wind level is within the range of ±25 m around the level of observation. This represents all of the WRF wind levels but dismisses some of the wind lidar levels as the lidar data have a finer vertical resolution. The comparison is restricted to the three days of the case studies to be discussed below (28 May; 6, 7 June 2018). The prevailing wind directions were northeast to southeast, and prevailing wind speeds range from 2 to 9 ms⁻¹. The root mean square error (RMSE) for the wind speed comparison calculates to 1.7 ms⁻¹. When eliminating the top two levels, the wind direction RMSE is reduced from 38 to 26^∘, indicating model inaccuracies towards the PBL top where wind shear effects are expected. Low wind speeds on 7 June possibly deteriorate the wind direction bias, as wind direction uncertainties are generally larger for low wind speeds. Further challenges for the wind direction estimation are the onset of convection during the observational morning hours with subsequent PBL rise and the calming winds towards the end of the observational days. In general we observed most outliers for the top comparison levels for wind direction, which could be related to a significant number of conspicuous low-wind-speed simulations and observations for these levels. This might be related to model uncertainties when estimating the PBL height, leading to misinterpretation of actual above-PBL observations with inside-PBL simulations and vice versa.

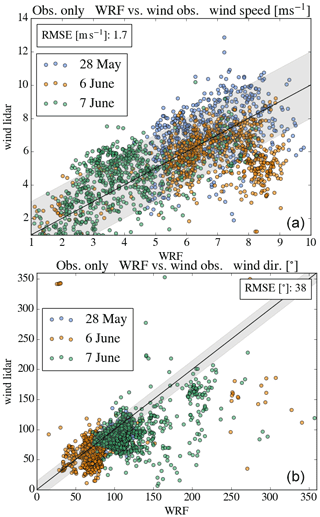
Figure 4 Comparison of WRF wind estimates and wind lidar observations for the observational period between 07:00 and 17:00 UTC for the three days of interest 28 May (blue), 6 June (orange), and 7 June (green). Shaded areas include roughly 80 % of the data points for ±2 ms⁻¹ for wind speed in (a) and include roughly 50 % of wind direction measurements in a $\pm \mathrm{15}{}^{\circ }$ range in (b). Wind direction simulations differ most from the observations for 7 June (green), a day with generally lower wind speeds than the other two discussed cases. This indicates wind information uncertainties when it comes to low wind speeds. For the wind direction comparison, note that values close to 0 and 360^∘ represent virtually the same wind direction but may introduce an error to the root mean square error (RMSE) calculations.

3.2 Lagrangian methane dispersion via FLEXPART

WRF wind fields drive the trajectory calculations in FLEXPART. The model simulates trajectories for 50 000 particles for every USCB coal mining shaft reported by the E-PRTR and the CoMet database (Gałkowski et al., 2021) with a total mass of 10⁵ kgĊH₄. The simulations do not consider background CH₄. The model releases particles in a 10 m ×10 m ×10 m box on the ground. The modeling period starts at 00:10 UTC the day of interest and continues until 17:50 UTC, which results in 17.7 h simulation time. We chose the grid output option in FLEXPART with 100×100 boxes and a spatial resolution of roughly 1.3 km stacked in 24 layers up to 3 km altitude. The simulated XCH₄ measurements are the sums of all boxes above each pixel enclosing an EM27/SUN location. The 6 min FLEXPART output is interpolated to the observational time interval, which is generally one measurement per minute. After unit conversion, the simulated methane enhancement is compared to the measured upwind–downwind difference ΔXCH₄.

The FLEXPART simulations are iterated with slightly different meteorological parameters to provide an uncertainty analysis. There are seven ensemble runs: the CONTROL run with best-guess input, the WINDp5 run with $+\mathrm{5}{}^{\circ }$ wind direction change of the whole wind field, the WINDm5 run with $-\mathrm{5}{}^{\circ }$ wind direction change of the whole wind field, the SPEEDp06 run with the wind speed increased by 0.9 m s⁻¹, the SPEEDm06 run with the wind speed decreased by 0.9 m s⁻¹, the PBLp100 run with the PBL height increased by 100 m, and the PBLm100 run with the PBL height decreased by 100 m. We use the same ensemble setup as discussed by Kostinek et al. (2021).

We further used the FLEXPART simulations for modeling the air mass travel time from the upwind to the downwind instruments (Fig. 5). To this end, we implemented a virtual methane source at the upwind measurement location at the beginning of each observational period. Then, we estimated the air mass travel time by recording the time required for the virtual tracer plume to cross the tangent point of the downwind measurement location, i.e., the point that was closest to the downwind location along the PBL-averaged wind direction. Given that the distance between upwind and downwind locations exceeds 50 km for some cases, estimated travel times range between 1.5 and 4.6 h. Thus, in order for the upwind measurement to be representative of the background conditions for the later downwind measurement, we consider the air mass travel time between the two measurements by subtracting the respective time-shifted upwind measurements when calculating ΔXCH₄. The travel time is calculated once for every case study beginning with the first upwind measurement, which is part of the inversion process, and ending when the virtual tracer reaches the respective downwind instrument. To account for possible background methane variability, we altered the simulated travel time by ±30 min and calculated the average methane enhancement for each individually time-shifted period. The difference between minimum and maximum averaged ΔXCH₄ of these periods is included in the emission estimation routine to represent the error related to background methane uncertainties.

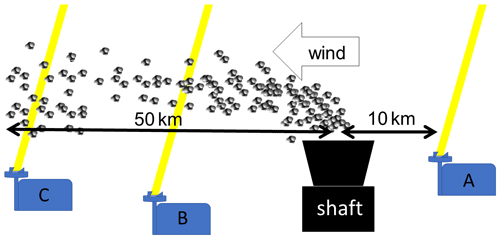
Figure 5 Lagrangian time lag sketch. Instrument A measures background methane (upwind). The methane enhancements induced by the emissions of the shaft are calculated by subtracting the background (upwind) measurements from the downwind observations of instruments B and C. Depending on wind speed, the air mass measured by instrument A will be at instrument B and C after different travel times.

4 Emission estimates via Phillips–Tikhonov regularization

In order to estimate the shaft emissions from the mismatch between measured and simulated methane enhancements ΔXCH₄, we use a Phillips–Tikhonov inverse method. We set it up such that the state vector x consists of m dimensionless factors that scale the emissions of each coal mine ventilation shaft considered by the FLEXPART simulations. We assume the scaling factors to be constant for each day of measurement; i.e., we impose the assumption of the source strength being constant over the time of a day. FLEXPART is the forward model K (m × n) relating the emissions of the n shafts to m ΔXCH₄ measurements. The measurement vector y contains the ΔXCH₄ enhancements, observed at 1 min intervals, translated from units of parts per billion (ppb) into total mass column enhancements (kg m⁻²). The Phillips–Tikhonov inverse method then delivers the estimated state vector x_λ by minimizing a two-term cost function consisting of a measurement term and an a priori term (Phillips, 1962; Tikhonov, 1963; Twomey, 1963):

$$\begin{array}{}\text{(1)}& {\mathit{x}}_{\mathit{\lambda }}=\mathrm{argmin}\left\{\Vert {\mathbf{S}}_{\mathit{ϵ}}^{-\frac{\mathrm{1}}{\mathrm{2}}}(\mathbf{K}\mathit{x}-\mathit{y}){\Vert }_{\mathrm{2}}^{\mathrm{2}}+{\mathit{\lambda }}^{\mathrm{2}}\Vert \mathbf{W}(\mathit{x}-{\mathit{x}}_{\mathrm{a}}){\Vert }_{\mathrm{2}}^{\mathrm{2}}\right\},\end{array}$$

with S_ϵ the error covariance matrix, λ the regularization parameter, W the weighting operator, x_a the a priori state vector, and $\left|\right|\cdot |{|}_{\mathrm{2}}$ representing the L₂ norm. S_ϵ contains the averaged standard deviation of the FLEXPART simulation ensemble summed in quadrature with the XCH₄ background variability and the measurement noise. Note that, for simplicity, we did not consider correlations in S_ϵ. The estimated background error ranges between 0.3 and 2.2 ppb for the individual case studies based on the differences of minimum and maximum average ΔXCH₄ calculated under consideration of ±30 min time shifts of the simulated methane travel times. The measurement noise amounts to 0.6 ppb, calculated as the standard deviation of the averaged measurements of The Glade (E) and Za Miastem (N) from 07:00 to 10:00 UTC on 28 May 2018 (see top panel in Fig. 7). W is a diagonal matrix with elements $\frac{\mathrm{1}}{x_{a,j}},j=\mathrm{1},\mathrm{\dots },m$, which renders the second cost term dimensionless (Butz et al., 2012). Technically, we transform the Phillips–Tikhonov regularization problem into a plain least-squares fit using the definitions (Hansen and O'Leary, 1993; Hansen, 1999; Golub and Von Matt, 1997)

$$\begin{array}{}\text{(2)}& \mathbf{C}=\left[\begin{array}{c}{\mathbf{S}}_{\mathit{ϵ}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathbf{K}\\ \mathit{\lambda }\mathbf{W}\end{array}\right]\text{ and }\mathit{d}=\left[\begin{array}{c}{\mathbf{S}}_{\mathit{ϵ}}^{-\frac{\mathrm{1}}{\mathrm{2}}}\mathit{y}\\ \mathit{\lambda }\mathbf{W}{\mathit{x}}_{\mathrm{a}}\end{array}\right],\end{array}$$

which transforms Eq. (1) to

$$\begin{array}{}\text{(3)}& {\mathit{x}}_{\mathit{\lambda }}=\mathrm{argmin}\left\{\Vert \mathbf{C}\mathit{x}-\mathit{d}{\Vert }_{\mathrm{2}}^{\mathrm{2}}\right\},\end{array}$$

and is treatable by a standard least-squares solver (e.g., python module scipy.optimize.lsq_linear).

The a priori information x_a for each ventilation shaft is taken from the annual E-PRTR emission inventory updated by Gałkowski et al. (2021). The a priori generally guides the minimization process towards physically reasonable solutions if the inverse problem tends to be ill-posed, e.g., when there is insufficient measurement information on some of the state vector elements. However, the solution is dependent on the regularization parameter λ, which has to be found by trading the propagation of measurement errors against influence of the a priori. Here, we use the L-curve criterion to determine the regularization parameter λ for each individual case study (e.g., Hansen, 1999). The L-curve is a graphical representation of the mismatch between measurements and simulations $\Vert \mathbf{K}{\mathit{x}}_{\mathit{\lambda }}-\mathit{y}{\Vert }_{\mathrm{2}}$ plotted against the norm of the state vector $\Vert {\mathit{x}}_{\mathit{\lambda }}{\Vert }_{\mathrm{2}}$ evaluated for a range of λ (see Fig. 9). The plot typically looks like an L. For small λ, the measurement term dominates the cost function, and the estimate x_λ becomes noisy and drives large deviations from the a priori. For large λ, the a priori term dominates the cost function, and the estimate x_λ ignores the measurements and produces a large norm of the measurement term. The corner of the L indicates a reasonable regularization parameter for the given minimization problem and is graphically chosen. In addition, we found that the shape of the L-curve is sensitive to forward model errors, e.g., when errors in the FLEXPART trajectories and the driving wind fields suggest a spurious, erroneous link between emissions and methane enhancements. Obvious distortions of the L-curve shape are used as a criterion to filter out periods when the forward model does not represent the actual dispersion conditions.

Besides the L-curve, the regularized inversion approach holds another diagnostic measure: the emissions averaging kernel matrix A_λ with dimensions m × m. It is defined via the gain matrix G_λ (Rodgers, 2000; Butz et al., 2012; Borsdorff et al., 2014).

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathbf{A}}_{\mathit{\lambda }}={\mathbf{G}}_{\mathit{\lambda }}\mathbf{K}\text{(5)}& {\displaystyle }{\mathbf{G}}_{\mathit{\lambda }}={\left({\mathbf{K}}^T{\mathbf{S}}_{\mathit{ϵ}}^{-\mathrm{1}}\mathbf{K}+{\mathit{\lambda }}^{\mathrm{2}}\cdot {\mathbf{W}}^T\mathbf{W}\right)}^{-\mathrm{1}}{\mathbf{K}}^T{\mathbf{S}}_{\mathit{ϵ}}^{-\mathrm{1}}\end{array}$$

The averaging kernel matrix, for a given regularization strength λ, diagnoses how information propagates from the true and a priori states, x_true and x_a, into the emission estimate.

$$\begin{array}{}\text{(6)}& {\mathit{x}}_{\mathit{\lambda }}={\mathbf{A}}_{\mathit{\lambda }}{\mathit{x}}_{\mathrm{true}}+(\mathbf{1}-{\mathbf{A}}_{\mathit{\lambda }}){\mathit{x}}_{\mathrm{a}}\end{array}$$

The rows of A_λ are called the averaging kernels, quantifying how an estimated state vector element calculates from the other state elements and what portion comes from the prior. For our purposes, the averaging kernels quantify how the emission estimate for a ventilation shaft is affected by the neighboring shafts and whether there is sufficient measurement information. In the perfect case, the emissions averaging kernel is unity for the shaft under consideration and zero for all other shafts, indicating that the shaft can be perfectly resolved and discriminated from neighboring sources and that it is well constrained by measurement information. In reality, groups of neighboring sources and sources behind each other along the trajectory are not resolvable, and some shafts only marginally affect our measurements, implying broader and smaller emissions averaging kernels.

The errors due to measurement noise, background methane variability, and atmospheric transport incorporated in S_ϵ are propagated into the a posteriori error covariance for the emission estimates via

$$\begin{array}{}\text{(7)}& {\mathbf{S}}_{x,\mathit{\lambda }}={\mathbf{G}}_{\mathit{\lambda }}{\mathbf{S}}_{\mathit{ϵ}}{\mathbf{G}}_{\mathit{\lambda }}^T,\end{array}$$

where we report the square root of the diagonal as the error bars of the shaft-wise emission estimates and the square root of the sum of the entire covariance matrix as the error of the total emissions aggregated over all shafts. For the case studies discussed in Sect. 5, the emission errors due to measurement noise range between 0.62 and 4.46 kt a⁻¹, which is small compared to the errors introduced by the dispersion modeling ensemble that range between 27 and 143 kt a⁻¹. Errors related to background methane variability introduced by a ±30 min time shift of the air mass travel time range between 0.83 and 8.5 kt a⁻¹.

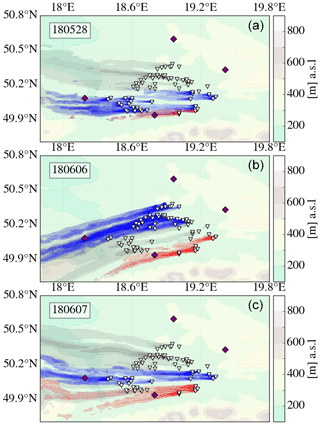
Figure 6 FLEXPART simulations of CH₄ trajectories released from the USCB ventilation shafts for 28 May (a), 6 June (b), and 7 June 2018 (c) (simulation at 12:04 UT). Red, blue, and grey shadings indicate trajectories that went over Pustelnik (S), Raciborz (W), or none of the observation sites, respectively. Background shading indicates topography.

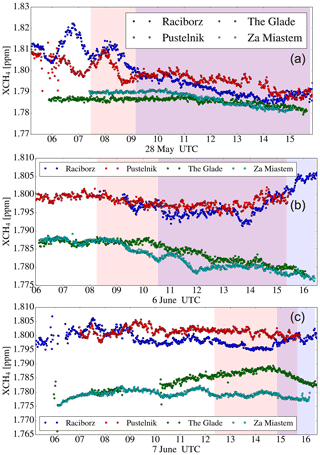
Figure 7 XCH₄ for 28 May (a), 6 June (b), and 7 June (c) 2018 at the stations Raciborz (W, blue), Pustelnik (S, red), The Glade (E, green), and Za Miastem (N, cyan). Background shadings indicate the time frames used for further analysis considering the individual travel times (light red for Pustelnik – S, blue for Raciborz – W, purple for both Raciborz and Pustelnik).

5 Case studies

We report on six case studies on three different days of the CoMet campaign. For the days 28 May and 6 and 7 June 2018, Fig. 6 illustrates typical FLEXPART trajectories of air masses around midday dispersing out of the USCB coal mine ventilation shafts. For all cases, easterly winds led to the southern station Pustelnik being influenced by a few southern shafts (red trajectories) and the western station Raciborz being influenced by many shafts in various parts of the basin (blue trajectories). The eastern station The Glade provides the background measurements, and the northern station Za Miastem was not used here since The Glade (E) was the better background station given the prevailing easterly winds.

Figure 7 depicts the corresponding XCH₄ measurements for all stations, indeed pointing at significantly elevated concentrations at the downwind sites typically amounting to ΔXCH₄ on the order of 10 ppb with some diurnal and day-to-day variability. For 28 May, the maxima during the morning hours at Pustelnik (S) and Raciborz (W) are most likely connected to nighttime methane accumulation and subsequent transport with rising convection and mixing during the morning hours. When considering the Lagrangian travel time of air masses, these morning hours are excluded from the period of investigation since we have to wait for the air masses from the upwind site The Glade (E) to arrive downwind at Pustelnik (S) and Raciborz (W). Therefore, the period of investigation starts later than the Pustelnik (S) and Raciborz (W) measurement records. For Pustelnik (S), travel times ranged between 1.3 and 2 h and for Raciborz (W) between 3 and 5.5 h; 7 June had the longest travel times linked to the slow wind speeds on that day (see Fig. 4). In particular, for 7 June, the consideration of the travel time implies that only a small fraction of the measurements at the end of the day is considered for the emission estimates. The stations The Glade (E) and Za Miastem (N) show roughly consistent background XCH₄ for 28 May and 6 June, but, on 7 June, significant differences indicate that the background concentration field was not homogeneous. Nonetheless, the FLEXPART trajectories point to The Glade (E) being representative of the background conditions for the downwind stations Raciborz (W) and Pustelnik (S). Following the procedures described in Sects. 3.2 and 4, we calculate observed ΔXCH₄ from the XCH₄ observations by subtracting the background record of The Glade (E) from the Pustelnik (S) and Raciborz (W) records, shifting the time series by the calculated Lagrangian travel times. Then, we estimate the shaft-wise emissions by the Phillips–Tikhonov technique.

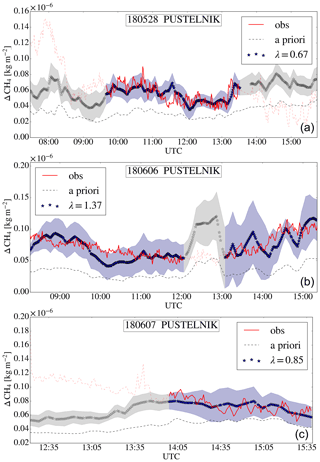
Figure 8 ΔXCH₄ for 28 May (a), 6 June (b), and 7 June (c) 2018 measured (red solid and dotted line) and simulated based on the a priori emissions (grey dashed) and on optimized emissions (dark grey and blue) at the station Pustelnik (S). The grey and blue shadings indicate the uncertainties due to measurement errors and atmospheric variability.

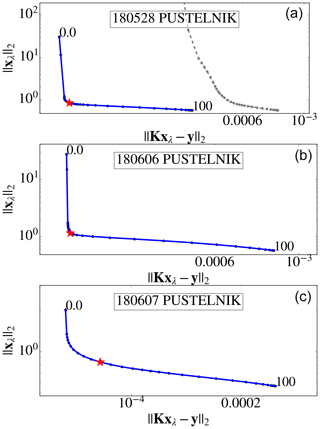
Figure 9 The L-curves for the three Pustelnik (S) case studies. Panel (a) additionally depicts the L-curve of the same case study (dashed grey line) but under consideration of the full data set including the morning and afternoon hours, which suffered from forward model errors and are omitted in the final analysis (blue curve). The regularization parameters, λ, range from 0 to 100. The red star marker depicts the respective λ used for the emission estimation.

5.1 Southern station Pustelnik

Focusing on the Pustelnik (S) records first, Fig. 8 illustrates the measured and simulated ΔXCH₄ enhancements (translated into units of kg m⁻²) and the time periods used for estimating emission rates (blue shading). Generally, FLEXPART simulations using the a priori emissions based on E-PRTR underestimate the enhancements substantially for all cases. The FLEXPART simulations with optimized emission rates fit the measurements well. Residual discrepancies range between $\mathrm{2.35}\times {\mathrm{10}}^{-\mathrm{8}}$ and $\mathrm{4.56}\times {\mathrm{10}}^{-\mathrm{8}}$ kg m⁻² ($\mathrm{2.62}\times {\mathrm{10}}^{-\mathrm{8}}$ and $\mathrm{4.72}\times {\mathrm{10}}^{-\mathrm{8}}$ kg m⁻²) in terms of mean bias (root mean square error). The regularization strength for optimizing the emissions was determined via the L-curves depicted in Fig. 9, for which the L-shape is clearly recognizable. The corner of the L-curve and the corresponding regularization parameter λ is identified by visual inspection. Beside excluding data at the start of the daily time series due to the travel time, we also exclude data that we diagnosed to be affected by systematic forward model errors. The periods before 10:00 and after 13:30 UTC on 28 May (Fig. 8, upper panel) are an illustrative example. For these periods, we find substantial deviations between the measured and modeled time series that the optimization cannot resolve by adjusting emission rates. We expect that such patterns originate from systematic errors in the wind fields that drive FLEXPART. If we include these periods in our optimization scheme, we end up with distorted L-curves (Fig. 9, upper panel, grey dashed line). Thus, inspection of the L-curve provides us with a diagnostic tool to identify periods that are affected by forward model errors, which we then exclude. The other excluded periods are around noon on 6 June and the beginning of 7 June (faint colors in Fig. 8).

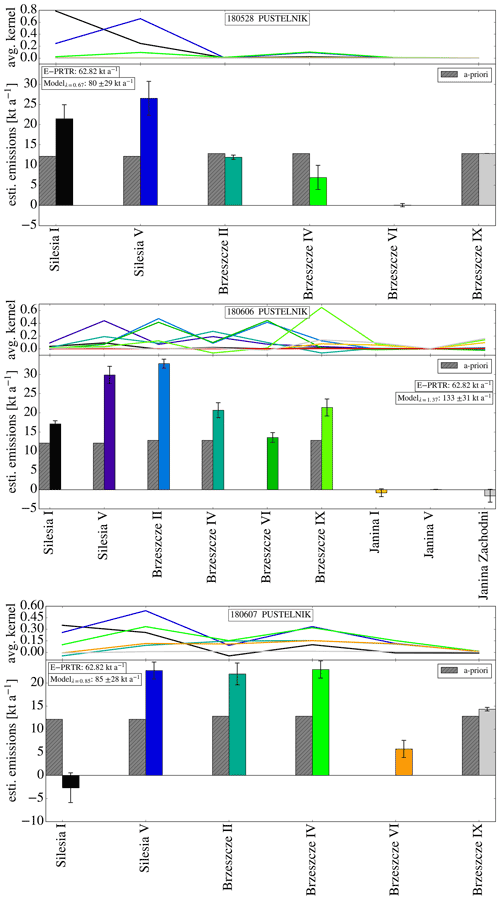
Figure 10 Shaft-wise emission estimates (lower sub-panels) for the three case studies at the southern station Pustelnik and the corresponding emissions averaging kernels (upper sub-panels). Colors of the shaft-wise emission estimates resemble colors of the emissions averaging kernel. Error bars contain atmospheric variability and observational uncertainty (measurement noise and background variability). Grey bars illustrate the a priori emission estimates.

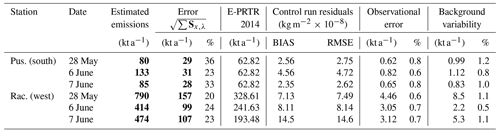
After selecting the data periods well represented by the FLEXPART simulations and choosing a suitable regularization parameter, we estimate the compatible shaft-wise emission rates illustrated in Fig. 10. Before evaluating the estimates, it is mandatory to inspect the emissions averaging kernels (upper sub-panels in Fig. 10), which encode the information on whether individual shafts or groups of shafts can be resolved. For 28 May (upper panel in Fig. 10), the emissions averaging kernels are greater than 0.7 and well positioned for the two Silesia shafts, while, for the Brzeszcze shafts, the emissions averaging kernels are small, indicating that there is very little measurement sensitivity to these shafts. Low sensitivity might be caused by air mass trajectories going over these shafts only for a short period of time. For the Silesia shafts, the estimated emission rates are substantially greater than the E-PRTR-based prior. On 6 June (middle panel in Fig. 10), the emissions averaging kernels indicate substantial sensitivity to Silesia V and Brzeszcze II, VI, and IX, as well as some sensitivity to Brzeszcze IV, but the emissions averaging kernels for Brzeszcze II and VI are double-peaked at each of the shafts, indicating the shafts cannot be resolved individually, e.g., because trajectories went over both shafts most of the time. A similar double-peaked emissions averaging kernel occurs for Silesia V and Brzeszcze VI. The shaft that can be best resolved is Brzeszcze IX. Generally, the optimized emissions are again significantly greater than the priors. For Brzeszcze VI, the prior even indicates zero emissions, while our estimate exceeds 10 kt a⁻¹. On 7 June (middle panel in Fig. 10), sensitivity is considerable for Silesia I and V, Brzeszcze IV, and to a lesser degree Brzeszcze II, but generally the emissions averaging kernels are not single-peaked but distributed among several shafts, which fits the rather unstable wind conditions on that day. It is noteworthy that we find small emissions for Silesia I on 7 June, while for the other days Silesia I showed emissions of 15–20 kt a⁻¹. This might point at day-to-day variability of the ventilation. Aggregating the emissions over all shafts (Table 2), we find that on all three days the optimized emissions are substantially greater than the prior. On 28 May and 7 June, the total optimized and prior emissions are compatible within the error bars, but on 6 June, our estimates indicate emissions twice as high as the prior: 133±31 kt a⁻¹ compared to 63 kt a⁻¹. The difference of the total emission estimates from the other days is largely due to better sensitivity to all the Brzeszcze shafts and to the larger respective emission estimates.

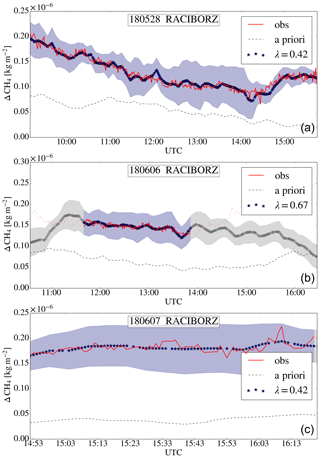
Figure 11 ΔXCH₄ for 28 May (a), 6 June (b), and 7 June (c) 2018 measured (red solid and dashed line) and simulated based on the a priori emissions (grey dashed) and on optimized emissions (dark grey and blue) at the station Raciborz (W). The grey and blue shadings indicate the uncertainties due to measurement errors and atmospheric variability.

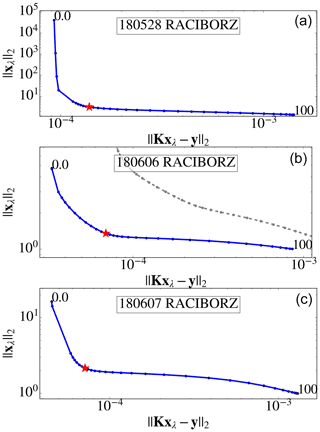
Figure 12 The L-curves for the three Raciborz (W) case studies. Panel (b) additionally depicts the L-curve of the same case study (dashed grey line) but under consideration of the full data set including the morning and afternoon hours, which suffered from forward model errors and are omitted in the final analysis (blue curve). The regularization parameters, λ, range from 0 to 100. The red star marker depicts the respective λ used for the emission estimation.

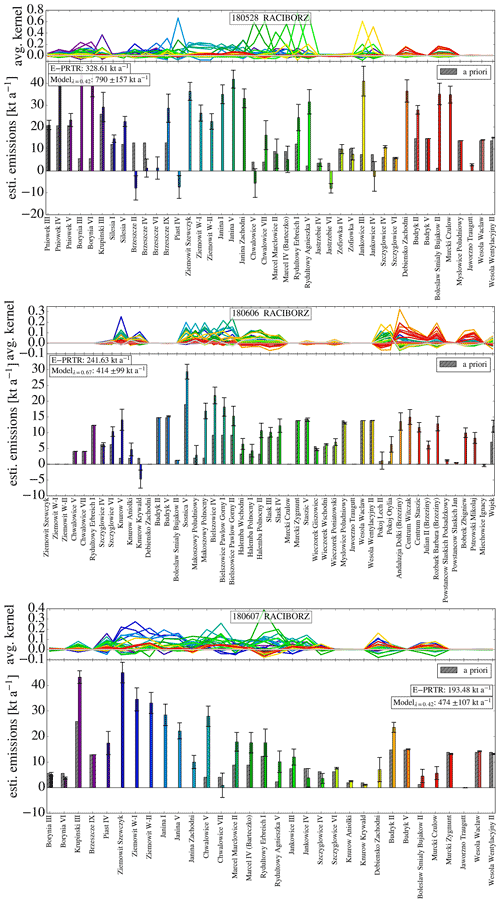
Figure 13 Shaft-wise emission estimates (lower sub-panels) for the three case studies at the western station Raciborz and the corresponding emissions averaging kernels (upper sub-panels). Colors of the shaft-wise emission estimates resemble colors of the emissions averaging kernel. Error bars contain atmospheric variability and observational uncertainty (measurement noise and background variability). Grey bars illustrate the a priori emission estimates.

5.2 Western station Raciborz

In contrast to the case studies for Pustelnik (S), the FLEXPART simulations indicate that the western station Raciborz is influenced by a large and varying number of shafts (between 30 and 50 shafts for the three days discussed here). Figures 11 and 12 show the fits to the ΔXCH₄ observations for the prior and optimized emission estimates and the L-curves for the selection of the regularization parameter, respectively. For 6 June, we again find that the FLEXPART simulations could not represent our measurements at the beginning and end of the time series, and therefore we excluded these periods based on visual inspection of distortions of the L-curve. Overall, after optimization the simulated ΔXCH₄ records fit the observations well, while simulations with prior emissions show substantially smaller-than-observed ΔXCH₄. The residual differences between simulations with optimized emissions and observations range between $\mathrm{7.13}\times {\mathrm{10}}^{-\mathrm{8}}$ and $\mathrm{1.45}\times {\mathrm{10}}^{-\mathrm{7}}$ kg m⁻² ($\mathrm{7.49}\times {\mathrm{10}}^{-\mathrm{8}}$ and $\mathrm{1.46}\times {\mathrm{10}}^{-\mathrm{7}}$ kg m⁻²) in terms of mean bias (root mean square error).

Figure 13 illustrates the shaft-wise emission estimates and the corresponding emissions averaging kernels (upper sub-panels). Due to the large number of shafts involved, the picture is less clear than for the Pustelnik (S) station. The emissions averaging kernels show that it is typically groups of shafts to which the measurements have good sensitivity but that, mostly, individual shafts cannot be resolved. Overall, the optimization points at emissions greater than the prior. When aggregated over all the shafts (Table 2), the optimized emissions are a factor of 2.4 (28 May), 1.7 (6 June), and 2.4 (7 June) greater than the prior emissions, and the differences are greater than the error bars estimated from measurement errors and the ensemble simulations representing transport variability. On 28 May, our estimates indicate large contributions from ventilation associated with the southwestern part of the USCB. On 6 June, the more northern and central mines show emissions greater than the prior, which is zero for some of the mines (e.g., Centrum Witczak/Staszic and Julian II/Rozbark Barbara). On 7 June, the number of contributing shafts is less than for the other days, and the estimates point at large emissions from ventilation of Ziemowit, Janina, and Chwałowicze V.

Table 2 Overview of all case studies including respective emission sums and their errors (bold numbers). Mean bias and root mean square error (RMSE) of the CONTROL run residuals refer to the regularized solution. The errors due to observational uncertainties and due to background methane variability are listed in the last four columns.

6 Discussion and conclusion

We estimated CH₄ emissions from coal mine ventilation facilities in the USCB during the CoMet campaign in May–June 2018. To this end, we deployed four EM27/SUN spectrometers in a network configuration enclosing the USCB. Combining pairs of upwind–downwind XCH₄ observations with trajectory simulations by the Lagrangian particle dispersion model FLEXPART, we attributed the observed ΔXCH₄ enhancements to the emission rates of the facilities. The trajectory calculations were driven by wind fields simulated by WRF under assimilation of wind measurements by three wind lidars distributed throughout the region. The trajectory calculations also enabled us to take into account the travel time of air masses between the upwind and downwind stations. For emission estimation, we used a Phillips–Tikhonov regularization approach together with the L-curve criterion for selecting a well-suited regularization parameter. The regularization scheme comes with the emissions averaging kernel diagnostics that allow for quantifying which facilities or groups of facilities the measurements are sensitive to. For estimating errors, we constructed an ensemble of seven FLEXPART runs, each with slightly perturbed atmospheric parameters (wind speed, wind direction, PBL height).

Upscaling our emission estimates to annual emissions, we find higher emission rates than listed by E-PRTR. Other studies (Luther et al., 2019; Kostinek et al., 2021; Fiehn et al., 2020) have shown better agreement between their instantaneous estimates and the E-PRTR inventory, while, in our study, only two out of six cases are compatible with the E-PRTR inventory within the error range (see Table 2). The other four cases suggest 1.7 to 2.4 times higher emissions than reported by the E-PRTR. The comparisons with E-PRTR are only of an illustrative nature. Depending on the under-ground mining activities, the emissions from the mining process are highly variable in time, and thus our measurements are certainly not representative of the annual total reported by E-PRTR. In order to constrain the latter, a permanent observatory network would need to be operated with reasonably dense sampling throughout the year.

Our emissions estimates for the totals of all contributing facilities show errors in the range between 23 % and 36 %. Measurement errors (0.62 to 4.46 kt a⁻¹) and background-variability-induced errors (0.83 to 8.5 kt a⁻¹) are negligibly small compared to errors induced by uncertainties of the wind fields (27 to 143 kt a⁻¹). As hinted at by the emissions averaging kernels, estimates for individual shafts are correlated, and these correlations were taken into account when calculating the aggregated total emissions. For all cases, these background concentrations were taken from the measurements conducted at the eastern station The Glade since the trajectory calculations showed that it was more representative for the background than the northern station Za Miastem. While for 28 May and 6 June, the two stations show similar concentrations (Fig. 7), The Glade (E) records higher XCH₄ than Za Miastem (N) on 7 June. Thus, the background concentration field has some spatial variability, which might be connected to remote sources such as the Krakow urban region affecting The Glade (E) but not Za Miastem (N) (Menoud et al., 2021). In the future, we will aim at estimating errors due to spatial background variability by running a model that includes all known sources in a larger area around the target region or by deploying more spectrometers.

Our inverse method was set up such that the parameters to be estimated included all the individual CH₄ ventilation shafts for which the trajectory calculations indicated contributions to the measurements. The problem requires regularization since CH₄ plumes might mask each other (e.g., shafts located behind another shaft along the trajectory), since the detected contributions might have occurred only for a short period, and since, due to errors in the wind fields, the trajectories might indicate contributions when there were actually none or vice versa (e.g., for trajectories barely hitting the downwind station). The Phillips–Tikhonov regularization with L-curve criterion provides useful tools to diagnose the robustness and information content of the problem. The L-curve shows distortions for episodes when the FLEXPART trajectories cannot represent the true link between emissions and downwind concentrations. Thus, inspecting the L-curve allows for excluding episodes affected by these simulation errors. The emissions averaging kernels are useful to identify the shafts or groups of shafts for which the emissions can be reliably estimated from the observations. For our configurations, we found that we can resolve emissions of individual shafts for the Pustelnik (S) downwind station where only a few comparatively close facilities contribute to the ΔXCH₄ enhancements. For the Raciborz (W) station with a much larger catchment area, we can typically resolve groups of shafts along the main wind direction, but disentangling individual shafts is not possible when they are close to each other or behind each other along the air mass trajectory. Nonetheless, we argue it is useful to set up the problem in terms of individual shafts instead of a priori aggregating shaft clusters since inspecting the emissions averaging kernels provides a tool to check which shafts can be resolved and since the aggregated total emissions and their errors can be calculated a posteriori.

CH₄ emissions from sources other than coal mining are not considered in our FLEXPART simulations; i.e., the pairwise ΔXCH₄ enhancements are assumed to be caused only by the ventilation shafts. Kostinek et al. (2021) have inspected EDGAR v4.3.2 for CH₄ emissions from sources that are not related to coal mining activities such as landfills, wastewater treatment, and livestock in the USCB. They found that these other sources amount to roughly 14 % of the USCB total CH₄ emissions and that the larger contributions stem form the northwest of the basin, which our measurements are not sensitive to. The CoMet inventory (Gałkowski et al., 2021) lists annual emission estimates for 4 of 16 landfills relevant for our case studies, which in total amount to 0.97 kt a⁻¹. We expect similar emission estimates for the other 12 landfills reported with undefined emissions. Thus, we assume that contributions from sources other than coal mining are small compared to our error bars. We did not consider chemical reactions such as oxidation of methane with OH, since the timescales relevant for this study are too short for oxidation to have a significant influence on the emission estimations.

Overall, our study shows that deploying sun-viewing spectrometers in an ad hoc network configuration around the USCB allows for estimating CH₄ emissions from coal mine ventilation facilities with some resolution for individual facilities and groups of them, depending on the deployment location. Given that the errors are dominated by uncertainties in the wind fields driving the trajectory calculations, it is essential to validate model winds by local wind data or, as in our case, to assimilate local wind lidar measurements. In the view of developing such networks toward a monitoring capacity, priority should be put on making the networks permanent for better temporal representativeness of the observations and on making the networks denser in order to gain sensitivity to more shafts and to better quantify spatial variability in the background concentrations. In addition to the monitoring aspect, permanent networks could also validate satellite missions, and the different ground-based and spaceborne emission estimation approaches could be consolidated.

Appendix A

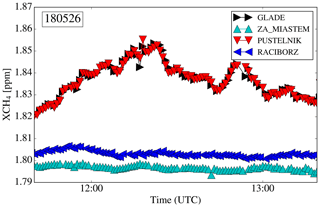
Figure A1 Calibrated XCH₄ measurements from 26 May. The instruments for The Glade (E) and Pustelnik (S) measured side-by-side at the station Pustelnik. The other two instruments measured at their respective campaign locations. The calibration of The Glade (E) towards the other instruments is based on these measurements.