the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Investigation of ice cloud modeling capabilities for the irregularly shaped Voronoi ice scattering models in climate simulations
Ming Li
Yiran Peng
Hiroshi Ishimoto
Yanluan Lin
Takashi Y. Nakajima
Anthony J. Baran
Zengyuan Guo
Yonghui Lei
Jiancheng Shi
Both weather–climate models and ice cloud remote sensing applications need to obtain effective ice crystal scattering (ICS) properties and the parameterization scheme. An irregularly shaped Voronoi ICS model has been suggested to be effective in remote sensing applications for several satellite programs, e.g., Himawari-8, GCOM-C (Global Change Observation Mission–Climate) and EarthCARE (Earth Cloud Aerosol and Radiation Explorer). As continuation work of Letu et al. (2016), an ice cloud optical property parameterization scheme (Voronoi scheme) of the Voronoi ICS model is employed in the Community Integrated Earth System Model (CIESM) to simulate the optical and radiative properties of ice clouds. We utilized the single-scattering properties (extinction efficiency, single-scattering albedo and asymmetry factor) of the Voronoi model from the ultraviolet to the infrared, combined with 14 408 particle size distributions obtained from aircraft measurements to complete the Voronoi scheme. The Voronoi scheme and existing schemes (Fu, Mitchell, Yi and Baum-yang05) are applied to the CIESM to simulate 10-year global cloud radiative effects during 2001–2010. Simulated globally averaged cloud radiative forcings at the top of the atmosphere (TOA) for Voronoi and the other four existing schemes are compared to the Clouds and the Earth's Radiant Energy System Energy Balanced and Filled (EBAF) product. The results show that the differences in shortwave and longwave globally averaged cloud radiative forcing at the TOA between the Voronoi scheme simulations and EBAF products are 1.1 % and 1.4 %, which are lower than those of the other four schemes. Particularly for regions (from 30∘ S to 30∘ N) where ice clouds occur frequently, the Voronoi scheme provides the closest match with EBAF products compared with the other four existing schemes. The results in this study fully demonstrated the effectiveness of the Voronoi ICS model in the simulation of the radiative properties of ice clouds in the climate model.
- Article
(1613 KB) - Full-text XML
- BibTeX
- EndNote
Ice clouds cover about 20 %–30 % of the global area (Rossow and Schiffer, 1991; Wang et al., 1996; Stubenrauch et al., 2013), and they strongly affect the earth's energy budget and climate system mainly due to their optical and radiative properties (Liou, 1986, 1992; Baran, 2012; Ramaswamy and Ramanathan, 1989). The radiative properties of ice clouds mainly depend on their optical properties (e.g., scattering albedo and optical thickness), which are significantly influenced by the microphysical properties (e.g., ice particle sizes and habits) of ice clouds (Baran, 2009; Yang et al., 2015, 2018). Based on the accurate knowledge of ice particle sizes and habits, the single-scattering properties (e.g., extinction efficiency, single-scattering albedo and asymmetry factor) of ice particles can be calculated by using the light scattering computational method to develop the ice crystal scattering (ICS) model/database. Combined with the single-scattering properties of the ICS model/database and size distributions, the optical properties of ice clouds can be simulated through the parameterization scheme, and the radiative properties of ice clouds can be further simulated based on the radiative transfer theory.
At present, satellite remote sensing and weather–climate models are two effective ways to understand the ice cloud optical and radiative properties through the ice cloud optical property parameterization scheme in radiative transfer models. However, numerous field observations (Rossow and Schiffer, 1999; Lawson et al., 2006; Heymsfield et al., 2017; Lawson et al., 2019), e.g., the First International Satellite Cloud Climatology Project (ISCCP) Regional Experiment (FIRE-I) in 1986 and 1991 (Rossow and Schiffer, 1999) and the European cirrus experiment in 1989 (Liou, 1992), have shown that ice clouds contain a large variety of non-spherical ice particle sizes and habits, which can lead to inaccurate simulations of the optical and radiative properties of ice clouds in nature. Our understanding of how ice particle habits affect the optical and radiative properties of ice clouds is still limited (Heymsfield and Miloshevich, 2003; van Diedenhoven et al., 2014; van Diedenhoven, 2018). The current insufficient knowledge of the ice cloud microphysical properties and the ice particle single-scattering properties contributes to inadequate representation of the optical properties in the parameterization scheme, which can directly lead to uncertainties in the simulated radiative properties of ice clouds (Zhang et al., 2015; Yang et al., 2015, 2018; Yi et al., 2017; van Diedenhoven and Cairns, 2020). Thus, the accurate representation of the microphysical properties of ice clouds and ice particle single-scattering properties is essential for the parameterization of ice cloud optical properties and the study of the radiative properties of ice clouds in both satellite remote sensing and weather–climate models. In terms of current light scattering computational methods, it is still difficult for one specific method to accurately calculate the single-scattering properties for non-spherical particles with a different size parameter (SZP), which is defined as the ratio of the equivalent-volume sphere's circumference dimension (or π times particle maximum diameters) to the incident wavelength (Nakajima et al., 2009; Baran, 2012; Yang et al., 2015). The existing light scattering computational methods for non-spherical particles can be generally divided into the approximation method (AM) based on the ray-tracing techniques (Wendling et al., 1979), as well as the numerical simulation (NM) method based on the approximate solutions of Maxwell equations. The AM method is suitable for non-spherical particles with very large SZPs. The geometrical optics approximation (GOA) method is a typical AM method. This method can capture the halo phenomenon of large hexagonal ice particles in the visible wavelength. However, the AM method has difficulties in accurately simulating the single-scattering properties for particles with small and moderate SZPs. The NM method is suitable for particles with small SZPs and can be divided into the volume- and surface-based methods depending on how Maxwell equations are solved. The volume-based NM method includes the finite-difference time domain (FDTD) (Yee, 1966; Yang and Liou, 1996b) and discrete dipole approximation (DDA) methods (Draine and Flatau, 1994; Yurkin and Hoekstra, 2007). A typical method of the surface-based method is the T-matrix method (Havemann and Baran, 2001; Mishchenko and Travis, 1998). However, the NM method requires discretization of the whole volume/surface of the scatterer and has rather high computational demands (Nakajima et al., 2009), so it is difficult to efficiently calculate the single-scattering properties for particles with moderate and large SZPs. Later, the invariant imbedding T-matrix (II-TM) (Bi et al., 2013a; Bi and Yang, 2014) and physical-geometric optics hybrid (PGOH) method (Bi et al., 2011) were developed for particles with small to moderate SZPs. Combined with the advantages of the AM and NM methods, several improved GOA methods including the geometric optics integral equation (GOIE) (Yang and Liou, 1996a; Ishimoto et al., 2012) and improved geometric-optics method (IGOM) (Yang and Liou, 1995, 1996a; Bi et al., 2010) have been developed. The GOIE and IGOM methods are useful for particles with moderate SZPs, and therefore they can bridge the gap between the AM and NM methods. Thus, the light scattering computation of particles with different SZPs can be completed by a combination of the AM and NM methods.
With the development of the ICS model/database, numerous parameterization schemes of the ice cloud optical properties have been developed for use in ice cloud remote sensing and weather–climate model applications (Yang et al., 2015, 2018). In terms of weather–climate model applications, Fu (1996) developed a parameterization scheme (referred to as the Fu scheme hereafter) using the GOA-based ICS database for the randomly oriented hexagonal particle (Takano and Liou, 1989). The Fu scheme was subsequently applied to the Fu–Liou radiative transfer model for use in the climate models (Fu, 1996, 2007). Mitchell et al. (1996b, 2006) used the modified anomalous diffraction approximation (MADA) method (Mitchell and Arnott, 1994) to generate an ICS database for a habit mixture and completed a parameterization scheme (referred to as the Mitchell scheme hereafter) combined with the bimodal size distributions (Mitchell et al., 1996a). The Mitchell scheme was then employed in the National Center for Atmospheric Research Community Atmosphere Model (CAM). Yang et al. (2000) used the IGOM and FDTD methods to develop an ICS database for six ice particle habits. However, this database contains several inconsistencies in the spectral regions caused by differences in particle habits and computational methods. Later, Yang et al. (2013) utilized the Amsterdam DDA (Yurkin et al., 2007; Yurkin and Hoekstra, 2011), T-matrix (Mishchenko et al., 1996) and improved IGOM (Bi et al., 2009) methods to generate a spectrally consistent ICS database for 11 ice particle habits. Yi et al. (2013) employed the ICS database of Yang et al. (2013) and developed a parameterization scheme (referred to as the Yi scheme hereafter) for use in the CAM. For ice cloud remote sensing applications, Baum et al. (2005a, b) used the ICS database of Yang et al. (2000) to develop a parameterization scheme (referred to as the Baum-yang05 scheme hereafter) for the MODIS Collection 5 ice cloud product. C.-Labonnote et al. (2000, 2001) and Doutriaux-Boucher et al. (2000) developed an ICS database for the inhomogeneous hexagonal monocrystal (IHM) model containing embedded inclusions (air bubbles and aerosols) and developed a parameterization scheme for use in the ice cloud retrievals from the French satellite Polarization and Directionality of the Earth's Reflectance (POLDER) measurements (Deschamps et al., 1994). Ishimoto et al. (2012) and Letu et al. (2016) developed an ICS database by using a combination method of the FDTD, GOIE and geometric-optics method (GOM) for an irregularly shaped Voronoi model based on in situ microphysical measurements. Letu et al. (2016, 2020) demonstrated that the Voronoi model can effectively retrieve the ice cloud microphysical properties from satellite measurements. Furthermore, the Voronoi model has been adopted for generating official ice cloud products for the Second Generation Global Imager (SGLI)/Global Change Observation Mission–Climate (GCOM-C) (Letu et al., 2012, 2016; Nakajima et al., 2019), AHI/Himawari-8 (Letu et al., 2018) and the Multi-Spectral Imager (MSI)/Earth Cloud Aerosol and Radiation Explorer (EarthCARE) satellite programs (Illingworth et al., 2015), which will be launched in 2023. These studies demonstrated the superiority of the Voronoi model in the ice cloud remote sensing applications. However, the performance of the Voronoi model in the climate model simulations has not been investigated quantitatively.
Motivated by the abovementioned situations, this study aims to quantify the effects of the Voronoi model on the optical and radiative properties of ice clouds in a climate model in comparison with the other ice cloud optical property schemes (Fu, Mitchell, Yi and Baum-yang05). To achieve this goal, we develop an ice cloud optical property parameterization scheme (referred to as the Voronoi scheme hereafter) for the Voronoi model. The Voronoi scheme and the other schemes are employed in the Community Integrated Earth System Model (CIESM) (Lin et al., 2020) to simulate shortwave and longwave fluxes at the top of the atmosphere (TOA). The CIESM-based simulations from the five schemes are compared with the Earth's Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) products. This study addresses the following questions through the comparison. How different is the Voronoi scheme from the other schemes? How and to what extent does the Voronoi scheme affect the radiative effects of ice clouds? What are the possible reasons for the impacts of the Voronoi scheme?
This paper is organized as follows. Sections 2 and 3 introduce the data and methodology used in this study, and Sect. 4 demonstrates the influence of the Voronoi model on the cloud radiative properties through the radiative transfer model and climate model. Section 5 presents the summary and conclusions of this study.
2.1 Single-scattering property database for the Voronoi model
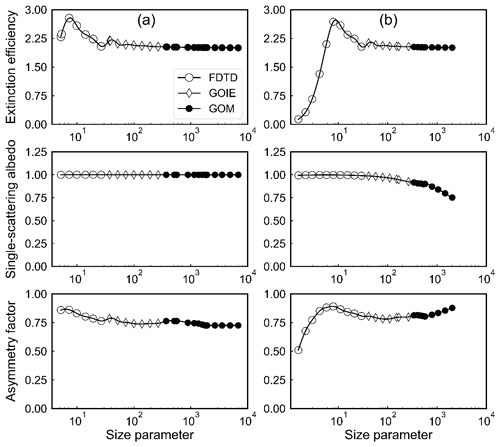
In this study, the single-scattering property database of the Voronoi model developed by Ishimoto et al. (2012) and Letu et al. (2016) is used in the parameterization process. The single-scattering properties including the extinction efficiency, single-scattering albedo and asymmetry factor of the Voronoi model from the ultraviolet to the infrared are utilized to calculate the shortwave and longwave optical properties of ice clouds. The single-scattering properties of the Voronoi model are calculated by a combination of methods of FDTD, GOIE and GOM. This combination method implements a treatment of particle edge effects well (Ishimoto et al., 2012). With this treatment, the gaps between the results calculated by the FDTD and those by the GOIE are relatively small, which can lead to consistency in the single-scattering properties of ice particles. Figure 1a and b show the extinction efficiency, single-scattering albedo and asymmetry factor for Voronoi models that vary with SZPs at wavelengths of 0.64 and 2.21 µm, respectively. Note that the FDTD and GOIE methods are used for small (SZP < 40) and moderate (SZP < 300) ice particles, respectively, and the GOM method is used for large (SZP > 300) particles. The extinction efficiency at wavelengths of 0.64 and 2.21 µm has a peak value when the SZP approximately equals 10 and decreases to be a constant value of 2 with increasing SZPs larger than 100. The single-scattering albedo at both wavelengths is close to 1, which is related to the high values of the real part in the refractive index. The asymmetry factor decreases with the increasing SZPs at the wavelength of 0.64 µm. At the wavelength of 2.21 µm, the asymmetry factor increases for the SZPs smaller than 10 and larger than 300.
2.2 Aircraft-based measurements of the particle size distributions
To generate the parameterization scheme of ice cloud optical properties for application in the climate model simulations, particle size distributions (PSDs) of the Voronoi model need to be assumed in ice clouds. In this study, we utilized 14 408 PSDs derived from in situ aircraft-based measurements obtained in 11 field campaigns (available http://stc-se.com/data/bbaum/Ice_Models/microphysical_data.html, last access: 1 February 2021) (Heymsfield et al., 2013). These data confirm that the particle phase is unambiguously ice after filtering by cloud temperature ( ∘C). For the fitting of PSDs for the Voronoi model, we adopt the gamma distribution form as follows:
where L is the particle maximum dimension, n(L) is the particle concentration per unit volume (e.g., 1 cm−3), N0 is the intercept, λ is the slope, and μ is the dispersion. The physical meaning of the PSD is that n(L) times dL is the number of particles per unit area.
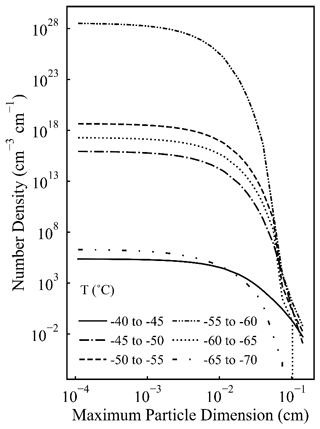
As shown in Fig. 2, the particle concentration decreases with increasing L for all ranges. When the temperature is between −60 and −55∘C, the particle concentration is the largest, and it decreases most sharply with increasing L. When the temperature is between −45 and −40∘C, as well as between −65 and −70∘C, the particle concentration is the smallest, and it decreases slowly with increasing L.
2.3 Satellite data used in the validation
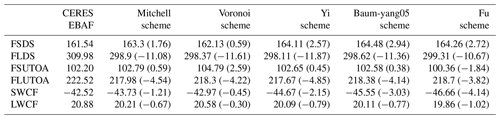
To evaluate the cloud radiative effects for different schemes of the ICS model, we adopted the CERES EBAF Ed4.1 products (available https://ceres.larc.nasa.gov/data/, last access: 6 May 2021) (Draine and Flatau, 1994; Doelling et al., 2016) from 2001 to 2010 as validation data. The “toa_cre_sw_mon” and “toa_cre_lw_mon” EBAF products are used for comparisons with the simulated shortwave and longwave cloud radiative effects from all five schemes. The “toa_cre_sw_mon” and “toa_cre_lw_mon” products are monthly mean shortwave and longwave cloud radiative effects at the TOA, and they are calculated as all-sky fluxes minus total region clear-sky fluxes for shortwave and longwave spectra. The “toa_sw_all_mon” and “toa_lw_all_mon” EBAF products are monthly mean all-sky outgoing shortwave and longwave fluxes at the TOA, and they are used for comparisons with simulated upwelling shortwave flux at the TOA (FSUTOA) and upwelling longwave flux at the TOA (FLUTOA) from all schemes. The “sfc_sw_down_all_mon” and “sfc_lw_down_all_mon” are monthly mean all-sky downwelling shortwave and longwave fluxes at the surface, and they are used for comparisons with simulated downwelling shortwave flux at the surface (FSDS) and downwelling longwave flux at the surface (FLDS) from all schemes. The spatial and temporal resolution of EBAF data is latitude by longitude and monthly means.
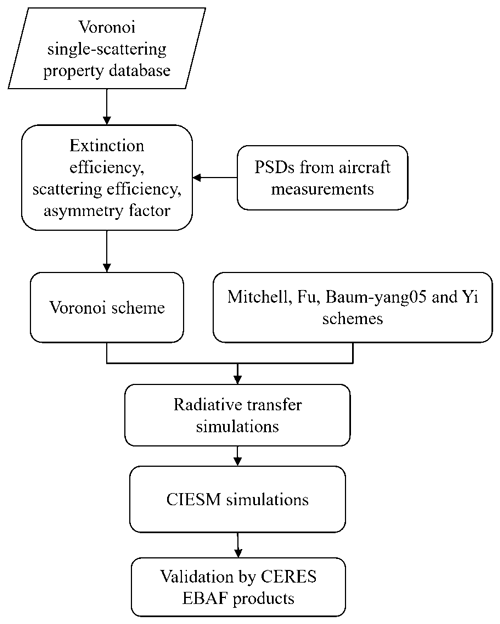
The main flowchart of this study is described in Fig. 3. Firstly, we developed the parameterization scheme of the Voronoi ICS model by using the aforementioned single-scattering properties of the Voronoi ICS database and large amounts of PSDs. Then, the Voronoi scheme and the other four existing schemes (Fu, Mitchell, Yi and Baum-yang05) were evaluated through simulations of shortwave upward and downward flux profiles in the rapid radiative transfer model for general circulation models (RRTMG). The RRTMG was utilized to understand how the different optical properties of the five schemes influence the upward and downward fluxes under several idealized conditions. Furthermore, all schemes were applied to the CIESM to simulate global shortwave and longwave cloud radiative forcing at the TOA from 2000 to 2010, among which the first year was removed for reaching the equilibrium state and the last 10 years were evaluated by EBAF products. The CIESM was employed to evaluate the effectiveness of the Voronoi ICS model in the simulations of ice cloud radiative properties compared with the other four schemes in the climate system.
3.1 Parameterization of ice cloud optical properties
To better understand the ice cloud modeling capabilities of the Voronoi model in the climate model and explain how ice clouds play a role in the climate system, it is necessary to introduce the main scattering parameters to evaluate the Voronoi ICS model through the parameterization scheme. The main radiative transfer processes can be simply attributed to extinction, scattering and absorption coefficients (Liou, 1986, 1992), which are calculated by Eq. (2).
where βe,s,a is the extinction, scattering and absorption coefficients and σ is the cross section (See Table A1 for a list of acronyms). The single-scattering albedo and co-albedo can be defined as the ratio of the scattering and absorption coefficients to the extinction coefficient in the form of Eq. (3).
where ϖ and 1−ϖ are single-scattering albedo and co-albedo, respectively. Based on the extinction coefficient, the optical depth can be defined by Eq. (4).
where τ is the optical depth, and z is the outer boundary of the atmosphere. In the assumption of plane-parallel atmospheres, changes in the diffuse intensity penetrating from below the layer considering multiple scattering processes can be given by Eq. (5).
where P is the phase function corresponding to a volume of ice particles. denotes the redirection of the incoming intensity defined by ( to the outgoing intensity defined by (μϕ). I indicates the total (direct plus diffuse) radiance, B indicates Planck's function associated with thermal emissions, and Θ is the scattering angle. Therefore, the extinction coefficients, single-scattering albedo and phase function are fundamental driving parameters within the transfer of diffuse intensity.
Based on these principles, in this study, we completed the Voronoi scheme by using the single-scattering properties of the Voronoi model and 14 408 groups of PSDs data. The parameterization of the ice cloud optical properties for the Voronoi scheme are developed following Eqs. (6)–(15). Firstly, the spectral ice cloud optical properties (mass-averaged extinction coefficients, single-scattering albedo and asymmetry factor) for the Voronoi scheme are calculated for all PSDs given by Eqs. (6)–(9).
where De is the effective particle diameter, and V and A are volume and projected area of the Voronoi models. Kext(λ) is spectral mass-averaged extinction coefficients (m2 g−1), ϖ(λ) is the spectral single-scattering albedo, and g(λ) is the spectral asymmetry factor. Qext, g and Qsca are extinction efficiency, asymmetry factor and scattering efficiency for Voronoi models.
Then, based on the spectral bulk optical properties including Kext(λ), ϖ(λ) and g(λ) of ice clouds, the band-averaged optical properties are calculated to apply the parameterization scheme in RRTMG and CIESM following Eqs. (10)–(12).
where , and are band-averaged and mass-averaged extinction coefficients, single-scattering albedo, and asymmetry factor for the Voronoi scheme, respectively. E is assigned by the solar constant provided by Chance and Kurucz (2010) for the shortwave spectrum and is replaced with the Planck function B(T) for the longwave spectrum, and T is an assumed cloud temperature of 233 K according to Liou (1992). The coefficients of the polynomial expressions of the ice cloud band-averaged optical properties as functions of De are determined in each band interval to develop the Voronoi scheme for shortwave and longwave spectra as shown in Eqs. (13)–(15).
where a, b and c are coefficients as functions of band intervals.
In terms of the other four existing schemes, the band-averaged optical properties of the Mitchell, Yi and Baum-yang05 schemes are developed as functions of De following Eqs. (13–15). Coefficients of the Mitchell scheme can be obtained from the CIESM. Values of coefficients for the Yi and Baum-yang05 schemes are listed in Appendix A (Tables A1, A2, A3, and A4) provided from Zhao et al. (2018). Coefficients of the Fu scheme (default scheme in RRTMG) are obtained from the existing ice cloud band-averaged optical properties from RRTMG. Formulation of the Fu scheme is similar to the Mitchell and Baum-yang05 schemes except for using the generalized effective diameter (Fu, 1996). The generalized effective diameter of the Fu scheme is unified into De for comparability.
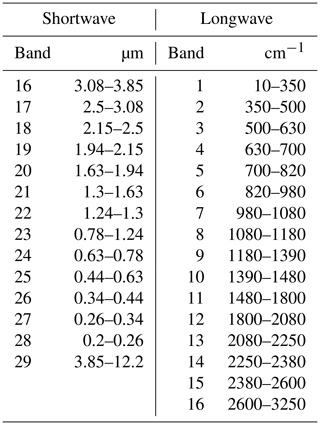
3.2 RRTMG and CIESM simulation experiments
The version of the RRTMG used in this study is the current version of the radiative transfer code applied in the CIESM (Mlawer et al., 1997; Iacono et al., 2008; Clough et al., 2005; (available from http://rtweb.aer.com/, last access: 5 January 2021). RRTMG utilizes the correlated-k approach to calculate shortwave fluxes and heating rates efficiently and accurately for application in climate models. The version of RRTMG utilizes a two-stream method for radiative transfer calculation. RRTMG has 14 bands for the shortwave spectrum and 16 longwave bands (see Table 1). Since the wavelength range is from 0.2 to 15 µm for the single-scattering property database of the Voronoi ICS model, ice cloud bulk optical properties of the default scheme (the Mitchell scheme) remain unchanged when bands are larger than 15 µm. To quantify the radiative flux differences caused by the five schemes under the same conditions, we design an assumed ice cloud case in a standard tropical atmospheric profile in the RRTMG. The RRTMG settings are as follows: ice effective radius is set to 45 µm, the ice water path is set to 60 g m−2, the ice cloud top pressure/height is between 125.1 and 245.5 hPa, the cloud fraction is 50 %, and the solar zenith angles is set to 60∘. The vertical resolution is 60 levels for the standard tropics. The RRTMG is run by the five ice cloud schemes under the same conditions; thus relative difference in fluxes can be explained by difference among the five schemes. The five schemes are implemented in the CIESM to calculate the FSDS, FLDS, FSUTOA, FLUTOA, shortwave cloud forcing (SWCF) and longwave cloud forcing (LWCF). SWCF is defined as Eq. (16), LWCF is defined the same as SWCF but for the longwave spectrum.
where Fcloudy and Fclear are the difference between downward and upward fluxes for cloudy and clear conditions, respectively. The CIESM is operated in two ways: (1) the CIESM is run with the default Mitchell scheme for ice clouds and the default water cloud scheme to obtain SWCF and LWCF for the Mitchell scheme, and (2) the CIESM is run by using the other four schemes (the Voronoi, Yi, Baum-yang05 and Fu schemes) in place of the Mitchell scheme, along with the default liquid water cloud scheme. Liquid water clouds adopt a spherical particle model, whose single-scattering properties are derived from the Lorenz–Mie theory (van de Hulst, 1957). Because the CIESM is unable to separate ice clouds from liquid clouds efficiently, the SWCF and LWCF for the five schemes are under the same liquid water cloud parameterization, and their differences are attributed to different ice habits and their scattering and absorption properties within the five schemes. The CIESM run is integrated for 11 years in 1-month increments; the initial first year is used for state initialization and stabilization, and the runs from the last 10 years were utilized for analysis. Horizontal and vertical resolution of CIESM run experiment is set to and 31 levels, respectively. The run is driven by prescribed climatological sea surface temperature and sea ice fraction with an annual cycle in the year 2000.
4.1 Band-averaged optical properties of the ice cloud
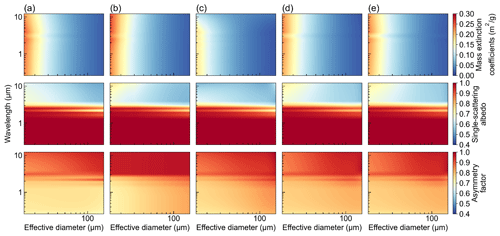
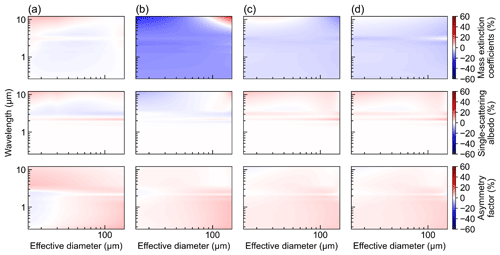
Based on the integration over both PSDs and band intervals, band-averaged bulk optical properties of the Voronoi scheme are compared with the Mitchell, Fu, Baum-yang05 and Yi schemes in Fig. 4. The differences in ice cloud optical properties between the Voronoi and the other four existing schemes are shown in Fig. 5. Since the Fu scheme uses generalized effective diameter, the remaining four schemes use De. Horizontal axes in both Figs. 4 and 5 are unified into De for comparability. Parameterized mass extinction coefficients, single-scattering albedo and asymmetry factor are plotted as functions of the De from 10 to 150 µm and 14 selected bands.
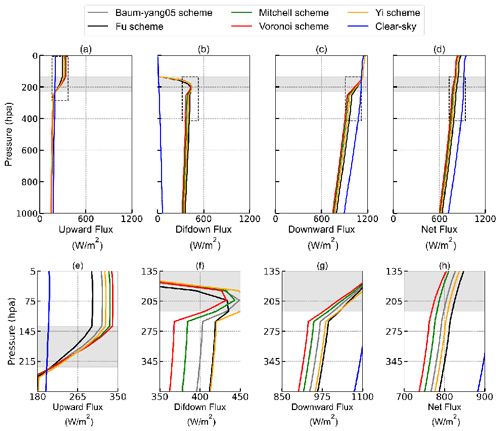
Figure 6Shortwave (a) upward fluxes, (b) diffuse downward fluxes, (c) downward total fluxes and (d) net fluxes for the Voronoi, Mitchell, Fu, Baum-yang05 and Yi schemes and clear conditions (blue line) for standard tropical atmospheric profile. Graphics in dotted black box are magnified and displayed in (e)–(h).
In Fig. 4, mass extinction coefficients obtained from the five schemes show a uniformly negative correlation with De. Mass extinction coefficients exceed up to 0.2 m2 g−1 for De smaller than 20 µm and approach 0 for De larger than 100 µm. This could be partly related to the majority of small particles in PSDs for the five schemes. Note that there is a minimum of mass extinction coefficients between 3.08 and 3.85 µm. It could be because the real part of the refractive index reaches the minimum at 3 µm (Warren and Brandt, 2008; Yang et al., 2013). This could weaken the scattering and extinction efficiency of ice particles. The single-scattering albedos obtained from the five schemes approach 1.0 in visible bands (0.2–0.78 µm). In near-infrared bands (0.78–3.85 µm), the single-scattering albedos are inversely proportional to De. This result is related to the large real part in visible bands and small imaginary part of the complex refractive index of ice particles. The asymmetry factor obtained from the five schemes increases with increasing wavelength for all De. From the visible to near-infrared band, the asymmetry factor increases with the increasing De.
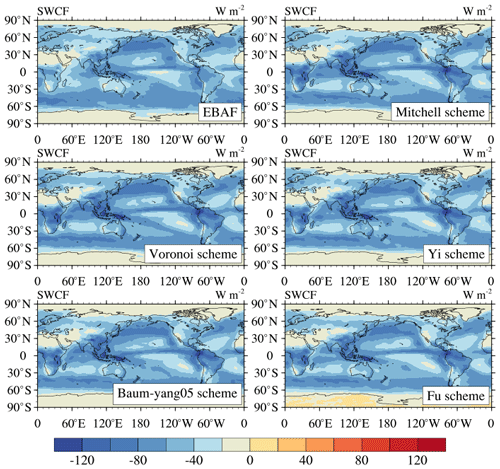
Figure 7The 10-year globally averaged CIESM-based TOA SWCF simulations for the Voronoi, Mitchell, Fu, Baum-yang05 and Yi schemes and corresponding CERES EBAF products during 2001–2010.
In Fig. 5, differences in mass extinction coefficients between the Voronoi scheme and the other four schemes show that the Voronoi scheme has slightly larger values than the Fu, Yi and Baum-yang05 schemes but is smaller than the Mitchell scheme. For the single-scattering albedo, the Voronoi scheme has a slightly larger single-scattering albedo than the Fu and Mitchell schemes and lower single-scattering albedo than the Baum-yang05 and Yi schemes in infrared bands. This result may be because large ice particles are closer to geometric optics and have a greater proportion of absorption than small ice particles. The low asymmetry factor of the Voronoi scheme is because the multifaceted shapes of the Voronoi ice model can result in significant side and backward scattering and reduced forward scattered energy. Since the impacts of different size distribution assumptions on the bulk optical properties of ice cloud parameterization are negligible (Heymsfield et al., 2013, 2017), differences in band-averaged bulk optical properties between the five schemes are originally rooted in different habits of ice particles and their single-scattering properties.
4.2 RRTMG simulation results
After the parameterization, band-averaged optical properties of ice cloud from the five schemes (Fu, Mitchell, Yi, Baum-yang05 and Voronoi) are subsequently parameterized as functions of De and 14 bands as shown in Fig. 4. To illustrate and quantify the influence of optical properties of ice cloud on its radiative effects, an ideal experiment is designed to test the response of radiative flux to the five ice cloud schemes under the same idealized conditions. Band-averaged optical properties for the five schemes are subsequently implemented in RRTMG to simulate radiative fluxes under prescribed ice clouds in standard tropical profiles (Anderson et al., 1986) which have a high proportion of ice cloud coverage (Massie et al., 2002; Stubenrauch et al., 2013). According to observations of Hong and Liu (2015), top and bottom pressures of ice cloud layer are set to 125.1 and 245.5 hPa, respectively, the De is set to 45 µm, and ice water paths equal 60 g m−2.
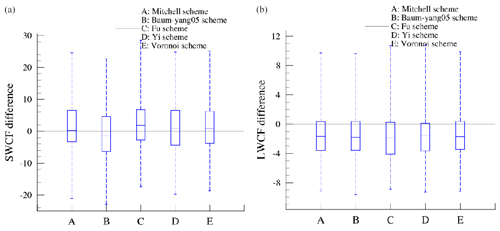
Figure 10Box analysis of zonal distributions of 10-year annual mean SWCF (a) and LWCF (b) difference between the Mitchell, Voronoi, Fu, Baum-yang05 and Yi schemes and EBAF products, respectively.
Shortwave radiative flux profiles of cloudy sky for the five schemes and clear-sky conditions are shown in Fig. 6. Specific comparison of the five schemes inside the dotted black region are enlarged and shown in the bottom row. In Fig. 6, upward fluxes of the five schemes gradually increase from cloud bottom to cloud top, reaching the maximum at the cloud top. The Voronoi and Mitchell schemes have higher upward fluxes and lower downward diffuse fluxes than the other three schemes. Figure 6 shows 6–30 W m−2 differences in TOA upward fluxes, 10–40 W m−2 differences in surface downward diffuse fluxes, 10–30 W m−2 differences in surface net fluxes and 8–42 W m−2 differences in TOA net fluxes owing to the five different ice cloud schemes. The radiative properties for the Voronoi scheme in shortwave fluxes can be explained by its lower asymmetry factor than the other four schemes, leading to smaller proportion of forward scattering and larger backward scattering and thus less shortwave flux reaching the ground and more upward flux for the Voronoi scheme compared with the other four schemes.
4.3 Climate model simulation results
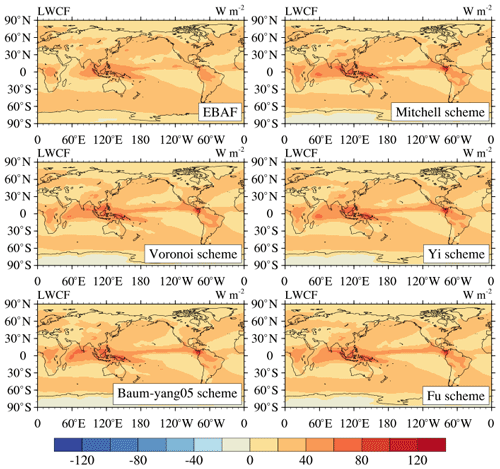
As shown in RRTMG simulations in Sect. 4.2, the influence of the five ice cloud schemes (Voronoi, Yi, Mitchell, Baum-yang05 and Fu schemes) on the radiative effects is evaluated under standard tropical atmospheric profiles and with assumptions of idealized ice cloud microphysical properties as input data. Simulation results based upon the radiative transfer model are capable of showing differences in ice cloud radiative effects for the five schemes under some specific conditions but are unable to demonstrate comprehensive the performance of the five schemes corresponding to real and complex atmospheric situations. To study the ice cloud modeling capabilities of the five schemes in the climate model, the Voronoi, Yi, Baum-yang05 and Fu schemes are applied in the CIESM. Upwelling and downwelling fluxes and TOA SWCF and LWCF from CIESM simulations for the five schemes compared with CERES EBAF products are plotted in Figs. 7 and 8, and their globally averaged values are listed in Table 2. The results show that the Voronoi scheme produced a lower difference of approximately −0.45 W m−2 (1.1 %) for the TOA shortwave cloud radiative forcing and −0.30 W m−2 (1.4 %) for the TOA longwave cloud radiative forcing compared with the four existing schemes. For FSDS, the Voronoi scheme has the smallest downwelling fluxes at the surface and is the closest to the EBAF products due to the Voronoi scheme scatter having the least energy in the forward direction. For FSUTOA, the Voronoi scheme possesses the largest upwelling fluxes compared to the other four schemes due to its strong backward scattering. For the longwave spectrum, the effects of the Voronoi scheme on the FLDS and FLUTOA are negligible.
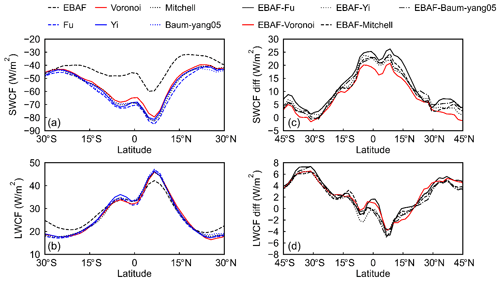
To discuss the influence of the five schemes on the global distributions of SWCF and LWCF, the zonal average analysis is shown in Fig. 9. Results show that the SWCF of CIESM simulations is stronger than the EBAF results in tropical regions. This might be because the CIESM overestimates ice and liquid cloud fraction in low latitudes compared with the observations (Eidhammer et al., 2014; Kay et al., 2016). Note that the Voronoi scheme exhibits weaker cooling effects in tropical regions than the other four existing schemes. According to the definitions of the SWCF and LWCF, the highest TOA upward fluxes of the Voronoi scheme can produce the lowest TOA net fluxes, which means the Voronoi scheme can produce the smallest negative TOA SWCF among the five schemes. Figure 10 displayed the distribution of differences between the five schemes and the CERES EBAF product. The difference boxes of the Voronoi scheme are the most concentrated on the zero line, and its statistical deviation is the smallest, which means the spatial distribution of cloud radiative effects of the Voronoi scheme is closer to EBAF products compared with the other four existing schemes.
The optical property parameterization (Voronoi scheme) of the Voronoi ice crystal scattering (ICS) model is investigated for simulations of the ice cloud radiative properties in the Community Integrated Earth System Model (CIESM). The Voronoi scheme is completed based on the single-scattering properties of the Voronoi ICS database and particle size distributions from in situ observations. The band-averaged optical properties of ice clouds including the mass extinction coefficients, single-scattering albedo and asymmetry factor of the Voronoi scheme are applied in the CIESM climate model and compared with those of the four existing schemes (Baum-yang05, Fu, Yi and Mitchell). The results show that the Voronoi scheme has a distinct feature of having the lowest asymmetry factor in the shortwave bands. This feature could be related to the complex multifaceted shape of the Voronoi ICS model and suggests that the Voronoi scheme can produce relatively stronger backward scattering compared with the other schemes.
Radiative properties of ice clouds are firstly assessed in the rapid radiative transfer model for general circulation models (RRTMG) in the CIESM. The profiles of upward and downward fluxes from different ice cloud schemes are simulated for the prescribed atmospheric condition. The RRTMG results show that the Voronoi scheme has the highest upward flux at the top of the atmosphere (TOA) and lowest downward flux at the surface when the solar zenith angle equals 60∘. Therefore, the net flux of the Voronoi scheme is largest at the TOA and smallest at the surface compared with the other schemes, which is mostly due to its lowest asymmetry factor.
The five schemes (Baum-yang05, Fu, Yi, Mitchell and Voronoi) are then applied to the CIESM to simulate shortwave and longwave global total cloud radiative forcing at the TOA during 2001–2010. The accuracy of simulated 10-year global total cloud radiative forcing from different schemes is evaluated with the Clouds and the Earth's Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) product. The results show that the Voronoi scheme produced a lower difference for the TOA shortwave and longwave cloud radiative forcing compared with the four existing schemes. Especially for the region (from 30∘ S to 30∘ N) where the ice clouds occur frequently, the Voronoi scheme provides the closest match with the CERES EBAF product.
In conclusion, simulations of globally averaged shortwave and longwave cloud radiative forcing at the TOA from the five schemes are investigated through the EBAF product. We find that the Voronoi scheme present a better agreement with EBAF products than the other schemes, especially in the tropical region, which confirmed that the Voronoi ICS model has the possibility of having ice cloud modeling capabilities in the climate model of the CIESM.
| L | Particle maximum diameter (µm) |
| λ | Wavelength (µm) |
| SZP | Size parameter (unitless) |
| n(L) | Particle concentration (cm−3) |
| N0 | Intercept coefficient of n(L) (unitless) |
| λ∗ | Slope coefficient of n(L) (unitless) |
| μ | Dispersion coefficient of n(L) (unitless) |
| PSD | Particle size distribution defined by N0, λ∗, μ and L |
| TOA | Top of atmosphere |
| βe,s,a | Extinction, scattering and absorption coefficients |
| σe,s,a | Extinction, scattering and absorption cross section |
| θ | Inclination to the upward normal direction scattering angle |
| Cosines of θ and incoming and outgoing intensity direction, respectively | |
| Incoming and outgoing intensity azimuthal angle with reference to the x axis, respectively | |
| P | Phase function regulated by and ϕ′ |
| z | Upper limit of the outer boundary |
| τ | Optical thickness |
| I | Total (direct plus diffuse) radiance |
| B[T] | Planck's function |
| Source function | |
| De | Effective particle diameter |
| Qext, sca(λ,L) | Extinction efficiency and scattering efficiency |
| V(L) | Ice particle volume (µm3) |
| A(L) | Average geometrical cross section (µm2) |
| Spectral and band-averaged mass extinction coefficients | |
| Spectral and band-averaged single-scattering albedo | |
| Spectral and band-averaged asymmetry factor | |
| N | Cloud fraction |
| Fcloudy | Net fluxes of cloudy conditions |
| Fclear | Net fluxes of clear conditions |
| FSDS | Downwelling shortwave flux at the surface |
| FLDS | Downwelling longwave flux at the surface |
| FSUTOA | Upwelling shortwave flux at the top of atmosphere |
| FLUTOA | Upwelling longwave flux at the top of atmosphere |
| SWCF | Shortwave cloud forcing |
| LWCF | Longwave cloud forcing |
The RRTMG code is available at http://rtweb.aer.com/rrtmg_sw_code.html (AER-RC, 2020) (last access: 5 January 2021), and the CERES level 3 EBAF products are available at https://ceres.larc.nasa.gov/data/ (NASA/LARC/SD/ASDC, 2019) (last access: 6 May 2021).
ML developed the ice cloud optical property parameterizations (Voronoi scheme) based on the single-scattering properties of the Voronoi models and compared the band-averaged optical properties of the Voronoi scheme with the other four schemes (Mitchell, Yi, Baum-yang05 and Fu). ML also compared the upward and downward flux profiles from the five schemes through RRTMG standalone simulations and radiative properties of the five schemes in CAM5 model simulations, as well as downloaded the CERES products and wrote the initial draft of the manuscript. HL designed the aims and structures of this study and assisted in developing the parameterization of ice cloud optical properties based on the Voronoi models. HL also provided the single-scattering property database of Voronoi models and helped in analyzing the single-scattering properties of Voronoi models, as well as guided the writing and revisions of the manuscript. YP and YL assisted in developing the ice cloud optical property parameterization and provided the climate models, as well as guided the settings of climate model runs and reviewing the manuscript. HI developed the single-scattering property database of Voronoi models, provided the database of Voronoi models and helped in the parameterization of ice cloud optical properties based on the single-scattering properties of Voronoi models. TYN provided the single-scattering property database of Voronoi models and especially assisted in guiding the flowchart of this study and reviewing the manuscript. AJB guided the development of the ice cloud optical property parameterization and reviewed the paper. ZG assisted with the runs and design of the climate model simulations and helped with the review of the manuscript. YL assisted in analyzing the results and guided the flowchart of the study, as well as reviewed the manuscript. JS assisted in designing the aims and structures of this study, guided the writing of the paper and helped review the manuscript.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (grant no. 2019QZKK0206), the National Natural Science Foundation of China (grant nos. 42025504, 41771395, 42175096) and the International Partnership Programme of Bureau of International Co-operation Chinese Academy of Sciences (contract no. 181811KYSB20190014).
This research has been supported by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (grant no. 2019QZKK0206), the National Natural Science Foundation of China (grant nos. 42025504, 41771395, 42175096) and the International Partnership Programme of Bureau of International Co-operation Chinese Academy of Sciences (contract no. 181811KYSB20190014).
This paper was edited by Martina Krämer and reviewed by four anonymous referees.
AER-RC: RRTMG_SW, Atmospheric and Environmental Research R&C, [data set], https://github.com/AER-RC/RRTMG_SW (last access: 5 January 2021), 2020.
Anderson, G. P., Clough, S. A., Kneizys, F. X., Chetwynd, J. H., and Shettle, E. P.: AFGL atmospheric constituent profiles (0.120 km), Tech. Rep. AFGL-TR-86-0110, Air Force Geophys. Lab., Hanscom Air Force Base, Bedford, Mass., 1986.
Baran, A. J.: A review of the light scattering properties of cirrus, J. Quant. Spectrosc. Ra., 110, 1239–1260, 2009.
Baran, A. J.: From the single-scattering properties of ice crystals to climate prediction: A way forward, Atmos. Res., 112, 45–69, 2012.
Baum, B. A., Heymsfield, A. J., Yang, P., and Bedka, S. T.: Bulk scattering properties for the remote sensing of ice clouds, Part I: Microphysical data and models, J. Appl. Meteorol., 44, 1885–1895, 2005a.
Baum, B. A., Yang, P., Heymsfield, A. J., Platnick, S., King, M. D., Hu, Y. X., and Bedka, S. T.: Bulk scattering properties for the remote sensing of ice clouds, Part II: Narrowband models, J. Appl. Meteorol., 44, 1896–1911, 2005b.
Bi, L. and Yang, P.: Accurate simulation of the optical properties of atmospheric ice crystals with the invariant imbedding T-matrix method, J. Quant. Spectrosc. Ra., 138, 17–35, 2014.
Bi, L., Yang, P., Kattawar, G., and Kahn, R.: Single-scattering properties of triaxial ellipsoidal particles for a size parameter range from the Rayleigh to geometric-optics regimes, Appl. Opt., 48, 114–126, 2009.
Bi, L., Yang, P., and Kattawar, G. W.: Edge-effect contribution to the extinction of light by dielectric disks and cylindrical particles, Appl. Opt., 49, 4641–4646, 2010.
Bi, L., Yang, P., Kattawar, G. W., Hu, Y. X., and Baum, B. A.: Scattering and absorption of light by ice particles: Solution by a new physical-geometric optics hybrid method, J. Quant. Spectrosc. Ra., 112, 1492–1508, 2011.
Bi, L., Yang, P., Kattawar, G. W., and Mishchenko, M. I.: A numerical combination of extended boundary condition method and invariant imbedding method applied to light scattering by large spheroids and cylinders, J. Quant. Spectrosc. Ra., 123, 17–22, 2013a.
Bi, L., Yang, P., Kattawar, G. W., and Mishchenko, M. I.: Efficient implementation of the invariant imbedding T-matrix method and the separation of variables method applied to large nonspherical inhomogeneous particles, J. Quant. Spectrosc. Ra., 116, 169–183, 2013b.
C.-Labonnote, L., Brogniez, G., Doutriaux-Boucher, M., Buriez, J.-C., Gayet, J.-F., and Chepfer, H.: Modeling of light scattering in cirrus clouds with inhomogeneous hexagonal monocrystals, Comparison with in-situ and ADEOS-POLDER measurements, Geophys. Res. Lett., 27, 113–116, 2000.
C.-Labonnote, L., Brogniez, G., Buriez, J.-C., Doutriaux-Boucher, M., Gayet, J.-F., and Macke, A.: Polarized light scattering by inhomogeneous hexagonal monocrystals: Validation with ADEOS-POLDER measurements, J. Geophys. Res.-Atmos., 106, 12139–12153, 2001.
Chance, K. and Kurucz, R. L.: An improved high-resolution solar reference spectrum for earth's atmosphere measurements in the ultraviolet, visible, and near infrared, J. Quant. Spectrosc. Ra., 111, 1289–1295, 2010.
Clough, S. A., Shephard, M. W., Mlawer, E. J., Delamere, J. S., Iacono, M. J., Cady-Pereira, K., Boukabara, S., and Brown, P. D.: Atmospheric radiative transfer modeling: a summary of the AER codes, J. Quant. Spectrosc. Radiat. Transfer, 91, 233–244, https://doi.org/10.1016/j.jqsrt.2004.05.058, 2005.
Deschamps, P. Y., Breon, F. M., Leroy, M., Podaire, A., Bricaud, A., Buriez, J. C., and Seze, G.: The Polder Mission – Instrument Characteristics and Scientific Objectives, IEEE T. Geosci. Remote, 32, 598–615, 1994.
Doelling, D. R., Sun, M., Nguyen, L. T., Nordeen, M. L., Haney, C. O., Keyes, D. F., and Mlynczak, P. E.: Advances in Geostationary-Derived Longwave Fluxes for the CERES Synoptic (SYN1deg) Product, J. Atmos. Ocean. Tech., 33, 503–521, 2016.
Doutriaux-Boucher, M., Buriez, J.-C., Brogniez, G., C.-Labonnote, L., and Baran, A.: Sensitivity of retrieved POLDER directional cloud optical thickness to various ice particle models, Geophys. Res. Lett., 27, 109–112, 2000.
Draine, B. T. and Flatau, P. J.: Discrete-Dipole Approximation for Scattering Calculations, J. Opt. Soc. Am. A, 11, 1491–1499, 1994.
Eidhammer, T., Morrison, H., Bansemer, A., Gettelman, A., and Heymsfield, A. J.: Comparison of ice cloud properties simulated by the Community Atmosphere Model (CAM5) with in-situ observations, Atmos. Chem. Phys., 14, 10103–10118, https://doi.org/10.5194/acp-14-10103-2014, 2014.
Fu, Q. A.: An accurate parameterization of the solar radiative properties of cirrus clouds for climate models, J. Climate, 9, 2058–2082, 1996.
Fu, Q. A.: A new parameterization of an asymmetry factor of cirrus clouds for climate models, J. Atmos. Sci., 64, 4140–4150, 2007.
Havemann, S. and Baran, A. J.: Extension of T-matrix to scattering of electromagnetic plane waves by non-axisymmetric dielectric particles: application to hexagonal ice cylinders, J. Quant. Spectrosc. Ra., 70, 139–158, 2001.
Heymsfield, A. J. and Miloshevich, L. M.: Parameterizations for the cross-sectional area and extinction of cirrus and stratiform ice cloud particles, J. Atmos. Sci., 60, 936–956, 2003.
Heymsfield, A. J., Schmitt, C., and Bansemer, A.: Ice Cloud Particle Size Distributions and Pressure-Dependent Terminal Velocities from In Situ Observations at Temperatures from 0∘ to −86∘ C, J. Atmos. Sci., 70, 4123–4154, 2013.
Heymsfield, A. J., Krämer, M., Luebke, A., Brown, P., Cziczo, D. J., Franklin, C., Lawson, P., Lohmann, U., McFarquhar, G., Ulanowski, Z., and Van Tricht, K.: Cirrus Clouds, Meteor. Mon., 58, 1–26, 2017.
Hong, Y. L. and Liu, G. S.: The Characteristics of Ice Cloud Properties Derived from CloudSat and CALIPSO Measurements, J. Climate, 28, 3880–3901, 2015.
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008.
Illingworth, A. J., Barker, H. W., Beljaars, A., Ceccaldi, M., Chepfer, H., Clerbaux, N., Cole, J., Delanoe, J., Domenech, C., Donovan, D. P., Fukuda, S., Hirakata, M., Hogan, R. J., Huenerbein, A., Kollias, P., Kubota, T., Nakajima, T., Nakajima, T. Y., Nishizawa, T., Ohno, Y., Okamoto, H., Oki, R., Sato, K., Satoh, M., Shephard, M. W., Velazquez-Blazquez, A., Wandinger, U., Wehr, T., and van Zadelhoff, G.-J.: The earthcare satellite, The Next Step Forward in Global Measurements of Clouds, Aerosols, Precipitation, and Radiation, B. Am. Meteorol. Soc., 96, 1311–1332, 2015.
Ishimoto, H., Masuda, K., Mano, Y., Orikasa, N., and Uchiyama, A.: Irregularly shaped ice aggregates in optical modeling of convectively generated ice clouds, J. Quant. Spectrosc. Ra., 113, 632–643, 2012.
Kay, J., Bourdages, L., Miller, N., Morrison, A., Yettella, V., Chepfer, H., and Eaton, B.: Evaluating and improving cloud phase in the Community Atmosphere Model version 5 using spaceborne lidar observations, J. Geophys. Res.-Atmos., 121, 4162–4176, https://doi.org/10.1002/2015JD024699, 2016.
Lawson, R. P., Baker, B., Pilson, B., and Mo, Q. X.: In situ observations of the microphysical properties of wave, cirrus, and anvil clouds, Part II: Cirrus clouds, J. Atmos. Sci., 63, 3186–3203, 2006.
Lawson, R. P., Woods, S., Jensen, E., Erfani, E., Gurganus, C., Gallagher, M., Connolly, P., Whiteway, J., Baran, A. J., May, P., Heymsfield, A., Schmitt, C. G., McFarquhar, G., Um, J., Protat, A., Bailey, M., Lance, S., Muehlbauer, A., Stith, J., Korolev, A., Toon, O. B., and Kramer, M.: A Review of Ice Particle Shapes in Cirrus formed In Situ and in Anvils, J. Geophys. Res.-Atmos., 124, 10049–10090, 2019.
Letu, H., Nakajima, T. Y., and Matsui, T. N.: Development of an ice crystal scattering database for the global change observation mission/second generation global imager satellite mission: investigating the refractive index grid system and potential retrieval error, Appl. Opt., 51, 6172–6178, 2012.
Letu, H., Ishimoto, H., Riedi, J., Nakajima, T. Y., C.-Labonnote, L., Baran, A. J., Nagao, T. M., and Sekiguchi, M.: Investigation of ice particle habits to be used for ice cloud remote sensing for the GCOM-C satellite mission, Atmos. Chem. Phys., 16, 12287–12303, https://doi.org/10.5194/acp-16-12287-2016, 2016.
Letu, H. S., Nagao, T. M., Nakajima, T. Y., Riedi, J., Ishimoto, H., Baran, A. J., Shang, H. Z., Sekiguchi, M., and Kikuchi, M.: Ice Cloud Properties From Himawari-8/AHI Next-Generation Geostationary Satellite: Capability of the AHI to Monitor the DC Cloud Generation Process, IEEE T. Geosci. Remote, 57, 3229–3239, 2018.
Letu, H. S., Yang, K., Nakajima, T. Y., Ishimoto, H., Nagao, T. M., Riedi, J., Baran, A. J., Ma, R., Wang, T. X., Shang, H. Z., Khatri, P., Chen, L. F., Shi, C. X., and Shi, J. C.: High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite, Remote Sens. Environ., 239, 1–16, https://doi.org/10.1016/j.rse.2019.111583, 2020.
Lin, Y., Huang, X., Liang, Y., Qin, Y., Xu, S., Huang, W., Xu, F., Liu, L., Wang, Y., Peng, Y., Wang, L., Xue, W., Fu, H., Zhang, G. J., Wang, B., Li, R., Zhang, C., Lu, H., Yang, K., Luo, Y., Bai, Y., Song, Z., Wang, M., Zhao, W., Zhang, F., Xu, J., Zhao, X., Lu, C., Chen, Y., Luo, Y., Hu, Y., Tang, Q., Chen, D., Yang, G., and Gong, P.: Community Integrated Earth SystemModel (CIESM): Description andevaluation., J. Adv. Model. Earth Sys., 12, e2019MS002036, https://doi.org/10.1029/2019MS002036, 2020.
Liou, K. N.: Influence of Cirrus Clouds on Weather and Climate Processes – a Global Perspective, Mon. Weather Rev., 114, 1167–1199, 1986.
Liou, K.-N.: Radiation and cloud processes in the atmosphere: theory, observation and modeling, Oxford monographs on geology and geophysics, 20, Oxford University Press, New York, 487 pp., 1992.
Massie, S., Gettelman, A., Randel, W., and Baumgardner, D.: Distribution of tropical cirrus in relation to convection, J. Geophys. Res.-Atmos., 107, 4591, https://doi.org/10.1029/2001JD001293, 2002.
Mishchenko, M. I. and Travis, L.: Capabilities and Limitations of a Current FORTRAN Implementation of the T-matrix Method for Randomly Oriented, Rotationally Symmetric Scatterers, J. Quant. Spectrosc. Ra., 60, 309–324, 1998.
Mishchenko, M. I., Travis, L. D., and Mackowski, D. W.: T-matrix computations of light scattering by nonspherical particles: A review, J. Quant. Spectrosc. Ra., 55, 535–575, 1996.
Mitchell, D. L. and Arnott, W. P.: A Model Predicting the Evolution of Ice Particle-Size Spectra and Radiative Properties of Cirrus Clouds, 2. Dependence of Absorption and Extinction on Ice Crystal Morphology, J. Atmos. Sci., 51, 817–832, 1994.
Mitchell, D. L., Chai, S. K., Liu, Y. G., Heymsfield, A. J., and Dong, Y. Y.: Modeling Cirrus Clouds. Part I: Treatment of Bimodal Size Spectra and Case Study Analysis, J. Atmos. Sci., 53, 2952–2966, 1996a.
Mitchell, D. L., Yangang, L., and Macke, A.: Modeling Cirrus Clouds, Part II: Treatment of Radiative Properties, J. Atmos. Sci, 53, 2967–2988, 1996b.
Mitchell, D. L., Baran, A. J., Arnott, W. P., and Schmitt, C.: Testing and comparing the modified anomalous diffraction approximation, J. Atmos. Sci., 63, 2948–2962, 2006.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 102, 16663–16682, https://doi.org/10.1029/97jd00237, 1997.
NASA/LARC/SD/ASDC: CERES Energy Balanced and Filled (EBAF) TOA and Surface Monthly means data in netCDF Edition 4.1, NASA Langley Atmospheric Science Data Center DAAC, [data set], https://doi.org/10.5067/TERRA-AQUA/CERES/EBAF_L3B.004.1 (last access: 6 May 2021), 2019.
Nakajima, T., Nakajima, T., Yoshimori, K., Mishra, S., and Tripathi, S.: Development of a light scattering solver applicable to particles of arbitrary shape on the basis of the surface-integral equations method of Müller type, I. Methodology, accuracy of calculation, and electromagnetic current on the particle surface, Appl. Opt., 48, 3526–3536, 2009.
Nakajima, T. Y., Ishida, H., Nagao, T. M., Hori, M., Letu, H., Higuchi, R., Tamaru, N., Imoto, N., and Yamazaki, A.: Theoretical basis of the algorithms and early phase results of the GCOM-C (Shikisai) SGLI cloud products, Prog. Earth Planet Sc., 6, 1–25, https://doi.org/10.1186/s40645-019-0295-9, 2019.
Ramaswamy, V. and Ramanathan, V.: Solar Absorption by Cirrus Clouds and the Maintenance of the Tropical Upper Troposphere Thermal Structure, J. Atmos. Sci., 46, 2293–2310, 1989.
Rossow, W. B. and Schiffer, R. A.: Isccp Cloud Data Products, B. Am. Meteorol. Soc., 72, 2–20, 1991.
Rossow, W. B. and Schiffer, R. A.: Advances in understanding clouds from ISCCP, B. Am. Meteorol. Soc., 80, 2261–2287, 1999.
Stubenrauch, C. J., Rossow, W. B., Kinne, S., Ackerman, S., Cesana, G., Chepfer, H., Di Girolamo, L., Getzewich, B., Guignard, A., Heidinger, A., Maddux, B. C., Menzel, W. P., Minnis, P., Pearl, C., Platnick, S., Poulsen, C., Riedi, J., Sun-Mack, S., Walther, A., Winker, D., Zeng, S., and Zhao, G.: Assessment of Global Cloud Datasets from Satellites: Project and Database Initiated by the GEWEX Radiation Panel, B. Am. Meteorol. Soc., 94, 1031–1049, 2013.
Takano, Y. and Liou, K. N.: Solar Radiative-Transfer in Cirrus Clouds, 1. Single-Scattering and Optical-Properties of Hexagonal Ice Crystals, J. Atmos. Sci., 46, 3–19, 1989.
van de Hulst, H. C.: Light scattering by small particles, Wiley, New York, 470 pp., 1957.
van Diedenhoven, B.: Remote Sensing of Crystal Shapes in Ice Clouds, 197–250, https://doi.org/10.1007/978-3-319-70808-9, 2018.
van Diedenhoven, B. and Cairns, B.: A Flexible Parameterization for Shortwave and Longwave Optical Properties of Ice Crystals and Derived Bulk Optical Properties for Climate Models, J. Atmos. Sci., 77, 1245–1260, 2020.
van Diedenhoven, B., Fridlind, A. M., Cairns, B., and Ackerman, A. S.: Variation of ice crystal size, shape, and asymmetry parameter in tops of tropical deep convective clouds, J. Geophys. Res.-Atmos., 119, 11809–11825, 2014.
Wang, P. H., Minnis, P., McCormick, M. P., Kent, G. S., and Skeens, K. M.: A 6-year climatology of cloud occurrence frequency from stratospheric aerosol and gas experiment II observations (1985–1990), J. Geophys. Res.-Atmos., 101, 29407–29429, 1996.
Warren, S. G. and Brandt, R. E.: Optical constants of ice from the ultraviolet to the microwave: A revised compilation, J. Geophys. Res.-Atmos., 113, D14220, https://doi.org/10.1029/2007JD009744, 2008.
Wendling, P., Wendling, R., and Weickmann, H.: Scattering of solar radiation by hexagonal ice crystals, Appl. Opt., 18, 2663–2671, 1979.
Yang, P. and Liou, K. N.: Light-Scattering by Hexagonal Ice Crystals – Comparison of Finite-Difference Time-Domain and Geometric Optics Models, J. Opt. Soc. Am. A., 12, 162–176, 1995.
Yang, P. and Liou, K. N.: Geometric-optics-integral-equation method for light scattering by nonspherical ice crystals, Appl. Opt., 35, 6568–6584, 1996a.
Yang, P. and Liou, K. N.: Finite-difference time domain method for light scattering by small ice crystals in three-dimensional space, J. Opt. Soc. Am. A., 13, 2072–2085, 1996b.
Yang, P., Liou, K. N., Wyser, K., and Mitchell, D.: Parameterization of the scattering and absorption properties of individual ice crystals, J. Geophys. Res.-Atmos., 105, 4699–4718, 2000.
Yang, P., Bi, L., Baum, B. A., Liou, K. N., Kattawar, G. W., Mishchenko, M. I., and Cole, B.: Spectrally Consistent Scattering, Absorption, and Polarization Properties of Atmospheric Ice Crystals at Wavelengths from 0.2 to 100 µm, J. Atmos. Sci., 70, 330–347, 2013.
Yang, P., Liou, K. N., Bi, L., Liu, C., Yi, B. Q., and Baum, B. A.: On the Radiative Properties of Ice Clouds: Light Scattering, Remote Sensing, and Radiation Parameterization, Adv. Atmos. Sci., 32, 32–63, 2015.
Yang, P., Hioki, S., Saito, M., Kuo, C. P., Baum, B. A., and Liou, K. N.: A Review of Ice Cloud Optical Property Models for Passive Satellite Remote Sensing, Atmosphere, 9, 499, https://doi.org/10.3390/atmos9120499, 2018.
Yee, K. S.: Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media, IEEE T. Antenn. Propag., 14, 302–307, 1966.
Yi, B. Q., Yang, P., Baum, B. A., L'Ecuyer, T., Oreopoulos, L., Mlawer, E. J., Heymsfield, A. J., and Liou, K. N.: Influence of Ice Particle Surface Roughening on the Global Cloud Radiative Effect, J. Atmos. Sci., 70, 2794–2807, 2013.
Yi, B. Q., Rapp, A. D., Yang, P., Baum, B. A., and King, M. D.: A comparison of Aqua MODIS ice and liquid water cloud physical and optical properties between collection 6 and collection 5.1: Cloud radiative effects, J. Geophys. Res.-Atmos., 122, 4550–4564, 2017.
Yurkin, M. A. and Hoekstra, A. G.: The discrete dipole approximation: An overview and recent developments, J. Quant. Spectrosc. Ra., 106, 558–589, 2007.
Yurkin, M. A. and Hoekstra, A.: The discrete-dipole-approximation code ADDA: Capabilities and known limitations, J. Quant. Spectrosc. Ra., 112, 2234–2247, https://doi.org/10.1016/j.jqsrt.2011.01.031, 2011.
Yurkin, M. A., Maltsev, V. P., and Hoekstra, A. G.: The discrete dipole approximation for simulation of light scattering by particles much larger than the wavelength, J. Quant. Spectrosc. Ra., 106, 546–557, 2007.
Zhang, H., Chen, Q., and Xie, B.: A new parameterization for ice cloud optical properties used in BCC-RAD and its radiative impact, J. Quant. Spectrosc. Ra., 150, 76–86, 2015.
Zhao, W. J., Peng, Y. R., Wang, B., Yi, B. Q., Lin, Y. L., and Li, J. N.: Comparison of three ice cloud optical schemes in climate simulations with community atmospheric model version 5, Atmos. Res., 204, 37–53, 2018.