Methodology to determine the coupling of continental clouds with surface and boundary layer height under cloudy conditions from lidar and meteorological data

The states of coupling between clouds and surface or boundary layer have been investigated much more extensively for marine stratocumulus clouds than for continental low clouds, partly due to more complex thermodynamic structures over land. A manifestation is a lack of robust remote sensing methods to identify coupled and decoupled clouds over land. Following the idea for determining cloud coupling over the ocean, we have generalized the concept of coupling and decoupling to low clouds over land, based on potential temperature profiles. Furthermore, by using ample measurements from lidar and a suite of surface meteorological instruments at the U.S. Department of Energy's Atmospheric Radiation Measurement Program's Southern Great Plains site from 1998 to 2019, we have developed a method to simultaneously retrieve the planetary boundary layer (PBL) height (PBLH) and coupled states under cloudy conditions during the daytime. The new lidar-based method relies on the PBLH, the lifted condensation level, and the cloud base to diagnose the cloud coupling. The coupled states derived from this method are highly consistent with those derived from radiosondes. Retrieving the PBLH under cloudy conditions, which has been a persistent problem in lidar remote sensing, is resolved in this study. Our method can lead to high-quality retrievals of the PBLH under cloudy conditions and the determination of cloud coupling states. With the new method, we find that coupled clouds are sensitive to changes in the PBL with a strong diurnal cycle, whereas decoupled clouds and the PBL are weakly related. Since coupled and decoupled clouds have distinct features, our new method offers an advanced tool to separately investigate them in climate systems.

1 Introduction

A large fraction of low clouds is driven by surface fluxes through the conduits of the planetary boundary layer (PBL) over land (e.g., Betts, 2009; Ek and Holtslag, 2004; Golaz et al., 2002; Teixeira and Hogan, 2002; Zheng et al., 2020; Wei et al., 2020; Santanello et al., 2018). This is a coupled cloud–surface system (Cheruy et al., 2014; Zheng and Rosenfeld, 2015; Wu et al., 1998). However, not all low clouds respond to surface forcing. Those clouds without close interactions with the local surface are considered to be in a decoupled state. Given that the PBL is, by definition, the lowest atmospheric layer influenced by the underlying surface (Stull, 1988), to what degree the PBL top overlaps with cloud bases becomes a good criterion to separate coupled and decoupled low clouds.

Conventionally, the “coupled state” of a cloud-topped marine boundary layer implies that the moist conserved variables are vertically well mixed within the PBL (Bretherton and Wyant, 1997; Dong et al., 2015; Zheng and Li, 2019; Zheng et al., 2018, 2021). However, such a definition cannot be simply applied to clouds over land since the definition and the determination methods of the PBL over land differ from those over ocean (Garratt, 1994; Vogelezang and Holtslag, 1996). The concept of coupled and decoupled states is typically used to characterize marine stratocumulus clouds due to their large-scale coverages (Nicholls, 1984). Since stratocumulus only constitutes a relatively small portion of continental clouds (Warren et al., 1986), we attempt to extend the concept of coupling and decoupling to characterize low clouds over land. Due to the relatively complex thermodynamics, the moisture conserved variables (e.g., total water mixing ratio and liquid potential temperature) may not be a constant in the coupled sub-cloud layer (Driedonks, 1982; Stull, 1988).

Following parcel theory, the lifted condensation level (LCL) has been used to diagnose a coupled cloud, based on the distance between the LCL and the cloud base (e.g., Dong et al., 2015; Glenn et al., 2020; Zheng and Rosenfeld, 2015; Zheng et al., 2020). When potential temperature and humidity are uniformly distributed in the vertical, the LCL should be consistent with the cloud base for coupled cases. However, the cloud base for coupled cases can considerably differ from the LCL over land because potential temperature and humidity have large variabilities in the vertical scale within the PBL over land (Driedonks, 1982; Guo et al., 2016, 2021; Stull, 1988; Su et al., 2017a). To address the limitation in the LCL method, we attempt to develop a remote sensing method to distinguish coupled and decoupled clouds over land.

Since the PBL height (PBLH) is the maximum height directly influenced by surface fluxes, we consider coupling with the PBL equivalent to coupling with the land surface. Thus, we use the PBLH as a critical parameter to diagnose the coupling between clouds and the land surface. The degree of coupling may thus be gauged in terms of quantitative differences between the cloud base and the PBL top. Such differences can be determined in a height coordinate system or in a potential temperature coordinate system (Kasahara, 1974). For this purpose, ground-based lidar has great potential because it can continuously track the development of the PBL (Demoz et al., 2006; Hageli et al., 2000; Sawyer and Li, 2013; Su et al., 2017b, 2018) and clouds (Clothiaux et al., 2000; Platt et al., 1994; Zhao et al., 2014) at high temporal and vertical resolutions.

By jointly using lidar measurements and meteorological data from the U.S. Department of Energy's Atmospheric Radiation Measurement (ARM) Southern Great Plains (SGP) site (36.6^∘ N, 97.48^∘ W), we attempt to identify coupled and decoupled low clouds during the daytime. Unlike previous studies that use the LCL or radiosonde (RS) data to diagnose coupled clouds (e.g., Dong et al., 2015; Zheng and Rosenfeld, 2015), this study developed a lidar-based method to determine the status of cloud coupling over land at a high temporal resolution.

The paper is organized as follows. Section 2 describes the measurements and data. Section 3 describes the new methodology in terms of the definition and implementation. The performance of the method is demonstrated in Sect. 4, and a summary is presented in Sect. 5.

2 Data descriptions

2.1 Radiosonde

RS launches took place at least four times per day at the ARM SGP site, usually at 00:30, 06:30, 12:30, and 18:30 local time (LT). Holdridge et al. (2011) provide technical details about the ARM RS (https://www.arm.gov/capabilities/instruments/sonde, last access: 2 December 2021). In this study, we consistently use daylight saving time (coordinated universal time −5 h) as local time throughout the year to avoid inconsistencies between summer and winter. Besides the routine measurements, there are fewer but still considerable numbers of RS data obtained at other times of the day (e.g., 09:30, 12:00, 13:00, 15:30, and 19:00 LT). These supplemental RS samples at other times comprise ∼ 10 % of the total number of cases. RS data from 06:30–19:00 LT are utilized in this study. The vertical resolution of RS data varies according to the rising rate of the balloon, but measurements are generally taken ∼ 10 m apart. We further vertically average the RS data to achieve a vertical resolution of 5 hPa.

There are several methods to determine PBLH from RS-measured potential temperature (θ), pressure, and humidity profiles. They include, among others, the parcel method (Holzworth, 1964), the gradient methods (Stull, 1988; Seidel et al., 2010), and the Richardson number method (Vogelezang and Holtslag, 1996). After examining the previous methods, Liu and Liang (2010) proposed a different approach to determine the PBLH that is valid under different thermodynamic conditions. The robust performance was demonstrated over the SGP site and in other major field campaign sites around the world (Liu and Liang, 2010). Thus, we adopted this method to calculate PBLH from RS data in this study. By using the water vapor mixing ratio (WVMR), the potential temperature is corrected as the virtual potential temperature, θ_v (θ_v = θ(1+0.61 WVMR)). The virtual potential temperature does not include a correction for the liquid water content profile, as this is challenging to measure in many conditions. Therefore, the virtual potential temperature is not conserved during moist convection. Since we mainly focus on the sub-cloud atmosphere, this is not a serious problem. Moreover, for available datasets, we use scaled RS moisture profiles normalized by the total precipitable water vapor derived from the microwave radiometer (https://www.arm.gov/capabilities/vaps/lssonde, last access: 2 December 2021, Revercomb et al., 2003).

2.2 Micropulse lidar (MPL) system

MPL backscatter profiles were collected at the SGP site from September 1998 to July 2019 with high continuity (Campbell et al., 2002). Technical details and data availability can be found at the website https://www.arm.gov/capabilities/instruments/mpl, last access: 1 December 2021. The backscatter profiles have a vertical resolution of 30 m. MPL signals have an initial temporal resolution of 10–30 s and are averaged every 10 min for this study. Due to the inherent problem of lidar observations, there is a ∼ 0.2 km near-surface blind zone. Following the standard lidar-data processing, background subtraction, signal saturation and overlapping, and after-pulse and range corrections are applied to the raw MPL data (Campbell et al., 2002, 2003). Questionable data are excluded based on the quality-control flags.

2.3 Cloud product

The MPL can be used to detect cloud layers based on signal gradients (Platt et al., 1994). Lidar-based methods are accurate for determining the cloud-base height (CBH) but may miss information about the cloud top due to the signal saturation within an optically thick cloud (Clothiaux et al., 2000). Under this condition, the cloud radar provides a better estimation of the cloud-top height (CTH). In this study, we directly use an existing quality-controlled cloud product, CLDTYPE/ARSCL (https://www.arm.gov/capabilities/vaps/cldtype, last access: 1 December 2021), which combines information from the MPL, ceilometer, and cloud radar to determine the vertical boundaries of clouds (ARM Data Center, 2021; Flynn et al., 2017). For the lowest cloud base, the best estimation from laser-based techniques (i.e., MPL and ceilometer) is used. The original temporal resolution of the CLDTYPE/ARSCL product is 1 min, averaged to a 10 min temporal resolution. To avoid averaging jumps in signal between different clouds, a cloud is considered to be continuous if its base height varies less than 0.25 km between two consecutive profiles.

3 Methodology

3.1 Definition of coupled and decoupled clouds based on thermodynamics

The definition of the state of cloud–surface coupling over land is a critical question. For marine stratocumulus, coupled clouds are identified when the liquid water potential temperature varies less than a certain threshold (i.e., 0.5 K) below the cloud base (Jones et al., 2011). We try to extend the concept of coupling and decoupling to clouds over land. The PBL over land is typically buoyancy driven and controlled by surface fluxes during the daytime. We consider a cloud is in the coupled state when it strongly interacts with the buoyancy fluxes within the PBL.

Figure 1 presents the idealized vertical profiles of virtual potential temperature (θ_v) under the clear sky, coupled cloud, and decoupled cloud. A superadiabatic surface layer exchanges the heat fluxes between the surface and PBL. The outer layer and entrainment zone are turbulently coupled with the surface and, thus, are considered as the coupled regime. Meanwhile, the free atmosphere is considered as the decoupled regime. Theoretically, θ_v is constant in the outer layer and follows the wet adiabatic lapse rate in the cloud layer. Although the profiles of θ_v in the real atmosphere can largely differ from the idealized profiles, the relative position between the cloud layer and capping inversion of entrainment zone is clear. For the coupled cases, the cloud base is below the capping inversion of entrainment zone. For the decoupled cases, the cloud base is above the capping inversion. Based on this feature, we can use the profiles of virtual potential temperature (θ_v) in the sub-cloud layer to determine the coupling state of continental clouds. It should be noted that the virtual potential temperature is not conserved in a moist adiabatic process and thus would decrease within a cloud layer. On the other hand, the liquid potential temperature remains a near-constant within the stratocumulus. Since we use the profiles of potential temperature in the sub-cloud layer to diagnose the cloud coupling, there is no difference in the identification results by using the virtual potential temperature.

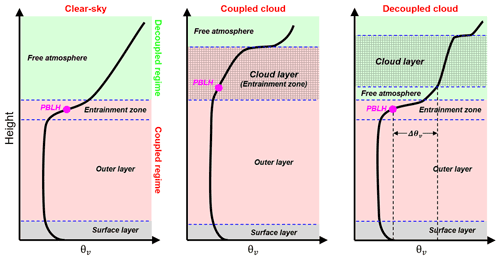
Figure 1 Idealized vertical profiles of virtual potential temperature (θ_v) under the clear sky, coupled cloud, and decoupled cloud over land. The surface layer, outer layer entrainment zone, and free atmosphere are divided by the dashed blue lines. The cloudy layer is marked as the shaded area, and PBLH is marked as the pink point. Red and green zones indicate the coupled and decoupled regime, respectively. Elements (e.g., turbulence, heat fluxes, cloud) in the coupled regime are directly affected by the PBL processes, while these elements are not directly affected by the PBL processes in the decoupled regime. For the coupled cases, the cloud base is below the capping inversion of entrainment zone. For the decoupled cases, the cloud base is above the capping inversion.

Following the previous studies (Jones et al., 2011; Dong et al., 2015), we attempt to use the variations in the potential temperature within the sub-cloud layer to diagnose the cloud coupling. For determining a suitable threshold, we first look at several examples of profiles of θ_v and WVMR from the RS (Fig. 2). If the CBH is lower than the PBLH, the cloud is affected by turbulence and buoyancy fluxes in the PBL, such as the cases shown in Fig. 2a. Note that the PBLH is not an absolute boundary limiting turbulence and buoyancy fluxes. Due to the overshooting of rising air parcels, we use a range to screen the condition of coupled clouds. As shown in Fig. 2b, even when the CBH is slightly above the PBLH, WVMR and θ_v are still relatively consistent between the cloud layer and the PBL and show large step signals at the cloud top.

Figure 2c–d show a clear inversion layer between the cloud base and the PBL top, and the difference in θ_v between the CBH and the PBLH (Δθ_v) is relatively large. Such a notable inversion layer prevents the buoyancy fluxes within the PBL from reaching the cloud base, leading to the decoupling between the cloud and the PBL. Overall, we consider Δθ_v as the key factor to determine cloud coupling. In Fig. 2, Δθ_v for coupled cases (a–c) is −0.32 and 0.31 K, respectively, and Δθ_v for decoupled cases (d–e) is 1.47 and 5.0 K, respectively.

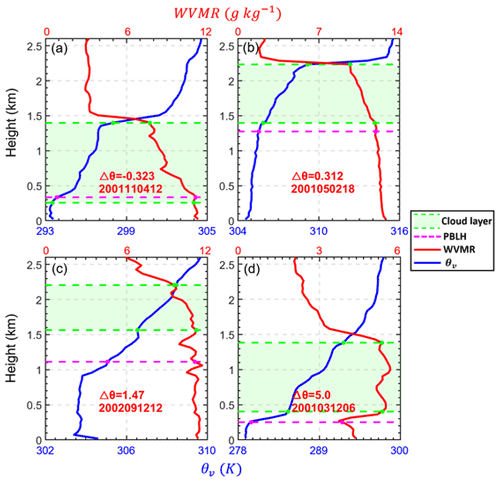
Figure 2 Virtual potential temperature (θ_v, blue lines) and water vapor mixing ratio (WVMR, red lines) profiles from radiosonde (RS) over the Southern Great Plains site for different cases. The differences in virtual potential temperature between the cloud base and the planetary boundary layer (PBL) top are expressed as $\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{v}}({\mathit{\theta }}_{\mathrm{v}}^{\mathrm{CBH}}-{\mathit{\theta }}_{\mathrm{v}}^{\mathrm{PBLH}})$. The time of each radiosonde launch is marked in each panel as “YYYYMMDDHH”, where YYYY, MM, DD, and HH indicate the year, month, day, and local time, respectively. Green regions are cloud layers, and dashed green lines indicate their boundaries. The cloud layer is obtained from the CLDTYPE/ARSCL data. PBLHs is derived from RS data and is marked as dashed pink lines.

Therefore, instead of giving a height range to limit the differences between CBH and PBLH, we consider using the differences in θ_v between CBH and PBLH to determine the threshold for distinguishing coupled and decoupled clouds. For convenience, we use Δθ_v to refer to the difference in θ_v between the CBH and the PBLH ($\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{v}}={\mathit{\theta }}_{\mathrm{v}}^{\mathrm{CBH}}-{\mathit{\theta }}_{\mathrm{v}}^{\mathrm{PBLH}})$. For decoupled cases, the cloud base is above the capping inversion of the entrainment zone. There is a notable inversion in θ_v between PBL top and decoupled cloud base. Thus, we identify the cases satisfying Δθ_v>δ_s as being in a decoupled state. Correspondingly, we identify the cases satisfying Δθ_v<δ_s as being in a coupled state. We set the range of CBH to between 0 and 4 km and excluded cases of deep convection (i.e., CBH < 4 km and CTH > 6.5 km). In the previous studies for marine clouds, the difference in the potential temperature between the CBH and the near surface is used as the criterion (Jones et al., 2011; Dong et al., 2015). However, we use the potential temperature at the PBL top instead of the potential temperature near the surface. This change is due to the relatively complex thermodynamic structure over the land. The large variation in the potential temperature within the surface layer would notably affect the result. Hence, we use the potential temperature above the PBL top to replace those values near the surface.

As the basic framework of PBL, the slab model assumes that θ_v is constant within the PBL (Wallace and Hobbs, 2006). Under this assumption, δ_s can be set as 0. However, there are certain variations in θ_v within the PBL, which can cause inversions with relatively small magnitudes between the cloud base and PBL top. Figure 3a presents the inversion strength in θ_v within PBL during the daytime. Specifically, inversions represent the layers with continuously increased structures of θ_v. For an inversion layer, the inversion strength is calculated as the differences in θ_v between the top and bottom of the layer. The inversions near the surface or across the PBL top are excluded. Besides the capping inversion and surface inversion, the inversion strength within PBL is typically below 1 K. Therefore, we set δ_s as 1 K, which is the same as the criterion for determining stable or convective conditions (Liu and Liang, 2010). Furthermore, we demonstrate the probability density function (PDF) of Δθ_v for the low-cloud cases. Coupled and decoupled clouds are classified by the threshold of δ_s (1 K). Through the development of PBL, boundary layer clouds frequently occur in the entrainment zone and form a coupled cloud–PBL system. For such coupled systems, θ_v at cloud top and PBL top is highly consistent for the majority of cases. Thus, the PDF of Δθ_v shows significantly high values for the range of −2 to 0.5 K in the coupled regime. Meanwhile, the PDF of Δθ_v is evenly distributed in the decoupled regime. Since we only analyze low clouds, the PDF of Δθ_v slowly decreases when Δθ_v is above 10 K.

Based on the variations in θ_v within the PBL, we set δ_s as 1 K. However, it should be noted that it is not an absolute value. A similar threshold of 0.5 K has been used for marine stratocumulus (Jones et al., 2011; Dong et al., 2015). Comparing to the marine condition, θ_v shows greater variabilities over land. Hence, the threshold is correspondingly larger. On the other hand, since the threshold of 1 K is in the low PDF regime (Fig. 3b), the small changes in this value would not notably affect the identifications. Specifically, a 0.1 K difference in δ_s will lead to a 0.5 % difference in the identification of coupled cloud.

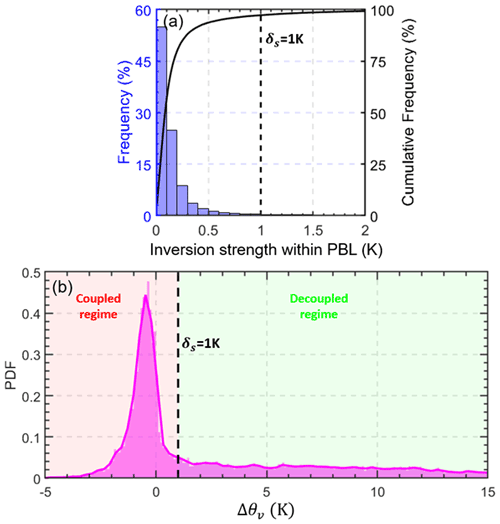
Figure 3 (a) Blue bars represent the inversion strength of θ_v within the PBL. The inversion strength is derived from the radiosonde during daytime (08:00–19:00 LT). The inversions near the surface or across PBL top are excluded. The solid black line represents the cumulative frequency. (b) Pink area represents the probability density function (PDF) of the differences in the virtual potential temperature between cloud-base height (CBH) and PBLH ($\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{v}}={\mathit{\theta }}_{\mathrm{v}}^{\mathrm{CBH}}-{\mathit{\theta }}_{\mathrm{v}}^{\mathrm{PBLH}})$. By using a threshold of Δθ_v<δ_s (1 K), we can identify the coupled cloud regime.

Similar to the previous studies (Jones et al., 2010; Dong et al., 2015; Zheng and Rosenfeld, 2015), we identified the coupled clouds as the thermodynamics coupling between surface and cloud base. However, it is an open question whether the entire cloud layer is coupled for coupled cases. It depends on whether the liquid water potential temperature is conserved within the cloud layer, which represents a moisture adiabatic process. This issue is closely related to the cloud types. In the cloud parameterizations, the entire stratocumulus layer is considered to be well-mixed, while the cumulus-capped layer is usually partially mixed (Lock, 2000). For stratocumulus clouds, the entire cloud layer and PBL are typically fully coupled with surface, when the cloud base is coupled with surface. For the cumulus-capped PBL, the entire cloud layer may not be completely coupled, despite the coupling between cloud base and surface. The well-established parameterizations are supported by many observational studies (e.g., Betts, 1986; Storer et al., 2015; Berkes et al., 2016; de Roode and Wang. 2006; Ott et al., 2009).

3.2 Lidar-based method to identify coupled and decoupled clouds

3.2.1 Method description

Given the rapid change in clouds over land, RS observations have limitations when it comes to tracking cloud development due to the coarse temporal resolution and drifting of the balloon. We thus further developed a lidar-based method to identify the coupled states of clouds based on our new algorithm for retrieving the PBLH that can better track the diurnal variations in PBLH than conventional lidar-based approaches (Su et al., 2020). We adapted this algorithm for retrieving the PBLH and developed a new scheme to deal with cloudy conditions. Following the original method (Su et al., 2020), the rainy cases are eliminated in the quality-control process. The principles behind the PBLH algorithm are stated next for completeness.

Table 1 List of parameters in the flowchart of DTDS (Fig. 4).

Our new PBLH algorithm can retrieve the PBL variability from the MPL under different thermodynamic stability (thus named the DTDS algorithm) conditions, taking into account the vertical coherence and temporal continuity of the PBLH. First, we identify the local maximum positions (LMPs; range: 0.25–4 km) in profiles of the wavelet covariance transform function derived from lidar backscatter (Brooks, 2003). These LMPs are the potential positions of the PBLH. We can use the PBLH derived from morning RS soundings as the starting point. Without morning RS soundings, the algorithm can still work well, with the lowest LMPs selected as the starting point, which reduces by 0.02–0.05 the correlation coefficient between MPL-derived and RS-derived PBLHs (Su et al., 2020).

To ensure good continuity, we select the closest LMP to the earlier position of the PBLH. Different stages of PBL development are considered. DTDS-derived PBLHs likely increase during the growth stage and decrease during the decaying stage, but the algorithm is also able to identify decreases during the growth stage or increases during the decaying stage based on the selection scheme described by Su et al. (2020). There are multiple step signals in the backscatter profiles when complex aerosol structures (e.g., the residual layer) are present, leading to multiple LMPs. Based on temporal continuity, we select the appropriate LMP as the position of the PBL top. However, PBLH retrievals still suffer from relatively low accuracies under stable conditions because of the weak vertical mixing and residual layer.

Clouds induce strong step signals in the lidar backscatter, further considerably affecting PBLH retrievals. Su et al. (2020) only considered cases where the low cloud top coincided with the previous PBL top, excluding other low-cloud cases (> 60 % of all low-cloud cases). Here, we specifically consider coupled and decoupled states of low clouds. Due to the MPL's ∼ 0.2 km blind zone, we only analyze the PBLH and CBH above 0.2 km. Figure 4 presents the flowchart describing the updated DTDS algorithm. In particular, we jointly use PBL development and the LCL to diagnose the states of coupling or decoupling. In ideal situations, LCL, PBLH, and CBH are highly consistent with each other for coupled clouds. But for real conditions, we only require that either the LCL or the PBLH coincides with the CBH for identifying coupled cases, with another parameter serving as an additional constraint. Specifically, a coupled cloud needs to occur within a certain range of LCL and the previous position of the PBL top.

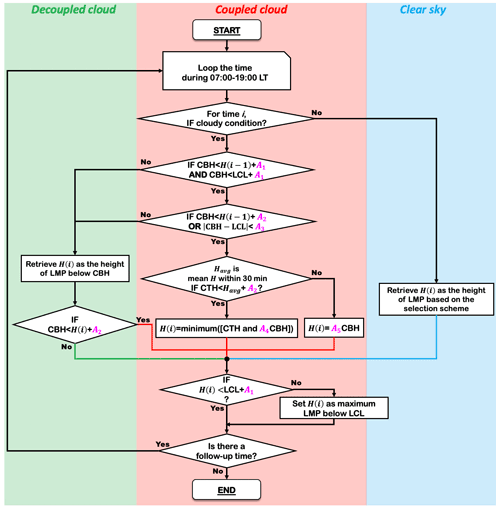
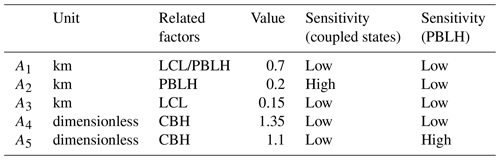
Figure 4 The flowchart of the updated DTDS algorithm. In this diagram, H(i) is the retrieved planetary boundary layer height (PBLH) at time i. CBH and CTH represent the base and top heights, respectively, of the lowest cloud at time i. The PBLH part for selecting the suitable local maximum position (LMP) follows Su et al. (2020), and a detailed scheme for identifying a coupled cloud is added to the DTDS algorithm. LCL stands for lifted condensation level. Five empirical parameters (A₁, A₂, A₃, A₄, and A₅) are set as 0.7, 0.2, 0.15, 1.35, and 1.1, respectively.

For the DTDS algorithm, five empirical parameters are used, including A₁, A₂, A₃, A₄, and A₅. As listed in the Table 1, A₁–A₅ are set as 0.7, 0.2, 0.15, 1.35, and 1.1, respectively. A cloud at time i is identified as being in the coupled state if the CBH is less than [$H(i-\mathrm{1})+\mathrm{0.2}$ km (A₂)] and [LCL +0.7 km (A₁)]. This step moves 39.5 % of low-cloud cases to the category of decoupled clouds. A cloud is also considered to be in a coupled state if the CBH is coincident with the LCL within 0.15 km (A₃), and the CBH is less than [$H(i-\mathrm{1})+\mathrm{0.7}$ km (A₁)], where H(i−1) represents the PBLH at time (i−1). This step further moves 17.8 % of the remaining cases to the category of decoupled clouds.

The LCL is calculated from surface meteorological data (relative humidity, temperature, pressure) at the SGP site based on an exact expression (Romps, 2017). Specifically, Romps (2017) proposed an exact, explicit, analytic expression for LCL as a function of surface meteorology. Compared to the previous approximate expressions, some of which may have an uncertainty in the order of hundreds of meters, the Romps expression can be considered as the precise value. The uncertainty of empirical vapor pressure data may lead to a bias of ∼ 5 m (Romps, 2017), which may be neglected in the analyses.

After determining the coupling or decoupling state of a cloud, we retrieve H(i) (i.e., PBLH at time i) based on the cloud state. For decoupled cases, we use the same strategy for a clear sky to retrieve the PBLH. Based on the selection scheme in the DTDS algorithm, the LMP below the CBH is selected as H(i). For coupled cases, we jointly use CBH and CTH to determine PBLH. During the warm season, active cumulus often occurs in the upper part of the PBL with strong surface heating, so the CBH can be generally regarded as the PBLH (Stull, 1988; Wallace and Hobbs, 2006). Under this condition, the CBH coincides with the previous PBL top. Therefore, if [$\mathrm{CTH}\ge {\mathrm{PBLH}}_{\mathrm{30}\min }+\mathrm{0.2}$ km (A₂)], we set H(i)=A₅CBH, where PBLH_30 min is the average value of the PBLH within 30 min of the prior time i. Hence, A₅ would be a critical parameter for the PBLH estimation. On the other hand, if [$\mathrm{CTH}<{\mathrm{PBLH}}_{\mathrm{30}\min }+\mathrm{0.2}$ km (A₂)], we set H(i) equal to the minimum between CTH and the product A₄ × CBH. This step is designed for thin clouds or some stratiform clouds. In particular, A₅ × CBH can be notably larger than the CTH for a thin cloud. Under this situation, we tend to use CTH to denote the PBL top. This step has little impact on the detection of surface–cloud coupling but can ensure that the CTH of the coupled cloud is always higher than the retrieved PBLH to fit the real situation.

After retrieving H(i), we consider that the cloud above the PBLH is still coupled if [$\mathrm{CBH}<H\left(i\right)+\mathrm{0.2}$ km (A₂)]. Moreover, we added an upper limit for all PBLH retrievals. If [$H\left(i\right)>\mathrm{LCL}+\mathrm{0.7}$ km (A₁)], we adjust H(i) as the maximum LMP below the LCL. The new DTDS method combines lidar measurements and surface meteorological observations and can simultaneously retrieve the PBLH and cloud states.

3.2.2 Selection of empirical parameters

The states of coupling and decoupling are diagnostic parameters rather than explicit expressions. Similar to the other methods for retrieving PBLH (e.g., Brooks, 2003; Liu and Liang, 2010), multiple empirical parameters are used to determine PBLH. Table 1 lists the five empirical parameters in the algorithm. These parameters are related with three factors, including LCL, PBLH, and CBH. The sensitivity to the selection of these parameters is presented. The detailed impacts of variations in these parameters on the retrievals of cloud coupling and PBLH will be discussed in this section.

Note that we used the CTH and A₄ × CBH as the upper limits for PBLH retrievals in the DTDS algorithm. For coupled cases, these two limits are generally close to or above the position of the PBL top. Only 2 % (3 %) of total cases meet the condition that the RS-derived PBLH is 0.25 km higher than the CTH (A₄ × CBH). Section 4 presents the detailed relationships between CBH, CTH, and PBLH. In the DTDS method, CTH serves as the upper limit for PBLH under the condition of coupled shallow cumulus.

Similar to previous studies, we can also use the LCL as the standard to identify coupled clouds (Dong et al., 2015; Zheng and Rosenfeld, 2015). We assume a cloud is coupled if |CBH-LCL|<Δh. By using ∼ 7500 RS profiles, the cloud coupling state derived from the virtual potential temperature method (Sect. 3.1) is considered as the ground truth for evaluation. Figure 5a shows the commission errors and omission errors for different criteria. Here, the commission error is calculated as the percentage of decoupled clouds misidentified as coupled clouds. The commission error can also be called a “false positive”, as the former is a common term for describing the nature of an error in identification. The omission error is calculated as the percentage of coupled clouds that have not been identified under this criterion. By using the LCL, we can obtain a relatively low commission error if the criterion is less than 0.15 km and a relatively low omission error if the criterion is greater than 0.7 km. Thus, we set A₁ and A₃ as 0.7 and 0.15 in the DTDS method to exclude and to select cases of coupled clouds. We can also use the RS-derived PBLH as the criterion (Fig. 5b).

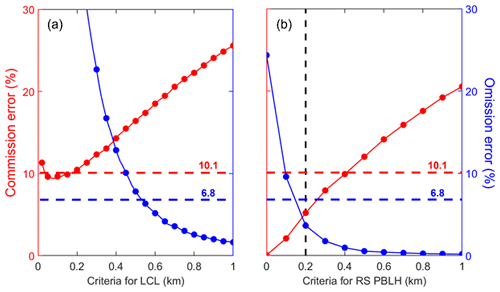
Figure 5 Commission errors and omission errors of coupled cloud identifications (a) for different criteria for the lifted condensation level (LCL) and (b) for different criteria for the planetary boundary layer height (PBLH). “Criteria for LCL” means coupled clouds are identified if |CBH−LCL| < criteria for LCL. Similarly, “Criteria for RS PBLH” means coupled clouds are identified if CBH − RS PBLH < criteria for RS PBLH. The dashed red and blue lines indicate the commission and omission errors, respectively, for the DTDS algorithm. CBH stands for cloud-base height, and RS stands for radiosonde. By using ∼ 7500 RS profiles, the cloud coupling state derived from the virtual potential temperature method (Sect. 3.1) is considered as the ground truth for evaluation.

Despite the coarse temporal resolution, the RS-derived PBLH can be a good criterion to use to distinguish between coupling and decoupling. If we consider a coupled cloud as a cloud where CBH < RS-derived PBLH + 0.2 km, both commission and omission errors are ∼ 5 %. Therefore, we primarily use [PBLH + 0.2 km (A₂)] in the DTDS method to identify coupled and decoupled regimes. As cloud can considerably affect with lidar backscattering and generate large signal variations, we jointly use lidar backscattering, the previous position of PBL top, and LCL to determine the surface–cloud coupling and PBLH. In particular, the LCL constraint in the algorithm notably reduces the absolute biases in PBLH retrievals under cloudy conditions by 9.3 %.

Moreover, we test the sensitivity of selecting these empirical parameters. Figure 6 presents the commission errors and omission errors in the identifications of coupled clouds for selecting different values of empirical parameters. Among these parameters, A₂ is the critical one, which would notably affect the identification results. In general, A₂ determines the maximum differences between PBLH and CBH for coupled cases. If [CBH − PBLH > A₂], we consider the cloud is under the decoupled state. Thus, the identification method is quite sensitive to A₂. Selecting a low value of A₂ would neglect many coupled cases, which leads to a high omission error. Meanwhile, selecting a high value of A₂ would misclassify many coupled cases, which leads to a high commission error. After a trail and error, A₂ is set as 0.2 km to balance the omission and commission errors. The selections for other parameters are not sensitive for the coupled cloud identifications. We can choose them from a reasonable range.

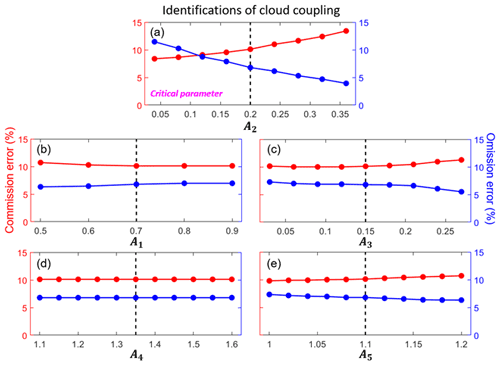
Figure 6 Commission errors (red line) and omission errors (blue line) of coupled cloud identifications for selecting different values of empirical parameters (A₁, A₂, A₃, A₄, A₅) in the DTDS algorithm. Dashed black lines indicate the default values. For each test, one parameter is variable, while other parameters are set as default values. For identifications of cloud coupling, A₂ is the critical parameter.

As a by-product of this method, we also pay attention to the PBLH retrievals under cloudy conditions. Figure 7 presents the mean absolute biases and correlation coefficients between PBLH derived from lidar and radiosonde for selecting different values of empirical parameters. To match the scope of this study, we only analyze the low-cloud conditions. For retrieving PBLH under cloudy conditions, A₂ is the critical parameter. The variations in correlation coefficients under different values of empirical parameters are small with a range of 0.81–0.82. However, the absolute biases can considerably differ under different values of A₅. In general, A₅ represents the ratio between CBH and PBLH under coupled conditions. If A₅ is above 1.1, PBLH retrievals under cloudy conditions are overestimated. We set A₅ as 1.1 to achieve a relatively low bias and a relatively high correlation coefficient at the same time. For other parameters, the selections from reasonable ranges would not notably affect the PBLH retrievals.

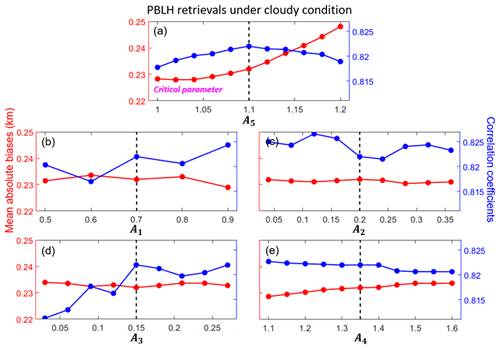
Figure 7 Red lines indicate the mean absolute biases between PBLH derived from lidar and radiosonde for selecting different values of empirical parameters (A₁, A₂, A₃, A₄, A₅) in the DTDS algorithm. Here, we only analyze the low-cloud cases. Blue lines indicate the corresponding correlation coefficients between PBLH derived from lidar and radiosonde. Dashed black lines indicate the default values. For each test, one parameter is variable, while other parameters are set as default values. For PBLH retrievals under cloudy conditions, A₅ is the critical parameter.

In short, selections of these empirical parameters are based on the overall relationship between cloud and PBL under the coupled and decoupled states. In our method, the selection of A₂ is critical for the identifications of coupled clouds, while the selection of A₅ is critical for the PBLH retrievals under cloudy conditions. The selections of other parameters are not sensitive.

4 Results

Figure 8 illustrates four examples of PBLH retrievals and cloud states derived from the DTDS algorithm for 27 October 2011, 31 July 2002, 19 March 2000, and 1 May 2012. Figure 8a depicts coupled shallow cumulus occurring at noontime at the PBL top. With a weak surface flux of ∼ 200 W m⁻², this shallow cumulus cloud appeared for less than an hour. Figure 8b shows a developed coupled cumulus cloud. With a strong surface flux of ∼ 500 W m⁻², this coupled cloud continuously developed during the daytime. Figure 8c presents the case of a daylong coupled cloud. After the passage of a frontal system that day, stratocumulus occurred during the morning with a cloud thickness of 0.5 km. Through the development of the PBL, the thick stratocumulus cloud was broken up by the strong turbulences, transforming into shallow cumulus clouds. Figure 8d shows the case of an active coupled cloud, which is generally associated with a large amount of convective available potential energy. Even though coupled clouds can differ in appearance and variability throughout the day, the common feature is the coherent variation between the cloud base and the PBL top. The LCL is a relevant parameter and can differ from the PBLH and the CBH for some coupled cases (e.g., Fig. 8b–c).

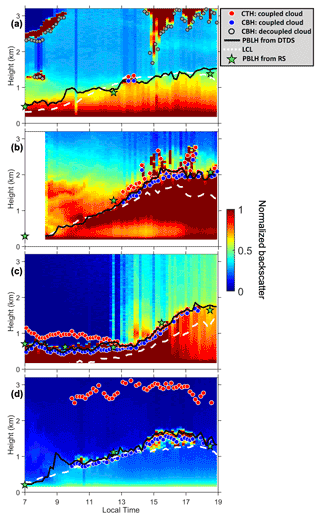
Figure 8 Daily backscatter profiles: (a) short-lived coupled cloud, (b) developed coupled cloud, (c) daylong coupled cloud, and (d) active coupled cloud. Backscatter is normalized to a range of 0–1 in arbitrary units. Red dots and blue dots indicate cloud-top heights (CTHs) and cloud-base heights (CBHs) of coupled clouds. Grey dots mark CBHs for decoupled clouds. Black lines and green stars mark the planetary boundary layer height (PBLH) retrieved from the DTDS algorithm and from radiosonde (RS) soundings, respectively. Dashed white lines represent lifted condensation levels (LCLs).

The identification accuracy, or disparity between different methods, is evaluated in terms of the selected criteria, for which the identification method based on Δθ_v is regarded as the “truth”, as described in Sect. 3.1. Hereafter, all results are analyzed for the period of 10:00–19:00 LT, so early-morning data are not used. The commission error is 10.1 %, and the omission error is 6.8 % for the DTDS method. Note that lidar-based PBLH methods generally suffer from relatively low accuracy under stable atmospheric conditions. Following Liu and Liang (2010), we identified stable PBLs from RS measurements. Since coupled clouds are driven by relatively strong buoyancy fluxes, only 1 % of total cases of coupled clouds occurred under stable PBL conditions during the study period (07:00–19:00 LT). Therefore, the relatively low accuracy for stable PBLs is not a major problem in this study.

Figure 5 also compares the accuracy between the DTDS and LCL methods. Based on the LCL alone, we cannot choose an appropriate criterion to achieve a lower commission error and omission error simultaneously. Thus, we do not use the LCL as the single standard to detect the coupling and decoupling of low clouds in our study. As diagnostic parameters, different methods inevitably produce different results regarding coupling and decoupling. Although we consider the method based on Δθ_v as the standard, it still suffers from uncertainties arising from balloon drifting. From this perspective, it is hard to conclude which method is the best. Since it determines the PBLH based on aerosol backscattering, the lidar-based method may be more representative of the coupling between a cloud and the aerosol layer near the surface when clear skies occur, at least during a short window of time.

Figure 9a–b present the occurrence frequencies of the CBH and the CTH at different heights. Despite the same variation ranges, clouds are mostly coupled if the CBH is lower than 1 km, while decoupled clouds dominate if the CBH is higher than 3 km. Figure 9c–d show the changes in the coupled fraction (ratio of coupled cases to total cases) with different CBHs and CTHs. The coupled fraction is about 90 % if the CBH is lower than 1 km and decreases to 2 % for CBHs above 3 km. Although the CBHs for coupled cases are generally less than 3 km, CTHs for coupled cases can be much higher. Coupled clouds still account for around 10 % of the cases with CTHs above 6 km.

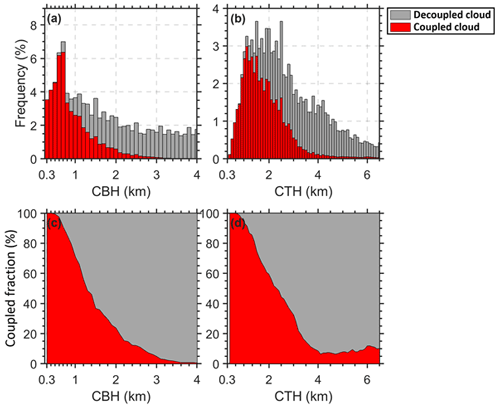
Figure 9 The height-dependent occurrence frequencies of (a) the cloud-base height (CBH) and (b) the cloud-top height (CTH) for coupled clouds (red bars) and decoupled clouds (grey bars). The relative occurrence frequencies of (c) the CBH and (d) the CTH for coupled clouds (red area) and decoupled clouds (grey area).

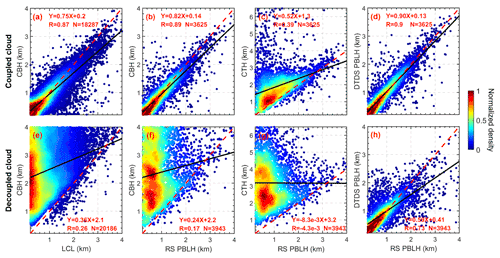
Figure 10 The relationships between (a) LCL and CBH, (b) CBH and RS-derived PBLH, (c) CTH and RS-derived PBLH for coupled clouds, and (d) DTDS-derived PBLH and RS-derived PBLH. Panels (e)–(h) are similar to panels (a)–(d) but for decoupled clouds. Black lines represent the linear regressions. The linear fitting functions, correlation coefficients (R), and sampling numbers (N) are given in each panel.

Figure 10 shows scatter plots between CBH, CTH, PBLH, and LCL for coupled and decoupled clouds. For coupled clouds, there is a generally strong correlation between CBH, LCL, and PBLH, contrary to the weak relationships of decoupled cases. The relationship between CTH and RS-derived PBLH is complicated. For shallow cumulus clouds, their tops can be considered as PBL tops for the coupled state, while the cloud top is considerably above the position of the PBL top for active cumulus clouds. We also note that the accuracy of CTH retrievals is generally lower than the accuracy of CBH retrievals (Clothiaux et al., 2000). As CTH is not a criterion for cloud coupling, the accuracy of CTH would not affect the identification of coupled cloud but may affect the PBLH retrievals for the coupled cloud cases. Meanwhile, despite the laser-based detection of CBH being considered the standard method (Platt et al., 1994; Clothiaux et al., 2000; Lim et al., 2019), the CBH retrievals from ceilometer or lidar still bear some uncertainties, which can potentially lead to a mean bias of 0.1 km (Silber et al., 2018). In our method, a systematic increase of 0.1 km in the CBH can lead to an increase of 2.1 % in omission errors and a decrease of 1 % in commission errors.

After identifying the coupling state of clouds, it is feasible to retrieve the PBLH under cloudy conditions. In particular, the DTDS-derived PBLH needs to resort to the cloud position for coupled cloud cases. For decoupled cloud cases, on the other hand, the PBLH below clouds is sought to avoid cloud interference. For coupled clouds, DTDS-derived PBLHs show a strong correlation with RS-derived PBLHs with a correlation coefficient (R) of ∼ 0.9 (Fig. 10d). For decoupled cases, the correlation between DTDS-derived PBLHs and RS-derived PBLHs is generally good (R=0.73) but worse than the correlation for coupled cases (Fig. 10h). As pointed out in previous studies (Chu et al., 2019; Hageli et al., 2000; Lewis et al., 2013; Su et al., 2017b), it has been a persistent problem to retrieve the PBLH under cloudy conditions since the strong backscattering and step signals from cloud interference would be excluded to avoid interfering with the retrievals. The PBLH determined by our method under a cloudy condition is much more reasonable. Moreover, due to the different definitions of the PBLH and aerosol stratification within the PBL, there are always considerable differences between lidar- and RS-derived PBLHs, which cannot be eliminated by a specific algorithm (Chu et al., 2019; Su et al., 2020).

5 Summary

In this study, we proposed a novel method for distinguishing between coupled and decoupled low clouds over land. Based on the understanding of PBL processes and quantitative analyses, we developed a lidar-based method (DTDS) to identify the coupling state of low clouds over the SGP site. In practice, we identified a coupled cloud when the position of the cloud base was generally close to or lower than the previous position of the PBL top, with the LCL serving as an additional restriction. Compared to using the LCL alone, the coupled states identified by the DTDS method show better consistency with the results derived from radiosondes, with about 10 % differences between the lidar-based retrievals and radiosonde results.

Not only the coupled state but also the PBLH under cloudy conditions is retrieved by the method. A long-lasting problem with lidar retrieval of PBLH is either incapability of retrieval or large uncertainties induced by the occurrence of low clouds (e.g., Chu et al., 2019; Hageli et al., 2000; Lewis et al., 2013); we address this issue by separately considering the coupled and decoupled state of low clouds. Specifically, in coupled conditions, the position of the coupled cloud serves as a good reference for identifying the PBLH. In decoupled conditions, the large backscatter and step signals from clouds would be excluded to avoid interfering with the retrievals. With our method, cloudy conditions are well handled.

With the new method, we study the difference of cloud–PBL interactions in coupled and decoupled conditions. In contrast to the sensitive responses of coupled clouds to changes in the PBLH and buoyancy, the decoupled clouds and the PBLH are weakly related. Due to their different relationships with the PBL, a robust differentiation between the coupled and decoupled low clouds is critical for further investigating the coupled land–atmosphere system and aerosol–cloud interactions. Our methodology paves a solid ground for such pursuits.