Responses of CIPS/AIM noctilucent clouds to the interplanetary magnetic field

This study investigates the link between the interplanetary magnetic field (IMF) B_y component and the noctilucent clouds (NLCs) measured by the Cloud Imaging and Particle Size (CIPS) experiment onboard the Aeronomy of Ice in the Mesosphere (AIM) satellite. The mean ice particle radius in NLCs is found to be positively correlated with IMF B_y in the Southern Hemisphere (SH) and negatively correlated with IMF B_y in the Northern Hemisphere (NH), respectively, on a day-to-day timescale in most of the 20 summer seasons during the 2007–2017 period with a near 0 d lag time, and the response in the SH is stronger than that in the NH. Moreover, the albedo, ice water content and frequency of occurrence of NLCs present positive correlation with IMF B_y in the SH but no significant correlation in the NH. The superposed epoch analysis (SEA) further indicates the r_m on average changes by about 0.73 nm after IMF B_y reversals, which is significant at the 90 % confidence level in Monte Carlo sensitivity tests. Our results suggest an IMF B_y-driven pathway: the influence of the solar wind on the polar ionospheric electric potential affects the nucleation processes in NLCs and consequently the ice particle radius and NLC brightness.

1 Introduction

1.1 NLCs

The noctilucent clouds (NLCs), also known as polar mesospheric clouds (PMCs), are the highest and coldest clouds in the terrestrial atmosphere, forming in the high-latitude summer mesosphere at ∼83 km altitude, where the temperature can drop to ∼140 K or lower. The long-term trends in NLCs are thought to be associated with global climate change. NLCs are susceptible to perturbations from lower-atmospheric activities such as gravity waves (Gao et al., 2018) and planetary waves (France et al., 2018). NLCs are strongly influenced by both solar and lunar tides, with diurnal and semidiurnal variations observed in the NLC properties (Fiedler and Baumgarten, 2018; Stevens et al., 2017; von Savigny et al., 2017). NLCs can also be affected by solar activities on various timescales, including solar proton events (Bardeen et al., 2016; Winkler et al., 2012), the 27 d solar rotation (Robert et al., 2010; Thomas et al., 2015; Thurairajah et al., 2017) and the 11-year solar cycle (Dalin et al., 2018; DeLand and Thomas, 2019; Hervig et al., 2019). To distinguish the contribution of solar activity to polar mesospheric clouds from that of climate change, it is important to clarify the mechanisms of the solar influence on NLCs. Based on the observed modest anti-correlation in NLCs with the 27 d and 11-year solar variations, both photodissociation and dynamic origins have been proposed in which the solar ultraviolet irradiance as characterized by the Lyman alpha (Ly-α) index is supposed to play a key role by altering the water vapor and temperature in the NLC region (Dalin et al., 2018; Thomas et al., 2015), while in general the exact mechanism is still unclear. In this paper, the interplanetary magnetic field (IMF) B_y rather than the Ly-α is applied as the solar activity index to explore the solar wind–NLC link, and new hypotheses are discussed in the next section.

1.2 IMF B_y-related mechanisms for NLC–solar link

The main IMF B_y-related process is the change in ionospheric potential in polar cap regions, which determines the flow of the regional downward ionosphere–earth current density J_Z. The current flow is part of the global atmospheric electric circuit (GEC), with ionospheric potential being ∼250 kV positive relative to earth's surface, maintained by the global thunderstorms and electrified clouds (Slyunyaev et al., 2019; Williams and Mareev, 2014). The earth experiences a Lorentz electric field applied by the cross-product of solar wind magnetic field and velocity, which is mainly northward (southward) for positive (negative) IMF B_y, and observations have shown that the IMF B_y-dependent daily averaged perturbation of ionospheric potential ranges from −30 to 30 kV at high geomagnetic latitudes and is opposite in the SH and NH (Tinsley and Heelis, 1993).

A possible link may exist between the solar wind B_y variations and polar surface meteorology through the ionospheric potential, which has been supported by a variety of observations, in terms of polar surface pressure (Lam et al., 2013), geopotential height (Lam et al., 2014), temperature (Freeman and Lam, 2019; Lam et al., 2018) and below-cloud irradiance (Frederick et al., 2019; Frederick and Tinsley, 2018; Tinsley et al., 2021). It should be noted that these observations are characterized by two features: the responses in the SH and NH are opposite, in line with the opposite IMF B_y-induced ionospheric potential in the SH and NH; the delay time is short, lasting only a few days or less. A hypothesis has been proposed to explain the above observations: firstly, solar wind B_y induces changes in the ionospheric electric potential, as well as the downward current density J_Z in the GEC; secondly, the microphysical processes inside clouds are sufficiently sensitive to space charge generated by J_Z so that the cloud properties such as infrared opacity and albedo will consequently be affected. Finally, polar surface meteorology will be influenced by cloud radiative forcing (Lam and Tinsley, 2016). The invoked cloud microphysical changes have been detailed for individual aerosol–droplet collisions (Zhang et al., 2018, 2019; Zhang and Tinsley, 2017, 2018), but direct measurements in clouds and modeling are required to test this hypothesis.

In comparison with the tropospheric clouds within which many factors are involved, the polar mesospheric clouds provide a relatively pure scenario to study the role played by electric charges in the microphysical process of clouds. By extending the above “solar–GEC–cloud microphysics–tropospheric meteorology” hypothesis, it is straightforward to propose the “IMF B_y–ionospheric potential–NLC microphysics–NLC brightness” hypothesis for the polar mesospheric clouds: IMF B_y induces changes in polar ionospheric potential, which will modulate the charge distribution on meteoric smoke particles (MSPs) with major implications for the nucleation rate and ice particle formation processes in NLCs and ultimately affect the macroscopic properties of NLCs.

1.3 Nucleation processes in NLCs

The formation of ice particles in NLCs is still not well understood, as a variety of factors are involved in the microphysical process, among which the nucleate rate and number density of ice nuclei contribute the most important uncertainties (Rapp and Thomas, 2006). Although the homogeneous nucleation has been considered feasible (Murray and Jensen, 2010), the extreme conditions required make the homogeneous nucleation unlikely to occur at the typical mesospheric supersaturation level (Tanaka et al., 2022). The heterogeneous nucleation instead is thought to be more effective by providing pre-existing ice nuclei, for which candidates such as ion clusters, soot, sulfate aerosols and meteoric smoke particles have been proposed (Rapp and Thomas, 2006). MSPs are abundant in the mesosphere and considered to be most likely; evidence that ice particles contain small numbers of MSPs has been provided by observations (Hervig et al., 2012). The exact nucleation process of MSPs is still poorly known, due to the lack of laboratory measurements at the mesospheric condition.

The MSPs are generated by meteor ablation in the upper mesosphere and lower thermosphere, with the radius ranging from sub-nanometer to nanometer size. The 2-D simulations involving the middle-atmospheric circulation revealed that the MSPs will move upward along with the strong updrafts in the summer mesosphere and are then transported to winter mesosphere by the meridional winds and finally sink down into the stratosphere by the downwelling (Megner et al., 2008a, b). The global mass redistribution of MSPs results in a pronounced reduction in MSP concentration and lifetime in the summer mesosphere, and thus the conventional idea of nucleation on MSPs is challenged.

The above dilemma can be resolved when the charged MSPs are taken into consideration because the MSPs' charge can effectively reduce the critical radius of ice nuclei at low temperature, allowing the charged MSPs to act as ice nuclei (Gumbel and Megner, 2009; Megner and Gumbel, 2009). It should be noted that the galactic cosmic rays can generate continuous ions throughout the atmosphere, and the charged molecular clusters are found to grow much faster than neutral clusters. The so-called ion-mediated nucleation (IMN) is of great important for the formation of cloud condensation nuclei in the atmosphere and has been studied for decades (Yu and Turco, 2000; Yu et al., 2008). The distribution of charges on MSPs becomes important with regards to the above assumption, while the efficiency of MSPs collecting electrons in the mesosphere is still unclear. Because the mobility of electrons is much greater than that of positive ions, negative charging is supposed to be dominant in the upper mesosphere, and rocket-borne measurements show that about 10 % of MSPs are negatively charged (Plane et al., 2014; Robertson et al., 2014). The NLCs are located in the D-region ionosphere, where the electric environment is sensitive to disturbances from solar winds. This provides a possible way through which solar activity may impact the NLCs through an electrically related mechanism.

The Cloud Imaging and Particle Size (CIPS) experiment onboard the Aeronomy of Ice in the Mesosphere (AIM) satellite began observing the NLCs in 2007, and 20-summer-season data in the SH and NH from 2007 to 2017 are available now. Therefore, we investigated the hypothetical IMF B_y-driven solar–NLC link in this study. The paper is structured as follows: Sect. 2 provides a brief description of the CIPS data and solar wind data. Section 3 presents the results of NLC correlation with IMF B_y during the 20 NLC seasons on the day-to-day scale, as well as the superposed epoch analysis for NLCs' response to IMF B_y reversals. Section 4 discusses the results, and Sect. 5 summarizes our main conclusions.

2 Data

2.1 CIPS/AIM data

The AIM satellite was launched on 25 April 2007 to a sun-synchronous polar orbit whose local time is mainly midday–midnight at high-latitude regions. The CIPS experiment onboard AIM comprises a panoramic UV nadir imager, consisting of four cameras operating at 265 nm, with a field of view of $\mathrm{120}{}^{\circ }\times \mathrm{80}{}^{\circ }$ and a horizontal spatial resolution of 5 km×5 km. This platform observes the scattered radiance from NLCs and images the NLCs of the ∼40–85^∘ latitude zone for the summer hemisphere ∼15 times per day. The CIPS has provided NLC data from the 2007 summer season until now, in terms of ice particle radius, albedo and ice water content (IWC), and detailed descriptions of the CIPS data products, calibration, retrieval algorithms, and retrieval uncertainties have been published (Carstens et al., 2013; Lumpe et al., 2013). The CIPS level 2 orbit data provide rectangular images of NLC properties for each of the 15 orbit strips per day, in which a single pixel represents a 25 km² (5 km×5 km) area anywhere on the globe, and a 5800 km×1000 km strip region is covered; thus the cloud cover as well as the frequency of occurrence (FO) of NLCs can be obtained by counting the number of pixels showing them in the images. This study applied the version 5.20 CIPS polar mesospheric cloud level 2 data to investigate the response of NLCs to solar variations during 10 NLC seasons (from 2007 to 2016) in the NH and 10 NLC seasons (from 2007/2008 to 2016/2017) in the SH.

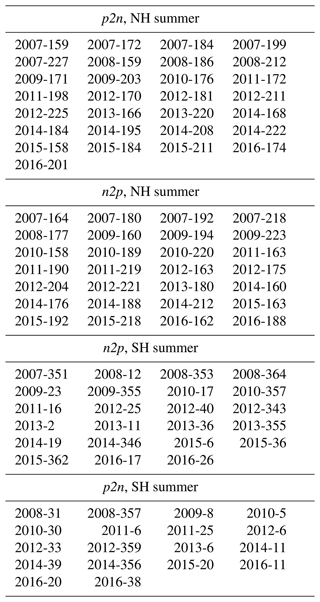
Table 1 Dates (year-day of year) of p2n and n2p IMF B_y reversals during 2007 and 2017 in NH and SH summer.

Figure 1 Daily averaged IMF B_y, mean ice particle radius (r_m), mean albedo (Alb_m), mean ice water content (IWC_m) and cloud cover observed by CIPS for the NH (a, c, e, g, i) and SH (b, d, f, h, j) for each of the NLC seasons from 2007 through 2017.

2.2 Solar wind data

The solar wind B_y data in geocentric solar magnetospheric (GSM) format were downloaded online from the GSFC/SPDF OMNI web interface (https://omniweb.gsfc.nasa.gov/form/dx1.html, last access: 25 FEbruary 2022). In the GSM coordinate system, the origin is located at the center of the earth; X points towards the sun; Z lies in the plane of the X and geomagnetic dipole and is perpendicular to X (roughly northward); and Y completes the right-hand coordinate system, stretching toward the dusk. The solar wind structures are fairly complex, varying from two-sector to four-sector and sometimes irregularly; therefore, during a 27 d solar rotation period, the IMF B_y can reverse two or four or more times, unlike other solar indexes such as Ly-α or F10.7, which show a regular 27 d period. In order to apply the widely used superposed epoch analysis (SEA) method, the key days of B_y reversals are listed in Table 1, which have been selected to ensure that during the 5 d period before and after the key day there are no NLC data missed and that the direction of IMF B_y is relatively stable. The IMF B_y changing from positive to negative (from negative to positive) is denoted by p2n (n2p). Four groups of dates during 2007 and 2017 are listed in Table 1, corresponding to the n2p (28 cases) and p2n (29 cases) reversals during NH summer and the n2p (23 cases) and p2n (18 cases) reversals during SH summer, respectively.

3 Results

3.1 Correlation analysis of day-to-day responses of NLCs to IMF B_y

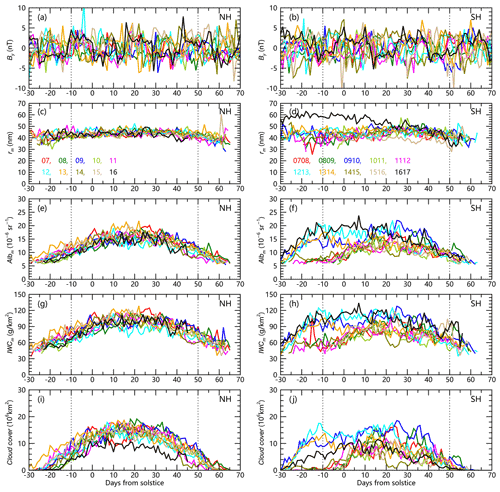
Figure 1 shows the variations in the daily averaged solar wind magnetic field and NLC properties during the NLC seasons from 2007 through 2017. The daily averaged IMF B_y varies between −5 and 5 nT, as shown in Fig. 1a and b, and the periods of IMF B_y variations are complex, as noted above. Figure 1c–h show the intensity of NLCs in terms of mean ice particle radius (r_m), mean albedo (Alb_m) and mean ice water content (IWC_m), while Fig. 1i and j show the cloud cover of NLCs, as calculated by counting of pixels, which is linearly proportional to FO. In order to diminish noise, the NLC data in the latitude bands 65–85^∘ are used because the NLCs are rarely observed by CIPS below 65^∘ latitude, and an albedo threshold of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ sr⁻¹ was applied. The intensity and coverage of NLC peak ∼20 d after the solstice and show strong seasonal variations, with the exception of the mean ice particle radius, r_m.

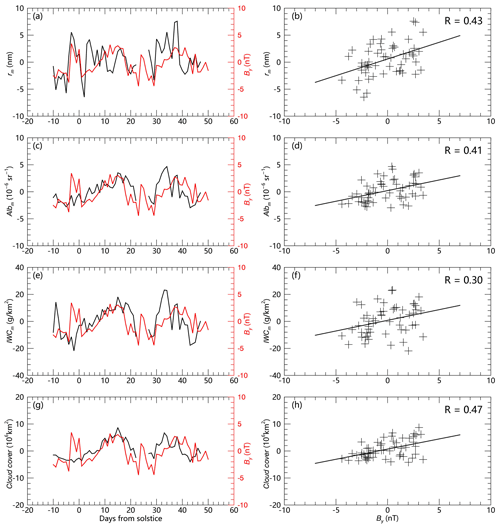
Figure 2 The left panels (a, c, e, g) show the relationships of the daily IMF B_y (red curves) with the anomaly of mean ice particle radius (r_m), mean albedo (Alb_m), mean ice water content (IWC_m) and cloud cover in the 2008/2009 NLC season for the SH. The anomaly of NLC data is obtained by removing the 40 d running mean. The right panels (b, d, f, h) present the correlation coefficients between the daily IMF B_y and the anomaly of NLC characters.

Figure 2 (left) shows the relationship between daily IMF B_y with the NLC intensity and covers the anomaly in the 65–85^∘ latitude zone for the 2008/2009 season in the SH, with the anomaly obtained by removing the 40 d running mean. The corresponding correlation coefficients are present in the right panel, indicating a clear positive relationship between the NLC brightness and the B_y component of solar wind magnetic fields in the SH. Figure 3 further shows the correlation coefficients of NLC intensity and coverage anomaly in the 65–85^∘ latitude zone with IMF B_y for each of the 20 summertime seasons, from 2007 to 2016 in the NH and from 2007/2008 to 2016/2017 in the SH. To remove the seasonal variation, the solar signals are extracted by subtracting the 40 d smoothed CIPS data. To avoid the no-cloud days, only the CIPS data during the period of 10 d before and 50 d after the solstice day are used (Fig. 1). The link between the anomalous mean ice particle radius r_m with IMF B_y is conspicuous, with positive correlation coefficients in all of the SH summer seasons and negative correlations in most of the NH summer seasons (Fig. 3a). These opposite responses in the SH and NH are consistent with the opposite ionospheric potential changes in the SH and NH caused by IMF B_y. Further, the response was stronger in the SH, with the correlation coefficient being about twice that in the NH. In NLCs, the larger the ice particle size is, the greater the albedo and IWC are; namely, the mean ice particle radius is normally positively correlated with the albedo and IWC (Lumpe et al., 2013), and the 20-season CIPS data show a correlation coefficient of ∼0.52 between r_m and Alb_m and of ∼0.35 for r_m and IWC_m. Conversely, the cloud cover of NLCs will also change in pace with the formation and growth process of ice particle radius, and the 20-season CIPS data also show a correlation coefficient of ∼0.48 between r_m and FO. It is thus reasonable to speculate that the albedo, IWC and FO will respond to IMF B_y in concert with ice particle radius, and Fig. 3b–d show that the correlation coefficients between the anomaly of Alb_m, IWC_m and FO with IMF B_y are pronounced in the SH, but not in the NH.

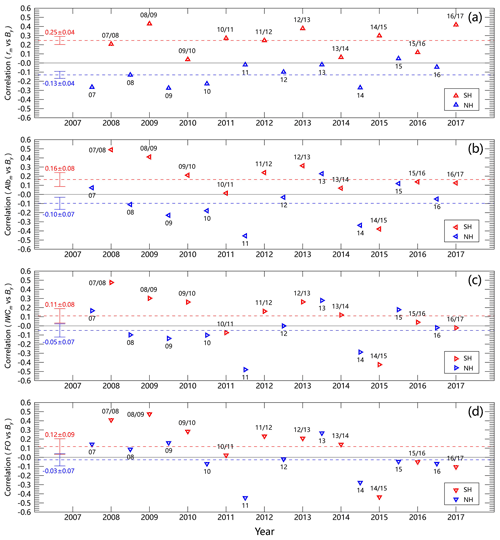
Figure 3 Correlation coefficients between the anomaly of r_m, Alb_m, IWC_m and IMF B_y from 2007 to 2017, with red and blue symbols representing the seasonal correlation coefficients and dashed red and blue lines illustrating the mean correlation coefficients for the SH and NH, respectively.

We have also tried to roughly estimate the column number density of ice particles, N_ice, based on the CIPS data of IWC and ice particle radius r. Assuming the mass of ice particle m_ice to be ${\mathit{\rho }}_{\text{ice}}\mathrm{4}\mathit{\pi }{r}^{\mathrm{3}}/\mathrm{3}$, where ρ_ice=0.92 g cm⁻³, the ice particle concentration N_ice will be approximately equal to the ice water content divided by the mass of the ice particle, $\text{IWC}/m_{\text{ice}}$. It is of great interest to study the correlation of ice particle concentration with IMF B_y, since it can reveal the microphysical process during the NLCs' responses to solar wind magnetic fields. The results show that the correlation coefficient between ice particle concentration with IMF B_y is −0.14 ± 0.06 in the SH and 0.09 ± 0.04 in the NH, which are surprisingly opposite to that of r_m and IWC_m shown in Fig. 3. In the dry NLC region, ice particles compete for the limited water vapor, resulting in an anticorrelation between the ice particle concentration and ice particle radius, which have been verified by observation and simulation (Hervig et al., 2009; Wilms et al., 2016). Our above results support this anticorrelation again, implying that the solar wind may firstly increase or decrease the nucleate rate and ice particle number density in NLCs, then decrease or increase the ice particle radius.

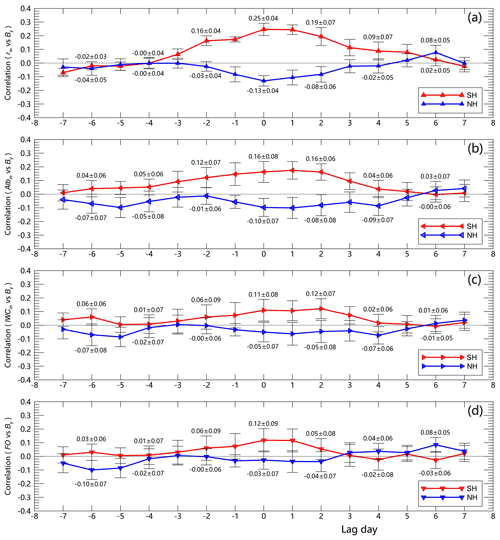
Figure 4 Correlation coefficients between the anomaly of r_m, Alb_m, IWC_m and IMF B_y for time lags varying from −7 to 7 d, with red and blue lines representing the mean correlation coefficients and error bars illustrating the standard deviation of the mean for the SH and NH, respectively.

NLCs are dominantly influenced by the solar tides with the diurnal variation, and the NLC occurrences are usually more frequent at the local time of morning (Fiedler and Baumgarten, 2018; Stevens et al., 2017). In addition, the NLCs can also be affected by the lunar tides, and the longitudinal variations in NLCs attributed to the non-migrating lunar tides have been found (Liu et al., 2016; von Savigny et al., 2017). To check whether the local time differences between the descending and ascending branches of the AIM satellite will affect the results in Fig. 3, we separate the CIPS data of the descending and ascending branches into two groups. Similarly, in order to check the longitudinal variations, the CIPS data are divided into two groups in terms of the longitude ranges of $(-\mathrm{180}{}^{\circ },\mathrm{0}{}^{\circ })$ and $(\mathrm{0}{}^{\circ },\mathrm{180}{}^{\circ })$. The correlation coefficients for the above two scenarios have been calculated and listed in Table 2, and the results for all of them are consistent with the results shown in Fig. 3. In summary, the correlation coefficients are found to not be affected by the local time variations and longitudinal variations in the CIPS data caused by the tide effects. This further proves that our results are robust.

Table 2 The correlation coefficients of NLC properties with IMF B_y under different selections of satellite branches and longitudinal ranges for CIPS data.

Furthermore, Fig. 4 shows the mean correlation coefficients for time lags varying from −7 to 7 d. The error bars illustrate the standard deviation of the mean, which is calculated from the 10 seasonal correlation coefficients and is also given in Fig. 3 at 0 d lag time. A very short delay time was observed (Fig. 4), with the maximum correlations occurring near 0 d, implying a microphysical response in NLCs to IMF B_y similar to the short delay time that has also been observed in the solar–troposphere studies. In previous studies of the link between Ly-α and NLCs, the proposed mechanisms involving photodissociation, heating or circulation all required longer time. The photodissociation process accounts for a negative correlation for the H₂O in the mesosphere and the 27 d solar irradiance variations, with a phase lag of about 6–7 d, which can be attributed to the lifetime of H₂O at those altitudes (Shapiro et al., 2012). Satellite observations showed the time lag for the water response 27 d solar rotation of about 0–3 d and for the temperature response of about 0–8 d, depending on altitudes, and the time lag between NLC property variations and solar Ly-α ranges from 0 to 3 d in the NH and from 6 to 7 d in the SH, depending on instruments and properties (Thomas et al., 2015; Thurairajah et al., 2017). In contrast, the IMF B_y-related processes of ionospheric potential changes respond quickly to solar wind magnetic field reversals. In summary, the nearly zero lag time of NLC properties responding to IMF B_y variations implies a mechanism of electrodynamic origin rather than thermodynamic origin.

In order to further verify the response of NLCs to solar wind at different latitudes, the approaches in Fig. 3 were repeated for the five latitude bands of 80–85, 75–80, 70–75, 65–70 and 60–65^∘, respectively. The correlation coefficients of the anomaly of NLC properties with IMF B_y are shown in Fig. 5, and the slope of the anomaly of NLC properties versus IMF B_y is given in Fig. 6. Figures 5a and 6a show that in the SH, the correlation and sensitivity of ice particle radius r_m to IMF B_y are both greater at higher latitudes, in agreement with the ionospheric potential perturbations caused by IMF B_y changes, while in the NH the correlation and sensitivity are just about half of that in the SH but still significant at latitudes higher than 65^∘. For the 60–65^∘ latitude region, the results are not significant; this may be because at lower latitudes the IMF B_y-induced processes are too weak and because the rare NLC occurrences at lower latitudes entail weaker signal-to-noise ratio. Figures 5b–d and 6b–d show that the responses of the anomaly of Alb_m, IWC_m and FO to IMF B_y are noticeable for high latitudes in the SH and obvious for Alb_m only at latitudes higher than 75^∘ in the NH but are not obvious for IWC_m and FO in the NH. Dividing the slope given in Fig. 6 by the yearly averaged NLC properties in 65–85^∘ latitude bands, the relative slope can be obtained: (0.71 % ± 0.16 %) nT⁻¹ in the SH and (−0.28 % ± 0.08 %) nT⁻¹ in the NH for r_m, (1.36 % ± 0.59 %) nT⁻¹ in the SH and (−0.52 % ± 0.32 %) nT⁻¹ in the NH for Alb_m, (0.74 % ± 0.48 %) nT⁻¹ in the SH and (−0.26 % ± 0.28 %) nT⁻¹ in the NH for IWC_m and (2.28 % ± 1.73 %) nT⁻¹ in the SH and (−0.38 % ± 0.60 %) nT⁻¹ in the NH for FO. In consideration of the ∼5 nT amplitude of IMF B_y variation during solar wind reversals, the responses of NLC intensity and coverage to IMF B_y are not negligible. The correlation coefficient of ice particle column number density N_ice with IMF B_y can also be obtained for different latitudes varying from 85 to 60^∘: −0.14 ± 0.06, −0.13 ± 0.05, −0.09 ± 0.03, −0.03 ± 0.04 and −0.004 ± 0.07 in the SH and 0.06 ± 0.05, 0.09 ± 0.05, 0.12 ± 0.04, 0.04 ± 0.04 and 0.01 ± 0.04 in the NH. Again, the correlation coefficient of ice particle concentration with solar wind magnetic field is opposite to that of mean ice particle radius and ice water content. However, it should be noted that due to the detection threshold of the CIPS instrument for ice particles with radii greater than 10–15 nm, the variation in the invisible smaller ice particles' concentration is unknown.

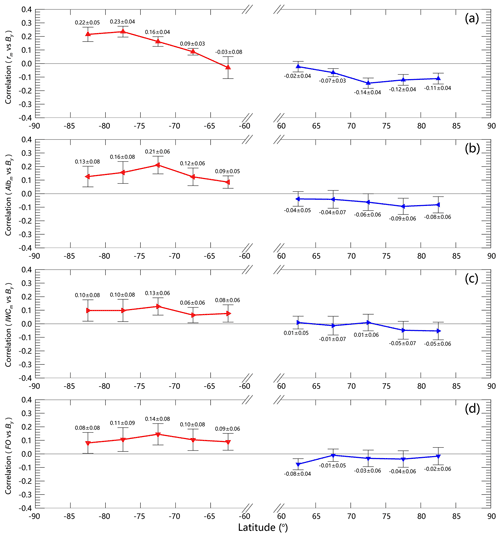
Figure 5 Correlation coefficients between the anomaly of r_m, Alb_m, IWC_m and IMF B_y at different latitude bands, with red and blue lines representing the mean correlation coefficients and error bars illustrating the standard deviation of the mean for the SH and NH, respectively.

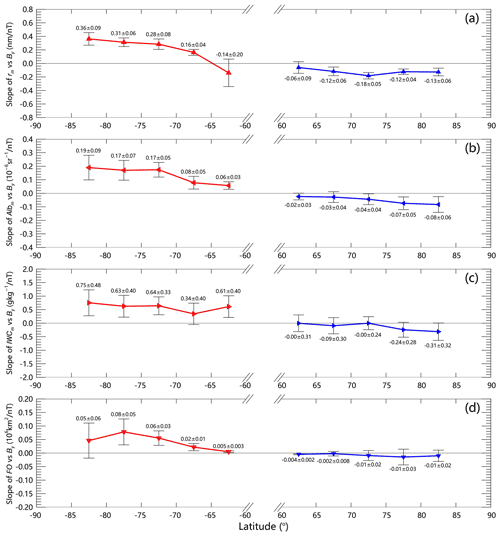
Figure 6 Slope of the anomaly of r_m, Alb_m and IWC_m versus IMF B_y at different latitude bands, with red and blue lines representing the mean slope and error bars illustrating the standard deviation of the mean for the SH and NH, respectively.

In addition, other solar wind parameters such as IMF B_z, A_p index and Ly-α irradiance have also been examined by the same processes; however, no correlations were found for them at 0 d lag time. The solar wind magnetic field line has an Archimedes spiral pattern (i.e., IMF B_x is negatively proportional to IMF B_y), and a correlation coefficient of about −0.67 between them was obtained during the period of 2007 to 2017; thus similar correlations also exist between IMF B_x and NLC properties, but with the opposite sign. The IMF B_z corresponds to a dawn–dusk solar wind electric field and thus can generate a dawn–dusk ionospheric potential drop for both hemispheres, while the sun-synchronous orbit of AIM is designed to be midday–midnight with a rare opportunity to pass the dawn–dusk regions; thus the zero correlations with IMF B_z observed for NLCs are just as expected.

3.2 Superposed epochs for NLCs' response to IMF B_y reversals

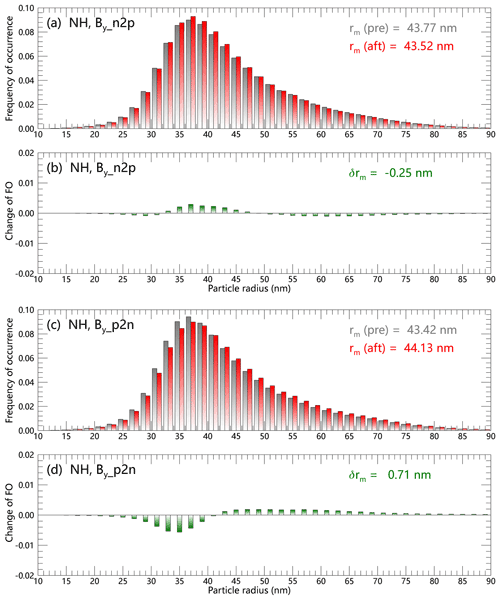
The superposed epoch analysis is frequently applied in the studies of atmospheric responses to short-term solar variations, in which solar signals are more obvious and easier to be extracted than for decadal or longer-term variations. Although the NLCs only occur in summer, during the 20-season period of CIPS data enough IMF B_y reversal cases have been accumulated, as listed in Table 1, allowing the SEA method to be used to explore the NLCs' responses. In the SEA method, the ice particle radius distribution is denoted by f(r), where the distribution is of the values of r over the array of pixels on a given day. The averages of f(r) during 3 d before and 3 d after the key day are denoted by f_3-pre and f_3-aft, respectively, then the changes in ice particle radius distribution δf during IMF B_y reversals are given by $\mathit{\delta }f=f_{\text{3-aft}}-f_{\text{3-pre}}$. The results of δf for the n2p and p2n IMF B_y reversals in the SH given in Table 1 are illustrated in Fig. 7, with an albedo threshold of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ sr⁻¹. The mean ice particle radius r_m can be calculated by integrating the product of the radius and its distribution, $r_{\mathrm{m}}=\sum rf\left(r\right)$; thus the changes in r_m during IMF B_y reversals are obtained by $\mathit{\delta }{r}_{\mathrm{m}}=r_{\mathrm{m},\text{3\_aft}}-r_{\mathrm{m},\text{3\_pre}}=\sum r\mathit{\delta }f$, and the values of δr_m are given in each panel of Fig. 7. For n2p and p2n IMF B_y reversals, the polar ionospheric electric potential will increase or decrease in the SH, and the r_m increases (decreases) by about 0.88 nm (1.07 nm) in the SH, as shown in Fig. 7. Similarly, the results of the NH are illustrated in Fig. 8. For n2p and p2n IMF B_y reversals, the polar ionospheric electric potential will decrease or increase in the NH, and the r_m decreases (increases) by about 0.25 nm (0.71 nm) in the NH, as shown in Fig. 8. Generally, the ice particle average radius changes by about 0.73 nm during IMF B_y reversals, and the responses in the SH are stronger than those in the NH. The results in Figs. 7 and 8 were subject to Monte Carlo sensitivity tests, in which the same number of key days as in Table 1 were randomly generated, and δr_m can be calculated by SEA. By repeating this process 1000 times, the distribution of δr_m is obtained, showing that the results in Figs. 7 and 8 are significant at the 90 % confidence level.

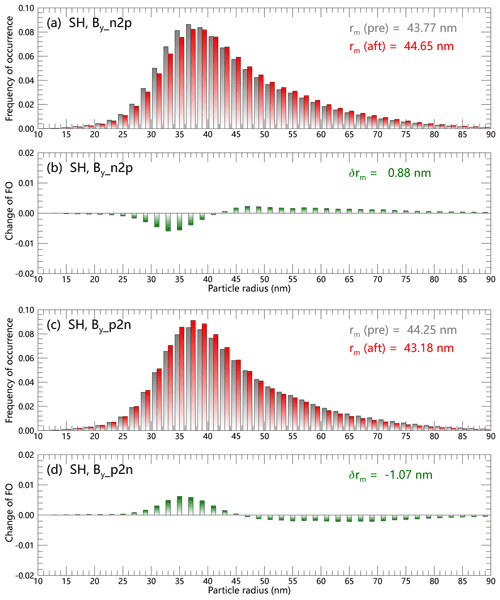
Figure 7 Changes in ice particle radius distribution δf(r) during n2p and p2n IMF B_y reversals in the Southern Hemisphere. The distributions of r over all pixels 3 d before (after) the key days are indicated by the gray (red) bars, and the changes between them are shown by the green bars.

Figure 8 Similar to Fig. 7, but for the results of the Northern Hemisphere.

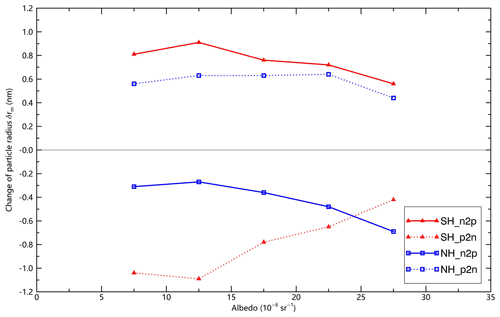
In addition, we also investigate the responses of NLCs to IMF B_y reversals for different brightness of noctilucent clouds. The NLCs were placed into five groups according to albedo: 5–$\mathrm{10}\times {\mathrm{10}}^{-\mathrm{6}}$, 10–$\mathrm{15}\times {\mathrm{10}}^{-\mathrm{6}}$, 15–$\mathrm{20}\times {\mathrm{10}}^{-\mathrm{6}}$, 20–$\mathrm{25}\times {\mathrm{10}}^{-\mathrm{6}}$ and 25–$\mathrm{30}\times {\mathrm{10}}^{-\mathrm{6}}$ sr⁻¹, respectively. It should be noted that the NLCs with albedo less than $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ sr⁻¹ are viewed as noise, and the proportion of NLCs with albedo greater than $\mathrm{30}\times {\mathrm{10}}^{-\mathrm{6}}$ sr⁻¹ is negligible. Figure 9 shows that for varying NLC albedos, the particle radius r_m changes during IMF B_y reversals are consistent with the results in Figs. 7 and 8, verifying that both the dark and the light NLCs are sensitive to IMF B_y reversals. On the other hand, the NLCs with greater albedo usually have greater mean ice particle radius; thus the results in Fig. 9 also indicate that both the small and large ice particles are sensitive to IMF B_y reversals. In addition, the results in Fig. 9 also support the idea that the responses of NLCs to IMF B_y are stronger in the SH than that in the NH.

Figure 9 The influences of IMF B_y reversals on the ice particle radius changes δr_m at different NLC brightness.

4 Discussion

Our results support the existence of a link between NLCs and solar wind magnetic fields, characterized by the two features of opposite responses in the SH and NH in conjunction with a short lag time of 1 d at most, similar to the previously introduced solar–troposphere link. The “IMF B_y–ionospheric potential–NLC microphysics–NLC brightness” hypothesis can be applied to explain the IMF B_y-driven solar–NLC link: IMF B_y will firstly change the ionospheric potential as well as the downward electric current J_Z in polar regions and subsequently change the fraction of negatively charged MSPs and the nucleation processes in NLCs; finally the ice particle radius, ice particle concentration, IWC and albedo will be affected.

As introduced in Sect. 1.2, the increase in IMF B_y will cause the ionospheric potential as well as the ionosphere–earth current density J_Z in the polar cap to increase (decrease) in the SH (NH). The downward atmospheric current density J_Z is of great interest in the studies of tropospheric clouds, since positive (negative) space charges can be induced at the cloud top (bottom) boundaries, which has been verified by in situ observations (Nicoll and Harrison, 2016). As the electric current flows through cloud boundaries, due to the changes in conductivity, gradients of electric field are created, requiring the formation of space charges according to Gauss's law (Zhou and Tinsley, 2007, 2012). The NLCs are located in the D-region ionosphere, where the ionization and conductivity are caused by solar radiation and thus increase with altitude. Similarly, net positive space charges will be accumulated in the NLC region as the downward current J_Z flows through. Moreover, as the ionization varies nearly exponentially with altitude in the D-region ionosphere, the gradient of electric field is larger at lower altitudes. As a result, the number of net space charges accumulated in the bottom of NLCs or lower will be larger than in the upper region of NLCs. Given that the ionization rate of the D-region ionosphere depends on solar radiation, the effect of IMF B_y on the ionization rate as well as positive ion concentration should be negligible; thus the net positive space charges are mainly generated by the reduction in electrons.

The MSPs are dominatingly negatively charged because electrons are easier to collect by MSPs as compared to positive ions, consistent with rocket-borne measurements (Plane et al., 2014; Robertson et al., 2014). In consideration of the fact that the net positive space charges induced by the downward current J_Z will reduce the concentration of electrons, a reduction in negatively charged MSPs is also required. And due to the exponential changes in conductivity, the number of negatively charged MSPs in the bottom of NLCs or lower will decrease more significantly than that in the upper region of NLCs. Upward vertical winds are dominant in the summer mesosphere and are able to carry the MSPs at the bottom of NLCs or lower to pass through the supersaturation region. As mentioned above, the reduction in negatively charged MSPs at lower altitudes is larger than that at higher altitudes, and the effect of current J_Z on the nucleation processes of NLCs through the negatively charged MSPs may be further amplified by the upward winds.

As introduced in Sect. 1.3, the critical radius of ice nuclei for the negatively charged MSPs is smaller than that of the neutral MSPs and will decrease to nearly zero at extremely low temperature. Based on the assumption that the charged MSPs are more efficient than neutral MSPs to form ice nuclei, the concentration of negatively charged MSPs will play an important role in the nucleation rate in NLCs. In addition, studies show that the decrease in nucleation rate will reduce the ice particle concentration, and given the limited amount of water vapor, larger ice particles will be yielded, and brighter NLC will be observed (Wilms et al., 2016).

Our results can be explained in the following pathway: when the IMF B_y increases, the ionospheric potential and the downward current J_Z will increase in the SH, and the net positive space charges increase, requiring a reduction in the number density of negatively charged MSPs in the NLC region. Therefore, the nucleation rate dominated by the negatively charged MSPs will decrease, and fewer ice particles will be formed. Due to the limited amount of water vapor, the mean particle radius will be larger, and characters such as the albedo, IWC and cloud occurrence will increase. Conversely, the response of the downward current J_Z to IMF B_y in the NH is opposite to that of the SH; thus the NLCs in the NH change in an opposite way to that of the SH.

Polar mesosphere summer echoes (PMSEs) are very strong radar echoes scattered by the electron-number-density irregularities at the polar summer mesopause altitudes of about 75–100 km, and the electron structures are thought to be caused by the neutral air turbulence in combination with the charged ice aerosol particles in the NLCs (Rapp and Lübken, 2004). Note that the NLCs are absent in the winter hemisphere, whereas polar mesosphere winter echoes (PMWEs) were still observed at much lower altitudes of 55–85 km. PMWEs are suggested to be caused by the neutral air turbulence together with the charged MSPs (Strelnikov et al., 2021). A possible link is expected to exist between PMSEs and PMWEs with IMF B_y for two reasons: first, the PMSE is sensitive to ice particle radius and concentration, due to the fact that ice particles can affect the diffusion of electrons (Rapp and Lübken, 2004). Our results show that the ice particle radius is sensitive to solar wind; thus it is necessary to check whether this response has further influence on the PMSE. Second, as mentioned in the above microphysical process, the IMF B_y is supposed to have a major effect on the charging process of the MSPs, and the latter plays a more direct role in PMSEs and PMWEs. In brief, investigating the response of PMSEs and PMWEs to IMF B_y will be helpful for understanding the link between solar wind and the mesosphere, while the relevant work is beyond the scope of this paper.

In conclusion, our results suggest a new possible explanation for the link between solar activity and NLCs. The IMF B_y-related mechanisms are concerned more about the microphysical process of ice nuclei formation, namely, the charging of MSPs and its influence on nucleation rate, while the Ly-α-related mechanism focuses more on the photodissociation, heat and dynamic processes, which will affect IWC with a longer time lag. Unlike the Ly-α irradiance, which has a regular 27 d period as well as an 11-year period, the IMF B_y varies in a more complex way; thus its effect on NLCs, as in the correlations, is not just the 27 d period. To better understand the effect of solar activity on NLCs at different lags, periods and latitudes, the IMF B_y and Ly-α should both be considered in future works.

5 Conclusion

The responses of NLCs to solar wind magnetic fields were investigated using the CIPS/AIM data. Our findings suggest that such a solar–NLC link exists. The mean ice particle radius in NLCs was positively (negatively) correlated with the IMF B_y in the SH (NH) on the day-to-day timescale in the majority of NLC seasons during the period of 2007–2017, with a short lag time of 1 d at most. The correlation and sensitivity of r_m versus IMF B_y were stronger in the SH, about twice that in the NH, and more conspicuous at higher latitudes. Similar responses of albedo, IWC and FO in NLCs with IMF B_y were also noticeable in the SH but not obvious in the NH. The superposed epoch analysis provides further insights into the mean ice particle radius responses during n2p and p2n IMF B_y reversals in the SH and NH, and results show that the r_m changes on average by about 0.73 nm following IMF B_y reversals, which is significant at the 90 % confidence level in the Monte Carlo sensitivity tests. The solar–NLC links are interpreted from the perspective of an IMF B_y-driven mechanism: opposite ionospheric electric potential changes in the SH and NH are induced by the IMF B_y, which will change the downward current density J_Z flowing through the NLC region and thus influence the charging of MSPs. Given that the negatively charged MSPs play an important role in the nucleation processes in NLCs, the ice particle radius as well as the brightness of NLCs will be affected. However, it is necessary to further understand the underlying processes of NLCs proposed in the above mechanism and to implement and verify them in polar mesospheric cloud modeling.