The influence of surface charge on the coalescence of ice and dust particles in the mesosphere and lower thermosphere

Agglomeration of charged ice and dust particles in the mesosphere and lower thermosphere is studied using a classical electrostatic approach, which is extended to capture the induced polarisation of surface charge. Collision outcomes are predicted whilst varying the particle size, charge, dielectric constant, relative kinetic energy, collision geometry and the coefficient of restitution. In addition to Coulomb forces acting on particles of opposite charge, instances of attraction between particles of the same sign of charge are discussed. These attractive forces are governed by the polarisation of surface charge and can be strong at very small separation distances. In the mesosphere and lower thermosphere, these interactions could also contribute to the formation of stable aggregates and contamination of ice particles through collisions with meteoric smoke particles.

1 Introduction

A significant fraction of the cosmic dust and meteoroid material that hits the Earth remains in the atmosphere for extended periods of time and is a source of solid dust particles, denoted as meteoric smoke particles (MSPs) (Megner et al., 2006; Rapp et al., 2012). MSPs are formed by an ablation process, whereby meteoroids colliding with atmospheric particles experience strong deceleration and are heated to evaporation temperatures. Meteoric and atmospheric species form an expanding column of partially ionised gas behind the meteoroid, which is observed as a meteor (see, e.g., Mann et al., 2011). Part of the meteoroid material vaporises, and the released small solid particles and gaseous species are incorporated into the atmosphere where they grow further to form MSPs (see, e.g., Megner et al., 2006; Brooke et al., 2017). The coalescence or condensation mechanisms leading to dust agglomerates is considered to be an important aspect of atmospheric physics and chemistry. A better understanding of these mechanisms could help to establish the significance of particles containing refractory materials that are present in the upper mesosphere and lower thermosphere, in short, the mesosphere and lower thermosphere (MLT) region of 60 to 130 km. These small solid particles could also play a role in the formation of ice clouds by providing a core for heterogeneous condensation that is more effective than homogeneous nucleation. During summer, at high and mid latitudes, the temperature near the mesopause reaches a minimum and can fall below the freezing point of water (Lübken, 1999), and clouds of ice particles, polar mesospheric clouds (PMCs), can form at heights of 80 to 85 km (Hervig et al., 2001). These are also observed from Earth after sunset and are known as noctilucent clouds (NLCs). Because NLCs may be an indicator of climate change (Lübken et al., 2018), it is important to understand the possible role of meteoric smoke in the coalescence of ice particles, although the growth of the meteoric smoke is an interesting topic of research in itself.

Models of coagulation (Megner et al., 2006; Bardeen et al., 2008; Brooke et al., 2017) take into consideration the convection of dust particles in global atmospheric circulation, the influence of gravitational force and the Brownian motion. The models also assume that particles stick together after a collision, which is not always the case. The outcome can depend on the relative velocity of the colliding particles and the elasticity of a collision as defined by the coefficient of restitution, which can vary according to the composition of a particle. Dust charging, which can cause particles to experience either strong attractive or repulsive forces, could also play a role in the growth process. This consideration has not previously been included in modelling the collisional dust growth in the MLT but has been studied for droplets in tropospheric clouds (Zhang et al., 2019).

In this paper, we investigate the influence of surface charge on the particle agglomeration processes. We apply models that are developed to describe electrostatic interactions between charged dielectric spheres and are based on solutions presented by Bichoutskaia et al. (2010) and Filippov et al. (2019). These theories predict collision outcomes according to the variables of particle size, charge, dielectric constant, relative kinetic energy, collision geometry and the coefficient of restitution. The presence of negative, positive and neutral particles in the MLT region implies that Coulomb forces between oppositely charged objects are the main attractive component of any electrostatically driven dust agglomeration process. However, in addition to the strong attractive interaction between oppositely charged particles, attractive interactions between particles of the same sign of charge can also take place at small separation distances, leading to the formation of stable aggregates. This attractive force is governed by the polarisation of surface charge, leading to regions of negative and positive surface charge density close to the point of contact between colliding particles (Stace et al., 2011). The strength of the resulting attractive electrostatic force depends on the particle composition, as the value of the dielectric constant determines the extent of polarisation of the bound surface charge. Previously, the model has successfully explained the effects of like-charge attraction in a range of coalescence processes such as the agglomeration of single particles and small clusters derived from a metal oxide composite (Lindgren et al., 2018b), aerosol growth in the atmosphere of Titan (Lindgren et al., 2017) and the self-assembly behaviour of charged micro-colloids (Naderi Mehr et al., 2020). Interactions between pairs of neutral and charged particles also depend on the polarisation of surface charge, but these take place in the absence of a Coulomb barrier (see below). In atmospheric science, the method of image charges is routinely used to study collision outcomes if particles can be approximated by conducting spheres (or having the dielectric constant greater than 80). The image charge model can also be applied to study qualitatively the interaction between dielectric particles if the value of the image charge is corrected as $q^{\prime }=\frac{{\mathit{ϵ}}_{\mathrm{1}}-{\mathit{ϵ}}_{\mathrm{2}}}{{\mathit{ϵ}}_{\mathrm{1}}+{\mathit{ϵ}}_{\mathrm{2}}}q$, where ϵ₁ and ϵ₂ are the dielectric constants, q^′ is image charge, and q is real charge (Jackson, 1999). In contrast, quantitatively accurate theoretical studies of interacting dielectric spheres began only quite recently.

Table 1 Common particulates found in the MLT region which are considered in this study.

The focus of this work is on aggregation processes relevant to mesospheric conditions and, in particular, at high latitudes. The MLT region offers unique conditions in terms of the electrostatic environment, composition and physical parameters such as temperature and pressure. The pressure at 60 km is less than 1 hPa and decreases further with increasing altitude; therefore, particles interact essentially in a vacuum, and consequently, in these simulations the dielectric constant of the surrounding medium is taken to be 1. To investigate the growth of meteoric smoke particles, we consider charged and neutral metal oxides particles with radii ranging from 0.2 to 5 nm, as shown in Table 1. To simulate the growth of ice onto the meteoric smoke, we examine the interactions between metal oxide particulates and large ice particles ranging in size from 10 to 100 nm and with charges 0 to −5e. As these particles typically possess a low charge (or single charge arising, for example, from either a photoionisation event that removes a single electron from a molecule on the particle or the attachment of an ambient air ion) the charge distribution is best represented by a point free charge residing on the surface. For this case, we have extended the numerical method developed in Lindgren et al. (2018a) to allow for description of particle charge in the form of point charge(s) residing on its surface, similar to a solution proposed in Filippov et al. (2019) but based on a numerical method. Comparisons with a uniform distribution of free surface charge, as described in Bichoutskaia et al. (2010), shows that, for particles with radii greater than 10 nm, the choice of a specific form of surface charge distribution does not affect the calculated electrostatic energy between particles; however, the difference does become important for sub-nanometre particles.

The remaining parts of the paper are organised as follows. In Sect. 2, we describe the ionospheric dusty plasma in the region where we study dust growth. In Sect. 3, the range of relative velocities for collisions leading to aggregation is calculated for all collision scenarios that are considered suitable to describe the interactions between ice and dust particles in the mesosphere. These velocity ranges are subsequently used to calculate the percentage aggregation outcome. The orientational geometry of the collisions is discussed, and a quantitative estimation of the electrostatic interaction energy profile is presented for collisions between like-charged particles. Section 4 focuses on specific cases of aggregation between like-charged dust and ice particles, and Sect. 5 deals with aggregation between small charged dust particulates. A brief discussion of the results is provided separately in Sect. 6.

2 Ionospheric dusty plasma conditions

The MLT overlaps with the D-region ionosphere, where the major ionisation process under quiet conditions above 80 km is due to solar radiation and geo-coronal UV radiation, and galactic cosmic rays become an important source of ionisation below 80 km. At high latitudes, where ice clouds can form, the precipitation of high-energy electrons and protons that form in the Sun–magnetosphere interactions and enter the ionosphere during geo-magnetically perturbed conditions promote further ionisation. This increases the ionisation rate by up to several orders of magnitude (Gumbel et al., 2003).

The dust particles in the MLT are, hence, embedded in a low-pressure atmosphere with a small but highly variable degree of ionisation. They collect and emit electrons and ions and some of the dust particles acquire a net equilibrium surface charge in a balance when the currents of incoming and outgoing charged particles are equal. The number density of plasma particles is variable. The impact of photons causes photoelectron emission and the detachment of electrons from negatively charged dust. Photoionising solar X-ray, extreme UV (EUV) and UV fluxes can be variable, and other sources of ionising radiation include aurora and geo-corona, as well as elves and sprites formed in the atmosphere (Barrington-Leigh et al., 2001). The dust number density is of a similar order as that of the free electrons and ions; all particles with charge collectively form a dusty plasma. In model calculations, the dust charge has been simulated by taking into account the capture of plasma particles, photo detachment and photoionisation (Baumann et al., 2013, 2015). The time to reach equilibrium charge varies from around 100 s in quiet conditions to less than 1 s in a meteor (Mann et al., 2011, 2019).

Different assumptions have been made regarding the composition of particles. Hervig et al. (2012) describe the polar mesospheric cloud particles that are observed with extinction measurements as a mixture of ice and meteoric smoke and suggest wüstite and magnesiowüstite as possible smoke materials. To simulate dust conditions in the laboratory, Plane et al. (2015) consider olivine and pyroxene and Duft et al. (2019) iron silicate. A number of laboratory experiments and ion chemistry considerations could also constrain expected MSP dust composition, revealing that FeO and MgO are rapidly oxidised by O₃ and O₂ and recombine with H₂O and CO₂ (Plane et al., 2015). Hence, the existence of these oxides as pure particles is unlikely. Bearing this in mind, we chose our sample materials mentioned above as analogues for materials with different dielectric constants. There has been no successful analysis made so far of the composition of collected MSPs, which is because of difficulties in the collection process and because of different sources of contamination (Hedin et al., 2014). Rapp et al. (2012) used in situ rocket observations to constrain the work function of the MSP material and to infer Fe and Mg hydroxides as possible initial compounds from that. Robertson et al. (2009) pointed out that rocket measurements of dust particles using charge detection can be misinterpreted when there are approximately equal numbers of positively and negatively charged MSPs; they also point out the importance of charge interactions for understanding the coagulation process.

3 Collision dynamics

Temperatures close to the mesopause at high latitudes fall during summer to the range of 130 to 150 K; however, observational studies have shown this to be variable (Lübken, 1999). Such low temperatures have a significant effect on the nature of water droplets, as according to the appropriate phase diagram (Journaux et al., 2020; Hudait and Molinero, 2016), ice particles are in a soft ice state and may absorb some of the kinetic energy present during a collision. This possibility has implications for the outcome of all collisions between small metal oxide particulates and ice particles, which, at short separation distances, can exhibit a strong attraction, even when both particles have a charge of the same sign (Bichoutskaia et al., 2010). However, for like-charged particles with low velocities, this attractive region is largely inaccessible due to the presence of a large repulsive Coulomb energy barrier (E_Coul) which prevents their aggregation. In addition to the Coulomb barrier, other factors affect aggregation during a collision; these include the binding energy as defined by the interaction energy at the point of contact (E₀), the coefficient of restitution (k_r), the Maxwell–Boltzmann distribution of particle velocities at a defined temperature and the composition of colliding particles (as defined by the dielectric constant and particle density).

The total kinetic energy of a system containing two colliding particles is the sum of the relative kinetic energy with respect to the centre of mass (K_rel), and the kinetic energy of the centre of mass (K_cm) is as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }{K}_{\text{tot}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\mu }{v}_{\text{rel}}^{\mathrm{2}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}M{v}_{\text{cm}}^{\mathrm{2}},\end{array}$$

where $\mathit{\mu }=\frac{m_{\mathrm{1}}{m}_{\mathrm{2}}}{m_{\mathrm{1}}+m_{\mathrm{2}}}$ is the reduced mass of the colliding particles, $M=m_{\mathrm{1}}+m_{\mathrm{2}}$, $v_{\text{rel}}=v_{\mathrm{1}}-v_{\mathrm{2}}$, and $v_{\text{cm}}=\frac{\sum m_j{v}_j}{M}$ ($j=\mathrm{1},\mathrm{2}$). The kinetic energy of the centre of mass is unaffected by changes in the inter-particle interaction energy; however, due to the law of conservation of energy, the loss or gain of electrostatic interaction energy between the colliding particles leads to corresponding changes in the relative kinetic energy. At the point where the electrostatic interaction energy is at the maximum (E_Coul), the relative kinetic energy of the colliding pair is at the minimum. Once over the barrier and immediately before the collision the kinetic energy is at its highest, i.e. $K_{\text{rel}}^{\text{before}}=K_{\text{rel}}^{\text{initial}}-E_{\mathrm{0}}$, and in an inelastic collision, it is reduced to $K_{\text{rel}}^{\text{after}}=k_{\mathrm{r}}^{\mathrm{2}}\times K_{\text{rel}}^{\text{before}}$. If k_r=1, the collision is elastic, and the kinetic energy does not change during the collision. The minimum relative initial velocity colliding particles require to overcome the Coulomb barrier is therefore as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{v}_{\text{rel}}^{\text{min}}=\sqrt{{\displaystyle \frac{\mathrm{2}{E}_{\text{Coul}}}{\mathit{\mu }}}}.\end{array}$$

If the loss of kinetic energy during a collision ($K_{\text{rel}}^{\text{before}}-K_{\text{rel}}^{\text{after}}$) is greater than the excess kinetic energy as compared to the Coulomb barrier ($K_{\text{rel}}^{\text{initial}}-E_{\text{Coul}}$), then the particles are trapped behind the barrier. The maximum relative initial velocity ($v_{\text{rel}}^{\text{max}}$), above which coalescence is not possible, is derived from the situation where, during a collision, insufficient kinetic energy is removed through the action of the coefficient of restitution and the particles fly apart. This maximum initial velocity is given by the following:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{v}_{\text{rel}}^{\text{max}}=\sqrt{{\displaystyle \frac{\mathrm{2}\left[(E_{\text{Coul}}-E_{\mathrm{0}})/k_{\mathrm{r}}^{\mathrm{2}}+E_{\mathrm{0}}\right]}{\mathit{\mu }}}}.\end{array}$$

The above collision scenarios are illustrated in Fig. 1 based on an example case of a small SiO₂ particle colliding with a larger ice particle, with both carrying a negative charge of $q_{\mathrm{1}}=q_{\mathrm{2}}=-\mathrm{1}e$. A total of three possible outcomes are described. If the relative kinetic energy of the colliding particles is smaller than the height of the Coulomb barrier (case 1) then the particles always repel one another without energy loss. If the particles collide inelastically with a relative kinetic energy sufficient to overcome the Coulomb barrier, the loss of kinetic energy during a collision may prevent their subsequent separation and lead to the formation of a stable, or metastable, aggregate (case 2). If the energy loss during such a collision is not sufficient to stabilise the pair, the particles rebound and separate (case 3). The latter case may be applicable in warmer regions of the atmosphere where particles move with higher velocities. In this work, we consider a wide range of particle velocities in order to identify a wide range of possible collision outcomes. The probability distribution for the relative velocity of two colliding particles in the form of a Maxwell–Boltzmann distribution at temperature T is given by Müller-Kirsten (2013) as follows:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }P\left(v_{\text{rel}}\right)=\sqrt{{\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}}{\left({\displaystyle \frac{\mathit{\mu }}{kT}}\right)}^{\mathrm{3}/\mathrm{2}}{v}_{\text{rel}}^{\mathrm{2}}{e}^{-\frac{\mathit{\mu }{v}_{\text{rel}}^{\mathrm{2}}}{\mathrm{2}kT}}.\end{array}$$

In Fig. 2, representative examples for the Maxwell–Boltzmann distribution of the relative velocities are shown for collisions between SiO₂ particles carrying a charge of $q_{\mathrm{2}}=-\mathrm{1}e$ and ice particles with q₁=0, −1e and −2e at T=150 K. If the surface charge is represented by a point charge residing on the particle's surface, then the orientational geometry of a collision becomes important. Figure 3 shows the geometries considered in this study, both for collisions between ice particles and small metal oxide particulates (Fig. 3a) and for collisions between metal oxide particles (Fig. 3b and c).

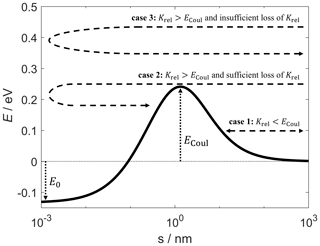
Figure 1 Possible outcomes for a collision between like-charged particles. The total energy is schematically split into two components, i.e. the electrostatic interaction energy (solid) and the relative kinetic energy (dashed). The electrostatic interaction energy profile is calculated for a collision between an ice particle (r₁=3 nm) and a SiO₂ particle (r₂=0.5 nm), with both particles carrying a charge of $q_{\mathrm{1}}=q_{\mathrm{2}}=-\mathrm{1}e$.

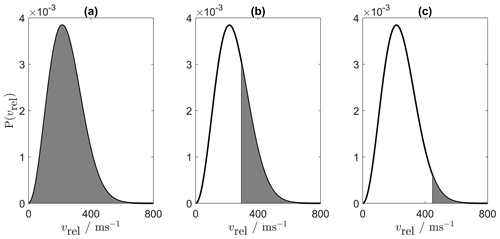
Figure 2 Aggregation probability, indicated by the shaded area, for a collision between a SiO₂ particle (r₂=0.2 nm, $q_{\mathrm{2}}=-\mathrm{1}e$) and an ice particle (r₁=30 nm), as defined by the Maxwell–Boltzmann distribution of the relative velocity at T=150 K. (a) In the case of a neutral ice particle (q₁=0), the probability of aggregation is 1 as P(v_rel) is integrated in the velocity range of [0,1192] m s⁻¹. (b) For $q_{\mathrm{1}}=-\mathrm{1}e$, the probability of aggregation is 0.293 as P(v_rel) is integrated in the velocity range of [295,1219] m s⁻¹. (c) For $q_{\mathrm{1}}=-\mathrm{2}e$, the probability of aggregation is 0.034 as P(v_rel) is integrated in the velocity range of [450,1260] m s⁻¹. The values of $v_{\text{rel}}^{\text{min}}$ and $v_{\text{rel}}^{\text{max}}$ are taken from Table 2.

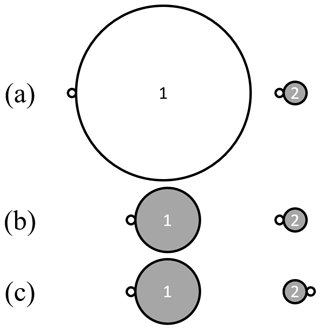
Figure 3 Position of the point charge on the surface of colliding particles depicted by a small open circle. Panel (a) shows an ice particle (1) and a small oxide particulate (2), and panels (b, c) show two oxide particles (1 and 2).

Previous studies by Bichoutskaia et al. (2010) have shown conclusively that, between like-charged particles, attraction is strongly size dependent, such that particles carrying the same amount of charge should have dissimilar sizes. This effect becomes more noticeable with the increase in the ratio of particle radii, $r_{\mathrm{1}}/r_{\mathrm{2}}$; as the ratio increases, surface charge polarisation becomes more pronounced, leading to strong attraction at short separation distances and a reduction in the Coulomb barrier. This effect is illustrated in Fig. 4a, which shows electrostatic interaction energy profiles as a function of separation distance for collisions between like-charged ice and SiO₂ particles ($q_{\mathrm{1}}=q_{\mathrm{2}}=-\mathrm{1}e$) as the size of the ice particle varies between r₁=10, 20 and 30 nm. As the ice particle becomes larger, the height of the Coulomb barrier decreases, which in turn can affect the outcome of a collision. Note that Fig. 4 refers to a collision geometry shown in Fig. 3a, which favours the attractive interaction between two particles, each with a point charge located on their surface.

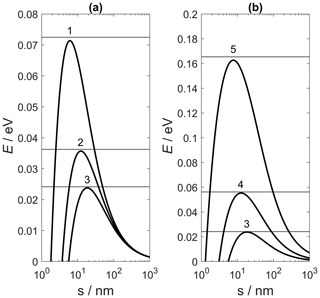
Figure 4 Electrostatic interaction energy as a function of the surface-to-surface separation distance, s, between an ice particle and a SiO₂ particle (r₂=0.2 nm; $q_{\mathrm{2}}=-\mathrm{1}e$) in the geometry shown in Fig. 3a, as calculated by the point charge model analogous to Filippov et al. (2019). Horizontal lines indicate the value of the Coulomb energy barrier obtained using the uniform surface charge model. (a) The charge of the ice particle is $q_{\mathrm{1}}=-\mathrm{1}e$, and the radius varies as r₁=10 nm (line 1), 20 nm (line 2) and 30 nm (line 3). (b) The radius of the ice particle is r₁=30 nm, and the charge varies as $q_{\mathrm{1}}=-\mathrm{1}e$ (line 3), −2e (line 4) and −5e (line 5). Note the change in scale on the y axis.

In this example, the SiO₂ particle approaches the ice particle from the direction opposite to the location of the point charge on the latter, and this collision corresponds to the least repulsive interaction. An equivalent scenario has been considered assuming a uniform distribution of surface charge on both particles, following the approach described in Bichoutskaia et al. (2010). The height of the Coulomb barrier obtained using a uniform distribution of surface charge is depicted in Fig. 4 by horizontal lines. For the size of particles considered in this work, these two approximations give very similar results. Although the height of the Coulomb barrier is strongly influenced by the size of the large ice particle (Fig. 4a), it shows no change with variations in the sizes of the SiO₂ particles considered here.

The height of the Coulomb barrier is affected even more greatly when the charge of colliding particles is changed. In the case considered in Fig. 4b, the charge on the ice particle was increased from $q_{\mathrm{1}}=-\mathrm{1}e$ to −5e to show the almost linear dependence of the barrier on charge variation, in accordance with the leading Coulomb energy term $E\propto \frac{q_{\mathrm{1}}{q}_{\mathrm{2}}}{r}$. The variation in the electrostatic energy with particle size shown in Fig. 4a is a more subtle effect related to surface charge polarisation (note the change of scale along y axis in Fig. 4b).

4 Aggregation of like charged metal oxide and ice particles

Consider first the aggregation of negatively charged metal oxides and ice particles. Table 2 shows values of $v_{\text{rel}}^{\text{min}}$ and $v_{\text{rel}}^{\text{max}}$ calculated using Eqs. (2) and (3) with k_r=0.9. Integrating the probability distribution shown in Fig. 2 between these limits gives the probability of aggregation, and the results are presented in Table 2, where aggregation is expressed as a percentage of all collisions. Table 2 summarises results for the aggregation of a metal oxide particle, with a fixed size and charge, with ice particles of varying size and charge. These data show that large ice particles with low charge have the highest probability of coalescence with like-charged metal oxide particles. However, in many cases the Coulomb barrier prevents the aggregation of particles with the kinetic energies typically found in the MLT region (kT=12.9 meV at T=150 K), assuming that thermal motion is the predominant contribution to velocity. The barrier can be overcome by a small number of high kinetic energy particles found in the tail of the Maxwell–Boltzmann distribution of molecular speeds at 150 K. For these particular interactions, the free charge on the surface of both colliding particles is described by a point charge with the geometry shown in Fig. 3a, and the change in electrostatic interaction energy is due to a redistribution of bound charge (polarisation effects). Note that, for ice particles with higher charges, a uniform distribution of free charge might be more appropriate. As mentioned previously, if the initial relative velocity of the incoming particles is smaller than $v_{\text{rel}}^{\text{min}}$, the two like-charged particles repel (case 1 shown in Fig. 1); however, if it is greater than $v_{\text{rel}}^{\text{max}}$, the particles do not coalesce but instead fly apart due to the residual excess kinetic energy (case 3). Therefore, only collisions with a relative initial velocity greater than $v_{\text{rel}}^{\text{min}}$ and smaller than $v_{\text{rel}}^{\text{max}}$ lead to coalescence. In these examples, a change in the coefficient of restitution would not affect the probability of aggregation as it only reduces $v_{\text{rel}}^{\text{max}}$, and values of the latter that fall within the temperature range appropriate for these calculations have extremely low probabilities.

Table 2 Energetic considerations and the percentage of aggregation for SiO₂–ice collisions at T=150 K and k_r=0.9 (the surface point charge model). The SiO₂ particle has a fixed radius and charge (r₂=0.2 nm, $q_{\mathrm{2}}=-\mathrm{1}e$), and the size and charge of ice particle is varied. The collision geometry is shown in Fig. 3a. The interactions of the MgO and FeO particles with ice show the same trend (see Tables A1 and A2 in the Appendix).

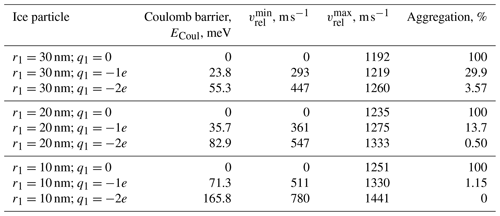
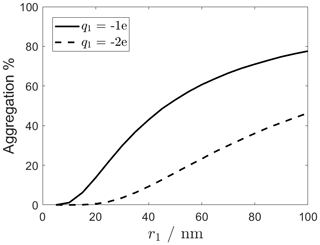
Figure 5 shows coalescence results where the size of the ice particle has been increased to 100 nm. These data reinforce the fact that, for like-charged collisions, an increase in the size of the ice particle from 10 to 100 nm can lead to an order of magnitude increase in the probability of aggregation. Also given in Fig. 5 are data calculated for a charge of −2e on the ice particle. In this case, the probability of aggregation is increased from zero (for r₁<20 nm) to more than 40 % (for r₁≈100 nm), thus providing a mechanism whereby ice particles can increase their charge, but still participate in aggregation processes. The results in Table 2 and Fig. 5 demonstrate that there are several routes whereby ice particles can become contaminated by both neutral and like-charged MSPs. These calculations on the coalescence of ice particles and dust are supported by the experimental observations of Hervig et al. (2012), who have identified the presence of meteoric smoke in ice particles. Our results also point to coagulation rather than condensation as a possible growth mechanism. Further studies are, however, required to help us understand how the collision probabilities influence the magnitudes of rate coefficients for coagulation.

Figure 5 Aggregation probability, presented as percentage, for a collision between a SiO₂ particle (r₂=0.2 nm; $q_{\mathrm{2}}=-\mathrm{1}e$) and an ice particle ($q_{\mathrm{1}}=-\mathrm{1}e$ and $q_{\mathrm{1}}=-\mathrm{2}e$) whose size varies from r₁=1 to 100 nm.

5 Aggregation of metal oxide and silica particles

The abundant presence of metal oxide and silica particles in meteoric smoke in the MLT region (Plane et al., 2015) leads to a possibility that these may also aggregate, and with radii ranging from 0.2 to 5 nm, these are amongst the smallest particles found in this region of atmosphere. Their size means that if the point charge approximation is used to describe the surface charge, then the exact location of the point charge on the surface of each colliding particle becomes very important because, as shown previously by Filippov et al. (2019), collision geometry can alter the strength of the electrostatic interaction. This statement does not apply to most like-charged interactions because, as shown in Table 3, the height of the Coulomb barrier prevents very small like-charged particles (less than 5 nm radius) from aggregating. Note that collisions between like-charged silica particles have lower energy barriers than those calculated for collisions between iron oxide particles. For collisions involving larger particles (r₁=5 nm), despite the lower energy barriers, the minimum initial velocity ($v_{\text{rel}}^{\text{min}}$) required to overcome the barriers for SiO₂ are still higher for than those for FeO particles. These effects arise from differences in density and mass.

Table 3 Energetic considerations and the percentage of aggregation for SiO₂–SiO₂ and FeO–FeO collisions at T=150 K and k_r=0.9 (the surface point charge model). Particle 2 has a fixed radius and charge (r₂=0.2 nm; $q_{\mathrm{2}}=-\mathrm{1}e$), and the size and charge of particle 1 is varied. The collision geometry is shown in Fig. 3b.

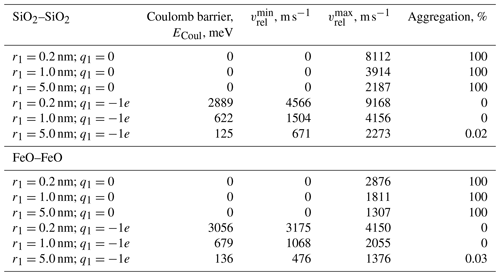
For collisions between charged and neutral particles, the Coulomb barrier is always zero, and their aggregation is driven by polarisation effects. Again, orientation of the particles becomes important, and here, two limiting cases are considered. Table 3 corresponds to the case where the point charge on the surface of particle 2 faces the neutral particle 1 (geometry shown in Fig. 3b, but we now assume that particle 1 is neutral). In this configuration, there is strong attraction as the point charge approaches the neutral particle leading to a redistribution (polarisation) of surface charge on the latter. This leads to a significant increase in the binding energy between the particles (E₀) and results in coalescence through the subsequent action of the coefficient of restitution. Irrespective of particle composition, the absence of a Coulomb barrier results in aggregation for all of the examples examined in Table 3.

Table 4 Energetic considerations and the percentage of aggregation for SiO₂–SiO₂ and FeO–FeO collisions at T=150 K and k_r=0.9 (the surface point charge model). Particle 2 has a fixed charge ($q_{\mathrm{2}}=-\mathrm{1}e$), particle 1 is neutral (q₁=0) and the size of both particles is varied. The collision geometry is shown in Fig. 3c.

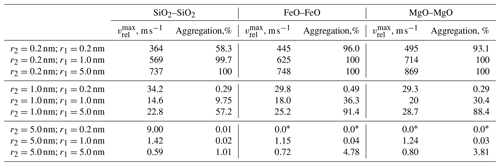
^* Zero within the accuracy of our calculations.

The data displayed in Table 4 correspond to the case least favourable to aggregation between neutral and charged particles. Here, the point charge on the surface of particle 2 faces away from the neutral particle 1 (the geometry is shown in Fig. 3c, but particle 1 is neutral). In this orientation, collisions with the smallest charged particles (r₂=0.2 nm) strongly favour aggregation often resulting in a 100 % coalescence outcome, even though the maximum relative initial velocity of colliding particles required for coalescence is significantly lower. When the charged particle is very small, the interaction resembles a point charge – a neutral particle case, which is always attractive. Note that the aggregation remains almost complete (100 %) even when both charged and neutral particles are extremely small ($r_{\mathrm{1}}=r_{\mathrm{2}}=\mathrm{0.2}$ nm) and highly polarisable (FeO and MgO). In general, there are distinct differences between the aggregation outcomes for SiO₂ particles and the more polarisable FeO particles, with the FeO collisions consistently having higher percentage aggregation and MgO particles lying somewhere between the two. For the geometry shown in Fig. 3c, the aggregation percentage drops very significantly as the size of the charged particle 2 grows. This is because any surface polarisation response on the neutral particle due to the presence of a point charge on the surface of particle 2 is now hindered by the volume of the charged particle itself. Finally, when the charged particle is large and the neutral one is very small, surface polarisation effects on the neutral particle are negligible and aggregation does not occur. This can be illustrated by comparing the following two examples: if $r_{\mathrm{2}}/r_{\mathrm{1}}=\mathrm{10}$ (the radius of the charged particle is 10 times bigger than that of neutral particle), then the aggregation is 0 %, and if $r_{\mathrm{1}}/r_{\mathrm{2}}=\mathrm{10}$ (the radius of the neutral particle is 10 times bigger than that of charged particle), then the aggregation is 100 % (Table 4).

Finally, if the results given in Tables 3 and 4 for the percentage of aggregation are compared, it can be seen that there are differences that depend on how the point charges are orientated on these particles, all of which have comparatively low dielectric constants. In all instances where a charge is pointing towards a large polarisable particle (Table 3; when q₁=0 and $q_{\mathrm{2}}=-\mathrm{1}e$), the aggregation is 100 %. However, when in Table 4 the charge is located at 180^∘ from the adjacent particle (case 3c in Fig. 3), the aggregation drops to 58 % when, in the least polarisable particle pair, SiO₂, the neutral particle has a radius of 0.2 nm. As the dielectric constant increases on moving to MgO and FeO, the particles become more polarisable and the percentage aggregation increases.

6 Brief discussion of main results and conclusions

This work is focused on the description of the basic principles underpinning the coalescence of ice and dust particles in thermal motion. Specific examples considered in this study examine the coalescence between particles, commonly found in the mesosphere, at the temperature T=150 K, which is typical of this region of the atmosphere. Pair interactions of charged particulates follow the Coulomb law with an additional contribution from the attraction between like-charged and neutral-charged pairs driven by the induced polarisation of the particle surface charge. The latter interactions can be significant at short separation distances between interacting particles. Low temperatures in the MLT region imply that the colliding particles are not very energetic, and for a like-charged pair, the relative kinetic energy is often insufficient to overcome the Coulomb barrier. However, the high energy tail of the Maxwell–Boltzmann distribution of the relative velocity at T=150 K provides an adequate amount of collisions leading to aggregation both between like-charged particles of ice and dust and between dust particulates themselves.

The like-charged attraction is more common (and stronger) between particles with low charge. This collision scenario can be described by a localised, point surface charge model and one where the charge is assumed to be uniformly distributed over the entire surface of a particle. An earlier study by Filippov et al. (2019) of the interaction between positively charged particles, showed that, for particles with low dielectric constants, there is a difference in the predicted behaviour between these two models. As the dielectric constant increased in value, results from the two models became equivalent. Similarly, differences in orientational geometry of a collision (extreme scenarios are shown in Fig. 3b and c) were also found to be evident at low dielectric constants, but again, these disappeared as the value of the dielectric constant increased. The presented results provide a basis for future work to estimate the coagulation rates between particles of a given size and charge and their variation with temperature.

Appendix A

Table A1 Energetic considerations and the percentage of aggregation for FeO–ice collisions at T=150 K and k_r=0.9 (the surface point charge model). The FeO particle has the fixed radius and charge (r₂=0.2 nm, $q_{\mathrm{2}}=-\mathrm{1}e$), and the size and charge of the ice particle is varied. The collision geometry is shown in Fig. 3a.

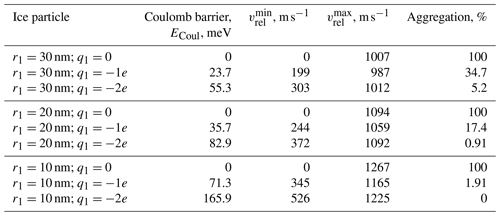
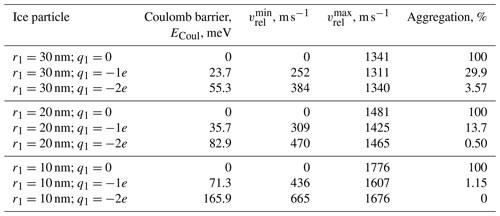
Table A2 Energetic considerations and the percentage of aggregation for MgO–ice collisions at T=150 K and k_r=0.9 (the surface point charge model). The MgO particle has the fixed radius and charge (r₂=0.2 nm, $q_{\mathrm{2}}=-\mathrm{1}e$), and the size and charge of ice particle is varied. The collision geometry is shown in Fig. 3a.