On the importance of atmospheric loss of organic nitrates by aqueous-phase ●OH oxidation

Organic nitrates are secondary species in the atmosphere. Their fate is related to the chemical transport of pollutants from polluted areas to more distant zones. While their gas-phase chemistry has been studied, their reactivity in condensed phases is far from being understood. However, these compounds represent an important fraction of organic matter in condensed phases. In particular, their partition to the aqueous phase may be especially important for oxidized organic nitrates for which water solubility increases with functionalization. This work has studied for the first time the aqueous-phase •OH-oxidation kinetics of four alkyl nitrates (isopropyl nitrate, isobutyl nitrate, 1-pentyl nitrate, and isopentyl nitrate) and three functionalized organic nitrates (α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate) by developing a novel and accurate competition kinetic method. Low reactivity was observed, with k_OH ranging from 8×10⁷ to 3.1×10⁹ L mol⁻¹ s⁻¹ at 296±2 K. Using these results, a previously developed aqueous-phase structure–activity relationship (SAR) was extended, and the resulting parameters confirmed the extreme deactivating effect of the nitrate group, up to two adjacent carbon atoms. The achieved extended SAR was then used to determine the •OH-oxidation rate constants of 49 organic nitrates, including hydroxy nitrates, ketonitrates, aldehyde nitrates, nitrooxy carboxylic acids, and more functionalized organic nitrates such as isoprene and terpene nitrates. Their multiphase atmospheric lifetimes towards •OH oxidation were calculated using these rate constants, and they were compared to their gas-phase lifetimes. Large differences were observed, especially for polyfunctional organic nitrates: for 50 % of the proposed organic nitrates for which the •OH reaction occurs mainly in the aqueous phase (more than 50 % of the overall removal), their •OH-oxidation lifetimes increased by 20 % to 155 % under cloud/fog conditions (liquid water content LWC = 0.35 g m⁻³). In particular, for 83 % of the proposed terpene nitrates, the reactivity towards •OH occurred mostly (>98 %) in the aqueous phase, while for 60 % of these terpene nitrates, their lifetimes increased by 25 % to 140 % compared to their gas-phase reactivity. We demonstrate that these effects are of importance under cloud/fog conditions but also under wet aerosol conditions, especially for the terpene nitrates. These results suggest that considering aqueous-phase •OH-oxidation reactivity of biogenic nitrates is necessary to improve the predictions of their atmospheric fate.

1 Introduction

Nitrogen oxides (NO${}_x=\mathrm{•}\mathrm{NO}+\mathrm{•}{\mathrm{NO}}_{\mathrm{2}}$) intensely impact air quality and the environment as they play key roles in the production of relevant air pollutants such as ozone (O₃), nitrous acid (HONO), nitric acid (HNO₃), and secondary organic aerosol (SOA). Their atmospheric chemistry controls the concentrations of the three main oxidants, O₃, •OH, and NO₃• radicals. The past few decades have witnessed important reductions in NO_x direct emissions in Europe or North America, resulting in changes in their atmospheric fate, by increasing the relative importance of their conversion to organic nitrates (Romer Present et al., 2020). The latter are secondary organic compounds, which are formed by the reactivity of NO_x with volatile organic compounds (VOCs). Owing to their long atmospheric lifetimes (much longer than for NO_x), organic nitrates can be transported from polluted to remote areas. During their long-range transport, these compounds may (1) release back NO_x far from NO_x sources via direct photolysis and/or •OH oxidation or (2) act as a definitive sink of atmospheric NO_x by hydrolysis of the nitrate group and/or by deposition. Organic nitrates thus act as sinks and reservoirs of NO_x, leading to a broader spatial distribution of NO_x and thus spreading the ozone, HONO, and SOA formation from the local to the regional scale. For this reason, understanding and considering the reactivity of organic nitrates is necessary for accurately predicting their atmospheric fates and impacts on air quality.

The gas-phase chemistry of organic nitrates has been studied through kinetic experiments focusing on their •OH oxidation (Bedjanian et al., 2018; Picquet-Varrault et al., 2020; Treves and Rudich, 2003; Wängberg et al., 1996; Zhu et al., 1991) and direct photolysis (Clemitshaw et al., 1997; Picquet-Varrault et al., 2020; Suarez-Bertoa et al., 2012). These experiments provide data for different types of organic nitrates, including alkyl nitrates, ketonitrates, hydroxy nitrates, dinitrates, cyclonitrates, and alkene nitrates, and provide knowledge on their gas-phase atmospheric fate. Although alkyl and alkene nitrates are highly volatile, polyfunctional organic nitrates may show much lower volatility and they can partition to condensed phases as aqueous and aerosol phases. Their presence in submicron particles has been observed in a fraction ranging from 5 % to 77 % (in mass) of organic aerosol in Europe and North America (Kiendler-Scharr et al., 2016; Lee et al., 2019). Despite this fact, their reactivities in condensed phases have been poorly explored. Most studies have focused on hydrolysis, a reaction that is extremely structure dependent, mostly occurring in tertiary or allylic nitrates (Hu et al., 2011; Liu et al., 2012), while the non-hydrolyzable fraction of α- and β-pinene particulate organic nitrate ranges from 68 % to 91 % in mass (Takeuchi and Ng, 2019). To our knowledge, only one study experimentally determined the photolysis kinetics of organic nitrates in the aqueous phase (Romonosky et al., 2015) and concluded that the •OH removal processes should have a higher relevance. However, there have been no attempts to experimentally determine their aqueous-phase •OH-oxidation reactivity.

Aqueous-phase •OH-oxidation processes play a key role in the removal and production of water-soluble compounds in the atmosphere (Herrmann et al., 2015). The determination of kinetic rate constants is essential to understand their lifetimes and to develop more precise models to predict pollution events and the scale of pollutant transport. Determining aqueous-phase •OH-oxidation second-order rate constants (k_OH) may be done by competition kinetic methods consisting of a comparison between the decay of the target compound versus a reference compound, for which the k_OH value is well known. Many studies have used the thiocyanate anion (SCN⁻) as the reference compound. Its decay can be easily followed by online spectroscopic measurement of the formed radical anion (SCN)₂•⁻ in the presence and absence of the target compound (Herrmann, 2003). This technique, however, is not well suited for species with low reactivity for which k_OH≤10⁹ L mol⁻¹ s⁻¹, i.e., more than 10 times lower than $k_{\mathrm{OH}+{\text{SCN}}^{-}}=\mathrm{1.12}(\pm \mathrm{0.20})\times {\mathrm{10}}^{\mathrm{10}}$ L mol⁻¹ s⁻¹. In this case, the target species should reach high concentrations to be able to compete with the thiocyanate anion. These high concentrations may interfere with the measurements. Other indirect methods use offline measurements for monitoring the target and reference compounds. However, most of these methods use reference compounds for which k_OH values have not been so widely explored, thus inducing important uncertainties in the experimentally determined k_OH values (Herrmann, 2003).

The aim of this work was to accurately determine aqueous-phase k_OH rate constants by developing a new online competition kinetic method, which is well suited to species with low reactivity. The effectiveness and the relevance of the method were validated on compounds for which k_OH rate constants are well known. Then, the method was used to determine the k_OH rate constants of some organic nitrates, and the results were used to extend the aqueous-phase structure–activity relationship (SAR) developed earlier (Monod and Doussin, 2008; Doussin and Monod, 2013) to the nitrate group. Furthermore, the prediction of k_OH rate constants for other atmospherically relevant organic nitrates in the aqueous phase was performed with the extended SAR. Finally, the potential multiphase fate of these compounds in the atmosphere was estimated.

2 Experimental

2.1 Principle

The originality of this work relies on a competition kinetic method monitored by online decay measurements of the reference compound in the reactor's headspace using a proton transfer reaction mass spectrometer (PTR-MS). Concerning the target compounds, depending on their properties (solubility, volatility, and instrumental response), their kinetic decays were monitored in the reactor's headspace by PTR-MS or offline by ultra-high-performance liquid chromatography photodiode array detector (UHPLC-UV). The developed method employed methanol as the reference compound because (i) its k_OH rate constant, 9.7 (±1.5) ×10⁸ L mol⁻¹ s⁻¹ at 298 K, is widely accepted (Table S1); (ii) this value is relevant for competitive kinetics relative to species with low reactivity; and (iii) its extremely sensitive quantification by PTR-MS was expected to not suffer from any interferences with the selected organic nitrates (Aoki et al., 2007; Lindinger et al., 1998).

Due to the known sensitivity of organic nitrates to photolysis (Romonosky et al., 2015), aqueous •OH radicals were generated in the dark by the Fenton reaction (Reaction R1) (Neyens and Baeyens, 2003) by dropwise addition of a solution of Fe²⁺ to an acidic solution of H₂O₂ in excess containing methanol and the target compound.

$$\begin{array}{}\text{(R1)}& {\mathrm{Fe}}^{\mathrm{2}+}+{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\to {\mathrm{Fe}}^{\mathrm{3}+}+\mathrm{•}\mathrm{OH}+{\mathrm{OH}}^{-}\end{array}$$

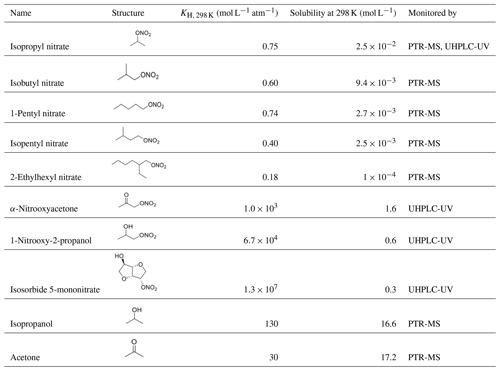
The method was validated using isopropanol and acetone as target compounds, whose •OH-oxidation rate constants are well known (Table S1). The method was then used to determine new k_OH values for four alkyl nitrates (isopropyl nitrate, isobutyl nitrate, 1-pentyl nitrate, and isopentyl nitrate) and three polyfunctional organic nitrates (α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate); see Table 1. Furthermore, a tentative study of 2-ethylhexyl nitrate k_OH rate constant was performed using this method, but it was limited by its very low solubility.

Table 1 Chemical structures and properties of the studied organic nitrates. Henry's law constants were obtained from Sander (2015) except for 2-ethylhexyl nitrate and isosorbide 5-mononitrate, which were calculated using the SAR developed by Raventos-Duran et al. (2010). Organic nitrate solubilities were calculated using the model WSKOWWIN™.

Figure 1 Experimental setup for the competition kinetics method.

2.2 Experimental setup and protocol

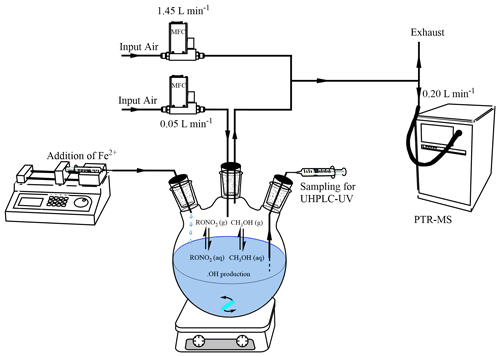
The aqueous-phase reactor consisted of a 1 L three-neck round-bottom flask closed hermetically with rubber caps (Fig. 1). A Razel syringe pump at 0.33 mL min⁻¹ was used with a glass syringe to add dropwise a solution of Fe²⁺ into the reactor's aqueous solution. A second syringe was also connected to the reactor to add the target and the reference compounds and to sample the aqueous phase when necessary. The reactor's aqueous solution was continuously stirred before and during the reaction with a magnetic stirrer. A flow of synthetic air constantly guided a fraction of the headspace gas phase to the PTR-MS instrument, with a flow of 0.050 L min⁻¹ using a mass flow controller (Brooks SLA Series). A 1:30 dilution was performed downward of the reactor's flow using synthetic air at 1.450 L min⁻¹. All experiments were performed at room temperature (296±2 K).

In each experiment, the Fe²⁺ solution consisted of 5–10 mL of FeSO₄•7H₂O (0.02–0.06 mol L⁻¹), added dropwise to the solution of 400 mL of H₂O₂ (in excess, i.e., 0.004 mol L⁻¹) acidified by H₂SO₄ (0.005 mol L⁻¹), to keep pH = 2.5 (Micro pH electrode, Thermo) during the reaction. Concentrations and volumes of the Fe²⁺ solution were varied in order to optimize the •OH attack on the reference and the target compounds. All experiments and their initial conditions are compiled in Table S2. The Fe²⁺ solution was used as the limiting reagent to minimize its possible interference with the organic nitrate reaction products. In addition, it was verified in control experiments that H₂O₂, used in excess, did not react with any of the target compounds. Furthermore, control experiments at pH = 2.5 confirmed that none of the organic nitrates underwent hydrolysis at significant rates under our experimental conditions.

Prior to each experiment, the reactor's headspace was extensively purged with pure air for 1 h while PTR-MS measurements were set for stabilization purposes. The target compound and methanol were then added directly into the aqueous phase, and the reactor's headspace signal was monitored for 30 min before the reaction with constant stirring of the solution to determine the first-order rate constant of evaporation (k_vap) of each compound under the reaction conditions. The reaction was then started by adding dropwise the Fe²⁺ solution for 15 to 30 min (depending on the volume of Fe²⁺ added). During experiments performed with isopropyl nitrate, α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate, the aqueous phase was sampled every 3 min for offline measurements by UHPLC-UV. Once the flow of Fe²⁺ was stopped, the system was kept stirring for another 30 min while continuously monitoring the reactor's headspace.

2.3 Methodology

In such a competition between the target compound (X) and methanol (M) towards •OH radicals (Reaction R2),

$$\begin{array}{}\text{(R2)}& \text{X/M}+\mathrm{•}\mathrm{OH}\to \text{Products},\end{array}$$

in the absence of direct photolysis, the second-order kinetic rate constant of the target compound, k_OH,X (in L mol⁻¹ s⁻¹), is directly obtained from the slope ($k_{\mathrm{OH},\mathrm{X}}/k_{\mathrm{OH},\mathrm{M}}$) of the linear plot of $\ln \left(\right[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}/\left[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)}\right)$ versus $\ln \left(\right[\mathrm{M}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}/\left[\mathrm{M}{]}_{t\left(\mathrm{aq}\right)}\right)$ derived from Eq. (1).

$$\begin{array}{}\text{(1)}& \ln {\displaystyle \frac{[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}}{[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)}}}={\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot \ln {\displaystyle \frac{[\mathrm{M}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}}{[\mathrm{M}{]}_{t\left(\mathrm{aq}\right)}}},\end{array}$$

where $[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}/[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)}$ represents the aqueous-phase concentration relative decay of the target compound, and $[\mathrm{M}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}/[\mathrm{M}{]}_{t\left(\mathrm{aq}\right)}$ represents the aqueous-phase concentration relative decay of methanol.

Using the Fenton Reaction (R1), •OH radicals were generated within the aqueous phase and could not reach the headspace in sufficient numbers to react significantly with the target compounds in the gas phase. This was confirmed by the validation experiments (Sect. 3.1) where the values found for $k_{\mathrm{OH},\mathrm{X}}/k_{\mathrm{OH},\mathrm{M}}$ ratios were those of the aqueous-phase reactions and not those of the gas phase, which are a factor of 2 to 3 higher.

Headspace analyses were based on the direct proportionality between aqueous- and gas-phase concentrations of the analytes (Karl et al., 2003). Therefore, in cases where both the target and the reference compounds were monitored by PTR-MS, Eq. (1) can be written as Eq. (2) (see Appendix A for detailed explanations).

$$\begin{array}{}\text{(2)}& \ln {\displaystyle \frac{{\text{ncps(X)}}_{\mathrm{0}}}{{\text{ncps(X)}}_t}}={\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot \ln {\displaystyle \frac{{\text{ncps(M)}}_{\mathrm{0}}}{{\text{ncps(M)}}_t}},\end{array}$$

where ncps(X) and ncps(M) are the normalized count rates of the target compound and methanol, respectively; i.e., $\text{ncps(X)}=\sum \mathrm{cps}\left({\mathrm{X}}^{+}\right)/\mathrm{cps}\left({\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right)$ and $\text{ncps(M)}=\sum \mathrm{cps}\left({\mathrm{M}}^{+}\right)/\mathrm{cps}\left({\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right)$. The normalization of the H₃O⁺ count rate removes any signal variability due to fluctuating performance of the ion source.

Depending on the properties of the investigated organic nitrates (i.e., their water solubility, volatility, and instrumental response), different treatments were applied to determine their kinetic decays. All the very volatile compounds were monitored in the reactor's headspace by PTR-MS: this comprised the target alkyl nitrates (for which Henry's law constant K_H<1 mol L⁻¹ atm⁻¹), as well as methanol, acetone, and isopropanol (K_H<300 mol L⁻¹ atm⁻¹). Furthermore, due to the low water solubility of alkyl nitrates, their initial concentrations were limited to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ mol L⁻¹. On the other hand, the target polyfunctionalized organic nitrates were much less volatile (K_H>1000 mol L⁻¹ atm⁻¹), and their detection by PTR-MS was more problematic; their relative decays were monitored in the aqueous phase by offline UHPLC-UV. For these compounds, the determination of the aqueous-phase •OH-oxidation rate constant was performed by plotting the relative decay of the aqueous-phase concentration $\left(\ln \right([\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}/[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)})$ against the relative decay of the reference compound signal in the gas phase ($\ln \left(\mathrm{ncps}\right(\mathrm{M}{)}_{\mathrm{0}}/\mathrm{ncps}\left(\mathrm{M}{)}_t\right)$ as shown in Eq. (3):

$$\begin{array}{}\text{(3)}& \ln {\displaystyle \frac{[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}}{[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)}}}={\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot \ln {\displaystyle \frac{\mathrm{ncps}(\mathrm{M}{)}_{\mathrm{0}}}{\mathrm{ncps}(\mathrm{M}{)}_t}}.\end{array}$$

In addition, for the most volatile molecules (i.e., alkyl nitrates), further corrections were performed to subtract the contribution of evaporation to the overall reaction decay. Their high volatilities induced a substantial decay in their concentrations that was systematically measured prior to the start of the reaction, inferring a specific first-order rate constant of evaporation (k_vap) of each compound under the reaction conditions. While for methanol, acetone, or isopropanol the evaporation decay was negligible, for the alkyl nitrates it accounted for 2 % to 20 % of the molecule's consumption during the reaction. To consider this contribution, Eq. (4) was used instead of Eq. (2) for volatile alkyl nitrates:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{1}}{t}}\cdot \ln {\displaystyle \frac{\mathrm{ncps}{\left(\mathrm{X}\right)}_{\mathrm{0}}}{\mathrm{ncps}{\left(\mathrm{X}\right)}_t}}=k_{\mathrm{vap}}+{\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot {\displaystyle \frac{\mathrm{1}}{t}}\cdot \ln {\displaystyle \frac{\mathrm{ncps}(\mathrm{M}{)}_{\mathrm{0}}}{\mathrm{ncps}(\mathrm{M}{)}_t}},\end{array}$$

where t is the reaction time (in seconds). Plotting $\mathrm{1}/t\cdot \ln (\mathrm{ncps}{\left(\mathrm{X}\right)}_{\mathrm{0}}/\mathrm{ncps}{\left(\mathrm{X}\right)}_t)$ versus $\mathrm{1}/t\cdot \ln (\mathrm{ncps}{\left(\mathrm{M}\right)}_{\mathrm{0}}/\mathrm{ncps}{\left(\mathrm{M}\right)}_t)$ resulted in a straight line with a slope of $k_{\mathrm{OH},\mathrm{X}}/k_{\mathrm{OH},\mathrm{M}}$ and an intercept of k_vap. The value of k_vap was determined during the 30 min prior to the reaction, and its value was fixed in Eq. (4). This treatment was not necessary for methanol, acetone, or isopropanol, due to their lower volatilities. For isopropyl nitrate, whose decay was also monitored in the aqueous phase by UHPLC-UV, Eq. (5) was used (in addition to Eq. 4):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\mathrm{1}}{t}}\cdot \ln {\displaystyle \frac{[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{aq}\right)}}{[\mathrm{X}{]}_{t\left(\mathrm{aq}\right)}}}=k_{\mathrm{vap}}+{\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot {\displaystyle \frac{\mathrm{1}}{t}}\cdot \ln {\displaystyle \frac{\mathrm{ncps}(\mathrm{M}{)}_{\mathrm{0}}}{\mathrm{ncps}(\mathrm{M}{)}_t}}.\end{array}$$

In summary, the aqueous-phase •OH-oxidation rate constants of isopropanol and acetone were determined using Eq. (2), while Eq. (3) was used for determining the rate constants of α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate. For isobutyl nitrate, 1-pentyl nitrate, and isopentyl nitrate, compounds which undergo a significant evaporation decay, Eq. (4) was used. Finally, isopropyl nitrate was chosen for intercomparing both methods as it is water soluble and volatile enough to be monitored by both analytical techniques; its aqueous-phase k_OH was determined by both Eqs. (4) and (5).

2.4 Analytical measurements

2.4.1 PTR-MS

A commercial high-sensitivity quadrupole PTR-MS (IONICON Analytik GmbH) was used to monitor the concentration decay of the reference compound (methanol) and seven target compounds (acetone, isopropanol, isopropyl nitrate, isobutyl nitrate, 1-pentyl nitrate, isopentyl nitrate, and 2-ethylhexyl nitrate) during the reaction. The drift tube voltage was 600 V, the reactor chamber pressure was 2.19 mbar, and the drift tube temperature was 333 K. These values correspond to an $E/N$ value of 136 Td (Townsend, with 1 Td = 10⁻¹⁷ V cm⁻²), where E is the electric field strength (V cm⁻¹), and N is the ambient air number density within the drift tube (molecule cm⁻³). Measurements were performed using the multiple ion detection (MID) mode on a short list of 11–13 preselected $m/z$ values resulting in measurement cycles of 25–35 s. This list includes the hydronium ion isotope H${}_{\mathrm{3}}^{\mathrm{18}}$O⁺ ($m/z=\mathrm{21}$) and its water clusters, H₂O•H₃O⁺ and (H₂O)₂•H₃O⁺ ($m/z=\mathrm{37}$ and $m/z=\mathrm{55}$, respectively) as well as parasitic ions NO⁺ and O${}_{\mathrm{2}}^{+}$ ($m/z=\mathrm{30}$ and $m/z=\mathrm{32}$) for diagnostic purposes. The remaining ions correspond to the protonated reference compound, methanol ($m/z=\mathrm{33}$), and to the 5–7 major products of organic nitrates. The individual fragmentation patterns of the organic nitrates determined during a series of preliminary measurements in scan mode (21–200 amu) are listed in Table S3. Data were corrected by normalizing the ion signals with the number of hydronium ions in the drift tube, calculated by multiplying by 500 the signal at $m/z=\mathrm{21}$.

Isopentyl nitrate and 2-ethylhexyl nitrate were analyzed by PTR-MS for the first time. The other compounds, isopropyl nitrate, isobutyl nitrate, and 1-pentyl nitrate, were previously investigated by Duncianu et al. (2017) and Aoki et al. (2007). Table S3 compiles detected fragments and their relative intensities for all the studied organic nitrates in this work. Compared to the previous studies, similar trends in the fragmentation of organic nitrates were found. Fragments with the highest relative intensities correspond to the R⁺ fragment, produced after the nitrate group loss in the drift tube, and to the NO${}_{\mathrm{2}}^{+}$ ion, which was detected for all organic nitrates, except for 2-ethylhexyl nitrate. Other relevant fragments were the RO⁺ fragment and/or other ions (such as C₃H${}_{\mathrm{5}}^{+}$, C₃H${}_{\mathrm{7}}^{+}$, C₄H${}_{\mathrm{9}}^{+}$) which were formed by further fragmentation of the R⁺ fragment.

The minimum standard sensitivity normalized to 10⁶ hydronium ions for all organic nitrates was determined prior to the start of the reaction, by calculating the maximum possible gas-phase concentrations assuming the Henry's law equilibrium (see Table S3). The sensitivities range from 3 to 7 ncps ppbv⁻¹ for all organic nitrates. From these sensitivities, it was calculated that in the reactor's headspace the target organic nitrates were detectable at concentrations higher than $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{7}}$ mol L⁻¹ in the aqueous phase.

For methanol, assuming Henry's law equilibrium, using a K_H=204 mol L⁻¹ atm⁻¹ (average value out of those reported in Sander, 2015), the minimum standard sensitivity normalized to 10⁶ hydronium ions would be 9±1 ncps ppbv⁻¹, corresponding to an effective sensitivity >360 cps ppbv⁻¹ at the typical H₃O⁺ count rate of 4×10⁷ cps. Under these conditions, it would be detectable in the reactor's headspace at aqueous concentrations higher than $\mathrm{9}\times {\mathrm{10}}^{-\mathrm{6}}$ mol L⁻¹.

2.4.2 UHPLC-UV

All the investigated organic nitrates show an intense UV absorption around 200 nm (Fig. S1). Aliquots of the solution were sampled every 3 min from the reactor and the least volatile target compounds were quantified by UHPLC-UV (Thermo Scientific Accela 600) at 200 nm. The device was equipped with a Hypersil Gold C18 column (50×2.1 mm) with a particle size of 1.9 µm and an injection loop of 5 µL. A binary eluent of H₂O and CH₃CN was used for all analyses at a flow rate of 400 µL min⁻¹. Two gradients were used depending on the compounds' polarity. For isopropyl nitrate, the gradient started from ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{CH}}_{\mathrm{3}}\mathrm{CN}$ $\mathrm{80}/\mathrm{20}$ ($v/v$) to $\mathrm{50}/\mathrm{50}$ ($v/v$) for 3 min, held at this proportion for 1 min, and then set back to $\mathrm{80}/\mathrm{20}$ ($v/v$) within 10 s until the end of the run, at minute 5 (method A). For more polar compounds, i.e., α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate, a similar gradient was employed but the initial and final proportions were ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{CH}}_{\mathrm{3}}\mathrm{CN}$ $\mathrm{90}/\mathrm{10}$ ($v/v$) in order to optimize their retention times (method B).

Calibration curves were optimized to obtain good linearity between $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ mol L⁻¹ with a R²>0.9995. The retention times were 0.9, 1.1, 1.2, and 2.4 min for 1-nitrooxy-2-propanol, isosorbide 5-mononitrate, α-nitrooxyacetone, and isopropyl nitrate, respectively. Limits of detection are $\mathrm{9}\times {\mathrm{10}}^{-\mathrm{6}}$ mol L⁻¹ for isopropyl nitrate and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ mol L⁻¹ for the other three compounds.

2.5 Reagents

Chemicals were commercially available and used as supplied: isopropyl nitrate (96 %, Sigma-Aldrich), isobutyl nitrate (98 %, Sigma-Aldrich), 2-ethylhexyl nitrate (97 %, Sigma-Aldrich), 1-pentyl nitrate (98 %, TCI Chemicals), isopentyl nitrate (98 %, TCI Chemicals), isosorbide 5-mononitrate (98 %, Acros Organics), H₂O₂ (30 %, non-stabilized, Acros Organics), FeSO₄•7H₂O (99 %, Sigma-Aldrich), H₂SO₄ (95 %–98 %, Merck), chloroacetone (95 %, Sigma-Aldrich), AgNO₃ (99 %, VWR Chemicals), KI (98 %, Sigma-Aldrich), and NaBH₄ (98 %, Sigma-Aldrich). Methanol (Fisher Chemical), acetonitrile (Fisher Optima), and isopropanol (Honeywell) were LC/MS grade and used as supplied. Acetone (Carlo Erba Reagents) and ether (Fisher Chemical) were HPLC grade. Tap water was purified with a Millipore Milli-Q system (18.2 MΩ cm and TOC <2 ppb).

Non-commercial organic nitrates, i.e., α-nitrooxyacetone and 1-nitrooxy-2-propanol, were synthesized and purified. α-Nitrooxyacetone was synthesized by the nucleophilic substitution reaction of iodoacetone which was synthesized previously from chloroacetone. The ketone group from α-nitrooxyacetone was reduced to produce 1-nitrooxy-2-propanol. See Sect. S1 in the Supplement for further details.

3 Results and discussion

3.1 Validation of the kinetic method

Three different kinds of validation experiments were performed. Their goals were (1) to verify that the partition of the reactants between the aqueous phase and the gas phase (in the reactor's headspace) was rapidly reached during the reaction; (2) to intercompare the two methods (PTR-MS and UHPLC-UV); and (3) to validate the aqueous-phase kinetic k_OH rate constants using well-known values, i.e., those of acetone and isopropanol.

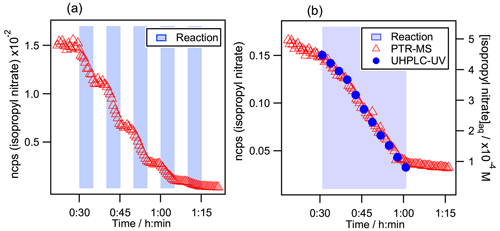
Figure 2 Kinetic decays of isopropyl nitrate during its aqueous-phase •OH oxidation. (a) Monitored by PTR-MS during several sequential additions of the Fe²⁺ solution. Initial conditions in the reactor were [Isopropyl nitrate]${}_{\mathrm{0}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ mol L⁻¹, [H₂O₂]${}_{\mathrm{0}}=\mathrm{4}\times {\mathrm{10}}^{-\mathrm{3}}$ mol L⁻¹, and [H₂SO₄]${}_{\mathrm{0}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ mol L⁻¹. (b) Intercomparison between PTR-MS and UHPLC-UV detection. Initial conditions were [Isopropyl nitrate]${}_{\mathrm{0}}=\mathrm{6}\times {\mathrm{10}}^{-\mathrm{4}}$ mol L⁻¹, [CH₃OH]${}_{\mathrm{0}}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$ mol L⁻¹, [H₂O₂]${}_{\mathrm{0}}=\mathrm{4}\times {\mathrm{10}}^{-\mathrm{3}}$ mol L⁻¹, and [H₂SO₄]${}_{\mathrm{0}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ mol L⁻¹. In both graphs, the time is set to 0 when isopropyl nitrate is injected. Blue background indicates periods when the solution of Fe²⁺ (0.06 mol L⁻¹) was dripped into the reactor to produce •OH radicals.

Figure 2a shows the headspace signal measured by PTR-MS during the aqueous-phase •OH oxidation of isopropyl nitrate. The light blue background indicates periods when the solution of Fe²⁺ (0.06 mol L⁻¹) was dripped into the reactor to produce •OH radicals. One can clearly observe how the isopropyl nitrate signal decay starts immediately at the beginning of the addition of Fe²⁺ and ceases promptly when it is stopped. The partition between the aqueous phase and the reactor's headspace is therefore swiftly reached and is faster than the PTR-MS measurement cycle rate (25 s for the shortest cycle).

Figure 2b shows the isopropyl nitrate decay during its aqueous-phase •OH-oxidation while monitoring its concentration with the PTR-MS and the UHPLC-UV. It is clear from the figure that the kinetics are identical for both methods. Furthermore, the ratios of $k_{\mathrm{OH},\mathrm{isopropryl}\mathrm{nitrate}}/k_{\mathrm{OH},\mathrm{methanol}}$ were 0.29 (±0.06) and 0.31 (±0.06) using the PTR-MS method, Eq. (4), and the UHPLC-UV one, Eq. (5), respectively. These results obtained for isopropyl nitrate confirm that its gas-phase concentrations in the reactor's headspace are proportional to its aqueous-phase concentrations. In addition, this proves that there is no •OH attack in the gas phase: the ratios of $k_{\mathrm{OH},\mathrm{X}}/k_{\mathrm{OH},\mathrm{M}}$ observed are significantly different from the gas-phase rate constant ratios, which are about 2 or 3 times higher. Furthermore, it shows that there are no further interferences in the reaction other than the compound evaporation.

The validation of the method was achieved by determining the aqueous-phase •OH-oxidation rate constants for acetone and isopropanol, which have been extensively studied in the literature (Table S1). Both compound decays were monitored in the reactor's headspace with the PTR-MS, and their k_OH values were determined using Eq. (2). The experiments were triplicated. The uncertainty of the rate constant was calculated by the propagation of the standard deviation of the three values and the methanol rate constant uncertainty.

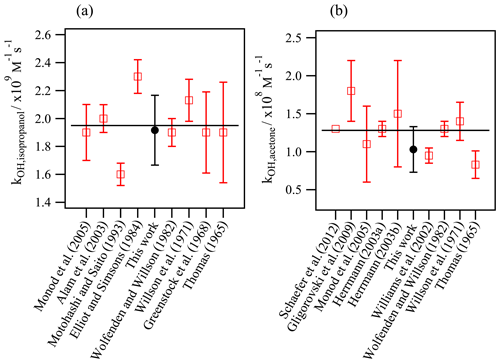
Figure 3 Validation experiments: determination of the aqueous-phase k_OH values using the new developed method and comparison with the reported values in the literature for (a) isopropanol and (b) acetone. The horizontal line represents the average value of the previous studies.

Figure 3 compares the experimentally determined k_OH values for acetone and isopropanol in this work with the previous values reported in the literature. The determined rate constants, 1.9 (±0.1) ×10⁹ L mol⁻¹ s⁻¹ for isopropanol and 1.0 (±0.2) ×10⁸ L mol⁻¹ s⁻¹ for acetone, agree very well with the reported values within the experimental uncertainties.

These results show the relevance of the developed method for accurately determining the aqueous-phase •OH-oxidation rate constant of any semivolatile or non-volatile compound detectable either by PTR-MS or by UHPLC-UV. Hereafter, the new rate constants for organic nitrates are presented and discussed.

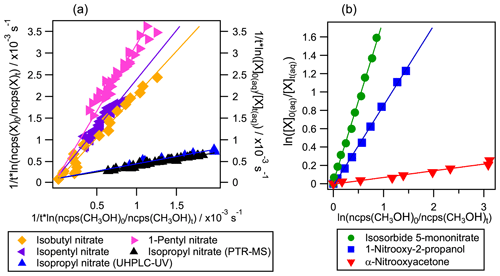
Figure 4 Examples of competition kinetic results for the studied organic nitrates using the new developed method: experiments 8, 14, 16, 19, 21, 24, and 26 (listed in Table S2). In panel (a) molecules were monitored in the reactor's headspace by PTR-MS (left axis and horizontal axis) except for isopropyl nitrate which was also monitored by UHPLC-UV (right axis). In panel (b) methanol was monitored in the reactor's headspace by PTR-MS (horizontal axis) while the polyfunctional organic nitrates were followed by UHPLC-UV (left axis).

3.2 New aqueous-phase k_OH determinations: application of the kinetic method to organic nitrates

Aqueous-phase k_OH for organic nitrates were determined for the first time using the developed competition method. The kinetic rate constants were calculated by Eq. (4) for isobutyl nitrate, 1-pentyl nitrate, and isopentyl nitrate; by Eq. (3) for α-nitrooxyacetone, 1-nitrooxy-2-propanol, and isosorbide 5-mononitrate; and by Eqs. (4) and (5) for isopropyl nitrate. Figure 4 shows some examples of the linear regressions obtained for each organic nitrate where the slope corresponds to the $k_{\mathrm{OH},\mathrm{X}}/k_{\mathrm{OH},\mathrm{M}}$ ratio. It evidences the diversity of values obtained for the studied organic nitrates, which all fall within less than an order of magnitude from that of methanol, thus confirming that this reference is appropriate for the studied molecules.

Table 2 Aqueous-phase •OH-oxidation rate constants for eight organic nitrates: comparison between the experimental rate constants (k_OH exp) and the simulated ones (k_OH sim) using the extended SAR. Calculations use the SAR parameters indicated in Table 4. The factor Δ is the relative difference between the simulated and the experimental rate constant (Eq. 10). n stands for the number of experimental determinations of each rate constant (note that for isopropyl nitrate six experiments were performed; in three of them the value was determined twice using both Eqs. (4) and (5), thus resulting in nine determinations). Experimental uncertainties are 95 % confidence interval.

The determined aqueous-phase •OH-oxidation rate constants for the organic nitrates are compiled in Table 2. Uncertainties were calculated by propagating the standard deviation of the replicates with the uncertainty of the methanol k_OH rate constant. Then, to account for the small number of experiments performed for some molecules, the uncertainties are given by the confidence limits of 95 % given by Student's t distribution. This explains why the value obtained for 1-pentyl nitrate shows the largest uncertainty as its k_OH was determined by only two experiments. Data for 2-ethylhexyl nitrate showed inconsistency compared to the other alkyl nitrates (significantly lower value with respect to its chemical structure). It is possible that even with a low initial concentration ($\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ mol L⁻¹), well below its solubility threshold ($\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ mol L⁻¹), the complete dissolution of the compound was not achieved when the reaction started, thus inducing an incorrect rate constant value. Furthermore, it is suspected, from its structure, to present some surface activity, thus preventing this compound from dissolving into the bulk water.

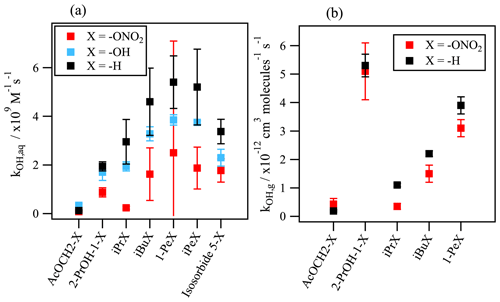
Figure 5 Comparison between the k_OH values for organic nitrates, the corresponding alcohols, and non-substituted homolog compounds (a) in the aqueous phase and (b) in the gas phase. Aqueous-phase k_OH values were taken from Reuvers et al. (1973) and Adams et al. (1965) for alcohols; Getoff (1991) and Rudakov et al. (1981) for H-substituted compounds; and the predictions using the SAR for hydroxy acetone and the –OH and –H substituted homologs of isosorbide 5-mononitrate. Gas-phase k_OH values were taken from Atkinson et al. (1982); Atkinson and Aschmann (1989); Becker and Wirtz (1989); Bedjanian et al. (2017); Suarez-Bertoa et al. (2012); Talukdar et al. (1997); Treves and Rudich (2003); and Zhu et al. (1991) for organic nitrates as well as from Atkinson et al. (1997, 1992) and Atkinson (2003) for H-substituted homologs.

Even though there are no other data available in the literature to compare with, the k_OH values obtained for the other organic nitrates are consistent regarding the chemical structures: they reflect that the rate constant increases with the number of reactive sites. In more detail, the chemical structure of the organic nitrate and the position of the nitrate group plays an important role in the •OH-oxidation rate constant. Figure 5a compares these values with the rate constants of their corresponding alcohols and non-functionalized molecules. It shows how the •OH oxidation is reduced when the nitrate group (–ONO₂) is replacing an alcohol group (–OH) or hydrogen (–H). The nitrate group attached to a primary carbon atom (i.e., isobutyl nitrate, 1-pentyl nitrate, isopentyl nitrate, α-nitrooxyacetone, and 1-nitrooxy-2-propanol) slows down the reactivity by a factor of 1.7 to 3.1 in comparison to their H-substituted homologs (isobutane, pentane, isopentane, acetone, and isopropanol). For isopropyl nitrate, a secondary organic nitrate, the •OH attack is reduced by an order of magnitude compared to n-propane.

A reduction of the reactivity caused by the presence of the nitrate group also occurs in the gas phase but in a much slighter manner (Fig. 5b). It has been discussed that the nitrate group has an electron-withdrawing nature that strengthens the C–H bond of the α- and the β-carbon atoms, thus lowering the hydrogen abstraction (Atkinson et al., 1982). However, the reduction of the reactivity is clearly more pronounced in the aqueous phase, implying a solvent kinetic effect that can more effectively lower the reactivity. This could be induced by the stabilization of the reactant (Koner et al., 2007) or by the formation of a solvent barrier provoked by the nitrate group solvation which could hinder the attack of the hydroxyl radical. The latter inhibiting effect could hinder the •OH attack further than the β position, up to the γ position.

In order to evaluate this question and to predict the reactivity of other organic nitrates with •OH radicals in the aqueous phase, we have investigated a structure–activity relationship (SAR).

3.3 Structure–activity relationship (SAR) for •OH-oxidation rate constants for organic nitrates

3.3.1 SAR principles

Using the experimentally determined aqueous-phase •OH-oxidation rate constants, the aqueous-phase SAR previously developed by Monod and Doussin (2008) and Doussin and Monod (2013) was extended to organic nitrates. Briefly, the principle of the estimation assumes that the overall rate constant for the •OH-radical-induced H abstraction is equal to the sum of each kinetic rate of each reactive site. These partial kinetic rate constants are determined by considering the chemical environment of the function along the carbon skeleton. Each –CH₃, –CH₂–, –CH<, –OH, and –CHO function of the molecule is associated with a group kinetic rate constant: k(group). To consider both field and resonance effects, the rate constants k associated with each H-bearing function are modulated with both the α-neighboring effect (represented by the F parameters) and the β-neighboring effect (represented by the G parameters). This aqueous-phase SAR can predict the •OH-oxidation rate constants of alkanes, alcohols, diols, geminal diols, carbonyls, carboxylic acids, carboxylates, and cyclic compounds as well as polyfunctional molecules. For organic nitrates, in addition to the F(–ONO₂) and G(–ONO₂) parameters, one specific parameter, H(–ONO₂), was included to test the influence of the nitrate group on the reactivity on distant reactive sites in γ position, Eq. (6):

$$\begin{array}{}\text{(6)}& \begin{array}{rl}k& =\sum _{i=\mathrm{1}}^n\left(k\left(i\right)\cdot \prod \mathrm{F}\left(\mathit{\alpha }\text{group}\right)\cdot \prod \mathrm{G}\left(\mathit{\beta }\text{group}\right)\right.\\ & \left.\cdot \prod {\mathrm{H}}_{{\mathrm{ONO}}_{\mathrm{2}}}\left(\mathit{\gamma }\text{group}\right)\cdot C\left(\text{ring}\right)\right),\end{array}\end{array}$$

where k(i) is the partial rate constant for a –CH<, –CH₂–, –CH₃, –CHO, or –OH; $\prod \mathrm{F}\left(\mathit{\alpha }\text{-group}\right)\cdot \mathrm{G}\left(\mathit{\beta }\text{-group}\right)$ is the product of all the contribution factors of the different neighboring groups for a reactive site in the α and β positions, respectively; $H_{{\mathrm{ONO}}_{\mathrm{2}}}\left(\mathit{\gamma }\text{-group}\right)$ is the contribution factor specific of the nitrate function for a reactive site in the γ position; and C(ring) is a contribution factor which represent the ring effect strains and only affects reactive positions inside a ring. Detailed examples where Eq. (6) is applied to calculate the organic nitrates aqueous-phase k_OH can be found in Sect. S2.

In order to include in this new extended SAR a complex polyfunctional molecule such as isosorbide 5-mononitrate, which comprises two 5-atom cycloether structures, the neighboring effects of ethers and cycloethers have also been determined, i.e., F(–O–), G(–O–), and a parameter X(–O–) used to calculate the ring effect strains for cycloethers by multiplying the existing C(ring) factor by a X(–O–) contribution factor which indicates the presence of one or two oxygen atoms in the ring.

Furthermore, as with all carbonyl compounds, α-nitrooxyacetone can be hydrated in water, leading to an equilibrium with its geminal diol form; thus, the equilibrium constant, K_hyd, is defined if water activity is considered to be unity by Eq. (7).

$$\begin{array}{}\text{(7)}& K_{\mathrm{hyd}}={\displaystyle \frac{\left[\text{gem-diol}\right]}{\left[\text{carbonyl}\right]}}\end{array}$$

The reactivity of these partner molecules toward •OH radicals can be significantly different (Doussin and Monod, 2013), however, the experimental determination only refers to the global rate constant, defined by Eq. (8).

$$\begin{array}{}\text{(8)}& k_{\mathrm{overall}}={\displaystyle \frac{K_{\mathrm{hyd}}\cdot k_{\text{gem-diol}}+k_{\mathrm{carbonyl}}}{K_{\mathrm{hyd}}+\mathrm{1}}},\end{array}$$

where k_overall is the overall rate constant for the •OH oxidation, and k_gem-diol and k_carbonyl are the calculated rate constants for the related species. When performing the SAR calculation, this equilibrium was considered, and descriptors were proposed to determine both the carbonyl + •OH and gem-diol + •OH rate constants, and the overall rate constant was calculated to be compared with the experimental data.

Due to the absence of any experimental determination of K_hyd in the literature for organic nitrates, a specific experiment was performed to determine the hydration constant of α-nitrooxyacetone. This was done by dissolving the compound in D₂O and measuring the NMR ratios between the signals associated with the geminal diol configuration and the ones associated with the carbonyl form. Details on these experiments as well as the α-nitrooxyacetone NMR spectra are presented in Sect. S3. The hydration constant for α-nitrooxyacetone was determined to be $K_{\mathrm{hyd}}=\mathrm{0.048}\pm \mathrm{0.002}$ at 298 K.

3.3.2 Database for the extended SAR

A dataset of 24 experimental k_OH rate constants for linear ethers and 8 for cycloethers from the literature complemented by 7 organic nitrate k_OH rate constants determined in this work were used together to determine the contribution factors of each group. Table S4 compiles all compounds with the corresponding values of experimental k_OH rate constants and their associated uncertainties. The rate constants of •OH oxidation of all mentioned ethers were previously determined using competition kinetic methods. The rate constants were recalculated considering updated values for the reference compounds. For the latter, recommended values were chosen in most cases; however, when no recommendation was mentioned in the literature or when more recent studies were published, average values were calculated (Table S1). Outlier values were discarded by using Dixon's Q test.

The F, G, H, and X parameters were varied simultaneously using the Microsoft^® Excel^® Solver routine to solve the multivariate linear regressions in order to minimize the sum of the square difference between calculated and experimental values normalized by the experimental uncertainties (Eq. 9).

$$\begin{array}{}\text{(9)}& Q=\sum _i{\displaystyle \frac{(k_{i,\exp }-k_{i,\mathrm{sim}}{)}^{\mathrm{2}}}{{\mathit{\sigma }}_i^{\mathrm{2}}}},\end{array}$$

where k_i,exp and k_i,sim are the experimental and simulated k_OH values, respectively, for compound i, and σ_i is the experimental uncertainty. This target Q value allowed us to give priority, in the simulations, to experimental data determined with low uncertainties, thus improving the reliability of the SAR compared to the previous developments. The experimental uncertainties were determined thoroughly for organic nitrates (Sect. 4.2) and were directly used for the SAR. For ethers, the associated experimental uncertainties were recalculated by considering not only the linear plot uncertainties but also the uncertainties associated with the values for the reference compound, using the propagation of uncertainty. For the values reported with no uncertainty, we arbitrarily assigned a 100 % uncertainty to prevent an excessive contribution of unclear determinations. This was the case, for example, for all the determinations reported in the works from Anbar et al. (1966) and Eibenberger (1980).

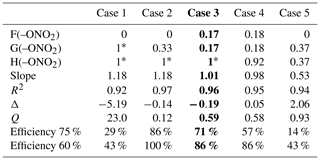
The preexisting parameters of the SAR were not modified, and they were used as reported in Doussin and Monod (2013) and Monod and Doussin (2008). To calculate the new parameters, in a first step, a rough estimation of the ether parameters (F(–O), G(–O–), and X(–O–)) was performed using our dataset by starting from different initial conditions. In a second step, a test of different constraints on organic nitrate parameters was performed using the ether parameters estimated in the first step (for isosorbide 5-mononitrate). Due to the restricted database for organic nitrates, constraints were settled on for the values of F(–ONO₂), G(–ONO₂), and H(–ONO₂), and five different cases were tested (Table 3) in order to find the best compromise between a minimum number of independent variables and a realistic parameterization of the possible long-range deactivating effects of the nitrate group. The five different cases were developed to investigate if the deactivating effect affects only the reactive sites in α position to the nitrate group (case 1) or reaches the reactive sites in β position (case 2 and case 3) or in γ position (case 4 and case 5). In the final step, once the optimal case was selected, all the new parameters were simultaneously adjusted using the whole dataset (Table 4).

Table 3 SAR tests on organic nitrate parameters: five case tests evaluated the nitrate group influence. Constraints imposed are the following: values fixed to 1 (i.e., no influence on the reactivity) marked by *; F(–ONO₂)=G(–ONO₂) for case 3 and case 4; and G(–ONO₂)=H(–ONO₂) for case 5. In bold is the selected case. The slope is the correlation slope between the simulated and the experimental k_OH rate constants, and R² is the corresponding correlation coefficient. The Δ factor is the relative difference between the simulated and the experimental rate constant. Q is the sum of the square difference between calculated and experimental values normalized by the experimental uncertainties. Efficiencies at 75 % and 60 % represent the percentage of organic nitrates with $\left|\mathrm{\Delta }\right|<\mathrm{0.25}$ and $\left|\mathrm{\Delta }\right|<\mathrm{0.40}$, respectively.

Table 4 SAR results: new calculated neighboring effects parameters for ethers, cyclic ethers and organic nitrates (using case 3 constraints).

3.3.3 SAR results

The results obtained for the five cases tested are shown in Table 3. Different parameters were evaluated in order to choose the optimal case. The correlation slope between the simulated and the experimental k_OH rate constants as well as their correlation coefficient, the Q values, and the relative difference between the simulated and the experimental rate constant was calculated for each organic nitrate using Eq. (10):

$$\begin{array}{}\text{(10)}& \mathrm{\Delta }={\displaystyle \frac{k_{\exp }-k_{\mathrm{sim}}}{k_{\exp }}},\end{array}$$

where the sum of all the individual Δ factors is given in Table 3. A value close to 0 indicates the absence of any significant bias.

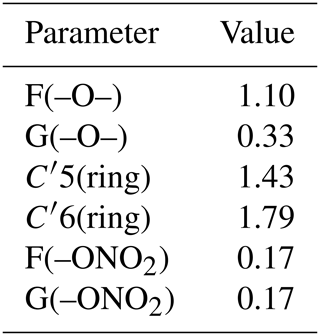
In all cases, each contribution factor for organic nitrates which was varied resulted in a value lower than 1, and the nearer to the nitrate group, the lower the value, confirming the deactivating effect of the group. Nonetheless, when cases 1, 2, and 5 were run, the calculated value for F(–ONO₂) dropped to 0, meaning a total suppression of the H-abstraction in the α position, which is unlikely, thus discarding these three cases. In the two remaining cases (3 and 4), the nitrate group impacts on the reactivity up to the β or the γ position, respectively. Most of the evaluation parameters are very similar in both cases, but case 4 is much less constrained than case 3, which holds only one variable (Table 3). Case 3 was thus selected as the optimal case. Furthermore, the value obtained for H(–ONO₂) in case 4 (0.92) is close to unity, thus showing a very slight influence of the nitrate group in the γ position, and the difference between this value and unity potentially falls in the experimental uncertainties. The results indicate that the impact of the nitrate group on the reactivity towards •OH radicals only affects the α- and the β-reactive sites. This means that the reduced reactivity (observed in Fig. 5) is caused by the electron-withdrawing effect of the nitrate group which is enhanced in the aqueous phase.

In the final step, using case 3 constraints, all the new parameters were simultaneously adjusted using the whole dataset, and the results are listed in Table 4. The resulting neighboring factors for organic nitrates are F(–ONO₂)= G(–ONO₂)=0.17. For ethers, the results show that F(–O–) = 1.10, which is a value higher than unity, and G(–O–) = 0.33, which is lower than 1. This reveals an influence similar to the –OH group, for which F(–OH) = 2.10 and G(–OH) = 0.44. For these groups, the α position is activating due to a positive mesomeric effect, whereas the β position is deactivating due to the oxygen electron-withdrawing effect. Furthermore, the resulting value for X(–O–) = 1.79 reflects that the presence of oxygen atoms in a ring increases the reactivity of the molecule.

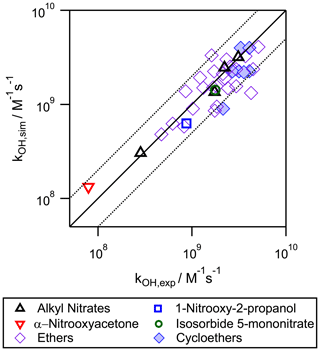
Figure 6 Correlation plot between the experimental and the simulated aqueous-phase •OH-oxidation rate constants for organic nitrates and ethers. The solid line corresponds to the 1:1 regression, and the dotted lines represent the limits where the simulated rate constants deviate from the experimental ones by a factor of 2.

Figure 6 shows the correlation between the calculated versus the experimental k_OH values, and it is compared to the 1:1 regression line. It shows good linearity covering a wide range of reactivities (over 2 orders of magnitude). The efficiency of the proposed extended SAR for organic nitrates, ethers, and cycloethers was studied by calculating the relative difference between the simulated and the experimental rate constants (Δ factor, see Eq. 10). Overall, for 51 % of the experimental values, the efficiency was better than 75 % ($\left|\mathrm{\Delta }\right|<\mathrm{0.25}$) and better than 60 % ($\left|\mathrm{\Delta }\right|<\mathrm{0.4}$) for 69 % of experimental values. For organic nitrates, six out of the seven studied molecules presented an efficiency better than 60 %. Compared to the previous versions of the SAR tested for other functional groups (Doussin and Monod, 2013; Monod and Doussin, 2008), the efficiencies were slightly lower. This may be due to the way the SAR parameters were calculated in this work. While the previous SAR aimed at minimizing Δ for a maximum number of values, in this work, a good efficiency was prioritized for the experimental values with low uncertainties using Eq. (9). Several arguments provide some evidence on the reliability of the application of the SAR to other compounds: (i) there are only a few discrepancies (deviations by a factor of 2) between the experimental and simulated values, even for low-weighted experimental values; (ii) the resolved parameters were chemically coherent; (iii) a wide range of reactivities were covered (2 orders of magnitude); and (iv) the good agreement between the simulated and the experimental k_OH values (within uncertainties) for isosorbide 5-mononitrate (Table 2). Being a highly complex polyfunctional compound (bearing two ring, two ether, one alcohol, and one nitrate groups), its good result gives some validation of the extended SAR application to polyfunctional compounds.

Due to the restricted database used here to build the extended SAR, the –ONO₂ contribution factors could not elucidate the differences between the F(–ONO₂) and G(–ONO₂) contribution factors. We acknowledge that the differences between the two factors may be significant as it happens for the gas-phase reactions (Jenkin et al., 2018). In order to better assess the detailed influence of the nitrate group to each carbon, more experimental determinations of the kinetic rate constants should be done for the reactivity of these compounds in the aqueous phase. However, as we have found a good agreement between the simulated values and the experimental ones, the present SAR is useful to estimate the importance of aqueous-phase •OH oxidation for organic nitrates in the atmosphere.

The extended SAR was used to calculate the •OH-oxidation rate constants of several atmospherically relevant compounds, such as hydroxy nitrates, isoprene nitrates, and terpene nitrates. The atmospheric fate of these molecules is discussed in the next section.

4 Atmospheric implications

In light of these results on the aqueous-phase •OH oxidation of organic nitrates, we estimated the importance of these processes in the atmosphere. We used the developed SAR to predict the k_OH rate constants of other atmospherically relevant organic nitrates to evaluate if the aqueous-phase •OH oxidation has a significant role in their atmospheric lifetimes. Some of the evaluated organic nitrates have been detected in field campaigns (Beaver et al., 2012; Li et al., 2018); they are expected products from isoprene or monoterpenes photooxidation (Lee et al., 2014), or they are small polyfunctional nitrates that may be formed by the fragmentation of terpene nitrates or by the oxidation of alkyl nitrates (Picquet-Varrault et al., 2020; Treves and Rudich, 2003). By selecting organic nitrates potentially relevant to atmospheric chemistry, as well as those mentioned in the literature, we listed 49 compounds that were divided into seven categories depending on their functionalization and chemical structure: 6 alkyl nitrates, 7 hydroxy nitrates, 7 ketonitrates, 5 aldehyde nitrates, 5 nitrooxy carboxylic acids, 7 other polyfunctional nitrates containing more than one oxygenated group, and 12 terpene nitrates corresponding to highly oxidized organic nitrates formed by the oxidation of terpenes, such as α- and β-pinene, limonene, and myrcene. Table S5 appends all the studied molecules and their chemical structures and properties under the scenarios studied below.

Inspired by the work of Epstein and Nizkorodov (2012), considering various aqueous-phase scenarios from cloud/fog conditions to wet aerosols, we evaluated the atmospheric phase partition of these 49 relevant organic nitrates, and we estimated the importance of the •OH-oxidation reaction in the aqueous phase. Finally, the atmospheric multiphase •OH-oxidation lifetimes of these compounds under cloud/fog conditions were calculated and compared to their gas-phase lifetimes.

4.1 Aqueous- and aerosol-phase partition of organic nitrates

The partition of atmospherically relevant organic nitrates between the aqueous, gas, and aerosol phases was evaluated. The partition between the gas and aqueous phases was calculated using Eq. (11):

$$\begin{array}{}\text{(11)}& K_{\mathrm{gas}/\mathrm{aq}}={\displaystyle \frac{n_{\mathrm{X},\mathrm{gas}}}{n_{\mathrm{X},\mathrm{aq}}}}={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{W}}}{L_{\mathrm{WC}}{K}_{\mathrm{H}}RT}},\end{array}$$

where n_X,gas and n_X,aq are the number of moles of compound X that are present in the gas and aqueous phases, respectively; ρ_W is the density of water (in g m⁻³); L_WC is the liquid water content (LWC in g m⁻³); K_H is the effective Henry's law constant (in mol L⁻¹ atm⁻¹); R is the ideal gas constant equal to 0.082 atm L mol⁻¹ K⁻¹; and T is the temperature in kelvin.

The partition between the gas and the aerosol phases was calculated using Eq. (12):

$$\begin{array}{}\text{(12)}& K_{\mathrm{gas}/\mathrm{aer}}={\displaystyle \frac{n_{\mathrm{X},\mathrm{gas}}}{n_{\mathrm{X},\mathrm{aer}}}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{M_{\mathrm{aer}}}{\mathit{\gamma }}_{\mathrm{X}}{P}_{\mathrm{X}}^{\mathrm{vap}}}{C_{\mathrm{aer}}RT}},\end{array}$$

where n_X,aer is the number of moles of compound X that are present in the aerosol phase, $\stackrel{\mathrm{‾}}{M_{\mathrm{aer}}}$ is the mean organic molar mass in the aerosol phase (in g mol⁻¹), γ_X is the activity coefficient of compound X, $P_{\mathrm{X}}^{\mathrm{vap}}$ is its saturation vapor pressure (in atm), and C_aer is the total organic aerosol mass concentration (in g m⁻³). Combining Eqs. (11) and (12), one obtains the fraction of any compound in each phase. The concentration of a compound in each phase depends on the values of K_H and $P_{\mathrm{X}}^{\mathrm{vap}}$.

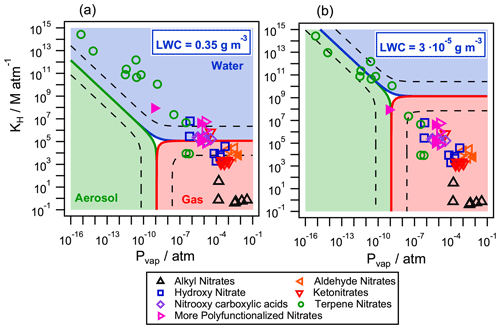
Figure 7 Partition of atmospherically relevant organic nitrates in the aqueous phase (blue), the gas phase (red), and the aerosol phase (green) for two different air parcels with (a) LWC = 0.35 g m⁻³ (cloud/fog conditions) and (b) LWC = $\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ (wet aerosol conditions). The temperature was set to 298 K and the aerosol mass concentration to $C_{\mathrm{aer}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ with a $\stackrel{\mathrm{‾}}{M_{\mathrm{aer}}}=\mathrm{200}$ g mol⁻¹. The dashed lines represent the limits where the concentration of one compound exceeds 95 % in each phase. Filled markers represent organic nitrates derived from isoprene.

The partition was studied for two representative atmospheric conditions: (i) under typical cloud/fog conditions with a LWC=0.35 g m⁻³ (Fig. 7a) and (ii) under wet aerosol conditions with a lower $\mathrm{LWC}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ (Fig. 7b) (Herrmann et al., 2015). The aerosol mass concentration was set to $C_{\mathrm{aer}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ with a $\stackrel{\mathrm{‾}}{M_{\mathrm{aer}}}=\mathrm{200}$ g mol⁻¹ and T=298 K. The values of K_H were calculated using the SAR developed by Raventos-Duran et al. (2010), and the values of $P_{\mathrm{X}}^{\mathrm{vap}}$ were calculated with the group contribution method by Nannoolal et al. (2004, 2008). Both values were taken from the GECKO-A website (http://geckoa.lisa.u-pec.fr/generateur_form.php, last access: 16 May 2020). The activity coefficient was assumed to be 1 due to the lack of experimental or simulated data, while, in a real organic aerosol, γ_X can range from 0.8 to 10 (Wania et al., 2014). It is worth noting that, in the atmosphere, the equilibrium may not be instantaneous. In their kinetic flux model, Shiraiwa and Seinfeld (2012) demonstrate that equilibrium is achieved on the order of seconds or minutes for the phase partitioning of relatively high volatility organic compounds into liquid particles, while the equilibration timescale ranges from hours to days for semisolid viscous particles, low volatility species, or large particle sizes and thus can be subject to equilibrium shifts by faster chemical reactions in each phase. However, these considerations are beyond the scope of the study, as the goal was to determine how aqueous-phase chemistry can affect the fate of organic nitrates even at very low LWC. Thus, Eq. (12) was used to understand if the partition into the aerosol phase is important compared to the aqueous phase and the gas phase, under the two investigated conditions.

Figure 7 shows the partition of the selected 49 relevant organic nitrates in the three phases. Under cloud/fog conditions (LWC=0.35 g m⁻³, Fig. 7a), all compounds partition between the aqueous phase (blue) and the gas phase (red). The presence of terpene nitrates in the aqueous phase is highly significant: 10 out of the 12 studied molecules are present in the aqueous phase in proportions higher than 95 %. Under the same conditions, small functionalized nitrates (with five carbons or less) partition in both phases depending on their functionalization. No significant partition to the aerosol phase is observed under these conditions. Under wet aerosol conditions ($\text{LWC}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³, Fig. 7b), small organic nitrates are only present in the gas phase (red). High-molecular-mass compounds such as terpene nitrates equally partition between the aqueous (blue) and the aerosol phases (green).

These results show that, depending on their reactivity, the compounds which mainly partition into the aqueous phase may show a different atmospheric lifetime compared to the one assessed if only the gas-phase reactions are considered.

4.2 •OH-oxidation multiphase lifetimes of organic nitrates

The atmospheric reactivity of each of the 49 organic nitrates with •OH radicals in the gas phase was compared to the aqueous-phase one using the W value defined in Eq. (13):

$$\begin{array}{}\text{(13)}& W={\displaystyle \frac{\frac{\mathrm{d}{n}_{\mathrm{X},\mathrm{gas}}}{\mathrm{d}t}}{\frac{\mathrm{d}{n}_{\mathrm{X},\mathrm{aq}}}{\mathrm{d}t}}}={\displaystyle \frac{{\mathit{\rho }}_W}{L_{\mathrm{WC}}{K}_{\mathrm{H}}RT}}{\displaystyle \frac{k_{\mathrm{OH},\mathrm{gas}}[\mathrm{OH}{]}_{\mathrm{gas}}}{k_{\mathrm{OH},\mathrm{aq}}[\mathrm{OH}{]}_{\mathrm{aq}}}},\end{array}$$

where k_OH,gas and k_OH,aq are the gas-phase and aqueous-phase •OH-oxidation rate constants, respectively (in mol L⁻¹ s⁻¹, with L being the volume unit of air and atmospheric water for k_OH,gas and k_OH,aq, respectively). [OH]_gas and [OH]_aq (in mol L⁻¹ of air and mol L⁻¹ of atmospheric water, respectively) are the concentrations of hydroxyl radicals in the gas and the aqueous phases.

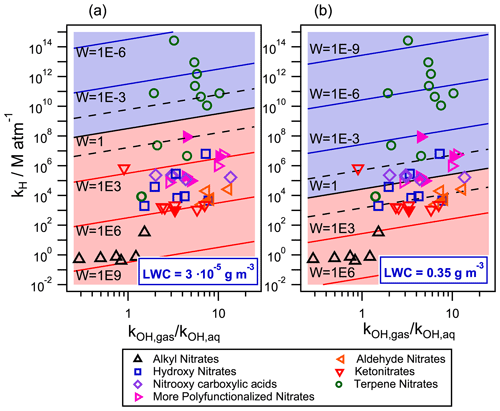
Figure 8 Gas–aqueous partition and reactivity (towards •OH-oxidation) of 49 organic nitrates for two different air parcels with (a) LWC = 0.35 g m⁻³ (cloud/fog conditions) and (b) LWC = $\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ (wet aerosol conditions) at 298 K. The •OH radical concentrations were set to $\mathrm{2.32}\times {\mathrm{10}}^{-\mathrm{15}}$ mol L⁻¹ (1.4×10⁶ molecules cm⁻³) in the gas phase and to 10⁻¹⁴ mol L⁻¹ in the aqueous phase. Filled markers represent organic nitrates derived from isoprene.

Figure 8 compares the •OH reactivity of organic nitrates in the aqueous and the gas phases for cloud/fog conditions (Fig. 8a) and for wet aerosol conditions (Fig. 8b) described in the previous section. The •OH radical concentrations were set to 1.4×10⁶ molecules cm⁻³ ($\mathrm{2.32}\times {\mathrm{10}}^{-\mathrm{15}}$ mol L⁻¹) in the gas phase and 10⁻¹⁴ mol L⁻¹ in the aqueous phase (Tilgner et al., 2013). The k_OH,aq rate constants were calculated using the extended SAR developed in this work (Eq. 6). Neighboring factors for nitrate and ether groups were those calculated in this work (Table 4), while all other parameters were taken from Doussin and Monod (2013) and Monod and Doussin (2008). Equation (8) was employed for compounds containing carbonyl groups. For organic nitrates containing a carboxylic acid functional group, the contributions of both the protonated molecule and its conjugated base were considered. For these compounds, the pH was set to 5 and 3 for cloud/fog conditions and for wet aerosol conditions, respectively. The experimental k_OH,gas values were used when available (references in Fig. 5). They were complemented, when necessary, using the gas-phase SAR developed by Jenkin et al. (2018). The GROHME method was used to obtain the K_hyd for compounds containing a carbonyl group (Raventos-Duran et al., 2010). Both the simulated k_OH,gas and K_hyd were taken from the GECKO-A website (http://geckoa.lisa.u-pec.fr/generateur_form.php, last access: 16 May 2020).

The y axis of Fig. 8 represents the effective Henry's law constant for each molecule. The ratio of gas- to aqueous-phase •OH-oxidation rate constant (in liters of air per liter of atmospheric water) is shown in the x axis. Isopleths show the W values. A W value lower than 1 (blue background) implies that more than 50 % of the target compound is consumed in the aqueous phase. The two dashed isopleths above and below the W=1 isopleth represent the limits for aqueous- and gas-phase processing exceeding 95 %, respectively.

Under cloud/fog conditions (Fig. 8a), most of the studied compounds present important aqueous-phase processing. Most of the terpene nitrates are highly functionalized and have a high molecular weight; they are almost absent in the gas phase, and their •OH oxidation is solely governed by their aqueous-phase kinetics. Only two terpene nitrates, which are first-generation reaction products of α- and β-pinene NO₃•-oxidation (Li et al., 2018), have a sufficiently low K_H for their •OH removal to take place mostly in the gas phase (≈93 %) due to their low functionalization.

For smaller functionalized organic nitrates, the gas-phase •OH-oxidation reaction is important. However, one can see that an important fraction of the compounds is located between the dashed isopleths, meaning that both the gas- and the aqueous-phase processing are relevant in their atmospheric loss towards •OH radicals. This behavior is highly related to the functionalization of the organic nitrate. For small ketonitrates and aldehyde nitrates, their loss is mainly taking place in the gas phase. With the increase of polarity, such as for hydroxy nitrates, and even more substantially for nitrooxy carboxylic acids, the aqueous-phase •OH oxidation becomes more important. For organic nitrates with more than one oxidized group, their processing in the aqueous phase becomes the major loss process. This observation could be relevant for atmospheric chemistry since some products of isoprene photooxidation are highly functionalized organic nitrates (Fisher et al., 2016).

Figure 8b shows the relative importance of aqueous-phase •OH oxidation under wet aerosol conditions ($\text{LWC}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³). Under these conditions, the aqueous-phase •OH oxidation is relevant for most of the terpene nitrates. However, under these conditions, these compounds should also partition to the aerosol phase (Fig. 7b). In this phase, not only the •OH-oxidation kinetic rate constants may differ from the gas- and the aqueous-phase ones but also other oxidants, such as singlet oxygen or the triplet excited state of dissolved organic matter, can play a crucial role in the atmospheric loss of these compounds (Kaur and Anastasio, 2018; Manfrin et al., 2019). Therefore, this chemistry should be included to precisely evaluate the atmospheric loss of terpene nitrates at these conditions. For small organic nitrates, the gas-phase •OH-oxidation reaction remains their major loss pathway. Figure 8 shows that for most of the compounds for which the aqueous phase is the major loss process, the ratio $k_{\mathrm{OH},\mathrm{gas}}/k_{\mathrm{OH},\mathrm{aq}}$ is higher than 1, thus inducing a slower consumption in the aqueous phase. This point is specifically investigated in Fig. 9 and Table S5.

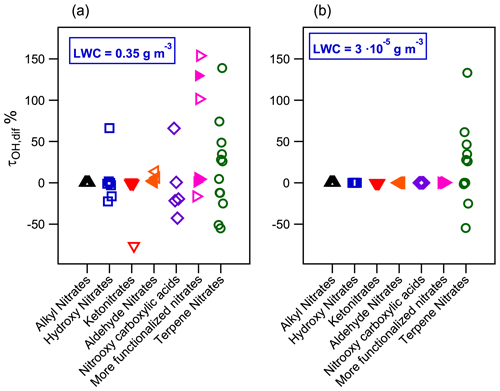
Figure 9 Relative difference of •OH-oxidation lifetimes between an air parcel with and without liquid water at (a) LWC = 0.35 g m⁻³ and (b) LWC = $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ g m⁻³ for atmospherically relevant organic nitrates. Filled markers represent organic nitrates derived from isoprene.

Multiphase •OH-oxidation lifetimes (τ_{OH,multiphase}) were calculated for each organic nitrate by considering the •OH reactivity both in the atmospheric aqueous phase and gas phase using Eq. (14):

$$\begin{array}{}\text{(14)}& \begin{array}{rl}& {\mathit{\tau }}_{\mathrm{OH},\mathrm{multiphase}}\\ & ={\displaystyle \frac{\mathrm{1}}{{\mathrm{\Phi }}_{\mathrm{aq}}{k}_{\mathrm{OH},\mathrm{aq}}[\mathrm{OH}{]}_{\mathrm{aq}}+{\mathrm{\Phi }}_{\mathrm{gas}}{k}_{\mathrm{OH},\mathrm{gas}}[\mathrm{OH}{]}_{\mathrm{gas}}}},\end{array}\end{array}$$

where Φ_aq and Φ_gas are the fractions of each compound present in the aqueous and gas phases, respectively.

Under cloud/fog conditions, the multiphase •OH-oxidation lifetimes range from hours to several days, and they are compiled in Table S5. Their τ_{OH,multiphase} is dependent on the chemical structure of the molecules. Large molecules, such as terpene nitrates, or compounds with reactive groups such as aldehyde nitrates show low •OH-oxidation lifetimes (from 6 to 27 h). For most of the other organic nitrates, their lifetimes range from 1 d to 1 week, such as primary alkyl nitrates, hydroxy nitrates, ketonitrates with more than three carbon atoms, or organic nitrates containing more than one different functional group. The last category contains four important isoprene-derived nitrates for which multiphase •OH-oxidation lifetimes are 1 d for C₅ dihydroxy dinitrate, 1 d for methacrolein nitrate, and 2 and 4 d for the two isomeric forms of methylvinyl nitrate. The most persistent molecules towards •OH that are present are small (≤3 carbon atoms), they bear reactivity-inhibiting functional groups such as carboxylic groups, or they combine more than one nitrate group. The multiphase •OH-oxidation lifetimes for these molecules can reach 28 d. Isopropyl nitrate and α-nitrooxyacetone, compounds which have been widely detected in the atmosphere, present very low atmospheric reactivity towards •OH radicals (24 and 19 d, respectively).

Among the selected organic nitrates, some compounds bear their nitrate group on a tertiary carbon; these species may undergo very fast hydrolysis (Darer et al., 2011; Jacobs et al., 2014). Their lifetimes with respect to hydrolysis range from 1 min to 8.8 h (Takeuchi and Ng, 2019). Therefore, for most of these compounds, their hydrolysis is likely the main loss reaction in the atmosphere. Nevertheless, as mentioned in Sect. 1, the non-hydrolyzable fraction of organic nitrates ranges from 68 % to 91 % for α-pinene- and β-pinene-derived organic nitrates; thus, for most of these organic nitrates this reaction does not occur.

Photolysis is also a likely sink for organic nitrates, mostly for carbonyl nitrates. Gas-phase photolysis lifetimes have been experimentally determined or simulated for 11 of these compounds, and they range from 0.5 to 15 h (Barnes et al., 1993; Müller et al., 2014; Picquet-Varrault et al., 2020; Suarez-Bertoa et al., 2012). At these rates, gas-phase photolysis is expected to be the main chemical loss process for low-molecular-weight carbonyl nitrates. On the other hand, to our knowledge, no aqueous-phase photolysis lifetimes have been experimentally determined for carbonyl nitrates. Meanwhile, Romonosky et al. (2015) investigated molar absorptivity of a series of β-hydroxynitrates in the aqueous phase, and, assuming similar quantum yields as in the gas phase, they calculated the photolysis rate constant ratios between the gas and aqueous phases. Using their approach, aqueous-phase photolysis is likely a major sink for water-soluble carbonyl nitrates as it likely occurs for most isoprene-derived nitrates. However, their results show that •OH oxidation in the aqueous phase or the gas phase is a more significant loss process than photolysis for β-hydroxynitrates. This could be the case for atmospherically relevant species such as C₅ dihydroxy dinitrate or for terpene nitrates. For the latter, their •OH-oxidation lifetimes fall in the same range as the photolysis lifetimes reported for carbonyl nitrates in the gas phase; thus, both processes may be relevant for terpene nitrates including those containing carbonyl groups, but further experimental studies would deserve attention to confirm this.

To assess the impact that aqueous-phase •OH oxidation has on organic nitrate lifetimes, the •OH-oxidation lifetime relative difference was calculated (τ_OH,dif) for each compound using Eq. (15):

$$\begin{array}{}\text{(15)}& {\mathit{\tau }}_{\mathrm{OH},\mathrm{dif}}\mathit{\%}={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{OH},\mathrm{multiphase}}-{\mathit{\tau }}_{\text{OH,gas phase}}}{{\mathit{\tau }}_{\text{OH,gas phase}}}}\cdot \mathrm{100},\end{array}$$

where τ_{OH, multiphase} derives from Eq. (14), and τ_{OH,gas phase} is the •OH-oxidation lifetime of a compound considering only the gas phase. For molecules barely partitioning into the aqueous phase, the τ_OH,dif value is close to zero. For molecules partitioning into the aqueous phase, a positive value of τ_OH,dif indicates that the aqueous-phase reactivity increases the atmospheric lifetime of the molecule, while a negative value implies a faster atmospheric removal via aqueous-phase reactivity.

Figure 9a shows τ_OH,dif for the studied organic nitrates. For the families of compounds such as alkyl nitrates, most of the ketonitrates and aldehyde nitrates, which barely partition into the aqueous phase, show that their lifetimes remain unchanged compared to the gas-phase reactivity. Substantial atmospheric loss is expected for hydroxy nitrates, nitrooxy carboxylic acids, and organic nitrates with more than one oxidized group as in the case of some isoprene and terpene nitrates. Their τ_OH,dif ranges from −75 % to +155 %, implying that their global •OH-oxidation lifetimes may be either shortened or lengthened when the aqueous phase is considered, depending on the chemical structure of the molecule. Figure 9 shows that for most of these compounds, especially many terpene nitrates and some polyfunctionalized isoprene nitrates, their atmospheric lifetimes significantly increase (by a factor that can exceed 140 %), thus showing that their atmospheric lifetimes should be even longer than what is predicted from gas-phase reactions. This effect might be enhanced considering that aqueous •OH concentrations might be lower than the one used in Eq. (14), i.e., $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{14}}$ M. This value corresponds to aqueous concentrations of •OH in polluted/urban cloud droplets (Tilgner et al., 2013). Nevertheless, for remote cloud droplets or wet aerosols, the aqueous •OH concentration might be 2 to 10 times lower (Arakaki et al., 2013). These lower concentrations would induce an increase in the •OH-oxidation lifetimes of molecules partitioning into the aqueous phase.

Figure 9b shows that under wet aerosol conditions, only terpene nitrate •OH-oxidation lifetimes are affected when considering the aqueous phase. Under this LWC condition, the proposed terpene nitrates partition both in the aqueous phase and the aerosol phase (Fig. 7b). In the aerosol phase, not only the •OH-oxidation kinetic rate constants may differ from the gas- and the aqueous-phase ones but also other oxidants can play a crucial role in the atmospheric loss of these compounds (Kaur and Anastasio, 2018; Manfrin et al., 2019). Further studies comprising this reactivity are thus needed to better understand the fate of organic nitrates in all atmospheric phases.

5 Conclusions

A new competition kinetic method was developed to accurately determine the aqueous-phase •OH-oxidation rate constants of species with low reactivity such as organic nitrates, using a robust reference compound such as methanol. The method was applied to determine new •OH-oxidation kinetics of seven organic nitrates (isopropyl nitrate, isobutyl nitrate, 1-pentyl nitrate, isopentyl nitrate, α-nitrooxyacetone, 1-nitrooxy-2-propanol, isosorbide 5-mononitrate), which are compounds for which the aqueous-phase •OH-oxidation reaction was investigated for the first time. It was found that the nitrate group provokes an important deactivation of the •OH attack, similar to the corresponding gas-phase reactions but enhanced by solvent kinetic effects. A previously developed SAR method was extended to include the nitrate group, allowing the prediction of aqueous-phase kinetics for these atmospherically relevant compounds. The resulting SAR parameters for the nitrate group confirmed the extreme deactivating effect of the nitrate group, up to two adjacent carbon atoms. The achieved SAR was then used to evaluate the multiphase fate of 49 organic nitrates of atmospheric relevance, including hydroxy nitrates, ketonitrates, aldehyde nitrates, nitrooxy carboxylic acids, and more functionalized organic nitrates. Among these compounds, polyfunctional organic nitrates were found to be extremely impacted by the aqueous-phase •OH oxidation not only due to their very high water solubility but also due to their reduced reactivity in this solvent. For 50 % of the proposed organic nitrates for which the •OH reaction occurs mainly in the aqueous phase (more than 50 % of the overall removal), their •OH-oxidation lifetimes increased by 20 % to 155 % under cloud/fog conditions. This was even more pronounced for terpene nitrates: for 83 % of them, the reactivity towards •OH occurred mostly (>98 %) in the aqueous phase under fog/cloud conditions, while for 60 % of these terpene nitrates their lifetimes increased by 25 % to 140 % compared to their gas-phase reactivity. We demonstrate that these effects are of importance under cloud/fog conditions but also under wet aerosol conditions, especially for the terpene nitrates. These results suggest that considering aqueous-phase •OH-oxidation reactivity of biogenic organic nitrates is necessary to improve the predictions of their atmospheric fates and transport, and they should result in a better assessment of the distribution of air pollution, SOA formation, and NO_x chemistry.

Appendix A: Determining aqueous-phase k_OH by monitoring the headspace with the PTR-MS

Since the organic compounds were diluted in the aqueous phase, headspace analyses were based on the direct proportionality between water and gas-phase concentrations of the analytes (Karl et al., 2003). Furthermore, the influence of the gas-phase •OH oxidation was negligible in our system. Equation (1) can be written as

$$\begin{array}{}\text{(A1)}& \ln {\displaystyle \frac{[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{g}\right)}}{[\mathrm{X}{]}_{t\left(\mathrm{g}\right)}}}={\displaystyle \frac{k_{\mathrm{OH},\mathrm{X}}}{k_{\mathrm{OH},\mathrm{M}}}}\cdot \ln {\displaystyle \frac{[\mathrm{M}{]}_{\mathrm{0}\left(\mathrm{g}\right)}}{[\mathrm{M}{]}_{t\left(\mathrm{g}\right)}}},\end{array}$$

where $\ln \left(\right[\mathrm{X}{]}_{\mathrm{0}\left(\mathrm{g}\right)}/\left[\mathrm{X}{]}_{t\left(\mathrm{g}\right)}\right)$ and $\ln \left(\right[\mathrm{M}{]}_{\mathrm{0}\left(\mathrm{g}\right)}/\left[\mathrm{M}{]}_{t\left(\mathrm{g}\right)}\right)$ represent the gas-phase concentration relative decay of the target compound and methanol, respectively. The gas-phase relative decays of both methanol and (in some cases) the target compound were monitored by the PTR-MS instrument. The PTR-MS measured quantities in counts per second (cps), which can be related to absolute headspace concentrations using Eq. (A2),

$$\begin{array}{}\text{(A2)}& {\left[\mathrm{X}\right]}_{\mathrm{g}}={\displaystyle \frac{\mathrm{1}}{k_{R_{\mathrm{rate}}}{t}_{R_{\mathrm{time}}}}}\cdot {\displaystyle \frac{\sum \mathrm{cps}\left({\mathrm{X}}^{+}\right)}{\mathrm{cps}\left({\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}\right)}},\end{array}$$

where $\sum \mathrm{cps}\left({\mathrm{X}}^{+}\right)$ is the sum of the counts per second of all the fragments which correspond to compound X; the cps(H₃O⁺) values are the counts per second of the hydronium ions that protonate the molecule; $k_{R_{\mathrm{rate}}}$ is the protonation rate constant for compound X in the PTR-MS drift tube; and $t_{R_{\mathrm{time}}}$ is the time spent by the molecule in the drift tube. Combining Eqs. (A1) and (A2), one obtains Eq. (2).