the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluated kinetic and photochemical data for atmospheric chemistry: volume VIII – gas-phase reactions of organic species with four, or more, carbon atoms ( ≥ C4)
Abdelwahid Mellouki
Markus Ammann
R. Anthony Cox
John N. Crowley
Hartmut Herrmann
Michael E. Jenkin
V. Faye McNeill
Jürgen Troe
Timothy J. Wallington
This article, the eighth in the series, presents kinetic and photochemical data sheets evaluated by the IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation. It covers the gas-phase thermal and photochemical reactions of organic species with four, or more, carbon atoms (≥ C4) available on the IUPAC website in 2021, including thermal reactions of closed-shell organic species with HO and NO3 radicals and their photolysis. The present work is a continuation of volume II (Atkinson et al., 2006), with new reactions and updated data sheets for reactions of HO (77 reactions) and NO3 (36 reactions) with ≥ C4 organics, including alkanes, alkenes, dienes, aromatics, oxygenated, organic nitrates and nitro compounds in addition to photochemical processes for nine species. The article consists of a summary table (Table 1), containing the recommended kinetic parameters for the evaluated reactions, and a supplement containing the data sheets, which provide information upon which recommendations are made.
- Article
(138 KB) - Full-text XML
-
Supplement
(3650 KB) - BibTeX
- EndNote
In the mid-1970s, it was appreciated that there was a need for the establishment of an international panel to produce a set of critically evaluated rate parameters for reactions of interest for atmospheric chemistry. To this end, the CODATA Task Group on Chemical Kinetics, under the auspices of the International Council of Scientific Unions (ICSU), was formed in 1977 and tasked to produce an evaluation of relevant, available kinetic and photochemical data. The first evaluation by this international committee was published in J. Phys. Chem. Ref. Data in 1980 (Baulch et al., 1980), followed by supplements in 1982 (Baulch et al., 1982) and 1984 (Baulch et al., 1984). In 1986 the IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry superseded the original CODATA Task Group for Atmospheric Chemistry. The subcommittee continued its data evaluation programme with supplements published in 1989 (Atkinson et al., 1989), 1992 (Atkinson et al., 1992), 1997 (Atkinson et al., 1997a), 1997 (Atkinson et al., 1997b), 1999 (Atkinson et al., 1999) and 2000 (Atkinson et al., 2000).
The gas-phase evaluation work was expanded to include heterogeneous reactions of gases on solid and liquid substrates in 2005. Aqueous-phase reactions of atmospheric importance were added in 2015. The IUPAC group's work now includes over 1400 gas-phase, heterogeneous and aqueous-phase reactions of importance in atmospheric chemistry. Reflecting the broader scope, the group changed its name to the IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation in 2013. Cox (2012) and Cox et al. (2018) discuss the history of IUPAC data evaluations and their role in addressing the critical societal challenges of stratospheric ozone loss, tropospheric ozone formation, acid rain, urban air pollution, aerosol formation and climate change.
In 2000 the evaluation was made available on the World Wide Web (http://iupac.pole-ether.fr, last access: 25 January 2021). The IUPAC website hosts an interactive database with a search facility and hyperlinks between the summary table and the data sheets, both of which can be downloaded as individual Word and PDF files. Work is underway to convert the data sheets to machine-readable XML files, which will enable the automatic transfer of IUPAC-recommended data into atmospheric models. The IUPAC group continues to update and extend the set of evaluated reactions. To enhance the accessibility of this updated material to the scientific community, the evaluation has been published as a series of articles in Atmospheric Chemistry and Physics (Atkinson et al., 2004, 2006, 2007, 2008; Crowley et al., 2010; Ammann et al., 2013; Cox et al., 2020). We present here in volume VIII new data sheets for gas-phase thermal and photochemical initiation reactions of organic species with four, or more, carbon atoms. The coverage of this volume includes evaluation of the thermal reactions of the organic species with HO and NO3 radicals and photolysis. The reactions with O3 are included in a separate volume within this series (Cox et al., 2020), along with the chemistry of the Criegee intermediates produced. The coverage of the evaluation was previously limited to the reactions of ≤ C3 organics, selected larger species (n-butane, isoprene, 2-methyl-but-3-en-2-ol and α-pinene) and some related oxygenated products (Atkinson et al., 2006). This has been substantially increased to include all C4 alkanes and alkenes, benzene and toluene, monoterpenes and sesquiterpenes and related oxygenated products. This volume therefore presents evaluations for 97 new reactions and updates for 25 reactions of organic species with four, or more, carbon atoms.
For each reaction covered in this volume, a data sheet with details about, for example, experimental methods and a justification of the choice of preferred value is available in the Supplement. The data sheets covering gas-phase reactions are principally of two types: (i) those for individual thermal reactions and (ii) those for the individual photochemical reactions.
2.1 Thermal reactions
The data sheets begin with a statement of the reactions including known/potential product channels when this information is available. The available kinetic data on the reactions are summarized under two headings: (i) absolute rate coefficients and (ii) relative rate coefficients. Under both headings, we list the published experimental data as absolute rate coefficients. If the temperature coefficient has been measured, the results are given in a temperature-dependent form over a stated temperature range. For bimolecular reactions, the temperature dependence is usually expressed in the normal Arrhenius form, k= A exp(), where . For a few bimolecular reactions, we have listed temperature dependencies in alternative forms such as k= C( K)nexp() or k= ET2exp(), where the original authors have found that alternative expressions give a better fit to the data. In our recommendations we seek to provide simple Arrhenius expressions that describe the kinetics over the atmospherically relevant temperature range (200–300 K). More complex expressions which are often needed to describe the kinetic behaviour over larger ranges of temperature are given in the “Comments on preferred values” section in the data sheets. Rate coefficients are given here in units of cubic centimetres per molecule per second (cm3 molecule−1 s−1). Note that “molecule” is not a unit recognized by IUPAC but is included for clarity. For pressure-dependent combination and dissociation reactions, the non-Arrhenius temperature dependence is used. This is discussed more fully in a subsequent section of this guide. Single temperature data are presented as such, and wherever possible the rate coefficient at, or close to, 298 K is quoted directly as measured by the original authors. This means that the listed rate coefficient at 298 K may differ slightly from that calculated from the Arrhenius parameters determined by the same authors. Rate coefficients at 298 K marked with an asterisk indicate that the value was calculated by extrapolation of a measured temperature range which did not include 298 K. The tables of experimental data are supplemented by a series of comments summarizing the experimental details. The abbreviations relating to experimental techniques that are used in the “Techniques/comments” and “Comments” sections are defined in the Appendix.
Table 1Summary of recommended rate coefficients for organic (≥ C4) reactions.
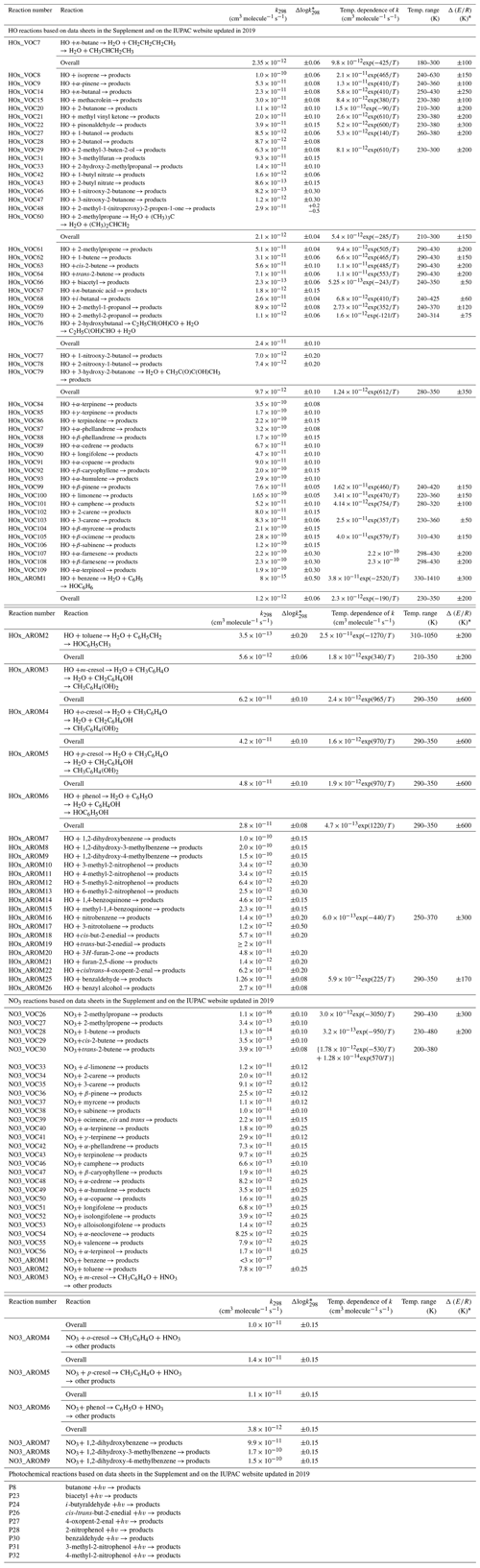
* The cited uncertainty corresponds approximately to 95 % confidence limits.
For measurements of relative rate coefficients, wherever possible the comments contain the actual measured ratio of rate coefficients together with the rate coefficient of the reference reaction used to calculate the absolute rate coefficient listed in the data table. The absolute value of the rate coefficient given in the table may be different from that reported by the original author, owing to a different choice of rate coefficient of the reference reaction. Whenever possible the reference rate coefficient data are those preferred in the present evaluation.
The preferred values in the data sheets are based on our consideration of the suitability of the experimental method and coverage of applicable parameter space (temperature, total pressure of diluent gas, partial pressure of gas-phase species) within the atmospherically relevant range. The general approach and methods used have been reviewed by Cox (2012). It is recognized that preferred values may change with publication of new data, and such changes are updated on the website. The preferred rate coefficients are presented (i) at a temperature of 298 K and (ii) in temperature-dependent form over a stated temperature range. This is followed by a statement of the uncertainty limits in log k at 298 K and the uncertainty limits in (), for the mean temperature in the range. Some comments on the assignment of uncertainties are given later in this guide to the data sheets. The “Comments on preferred values” describe how the selection was made and give any other relevant information. The extent of the comments depends upon the present state of our knowledge of the particular reaction in question. The data sheets are concluded with a list of the relevant references.
2.2 Conventions concerning rate coefficients
All of the reactions are considered to be elementary processes. Thus the rate expression is derived from a statement of the reaction, e.g.
Note that the stoichiometric coefficient for A, i.e. 2, appears in the denominator before the rate of change of [A] (which is equal to 2k[A]2) and as a power on the right-hand side. Representations of k as a function of temperature characterize simple “direct” bimolecular reactions. Sometimes it is found that k also depends on the pressure and the nature of the bath gas. This may be an indication of complex formation during the course of the bimolecular reaction, which is always the case in combination reactions. In the following sections the representations of k which are adopted in these cases are explained.
2.3 Treatment of combination and dissociation reactions
Unlike simple bimolecular reactions such as those considered in Sect. 2.2, combination reactions
and the reverse dissociation reactions
are composed of sequences of different types of physical and chemical elementary processes. Their rate coefficients reflect the more complicated sequential mechanism and depend on the temperature, T, and the nature and concentration of the third body, M. In this evaluation, the combination reactions are described by a formal second-order rate law:
while dissociation reactions are described by a formal first-order rate law:
In both cases, k depends on the temperature and on the concentration of M, i.e. [M]. To rationalize the representations of the rate coefficients used in this evaluation, we first consider the Lindemann–Hinshelwood reaction scheme. The combination reactions follow an elementary mechanism of the form
while the dissociation reactions are characterized by
Assuming quasi-stationary concentrations for the highly excited unstable species AB* (i.e. that d[AB*]/dt ≈ 0), it follows that the rate coefficient for the combination reaction is given by
while that for the dissociation reaction is given by
In these equations the expressions before the parentheses represent the rate coefficients of the process initiating the reaction, whereas the expressions within the parentheses denote the fraction of reaction events which, after initiation, complete the reaction to products. In the low-pressure limit ([M] → 0) the rate coefficients are proportional to [M]; in the high-pressure limit ([M] →∞) they are independent of [M]. It is useful to express k in terms of the limiting low-pressure and high-pressure rate coefficients:
From this convention, the Lindemann–Hinshelwood equation is obtained:
It follows that, for combination reactions, and k∞=k1, while, for dissociation reactions, and . Since detailed balancing applies, the ratio of the rate coefficients for combination and dissociation at a fixed T and [M] is given by the equilibrium constant .
Starting from the high-pressure limit, the rate coefficients fall off with decreasing third-body concentration [M], and the corresponding representation of k as a function of [M] is termed the “falloff curve” of the reaction. In practice, the above Lindemann–Hinshelwood expressions do not suffice to characterize the falloff curves completely. Because of the multistep character of the collisional deactivation (k2[M]) and activation (k−2[M]) processes, and energy and angular momentum dependences of the association (k1) and dissociation (k−1) steps, as well as other phenomena, the falloff expressions have to be modified. This can be done by including a broadening factor F in the Lindemann–Hinshelwood expression (Troe, 1979):
The broadening factor F depends on the ratio , which is proportional to [M], and can be used as a measure of “reduced pressure”. The first factors on the right-hand side represent the Lindemann–Hinshelwood expression, and the additional broadening factor F, at not too high temperatures, is approximately given by (Troe, 1979)
where log = log10 and N≈ [0.75–1.27 log Fc].
When Fc decreases, the falloff curve broadens and becomes asymmetric (i.e. . The given equation for F then becomes insufficient and should be replaced, for example, by
where [ln2ln(] [0.8 + 0.2 xq], 1)ln() and ln = loge (Troe and Ushakov, 2014). While the former equation for log F appears acceptable as long as Fc≥ 0.6, the latter equation for F should be used for Fc≤ 0.6. With these equations, falloff curves are represented in terms of the three parameters k0 (being proportional to [M]), k∞ and Fc.
The parameters k0,k∞ and Fc depend on details of the intra- and intermolecular dynamics and in principle can be calculated. If the required information is not available, one has to obtain them by fitting experimental falloff curves with the expressions given above. Nevertheless, one may estimate Fc to be typically of the order of 0.49, 0.44, 0.39 and 0.35, if the reactants A and B in total have r= 3, 4, 5, and 6 external rotational degrees of freedom, respectively (Cobos and Troe, 2003; for the reaction HO + NO2+ M, for example, one would have r= 5 and Fc≈ 0.39); Fc may be lower if low-frequency vibrations in A or B are relevant in addition to the rotations and if collisions are inefficient. Over the range 200–300 K, often one can neglect a temperature dependence of Fc (for detailed calculations of Fc, including a dependence on the bath gas M, see, for example, Troe 1983; Troe and Ushakov, 2011, 2014). The accuracy of F(x) as given above is estimated to be about 10 %. Larger differences between experimentally fitted Fc often are an indication of inadequate falloff extrapolations to k0 and/or k∞. In this case, the apparent values for k0, k∞ and Fc can still provide a satisfactory representation of the considered experimental data, in spite of the fact that k0 and/or k∞ are not the real limiting values. If falloff curves are fitted in different ways, changes in Fc require changes in the limiting k0 and k∞. In the present evaluation, we generally follow the experimentally fitted values for k0, k∞ and Fc, provided that Fc does not differ too much from the standard values given above and theoretically modelled values. If large deviations are encountered, the experimental data are re-evaluated using Fc values as given above. Values of k∞ for combination reactions without a barrier often have only weak temperature dependences, which in practice can be neglected.
Besides the energy-transfer mechanism, i.e. Reactions (1), (−1), and (2), a second mechanism may become relevant for some reactions considered here. This is the radical-complex (or chaperon) mechanism,
which, in the low-pressure range, leads to k0= ( [M]. For some tri- and tetra-atomic adducts AB, e.g. O + O2→ O3 and HO + C6H6→ HOC6H6, the value of k0 may exceed that from the energy-transfer mechanism and show stronger temperature dependences (Luther et al., 2005; Teplukhin and Babikov, 2016). This mechanism may also influence high-pressure experiments when k0 from the radical-complex mechanism exceeds k∞ from the energy-transfer mechanism (Oum et al., 2003). In this case falloff over wide pressure ranges cannot be represented by contributions from the energy-transfer mechanism alone, in particular when measurements at pressures above about 1×106 Pa are taken into consideration.
The dependence of k0 and k∞ on temperature T is represented in the form except for cases with an established energy barrier in the potential. We have used this form of temperature dependence because it usually gives a better fit to the data over a wider range of temperature than the Arrhenius expression does. It should be emphasized that the chosen form of the temperature dependence is often only adequate over limited temperature ranges such as 200–300 K. Obviously, the relevant values of n are different for k0 and k∞. In this evaluation, values of k0 are given for selected examples of third bodies M, and if possible for M= N2, O2 or air.
2.4 Treatment of complex-forming bimolecular reactions
Bimolecular reactions may follow the “direct” pathway
and/or involve complex formation, in the simplest way characterized by the steps
(there may be additional pathways following from AB*; direct and complex-forming pathways may or may not be coupled). Assuming quasi-stationary concentrations of AB* (i.e. that d[AB*]]dt ≈ 0 as in Sect. 2.3), a Lindemann–Hinshelwood-type analysis leads to
The rate constants for association (kAss) and for chemical activation leading to product formation (kCA) then are given by
Note that kAss and kCA are dependent on the nature and concentration of the third body M, in addition to their temperature dependence. In reality, as for combination and dissociation reactions, the given expressions for kAss and kCA have to be extended by suitable broadening factors F to account for the multistep character of processes (2) and the energy and angular momentum dependences of processes (1), (−1) and (5). These broadening factors, however, generally differ for kAss and kCA; also they generally differ from those of simple combination reactions described in Sect. 2.3. One should note that association and chemical activation here are coupled such that their joint treatment is complicated. Some simplification is reached when the processes first are treated separately and the coupling is introduced at the end (Troe, 2015). The corresponding rate constants of the separated processes are denoted by kAss* and and are given by
and
then corresponds to the rate constant of a combination reaction described in Sect. 2.3 and has a broadening factor . has to be treated in a different way and is expressed in the form
with [M] and a broadening factor (Stewart et al., 1989). The latter factor is generally larger than (Troe, 2015). The rate parameters and depend on the molecular parameters and can be calculated theoretically or fitted experimentally (after the coupling between association and chemical activation has been accounted for). In practice one may try to represent the rate constants in the form of rate constants of separated processes and . Coupling these rate constants then leads to a full representation of the rate constants in terms of the six rate parameters , kCA,∞ and FCA,c. If one neglects the coupling and fits these parameters directly from the experiments (Miller and Klippenstein, 2001), however, one has to be aware of the fact that the values obtained do not correspond to those of separated, single-channel, association and chemical activation processes (for more details, see Troe, 2015).
As a consequence of the multistep character of complex-forming bimolecular reactions, a variety of temperature and pressure dependences of kAss and kCA are observed. The low-pressure limit of the total rate constants , i.e. , because of different energy and angular momentum dependences of the specific rate constants k1, k−1 and k5, may increase or decrease with temperature, the latter with the possibility of a change with an increase above a certain temperature. ktot, as given above, may increase with pressure from kCA,0 to k1, with M = H2O often being a particularly efficient third body in the pressure-dependent range. The pressure dependence generally becomes less apparent with increasing temperature. Finally, the further fate of an addition product AB is of importance. It may be collisionally reactivated to energies where k5 ≫ k−1, such that formation of C+D is enhanced (in comparison to energies where ). There is also the possibility that A–M (or B–M) complexes are formed which react in a chaperon mechanism with B (or A) and then form products. M= H2O here may be particularly efficient. Without detailed theoretical analysis, in general, it will be difficult to disentangle the intrinsic mechanism. Therefore, reference to theoretical work is given for selected reactions.
2.5 Photochemical reactions
The data sheets begin with a list of feasible primary photochemical processes for wavelengths usually down to 185 nm, along with the corresponding enthalpy changes at 0 K where possible or alternatively at 298 K. Calculated threshold wavelengths corresponding to these enthalpy changes are also listed, bearing in mind that the values calculated from the enthalpy changes at 298 K are not true “threshold values”. This is followed by tables which summarize the available experimental data for (i) absorption cross sections and (ii) quantum yields. These data are supplemented by a series of comments. The next table lists the preferred absorption cross section data and the preferred quantum yields at appropriate wavelength intervals. For absorption cross sections, the intervals are usually 1, 5 or 10 nm. Any temperature dependence of the absorption cross sections is also given where possible. The aim in presenting these preferred data is to provide a basis for calculating atmospheric photolysis rates. For absorption continua, the temperature dependence is often represented by Sulzer–Wieland-type expressions (Astholz et al., 1981). Alternatively a simple empirical expression of the form log is used. The comments again describe how the preferred data were selected and include other relevant points. The photochemical data sheets are concluded with a list of references.
2.6 Conventions concerning absorption cross sections
These are presented in the data sheets as “absorption cross sections per molecule, base e.” They are defined according to the following equation:
where I0 and I are the incident and transmitted light intensities, [N] is the number concentration of absorber (expressed in molecule cm−3), l is the path length (expressed in cm) and σ is the absorption cross section (units of cm2 molecule−1). Note that “molecule” is not a unit recognized by IUPAC but is included here for clarity. Other definitions and units are frequently quoted. The closely related quantities “absorption coefficient” and “extinction coefficient” are often used, but care must be taken to avoid confusion in their definition; see Calvert (1990) for definitions and discussion. It is always necessary to know the units of concentration and of path length and the type of logarithm (base e or base 10) corresponding to the definition. The decadic molar absorption coefficient, ε, is often quoted, particularly in the older literature, and is defined as
where [A] is the concentration of the absorber expressed in units of moles per cubic decimetre (moles dm−3). While ε is often called an extinction coefficient, the term “extinction” should more properly be used for the sum of absorption and scattering. To convert from ε (base 10, units of dm3 mol−1 cm−1) to σ (base e, units of cm2 molecule−1), multiply it by .
2.7 Assignment of uncertainties
Under the heading “reliability,” estimates have been made of the absolute accuracies of the preferred values of k at 298 K and of the preferred values of over the quoted temperature range. The accuracy of the preferred rate coefficient at 298 K is quoted as the term Δ log k, where Δlog k=d and d is defined by the equation, log k=c ± d. This is equivalent to the statement that k is uncertain to a factor of f, where d= log f. The accuracy of the preferred value of is quoted as the term , where and g is defined by the equation . d and g are uncertainties corresponding approximately to 95 % confidence limits. For second-order rate coefficients listed in this evaluation, an estimate of the uncertainty at any given temperature within the recommended temperature range may be obtained from the equation:
The assignment of these absolute uncertainties in k and is our subjective assessment. They are not determined by a rigorous, statistical analysis of the database, which is generally too limited to permit such an analysis. Rather, the uncertainties are based on our knowledge of the techniques, the difficulties of the experimental measurements, the potential for systematic errors and the number of studies conducted and their agreement or lack thereof. Experience shows that for rate measurements of atomic and free radical reactions in the gas phase, the precision of the measurement, i.e. the reproducibility, is usually good. Thus, for single studies of a particular reaction involving one technique, standard deviations, or even 95 % confidence limits, of ±10 % or less are frequently reported in the literature. However, when we compare data for the same reaction studied by more than one group of investigators and involving different techniques, the rate coefficients sometimes differ by a factor of 2 or even more. This can only mean that one or more of the studies has involved large systematic uncertainty, which is difficult to detect. The differences between various measurements could be due to multiple reasons, such as insufficient purity of compounds, unknown/unexpected impurities, wall adsorption and decomposition, insufficient time resolution for the initial elementary step, opposing and parallel reactions or unexpected decomposition products from the primary product. This is hardly surprising since, unlike molecular reactions, it is not always possible to study atomic and free radical reactions in isolation, and consequently mechanistic and other difficulties frequently arise. On the whole, our assessment of uncertainty limits tends towards the cautious side. Thus, in the case where a rate coefficient has been measured by a single investigation using one particular technique and is unconfirmed by independent work, we typically suggest an uncertainty of a factor of 2.
In contrast to the usual situation for the rate coefficients of thermal reactions, where inter-comparison of results of a number of independent studies permits a realistic assessment of reliability, for many photochemical processes there is a scarcity of data. Thus, we do not feel justified at present in assigning uncertainty limits to the parameters reported for the photochemical reactions.
| A | absorption |
| API | atmospheric pressure ionization |
| AS | absorption spectroscopy |
| CCD | charge-coupled detector |
| CEAS | cavity-enhanced absorption spectroscopy |
| CIMS | chemical ionization mass spectroscopy/spectrometry |
| CL | chemiluminescence |
| CRDS | cavity ring-down spectroscopy |
| DF | discharge flow |
| EPR | electron paramagnetic resonance |
| F | flow system |
| FP | flash photolysis |
| FTIR | Fourier transform infrared |
| FTS | Fourier transform spectroscopy |
| GC | gas chromatography/gas chromatographic |
| HPLC | high-performance liquid chromatography |
| IBBCEAS | incoherent broadband cavity enhanced absorption spectroscopy |
| IR | infrared |
| LIF | laser-induced fluorescence |
| LMR | laser magnetic resonance |
| LP | laser photolysis |
| MM | molecular modulation |
| MS | mass spectrometry/mass spectrometric |
| P | steady-state photolysis |
| PLP | pulsed laser photolysis |
| PR | pulse radiolysis |
| RA | resonance absorption |
| RF | resonance fluorescence |
| RR | relative rate |
| S | static system |
| TDLS | tunable diode laser spectroscopy |
| ToF | time of flight |
| UV | ultraviolet |
| UVA | ultraviolet absorption |
| VUVA | vacuum ultraviolet absorption |
All relevant data and supporting information have been provided in the Supplement. The detailed reaction data sheets are also available on the IUPAC Task Group on Atmospheric Chemical Kinetics Data Evaluation website at http://iupac.pole-ether.fr/ (IUPAC, 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-21-4797-2021-supplement.
All authors defined the scope of the work. AM, TJW, JNC, MEJ and RAC developed and drafted the data sheets and manuscript. All authors reviewed, refined and revised the manuscript and data sheets.
The authors declare that they have no conflict of interest.
The chairman and members of the task group wish to express their appreciation to IUPAC for the help which facilitated the preparation of this evaluation. We also acknowledge support from the following organizations: EU Framework Program 6 and 7 and Horizon 2020, the UK Natural Environmental Research Council, the Swiss National Science Foundation, the Centre National de la Recherche Scientifique-Institut National des Sciences de l'Univers (CNRS-INSU), Orléans University and Observatoire des Sciences de l'Univers en région Centre (OSUC). We thank Cathy Boone and Phuong Nguyen for constructing, developing and maintaining the website.
This paper was edited by Ulrich Pöschl and reviewed by Cornelius Zetzsch and Geert Moortgat and three anonymous referees.
Ammann, M., Cox, R. A., Crowley, J. N., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VI – heterogeneous reactions with liquid substrates, Atmos. Chem. Phys., 13, 8045–8228, https://doi.org/10.5194/acp-13-8045-2013, 2013.
Astholz, D. C., Brouwer, L., and Troe, J.: High-temperature ultraviolet-absorption spectra of polyatomic molecules in shock waves, Ber. Bunsen. Phys. Chem., 85, 559–564, 1981.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement III, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 18, 881–1097, 1989.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement IV, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 21, 1125–1568, 1992.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Rossi, M. J., and Troe, J.: Evaluated kinetic, photochemical, and heterogeneous data for atmospheric chemistry: Supplement V, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 26, 521–1011, 1997a.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement VI, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 26, 1329–1499, 1997b.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement VII, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 28, 191–393, 1999.
Atkinson, R., Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry, Supplement VIII, IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry, J. Phys. Chem. Ref. Data, 29, 167–266, 2000.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I – gas phase reactions of Ox, HOx, NOx, and SOx species, Atmos. Chem. Phys., 4, 1461–1738, https://doi.org/10.5194/acp-4-1461-2004, 2004.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., Troe, J., and IUPAC Subcommittee: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume II – gas phase reactions of organic species, Atmos. Chem. Phys., 6, 3625–4055, https://doi.org/10.5194/acp-6-3625-2006, 2006.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume III – gas phase reactions of inorganic halogens, Atmos. Chem. Phys., 7, 981–1191, https://doi.org/10.5194/acp-7-981-2007, 2007.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume IV – gas phase reactions of organic halogen species, Atmos. Chem. Phys., 8, 4141–4496, https://doi.org/10.5194/acp-8-4141-2008, 2008.
Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Troe, J., and Watson, R. T.: Evaluated kinetic and photochemical data for atmospheric chemistry, CODATA Task Group on Chemical Kinetics, J. Phys. Chem. Ref. Data, 9, 295–471, 1980.
Baulch, D. L., Cox, R. A., Crutzen, P. J., Hampson Jr., R. F., Kerr, J. A., Troe, J., and Watson, R. T.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement I, CODATA Task Group on Chemical Kinetics, J. Phys. Chem. Ref. Data, 11, 327–496, 1982.
Baulch, D. L., Cox, R. A., Hampson Jr., R. F., Kerr, J. A., Troe, J., and Watson, R. T.: Evaluated kinetic and photochemical data for atmospheric chemistry: Supplement II, CODATA Task Group on Gas Phase Chemical Kinetics, J. Phys. Chem. Ref. Data, 13, 1259–1380, 1984.
Calvert, J. G.: Glossary of atmospheric chemistry terms, Pure Appl. Chem., 62, 2167–2219, 1990.
Cobos, C. J. and Troe, J.: Prediction of reduced falloff curves for recombination reactions at low temperatures, Z. Phys. Chem., 217, 1–14, 2003.
Cox, R. A.: Evaluation of laboratory kinetics and photochemical data for atmospheric chemistry applications, Chem. Soc. Rev., 41, 6231–6246, 2012.
Cox, R. A., Ammann, M., Crowley, J. N., Herrmann, H., Jenkin, M. E., McNeill, V. F., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: IUPAC in the (real) clouds: 40 years of evaluating atmospheric chemistry data, Chemistry International, 40, 10–13, https://doi.org/10.1515/ci-2018-0404, 2018.
Cox, R. A., Ammann, M., Crowley, J. N., Herrmann, H., Jenkin, M. E., McNeill, V. F., Mellouki, A., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VII – Criegee intermediates, Atmos. Chem. Phys., 20, 13497–13519, https://doi.org/10.5194/acp-20-13497-2020, 2020.
Crowley, J. N., Ammann, M., Cox, R. A., Hynes, R. G., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume V – heterogeneous reactions on solid substrates, Atmos. Chem. Phys., 10, 9059–9223, https://doi.org/10.5194/acp-10-9059-2010, 2010.
IUPAC, Task Group on Atmospheric Chemical Kinetic Data Evaluation: Evaluated kinetic data, available at: http://iupac.pole-ether.fr/, last access: 25 January 2021.
Luther, K., Oum, K., and Troe, J.: The role of the radical-complex mechanism in the ozone recombination/dissociation reaction, Phys. Chem. Chem. Phys., 7, 2764–2770, 2005.
Miller, J. and Klippenstein, S. J.: The reaction between ethyl and molecular oxygen: Further analysis, Int. J. Chem. Kinet., 33, 654–668, 2001.
Oum, K., Sekiguchi, K., Luther, K., and Troe, J.: Observation of unique pressure effects in the combination reaction of benzyl radicals in the gas to liquid transition region, Phys. Chem. Chem. Phys., 5, 2931–2933, 2003.
Stewart, P. H., Larson, C. W., and Golden, D. M.: Pressure and temperature dependence of reactions proceeding via a bound complex, 2. An application to 2 CH3→ C2H5+ H, Combust. Flame, 75, 25–31, 1989.
Teplukhin, A. and Babikov, D.: A full-dimensional model of ozone forming reaction: the absolute value of the recombination rate coefficient, its pressure and temperature dependencies, Phys. Chem. Chem. Phys., 18, 19194–19206, 2016.
Troe, J.: Theory of thermal unimolecular reactions in the fall-off range, I. Strong collision rate constants, Ber. Bunsen. Phys. Chem., 87, 161–169, 1983.
Troe, J.: Predictive possibilities of unimolecular rate theory, J. Phys. Chem., 83, 114–126, 1979.
Troe, J.: Simplified representation of partial and total rate constants of complex-forming bimolecular reactions, J. Phys. Chem. A, 119, 12159–12165, 2015.
Troe, J. and Ushakov, V. G.: Revisiting falloff curves of thermal unimolecular reactions, J. Chem. Phys., 135, 054304, https://doi.org/10.1063/1.3615542, 2011.
Troe, J. and Ushakov, V. G.: Representation of “Broad” Falloff Curves for Dissociation and Recombination Reactions, Z. Phys. Chem., 228, 1–10, 2014.





