Global modeling of heterogeneous hydroxymethanesulfonate chemistry

Hydroxymethanesulfonate (HMS) has recently been identified as an abundant organosulfur compound in aerosols during winter haze episodes in northern China. It has also been detected in other regions although the concentrations are low. Because of the sparse field measurements, the global significance of HMS and its spatial and seasonal patterns remain unclear. Here, we modify and add to the implementation of HMS chemistry in the GEOS-Chem chemical transport model and conduct multiple global simulations. The model accounts for cloud entrainment and gas–aqueous mass transfer within the rate expressions for heterogeneous sulfur chemistry. Our simulations can generally reproduce quantitative HMS observations from Beijing and show that East Asia has the highest HMS concentration, followed by Europe and North America. The simulated HMS shows a seasonal pattern with higher values in the colder period. Photochemical oxidizing capacity affects the competition of formaldehyde with oxidants (such as ozone and hydrogen peroxide) for sulfur dioxide and is a key factor influencing the seasonality of HMS. The highest average HMS concentration (1–3 µg m⁻³) and HMS ∕ sulfate molar ratio (0.1–0.2) are found in northern China in winter. The simulations suggest that aqueous clouds act as the major medium for HMS chemistry while aerosol liquid water may play a role if its rate constant for HMS formation is greatly enhanced compared to cloud water.

1 Introduction

Organosulfur (OS) compounds have been detected in secondary organic aerosols (SOAs). The OS compounds affect the physicochemical properties of aerosols such as hygroscopicity, acidity, and viscosity, and ultimately the climate and health effects of aerosols (Surratt et al., 2007; Farmer et al., 2010; Sorooshian et al., 2015; Estillore et al., 2016; Riva et al., 2019). The identified OS compounds include organosulfates (${\mathrm{ROSO}}_{\mathrm{3}}^{-}$), sulfoxides (RSOR^′), sulfones (RSO₂R^′), and sulfonates (${\mathrm{RSO}}_{\mathrm{3}}^{-}$) (Brüggemann et al., 2020). Sulfonates include methanesulfonate (${\mathrm{CH}}_{\mathrm{3}}{\mathrm{SO}}_{\mathrm{3}}^{-}$, deprotonated MSA, methanesulfonic acid) and hydroxyalkylsulfonates ($\mathrm{RCH}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}$) (Song et al., 2019a). These classes of OS compounds may differ widely in their formation mechanisms, concentration levels, and spatiotemporal distributions. Organosulfates and MSA are the two most studied OS species or classes (Bates et al., 1992; Huang et al., 2017; Brüggemann et al., 2020). Organosulfates are primarily formed by the reactive uptake of gas-phase epoxides on acidic sulfate particles (Froyd et al., 2010; Surratt et al., 2010; Xu et al., 2015). The most abundant organosulfate observed in ambient fine particulate matter (PM_2.5) is the isoprene-derived methyltetrol sulfate (${\mathrm{C}}_{\mathrm{5}}{\mathrm{H}}_{\mathrm{11}}{\mathrm{SO}}_{\mathrm{7}}^{-}$), with an average concentration of 1.8 µg m⁻³ found during August 2015 in Atlanta, Georgia, USA (Hettiyadura et al., 2019). MSA is produced primarily by the oxidation of biogenic dimethyl sulfide (DMS, mainly from marine phytoplankton) and is likely the major organosulfur species in many regions over the oceans (Chen et al., 2018; Hodshire et al., 2019). The concentrations of aerosol-phase MSA in marine environments range from tens to a few hundred ng m⁻³ (Phinney et al., 2006; Sciare et al., 2009; Huang et al., 2017).

Recently, high mass concentrations of hydroxymethanesulfonate (HMS, ${\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}$), the most abundant hydroxyalkylsulfonate species commonly found in the atmosphere, have been detected in winter in Beijing, China using an aerosol mass spectrometer by Song et al. (2019a), using an improved ion chromatography method by Ma et al. (2020), and using a UHPLC-LTQ-Orbitrap mass spectrometry by Wei et al. (2020). The mass spectrometry quantification of HMS in ambient aerosols may be subject to the interference of other inorganic and organic sulfur compounds, as suggested by Dovrou et al. (2019). Another difficulty with interpreting HMS in the observational record is the potential for HMS to decompose during sample storage and analysis (Ma et al., 2020; Moch et al., 2020). The average HMS concentration in the 2015/16 and 2016/17 winters in Beijing was observed to be 1.9 µg m⁻³ (Ma et al., 2020). The highest daily average HMS concentration reached 15 µg m⁻³, accounting for 6 % of PM_2.5 concentration (Ma et al., 2020). Song et al. (2019a) argued that HMS was likely the major organosulfur compound during winter haze events in northern China. Prior to the two studies, only low levels of HMS, with averages on the order of 0.01 µg m⁻³, had been observed in the United States, Japan, and Germany (Dixon and Aasen, 1999; Suzuki et al., 2001; Scheinhardt et al., 2014). More recently, Moch et al. (2020) reported observational evidence for a ubiquitous presence of HMS across 160 locations in North America, Europe, and Asia. Most of the observations of HMS reported by Moch et al. (2020) were unquantified, but mass concentrations of up to 7.6 µg m⁻³ were reported for Shijiazhuang, China and up to 0.6 µg m⁻³ for Singapore.

Our knowledge of the chemical mechanism for HMS stems largely from studies in the 1980s when it was recognized as part of the aqueous sulfur chemistry (Pandis and Seinfeld, 1989). Field measurements of cloud water in the Los Angeles Basin showed the coexistence of H₂O₂ and S(IV) that was much larger than expected based on the phase equilibrium with gaseous SO₂ (Richards et al., 1983). The formation of HMS by the reaction of dissolved SO₂ and HCHO was postulated, and then proved, to explain the observed excess of S(IV) (Munger et al., 1986). The laboratory experiments from several groups determined the kinetics and thermodynamics of HMS reactions in aqueous solutions (Boyce and Hoffmann, 1984; Deister et al., 1986; Dong and Dasgupta, 1986; Kok et al., 1986; Olson and Fessenden, 1992). Briefly, both formation and decomposition of HMS depend strongly on pH, i.e., the hydrogen ion activity expressed on a logarithmic scale. HMS is resistant to oxidation by H₂O₂ and O₃ but reacts with hydroxyl radicals (OH) in the aqueous phase. These studies suggested that the atmospheric conditions favorable for the formation and stability of HMS involved abundant gas-phase SO₂ and HCHO, high aqueous water content, low temperature, intermediate pH, and low photochemical activity.

The integration and reconciliation of data from field observations, laboratory experiments, and chemical modeling are crucial for obtaining a better understanding of how HMS is processed in the atmosphere. Moch et al. (2020) recently implemented in-cloud HMS chemistry into the GEOS-Chem chemical transport model to explore its large-scale spatiotemporal distribution. The HMS chemistry is heterogeneous in nature since the reactions occur in the aqueous phase with reactants transported from the gas phase (Jacob, 2000). Sometimes heterogeneous chemistry is referred to as multiphase chemistry (Ravishankara, 1997). As shown in Fig. 1, the overall heterogeneous reaction rates are controlled not only by rate constants in the aqueous phase but also by mass transfer limitations between the gas and aqueous phases (Jacob, 1986; Ravishankara, 1997; Seinfeld and Pandis, 2016). In partly cloudy conditions, heterogeneous reactions may also be influenced by the entrainment and detrainment of air into and out from clouds (Holmes et al., 2019). Building upon Moch et al. (2020), the current study designed and conducted multiple GEOS-Chem global model simulations, in order to explore the controlling factors and processes of the spatiotemporal distribution of HMS, including cloud entrainment and gas–aqueous mass transfer limitations, kinetics and thermodynamics of HMS chemistry, and the formation media of HMS. The model is driven by the kinetic and thermodynamic data obtained from available laboratory experiments. The simulated results are compared with observations made in four field campaigns. Compared with the control simulation that follows the parameterization in the standard GEOS-Chem model, the default simulation improves treatments of entrainment and mass transfer processes for heterogeneous cloud sulfur chemistry. Both aqueous cloud droplets (Jacob, 1986; Olson and Hoffmann, 1989; Moch et al., 2018; Moch et al., 2020) and aqueous aerosols (Song et al., 2019a; Ma et al., 2020) have been suggested to provide the media for HMS reactions. However, kinetic and thermodynamic data have been determined only in dilute solutions, which are suitable for application in clouds. The lack of corresponding data in concentrated solutions poses a key challenge to modeling HMS chemistry for aerosol water. Therefore, following Moch et al. (2020) we assume that cloud water serves as the only medium in the control and default simulations. The role of aerosol water is explored through sensitivity simulations. Aerosol water chemistry also considers the physiochemical processes in Fig. 1, allowing an evaluation of the importance of the two aqueous media.

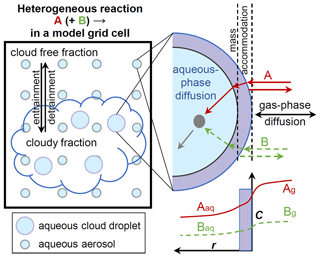
Figure 1 Schematic of physicochemical processes that control the heterogeneous reaction of a molecule A (with another molecule B) in a model grid cell. (Left). Entrainment and detrainment of air into and out from clouds. The volume occupied by aqueous clouds in the grid cell is represented by the cloud fraction (f_c), which is provided by the MERRA-2 meteorological reanalysis in this study. The cloud-free fraction is thus 1−f_c. Aqueous aerosols are assumed to be evenly distributed in the grid cell. For aqueous cloud droplets and aqueous aerosols, the same mass transport processes are considered and are shown in the right panel. (Top Right). Gas-phase, interfacial, and aqueous-phase mass transport limitations for the molecules A and B. (Bottom Right). Concentration (C) profiles of A and B are a function of radial distance (r) from the surface of a spherical particle. The subscripts g and aq refer to gas and aqueous phases, respectively. The concentrations are in arbitrary units and their scales are different for gas and aqueous phases. The entrainment/detrainment processes for clouds have been described in detail by Holmes et al. (2019). The right panel is adapted from Fig. 4 in Ravishankara (1997).

This article is organized as follows. In the Methods section, we first provide an overview of the aqueous chemical reactions for HMS, including its formation, decomposition, and oxidation (Sect. 2.1). From existing laboratory studies, we critically estimate the best values and uncertainties of their rate constants. The general configuration of the GEOS-Chem model is described in Sect. 2.2, including its version, simulation period, spatial and temporal resolutions, meteorological field, chemical mechanisms, and underlying emissions. A brief introduction of sulfur simulation in the standard model is given in Sect. 2.3. The two major simulations in this study, control and default, are described in Sect. 2.4 and 2.5, respectively. Based on settings in the standard model, the control simulation implements heterogeneous HMS chemistry using cloud as the only aqueous medium (Moch et al., 2020). We find that the in-cloud SO₂ titration by various reactants is inappropriately represented in the control simulation, very likely leading to an overestimation of HMS formation. The default simulation fixes this issue. Section 2.6 describes the sensitivity simulations designed to investigate the key factors leading to uncertainty in the modeled HMS levels. In the Results and discussion section, we first show in Sect. 3.1 the spatial and seasonal distributions of HMS from the default simulation and discuss the underlying factors. Differences in the modeled HMS between the default and control simulations are presented and discussed in Sect. 3.2. Section 3.3 demonstrates the key uncertain parameters and processes in the HMS model identified from sensitivity simulations. Sect. 3.4 compares the observations of HMS in four different regions with these model results. The knowledge gained in this study and the remaining gaps are summarized in Sect. 3.5. Finally, the conclusions are given in Sect. 4.

2 Methods

2.1 Kinetics and thermodynamics of HMS chemistry

Hydroxymethanesulfonic acid (HMSA, CH₂(OH)SO₃H) is a diacid with pK_a1<0 (Reaction R1) and pK_a2∼12 (Reaction R2). Thus, it primarily exists as HMS (${\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}$) in tropospheric clouds and aerosols. In the aqueous phase, HMS is produced by the nucleophilic addition of ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ and ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ to the carbonyl C atom of HCHO (Reactions R3–R6). As ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ is a much stronger nucleophile than ${\mathrm{HSO}}_{\mathrm{3}}^{-}$, the rate constant of ${\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$, k₂, is a few orders of magnitude higher than that of ${\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{HSO}}_{\mathrm{3}}^{-}$, k₁, as shown in Table 1. HCHO_(aq) refers to the free, unhydrated formaldehyde dissolved in the aqueous phase, and maintains an equilibrium with its hydrated form, CH₂(OH)₂ (methylene glycol). The equilibrium constant of Reaction (R7), K_h, represents the extent of hydration (Eq. 1). Reactions (R1)–(R6) are all reversible and can be summarized by Reaction (R8). ${\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T$ is the sum of SO₂⋅H₂O, ${\mathrm{HSO}}_{\mathrm{3}}^{-}$, and ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ (Eq. 2). k_f (M⁻¹ s⁻¹) and k_d (s⁻¹) represent the forward and backward reaction (HMS formation and decomposition) rate constants of Reaction (R8) and K_eq (M⁻¹) is its equilibrium constant (Eq. 3). k_f is a combination of k₁ and k₂ weighted by the fractions of ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ and ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ in ${\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T$ (Eqs. 4–6). K_s1 and K_s2 denote the first and second dissociation constants for dissolved SO₂ (Table 2). Figure 2 shows the values of k_f and k_d obtained from the available laboratory experiments as a function of pH (Blackadder and Hinshelwood, 1958; Sørensen and Andersen, 1970; Boyce and Hoffmann, 1984; Deister et al., 1986; Dong and Dasgupta, 1986; Kok et al., 1986; Lagrange et al., 1999). In general, we find a large discrepancy for k_f and good agreement for k_d.

$$\begin{array}{}\text{(R1)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}\mathrm{H}\leftrightarrow {\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}+{\mathrm{H}}^{+}\text{(R2)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}\leftrightarrow {\mathrm{CH}}_{\mathrm{2}}\left({\mathrm{O}}^{-}\right){\mathrm{SO}}_{\mathrm{3}}^{-}+{\mathrm{H}}^{+}\text{(R3)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}}\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{HSO}}_{\mathrm{3}}^{-}+{\mathrm{H}}^{+}\text{(R4)}& {\displaystyle }{\mathrm{HSO}}_{\mathrm{3}}^{-}\leftrightarrow {\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}+{\mathrm{H}}^{+}\text{(R5)}& {\displaystyle }{\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{HSO}}_{\mathrm{3}}^{-}\stackrel{k_{\mathrm{1}}}{⟷}{\mathrm{CH}}_{\mathrm{2}}\left(\mathrm{OH}\right){\mathrm{SO}}_{\mathrm{3}}^{-}\text{(R6)}& {\displaystyle }{\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}\stackrel{k_{\mathrm{2}}}{⟷}{\mathrm{CH}}_{\mathrm{2}}\left({\mathrm{O}}^{-}\right){\mathrm{SO}}_{\mathrm{3}}^{-}\text{(R7)}& {\displaystyle }{\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{CH}}_{\mathrm{2}}{\left(\mathrm{OH}\right)}_{\mathrm{2}}\text{(R8)}& {\displaystyle }{\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T\leftrightarrow \mathrm{HMS}\end{array}$$

$$\begin{array}{}\text{(1)}& {\displaystyle }{K}_{\mathrm{h}}=\left[{\mathrm{CH}}_{\mathrm{2}}{\left(\mathrm{OH}\right)}_{\mathrm{2}}\right]/{\left[\mathrm{HCHO}\right]}_{\mathrm{aq}}\text{(2)}& {\displaystyle }{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}=\left[{\mathrm{SO}}_{\mathrm{2}}\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]+\left[{\mathrm{HSO}}_{\mathrm{3}}^{-}\right]+\left[{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}\right]\text{(3)}& {\displaystyle }{K}_{\mathrm{eq}}=\left[\mathrm{HMS}\right]/\left({\left[\mathrm{HCHO}\right]}_{\mathrm{aq}}{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}\right)=k_{\mathrm{f}}/k_{\mathrm{d}}\text{(4)}& {\displaystyle }{k}_{\mathrm{f}}=k_{\mathrm{10}}{x}_{{\mathrm{HSO}}_{\mathrm{3}}^{-}}+k_{\mathrm{11}}{x}_{{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}}\text{(5)}& {\displaystyle }\begin{array}{rl}{x}_{{\mathrm{HSO}}_{\mathrm{3}}^{-}}=& \left[{\mathrm{HSO}}_{\mathrm{3}}^{-}\right]/{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}=K_{s\mathrm{1}}\left[{\mathrm{H}}^{+}\right]/\\ & \left({\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}+K_{s\mathrm{1}}\left[{\mathrm{H}}^{+}\right]+K_{s\mathrm{1}}{K}_{s\mathrm{2}}\right)\end{array}\text{(6)}& {\displaystyle }\begin{array}{rl}{x}_{{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}}=& \left[{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}\right]/{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}=K_{s\mathrm{1}}{K}_{s\mathrm{2}}/\\ & \left({\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}+K_{s\mathrm{1}}\left[{\mathrm{H}}^{+}\right]+K_{s\mathrm{1}}{K}_{s\mathrm{2}}\right)\end{array}\end{array}$$

Table 1 Aqueous-phase reaction rate expressions.

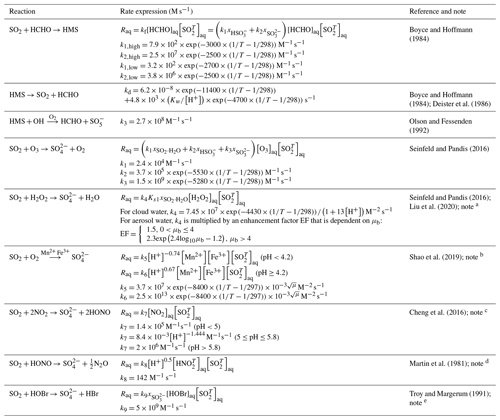
The chemical reaction equations are used to indicate major reactants and products and may not be balanced in terms of stoichiometry and charge. $x_{{\mathrm{SO}}_{\mathrm{2}}\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\left[{\mathrm{SO}}_{\mathrm{2}}\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]/{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}={\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}/\left({\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}+K_{s\mathrm{1}}\left[{\mathrm{H}}^{+}\right]+K_{s\mathrm{1}}{K}_{s\mathrm{2}}\right)$ ^a EF is obtained by fitting the experimental data shown in Fig. 2C in Liu et al. (2020). μ_b is the molality-based ionic strength (mol kg⁻¹). ^b The relationship between k and μ is: $k/k^{\mathit{\mu }=\mathrm{0}}={\mathrm{10}}^{b\left(\sqrt{\mathit{\mu }}/\left(\mathrm{1}+\sqrt{\mathit{\mu }}\right)\right)}\approx {\mathrm{10}}^{b\sqrt{\mathit{\mu }}}$, in which b is in range of −4 to −2 (Shao et al., 2019). ^c k₇ is believed to be the lower limit (Cheng et al., 2016). ^d ${\left[{\mathrm{HNO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}$ is the total dissolved HONO and NO${}_{\mathrm{2}}^{-}$. ^e k₉ is determined at 25 ^∘C, μ=0.5 M. We consider the reaction of HOBr and SO${}_{\mathrm{3}}^{\mathrm{2}-}$ but not the one between HOBr and HSO${}_{\mathrm{3}}^{-}$, which is included in the standard GEOS-Chem model. The original lab experiments (Liu, 2002) seemed to be interfered by Br₂, a stronger oxidizing reagent which also reacts with HSO${}_{\mathrm{3}}^{-}$. A recent study by Liu and Abbatt (2020) suggested that the rate constant of HOBr and HSO${}_{\mathrm{3}}^{-}$ was much lower that of HOBr and SO${}_{\mathrm{3}}^{\mathrm{2}-}$.

2.1.1 HMS formation

Boyce and Hoffmann (1984) determined the following kinetic parameters at ionic strength μ=1 M, pH from 0 to 3.5: $k_{\mathrm{1}}=\mathrm{7.9}\times {\mathrm{10}}^{\mathrm{2}}$ M⁻¹ s⁻¹ and $k_{\mathrm{2}}=\mathrm{2.5}\times {\mathrm{10}}^{\mathrm{7}}$ M⁻¹ s⁻¹ (both at 298 K). The enthalpies of activation Δ^‡H₁ and Δ^‡H₂ were 25 and 20 kJ mol⁻¹, respectively. These parameters were calculated assuming $K_{s\mathrm{1}}=\mathrm{1.45}\times {\mathrm{10}}^{-\mathrm{2}}$ M and $K_{s\mathrm{2}}=\mathrm{6.31}\times {\mathrm{10}}^{-\mathrm{8}}$ M, which were in fact for dilute solutions (μ≈0 M). According to Boyce and Hoffmann (1984), application of the Davies equation to correct for the ionic strength effects on K_s1 and K_s2 yielded $k_{\mathrm{1}}=\mathrm{4.5}\times {\mathrm{10}}^{\mathrm{2}}$ M⁻¹ s⁻¹, $k_{\mathrm{2}}=\mathrm{5.4}\times {\mathrm{10}}^{\mathrm{6}}$ M⁻¹ s⁻¹ (both at 298 K), Δ^‡H₁=22 kJ mol⁻¹, and Δ^‡H₂=21 kJ mol⁻¹. Boyce and Hoffmann (1984) also used a higher K_h of 1.8×10³ than the value of 1.3×10³ obtained in a more recent study by Winkelman et al. (2002) (Table 2). We further adjust the kinetics based on this recent K_h and obtain $k_{\mathrm{1}}=\mathrm{3.2}\times {\mathrm{10}}^{\mathrm{2}}$ M⁻¹ s⁻¹ and $k_{\mathrm{2}}=\mathrm{3.8}\times {\mathrm{10}}^{\mathrm{6}}$ M⁻¹ s⁻¹.

Table 2 Equilibrium reactions.

^* The Henry's law constant of HOBr is very uncertain, ranging from 90 to 6000 M atm⁻¹. HOBr can undergo acid dissociation and has a pK_a of 8.65 at 25 ^∘C. We do not consider its acid dissociation because it is only partially dissociated in the interested pH range and because of the high uncertainty of its intrinsic Henry's law constant.

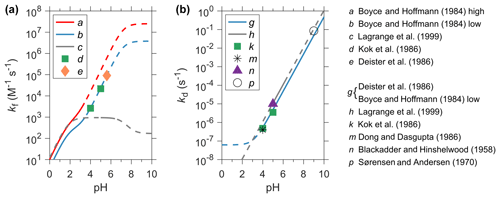
Figure 2 Comparison of rate constants for the formation (panel a, k_f in M⁻¹ s⁻¹) and decomposition (panel b, k_d in s⁻¹) of HMS from the available laboratory studies. Data are shown as a function of pH. Unless otherwise noted, rate constants are determined at or corrected to 25 ^∘C and under dilute conditions (μ<0.01 M). For a, b, c, g, and h, the solid curves show the range of pH at which these experiments are performed, whereas the dash curves indicate the extrapolated values. Other experiments (d, e, k, m, n, and p) are performed at discrete pH and shown by symbols. (a) the high k_f is from Boyce and Hoffmann (1984) at μ=1 M. (b) the low k_f is also from Boyce and Hoffmann (1984) and corrected for μ and K_h. (c) Lagrange et al. (1999): $k_{\mathrm{f}}=K_{\mathrm{h}}\times \left(\mathrm{0.73}\times x_{{\mathrm{HSO}}_{\mathrm{3}}^{-}}+\mathrm{0.13}\times x_{{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}}\right)$ M⁻¹ s⁻¹. (d) Kok et al. (1986): the reported k_f is limited by the dehydration rate of CH₂(OH)₂, k_dh, and is thus corrected here. (e) is calculated using the k_d and K_eq determined by Deister et al. (1986) and is also corrected for k_dh. The calculated k_f values are 2.6×10³, 2.2×10⁴, and 9.1×10⁴ M⁻¹ s⁻¹, respectively, at pH = 4, 5, and 5.6 in (d) and (e). For comparison, the extrapolation of the low k_f data (b) are 2.7×10³, 2.4×10⁴, and 9.3×10⁴ M⁻¹ s⁻¹, respectively, at pH = 4, 5, and 5.6. (g) k_d is calculated using the K_eq from Deister et al. (1986) and the low k_f from Boyce and Hoffmann (1984). (h) Lagrange et al. (1999): $k_{\mathrm{d}}=\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{4}}\times \left(K_w/\left[{\mathrm{H}}^{+}\right]\right)$ at μ=1 M in the presence of H₂O₂. (k) Kok et al. (1986) measured k_d of 4.8 × 10⁻⁷ and 3.5 × 10⁻⁶ s⁻¹, respectively, at pH 4 and 5. (m) Dong and Dasgupta (1986) measured K_eq at pH 4 and μ= 0.05 M, which translated to a k_d of 4 × 10⁻⁷ s⁻¹. (n) Blackadder and Hinshelwood (1958): $k_{\mathrm{d}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ at pH 5 and μ≈0.1 M. (p) Sørensen and Andersen (1970): $k_{\mathrm{d}}=\mathrm{8.5}\times {\mathrm{10}}^{-\mathrm{2}}$ s⁻¹ at pH 9 and μ=0.1 M. For comparison, values of k_d calculated by (g) are 5.4 × 10⁻⁷, 4.9 × 10⁻⁶, and 4.8 × 10⁻² s⁻¹ at pH 4, 5, and 9, respectively.

Therefore, two sets of HMS formation kinetic data can be obtained from Boyce and Hoffmann (1984) and are designated here as the high and low rate constants, as shown in Table 1 and Fig. 2. The high rate constants are the same as those used in Moch et al. (2020). The calculated high and low k_f differ by a factor of about 3 at pH < 2 and by a factor of about 6 at pH > 4. The low k_f agrees very well (within a factor of 1.1) with the results determined by Kok et al. (1986) and Deister et al. (1986) at higher pH 4, 5, and 5.6 (Fig. 2). The low kinetic data are also closer to the rate constants from the recent quantum chemical calculations by Zhang et al. (2019) (k₁=0.9  M⁻¹ s⁻¹, $k_{\mathrm{2}}=\mathrm{2}\times {\mathrm{10}}^{\mathrm{6}}$ M⁻¹ s⁻¹, at 298 K). Consequently, the low formation rate constants from Boyce and Hoffmann (1984) are adopted for the default model simulation, while the high ones are used in a sensitivity simulation. Lagrange et al. (1999) proposed another value of k_f which was about 1–4 orders of magnitude smaller than the low k_f from Boyce and Hoffmann (1984) at pH > 4 (Fig. 2). The simulated HMS concentration is negligible everywhere when applying the k_f from Lagrange et al. (1999) in the model, and thus, will not be discussed further.

2.1.2 HMS decomposition

The most complete analysis of K_eq was done by Deister et al. (1986). We calculate the expression of k_d using the low k_f from Boyce and Hoffmann (1984) and K_eq from Deister et al. (1986) (Eq. 3 and Table 1). As shown in Fig. 2, k_d estimated in this way agrees within a factor of about 2 with results from the other laboratory studies (Blackadder and Hinshelwood, 1958; Sørensen and Andersen, 1970; Dong and Dasgupta, 1986; Kok et al., 1986; Lagrange et al., 1999). Therefore, this expression of k_d is adopted in the default simulation, and its value is doubled in a sensitivity simulation. If we use the high k_f from Boyce and Hoffmann (1984) and the K_eq from Deister et al. (1986), we will obtain a k_d that is several times higher than estimates from the other studies. This may serve as circumstantial evidence in favor of the low k_f. Moch et al. (2020) uses a value of 3.6 × 10³ s⁻¹ for k_d following Diester et al. (1986).

2.1.3 HMS oxidation

HMS is resistant to oxidation by H₂O₂ and O₃ but can be oxidized by OH in the aqueous phase (Martin et al., 1989; Olson and Fessenden, 1992). Reaction (R9) produces HCHO and peroxysulfate radical (${\mathrm{SO}}_{\mathrm{5}}^{-}$) with a rate constant of 2.7×10⁸ M⁻¹ s⁻¹ (Olson and Fessenden, 1992) (Table 1). This value is lower by a factor of about 4 than the results reported in two earlier laboratory studies (Martin et al., 1989; Deister et al., 1990). Olson and Fessenden (1992) argued that these two studies were subject to artifacts and interferences from secondary reactions.

$$\begin{array}{}\text{(R9)}& \mathrm{HMS}+{\mathrm{OH}}_{\left(\mathrm{aq}\right)}\stackrel{{\mathrm{O}}_{\mathrm{2}}}{⟶}{\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}+{\mathrm{SO}}_{\mathrm{5}}^{-}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

The second source of uncertainty in Reaction (R9) arises from estimating aqueous OH concentrations. Aqueous OH is a short-lived species that can be transferred from the gas phase and generated/scavenged in the aqueous phase. Its sources and sinks, which are linked to photochemical processes (e.g., photolysis of nitrate and peroxides), transition metal ions (Fenton reactions), and/or reactions with halogen anions and organic matter, are not yet fully understood (Tilgner and Herrmann, 2018). Currently, there exist significant discrepancies between the modeled and measured [OH]_aq levels. A comprehensive overview has shown that [OH]_aq from different model studies ranges from 3 × 10⁻¹⁵ to 8 × 10⁻¹² M for cloud droplets and from 1 × 10⁻¹⁶ to 8 × 10⁻¹² M for aqueous aerosols. On the other hand, data ranges of the measured [OH]_aq are 0.5–7 × 10⁻¹⁵ M for clouds and 0.1–6 × 10⁻¹⁵ M for aerosols (Tilgner and Herrmann, 2018). On average, the modeled [OH]_aq is 2 orders of magnitude higher than the measured values. This large gap is believed to result from the limitations of both models and measurements. The bulk measurements of [OH]_aq may underestimate its concentrations in real aerosols and clouds due to lack of replenishment of important oxidations and OH precursors from the gas phase under the dark conditions of sample storage and treatment (Tilgner and Herrmann, 2018). On the other hand, the multiphase models may significantly overpredict [OH]_aq because they only partially consider the complex organic aqueous chemistry. The reasonable estimates of [OH]_aq in real aerosols and clouds seem to be 1 order of magnitude lower than modeled concentrations and 1 order of magnitude higher than measured levels (Tilgner and Herrmann, 2018). Since GEOS-Chem does not have a detailed representation of aqueous OH chemistry, we follow Moch et al. (2020) and simply estimate [OH]_aq using the modeled [OH]_g and a pseudo Henry's law constant $H_{\mathrm{OH}}^{\ast }$ (Eq. 7). In the default simulation, $H_{\mathrm{OH}}^{\ast }$ is set to 4 × 10⁻²⁰ M cm³ molecules⁻¹. $H_{\mathrm{OH}}^{\ast }$ is more than 1 order of magnitude lower than its intrinsic Henry's law constant, H_OH (Table 2), reflecting our presumption that the various organic and inorganic compounds in the aqueous phase act as a net sink for OH radicals. A global mean [OH]_g of about 1 × 10⁶ molecules cm⁻³ implies a mean [OH]_aq of 4 × 10⁻¹⁴ M, 1 order of magnitude higher than the mean of the above-mentioned measured [OH]_aq. Moch et al. (2020) use a value for $H_{\mathrm{OH}}^{\ast }$ of 1 × 10⁻¹⁹ M cm³ molecules⁻¹ based on Jacob et al. (2005).

$$\begin{array}{}\text{(7)}& {\left[\mathrm{OH}\right]}_{\mathrm{aq}}={\left[\mathrm{OH}\right]}_{\mathrm{g}}\times H_{\mathrm{OH}}^{\ast }\end{array}$$

The products of Reaction (R9) are HCHO_(aq) and ${\mathrm{SO}}_{\mathrm{5}}^{-}$. Interestingly, the net effect of HMS formation (Reaction R8) and its subsequent oxidation (Reaction R9) is the oxidation of ${\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T$ by OH_(aq), which thus represents an indirect oxidation pathway for SO₂. The sinks for ${\mathrm{SO}}_{\mathrm{5}}^{-}$ are mainly the reactions with ${\mathrm{O}}_{\mathrm{2}}^{-}$, HCOO⁻, and itself (Reactions R10–R12). The reaction of ${\mathrm{SO}}_{\mathrm{5}}^{-}$ and ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ is slow (Jacob et al., 1989). The peroxymonosulfate radical (${\mathrm{HSO}}_{\mathrm{5}}^{-}$) produced by Reactions (R10) and (R11) can oxidize ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ to sulfate (Reaction R13) with a similar rate constant to ${\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{HSO}}_{\mathrm{3}}^{-}$ (Betterton and Hoffmann, 1988). The sulfate radical (${\mathrm{SO}}_{\mathrm{4}}^{-}$) produced by Reaction (R12) is a very strong oxidant and can react rapidly with ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ and ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ (Reactions R14 and R15) as well as with many other species such as Cl⁻, ${\mathrm{NO}}_{\mathrm{2}}^{-}$, ${\mathrm{O}}_{\mathrm{2}}^{-}$, HCOO⁻, and HO₂ (Jacob, 1986). The rate constants for Reactions (R10)–(R15) can be found in Jacob et al. (1989). It is convenient to define the sulfate yield as the number of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions produced due to each attack of OH_(aq) on HMS. If ${\mathrm{SO}}_{\mathrm{5}}^{-}$ reacts with ${\mathrm{O}}_{\mathrm{2}}^{-}/{\mathrm{HCOO}}^{-}$ (Reactions R10 and R11) and the product ${\mathrm{HSO}}_{\mathrm{5}}^{-}$ oxidizes ${\mathrm{HSO}}_{\mathrm{3}}^{-}$ (Reaction R13), the yield is 2. If ${\mathrm{SO}}_{\mathrm{5}}^{-}$ undergoes self-reaction (Reaction R12) and the produced ${\mathrm{SO}}_{\mathrm{4}}^{-}$ reacts with ${\mathrm{HSO}}_{\mathrm{3}}^{-}/{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ (Reactions R14 and R15), a reaction chain is triggered as the products include ${\mathrm{SO}}_{\mathrm{5}}^{-}$. In certain conditions, the sulfate yield can reach 20 or more (Jacob et al., 1989). However, as mentioned above, other oxidizable species also compete for ${\mathrm{SO}}_{\mathrm{4}}^{-}$, thereby terminating this chain and leading to a sulfate yield of 1. In remote environments where SO₂ is very low, ${\mathrm{HSO}}_{\mathrm{5}}^{-}$ may be a stable species, resulting in a sulfate yield < 1. Our low [OH]_aq assumption implies the existence of important oxidizable species, and therefore, the chain propagation is limited. As in Moch et al. (2020) the sulfate yield is assumed to be 2 in our simulations.

$$\begin{array}{}\text{(R10)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{5}}^{-}+{\mathrm{O}}_{\mathrm{2}}^{-}\stackrel{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{⟶}{\mathrm{HSO}}_{\mathrm{5}}^{-}+{\mathrm{O}}_{\mathrm{2}}+{\mathrm{OH}}^{-}\text{(R11)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{5}}^{-}+{\mathrm{HCOO}}^{-}\stackrel{{\mathrm{O}}_{\mathrm{2}}}{⟶}{\mathrm{HSO}}_{\mathrm{5}}^{-}+{\mathrm{O}}_{\mathrm{2}}^{-}+{\mathrm{CO}}_{\mathrm{2}}\text{(R12)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{5}}^{-}+{\mathrm{SO}}_{\mathrm{5}}^{-}\to \mathrm{2}{\mathrm{SO}}_{\mathrm{4}}^{-}+{\mathrm{O}}_{\mathrm{2}}\text{(R13)}& {\displaystyle }{\mathrm{HSO}}_{\mathrm{5}}^{-}+{\mathrm{HSO}}_{\mathrm{3}}^{-}\to \mathrm{2}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+\mathrm{2}{\mathrm{H}}^{+}\text{(R14)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{4}}^{-}+{\mathrm{HSO}}_{\mathrm{3}}^{-}\stackrel{{\mathrm{O}}_{\mathrm{2}}}{⟶}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{SO}}_{\mathrm{5}}^{-}+{\mathrm{H}}^{+}\text{(R15)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{4}}^{-}+{\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}\stackrel{{\mathrm{O}}_{\mathrm{2}}}{⟶}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{SO}}_{\mathrm{5}}^{-}\end{array}$$

2.1.4 Phase equilibrium

The gas/aqueous phase equilibriums of HCHO (Reaction R16) and SO₂ (Reaction R17) are described by intrinsic Henry's law constants, H_HCHO and $H_{{\mathrm{SO}}_{\mathrm{2}}}$, respectively (Table 2). HCHO_(aq) is subject to hydration and the apparent Henry's law constant, $H_{\mathrm{HCHO}}^{\ast }$, is much larger than H_HCHO (Eq. 8). SO₂⋅H₂O dissociates twice in the aqueous phase and thus $H_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }$ depends on pH (Eq. 9). The rates for the hydration of HCHO_(aq) (k_h in Table 2) and the acid dissociations of SO₂⋅H₂O (Schwartz and Freiberg, 1981) are fast enough and we assume that these reactions are always in equilibrium.

$$\begin{array}{}\text{(R16)}& {\displaystyle }{\mathrm{HCHO}}_{\left(\mathrm{g}\right)}\leftrightarrow {\mathrm{HCHO}}_{\left(\mathrm{aq}\right)}\text{(R17)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{SO}}_{\mathrm{2}}\cdot {\mathrm{H}}_{\mathrm{2}}\mathrm{O}\end{array}$$

$$\begin{array}{}\text{(8)}& {\displaystyle }\begin{array}{rl}{H}_{\mathrm{HCHO}}^{\ast }=& \left(\left[{\mathrm{CH}}_{\mathrm{2}}{\left(\mathrm{OH}\right)}_{\mathrm{2}}\right]+{\left[\mathrm{HCHO}\right]}_{\mathrm{aq}}\right)/{\left[\mathrm{HCHO}\right]}_{\mathrm{g}}\\ & =H_{\mathrm{HCHO}}\left(\mathrm{1}+K_{\mathrm{h}}\right)\cong H_{\mathrm{HCHO}}{K}_{\mathrm{h}}\end{array}\text{(9)}& {\displaystyle }\begin{array}{rl}{H}_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }=& {\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}/{\left[{\mathrm{SO}}_{\mathrm{2}}\right]}_{\mathrm{g}}\\ & =H_{{\mathrm{SO}}_{\mathrm{2}}}\left(\mathrm{1}+K_{s\mathrm{1}}/\left[{\mathrm{H}}^{+}\right]+K_{s\mathrm{1}}{K}_{s\mathrm{2}}/{\left[{\mathrm{H}}^{+}\right]}^{\mathrm{2}}\right)\end{array}\end{array}$$

2.2 General model description

We perform global simulations of heterogeneous HMS chemistry using the three-dimensional GEOS-Chem chemical transport model (version 12.1.0, Doi: https://doi.org/10.5281/zenodo.1553349, The International GEOS-Chem User Community, 2018). The simulations are driven by the Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2) reanalysis meteorology from the NASA Goddard Earth Observing System (Gelaro et al., 2017). The original MERRA-2 has a resolution of 0.625^∘ (longitude) × 0.5^∘ (latitude) and is degraded to 5^∘ × 4^∘ for input into the simulations. There are 47 vertical layers in the atmosphere from surface to the mesosphere. The simulations are conducted for 18 months starting from March 2015. The first 6 months are used for initialization and we focus on the 1-year simulation results from September 2015 to August 2016. These months are selected to obtain a continuous boreal winter. We use the tropospheric chemistry mechanism with detailed reactions for O₃-NO_x-VOC (volatile organic compound)-aerosol-halogen interactions. The time step for species advection, vertical mixing, and convection is set to 10 min. The time step is 20 min for emissions, dry deposition, photolysis, and chemistry, as recommended by Philip et al. (2016). The simulated aerosol species include secondary inorganic (sulfate, nitrate, and ammonium) and organic aerosols, primary organic aerosols, black carbon, dust, and sea salt.

Emissions are calculated using HEMCO (the Harvard-NASA Emissions Component, version v2.1.010) (Keller et al., 2014). The global anthropogenic emissions of SO₂, NO_x, NH₃, CO, VOCs, black carbon, and organic carbon are from the Community Emissions Data System (CEDS) (Hoesly et al., 2018). Emissions are overwritten by regional inventories wherever available: EMEP (European Monitoring and Evaluation Programme) over Europe (http://www.emep.int/index.html, last access: 10 June 2020), MIX over Asia (Li et al., 2017), DICE (Diffuse and Inefficient Combustion Emissions) over Africa (Marais and Wiedinmyer, 2016), NEI (National Emissions Inventory) over the United States (Travis et al., 2016), CAC (Criteria Air Contaminants) over Canada (http://wiki.seas.harvard.edu/geos-chem/index.php/CAC_anthropogenic_emissions, last access: 10 June 2020), and MEIC (Multi-resolution Emission Inventory) over China (Zheng et al., 2018). Primary emissions of sulfate constitute 1.4 %–5 % of total anthropogenic sulfur emissions in different regions of the world. Aircraft emissions are from the Aviation Emissions Inventory Code (Simone et al., 2013). Biomass burning emissions are from the Global Fire Emissions Database (GFED, version 4) (van der Werf et al., 2017). Biogenic VOC emissions are calculated by the Model of Emissions of Gases and Aerosols from Nature (MEGAN, version 2.1) (Guenther et al., 2012). Mineral dust emissions follow Duncan et al. (2007) and are distributed in one fine- and three coarse-size bins. Anthropogenic emissions of fine dust aerosols are from the Anthropogenic Fugitive, Combustion, and Industrial Dust (AFCID) inventory (Philip et al., 2017). Sea-salt aerosols in two size bins (fine and coarse) are simulated based on Jaeglé et al. (2011). Other emissions include volcanic SO₂ emissions (Ge et al., 2016), oceanic DMS emissions (Lana et al., 2011), lightning and soil NO_x emissions (Hudman et al., 2012; Murray et al., 2012), and natural NH₃ emissions from the GEIA (Global Emissions InitiAtive) inventory (http://www.geiacenter.org, last access: 10 June 2020).

Because of the importance of acidity for heterogeneous HMS chemistry, more details are provided for the calculation of cloud water and aerosol pH. The standard model calculates cloud water pH iteratively with an initial estimate of 4.5, as described in Alexander et al. (2012). The ions considered in the electroneutrality equation are NH${}_{\mathrm{4}}^{+}$, H⁺, OH⁻, SO${}_{\mathrm{4}}^{\mathrm{2}-}$, NO${}_{\mathrm{3}}^{-}$, HSO${}_{\mathrm{3}}^{-}$, SO${}_{\mathrm{3}}^{\mathrm{2}-}$, HCO${}_{\mathrm{3}}^{-}$, and CO${}_{\mathrm{3}}^{\mathrm{2}-}$. HSO${}_{\mathrm{3}}^{-}/$ SO${}_{\mathrm{3}}^{\mathrm{2}-}$ and HCO${}_{\mathrm{3}}^{-}/$ CO${}_{\mathrm{3}}^{\mathrm{2}-}$ are from the scavenging of SO₂ and CO₂. SO${}_{\mathrm{4}}^{\mathrm{2}-}$ is assumed to be the only form of sulfate and is obtained from the cloud scavenging of aerosols. NH${}_{\mathrm{4}}^{+}$ and NO${}_{\mathrm{3}}^{-}$ are from the scavenging of both aerosols and gases (NH₃ and HNO₃). The scavenging efficiencies of aerosols and gases are assumed to be 0.7 and unity, respectively. The ISORROPIA II (version 2.2) thermodynamic equilibrium model (Fountoukis and Nenes, 2007) is used to calculate the inorganic aerosol water content (m³ H₂O m⁻³ air) and pH, including the following gas and aerosol species: NH₃, HNO₃, ammonium, nitrate, sulfate, and fine sea-salt aerosols.

2.3 Sulfur simulation in the standard model

The sulfur simulation in GEOS-Chem has been developed and improved based on multiple studies (Chin et al., 2000; Park et al., 2004; Alexander et al., 2005, 2009; Chen et al., 2017; Shao et al., 2019). The simulated sulfur species include DMS, SO₂, MSA, and sulfate. It includes primary emissions of DMS, SO₂, and sulfate (Sect. 2.2). SO₂, MSA, and sulfate can also be formed by chemical reactions. The model contains three gas-phase reactions of DMS oxidation, producing SO₂ and MSA (Reactions R18–R20). An expanded chemistry mechanism for DMS can be found in Chen et al. (2018). The oxidation of SO₂ to sulfate occurs in the gas phase by OH (Reaction R21) and in the aqueous clouds. The aqueous-phase oxidants are O₃, H₂O₂, O₂ (catalyzed by transition metal ions Mn²⁺ and Fe³⁺), and HOBr (Reactions R22–R25). The effect of the heterogeneity in cloud droplet pH on sulfate production rates is accounted for using the parameterization by Yuen et al. (1996) and Fahey and Pandis (2001). This parameterization is restricted over the ocean since the heterogeneity in pH is believed to be caused by alkaline sea-salt aerosols (Alexander et al., 2012). The model also includes the oxidation of SO₂ by O₃ on sea-salt aerosol surface (Reaction R26) (Alexander et al., 2005).

$$\begin{array}{}\text{(R18)}& {\displaystyle }{\mathrm{DMS}}_{\left(\mathrm{g}\right)}+{\mathrm{OH}}_{\left(\mathrm{g}\right)}\to {\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{HCHO}}_{\left(\mathrm{g}\right)}\text{(R19)}& {\displaystyle }{\mathrm{DMS}}_{\left(\mathrm{g}\right)}+{\mathrm{OH}}_{\left(\mathrm{g}\right)}\to \mathrm{0.75}{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+\mathrm{0.25}{\mathrm{MSA}}_{\left(\mathrm{g}\right)}\text{(R20)}& {\displaystyle }\begin{array}{rl}& {\mathrm{DMS}}_{\left(\mathrm{g}\right)}+{\mathrm{NO}}_{\mathrm{3}\left(\mathrm{g}\right)}\to {\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{HCHO}}_{\left(\mathrm{g}\right)}\\ & +{\mathrm{HNO}}_{\mathrm{3}\left(\mathrm{g}\right)}\end{array}\text{(R21)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{OH}}_{\left(\mathrm{g}\right)}\stackrel{\mathrm{M}}{⟶}{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}\left(\mathrm{g}\right)}+{\mathrm{HO}}_{\mathrm{2}\left(\mathrm{g}\right)}\text{(R22)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+{\mathrm{O}}_{\mathrm{3}\left(\mathrm{aq}\right)}\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{O}}_{\mathrm{2}\left(\mathrm{aq}\right)}\text{(R23)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}\left(\mathrm{aq}\right)}\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\text{(R24)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+{\mathrm{O}}_{\mathrm{2}\left(\mathrm{aq}\right)}\stackrel{{\mathrm{Mn}}^{\mathrm{2}+}{\mathrm{Fe}}^{\mathrm{3}+}}{⟶}{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\text{(R25)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+{\mathrm{HOBr}}_{\left(\mathrm{aq}\right)}\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{HBr}}_{\left(\mathrm{aq}\right)}\text{(R26)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{g}\right)}+{\mathrm{O}}_{\mathrm{3}\left(\mathrm{g}\right)}+\text{fine\hspace{0.17em} sea\hspace{0.17em} salt}\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+{\mathrm{O}}_{\mathrm{2}}\end{array}$$

2.4 Control simulation

Based on the standard model v12.1.0, we implement heterogeneous HMS chemistry and assume that cloud water provides the only aqueous medium, following Moch et al. (2020). As described in Sect. 2.1, HMS is produced by dissolved SO₂ and HCHO, undergoes decomposition, and is oxidized to sulfate by aqueous OH. Two other cloud sulfate formation pathways are also incorporated (Wang et al., 2020), in which SO₂ is oxidized by NO₂ and HONO (Reactions R27 and R28).

$$\begin{array}{}\text{(R27)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+\mathrm{2}{\mathrm{NO}}_{\mathrm{2}\left(\mathrm{aq}\right)}\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+\mathrm{2}{\mathrm{HONO}}_{\left(\mathrm{aq}\right)}\text{(R28)}& {\displaystyle }{\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T+{\mathrm{HONO}}_{\left(\mathrm{aq}\right)}^T\to {\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}+\mathrm{0.5}{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\left(\mathrm{aq}\right)}\end{array}$$

Tables 1 and 2 show all the rate constants of aqueous-phase reactions and the Henry's law constants of the reactants. The solubilities of transition metals Fe and Mn are reduced following Shao et al. (2019). Ten advected tracers are added: one is the aerosol HMS species and the others represent different sulfate formation pathways. Transport and deposition of these tracers are treated in the same way as the sulfate tracer as in Moch et al. (2020). In addition, several other changes are made in the control simulation to the standard model. First, we update the dry deposition scheme and the reactive uptake coefficients of NO₂, NO₃, and N₂O₅ on aerosols, following Jaeglé et al. (2018) and Shah et al. (2018). Second, this simulation includes some updates developed by Luo et al. (2019, 2020) in the treatments of wet processes, including spatially and temporally varying in-cloud condensation water contents, empirical washout rates for water-soluble aerosols and nitric acid, the cloud fraction available for aqueous chemistry, and rainout efficiencies for water-soluble aerosols and gases. Third, more ions are included in the cloud water pH calculation. We consider Ca²⁺, Mg²⁺, NH${}_{\mathrm{4}}^{+}$, Na⁺, H⁺, OH⁻, Cl⁻, SO${}_{\mathrm{4}}^{\mathrm{2}-}$, NO${}_{\mathrm{3}}^{-}$, NO${}_{\mathrm{2}}^{-}$, HSO${}_{\mathrm{3}}^{-}$, SO${}_{\mathrm{3}}^{\mathrm{2}-}$, HCO${}_{\mathrm{3}}^{-}$, CO${}_{\mathrm{3}}^{\mathrm{2}-}$, HCOO⁻, CH₃COO⁻, HMS, and ${\mathrm{CH}}_{\mathrm{3}}{\mathrm{SO}}_{\mathrm{3}}^{-}$. The Newton–Raphson method is used to find the solution to the cubic electroneutrality equation, following Luo et al. (2020) and Moch et al. (2020). Ca²⁺ and Mg²⁺ are assumed to constitute 3 % and 0.6 %, respectively, of the dust by mass (Claquin et al., 1999; Fairlie et al., 2010; Nickovic et al., 2012; Shao et al., 2019; Moch et al., 2020). Only Na⁺ and Cl⁻ from sea-salt aerosols are considered. HMS and ${\mathrm{CH}}_{\mathrm{3}}{\mathrm{SO}}_{\mathrm{3}}^{-}$ are from the cloud scavenging of aerosols. NO${}_{\mathrm{2}}^{-}$, HCOO⁻, and CH₃COO⁻ are from the scavenging of HONO, HCOOH, and CH₃COOH, respectively. Fourth, HMS, ${\mathrm{CH}}_{\mathrm{3}}{\mathrm{SO}}_{\mathrm{3}}^{-}$, and Ca²⁺ and Mg²⁺ in fine dust are included in the ISORROPIA calculations. We assume the same hygroscopicity of HMS and MSA as sulfate (Xu et al., 2020).

We evaluate the performance of the control simulation by comparing it with the standard GEOS-Chem v12.1.0 (GC12.1.0). Figure S1 in the Supplement shows the horizontal distributions of surface ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and SO₂ concentrations. The global average ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ in the control simulation is reduced by 24 % compared to GC12.1.0. The updates in the treatments of wet processes by Luo et al. (2019, 2020) are primarily responsible for this difference. The ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations modeled in the control simulation are consistent with the improved model results in Luo et al. (2020), which have been found to agree well with ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ observed in the United States, Europe, and Asia (Luo et al., 2020). Moreover, since GC12.1.0 was released in late 2018, it is necessary to compare it with a more recent model version. Accordingly, we conduct a simulation using the standard GEOS-Chem v12.7.0 (GC12.7.0, released in February 2020, http://wiki.seas.harvard.edu/geos-chem/index.php/GEOS-Chem_12, last access: 10 June 2020). We find that the global average ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ in GC12.7.0 only differs little (3 %) compared with that in GC12.1.0 (Fig. S2 in the Supplement).

Below, we provide details on the calculation of cloud sulfur chemistry and highlight the need for more accurate representations of in-cloud SO₂ titration by various reactants, which include O₃ (Reaction R22), H₂O₂ (Reaction R23), O₂ (Reaction R24), HOBr (Reaction R25), NO₂ (Reaction R27), HONO (Reaction R28), and HCHO (Reaction R8). Cloud sulfur chemistry is calculated locally in the model grid cells where aqueous clouds are present. f_c (dimensionless, $\le f_{\mathrm{c}}\le \mathrm{1}$) denotes the fraction of aqueous cloud in a grid cell, and L (m³ H₂O m⁻³ air) denotes the in-cloud liquid water content. In each chemistry time step (Δt=20 min), the losses of SO₂ in the above reactions (R8, R22–R25, R27, and R28) are calculated. Reaction (R24) is treated as a first-order reaction of SO₂ (O₂ is in large excess), while the other reactions are second order. The first- and second-order rate constants for the aqueous reaction of ${\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T$ and $X_{i_{\left(\mathrm{aq}\right)}}$, $k_{\mathrm{1},\mathrm{aq},i}$ (s⁻¹) and $k_{\mathrm{2},\mathrm{aq},i}$ (M⁻¹ s⁻¹), are obtained by Eq. (10) from the kinetic data in Table 1. X_i ($i=\mathrm{1}:\mathrm{7}$) represents the ith reactant with SO₂. R_aq,i is the reaction rate (M s⁻¹). $k_{\mathrm{1},\mathrm{aq},i}$ and $k_{\mathrm{2},\mathrm{aq},i}$ are used to derive the first- and second-order rate constants for the heterogeneous reaction of SO_2(g) and $X_{i_{\left(\mathrm{g}\right)}}$, $k_{\mathrm{1},\mathrm{g},i}$ (s⁻¹) and $k_{\mathrm{2},\mathrm{g},i}$ (mol mol⁻¹ s⁻¹) (Eq. 11). $H_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }$ and $H_{X_i}$ indicate their Henry's law constants. $f_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}$ and f_g,Xi are the gas-phase partitioning fractions of SO₂ and X_i, respectively (Eq. 12). R is the gas constant. T (K) is the temperature. P (atm) is atmospheric pressure. The loss of SO₂ over time Δt, $\mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}$, is solved analytically (Eq. 13). ${\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}$ and ${\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}$ are the mixing ratios (mol mol⁻¹) for SO_2(g) and $X_{i_{\left(\mathrm{g}\right)}}$ at the beginning of this time step. The grid-average losses of SO_2(g) from all seven reactions are limited by the availability of SO_2(g) within the cloud fraction f_c.

$$\begin{array}{}\text{(10)}& {\displaystyle }\begin{array}{rl}{k}_{\mathrm{1},\mathrm{aq},i}=& R_{\mathrm{aq},i}/{\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}\text{ and }{k}_{\mathrm{2},\mathrm{aq},i}\\ & =R_{\mathrm{aq},i}/\left({\left[{\mathrm{SO}}_{\mathrm{2}}^T\right]}_{\mathrm{aq}}{\left[X_i\right]}_{\mathrm{aq}}\right)\end{array}\text{(11)}& {\displaystyle }\begin{array}{rl}{k}_{\mathrm{1},\mathrm{g},i}=& k_{\mathrm{1},\mathrm{aq},i}{H}_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }{f}_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}\text{LRT}\text{ and }\\ & k_{\mathrm{2},\mathrm{g},i}=k_{\mathrm{2},\mathrm{aq},i}{H}_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }{f}_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}{H}_{X_i}{f}_{\mathrm{g},{\mathrm{X}}_i}\mathrm{PLRT}\end{array}\text{(12)}& {\displaystyle }\begin{array}{rl}{f}_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}=& {\left(\mathrm{1}+H_{{\mathrm{SO}}_{\mathrm{2}}}^{\ast }\text{LRT}\right)}^{-\mathrm{1}}\text{ and }\\ & f_{\mathrm{g},{\mathrm{X}}_i}={\left(\mathrm{1}+H_{X_i}\mathrm{LRT}\right)}^{-\mathrm{1}}\end{array}\text{(13)}& {\displaystyle }\begin{array}{rl}& \mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}=\\ & \left\{\begin{array}{l}{\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}\left[\mathrm{1}-\exp \left(-k_{\mathrm{1},\mathrm{g},i}\mathrm{\Delta }t\right)\right],\mathrm{1}\mathrm{st}\mathrm{order}\\ \frac{{\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}{\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}\left(C-\mathrm{1}\right)}{{\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}C-{\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}},C=\\ \exp \left[\left({\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}-{\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}\right)k_{\mathrm{2},\mathrm{g},i}\mathrm{\Delta }t\right]\mathrm{2}\mathrm{nd}\mathrm{order}\end{array}\right.\end{array}\end{array}$$

Since multiple in-cloud reactions consume SO₂ simultaneously, it is important to allow them to compete effectively and fairly. As shown in Eq. (13), the contribution of the ith reaction to the total SO_2(g) loss depends on its rate constant ($k_{\mathrm{1},\mathrm{g},i}$ or $k_{\mathrm{2},\mathrm{g},i}$), its relative abundance (${\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}/{\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}$), and the choice of Δt. Ideally, Δt should be smaller than the lifetime (τ_i) of SO_2(g) for any ith reaction. τ_i is the inverse of the pseudo-first-order rate constant, $k_{\mathrm{1},\mathrm{g},i}^{\sim }$, which equals to $k_{\mathrm{1},\mathrm{g},i}$ for a first-order reaction and to $k_{\mathrm{2},\mathrm{g},i}{\left[X_{it=\mathrm{0}}\right]}_{\mathrm{g}}$ for a second-order reaction. Figure 3 shows the probability density distributions of the calculated $k_{\mathrm{1},\mathrm{g},i}^{\sim }$ and the total rate constant for the seven reactions, $\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{g},i}^{\sim }$, in the lower troposphere for a randomly selected week in boreal summer. $k_{\mathrm{1},\mathrm{g},i}^{\sim }$ (and thus τ_i) can vary by several orders of magnitude in different model grid cells. Notably, there is a > 50 % possibility that the lifetime of SO_2(g) is smaller than 20 min, the Δt used in this simulation. The rapid consumption of SO_2(g) is mainly via O₃ and H₂O₂, as shown in Fig. 3 and Table S1 in the Supplement (statistics of probability distributions). The other five reactions consuming SO₂ (HCHO, TMI+O₂, NO₂, HONO, and HOBr) can be considered as minor pathways. This means that using Δt=20 min for the sulfur chemistry will in general lead to an underestimation of the contribution of O₃ and H₂O₂ and an overestimation of the importance of the other reactants such as HCHO. An example is provided in Text S1 in the Supplement to conceptually explain the effect of Δt on the competition of different reactions. We conduct a sensitivity simulation in which Δt is set to 10 min and, as we expect, the ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations through the cloud O₃ chemistry increase significantly (Fig. S3 in the Supplement). A simple way to solve this problem is to reduce Δt. The possibility of τ<Δt decreases to only 4 % when Δt=1 min (Fig. 3 and Table S1). Also, most (> 80 %) of the cases of τ<1 min arise from the rapid reaction of ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ with O_3(aq) when cloud water pH is high. The remaining cases are from the reactions of ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$ with HOBr_(aq) and HCHO_(aq). The other four reactions can hardly lead to τ<1 min. We change the time step to 1 min when calculating in-cloud SO₂ titration in the default simulation (Sect. 2.5).

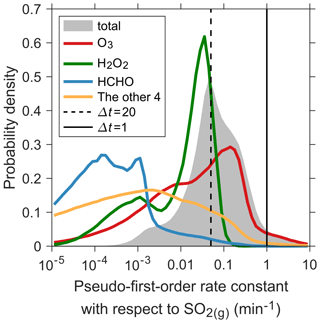
Figure 3 Probability density distributions of the pseudo-first-order rate constants with respect to SO_2(g) for cloud reactions in the control simulation. The shaded area shows the sum of rate constants for the seven reactions consuming SO₂. The red, green, blue, and orange curves indicate the distributions for reactions with O₃, H₂O₂, HCHO, and the sum of rate constants for the other four reactions consuming SO₂ (TMI+O₂, NO₂, HONO, and HOBr), respectively. Data shown are for the first week of July and in the lower troposphere (13 vertical layers above surface up to about 800 hPa). Since the chemistry time step (Δt) of this simulation is 20 min, there are 504 steps in this week. The total number of data points is 72 × 46 (number of 5^∘ × 4^∘ grids) × 13 (vertical layers) × 504 $\approx \mathrm{2.2}\times$ 10⁷. About 1.4 × 10⁷ data points have aqueous clouds (cloud fraction f_c>0), accounting for about 2∕3. The probability density distributions are plotted based on these data points. The dashed and solid vertical black lines indicate the rate constants corresponding to Δt of 20 and 1 min, respectively.

Another issue in the control simulation is, in a partly cloudy ($<f_{\mathrm{c}}<\mathrm{1}$) model grid, that the mixing of air between the cloudy fraction (f_c) and the cloud-free fraction (1−f_c) occurs in the same timescale as the chemistry time step of the model (Holmes et al., 2019). In each time step, the grid-average loss of SO_2(g) from all in-cloud reactions cannot exceed the amount of SO_2(g) available within the cloudy fraction and at the beginning of this time step (Eq. 14). This so-called “cloud-partitioning method” is unphysical as the entrainment/detrainment rates are affected by the setting of the chemistry time step (Holmes et al., 2019). Since many chemical transport models such as GEOS-Chem do not resolve individual clouds, Holmes et al. (2019) developed a more realistic and stable “entrainment-limited uptake” method, which accounts for cloud entrainment/detrainment within the chemical rate expression. We apply this method to the default simulation (Sect. 2.5).

$$\begin{array}{}\text{(14)}& \sum _{i=\mathrm{1}}^{\mathrm{7}}\mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}\le f_{\mathrm{c}}{\left[{\mathrm{SO}}_{\mathrm{2},t=\mathrm{0}}\right]}_{\mathrm{g}}\end{array}$$

2.5 Default simulation

Three major changes are made in this simulation based on the control simulation, as mentioned in Sect. 2.4. The first is applying the entrainment-limited uptake method developed by Holmes et al. (2019) to more realistically model the entrainments and detrainments of air in cloudy grid cells. The second is reducing the time step to 1 min when calculating cloud sulfur reactions to better quantify the competition of different chemical pathways consuming SO₂. The third is adding the reaction of H₂O₂ and SO₂ in aerosol water using the kinetic data reported recently by Liu et al. (2020). The control simulation only includes the reaction of H₂O₂ and SO₂ in cloud water. Figure S4 in the Supplement shows the horizontal distributions of surface ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and SO₂ concentrations in the control and default simulations, and only very small differences (4 % for ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and 1 % for SO₂) are found for their global average values.

In the entrainment-limited uptake method (Holmes et al., 2019), the first-order loss rate of SO_2(g) in a model grid cell due to heterogeneous cloud chemistry, k₁ (s⁻¹), depends on the cloud fraction (f_c), the detrainment rate (k_c, s⁻¹), and the in-cloud total pseudo-first-order rate constant, $k_{\mathrm{1},\mathrm{g}}^{\ast }=\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{g},i}^{\ast }$ (s⁻¹) (Eq. 15). As shown in Holmes et al. (2019), the entrainment/detrainment (k_c term) limits its reactive uptake. In a completely cloudy condition (f_c=1), Eq. (15) reduces to $k_{\mathrm{1}}=\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{g},i}^{\ast }$. k_c is the reverse of the in-cloud residence time of air (τ_c), which varies with cloud types and ranges from 15 to 120 min for stratus and cumulus clouds (Holmes et al., 2019). We use τ_c=30 min in this work since MERRA-2 does not provide this information. A sensitivity simulation shows that assuming a τ_c of 60 min decreases the global average surface ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentration by 10 %. Holmes et al. (2019) have pointed out that future studies are needed to specify the spatiotemporal variability of τ_c in the global reanalysis data sets. Within the cloudy fraction of a model grid cell, as shown in Fig. 1 and Eq. (16), the heterogeneous reaction rates are limited by a series of resistances associated with the mass transfer processes from the gas phase to the aqueous phase, including gas-phase diffusion, transfer of the reactants across the air–water interface, and aqueous-phase diffusion (Ravishankara, 1997; Jacob, 2000). In Eq. (16), the ${\mathit{\alpha }}_{{\mathrm{SO}}_{\mathrm{2}}}$ term represents the limitation due to mass accommodation at the air–water interface and the $D_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}$ term represents that due to gas-phase diffusion. A dimensionless parameter Q, whose expression is given by Eq. (17) ($\mathrm{0}<Q<\mathrm{1}$), is used to account for aqueous-phase mass transport limitations when calculating $k_{\mathrm{1},\mathrm{aq},i}$ and $k_{\mathrm{2},\mathrm{aq},i}$ (Eq. 10).

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{\mathrm{1}}{k_{\mathrm{1}}}}={\displaystyle \frac{\mathrm{1}-f_{\mathrm{c}}}{f_{\mathrm{c}}{k}_{\mathrm{c}}}}+{\displaystyle \frac{\mathrm{1}}{f_{\mathrm{c}}{k}_{\mathrm{1},\mathrm{g}}^{\ast }}}={\displaystyle \frac{\mathrm{1}-f_{\mathrm{c}}}{f_{\mathrm{c}}{k}_{\mathrm{c}}}}+{\displaystyle \frac{\mathrm{1}}{f_{\mathrm{c}}\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{g},i}^{\ast }}}\text{(16)}& {\displaystyle \frac{\mathrm{1}}{k_{\mathrm{1},\mathrm{g},i}^{\ast }}}={\displaystyle \frac{\mathrm{1}}{k_{\mathrm{1},\mathrm{g},i}^{\sim }}}+{\displaystyle \frac{\mathrm{4}}{A{v}_{{\mathrm{SO}}_{\mathrm{2}}}{\mathit{\alpha }}_{{\mathrm{SO}}_{\mathrm{2}}}}}+{\displaystyle \frac{r}{A{D}_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}}}\text{(17)}& {\displaystyle }Q=\mathrm{3}\left({\displaystyle \frac{\coth q}{q}}-{\displaystyle \frac{\mathrm{1}}{q^{\mathrm{2}}}}\right)q=r\sqrt{{\displaystyle \frac{\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{aq},i}^{\sim }}{D_{\mathrm{aq}}}}}\end{array}$$

Here, r is the radius of cloud droplets and is assumed to be 10⁻⁵ m. A (m² m⁻³ air) is the surface area density of cloud droplets and is derived using L and r. $v_{{\mathrm{SO}}_{\mathrm{2}}}$ (m s⁻¹) is the molecular mean speed of SO₂ (Eq. 18). ${\mathit{\alpha }}_{{\mathrm{SO}}_{\mathrm{2}}}$ (dimensionless) is the mass accommodation coefficient of SO₂ (Table 3). $D_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}$ (m² s⁻¹) is the gas-phase diffusion coefficient of SO₂ (Eq. 19). q is a dimensionless parameter determined by r, D_aq, and $k_{\mathrm{1},\mathrm{aq},i}^{\sim }$ (the pseudo-first-order rate constant with respect to ${\mathrm{SO}}_{\mathrm{2}\left(\mathrm{aq}\right)}^T$ for the ith reaction). For a first-order and second-order reaction, $k_{\mathrm{1},\mathrm{aq},i}^{\sim }$ is equal to $k_{\mathrm{1},\mathrm{aq},i}$ and $k_{\mathrm{2},\mathrm{aq},i}{\left[X_i\right]}_{\mathrm{aq}}$, respectively (Eq. 10). D_aq is the aqueous-phase diffusion coefficient (10⁻⁹ m² s⁻¹) (Song et al., 2019a). $M_{{\mathrm{SO}}_{\mathrm{2}}}$ (g mol⁻¹) represents the molar mass of SO₂. ρ_n,air (molecule cm⁻³) is the number density of air. $k_{\mathrm{1},\mathrm{g},i}^{\sim }$ (s⁻¹) is the pseudo-first-order rate constant with respect to SO_2(g) for the ith aqueous-phase reaction, and is equal to $k_{\mathrm{1},\mathrm{g},i}$ and $k_{\mathrm{2},\mathrm{g},i}{\left[X_i\right]}_{\mathrm{g}}$ for the first-order and second-order reactions, respectively. In addition, as illustrated in Fig. 1, the second-order reaction rate may also be limited by the mass transfer of X_i. Thus, the in-cloud pseudo-second-order rate constant, $k_{\mathrm{2},\mathrm{g},i}^{\ast }$, is given by Eq. (20). $v_{X_i}$, ${\mathit{\alpha }}_{X_i}$, and $D_{\mathrm{g},{\mathrm{X}}_i}$ are the molecular mean speed, the mass accommodation coefficient, and the gas-phase diffusion coefficient of X_i, respectively. $v_{X_i}$ and $D_{\mathrm{g},{\mathrm{X}}_i}$ are calculated similarly to Eqs. (18) and (19). ${\mathit{\alpha }}_{X_i}$ can be found in Table 3.

$$\begin{array}{}\text{(18)}& {\displaystyle }{v}_{{\mathrm{SO}}_{\mathrm{2}}}=\sqrt{\mathrm{8}RT}/\left(\mathit{\pi }{M}_{{\mathrm{SO}}_{\mathrm{2}}}\right)\text{(19)}& {\displaystyle }\begin{array}{rl}& D_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}=\\ & {\displaystyle \frac{\mathrm{9.45}\times {\mathrm{10}}^{\mathrm{13}}\times \sqrt{T\times \left(\mathrm{3.47}\times {\mathrm{10}}^{-\mathrm{2}}+\mathrm{1}/M_{{\mathrm{SO}}_{\mathrm{2}}}\right)}}{{\mathit{\rho }}_{\mathrm{n},\mathrm{air}}}}\end{array}\text{(20)}& {\displaystyle }\begin{array}{rl}& {\displaystyle \frac{\mathrm{1}}{k_{\mathrm{2},\mathrm{g},i}^{\ast }}}={\displaystyle \frac{\mathrm{1}}{k_{\mathrm{2},\mathrm{g},i}}}+\mathrm{MAX}\\ & \left({\displaystyle \frac{\mathrm{4}{\left[X_i\right]}_{\mathrm{g}}}{A{v}_{{\mathrm{SO}}_{\mathrm{2}}}{\mathit{\alpha }}_{{\mathrm{SO}}_{\mathrm{2}}}}}+{\displaystyle \frac{r{\left[X_i\right]}_{\mathrm{g}}}{A{D}_{\mathrm{g},{\mathrm{SO}}_{\mathrm{2}}}}}{\displaystyle \frac{\mathrm{4}{\left[{\mathrm{SO}}_{\mathrm{2}}\right]}_{\mathrm{g}}}{A{v}_{X_i}{\mathit{\alpha }}_{X_i}}}+{\displaystyle \frac{r{\left[{\mathrm{SO}}_{\mathrm{2}}\right]}_{\mathrm{g}}}{A{D}_{\mathrm{g},{\mathrm{X}}_i}}}\right)\end{array}\end{array}$$

As mentioned in Sect. 2.4, we do not change the chemistry time step of the model (Δt=20 min) but only the time step (to 1 min) when identifying cloud SO₂ reactions. For each 1 min time step, the loss of SO_2(g) for the ith reaction, $\mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}$, is solved analytically using Eq. (13), in which $k_{\mathrm{1},\mathrm{g},i}$ and $k_{\mathrm{2},\mathrm{g},i}$ are replaced by $k_{\mathrm{1},\mathrm{g},i}^{\ast }$ from Eq. (16) and $k_{\mathrm{2},\mathrm{g},i}^{\ast }$ from Eq. (20), respectively. This change reflects the mass transport limitations. The grid-average first-order loss rate of SO_2(g), k₁, is calculated using Eq. (15), in which $\sum _{i=\mathrm{1}}^{\mathrm{7}}{k}_{\mathrm{1},\mathrm{g},i}^{\ast }$ is replaced by the in-cloud total pseudo-first-order rate constant estimated from $\sum _{i=\mathrm{1}}^{\mathrm{7}}\mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}$. The grid-average loss of SO_2(g) and the contributions of different reactions are then calculated using k₁ and $\mathrm{\Delta }{{\mathrm{SO}}_{\mathrm{2}}}_{\mathrm{g},i}$. The mixing ratios of the relevant chemical species are updated at the end of this 1-min time step and used as initial condition for the next time step. The calculations are repeated 20 times in a chemistry time step.

Table 3 Mass accommodation coefficients on aqueous surfaces.

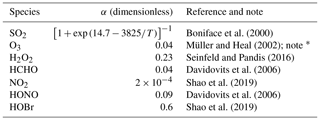
^* The α of O₃ is very uncertain with the upper limit approaching unity.

Table 4 Description of model simulations.

The cloud water pH and rate constants for the heterogeneous reaction of SO_2(g) and $X_{i_{\left(\mathrm{g}\right)}}$ are calculated only at the beginning of each chemistry time step. We conduct a sensitivity simulation that redoes cloud SO₂ calculations using the cloud water pH and rate constants estimated at the end of each chemistry time step. The resulting change is insignificant (global mean ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentration decreases by <2 %). The aqueous-phase sulfur reactions are hard-coded into the model. Ideally, further model development of cloud chemistry should apply the advanced numerical solvers generated by the Kinetic PreProcessor (KPP), which may not only allow a full coupling of gas-phase and cloud chemistry but also make it easier for the model to incorporate additional aqueous reactions (Fahey et al., 2017; Viral Shah, personal communication, 18 December 2019).

The implementation of sulfur chemistry in aerosol water is similar to that for cloud sulfur chemistry. As shown in Fig. 1, the heterogeneous reaction rates are also controlled by the mass transfer of reactants from the gas to the aqueous phase. The difference is that aerosols (and aerosol water) can be considered evenly distributed in a model grid cell, and it is unnecessary to include the entrainment/detrainment processes. The major difficulty in parameterizing the aerosol water sulfur chemistry is the lack of suitable reaction rate constants. Liu et al. (2020) have recently found that the high ionic strength of deliquesced aerosols significantly enhances the rate constants for the reaction of H₂O₂ and SO₂. The enhancement factor (EF) relative to its rate constant in dilute solutions is derived by fitting the data in Liu et al. (2020) as a function of the molality-based ionic strength, μ_b (mol kg⁻¹) (Table 1). The water content, pH, μ_b, and the absorbed water volume fraction of inorganic aerosols are calculated by the ISORROPIA II model (Sect. 2.2). The aerosol water volume fraction of 0.25 is used as a threshold for the occurrence of aqueous reactions as it governs the transition of aerosols to a liquid state (Bateman et al., 2016).

2.6 Sensitivity simulations

In addition to the control and default simulations, we conduct ten sensitivity simulations to investigate the key factors leading to uncertainty in the modeled HMS concentrations. As shown in Table 4, all these sensitivity simulations are based on the default simulation. HiKf, HiKd, and HiOH make changes to HMS formation, decomposition, and oxidation, respectively, in heterogeneous cloud chemistry. HiKf uses the high k_f instead of the low k_f in the default simulation (Sect. 2.1.1). HiKd increases k_d by a factor of 2, the upper limit of its estimate (Sect. 2.1.2). HiOH increases [OH]_aq by a factor of 10, matching its average value in current multiphase models (Sect. 2.1.3). CWpH considers less ions, i.e., NH${}_{\mathrm{4}}^{+}$, H⁺, OH⁻, SO${}_{\mathrm{4}}^{\mathrm{2}-}$, NO${}_{\mathrm{3}}^{-}$, HSO${}_{\mathrm{3}}^{-}$, SO${}_{\mathrm{3}}^{\mathrm{2}-}$, HCO${}_{\mathrm{3}}^{-}$, CO${}_{\mathrm{3}}^{\mathrm{2}-}$, HMS, and ${\mathrm{CH}}_{\mathrm{3}}{\mathrm{SO}}_{\mathrm{3}}^{-}$, in cloud water pH calculations.

AWOH, AWK0, and AWKE examine the potential role of aerosol water in heterogeneous HMS chemistry (Table 4). Since the rate constants of HMS chemical reactions in concentrated solutions have not been determined experimentally, we have to make assumptions about these data. AWOH implements the oxidation of HMS by OH in aerosol water and assumes the same rate constant as those for cloud water. AWK0 adds the formation and decomposition of HMS in aerosol water also using the rate constants for cloud water. Theoretically, we anticipate that the rate constant of HMS formation, k_f, in concentrated solutions should be enhanced relative to dilute solutions (Song et al., 2019a), similar to the situation found for the reaction of H₂O₂ and SO₂. AWKE arbitrarily increases k_f by the same EF for the H₂O₂ and SO₂ reaction (Table 1). The implementation of the above chemical reactions of HMS in aerosol water follows the approach described in Sect. 2.5.

Three sensitivity simulations, HiNH3, HiFA, and AppHet, focus on East Asia (Table 4). SO₂, HCHO, and NH₃ emissions may influence the modeled HMS. Although SO₂ emissions are well understood, recent studies have shown that there may be large uncertainties in emissions of NH₃ and HCHO in China (Pan et al., 2018; Kong et al., 2019; Liu et al., 2019; Song et al., 2019a). An inverse study found that the MEIC inventory underestimated NH₃ emissions by 30 % nationally and by > 40 % in eastern and central regions using observations over the same time period as our study (Kong et al., 2019). HiNH3 increases the anthropogenic emissions of NH₃ in MEIC by 50 %. Less information is available regarding the emissions of HCHO due to its sparse observations and complex chemistry. Model–observation comparisons in Beijing suggested a strong underestimation of HCHO emissions during winter (Song et al., 2019a). Mobile and residential emission sources may be responsible for its underestimation (Jaeglé et al., 2018; Song et al., 2019a). HiFA increases HCHO emissions from the transportation and residential sectors by a factor of 5. Chemical transport models commonly underestimate ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ during winter haze episodes in China (Chu et al., 2020), and thus some studies have adopted an apparent heterogeneous parameterization for SO₂ reactive uptake in order to compensate for the missing ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (Zheng et al., 2015; Cheng et al., 2016; Chu et al., 2016; Wang et al., 2016; Liu et al., 2019; Li et al., 2020). This parameterization is applied in AppHet during the cold season, in which the reactive uptake coefficient of SO₂ increases from 2 × 10⁻⁵ to 5 × 10⁻⁵ with 50 % < RH ≤ 100 % (Zheng et al., 2015).

3 Results and discussion

3.1 Spatial and seasonal distributions in the default simulation

The horizontal distributions of HMS concentration in the surface layer and the vertical profiles of its zonal average are shown in Fig. 4 (DJF: December–January–February and JJA: June–July–August) and Fig. S5 in the Supplement (MAM: March–April–May and SON: September–October–November). The concentration unit is µg sm⁻³, where 1 sm³ equals 1 m³ at standard temperature and pressure (273.15 K and 1013.25 hPa). The molar ratio of HMS to sulfate, also shown in Figs. 4 and S5 in the Supplement, is a useful metric to assess the significance of HMS in sulfur chemistry. Higher HMS concentrations and HMS ∕ sulfate ratios are found over the continental regions in the Northern Hemisphere. The vertical profiles indicate that most HMS exists in the lower troposphere. These features are expected because the precursors of HMS, SO₂ and HCHO, are more abundant in these regions compared with elsewhere (Fig. S6 in the Supplement).

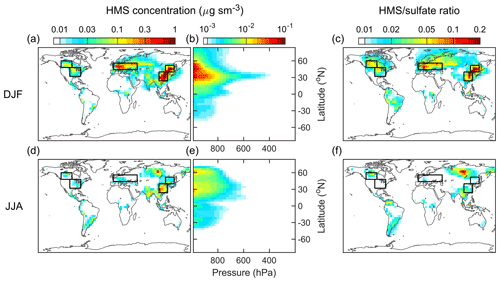
Figure 4 Distributions of HMS concentrations and the molar ratios of HMS to sulfate modeled by the default simulation. Top and bottom panels show results for DJF (December–January–February) and JJA (June–July–August), respectively. (a), (c), (d), and (f) are the horizontal distributions in the surface layer. (b) and (e) are the vertical distributions of the zonal averages from surface to 200 hPa. The concentration unit is µg sm⁻³, where 1 sm³ equals 1 m³ at 273.15 K and 1013.25 hPa. The color bars are not linear and differ in the three columns. The same color bars are used for each pair of the top and bottom panels. The black-outline boxes indicate the three regions selected for quantitative analysis.

The surface HMS concentrations and HMS ∕ sulfate molar ratios exhibit distinct seasonal patterns with maxima in DJF (boreal winter) and minima in JJA (boreal summer), and thus our analyses focus on these two seasons. It is noted that there are hotspots of HMS in JJA in Siberia that are linked to massive forest fires in that region in July 2016 (Sitnov et al., 2017). As highlighted in Fig. 4, three regions with relatively high HMS levels, East Asia (EA), Europe (EU), and North America (NA), are selected for quantitative analysis. Figure 5 shows the statistics of HMS levels from the default simulation with comparisons to other simulations. The average HMS concentrations in DJF (JJA) are 0.59 (0.09), 0.16 (0.013), 0.055 (0.015) µg sm⁻³, for EA, EU, and NA, respectively. The average HMS ∕ sulfate ratios in DJF (JJA) are 0.09 (0.01), 0.06 (0.006), 0.04 (0.009), for EA, EU, and NA, respectively. The wintertime in East Asia, northern China in particular, has both the highest HMS concentration and highest HMS ∕ sulfate ratio. The average HMS concentrations (1–3 µg sm⁻³) and HMS ∕ sulfate ratios (0.1–0.2) are found during the winter season in northern China (Fig. S7).

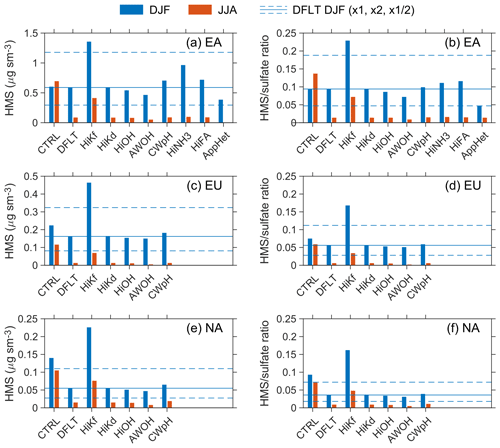
Figure 5 Comparison of the modeled surface HMS concentrations (a, c, e) and HMS ∕ sulfate molar ratios (b, d, f) from different simulations for three regions and two seasons. EA, EU, and NA are East Asia, Europe, and North America, respectively. DJF and JJA represent December–January–February and June–July–August, respectively. The solid and dashed lines indicate the DJF value from the default (DFLT) simulation and its double and half. The vertical axis differs in the left panels.

As mentioned in Sect. 1, previous studies have suggested that the formation and existence of HMS in the condensed phase are generally favored under the following conditions: high precursor (SO₂ and HCHO) concentrations, low photochemical oxidant levels, low temperature, abundant aqueous water, and moderate acidity (Munger et al., 1984, 1986; Moch et al., 2018; Song et al., 2019a; Ma et al., 2020). The seasonal variability of HMS does not follow that of the precursor levels (Fig. S6 in the Supplement). The seasonal variation of the geometric mean of the two precursors, $\sqrt{{\mathrm{SO}}_{\mathrm{2}}\times \mathrm{HCHO}}$, is weak because of their opposite seasonality (more SO₂ but less HCHO in winter). The cloud liquid water content (L) in the lower troposphere shows a spatial distribution with higher values over the ocean and lower values over land (Fig. S8). There is no consistent seasonal pattern of L between DJF and JJA over the three regions (EA, EU, and NA). The modeled cloud water pH exhibits a seasonal difference. The average pH in DJF (JJA) is 4.3 (5.8), 4.7 (5.6), and 4.7 (5.7) for EA, EU, and NA, respectively. The higher pH in JJA is related to more abundant gaseous NH₃ (Fig. S8 in the Supplement), given the buffer capacity of NH₃ in moderating the acidity of atmospheric condensed water (Song et al., 2019b).

One of the above-mentioned factors favoring HMS is the moderate acidity. This term is somewhat ambiguous but is used to represent the pH range that allows for relatively rapid formation and slow decomposition of HMS. We show in Fig. 2 that both k_f and k_d increase with pH. The lifetime of HMS with respect to decomposition is about 60, 6, and 0.6 hours at pH 5, 6, and 7, respectively, at 298 K, and is even larger at lower T. For the range of pH in the three regions (its average from 4.3 to 5.8), the decomposition of HMS is so slow that its chemical equilibrium is difficult to achieve. Accordingly, the modeled HMS levels are predominantly controlled by formation kinetics. This is supported by the results from the HiKd simulation, in which k_d × 2 makes little difference in the modeled HMS compared to the default simulation (Fig. 5). The higher cloud pH in JJA should lead to faster HMS formation rates than those in DJF. However, in the default simulation, the modeled HMS levels show an opposite pattern. This is believed to be linked to the different photochemical oxidizing abilities in the two seasons. Globally, the two main aqueous oxidants for SO₂ are O₃ and H₂O₂, which compete with HCHO. The competition of different pathways can be influenced by the levels of these gases, T (changing gas solubilities and rate constants), and pH (changing rate constants). O₃, H₂O₂, and HCHO all have higher concentrations in JJA (Fig. S6). The lower T in DJF favors the H₂O₂ reaction most and the O₃ reaction least. Notably, the response of the O₃ reaction to pH is essentially the same as that for HCHO since both react rapidly with ${\mathrm{SO}}_{\mathrm{3}}^{\mathrm{2}-}$. The HCHO + SO₂ reaction is significant only when the two photochemical oxidants are inefficient.

3.2 Difference between the default and control simulations

Compared with the default simulation, the control simulation realizes very different spatial and seasonal distributions of HMS concentrations and HMS ∕ sulfate molar ratios (Fig. S9 in the Supplement). Figure 6 shows the differences in surface HMS concentrations for DJF and JJA. The corresponding information for MAM and SON is presented in Fig. S10 in the Supplement. Two features are evident. First, a weak seasonality is found for the control simulation, but for the default simulation, HMS is much more abundant in DJF. Second, the control simulation predicts significantly higher HMS concentrations almost everywhere except in parts of East Asia and Europe in DJF. Interestingly, the only region where the default simulation gives higher HMS concentrations is wintertime in northern China, the focus of several studies (Moch et al., 2018; Song et al., 2019a; Ma et al., 2020). Specifically, as shown in Fig. 5, the average HMS concentrations modeled by the control simulation in DJF (JJA) are 0.60 (0.70), 0.22 (0.12), 0.14 (0.11) µg sm⁻³, respectively, for East Asia (EA), Europe (EU), and North America (NA). The average HMS ∕ sulfate ratios inferred from the control simulation in DJF (JJA) are 0.09 (0.14), 0.08 (0.06), 0.09 (0.07), respectively, for EA, EU, and NA.

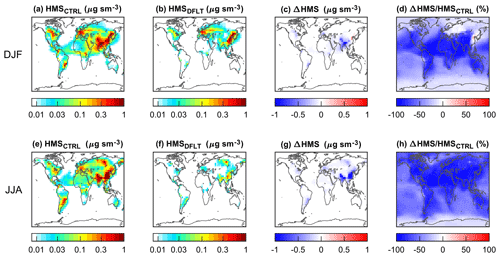
Figure 6 Surface concentrations of HMS from the control (CTRL) and default (DFLT) simulations in two seasons. Top and bottom panels show results for DJF (December–January–February) and JJA (June–July–August), respectively. (c) is the absolute difference between these two simulations: b−a. (d) is their relative difference: $(b/a-\mathrm{1})\times \mathrm{100}$ %. Similarly, (g) is the absolute difference between (e) and (f): f−e, and (h) the relative difference between them: $(f/e-\mathrm{1})\times \mathrm{100}$ %. The color bars in (a), (b), (e), and (f) are not linear.

As described in Sect. 2.5, based on the control, the default simulation improves the representations of heterogeneous cloud sulfur chemistry in the model by applying the entrainment-limited uptake method from Holmes et al. (2019) and by reducing the time step when calculating aqueous sulfur reactions. These changes allow for a more realistic simulation of entrainments and detrainments of air in partly cloudy grid cells and for an effective competition of different aqueous reactions consuming SO₂. In the control simulation, the time step for calculating in-cloud sulfur reactions is the same as the chemistry time step of the model, Δt=20 min. But there may be a > 50 % possibility that the lifetime of in-cloud SO₂ is less than this Δt, as shown in Fig. 3 and described in Sect. 2.4. Given that the main reactants with in-cloud SO₂ are O₃ and H₂O₂, this setting leads to a general underestimation of the contribution of O₃ and H₂O₂ and an overestimation of importance of the minor reactants such as HCHO. The bias is larger in JJA than in DJF, as suggested by the probability distribution statistics for the in-cloud lifetime of SO₂ (Table S1 in the Supplement).

3.3 Key uncertain factors

Section 2.6 and Table 4 describe the ten sensitivity simulations we conduct with an aim to find out the key parameters and processes leading to HMS modeling uncertainties. All of these simulations are modified based on the default simulation and can be classified into three groups: heterogeneous cloud chemistry (HiKf, HiKd, HiOH, and CWpH); heterogeneous aerosol water chemistry (AWOH, AWK0, and AWKE); and East Asia only (HiNH3, HiFA, and AppHet). A comparison of the surface HMS concentrations and HMS ∕ sulfate molar ratios from these sensitivity simulations is provided in Fig. 5, focusing on three regions (EA, EU, and NA) and two seasons (DJF and JJA).

First, we examine the sensitivity simulations in terms of the formulation of heterogeneous cloud chemistry. HiKf, HiKd, HiOH, and CWpH make changes in HMS formation, decomposition, oxidation, and cloud water pH calculations, respectively. The surface HMS concentrations and HMS ∕ sulfate ratios in the latter three indicate relative differences of less than ±20 % compared to the default simulation. However, HiKf shows a very large increase, by a factor of 2 to 6, in modeled HMS. This is expected since the high and low k_f differ by a factor of about 3 at pH < 2 and by a factor of about 6 at pH > 4 (Sect. 2.1.1). As described in Sect. 2.1.3, the formation of HMS and its oxidation by OH represent an indirect oxidation pathway for SO₂. The sulfate yield, defined as the number of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions produced due to each attack of OH on HMS, is set to 2 in our simulations. The small difference between the HiOH and default simulations suggests that this indirect pathway should be insignificant.

Second, three sensitivity simulations are conducted for East Asia, as it is found most suitable for the existence of HMS. HiNH3 and HiFA increase the concentrations for modeled HMS in DJF by 60 % and 20 %, respectively, whereas the concentrations by AppHet are decreased by about 30 %. The changes due to HiNH3 and HiFA are much smaller in JJA (Fig. 5). The increase of HMS in HiNH3 can be attributed to higher cloud water pH, and its decrease in AppHet should be related to a decrease in SO₂ available for cloud chemistry. Interestingly, HiNH3 increases the HMS ∕ sulfate ratios in DJF by only 20 %. The higher cloud water pH enhances the formation of sulfate through the pH-sensitive pathways such as the reaction of SO₂ with O₃.

Third, AWOH, AWK0, and AWKE explore the potential role of heterogeneous aerosol water HMS chemistry. The challenge of modeling aerosol water HMS chemistry is the lack of its reaction rate constants in concentrated aqueous solutions. We use the rate constants from dilute solutions in AWOH and AWK0. The oxidation of HMS by OH in aerosol water leads to losses of 10 %–20 % (DJF) and 40 %–60 % (JJA) (Fig. 5). The formation and decomposition of HMS in aerosol water result in negligible changes in the modeled HMS concentrations, as shown in Fig. 7 (DJF) and Fig. S11 (the other seasons). Results from AWKE suggest that aerosol water might play a role in the formation of HMS only when the k_f is strongly enhanced in concentrated solutions like the rate constant of the SO₂ reaction with H₂O₂.

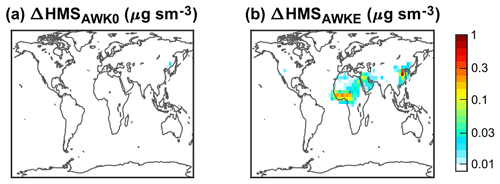
Figure 7 Difference in surface HMS concentrations in DJF (December–January–February) between two sensitivity simulations (AWK0 a and AWKE b) and the default simulation (DFLT). The color bar is not linear.

Overall, our sensitivity simulations suggest that the key uncertain parameter in the model is k_f. Based on existing experimental results, the low value for k_f seems more reasonable (Sect. 2.1.1). The key uncertain process is modeling the aerosol water chemistry of HMS in the absence of reliably defined rate constants.

3.4 Comparison with prior observations

The quantitative observations of HMS in ambient aerosols remain sparse (Moch et al., 2020) and we provide here a comparison between the observations at four sites and two model simulations (control and default) in Table 5. Since these observations have been collected over the past three decades while our simulations cover only one year, it is more appropriate to use the molar ratios of HMS ∕ ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ or HMS/MSA rather than absolute HMS concentrations. The measurement techniques of HMS in different studies were different (Table 5) and their effects on the reported results are unclear. Moreover, observations of HMS may be subject to measurement artifacts that may make quantitative comparisons between model results and observations difficult (Ma et al., 2020; Moch et al., 2020). Among the observations shown in Table 5, the highest HMS ∕ ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ratio of 11 % has been found in winter in Beijing by Ma et al. (2020). Model results from both default and control simulations agree well with this observed ratio. Less HMS was observed in other regions, including New Mexico (USA), Germany, and Osaka Bay (Japan). The default simulation overestimates the HMS ∕ ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ or HMS/MSA ratios by a factor of 2–3, whereas the control simulation overestimates these ratios by an order of magnitude.

Table 5 Comparison between observations and model simulations.

^a PM₁ (particles smaller than 1 µm) samples of 11 PM₂ samples were collected with each sampled for several days. HMS detection method: ion chromatography. ^b Size-segregated (five stages under 10 µm) daily aerosol samples of 154 data sets were collected at nine sites. HMS detection method: capillary electrophoresis. ^c PM_2.5 samples of 77 were collected with 69 daily and eight half-day samples. HMS detection method: ion chromatography. ^d Size-segregated (four stages under 7 µm) aerosol samples of four data sets were collected with each sampled for 11–25 d. HMS detection method: proton nuclear magnetic resonance (¹H NMR).

A more detailed comparison of the model with observations in Beijing is provided below (Ma et al., 2020). These samples from Beijing were stored at −20 ^∘C between sample collection and analysis, had HCHO added to solution during sample extraction, and were examined by ion chromatography using a more acidic eluent than normal all in order to limit HMS decomposition and misidentification. The observations in Ma et al. (2020) cover 73 d in winter and 11 polluted days in other seasons. The data for the other seasons is presented only in their discussion paper. Because of the coarse resolution of global model, we do not expect our simulations to capture the day-to-day variability that is observed at a single site. Accordingly, we examine the ability of our simulations to reproduce the observed relationships between HMS and its influencing factors. Figure 8 provides scatter plots of HMS concentrations (and HMS ∕ ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ratios) versus two variables (O₃ and RH) and compares the data from observations and model simulations (control and default). The level of O₃ represents photochemical oxidizing capacity and RH may indicate the abundance of aqueous water in the lower troposphere.

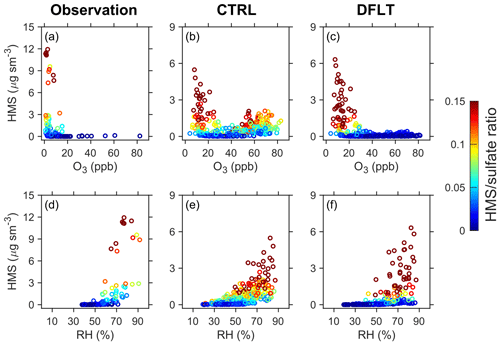
Figure 8 Relationship between HMS concentrations and O₃ mixing ratios (top) and RH (bottom) in northern China. Data from observations, the control (CTRL), and the default (DFLT) simulations are presented in (a) and (d), (b) and (e), and (c) and (f), respectively. HMS ∕ sulfate molar ratios are indicated by the color scale. The observational data in (a) and (d) were collected in Beijing by Ma et al. (2020). There were 69 daily (and 8 half-day) samples in the 2015/16 and 2016/17 winter seasons. The model data are obtained from the grid cell covering Beijing with 366 daily samples. The vertical axes differ in the panels of observations and model simulations.

We find a similar relationship between HMS and O₃ from the observations and default simulation (Fig. 8). Significant HMS levels are observed and modeled only under low O₃ conditions (< 20 ppb). However, the control simulation obtains another cluster of days with high HMS levels when O₃ is abundant (> 40 ppb). This cluster is linked to the inappropriate representation of heterogeneous cloud sulfur chemistry in the control simulation. The large time step for SO₂ titration excessively favors the reaction of SO₂ with HCHO, as described in Sect. 2.4 and Fig. 3. It should be noted in Ma et al. (2020) that only 11 daily samples had O₃ levels larger than 20 ppb. There might be a possibility that the days with high levels of both HMS and O₃ were missed in their sampling coverage, but we think it is unlikely given the rapid oxidation of SO₂ by the photochemical oxidants (gaseous OH and aqueous O₃ and H₂O₂) under such conditions.

The scatter plots of HMS and RH show a similar exponential-like relationship in the observations and model simulations (Fig. 8). Such an exponential-like relationship has been interpreted to support the hypothesis that HMS is produced through aerosol water (Song et al., 2019a; Ma et al., 2020). This is because the amount of aerosol water also exhibits an exponential relationship with RH (Song et al., 2018, 2019b). Interestingly, our model simulations using aqueous clouds as the only medium can obtain a similar relationship between HMS and RH, which reduces the credibility of this aerosol water hypothesis and lends support to the hypothesis that cloud water is a dominant medium for HMS formation (Moch et al., 2018, 2020). Global atmospheric models, including the numerical weather prediction model employed in the MERRA-2 reanalysis, are usually not capable of resolving subgrid cloud processes, and cloud properties are parameterized using an RH-related statistical scheme (Molod, 2012; Molod et al., 2015). Thus, it is not surprising to find a relationship between RH and HMS in the simulations.

3.5 Knowledge gained and remaining gaps

The different spatiotemporal patterns of the HMS levels modeled by the control and default simulations indicate the importance of an appropriate representation of heterogeneous cloud sulfur chemistry. Our modeling suggests that photochemical oxidizing capacity is a key influencing factor for HMS formation because it affects the competition of HCHO with oxidants (e.g., O₃ and H₂O₂) for SO₂. This factor is partly responsible for the distinct seasonality in HMS modeled by the default simulation. On a regional scale, the most suitable place for the formation and existence of HMS is parts of East Asia in the lower troposphere during the cold season. Aqueous clouds are the major medium for HMS chemistry since the model simulations can reasonably reproduce both the observed HMS levels and the relationship between in situ HMS and RH when assuming this as the only medium. Aerosol water may play a role if the rate constant of HMS formation is greatly enhanced in concentrated solutions. This finding is consistent with several studies (Jacob, 1986; Olson and Hoffmann, 1989; Whiteaker and Prather, 2003; Moch et al., 2018, 2020). Quantitative observations of HMS are sparse, and more data are required to validate the model. The quantification of HMS in different seasons and over different photochemical conditions, with samples analyzed shortly after collection to minimize potential HMS decomposition, is particularly valuable.

Two knowledge gaps are identified from our sensitivity simulations. First, the key uncertain factor in the model is k_f, the rate constant for HMS formation. Large discrepancies exist among existing laboratory experiments (Fig. 2), and future laboratory studies are required to narrow its uncertainty. Second, the lack of kinetic and thermodynamic data for HMS chemistry in concentrated solutions poses a key challenge to modeling HMS processing in aerosol water, and new laboratory studies are needed. Also, we did not consider the uncertainty in the meteorological reanalysis. Although MERRA-2 assimilates extensive observations and represents the atmospheric states accurately, cloud properties are modeled exclusively. Studies have shown biases in seasonal and spatial variations of cloudiness when comparing the reanalysis data with lidar and satellite observations (Kennedy et al., 2011; Stengel et al., 2018; Miao et al., 2019). Previous work has found that simulated HMS is extremely sensitive to cloud distributions and properties, and these biases in MERRA-2 cloud properties have been identified as a possible source of error for simulation of HMS driven by MERRA-2 (Moch et al., 2018, 2020).

Recently, the quantum chemical calculations by Chen and Zhao (2020) suggested that hydroxymethyl sulfite (HMSi), an isomer of HMS, might also be produced by an aqueous reaction of HCHO and SO₂. The laboratory experiments of De Haan et al. (2020) demonstrated that HMS was one of the major products from the aqueous processing of glyoxal monobisulfite (CH(OH)₂CH(OH)SO${}_{\mathrm{3}}^{-}$), the adduct of glyoxal and SO₂. These new mechanisms need to be considered in future model studies.

4 Conclusions

Based on appropriate implementation of heterogeneous HMS chemistry and assuming aqueous clouds as the only medium, the global GEOS-Chem model can reasonably reproduce the observations of HMS in Beijing and three other sites. The modeled HMS concentrations and HMS ∕ sulfate ratios show a clear seasonal pattern with higher values in the cold period. The spatial distributions of HMS in descending order are East Asia, Europe, and North America. Our model simulations find the highest average HMS concentrations (1–3 µg m⁻³) and HMS ∕ sulfate molar ratios (0.1–0.2) in northern China during the winter season. Photochemical oxidizing capacity affects the competition of HCHO with oxidants (e.g., O₃ and H₂O₂) for SO₂, and is a key factor influencing HMS formation. Aqueous clouds act as the primary medium for HMS chemistry, agreeing with prior studies (Moch et al., 2018, 2020), while aerosol liquid water could play a role if the rate constant for HMS formation is greatly enhanced.

This study identifies future research needs. Laboratory experiments should reduce the uncertainty in the formation rate constant of HMS and determine the kinetics for HMS chemistry in concentrated solutions. More field observations of HMS, especially its quantification in different seasons and photochemical conditions, are helpful to validate the model. It is important for future observations of HMS to limit possible HMS decomposition so that the observations can be compared directly with model results. Limiting HMS decomposition can be achieved by analyzing samples shortly after collection and by using analysis methods that are designed to limit HMS decomposition (Dovrou et al., 2019; Ma et al., 2020; Moch et al., 2020). The coarse resolution of the global model does not allow it to capture day-to-day observations at a single site, and we are preparing another paper to demonstrate the capacities of regional model with a finer resolution to reproduce individual haze events in northern China.