Technical note: The enhancement limit of coagulation scavenging of small charged particles

We show that the limit of the enhancement of coagulation scavenging of charged particles is 2, that is, doubled compared to the neutral case. Because the particle survival probability decreases exponentially as the coagulation sink increases, everything else being equal, the doubling of the coagulation sink can amount to a dramatic drop in survival probability – squaring the survival probability, p², where p≤1 is the survival probability in the neutral case. Thus, it is imperative to consider this counterbalancing effect when studying ion-induced new-particle formation and ion-enhanced new-particle growth in the atmosphere.

1 Introduction

There are many situations in atmospheric phenomena where we care about total particle number, and especially total particle number above some critical size. An example is cloud activation, where the total number of cloud condensation nuclei is often estimated to be the total number of particles with diameters d_p≥50 nm (𝒩₅₀) or perhaps d_p≥100 nm (𝒩₁₀₀), depending on updraft velocity (Rosenfeld et al., 2019; Pierce and Adams, 2007; Pierce et al., 2012; Gordon et al., 2017; Lee et al., 2019). When new-particle formation, also known as nucleation, or emission is dominated by much smaller particles, we care not only about the formation or emission rate but also the survival probability of the newly formed particles as they grow to the critical size.

The particle survival probability decreases exponentially as the coagulation sink increases (Kulmala et al., 2017; Kerminen and Kulmala, 2002; Lehtinen et al., 2007; Li and McMurry, 2018). The counterbalancing role of growth rate and coagulation sink is well known, for example as studied by Kulmala et al. (2017). Additionally, the presence of charge can increase new-particle formation rates in both acid–base (Merikanto et al., 2016) and organic (Kirkby et al., 2016) systems. Charge can also increase the growth rate of small particles due to the polar enhancement of gas–particle collision parameters (Lehtipalo et al., 2018), though this effect tends to be negligible once particles are bigger than 2 nm. Yet, the direct role of charge in the counterbalancing of growth rate and coagulation sink has received less attention. Here, we focus on the effect of charge on the coagulation sink – we investigate the limit of the enhancement in the coagulation sink of charged particles that can take place in the atmosphere or in experiments. We show that this enhancement limit is asymptotically 2; that is, the coagulation sink of charged particles is double that of the otherwise same neutral particles.

Small charged particles are intrinsically out of equilibrium (Gonser et al., 2014; Hoppel and Frick, 1986; Hõrrak et al., 2008; López-Yglesias and Flagan, 2013a, b; Gopalakrishnan et al., 2013). The thermal equilibrium charge distribution on particles of diameter d_p is given via the probability density function, $p_i^{\mathrm{eq}}$, assuming positive and negative ion mobilities are the same; see the similar expression provided by Gunn and Woessner (1956) for different mobilities.

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{p}_i^{\mathrm{eq}}\left(d_{\mathrm{p}}\right)& =\mathcal{A}\exp \left(-{\displaystyle \frac{e^{\mathrm{2}}}{\mathrm{4}\mathit{\pi }{\mathit{ϵ}}_{\mathrm{0}}{k}_{B}T}}{\displaystyle \frac{i^{\mathrm{2}}}{d_{\mathrm{p}}}}\right)\\ & =\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}{\displaystyle \frac{d_{\mathrm{C}}}{d_{\mathrm{p}}}}}\exp \left(-{\displaystyle \frac{i^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{d_{\mathrm{C}}}{d_{\mathrm{p}}}}\right)\end{array}\end{array}$$

In Eq. (1), 𝒜 is normalization factor of the distribution, k_B is the Boltzmann constant, e is the elementary charge, i is the charge on the particles, and ϵ₀ is the permittivity of free space. The first quotient in Eq. (1) is a scale length – which we call the Coulomb diameter and is shown in Eq. (2).

$$\begin{array}{}\text{(2)}& d_{\mathrm{C}}={\displaystyle \frac{e^{\mathrm{2}}}{\mathrm{2}\mathit{\pi }{\mathit{ϵ}}_{\mathrm{0}}{k}_{B}T}}\end{array}$$

At 300 K, d_C=111.4 nm. For particles smaller than the Coulomb diameter, the energy of even a single elementary charge is well above the thermal energy. This means that for d_p≪d_C, any significant charging is far away from equilibrium. It also means that there are two critical sizes for collisions of oppositely charged particles: actual contact, when charge reduction (neutralization) formally occurs, but also passage to within d_C, when charge reduction is viable (López-Yglesias and Flagan, 2013a, b; Gopalakrishnan and Hogan, 2012; Ouyang et al., 2012; Chahl and Gopalakrishnan, 2019). There are thus two possible rate-limiting events, in addition to an expected pressure dependence due to third-body collisions within the Coulomb threshold. Even considering relatively inefficient diffusion neutralization by primary ions (Mahfouz and Donahue, 2020), the steady-state charged fraction for particles smaller than 7 nm in diameter is extremely small (López-Yglesias and Flagan, 2013a); relatedly, this is why standard scanning particle sizers are ineffective below this diameter.

For particles larger than roughly 10 nm, the dominant mechanism for gaining and losing charge (in the atmosphere) is diffusion charging, either from primary ions or other sub-10 nm particles if these represent a large fraction of extremely small and mobile ions. For d_p<d_C, most of the particles are neutral – see for example the studies by López-Yglesias and Flagan (2013a) and Hoppel and Frick (1986) – and yet at steady state the rate of particle neutralization must be balanced by diffusion charging. Thus, the collision rate of ions with the (relatively rare by number) charged fraction must equal the collision rate of ions with the (dominant) neutral particles, and the overall collision rate of small charged particles with larger particles will be double that of corresponding neutral particles. Relatively small particles are also exceptionally mobile. We show that the coagulation loss of said small charged particles can be double that of small neutral particles. As shown in Sects. 2 and 3 below, this limiting behavior holds only when the background particles are significantly smaller than d_C; this may occur frequently in experiments, and cannot be neglected in the atmosphere, especially in the troposphere.

2 Analytic derivation of the limiting behavior for charge coagulation enhancement

We present a simple derivation of this limiting behavior, where the presence of charge leads to the doubling of coagulation losses. For particles with d_p<100 nm, there are only three relevant charge states ($-,\mathrm{0},+$) with particles either singly charged or neutral; the fraction of particles with two or more charges is truly negligible (López-Yglesias and Flagan, 2013a). We assume a collision coefficient, $\stackrel{\mathrm{̃}}{\mathit{\beta }}$, and a charge enhancement α for opposite charges; for this derivation only, we assume ${\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\mp }=\mathit{\alpha }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\mp }=\mathit{\alpha }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\mathrm{0}}$, where the subscripts on $\stackrel{\mathrm{̃}}{\mathit{\beta }}$ refer to the charge state of the coagulating particles. That is, ${\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\mp }$ means $\stackrel{\mathrm{̃}}{\mathit{\beta }}$ when the first particle has a positive charge and the second a negative one or the first negative and the second positive – in other words, the coagulating particles have opposing charges. Likewise, we also assume ${\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\pm }=\mathit{\gamma }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\pm }=\mathit{\gamma }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\mathrm{0}}$, where γ is the reduction factor for charges of the same sign; like before, ${\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\pm }$ means $\stackrel{\mathrm{̃}}{\mathit{\beta }}$ of two particles carrying the same charge. Additionally, we define ${\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\pm }={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\mathrm{0}}={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\mathrm{0}}$; that is, we drop the two subscripts for one when the coagulation involves a neutral particle as we assume a neutral–neutral collision rate is the same as neutral–charged collision rate. All of this is to say we assume that the order of charges does not matter; α is the enhancement factor due to like–unlike coagulation; γ is the suppression factor due to the like–like coagulation; the neutral–neutral coagulation is the same as the neutral–charged coagulation; all particles have at most one charge.

Because all particles are at most singly charged in this limiting derivation, this applies to bigger particles comprising the coagulation sink, $N_{\mathrm{CoagS},\mathit{\{}-,\mathrm{0},+\mathit{\}}}$, as well as smaller particles potentially lost to coagulation, $N_{\mathit{\{}-,\mathrm{0},+\mathit{\}}}$. That is, $N_{\mathrm{CoagS},-}$ is the number of monodisperse particles in the coagulation sink (bigger particles) which have a negative charge, and N₋ is the number of monodisperse newly formed (or smaller) particles which have a negative charge. We assume that positive and negative mobilities of smaller particles, including primary ions or newly formed particles, are the same. As such, the number of positive and negative bigger particles is the same – that is, $N_{\mathrm{CoagS},-}=N_{\mathrm{CoagS},+}=N_{\mathrm{CoagS},\pm }$. We assume the “diffusion charging” rates – $R_{\mathit{\{}-,\mathrm{0},+\mathit{\}}}$ – of smaller particles to bigger particles are in equilibrium such that $R_{-}=R_{+}=R_{\mathrm{0}}$. We write R_k as the rate of ions or smaller particles, $N_{\mathit{\{}-,\mathrm{0},+\mathit{\}}}$, coagulating with bigger particles, $N_{\mathrm{CoagS},\mathit{\{}-,\mathrm{0},+\mathit{\}}}$, to form a particle of charge k. Here, k is −1, 0, or +1, and so without confusion, we call those states −, 0, and +. We assume the negative and positive mobilities are the same; in the atmosphere, they are different, but this assumption will help us realize the limit. As such, we use R_± to mean R₋ or R₊ like before; note that if the subscript ± appears alongside ∓ in the equations below, it means the charges are opposite.

Accordingly, we define the diffusion charging rates and set them in equilibrium in Eq. (3).

$$\begin{array}{}\text{(3)}& {\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\pm }{N}_{\mathrm{CoagS},\mathrm{0}}{N}_{\pm }=R_{\pm }=R_{\mathrm{0}}={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mp ,\pm }{N}_{\mathrm{CoagS},\mp }{N}_{\pm }\end{array}$$

From Eq. (3), $N_{\mathrm{CoagS},\mathrm{0}}=\mathit{\alpha }{N}_{\mathrm{CoagS},\mp }$. Then, the coagulation sinks for neutral and charged particles are shown in Eqs. (4) and (5), respectively.

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}{\mathrm{CoagS}}_{\mathrm{0}}& ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}\left(N_{\mathrm{CoagS},\mathrm{0}}+N_{\mathrm{CoagS},+}+N_{\mathrm{CoagS},-}\right)\\ & ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}\left(N_{\mathrm{CoagS},\mathrm{0}}+\mathrm{2}{N}_{\mathrm{CoagS},\pm }\right)\\ & ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}{N}_{\mathrm{CoagS},\mathrm{0}}\left(\mathrm{1}+\mathrm{2}/\mathit{\alpha }\right)\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}{\mathrm{CoagS}}_{\pm }& ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0},\pm }{N}_{\mathrm{CoagS},\mathrm{0}}+{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mp ,\pm }{N}_{\mathrm{CoagS},\mp }+{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\pm ,\pm }{N}_{\mathrm{CoagS},\pm }\\ & ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}{N}_{\mathrm{CoagS},\mathrm{0}}+\mathit{\alpha }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}{N}_{\mathrm{CoagS},\mp }+\mathit{\gamma }{\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}{N}_{\mathrm{CoagS},\pm }\\ & ={\stackrel{\mathrm{̃}}{\mathit{\beta }}}_{\mathrm{0}}{N}_{\mathrm{CoagS},\mathrm{0}}\left(\mathrm{2}+\mathit{\gamma }/\mathit{\alpha }\right)\end{array}\end{array}$$

Finally, we define the ratio of the coagulation sinks in Eq. (6).

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{{\mathrm{CoagS}}_{\pm }}{{\mathrm{CoagS}}_{\mathrm{0}}}}={\displaystyle \frac{\left(\mathrm{2}+\mathit{\gamma }/\mathit{\alpha }\right)}{\left(\mathrm{1}+\mathrm{2}/\mathit{\alpha }\right)}}\end{array}$$

Therefore, ${\mathrm{CoagS}}_{\pm }/{\mathrm{CoagS}}_{\mathrm{0}}\to \mathrm{2}$ as α≫2 and γ≪1. This is the limit when the presence of the charge significantly increases or decreases the collision of particles. The other limit is ${\mathrm{CoagS}}_{\pm }/{\mathrm{CoagS}}_{\mathrm{0}}=\mathrm{1}$ as $\mathit{\alpha }=\mathit{\gamma }=\mathrm{1}$, when the presence of charge is insignificant – that is, charge is “screened”. This shows that in the limit of a coagulation sink comprised of relatively small particles (that is because the first limit, α≫2 and γ≪1, only happens if the coagulation sink is comprised of smaller particles as shown in Fig. 1), coagulation can be greatly enhanced for small charged particles compared to neutral particles of the same size.

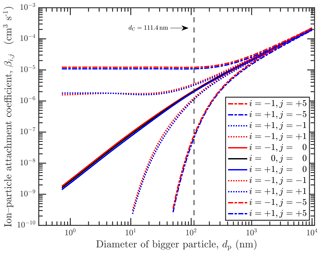
Figure 1 Ion–particle flux attachment coefficient (López-Yglesias and Flagan, 2013a, b) kernel of primary ion with charge i and a particle of size d_p. The colors refer to the charge of the smaller particles (modeled as primary ions): red is negative, blue is positive, and black is neutral. The line styles refer to the charge of the bigger particle (j): dashed–dotted is ±5, dotted is ±1, and continuous is 0. Also shown is the Coulomb diameter, d_C, at 111.4 nm. Neutralization coefficients (attachment between particles of opposite charge) tend toward an asymptotic value for d_p<d_C.

3 Computed static limit

To illustrate this derived limit further, we use primary ions as a limit for the smallest particles. We compute the limiting behavior from available data, assuming that the coagulation between smaller particles and bigger particles is the same as the coagulation of primary ions with bigger particles. In this case, we study the coagulation sink ratio, defined by ${\mathrm{CoagS}}_i/{\mathrm{CoagS}}_{\mathrm{0}}$ for charges $i=\pm \mathrm{1}$. Further,

$$\begin{array}{}\text{(7)}& {\mathrm{CoagS}}_i=\underset{\mathrm{\infty }>d_{\mathrm{p}}\ge d_{{\mathrm{p}}^{*}}}{\int }\sum _j{\mathit{\beta }}_{i,j}\left(d_{{\mathrm{p}}^{*}},d_{\mathrm{p}}\right)n_j\left(d_{\mathrm{p}}\right)\mathrm{d}{d}_{\mathrm{p}},\end{array}$$

where $d_{{\mathrm{p}}^{*}}$ is the diameter whence particles are formed, β is the particle–particle coagulation kernel with charges i and j, and n is the particle number density or size distribution. For ease, we take n as monodisperse distributions, thereby simplifying Eq. (7) by dropping the integration.

We assume the smallest particles (at $d_{{\mathrm{p}}^{*}}$) have characteristics similar to those of primary ions found in the atmosphere. To this end, we utilize the ion–particle attachment coefficients (for β) and the corresponding charge fraction distributions as reported by López-Yglesias and Flagan (2013a, b). The ion–particle attachment coefficients are shown in Fig. 1. We note that López-Yglesias and Flagan (2013a) do not report the case where a neutral extremely small “particle” is colliding with a bigger particle, akin to a neutral “ion” colliding with a bigger particle, and so we have extrapolated that an acceptable form is similar to the average of positive and negative ions' attachment coefficients to a neutral particle. This averaging leads to similar results found elsewhere for the neutral–neutral attachment coefficients of particles of those sizes. We opted to use this averaging as opposed to the commonly used expression to ensure we use all data below from the same source.

In Fig. 2, we show the coagulation sink ratio converging onto exactly 2 for both negative and positive when the size of the bigger particles (comprising the coagulation sink) is less than around 10 nm. And for particles bigger than 100 nm, we show that the coagulation sink ratios also converge exactly onto 1. They tend to diverge slightly as the particle sizes grow much bigger because of the charging asymmetry between positive and negative ions observed in the atmosphere.

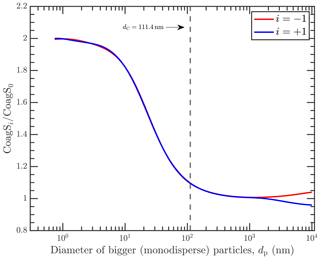
Figure 2 The ratio of the coagulation sink of charged ($i=\pm \mathrm{1}$) to neutral nucleating particles (modeled as primary ions). The colors refer to the charge of the primary ions: red is negative and blue is positive. Also shown is the Coulomb diameter, d_C, at 111.4 nm. For d_p≪d_C, the coagulation sink for charged particles approaches a limit of twice the coagulation sink for neutral particles.

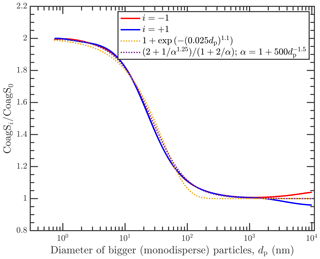
Figure 3 Coagulation sink ratios shown in Fig. 2, along with two parameterizations capturing the limiting behavior.

For convenience, we present two parameterizations that capture this limiting behavior in Fig. 3. The first parameterization is based on an exponential function and takes the form $\mathrm{1}+\exp (-(\mathrm{0.025}{d}_{\mathrm{p}}{)}^{\mathrm{1.1}})$. The second parameterization is based on the limiting behavior presented earlier. We observe that as α≫1, then by definition γ≪1. As such, the ratio $\mathit{\gamma }/\mathit{\alpha }$ decreases faster than $\mathrm{1}/\mathit{\alpha }$. The relationship between α and γ is not simply reciprocal, $\mathit{\gamma }\ne \mathrm{1}/\mathit{\alpha }$. But this is at most a caveat expressed in the kth dependency in $\left(\mathrm{2}+\mathrm{1}/{\mathit{\alpha }}^k\right)/\left(\mathrm{1}+\mathrm{2}/\mathit{\alpha }\right)$, where $\mathrm{1}\le k\le \mathrm{3}$ for most cases by observation. What remains is the functional form of α in size, α(d_p). This functional form of α depends weakly on the number of charges, and the size is the leading factor. From observation, $\mathit{\alpha }\approx \mathrm{1}+\mathrm{500}{d}_{\mathrm{p}}^{-\mathrm{1.5}}$ for $j=\pm \mathrm{1}$ and $\mathit{\alpha }\approx \mathrm{1}+\mathrm{5000}{d}_{\mathrm{p}}^{-\mathrm{1.5}}$ for $j=\pm \mathrm{5}$.

4 Conclusions

We have shown that the limit of the enhancement of coagulation scavenging of charged particles is 2 – double that of neutrals. Particle survival probabilities decrease exponentially as the coagulation sink increases (Kulmala et al., 2017), and so all being equal, the doubling of the coagulation sink can amount to a noticeable drop in the survival probability. In other words, if the survival probability of neutral particles is p, then the survival probability of charged particles is p² where p≤1. We note that ion-induced new-particle formation and ion-enhanced new-particle growth only matter if there is an abundance of ions – and therefore charges – available. Thus, it is imperative to consider this counterbalancing (blunting) effect when studying ion-induced new-particle formation and ion-enhanced new-particle growth in the atmosphere.