the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A-Train estimates of the sensitivity of the cloud-to-rainwater ratio to cloud size, relative humidity, and aerosols
Anita D. Rapp
Precipitation efficiency has been found to play an important role in constraining the sensitivity of the climate through its role in controlling cloud cover, yet its controls are not fully understood. Here we use CloudSat observations to identify individual contiguous shallow cumulus cloud objects and compute the ratio of cloud water path to rainwater (WRR) path as a proxy for warm-rain efficiency. Cloud objects are then conditionally sampled by cloud-top height, relative humidity, and aerosol optical depth (AOD) to analyze changes in WRR as a function of cloud size (extent). For a fixed cloud-top height, WRR increases with extent and environmental humidity following a double power-law distribution, as a function of extent. Similarly, WRR increases, holding average relative humidity at or below 850 mb constant. There is little relationship between WRR and AOD when conditioned by cloud-top height, suggesting that, once rain drop formation begins, aerosols may not be as important for WRR as cloud size and depth. Consistent with prior studies, results show an increase in WRR with sea-surface temperature. However, for a given depth and SST, WRR is also dependent on cloud size and becomes larger as cloud size increases. Given that larger objects become more frequent with increasing SST, these results imply that increasing precipitation efficiencies with SST are due not only to deeper clouds with greater cloud water contents but also to the propensity for larger clouds which may have more protected updrafts.
- Article
(4011 KB) - Full-text XML
- BibTeX
- EndNote
Low cloud cover continues to be a dominant source of uncertainty in projecting future climate (e.g., Bony and Dufresne, 2005; Dufresne and Bony, 2008; Vial et al., 2013), with variations in shallow cumulus distributions explaining much of the differences in climate-model-derived estimates of climate sensitivity (e.g., Wyant et al., 2006; Medeiros and Stevens, 2011; Nam et al., 2012). This stems from climate models' inability to simulate shallow cumulus clouds and their impacts, due in part to the low temporal and spatial resolution of these models (e.g., Stevens et al., 2002), as well as the fact that small-scale processes important for cloud development, including turbulence and convection, must be parameterized (e.g., Tiedtke, 1989; Zhang and McFarlane, 1995; Bretherton et al., 2004). Studies have shown precipitation efficiency is a key parameter used to constrain cloud parameterizations within climate models (Rennó et al., 1994; Del Genio et al., 2005; Zhao, 2014; Lutsko and Cronin, 2018). Nam et al. (2012) hypothesized that shallow cumulus clouds are too reflective in climate models, possibly because model precipitation efficiencies are too weak. This results in excess cloud water, which increases cloud optical depth and shallow cumulus reflectance. Prior observational and modeling studies found the precipitation efficiency of shallow cumulus clouds increases as sea-surface temperature (SST) increases in response to climate change (Lau and Wu, 2003; Bailey et al., 2015; Lutsko and Cronin, 2018). Factors including environmental moisture (e.g., Heus and Jonker, 2008; Schmeissner et al., 2015), entrainment (e.g., Korolev et al., 2016; Pinsky et al., 2016b, a), and aerosols (e.g., Koren et al., 2014; Dagan et al., 2016; Jung et al., 2016b, a) help regulate both thermodynamic and dynamical processes that promote favorable conditions important to not only warm-rain production but also the efficiency of the conversion of cloud water to precipitation. To better constrain cloud parameterizations of these processes and subsequently climate sensitivity to low cloud cover, more observation-based studies analyzing physical processes influencing warm-rain efficiencies are needed.
In an ideal shallow cumulus cloud, liquid water content increases adiabatically from cloud base to top. However, liquid water content is generally only 50–80 % of the adiabatic values due to entrainment (Gerber et al., 2008; Blyth et al., 2013; Watson et al., 2015). Evaporation induced by cloud edge mixing impacts not only shallow cumulus updraft strength but also the number and size of droplets within a cloud (Lu et al., 2012), with increased evaporation potentially reducing the number and size of available droplets. Using a large-eddy simulation (LES), Moser and Lasher-Trapp (2017) found the influence of entrainment decreases from cloud edge to center of individual shallow cumulus clouds as they grow larger. This results in liquid water content at cloud center being closer to adiabatic in larger clouds, because fewer droplets evaporate away at cloud center. This implies that the collision–coalescence process is more efficient at cloud center, because there is more cloud water available to be collected by large droplets. As a result, smaller droplets originating near cloud top may be more likely to continuously grow larger as they fall, potentially reaching raindrop size near cloud base. At cloud edge, there are not only fewer droplets but also smaller droplets, potentially reducing collision–coalescence efficiencies there. This is consistent with other LES results that found shallow cumulus updrafts are more insulated from entrainment as they increase in size (e.g., Heus and Jonker, 2008; Burnet and Brenguier, 2010; Tian and Kuang, 2016).
LES and limited field-campaign observational studies have shown that cloud updrafts become more protected not only as cloud size increases but also as relative humidity (RH) increases (e.g., Heus and Jonker, 2008; Schmeissner et al., 2015). Using a model, Romps (2014) found precipitation efficiency to be closely related to RH, defining the lower bound of precipitation efficiency as ≥ 1 − RH. Therefore, the precipitation efficiency at any given level of the atmosphere should increase with increasing RH in response to lower evaporation rates. This suggests that lower RH would result in increased evaporation rates and lower warm-rain efficiencies. Prior studies have defined precipitation efficiency in two ways: (1) as the large-scale precipitation efficiency and (2) as the cloud microphysical precipitation efficiency. Generally, observational studies have based their definition of precipitation efficiency on the large-scale definition, which has simply been defined as the ratio of surface rain rate to the sum of both vapor mass flux in/out of a cloud and surface evaporation (e.g., Chong and Hauser, 1989; Tao et al., 2004; Sui et al., 2007), whereas the cloud microphysical definition, or the ratio of surface rain rate to the sum of vapor condensation and deposition rates, has been primarily used in cloud modeling studies (e.g., Li et al., 2002; Sui et al., 2005; Gao et al., 2018). Although both the large-scale and cloud microphysical definitions of precipitation efficiency are useful (Sui et al., 2005, 2007), variations in the ratio of cloud water to rainwater (WRR) in response to changes in evaporation can theoretically be used as a proxy for warm-rain efficiency based on the cloud microphysical definition. From this coupled with LES results showing that shallow cumulus updrafts are more protected as clouds grow in size and/or RH increases, we hypothesize larger droplets will be evident closer to the cloud base and increase WRR in larger cloud objects, because the cloud core of larger cloud objects is more protected from entrainment.
While perhaps not as important as organization (Minor et al., 2011) or cloud size (Jiang and Feingold, 2006), it is widely understood that aerosol concentrations act to suppress warm-rain production (Twomey, 1974; Albrecht, 1989) by increasing the cloud droplet concentration and reducing cloud droplet sizes (Squires, 1958). Albrecht (1989) found that increasing precipitation efficiency within a model is equivalent to decreasing the amount of cloud concentration nuclei (CCN), which reduces the mass concentration of cloud water within a cloudy layer. Similarly, Saleeby et al. (2015) used a cloud model to recently show that the number concentration of smaller cloud drops increases, but the number concentration of rain drops decreases as CCN increase in the presence of increasing aerosols. Lebsock et al. (2011) used CloudSat and Moderate Resolution Imaging Spectroradiometer (MODIS) observations to show that, as drop size decreases, the ratio of rainwater to cloud water also decreases. Together, these studies suggest the number of large droplets able to fall at sufficient terminal velocities to initiate collision–coalescence and continue growing to large enough sizes to fall out as rain decreases with increasing aerosol concentrations, which would reduce WRR.
Earlier studies have used satellite observations to infer the relationship between precipitation efficiency and both sea-surface temperature (Lau and Wu, 2003) and drop size (Lebsock et al., 2011). However, the relationship between cloud water and precipitation as shallow cumulus clouds grow larger, environmental moisture increases, and/or as aerosol loading varies has only been investigated using cloud models (e.g., Abel and Shipway, 2007; van Zanten et al., 2011; Franklin, 2014; Saleeby et al., 2015; Moser and Lasher-Trapp, 2017; Hoffmann et al., 2017) and limited field-campaign observations (e.g., Rauber et al., 2007; Gerber et al., 2008; Burnet and Brenguier, 2010; Watson et al., 2015; Jung et al., 2016b). While these case and model studies provide insight into the physical processes, it is unclear how well they represent the shallow cumulus clouds observed globally. Satellites can observe a large enough sample size of shallow cumulus clouds over different regions and during different stages of their life cycle to gain a more holistic view of this relationship. Prior studies have used TRMM and Global Precipitation Measurement Mission (GPM) observations to analyze warm-rain production and efficiency (e.g., Lau and Wu, 2003). Unfortunately, TRMM and GPM are precipitation radars operating at the Ku- and Ka-bands not capable of observing the non-raining portions of clouds or light precipitation. Building off work in Smalley and Rapp (2020) that analyzed the relationship between rain likelihood and cloud size, this study uses the higher-sensitivity radar of CloudSat in addition to MODIS observations to test the hypothesis that WRR is higher in larger shallow cumulus clouds and is modulated by RH and aerosol loading.
To determine if larger shallow cumulus clouds are more efficient at producing warm rainfall, this study uses the CloudSat Cloud Profiling Radar (CPR; Tanelli et al., 2008) to identify individual contiguous shallow cumulus cloud objects. The CPR is a near-nadir-pointing 94 GHz radar that can observe raining and non-raining cloud drops. It allows us to analyze the horizontal distribution of cloud within a horizontal footprint of 1.4 × 1.8 km and the vertical distributions of clouds within a 240 m bin within each CloudSat pixel.
Contiguous cloudy regions are initially identified using the 2B-GEOPROF (Marchand et al., 2008) cloud mask confidence values ≥ 20, which removes orbit elements that may be influenced by ground clutter (Marchand et al., 2008). An additional limitation of CloudSat is its inability to sense the smallest cloud droplets (e.g., Lamer et al., 2020). Smalley and Rapp (2020) addressed this by including CALIPSO measurements, which are sensitive to the smallest cloud droplets, in their identification of contiguous cloudy regions. However for this study, cloud objects must not be missing any reflectivity values. As a result, some cloud object edges may not be the true edge, and some of our defined cloud objects may be connected to other cloud objects. Before identifying cloud objects, 2C-RAIN-PROFILE (Lebsock and L'Ecuyer, 2011) modeled reflectivity is mapped onto the two-dimensional cloud mask field. As outlined by the prior literature (e.g., L'Ecuyer and Stephens, 2002; Mitrescu et al., 2010; Lebsock and L'Ecuyer, 2011), modeled reflectivity adjusts the raw reflectivity for multi-scattering and attenuation when it is raining. As described by Smalley and Rapp (2020), we use a lower-tropospheric stability threshold of 18.55 K (Klein and Hartmann, 1993) to separate cloud objects occurring in environments favoring stratocumulus development from those occurring in environments favoring shallow cumulus development. To ensure that none of the cloud objects examined here contain ice, we only include cloud objects with tops entirely below the freezing level as defined in 2C-PRECIP-COLUMN (Haynes et al., 2009).
Shallow cumulus cloud objects are then identified using the methodology described by Smalley and Rapp (2020) using the combined two-dimensional reflectivity field, with only single-layer cloud objects included. We use the incidence precipitation flag from 2C-PRECIP-COLUMN (rain possible, probable, or certain) to identify raining cloud objects and the raining pixels within them. Using all three rain flags helps us identify pixels only producing light drizzle that might be evaporating before reaching the surface to those producing heavier rainfall (Haynes et al., 2009). This range of rainfall is incorporated into the integrated precipitation water path product from 2C-RAIN-PROFILE (Lebsock, 2018), and we use this product to determine the average rainwater path (WP) for each cloud object, only including WP associated with raining pixels in the average. We then store the median cloud-top height and maximum along-track extent (hereafter extent) of each cloud object for later analysis.
Although CloudSat 2B-CWC-RVOD (Austin et al., 2009) does provide a cloud water path (WC) product, the rain drop size distribution used in 2B-CWC-RVOD is not the same as that used in 2C-RAIN-PROFILE. Additionally, Christensen et al. (2013) found that the 2B-CWC-RVOD algorithm struggles to filter out precipitation-sized droplets in the presence of light precipitation and drizzle, which results in an overestimation of cloud water. This, coupled with differences in assumed drop size distributions by 2B-CWC-RVOD and 2C-RAIN-PROFILE, makes 2B-CWC-RVOD WC not ideal for this study, so we instead use MODIS WC. Cho et al. (2015) found that MODIS effective radius and optical depth retrieval failure rates are higher in regions of broken trade cumulus than regions of predominantly stratocumulus, and they primarily attributed this to the presence of partially filled and inhomogeneous cloudy pixels. They also found that a large fraction of unexplained MODIS retrieval failures are related to the presence of precipitation after comparing MODIS failure rates to non-precipitating and precipitating pixels classified by CloudSat. This is attributed to a higher frequency of failures due to effective radius being too large. Considering the retrieval of effective radius and optical depth is required to derive WC and higher failure rates within broken trade cumulus, we suspect unavoidable sampling bias exists in WC matched to the smallest cloud objects and/or those containing large droplets and heavy rain. However on a global scale, prior studies have found the uncertainties in MODIS WC are small in comparison to other satellite retrievals (e.g., Seethala and Horvath, 2010; Lebsock and Su, 2014), with the global mean of MODIS WC being within 5 g m−2 of WC determined using the Advanced Microwave Scanning Radiometer for Earth Observing System (Seethala and Horvath, 2010). Given potential uncertainties in WC, we tested the sensitivity of our results to only including MODIS pixels with a minimum WC > 0, 20, and 30 g m−2 in our analysis, and we found that the overall interpretation of our results does not change depending on the minimum WC threshold used. Even though our overall results do not change using a WC threshold below 30 g m−2, we use the conservative estimate of WC (≥ 30 g m−2), which is based on an uncertainty estimate of 28 g m−2 from Jolivet and Feijt (2005), coupled with an estimated uncertainty of 36 g m−2 which was determined using error in effective radius and optical depth from Platnick and Valero (1995). Due to horizontal resolution differences between CloudSat and MODIS, one CloudSat pixel may overlap multiple MODIS pixels within a surrounding 3 × 3 km grid. As a result, WC is then calculated for each CloudSat pixel by averaging the nearest nine non-zero MOD-06-1KM (Platnick et al., 2003) pixels within a 3 × 3 km grid surrounding each CloudSat pixel, which have been previously matched to the CloudSat track in the MOD-06-1KM product (Cronk and Partain, 2018). There could be concerns that averaging WC within the nearest nine MODIS pixels may not properly represent the WC at the appropriate scales relative to the horizontal footprint of each CloudSat pixel; however we tested our results using WC within the nearest MODIS pixel and found that our overall results do not change. We then stored and analyzed the mean WC associated with each cloud object.
WRR of each shallow cumulus cloud object is calculated as . Note that this is a proxy for true warm-rain efficiency, because mass flux of water in and out of a cloud cannot be determined without a model; however, this ratio has been used by prior observational studies to analyze the amount of cloud water converted to rainwater (e.g., Lebsock et al., 2011).
Considering Rayleigh reflectivity is a function of the drop size distribution to the 6th power, it is expected that the maximum reflectivity in non-raining cloud objects will occur near cloud top and then shift downward as a cloud transitions from non-raining to raining. Wang et al. (2017) used the vertical reflectivity gradient (VGZ) to investigate warm-rain onset. They found VGZ (positive down) reverses sign (positive to negative) when clouds transition from non-raining to raining. Given previous studies and results shown in Smalley and Rapp (2020) finding rain is more likely as clouds grow larger in extent, it is hypothesized that the negative VGZ within individual raining cloud objects will increase in magnitude as cloud objects increase in extent. The methodology developed by Wang et al. (2017) is applied to find the VGZ for each pixel within every shallow cumulus cloud object. VGZ at cloud object center pixel (VGZCP) will then be compared to VGZ at cloud object edge pixel (VGZEP) to infer the impact of mixing on cloud object cores as a function of cloud size and RH.
The influence of aerosols on the relationship between WRR and cloud object size is determined using Aqua MODIS Level 3 daily 550 nm aerosol optical depth (AOD) (Ruiz-Arias et al., 2013). Each cloud object is matched to the nearest 1∘ × 1∘ grid box AOD value. Note that AOD may not necessarily scale with the number of CCN due to its dependence on particle size, and that aerosol type varies globally. Additionally, AOD, being column-integrated, does not give any information about where the aerosols are within the atmospheric column, so high AOD does not necessarily mean that aerosols are occurring within the cloud layer. Finally, multiple studies have shown that AOD depends on relative humidity (Su et al., 2008; Michel Flores et al., 2012; Neubauer et al., 2017; Liu and Li, 2018). This results in aerosols swelling due to the uptake of water and an underestimation of the first indirect aerosol effect (Liu and Li, 2018). These conditions are not considered in this study but may factor into WRR.
As in Smalley and Rapp (2020), this analysis is constrained to only marine shallow cumulus clouds between 60∘ N and 60∘ S. Measurements are constricted to June 2006 and December 2010 because CloudSat stopped taking nighttime measurements after 2010 due to a battery anomaly (Witkowski et al., 2012). RH is classified using 6-hourly ECMWF-AUX (Cronk and Partain, 2017). However, because lateral mixing at shallow cumulus edges would most likely be entraining boundary layer air (see review by de Rooy et al., 2013), we tested the sensitivity of our results to RH at different pressure levels (850 and 950 mb) in the lower atmosphere and at the surface, and the average RH at or below 850 mb. We found that, while the magnitudes slightly change, the overall interpretation of our results does not depend on our definition of RH. As a result, we classify RH as the average RH at or below 850 mb and match it to each cloud object. Cloud-top height, RH, VGZ, and AOD are used to control and analyze the relationship between WRR and cloud object extent.
Similar to Smalley and Rapp (2020), the spatial distribution of WP, WC, WRR, and AOD, as well as the extent of raining shallow cumulus cloud objects, is analyzed by binning them to a 2.5∘ × 2.5∘ global grid.
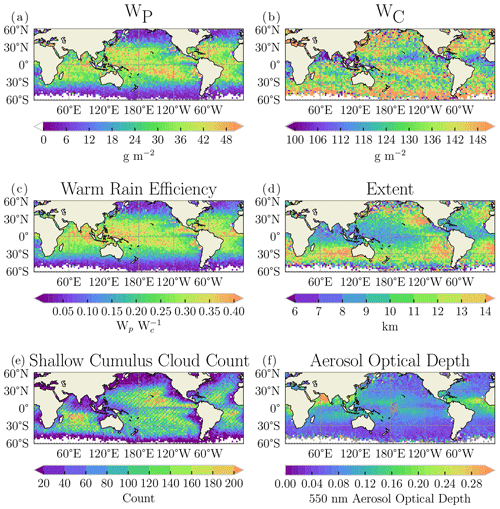
Figure 1The spatial distribution of integrated precipitation water path (WP), cloud water path (WC), warm-rain efficiency, extent, number of shallow cumulus cloud objects, and aerosol optical depth is shown in panels (a)–(f), respectively. Cloud objects are binned onto a 2.5∘ × 2.5∘ spatial grid, and any grid box containing no data is white.
Figure 1a shows the spatial distribution of WP over the global ocean basins, with WP increasing equatorward. This is consistent with the prior literature that found raining shallow cumulus clouds are most frequent within the tropics (e.g., Smalley and Rapp, 2020). WP is largest near the Inter-Tropical Convergence Zone (ITCZ), South Pacific Convergence Zone (SPCZ), and tropical warm pool, with values exceeding 45 g m−2. Deep convection is more frequent here (e.g., Waliser and Gautier, 1993), so some objects may be transitioning from raining shallow cumulus to deeper convection. The results likely include a mix of frequently occurring tropical raining shallow cumulus clouds and the early stages of developing deep convection possibly resulting in large WP over the tropics.
Spatial patterns in WC (Fig. 1b) within the tropics generally follow WP, with values ranging between 110 and 150 g m−2 in the tropics. We find that relative humidity generally decreases from median values near 90 % in the tropics to median values near 80 % north or south into the midlatitudes (not shown); this is consistent with modeling studies that found less cloud water evaporates away in wetter environments (e.g., Tian and Kuang, 2016). Considering boundary layer depth scales with SST (e.g., Wood and Bretherton, 2004), the boundary layer is generally deeper over the tropical oceans than the sub-tropical oceans. This supports deeper clouds (e.g., Short and Nakamura, 2000; Rauber et al., 2007; Smalley and Rapp, 2020) and could also help explain why WC and WP are largest in the tropics.
Figure 1c shows the spatial patterns in WRR follow spatial patterns in WP, with values increasing equatorward. Shallow cumulus cloud object WRR is largest within the ITCZ, SPCZ, and tropical warm pool, with values > 0.35. This is consistent with Lau and Wu (2003), who found precipitation efficiency is positively correlated with SST (e.g., Lau and Wu, 2003), and implies that WRR is higher in wetter environments.
Patterns in spatial extent shown in Fig. 1d are similar to those found by Smalley and Rapp (2020), who used combined CloudSat–CALIPSO to define extent, with extent decreasing from the stratocumulus regions west into the trade cumulus regions and north of the trade cumulus and stratocumulus regions into the ITCZ. Interestingly, Fig. 1c shows WRR also peaks in the southeast Pacific stratocumulus region, implying that WRR is high in regions with relatively low SST. However, Fig. 1e shows that fewer than 40 shallow cumulus objects are observed in a given grid box over this region in a 4-year period, reducing confidence in WRR here. Together, Fig. 1c and d indicate that the relationship between WRR and extent is complicated and potentially depends on cloud depth (which increases in the tropics) and on environmental conditions including RH and aerosol loading.
To determine how WRR depends on cloud size, Fig. 2 shows WRR as a function of cloud object extent. Note that we estimate the uncertainty in median WRR at any given extent by bootstrapping WRR at a given extent 10 000 times with replacement. Error in WRR median is then classified as ±1 standard deviation of the bootstrapped sample distribution of median values. Similar error estimates are shown in Figs. 3–5 later in this section. WRR follows a double power-law relationship, with WRR < 0.25 for cloud objects < 8.4 km and approaching 0.30 for cloud objects > 8.4 km. There is also very little spread in median WRR at a given extent, which gives us confidence that this relationship is real. Similar to these results, earlier studies have shown a double power-law distribution in shallow cumulus size (e.g., Benner and Curry, 1998; Trivej and Stevens, 2010), which will be discussed in further detail later.
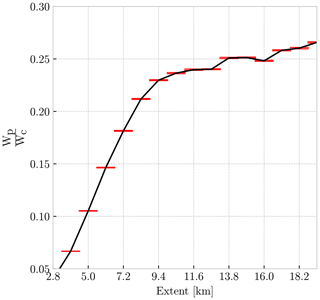
Figure 2The median ratio of cloud water to rainwater at a given maximum size (extent). The red error bars represent ±1 standard deviation of a bootstrapped distribution of medians at a given extent.
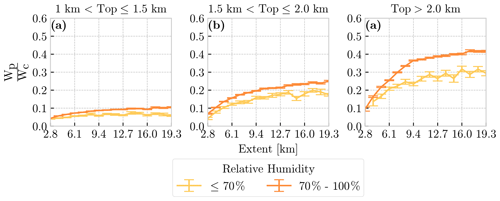
Figure 3The median ratio of cloud water to rainwater at a given maximum size (extent). The different line colors represent cloud objects separated by < 850 mb relative humidity (RH). Error bars represent ±1 standard deviation of a bootstrapped distribution of medians at a given extent and RH.
To address the impact of RH and cloud depth on WRR, Fig. 3 shows the relationship between WRR and cloud object extent conditioned using cloud-top height and RH at or below 850 mb. Holding RH constant, WRR depends strongly on cloud-top height, with WRR nearly doubling for each 0.5 km increase in cloud-top height for a given extent in the most humid environments. For a given RH and top height, there is also an increase in WRR with extent. Holding top height constant, there is also an increase in WRR with increasing RH, with no overlap in median WRR error at a given extent or RH. However, increases in WRR are dominated by changing cloud size (depth and extent).
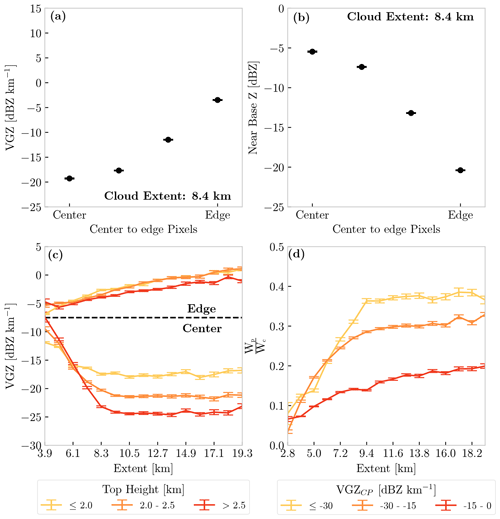
Figure 4Panel (a) shows the median change in the vertical reflectivity (VGZ) from the center to edge of all cloud objects with an extent of 8.4 km. Panel (b) shows the median change in near-base reflectivity (Z) from the center to edge of all cloud objects with an extent of 8.4 km. Panel (c) shows the median vertical reflectivity gradient (VGZ) at the center and edge of different-sized (extent) raining cloud objects. Different lines represent cloud objects separated by top height. Panel (d) shows the median ratio of cloud water to rainwater () at a given median size (extent). The different line colors represent cloud objects separated by the vertical reflectivity gradient on the center pixel (VGZCP) of all cloud objects. Error bars represent ±1 standard deviation of a bootstrapped distribution of median VGZ and Z for a given pixel from cloud object edge to center (a, b), as well as VGZ and at a given extent (c, d).
To support the hypothesis that larger shallow cumulus clouds are able to sustain a larger droplet field within their cores to increase the precipitation efficiency, the variation in the VGZ across individual cloud objects is examined. We expect that VGZ will be a larger negative value near cloud center than cloud edge, especially as cloud size increases. As an example, Fig. 4a shows the change in median VGZCP to VGZEP for cloud objects with an extent of 8.4 km. VGZ decreases from −3.48 dBZ km−1 at cloud object edge to −20.3 dBZ km−1 at cloud object center. Given the relationship between reflectivity and drop size, a negative VGZCP implies that drop growth is occurring from near cloud top to near cloud base close to cloud object center, suggesting that larger droplets may be present near cloud base near cloud object center compared to the edge. To directly analyze drop size near cloud base, Fig. 4b shows the spread in median near-base reflectivity for cloud objects with an extent of 8.4 km. Figure 4b confirms that cloud drops are largest near cloud object center, with a median reflectivity of −5.28 dBZ. Reflectivity values, and subsequent drop sizes, then decrease, moving from cloud object center to cloud object edge, with edge values of −17.96 dBZ. Figure 4a coupled with Fig. 4b implies, at least for extents of 8.4 km, that drops grow larger near cloud object centers and may be more protected from mixing.
Figure 4c shows the relationship between VGZCP and VGZEP as a function of extent and top height. For a constant cloud-top height, VGZCP again follows a double power-law distribution. Specifically, the magnitude of the VGZCP rapidly increases from approximately 10 to 20 dBZ km−1 as extent approaches 8.4 km, while it plateaus around 20 dBZ km−1 for extents > 8.4 km. Conversely, VGZEP decreases in magnitude, approaching 0 dBZ km−1 for the largest cloud object extents. However, it does not decrease as fast as VGZCP, implying that the change in vertical reflectivity gradient in the center of cloud is driving changes in differences from center to edge. Figure 4c also shows that the change in VGZCP depends on cloud-top height for extents > 5.6 km, with larger magnitudes for the tallest clouds. Narrowing this down to the possible influence of entrainment on cloud object updrafts from cloud edge to center, this is also consistent with previous modeling studies that found that larger shallow cumulus cloud cores are more insulated from entrainment (e.g., Burnet and Brenguier, 2010; Tian and Kuang, 2016), a more adiabatic cloud core of developing cumulus as shown in Fig. 2 from Moser and Lasher-Trapp (2017), and a higher probability of rainfall (e.g., Smalley and Rapp, 2020) in observations.
To determine how VGZCP influences the relationship between WRR and extent, Fig. 4d shows WRR as a function of extent conditioned by top height and VGZCP, with WRR increasing as the magnitude of VGZCP increases; however, changes in WRR are not distinct when the magnitude of VGZCP is larger than −15 dBZ km−1 for extents < 7 km. This, coupled with Fig. 4c, illustrates that, as shallow cumulus grow deeper and wider, drops at the center of the cloud can grow larger and scavenge more available cloud water. This is consistent with larger shallow cumulus clouds being more efficient at producing rainfall, perhaps in part because they are less influenced by environmental mixing.
Until this point, this paper has focused on how cloud size and RH impact WRR. However, it is also understood that aerosol concentrations influence both the number and size of droplets within a cloud, with larger aerosol concentrations resulting in a greater number of smaller droplets (e.g., Twomey, 1974; Albrecht, 1989). As a result, we hypothesize that increasing aerosol concentrations, which vary regionally (Fig. 1f), increase the ratio of cloud droplets to rain drops, thus reducing WRR.
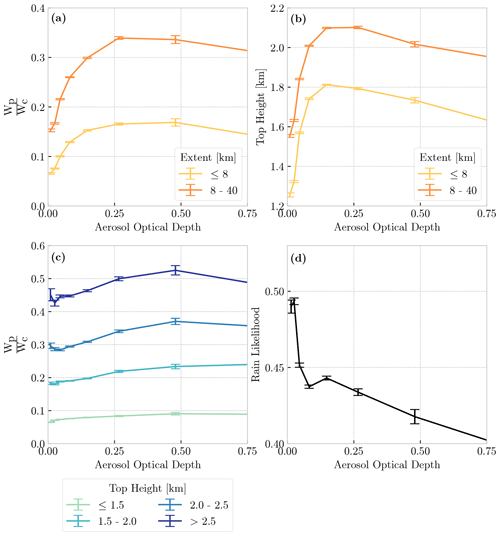
Figure 5Panel (a) shows the relationship between median warm-rain efficiency and MODIS 550 nm aerosol optical depth. Panel (b) shows the relationship between median cloud-top height and aerosol optical depth. Panel (c) shows the relationship between warm-rain efficiency and aerosol optical depth. Line colors in panels (a) and (b) represent cloud objects separated by extent, while line colors in panel (c) represent cloud objects separated by top height. Panel (d) shows the ratio of raining cloud objects to non-raining cloud objects (rain likelihood) at a given aerosol optical depth. For panels (a), (b), and (c), error bars represent ±1 standard deviation of a bootstrapped distribution of raining cloud objects to determine the uncertainty in and top height at a given aerosol optical depth, whereas the error bars shown in panel (d) represent ±1 standard deviation of a bootstrapped distribution of raining and non-raining cloud objects to determine rain likelihood uncertainty at a given aerosol optical depth.
Figure 5a shows the relationship between WRR and AOD, conditioned by top height. On first glance, it appears that WRR increases as a function of AOD, which contradicts the expectation of a shift in drop size distribution towards fewer large drops to initiate collision–coalescence, which would reduce the amount of cloud water converted to rainwater. However, disentangling aerosol–cloud interactions from other meteorological variables is quite difficult, as increasing aerosol concentrations are often correlated with other environmental variables (e.g., Koren et al., 2014).
Given the strong dependence of WRR on top height, we further examine the relationship between AOD and top height (Fig. 5b), conditioned by extent. The curves shown in Fig. 5a look similar to those shown in Fig. 5b, suggesting the positive correlation between aerosols and top height are responsible for the observed relationship between AOD and WRR. Indeed, Fig. 5c further supports this assertion. When conditioned by top height, WRR shows little dependence on AOD and suggests that the conversion from WC to WP is more sensitive to cloud depth than aerosols. While these results seem counterintuitive, this analysis examines clouds in which precipitation has been detected. Figure 5d shows the likelihood of rain occurrence at a given AOD determined by the ratio of raining cloud objects to the total number of cloud objects. As expected, Fig. 5d shows that the likelihood of rain decreases as AOD increases, with rain likelihood of about 50 % in the cleanest environments decreasing to about 40 % for an AOD approaching 0.75. These results imply that, once the condensation–coalescence is initiated, aerosol loading has a smaller impact on the conversion of cloud water to rain than other cloud or environmental characteristics.
This study has emphasized the potential for the decreasing impact of entrainment on cloud cores, resulting in higher WRR, as cloud size increases; however, it is important to point out other factors related to cloud size that may also impact WRR. Figure 3 shows WRR is higher when cloud objects are taller, which may be simply because we are sampling more mature clouds that have had more time for the collision–coalescence process to result in rain formation. Deeper shallow cumulus not only live longer, which would give cloud droplets more time to grow to raindrop size (e.g., Burnet and Brenguier, 2010), but they are more likely to have more intense updrafts, which could result in more water vapor being transported to higher altitudes within a cloud. Stronger updrafts are then more likely to be able to suspend cloud droplets higher in the cloud for longer periods of time, which allows them to grow larger before they begin to fall and collision–coalescence is initiated. Once cloud droplets do begin to fall, they are not only potentially larger but able to collect more droplets over a larger distance than droplets falling through a shallower cloud. This could potentially result in higher WRR; however there is likely a lag between the peaks in cloud water path and rainwater path as cloud drops grow to raindrop size in a developing cloud. Earlier modeling studies have also noted that turbulent flow potentially enhances the likelihood of warm-rain formation (e.g., Brenguier and Chaumat, 2001; Seifert et al., 2010; Wyszogrodzki et al., 2013; Franklin, 2014; Seifert and Onishi, 2016; Chen et al., 2018). Seifert et al. (2010) found that turbulence effects are largest near cloud tops in shallow cumulus clouds, which they note is an important region for initial rain formation. While these additional processes may impact WRR, the satellite observations used in this study are instantaneous snapshots in time. We attempted to remove some of these life cycle impacts by binning cloud objects by top height. Within a given cloud-top height bin, WRR (Fig. 3) and the magnitude of VGZCP (Fig. 4c) still increase as a function of extent. While we acknowledge that this cannot fully remove these impacts, these results support the idea that processes other than those related to cloud lifetime, like lateral entrainment, may also influence the WRR of shallow cumulus clouds of different horizontal sizes.
It is surprising that this study identifies shallow cumulus cloud objects larger than 10 km. This suggests that some stratocumulus clouds are not being filtered out of this dataset by our lower-tropospheric stability threshold. However, a majority of cloud objects that we identify have extents below 10 km. This is consistent with Fig. 1e, which shows that a majority of cloud objects occur over regions generally associated with shallow cumulus clouds. To further test this, we performed the same analysis over the South Pacific trade region but excluded the southeast stratocumulus region, and we still find few large cloud objects with our overall results and interpretation not changing. This suggests that the predominant type of entrainment impacting these cloud objects would be lateral entrainment at cloud edges (see review by de Rooy et al., 2013) and that these are indeed shallow cumulus.
At the small end of the shallow cumulus horizontal size spectrum, CloudSat is limited to observing cloud objects no smaller than 1.4 × 1.8 km. Given prior ground observational studies, it is likely that there is a significant population of shallow cumulus cloud objects not identified by our study (e.g., Kollias et al., 2003; Mieslinger et al., 2019) due to non-uniform beam filling effects. Battaglia et al. (2020) noted that this results in an underestimation of path-integrated attenuation, potentially introducing error into the retrieval of WP. Unfortunately, this limitation is unavoidable given CloudSat's horizontal resolution.
This study uses the methodology described by Smalley and Rapp (2020) to classify a large global shallow cumulus cloud object dataset from CloudSat and determine the relationship between WRR, cloud extent, RH, and aerosol loading. We find that WRR increases as a function of cloud size (top height and extent) and RH. Benner and Curry (1998) found a double power-law distribution in shallow cumulus thickness as a function of cloud diameter, and Trivej and Stevens (2010) hypothesized that the shift from one power-law distribution to another results from small shallow cumulus clouds that can rapidly grow in size until reaching the trade inversion. We find a similar relationship between WRR and extent, showing that one distribution exists with WRR increasing faster for extents < 8.4 km and then slowly increasing above this breakpoint. Trivej and Stevens (2010) also found that environmental factors, particularly RH, become important once cloud-top height reaches the trade inversion. Our results show that WRR is most sensitive to RH above an extent of 8.4 km, which we assume represents the average extent where cloud objects reach the trade inversion.
Unexpectedly, we find that, for a fixed cloud depth, WRR is fairly insensitive to AOD. One explanation may be that, although high AOD values do occur over the global ocean basins, the majority of cloud objects being sampled still form in relatively clean air, so the minority of cloud objects occurring over polluted regions have a small impact on the overall statistics. Another explanation may be that this analysis only includes precipitating clouds, so once collision–coalescence is initiated, the amount of cloud water converted to rainwater is less influenced by aerosol concentrations.
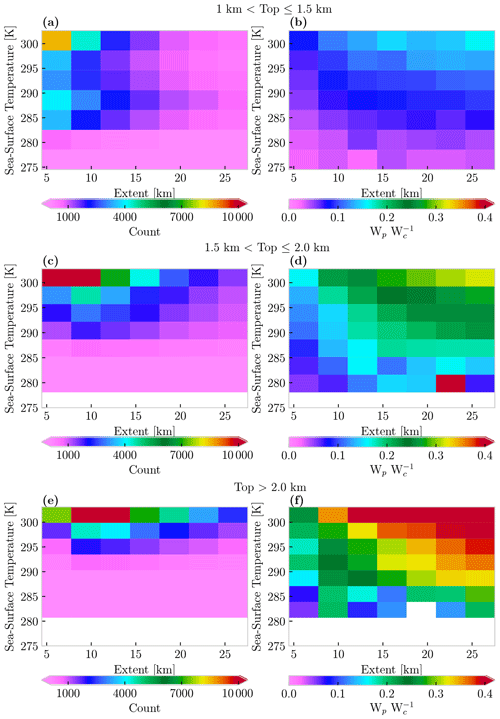
Figure 6The two-dimensional distribution of extent as a function of sea-surface temperature, conditioned by cloud-top height, is shown in panels (a), (c), and (e). The median ratio of cloud water to rainwater () as a function of extent and sea-surface temperature is shown in panels (b), (d), and (f).
Past studies conclude that precipitation efficiency increases as SST increases (Lau and Wu, 2003; Bailey et al., 2015; Lutsko and Cronin, 2018). Considering warmer SSTs tend to result in deeper clouds (e.g., Wood and Bretherton, 2004) and more humid environments (e.g., Chen and Liu, 2016), it is reasonable to expect that WRR would increase in response (e.g., Lau and Wu, 2003). Our results show that WRR is highest near the Equator, where SSTs are warmest. However, the general relationship between cloud size (depth and extent), RH, and WRR suggests that WRR is more sensitive to cloud size than RH. To directly address the SST dependence, Fig. 6 shows the frequency distribution of extents and the median WRR, both as a function of cloud-top height and SST. For a given cloud-top height, WRR does increase as a function of SST. However, for a fixed SST, WRR also increases as extent increases. Additionally, Fig. 6 shows that the frequency distribution of cloud object sizes shifts toward more frequent larger extents with increasing SST. Together, these suggest that increasing WRR with SST shown in past studies results not only from the deepening clouds but also from the shift towards more frequent larger clouds.
The prior literature has shown that modeled shallow cumulus cores become more adiabatic as they grow larger (Moser and Lasher-Trapp, 2017), potentially resulting in larger drops. Figure 6 and our analysis of the relationship between VGZCP, extent, and WRR suggest drop growth is being enhanced near the base at the center of larger cloud objects, potentially resulting in more cloud water being scavenged by larger droplets and more efficient autoconversion and accretion processes. Most climate models parameterize autoconversion and accretion as functions of cloud and precipitation properties (e.g., Lohmann and Roeckner, 1996; Liu and Daum, 2004; Morrison et al., 2005; Lim and Hong, 2010; Lee and Baik, 2017), but recently enhancement factors that depend on variations and covariations in WC and WP have been introduced to correct for biases due to subgrid-scale WC and WP inhomogeneity (e.g., Lebsock et al., 2013; Boutle et al., 2014; Witte et al., 2019). Presumably, the dependence of these enhancement factors on WC variability would capture the increase in WRR with cloud depth shown here; however it is unclear if these enhancement factors based on the variance in WC and WP capture the effects of cloud extent on WC and WP, and subsequently WRR. Our dataset provides an opportunity for a future analysis that could focus on investigating the relationship between subgrid-scale variability in WC, WP, WRR, and extent, which could help improve our understanding and simulation of precipitating shallow cloud processes in climate models.
ECMWF-AUX (Cronk and Partain, 2017), MOD-06-1KM (Cronk and Partain, 2018), 2B-GEOPROF (Marchand et al., 2008), 2C-RAIN-PROFILE (Lebsock and L'Ecuyer, 2011), and 2C-PRECIP-COLUMN (Haynes et al., 2009) were acquired from the CloudSat Data Processing Center and can be obtained from http://www.cloudsat.cira.colostate.edu (last access: 20 July 2020).
Please contact the authors for access to any dataset created by the analysis and/or the code used to process the CloudSat/MODIS data.
KMS performed the analysis, while KMS and ADR wrote and edited the manuscript.
The authors declare that they have no conflict of interest.
We thank the two anonymous reviewers for their comments and suggestions that helped improve and clarify this paper.
This research has been supported by the National Aeronautics and Space Administration (grant no. NNX14AO72G).
This paper was edited by Timothy Garrett and reviewed by two anonymous referees.
Abel, S. J. and Shipway, B. J.: A comparison of cloud-resolving model simulations of trade wind cumulus with aircraft observations taken during RICO, Q. J. Roy. Meteor. Soc., 133, 781–794, https://doi.org/10.1002/qj.55, 2007. a
Albrecht, B. A.: Aerosols, Cloud Microphysics, and Fractional Cloudiness, Science, 245, 1227–1230, https://doi.org/10.1126/science.245.4923.1227, 1989. a, b, c
Austin, R. T., Heymsfield, A. J., and Stephens, G. L.: Retrieval of ice cloud microphysical parameters using the CloudSat millimeter-wave radar and temperature, J. Geophys. Res.-Atmos., 114, D00A23, https://doi.org/10.1029/2008JD010049, 2009. a
Bailey, A., Nusbaumer, J., and Noone, D.: Precipitation efficiency derived from isotope ratios in water vapor distinguishes dynamical and microphysical influences on subtropical atmospheric constituents, J. Geophys. Res.-Atmos., 120, 9119–9137, https://doi.org/10.1002/2015JD023403, 2015. a, b
Battaglia, A., Kollias, P., Dhillon, R., Lamer, K., Khairoutdinov, M., and Watters, D.: Mind the gap – Part 2: Improving quantitative estimates of cloud and rain water path in oceanic warm rain using spaceborne radars, Atmos. Meas. Tech., 13, 4865–4883, https://doi.org/10.5194/amt-13-4865-2020, 2020. a
Benner, T. C. and Curry, J. A.: Characteristics of small tropical cumulus clouds and their impact on the environment, J. Geophys. Res.-Atmos., 103, 28753–28767, https://doi.org/10.1029/98JD02579, 1998. a, b
Blyth, A. M., Lowenstein, J. H., Huang, Y., Cui, Z., Davies, S., and Carslaw, K. S.: The production of warm rain in shallow maritime cumulus clouds, Q. J. Roy. Meteor. Soc., 139, 20–31, https://doi.org/10.1002/qj.1972, 2013. a
Bony, S. and Dufresne, J.-L.: Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models, Geophys. Res. Lett., 32, L20806, https://doi.org/10.1029/2005GL023851, 2005. a
Boutle, I. A., Abel, S. J., Hill, P. G., and Morcrette, C. J.: Spatial variability of liquid cloud and rain: observations and microphysical effects, Q. J. Roy. Meteor. Soc., 140, 583–594, https://doi.org/10.1002/qj.2140, 2014. a
Brenguier, J.-L. and Chaumat, L.: Droplet Spectra Broadening in Cumulus Clouds, Part I: Broadening in Adiabatic Cores, J. Atmos. Sci., 58, 628–641, https://doi.org/10.1175/1520-0469(2001)058<0628:DSBICC>2.0.CO;2, 2001. a
Bretherton, C. S., McCaa, J. R., and Grenier, H.: A New Parameterization for Shallow Cumulus Convection and Its Application to Marine Subtropical Cloud-Topped Boundary Layers, Part I: Description and 1D Results, Mon. Weather Rev., 132, 864–882, https://doi.org/10.1175/1520-0493(2004)132<0864:ANPFSC>2.0.CO;2, 2004. a
Burnet, F. and Brenguier, J.-L.: The onset of precipitation in warm cumulus clouds: An observational case-study, Q. J. Roy. Meteor. Soc., 136, 374–381, https://doi.org/10.1002/qj.552, 2010. a, b, c, d
Chen, B. and Liu, C.: Warm Organized Rain Systems over the Tropical Eastern Pacific, J. Climate, 29, 3403–3422, https://doi.org/10.1175/jcli-d-15-0177.1, 2016. a
Chen, S., Yau, M. K., and Bartello, P.: Turbulence Effects of Collision Efficiency and Broadening of Droplet Size Distribution in Cumulus Clouds, J. Atmos. Sci., 75, 203–217, https://doi.org/10.1175/JAS-D-17-0123.1, 2018. a
Cho, H.-M., Zhang, Z., Meyer, K., Lebsock, M., Platnick, S., Ackerman, A. S., Di Girolamo, L., C.-Labonnote, L., Cornet, C., Riedi, J., and Holz, R. E.: Frequency and causes of failed MODIS cloud property retrievals for liquid phase clouds over global oceans, J. Geophys. Res.-Atmos., 120, 4132–4154, https://doi.org/10.1002/2015JD023161, 2015. a
Chong, M. and Hauser, D.: A Tropical Squall Line Observed during the COPT 81 Experiment in West Africa, Part II: Water Budget, Mon. Weather Rev., 117, 728–744, https://doi.org/10.1175/1520-0493(1989)117<0728:ATSLOD>2.0.CO;2, 1989. a
Christensen, M. W., Stephens, G. L., and Lebsock, M. D.: Exposing biases in retrieved low cloud properties from CloudSat: A guide for evaluating observations and climate data, J. Geophys. Res.-Atmos., 118, 12120–12131, https://doi.org/10.1002/2013JD020224, 2013. a
Cronk, H. and Partain, P.: CloudSat ECMWF-AUX Auxillary Data Product Process Description and Interface Control Document, Tech. Rep., Colorado State University, Fort Collins, Colorado, USA, 2017. a, b
Cronk, H. and Partain, P.: CloudSat MOD06-AUX Auxiliary Data Process Description and Interface Control Document, Tech. Rep., Colorado State University, Fort Collins, Colorado, USA, 2018. a, b
Dagan, G., Koren, I., Altaratz, O., and Heiblum, R. H.: Aerosol effect on the evolution of the thermodynamic properties of warm convective cloud fields, Sci. Rep.-UK, 6, 38769, https://doi.org/10.1038/srep38769, 2016. a
Del Genio, A. D., Kovari, W., Yao, M.-S., and Jonas, J.: Cumulus Microphysics and Climate Sensitivity, J. Climate, 18, 2376–2387, https://doi.org/10.1175/JCLI3413.1, 2005. a
de Rooy, W. C., Bechtold, P., Fröhlich, K., Hohenegger, C., Jonker, H., Mironov, D., Pier Siebesma, A., Teixeira, J., and Yano, J.-I.: Entrainment and detrainment in cumulus convection: an overview, Q. J. Roy. Meteor. Soc., 139, 1–19, https://doi.org/10.1002/qj.1959, 2013. a, b
Dufresne, J.-L. and Bony, S.: An Assessment of the Primary Sources of Spread of Global Warming Estimates from Coupled Atmosphere–Ocean Models, J. Climate, 21, 5135–5144, https://doi.org/10.1175/2008JCLI2239.1, 2008. a
Franklin, C. N.: The effects of turbulent collision–coalescence on precipitation formation and precipitation-dynamical feedbacks in simulations of stratocumulus and shallow cumulus convection, Atmos. Chem. Phys., 14, 6557–6570, https://doi.org/10.5194/acp-14-6557-2014, 2014. a, b
Gao, W., Liu, L., Li, J., and Lu, C.: The Microphysical Properties of Convective Precipitation Over the Tibetan Plateau by a Subkilometer Resolution Cloud-Resolving Simulation, J. Geophys. Res.-Atmos., 123, 3212–3227, https://doi.org/10.1002/2017JD027812, 2018. a
Gerber, H. E., Frick, G. M., Jensen, J. B., and Hudson, J. G.: Entrainment, Mixing, and Microphysics in Trade-Wind Cumulus, J. Meteorol. Soc. Jpn., 86A, 87–106, https://doi.org/10.2151/jmsj.86A.87, 2008. a, b
Haynes, J. M., Lecuyer, T. S., Stephens, G. L., Miller, S. D., Mitrescu, C., Wood, N. B., and Tanelli, S.: Rainfall retrieval over the ocean with spaceborne W-band radar, J. Geophys. Res., 114, D00A22, https://doi.org/10.1029/2008jd009973, 2009. a, b, c
Heus, T. and Jonker, H. J. J.: Subsiding Shells around Shallow Cumulus Clouds, J. Atmos. Sci., 65, 1003–1018, https://doi.org/10.1175/2007jas2322.1, 2008. a, b, c
Hoffmann, F., Noh, Y., and Raasch, S.: The Route to Raindrop Formation in a Shallow Cumulus Cloud Simulated by a Lagrangian Cloud Model, J. Atmos. Sci., 74, 2125–2142, https://doi.org/10.1175/JAS-D-16-0220.1, 2017. a
Jiang, H. and Feingold, G.: Effect of aerosol on warm convective clouds: Aerosol-cloud-surface flux feedbacks in a new coupled large eddy model, J. Geophys. Res.-Atmos., 111, D01202, https://doi.org/10.1029/2005JD006138, 2006. a
Jolivet, D. and Feijt, A. J.: Quantification of the accuracy of liquid water path fields derived from NOAA 16 advanced very high resolution radiometer over three ground stations using microwave radiometers, J. Geophys. Res.-Atmos., 110, D11204, https://doi.org/10.1029/2004JD005205, 2005. a
Jung, E., Albrecht, B. A., Feingold, G., Jonsson, H. H., Chuang, P., and Donaher, S. L.: Aerosols, clouds, and precipitation in the North Atlantic trades observed during the Barbados aerosol cloud experiment – Part 1: Distributions and variability, Atmos. Chem. Phys., 16, 8643–8666, https://doi.org/10.5194/acp-16-8643-2016, 2016a. a
Jung, E., Albrecht, B. A., Sorooshian, A., Zuidema, P., and Jonsson, H. H.: Precipitation susceptibility in marine stratocumulus and shallow cumulus from airborne measurements, Atmos. Chem. Phys., 16, 11395–11413, https://doi.org/10.5194/acp-16-11395-2016, 2016b. a, b
Klein, S. A. and Hartmann, D. L.: The Seasonal Cycle of Low Stratiform Clouds, J. Climate, 6, 1587–1606, https://doi.org/10.1175/1520-0442(1993)006<1587:TSCOLS>2.0.CO;2, 1993. a
Kollias, P., Albrecht, B. A., and Marks Jr., F. D.: Cloud radar observations of vertical drafts and microphysics in convective rain, J. Geophys. Res.-Atmos., 108, 4053, https://doi.org/10.1029/2001JD002033, 2003. a
Koren, I., Dagan, G., and Altaratz, O.: From aerosol-limited to invigoration of warm convective clouds, Science, 344, 1143–1146, https://doi.org/10.1126/science.1252595, 2014. a, b
Korolev, A., Khain, A., Pinsky, M., and French, J.: Theoretical study of mixing in liquid clouds – Part 1: Classical concepts, Atmos. Chem. Phys., 16, 9235–9254, https://doi.org/10.5194/acp-16-9235-2016, 2016. a
Lamer, K., Kollias, P., Battaglia, A., and Preval, S.: Mind the gap – Part 1: Accurately locating warm marine boundary layer clouds and precipitation using spaceborne radars, Atmos. Meas. Tech., 13, 2363–2379, https://doi.org/10.5194/amt-13-2363-2020, 2020. a
Lau, K. M. and Wu, H. T.: Warm rain processes over tropical oceans and climate implications, Geophys. Res. Lett., 30, 2290, https://doi.org/10.1029/2003GL018567, 2003. a, b, c, d, e, f, g
Lebsock, M. D.: Level 2C RAIN-PROFILE Product Process Description and Interface Control Document, Tech. Rep. D-20308, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California, USA, 2018. a
Lebsock, M. D. and L'Ecuyer, T. S.: The retrieval of warm rain from CloudSat, J. Geophys. Res.-Atmos., 116, D20209, https://doi.org/10.1029/2011JD016076, 2011. a, b, c
Lebsock, M. D. and Su, H.: Application of active spaceborne remote sensing for understanding biases between passive cloud water path retrievals, J. Geophys. Res.-Atmos., 119, 8962–8979, https://doi.org/10.1002/2014JD021568, 2014. a
Lebsock, M. D., L'Ecuyer, T. S., and Stephens, G. L.: Detecting the Ratio of Rain and Cloud Water in Low-Latitude Shallow Marine Clouds, J. Appl. Meteorol. Clim., 50, 419–432, https://doi.org/10.1175/2010JAMC2494.1, 2011. a, b, c
Lebsock, M. D., Morrison, H., and Gettelman, A.: Microphysical implications of cloud-precipitation covariance derived from satellite remote sensing, J. Geophys. Res.-Atmos., 118, 6521–6533, https://doi.org/10.1002/jgrd.50347, 2013. a
L'Ecuyer, T. S. and Stephens, G. L.: An Estimation-Based Precipitation Retrieval Algorithm for Attenuating Radars, J. Appl. Meteorol., 41, 272–285, https://doi.org/10.1175/1520-0450(2002)041<0272:AEBPRA>2.0.CO;2, 2002. a
Lee, H. and Baik, J.-J.: A Physically Based Autoconversion Parameterization, J. Atmos. Sci., 74, 1599–1616, https://doi.org/10.1175/JAS-D-16-0207.1, 2017. a
Li, X., Sui, C.-H., and Lau, K.-M.: Precipitation Efficiency in the Tropical Deep Convective Regime: A 2D Cloud Resolving Modeling Study, J. Meteorol. Soc. Jpn., 80, 205–212, https://doi.org/10.2151/jmsj.80.205, 2002. a
Lim, K.-S. S. and Hong, S.-Y.: Development of an Effective Double-Moment Cloud Microphysics Scheme with Prognostic Cloud Condensation Nuclei (CCN) for Weather and Climate Models, Mon. Weather Rev., 138, 1587–1612, https://doi.org/10.1175/2009MWR2968.1, 2010. a
Liu, J. and Li, Z.: Significant Underestimation in the Optically Based Estimation of the Aerosol First Indirect Effect Induced by the Aerosol Swelling Effect, Geophys. Res. Lett., 45, 5690–5699, https://doi.org/10.1029/2018GL077679, 2018. a, b
Liu, Y. and Daum, P. H.: Parameterization of the Autoconversion Process, Part I: Analytical Formulation of the Kessler-Type Parameterizations, J. Atmos. Sci., 61, 1539–1548, https://doi.org/10.1175/1520-0469(2004)061<1539:POTAPI>2.0.CO;2, 2004. a
Lohmann, U. and Roeckner, E.: Design and performance of a new cloud microphysics scheme developed for the ECHAM general circulation model, Clim. Dynam., 12, 557–572, https://doi.org/10.1007/BF00207939, 1996. a
Lu, C., Liu, Y., Niu, S., and Vogelmann, A. M.: Lateral entrainment rate in shallow cumuli: Dependence on dry air sources and probability density functions, Geophys. Res. Lett., 39, L20812, https://doi.org/10.1029/2012GL053646, 2012. a
Lutsko, N. J. and Cronin, T. W.: Increase in Precipitation Efficiency With Surface Warming in Radiative-Convective Equilibrium, J. Adv. Model. Earth Sy., 10, 2992–3010, https://doi.org/10.1029/2018MS001482, 2018. a, b, c
Marchand, R., Mace, G. G., Ackerman, T., and Stephens, G.: Hydrometeor Detection Using Cloudsat – An Earth-Orbiting 94 GHz Cloud Radar, J. Atmos. Ocean. Tech., 25, 519–533, https://doi.org/10.1175/2007JTECHA1006.1, 2008. a, b, c
Medeiros, B. and Stevens, B.: Revealing differences in GCM representations of low clouds, Clim. Dynam., 36, 385–399, https://doi.org/10.1007/s00382-009-0694-5, 2011. a
Michel Flores, J., Bar-Or, R. Z., Bluvshtein, N., Abo-Riziq, A., Kostinski, A., Borrmann, S., Koren, I., Koren, I., and Rudich, Y.: Absorbing aerosols at high relative humidity: linking hygroscopic growth to optical properties, Atmos. Chem. Phys., 12, 5511–5521, https://doi.org/10.5194/acp-12-5511-2012, 2012. a
Mieslinger, T., Horvath, A., Buehler, S. A., and Sakradzija, M.: The Dependence of Shallow Cumulus Macrophysical Properties on Large-Scale Meteorology as Observed in ASTER Imagery, J. Geophys. Res.-Atmos., 124, 11477–11505, https://doi.org/10.1029/2019JD030768, 2019. a
Minor, H. A., Rauber, R. M., Göke, S., and Di Girolamo, L.: Trade Wind Cloud Evolution Observed by Polarization Radar: Relationship to Giant Condensation Nuclei Concentrations and Cloud Organization, J. Atmos. Sci., 68, 1075–1096, https://doi.org/10.1175/2010JAS3675.1, 2011. a
Mitrescu, C., L'Ecuyer, T., Haynes, J., Miller, S., and Turk, J.: CloudSat Precipitation Profiling Algorithm–Model Description, J. Appl. Meteorol. Clim., 49, 991–1003, https://doi.org/10.1175/2009JAMC2181.1, 2010. a
Morrison, H., Curry, J. A., and Khvorostyanov, V. I.: A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models, Part I: Description, J. Atmos. Sci., 62, 1665–1677, https://doi.org/10.1175/JAS3446.1, 2005. a
Moser, D. H. and Lasher-Trapp, S.: The Influence of Successive Thermals on Entrainment and Dilution in a Simulated Cumulus Congestus, J. Atmos. Sci., 74, 375–392, https://doi.org/10.1175/JAS-D-16-0144.1, 2017. a, b, c, d
Nam, C., Bony, S., Dufresne, J.-L., and Chepfer, H.: The “too few, too bright” tropical low-cloud problem in CMIP5 models, Geophys. Res. Lett., 39, L21801, https://doi.org/10.1029/2012GL053421, 2012. a, b
Neubauer, D., Christensen, M. W., Poulsen, C. A., and Lohmann, U.: Unveiling aerosol–cloud interactions – Part 2: Minimising the effects of aerosol swelling and wet scavenging in ECHAM6-HAM2 for comparison to satellite data, Atmos. Chem. Phys., 17, 13165–13185, https://doi.org/10.5194/acp-17-13165-2017, 2017. a
Pinsky, M., Khain, A., and Korolev, A.: Theoretical analysis of mixing in liquid clouds – Part 3: Inhomogeneous mixing, Atmos. Chem. Phys., 16, 9273–9297, https://doi.org/10.5194/acp-16-9273-2016, 2016a. a
Pinsky, M., Khain, A., Korolev, A., and Magaritz-Ronen, L.: Theoretical investigation of mixing in warm clouds – Part 2: Homogeneous mixing, Atmos. Chem. Phys., 16, 9255–9272, https://doi.org/10.5194/acp-16-9255-2016, 2016b. a
Platnick, S. and Valero, F. P. J.: A Validation of a Satellite Cloud Retrieval during ASTEX, J. Atmos. Sci., 52, 2985–3001, https://doi.org/10.1175/1520-0469(1995)052<2985:AVOASC>2.0.CO;2, 1995. a
Platnick, S., King, M. D., Ackerman, S. A., Menzel, W. P., Baum, B. A., Riedi, J. C., and Frey, R. A.: The MODIS cloud products: algorithms and examples from Terra, IEEE T. Geosci. Remote, 41, 459–473, 2003. a
Rauber, R. M., Stevens, B., Ochs, H. T., Knight, C., Albrecht, B. A., Blyth, A. M., Fairall, C. W., Jensen, J. B., Lasher-Trapp, S. G., Mayol-Bracero, O. L., Vali, G., Anderson, J. R., Baker, B. A., Bandy, A. R., Burnet, E., Brenguier, J.-L., Brewer, W. A., Brown, P. R. A., Chuang, R., Cotton, W. R., Girolamo, L. D., Geerts, B., Gerber, H., Göke, S., Gomes, L., Heikes, B. G., Hudson, J. G., Kollias, P., Lawson, R. R., Krueger, S. K., Lenschow, D. H., Nuijens, L., O'Sullivan, D. W., Rilling, R. A., Rogers, D. C., Siebesma, A. P., Snodgrass, E., Stith, J. L., Thornton, D. C., Tucker, S., Twohy, C. H., and Zuidema, P.: Rain in Shallow Cumulus Over the Ocean: The RICO Campaign, B. Am. Meteorol. Soc., 88, 1912–1928, https://doi.org/10.1175/bams-88-12-1912, 2007. a, b
Rennó, N. O., Emanuel, K. A., and Stone, P. H.: Radiative-convective model with an explicit hydrologic cycle: 1. Formulation and sensitivity to model parameters, J. Geophys. Res.-Atmos., 99, 14429–14441, https://doi.org/10.1029/94JD00020, 1994. a
Romps, D. M.: An Analytical Model for Tropical Relative Humidity, J. Climate, 27, 7432–7449, https://doi.org/10.1175/JCLI-D-14-00255.1, 2014. a
Ruiz-Arias, J. A., Dudhia, J., Gueymard, C. A., and Pozo-Vázquez, D.: Assessment of the Level-3 MODIS daily aerosol optical depth in the context of surface solar radiation and numerical weather modeling, Atmos. Chem. Phys., 13, 675–692, https://doi.org/10.5194/acp-13-675-2013, 2013. a
Saleeby, S. M., Herbener, S. R., van den Heever, S. C., and L'Ecuyer, T.: Impacts of Cloud Droplet–Nucleating Aerosols on Shallow Tropical Convection, J. Atmos. Sci., 72, 1369–1385, https://doi.org/10.1175/JAS-D-14-0153.1, 2015. a, b
Schmeissner, T., Shaw, R. A., Ditas, J., Stratmann, F., Wendisch, M., and Siebert, H.: Turbulent Mixing in Shallow Trade Wind Cumuli: Dependence on Cloud Life Cycle, J. Atmos. Sci., 72, 1447–1465, https://doi.org/10.1175/jas-d-14-0230.1, 2015. a, b
Seethala, C. and Horvath, A.: Global assessment of AMSR-E and MODIS cloud liquid water path retrievals in warm oceanic clouds, J. Geophys. Res.-Atmos., 115, D13202, https://doi.org/10.1029/2009JD012662, 2010. a, b
Seifert, A. and Onishi, R.: Turbulence effects on warm-rain formation in precipitating shallow convection revisited, Atmos. Chem. Phys., 16, 12127–12141, https://doi.org/10.5194/acp-16-12127-2016, 2016. a
Seifert, A., Nuijens, L., and Stevens, B.: Turbulence effects on warm-rain autoconversion in precipitating shallow convection, Q. J. Roy. Meteor. Soc., 136, 1753–1762, https://doi.org/10.1002/qj.684, 2010. a, b
Short, D. A. and Nakamura, K.: TRMM Radar Observations of Shallow Precipitation over the Tropical Oceans, J. Climate, 13, 4107–4124, https://doi.org/10.1175/1520-0442(2000)013<4107:TROOSP>2.0.CO;2, 2000. a
Smalley, K. M. and Rapp, A. D.: The role of cloud size and environmental moisture in shallow cumulus precipitation, J. Appl. Meteorol. Clim., 59, 535–550, https://doi.org/10.1175/JAMC-D-19-0145.1, 2020. a, b, c, d, e, f, g, h, i, j, k, l
Squires, P.: The Microstructure and Colloidal Stability of Warm Clouds, Tellus, 10, 256–261, https://doi.org/10.1111/j.2153-3490.1958.tb02011.x, 1958. a
Stevens, D. E., Ackerman, A. S., and Bretherton, C. S.: Effects of domain size and numerical resolution on the simulation of shallow cumulus convection, J. Atmos. Sci., 59, 3285–3301, https://doi.org/10.1175/1520-0469(2002)059<3285:EODSAN>2.0.CO;2, 2002. a
Su, W., Schuster, G. L., Loeb, N. G., Rogers, R. R., Ferrare, R. A., Hostetler, C. A., Hair, J. W., and Obland, M. D.: Aerosol and cloud interaction observed from high spectral resolution lidar data, J. Geophys. Res.-Atmos., 113, D24202, https://doi.org/10.1029/2008JD010588, 2008. a
Sui, C.-H., Li, X., Yang, M.-J., and Huang, H.-L.: Estimation of Oceanic Precipitation Efficiency in Cloud Models, J. Atmos. Sci., 62, 4358–4370, https://doi.org/10.1175/JAS3587.1, 2005. a, b
Sui, C.-H., Li, X., and Yang, M.-J.: On the Definition of Precipitation Efficiency, J. Atmos. Sci., 64, 4506–4513, https://doi.org/10.1175/2007JAS2332.1, 2007. a, b
Tanelli, S., Durden, S. L., Im, E., Pak, K. S., Reinke, D. G., Partain, P., Haynes, J. M., and Marchand, R. T.: CloudSat's Cloud Profiling Radar After Two Years in Orbit: Performance, Calibration, and Processing, IEEE T. Geosci. Remote, 46, 3560–3573, https://doi.org/10.1109/TGRS.2008.2002030, 2008. a
Tao, W.-K., Johnson, D., Shie, C.-L., and Simpson, J.: The Atmospheric Energy Budget and Large-Scale Precipitation Efficiency of Convective Systems during TOGA COARE, GATE, SCSMEX, and ARM: Cloud-Resolving Model Simulations, J. Atmos. Sci., 61, 2405–2423, https://doi.org/10.1175/1520-0469(2004)061<2405:TAEBAL>2.0.CO;2, 2004. a
Tian, Y. and Kuang, Z.: Dependence of entrainment in shallow cumulus convection on vertical velocity and distance to cloud edge, Geophys. Res. Lett., 43, 4056–4065, https://doi.org/10.1002/2016gl069005, 2016. a, b, c
Tiedtke, M.: A Comprehensive Mass Flux Scheme for Cumulus Parameterization in Large-Scale Models, Mon. Weather Rev., 117, 1779–1800, https://doi.org/10.1175/1520-0493(1989)117<1779:ACMFSF>2.0.CO;2, 1989. a
Trivej, P. and Stevens, B.: The Echo Size Distribution of Precipitating Shallow Cumuli, J. Atmos. Sci., 67, 788–804, https://doi.org/10.1175/2009JAS3178.1, 2010. a, b, c
Twomey, S.: Pollution and the planetary albedo, Atmos. Environ., 8, 1251–1256, https://doi.org/10.1016/0004-6981(74)90004-3, 1974. a, b
van Zanten, M. C., Stevens, B., Nuijens, L., Siebesma, A. P., Ackerman, A. S., Burnet, F., Cheng, A., Couvreux, F., Jiang, H., Khairoutdinov, M., Kogan, Y., Lewellen, D. C., Mechem, D., Nakamura, K., Noda, A., Shipway, B. J., Slawinska, J., Wang, S., and Wyszogrodzki, A.: Controls on precipitation and cloudiness in simulations of trade-wind cumulus as observed during RICO, J. Adv. Model. Earth Sy., 3, M06001, https://doi.org/10.1029/2011MS000056, 2011. a
Vial, J., Dufresne, J.-L., and Bony, S.: On the interpretation of inter-model spread in CMIP5 climate sensitivity estimates, Clim. Dynam., 41, 3339–3362, https://doi.org/10.1007/s00382-013-1725-9, 2013. a
Waliser, D. E. and Gautier, C.: A Satellite-derived Climatology of the ITCZ, J. Climate, 6, 2162–2174, https://doi.org/10.1175/1520-0442(1993)006<2162:ASDCOT>2.0.CO;2, 1993. a
Wang, Y., Chen, Y., Fu, Y., and Liu, G.: Identification of precipitation onset based on Cloudsat observations, J. Quant. Spectrosc. Ra., 188, 142–147, https://doi.org/10.1016/j.jqsrt.2016.06.028, 2017. a, b
Watson, C. D., Smith, R. B., and Nugent, A. D.: Processes Controlling Precipitation in Shallow, Orographic, Trade Wind Convection, J. Atmos. Sci., 72, 3051–3072, https://doi.org/10.1175/JAS-D-14-0333.1, 2015. a, b
Witkowski, M., Vane, D., Livermore, T., Rokey, M., Barthuli, M., Gravseth, I. J., Pieper, B., Rodzinak, A., Silva, S., and Woznick, P.: CloudSat anomaly recovery and operational lessons learned, Tech. Rep., Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, California, USA, 2012. a
Witte, M. K., Morrison, H., Jensen, J. B., Bansemer, A., and Gettelman, A.: On the Covariability of Cloud and Rain Water as a Function of Length Scale, J. Atmos. Sci., 76, 2295–2308, https://doi.org/10.1175/JAS-D-19-0048.1, 2019. a
Wood, R. and Bretherton, C. S.: Boundary Layer Depth, Entrainment, and Decoupling in the Cloud-Capped Subtropical and Tropical Marine Boundary Layer, J. Climate, 17, 3576–3588, https://doi.org/10.1175/1520-0442(2004)017<3576:BLDEAD>2.0.CO;2, 2004. a, b
Wyant, M. C., Khairoutdinov, M., and Bretherton, C. S.: Climate sensitivity and cloud response of a GCM with a superparameterization, Geophys. Res. Lett., 33, L06714, https://doi.org/10.1029/2005GL025464, 2006. a
Wyszogrodzki, A. A., Grabowski, W. W., Wang, L.-P., and Ayala, O.: Turbulent collision-coalescence in maritime shallow convection, Atmos. Chem. Phys., 13, 8471–8487, https://doi.org/10.5194/acp-13-8471-2013, 2013. a
Zhang, G. and McFarlane, N. A.: Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian climate centre general circulation model, Atmos. Ocean, 33, 407–446, https://doi.org/10.1080/07055900.1995.9649539, 1995. a
Zhao, M.: An Investigation of the Connections among Convection, Clouds, and Climate Sensitivity in a Global Climate Model, J. Climate, 27, 1845–1862, https://doi.org/10.1175/JCLI-D-13-00145.1, 2014. a





