the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A predictive model for salt nanoparticle formation using heterodimer stability calculations
Sabrina Chee
Kelley Barsanti
Acid–base clusters and stable salt formation are critical drivers of new particle formation events in the atmosphere. In this study, we explore salt heterodimer (a cluster of one acid and one base) stability as a function of gas-phase acidity, aqueous-phase acidity, heterodimer proton transference, vapor pressure, dipole moment and polarizability for salts comprised of sulfuric acid, methanesulfonic acid and nitric acid with nine bases. The best predictor of heterodimer stability was found to be gas-phase acidity. We then analyzed the relationship between heterodimer stability and J4×4, the theoretically predicted formation rate of a four-acid, four-base cluster, for sulfuric acid salts over a range of monomer concentrations from 105 to 109 molec cm−3 and temperatures from 248 to 348 K and found that heterodimer stability forms a lognormal relationship with J4×4. However, temperature and concentration effects made it difficult to form a predictive expression of J4×4. In order to reduce those effects, heterodimer concentration was calculated from heterodimer stability and yielded an expression for predicting J4×4 for any salt, given approximately equal acid and base monomer concentrations and knowledge of monomer concentration and temperature. This parameterization was tested for the sulfuric acid–ammonia system by comparing the predicted values to experimental data and was found to be accurate within 2 orders of magnitude. We show that one can create a simple parameterization that incorporates the dependence on temperature and monomer concentration on J4×4 by defining a new term that we call the normalized heterodimer concentration, Φ. A plot of J4×4 vs. Φ collapses to a single monotonic curve for weak sulfate salts (difference in gas-phase acidity >95 kcal mol−1) and can be used to accurately estimate J4×4 within 2 orders of magnitude in atmospheric models.
- Article
(2996 KB) - Full-text XML
-
Supplement
(2721 KB) - BibTeX
- EndNote
Atmospheric aerosol particles represent the largest uncertainty in our understanding of global climate through their participation in cloud formation and the absorption and scattering of radiation (Kerminen et al., 2005; Kuang et al., 2009; Lohmann and Feichter, 2005; Merikanto et al., 2009; Spracklen et al., 2008). In particular, particle formation by nucleation is still not well understood and is difficult to represent in models (Kerminen et al., 2018). One of the dominant nucleation pathways is through salt formation, where the formation of a cluster is stabilized by the interactions between acid and base molecules, which enhances particle formation (Ball et al., 1999; Kirkby et al., 2011; Kürten et al., 2016; Nadykto and Yu, 2007; Nadykto et al., 2015; Wang et al., 2018). This nucleation pathway is particularly dominant in urban environments, where anthropogenic sources for acidic and basic gases are abundant (Ge et al., 2011; Kirkby et al., 2011; Qiu and Zhang, 2013; Weber et al., 1996; Wang et al., 2020). Although sulfuric acid (H2SO4, SA) is most commonly associated with atmospheric nucleation (Ball et al., 1999; Bzdek et al., 2012; Kirkby et al., 2011; Angelino et al., 2001; Weber et al., 1995), nitric acid (HNO3, NA) and methanesulfonic acid (CH3SO3H, MSA) have been also observed to be participants and may also play important roles in the initial stages of cluster growth (Afpel et al., 1979; Barsanti et al., 2009; Mäkelä et al., 2001; Smith et al., 2004, 2008; Weber et al., 1995), the latter of which we shall refer to henceforth as new particle formation (NPF).
Ammonia is the most abundant base in the atmosphere and its reaction with sulfuric acid has been well studied (Bzdek et al., 2010; Glasoe et al., 2015; Weber et al., 1996). Alkylamines have also garnered attention due to their high basicity and demonstrated ability to enhance NPF more than ammonia, despite their lower atmospheric abundance (Kurtén et al., 2008; Smith et al., 2010; Temelso et al., 2018; Waller et al., 2019; Kreinbihl et al., 2020).
Recently, computational efforts have focused on accurately representing the formation and growth of acid–base clusters (Smith et al., 2021). Myllys et al. (2016a) investigated the accuracy of the domain local pair natural orbital coupled cluster (DLPNO–CCSD(T)) method and found that it allows for the modeling of up to 10 molecules in a cluster, which had not been previously feasible with other highly accurate methods. The DLPNO–CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G** level of theory has become increasingly popular for modeling atmospheric processes such as cluster formation of sulfuric acid with ammonia, methylamine, dimethylamine, trimethylamine, guanidine, monoethanolamine, trimethylamine N-oxide and a variety of diamines (Myllys et al., 2016a; Ma et al., 2019; Xie et al., 2017; Myllys et al., 2020, 2018; Elm et al., 2016, 2017).
This large variety in systems studied has yielded insights into the factors that determine cluster formation and growth. Generally, the enhancing efficiency of the base on heterodimer stability and NPF is known to correlate with base strength, which has been attributed to a more favorable proton transfer and the formation of essentially nonvolatile ionic salts and has been shown to be generally true for the most abundant bases in the atmosphere: ammonia, methylamine, dimethylamine and trimethylamine (Almeida et al., 2013; Elm, 2017; Myllys et al., 2019b; Barsanti et al., 2009; Shen et al., 2020; Han et al., 2020; Kürten et al., 2014; Jen et al., 2014a). For many studies that observe both cluster and nanoparticle formation and growth, pKa has been often used as the metric for basicity. However, since pKa is, by definition, an aqueous measure of acidity, applying it to cluster and nanoparticle-sized systems does not take into account the drastically different environment. Indeed, in the study by Xie et al. (2017), monoethanolamine (pKa=9.5) enhanced NPF more than methylamine (pKa=10.6), despite methylamine being the stronger base according to their pKa values (Haynes, 2014). In that study, the lack of a base strength trend was attributed to the additional hydrogen bonding sites provided by the -OH group on monoethanolamine. In addition, we have recently studied the modeled formation rates of sulfuric acid and trimethylamine-N-oxide (TMAO), guanidine or dimethylamine, where TMAO, despite its lower basicity (pKa=4.7) to both guanidine (pKa=13.6) and dimethylamine (pKa=10.7), had similar formation rates to guanidine, which were much higher than those of dimethylamine (Myllys et al., 2020; Haynes, 2014). In these studies, pKa was insufficient to predict NPF enhancement.
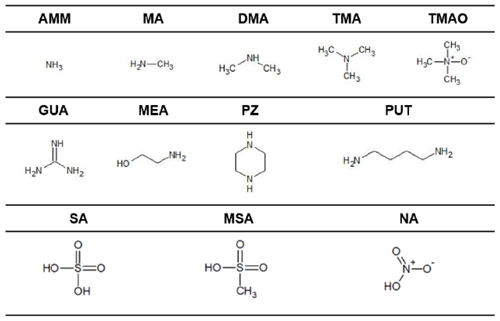
In this study, we aim to use these computational methods to identify what molecular properties predict heterodimer stability, or more specifically the Gibbs free energy of formation of the heterodimer (ΔGheterodimer), and, in turn, formulate a model to predict NPF rate. We specifically investigate the use of pKa in comparison to gas-phase acidity measures to predict proton transfer in the heterodimer as well as heterodimer stability. In addition, we examine if base vapor pressure has any correlation with heterodimer stability, as sulfuric acid is often cited to participate in NPF because of its low volatility and condensation onto clusters (Weber et al., 1996; Ball et al., 1999; Sipilä et al., 2010). Finally, we also calculate the dipole moment and polarizability of the studied base molecules to see if, in the absence of ions, they have any predictive capability of heterodimer stability. These observations extend to salts of SA, MSA and NA with nine bases: ammonia (AMM), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), trimethylamine N-oxide (TMAO), guanidine (GUA), monoethanolamine (MEA), putrescine (PUT) and piperazine (PZ) (Table 1).
In addition to these molecular properties, we further explore the relationship between heterodimer stability and NPF rate for SA salts. The goal of this work is to develop computationally efficient approaches for calculating NPF rate that can be applied to models that estimate the impacts of NPF on climate and air quality. We represent NPF rate as J4×4, the rate at which a cluster larger than four acid and four base molecules is formed. A cluster of this size can range in diameter from 1 to 1.5 nm, depending on the constituent acid and base. We analyze the relationship between heterodimer stability and the theoretically predicted J4×4 for sulfuric acid salts over a range of monomer concentrations from 105 to 109 molec cm−3 and temperatures from 248 to 348 K. The concentration of heterodimers was calculated from heterodimer stability, temperature and monomer concentrations for the case where acid and base monomer concentrations are approximately equal. This results in a parametrization for J4×4 as a function of heterodimer concentration that can be applied to any acid–base system. These results were compared to J1.7 rates measured at the CLOUD (Cosmics Leaving OUtdoor Droplets) chamber for SA–AMM salts. We note that the relationship between J4×4 and heterodimer concentration is not unique but depends on both temperature and monomer concentration. However, if the dependent variable is redefined as a term that we call the “normalized heterodimer concentration”, or Φ, then a simple monotonic relationship develops that can be used to predict J4×4 for weak salts of sulfuric acid, wherein their difference in gas-phase acidity (ΔGA) is greater than 95 kcal mol−1. We believe that this approach is generalizable to any acid–base system, allowing accurate predictions of NPF rates over a wide range of monomer concentration, temperature and ambient pressure.
Table 1Acid and base compounds in this study. Abbreviations are as follows: ammonia (AMM), methylamine (MA), dimethylamine (DMA), trimethylamine (TMA), trimethylamine N-oxide (TMAO), guanidine (GUA), monoethanolamine (MEA), putrescine (PUT) and piperazine (PZ), sulfuric acid (SA), methanesulfonic acid (MSA) and nitric acid (NA).
Two-component acid–base particle formation was studied by making systematic changes in temperature and concentration to understand the effects of simulation conditions and acid/base molecular properties on J4×4. Correlations of J4×4 with different molecular properties provided insight into the critical factors of cluster formation. Properties listed in Table 2 were examined as possible variables that may have a role in stabilizing clusters and enhancing particle formation.
Haynes (2014)Haynes (2014)Table 2Experimental and calculated properties examined in this study.

a Stull (1947), Aston et al. (1937, 1939), Swift and Hochanadel (1945), Matthews et al. (1950), EPISUITE v4.11. b Acidity of an acid HA or bases' conjugate acid BH+.
2.1 Cluster thermodynamics
In order to simulate cluster formation and growth, one must calculate accurate structures and thermochemical properties of neutral SA–base clusters up to the cluster size of four SA and four base molecules (4SA4base). Thermochemistry of clusters containing AMM, DMA, GUA and TMAO were taken from our previous studies (Myllys et al., 2018, 2019b, 2020). Thermochemistry of clusters with MEA, PUT and PZ were taken from a database (Elm, 2019), collected from original publications of Xie et al. (2017), Elm et al. (2017) and Ma et al. (2019). Available structures with MA and TMA were taken from Olenius et al. (2017) and, to be consistent with the level of theory used, structures were optimized and frequencies calculated at the ωB97X-D/6-31++G** level using rigid rotor–harmonic oscillator approximation, and electronic energies corrected at the DLPNO–CCSD(T)/aug-cc-pVTZ level with TightPNO, TightSCF and GRID4 keywords. In addition, for the missing structures, we performed a configurational sampling as explained in Kubečka et al. (2019). Briefly, to create the initial cluster structures, we used 3000 random guesses and 100 exploration loops, with a scout limit of four in the ABCluster program, and for each building block combination, we saved 300 of the lowest energy structures that were subsequently optimized by the tight-binding method GFN2-xTB with a very tight optimization criterion (Zhang and Dolg, 2016, 2015; Bannwarth et al., 2019). Based on the electronic energies, radius of gyration and dipole moments, we separated different conformers, which were then optimized using the ωB97X-D/6-31+G* level of theory. Based on the obtained electronic energies, we selected structures with a maximum of N kcal mol−1 from the lowest electronic energy (where N is the number of molecules in the cluster). For the lowest free energy clusters, Gibbs free-binding energies were calculated at the DLPNO–CCSD(T)/aug-cc-pVTZ//ωB97X-D/6-31++G** level of theory (Riplinger and Neese, 2013; Riplinger et al., 2013; Myllys et al., 2016a, b).
In addition of a full data set for SA–base clusters, we studied heterodimers of NA and MSA with the nine above-mentioned bases. The same quantum chemical methods were used as in SA–base calculations. In order to detect whether proton transfer was occurring in the heterodimer, the Molden program (Schaftenaar and Noordik, 2000) was used to visualize the global minimum structure. Gas-phase basicity and proton affinity values were computed using the same level of theory. Gaussian 16 RevA.03 (Frisch et al., 2016) was used to optimize geometries and calculate vibrational frequencies, and Orca version 4.2.1 (Neese, 2012) was used for single-point energy corrections.
2.2 Particle formation simulations
Theoretical methods allow us to perform particle formation simulations at conditions where particle formation rates are not experimentally measurable. This means that very low or high temperatures and vapor concentrations can be used to estimate J4×4. While some values in this range might not be directly “atmospherically relevant”, these calculations can lead to a deeper understanding of the non-linear behavior of nucleation as a function of vapor concentrations and/or temperature. It is also possible to study cluster formation of different compounds under identical conditions because there are no instrumental limitations or measurement biases. The calculated thermodynamic data sets for SA–base clusters were used as input in Atmospheric Cluster Dynamics Code (ACDC), the detailed theory of which is explained in McGrath et al. (2012). Briefly, the ACDC model simulated particle formation by solving the cluster distribution considering collision, evaporation and removal processes. The collision coefficients were computed from kinetic gas theory and the evaporation rates from quantum chemical Gibbs free energies assuming detailed balance. The model calculated the rate constants for each process among the population of clusters and vapor molecules and solved the discrete general dynamic equations for each cluster type. We have performed J4×4 simulations at temperatures of 248–348 K using SA and base vapor concentrations of [acid] = [base]=105–109 cm−3. Simulated J4×4 values are given in the Supplement. Simulations were performed for neutral clustering pathways at dry conditions due to computational (quantum chemical) restrictions. It should be noted that the cluster sampling procedure were performed at 298 K, and those structures and thermodynamic data (ΔH and ΔS) have been used in simulations at all temperatures. Thus, at lower or higher temperatures, slightly different global minimum structures might exist. Additionally, the simulation box size of four acid and four base molecules might be too small (i.e., critical cluster is outside of a box) at high temperatures and low concentrations. This leads overestimated particle formation rates, as discussed in Besel et al. (2020), where the effect of simulation settings was studied in the case of ammonia and sulfuric acid nucleation.
3.1 Heterodimer stability results
In the cluster formation process, the changes in enthalpy (ΔH) and entropy (ΔS) are always negative because hydrogen bond formation is an exothermic process in which the degrees of freedom are decreasing when isolated molecules become one entity. Gibbs free energy is calculated from ΔH and ΔS as a function of temperature by
where ΔG decreases as temperature decreases. Lower ΔGheterodimer values correspond to more stable heterodimers. However, while a negative ΔGheterodimer value indicates a spontaneous reaction in solution at standard conditions, heterodimer formation in the gas phase under atmospheric conditions also depends on the acid and base vapor concentrations. Table 3 presents enthalpies, entropies and Gibbs free energies of SA–base heterodimer formation at 298 K, and corresponding tables for MSA and NA are given in the Supplement. From these data, heterodimer stability can be calculated at other temperatures readily for all 27 salts studied here. Our calculated ΔGheterodimer value for SA–AMM indicates a less stable heterodimer than the SA–amines heterodimers, which is consistent with numerous other studies (Kurtén et al., 2008; Nadykto et al., 2011; Leverentz et al., 2013; Kupiainen et al., 2012). MA and MEA are the weakest heterodimer stabilizers among the amines; DMA, TMA and PZ are stronger and form approximately equally stable heterodimers. Of these nine bases, the most stable heterodimers are formed with TMAO, GUA and PUT.
Table 3Calculated enthalpy (ΔHheterodimer in kcal mol−1), entropy (ΔSheterodimer in cal (mol K)−1) and Gibbs free energy (ΔGheterodimer in kcal mol−1) for SA–base heterodimer formation at 298 K.
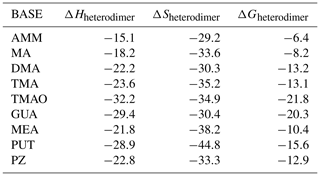
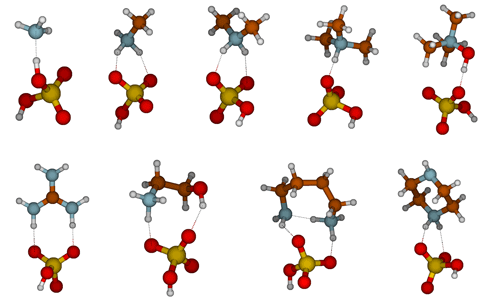
The molecular structures of SA–base heterodimers are presented in Fig. 1 and for MSA and NA heterodimers in the Supplement. AMM is the only base which is unable to accept a proton from SA in the heterodimer structure; the heterodimer is held together via one hydrogen bond between AMM and SA. All other base compounds accept a proton from SA and form an ion pair with the deprotonated SA, bisulfate. Protonated TMA and TMAO form only one hydrogen bond with bisulfate, whereas the other bases form two hydrogen bonds. In the SA–PUT heterodimer, PUT also forms an intramolecular hydrogen bond via its protonated and non-protonated amino groups.
3.2 Molecular properties that affect heterodimer stability (ΔGheterodimer)
3.2.1 Evaluation of gas-phase versus aqueous-phase acidity
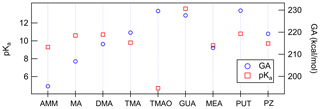
Figure 2 shows that gas-phase and aqueous-phase acidity values do not trend the same amongst the nine bases, wherein we define acidity of a base to be the acidity of the conjugate acid (i.e., the gas-phase or aqueous-phase acidity of NH3 refers to the acidity of the conjugate acid, ). For NR3 compounds, where R is either H or CH3, the gas-phase monomer acidities (GAs) directly follow the number of substitutions as AMM < MA < DMA < TMA. This means that when removing a proton from isolated gas-phase BH+ compound, the Gibbs free reaction energy has the largest value in the case of TMA. That is because the methyl groups stabilize cation formation by distributing the charge. In the aqueous-phase (pKa), however, the basicities have a different order: AMM < TMA < MA < DMA. This means that DMA has the largest proportion of protonated base cations in water solution. DMA has two methyl groups that facilitate protonation, and H-bond formation with water molecules provides additional stabilization. In the case of TMA, the hydration is very limited due to the steric hindrance of three methyl groups, and thus TMA has lower aqueous-phase basicity than DMA and MA. Because the basicity order of amines in the gas-phase directly follows the substitution order, the anomalous inversion of basicities in aqueous phase can be attributed to the stabilization effect of surrounding solvent molecules (Seybold and Shields, 2015).
In the gas phase, the strongest bases are, in decreasing order, PUT, TMAO and GUA, whereas in the aqueous phase the order is GUA, PUT and DMA. GUA is a very strong base both in gas and aqueous phases because its cationic form has six π electrons that are delocalized over the Y-shaped plane. This D3h-symmetric structure of guanidinium makes it extraordinarily stable. TMAO is very strong base in the gas phase because of its zwitterionic bond, where oxygen has a negative charge that strongly attracts H+. In the aqueous phase, polar solvent molecules are capable of stabilizing the zwitterionic bond in TMAO; thus, TMAO is the weakest base in the water solution. The reason why PUT is the strongest base in the gas phase is related to the change of its configuration between neutral and cationic forms. The neutral form of PUT is linear, but the cation is cyclic as the protonated and deprotonated amino groups are hydrogen bonded to each other as shown in Fig. 3. The Gibbs free energy difference between cyclic global minimum configuration and lowest acyclic local minimum configuration is 14.6 kcal mol−1, which is the additional stabilization caused by the H bond in gas phase. The gas basicity of PUT calculated based on the acyclic form would be 215.2 kcal mol−1, which is very close to that of DMA – and interestingly the pKa values of DMA and PUT are very close to each other. This could indicate that protonated PUT is in aqueous phase mainly in its acyclic form and is stabilized by H bonds with water molecules in the same manner as DMA.
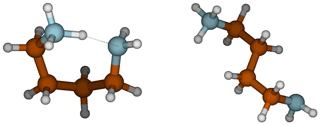
Figure 3Cyclic and acyclic configurations of protonated PUT. The lowest energy acyclic structure is 14.6 kcal mol−1 higher in free energy than the cyclic, global minimum structure.
As PUT and PZ are diamines, they can accept two protons and form cations. The PA and GA values for the second protonation reaction are significantly smaller than for the first protonation reaction: for PUT 130.6 and 125.2 kcal mol−1 and for PZ 121.0 and 113.3 kcal mol−1, respectively. While the PA and GA values can be measured for the first protonation reaction for each base, there was no experimental data found for the second protonation reaction. Experimental PA and GA values from Hunter and Lias (1998) are given in the Supplement, and good agreement with our calculated values is shown. PA, GA and pKa values are listed for SA, MSA and NA in the Supplement.
Because heterodimer stability has been shown to be a good proxy for J4×4, we have plotted the correlation between ΔGheterodimer and ΔGA and ΔpKa to probe the hypothesis that acid and base strength predict the formation of the heterodimer (Fig. 4). Here, ΔGA is defined to be the difference between the GA of the acid and the GA of the protonated base. And similarly the ΔpKa value is defined as the difference between the pKa of the acid and the pKa of the protonated base. All pKa values were taken from literature as bulk aqueous-phase dissociation constants, whereas GA values were calculated for this study. By definition, the larger the ΔGA, the less favorable the acid–base reaction is in the gas phase. Similarly, the more positive the ΔpKa, the less favorable the acid–base reaction is in the bulk aqueous phase.
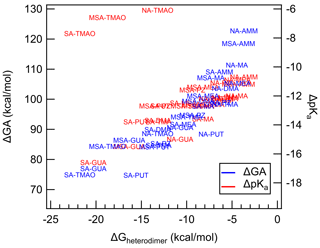
Figure 4Calculated ΔGA and ΔpKa plotted against ΔGheterodimer. Each data point represents an acid–base pair between either SA, NA or MSA with either AMM, MA, DMA, TMA, TMAO, GUA, MEA, PUT or PZ. Blue text represents ΔGA values, while red text represents ΔpKa values. Text markers are centered over the data point.
Over the observed ΔGA, as ΔGA increases, the less stable the heterodimer. The story is similar for ΔpKa: as ΔpKa increases, the heterodimer becomes less stable. However, for ΔpKa, TMAO salts seem to deviate drastically from the trend. Indeed, this is most likely because TMAO is more able to be stabilized by water molecules in the bulk aqueous phase and its proton exchange in the gas phase is not well represented by pKa (Myllys et al., 2021). Otherwise, the trend of ΔpKa matches up well with that of ΔGA. These results demonstrate that acid and base strength have a clear relationship with ΔGheterodimer and that ΔGA can be used in parameterizations of ΔGheterodimer. ΔGA is even less computationally intensive than ΔGheterodimer because it only models the removal of a proton from the original molecule in comparison to modeling the interactions of two molecules. In addition, GA values can be calculated for an array of acids and bases to get ΔGA for a larger combination of acids and bases rather than modeling ΔGheterodimer for each acid–base pair. For example, in this study, three acids and nine bases were studied: to calculate ΔGA for all combinations, only 12 reactions need to be simulated; in contrast, ΔGheterodimer would need to be calculated for each of the 27 salts. Because the GA values calculated here agree well with those experimentally determined in Hunter and Lias (1998), this modeling approach may be a simpler, more consistent method to predict GA values for yet-unstudied bases, including those that are atmospherically relevant.
Figure 5 illustrates how ΔGA is a better predictor of proton transfer in the gas phase than ΔpKa. In general, acid–base pairs with ΔGA of 103 kcal mol−1 or below undergo proton transfer, and thus ΔGA provides a threshold for cluster formation. This is consistent with the stronger trends between heterodimer stability and GA than heterodimer stability and pKa, the latter of which was affected by the solubilities of the acids and bases, which is not relevant to cluster formation and growth in the gas phase.
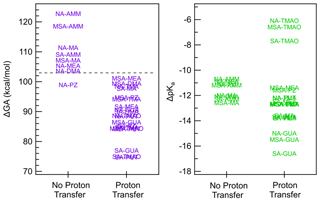
Figure 5ΔGA and ΔpKa values separated based on whether the heterodimer structure exhibits proton transfer. The dashed gray line on the ΔGA graph at 103 kcal mol−1 shows the cutoff point for proton transfer.
Interestingly, the NA–PZ salt is an anomaly in the cutoff for ΔGA in predicting proton transfer, with ΔGA value of 98.9 kcal mol−1, yet there is no proton transfer in the global minimum structures of heterodimer. However, there exists a local minimum structure in which proton transfer occurs that is only 1.8 kcal mol−1 higher in free energy than the global minimum. Figure 6 shows that in the proton transferred form of the NA–PZ pair, the second H-bond formation, which is needed to stabilize the anion–cation pair, is unfavorable because of the induced ring strain. Generally, NA is less likely to form two H bonds with a base than SA or MSA as the angle of O–N–O is 120∘, whereas the O–S–O angle in SA and MSA are 109∘, and therefore the ring strain would be high in NA salts (with an exception for GUA as shown in the Supplement). Overall, heterodimer proton transfer only occurs in clusters with a ΔGA smaller than 103 kcal mol−1 (NA–PUT) with the exception of NA–PZ. In general, this strengthens the idea that ΔGA is a better estimate of gas-phase reactivity than ΔpKa and emphasizes the importance of using thermodynamic constants that accurately represent the systems being studied.
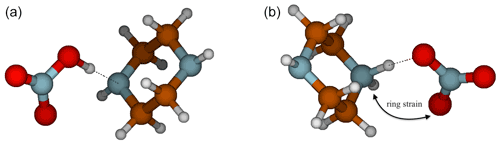
Figure 6Deprotonated (a) and protonated (b) conformers of PZ for the NA–PZ salt showing the ring strain necessary to form another intermolecular hydrogen bond.
ΔGA and ΔpKa values can and should be used in lab settings to gauge the likelihood of nucleation. For example, numerous studies, including those in our own lab, show that oxalic acid does not form particles with any of the methylated amines (MA, DMA, TMA) in a two-component system at 298 K (Arquero et al., 2017). The most negative ΔpKa value for these oxalic acid salts is −9.45, which is more positive than any of the systems studied here. Considering that NA–AMM does not form particles at room temperature even at high concentrations, its ΔpKa value of −10.7, or its ΔGA value of 122.65 kcal mol−1, could be used as a benchmark for predicting particle formation at room temperature. This cutoff is dependent on both temperature and the concentrations of precursor acid and base and should be viewed as a qualitative means for predicting NPF at room temperature. A more accurate means of estimating NPF rates that accounts for both temperature and precursor concentration is presented in Sect. 3.3.1. It is worth of mentioning that our model for using heterodimer stability to predict particle formation rates is valid only for acid–base clusters and not for organic acid–inorganic acid clusters. Thus, for instance a formation free energy value of oxalic acid–sulfuric acid heterodimer cannot be used to predict particle formation efficiency using any formula presented in this paper.
3.2.2 Factors that do not affect heterodimer stability
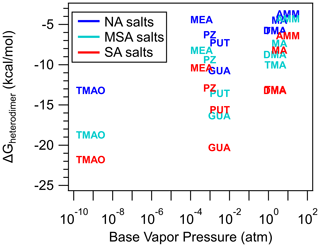
Figure 7 shows the relationship between base vapor pressure and heterodimer stability (ΔGheterodimer), which is plotted to explore the hypothesis that the volatility of the base, which is typically much higher than that of the accompanying acid, is a limiting factor that drives NPF. The lack of correlation suggests that acid–base reactive uptake, leading to salt formation, is the dominant mechanism and that volatility of the constituent acid and base plays a relatively minor role in heterodimer stability. However, volatility plays a key role in cluster and nanoparticle growth, wherein low volatility compounds in the atmosphere (i.e., H2SO4) are still very important for understanding NPF. It is important to emphasize that this lack of correlation between vapor pressure and heterodimer stability is only observable because the bases have different structural properties. Otherwise, if only AMM, MA, DMA and TMA were studied, then trends for vapor pressure and heterodimer stability would follow the trend of the more volatile base making a less stable heterodimer, which is untrue. Since the most well-studied bases in the atmosphere are AMM, MA, DMA and TMA, due to their relative abundance and contribution to NPF, it may be tempting to make conclusions on base behavior in NPF based solely on those four bases. However, these correlations – or lack thereof – highlight the importance of a wider breadth of study for us to better understand how bases behave in the atmosphere. This disappearance of a trend as more bases are included applies to the dipole moment and polarizability of the base as well (see Supplement). However, it is worth noting that while base vapor pressure does not affect heterodimer stability, it may have a larger role in determining particle composition as particles grow to a size that represents bulk systems (Lawler et al., 2016; Chen and Finlayson-Pitts, 2017; Myllys et al., 2020; Chee et al., 2019).
3.3 Heterodimer stability vs. J4×4
The stabilities of a heterodimer and other small clusters are known to affect the ability of a cluster to grow to a large aerosol particle (Almeida et al., 2013; Elm, 2017; Olenius et al., 2013). We now correlate ΔGheterodimer with calculated J4×4 for all nine bases with SA at varying conditions to observe the change in new particle formation rate over the temperature range of 248–348 K (Fig. 8a), and acid and base monomer concentrations from 105–109 molec cm−3 (Fig. 8b). For reference, a J of 0.1 cm−3 s−1 is also indicated, which can be viewed as a lower limit for observed atmospheric J4×4 (Kerminen et al., 2018). We emphasize that these some of the concentrations and temperatures might not be very common in the atmosphere. However, through these systematic changes in temperature and concentrations, we are able to gain insight into the predictors of cluster formation and growth.
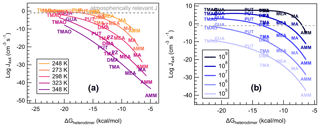
Figure 8Heterodimer stability (ΔGheterodimer) plotted against NPF rate (Jtheory) in varied conditions. (a) Vapor concentrations are constant: [acid] = [base] = 106 molec cm−3 at varying temperature: T=248, 273, 298, 323 and 348 K. (b) Temperature is constant: T=298 K at varying vapor concentrations: [acid] = [base] = 105, 106, 107, 108 and 109 molec cm−3. Text markers are centered over the data point.
Previously, theoretically calculated J4×4 for reactions of SA with DMA or AMM have been shown to be a good approximation for experimentally determined NPF rates observed at the CLOUD chamber (Myllys et al., 2019b). As Fig. 8a shows, J4×4 follows a lognormal relationship with ΔGheterodimer. This makes sense in that, for the most stable heterodimers like salts of TMAO and GUA, J4×4 approaches the kinetic limit and simply cannot form any faster. However, as heterodimer stability decreases, the evaporation of a heterodimer occurs faster than its collision with vapor molecules or other clusters, which results in a reduction in J4×4. In contrast, when temperature is held constant and base concentration is varied (Fig. 8b), the fit curve shape remains the same as J4×4 is shifted upwards with increasing starting concentrations until the kinetic limit is reached. The changing relationship between ΔGheterodimer and J4×4 with varying temperature can be attributed to the change in the thermodynamics of the reaction, while the shift in NPF rate with respect to ΔGheterodimer with varying concentration can be attributed to the relatively higher number of collisions in a shorter period of time. This behavior matches the relationship of J with temperature and concentration found in classical nucleation theory (Arstila et al., 1999; Trinkaus, 1983; Vehkamäki et al., 2002):
where J is the nucleation rate, Z is a kinetic pre-factor, W is the work of formation of the critical nucleus and p(1,2) and W(1,2) are the number concentration and cluster formation energy, respectively. J is directly proportional to heterodimer concentrations (p(1,2), which is related to the monomer concentrations of acid and base), whereas temperature contributes from within the exponential expression, which matches the behavior seen in Fig. 8.
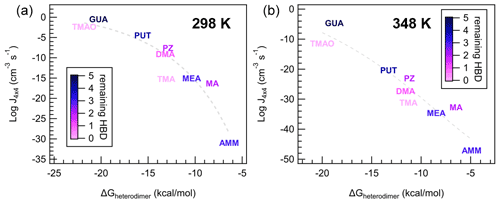
Figure 9Individual data points and trendlines from Fig. 8a colored according to the number of remaining hydrogen bond donors (HBDs) on the heterodimer. Panel (a) indicates data from the 298 K case and (b) indicates data from the 348 K case, at [acid] = [base] = 106 molec cm−3.
Interestingly, as temperature increases, this lognormal relationship transitions to linear, with a larger spread of data points around the trendline. Practically, this implies that ΔGheterodimer predicts theoretical J4×4 well at cold temperatures, but additional factors become more prominent at warmer temperatures. To understand what processes are important for J4×4, we scaled the color on each of the bases to the number of hydrogen bond donors (HBDs) remaining on the heterodimer after the proton was transferred at two temperatures (Fig. 9). The number of remaining HBDs was determined by counting the number of polar hydrogens on the base molecule minus the hydrogen donated by SA (if the proton transfer reaction occurred). Although other intermolecular H bonds exist, those were not subtracted because as the cluster grows, those bonds are broken as the base shifts to accommodate an additional molecule. SA salts with MA, TMAO, PUT and GUA salts all demonstrate this behavior, where the intermolecular bonds present in the heterodimer for MA, PUT and GUA are rearranged with each added molecule to the cluster (see the Supplement).
With respect to the lognormal relationship between J4×4 and ΔGheterodimer, TMA and TMAO, and to a lesser extent, DMA, are below the trendline, and they have zero to one remaining HBDs. In contrast, AMM, MA, MEA, PZ and PUT have two to four remaining HBDs and are closest to the trendline. GUA is the only molecule that has five remaining HBDs, and consistently has a higher NPF rate than the trendline suggests. This behavior can be attributed to cluster growth being slightly dependent on how well the next molecules can “stick” onto the existing cluster, where if there are more remaining HBDs on a cluster, it is easier and faster for the cluster to grow. It is interesting that MA has higher NPF rates than the trendline compared to MEA, PUT and PZ despite having either the same or one fewer HBDs, but this may be attributed to the bulkiness of the alkyl groups attached to those amines, which may block the remaining HBDs from participating in stabilizing the growing cluster.
These findings are notable in that ΔGheterodimer trends consistently with J4×4, and deviations from these trendlines can be attributed to structural differences in the base, where a base with more HBDs available on the heterodimer would have higher predicted NPF rates than the trendline, with the inverse also being true. However, the ΔGheterodimer vs. J4×4 relationship varies strongly with temperature and concentration as described above, and as such is not conducive to predicting J4×4, which we attempt to remedy in the following two sections.
3.3.1 A generalized parameterization to predict J4×4
In order to combine simulated particle formation rates at different conditions for all acid–base systems, we calculated the heterodimer concentration, which is a function of ΔGheterodimer, temperature and the concentration of the gaseous acid and base monomers. The stability of a heterodimer defines its theoretical maximum concentration at given conditions assuming the system is at equilibrium. Assuming mass balance for the heterodimer formation reaction leads to the following concentration under equilibrium conditions:
The equilibrium concentration of the heterodimer [heterodimer] is dependent both on the Gibbs free formation energy ΔGheterodimer (calculated at reference concentration , where Pref is defined as 1 atm and Cref is in units of molec cm−3), and on the monomer concentrations [acid] and [base]. Here, we use heterodimer concentration to estimate J4×4 under any (atmospherically relevant) temperature or concentration. However, as different acid–base systems form particles via different pathways depending on acid-to-base ratios, the NPF mechanism may change when either the acid or base is in excess. Thus, the derivations here are directly applicable at situations when acid and base concentrations are close to equal.
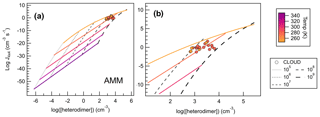
Figure 10Heterodimer concentration plotted against J4×4 for SA–AMM across 25 computational conditions (filled diamonds) from 248–348 K and monomer concentrations from 105–109 cm−3, where panel (a) shows the full set of conditions calculated for SA–AMM, and panel (b) shows a magnification of how CLOUD data compare to the computational dataset. Colored lines correlate to temperature trendlines that were drawn through all data points calculated at the same temperature. Dashed lines represent data points calculated at the same monomer concentrations. We calculated heterodimer concentrations for CLOUD data whose acid and base concentrations were within 50 % of each other according to Eq. (3). All CLOUD data points were collected at temperatures of either 248 or 273 K (colored circles corresponding to color scale) and with monomer concentrations between approximately 108–109 cm−3.
Figure 10a shows the temperature and concentration effects on heterodimer concentration for SA–AMM salts. As one would expect from Eq. (3), as concentration increases, heterodimer concentration increases by 2 orders of magnitude (as reflected in the [heterodimer] term). However, because temperature affects both the calculation of ΔGheterodimer and heterodimer concentration, this relationship is not as simple. In general, as temperature decreases, heterodimer concentration increases. As heterodimer concentration increases and temperature decreases, J4×4 also increases, though we begin to see J4×4 begin to saturate at 248 K and 109 cm−3. Through the use of heterodimer concentration, we have been able to combine the two factors, temperature and monomer concentration, into one term, where we can now use it to compare (or predict) J4×4.
To test the robustness of our calculations, heterodimer concentrations of CLOUD experiments were calculated using Eq. (3) and this study's calculated ΔGheterodimer values to compare our J4×4 calculations to CLOUD's measured J1.7 (Kirkby et al., 2011). Because heterodimer concentration can only be calculated for experiments run at approximately equal acid and base concentrations, all experiments that had more than a 50 % difference between monomer concentrations were excluded. A total of 21 measured J1.7 values met this criterion and are shown as filled circles in Fig. 10. When using the closest temperature trendlines (i.e., CLOUD data measured at 273 K was compared to 278 K model trend) to predict the CLOUD data, the difference between the predicted and measured J was within 2 orders of magnitude. On the other hand, if concentration trendlines were used to predict J (i.e., CLOUD vapor concentrations were near 108 molec cm−3 so the modeled 108 molec cm−3 trendline was used), differences of up to 4 orders of magnitude occurred. Trendline equations for SA–AMM are shown in the Supplement, as well as difference plots to show the accuracy of the trendlines as discussed.
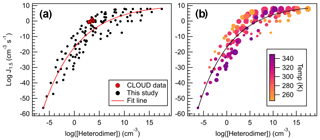
Figure 11Heterodimer concentration plotted against J4×4 for all calculated conditions for all sulfuric acid salts, wherein (a) all data are represented with black dots, and (b) data points are colored according to temperature and sized to reflect monomer concentrations (105–109 cm−3). Data were fitted to an exponential function, which can be found in the Supplement and Eq. (4).
All data calculated for this study are plotted in Fig. 11, which spans 100 K and 5 orders of magnitude in monomer concentrations. Indeed, concentration and temperature effects are minimized compared to the direct comparison between J4×4 and ΔGheterodimer (Fig. 8). Because more J4×4 values were calculated for AMM and GUA, data points were left as black points to avoid complicating the data. Data were fitted to give the following equation:
which can be used to approximate J4×4 rates given a calculated ΔGheterodimer, temperature and concentration. Because ΔGheterodimer requires significantly less computational power to calculate than J4×4, this trendline provides a method to quickly approximate J4×4 to within 10 orders of magnitude. This large spread of data is because of the wide range of temperatures and concentrations calculated in this study. In general, for concentrations less than 107 cm−3 and temperatures greater than 298 K, predicted J4×4 values are below the trendline. Similarly, for concentrations more than 107 cm−3 and temperatures greater than 298 K, predicted J4×4 values are above the trendline, which can be seen in Fig. 11b. It is important to keep in mind that this model was calculated in the absence of relative humidity, which may enhance J4×4 rates for those acid–base pairs with many free HBDs (Yang et al., 2018).
3.4 System-specific parameterization for weak bases using normalized heterodimer concentration (Φ)
Here, we attempt to reduce this uncertainty for nine salts of SA and further simplify the expression used to calculate J4×4. We accomplish this by incorporating heterodimer concentration and monomer concentrations into a new independent variable, the normalized heterodimer concentration, Φ:
It can be noted that Eq. (5) is same as Eq. (3) but with a square root around the concentration term.
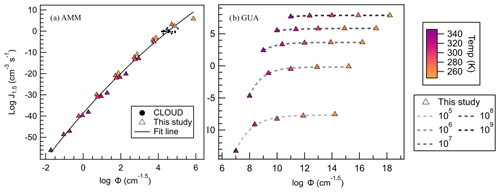
Figure 12(a) AMM–SA and (b) GUA–SA salts' J4×4 plotted against Φ, where triangles are colored according to the temperature of that point's calculation. CLOUD data are shown as black dots, and their Φ values were calculated according to Eq. (5). All trendlines used an exponential fit.
When applied to ammonia, a simple monotonic relationship between Φ and J4×4 becomes immediately apparent (Fig. 12a). Here, we observe that temperature affects the value of Φ minimally, and that the effects of temperature and concentration are incorporated in the dependent variable resulting in relatively minor data spread. Again, CLOUD Φ values were calculated for comparison, and CLOUD data are all predicted within 2 orders of magnitude of the best exponential fit to the data (fit equation available in the Supplement). The dispersion in J4×4 remains constant over all conditions explored.
As a contrast to the SA–AMM system, we also examined the behavior of the SA–GUA salt, a strong-acid and strong-base combination. Figure 12b shows that a monotonic relationship does not apply for such systems. In fact, at each concentration, J4×4 quickly reaches the kinetic limit and remains constant with temperature once monomer concentrations are above 107 cm−3. GUA is likely insensitive to changes in temperature because GUA is a strong base and forms more stable growing clusters than those of ammonia. In addition, at higher concentrations than 107 cm−3, collisions are occurring so quickly that if the cluster evaporates a monomer, another monomer is able to readily take its place. In this way, GUA salt J4×4 is largely dictated by monomer concentration rather than temperature.
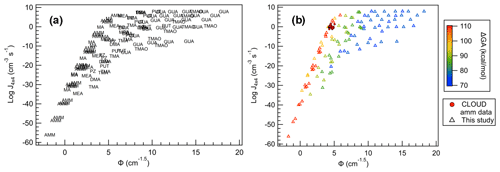
Figure 13All SA salts plotted with (a) base names as markers and (b) markers colored according to their ΔGA values. CLOUD observations are shown as filled circles.
When Φ is compared to J4×4 for all bases (Fig. 13a), we can immediately see that, in general, each base follows a unique trendline. Additionally, more bases follow the more monotonic behavior of SA–AMM than SA–GUA, and increase in the data dispersion follows increasing basicity. This is apparent when each of the base data points are colored according to their ΔGA values (Fig. 13b). In general, the larger ΔGA values correspond to more linear, less dispersed relationships between J4×4 and Φ, and as ΔGA decreases, J4×4 begins to saturate and dispersion increases. This change in behavior seems occur most dramatically as ΔGA decreases below 90 kcal mol−1 for the conditions shown here; however, it is likely for larger concentrations or lower temperatures, even the weakest of bases will saturate. The fact that ΔGA is directly linked to J4×4 saturation highlights how acid and base strength are crucial to understanding cluster formation and growth into particles.
Here, Φ can be used to predict J4×4 relatively accurately for specific bases, as demonstrated by the CLOUD J1.7 observations. However, for bases with ΔGA below approximately 90 kcal mol−1, prediction becomes more uncertain as the kinetic limit becomes easier to reach. This ΔGA cutoff of 90 kcal mol−1 means that the most abundant bases in the atmosphere, AMM, MA, DMA and TMA, are not expected to saturate in this model under atmospheric conditions and thus their J4×4 can be approximated relatively accurately using the results of this study. While this can only be used for experiments with acid and base monomer concentrations within 50 % of each other over the concentrations and temperatures studied, this is a powerful predictive tool using only the term, Φ, which only requires the calculation of one computational parameter, ΔGheterodimer.
Because each base has its own correlation between Φ and J4×4, the trendlines here cannot be generalized to bases that are not described. For those bases not described here, Eq. (4) should be used to approximate J4×4 to within 10 orders of magnitude.
Here, we have shown that heterodimer stability is largely predicted by the gas-phase acidity of the constituent acid and base across 27 acid–base pairs. In addition, we found that trends between heterodimer stability and physical properties such as volatility, dipole moment and polarizability did not hold for the wide variety of bases studied here, despite a trend existing for the smaller set of AMM, MA, DMA and TMA. We emphasize here the importance of studying a variety of bases with different structures and physical properties in order to make sure our understanding of salt NPF remains unbiased. We have also shown the relationship between J4×4 and heterodimer stability and how it was affected by temperature and concentration. We show that deviations from the lognormal relationship were attributed to the remaining HBDs available on the base molecule on the heterodimer. Then, in order to devise a simple model to predict J4×4, heterodimer stability values were used to calculate heterodimer concentrations. Indeed, the relationship between heterodimer concentration and J4×4 varied much less with changes to temperature and concentration compared to the relationship between ΔGheterodimer and J4×4. When compared to CLOUD experimental J1.7 data, the SA–AMM trendlines were able to predict J4×4 within 2 orders of magnitude when the closest temperature trendline was used. We found that heterodimer concentration can be parameterized into a expression that can predict J4×4. Because of this, the more difficult to calculate parameter of J4×4 could be replaced by the more easily acquired parameter of heterodimer stability. In addition, we have calculated a new parameter, the normalized heterodimer concentration, Φ, which minimized the effects of temperature and concentration even more than that of heterodimer concentration. We found that Φ reduces the complexity of calculating J4×4 by producing a single, monotonic trendline for SA–AMM, instead of 10 as it was for our calculations using heterodimer concentration as the independent variable. The ability of Φ to accurately predict J4×4 applies to SA salts of weaker bases, as stronger bases quickly saturated to reach the kinetic limit. This behavior was exhibited more strongly for salts that had a ΔGA value smaller than 90 kcal mol−1. It is important to emphasize that all of these predictions of J4×4 based on heterodimer stability is only possible for heterodimers made up of one acid and one base molecule, and not any other combination of molecules wherein the word heterodimer may apply.
In addition, we have presented a facile way of predicting J4×4 to within 10 orders of magnitude for salts of SA using a generalized parameterization (Eq. 4). We also present a method to more accurately predict J4×4 using the new parameter Φ for the nine SA salts studied here. It is important to note that, due to computational restrictions, all particle formation simulations are performed for two-component neutral clusters with an absence of relative humidity. Thus, theoretical results might vary compared to measured particle formation under atmospheric or laboratory conditions. Water enhancement of NPF is known to be greater with more available hydrogen bonding sites as shown in Yang et al. (2018), which may enhance the deviation from the lognormal relationship that was attributed to remaining HBDs on the heterodimer. The enhancing effect of ions on the NPF rate can be several orders of magnitude for systems where small neutral clusters are unstable (e.g., ammonium salts in this study) but is negligible with more stable clusters, like a strong acid and base pair (Myllys et al., 2019b). In addition, when more than two components are present at the same time in the atmosphere or even as a contaminant in laboratory, NPF can be largely enhanced due to synergistic effects (Glasoe et al., 2015; Jen et al., 2014b; Yu et al., 2012; Temelso et al., 2018; Myllys et al., 2019a). It is infeasible to explicitly study of all possible combinations of multi-component acid and base mixtures, but perhaps in the future the synergy between different compounds and the role of water vapor could be estimated using some simple parameters such as GA values and number of hydrogen bonding sites.
The Supplement contains the following information on the code and data used in this study:
-
monomer structures and properties,
-
methanesulfonic acid and nitric acid complexes,
-
acidity measures,
-
base dipole moment and polarizability,
-
boundary conditions in particle formation simulations,
-
simulated particle formation rates,
-
hydrogen bonding in clusters and
-
predictive expressions of J4×4 for ammonia.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-21-11637-2021-supplement.
NM performed the quantum chemical calculations and cluster formation simulations and initiated this study's design and supervised the data analysis process. SC curated, analyzed, investigated and visualized cluster data. SC prepared the bulk of the manuscript with contributions from NM, JNS and KB. JNS and KB acquired funding and supervised the project. All authors have read and agreed to the published version of the manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the CSC-IT Center for Science in Espoo, Finland, for computational resources.
This research has been supported by the Jenny ja Antti Wihurin Rahasto and the National Science Foundation (grant no. CHE-1710580).
This paper was edited by Ari Laaksonen and reviewed by two anonymous referees.
Afpel, B. R., Wall, S. M., Tokiwa, Y., and Haik, M.: Simultaneous nitric acid, particulate nitrate, and acidity measurements in ambient air, Atmos. Environ., 14, 549–554, 1979. a
Almeida, J., Schobesberger, S., Kurten, A., Ortega, I. K., Kupiainen-Maatta, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurten, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppa, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petaja, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipila, M., Stozhkov, Y., Stratmann, F., Tome, A., Trostl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamaki, H., and Kirkby, J.: Molecular Understanding of Sulphuric Acid–Amine Particle Nucleation in the Atmosphere, Nature, 502, 359–363, 2013. a, b
Angelino, S., Suess, D. T., and Prather, K. A.: Formation of Aerosol Particles from Reactions of Secondary and Tertiary Alkylamines: Characterization by Aerosol Time-of-Flight Mass Spectrometry, Environ. Sci. Technol., 35, 3130–3138, https://doi.org/10.1021/ES0015444, 2001. a
Arquero, K. D., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J.: Particle formation and growth from oxalic acid, methanesulfonic acid, trimethylamine and water: A combined experimental and theoretical study, Phys. Chem. Chem. Phys., 19, 28286–28301, https://doi.org/10.1039/c7cp04468b, 2017. a
Arstila, H., Korhonen, P., and Kulmala, M.: Ternary nucleation: Kinetics and application to water-ammonia-hydrochloric acid system, J. Aerosol Sci., 30, 131–138, https://doi.org/10.1016/S0021-8502(98)00033-0, 1999. a
Aston, B. J. G., Eidinoff, M. L., and Forster, W. S.: The Heat Capacity and Entropy, Heats of Fusion and Vaporization and the Vapor Pressure of Dimethylamine, J. Am. Chem. Soc., 61, 1539–1543, https://doi.org/10.1021/ja01875a061, 1939. a
Aston, J. G., Siller, C. W., and Messerly, G. H.: Heat Capacities and Entropies of Organic Compounds. III. Methylamine from 11.5 ∘K. To the Boiling Point. Heat of Vaporization and Vapor Pressure. The Entropy from Molecular Data, J. Am. Chem. Soc., 59, 1743–1751, https://doi.org/10.1021/ja01288a054, 1937. a
Ball, S. M., Hanson, D. R., Eisele, F. L., and McMurry, P. H.: Laboratory studies of particle nucleation: Initial results for H2SO4, H2O, and NH3 vapors, J. Geophys. Res.-Atmos., 104, 23709–23718, https://doi.org/10.1029/1999JD900411, 1999. a, b, c
Bannwarth, C., Ehlert, S., and Grimme, S.: GFN2-xTB – An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 15, 1652–1671, https://doi.org/10.1021/acs.jctc.8b01176, 2019. a
Barsanti, K. C., McMurry, P. H., and Smith, J. N.: The potential contribution of organic salts to new particle growth, Atmos. Chem. Phys., 9, 2949–2957, https://doi.org/10.5194/acp-9-2949-2009, 2009. a, b
Besel, V., Kubečka, J., Kurtén, T., and Vehkamäki, H.: Impact of Quantum Chemistry Parameter Choices and Cluster Distribution Model Settings on Modeled Atmospheric Particle Formation Rates, J. Phys. Chem. A, 124, 5931–5943, 2020. a
Bzdek, B. R., Ridge, D. P., and Johnston, M. V.: Size-Dependent Reactions of Ammonium Bisulfate Clusters with Dimethylamine, J. Phys. Chem. A, 114, 11638–11644, https://doi.org/10.1021/jp106363m, 2010. a
Bzdek, B. R., Zordan, C. A., Pennington, M. R., Luther, G. W., and Johnston, M. V.: Quantitative Assessment of the Sulfuric Acid Contribution to New Particle Growth, Environ. Sci. Technol., 46, 4365–4373, https://doi.org/10.1021/es204556c, 2012. a
Chee, S., Myllys, N., Barsanti, K. C., Wong, B. M., and Smith, J. N.: An Experimental and Modeling Study of Nanoparticle Formation and Growth from Dimethylamine and Nitric Acid, J. Phys. Chem. A, 123, 5640–5648, https://doi.org/10.1021/acs.jpca.9b03326, 2019. a
Chen, H. and Finlayson-Pitts, B. J.: New Particle Formation from Methanesulfonic Acid and Amines/Ammonia as a Function of Temperature, Environ. Sci. Technol., 51, 243–252, https://doi.org/10.1021/acs.est.6b04173, 2017. a
Elm, J.: Elucidating the Limiting Steps in Sulfuric Acid–Base New Particle Formation, J. Phys. Chem. A, 121, 8288–8295, https://doi.org/10.1021/acs.jpca.7b08962, 2017. a, b
Elm, J.: An Atmospheric Cluster Database Consisting of Sulfuric Acid, Bases, Organics, and Water, ACS Omega, 4, 10965–10974, https://doi.org/10.1021/acsomega.9b00860, 2019. a
Elm, J., Jen, C. N., Kurtén, T., and Vehkamäki, H.: Strong Hydrogen Bonded Molecular Interactions between Atmospheric Diamines and Sulfuric Acid, J. Phys. Chem. A, 120, 3693–3700, https://doi.org/10.1021/acs.jpca.6b03192, 2016. a
Elm, J., Passananti, M., Kurtén, T., and Vehkämaki, H.: Diamines Can Initiate New Particle Formation in the Atmosphere, J. Phys. Chem. A, 121, 6155–6164, https://doi.org/10.1021/acs.jpca.7b05658, 2017. a, b
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Petersson, G. A., Nakatsuji, H., Li, X., Caricato, M., Marenich, A. V., Bloino, J., Janesko, B. G., Gomperts, R., Mennucci, B., Hratchian, H. P., Ortiz, J. V., Izmaylov, A. F., Sonnenberg, J. L., Williams-Young, D., Ding, F., Lipparini, F., Egidi, F., Goings, J., Peng, B., Petrone, A., Henderson, T., Ranasinghe, D., Zakrzewski, V. G., Gao, J., Rega, N., Zheng, G., Liang, W., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Throssell, K., Montgomery Jr., J. A., Peralta, J. E., Ogliaro, F., Bearpark, M. J., Heyd, J. J., Brothers, E. N., Kudin, K. N., Staroverov, V. N., Keith, T. A., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A. P., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Millam, J. M., Klene, M., Adamo, C., Cammi, R., Ochterski, J. W., Martin, R. L., Morokuma, K., Farkas, O., Foresman, J. B., and Fox, D. J.: Gaussian16 Revision A.03, Gaussian Inc. Wallingford, CT, 2016. a
Ge, X., Wexler, A. S., and Clegg, S. L.: Atmospheric Amines – Part I. A Review, Atmos. Environ., 45, 524–546, https://doi.org/10.1016/j.atmosenv.2010.10.012, 2011. a
Glasoe, W., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D., McMurry, P., and Jen, C.: Sulfuric Acid Nucleation: An Experimental Study of the Effect of Seven Bases, J. Geophys. Res.-Atmos., 120, 1933–1950, 2015. a, b
Han, J., Wang, L., Zhang, H., Su, Q., Zhou, X., and Liu, S.: Determinant Factor for Thermodynamic Stability of Sulfuric Acid–Amine Complexes, J. Phys. Chem. A, 124, 10246–10257, https://doi.org/10.1021/acs.jpca.0c07908, 2020. a
Haynes, W. M.: CRC handbook of chemistry and physics, CRC press, 2014. a, b, c, d, e
Hunter, E. P. L. and Lias, S. G.: Evaluated Gas Phase Basicities and Proton Affinities of Molecules; Heats of Formation of Protonated Molecules, J. Phys. Chem. Ref. Data, 27, 413–656, https://doi.org/10.1063/1.555719, 1998. a, b
Jen, C. N., McMurry, P. H., and Hanson, D. R.: Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, https://doi.org/10.1002/2014JD021592, 2014a. a
Jen, C. N., McMurry, P. H., and Hanson, D. R.: Stabilization of Sulfuric Acid Dimers by Ammonia, Methylamine, Dimethylamine, and Trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, https://doi.org/10.1002/2014JD021592, 2014b. a
Kerminen, V.-M., Lihavainen, H., Komppula, M., Viisanen, Y., and Kulmala, M.: Direct observational evidence linking atmospheric aerosol formation and cloud droplet activation, Geophys. Res. Lett., 32, L14803, https://doi.org/10.1029/2005GL023130, 2005. a
Kerminen, V. M., Chen, X., Vakkari, V., Petäjä, T., Kulmala, M., and Bianchi, F.: Atmospheric new particle formation and growth: Review of field observations, Environ. Res. Lett., 13, 103003, https://doi.org/10.1088/1748-9326/aadf3c, 2018. a, b
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–433, https://doi.org/10.1038/nature10343, 2011. a, b, c, d
Kreinbihl, J. J., Frederiks, N. C., Waller, S. E., Yang, Y., and Johnson, C. J.: Establishing the structural motifs present in small ammonium and aminium bisulfate clusters of relevance to atmospheric new particle formation, J. Chem. Phys., 153, 034307, https://doi.org/10.1063/5.0015094, 2020. a
Kuang, C., McMurry, P. H., and McCormick, A. V.: Determination of cloud condensation nuclei production from measured new particle formation events, Geophys. Res. Lett., 36, 1–5, https://doi.org/10.1029/2009GL037584, 2009. a
Kubečka, J., Besel, V., Kurtén, T., Myllys, N., and Vehkamäki, H.: Configurational Sampling of Noncovalent (Atmospheric) Molecular Clusters: Sulfuric Acid and Guanidine, J. Phys. Chem. A, 123, 6022–6033, https://doi.org/10.1021/acs.jpca.9b03853, 2019. a
Kupiainen, O., Ortega, I. K., Kurtén, T., and Vehkamäki, H.: Amine substitution into sulfuric acid – ammonia clusters, Atmos. Chem. Phys., 12, 3591–3599, https://doi.org/10.5194/acp-12-3591-2012, 2012. a
Kürten, A., Jokinen, T., Simon, M., Sipilä, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tomé, A., Tröstl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid – Dimethylamine observed in real time under atmospheric conditions, P. Natl. Acad. Sci. USA, 111, 15019–15024, https://doi.org/10.1073/pnas.1404853111, 2014. a
Kürten, A., Bergen, A., Heinritzi, M., Leiminger, M., Lorenz, V., Piel, F., Simon, M., Sitals, R., Wagner, A. C., and Curtius, J.: Observation of new particle formation and measurement of sulfuric acid, ammonia, amines and highly oxidized organic molecules at a rural site in central Germany, Atmos. Chem. Phys., 16, 12793–12813, https://doi.org/10.5194/acp-16-12793-2016, 2016. a
Kurtén, T., Loukonen, V., Vehkamäki, H., and Kulmala, M.: Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 8, 4095–4103, https://doi.org/10.5194/acp-8-4095-2008, 2008. a, b
Lawler, M. J., Winkler, P. M., Kim, J., Ahlm, L., Tröstl, J., Praplan, A. P., Schobesberger, S., Kürten, A., Kirkby, J., Bianchi, F., Duplissy, J., Hansel, A., Jokinen, T., Keskinen, H., Lehtipalo, K., Leiminger, M., Petäjä, T., Rissanen, M., Rondo, L., Simon, M., Sipilä, M., Williamson, C., Wimmer, D., Riipinen, I., Virtanen, A., and Smith, J. N.: Unexpectedly acidic nanoparticles formed in dimethylamine–ammonia–sulfuric-acid nucleation experiments at CLOUD, Atmos. Chem. Phys., 16, 13601–13618, https://doi.org/10.5194/acp-16-13601-2016, 2016. a
Leverentz, H. R., Siepmann, J. I., Truhlar, D. G., Loukonen, V., and Vehkamäki, H.: Energetics of Atmospherically Implicated Clusters Made of Sulfuric Acid, Ammonia, and Dimethyl Amine, J. Phys. Chem. A, 117, 3819–3825, https://doi.org/10.1021/jp402346u, 2013. a
Lohmann, U. and Feichter, J.: Global indirect aerosol effects: a review, Atmos. Chem. Phys., 5, 715–737, https://doi.org/10.5194/acp-5-715-2005, 2005. a
Ma, F., Xie, H.-B., Elm, J., Shen, J., Chen, J., and Vehkamaki, H.: Piperazine enhancing sulfuric acid-based new particle formation: implications for the atmospheric fate of piperazine, Environ. Sci. Technol., 53, 8785–8795, 2019. a, b
Mäkelä, J. M., Ylikoivisto, S., Hiltunen, V., Seidl, W., Swietlicki, E., Teinilä, K., Sillanpää, M., Koponen, I. K., Paatero, J., Rosman, K., and Hämeri, K.: Chemical composition of aerosol during particle formation events in boreal forest, Tellus B, 53, 380–393, https://doi.org/10.3402/tellusb.v53i4.16610, 2001. a
Matthews, J., Sumner, J. F., and Moelwyn-Hughes, E.: The Vapour Pressures of Certain Liquids, T. Faraday Soc., 46, 797–803, 1950. a
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012. a
Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J., and Carslaw, K. S.: Impact of nucleation on global CCN, Atmos. Chem. Phys., 9, 8601–8616, https://doi.org/10.5194/acp-9-8601-2009, 2009. a
Myllys, N., Elm, J., Halonen, R., Kurtén, T., and Vehkamäki, H.: Coupled Cluster Evaluation of the Stability of Atmospheric Acid–Base Clusters with up to 10 Molecules, J. Phys. Chem. A, 120, 621–630, https://doi.org/10.1021/acs.jpca.5b09762, 2016a. a, b, c
Myllys, N., Elm, J., and Kurtén, T.: Density Functional Theory Basis Set Convergence of Sulfuric Acid-Containing Molecular Clusters, Comput. Theor. Chem., 1098, 1–12, https://doi.org/10.1016/j.comptc.2016.10.015, 2016b. a
Myllys, N., Ponkkonen, T., Passananti, M., Elm, J., Vehkamäki, H., and Olenius, T.: Guanidine: A Highly Efficient Stabilizer in Atmospheric New-Particle Formation, J. Phys. Chem. A, 122, 4717–4729, https://doi.org/10.1021/acs.jpca.8b02507, 2018. a, b
Myllys, N., Chee, S., Olenius, T., Lawler, M., and Smith, J. N.: Molecular-Level Understanding of Synergistic Effects in Sulfuric Acid–Amine–Ammonia Mixed Clusters, J. Phys. Chem. A, 123, 2420–2425, https://doi.org/10.1021/acs.jpca.9b00909, 2019a. a
Myllys, N., Kubečka, J., Besel, V., Alfaouri, D., Olenius, T., Smith, J. N., and Passananti, M.: Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 19, 9753–9768, https://doi.org/10.5194/acp-19-9753-2019, 2019b. a, b, c, d
Myllys, N., Ponkkonen, T., Chee, S., and Smith, J.: Enhancing Potential of Trimethylamine Oxide on Atmospheric Particle Formation, Atmosphere, 11, 35, https://doi.org/10.3390/atmos11010035, 2020. a, b, c, d
Myllys, N., Myers, D., Chee, S., and Smith, J. N.: Molecular properties affecting the hydration of acid–base clusters, Phys. Chem. Chem. Phys., 23, 13106–13114, https://doi.org/10.1039/D1CP01704G, 2021. a
Nadykto, A., Herb, J., Yu, F., Xu, Y., and Nazarenko, E.: Estimating the Lower Limit of the Impact of Amines on Nucleation in the Earth's Atmosphere, Entropy, 17, 2764–2780, https://doi.org/10.3390/e17052764, 2015. a
Nadykto, A. B. and Yu, F.: Strong Hydrogen Bonding between Atmospheric Nucleation Precursors and Common Organics, Chem. Phys. Lett., 435, 14–18, https://doi.org/10.1016/j.cplett.2006.12.050, 2007. a
Nadykto, A. B., Yu, F., Jakovleva, M. V., Herb, J., and Xu, Y.: Amines in the Earth's Atmosphere: A Density Functional Theory Study of the Thermochemistry of Pre-Nucleation Clusters, Entropy, 13, 554–569, 2011. a
Neese, F.: The ORCA Program System, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2, 73–78, https://doi.org/10.1002/wcms.81, 2012. a
Olenius, T., Kupiainen-Määttä, O., Ortega, I. K., Kurtén, T., and Vehkamäki, H.: Free Energy Barrier in the Growth of Sulfuric Acid–Ammonia and Sulfuric Acid–Dimethylamine Clusters, J. Chem. Phys., 139, 084312, https://doi.org/10.1063/1.4819024, 2013. a
Olenius, T., Halonen, R., Kurtén, T., Henschel, H., Kupiainen-Määttä, O., Ortega, I. K., Jen, C. N., Vehkamäki, H., and Riipinen, I.: New Particle Formation from Sulfuric Acid and Amines: Comparison of Mono-, Di-, and Trimethylamines, J. Geophys. Res.-Atmos., 122, 7103–7118, https://doi.org/10.1002/2017JD026501, 2017. a
Qiu, C. and Zhang, R.: Multiphase chemistry of atmospheric amines, Phys. Chem. Chem. Phys., 15, 5738, https://doi.org/10.1039/c3cp43446j, 2013. a
Riplinger, C. and Neese, F.: An Efficient and Near Linear Scaling Pair Natural Orbital Based Local Coupled Cluster Method, J. Chem. Phys., 138, 034106, https://doi.org/10.1063/1.4773581, 2013. a
Riplinger, C., Sandhoefer, B., Hansen, A., and Neese, F.: Natural Triple Excitations in Local Coupled Cluster Calculations with Pair Natural Orbitals, J. Chem. Phys., 139, 134101, https://doi.org/10.1063/1.4821834, 2013. a
Schaftenaar, G. and Noordik, J. H.: Molden: a pre-and post-processing program for molecular and electronic structures, J. Comput. Aid. Mol. Des., 14, 123–134, 2000. a
Seybold, P. G. and Shields, G. C.: Computational estimation of pKa values, WIREs Computational Molecular Science, 5, 290–297, https://doi.org/10.1002/wcms.1218, 2015. a
Shen, J., Elm, J., Xie, H.-B., Chen, J., Niu, J., and Vehkamäki, H.: Structural Effects of Amines in Enhancing Methanesulfonic Acid-Driven New Particle Formation, Environ. Sci. Technol., 54, 13498–13508, https://doi.org/10.1021/acs.est.0c05358, 2020. a
Sipilä, M., Berndt, T., Petäjä, T., Brus, D., Vanhanen, J., Stratmann, F., Patokoski, J., Mauldin III, R. L., Hyvärinen, A.-P., Lihavainen, H., and Kulmala, M.: The Role of Sulfuric Acid in Atmospheric Nucleation, Science, 327, 1243–1247, 2010. a
Smith, J. N., Moore, K. F., Mcmurry, P. H., and Eisele, F. L.: Atmospheric Measurements of Sub-20 nm Diameter Particle Chemical Composition by Thermal Desorption Chemical Ionization Mass Spectrometry, Aerosol Sci. Technol., 38, 100–110, https://doi.org/10.1080/02786820490249036, 2004. a
Smith, J. N., Dunn, M. J., VanReken, T. M., Iida, K., Stolzenburg, M. R., McMurry, P. H., and Huey, L. G.: Chemical composition of atmospheric nanoparticles formed from nucleation in Tecamac, Mexico: Evidence for an important role for organic species in nanoparticle growth, Geophys. Res. Lett., 35, L04808, https://doi.org/10.1029/2007GL032523, 2008. a
Smith, J. N., Barsanti, K. C., Friedli, H. R., Ehn, M., Kulmala, M., Collins, D. R., Scheckman, J. H., Williams, B. J., and McMurry, P. H.: Observations of aminium salts in atmospheric nanoparticles and possible climatic implications, P. Natl. Acad. Sci. USA, 107, 6634–6639, https://doi.org/10.1073/pnas.0912127107, 2010. a
Smith, J. N., Draper, D. C., Chee, S., Dam, M., Glicker, H., Myers, D., Thomas, A. E., Lawler, M. J., and Myllys, N.: Atmospheric clusters to nanoparticles: Recent progress and challenges in closing the gap in chemical composition, J. Aerosol Sci., 153, 105733, https://doi.org/10.1016/j.jaerosci.2020.105733, 2021. a
Spracklen, D. V., Carslaw, K. S., Kulmala, M., Kerminen, V.-M., Sihto, S.-L., Riipinen, I., Merikanto, J., Mann, G. W., Chipperfield, M. P., Wiedensohler, A., Birmili, W., and Lihavainen, H.: Contribution of particle formation to global cloud condensation nuclei concentrations, Geophys. Res. Lett., 35, L06808, https://doi.org/10.1029/2007GL033038, 2008. a
Stull, D. R.: Vapor Pressure of Pure Substances. Organic and Inorganic Compounds, Ind. Eng. Chem., 39, 517–540, https://doi.org/10.1021/ie50448a022, 1947. a
Swift, E. and Hochanadel, H. P.: The Vapor Pressure of Trimethylamine from 0 to 40∘, J. Am. Chem. Soc., 67, 880–881, https://doi.org/10.1021/ja01221a508, 1945. a
Temelso, B., Morrison, E. F., Speer, D. L., Cao, B. C., Appiah-Padi, N., Kim, G., and Shields, G. C.: Effect of Mixing Ammonia and Alkylamines on Sulfate Aerosol Formation, J. Phys. Chem. A, 122, 1612–1622, https://doi.org/10.1021/acs.jpca.7b11236, 2018. a, b
Trinkaus, H.: Theory of the nucleation of multicomponent precipitates, Phys. Rev. B, 27, 7372–7378, https://doi.org/10.1103/PhysRevB.27.7372, 1983. a
Vehkamäki, H., Kulmala, M., Napari, I., Lehtinen, K. E., Timmreck, C., Noppel, M., and Laaksonen, A.: An improved parameterization for sulfuric acid-water nucleation rates for tropospheric and stratospheric conditions, J. Geophys. Res.-Atmos., 107, AAC 3-1–AAC 3-10, https://doi.org/10.1029/2002JD002184, 2002. a
Waller, S. E., Yang, Y., Castracane, E., Kreinbihl, J. J., Nickson, K. A., and Johnson, C. J.: Electrospray Ionization-Based Synthesis and Validation of Amine-Sulfuric Acid Clusters of Relevance to Atmospheric New Particle Formation, J. Am. Soc. Mass Spectr., 30, 2267–2277, https://doi.org/10.1007/s13361-019-02322-3, 2019. a
Wang, C. Y., Jiang, S., Liu, Y. R., Wen, H., Wang, Z. Q., Han, Y. J., Huang, T., and Huang, W.: Synergistic Effect of Ammonia and Methylamine on Nucleation in the Earth's Atmosphere. A Theoretical Study, J. Phys. Chem. A, 122, 3470–3479, https://doi.org/10.1021/acs.jpca.8b00681, 2018. a
Wang, M., Kong, W., Marten, R., He, X.-C., Chen, D., Pfeifer, J., Heitto, A., Kontkanen, J., Dada, L., Kürten, A., Yli-Juuti, T., Manninen, H. E., Amanatidis, S., Amorim, A., Baalbaki, R., Baccarini, A., Bell, D. M., Bertozzi, B., Bräkling, S., Brilke, S., Murillo, L. C., Chiu, R., Chu, B., De Menezes, L.-P., Duplissy, J., Finkenzeller, H., Carracedo, L. G., Granzin, M., Guida, R., Hansel, A., Hofbauer, V., Krechmer, J., Lehtipalo, K., Lamkaddam, H., Lampimäki, M., Lee, C. P., Makhmutov, V., Marie, G., Mathot, S., Mauldin, R. L., Mentler, B., Müller, T., Onnela, A., Partoll, E., Petäjä, T., Philippov, M., Pospisilova, V., Ranjithkumar, A., Rissanen, M., Rörup, B., Scholz, W., Shen, J., Simon, M., Sipilä, M., Steiner, G., Stolzenburg, D., Tham, Y. J., Tomé, A., Wagner, A. C., Wang, D. S., Wang, Y., Weber, S. K., Winkler, P. M., Wlasits, P. J., Wu, Y., Xiao, M., Ye, Q., Zauner-Wieczorek, M., Zhou, X., Volkamer, R., Riipinen, I., Dommen, J., Curtius, J., Baltensperger, U., Kulmala, M., Worsnop, D. R., Kirkby, J., Seinfeld, J. H., El-Haddad, I., Flagan, R. C., and Donahue, N. M.: Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 581, 184–189, https://doi.org/10.1038/s41586-020-2270-4, 2020. a
Weber, R. J., McMurry, P. H., Eisele, F. L., and Tanner, D. J.: Measurement of Expected Nucleation Precursor Species and 3–500-nm Diameter Particles at Mauna Loa Observatory, Hawaii, J. Atmos. Sci., 52, 2242–2257, https://doi.org/10.1175/1520-0469(1995)052<2242:MOENPS>2.0.CO;2, 1995. a, b
Weber, R. J., Marti, J. J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A.: Measured Atmospheric New Particle Formation Rates: Implications for Nucleation Mechanisms, Chem. Eng. Commun., 151, 53–64, https://doi.org/10.1080/00986449608936541, 1996. a, b, c
Xie, H.-B., Elm, J., Halonen, R., Myllys, N., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Fate of Monoethanolamine: Enhancing New Particle Formation of Sulfuric Acid as an Important Removal Process, Environ. Sci. Technol., 51, 8422–8431, https://doi.org/10.1021/acs.est.7b02294, 2017. a, b, c
Yang, Y., Waller, S. E., Kreinbihl, J. J., and Johnson, C. J.: Direct Link between Structure and Hydration in Ammonium and Aminium Bisulfate Clusters Implicated in Atmospheric New Particle Formation, J. Phys. Chem. Lett., 9, 5647–5652, https://doi.org/10.1021/acs.jpclett.8b02500, 2018. a, b
Yu, H., McGraw, R., and Lee, S.-H.: Effects of Amines on Formation of Sub-3 nm Particles and Their Subsequent Growth, Geophys. Res. Lett., 39, L02807, https://doi.org/10.1029/2011GL050099, 2012. a
Zhang, J. and Dolg, M.: ABCluster: The Artificial Bee Colony Algorithm for Cluster Global Optimization, Phys. Chem. Chem. Phys., 17, 24173–24181, https://doi.org/10.1039/C5CP04060D, 2015. a
Zhang, J. and Dolg, M.: Global Optimization of Clusters of Rigid Molecules using the Artificial Bee Colony Algorithm, Phys. Chem. Chem. Phys., 18, 3003–3010, https://doi.org/10.1039/C5CP06313B, 2016. a