the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimating the potential cooling effect of cirrus thinning achieved via the seeding approach
Jiaojiao Liu
Cirrus thinning is a newly emerging geoengineering approach to mitigate global warming. To sufficiently exploit the potential cooling effect of cirrus thinning with the seeding approach, a flexible seeding method is used to calculate the optimal seeding number concentration, which is just enough to prevent homogeneous ice nucleation from occurring. A simulation using the Community Atmosphere Model version 5 (CAM5) with the flexible seeding method shows a global cooling effect of W m−2, which is approximately two-thirds of that from artificially turning off homogeneous nucleation ( W m−2). However, simulations with fixed seeding ice nuclei particle number concentrations of 20 and 200 L−1 show a weak cooling effect of W m−2 and warming effect of 0.35±0.28 W m−2, respectively. Further analysis shows that cirrus seeding leads to a significant warming effect of liquid and mixed-phase clouds, which counteracts the cooling effect of cirrus clouds. This counteraction is more prominent at low latitudes and leads to a pronounced net warming effect over some low-latitude regions. The sensitivity experiment shows that cirrus seeding carried out at latitudes with solar noon zenith angles greater than 12∘ could yield a stronger global cooling effect of −2.00 ± 0.25 W m−2. Overall, the potential cooling effect of cirrus thinning is considerable, and the flexible seeding method is essential.
- Article
(11848 KB) - Full-text XML
- BibTeX
- EndNote
Global warming has been proven by observations and has demonstrated many adverse effects on the environment and economy (Alexander et al., 2006; Feely et al., 2009; Lenton et al., 2019; Milne et al., 2009; Myhre et al., 2013). Saving energy and reducing greenhouse gas emissions are regarded as the primary strategies to counteract global warming, but these strategies may not be satisfactory (Fuss et al., 2018; IEA, 2019; Rogelj et al., 2015; Solomon et al., 2009). Therefore, geoengineering as a backup tool against climate warming has been receiving increasing attention in recent years (e.g., Gasparini et al., 2020; Jones et al., 2018; Keith and MacMartin, 2015; Lawrence et al., 2018; Lohmann and Gasparini, 2017; Macnaghten and Owen, 2011). Geoengineering is usually divided into two categories: carbon dioxide removal (CDR), which aims to permanently eliminate CO2 from the atmosphere, and solar radiation management (SRM), which proposes artificial intervention in the radiation budget (Caldeira et al., 2013; Heutel et al., 2018; Irvine et al., 2016; Kravitz et al., 2011; Vaughan and Lenton, 2011).
It is well known that cirrus clouds (ice clouds) typically reflect less incoming solar radiation but block more of Earth's outgoing longwave radiation, which warms our planet (Berry and Mace, 2014; Hong et al., 2016; Matus and L'Ecuyer, 2017). Cirrus thinning geoengineering, which allows more longwave radiation to escape to space, leading to a cooling effect on the planet, has been investigated as a new SRM approach and has been proposed in Geoengineering Model Intercomparison Project Phase 6 (GeoMIP6; Kravitz et al., 2015). In GeoMIP6, cirrus thinning is simulated by artificially increasing the sedimentation velocity of ice crystals (ICs). Simulations with this idealized approach indicate that cirrus thinning can produce the desired globally averaged cooling effect ( W m−2; e.g., Gasparini et al., 2017; Jackson et al., 2016; Muri et al., 2014). Considering the physical feasibility, simulating cirrus thinning by seeding with ice nuclei particles (INPs) is a better approach that can prevent homogeneous nucleation from occurring, thereby decreasing the number concentration of ICs (e.g., Gruber et al., 2019; Storelvmo and Herger, 2014; Storelvmo et al., 2013). Previous studies have shown that the cooling effect achieved via the seeding approach is sensitive to the seeding number concentration (Nseed), and even the strongest cooling effects are not strong enough (above −1.0 W m−2; e.g., Gasparini and Lohmann, 2016; Gasparini et al., 2017; Penner et al., 2015). Note that the Nseed used in these model simulations is fixed (usually in the range of 0.1 to 200 L−1), and the seeding strategy is uninterrupted (i.e., seeding occurs at every model time step). This study shows that the potential cooling effect of cirrus thinning cannot be sufficiently exploited due to the fixed seeding method. Moreover, a flexible seeding method is introduced to calculate the optimal Nseed (Nseedopt) based on the cirrus formation condition. The major purpose of this study is to estimate the potential cooling effect of cirrus thinning achieved via the seeding approach.
In this study, the cooling effects of cirrus thinning with different seeding methods are estimated. The paper is organized as follows. The flexible seeding method and its advantages are introduced in Sect. 2. This section also introduces the models and experimental designs that are employed. Comparisons of the cooling effects among different seeding methods and the main mechanism for the cooling effect are presented in Sect. 3. Finally, Sect. 4 presents the conclusions and discussion.
2.1 Cirrus thinning by seeding with ice nuclei particles
To better understand the seeding methods used in this study, it is necessary to briefly introduce the mechanism of cirrus thinning by seeding with INPs. In cirrus clouds, ICs are formed by homogeneous nucleation on soluble aerosol particles or heterogeneous nucleation on insoluble aerosol particles (Pruppacher and Klett, 1998). As ice-phase supersaturation (Si) rises, heterogeneous nucleation occurs earlier with the aid of INPs (i.e., insoluble aerosols). A few ICs (usually less than 100 L−1) are generated due to the relatively low number concentration of INPs. These newly formed ICs consume water vapor via deposition growth and then hinder Si from rising (DeMott et al., 2003; Hoose and Möhler, 2012; Lohmann et al., 2008). The threshold Si for homogeneous nucleation (Sihom) is relatively higher. Therefore, homogeneous nucleation cannot occur (i.e., Si cannot reach Sihom) if there are enough newly formed ICs from heterogeneous nucleation. However, homogeneous nucleation can produce a large number of ICs once it takes place (usually much greater than 100 L−1) because the number concentration of soluble aerosols in the upper troposphere is abundant (Barahona and Nenes, 2009; Kärcher, 2002). Therefore, seeding the clouds with a few INPs (usually less than 100 L−1) can prevent Si from reaching Sihom (Barahona and Nenes, 2009; Liu and Penner, 2005; McGraw et al., 2020). As a result, the in-cloud IC number concentration (Ni) is usually decreased, which decreases the cirrus cloud optical depth (i.e., cirrus thinning; Storelvmo and Herger, 2014; Storelvmo et al., 2013).
2.2 Models and parameterizations
In this study, we use a cloud parcel model to illustrate the impact of seeding on the ice nucleation process. The parcel model presents the IC formation process in an adiabatically rising air parcel with a constant updraft vertical velocity (W). Equations that describe the evolution of temperature (T), pressure (P), ice water mixing ratio (Qi), and ice particle size (Ri) can be found in Pruppacher and Klett (1998). The Si is diagnosed from the conservation equation of total water (i.e., water vapor plus ice water). The homogeneous nucleation rate (J) of sulfate aerosol particles is calculated based on the water activity (Koop et al., 2000). The heterogeneous frozen fraction of dust aerosol particles is calculated by the classical nucleation theory (CNT; following Barahona and Nenes, 2009) with a freezing efficiency of 1.0 (i.e., 100 % dust aerosols can act as INPs). More details about this cloud parcel model can be found in Shi and Liu (2016).
The climate model used in this study is version 5.3 of the Community Atmosphere Model (CAM5; Neale et al., 2012) with an improved ice nucleation parameterization that considers the effect of preexisting ICs and in-cloud vertical velocity fluctuations (Shi et al., 2015; Shi and Liu, 2016). The ice nucleation parameterization considers the competition between heterogeneous freezing on coarse-mode dust aerosol particles and homogeneous freezing on sulfate aerosol particles. Here, 100 % coarse-mode dust aerosols can act as INPs (Liu and Penner, 2005; Shi et al., 2015). Considering that sulfate aerosol particles may transform into a glassy state at very low temperatures (Murray et al., 2010), homogeneous nucleation is switched off below −68 ∘C (∼205 K), which could cause the modeled Ni to be close to observations (Shi et al., 2013). Note that there is no homogeneous nucleation in mixed-phase clouds (0 ∘C ∘C). The sub-grid vertical velocity (Wsub) derived from the turbulent kinetic energy is used to drive ice nucleation parameterization (Gettelman et al., 2010). The effect of preexisting ICs on ice nucleation is parameterized by reducing the vertical velocity for ice nucleation (Wpre; Barahona et al., 2014; Kärcher et al., 2006; Shi et al., 2015). In the improved ice nucleation parameterization, the newly nucleated IC number concentration (Ninuc) is calculated as a function of T, P, Si, Wsub, Wpre, the number concentration of coarse-mode dust aerosols (Ndust), and the number concentration of sulfate aerosols (Nsul). The cloud microphysics is represented by a two-moment scheme (Morrison and Gettelman, 2008).
2.3 Flexible seeding method
According to the mechanism of cirrus thinning caused by seeding with INPs, it is clear that Nseedopt is the minimal number concentration to prevent homogeneous nucleation from occurring. If Nseed is less than Nseedopt (underseeding), the newly formed ICs from heterogeneous nucleation are insufficient; thus, homogeneous nucleation still occurs and produces a relatively large Ninuc. If Nseed is larger than Nseedopt (overseeding), despite homogeneous nucleation being suppressed, Ninuc remains somewhat larger due to excessive Nseed. Notably, in terms of consuming water vapor and hindering homogeneous nucleation, it is clear that ICs are superior to INPs (Pruppacher and Klett, 1998; Kärcher et al., 2006; Shi et al., 2015). In other words, ICs can act as cheaper, cleaner, and safer INPs. Therefore, ICs are used as the seeding material in the flexible seeding method introduced by this study. The formulas for calculating Nseedopt are introduced in the Appendix. Nseedopt is a function of cirrus ambient conditions, aerosol properties, and radius of seeding ICs (Rseed). Rseed is a tunable given parameter. It is important to point out that seeding with ICs occurs only where homogeneous nucleation would occur without seeding (i.e., flexible seeding strategy).
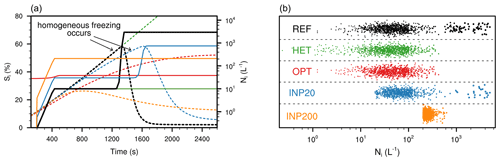
Figure 1Schematic diagram of different seeding methods, reference results without seeding (REF, black), pure heterogeneous nucleation (HET, green), seeding with the optimal number concentration of ICs (OPT, red), seeding with 20 L−1 of INPs (INP20, blue), and seeding with 200 L−1 of INPs (INP200, orange). The optimal seeding method uses ICs with the radius of 25 µm. Panel (a) shows simulation results from the parcel model with given initial conditions (P=330 hPa, T=220 K, W=0.3 m s−1, Ndust=10 L−1, and Nsul=500 000 L−1). The solid lines denote the total number concentrations of ICs in the parcel (Ni, units: L−1), which include the seeding ICs and the newly formed ICs, and the dashed lines denote ice supersaturation (Si, units: %). The arrows point to the beginning of homogeneous nucleation. Panel (b) shows the Ni from ice nucleation parameterizations driven by the same 1000 datasets of input variables (one dot denotes one offline result), which are sampled from the CAM5 simulation. The horizontal coordinate axis is Ni, and the vertical coordinate axis is meaningless.
Figure 1a illustrates the advantage of Nseedopt. Parcel model results show that without seeding (REF, black lines), heterogeneous nucleation takes place at Si>10 % and produces 10 L−1 of ICs. Because these newly formed ICs are too few in number to prevent Si from increasing, homogeneous nucleation takes place at Si>Sihom (∼56 %) and produces a large number of ICs (2937 L−1). The final Ni (i.e., Ninuc) is 2947 L−1. In the simulation with pure heterogeneous nucleation (HET, green lines), the final Ni is 10 L−1. In the simulation with seeding of 28 L−1 (Nseedopt is 28 L−1) of ICs (OPT, red lines), the newly formed ICs from heterogeneous nucleation (10 L−1) and seeding ICs are just enough to prevent Si from reaching Sihom. The final Ni (i.e., Ninuc+Nseedopt) is 38 L−1. In the simulation with seeding of 20 L−1 of coarse-mode dust aerosol particles (INP20, blue lines, underseeding), heterogeneous nucleation produces more ICs (30 L−1) than the REF simulation. However, homogeneous nucleation still occurs and produces 715 L−1 of ICs. The final Ni is 745 L−1. In the simulation with seeding of 200 L−1 of coarse-mode dust aerosol particles (INP200, orange lines, overseeding), the newly formed ICs from heterogeneous nucleation (210 L−1) are large enough to prevent homogeneous nucleation from occurring. The final Ni is 210 L−1. Overall, seeding with INPs/ICs can lead to a lower Ni, and Ni from the OPT simulation is closest to the HET simulation.
Additionally, we run large-ensemble ice nucleation offline experiments to show the advantage of the flexible seeding strategy (Fig. 1b). A total of 1000 cirrus formation cases are sampled from the CAM5 simulation without seeding. The input variables (T, P, Si, Wsub, Ndust, and Nsul) used to drive ice nucleation parameterization in CAM5 are used to drive these offline experiments. Homogeneous nucleation events account for 7.4 % (i.e., 74 homogeneous nucleation cases). Five experiments corresponding to the parcel model simulations are carried out. Each experiment is driven by the same 1000 cases. In the two fixed seeding experiments (i.e., the INP20 and INP200 experiments), INPs (i.e., coarse-mode dust aerosols) are added for all 1000 cases, even if there was no homogeneous nucleation (i.e., uninterrupted seeding strategy). Compared with the REF experiment, all large Ni cases (dots with Ni>500 L−1) totally vanish in the HET experiment because only heterogeneous nucleation events occur. The Ni distribution in the OPT experiment is similar to that in the HET experiment, except for some low Ni (<10 L−1) cases. In the INP20 experiment, there are some large Ni cases because homogeneous nucleation still occurs in 36 cases. In the INP200 experiment, there are no large Ni cases because almost all homogeneous nucleation cases are suppressed, whereas the Ni from all cases is greater than 200 L−1 due to the large Nseed. In short, the flexible seeding method is better than the fixed seeding method.
2.4 Experimental setups
CAM5 model experiments are carried out to estimate the cooling effect of cirrus thinning. Table 1 summarizes all the experiments performed in this study. The REF, HET, OPT, INP20, and INP200 experiments correspond to the offline experiments discussed above. In the INP20 and INP200 experiments, the Ndust used for driving ice nucleation parameterization (cirrus clouds only) increases by 20 and 200 L−1 (i.e., the Ndust from the aerosol module plus 20 and 200 L−1), respectively. Note that the seeding INPs are added at every model time step but only impact the ice nucleation process (i.e., theNdust in the aerosol module is not influenced by the seeding INPs). In the OPT experiment, the seeding ICs are directly added into the cloud microphysics scheme. As a result, these seeding ICs would affect both the ice nucleation process and other cloud microphysics processes. Notably, it is unnecessary to consider water conservation because the seeding ICs are made from ambient atmospheric water vapor.
Additionally, we set up two sensitivity experiments for the flexible seeding method (Table 1). First, the tunable parameter Rseed is investigated. Rseed is 10 µm in the R10 experiment, whereas Rseed is 50 µm in the OPT experiment. Second, the seeding region is investigated. Cirrus thinning also leads to more incoming solar radiation (warming effect), which counteracts the cooling effect from more outgoing longwave radiation, especially for the low solar noon zenith angle regions (Storelvmo and Herger, 2014; Storelvmo et al., 2014). Furthermore, this study also finds that the cooling effect over low-latitude regions is less susceptible to cirrus seeding for other reasons (see Sect. 3.1). Thus, another sensitivity experiment with a specific geographical target (i.e., the GT experiment) is examined. Similar to the study of Storelvmo and Herger (2014), cirrus seeding is only carried out at latitudes where the solar noon zenith angles are greater than 12∘, which compose approximately 80 % of the Earth's surface.
In this study, all CAM5 experiments are atmosphere-only simulations with the same prescribed climatological ocean surface conditions. All experiments run for 11 model years at a horizontal resolution of and a model time step of 30 min. The first year is considered to be a spin-up period, and the last 10 years are used in the analyses. The standard deviations, which are estimated from the averages of each year, are used for variability analysis.
3.1 Comparisons among different seeding methods
First, we analyze the impact of cirrus seeding on the ice nucleation process (Fig. 2). The contribution of homogeneous nucleation to cirrus formation (Fhom) is essential for the radiative properties of cirrus clouds (Jensen et al., 2013; Shi and Liu, 2016). Here, Fhom is quantified as the ratio of the homogeneous nucleation occurrence frequency to the ice nucleation occurrence frequency (Fnuc). In the REF experiment, Fhom is low near dust source regions (e.g., the Saharan Desert and Arabian Desert). Fhom is high over other tropical regions due to the large Wsub (not shown). Generally, Fhom is low (<20 %) in most regions, which is consistent with observations that heterogeneous nucleation is the dominant mechanism for cirrus formation (Cziczo et al., 2013; Jensen et al., 2013). Although Fhom from the INP20 experiment is decreased substantially, there are still some homogeneous freezing events (3.38 % of all cirrus and 5.20 % at 233 hPa). In the INP200 experiment, there are only a few homogeneous freezing events (0.42 % of all cirrus and 0.63 % at 233 hPa) due to the larger Nseed of INPs. Both the INP20 and INP200 experiments show that the averaged number concentrations of ICs produced from heterogeneous freezing events (Nihet) are increased. This increase would lead to more intense competition between homogeneous and heterogeneous nucleation. As a result, the averaged number concentrations of ICs produced from homogeneous freezing events (Nihom) from the INP20 and INP200 experiments are substantially decreased compared with the number concentration of ICs from the REF experiment. As expected, Fhom and Nihom are zero from the HET and OPT experiments. It is noteworthy that a large number of small ICs (e.g., homogeneous nucleation occurs) would exist for a long time, consuming water vapor via deposition growth and then hindering subsequent ice nucleation (Shi et al., 2015). Therefore, Fnuc from the REF experiment is very low (<4 %) in most regions, and Fnuc from the cirrus thinning experiments (i.e., the HET, OPT, INP20, and INP200 experiments) is obviously increased due to the decreases in Fhom and Nihom. This finding suggests that the impact of cirrus seeding (including the HET experiment) on the ice nucleation process is very complicated. There is not only the direct instantaneous impact but also the indirect impact caused by subsequent changes.
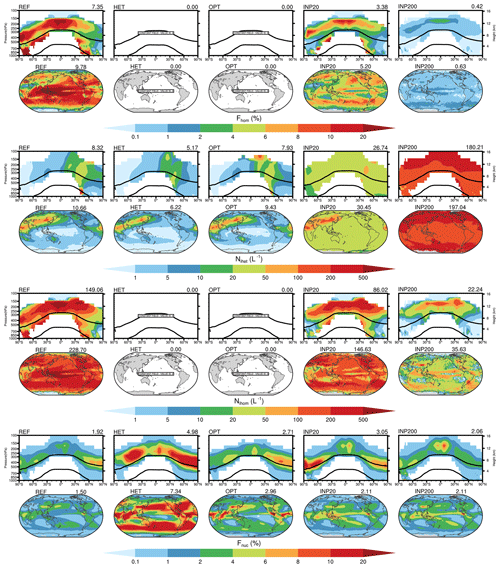
Figure 2Annual zonal mean and 233 hPa spatial distribution of the homogeneous nucleation contribution to cirrus formation (Fhom, first panel), averaged IC number concentration produced from heterogeneous freezing events (Nihet, second panel) and from homogeneous freezing events (Nihom, third panel), and ice nucleation occurrence frequency (Fnuc, last panel). Experimental names are shown in the upper left corner, and global mean values are shown in the upper right corner. The two black lines are 0 and −37 ∘C isotherms. The results are sampled from model grids where Fnuc is greater than 0.1 %.
Figure 3 shows the impact of cirrus seeding on cloud properties. In the cloud microphysics scheme, the in-cloud IC number concentration (i.e., Ni) mainly depends on the ice nucleation process (i.e., Ninuc, Shi et al., 2015; Shi and Liu, 2016). Therefore, the annual averaged Ni from the cirrus thinning experiments is decreased significantly in most cirrus clouds (ice clouds), especially from the HET and OPT experiments. The Ni from the INP20 experiment is not significantly decreased over the tropical regions because there are still many homogeneous freezing events (Fhom and Nihom in Fig. 2). Compared with the REF experiment, Ni from the INP200 experiment is obviously increased in the tropical upper troposphere and the polar troposphere. This increase occurs because the homogeneous nucleation contribution (i.e., ) from the REF experiment is relatively low, and the heterogeneous nucleation contribution (i.e., Fnuc×Nihet) from the INP200 experiment increases dozens of times over these regions (Fig. 2). Similarly, the vertically integrated Ni (i.e., column Ni) from the HET and OPT experiments is significantly decreased in most regions. In contrast, the changes in column Ni from the INP20 and INP200 experiments are not notable. The changes in ice water content (IWC) and ice water path (IWP) from the INP20 and INP200 experiments are also non-significant in most regions. In the HET and OPT experiments, both Ni and IWC in the middle and lower mixed-phase clouds are obviously increased. The main reason might be that the deep convective activity becomes more vigorous because cirrus thinning reduces atmospheric stability via the radiative budget (not shown). The ratio of ice to total cloud condensate detrained from the convective parameterizations is a linear function of temperature between −40 and −10 ∘C (Morrison and Gettelman, 2008). Furthermore, the ICs can grow through the Bergeron process in mixed-phase clouds (Morrison and Gettelman, 2008). This might be the reason that the relative increases in IWC in mixed-phase clouds are stronger than the relative increases in Ni. Although the increases in IWC in mixed-phase clouds counteract the decreases in IWC in ice clouds to some extent, the IWP is still significantly decreased in most regions from the HET and OPT experiments. However, the IWP is significantly increased over a few regions (e.g., central Africa and northern Brazil) because the decreases in IWC in ice clouds are slight and even smaller than the increases in IWC in mixed-phase clouds over those regions (not shown). The changes in liquid water content (LWC) and liquid water path (LWP) from the INP20 and INP200 experiments are non-significant in most regions, whereas both the LWC and LWP from the HET and OPT experiments are significantly decreased in some low- and mid-latitude regions. One possible reason is that falling ICs accrete by riming of cloud droplets (Gasparini et al., 2017; Storelvmo et al., 2013), and the conversion efficiency of cloud droplets to precipitation is increased. Another possible reason is that cirrus thinning leads to stronger convective precipitation (Kristjánsson et al., 2015; Storelvmo and Herger, 2014), which would consume more cloud water (Gasparini et al., 2017; Rapp et al., 2011). The above analyses are in agreement with previous studies, which show that cirrus thinning might result in complex impacts on mixed-phase and liquid clouds (Gasparini and Lohmann, 2016; Gruber et al., 2019).
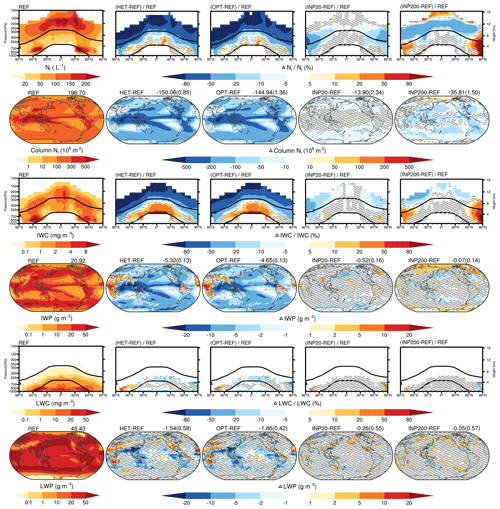
Figure 3Annual zonal mean of in-cloud IC number concentration (Ni, first row), ice water content (IWC, third row), and liquid water content (LWC, fifth row) from the REF experiment (first column) and the relative changes from the HET, OPT, INP20, and INP200 experiments with respect to the REF experiment (second to fifth columns). The corresponding spatial distributions of vertically integrated Ni (column Ni, second row), ice water path (IWP, fourth row), and liquid water path (LWP, sixth row) from the REF experiment and the differences (“Δ”) from the HET, OPT, INP20, and INP200 experiments with respect to the REF experiment. Global mean values are shown in the upper right corner, and the standard deviations calculated from the difference of each year for 10 years are shown in brackets. The shadow denotes that the differences between two experiments are not significant at the 95 % level based on Student's t test.
Table 2Global annual mean cloud radiative effect from all experiments∗. The corresponding standard deviations calculated from the difference of each year for 10 years are shown in brackets.
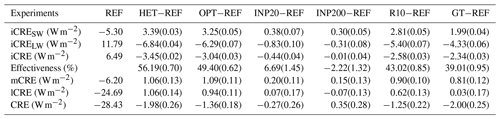
∗ Shown are the ice cloud shortwave radiative effect (iCRESW), ice cloud longwave radiative effect (iCRELW), ice cloud radiative effect (iCRE), cirrus seeding effectiveness (Effectiveness), mixed-phase cloud radiative effect (mCRE), liquid cloud radiative effect (lCRE), and the all cloud radiative effect (CRE).
The cooling effect of cirrus thinning is usually quantified by the anomaly in cloud radiative effect (ΔCRE; Mitchell and Finnegan, 2009; Storelvmo and Herger, 2014). For convenience of expression, “Δ” indicates the difference between the cirrus thinning experiments and the REF experiment. In addition to the model standard diagnostics of CRE, CRE from ice clouds (iCRE), mixed-phase clouds (mCRE), and liquid clouds (lCRE) is also diagnosed separately. Note that cirrus clouds are clouds at temperatures below −37 ∘C and above 440 hPa (Boucher et al., 2013), so we refer to them as ice clouds in this study. Furthermore, the cooling radiative effect is quantified by a negative value, even if it has been declared a cooling effect. For convenience, the global annual mean cloud radiative effects from all experiments are listed in Table 2.
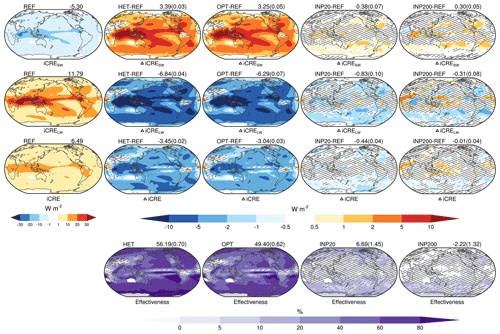
Figure 4The annual mean spatial distribution of ice cloud shortwave radiative effect (iCRESW, first row), ice cloud longwave radiative effect (iCRELW, second row), ice cloud radiative effect (iCRE = iCRESW+iCRELW, third row), and cirrus seeding effectiveness (fourth row) from the REF experiment (first column) and the differences (“Δ”) from the HET, OPT, INP20, and INP200 experiments with respect to the REF experiment (second to fifth columns). Note that regions with absolute value of iCRE < 1.0 W m−2 from the REF experiment are excluded for calculating cirrus seeding effectiveness. Global mean values are shown in the upper right corner, and the corresponding standard deviations calculated from the difference of each year for 10 years are shown in brackets. The shadow denotes that the differences between two experiments are not significant at the 95 % level based on Student's t test.
The iCRE and its shortwave (iCRESW) and longwave (iCRELW) components are analyzed first (Fig. 4). The globally averaged iCRE from the REF experiment is 6.49 W m−2 (net warming effect), with a shortwave component (iCRESW) of −5.30 W m−2 (cooling effect) and a longwave component (iCRELW) of 11.79 W m−2 (stronger warming effect). This globally averaged iCRE is within the possible range reported in recent studies (4.5–6.8 W m−2; Gasparini and Lohmann, 2016; Gasparini et al., 2020; Hong et al., 2016; Lohmann and Gasparini, 2017; Muench and Lohmann, 2020). The globally averaged iCRESW from the HET, OPT, INP20, and INP200 experiments increases (less negative, warming effect) by 3.39, 3.25, 0.38, and 0.30 W m−2, respectively. The decrease in iCRELW (cooling effect) from all cirrus thinning experiments is stronger, especially from the HET (−6.84 W m−2) and OPT (−6.29 W m−2) experiments. Although ΔiCRELW from the HET and OPT experiments shows significant cooling effects over most regions, there are still a few regions with warming effects (central Africa and northern Brazil) due to higher ice cloud occurrence frequencies (not shown). The spatial patterns of ΔiCRESW and ΔiCRELW are generally in agreement with the changes in IWP and column Ni (Fig. 3). In terms of ΔiCRE, the HET (−3.45 W m−2) and OPT (−3.04 W m−2) experiments show much stronger cooling effects than the INP20 (−0.44 W m−2) and INP200 (−0.01 W m−2) experiments. Following Gasparini et al. (2020), the cirrus seeding effectiveness () is used to show what proportion of iCRE is eliminated by cirrus seeding. The globally averaged cirrus seeding effectiveness from the HET and OPT experiments is 56.19 % and 49.40 %, respectively. These values are much higher than those from the INP20 (6.69 %) and INP200 (−2.22 %) experiments. The fixed seeding method restricts the cirrus seeding effectiveness. Notably, over some tropical regions, the cirrus seeding effectiveness from the HET and OPT experiments is somewhat low, although the ΔiCRE is relatively strong (< −5 W m−2). One reason is that iCRE is relatively strong (> 10 W m−2), but convective detrainment (anvil cirrus, which is not influenced by cirrus seeding) contributes more to iCRE (not shown). Another reason is that the ratio of ΔiCRESW to ΔiCRELW is higher over tropical areas due to the small solar noon zenith angles (not shown).
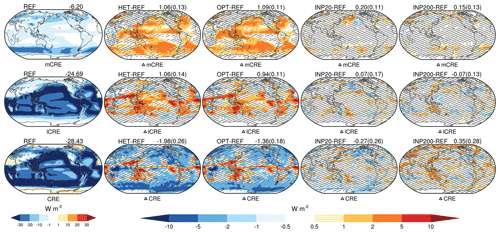
Figure 5Similar to Fig. 4 but for the mixed-phase cloud radiative effect (mCRE, first row), liquid cloud radiative effect (lCRE, second row), and the all cloud radiative effect (CRE, third row).
In addition to iCRE, mCRE and lCRE are also obviously influenced by cirrus thinning (Fig. 5). Compared with the REF experiment, mCRE from the HET and OPT experiments is significantly increased in most ocean regions. The corresponding globally averaged ΔmCRE is 1.06 and 1.09 W m−2, respectively. This warming effect (i.e., positive ΔmCRE) mainly comes from the increasing longwave component (not shown), which is consistent with the increase in IWC in mixed-phase clouds (Fig. 3). The globally averaged lCRE from the HET and OPT experiments increases (warming effect) by 1.06 and 0.94 W m−2, respectively. The ΔlCRE is strong (>2 W m−2) over some low- and mid-latitude regions that couple with the decreases in LWP (Fig. 3). Both ΔmCRE and ΔlCRE from the HET and OPT experiments show that the globally averaged values are several times larger than the corresponding standard deviations (0.11–0.14). This finding indicates that cirrus thinning with the HET/OPT method leads to a significant globally averaged warming effect from mixed-phase clouds (ΔmCRE) and liquid clouds (ΔlCRE), although ΔmCRE and ΔlCRE are not statistically significant in most regions. Unlike the HET and OPT experiments, both ΔmCRE and ΔlCRE from the INP20 and INP200 experiments are weak and uncertain. The overall cooling effect of cirrus thinning (i.e., ΔCRE) from the HET and OPT experiments is W m−2 and W m−2, respectively (Fig. 5). Compared with the cooling effect of ice clouds (i.e., ΔiCRE, Fig. 4), these values drop by approximately half due to the warming effect exerted by mixed-phase and liquid clouds. The INP20 and INP200 experiments show a weak cooling effect ( W m−2), and even a small warming effect (0.35±0.28 W m−2), respectively. It is clear that cirrus seeding with the flexible method could produce a notable global cooling effect, which is much better than the fixed methods. Furthermore, the cooling effect with the flexible seeding method is significant over most midlatitude and high-latitude regions. Some low-latitude regions show a pronounced warming effect because cirrus seeding leads to a stronger warming effect introduced by mixed-phase and liquid clouds (i.e., ΔmCRE and ΔlCRE). This finding suggests that cirrus seeding over low-latitude regions might be redundant.
3.2 Sensitivity experiments with the flexible seeding method
To better understand cirrus thinning with the flexible seeding method, this section investigates sensitivity experiments of the cooling effect on Rseed (R10 experiment) and the seeding region (GT experiment).
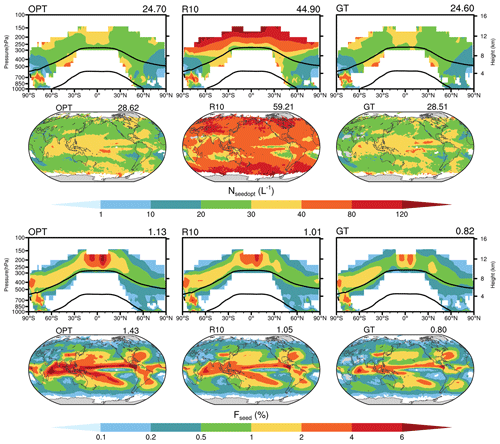
Figure 6Annual zonal mean and 233 hPa spatial distribution of the optimal seeding number concentration (Nseedopt, first panel) and seeding frequency (Fseed, second panel). The names of the experiments are shown in the upper left corner, and globally mean values are shown in the upper right corner. The results are sampled from model grids where Fseed is greater than 0.1 %.
Figure 6 shows the seeding number concentration (Nseedopt) and seeding frequency (Fseed). As expected, the OPT and GT experiments show similar Nseedopt in midlatitude and high-latitude regions. In these two experiments, Nseedopt is less than 40 L−1 in most regions. Because Nseedopt increases with decreasing Rseed (see Appendix), Nseedopt from the R10 experiment is larger than that from the OPT and GT experiments. In these seeding experiments (i.e., the OPT, R10, and GT experiments), it becomes easier for the ice nucleation process to reach Sihom (i.e., cirrus seeding occurs) because the large number of long-lived small ICs produced by homogeneous nucleation is cut off. As a result, Fseed from the seeding experiments is much larger than the homogeneous freezing occurrence frequency (Fhom×Fnuc) from the REF experiment (much less than 1 %, Fig. 2). However, Fseed from the seeding experiments is still relatively low (<4 %) in most regions. Fseed from the GT experiment is even lower than 2 % in most regions. The smaller ICs usually have a longer lifetime in cirrus clouds, so Fseed from the R10 experiment (1.01 % of all cirrus and 1.05 % at 233 hPa) is lower than that from the OPT experiment (1.13 % of all cirrus and 1.43 % at 233 hPa). Similar to the spatial distribution of Fhom from the REF experiment, Fseed from the cirrus seeding experiments is much higher in the low-latitude regions. This is the reason that the globally averaged Fseed from the GT experiment (0.82 % of all cirrus and 0.80 % at 233 hPa) is about one-third lower than that from the OPT experiment.
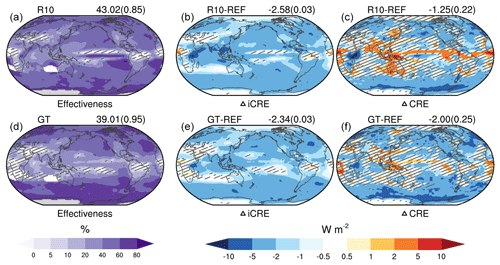
Figure 7Similar to Fig. 4 but for ΔiCRE (b, e), ΔCRE (c, f), and cirrus seeding effectiveness (a, d) from the R10 (a–c) and GT (d–f) experiments.
Figure 7 shows the cooling effects from the R10 and GT experiments. The globally averaged ΔiCRE from the R10 experiment is −2.58 W m−2. This ice cloud cooling effect is obviously weaker than that from the OPT experiment (−3.04 W m−2) because the seeding ICs in the R10 experiment (larger Nseedopt and smaller Rseed) could exist for a longer time in cirrus clouds. Correspondingly, the cirrus seeding effectiveness from the R10 experiment (43.02 %) is also less than that from the OPT experiment (49.40 %). Similar to the OPT experiment, the R10 experiment also shows that cirrus seeding induces an obvious global warming effect of mixed-phase and liquid clouds (ΔmCRE and ΔlCRE, Table 2). Notably, these warming effects (i.e., ΔmCRE and ΔlCRE) are weaker than those from the OPT experiments (Table 2). Thus, ΔCRE from the R10 experiment is W m−2, which is close to that from the OPT experiment ( W m−2). Compared with the OPT experiment, ΔiCRE from the GT experiment becomes weaker over the regions without seeding (Figs. 7 and 4). Thus, the globally averaged ΔiCRE only decreases by −2.34 W m−2 from the GT experiment. Correspondingly, the cirrus seeding effectiveness from the GT experiment is also obviously less than that from the OPT experiment, except in high-latitude regions. As mentioned in Sect. 3.1, cirrus seeding would lead to a strong warming effect of mixed-phase and liquid clouds at low latitudes. As expected, in the GT experiment, this warming effect is constrained to some extent (Table 2). The globally averaged cooling effect (ΔCRE) from the GT experiment is W m−2, which is much stronger than that from the OPT experiment ( W m−2) and even stronger than that from the HET experiment ( W m−2). This finding suggests that cirrus seeding without low solar noon zenith angle regions might produce a better global cooling effect.
The major purpose of this study is to estimate the potential cooling effect of cirrus thinning. Based on the mechanism of cirrus thinning by the seeding approach, a flexible seeding method is used to calculate the optimal seeding number concentration, which is just enough to prevent homogeneous ice nucleation from happening. Furthermore, the cirrus seeding approach could move further by injecting ice crystals (ICs) instead of ice nuclei particles (INPs). In terms of hindering homogeneous nucleation and environmental safety, ICs are better than INPs. More importantly, the problem of INP transportation discussed in previous studies might be solved because ICs can be made from ambient atmospheric water vapor.
Both parcel model simulations and large-ensemble ice nucleation offline experiments show that the flexible seeding method has obvious advantages over the fixed seeding method. Furthermore, the CAM5 simulations with the flexible seeding method (implementing seeding globally) show a notable global cooling effect, W m−2 from seeding with ICs of 50 µm (OPT experiment) and W m−2 from seeding with ICs of 10 µm (R10 experiment). However, simulations with fixed seeding number concentrations of 20 and 200 INPs L−1 show a weak cooling effect of W m−2 and a warming effect of 0.35±0.28 W m−2, respectively. Note that some previous work using CAM5 with the fixed seeding method showed a notable cooling effect ( W m−2; e.g., Storelvmo and Herger, 2014; Storelvmo et al., 2014). This is attributed to the contribution of homogeneous nucleation to cirrus formation (Fhom) from the default CAM5 model used in their study (Penner et al., 2015). The Fhom from default CAM5 simulations is relatively higher because the default version neglects the effect of preexisting ICs (Shi et al., 2015). Penner et al. (2015) tuned the main ice nucleation mechanism in CAM5 to limit Fhom and found that cirrus thinning with a fixed seeding number concentration cannot produce a definite global cooling effect. In this study, Fhom is also limited to a low level (Fig. 2). Our results with the fixed seeding method are similar to the study of Penner et al. (2015). However, with the benefits of the flexible seeding method, cirrus seeding could produce a considerable cooling effect.
This study also analyzes the main mechanism for the cooling effect achieved via cirrus seeding. Simulation results show that cirrus seeding not only impacts ice clouds, but also significantly impacts mixed-phase and liquid clouds. In terms of ice clouds, cirrus thinning with the flexible seeding method could lead to a notable cooling effect. However, cirrus seeding also leads to a significant warming effect of mixed-phase and liquid clouds, which counteracts the cooling effect of cirrus clouds. Because the counteraction is more prominent over low-latitude regions, the low-latitude regions are less susceptible to cirrus seeding. This finding agrees with the previous finding that cirrus thinning is more effective at mid and high latitudes because of more insolation caused by cirrus thinning when the sun is overhead (Storelvmo et al., 2014). The warming effect of liquid clouds from the OPT experiment (0.94±0.11 W m−2) is similar to the study of Gasparini et al. (2017; Table 5, 0.96±0.25 W m−2 from the ECHAM-HAM model simulation with seeding of 1 L−1 of 50 µm INPs). There seems to be a relatively solid mechanism whereby cirrus thinning reduces atmospheric stability, leading to the warming effect of liquid clouds. However, the warming effect of mixed-phase clouds from the OPT experiment (1.09±0.11 W m−2) is several times stronger than that reported in their results (0.15±0.10 W m−2). This difference suggests that the climatic response to cirrus seeding is complex and might differ among different climate models and seeding methods. Finally, it is necessary to point out that the compensating effects introduced in this study (i.e., the warming effect of mixed-phase and liquid clouds) are derived from the atmosphere-only simulations, and with prescribed ocean surface conditions, the coupled model simulations might show different results (e.g., Gasparini et al., 2017).
Sensitivity experiments with the flexible seeding method show that the seeding method with smaller ICs (i.e., the R10 experiment) leads to a weaker global cooling effect of ice clouds due to the larger seeding number concentration and smaller ICs. The warming effects of mixed-phase and liquid clouds are also reduced to some extent because the convective activity from the R10 experiment is not as strong as that from the OPT experiment (not shown). Thus, the global cooling effect from seeding with smaller ICs ( W m−2) is not obviously weaker than seeding with larger ICs ( W m−2). Avoiding seeding over low-latitude regions can limit some warming effects due to changes in mixed-phase and liquid clouds and thus lead to a more pronounced global cooling effect. Sensitivity experiments show that seeding carried out at latitudes with solar noon zenith angles greater than 12∘ yields a stronger global cooling effect of W m−2, which is close to that of artificially turning off homogeneous nucleation over the whole Earth ( W m−2). In addition, we carried out sensitivity experiments with other threshold values (23.5, 18, and 8∘). With increasing thresholds, the global cooling effect of ice clouds decreases, and the global warming effects of mixed-phase and liquid clouds also decrease. The overall cooling effect is maximized when using a solar zenith angle threshold of 12∘. In short, the global cooling effect is more sensitive to seeding regions than to the radius of seeding ICs. The global cooling effect can thus be maximized when limiting seeding to the most suitable regions and times of the year. However, estimating the cooling effect of cirrus seeding based on commercial airliners (i.e., with a limited time and place) is more realistic. We plan to investigate this method in our future work.
For the ice nucleation parameterization with the preexisting IC effect, the seeding ICs are considered to be preexisting ICs. The optimal number concentration of ICs (Nseedopt) depends on the ice nucleation parameterization, especially for its treatment of the preexisting IC effect.
Without the preexisting ICs or seeding ICs, the temporal evolution of Si is governed by the following (Kärcher et al., 2006):
where the parameters a1, a2, and a3 only depend on the ambient temperature and pressure. W is the updraft velocity, and denotes the growth rate of newly nucleated ICs. To account for the effect of preexisting ICs and seeding ICs, the deposition growth of preexisting ICs and seeding ICs are added to Eq. (A1):
Equation (A2) can be rewritten as the following form:
The effect of preexisting ICs on ice nucleation can be taken as reducing the vertical velocity (Wpre; Barahona et al., 2014). Details about how to calculate Wpre are introduced in Shi et al. (2015). Here, the reduced vertical velocity from seeding ice (i.e., Wseed) is similar to Wpre. Wseed is a function of seeding ice number concentration (Nseed) and its radius (Rseed). Assuming all seeding ICs have the same Rseed, the growth rate is given by
where ρi is the ice density, and mw is the mass of a water molecule. , . α is the water vapor deposition coefficient on ice, νth is the thermal speed, nsat is the water vapor number density at ice saturation, and D is the water vapor diffusion coefficient from the gas phase to the ice phase (Kärcher et al., 2006).
Under a given Rseed, Wseed increases with increasing Nseed. That is, the more ICs that are added, the more they will reduce W. The minimal Nseed (i.e., Nseedopt) is calculated based on the minimal Wseed, which can prevent homogeneous ice nucleation from occurring. The default ice nucleation parameterization (Liu and Penner, 2005; LP parameterization) provides a threshold updraft velocity (Wthre) for homogeneous ice nucleation,
where T is the ambient temperature, , . NINP is the INP (e.g., dust aerosol particle) number concentration. Homogeneous ice nucleation does not occur (i.e., only heterogeneous nucleation) if the effective updraft velocity (Weff, ) is less than Wthre. Thus, the minimal Wseed is calculated as . If Wseed<0, there is no need for seeding. The minimal number concentration of seeding ICs (i.e., Nseedopt) can be calculated based on Eqs. (A5) and (A6) at threshold Si for homogeneous freezing (Sihom). In this study, with the given Rseed, Nseedopt is given by
Because the impact of deposition growth on preexisting ICs is neglected in calculating Wpre (Barahona et al., 2014; Shi et al., 2015), the increase in Rseed caused by deposition growth during the ice nucleation process is also neglected. As a result, Nseedopt might be overestimated, especially for a small given Rseed. The LP parameterization provides a critical number concentration of INPs (Nlim) for the only heterogeneous freezing scenario. Nseedopt cannot exceed Nlim because ICs are superior to INPs in hindering homogeneous nucleation.
The modified code of CAM5 and the output data used in this study are available online at https://doi.org/10.5281/zenodo.4507001 (Liu and Shi, 2021).
JL derived the formula for optimal seeding number concentrations. XS and JL designed the model experiments and developed the model code. JL processed and analyzed the raw model output data and wrote the paper. XS helped to explain the results. Both authors contributed to improving and reviewing the manuscript.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors would like to thank Blaž Gasparini for suggesting plotting the cirrus seeding effectiveness. The model simulation was conducted in the High Performance Computing Center of Nanjing University of Information Science & Technology.
This research has been supported by the National Key Research and Development Program of China (grant no. 2018YFC1507001) and the National Natural Science Foundation of China (grant nos. 41775095 and 42075145).
This paper was edited by Martina Krämer and reviewed by Blaž Gasparini and one anonymous referee.
Alexander, L. V., Zhang, X., Peterson, T. C., Caesar, J., Gleason, B., Klein Tank, A. M. G., Haylock, M., Collins, D., Trewin, B., Rahimzadeh, F., Tagipour, A., Rupa Kumar, K., Revadekar, J., Griffiths, G., Vincent, L., Stephenson, D. B., Burn, J., Aguilar, E., Brunet, M., Taylor, M., New, M., Zhai, P., Rusticucci, M., and Vazquez-Aguirre, J. L.: Global observed changes in daily climate extremes of temperature and precipitation, J. Geophys. Res., 111, D05109, https://doi.org/10.1029/2005JD006290, 2006.
Barahona, D. and Nenes, A.: Parameterizing the competition between homogeneous and heterogeneous freezing in ice cloud formation – polydisperse ice nuclei, Atmos. Chem. Phys., 9, 5933–5948, https://doi.org/10.5194/acp-9-5933-2009, 2009.
Barahona, D., Molod, A., Bacmeister, J., Nenes, A., Gettelman, A., Morrison, H., Phillips, V., and Eichmann, A.: Development of two-moment cloud microphysics for liquid and ice within the NASA Goddard Earth Observing System Model (GEOS-5), Geosci. Model Dev., 7, 1733–1766, https://doi.org/10.5194/gmd-7-1733-2014, 2014.
Berry, E. and Mace, G. G.: Cloud properties and radiative effects of the Asian summer monsoon derived from A-Train data: cloud ice water and radiative effects, J. Geophys. Res. Atmos., 119, 9492–9508, https://doi.org/10.1002/2014JD021458, 2014.
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S. K., Sherwood, S., Stevens, B., and Zhang, X. Y.: Clouds and Aerosols, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, USA, 2013.
Caldeira, K., Bala, G., and Cao, L.: The Science of Geoengineering, Annu. Rev. Earth Pl. Sc., 41, 231–256, https://doi.org/10.1146/annurev-earth-042711-105548, 2013.
Cziczo, D. J., Froyd, K. D., Hoose, C., Jensen, E. J., Diao, M., Zondlo, M. A., Smith, J. B., Twohy, C. H., and Murphy, D. M.: Clarifying the Dominant Sources and Mechanisms of Cirrus Cloud Formation, Science, 340, 1320–1324, https://doi.org/10.1126/science.1234145, 2013.
DeMott, P. J., Cziczo, D. J., Prenni, A. J., Murphy, D. M., Kreidenweis, S. M., Thomson, D. S., Borys, R., and Rogers, D. C.: Measurements of the concentration and composition of nuclei for cirrus formation, P. Natl. Acad. Sci. USA, 100, 14655–14660, https://doi.org/10.1073/pnas.2532677100, 2003.
Feely, R., Doney, S., and Cooley, S.: Ocean Acidification: Present Conditions and Future Changes in a High-CO2 World, Oceanography, 22, 36–47, https://doi.org/10.5670/oceanog.2009.95, 2009.
Fuss, S., Lamb, W. F., Callaghan, M. W., Hilaire, J., Creutzig, F., Amann, T., Beringer, T., de Oliveira Garcia, W., Hartmann, J., Khanna, T., Luderer, G., Nemet, G. F., Rogelj, J., Smith, P., Vicente, J. L. V., Wilcox, J., del Mar Zamora Dominguez, M., and Minx, J. C.: Negative emissions – Part 2: Costs, potentials and side effects, Environ. Res. Lett., 13, 063002, https://doi.org/10.1088/1748-9326/aabf9f, 2018.
Gasparini, B. and Lohmann, U.: Why cirrus cloud seeding cannot substantially cool the planet, J. Geophys. Res.-Atmos., 121, 4877–4893, https://doi.org/10.1002/2015JD024666, 2016.
Gasparini, B., Münch, S., Poncet, L., Feldmann, M., and Lohmann, U.: Is increasing ice crystal sedimentation velocity in geoengineering simulations a good proxy for cirrus cloud seeding?, Atmos. Chem. Phys., 17, 4871–4885, https://doi.org/10.5194/acp-17-4871-2017, 2017.
Gasparini, B., McGraw, Z., Storelvmo, T., and Lohmann, U.: To what extent can cirrus cloud seeding counteract global warming?, Environ. Res. Lett., 15, 054002, https://doi.org/10.1088/1748-9326/ab71a3, 2020.
Gettelman, A., Liu, X., Ghan, S. J., Morrison, H., Park, S., Conley, A. J., Klein, S. A., Boyle, J., Mitchell, D. L., and Li, J.-L. F.: Global simulations of ice nucleation and ice supersaturation with an improved cloud scheme in the Community Atmosphere Model, J. Geophys. Res., 115, D18216, https://doi.org/10.1029/2009JD013797, 2010.
Gruber, S., Blahak, U., Haenel, F., Kottmeier, C., Leisner, T., Muskatel, H., Storelvmo, T., and Vogel, B.: A Process Study on Thinning of Arctic Winter Cirrus Clouds With High-Resolution ICOn-ART Simulations, J. Geophys. Res., 124, 5860–5888, 2019.
Heutel, G., Moreno-Cruz, J., and Shayegh, S.: Solar geoengineering, uncertainty, and the price of carbon, J. Environ. Econ. Manag., 87, 24–41, https://doi.org/10.1016/j.jeem.2017.11.002, 2018.
Hong, Y., Liu, G., and Li, J.-L. F.: Assessing the Radiative Effects of Global Ice Clouds Based on CloudSat and CALIPSO Measurements, J. Climate, 29, 7651–7674, https://doi.org/10.1175/JCLI-D-15-0799.1, 2016.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
IEA: World Energy Outlook 2019, available at: https://www.iea.org/reports/world-energy-outlook-2019 (last access: 21 May 2020), 2019.
Irvine, P. J., Kravitz, B., Lawrence, M. G., and Muri, H.: An overview of the Earth system science of solar geoengineering: Overview of the earth system science of solar geoengineering, WIREs Clim. Change, 7, 815–833, https://doi.org/10.1002/wcc.423, 2016.
Jackson, L. S., Crook, J. A., and Forster, P. M.: An intensified hydrological cycle in the simulation of geoengineering by cirrus cloud thinning using ice crystal fall speed changes, J. Geophys. Res.-Atmos., 121, 6822–6840, https://doi.org/10.1002/2015JD024304, 2016.
Jensen, E. J., Diskin, G., Lawson, R. P., Lance, S., Bui, T. P., Hlavka, D., McGill, M., Pfister, L., Toon, O. B., and Gao, R.: Ice nucleation and dehydration in the Tropical Tropopause Layer, P. Natl. Acad. Sci. USA, 110, 2041–2046, https://doi.org/10.1073/pnas.1217104110, 2013.
Jones, A. C., Hawcroft, M. K., Haywood, J. M., Jones, A., Guo, X., and Moore, J. C.: Regional Climate Impacts of Stabilizing Global Warming at 1.5 K Using Solar Geoengineering, Earths Future, 6, 230–251, https://doi.org/10.1002/2017EF000720, 2018.
Kärcher, B.: A parameterization of cirrus cloud formation: Homogeneous freezing of supercooled aerosols, J. Geophys. Res., 107, 4010, https://doi.org/10.1029/2001JD000470, 2002.
Kärcher, B., Hendricks, J., and Lohmann, U.: Physically based parameterization of cirrus cloud formation for use in global atmospheric models, J. Geophys. Res., 111, D01205, https://doi.org/10.1029/2005JD006219, 2006.
Keith, D. W. and MacMartin, D. G.: A temporary, moderate and responsive scenario for solar geoengineering, Nat. Clim. Change, 5, 201–206, https://doi.org/10.1038/nclimate2493, 2015.
Koop, T., Luo, B., Tsias, A., and Peter, T.: Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 406, 611–614, https://doi.org/10.1038/35020537, 2000.
Kravitz, B., Robock, A., Boucher, O., Schmidt, H., Taylor, K. E., Stenchikov, G., and Schulz, M.: The Geoengineering Model Intercomparison Project (GeoMIP), Atmos. Sci. Lett., 12, 162–167, https://doi.org/10.1002/asl.316, 2011.
Kravitz, B., Robock, A., Tilmes, S., Boucher, O., English, J. M., Irvine, P. J., Jones, A., Lawrence, M. G., MacCracken, M., Muri, H., Moore, J. C., Niemeier, U., Phipps, S. J., Sillmann, J., Storelvmo, T., Wang, H., and Watanabe, S.: The Geoengineering Model Intercomparison Project Phase 6 (GeoMIP6): simulation design and preliminary results, Geosci. Model Dev., 8, 3379–3392, https://doi.org/10.5194/gmd-8-3379-2015, 2015.
Kristjánsson, J. E., Muri, H., and Schmidt, H.: The hydrological cycle response to cirrus cloud thinning, Geophys. Res. Lett., 42, 10807-10815, https://doi.org/10.1002/2015GL066795, 2015.
Lawrence, M. G., Schäfer, S., Muri, H., Scott, V., Oschlies, A., Vaughan, N. E., Boucher, O., Schmidt, H., Haywood, J., and Scheffran, J.: Evaluating climate geoengineering proposals in the context of the Paris Agreement temperature goals, Nat. Commun., 9, 3734, https://doi.org/10.1038/s41467-018-05938-3, 2018.
Lenton, T. M., Rockström, J., Gaffney, O., Rahmstorf, S., Richardson, K., Steffen, W., and Schellnhuber, H. J.: Climate tipping points – too risky to bet against, Nature, 575, 592–595, https://doi.org/10.1038/d41586-019-03595-0, 2019.
Liu, J. and Shi, X.: Model code, simulation output data, and all scripts for the paper “Estimating the potential cooling effect of cirrus thinning achieved via the seeding approach”, Version 1.0, Zenodo [data set], https://doi.org/10.5281/zenodo.4507001, 2021.
Liu, X. and Penner, J. E.: Ice nucleation parameterization for global models, Meteorol. Z., 14, 499–514, https://doi.org/10.1127/0941-2948/2005/0059, 2005.
Lohmann, U. and Gasparini, B.: A cirrus cloud climate dial?, Science, 357, 248–249, https://doi.org/10.1126/science.aan3325, 2017.
Lohmann, U., Spichtinger, P., Jess, S., Peter, T., and Smit, H.: Cirrus cloud formation and ice supersaturated regions in a global climate model, Environ. Res. Lett., 3, 045022, https://doi.org/10.1088/1748-9326/3/4/045022, 2008.
Macnaghten, P. and Owen, R.: Good governance for geoengineering, Nature, 479, 293–293, https://doi.org/10.1038/479293a, 2011.
Matus, A. V. and L'Ecuyer, T. S.: The role of cloud phase in Earth's radiation budget: cloud phase in earth's radiation budget, J. Geophys. Res.-Atmos., 122, 2559–2578, https://doi.org/10.1002/2016JD025951, 2017.
McGraw, Z., Storelvmo, T., David, R. O., and Sagoo, N.: Global Radiative Impacts of Mineral Dust Perturbations Through Stratiform Clouds, J. Geophys. Res.-Atmos., 125, e2019JD031807, https://doi.org/10.1029/2019JD031807, 2020.
Milne, G. A., Gehrels, W. R., Hughes, C. W., and Tamisiea, M. E.: Identifying the causes of sea-level change, Nat. Geosci., 2, 471–478, https://doi.org/10.1038/ngeo544, 2009.
Mitchell, D. L. and Finnegan, W.: Modification of cirrus clouds to reduce global warming, Environ. Res. Lett., 4, 045102, https://doi.org/10.1088/1748-9326/4/4/045102, 2009.
Morrison, H. and Gettelman, A.: A New Two-Moment Bulk Stratiform Cloud Microphysics Scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and Numerical Tests, J. Climate, 21, 3642–3659, https://doi.org/10.1175/2008JCLI2105.1, 2008.
Muench, S. and Lohmann, U.: Developing a Cloud Scheme With Prognostic Cloud Fraction and Two Moment Microphysics for ECHAM-HAM, J. Adv. Model. Earth Sy., 12, e2019MS001824, https://doi.org/10.1029/2019MS001824, 2020.
Muri, H., Kristjánsson, J. E., Storelvmo, T., and Pfeffer, M. A.: The climatic effects of modifying cirrus clouds in a climate engineering framework, J. Geophys. Res.-Atmos., 119, 4174–4191, https://doi.org/10.1002/2013JD021063, 2014.
Murray, B. J., Wilson, T. W., Dobbie, S., Cui, Z., Al-Jumur, S. M. R. K., Möhler, O., Schnaiter, M., Wagner, R., Benz, S., Niemand, M., Saathoff, H., Ebert, V., Wagner, S., and Kärcher, B.: Heterogeneous nucleation of ice particles on glassy aerosols under cirrus conditions, Nat. Geosci., 3, 233–237, https://doi.org/10.1038/ngeo817, 2010.
Myhre, G., Shindell, D., Bréon, F.-M., Collins, W., Fuglestvedt, J., Huang, J., Koch, D., Lamarque, J.-F., Lee, D., Mendoza, B., Nakajima, T., Robock, A., Stephens, G., Takemura, T., and Zhang, H.: Anthropogenic and Natural Radiative Forcing, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, USA, 2013.
Neale, R. B., Gettelman, A., Park, S., Conley, A. J., Kinnison, D., Marsh, D., Smith, A. K., Vitt, F., Morrison, H., Cameron-Smith, P., Collins, W. D., Iacono, M. J., Easter, R. C., Liu, X., and Taylor, M. A.: Description of the NCAR Community Atmosphere Model (CAM 5.0), NCAR Tech. Note NCAR/TN-485 + STR, Natl. Cent. for Atmos. Res, Boulder, Co, USA, 289 pp., 2012.
Penner, J. E., Zhou, C., and Liu, X.: Can cirrus cloud seeding be used for geoengineering?, Geophys. Res. Lett., 42, 8775–8782, https://doi.org/10.1002/2015GL065992, 2015.
Pruppacher, H. and Klett, J.: Microphysics of Clouds and Precipitation: second revised and enlarged edition with an introduction to cloud chemistry and cloud electricity, Kluwer, Dordrecht, 1998.
Rapp, A., Kummerow, C., and Fowler, L.: Interactions between warm rain clouds and atmospheric preconditioning for deep convection in the tropics. J. Geophys. Res.-Atmos., 116, D23210, https://doi.org/10.1029/2011JD016143, 2011.
Rogelj, J., Luderer, G., Pietzcker, R. C., Kriegler, E., Schaeffer, M., Krey, V., and Riahi, K.: Energy system transformations for limiting end-of-century warming to below 1.5 ∘C, Nat. Clim. Change, 5, 519–527, https://doi.org/10.1038/nclimate2572, 2015.
Shi, X. and Liu, X.: Effect of cloud-scale vertical velocity on the contribution of homogeneous nucleation to cirrus formation and radiative forcing, Geophys. Res. Lett., 43, 6588–6595, https://doi.org/10.1002/2016GL069531, 2016.
Shi, X., Liu, X., and Zhang, K.: Effects of pre-existing ice crystals on cirrus clouds and comparison between different ice nucleation parameterizations with the Community Atmosphere Model (CAM5), Atmos. Chem. Phys., 15, 1503–1520, https://doi.org/10.5194/acp-15-1503-2015, 2015.
Shi, X., Wang, B., Liu, X., and Wang, M.: Two-moment bulk stratiform cloud microphysics in the Grid-point Atmospheric Model of IAP LASG (GAMIL), Adv. Atmos. Sci., 30, 868–883, https://doi.org/10.1007/s00376-012-2072-1, 2013.
Solomon, S., Plattner, G.-K., Knutti, R., and Friedlingstein, P.: Irreversible climate change due to carbon dioxide emissions, P. Natl. Acad. Sci. USA, 106, 1704–1709, https://doi.org/10.1073/pnas.0812721106, 2009.
Storelvmo, T., Boos, W., and Herger, N.: Cirrus cloud seeding: a climate engineering mechanism with reduced side effects?, Philos. T. Roy. Soc. A., 372, 20140116, https://doi.org/10.1098/rsta.2014.0116, 2014.
Storelvmo, T. and Herger, N.: Cirrus cloud susceptibility to the injection of ice nuclei in the upper troposphere, J. Geophys. Res.-Atmos., 119, 2375–2389, https://doi.org/10.1002/2013JD020816, 2014.
Storelvmo, T., Kristjánsson, J., Muri, H., Pfeffer, M. A., Barahona, D., and Nenes, A.: Cirrus cloud seeding has potential to cool climate, Geophys. Res. Lett., 40, 178–182, https://doi.org/10.1029/2012GL054201, 2013.
Vaughan, N. E. and Lenton, T. M.: A review of climate geoengineering proposals, Climatic Change, 109, 745–790, https://doi.org/10.1007/s10584-011-0027-7, 2011.
- Abstract
- Introduction
- Methods and experiments
- Estimating the cooling effect of cirrus thinning
- Conclusions and discussion
- Appendix A: The formula of optimal seeding number concentration (Nseedopt)
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods and experiments
- Estimating the cooling effect of cirrus thinning
- Conclusions and discussion
- Appendix A: The formula of optimal seeding number concentration (Nseedopt)
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References






