the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The absorption Ångstrom exponent of black carbon with brown coatings: effects of aerosol microphysics and parameterization
Xiaolin Zhang
Mao Mao
Shihao Tang
The aerosol absorption Ångstrom exponent (AAE) is a crucial optical parameter for apportionment and characterization. Due to considerable inconsistences associated with observations, numerical research is a powerful means to give a better understanding of the AAE of aged black carbon (BC) aerosols. Numerical studies of the AAE of polydisperse BC aggregates with brown coatings using the exact multiple-sphere T-matrix method (MSTM) are performed. The objective of the study is to thoroughly assess the AAE of coated BC influenced by their observation-based detailed microphysics and then provide a new AAE parameterization for application. At odds with our expectations, more large-sized BC particles coated by thin brown carbon can have an AAE smaller than 1.0, indicating that BC aerosols internally mixing with brown carbon can even show lower AAE than pure BC particles. The AAE of BC with brown coatings is highly sensitive to the absorbing volume fraction of the coating, coated volume fraction of BC, shell ∕ core ratio, and particle size distribution with a wide variation, whereas the impacts of BC geometry and BC position within the coating are negligible. The AAE of BC with brown coatings can be larger than 3.0 if there are plenty of small-sized coated BC particles, heavy coating, or a large amount of brown carbon. However, the AAE of BC with non-absorbing coating appears to be weakly sensitive to particle microphysics with values around 1.0 (i.e., 0.7–1.4), suggesting the substantial role of the absorbing volume fraction of the coating in AAE determination. With more realistic BC geometries, our study also indicates that the occurrence of brown carbon may not be confidently determined unless AAE > 1.4. The currently popular core–shell Mie model reasonably approximates the AAE of fully coated BC by brown carbon, whereas it underestimates the AAE of partially coated or externally attached BC and underestimates more for a lower coated volume fraction of BC. In addition, we present a parameterization of the AAE of coated BC with a size distribution on the basis of numerical results, which can act as a guide for the AAE response to the absorbing volume fraction of the coating, coated volume fraction of BC, and shell ∕ core ratio. The proposed parameterization of coated BC AAE generates a decent prediction for moderate BC microphysics, whereas caution should be taken in applying it for extreme cases, such as externally attached coated BC morphology. Our findings could improve the understanding and application of the AAE of BC with brown coatings.
- Article
(1392 KB) - Full-text XML
-
Supplement
(173 KB) - BibTeX
- EndNote
Black carbon (BC) aerosols exert a momentous influence on both global and regional climates on account of their strong scattering and absorption of radiation (e.g., Ramanathan and Carmichael, 2008; Guo et al., 2014; Zhang et al., 2015). Meanwhile, BC tends to be coated by secondary aerosol compositions (such as organics) with the aging process, resulting in a complicated mixing state and morphology (Schwarz et al., 2008; Myhre, 2009). Among BC coatings, in addition to non-absorbing components, the absorbing organics, named brown carbon (BrC), absorb radiation in the ultraviolet and visible spectra (Clarke et al., 2007). The largest uncertainty in the estimation of BC climate effects is rooted in uncertainties in determining the optical properties determined by complex microphysical properties (Zhang et al., 2019a). As one of the most significant optical properties, the absorption Ångstrom exponent (AAE) describes the wavelength variation in particle absorption, whereas the understanding of aged BC AAE is still limited due to internal mixing with non-absorptive and absorbing coatings (e.g., Zhang et al., 2008; Shiraiwa et al., 2010). The lack of an accurate understanding and parameterization of the AAE of aged BC has been a pivotal limitation to the assessment of BC radiative effects.
The concept of AAE is intensively employed for aerosol characterization, as it is considered to be a special parameter of aerosol species (e.g., C. Liu et al., 2018). For instance, the AAE of pure BC is predicted to be wavelength-independent with a value of 1.0 for particle size less than 50 nm (e.g., Moosmüller et al., 2011), whilst BrC and dust are assumed to have high AAEs (e.g., Russell et al., 2010). Therefore, in ambient measurements, large AAE is considered to indicate that aerosols originate from dust or biofuel and/or biomass burning, while small AAE near 1.0 is understood to indicate that aerosols are BC-rich particles due to the burning of fossil fuel (Russell et al., 2010). BrC contributes no absorption at near-infrared wavelengths and absorbs more at shorter wavelengths, whereas BC typically shows an AAE of 1.0 at near-infrared and visible wavelengths (e.g., Kirchstetter and Thatcher, 2012). The AAE cannot unambiguously be utilized to quantify the separation of BrC absorption from BC absorption despite their distinctive functions of incident wavelength (e.g., Schuster et al., 2016). Additionally, the effects of specified AAE values on the attribution of BC and BrC light absorption are also investigated (Lack and Langridge, 2013).
For estimating the AAEs of BC particles, numerous experiments have been conducted by measuring their absorption at different wavelengths. The soot from diesel shows an AAE of 1.1, while carbon particles generated from spark exhibit an AAE value of 2.1 (Schnaiter et al., 2003). After extracting organics, values of AAE ranging from 0.6 to 1.3 for aerosols inside a tunnel or close to a roadway are found (Kirchstetter et al., 2004). The AAE of BC-dominated aerosols produced with mustard oil is observed to be ∼1.3 (e.g., Chakrabarty et al., 2013). For brown coatings, Hoffer et al. (2006) extract humic-like substances with water from the fine fraction of biomass burning aerosols and introduce an BrC AAE of 6.0–7.0. Obviously, reported AAE values of BC particles and their brown coatings are not concordant in different studies, and this may be in association with their complicated microphysical properties, such as particle size, mixing state, and chemical component.
In spite of providing referential AAE values of BC particles and their brown coatings with measurements, the causes of the AAEs are generally not clear. For instance, what is the principal factor in particle microphysics that leads to complicated AAEs? Is it the size distribution, mixing state, or composition of BC coating? To our knowledge, the measurements have difficulties addressing these questions, whereas a numerical study is a powerful method that can reveal the mechanism behind complicated BC AAE. To improve our understanding of the AAEs of pure BC and coated BC, numerical investigations have been carried out. On the basis of the core–shell Mie theory, Lack and Cappa (2010) investigate the impacts of brown and clear carbon on BC AAE and show that BC coated in non-absorbing organics can have an AAE as high as 1.6, which complicates attributing measured absorption to BrC within ambient aerosols. Nonetheless, the core–shell Mie structure is in debate (e.g., Cappa et al., 2012), as lacy or compact fractal aggregates are widely accepted for BC geometries (e.g., Liu and Mishchenko, 2018; Liu et al., 2019). With more realistic geometries of BC aggregates, C. Liu et al. (2018) numerically investigate the AAEs of bare BC and fully coated BC with non-absorptive coating and highlight the effect of particle size on the AAE. However, the impact of brown coatings on BC AAE is not clear, and meanwhile, no conclusive results for the influences of coating microphysics on BC AAE have been provided. This limits the AAE applications in aerosol–climate models, radiative transfer, and remote sensing due to the lack of a thorough understanding and further parameterization of the AAE of BC with brown coating affected by their microphysics.
Here, numerical studies of the AAE of polydisperse BC particles with brown coatings are systematically carried out according to our current understandings. An accurate multiple-sphere T-matrix method (MSTM) is used for numerical calculation of coated BC absorption properties and their AAE values. The aim is to evaluate the influences of particle microphysics, including the absorbing volume fraction of the coating, coated volume fraction of BC, BC position within coating, BC fractal dimension, shell ∕ core ratio, and size distribution, on the AAEs of BC particles with brown coatings, which hopefully contributes to understanding the BC AAEs and their parameterization for application. The performance of the core–shell Mie model for the AAE of coated BC is also evaluated.
2.1 Models of coated BC
It is observed that BC particles can be externally attached to, partially coated in, or fully encapsulated by coatings (China et al., 2013, 2015). This study considers a BC aggregate core with a spherical coating, following the coated BC models built by Zhang et al. (2018). Sketch maps of three typical coated BC structures considered here (i.e., externally attached, partially coated and fully coated) are portrayed in Fig. 1. For coated BC, the coated volume fraction of BC (F) is a crucial microphysical parameter characterizing its mixing state, and it is as follows:
where VBC inside and VBC are the volume of BC monomers encapsulated in coating and overall BC volume, respectively (see Fig. 1). With this definition, the externally attached, partially coated, and fully coated BC aggregates show F=0, , and F=1, respectively. For coated BC, the shell ∕ core ratio Dp∕Dc is an important microphysical parameter and is defined as the spherical equivalent particle diameter divided by the BC core diameter (Dc). The geometries of freshly emitted bare BC can typically be described by the fractal aggregate (e.g., Sorensen, 2001; Li et al., 2016), mathematically satisfying the statistic scaling rule with the following form:
where N, k0, Rg, a, and Df represent the monomer number, fractal prefactor, gyration radius, monomer radius, and fractal dimension, respectively. The fractal dimension Df is a parameter describing the compactness of BC aggregates, and due to the aging process in ambient air, BC can be coated by other species, such as organics, becoming compact (i.e., large Df) (e.g., Coz and Leck, 2011; Tritscher et al., 2011).
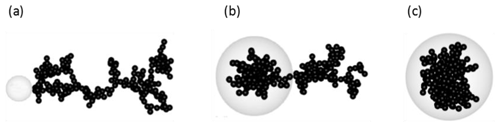
Figure 1Sketch maps of the geometries of coated black carbon. Examples of fractal black carbon aggregates containing 200 monomers are externally attached to (a), partially coated by (b), and fully coated in (c) organics, with the coated volume fractions of BC being 0.0, 0.5, and 1.0, respectively.
The details of the construction of coated BC models and mixing-state description using BC microphysical parameters are illustrated in Zhang et al. (2018). The k0 of BC aggregates in this study is assumed as 1.2 (Sorensen, 2001), and BC absorption does not change substantially with Df varying from 0.9 to 2.1 (Liu and Mishchenko, 2005). The shielding effect of N on the absorption of BC aggregates is an important topic, as larger N can induce more shielding and result in less efficient absorption (Liu and Mishchenko, 2007). This study considers an N value of 200 for accumulation BC, following the methods described in Zhang et al. (2017, 2018), because it is observed that BC particles are mostly in the accumulation mode. Two BC Df values of 2.8 and 1.8 for compact and lacy BC aggregates, respectively, are considered (e.g., C. Liu et al., 2018). The BC shell ∕ core ratio Dp∕Dc ranging from 1.1 to 2.7 is assumed based on recent observations shown in Liu et al. (2015) and Zhang et al. (2016).
2.2 Simulation of coated BC absorption
Given the models of coated BC built, their orientation-averaged absorption is accurately computed utilizing the powerful multiple-sphere T-matrix method (Mackowski, 2014). The MSTM is popularly utilized for plentiful numerical research on BC optical and radiative properties (e.g., Mishchenko et al., 2016). As it is meaningful to average bulk aerosol properties over a certain size distribution for atmospheric applications, a lognormal particle size distribution for an ensemble of coated BC is assumed following
where σg and rg demote the geometric standard deviation and geometric mean radius, respectively (e.g., Schwarz et al., 2008). Coated BC follows this size distribution, while r is the radius of the equivalent volume sphere that has the same volume as that of a coated BC aggregate. We assume rg as 0.075 µm (Yu and Luo, 2009) and σg to be 1.59 (Zhang et al., 2012), as coated BC in the accumulation mode is considered. Considering size distribution, coated BC bulk absorption properties are obtained based on the following equation:
The range of radius is set to be 0.05–0.5 µm with an equidistant interval of 0.005 µm for the averaging. The exact sizes of BC aggregates can be known on the basis of these coated BC sizes and shell ∕ core ratios.
We investigate the absorption properties of coated BC particles at multiple incident wavelengths between 350 and 700 nm in steps of 50 nm. We consider a typical BC refractive index of 1.85–0.71i (Bond and Bergstrom, 2006), as it is normally assumed to be wavelength-independent in near-visible and visible spectral regions (Moosmüller et al., 2009; Luo et al., 2018). For the refractive index of the coating of absorbing organics (i.e., brown carbon), this study assumes its real part to be a constant of 1.55 (Chakrabarty et al., 2010), whereas its imaginary part is substantially dependent on the incident wavelength over shorter visible and ultraviolet regions (e.g., Moosmüller et al., 2009; Alexander et al., 2008). The imaginary parts of BrC refractive indices at different wavelengths assumed in this study follow Kirchstetter et al. (2004) and are shown in Fig. S1 in the Supplement.
2.3 Calculating the absorption Ångstrom exponent of coated BC
Given that bulk absorption cross sections at various wavelengths are obtained, we calculate the absorption Ångstrom exponent of coated BC, a microphysical parameter describing the wavelength variation in particle absorption. As particle absorption decreases exponentially along with the increase in wavelength over the near-infrared and visible spectral region (e.g., Lewis et al., 2008), the AAE is defined in the form of or
where λ, Cabs, and C0 denote the incident wavelength, aerosol absorption cross section, and a wavelength-independent constant, respectively. The AAE is normally obtained with particle absorption at two wavelengths following
where 〈Cabs(λ1)〉 and 〈Cabs(λ2)〉 are the aerosol absorption cross sections at wavelengths of λ1 and λ2, respectively (e.g., Utry et al., 2014). Nonetheless, the AAE obtained from Eq. (7) is rather sensitive to observational wavelengths selected, and notable distinct AAE values can be obtained for different wavelength ranges (Moosmüller and Chakrabarty, 2011).
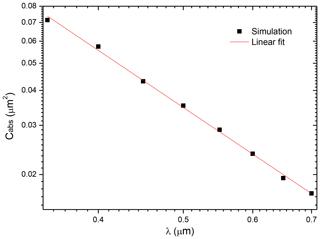
To acquire the most representational AAE, absorption cross sections of coated BC at the eight aforementioned wavelengths are applied, and the best AAE is obtained by fitting log-transformed absorption over the wavelength spectra based on a linear regression (see the second format in Eq. 6). Figure 2 gives an example for the AAE calculation, and the bulk absorption cross sections as a function of wavelength are illustrated in logarithmic scale. The black squares in the figure are calculated by the MSTM for BC particles partially coated by BrC (BC Df=2.8, , and F=0.5) with the aforementioned size distribution and refractive indices. The logarithmic absorption depicts an apparent linear variation in the figure, and the red line as a result of the linear fit becomes clear. Therefore, the negative of the line slope, i.e., 2.1, is the value of the AAE of BC coated by BrC with relevant microphysical parameters, and the AAE bias induced by wavelength selection may be averted by this fitting method. Note that the example shown gives a good linear relationship that is possibly not true for all coated BC cases, while this fit method still produces the best AAE representation.
3.1 Effects of coating structures on the AAE of BC coated by BrC
Due to various microphysical parameters, we first study their impacts on the AAE of BC coated by BrC for a fixed particle size distribution. Figure 3 depicts the AAE of BC aggregates coated by BrC calculated with the aforementioned methods for distinct shell ∕ core ratios and coated volume fractions of BC. The absorption properties are calculated over internally mixed BC–BrC ensembles with the aforementioned size distribution. BC fractal dimensions of 1.8 and 2.8 and coated volume fractions of BC ranging from 0.0 to 1.0 are selected for the investigation. For fully coated BC aggregates (i.e., F=1.0), an outermost off-center core–shell and concentric core–shell (Zhang et al., 2019a) are considered in Fig. 3, while the popular core–shell Mie model is also studied for comparison.
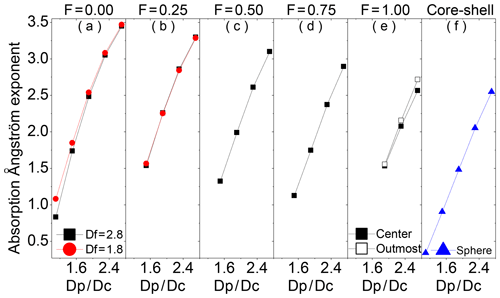
Figure 3The absorption Ångstrom exponent (AAE) of BC aggregates coated with brown carbon as a function of the shell ∕ core ratio (Dp∕Dc). The coated volume fractions of BC (F) of 0.00, 0.25, 0.5, 0.75, and 1.00, as well as the spherical core–shell structure, are considered (from left to right). Black squares and red circles indicate BC fractal dimensions of ∼2.8 and ∼1.8, respectively, while blue triangles denote spherical core–shell structures. For coating cases with F=1, black solid squares denote BC aggregates located at the particle geometric center, while black open squares indicate BC at an outermost position close to the coating boundary.
As evident in Fig. 3, the AAEs of BC coated by BrC are sensitive to the BC fractal dimension, coated volume fraction of BC, and shell ∕ core ratio. The AAE becomes much stronger with the shell ∕ core ratio becoming larger, indicating that thinly coated BC has a small AAE, whereas heavy coating results in a large AAE. BC particles having a larger F value exhibit a smaller AAE for the same BC Df and Dp∕Dc. Initiating from BC Df of 2.8, externally attached BC–BrC particles exhibit large AAE variation of 0.8–3.5 with Dp∕Dc ranging from 1.1 to 2.7 (see Fig. 3a). Meanwhile, for partially coated BC showing F=0.5, values of AAE vary from 1.3 to 3.1 with Dp∕Dc increasing in the range of 1.5–2.7. When BC aggregates are fully coated by BrC, with the increase in Dp∕Dc from 1.9 to 2.7, the AAE varies in a range of 1.5–2.6. The coated BC AAE is slightly sensitive to the BC position within brown coating, and its sensitivity becomes stronger as Dp∕Dc becomes larger. For fixed Dp∕Dc, the AAEs of coated BC with an off-center core–shell structure are slightly larger than those with a concentric core–shell structure, with differences within 0.2 (see Fig. 3e). The AAE of coated BC aggregates is also slightly sensitive to the Df of BC, and the sensitivity becomes weaker as Dp∕Dc or F increase. The AAEs of compact BC coated by BrC (i.e., BC Df=2.8) are generally smaller than those of lacy coated BC (i.e., BC Df=1.8), with differences less than 0.3, and there is almost no sensitivity of AAE to BC Df for F>0. The core–shell Mie model is widely utilized in aerosol–climate models, whereas its applicability to spectrally varying absorption properties has not been evaluated. Compared to the core–shell Mie model, BC aggregates coated by BrC with various coating microphysics have large AAE values, indicating that the assumption of the core–shell Mie model could underestimate BC AAE. This is probably because the absorption of BC coated by BrC calculated from the core–shell Mie model shows a slower increase with decreased wavelength than that calculated using realistic particle geometry. Moreover, this underestimation becomes stronger if BC aggregates with brown coating have a smaller F. For instance, fully coated BC shows slightly larger AAEs than those of concentric spherical coated BC with differences less than 0.2, whereas the differences can be as large as 1.0 for externally attached BC–BrC particles.
On the whole, the impacts of the BC fractal dimension and BC position within brown coating on the AAE of coated BC are generally negligible. Nevertheless, the AAE of BC coated by BrC is highly sensitive to the shell ∕ core ratio and coated volume fraction of BC, and of the two, the shell ∕ core ratio plays a more important role in the AAE determination, highlighting the significance of BC shell ∕ core ratio measurement in ambient air. The currently popular core–shell Mie model reasonably approximates the AAE of fully coated BC by BrC, whereas it underestimates the AAE of partially coated or externally attached BC and underestimates more for a smaller coated volume fraction of BC.
3.2 Effect of particle size distribution on the AAE of BC coated by BrC
The influence of particle size distribution on the AAE of BC aggregates (BC Df=2.8) coated by BrC at various shell ∕ core ratios is shown in Fig. 4. Coated volume fractions of BC with F=0.0, 0.5, and 1.0 corresponding to three typical BC coating states (i.e., externally attached, partially coated, and fully coated) are depicted, and BC is considered to be located at the geometric center for fully coated BC. The lognormal size distributions for coated BC with rg (x axis) in the range of 0.05–0.15 µm and σg assumed as the aforementioned 1.59 are considered.
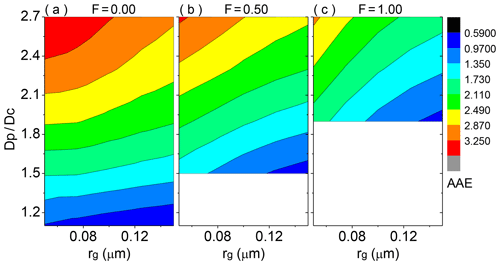
Figure 4The absorption Ångstrom exponent (AAE) of BC aggregates (BC fractal dimension of ∼2.8) coated by brown carbon with different shell ∕ core ratios (Dp∕Dc) and particle size distributions. Three coated volume fractions of BC, being 0.00, 0.50, and 1.00, are shown from left to right. For fully coated BC structure, BC is located at the particle geometric center. The geometric standard deviation (σg) for the lognormal distribution used is 1.59.
As clearly illustrated in Fig. 4, the AAE of BC aggregates coated by BrC is rather sensitive to size distribution, in addition to the shell ∕ core ratio and coated volume fraction of BC. The AAE of BC coated by BrC decreases with increasing rg; i.e., coated BC particles are larger. In addition, BC with different coating structures shows different dependences on particle size. For the externally attached structure, BC–BrC internally mixed particles with various distributions give large AAE variation with a range of 0.6–3.6, wherein thinly coated BC generally exhibits a small AAE less than 1.0. For BC partially coated by BrC with F=0.5 and fully coated BC with BC at the particle geometric center, their AAEs vary in ranges of 0.8–3.3 and 0.9–3.0, respectively. Comparing all three BC coating structures with Dp∕Dc fixed, the AAE of BC coated by BrC shows stronger variations in size distribution when F is larger. Generally, Fig. 4 indicates that BC coated by BrC gives larger AAEs for a higher shell ∕ core ratio, a lower coated volume fraction of BC, or a smaller particle size.
3.3 Effect of the absorbing volume fraction of the coating on the AAE of coated BC
The above simulations assume BC coated by BrC, whereas non-absorptive organic carbon can also exist in BC coatings in ambient air. While the organic coatings in the atmosphere may contain both absorbing and non-absorbing organics, the absorbing volume fraction of the coating (f) is a vital microphysical parameter characterizing the percentage of BrC in the whole coatings with the following equation:
where Vabsorbing is the volume of BrC, and Vnon-absorbing is the volume of non-absorbing coating. It should be noted that no one has ever definitively separated BrC from organic carbon. To a certain extent, the concept of f here may be treated as if the cases of BrC with imaginary parts of refractive indices less than those of Kirchstetter et al. (2004) are considered due to a range of BrC refractive indices being provided (Schuster et al., 2016). The absorbing and non-absorbing organics form internally mixed coatings with an effective refractive index determined by their volume fractions. The effective refractive index of the internally mixed coatings is generated on the basis of the popular volume-weighted average method, since it provides acceptable absorption properties for coated BC in the accumulation mode (Zhang et al., 2019a, b). For the refractive index of non-absorbing organics, its real part is assumed to be the same as that of absorbing organics (i.e., 1.55), while its imaginary part is considered to be 0. The key microphysical parameters of coated BC considered are summarized in Table 1.
Table 1Key microphysical properties of coated BC aggregates.

a Coated volume fraction of BC. b Shell ∕ core ratio of coated BC that is the spherical equivalent particle diameter divided by the BC core diameter. c Absorbing volume fraction of the coating. d Fractal dimension of BC aggregate.
Figure 5 shows the calculated AAE of coated BC (BC Df=2.8) with a distinct absorbing volume fraction of the coating and shell ∕ core ratio. Again, the externally attached BC, partially coated BC with F=0.5, and fully coated BC with BC at the particle geometric center are presented as different BC coating states. The absorption properties of coated BC particles are averaged with the aforementioned fixed size distribution (i.e., rg=0.075 µm, σg=1.59). The high sensitivity of coated BC AAE to the absorbing volume fraction of the coating is clearly depicted, and for fixed Dp∕Dc and F, the AAE increases exponentially with the incremental absorbing volume fraction of the coating. If the BC coating is non-absorbing organics (i.e., f=0.0), coated BC with various shell ∕ core ratios gives the AAE in ranges of 0.7–1.0, 1.0–1.0, and 1.0–1.2 for F=0.0, 0.5, and 1.0, respectively. These low AAEs of coated BC may potentially explain the small AAEs observed in the atmosphere (Schnaiter et al., 2005; Chakrabary et al., 2013; Gyawali et al., 2012). Nevertheless, as f is increased to 1.0, the AAEs for coated BC with F=0.0, 0.5, and 1.0 are enhanced by factors of 3.5, 3.0, and 3.2 for heavy coating with and by factors of 1.3, 1.3, and 1.5 for thin coating, respectively. Furthermore, the AAE of coated BC with a fixed F shows stronger variation in the absorbing volume fraction of the coating when the shell ∕ core ratio is larger. However, for a fixed Dp∕Dc, the variation of AAE in the absorbing volume fraction of the coating becomes weaker as F becomes higher.
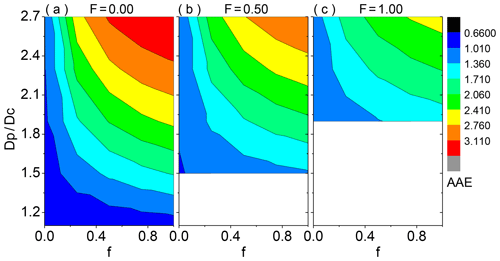
Figure 5The absorption Ångstrom exponent (AAE) of BC aggregates (BC fractal dimension of ∼2.8) coated by organics with different shell ∕ core ratios (Dp∕Dc) and absorbing volume fractions of the coating (f). Three coated volume fractions of BC, being 0.00, 0.50, and 1.00, are shown from left to right. For fully coated BC structure, BC is located at the particle geometric center.
To reveal the impact of the absorbing volume fraction of the coating on the AAE of coated BC under different size distributions, Fig. 6 depicts the AAE results of coated BC with the abovementioned three different coating structures. As the AAE of thinly coated BC shows small values with a narrow variation, heavily coated BC with a Dp∕Dc of 2.7 is considered for this sensitivity study. One can see that the AAE of coated BC is sensitive to both the size distribution and absorbing volume fraction of the coating, and stronger sensitivity of the AAE to size distribution is found when the absorbing volume fraction of the coating is larger. For non-absorbing coating, the AAE of externally attached BC with is slightly sensitive to size distribution, and its values are between 0.9 and 1.0. With more BC encapsulated in non-absorbing organics, the AAEs tend to be more sensitive to size distribution and are in ranges of 0.8–1.1 and 0.7–1.4 for F=0.5 and 1.0, respectively. This may be associated with the fact that intensified F enhances the absorption of BC coated by non-absorbing organics and its AAE is altered (Zhang et al., 2018). The AAE of BC coated by non-absorbing organics in our study is coincident with corresponding results presented in C. Liu et al. (2018) and L. Liu et al. (2018). With incremental absorbing coatings, the AAE increases sharply, showing large values in ranges of 2.9–3.6, 2.6–3.3, and 1.9–3.0 for BC coated by BrC with F=0.0, 0.5, and 1.0, respectively.
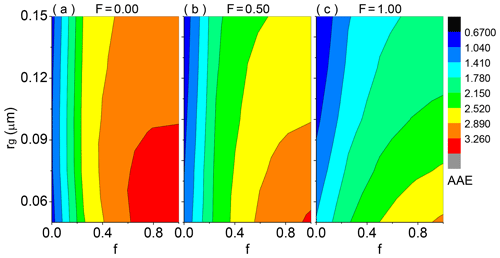
Figure 6The absorption Ångstrom exponent (AAE) of BC aggregates (BC fractal dimension of ∼2.8) coated by organics with different absorbing volume fractions of the coating (f) and particle size distributions. Three coated volume fractions of BC, being 0.00, 0.50, and 1.00, are shown from left to right. For fully coated BC structure, BC is located at the particle geometric center. The shell ∕ core ratio is 2.7, and the geometric standard deviation (σg) for the utilized lognormal distribution is 1.59.
In general, the absorbing volume fraction of the coating plays a more substantial role in the AAE determination than other sensitive microphysical parameters. The AAE of BC with non-absorbing coating shows weak sensitivity to size distribution, shell ∕ core ratio, and the coated volume fraction of BC, and a narrow AAE variation is seen with values around 1.0 (i.e., approximately 0.7–1.4). However, with an increasing absorbing volume fraction of the coating, the coated BC AAE increases exponentially and becomes strongly sensitive to size distribution, shell ∕ core ratio, and the coated volume fraction of BC with a wide variation. In addition, our results with more realistic geometries indicate that the occurrence of BrC can only be determined with confidence if the AAE of coated BC is larger than 1.4. This is generally consistent with the findings of Lack and Cappa (2010) produced by a core–shell Mie model, showing that BrC cannot be assigned with confidence unless AAE > ∼1.6.
3.4 Parameterization of the AAE of coated BC
After sensitivity analysis of all microphysical factors in the previous subsections, it apparently becomes feasible to parameterize the AAE of coated BC on the basis of the decomposition of the impacts of its microphysics. Among all microphysical parameters of coated BC, the absorbing volume fraction of the coating, coated volume fraction of BC, shell ∕ core ratio, and particle size distribution have significant effects on the AAE, whereas the impacts of the BC fractal dimension and BC position within the coating are comparatively negligible. Compared to the absorbing volume fraction of the coating, coated volume fraction of BC, and shell ∕ core ratio, the effect of particle size distribution on the AAE is comparatively complicated. Meanwhile, the impact of size distribution on the AAE is generally smaller than the other three important microphysical parameters and shows close sensitivities to the absorbing volume fraction of the coating and shell ∕ core ratio only for fully coated BC. Thus, to make the parameterization feasible, the absorbing volume fraction of the coating (f), coated volume fraction of BC (F), and shell ∕ core ratio (Dp∕Dc) are used for the AAE parameterization, whereas the size distribution is not considered (i.e., to be fixed). As discussed previously, the absorbing volume fraction of the coating, coated volume fraction of BC, and shell ∕ core ratio show a clearly monotonic impact on the AAE but to varying degrees. With other microphysical parameters fixed, the AAE of coated BC varies exponentially with each of these three parameters (i.e., f, Dp∕Dc, and F) and can be fitted well by power-law functions. To be more specific, for a fixed size distribution, the AAE of coated BC is assumedly expressed by
where k1–k6 denote the coefficients, indicating the significance of the relevant influence on the AAE of coated BC. Considering the aforementioned fixed size distribution (i.e., rg=0.075 µm, σg=1.59), which is commonly utilized in aerosol–climate models, the coefficients (with 95 % confidence range) can be fitted and the AAE of coated BC is given by
The fitting coefficients in Eq. (10) are acquired based on the smallest root mean square relative errors for all calculated values of AAE (R2=0.86). The correlation coefficient for parameterizing with three variables (i.e., f, Dp∕Dc, and F) is mildly smaller than that with one variable (i.e., using f, Dp∕Dc, or F and fixing the other two), and this is possibly associated with the lack of consideration of the combined interaction effects of f, Dp∕Dc, and F on the AAE in the parameterization. The influences of particle microphysics on the AAE of coated BC are obviously confirmed by corresponding coefficients in Eq. (10) with a quantitative understanding. High absolute values of fitting coefficients imply showing more significant impacts on the AAE of coated BC, while their negative or positive sign indicates the correlation sign. It is evident that the coated BC AAE is more sensitive to f and Dp∕Dc than F.
To confirm the capability of this parameterization to approximate the AAE of coated BC, Fig. 7 demonstrates absolute differences between the AAEs approximated by Eq. (10) and those from exact numerical simulations. It is clear that most of the approximated AAE results are in good agreement with the exact simulations, with differences less than 0.2. The externally attached BC shows relatively poor agreement compared to the partially and fully coated BC particles. However, considering that the partly and fully coated morphologies are dominant in aged BC based on observations (China et al., 2013, 2015), Fig. 7 reveals that this simple parameterization method we proposed gives rather accurate estimations of the AAE of coated BC with typical size distributions.
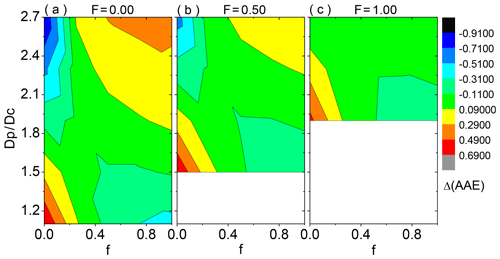
Figure 7Absolute differences between the absorption Ångstrom exponents (AAEs) approximated by Eq. (10) and those given by accurate numerical simulations. BC aggregates (BC fractal dimension of ∼2.8) coated by organics with different shell ∕ core ratios (Dp∕Dc) and absorbing volume fractions of the coating (f) are considered. Three coated volume fractions of BC, being 0.00, 0.50, and 1.00, are shown from left to right. For fully coated BC structure, BC is located at the particle geometric center.
3.5 Atmospheric implications
The theoretical results presented may show universal significance, as inorganic species contained in ambient BC coatings exhibit similar refractive indices to those of non-absorptive organics in this study. It is found that the absorbing volume fraction of the coating plays a crucial role in the AAE determination, and the AAE of BC with non-absorbing coating is weakly sensitive to particle microphysics with values around 1.0 (i.e., 0.7–1.4). However, the AAE of BC with brown coatings is highly sensitive to the absorbing volume fraction of the coating, coated volume fraction of BC, shell ∕ core ratio, and particle size distribution with a wide variation, while the effects of the BC fractal dimension and BC position within the coating are negligible. With BrC contained in the coating, the AAE can be larger than 3.0 for coated BC with more small particles, heavy coating, or more BrC. Although the volume of BrC seems to be responsible for the large AAE of coated BC, more BC encapsulated in brown coating or more large-sized coated BC particles reduce this effect. Interestingly, BC coated by thin BrC with a large size distribution (i.e., large rg) can have an AAE smaller than 1.0, and this implies that BC aerosols containing BrC can even show a lower AAE than pure BC particles, which challenges conventional beliefs. Meanwhile, the ambient measurement of small AAE (such as values near 1.0) does not exclude important contributions from BrC to absorption, since BC particles coated by BrC can give similar small AAE values based on our exact numerical simulation. Our results with more realistic geometries also indicate that the occurrence of BrC may not be confidently determined unless AAE > 1.4. Furthermore, the impacts of aerosol microphysics on coated BC AAE can be understood by Eq. (9) and can be quantitatively obtained by Eq. (10) for coated BC under a typical lognormal size distribution (i.e., rg=0.075 µm, and σg=1.59). The effects of various microphysical parameters on coated BC AAE are rather complex, and finding a best AAE parameterization is difficult. Nevertheless, with the help of Eqs. (9) and (10), the AAE of coated BC with brown coatings may be easily obtained if its key microphysics (i.e., size distribution, shell ∕ core ratio, absorbing volume fraction of the coating, and coated volume fraction of BC) are known.
The study numerically investigates the AAEs of polydisperse BC particles with brown coatings affected by their microphysics that are constrained within realistic ranges based on observations. The BC morphology is modeled by the fractal aggregate, whereas the MSTM is employed to exactly calculate the light absorption of coated BC. The results reveal that the AAE of BC with brown coatings is highly sensitive to the absorbing volume fraction of the coating, coated volume fraction of BC, shell ∕ core ratio, and particle size distribution with a broad variation, while the influences of BC position within the coating and the BC fractal dimension are generally negligible. Nevertheless, the AAE of BC with non-absorbing coating is weakly sensitive to particle microphysics with values around 1.0 (i.e., 0.7–1.4), indicating the substantial role of the absorbing volume fraction of the coating in determining the AAE. The AAE of BC with brown coatings can be larger than 3.0 for coated BC with more small particles, heavy coating, or more brown carbon. Meanwhile, BC coated by thin brown carbon with a large size distribution can show an AAE smaller than 1.0, implying that BC aerosols containing brown carbon can even show a lower AAE than pure BC particles, and this challenges conventional beliefs. With more realistic geometries, our study also indicates that the occurrence of brown carbon may not be confidently determined unless AAE > 1.4.
Although it is challenging to parameterize the AAE of coated BC based on various microphysical properties, we present a simple AAE parameterization method with key parameters (i.e., coated volume fraction of BC, shell ∕ core ratio, and absorbing volume fraction of the coating) for a known particle size distribution. For a typical lognormal size distribution (i.e., rg=0.075 µm, and σg=1.59), the complicated influences of sensitive microphysical parameters on the AAE of coated BC can be quantified with a good fitting correlation coefficient (R2=0.86). Overall, the work clearly demonstrates the distinctive importance of diverse microphysical properties for the AAE of coated BC. Nevertheless, caution may need to be taken with our results as a guide, since ambient observations of the microphysical properties of aged BC are still limited at present.
Data associated with this study are available at https://doi.org/10.5281/zenodo.3986854 (Zhang, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-9701-2020-supplement.
MM and XZ conceived the research plan. XZ performed the simulations and wrote the paper. All authors discussed the results and contributed to the final paper.
The authors declare that they have no conflict of interest.
We particularly appreciate Daniel W. Mackowski for the source codes of MSTM 3.0.
This work is financially supported by the National Natural Science Foundation of China (NSFC) (grant nos. 91644224 and 41505127) and the Natural Science Foundation of Jiangsu Province (grant no. BK20150901). This work is also supported by the Key Laboratory of Middle Atmosphere and Global Environment Observation (grant no. LAGEO-2019-04) and the Key Laboratory of Meteorological Disaster, Ministry of Education (grant no. KLME201810).
This paper was edited by Manvendra K. Dubey and reviewed by two anonymous referees.
Alexander, D. T. L., Crozier, P. A., and Anderson, J. R.: Brown Carbon Spheres in East Asian Outflow and their Optical Properties, Science, 321, 833–836, 2008.
Bond, T. C. and Bergstrom, R. W.: Light absorption by carbonaceous particles: an investigative review, Aerosol Sci. Tech., 40, 27–67, 2006.
Cappa, C. D., Onasch, T. B., Massoli, P., Worsnop, D. R., Bates, T. S., Cross, E. S., Davidovits, P., Hakala, J., Hayden, K. L., Jobson, B. T., Kolesar, K. R., Lack, D. A., Lerner, B. M., Li, S. M., Mellon, D., Nuaaman, I., Olfert, J. S., Petaja, T., Quinn, P. K., Song, C., Subramanian, R., Williams, E. J., and Zaveri, R. A.: Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 337, 1078–1081, 2012.
Chakrabarty, R. K., Moosmúller, H., Chen, L.-W. A., Lewis, K., Arnott, W. P., Mazzoleni, C., Dubey, M. K., Wold, C. E., Hao, W. M., and Kreidenweis, S. M.: Brown carbon in tar balls from smoldering biomass combustion, Atmos. Chem. Phys., 10, 6363–6370, https://doi.org/10.5194/acp-10-6363-2010, 2010.
Chakrabarty, R. K., Arnold, I. J., Francisco, D. M., Hatchett, B., Hosseinpour, F., Loria, M., Pokharel, A., and Woody, B. M.: Black and brown carbon fractal aggregates from combustion of two fuels widely used in Asian rituals, J. Quant. Spectrosc. Ra., 122, 25–30, 2013.
China, S., Mazzoleni, C., Gorkowski, K., Aiken, A. C., and Dubey, M. K.: Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles, Nat. Commun., 4, 2122, https://doi.org/10.1038/ncomms3122, 2013.
China, S., Scarnato, B., Owen, R. C., Zhang, B., Ampadu, M. T., Kumar, S., Dzepina, K., Dziobak, M. P., Fialho, P., Perlinger, J. A., Hueber, J., Helmig, D., Mazzoleni, L. R., and Mazzoleni, C.: Morphology and mixing state of aged soot particles at a remote marine free troposphere site: Implications for optical properties, Geophys. Res. Lett., 42, 1243–1250, 2015.
Clarke, A., McNaughton, C., Kapustin, V., Shinozuka, Y., Howell, S., Dibb, J., Zhou, J., Anderson, B., Brekhovskikh, V., Turner, H., and Pinkerton, M.: Biomass Burning and Pollution Aerosol over North America: Organic Components and Their Influence on Spectral Optical Properties and Humidification Response, J. Geophys. Res., 112, D12S18, https://doi.org/10.1029/2006JD007777, 2007.
Coz, E. and Leck, C.: Morphology and state of mixture of atmospheric soot aggregates during the winter season over Southern Asia – a quantitative approach, Tellus B, 63, 107–116, 2011.
Guo, S., Hu, M., Zamora, M. L., Peng, J. F., Shang, D. J., Zheng, J., Du, Z. F., Wu, Z., Shao, M., Zeng, L. M., Molina, M. J., and Zhang, R. Y.: Elucidating severe urban haze formation in China, P Natl. Acad. Sci. USA, 111, 17373–17378, 2014.
Gyawali, M., Arnott, W. P., Zaveri, R. A., Song, C., Moosmüller, H., Liu, L., Mishchenko, M. I., Chen, L.-W. A., Green, M. C., Watson, J. G., and Chow, J. C.: Photoacoustic optical properties at UV, VIS, and near IR wavelengths for laboratory generated and winter time ambient urban aerosols, Atmos. Chem. Phys., 12, 2587–2601, https://doi.org/10.5194/acp-12-2587-2012, 2012.
Hoffer, A., Gelencsér, A., Guyon, P., Kiss, G., Schmid, O., Frank, G. P., Artaxo, P., and Andreae, M. O.: Optical properties of humic-like substances (HULIS) in biomass-burning aerosols, Atmos. Chem. Phys., 6, 3563–3570, https://doi.org/10.5194/acp-6-3563-2006, 2006.
Kirchstetter, T. W. and Thatcher, T. L.: Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation, Atmos. Chem. Phys., 12, 6067–6072, https://doi.org/10.5194/acp-12-6067-2012, 2012.
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res., 109, D21208, https://doi.org/10.1029/2004JD004999, 2004.
Lack, D. A. and Cappa, C. D.: Impact of brown and clear carbon on light absorption enhancement, single scatter albedo and absorption wavelength dependence of black carbon, Atmos. Chem. Phys., 10, 4207–4220, https://doi.org/10.5194/acp-10-4207-2010, 2010.
Lack, D. A. and Langridge, J. M.: On the attribution of black and brown carbon light absorption using the Ångström exponent, Atmos. Chem. Phys., 13, 10535–10543, https://doi.org/10.5194/acp-13-10535-2013, 2013.
Lewis, K., Arnott, W. P., Moosmüller, H., and Wold, C. E.: Strong spectral variation of biomass smoke light absorption and single cattering albedo observed with a novel dual-wavelength photoacoustic instrument, J. Geophys. Res., 113, 280–288, 2008.
Li, W., Sun, J., Xu, L., Shi, Z., Riemer, N., Sun, Y., Fu, P., Zhang, J., Lin, Y., Wang, X., Shao, L., Chen, J., Zhang, X., Wang, Z., and Wang, W.: A conceptual framework for mixing structures in individual aerosol particles, J. Geophys. Res., 121, 13784–13798, 2016.
Liu, C., Chung, C. E., Yin, Y., and Schnaiter, M.: The absorption Ångström exponent of black carbon: from numerical aspects, Atmos. Chem. Phys., 18, 6259–6273, https://doi.org/10.5194/acp-18-6259-2018, 2018.
Liu, C., Xu, X., Yin, Y., Schnaiter, M., and Yung, Y.: Black carbon aggregates: A database for optical properties, J. Quant. Spectrosc. Ra., 222–223, 170–179, 2019.
Liu, D., Taylor, J. W., Young, D. E., Flynn, M. J., Coe, H., and Allan, J. D.: The effect of complex black carbon microphysics on the determination of the optical properties of brown carbon, Geophys. Res. Lett., 42, 613–619, 2015.
Liu, L. and Mishchenko, M. I.: Effects of aggregation on scattering and radiative properties of soot aerosols, J. Geophys. Res., 110, D11211, https://doi.org/10.1029/2004JD005649, 2005.
Liu, L. and Mishchenko, M. I.: Scattering and radiative properties of complex soot and soot-containing aggregate particles, J. Quant. Spectrosc. Ra., 106, 262–273, 2007.
Liu, L. and Mishchenko, M. I.: Scattering and Radiative Properties of Morphologically Complex Carbonaceous Aerosols: A Systematic Modeling Study, Remote Sens., 10, 1634, https://doi.org/10.3390/rs10101634, 2018.
Luo, J., Zhang, Y., Wang, F., and Zhang, Q.: Effects of brown coatings on the absorption enhancement of black carbon: a numerical investigation, Atmos. Chem. Phys., 18, 16897–16914, https://doi.org/10.5194/acp-18-16897-2018, 2018.
Mackowski, D. W.: A general superposition solution for electromagnetic scattering by multiple spherical domains of optically active media, J. Quant. Spectrosc. Ra., 133, 264–270, 2014.
Mishchenko, M. I., Dlugach, J. M., Yurkin, M. A., Bi, L., Cairns, B., Liu, L., Panetta, L. R., Travis, L., Yang, P., and Zakharova, N.: First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random media, Phys. Rep., 632, 1–75, 2016.
Moosmüller, H. and Chakrabarty, R. K.: Technical Note: Simple analytical relationships between Ångström coefficients of aerosol extinction, scattering, absorption, and single scattering albedo, Atmos. Chem. Phys., 11, 10677–10680, https://doi.org/10.5194/acp-11-10677-2011, 2011.
Moosmüller, H., Chakrabarty, R. K., and Arnott, W. P.: Aerosol light absorption and its measurement: A review, J. Quant. Spectrosc. Ra., 110, 844–878, 2009.
Moosmüller, H., Chakrabarty, R. K., Ehlers, K. M., and Arnott, W. P.: Absorption Ängström coefficient, brown carbon, and aerosols: basic concepts, bulk matter, and spherical particles, Atmos. Chem. Phys., 11, 1217–1225, https://doi.org/10.5194/acp-11-1217-2011, 2011.
Myhre, G.: Consistency between satellite-derived and modeled estimates of the direct aerosol effect, Science, 325, 187–190, 2009.
Ramanathan, V. and Carmichael, G.: Global and regional climate changes due to black carbon, Nat. Geosci., 1, 221–227, 2008.
Russell, P. B., Bergstrom, R. W., Shinozuka, Y., Clarke, A. D., DeCarlo, P. F., Jimenez, J. L., Livingston, J. M., Redemann, J., Dubovik, O., and Strawa, A.: Absorption Angstrom Exponent in AERONET and related data as an indicator of aerosol composition, Atmos. Chem. Phys., 10, 1155–1169, https://doi.org/10.5194/acp-10-1155-2010, 2010.
Schnaiter, M., Horvath, H., Möhler, O., Naumann, K.-H., Saathoff, H., and Söchck, O. W.: UV-VIS-NIR spectral optical properties of soot and soot-containing aerosols, J. Aerosol Sci., 34, 1421–1444, 2003.
Schnaiter, M., Linke, C., Möhler, O., Naumann, K. H., Saathoff, H., Wagner, R., and Schurath, U.: Absorption amplification of black carbon internally mixed with secondary organic aerosol, J. Geophys. Res., 110, D19204, https://doi.org/10.1029/2005JD006046, 2005.
Schuster, G. L., Dubovik, O., Arola, A., Eck, T. F., and Holben, B. N.: Remote sensing of soot carbon – Part 2: Understanding the absorption Ångström exponent, Atmos. Chem. Phys., 16, 1587–1602, https://doi.org/10.5194/acp-16-1587-2016, 2016.
Schwarz, J. P., Gao, R. S., Spackman, J. R., Watts, L. A., Thomson, D. S., Fahey, D. W., Ryerson, T. B., Peisch, J., Holloway, J. S., Trainer, M., Frost, G. J., Baynard, T., Lack, D. A., de Gouw, J. A., Warneke, C., and Del Negro, L. A.: Measurement of the mixing state, mass, and optical size of individual black carbon particles in urban and biomass burning emissions, Geophys. Res. Lett., 35, L13810, https://doi.org/10.1029/2008GL033968, 2008.
Shiraiwa, M., Kondo, Y., Iwamoto, T., and Kita, K.: Amplification of light absorption of black carbon by organic coating, Aerosol Sci. Tech., 44, 46–54, 2010.
Sorensen, C. M.: Light scattering by fractal aggregates: A review, Aerosol Sci. Tech., 35, 648–687, 2001.
Tritscher, T., Juranyi, Z., Martin, M., Chirico, R., Gysel, M., Heringa, M. F., DeCarlo, P. F., Sierau, B., Prevot, A. S. H., Weingartner, E., and Baltensperger, U.: Changes of hygroscopicity and morphology during ageing of diesel soot, Environ. Res. Lett., 6, 034026, https://doi.org/10.1088/1748-9326/6/3/034026, 2011.
Utry, N., Ajtai, T., Filep, A., Pinter, M., Torok, Z., Bozoki, Z., and Szabo, G.: Correlation between absorption Angstrom exponent of wintertime ambient urban aerosol and its physical and chemical properties, Atmos. Environ., 91, 52–59, 2014.
Yu, F. and Luo, G.: Simulation of particle size distribution with a global aerosol model: contribution of nucleation to aerosol and CCN number concentrations, Atmos. Chem. Phys., 9, 7691–7710, https://doi.org/10.5194/acp-9-7691-2009, 2009.
Zhang, K., O'Donnell, D., Kazil, J., Stier, P., Kinne, S., Lohmann, U., Ferrachat, S., Croft, B., Quaas, J., Wan, H., Rast, S., and Feichter, J.: The global aerosol-climate model ECHAM-HAM, version 2: sensitivity to improvements in process representations, Atmos. Chem. Phys., 12, 8911–8949, https://doi.org/10.5194/acp-12-8911-2012, 2012.
Zhang, R., Khalizov, A. F., Pagels, J., Zhang, D., Xue, H., and McMurry, P. H.: Variability in morphology, hygroscopicity, and optical properties of soot aerosols during atmospheric processing, P. Natl. Acad. Sci. USA, 105, 10291–10296, 2008.
Zhang, X.: xiaolinzhang/Data_FOR_ACP-2020-224: ACP-2020-224, https://doi.org/10.5281/zenodo.3986854, 2020.
Zhang, X., Rao, R., Huang, Y., Mao, M., Berg, M. J., and Sun, W.: Black carbon aerosols in urban central China, J. Quant. Spectrosc. Ra., 150, 3–11, 2015.
Zhang, X., Mao, M., Yin, Y., and Wang, B.: Absorption enhancement of aged black carbon aerosols affected by their microphysics: A numerical investigation, J. Quant. Spectrosc. Ra., 202, 90–97, 2017.
Zhang, X., Mao, M., Yin, Y., and Wang, B.: Numerical investigation on absorption enhancement of black carbon aerosols partially coated with nonabsorbing organics, J. Geophys. Res., 123, 1297–1308, 2018.
Zhang, X., Mao, M., and Yin, Y.: Optically effective complex refractive index of coated black carbon aerosols: from numerical aspects, Atmos. Chem. Phys., 19, 7507–7518, https://doi.org/10.5194/acp-19-7507-2019, 2019a.
Zhang, X., Jiang, H., Mao M., and Yin, Y.: Does optically effective complex refractive index of internal-mixed aerosols have a physically-based meaning?, Opt. Express, 27, 1216–1224, 2019b.
Zhang, Y., Zhang, Q., Cheng, Y., Su, H., Kecorius, S., Wang, Z., Wu, Z., Hu, M., Zhu, T., Wiedensohler, A., and He, K.: Measuring the morphology and density of internally mixed black carbon with SP2 and VTDMA: new insight into the absorption enhancement of black carbon in the atmosphere, Atmos. Meas. Tech., 9, 1833–1843, https://doi.org/10.5194/amt-9-1833-2016, 2016.