Strong sensitivity of the isotopic composition of methane to the plausible range of tropospheric chlorine

The ¹³C isotopic ratio of methane, δ¹³C of CH₄, provides additional constraints on the CH₄ budget to complement the constraints from CH₄ observations. The interpretation of δ¹³C observations is complicated, however, by uncertainties in the methane sink. The reaction of CH₄ with Cl is highly fractionating, increasing the relative abundance of ¹³CH₄, but there is currently no consensus on the strength of the tropospheric Cl sink. Global model simulations of halogen chemistry differ strongly from one another in terms of both the magnitude of tropospheric Cl and its geographic distribution. This study explores the impact of the intermodel diversity in Cl fields on the simulated δ¹³C of CH₄. We use a set of GEOS global model simulations with different predicted Cl fields to test the sensitivity of the δ¹³C of CH₄ to the diversity of Cl output from chemical transport models. We find that δ¹³C is highly sensitive to both the amount and geographic distribution of Cl. Simulations with Cl providing 0.28 % or 0.66 % of the total CH₄ loss bracket the δ¹³C observations for a fixed set of emissions. Thus, even when Cl provides only a small fraction of the total CH₄ loss and has a small impact on total CH₄, it provides a strong lever on δ¹³C. Consequently, it is possible to achieve a good representation of total CH₄ using widely different Cl concentrations, but the partitioning of the CH₄ loss between the OH and Cl reactions leads to strong differences in isotopic composition depending on which model's Cl field is used. Comparing multiple simulations, we find that altering the tropospheric Cl field leads to approximately a 0.5 ‰ increase in δ¹³CH₄ for each percent increase in how much CH₄ is oxidized by Cl. The geographic distribution and seasonal cycle of Cl also impacts the hemispheric gradient and seasonal cycle of δ¹³C. The large effect of Cl on δ¹³C compared to total CH₄ broadens the range of CH₄ source mixtures that can be reconciled with δ¹³C observations. Stronger constraints on tropospheric Cl are necessary to improve estimates of CH₄ sources from δ¹³C observations.

1 Introduction

The global budget of methane is of great interest due to methane's role as a greenhouse gas, ozone precursor, and sink of the hydroxyl radical. Despite extensive study, major uncertainties in the methane budget remain, with top-down and bottom-up estimates often yielding different results (Kirschke et al., 2013; Saunois et al., 2016, 2017, and references therein) for the strength of specific source types. Furthermore, the resumed increase of methane concentrations beginning in 2007 (Dlugokencky et al., 2009; Rigby et al., 2008) can be explained by multiple hypotheses including an increase in fossil fuel emissions (Turner et al., 2016; Thompson et al., 2015; Hausmann et al., 2016), an increase in fossil fuel emissions combined with a decrease in biomass burning (Worden et al., 2017), an increase in biogenic sources (Schaefer et al., 2016; Nisbet et al., 2016), or a decrease in hydroxyl concentrations (Turner et al., 2017; Rigby et al., 2017). Variations in hydroxyl concentrations may also be important for the decrease in methane growth from 1999 to 2006 (McNorton et al., 2016).

Observations and modeling of methane's carbon isotopes provide additional information on methane sources since individual sources differ in their ¹³C to ¹²C ratio (δ¹³C). Isotopic information can be used to better constrain methane sources (e.g., Thompson et al., 2015; Mikaloff Fletcher et al., 2004a, b) and infer how the source mixture changed over glacial (e.g., Hopcroft et al., 2018; Fischer et al., 2008; Bock et al., 2017), millennial (e.g., Ferretti et al., 2005; Houweling et al., 2008), and decadal timescales (e.g., Nisbet et al., 2016; Schaefer et al., 2016; Kai et al., 2011; Schwietzke et al., 2016; Thompson et al., 2018). However, there are considerable uncertainties in the processes that control methane's isotopic composition that may confound source apportionment studies. Many modeling studies use a single value for the isotopic ratio of each source, while in reality sources such as wetlands, biomass burning, and natural gas show large regional or environment-dependent variations in their isotopic signature (Ganesan et al., 2018; Brownlow et al., 2017; Dlugokencky et al., 2011; Schwietzke et al., 2016; Sherwood et al., 2017).

The isotopic composition of atmospheric methane is also sensitive to methane's sinks. Reaction with OH, the principal loss for atmospheric methane, has a kinetic isotope effect (KIE) of −5.4 ‰ ($\mathit{\alpha }=k_{\mathrm{13}}/k_{\mathrm{12}}=\mathrm{0.9946}$) to −3.9 ‰ (α=0.9961) (Saueressig et al., 2001; Cantrell et al., 1990) and contributes to the interhemispheric gradient of δ¹³C (Quay et al., 1991). Mass balance (Lassey et al., 2007) and observations of the seasonal cycle of δ¹³C versus methane concentration, however, suggest larger apparent KIE values, which may indicate a role for methane oxidation by chlorine (Cl) in the marine boundary layer (MBL) (Allan et al., 2001, 2007) since Cl has a KIE of −61.9 ‰ (α=0.938) at 297 K (Saueressig et al., 1995). Inclusion of the MBL Cl sink alters the source mixture inferred from inverse modeling of δ¹³CH₄ (Rice et al., 2016). Nisbet et al. (2019) point out that interannual variability in the CH₄ Cl sink could explain some of the variability of δ¹³C. Cl is also an important methane sink in the stratosphere, and the impact of this sink on surface δ¹³C is a source of uncertainty in modeling δ¹³C (Ghosh et al., 2015). Reaction with stratospheric Cl contributes approximately 0.23 ‰ to the δ¹³C of surface methane and makes a small contribution to the observed trend in surface δ¹³C over the last century (Wang et al., 2002).

The global concentration of Cl in the MBL and its role in the methane budget is still uncertain. Cl concentrations are highly variable and not well constrained by direct observations. Modeling work by Hossaini et al. (2016) and Sherwen et al. (2016) suggests that chlorine provides 2 %–2.5 % of tropospheric methane oxidation. This agrees well with estimates based on the isotopic fractionation, which also suggest Cl provides several percent of the total sink (Allan et al., 2007; Platt et al., 2004). However, Gromov et al. (2018) suggest that these are overestimates as values over 1 % are inconsistent with the δ¹³C of CO, which is a product of CH₄ oxidation. The recent modeling study of Wang et al. (2019) also suggests a value of 1 %. There is thus considerable uncertainty in the role of chlorine in the budget and isotopic composition of methane.

Here, we investigate the sensitivity of δ¹³C of CH₄ to intermodel diversity in tropospheric chlorine concentrations to better quantify how much uncertainty in the interpretation of δ¹³C is imposed by the uncertainty in Cl. Section 2 describes the modeling framework. We present results for total CH₄ and its isotopic composition compared to surface observations in Sect. 3 and discuss the implications for the global CH₄ budget in Sect. 4.

2 Methods

2.1 Model description

We simulate atmospheric methane with the Goddard Earth Observing System (GEOS) global earth system model (Molod et al., 2015; Nielsen et al., 2017). The model has 72 vertical levels extending from the surface to 1 Pa. We conduct simulations at C90 resolution on the cubed sphere, which corresponds to approximately 100 km horizontal resolution. The simulations' meteorology is constrained to the MERRA-2 reanalysis (Gelaro et al., 2017) using a “replay” method (Orbe et al., 2017). The GEOS replay agrees well with the tropospheric mean age of the Global Modeling Initiative (GMI) chemistry and transport model (CTM) (Orbe et al., 2017), which shows reasonable agreement with the age derived from SF₆ observations, albeit with an old bias in the Southern Hemisphere (Waugh et al., 2013). We thus expect the simulated interhemispheric transport time to be reasonable.

The GEOS CH₄ simulation can be interactively coupled to CO and OH (Elshorbany et al., 2016) or run independently with prescribed OH fields. We take the latter approach in this study, since this approach is able to capture many of the observed variations in atmospheric methane (Elshorbany et al., 2016). We prescribe the OH field following (Spivakovsky et al., 2000) but modify the OH to be approximately 20 % higher in the Northern Hemisphere than the Southern Hemisphere, consistent with the OH field produced by many global atmospheric chemistry models (Naik et al., 2013; Strode et al., 2015). This modification is designed to make our results more applicable to understanding the impacts of intermodel differences in Cl, since it makes our OH distribution more consistent with that produced by many chemistry–climate models (CCMs). The OH field varies monthly but repeats every year. We also include stratospheric losses for CH₄ from reaction with OH, Cl, and O¹D. These fields are prescribed from output of the GMI CTM (https://gmi.gsfc.nasa.gov, last access: 13 July 2020) (Strahan et al., 2007; Duncan et al., 2007).

We implement the CH₄ isotopes in GEOS by separately simulating ¹³CH₄ and ¹²CH₄ tracers. We then calculate total CH₄ as the sum of the two carbon isotopologues and calculate δ¹³C of CH₄ in per mil using the standard definition:

$$\begin{array}{}\text{(1)}& {\mathit{\delta }}^{\mathrm{13}}\mathrm{C}-{\mathrm{CH}}_{\mathrm{4}}\left(\mathrm{‰}\right)=\left(\left[{}^{\mathrm{13}}{\mathrm{CH}}_{\mathrm{4}}\right]/\left[{}^{\mathrm{12}}{\mathrm{CH}}_{\mathrm{4}}\right]/R_{\mathrm{std}}-\mathrm{1}\right)\cdot \mathrm{1000},\end{array}$$

where R_std=0.0112372 is the Peedee belemnite (PDB) isotopic standard (Craig, 1957). We partition each emission source into ¹²CH₄ and ¹³CH₄ emissions according to a source-specific δ¹³C value from the literature, provided in Table 1. We use the Craig (1957) R_std value to partition the sources since it is cited in the literature used in Table 1 (Houweling et al., 2000; Lassey, 2007), and so for consistency we use the same value in Eq. (1) to calculate the simulated δ¹³C of the CH₄ concentrations. We note, however, that the Global Monitoring Division (GMD) observations now use a slightly different standard, the Vienna PDB (VPDB) value of 0.011183 (Zhang and Li, 1990). A sensitivity study (not shown) confirms that the choice R_std has little effect on our results as long as the same value is used for the source partitioning as for the calculation of δ¹³C-CH₄ from simulated [¹³CH₄] and [¹²CH₄].

Table 1 Emission source references, description of interannual variability (IAV), and δ¹³C values.

^a δ¹³C values from Dlugokencky et al. (2011), Lassey et al. (2007), Monteil et al. (2011), Houweling et al. (2000), and references therein. ^b Values for 2004.

The reaction rates for CH₄+OH, CH₄+Cl, and CH₄+O¹D differ between the ¹²CH₄ and ¹³CH₄ simulations to account for the kinetic isotope effect (KIE). In particular, we assume α values of 0.987 and 0.938 for CH₄+O¹D and CH₄+Cl, respectively (Saueressig et al., 1995, 2001). Our standard simulation uses α_OH=0.9946 (Cantrell et al., 1990).

Methane from different sources is tracked individually using a “tagged tracer” approach, which allows us to simulate the spatial footprint of CH₄ and δ¹³C-CH₄ from individual sources. The soil sink is applied to each tracer as a fraction of its source, modified to account for faster loss of ¹²CH₄ to soil compared to ¹³CH₄ (α_soil=0.978) (Tyler et al., 1994). Figure S1 in the Supplement shows the July 2004 CH₄ and δ¹³C-CH₄ footprints of the biomass burning, wetland, and coal plus other geologic CH₄ sources from the tagged tracers to illustrate the tagged tracer approach. We note that the δ¹³C values of the surface methane from each source is heavier (less negative) than the emission value for that source (Table 1), especially in regions far from the source, because of the fractionating effects of the sinks. Figure S2 shows the corresponding footprints for January.

2.2 Description of simulations

We simulate the period from 1990 through 2004 and focus our analysis on 2004. We choose 2004 as our endpoint because it lies within the period when methane concentrations remained relatively flat, simplifying our analysis. Ending the simulations in 2004 also avoids much of the uncertainty about the causes of the resumed growth rate in recent years. The isotopic ratios of methane take longer to adjust to a perturbation than total methane (Tans, 1997). Since we wish to begin our simulations with a state that is as close as possible to “spun up”, we choose the initial condition for each tagged tracer based on its present-day distribution and proportion of the total CH₄ and scale it back to 1990 levels such that the total CH₄ is consistent with the global mean CH₄ from surface observations for 1990. We then iteratively adjusted the ¹²C- to ¹³C-CH₄ tracer ratios at the beginning of 1990 to yield a good match to global mean δ¹³C-CH₄ observations for 1998, when more δ¹³C-CH₄ observations are available. The same initial condition is used for the standard and sensitivity simulations.

We use interannually varying emissions of CH₄ from anthropogenic, biomass burning, and wetland sources. Emissions from anthropogenic sources such as oil and gas, energy production, industrial activities, and livestock come from the EDGAR version 4.2 inventory (European Commission, 2011). Biomass burning emissions come from the MACCity inventory (Granier et al., 2011). We treat forest fires as C3 burning and savannas as C4 burning for partitioning the biomass burning emissions between isotopologues. Wetland and rice emissions come from the Vegetation Integrative Simulator for Trace gases (VISIT) terrestrial ecosystem model (Ito and Inatomi, 2012), scaled by 0.69 and 0.895, respectively, for consistency with the Transcom-CH₄ study (Patra et al., 2011). Ocean (Houweling et al., 1999), termite (Fung et al., 1991), and mud volcano emissions (Etiope and Milkov, 2004) are also from the Transcom study (Patra et al., 2011) and have a seasonal cycle but no interannual variability. Initial tests with these emissions showed a substantial underestimate of the CH₄ growth rate. Consequently, we scale up all the emissions by 10 % for 1990–1998 and by 6.8 % for 1998–2004. We find the resulting emissions lead to a good simulation of the time series of surface CH₄ observations from the National Oceanic and Atmospheric Administration (NOAA) GMD (Dlugokencky et al., 2018), especially towards the end of the period (Fig. 1). The simulation has only a 0.1 % mean bias compared to the observations for 2004.

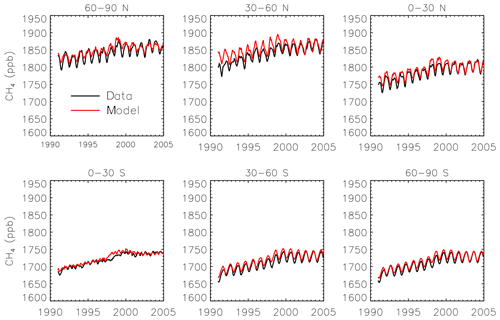
Figure 1 Monthly CH₄ observations from the GMD network (black) and simulated surface concentrations from SimStd (red) averaged over latitude bands.

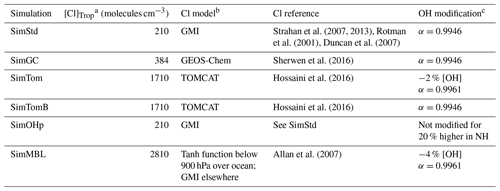
Our standard simulation (SimStd) uses Cl from the GMI CTM for the tropospheric as well as stratospheric loss of CH₄ by reaction with Cl. Tropospheric Cl concentrations are small in GMI since it does not include very short lived species, and reaction with Cl represents only 0.28 % of the total tropospheric CH₄ loss. We also conduct several sensitivity simulations in which we alter the tropospheric and lower stratospheric Cl fields (Table 2). Cl is not altered above 56 hPa. Sensitivity simulation SimGC uses Cl from the GEOS-Chem chemistry module within GEOS (Long et al., 2015; Hu et al., 2018). GEOS-Chem v11-02f with fully coupled tropospheric and stratospheric chemistry was used for this simulation, with halogen chemistry as described in Sherwen et al. (2016). SimGC has higher values of tropospheric Cl than SimStd (Figs. 3, 4) and leads to 0.66 % of the total CH₄ loss occurring via Cl. Both SimStd and SimGC are thus below the 1 % loss via Cl suggested by Gromov et al. (2018). We conduct a third sensitivity simulation, SimTom, which uses Cl from the TOMCAT model simulations that include chlorine sources from chlorocarbons (including very short lived substances), HCl from industry and biomass burning, and very short lived substances (Hossaini et al., 2016). This simulation leads to Cl accounting for 2.5 % of tropospheric CH₄ loss in our simulation. Finally, we conduct a fourth sensitivity simulation, SimMBL, which modifies the Cl over the oceans at altitudes below 900 hPa (Fig. 2d) to reflect the marine boundary layer distribution suggested by Allan et al. (2007). This Cl field is described by the following equation:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathrm{Cl}\mathit{\_}\mathrm{MBL}& =\mathrm{18}\times {\mathrm{10}}^{\mathrm{3}}\mathrm{atoms}{\mathrm{cm}}^{-\mathrm{3}}\cdot (\mathrm{1}+\tanh (\mathrm{3}\mathit{\lambda })\\ & \cdot \sin (\mathrm{2}\mathit{\pi }\cdot (t-\mathrm{90})/\mathrm{365}))\end{array},\end{array}$$

where λ is latitude in radians and t is the day of the year. Elsewhere SimMBL uses the Cl field from SimStd. This simulation has the highest percent of CH₄ loss occurring via Cl: 3.9 %. If we consider the loss of methane throughout the atmosphere rather than just the troposphere, then the percent lost via Cl increases to 1.6 %, 2.0 %, 3.6 %, and 5.0 % for SimStd, SimGC, SimTom, and SimMBL, respectively.

Figure 2 Annual zonal mean Cl field for (a) SimStd, (b) SimGC, (c) SimTom, and (d) SimMBL.

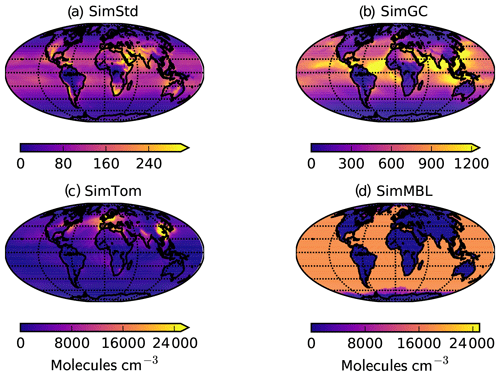
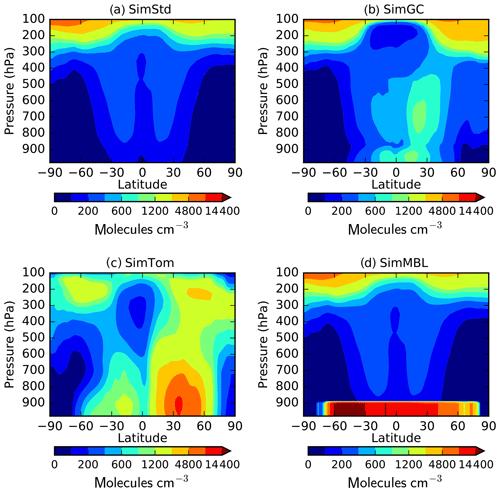
Figure 3 Annual mean surface concentrations of Cl in (a) SimStd, (b) SimGC, (c) SimTom, and (d) SimMBL. Note the different color scales between panels.

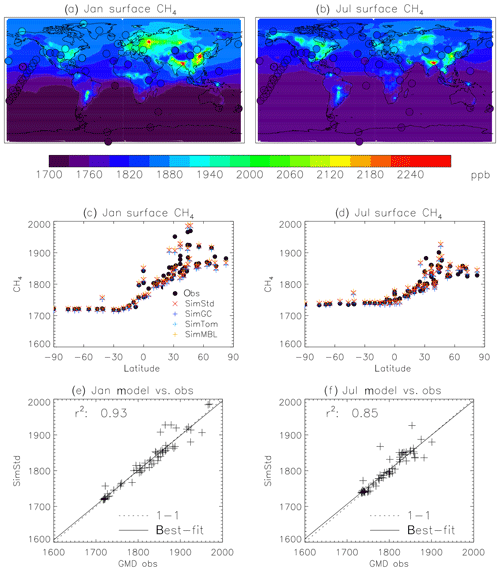
Figure 4 Comparison of 2004 simulated and observed surface CH₄ concentrations for January (a, c, e) and July (b, d, f). (a, b) Surface concentrations of CH₄ from SimStd are overplotted with the concentrations from the GMD observations in circles. (c, d) GMD observations (black circles), SimStd (red ×), SimGC (dark blue +), SimTom (light blue +), and SimMBL (orange +) CH₄ as a function of latitude. (e, f) SimStd CH₄ (ppb) at the observation locations versus the GMD observations (+ signs) as well as the regression line (solid) and one-to-one line (dashed).

Table 2 Oxidants for the standard and sensitivity simulations.

^a Concentration of Cl averaged over the troposphere. ^b Name of the model that generated the offline Cl field. ^c Changes to [OH] or α_OH compared to SimStd.

We designed the sensitivity experiments to alter the isotopic composition of CH₄ without greatly affecting the total CH₄. Consequently, we reduce the OH concentrations in the SimTom and SimMBL simulations by 2 % and 4 %, respectively, relative to the SimStd OH to offset the effect of increasing Cl. These changes are small compared to the uncertainty in global OH (Rigby et al., 2017). In addition, the SimTom and SimMBL simulations use α_OH=0.9961 (Saueressig et al., 2001) rather than α_OH=0.9946 (Cantrell et al., 1990) to avoid too much fractionation from the combined Cl and OH sinks. While these changes are necessary to maintain consistent total CH₄ and reasonable isotopic ratios, changing multiple factors in addition to Cl makes it difficult to quantify the impact of Cl alone. Consequently, we conduct an additional sensitivity study, called SimTomB, which uses the same Cl field as SimTom but retains the OH and α_OH values of SimStd. SimTomB is used in Sect. 3.3. This simulation becomes too heavy compared to observations, justifying the need to change α_OH in the main SimTom simulation. We also conduct a sensitivity simulation, SimOHp, that uses the same Cl field as SimStd but does not alter the hemispheric ratio of OH. Table 2 summarizes the standard and sensitivity simulations.

The four Cl distributions differ in their vertical and horizontal spatial distributions as well as their tropospheric mean (Figs. 2 and 3). The SimStd Cl is largest in the tropics, is nearly symmetric between hemispheres, and increases with altitude. Both SimGC and SimTom have Cl that is larger in the Northern Hemisphere than the Southern Hemisphere in the annual mean and reaches a minimum in the midtroposphere. However, the maximum in lower tropospheric Cl occurs in the tropics in SimGC but in the extratropics in SimTom. This midlatitude Cl maximum arises because SimTom has high Cl values over east Asia, whereas SimGC Cl is highest over ocean regions (Fig. 3). SimMBL has a strong maximum in the MBL compared to the free troposphere and land regions. Its annual mean Cl concentrations are higher in the Southern Hemisphere (Fig. 2) due to the larger ocean area in the Southern Hemisphere. However, SimMBL includes a strong seasonal shift in peak Cl between the hemispheres. SimStd and SimGC have more modest seasonal shifts, while Cl in SimTom remains concentrated in the Northern Hemisphere throughout the year (Fig. S3). All simulations repeat the same Cl field from year to year.

The sensitivity simulations listed above are designed to test the role of the Cl sink. We conduct an additional sensitivity study, SimWet, to illustrate the role of spatial variation in the isotopic source signature. SimWet parallels SimStd, but the isotopic composition of the wetland source uses spatial variation from Ganesan et al. (2018). The global mean source signature of the wetland emissions remains −60 ‰.

2.3 Observations

We use surface observations from the NOAA GMD Carbon Cycle Cooperative Global Air Sampling Network to evaluate our simulations. We use the monthly mean observations of total CH₄ (Dlugokencky et al., 2018) and δ¹³C of CH₄ (White et al., 2018) to compare to the monthly mean simulation results. The isotopic measurements were made at the Institute of Arctic and Alpine Research at the University of Colorado and are referenced to the VPDB scale (Zhang and Li, 1990). The analytical uncertainty of the isotopic measurements is 0.06 ‰. The variability between measurements taken in a given month may, however, be larger, so we use the maximum of analytical uncertainty and the within-month standard deviation as the uncertainty in the monthly mean. When multiple years of observations are averaged together, we use the pooled variance to calculate the standard error, thus reducing the error based on the number of years. The GMD observations are located at remote sites, shown in Fig. 4 for CH₄ in 2004. Measurements of δ¹³C of CH₄ are available at a subset of the sites, shown in Fig. 5.

Figure 5 Maps of the simulated surface δ¹³C of CH₄ in per mil for January (left) and July (right) overplotted with observations from the GMD sites (circles). The simulations are (a, b) SimStd, (c, d) SimGC, (e, f) SimTom, (g, h) SimMBL, and (i, j) SimWet.

3 Results and discussion

3.1 Evaluation of simulated CH₄

We find good agreement between the SimStd simulation and the GMD observations for CH₄ (Fig. 4) for 2004. We focus on these 2 months to represent the seasonal differences. The latitudinal distribution is well reproduced, and the simulation captures the elevated concentrations of CH₄ observed over Europe in January as well as the January versus July differences in concentration. Overall, the spatial correlation between SimStd and the observations is 0.93 in January and 0.85 in July. The sensitivity simulations described in Table 2 have little effect on the CH₄ distribution, as shown by the overlapping symbols in Fig. 4c, d.

3.2 Impact of Cl on the δ¹³C distribution

We next examine the distribution of δ¹³C in SimStd compared to observations. Figure 6 shows the time series of observed and simulated δ¹³C for 1998–2004 at the six GMD sites with δ¹³C records covering this time period. We begin the figure at 1998 rather than 1990 due to the lack of data availability in the earlier years. The standard and sensitivity simulations overestimate δ¹³C at the northernmost station, BRW. The observations at the other stations lie within the range of simulations, with most simulations underestimating the observations at the south pole. The differences between the different sensitivity simulations are large compared to the interannual variability in both observed and simulated δ¹³C. We focus our subsequent analysis on a single year, 2004.

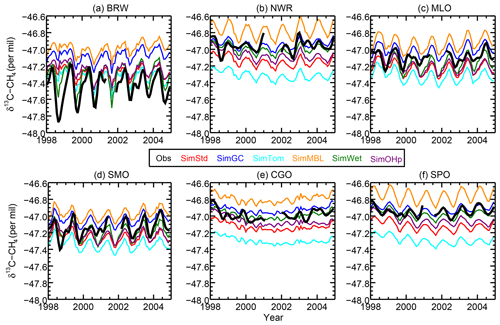
Figure 6 The time series of observed (black) and simulated (colors) δ¹³CH₄ at the six GMD sites with records extending back to 1998. BRW: 71.3^∘ N, 156.6^∘ W; NWR: 40.0^∘ N, 105.6^∘ W; MLO: 19.5^∘ N, 155.6^∘ W; CGO: 40.7^∘ S, 144.7^∘ E; and SPO: 90.0^∘ S, 24.8^∘ W.

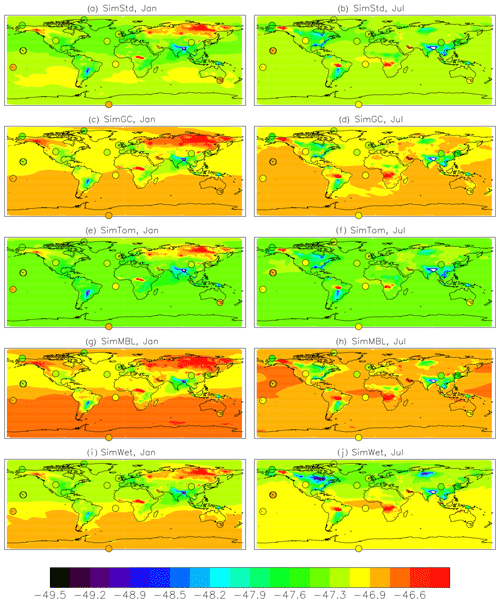
Figure 5a and b show both meridional and zonal variability in δ¹³C. Background values are less negative (heavier) in the Southern versus Northern Hemisphere (NH) (Fig. 7), a feature seen more strongly in the observations, but there is also variability due to the different source signatures. Areas of biomass burning, such as tropical Africa, show up as particularly heavy, while regions with large wetland and rice emissions, such as SE Asia, are particularly light. Another prominent feature is the isotopically heavy region in northern Eurasia (around 60^∘ N) in January, which we attribute to the influence of the geologic (including oil, gas, and coal) source in this region (Fig. S2). This signal is less evident in July, when greater influence from boreal wetlands lightens the isotopic mix. The spatial correlation (r²) between the SimStd and observed δ¹³C is 0.61 in January and 0.75 in July.

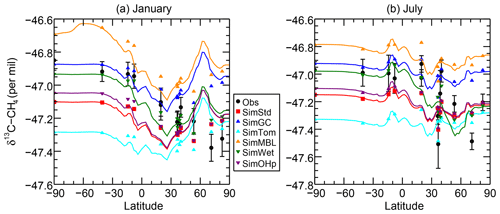
Figure 7 δ¹³C of CH₄ as a function of latitude in (a) January and (b) July 2004 for the GMD observations (black circles), SimStd (red), SimGC (dark blue), SimTom (cyan), SimMBL (orange), SimWet (green), and SimOHp (purple). Error bars represent the maximum of the analytical uncertainty (0.06 ‰) and the standard deviation of individual measurements in the month for each site. The colored lines represent the simulated zonal mean, while the colored symbols represent the simulation sampled at the location of the GMD observations.

The sensitivity simulations with altered oxidant concentrations alter the global values of δ¹³C, but the geographic patterns remain similar to that of SimStd. The larger Cl sink in SimGC leads to an overall less negative δ¹³C, which agrees better than SimStd with observations at Southern Hemisphere (SH) sites but worse in the NH (Figs. 6c, d and 7). The isotopic effect of the larger Cl sink in SimTom is compensated for by the lower OH and α_OH values used in that simulation, flattening the interhemispheric gradient (Figs. 6e, f and 7). In contrast, the very large MBL Cl concentrations in SimMBL lead to an overestimate (insufficiently negative) of the observed δ¹³C (Fig. 5g, h) but strengthen the interhemispheric gradient. We note that since all simulations began with the same initial conditions but have different sinks, the isotopic composition is not in steady state in 2004 and the results of the sensitivity simulations diverge further with additional years of simulation, with SimMBL becoming clearly inconsistent with observations. We note that while these results highlight the differences in δ¹³C imposed by changing Cl, the absolute values of δ¹³C, and hence their agreement with observations, would be different for CH₄ source mixtures with a different average δ¹³C.

Figure 7 reveals an underestimate in the interhemispheric gradient of δ¹³C in both SimStd and the sensitivity runs compared to the GMD observations. Table 3 presents the observed and simulated δ¹³C interhemispheric gradients calculated as the difference between the δ¹³C values averaged over all sites south of 30^∘ S and the average over sites north of 30^∘ N. SimStd and SimGC show similar underestimates of the observed gradient, and the underestimate is more severe in SimTom. The gradient is improved in SimMBL in January. The differences between simulations reflect differences in the locations where CH₄ oxidation occurs and the amount and location of isotopic fractionation due to Cl versus OH. Figure 8 shows that the higher Cl values over the NH, particularly China, in SimTom versus SimStd lead to more CH₄ loss occurring in the NH and higher (heavier) δ¹³C in the NH. This effect is particularly pronounced over China and Europe. Less fractionation by the OH sink in SimTom leads to lighter values in the SH. Conversely, SimMBL has more loss occurring over the SH oceans in January, leading to heavier δ¹³C in the SH (Fig. 9). This effect is not present in July, when the SimMBL Cl loss shifts to the NH (Fig. S4). The reduced hemispheric difference in OH in SimOHp leads to a small improvement in the hemispheric gradient in δ¹³C.

Table 3 Observed and simulated interhemispheric gradient in δ¹³C-CH₄.

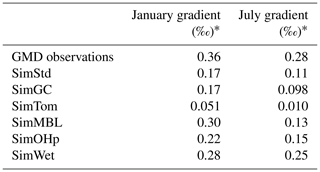
^* Average δ¹³C-CH₄ at GMD site locations south of 30^∘ S minus average δ¹³C-CH₄ at locations north of 30^∘ N.

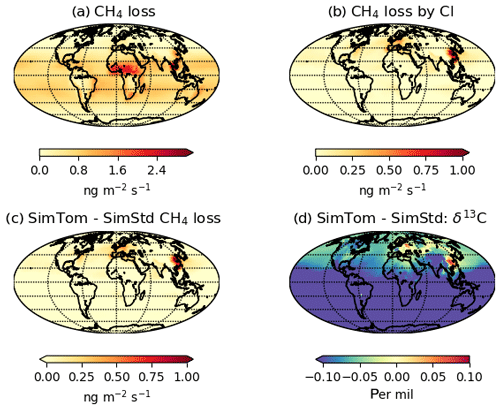
Figure 8 January (a) CH₄ loss and (b) CH₄ loss by Cl only in the SimTom simulation, as well as the difference in (c) CH₄ loss and (d) δ¹³C-CH₄ between the SimTom and SimStd simulations.

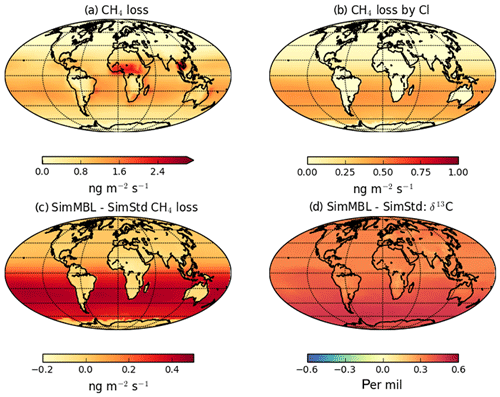
Figure 9 January (a) CH₄ loss and (b) CH₄ loss by Cl only in the SimMBL simulation, as well as the difference in (c) CH₄ loss and (d) δ¹³C-CH₄ between the SimMBL and SimStd simulations.

We further examine the seasonal cycle of δ¹³C in Fig. 10. We focus on the seasonal cycle at the South Pole Observatory (SPO) site because it is far from large CH₄ sources, and thus the seasonal cycle depends strongly on the seasonality of the CH₄ sinks. While all simulations lie mostly within the error bars of the observations, SimMBL has the largest seasonal cycle amplitude, overestimating the seasonal cycle at of the SPO observations with a δ¹³C value that is both too heavy in February–June and too light in August–November. In contrast, SimStd and the other sensitivity simulations underestimate the magnitude of the observed seasonal cycle at SPO. Figure S5 shows a large enhancement in the seasonal cycle amplitude between SimMBL and the other simulations for the Cape Grim site in Tasmania (CGO) but only a small change at other sites. This suggests that while MBL Cl is attractive as an explanation for the SH seasonality of δ¹³C, this explanation may be inconsistent with the inclusion of nonmarine Cl sources. However, since the seasonal cycle amplitude at SPO lies in between SimMBL and the other simulations, it is possible that at an MBL Cl source similar to that of SimMBL but with a smaller average value could reproduce the amplitude well.

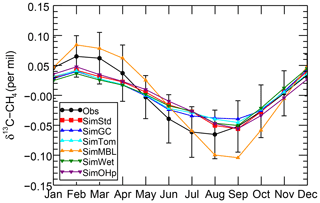
Figure 10 The seasonal cycle of δ¹³C of CH₄ at the SPO site with the annual mean removed averaged over 2002–2004 for the GMD observations (black), SimStd (red), SimGC (blue), SimTom (cyan), SimMBL (orange), SimWet (green), and SimOHp (purple). Error bars represent the standard error, calculated as the maximum of the pooled standard deviation or the analytical uncertainty (0.06 ‰), divided by the square root of the number of years of observations.

3.3 Quantifying the sensitivity of δ¹³C to CH₄ loss by Cl

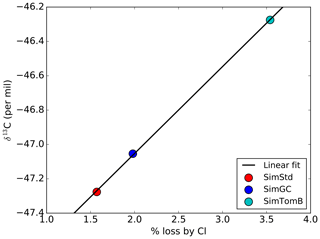
Given the substantial range in estimates for how much methane is lost by reaction with tropospheric Cl, it is important to quantify the sensitivity of global mean surface δ¹³C to the CH₄ loss by Cl. This analysis summarizes the global impact of the isotopic effect of the Cl differences between simulations discussed above. Figure 11 shows the global mean, area-weighted surface δ¹³C in 2004 as a function of the percent of CH₄ oxidized by Cl for SimStd, SimGC, and SimTomB, the three simulations with the same OH and emissions but different Cl. A strong linear relationship is evident between the oxidation by Cl and the surface δ¹³C. The slope of the linear regression line indicates the expected increase in surface δ¹³C for a change in the percent of CH₄ oxidized by Cl. Based on this analysis we expect that surface δ¹³C will increase by approximately 0.5 ‰ for each percent increase in CH₄ loss by Cl.

Figure 11 Area-weighted global mean surface δ¹³C for the SimStd (red), SimGC (blue), and SimTomB (cyan) simulations in 2004 as a function of the percent of CH₄ loss occurring by reaction with Cl. The linear best-fit line is shown in black.

3.4 Sensitivity of δ¹³C to the isotopic distribution of sources

Other factors in addition to the Cl distribution likely contribute to the mismatch between the observed and simulated interhemispheric gradients. Figure 5 shows the impact of the geologic source on the δ¹³C values over northern Asia. A bias in either the strength or the isotopic composition of this source will impact the interhemispheric gradient. Another likely contributing factor is our use of a globally uniform isotopic ratio for each source type. Ganesan et al. (2018) developed a global map of the isotopic signatures of wetland emissions. We use this map to impose spatially varying isotopic ratios on our SimWet simulation. SimWet increases the amplitude of the seasonal cycle in δ¹³C-CH₄ particularly for northern latitudes sites such as ALT, BRW, and MHD (Fig. S5). It has little effect on the seasonal cycle at the SH CGO and SPO sites, where SimMBL shows a large effect on the cycle. SimWet results in improved agreement with the observed interhemispheric gradient (Figs. 5, 7; Table 3). SimWet is better able to simultaneously match the δ¹³C-CH₄ observations at both the northernmost (BRW) and southernmost (SPO) sites shown in Fig. 6 than the other simulations, even though all simulations reproduce the latitudinal distribution of CH₄ well (Fig. 4). This highlights the importance of spatially varying isotopic ratios for the δ¹³C-CH₄ distribution. The size of the effect of including spatially varying ratios in wetland emissions depends on the strength of the wetland emissions as well as the other sources. Including spatially varying isotopic signature for other sources as well could further modify the simulated interhemispheric gradient, potentially correcting some of the flat gradient of, e.g., the SimTom simulation.

4 Conclusions

The role of Cl as a methane sink is a significant uncertainty in the global CH₄ budget, particularly with respect to isotopes. The global distribution of Cl is not well known from observations, and the Cl distributions simulated by global models vary widely from model to model. We investigated the sensitivity of the surface δ¹³C distribution of CH₄ to the intermodel diversity in tropospheric Cl using a series of sensitivity studies with a global 3D model. Given the uncertainties in CH₄ sources and their isotopic ratios, it is not possible to conclude from this study which Cl field is best. However, the differences between the simulations provide insight on the strong lever that tropospheric Cl exerts on the δ¹³C distribution.

Our standard and sensitivity simulations all reproduce well the geographic distribution of and temporal evolution of CH₄ observed at the GMD surface sites. However, imposing Cl distributions from a range of chemical transport models used in the scientific community leads to large differences in the simulated distribution of the δ¹³C of CH₄. The CH₄ sinks from Cl in our SimStd and SimGC simulations are both below 1 % of the total CH₄ sink, as suggested by Gromov et al. (2018). Yet the SimStd and SimGC simulations underestimate and overestimate, respectively, the observed δ¹³C in 2004, despite the fact that both include only a relatively small CH₄ sink from Cl.

Our ability to reproduce the observed latitudinal distribution of δ¹³C depends not only on the assumed value of global mean Cl, but also its geographic distribution. The detailed halogen chemistry model (TOMCAT) of Hossaini et al. (2016) places the maximum Cl values in the continental NH, in contrast to the large MBL Cl sink used in Allan et al. (2007) to explain SH observations. We find that the strong NH Cl maximum, along with the resulting reduction in OH fractionation required to maintain consistency with observations, acts to flatten the interhemispheric gradient of δ¹³C, while the MBL Cl sink increases the hemispheric differences in NH winter and also strengthens the seasonal cycle. However, the interhemispheric gradient is also influenced by spatial variation in the isotopic signatures of the sources and uncertainties in the soil sink, complicating this issue.

Two values for the fractionating effect of OH (α_OH) on δ¹³C (Cantrell et al., 1990; Saueressig et al., 2001) are widely cited in the literature. Combining the TOMCAT Cl fields with the α_OH of Saueressig et al. (2001) leads to an underestimate of observed δ¹³C, but combining it with the Cantrell et al. (1990) α_OH would lead to an overestimate. Reducing uncertainty in the fractionating effect of OH would thus improve our ability to constrain the role of Cl.

Observations of the δ¹³C of CH₄ provide an important tool for constraining the CH₄ budget. We find that the range of Cl fields available from current global models leads to a wide range of simulated δ¹³C values. Each percent increase in the amount of CH₄ loss occurring by reaction with Cl increases global mean surface δ¹³C of CH₄ by approximately 0.5 ‰. This relationship can be used to estimate the impact on methane's isotopic values from future model simulations of Cl. The choice of Cl field thus strongly impacts what CH₄ source mixture best fits δ¹³C observations. Better quantification of the role of Cl in the methane budget and further developing models of tropospheric halogens are therefore critical for interpreting the δ¹³C observations to their fullest potential.