The significant impact of aerosol vertical structure on lower atmosphere stability and its critical role in aerosol–planetary boundary layer (PBL) interactions

The aerosol–planetary boundary layer (PBL) interaction was proposed as an important mechanism to stabilize the atmosphere and exacerbate surface air pollution. Despite the tremendous progress made in understanding this process, its magnitude and significance still have large uncertainties and vary largely with aerosol distribution and meteorological conditions. In this study, we focus on the role of aerosol vertical distribution in thermodynamic stability and PBL development by jointly using micropulse lidar, sun photometer, and radiosonde measurements taken in Beijing. Despite the complexity of aerosol vertical distributions, cloud-free aerosol structures can be largely classified into three types: well-mixed, decreasing with height, and inverse structures. The aerosol–PBL relationship and diurnal cycles of the PBL height and PM_2.5 associated with these different aerosol vertical structures show distinct characteristics. The vertical distribution of aerosol radiative forcing differs drastically among the three types, with strong heating in the lower, middle, and upper PBL, respectively. Such a discrepancy in the heating rate affects the atmospheric buoyancy and stability differently in the three distinct aerosol structures. Absorbing aerosols have a weaker effect of stabilizing the lower atmosphere under the decreasing structure than under the inverse structure. As a result, the aerosol–PBL interaction can be strengthened by the inverse aerosol structure and can be potentially neutralized by the decreasing structure. Moreover, aerosols can both enhance and suppress PBL stability, leading to both positive and negative feedback loops. This study attempts to improve our understanding of the aerosol–PBL interaction, showing the importance of the observational constraint of aerosol vertical distribution for simulating this interaction and consequent feedbacks.

1 Introduction

Aerosols have a critical impact on the earth's climate through aerosol–cloud interactions (ACIs) and aerosol–radiation interactions (ARIs). They also continue to contribute to the considerable uncertainty in quantifying and interpreting the earth's changing radiation budget and hydrological cycles (Charlson et al., 1992; Ackerman et al., 2004; Boucher et al., 2013; Li et al., 2011, 2017a; Guo et al., 2017, 2019a). Despite the great advances made in the past decades in observational and modeling studies of aerosol effects, it is still a challenge to accurately quantify aerosol effects on the climate system due to an inadequate understanding of some mechanisms and strong variations in aerosol type, loading, and vertical distribution (Haywood and Boucher, 2000; Jacobson, 2001; Carslaw et al., 2013; Huang et al., 2015; Guo et al., 2016a; Z. Li et al., 2016; Wei et al., 2019a, b). Aerosols can interact with thermodynamic stability through ARI (Atwater, 1971; Bond et al., 2013). Absorbing aerosols can stabilize the atmosphere (Ramanathan et al., 2001; Wang et al., 2013; Ding et al., 2016) and may also enhance convection and precipitation under certain conditions (Menon et al., 2002; Li et al., 2017b).

Thermodynamic stability in the planetary boundary layer (PBL) dictates the PBL development (Stull, 1988; W. Zhang et al., 2018), thereby dominating the vertical dissipation of surface pollutants to some degree. Aerosols, in turn, have important feedbacks on the stability in the PBL, depending on aerosol properties, especially those of light-absorbing aerosols (e.g., black, organic, and brown carbon). However, due to large uncertainties in aerosol radiative forcing, it remains a challenge to quantify the impact of aerosols on thermodynamic stability and PBL development. Conventionally, increasing the aerosol absorption tends to stabilize the atmosphere, leading to a reduced PBL height (PBLH). A more stable atmosphere and lower PBLH will, in turn, increase the surface aerosol loading, which is the well-established positive feedback loop in the aerosol–PBL interaction (e.g., Wang et al., 2015; Ding et al., 2016; Petäjä et al., 2016; Dong et al., 2017; Zou et al., 2017; Q. Huang et al., 2018; Z. Wang et al., 2018; Wang et al., 2019). However, such a positive feedback loop may not be real for all situations and is subject to confounding factors such as aerosol type, aerosol vertical distribution, soil moisture, and PBL regime (Guo et al., 2019b; Lou et al., 2019). Geiß et al. (2017) reported the ambiguous relationship between surface aerosol loading and PBLH, while our previous study revealed weak correlations between surface pollutants and the PBLH in mountainous or clean regions (Su et al., 2018). Lou et al. (2019) showed that aerosols have a positive correlation with the PBLH under stable PBL conditions, indicating the importance of thermodynamic conditions in the PBL.

Among others, numerical models are one of the viable methods used to determine aerosol impacts on stability and PBL (e.g., Wang et al., 2014; Ding et al., 2016; Y. Wang et al., 2018; Zhou et al., 2018). The aerosol optical depth (AOD), a measure of aerosol columnar loading, is usually taken into account in model simulations. However, the aerosol vertical distribution in models is generally prescribed and may differ greatly from the real situation. With observational constraints, the role of aerosol vertical distributions in aerosol–PBL interactions warrants further investigation.

Ample observational datasets for Beijing are available, including aerosol vertical distributions derived from lidar, optical properties derived from the sun photometer, profiles of meteorological variables from radiosonde (RS), and surface PM_2.5 and meteorological parameters. Based on these measurements, a radiative transfer model is used to simulate the vertical profiles of aerosol radiative forcing that are employed to investigate the impact of aerosols on buoyancy in the lower atmosphere.

The paper is structured as follows. Section 2 introduces the datasets and methods used. Section 3 presents analyses of aerosol–PBL interactions under different aerosol vertical structures. Section 4 discusses the results with a brief summary.

2 Data and methods

2.1 Site description

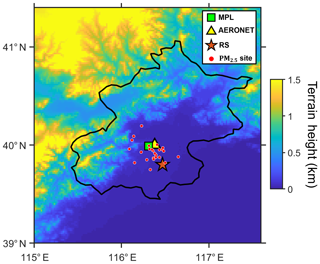
We utilized data from multiple sources in Beijing, a megacity located in the North China Plain. As one of the most densely populated and urbanized regions in the world, Beijing is a polluted region with high concentrations of absorbing aerosols (Zhang et al., 2019). The micropulse lidar (MPL) located in Beijing was operated continuously by Peking University (39.99^∘ N, 116.31^∘ E) from March 2016 to December 2018, with a temporal resolution of 15 s and a vertical resolution of 15 m. Due to incomplete laser pulse corrections, the near-surface lidar blind zone is ∼0.15 km. Background subtraction, saturation, after-pulse, overlap, and range corrections are applied to raw MPL data to calculate the normalized signals (Yang et al., 2013; Su et al., 2017a). MPL data on rainy days are excluded. Level 1.5 AOD and single-scattering albedos (SSAs) are employed at multiple wavelengths (i.e., 0.44, 0.5, 0.67, 0.87, and 1.02 µm) from the Beijing_RADI (40^∘ N, 116.38^∘ E) Aerosol Robotic Network (AERONET) site from 2011 to 2018 under cloud-free conditions (Holben et al., 1998; Smirnov et al., 2000; Zhang et al., 2017). The RS station (39.80^∘ N, 116.47^∘ E) in Beijing, operated by the China Meteorological Administration, is ∼25 km from the MPL site. The variables observed at the RS station include meteorological data and profiles of water vapor, temperature, pressure, and wind. The vertical resolution of the RS is altitude dependent and generally less than 8 m (Guo et al., 2016b; W. Zhang et al., 2018). The RS is routinely launched at 08:00 local time (LT) and 20:00 LT each day and is also launched at 14:00 LT in the summer (June–July–August). RS measurements were collected during 2011–2018. To reduce small-scale biases and to obtain a picture of the regional variation in particulate matter with a diameter smaller than 2.5 µm (PM_2.5), we acquire mean PM_2.5 data from 20 environmental monitoring stations located within 20 km from the lidar site, including one station at the Beijing Embassy of the United States. Figure 1 shows the topography of Beijing. The green square indicates the MPL site, and the yellow triangle indicates the AERONET station. The brown star represents the RS station, and the red–pink dots represent the PM_2.5 sites.

Figure 1 Topography of Beijing. The green square indicates the MPL site, and the yellow triangle indicates the AERONET station. The brown star shows the radiosonde (RS) station, and the red–pink dots show the PM_2.5 sites.

2.2 Statistical analysis methods

The statistical significance is tested by two independent statistical methods, namely least-squares regression and the Mann–Kendall (MK) tau test (Mann, 1945; Kendall, 1975; J. Li et al., 2016). Least-squares regression typically assumes a Gaussian data distribution in the trend analysis, whereas the MK test is a nonparametric test without any assumed functional form. The latter is more suitable for data that do not follow a certain distribution. To improve the robustness of the analysis, a relationship is considered significant when the confidence level is above 99 % for both the least-squares regression and the MK test. Hereafter, “significant” indicates that the correlation is statistically significant at the 99 % confidence level.

We primarily use the linear-fit method to build relationships between different parameters. The Pearson correlation coefficient derived from the linear regression analysis measures the degree to which the data fit a linear relationship. However, following our recent work (Su et al., 2018), inverse fitting $[f\left(x\right)=A/x+B]$ is used to establish the relationship between PBLH and PM_2.5. The magnitude of the correlation coefficient (R^†) is designed to measure the degree to which the data fit an inverse relationship. Since the relationship between the PBLH and PM_2.5 is nonlinear, the inverse fitting better characterizes this relationship.

2.3 PBLH and buoyancy derived from RS

The RS vertical resolution varies according to the balloon ascending rate. The RS records measurements every 1.2 s, which represents an approximate vertical resolution of 5–8 m. Prior to the retrieval of the PBLH, we further resample RS data to achieve a vertical resolution of 5 hPa with linear interpolation. We follow a well-established method developed by Liu and Liang (2010) to derive the PBLH based on profiles of the potential temperature gradient that takes into account different stability conditions. In this study, we only focus on PBLs driven by buoyancy, so PBLs driven by low-level jets are excluded using RS-derived wind profiles (Liu and Liang, 2010; Miao et al., 2018).

The static stability of the atmosphere is determined by the buoyancy force, which is expressed as (Wallace and Hobbs, 2006)

$$\begin{array}{}\text{(1)}& {\displaystyle }B={\displaystyle \frac{d^{\mathrm{2}}z}{\mathrm{d}{t}^{\mathrm{2}}}}={\displaystyle \frac{T^{\prime }-T}{T}}g=-g\mathrm{\Delta }z{\displaystyle \frac{\mathrm{1}}{\mathit{\theta }}}{\displaystyle \frac{\mathrm{d}\mathit{\theta }}{\mathrm{d}z}},\end{array}$$

where z is the height of the air parcel, and t indicates the time. T^′ represents the temperature of the parcel, T represents the temperature of the environment, and θ is the virtual potential temperature of the environment. An atmospheric layer is convective if the buoyancy is above zero and stable when the buoyancy is below zero. If the buoyancy is near zero, the atmosphere is neutral. We calculated buoyancy with a vertical resolution of 15 m. Based on the identification method for PBL type (Liu and Liang, 2010; W. Zhang et al., 2018), we present profiles of buoyancy forcing for stable, neutral, and convective PBLs (Fig. 2a). The results shown are averages from 3069 radiosonde measurements, of which 438 cases are convective PBLs, 714 cases are neutral PBLs, and 1916 cases are stable PBLs. The strongest upward or downward forcing occurs near the surface. Figure 2b–c further show the height-dependent correlation coefficients between buoyancy and PBLH–PM_2.5 with an interpolation window of 0.2 km. Note that the PBLH and surface PM_2.5 are fixed for the entire column, and the buoyancy is height dependent. Due to the insufficient development of the PBL, we do not use RS data at 08:00 LT here. To exclude the impact induced by the dragging effects of rainfall, we only consider cases without precipitation within the past 24 h. Strong upward buoyancy can uplift the PBLH and mitigate surface pollutants, especially in the lower atmosphere. Thus, we vertically average the buoyancy forcing profiles within the lowest 1 km (red line in Fig. 2b–c), defined as the lower atmosphere buoyancy (LAB). As shown in Fig. 3a–b, LAB and PM_2.5 are negatively correlated, and LAB and PBLH are positively correlated. LAB also has a significant negative correlation with absorbing aerosol optical depth (Fig. 3c). This may be due to the stabilizing effect of absorbing aerosols on the atmosphere, which is widely reported in many previous studies (H. Wang et al., 2015; Ding et al., 2016; Petäjä et al., 2016; Dong et al., 2017; Li et al., 2017b; X. Huang et al., 2018).

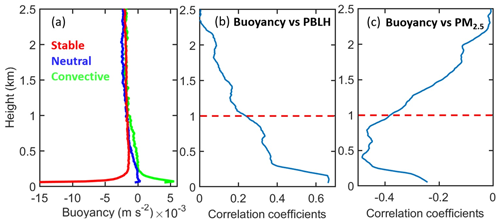
Figure 2 (a) Averaged vertical profiles of buoyancy forcing in stable, neutral, and convective PBLs. (b) Height-dependent correlation coefficients between buoyancy and PBLH. (c) Height-dependent correlation coefficients between buoyancy and surface PM_2.5. Note that the PBLH and surface PM_2.5 are fixed for the entire column, and the buoyancy is height dependent. The buoyancy in the lower atmosphere (<1 km) has the most important impact on the PBLH and surface PM_2.5. The buoyancy and PBLH are calculated from RS measurements made at 14:00 LT and 20:00 LT from 2011 to 2018.

2.4 PBLH and aerosol extinction coefficient derived from MPL

MPL data from Beijing were used to retrieve the PBLH during the daytime (08:00–19:00 LT). Many methods have been developed for retrieving the PBLH from MPL measurements, e.g., the signal threshold (Melfi et al., 1985), the maximum of the signal variance (Hooper and Eloranta, 1986), the minimum of the signal profile derivative (Flamant et al., 1997), and the wavelet transform (Cohn and Angevine, 2000; Davis et al., 2000; Su et al., 2017b; Chu et al., 2019). To derive the PBLH from MPL data, we adopted previous well-established approaches with several refinements, which have already been validated by long-term data collected at the Southern Great Plains site (Sawyer and Li, 2013; Su et al., 2020).

We initially identify the local maximum positions (range: 0.25–4 km) in the covariance transform function collocated with a signal gradient larger than a certain threshold. We further estimated the shot noise (σ) induced by background light and dark currents for each profile, and then set the threshold as 3σ. The initial PBLH retrieval (at 08:00 LT) is constrained by the PBLH value derived from the morning RS sounding. Then, the following PBLHs are retrieved using a stability-dependent model based on continuity. Boundary layer clouds are identified to diagnose the PBLH for cloudy cases. Figure 3d presents the comparison of summertime PBLH results derived from MPL and RS at 14:00 LT, showing good agreement (R=0.79).

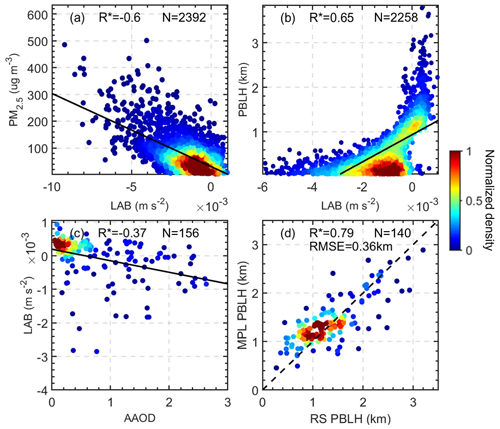
Figure 3 (a) The relationship between lower atmosphere buoyancy (LAB) and PM_2.5. (b) The relationship between LAB and PBLH. (c) The relationship between absorbing aerosol optical depth (AAOD) and LAB. In (a), (b), and (c), the LAB and PBLH are derived from RS measurements made at 14:00 and 20:00 LT, and AAOD is derived from AERONET measurements. The black solid lines indicate the best-fit lines from linear regression. (d) Comparison of PBLHs derived from the MPL and RS at 14:00 LT. Each panel gives the correlation coefficients (R), sample number (N), and root mean square error (RMSE). R with an asterisk indicates that the correlation is statistically significant at the 99 % confidence level. The color-shaded dots indicate the normalized sample density.

Multiple studies have provided a well-established algorithm to retrieve the vertical profiles of the aerosol extinction coefficient (AEC) from MPL data (e.g., Fernald, 1984; Klett, 1985; Liu et al., 2012). The Klett method is further used to retrieve extinction profiles (Klett, 1985). The column-averaged extinction-to-backscatter ratio (the so-called lidar ratio) is an important parameter in the retrieval process and is constrained using AERONET-derived AOD at 0.5 µm. The AEC is assumed to be equal within the blind zone. The overall uncertainties from the overlap function, the lidar ratio, the effects of multiple scattering, and noise fall within the range of 20 %–30 % in the retrieval process (He et al., 2006).

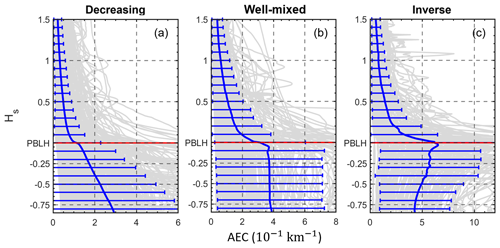
Figure 4 Normalized vertical profiles of the aerosol extinction coefficient (AEC) for (a) decreasing, (b) well-mixed, and (c) increasing (i.e., inverse) aerosol structures. The red line marks the position of the PBLH, the solid blue lines represent the average profiles of corresponding profiles, and error bars represent the standard deviations.

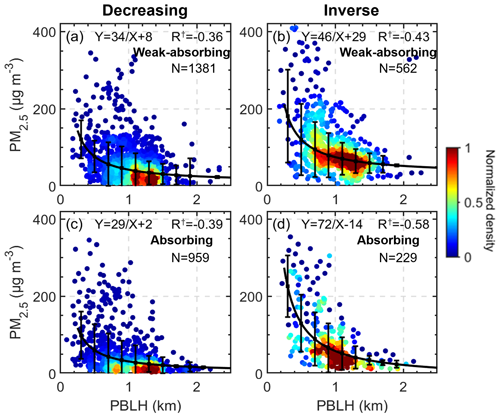
Figure 5 The relationship between MPL-derived PBLH and PM_2.5 for (a) weakly absorbing and (c) absorbing aerosols for the decreasing aerosol structure. The relationship between MPL-derived PBLH and PM_2.5 for (b) weakly absorbing and (d) absorbing aerosols for the increasing (i.e., inverse) aerosol structure. Black lines represent the inverse fits, and the whiskers indicate the standard deviations. The fitting functions and number of samples are given in each panel, along with the correlation coefficient (R^†) for the inverse fit.

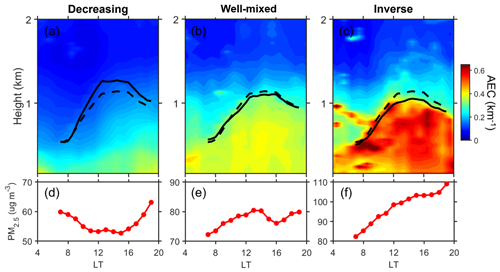
Figure 6 The averaged diurnal variations in AEC for (a) decreasing, (b) well-mixed, and (c) increasing (i.e., inverse) aerosol structures. Solid black lines indicate the averaged diurnal cycles of MPL-derived PBLH under the different aerosol structures. Dashed black lines represent the mean MPL-derived PBLH diurnal cycles. (d, e, f) The averaged diurnal variations in surface PM_2.5 under the different aerosol structures.

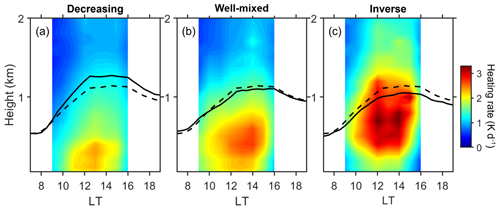
Figure 7 The averaged diurnal variations in aerosol radiative forcing in the vertical for (a) decreasing, (b) well-mixed, and (c) increasing (i.e., inverse) structures of aerosol loading. Solid black lines indicate the mean diurnal cycles of MPL-derived PBLH under different aerosol structures. Dashed black lines represent the mean MPL-derived PBLH diurnal cycles.

2.5 Estimation of the impacts of aerosols on buoyancy

To show vertical profiles of aerosol radiative forcing, the Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART) model (Ricchiazzi et al., 1998) was used to simulate the atmospheric heating rate (dT∕dt) induced by aerosols (Liu et al., 2012; Dong et al., 2017). Integrated aerosol inputs include AODs, SSAs (i.e., at 0.44, 0.67, 0.87, and 1.02 µm) retrieved from AERONET measurements, and AEC profiles at 0.5 µm obtained from the MPL. We also use Moderate Resolution Imaging Spectroradiometer surface reflectances as an additional input (https://modis.gsfc.nasa.gov/data/dataprod/mod09.php, last access: April 2019). We further use heating rates induced by aerosols to estimate the impact of aerosols on buoyancy.

Theoretically, the rate of change in buoyancy for a certain layer is expressed as

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& {\displaystyle \frac{\mathrm{d}B}{\mathrm{d}t}}={\displaystyle \frac{d}{\mathrm{d}t}}\left({\displaystyle \frac{T_{\mathrm{0}}-{\mathrm{\Gamma }}_{\mathrm{d}}\mathrm{\Delta }z-T}{T}}g\right)=\\ & {\displaystyle \frac{\left(\frac{\mathrm{d}{T}_{\mathrm{0}}}{\mathrm{d}t}-\frac{\mathrm{d}T}{\mathrm{d}t}\right)T+\frac{\mathrm{d}T}{\mathrm{d}t}({\mathrm{\Gamma }}_{\mathrm{d}}-\mathrm{\Gamma })\mathrm{\Delta }z}{T^{\mathrm{2}}}}g,\end{array}\end{array}$$

where most parameters are defined in the same way as in Eq. (1), and Γ_d (Γ) represents the dry adiabatic lapse rate (environmental lapse rate). We primarily focus on the rate of change in buoyancy during the noontime period (11:00–15:00 LT), when the PBL is well-developed and aerosol radiative forcing is strong. The rate of change in buoyancy (dB∕dt) induced by aerosols is largely determined by the aerosol heating rate, which can be produced by the radiative transfer model. Additional inputs include the environmental lapse rate and temperature obtained from noontime RS soundings in the summer. For other times, the environmental lapse rate and temperature are obtained from MERRA-2 reanalysis data, which assimilate coarse-resolution RS observations (Rienecker et al., 2011). In this way, we can estimate dB∕dt induced by aerosols with a primary focus on the daytime. Note that the errors in MERRA-2 data lead to uncertainties in the estimated dB∕dt. A 1–3 K uncertainty in MERRA-2 temperatures (Gelaro et al., 2017) leads to 1 %–3 % relative biases in the estimated dB∕dt. Considering the large variation in dB∕dt for different aerosol structures, the biases resulting from MERRA-2 data are not a serious issue.

3 Results

3.1 Classification of different aerosol structure scenarios

By altering the adiabatic heating rate of the atmosphere, the aerosol vertical distribution is of great importance to the PBL. Based on cloud-free AEC profiles in the PBL, aerosol vertical structures can be classified into three types: well-mixed, decreasing with height, and its inverse, increasing with height. If AEC varies by less than 20 % within the lowest 80 % of the PBL, it is considered a well-mixed structure. For the other cases, a decreasing structure indicates a peak in AEC near the surface, and the inverse structure indicates a peak in AEC in the middle or upper PBL.

To investigate the vertical variation in AEC within the PBL, the evolution of the PBLH has to be taken into account. Following previous studies (Ferrero et al., 2014; Kuang et al., 2016), vertical profiles were normalized by introducing a standardized height (H_s), calculated as follows:

$$\begin{array}{}\text{(3)}& H_{\mathrm{s}}={\displaystyle \frac{z-\mathrm{PBLH}}{\mathrm{PBLH}}},\end{array}$$

where z is the height above the ground, and H_s is 0 at the PBL top and −1 at ground level. Figure 4 shows the normalized vertical profiles of AEC derived from MPL data for different aerosol structures around noontime. The number of samples and percentages of decreasing, well-mixed, and increasing aerosol structures are 998 (51 %), 611 (32 %), and 330 (17 %), respectively. Since a temperature inversion located at the PBL top traps moisture and aerosols, there is a sharp decrease in the AEC profile from the PBL upper boundary to the free atmosphere. Variations in the aerosol vertical distribution largely depend on different conditions but share similar features among the different aerosol structure patterns. Despite complex aerosol vertical distributions, these three types of profiles can account for most of the cloud-free cases.

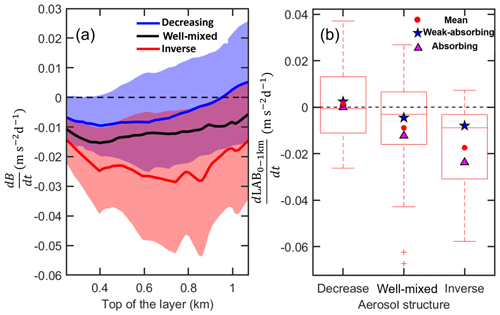
Figure 8 (a) The rate of change in buoyancy (dB∕dt) in a layer of the lowest atmosphere for decreasing (blue), well-mixed (black), and inverse (red) aerosol structures during noontime. The bottom of the layer is the surface, and the rate of change in buoyancy is subjected to the top of the layer. The shaded areas show the standard deviations of the rate of change in buoyancy. (b) Box-and-whisker plots showing the 10th, 25th, 50th, 75th, and 90th percentile values of the rate of change in LAB_0–1 km (integrated buoyancy within the lowest 1 km) during noontime. Red dots indicate the mean values, and blue stars and pink triangles show the means for weakly absorbing (SSA >0.9) and absorbing (SSA <0.85) cases.

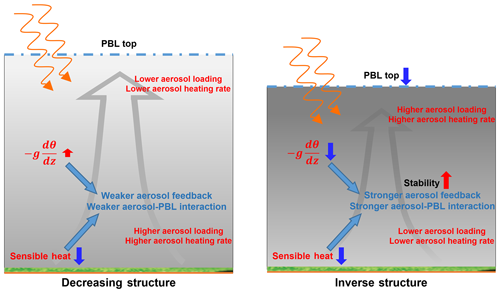
Figure 9 Schematic diagrams describing aerosol–PBL interactions when decreasing and inverse aerosol structures are present. The blue dash-dotted line indicates the top of the PBL. Orange curved arrows indicate solar radiation. The background grey arrow sketches the vertical transport of humidity, aerosols, and heat. The background greyscale indicates the pollution level.

3.2 BLH and PM_2.5 under different aerosol structure scenarios

Absorbing aerosols tend to have a positive feedback with the PBLH, and the aerosol vertical distribution plays a critical role in this process. We investigate the relationship between MPL-derived PBLH and PM_2.5 for absorbing (daily average SSA ≤0.85) or weakly absorbing (daily average SSA >0.9) aerosols for increasing and decreasing aerosol structures during 09:00–19:00 LT (Fig. 5). The PBLH–PM_2.5 relationships can represent the intensity of the aerosol–PBL interaction. In general, there are stronger correlations between PBLH and PM_2.5 for the inverse aerosol structure. This is likely caused by substantial heating in the upper PBL, facilitating the formation of a temperature inversion and further increasing the stability of the PBL. For the decreasing aerosol structure, aerosols may not significantly redistribute adiabatic energy. Hence, the PBLH–PM_2.5 correlation is relatively weak. Significant PBLH–PM_2.5 correlations are found for both absorbing and weakly absorbing cases, indicating that scattering aerosols may also play an important role in the aerosol–PBL interaction, especially for the inverse aerosol structure.

Figure 6 presents the averaged diurnal cycles of AEC, PBLH, and PM_2.5 for different aerosol vertical structures, classified based on the average AEC profiles during noontime. High humidity cases (surface relative humidity >90 %) and strong wind cases (wind speed >5 m s⁻¹) are excluded. Here, both AEC and PBLH are derived from MPL data. Data are collected on 371 available days, of which 191 have decreasing aerosol structures, 122 have well-mixed aerosol structures, and 58 have inverse aerosol structures. Multiple entangled factors can contribute to the formation of different aerosol structures within the PBL, including synoptic patterns, new particle formation, vertical turbulence, horizontal transport, and entrainment rates to name a few. In general, the inverse structure is characterized by higher aerosol loadings and lower PBLHs, whereas the decreasing structure is characterized by light pollution and a well-developed PBL. In theory, PM_2.5 should generally decrease with increasing PBLH in the morning due to the dilution effect. This situation is demonstrated clearly for decreasing aerosol structures. However, PM_2.5 continuously grows during the daytime when an inverse aerosol structure is present, regardless of the PBLH diurnal cycle. Even though many factors control the diurnal variations in aerosols and the PBL, the strong aerosol–stability interaction generates an unfavorable condition for the vertical dissipation of aerosols, so the surface aerosol loading can continuously accumulate due to emissions.

The correlations and statistical results concerning the PBLH and PM_2.5 provide hints about the differences in aerosol–PBL interactions for different aerosol structures. However, these results cannot explain the feedback loop and causality. Therefore, we further use the SBDART model with the constraint of ample observations to investigate the vertical profiles of radiative forcing induced by aerosols and its impacts on atmospheric stability.

3.3 Aerosol radiative forcing for different aerosol structures

Following the description in Sect. 2.5, we calculate the statistical means of aerosol radiative forcing in the vertical for decreasing, well-mixed, and inverse aerosol structures derived from the cases presented in Fig. 6. Figure 7 shows that the vertical distributions of the heating rate differ drastically among the different aerosol structures. For the inverse aerosol structure scenario, aerosols cause substantial heating in the upper PBL, facilitating the formation of a temperature inversion and further increasing the stability in the PBL. For the decreasing aerosol structure scenario, the abundance of aerosols at the bottom of PBL heats the lower PBL so can potentially enhance convection in the PBL.

There are considerable differences in the heating rate among the three distinct aerosol structures (Fig. 8), which affects the atmospheric buoyancy and stability differently. On average, aerosols generally suppress buoyancy in the lower atmosphere. Such an effect is quite notable for the inverse structure and is insignificant for the decreasing structure, with large standard deviations. Absorbing aerosols are not very helpful for stabilizing the lower atmosphere when a decreasing aerosol structure is present, but they play an important role when an inverse aerosol structure is present. As such, we expect the strongest aerosol–PBL interaction to occur for absorbing aerosol cases when an inverse aerosol structure is present, consistent with the results shown in Fig. 5.

Figure 9 shows schematic diagrams of the interactions between aerosols, stability, and the PBL when decreasing or inverse aerosol structures are present. Overall, both decreasing and inverse aerosol structures can cool the surface and suppress sensible heat, thus stabilizing the PBL. In both cases, aerosols have notable stabilizing effects near the surface.

When a decreasing aerosol structure is present, abundant aerosols near the surface generate a stronger aerosol heating rate in the lower PBL than in the upper PBL. Such aerosol radiative forcing lowers the potential temperature gradient (dθ∕dz) in the middle and upper PBL and can further strengthen vertical convection in the middle and upper PBL. The opposite aerosol effects on PBL stability lead to a relatively weak aerosol feedback and a relatively weak aerosol–PBL interaction. When an inverse aerosol structure is present, the significant heating effect on the upper PBL facilitates the formation of temperature inversion and further increases the stability and suppresses the PBLH. The notable increase in stability leads to the strong, positive aerosol feedback.

Highly variable aerosol vertical distributions cause large variations in the impact of aerosol on stability and thus exert important and highly variable influences on the aerosol–PBL interactions. Although aerosol stabilizes the PBL for the majority of cases, aerosol can also suppress stability in the lower atmosphere, when the aerosol heating effect is much stronger on the near surface than the upper PBL, and further lead to a potential negative feedback loop. The positive feedback loop leads to strong aerosol–PBL interactions, whereas the negative feedback loop leads to weak aerosol–PBL interactions. It explains the paradox of the different correlations between PBLH and surface pollutants since its magnitude, significance, and even sign reportedly vary or even reverse (Quan et al., 2013; Tang et al., 2016; Geiß et al., 2017; Su et al., 2018).

4 Summary and discussion

Based on integrated aerosol and meteorological measurements made in Beijing, the aerosol–PBL interaction is assessed for different aerosol vertical structures, i.e., decreasing, well-mixed, and inversely increasing with height. The aerosol–PBL relationships and the diurnal cycles of PBLH and PM_2.5 show distinct characteristics among the different aerosol vertical patterns. For the decreasing aerosol structure, PM_2.5 decreases in the morning with relatively large PBLH growth rates. In this situation, absorbing aerosols are not very helpful in stabilizing the lower atmosphere. For the inverse aerosol structure, PM_2.5 continuously grows during the daytime with relatively low PBLH growth rates. This phenomenon could be a sign of a strong aerosol–PBL interaction. The aerosol radiative forcing in the vertical for decreasing, well-mixed, and inverse aerosol structures differ drastically, with strong heating in the lower, middle, and upper PBL, respectively. Such a difference in the heating rate affects the atmospheric buoyancy and stability differently in the three distinct aerosol structures.

Turbulent fluxes and eddies in the PBL could spread out and redistribute the radiative effects induced by aerosols. Numerical models are needed to quantify the aerosol–PBL interaction and consequent feedbacks (e.g., Y. Wang et al., 2013; Ding et al., 2016; Z. Wang et al., 2018; Zhou et al., 2018). Aerosol vertical distributions vary greatly on both temporal and vertical scales and critically affect aerosol radiative effects. However, the aerosol vertical distribution is still poorly represented in numerical models, partly due to a lack of observational constraints. This study reveals the important role of the aerosol vertical distribution in aerosol–PBL interactions, which should be carefully taken into account in both observational analyses and model simulations.

This study used column-averaged aerosol properties from AERONET. However, the vertical variations in SSA and aerosol type remain unknown, inducing uncertainties in the estimation of aerosol effects. In the future, we plan to use aircraft data from field campaigns to better account for the influence of different types of aerosols with different properties.