Kinetics of the OH + NO₂ reaction: effect of water vapour and new parameterization for global modelling

The effect of water vapour on the rate coefficient for the atmospherically important, termolecular reaction between OH and NO₂ was determined in He–H₂O (277, 291, and 332 K) and N₂–H₂O bath gases (292 K). Combining pulsed-laser photolytic generation of OH and its detection by laser-induced fluorescence (PLP-LIF) with in situ, optical measurement of both NO₂ and H₂O, we were able to show that (in contrast to previous investigations) the presence of H₂O increases the rate coefficient significantly. We derive a rate coefficient for H₂O bath gas at the low-pressure limit ($k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) of $\mathrm{15.9}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹. This indicates that H₂O is a more efficient collisional quencher (by a factor of ≈6) of the initially formed HO–NO₂ association complex than N₂, and it is a factor of ≈8 more efficient than O₂. Ignoring the effect of water vapour will lead to an underestimation of the rate coefficient by up to 15 %, e.g. in the tropical boundary layer. Combining the new experimental results from this study with those from our previous paper in which we report rate coefficients obtained in N₂ and O₂ bath gases (Amedro et al., 2019), we derive a new parameterization for atmospheric modelling of the OH + NO₂ reaction and use this in a chemical transport model (EMAC) to examine the impact of the new data on the global distribution of NO₂, HNO₃, and OH. Use of the new parameters (rather than those given in the IUPAC and NASA evaluations) results in significant changes in the HNO₃∕NO₂ ratio and NO_x concentrations (the sign of which depends on which evaluation is used as reference). The model predicts the presence of HOONO (formed along with HNO₃ in the title reaction) in concentrations similar to those of HO₂NO₂ at the tropical tropopause.

1 Introduction

In our recent study of the title reaction (Amedro et al., 2019), we reported extensive measurements of the rate constant (k₁) for the termolecular reaction between OH and NO₂ (Reaction R1) in N₂ and O₂ bath gas over a large range of temperatures and pressures.

$$\begin{array}{}\text{(R1a)}& {\displaystyle }\mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}+\mathrm{M}& {\displaystyle }\to {\mathrm{HNO}}_{\mathrm{3}}+\mathrm{M},\text{(R1b)}& {\displaystyle }& {\displaystyle }\to \mathrm{HOONO}+\mathrm{M}.\end{array}$$

Reaction (R1) converts NO₂ to nitric acid (HNO₃) and peroxynitrous acid (HOONO), and its rate strongly influences the relative abundance of atmospheric NO_x (NO₂ + NO) and longer-lived “reservoirs” of NO_x, which include, for example, HNO₃ and organic nitrates. It also converts OH (the main initiator of atmospheric oxidation) to a long-lived reservoir (HNO₃). As the abundances of OH and NO_x directly impact on photochemical ozone formation and the lifetimes of greenhouse gases, Reaction (R1) may be considered one of the most important gas-phase processes in atmospheric science (Newsome and Evans, 2017). As outlined by Amedro et al. (2019), the rate coefficients and product branching for this reaction are dependent on pressure and temperature and also on the bath-gas identity, i.e. the identity of the collision partner (M in Reaction R1). The efficiency per collision of energy transfer from the initially “hot” association complex to bath gas can vary considerably, with more complex bath gases possessing more degrees of freedom and bonds with similar vibrational frequencies to those in the association complex being generally more efficient. In this sense, we may expect H₂O to be better than N₂ or O₂ in quenching [HO–NO₂]^#.

In this second part of our study of the reaction between OH and NO₂, we extend the experiments to H₂O and He bath gases. After N₂ (≈78 %) and O₂ (≈21 %), water vapour is the third most abundant gaseous species in the lower atmosphere. Its concentration is highly variable in time and space, varying in mixing ratio from a few percent at sea level to parts-per-million levels in the stratosphere. Most of the atmosphere's water vapour is present in the planetary boundary layer where its average mixing ratio on the global scale is ≈1 % but which may exceed 5 % in tropical regions.

The effect of water vapour on gas-phase radical reactions has been the subject of numerous studies (Buszek et al., 2011) and is sometimes interpreted in terms of formation of H₂O–radical complexes leading, via a chaperone-type mechanism, to an increase in the rate constant. An important example of this is the HO₂ self-reaction for which the rate constant increases by a factor of up to 2 in the presence of water vapour due to formation of an HO₂–H₂O complex (Lii et al., 1981; Kircher and Sander, 1984). Theoretical calculations (Allodi et al., 2006; Sadanaga et al., 2006; Thomsen et al., 2012) suggest that, under our experimental conditions, the fraction of OH and NO₂ clustered with H₂O is <0.1 %, which is insufficient to significantly impact on k₁.

On the other hand, the role of H₂O as a collision partner in termolecular, atmospheric reactions has rarely been reported though its potential impact has been highlighted (Troe, 2003). Indeed, water vapour is known to be a more efficient third-body collider, by up to an order of magnitude, compared to N₂ in termolecular reactions such as H + H + M, H + OH + M, and H + O₂ + M (Getzinger and Blair, 1969; Michael et al., 2002; Fernandes et al., 2008; Shao et al., 2019).

The conclusions of three previous experiments examining the role of H₂O in kinetic studies of Reaction (R1) are highly divergent, with the addition of H₂O found to (1) increase the rate coefficient (Simonaitis and Heicklen, 1972), (2) have no measurable effect (D'Ottone et al., 2001), or (3) even reduce it (Sadanaga et al., 2006). The overall aim of this research was to clarify these differences and provide quantitative data on the third-body efficiency of H₂O for the title reaction. Based on the kinetic data for the water-vapour effect reported in this paper and in N₂ and O₂ presented in the first part of this study (Amedro et al., 2019), we have generated a new parameterization for the overall rate coefficient, k₁, and examined its impact on atmospheric OH, NO_x, and NO_y in a global chemical transport model.

2 Experimental details

The details of the experimental set-up have been published previously (Wollenhaupt et al., 2000; Amedro et al., 2019), and only a brief description is given here.

2.1 PLP-LIF technique

The experiments were carried out in a quartz reactor of 500 cm³ volume, which was thermostatted to the desired temperature by circulating a 60:40 mixture of ethylene glycol–water. The pressure in the reactor was monitored with 100 and 1000 Torr capacitance manometers. Flow rates were chosen so that a fresh gas sample was available for photolysis at each laser pulse (laser frequency, 10 Hz), thus preventing build-up of products. Pulses of 248 nm laser light (≈20 ns) for OH generation from HNO₃, H₂O₂, and O₃∕H₂O precursors were provided by an excimer laser (Compex 205 F, Coherent) operated using KrF.

$$\begin{array}{}\text{(R2)}& {\displaystyle }& {\displaystyle }{\mathrm{HNO}}_{\mathrm{3}}+h\mathit{\nu }\left(\mathrm{248}\mathrm{nm}\right)\to \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}},\text{(R3)}& {\displaystyle }& {\displaystyle }{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}_{\mathrm{2}}+h\mathit{\nu }\left(\mathrm{248}\mathrm{nm}\right)\to \mathrm{2}\mathrm{OH},\text{(R4)}& {\displaystyle }& {\displaystyle }{\mathrm{O}}_{\mathrm{3}}+h\mathit{\nu }\left(\mathrm{248}\mathrm{nm}\right)\to \mathrm{O}\left({}^{\mathrm{1}}\mathrm{D}\right)+{\mathrm{O}}_{\mathrm{2}},\text{(R5)}& {\displaystyle }& {\displaystyle }\mathrm{O}\left({}^{\mathrm{1}}\mathrm{D}\right)+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}\mathrm{OH}.\end{array}$$

OH concentrations (10¹¹ to 10¹² molecule cm⁻³) were similar to those reported by Amedro et al. (2019) and the same arguments, which rule out a significant influence of secondary reactions, apply. The concentration ranges of the H₂O₂, HNO₃, and O₃ precursors are listed in the notes to Tables 1 and 2.

Table 1 Measurements of k₁ in He bath gas.

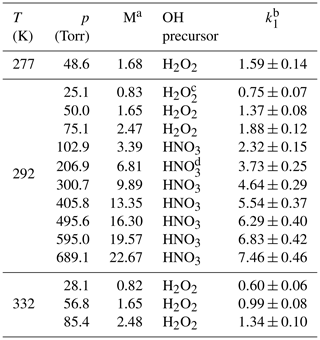
^a Molecular density M(He) in units of 10¹⁸ molecule cm⁻³. ^b Units of 10⁻¹² cm³ molecule⁻¹ s⁻¹. The errors are 2σ total uncertainty. ^c Concentration range of H₂O₂≈5–14×10¹³ molecule cm⁻³. ^d Concentration range of HNO₃≈5–9×10¹³ molecule cm⁻³.

Table 2 Measurements of k₁ in N₂–H₂O and He–H₂O bath gases.

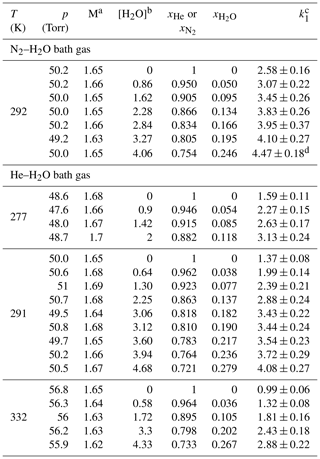
Unless otherwise indicated, the measurements were performed using H₂O₂ as OH precursor. The concentration range of H₂O₂ was 5–18×10¹³ molecule cm⁻³ for experiments in He–H₂O bath gas and 9–14×10¹³ molecule cm⁻³ for experiments in N₂–H₂O bath gas. ^a Molecular density M(He–H₂O) or M(N₂–H₂O) in units of 10¹⁸ molecule cm⁻³. ^b Units of 10¹⁷ molecule cm⁻³. ^c Units of 10⁻¹² cm³ molecule⁻¹ s⁻¹. Errors are 2σ total uncertainty. ^d Measurement performed using O₃–H₂O as OH precursor (with $\left[{\mathrm{O}}_{\mathrm{3}}\right]=\mathrm{2}\times {\mathrm{10}}^{\mathrm{13}}$ molecule cm⁻³).

OH was detected following excitation of the OH $A^{\mathrm{2}}\mathrm{\Sigma }(v^{\prime }=\mathrm{1})\leftarrow X^{\mathrm{2}}\mathrm{\Pi }(v^{\prime \prime }=\mathrm{0})$ transition (Q11(1) at 281.997 nm using a YAG-pumped dye laser (Quantel Brilliant B and Lambda-Physik Scanmate)). OH fluorescence was detected by a photomultiplier tube (PMT) screened by a 309 nm interference filter and a BG 26 glass cut-off filter.

2.2 Online absorption measurement of NO₂ and H₂O concentration

As discussed by Amedro et al. (2019), the determination of the NO₂ concentration is critical for accurate measurement of k₁. We therefore deployed in situ, broadband (405–440 nm), and single-wavelength (365 nm) optical absorption spectroscopy techniques. The former was located prior (in flow) to the quartz reactor; the latter was located behind the quartz reactor. Using the broadband cell, the NO₂ concentration was retrieved by least square fitting from 405 to 440 nm to a reference spectrum (Vandaele et al., 2002) and degraded to the resolution of our spectrometer. Simultaneously, we measured NO₂ at 365 nm using the absorption cross section of $\mathrm{5.89}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molecule⁻¹, which was determined previously by Amedro et al. (2019), who give a detailed description of the NO₂ concentration measurements and the choice of reference spectrum. For the temperatures used in this study, corrections to the NO₂ concentration due to formation of the N₂O₄ dimer were not necessary.

For the present experiments, a third absorption cell (l=40 cm) was placed downstream of the quartz reactor to measure the H₂O concentration at 184.95 nm. This set-up used a low-pressure mercury Pen-Ray lamp isolated with a 185 nm interference filter as light source. Optical extinction was converted to concentrations using a cross section of $\mathrm{7.14}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molecule⁻¹ (Cantrell et al., 1997).

2.3 Chemicals

N₂ and He (Westfalen, 99.999 %) were used without further purification. H₂O₂ (AppliChem, 50 wt %) was concentrated to >90 wt % by vacuum distillation. Anhydrous nitric acid was prepared by mixing KNO₃ (Sigma Aldrich, 99 %) and H₂SO₄ (Roth, 98 %) and condensing HNO₃ vapour into a liquid-nitrogen trap. NO (Air Liquide, 3.5) was purified of other nitrogen oxides by fractional vacuum distillation and then converted to NO₂ via reaction with a large excess of O₂. The NO₂ thus made was trapped in liquid N₂, and the excess O₂ was pumped out. The resulting NO₂ was stored as a mixture of ∼0.5 % NO₂ in N₂ or ∼5.5 % NO₂ in He. Distilled H₂O (Merck, liquid chromatography grade) was degassed before use and kept at constant temperature.

3 Results and discussion

3.1 Measurements of k₁ in He bath gas and comparison with literature

Our study of the role of H₂O as collision partner in Reaction (R1) was carried out in mixtures of He–H₂O and N₂–H₂O. In order to separate the effects of H₂O and He, we also required accurate rate coefficients for pure He bath gas, which we describe below. As for the N₂ and O₂ bath-gas datasets (Amedro et al., 2019), the experiments were carried out under pseudo-first-order conditions ([NO₂] ≫ [OH]) so that Eqs. (1)–(2) describe the decay of OH and the derivation of the bimolecular rate coefficient k₁.

$$\begin{array}{}\text{(1)}& [\mathrm{OH}{]}_t=[\mathrm{OH}{]}_{\mathrm{0}}\exp (-k^{\prime }t),\end{array}$$

where [OH]_t is the concentration (molecule cm⁻³) at time t after the laser pulse. k^′ is the pseudo-first-order rate coefficient and is defined as

$$\begin{array}{}\text{(2)}& k^{\prime }=k_{\mathrm{1}}\left[{\mathrm{NO}}_{\mathrm{2}}\right]+k_d,\end{array}$$

where k_d (s⁻¹) accounts for OH loss due to diffusion out of the reaction zone and reaction with its photolytic precursors such as HNO₃ or H₂O₂.

An exemplary dataset illustrating OH decays and a plot of k^′ versus [NO₂] is given in Fig. S1 of the Supplement.

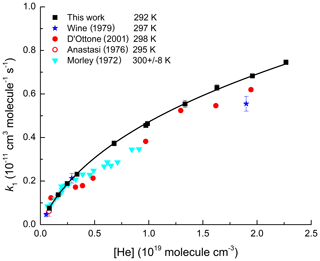
Figure 1 Values of k₁ from this study (black squares) as a function of He concentration at 292 K. Errors are 2σ statistical only. The solid line is a fit to our data using Eq. (4) with $k_{\mathrm{0}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, F_c=0.32, m=3.1, and n=0. Previous datasets at room temperature (Wine et al., 1979; D'Ottone et al., 2001; Anastasi and Smith; 1976; Morley and Smith, 1972) are displayed for comparison.

Values of k₁ obtained in He bath gas (25–690 Torr, 292 K) are summarized in Figs. 1 and 2 and listed in Table 1. The kinetics of termolecular reactions can be described by the Lindemann–Hinshelwood mechanism, whereby the rate constant at the low-pressure limit (k₀, units of cm⁶ molecule⁻² s⁻¹) is proportional to the pressure, and at the high-pressure limit (k_∞, units of cm³ molecule⁻¹ s⁻¹) is independent of pressure. In the intermediate pressure range, the fall-off regime, the rate coefficient is a function of both low-pressure (k₀) and high-pressure (k_∞) rate coefficients and the (reaction-partner-dependent) broadening factor F, which accounts for the lower rate constant measured in the fall-off regime than predicted by the Lindemann–Hinshelwood mechanism reactions (Troe, 1983). Under the conditions of temperature and pressure relevant for atmospheric chemistry, the title reaction is in the fall-off regime.

$$\begin{array}{}\text{(3)}& k={\displaystyle \frac{k_{\mathrm{0}}\left[M\right]k_{\mathrm{\infty }}}{k_{\mathrm{0}}\left[M\right]+k_{\mathrm{\infty }}}}F\end{array}$$

The solid lines in Figs. 1 and 2 are fits according to the Troe formalism for termolecular reactions (Troe, 1983) as adopted by the IUPAC panel in their evaluation of atmospheric reactions:

$$\begin{array}{}\text{(4)}& k\left(PT\right)={\displaystyle \frac{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}\left[\mathrm{M}\right]k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}\left[\mathrm{M}\right]+k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}}F,\end{array}$$

where T is the temperature in kelvin, [M] is the bath-gas concentration (molecule cm⁻³), and m and n are dimensionless temperature exponents.

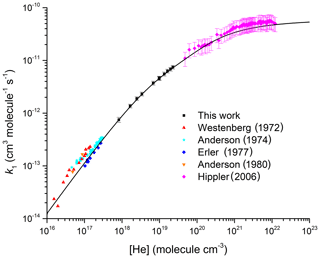
Figure 2 Comparison between the present dataset; the high-pressure measurements by Hippler et al. (2006); and the low-pressure measurements by Anderson et al. (1974), Westenberg and Dehaas (1972), Anderson (1980), and Erler et al. (1977). All measurements were made at room temperature. The black line is our parameterization with $k_{\mathrm{0}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, m=3.1, n=0, and F_c=0.32.

The broadening factor, F, is

$$\begin{array}{}\text{(5)}& \log F={\displaystyle \frac{\log F_{\mathrm{c}}}{\mathrm{1}+{\left[\log \left(\frac{k_{\mathrm{0}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}\left[M\right]}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/N\right]}^{\mathrm{2}}}},\end{array}$$

where N=(0.75–1.27 log F_c) and F_c is the broadening factor at the centre of the fall-off curve.

As discussed in some detail in the first part of our studies of the title reaction (Amedro et al., 2019), the low- or high-pressure rate constants for the title reaction (k₀ and k_∞) are not well defined by existing datasets, which do not deliver sufficiently accurate rate coefficient at very low pressures (<1 mbar) or at very high pressures (>500 bar). Studies in which k_∞ has been derived from rates of vibrational relaxation of OH (Smith and Williams, 1985; D'Ottone et al., 2005) return values of k_∞ that provide some constraint on its value, but the associated uncertainty is too large to consider this parameter well defined.

In our previous paper, Amedro et al. (2019) describe highly accurate measurements of k₁ over a wide range of temperatures and pressures in the fall-off regime. From measurements of k₁ in N₂ bath gas, we retrieved values for k₀ and k_∞ of $\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ and $\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, respectively, by fixing F_c to a value of 0.39, which has a theoretical basis (Cobos and Troe, 2003). The reasons for choosing this value of F_c are discussed in Amedro et al. (2019). Note that whereas k₀ is dependent on the bath gas used, at the high-pressure limit, k_∞ should be the same in N₂, O₂, He, or H₂O bath gases.

In Fig. 1 we display pressure-dependent rate coefficients (solid, black squares) obtained in He bath gas at 292 K. The black line is a fit (Eq. 4) to our data with k_∞ fixed to $\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹ and n=0 as derived from an extensive dataset obtained using N₂ bath gas (Amedro et al., 2019). For this dataset, the best fit is obtained with F_c=0.32, and $k_{\mathrm{0}}^{\mathrm{He}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹. When using F_c=0.39 (i.e. same value as that obtained in N₂ bath gas), the fit slightly overestimates (∼5 %) the measurements at pressures above ∼300 Torr, whereas it underestimates by 10 % at lower pressures (Fig. S2). We note that using a higher F_c=0.39 resulted in a lower value of $k_{\mathrm{0}}^{\mathrm{He}}$ equal to $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹. The T-dependence factor in He, m(He), was determined to be 3.1 over the temperature range from 277 to 332 K (Table 1 and Fig. S6).

The high precision of our measurements in He and N₂ indicates that different broadening factors (F_c) are required to interpret the pressure dependence of k₁ obtained in N₂ and He. This can be rationalized by considering that F_c is the product of strong-collision ($F_{\mathrm{c}}^{\mathrm{SC}}$) and weak-collision ($F_{\mathrm{c}}^{\mathrm{WC}}$) components (Eqs. 6–8) (Gilbert et al., 1983; Troe, 1983; Troe and Ushakov, 2011):

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{c}}\approx F_{\mathrm{c}}^{\mathrm{SC}}{F}_{\mathrm{c}}^{\mathrm{WC}},\text{(7)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{c}}^{\mathrm{SC}}\approx S_{\mathrm{K}}^{-\mathrm{0.62}}\approx {\left(\mathrm{1}+{\displaystyle \frac{r}{\mathrm{2}}}\right)}^{-\mathrm{0.62}},\text{(8)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{c}}^{\mathrm{WC}}\approx {\mathit{\beta }}_{\mathrm{c}}^{\mathrm{0.14}}.\end{array}$$

Here, S_K is the Kassel parameter, r is the total number of external rotational modes of the reactants (equal to 5 in the reaction between OH and NO₂), and β_c is the collision efficiency. While the strong collision component is independent of bath gas ($F_{\mathrm{c}}^{\mathrm{SC}}\approx \mathrm{0.46}$ for the title reaction) a change in $F_{\mathrm{c}}^{\mathrm{WC}}$ due to a lower collision efficiency (β_c) of He relative to N₂ is likely.

The collision efficiency for N₂, which was used to calculate F_c=0.39, was β_c(N₂)≈0.3 (Troe, 2001). The value of F_c=0.32 from our He data implies β_c(He)≈0.08, a factor of 3.7 times lower than β_c(N₂). A large difference in collision efficiency between N₂ and He is consistent with theoretical calculations (Glänzer and Troe, 1974; Troe, 2001; Golden et al., 2003).

In Fig. 1, we also compare our measurements of k₁ in He with data collected in the same pressure range using similar techniques. The three first measurements (Morley and Smith, 1972; Anastasi and Smith, 1976; Wine et al., 1979) used flash photolysis of H₂O as a OH precursor with detection of OH by resonance fluorescence. Morley and Smith (1972) reported rate coefficients at pressures of 20 to 280 Torr at room temperature with the NO₂ concentration calculated manometrically. Our parametrization agrees within the combined uncertainty of both measurements (Fig. S3). Anastasi and Smith (1976) reported one value of k₁ at 25 Torr of He, which is ≈20 % lower than our measurement. Wine et al. (1979) presented values of k₁ at three pressures of He. The agreement with our parameterization at the lowest two pressures is excellent but a deviation of ≈20 % is observed at the highest pressure (Fig. S4). As both studies measured NO₂ concentrations using optical absorption at 365 nm, the ≈20 % difference is significant. Most recently, D'Ottone et al. (2001) reported rate coefficients from 30 to 600 Torr of He using a very similar approach to ours, i.e. PLP-LIF technique with in situ measurements of NO₂ by absorption at 365 nm. The disagreement (up to 40 %) between our measurements and theirs exceed the combined reported uncertainty (Fig. S5). While it is unclear what could have caused the discrepancy, we note that the data of D'Ottone et al. (2001) are significantly more scattered and do not describe a smooth increase in rate coefficient with pressure as expected from termolecular reactions in the fall-off regime. This would appear to indicate an underestimation of the total uncertainty in their study.

Figure 2 extends the pressure range to additionally display data obtained in low-pressure flow tubes (Westenberg and Dehaas, 1972; Anderson et al., 1974; Erler et al., 1977; Anderson, 1980) and the high-pressure measurements by Hippler et al. (2006). At low pressures our data are in excellent agreement (within 10 %) with the data of Erler et al. (1977), but they predict values ≈40 % lower than those reported by Westenberg and Dehaas (1972) and Anderson (1980). The data of Anderson et al. (1974) display a large intercept ($\mathrm{4.9}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molecule⁻¹ s⁻¹) at zero pressure, which is attributed to a second-order heterogeneous removal rate constant. As indicated in a critical assessment of the low-pressure data by Amedro et al. (2019), it is unclear whether one can simply subtract a constant value equal to the intercept (obtained from a linear fit) to each data point. If we were to do so, the work by Anderson et al. (1974) would be in very good agreement with the low-pressure study by Erler et al. (1977) as well as with our parameterization extended to low pressures. Additionally, Amedro et al. (2019) demonstrated that, owing to the large asymmetric broadening of fall-off for this reaction, the assumption that the rate coefficient is in the low-pressure limit at N₂ pressures of 0.5 Torr < p<10 Torr is invalid and leads to underestimation of k₀. This observation is still true of datasets obtained at low pressures of He, so that while very good agreement is observed between our parameterization and individual rate coefficients obtained between 3 and 8 Torr of He, reported values of $k_{\mathrm{0}}^{\mathrm{He}}$ are 40 % lower than our values obtained from the fall-off analysis. As indicated in Fig. 2, our parameterization of k₁ in He is in very good agreement with the high-pressure data reported by Hippler et al. (2006).

3.2 Influence of H₂O on k₁

As mentioned above, the effect of water vapour on k₁ was determined in mixtures of H₂O with both N₂ and He. This is because the vapour pressure of H₂O at room temperature (≈17 Torr at 293 K) is too low to enable experiments in pure H₂O bath gas to be conducted using our instrument. The measurements were performed at low density ([M] $=\mathrm{1.6}\times {\mathrm{10}}^{\mathrm{18}}$ molecule cm⁻³; 50 Torr at 293 K) where the relative increase in k₁ in the presence of H₂O is pronounced, resulting in greater accuracy in the determination of $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$. Experimental data on the influence of H₂O on k₁ were obtained in N₂–H₂O and He–H₂O mixtures by varying the H₂O mixing ratio, $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, from 0.05 to 0.27 ([H₂O]=0.9–4.5×10¹⁷ molecule cm⁻³) while keeping the total pressure constant at 50 Torr. Under these conditions, the addition of H₂O resulted in an increase in k₁ up to a factor of 2 as illustrated by the datasets of Fig. 3 in which the increase in slope as more water vapour is added is proportional to the increase in k₁ (Eq. 2). At the highest concentration of water vapour (4.5×10¹⁷ molecule cm⁻³) the rate coefficient in He–H₂O increased by a factor of >3 compared to that obtained in pure He (see Table 1).

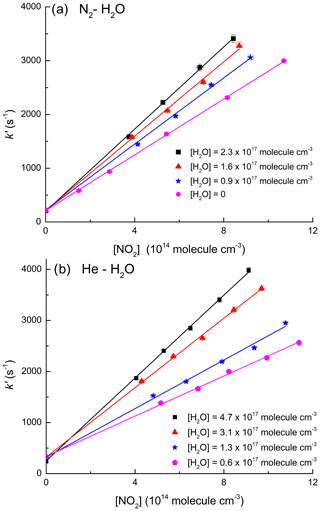
Figure 3 (a) Data obtained in N₂–H₂O bath gas (50 Torr, 292 K). (b) Data obtained in He–H₂O bath gas (50 Torr, 291 K). Both panels display first-order OH decay constants in various concentrations of NO₂ and different mole fractions of H₂O. The solid lines represent least squares linear fits to Eq. (2).

In order to determine the temperature dependence of the enhancement in k₁ caused by the presence of water, the experiments in He were carried out at three different temperatures (277, 291, and 332 K). The values of k₁ obtained from these experiments are plotted versus the mole fraction of H₂O in Fig. 4b. At the pressures used in our experiments, k₁ displays fall-off, precluding a direct measurement of $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$.

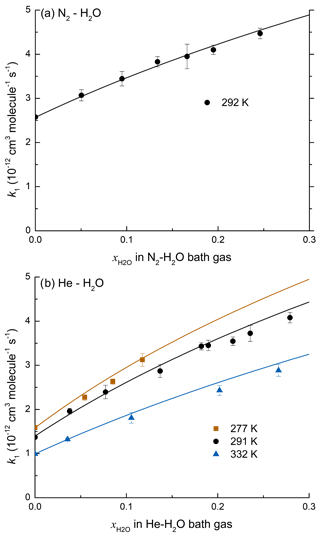
Figure 4 (a) k₁ as a function of $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ at 50 Torr N₂–H₂O and 292 K. The line represents a least squares multivariate fit (Eqs. 7 and 8) with $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻² s⁻¹, $k_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, F_c=0.39, m=3.6, $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{15.9}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, and o=3.4. (b) k₁ as a function of $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in He–H₂O mixtures at 277, 291, and 332 K. The solid lines represent a least squares multivariate fit (Eqs. 7 and 9 to 12) where $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻² s⁻¹, $k_{\mathrm{0}}^{\mathrm{He}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $F_{\mathrm{c}}^{\mathrm{He}}=\mathrm{0.32}$, m=3.1, $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{15.9}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.39}$, and o=3.4.

The total rate constant measured in, for example, a H₂O–N₂ bath gas is not equal to the sum of the individual rate constants calculated from the mixing ratios of N₂ and H₂O; i.e. $k_{{\mathrm{N}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\ne k_{{\mathrm{N}}_{\mathrm{2}}}+k_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$; $k_{{\mathrm{N}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is only equal to the sum of $k_{{\mathrm{N}}_{\mathrm{2}}}$ and $k_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ at the low-pressure limit (≪1 Torr in the case of the OH reaction with NO₂) and under certain conditions where gas mixtures are composed of strong colliders and/or have similar collision efficiencies (Troe, 1980; Burke and Song, 2017). Additionally, at the high-pressure end of the fall-off curve, the rate coefficient is independent of bath gas composition. To be able to make a reasonable prediction of this effect under atmospheric conditions, where the mole fraction of water vapour ($x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) can be as large as 0.05, we analysed our measurements using two different approaches to determine $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$. In the first case, the low-pressure rate constant in a N₂–H₂O mixture is defined as the sum of two individual low-pressure-limit rate constants,

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& k(p,T)=\\ & {\displaystyle \frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]+k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}}F,\end{array}\end{array}$$

where $x_{{\mathrm{N}}_{\mathrm{2}}}$ and $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are the mixing ratio for N₂ and H₂O, respectively; $k_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}$ and $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are low-pressure-limiting rate constants (units of cm⁶ molecule⁻² s⁻¹) for pure N₂ and H₂O; k_∞ is the high-pressure limit rate constant (units of cm³ molecule⁻¹ s⁻¹); T is the temperature in kelvin; [M] is the molecular density (molecule cm⁻³); and m, n, and o are dimensionless temperature exponents.

The broadening factor, F, is

$$\begin{array}{}\text{(10)}& \begin{array}{rl}& \log F=\\ & {\displaystyle \frac{\log F_{\mathrm{c}}}{\mathrm{1}+{\left[\log \left(\frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/N\right]}^{\mathrm{2}}}},\end{array}\end{array}$$

where N=(0.75–1.27log F_c) and F_c is the broadening factor at the centre of the fall-off curve.

In the second approach, we follow Burke and Song (2017), where, in addition to the low-pressure limiting rate coefficients, the broadening factors for each bath gas are also mixed linearly and $\log F^{{\mathrm{N}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is defined as

$$\begin{array}{}\text{(11)}& \log F^{{\mathrm{N}}_{\mathrm{2}}-{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=X_{{\mathrm{N}}_{\mathrm{2}}}\log F^{{\mathrm{N}}_{\mathrm{2}}}+X_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\log F^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},\end{array}$$

where

$$\begin{array}{}\text{(12)}& {\displaystyle }\begin{array}{rl}& X_{{\mathrm{N}}_{\mathrm{2}}}={\displaystyle \frac{x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}\left[\mathrm{M}\right]}{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]}},\\ & X_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}={\displaystyle \frac{x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}\left[M\right]}{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]}}\end{array};\text{(13)}& {\displaystyle }\begin{array}{rl}& \log F^{{\mathrm{N}}_{\mathrm{2}}}=\\ & {\displaystyle \frac{\log F_{\mathrm{c}}^{{\mathrm{N}}_{\mathrm{2}}}}{\mathrm{1}+{\left[\log \left(\frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/\left(\mathrm{0.75}-\mathrm{1.27}\log F_{\mathrm{c}}^{{\mathrm{N}}_{\mathrm{2}}}\right)\right]}^{\mathrm{2}}}}\end{array};\text{(14)}& {\displaystyle }\begin{array}{rl}& \log F^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\\ & {\displaystyle \frac{\log F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{\mathrm{1}+{\left[\log \left(\frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)\left[M\right]}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/\left(\mathrm{0.75}-\mathrm{1.27}\log F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right)\right]}^{\mathrm{2}}}};\end{array}\end{array}$$

where $F_{\mathrm{c}}^{{\mathrm{N}}_{\mathrm{2}}}$ and $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are the broadening factors at the centre of the fall-off curve for N₂ and H₂O.

In the case where two bath gases have identical (or very similar) values of F_c, the two approaches result in identical predictions and the first approach will be preferred for its simplicity. This is the case for N₂ and H₂O bath gases. However, when two bath gases have significantly different values of F_c (as is the case for He–H₂O mixtures; see below) the second approach provides a more accurate parameterization.

3.2.1 Parameterization of k₁ from data obtained in N₂–H₂O and He–H₂O bath gases

Values of k₁ obtained in N₂–H₂O and He–H₂O bath gases are listed in Table 2. Each rate coefficient obtained in N₂–H₂O bath gas was defined by five parameters: the mixing ratio of N₂ and H₂O ($x_{{\mathrm{N}}_{\mathrm{2}}}$ and $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$), the overall rate coefficient (k₁), the molecular density [M], and the temperature T. We performed a multivariate fit of the N₂–H₂O dataset with $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ as variable and all other parameters fixed with $k_{\mathrm{\infty }}=\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molecule⁻¹ s⁻¹, $k_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}=\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, and m=3.6 as derived in Amedro et al. (2019); o was fixed to 3.4 (see below) and F_c was held at 0.39, making the assumption that the broadening factors at the centre of the fall-off curve for H₂O and N₂ were identical. The fit to the data returned $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=(\mathrm{15.9}\pm \mathrm{0.7})\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹ where the uncertainty is 2σ (statistical only). The solid black line in Fig. 4a represents the parameterization for a varying fraction of H₂O in N₂ at a total pressure of 50 Torr using the parameters given above. Equating $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and $F_{\mathrm{c}}^{{\mathrm{N}}_{\mathrm{2}}}$ simplifies the analysis, though it is likely that $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}>F_{\mathrm{c}}^{{\mathrm{N}}_{\mathrm{2}}}$ as the collision efficiency (β_c) is likely to be larger for H₂O than for N₂. We found that the He–H₂O data cannot be modelled by assuming the same F_c for both He and H₂O bath gas, and the approach of Burke and Song (2017) was therefore preferred. In order to analyse the data, we fixed the following parameters: $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{15.9}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.39}$, $F_{\mathrm{c}}^{\mathrm{He}}=\mathrm{0.32}$, $k_{\mathrm{0}}^{\mathrm{He}}=\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, and m=3.1 to derive $o=\mathrm{3.4}\pm \mathrm{0.8}$ (2σ, statistical only), which describes the temperature dependence of the low-pressure limit in H₂O as depicted in Fig. 4b.

There is clearly some uncertainty related to the arbitrary use of $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.39}$. For example, if we were to analyse the data in N₂–H₂O using $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.6}$ and the linear mixing method, we would retrieve $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{10}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹, which is ≈50 % lower than our preferred value. The effect of the different analyses can be assessed by comparing the predicted impact of H₂O on k₁ at 80 % relative humidity, 1000 mbar, and 313 K. If we set $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.39}$, we predict that the effect of H₂O is to increase k₁ by 15 %, while choosing $F_{\mathrm{c}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{0.6}$ results in an increase of 20 %. Theoretical calculation of the relative values of F_c in N₂, O₂, and H₂O bath gases input would be useful to reduce this uncertainty. Our data indicate a significant positive trend in k₁ when adding H₂O. As discussed above, more efficient energy transfer from [HO–NO₂]^# in collision with H₂O compared to N₂ is intuitive and supported by the present dataset as well as that of Simonaitis and Heicklen (1972), who derived $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}=\mathrm{11}\times {\mathrm{10}}^{-\mathrm{30}}$ cm⁶ molecule⁻² s⁻¹. Given the complexity of the analysis, this may be considered to be in good agreement. This result is, however, not consistent with the observations of D'Ottone et al. (2001), who report no significant change in k₁ in 150 Torr of He when adding either 10 or 20 Torr of H₂O and is completely at odds with the conclusions of Sadanaga et al. (2006), who report a reduction in k₁ (by 18 %) when adding 29.1 mbar of H₂O at atmospheric pressure. If our value for $k_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is correct, D'Ottone et al. (2001) should have seen an increase in k₁ of ≈55 % and Sadanaga et al. (2006) should have observed an increase of ≈5 %.

A potential explanation for the very divergent observations of the effect of H₂O is the heterogeneous loss of NO₂ when adding H₂O. We tested for NO₂ loss in a set of experiments in which NO₂ and H₂O were monitored simultaneously while systematically varying the amount of H₂O. Our results indicated a reduction in the concentration of NO₂ by up to ≈20 % as we increased the concentration of H₂O up to 4.5×10¹⁷ molecule cm⁻³. Unless NO₂ is monitored in situ (as in our experiments), 20 % loss of NO₂ would lead to a similar size reduction in the OH decay constant and thus an underestimation of the rate coefficient. A fractional loss of NO₂ of this magnitude would explain why Sadanaga et al. (2006) found an apparent reduction in k₁ when adding H₂O.

However, the situation becomes more complex if NO₂ is converted to trace gases that are reactive towards OH. For this reason, we performed an additional experiment to investigate whether NO₂ was converted via reaction with H₂O on surfaces to HONO and/or HNO₃. Note that conversion of NO₂ to HONO at low pressures (e.g. 50 Torr) would result in an increase in the OH decay constant ($k_{\mathrm{OH}+\mathrm{HONO}}>k_{\mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}}$), whereas conversion of NO₂ to HNO₃ would result in a decrease ($k_{\mathrm{OH}+{\mathrm{HNO}}_{\mathrm{3}}}<k_{\mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}}$).

In order to test for the presence of HONO, we modified the broadband absorption set-up by replacing the halogen lamp with a deuterium lamp, allowing us to detect HONO around 350 nm as well as NO₂. The optical absorption of NO₂ and HONO (340–380 nm) was monitored in a flow of NO₂ (1.7×10¹⁵ cm⁻³) at 50 Torr of He in the absence and presence of H₂O ($\left[{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right]=\mathrm{4.5}\times {\mathrm{10}}^{\mathrm{17}}$ molecule cm⁻³, the maximum concentration used in this work). A depletion in NO₂ of 21 % (3.7×10¹⁴ molecule cm⁻³) was observed when H₂O was added. An analysis of the spectra with and without H₂O (Fig. S7) enabled us to establish an upper limit to the HONO concentration of $\approx \mathrm{1}\times {\mathrm{10}}^{\mathrm{13}}$ molecule cm⁻³, which would correspond to just 3 % of the NO₂ lost. At this concentration, HONO does not significantly increase the loss rate of OH (<3 % using a rate coefficient for reaction of OH with HONO of $\mathrm{6.0}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molecule⁻¹ s⁻¹ (IUPAC, 2019). In the same experiment, we also recorded the optical density at 185 nm, where H₂O, NO₂, and HNO₃ all absorb. Despite the large HNO₃ absorption cross section at this wavelength ($\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{17}}$ cm² molecule⁻¹; Dulitz et al., 2018) we found no evidence for HNO₃ formation, indicating that the NO₂ lost was not converted to gas-phase HNO₃. Given its great affinity for glass in the presence of H₂O, we expect that any HNO₃ formed is strongly partitioned to the walls of the reactor. The tests indicate that, on the timescales of our experiments, NO₂ is lost irreversibly on the humidified walls of our experiment. The maximum concentration of H₂O used in this experiment, 4.5×10¹⁷ molecule cm⁻³, corresponds to a relative humidity of 80 % (at 292 K) so that H₂O condensation is not expected.

It is difficult to establish whether our observations of significant NO₂ loss can explain the result of D'Ottone et al. (2001), who did not observe an enhancement in k₁. D'Ottone et al. (2001) did not state whether, in their experiments, NO₂ and H₂O were monitored simultaneously. Also, our observed loss of NO₂ is not necessarily transferable to other studies as the heterogeneous loss of NO₂ will vary from one experimental set-up to the next, as residence times and surface areas may vary substantially.

A very simple calculation serves to illustrate the role of water vapour as a third-body quencher for the title reaction. We consider, for example, the tropical boundary layer with a temperature of 30 ^∘C and a relative humidity of 80 % at a total pressure of 1 bar. The pressure of water vapour is 34 mbar, and those of O₂ and N₂ are then 210 and 756 mbar, respectively. A rough contribution of each quenching gas to the overall rate coefficient can be calculated from the respective low-pressure rate coefficients. For N₂, O₂, and H₂O these are (in units of 10⁻³⁰ cm³ molecule⁻¹ s⁻¹) 2.6, 2.0, and 15.9. Water vapour is therefore a factor of ≈8 more efficient than O₂, and a factor of ≈6 more efficient than N₂ as a quencher of the HO–NO₂ intermediate, which is qualitatively consistent with known strong binding (40 kJ mol⁻¹) in the HNO₃–H₂O complex (Tao et al., 1996).

For our tropical boundary layer case study, in which the O₂ pressure is only a factor of 6 greater than that of H₂O, we calculate that H₂O contributes more to the rate coefficient of the title reaction than O₂ does. Clearly, the neglect of including the quenching effect of H₂O leads to an underestimation (in the boundary layer) of the rate coefficient for this centrally important atmospheric reaction.

In order to assess both the effect of H₂O (this work) and the new parameterization for k₁ in N₂ and O₂ bath gases presented in the first part of this study (Amedro et al., 2019), we have used a 3-D chemical transport model (EMAC; see below) to explore the impact on a global scale.

3.3 Atmospheric modelling of the OH + NO₂ reaction including the effect of water vapour

The EMAC (ECHAM/MESSy Atmospheric Chemistry) model employed is a numerical chemistry and climate simulation system (Jöckel et al., 2006, 2010) using the fifth-generation ECMWF Hamburg general circulation model (ECHAM5; Roeckner et al., 2006) as core atmospheric general circulation model. For the present study, we applied EMAC (ECHAM5 version 5.3.02, MESSy version 2.53.0) in the T42L47MA resolution, i.e. with a spherical truncation of T42 (corresponding to a quadratic Gaussian grid of approx. 2.8^∘ by 2.8^∘ in latitude and longitude) with 47 vertical hybrid pressure levels up to 0.01 hPa. The model has been weakly nudged in spectral space, nudging temperature, vorticity, divergence, and surface pressure (Jeuken et al., 1996). The chemical mechanism scheme adopted (MOM; Mainz Organic Mechanism) includes oxidation of isoprene and saturated and unsaturated hydrocarbons, including terpenes and aromatics (Sander et al., 2019). Further, tracer emissions and model set-up are similar to the one presented in Lelieveld et al. (2016). EMAC model predictions have been evaluated against observations on several occasions (Pozzer et al., 2010; de Meij et al., 2012; Elshorbany et al., 2014; Yoon and Pozzer, 2014): for additional references, see http://www.messy-interface.org (last access: November 2019). For this study, EMAC was used in a chemical transport model (CTM mode) (Deckert et al., 2011), i.e. by disabling feedbacks from photochemistry on radiation and dynamics. Two years were simulated (2009–2010), with the first year used as spin-up time.

The following parameterization of k₁ was implemented in EMAC; values of each parameter are listed in Table 3.

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& k_{\mathrm{1}}(p,T)=\\ & {\displaystyle \frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{O}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{O}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-q}+,x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)M{k}_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{O}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{O}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-q}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)M+k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}}F\end{array}\end{array}$$

The broadening factor, log F, is

$$\begin{array}{}\text{(16)}& \begin{array}{rl}& \log F=\\ & {\displaystyle \frac{\log F_{\mathrm{c}}}{\mathrm{1}+{\left[\log \left(\frac{\left(x_{{\mathrm{N}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{N}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-m}+x_{{\mathrm{O}}_{\mathrm{2}}}{k}_{\mathrm{0}}^{{\mathrm{O}}_{\mathrm{2}}}{\left(\frac{T}{\mathrm{300}}\right)}^{-q}+x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{k}_{\mathrm{0}}^{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\left(\frac{T}{\mathrm{300}}\right)}^{-o}\right)M}{k_{\mathrm{\infty }}{\left(\frac{T}{\mathrm{300}}\right)}^{-n}}\right)/\left[\mathrm{0.75}-\mathrm{1.27}\log F_{\mathrm{c}}\right]\right]}^{\mathrm{2}}}}.\end{array}\end{array}$$

As described in Sect. 1, the reaction between OH and NO₂ forms not only HNO₃ but also HOONO. HOONO decomposes rapidly at typical boundary layer temperatures, but it is long lived with respect to thermal dissociation at the temperatures found in the upper troposphere and lower stratosphere (UTLS).

$$\begin{array}{}\text{(R6)}& \mathrm{HOONO}+\mathrm{M}\to \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}\end{array}$$

The rate constant (k₆) for thermal decomposition of HOONO was calculated from the channel-specific rate coefficient for its formation (k₁α) and an equilibrium coefficient: $k_{\mathrm{6}}=k_{\mathrm{1}}\mathit{\alpha }/K_{\mathrm{eq}}$, where $K_{\mathrm{eq}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{27}}\exp (\mathrm{10135}/T)$ (Burkholder et al., 2015; IUPAC, 2019) based on the analysis of Golden et al. (2003). The branching ratio to HOONO formation (α) was adapted from the present IUPAC recommendations for k_1a and k_1b, which were derived from experimental work (Hippler et al., 2006; Mollner et al., 2010) and theoretical analysis (Troe, 2012). The IUPAC recommendations were augmented with a pressure-independent HOONO yield of 0.035 to better represent the dataset of Mollner et al. (2010), who detected HOONO directly at room temperature. We assume α is independent of water vapour. The expression used and a plot of α at different temperatures and pressures is given in Fig. S8.

Table 3 Parameters for calculating k₁ using Eqs. (15) and (16).

^a Units of cm⁶ molecule⁻² s⁻¹. ^b Units of cm³ molecule⁻¹ s⁻¹. Note that k_∞ is independent of temperature (n=0).

In the absence of experimental data on the reactions of HOONO with OH or on its photolysis, we follow the approach of Golden and Smith (2000) and set these equal to those for HO₂NO₂:

$$\begin{array}{}\text{(R7)}& {\displaystyle }& {\displaystyle }\mathrm{HOONO}+\mathrm{OH}\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{NO}}_{\mathrm{3}},\text{(R8)}& {\displaystyle }& {\displaystyle }\mathrm{HOONO}+h\mathit{\nu }\to \mathrm{HO}+{\mathrm{NO}}_{\mathrm{2}}.\end{array}$$

In Fig. 5, we illustrate the global impact (annual average) of H₂O vapour on the rate coefficient. We plot the fractional reduction in k₁ at the Earth's surface when setting $x_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ to zero rather than using the EMAC global water-vapour fields. We focus on the boundary layer as the H₂O concentration is largest here and decreases rapidly with altitude.

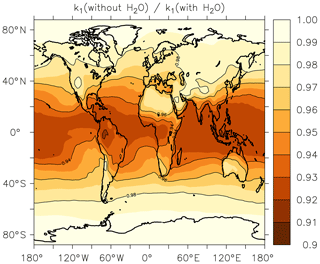
Figure 5 Annual-average effect of H₂O on k₁ expressed as the fractional change in the rate coefficient at the Earth's surface when setting the mole fraction of water vapour to zero in Eq. (15).

As expected, the greatest effect is found in warm, tropical regions where neglecting the impact of water vapour results in an average underestimation of the rate coefficient by up to ≈8 %. At higher or lower latitudes the effect is diminished and water vapour accounts for only 3 %–4 % of the overall rate coefficient at 40^∘ N or S. The presence of water vapour does not impact on values of k₁ above the boundary layer.

Our experimental data do not give insight into whether the H₂O-induced enhancement in k₁ is accompanied by a change in the branching ratio to favour either HNO₃ or HOONO. However, as the formation of HOONO is favoured at high pressures (more effective collisional deactivation), it is possible that the HOONO yield may be enhanced relative to HNO₃ in the presence of H₂O. If this is the case, the increase in rate coefficient at high water-vapour levels (e.g. in the tropical lower troposphere) may be to some extent offset by the subsequent thermal dissociation of HOONO in these warm regions.

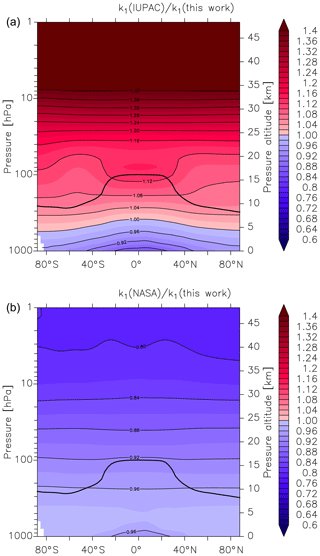
Figure 6 Global values of $\frac{k_{\mathrm{1}}^{\mathrm{IUPAC}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ (a) and $\frac{k_{\mathrm{1}}^{\mathrm{NASA}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ (b). k₁ is the overall rate coefficient (both channels) for Reaction R1 calculated using the parameters from this work ($k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}$) and those presently recommended by the IUPAC ($k_{\mathrm{1}}^{\mathrm{IUPAC}}$) and NASA ($k_{\mathrm{1}}^{\mathrm{NASA}}$) data evaluation panels. The black line represents the model tropopause.

As described by Amedro et al. (2019) (Fig. 1 of that paper), two expert panels (IUPAC, NASA) evaluating kinetic data for use in atmospheric modelling fail to reach consensus for the title reaction, with the preferred rate coefficients differing by as much as 50 % in the cold UTLS. For this reason, we have calculated values of $\frac{k_{\mathrm{1}}^{\mathrm{NASA}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ and $\frac{k_{\mathrm{1}}^{\mathrm{IUPAC}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ at different altitudes and latitudes (i.e. at different temperatures and pressures). We parameterized the rate coefficient using the expressions given in this work (Eq. 15, Table 3) and in the latest evaluations of IUPAC (k₁ last evaluated in 2017; IUPAC, 2019) and NASA (last evaluation published in 2015; Burkholder et al., 2015). As displayed in Fig. 6, values of $\frac{k_{\mathrm{1}}^{\mathrm{NASA}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ and $\frac{k_{\mathrm{1}}^{\mathrm{IUPAC}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ vary greatly with pressure and temperature and thus altitude. The NASA recommendations are always slightly lower but in good agreement (≤10 %) for most of the troposphere, with larger differences (($\frac{k_{\mathrm{1}}^{\mathrm{NASA}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$) always <1) only observed in the lower and mid-stratosphere. At altitudes above ≈30 km the ratio decreases to ≈0.8. A comparison with the rate coefficient derived from the IUPAC parameterization shows that $\frac{k_{\mathrm{1}}^{\mathrm{IUPAC}}}{k_{\mathrm{1}}^{\mathrm{this}\mathrm{work}}}$ varies from ≈0.9 at the surface to ≈1.1 at the tropopause but increases to >1.3 at the low pressures and temperatures that reign at 30 km and above. At high altitudes (low pressure and temperature) the rate coefficients that the evaluation panels recommend are strongly biased by choice of the rate coefficient (and its temperature dependence) at the low-pressure limit. As discussed by Amedro et al. (2019) the available experimental data at low pressures and temperatures are not of sufficient accuracy to use as basis for recommendation of k₀, and this is reflected in the highly divergent values of k₁ under these conditions.

As mentioned above, the atmospheric HNO₃∕NO₂ ratio is expected to be highly sensitive to the rate coefficient k₁, with an increase in k₁ resulting in an increase in the HNO₃∕NO₂ ratio and vice versa. The HNO₃∕NO₂ ratio also depends on the concentration of OH, and thus the effect of using different values of k₁ will be most apparent in regions where the greatest OH concentrations are found, i.e. at low latitudes. At higher latitudes, especially in winter months where solar insolation is weak and OH levels are relatively low, the HNO₃∕NO₂ ratio will also be impacted by night-time conversion of NO₂ to N₂O₅ and finally, via heterogeneous hydrolysis, to HNO₃. In Fig. 7 we plot zonally and yearly averaged model values of $\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{IUPAC}\right)/\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{this}\mathrm{work}\right)$ in the upper panel (Fig. 7a) and $\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{NASA}\right)/\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{this}\mathrm{work}\right)$ in the lower panel (Fig. 7b). Compared to the present parameterization of k₁, the IUPAC evaluation returns HNO₃∕NO₂ ratios that are between 0.9 and 1 throughout most of the lower and free troposphere (up to ≈5 km) and larger HNO₃∕NO₂ ratios (factor of 1.1 to 1.15) above ≈10 km especially at the tropical tropopause. The divergence between the HNO₃∕NO₂ ratios increases as we move further into the stratosphere with $\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{IUPAC}\right)/\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{this}\mathrm{work}\right)$ values as large as 1.2 to 1.3 above 25 km. At the same time, NO_x levels (NO_x = NO + NO₂) decrease by a factor of ≈0.95 (see Fig. S9). When we compare our parameterization with that of the NASA panel, the picture is largely reversed (lower panel, Fig. 7b). Again, we find reasonable agreement in the HNO₃∕NO₂ ratio in the lowermost atmosphere, but in this case lower values (0.8 to 0.9) in the lower stratosphere, which are accompanied by a factor of 1.06 change in NO_x concentrations (Fig. S9). For both the NASA and IUPAC parameterizations, the largest differences in the HNO₃∕NO₂ ratio compared to the present study are found higher in the atmosphere. The modelling studies confirm the simple calculation of Amedro et al. (2019; see Fig. 1 of their paper), showing that the IUPAC and NASA parameterizations result in very different values of k₁ in some parts of the atmosphere, and they will result in divergent predictions of partitioning of reactive nitrogen between NO_x and NO_y. Use of the parameterization based on the present dataset lies roughly between the two evaluations, with best agreement observed with NASA for the lower atmosphere. However, as previous laboratory studies had not identified the important role of H₂O in the title reaction, which could therefore not be incorporated in either of the previous parameterizations, any agreement at better than the 10 % level is fortuitous, reflecting random cancelling of systematic bias.

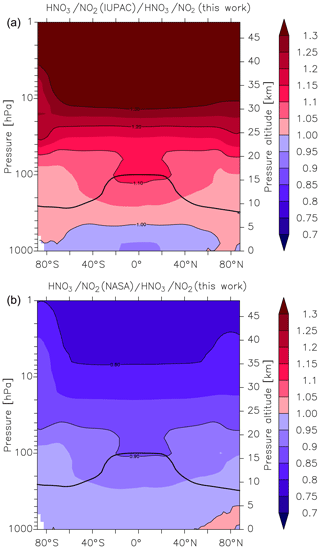
Figure 7 Effect of different parameterizations of k₁ on the global (zonal and yearly averaged) HNO₃ to NO₂ ratio. (a) $\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{IUPAC}\right)/\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{this}\mathrm{work}\right)$, (b) $\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{NASA}\right)/\frac{{\mathrm{HNO}}_{\mathrm{3}}}{{\mathrm{NO}}_{\mathrm{2}}}\left(\mathrm{this}\mathrm{work}\right)$. The black line represents the model tropopause.

As reaction with OH is the predominant sink for most atmospheric trace gases, its concentration largely defines the oxidizing power of the atmosphere (Lelieveld et al., 2004, 2008, 2016) and even changes of a few percent in its concentration are significant. An increase in the rate coefficient of the title reaction will reduce the atmospheric abundance of this centrally important radical. In Fig. S10 we illustrate the impact of using the parameterization of k₁ from the present study compared to the IUPAC and NASA recommendations. The upper panel in Fig. S10 plots the ratio of OH concentrations obtained when using the IUPAC parameterization and that from the present study, OH(IUPAC)/OH(this work). Throughout the troposphere OH(IUPAC)/OH(this work) deviates by only a few percent, with a value of 1.02 at the surface and 0.96 at the tropical tropopause. OH(NASA)/OH(this work) is also 1.02 at the surface but increases to 1.04 at the tropical tropopause as the NASA-derived value of k₁ is lower at the temperatures and pressures encountered in this part of the atmosphere. The weak effect of changing k₁ on OH at the surface reflects the fact that many reactions apart from that with NO₂ contribute to the overall sink term for OH in the lower troposphere.

Although our experiments do not give insight into the branching between formation of HOONO and HNO₃ in the title reaction, previous work predicts a significant yield of HOONO especially at low temperatures (see Fig. S8). As the lifetime of HOONO with respect to re-dissociation to reactants is short at, for example, boundary layer temperatures (≈1 s at 298 K and 1 bar pressure), its formation may be seen as an effective reduction in the rate coefficient for OH + NO₂ (Golden and Smith, 2000). However, its lifetime increases to several days at temperature and pressure conditions typical of the tropical tropopause (100 mbar, 220 K). As HOONO formation and loss are now parameterized (see above) in EMAC, we can explore its potential contribution to odd-nitrogen species in the atmosphere. The reaction between OH and NO₂ to form HOONO converts short-lived HO_x (HO_x = OH + HO₂) and NO_x (NO_x = NO + NO₂) into a longer-lived “reservoir” species, and in this sense it is similar to the reaction between HO₂ and NO₂ to form HO₂NO₂:

$$\begin{array}{}\text{(R9)}& {\mathrm{HO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}+\mathrm{M}\to {\mathrm{HO}}_{\mathrm{2}}{\mathrm{NO}}_{\mathrm{2}}+\mathrm{M},\end{array}$$

which is also thermally unstable, dissociating to reform HO₂ and NO₂. Unlike HOONO, for which there are no atmospheric measurements, much effort has been made to measure concentrations of HO₂NO₂ in colder regions of the atmosphere, and it is considered an important component of the NO_y budget at high altitudes (Nault et al., 2016). We therefore compared EMAC predictions of HOONO concentrations with those of HO₂NO₂. The results are displayed in Fig. 8, in which we plot the zonally averaged HOONO∕HO₂NO₂ ratio. Immediately apparent from Fig. 8 is that, compared to HO₂NO₂, HOONO is a minor component of NO_y in the warm, lower atmosphere. This reflects the difference in the thermal decomposition rate constant of the two trace gases, i.e. that of HO₂NO₂ being $\approx \mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹ in, for example, the middle troposphere at 400 mbar and 250 K, whereas HOONO decomposes a 10 times faster so that its lifetime is only ≈1000 s. In the UTLS region, the ratio increases further (HO₂NO₂ is a factor of 50 more long lived with respect to thermal decomposition at 100 mbar and 220 K), but the lifetimes of both gases under these conditions are sufficiently long that their concentrations are largely determined by their production rates and their losses due to photolysis and reaction with OH. The maximum ratio of HOONO to HO₂NO₂ is found at the tropical tropopause, where concentrations become comparable. As the modelled loss processes of HOONO and HO₂NO₂ (rate constants for photolysis and reaction with OH) are assumed to be identical, the occurrence of the maximum HOONO to HO₂NO₂ ratio at the tropical tropopause is related to the ratio of the (temperature-dependent) rate coefficients responsible for their formation (at 220 K and 100 mbar this favours HOONO formation by a factor of ≈2) and the model OH∕HO₂ ratio. Whilst this result indicates that HOONO could be an important reservoir of NO_x under certain conditions, we must bear in mind that there is great uncertainty associated not only with the branching ratio to HOONO formation in Reaction (R1b) but also with its loss processes (reaction with OH, photolysis), which remain unexplored experimentally. OH reacts with HO₂NO₂ via H abstraction from the H−OO group (IUPAC, 2019), and a similar mechanism is likely for HOONO. As the H−OO bond strength is likely to be greater in HOONO than in HO₂NO₂ (larger electron density around the peroxy bond), we may expect the rate coefficient to be lower for HOONO. A significantly lower rate coefficient for reaction with OH (or photolysis rate constant) could greatly increase the abundance of HOONO. If this were the case, airborne instruments that measure NO_x would likely also measure some fraction of HOONO following its rapid decomposition in warm inlet lines, as has been observed for HO₂NO₂ and CH₃O₂NO₂ (Nault et al., 2015; Silvern et al., 2018). Clearly, more experimental or theoretical data that better constrain the yield of HOONO and its atmospheric loss processes as well as atmospheric measurements are necessary in order to improve our understanding of the role of the reaction between OH and NO₂ throughout the atmosphere.

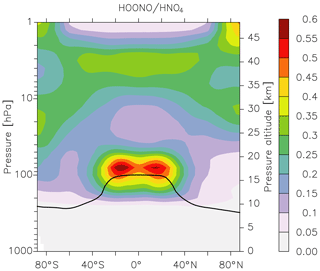
Figure 8 Model (EMAC) ratio of HOONO (formed in the reaction of NO₂ with OH) to HO₂NO₂ (formed in the reaction of NO₂ with HO₂) calculated using the present parameterization of k₁ and equating the (unknown) rate coefficients for loss of HOONO via reaction with OH or photolysis to those of HO₂NO₂. The black line represents the model tropopause.

4 Conclusions

We have made very precise and accurate measurements for the overall rate coefficient, k₁, of the reaction between OH and NO₂, which is of critical importance in atmospheric chemistry. Our experiments demonstrate clearly that the presence of H₂O increases significantly the overall rate coefficient (k₁) of the reaction between OH and NO₂. H₂O is found to be a more efficient collisional quencher (by a factor of ≈6) of the initially formed HO–NO₂ association complex than N₂ and a factor of ≈8 more efficient than O₂. A new parameterization of the rate coefficient for the title reaction that considers the roles of N₂, O₂, and H₂O as third-body quenchers (also using data from our previous paper; Amedro et al., 2019) has been incorporated into a global chemistry transport model to assess its impact on, for example, the HNO₃∕NO₂ ratio as well as NO_x and OH levels. Compared to existing evaluations of the kinetic data, use of the new parameters will result in significant changes (5 %–10 %) in the partitioning of NO_x and NO_y, the direction of the bias depending on which evaluation is used as reference and on region of the atmosphere. This work highlights the continuing importance of obtaining accurate laboratory kinetic data for those reactions that are central to our understanding of atmospheric chemistry and which provide anchor-points in chemical transport models.

Though the result is associated with great uncertainty owing to missing kinetic parameters for HOONO, the global model predicts the presence of HOONO in concentrations similar to those of HO₂NO₂ at the tropical tropopause. The present dataset addresses only the overall rate coefficient (k₁). Detailed experimental studies of the formation of HOONO (e.g. its yield at various temperatures and in the presence of H₂O) and on the fate of HOONO (OH kinetics, photolysis) are required to better assess its role as an NO_x and HO_x reservoir in cold parts of the atmosphere.