Modelling the relationship between liquid water content and cloud droplet number concentration observed in low clouds in the summer Arctic and its radiative effects

Low clouds persist in the summer Arctic with important consequences for the radiation budget. In this study, we simulate the linear relationship between liquid water content (LWC) and cloud droplet number concentration (CDNC) observed during an aircraft campaign based out of Resolute Bay, Canada, conducted as part of the Network on Climate and Aerosols: Addressing Key Uncertainties in Remote Canadian Environments study in July 2014. Using a single-column model, we find that autoconversion can explain the observed linear relationship between LWC and CDNC. Of the three autoconversion schemes we examined, the scheme using continuous drizzle (Khairoutdinov and Kogan, 2000) appears to best reproduce the observed linearity in the tenuous cloud regime (Mauritsen et al., 2011), while a scheme with a threshold for rain (Liu and Daum, 2004) best reproduces the linearity at higher CDNC. An offline version of the radiative transfer model used in the Canadian Atmospheric Model version 4.3 is used to compare the radiative effects of the modelled and observed clouds. We find that there is no significant difference in the upward longwave cloud radiative effect at the top of the atmosphere from the three autoconversion schemes (p=0.05) but that all three schemes differ at p=0.05 from the calculations based on observations. In contrast, the downward longwave and shortwave cloud radiative effect at the surface for the Wood (2005b) and Khairoutdinov and Kogan (2000) schemes do not differ significantly (p=0.05) from the observation-based radiative calculations, while the Liu and Daum (2004) scheme differs significantly from the observation-based calculation for the downward shortwave but not the downward longwave fluxes.

1 Introduction

Observations show a warming trend in the Arctic that is 2.5 times greater than the rest of the world (ACIA, 2005). One known uncertainty in our understanding of climate change is the effect of clouds on the radiation budget (Lohmann and Hoose, 2009), with particularly important consequences for Arctic climate. Microphysical properties of Arctic clouds are sensitive to changes in cloud condensation nuclei (CCN) concentrations (Coopman et al., 2018) as is cloud radiative effect (Rosenfeld et al., 2019). As observed at other latitudes for comparable liquid water content (LWC), smaller cloud droplets in the Arctic are associated with less shortwave radiation at the surface than larger droplets due to an increased reflectivity (Peng et al., 2002). However, the net radiative effect of cloud droplet size and number concentration can vary in sign in the Arctic due to the interplay between longwave and shortwave radiative effects when there are high surface albedo and large solar zenith angle (Curry et al., 1996). Overall, the radiative forcing from shortwave radiation due to cloud is controlled by cloud microphysical properties such as liquid water path (LWP), effective radius, cloud droplet number concentration (CDNC), as well as solar zenith angle and surface albedo (Curry et al., 1996). The longwave cloud radiative forcing is dominated by LWC, effective radius, phase and emission temperature of the cloud (Sedlar et al., 2010). Model simulations without shortwave radiation have been used to show that it can also impact Arctic stratus clouds by limiting their height as well as microphysical properties, demonstrating feedbacks between radiation and cloud properties (Olsson et al., 1998). In general, the impact of increasing the CDNC is more complicated than just reducing the cloud droplet size and increasing the cloud reflectance, as it may inhibit precipitation, cause smaller droplets to evaporate faster in non-precipitating clouds and/or suppress the breakup of clouds by precipitation (e.g. Rosenfeld et al., 2014). Depending on the amount of moisture in the free troposphere, changes in the CDNC may also positively or negatively affect the LWP via increased cloud top radiative cooling enhancing turbulent mixing (and hence entrainment) near the top of the cloud (Possner et al., 2017; Chen et al., 2015; Ackerman et al., 2004) or via precipitation. The present investigation involving the relationship between LWC and CDNC has also been found to vary geographically in other regions of the world (Gryspeerdt et al., 2019).

In cloud models, an important parameterization that affects the cloud microphysical properties, and thus cloud lifetime and radiative effects, is the autoconversion scheme, which converts cloud droplets to drizzle drops in order to simulate rain. These schemes are usually used instead of explicit calculations of the cloud droplet size distribution to reduce the computational cost and complexity of models. Autoconversion schemes can depend on variables such as cloud LWC, air density, CDNC and droplet radius. Some have a threshold below which the cloud does not simulate rain while others simulate continuous precipitation based on LWC. Autoconversion rates from different parameterizations can vary from 10⁻⁷ to 10⁻¹¹ kg m⁻³ s⁻¹ for marine boundary layer clouds (Wood, 2005b), thus the choice of autoconversion scheme can be significant. A recent study compared the output of six models (three large eddy simulations and three numerical weather prediction models) simulating clean Arctic conditions, showing that under very clean conditions, clouds can be very sensitive to cloud condensation nuclei (CCN) concentrations, with otherwise identical simulations from individual models producing different cloud properties, to the point that the LWC and radiative effects of the clouds were CCN-limited (Stevens et al., 2018). In that study, models with faster autoconversion rates were found to be generally less sensitive to changes in CDNC or CCN concentrations for all examined cloud properties. However, the study did not test different autoconversion parameterizations using the same model. Nor did the study compare the results of Arctic clouds with different CCN concentrations or rain formation schemes in the models (Stevens et al., 2018). Others have pointed out the inherent difficulty of reconciling the abstraction of autoconversion from the physical processes in the cloud as well (Mülmenstädt and Feingold, 2018).

Recent observations by Leaitch et al. (2016a) showed a strong linear relationship between LWC and CDNC in low-altitude, relatively horizontally homogeneous, liquid clouds in the summertime Canadian Arctic with weak influences by outside mixing processes aside from the top and bottom of the clouds. The clouds were formed as air advected over cold water, rather than by lifting, and as such differ significantly from the adiabatic cloud concept model. In these clouds, LWC was approximately constant from the top of the cloud to the bottom of the observations, implying that the cloud did not form by lifting and condensation (Leaitch et al., 2016a). The clouds were also persistent in time with no evidence of significant precipitation and hence likely in a quasi-equilibrium state. Instead of droplet size reducing with increasing CDNC, the volume mean diameter remained approximately constant, with a value near 20 µm (Leaitch et al., 2016a). Three possible physical explanations for the linear relationship between LWC and CDNC are discussed here. One possible cause is autoconversion, since the autoconversion of cloud water becomes less efficient at higher CDNC because relatively few droplets are converted to raindrops, thus the liquid in them stays as LWC rather than precipitating out, leading to higher cloud LWC (Albrecht, 1989). A second possible cause is the entrainment of dry air parcels into a cloud without mixing with the cloud droplets. This type of inhomogeneous mixing occurs when the evaporation timescale is shorter than the timescale to mix the entrained parcels within the cloud, which results in some droplets evaporating fully in and near the entrained parcel, lowering the CDNC as well as the LWC (Gerber et al., 2008; Jensen et al., 1985), which may lead to a nearly linear relationship between LWC and CDNC. In contrast, during homogeneous mixing, the evaporation timescale is longer than the mixing timescale, which results in most cloud droplets losing some water but not completely evaporating, thus lowering the LWC while the CDNC remains constant. During one of the flights, Leaitch et al. (2016a) noted that entrainment appeared to reduce the CDNC but not the LWC, which is inconsistent with the linear change observed overall. As such, while entrainment may be a possible driver of the linearity of the LWC–CDNC relationship on the other days, it is likely not the sole or main driver overall in our data set. A final possible cause is increased rates of cooling causing increased rates of condensation (and possibly supersaturation), which increases both the CDNC and LWC. A possible mechanism for this would be fog advecting over a colder surface, as when a water temperature gradient exists. The implication of autoconversion driving part of the observed linear relationship is that it provides evidence for the second aerosol indirect effect since higher CDNC suppress rainfall, leading to higher LWC.

Three of the cases observed during the Network on Climate and Aerosols: Addressing Key Uncertainties in Remote Canadian Environments (NETCARE) 2014 flight campaign had CDNC at or below the tenuous cloud regime (Leaitch et al., 2016a; Mauritsen et al., 2011). Mauritsen et al. (2011) proposed that a tenuous cloud regime exists when cloud formation is limited by the available CCN, wherein the low CDNC causes rapid growth from vapour deposition resulting in droplets large enough to fall. This was expanded by Leaitch et al. (2016a), who introduced the Mauritsen limit as a threshold for the aerosol concentration, below which an increase in the CCN (hence CDNC) results in net warming due to longwave effects. As such, clouds with aerosol concentrations below the Mauritsen limit are presumed to be in the tenuous-cloud regime. Previously determined numerical values of the Mauritsen limit have included 10 cm⁻³ (Mauritsen et al., 2011) and 16 cm⁻³ (Leaitch et al., 2016a), but the concept is not tied to specific droplet number concentrations, as the environment can affect the threshold (Leaitch et al., 2016a; Mauritsen et al., 2011).

In this study, we attempt to reproduce the observed linear relationship between LWC and CDNC using the Single-Column Model for Arctic Boundary Layer Clouds (SCM-ABLC), which is based on the fourth generation of the Canadian Atmospheric Global Climate Model (CanAM4) (von Salzen et al., 2013). Specifically, we examine whether autoconversion can explain the observed linear relationship between CDNC and LWC, since the SCM-ABLC does not include radiative feedbacks involved in increasing condensation rates or parameterizations of inhomogeneous mixing as it uses a first-order turbulence closure. Dry air above the cloud is allowed to mix into the cloud and evaporate cloud droplets, but this parameterization may not be sufficient to accurately account for the effect of stirring between cloudy and non-cloudy air that might result in inhomogeneous mixing (Gerber et al., 2008; Jensen et al., 1985). The simulated CDNC and LWC use three autoconversion schemes (Wood, 2005b; Liu and Daum, 2004; Khairoutdinov and Kogan, 2000) that are explored and compared. Changes in the radiative balance of the simulated clouds due to differences from the autoconversion schemes are examined using an offline version of the radiative transfer model in CanAM4.3 (see Sect. 2.3 for details).

2 Methods

2.1 Observations

This study uses observations from the NETCARE project (Abbatt et al., 2019). These data were collected during an aircraft campaign on board the Alfred Wegener Institute's Polar 6 aircraft based out of Resolute Bay, Nunavut (74^∘40^′48^′′ N, 94^∘52^′12^′′ W), in July 2014 (see Fig. 1). Only details relevant to this study are included below. A more extensive description of the details of the flight campaign can be found in Leaitch et al. (2016a).

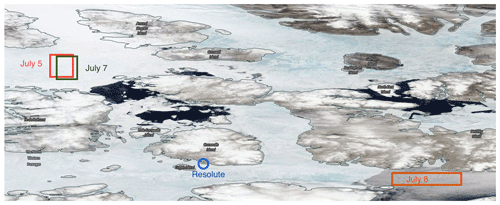
Figure 1 Satellite image from 8 July 2014 depicting Resolute Bay and the surrounding area, with rectangles showing the approximate locations of profiles on 5, 7 and 8 July. Retrieved from https://worldview.earthdata.nasa.gov/ (National Aeronautics and Space Administration, 2018).

Temperature, wind speed and relative humidity measurements from the Aircraft Integrated Meteorological Measurement System (AIMMS-20) were used in the creation of input profiles for the SCM-ABLC. Cloud properties were determined from the Forward Scattering Spectrometer Probe (FSSP-100, Particle Measuring Systems), which measured the number concentration and size distribution of cloud droplets, allowing the LWC and CDNC to be determined (Coelho et al., 2005). The FSSP was mounted in a canister under the port-side wing (Leaitch et al., 2016a), with modified tips to reduce shattering artefacts as per Korolev et al. (2011). These data were processed to account for the geometry of the FSSP (depth of field =0.298 cm, beam diameter =0.02 cm and the true air speed from the AIMMS-20). No corrections were applied for probe dead time or for coincidence effects since these were deemed to be negligible due to the low airspeed of the aircraft (∼65 m s⁻¹) and low CDNC (<131 cm⁻³) in this study, respectively. However, LWC may be underestimated due to droplets that were larger than the upper limits of the chosen FSSP sampling sizes (approximately 45 µm; Leaitch et al., 2016a). However, we expect that the number of larger droplets was negligible in this work, as the 95th percentile volume mean diameter observed in low-altitude clouds by Leaitch et al. (2016a) was 31 µm, far below the upper size limit. As per Leaitch et al. (2016a), no ice crystals or water droplets with diameter greater than 100 µm were detected by the PMS-2D-C greyscale probe in any of these clouds, suggesting that these clouds were not precipitating. However, the low-altitude clouds with very low droplet concentrations on 5 and 7 July had some droplets large enough in size (greater than 30 µm) that their settling speed was high enough to possibly be viewed as precipitation.

Vertical profiles

Flight sections through and near low clouds (defined as cloud top height ≤220 m) from 5, 7 and 8 July 2014 were included in this study and the profile locations and times chosen are shown in Table 1. Each profile contains a single trip either up or down by the aircraft and were chosen for segments when observations existed for at least 20 m in and above the cloud. Additionally, data points were excluded when any one of the instruments collecting the data that went into the input profiles malfunctioned. As many profiles as possible from the Leaitch et al. (2016a) study were included in this study. However, profiles either through very thin cloud layers or entirely within a cloud layer without any observations above the cloud were excluded.

Table 1 Details of the location and time of the low clouds examined in this study.

Our model represents spatially averaged conditions in cloudy and clear-sky grid cells separately for a better comparison with observations, so non-cloudy samples were removed before averaging data points in cloudy grid cells. This was accomplished by binning LWC data points in each profile into 10 m altitude bins. Bins were then categorized as being in cloud if more than 50 % of the LWC data points were greater than 0.01 g m⁻³. For bins deemed to be in cloud, only individual data points within each in-cloud bin with LWC greater than 0.01 g m⁻³ were included in the bin's average LWC. A similar procedure was applied to altitude bins considered to be out of cloud but with a condition that the average and individual LWC had to be less than 0.01 g m⁻³ in order to be included. Meteorological variables were also averaged into altitude bins, but only observations associated with LWC values included in the bin average were included in the analysis.

The SCM-ABLC only used a single input of CDNC for each profile. As such, a mean CDNC was calculated throughout the observed portion of the cloud by averaging the CDNC corresponding to each LWC data point in the in-cloud altitude bins over the number of data points in that bin. An average over all of the in-cloud altitude bins was then calculated and used as a fixed input in the SCM-ABLC. This two-step averaging procedure accounted for potential bias from the length of time that the aircraft flew at each altitude.

2.2 SCM-ABLC

2.2.1 Cloud physics and processes

Much of the model physics of the SCM-ABLC, from cloud processes and turbulence to the parameterizations of the ocean surface, is taken from the Canadian Atmospheric Global Climate Model, CanAM4 (von Salzen et al., 2013). However, the SCM-ABLC only models liquid clouds, excluding ice and mixed-phase clouds, and does not include aerosol processes. Clouds are produced by local turbulent mixing processes, which move moisture, heat and momentum down-gradient and are affected by surface fluxes. Cloud microphysical processes are prognostic, using a scheme based on the governing equations for water vapour and cloud liquid water outlined in Lohmann and Roeckner (1996) and Lohmann (1996) (von Salzen et al., 2013).

Eddy diffusivities calculated in the model depend on horizontal wind, height above ground, the gradient Richardson number and a mixing length (von Salzen et al., 2013). In the presence of cloud, the mixing length is set to 100 m (von Salzen et al., 2013), while in the absence of cloud, the mixing length is calculated from the parameterization by Lenderink and Holtslag (2004). Surface fluxes, including evaporation from the ocean, as well as heat and momentum fluxes, are simulated using an approach based on the Monin–Obukhov similarity theory (von Salzen et al., 2013).

The vertical size of the grid cells in SCM-ABLC is 10 m, which allows for a straightforward comparison with the flight observations since they are over a relatively narrow period in time and space with high temporal resolution (see Table 1) so that vertical features of the clouds are resolved on scales of a few metres. The modelled lower boundary was the ground, but the height of the upper boundary varied with the cloud top height and availability of measurements (see Table 1 for cloud top heights), though the upper boundary was always at least 20 m above the observed cloud top. The time step used was 900 s. The total run time was 300 h, which ensured that model results approach equilibrium for the given boundary conditions. Model results from the last 200 time steps (or 50 h) were then averaged.

Unsaturated air can be entrained into the cloud at the top and sides of the cloud as well as the bottom and affect microphysical properties in the cloud (e.g. Gerber et al., 2008). Entrained parcels have been found to exist on scales of metres in size and can reach up to tens of metres into the clouds before mixing homogenizes them with the rest of the cloud (Gerber et al., 2008). In the model, cloud parameterizations do not account for lateral mixing. While our 8 July flight observations are unlikely to have many entrained parcels due to the horizontal extent of the cloud, observations on 5 and 7 July are more likely to contain entrained parcels. Similar to other large-scale atmospheric models, air mixed into the cloud by vertical diffusion at the top and bottom of the cloud is immediately mixed with the cloudy air, assuming horizontally uniform thermodynamic cloud properties and CDNC.

2.2.2 Input profiles and boundary conditions

Inputs to the SCM-ABLC used aircraft observations of wind speed, relative humidity, LWC, CDNC and temperature. These inputs provided initial conditions for the model. Additionally, mean vertical profiles of CDNC, temperature, specific humidity and horizontal winds for each individual aircraft ascent or descent are generated and used to constrain meteorological conditions in the simulation by nudging (see the Supplement for details). Upper boundary conditions for cloud simulations representing the bottom of the free troposphere based on aircraft measurements were nudged as to remain constant over the duration of the model run. The lower boundary conditions at 10 m height for temperature and pressure were specified: the surface temperature was set to 273 K, as the flights were all near or over open water and ice edges, and the surface pressure was set to 1013 hPa. Between the surface and the altitude of the lowest observation-based initial condition, LWC, horizontal wind and temperature were calculated based on vertical diffusion with a first-order turbulence closure (von Salzen et al., 2013). Model output from the layers beneath the cloud were not considered in the analysis of results in the following sections.

2.2.3 Boundary layer heights

The choice of model domain vertical extent is important in the SCM-ABLC since processes above the boundary layer are not well-represented in the model due to the relatively long timescales and non-local character of free and upper tropospheric processes. For instance, the model does not account for the large-scale transport of air. On the other hand, mixing processes and cloud microphysical processes occur on timescales that are fast compared to large-scale transport of air so that it is sufficient to relax large-scale simulated thermodynamic conditions towards observed profiles. Consequently, we assume that the free troposphere in the model can be represented by the observations at those heights and that properties remain constant over the time period of the profile. For each case, the boundary layer height was estimated from the height of the base of the observed temperature inversion. The SCM-ABLC was then run for estimated modelled boundary layer heights within 30 m of that height. The height that resulted in a LWC profile most qualitatively similar to the observed was then used for all subsequent simulations for that case. The model LWC profile was averaged over the final 50 h of the simulation and then used for all later runs for that case. This procedure was repeated for all cases.

2.2.4 Autoconversion

Three autoconversion schemes detailed in the literature were used in the SCM-ABLC: Wood (2005b), Liu and Daum (2004), and Khairoutdinov and Kogan (2000). The latter two are herein abbreviated as L–D and K–K, respectively. These schemes are described below.

The autoconversion scheme presented by Khairoutdinov and Kogan (2000) separates liquid water in the model into two categories: cloud liquid water and drizzle. It predicts drizzle water and drizzle drop concentration using a prognostic scheme by fitting results from a large eddy scheme model (Khairoutdinov and Kogan, 2000). This scheme was found to be in good agreement with an explicit model for two cases with no rain and heavy drizzle that were analyzed by Khairoutdinov and Kogan (2000). It was developed for conditions found in the extra-tropics and mid-latitudes off the west coasts of continents, where stratocumulus cloud layers arise from upwelling of cold water in the ocean (Khairoutdinov and Kogan, 2000). As implemented in the CanAM4, the K–K scheme in the SCM-ABLC has been tuned so that the rate of conversion from cloud droplets to raindrops has been increased relative to the original parameterization (von Salzen et al., 2013). Tuning factors are commonly used in climate models, as autoconversion is usually underestimated due to missing processes and other factors (e.g. cloud homogeneity) (Williamson et al., 2015). A tuning factor of 2.5, based on simulations with version 4.3 of the Canadian Atmospheric Model (CanAM4.3), is used in this paper.

The scheme by Liu and Daum (2004) is based on similar principles to K–K but does not assume a fixed collection efficiency with respect to droplet radius (Liu and Daum, 2004). The different representation of the autoconversion process in the L–D scheme results in stronger dependencies on LWC and CDNC (Liu and Daum, 2004). It also increases the coefficient of variation (the ratio of standard deviation to the mean radius), which affects the threshold radius for autoconversion as broader droplet size distributions tend to have larger autoconversion rates (Liu and Daum, 2004). Unlike K–K, L–D has a threshold radius value before autoconversion begins, preventing rain processes below the threshold. However, this scheme has been shown to overestimate the autoconversion rate above the threshold compared to observation-based estimates for mid-latitude marine clouds (Wood, 2005b).

The Wood (2005b) scheme reduced the empirically calculated constant term in the L–D parameterization to 12 % of its original value based on a comparison with observation-based autoconversion rates in drizzling stratiform clouds that showed lower rates than predicted by L–D. Wood (2005b) also found that the K–K scheme did not over-predict rain as much as the L–D scheme in test cases (flight data described in Wood, 2005a) and suggested that the K–K scheme may be useful in situations other than those it was designed for (Wood, 2005b). The modified L–D scheme (referred to as the Wood scheme) produced more realistic dependencies of autoconversion on cloud LWC and CDNC compared to the original L–D scheme for drizzle in stratiform clouds (Wood, 2005b). All were originally developed for the mid-latitudes, so as part of our study we will be evaluating their performance in summer Arctic low clouds.

Three additional cases were simulated in the SCM-ABLC for diagnostic purposes. The first two cases eliminated the impacts of CDNC on the autoconversion rates. This was accomplished by keeping the CDNC constant while retaining the variation in meteorological conditions, such as temperature, relative humidity and wind speed. CDNC values of 5 and 112 cm⁻³, near the extreme observed values, were chosen to represent the range from the observations caused by CDNC. Only the Wood autoconversion scheme was used for these calculations for simplicity. The third case simulated no autoconversion by allowing the variable that represents rain water to be constantly zero, forcing all of the moisture in the clouds to remain in either cloud droplet or vapour form.

2.2.5 Cloud profiles

The cloud vertical extent produced by the SCM-ABLC can differ slightly between different autoconversion schemes and does so in some simulations. However, since the aircraft observations used in our comparisons do not include the entire cloud but only the uppermost part of it, we have focused on comparing the thicknesses equivalent to the observed portion of the clouds rather than examining the modelled vertical extent. For each observed profile, we used the thickness of cloud measured down from the modelled cloud top to the penetration depth of the aircraft into the cloud during the NETCARE flights. Parts of cloud below the lowest flight level of the aircraft were omitted to avoid only relying on model output.

2.3 Offline radiative transfer model

In addition to SCM-ABLC, this study uses an offline version of the radiative transfer model in CanAM4.3. The main attributes of the radiative transfer model are described in von Salzen et al. (2013) and references therein. Only profiles from 8 July are used for the radiative transfer calculations. The flights from 5 and 7 July were not analyzed due to the different solar zenith angles, the different surface albedos, the small number of available cloud profiles and the possible effects of a different regime at lower CDNC. This resulted in uncertainties that would have made meaningful comparisons difficult. We summarize the main aspects of the model below.

2.3.1 Model description

Solar and infrared fluxes and heating rates are computed using the Monte Carlo Independent Column Approximation (McICA), which can account for the cloud horizontal variability and vertical overlap (Pincus et al., 2003; Barker et al., 2008). Both the solar and infrared use two-stream solutions, the delta-Eddington approximation for the solar (Zdunkowski et al., 1982) and a perturbation approach for the infrared (Li, 2002).

Absorption by gases is computed using the correlated-k method (von Salzen et al., 2013; Lacis and Oinas, 1991). The optical properties of liquid clouds are computed separately, using the parameterizations referenced by von Salzen et al. (2013), for solar (Dobbie et al., 1999) and infrared (Lindner and Li, 2000) wave numbers.

Aerosols were omitted in the radiative transfer calculations due to their relatively small effects on the radiative fluxes compared to those due to the clouds.

2.3.2 Cloud profiles

The radiative transfer model required profiles of cloud properties including the effective radius, LWP, cloud fraction and cloud heights. These profiles were constructed by using model output of cloud properties, as described in Sect. 2.2.5. Clouds below the lowest flight level of the aircraft were again omitted to avoid only relying on model output in all but one of the simulations with the radiative transfer model. We ran a single case using averaged cloud microphysical properties from the observed part of the cloud in order to estimate the difference in radiative fluxes due to the difference in cloud thickness (see Sect. 3.2 for results). The LWC was then multiplied by the grid cell depth and integrated to yield the LWP needed as input to the radiative transfer model. The cloud amount was set to 1 (overcast) at the altitudes where there was cloud for both the SCM-ABLC and observed profiles. This allowed the optical depths of the modelled and observed clouds to be compared since their thicknesses were equal.

The radiative transfer calculations were performed using the cloud profiles constructed as described above using three configurations: cloud profiles from observations, cloud profiles from the SCM-ABLC and no clouds. The profile with no clouds was calculated by setting zero values for the cloud amount, LWP and effective radii. The radiative effects of clouds were computed by subtracting the clear-sky radiative fluxes from the radiative fluxes resulting from cloudy profiles.

2.3.3 Atmospheric state profiles

Profiles of pressure, temperature and water vapour profiles were created using the European Centre for Medium-Range Weather Forecasts (ECMWF) Re-Analysis (ERA)-Interim product by extracting the profiles closest in time and location to the aircraft profiles. The results were vertically interpolated to a vertical grid with 8866 levels spanning from the surface to ∼89 km, with each layer between 10 and 20 m thick. The temperature profiles from ERA-Interim were adjusted by a height-independent scaling factor defined by comparing the mean cloud temperatures from the ERA-Interim to the mean observed cloud temperatures, bringing the cloud temperatures closer to the observations. The surface skin temperature was chosen by rounding the temperature interpolation at the lowest level to the nearest degree. Trace gas profiles, including carbon monoxide, carbon dioxide, ozone, nitrous oxide, methane, oxygen, carbon tetrachloride, CFC-11 and CFC-12, were computed by interpolating a climatology from the ECMWF Integrated Forecasting System to all levels.

2.3.4 Surface albedo

The flight on 8 July took place over the open ocean, which we estimated to have a broadband surface albedo of 0.054 based on the solar zenith angle and the time of flight using the parameterization from Taylor et al. (1996). This value is consistent with ocean albedos used by other studies based on measurements (Henderson-Sellers and Huges, 1982; Kukla and Robinson, 1980; Budyko, 1956; Payne, 1972). Albedo values from 5 and 7 July were not used, as the profiles from 5 and 7 July are omitted from the radiative transfer calculations.

3 Results and discussion

3.1 SCM-ABLC

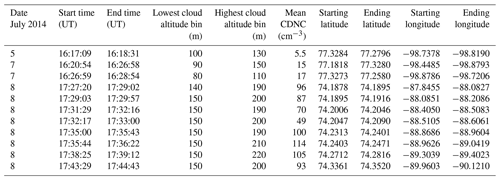
The green triangles in Fig. 2 show the observed mean LWC and CDNC from the profiles listed in Table 1 and Sect. 2.1. As observed by Leaitch et al. (2016a), the CDNC and LWC are linearly related, despite a slightly different definition of profiles. The variance in our observed relationship is low, with R²=0.987 (Table 2, “observed” case).

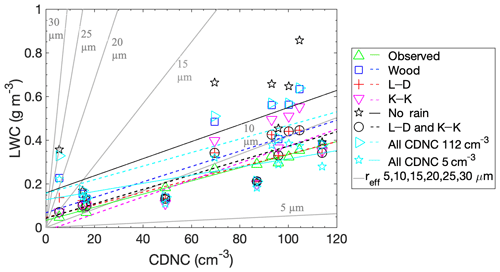
Figure 2 Observed and simulated LWC for three autoconversion schemes in SCM-ABLC, as a function of the observed CDNC specified in the model (symbols). Linear regressions are also shown for the observations and different parameterizations (lines). “No rain” corresponds to the LWC produced by the model with no autoconversion scheme. “L–D and K–K” corresponds to the combination of L–D (>20 cm⁻³) and K–K (<20 cm⁻³) schemes. “All CDNC 5 cm⁻³” and “all CDNC 112 cm⁻³” refer to the test cases of the Wood scheme that were run with all of the profiles having a constant CDNC of 5 and 112 cm⁻³, respectively, with the x axis values corresponding to which original CDNC values they had. The grey lines show the theoretical LWC for varying CDNC given the constant effective radii of the labels.

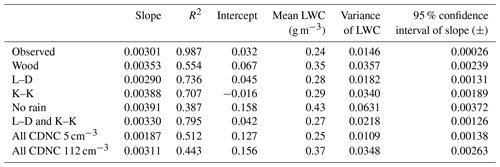
Table 2 Summary of linear fits of observations and model output. See the main text for description of cases. Here R² corresponds to the coefficient of determination, or the proportion of variance in LWC due to CDNC.

To determine whether autoconversion was an important source of the linear relationship observed between LWC and CDNC by Leaitch et al. (2016a), we used the SCM-ABLC to model the LWC for the profiles listed in Table 1 using the three different parameterizations of autoconversion (described in Sect. 2.2.4). Simulations were conducted with the K–K, L–D, and Wood autoconversion schemes; with two different constant CDNC; and with no autoconversion scheme (see Fig. 2 and Table 2 for the cases K–K, L–D, Wood, all CDNC 112 cm⁻³, all CDNC 5 cm⁻³ and no rain, respectively). Based on these results, we constructed a piecewise function based on the two linearizations of the closest-fitting results to observations, called “L–D and K–K” corresponding to the combination of L–D and K–K schemes, with the K–K scheme at CDNC <20 cm⁻³ and the L–D scheme at higher CDNC.

Overall, Fig. 2 shows that the linearity of the relationship observed between CDNC and LWC can be reproduced by all three autoconversion schemes. Nevertheless, the tested autoconversion schemes tend to overpredict the LWC compared to observations in most cases. The Wood scheme (blue squares) produces the highest variability in LWC and overpredicts the observations the most. The K–K scheme (magenta triangles) has the largest slope but overpredicts the least at lower CDNC, while the L–D scheme (red crosses) has the lowest slope and overpredicts the observations the least at higher CDNC. The slopes and variance in Table 2 show that the L–D scheme is closer to the observations than the Wood scheme in both measures, suggesting that the reduction in autoconversion implemented by Wood to the original L–D autoconversion scheme is not suitable for summer Arctic low clouds. In summary, the simulations with L–D and K–K parameterizations explain most of observed variability in LWC in Fig. 2.

Interestingly, simulations with the simplified parameterizations that do not account for effects of CDNC on autoconversion (“all CDNC 5 cm⁻³” and “all CDNC 112 cm⁻³”) also produce LWC values that are similar to the observed values for some of the flights but have lower R² values compared to results with L–D and K–K parameterizations (see Table 2). In addition, the relative size of the 95 % confidence interval from the all CDNC 112 cm⁻³ is large in comparison to the autoconversion cases and the observations (Table 2). This indicates that differences in meteorological conditions, cloud top height, boundary layer depth and the location of the inversion in the simulations that are associated with different aircraft profiles are partly responsible for the increase in LWC with CDNC, according to the linear regression in Fig. 2. Due to the lack of droplet sedimentation in the model, the droplets in the all CDNC 5 cm⁻³ case are likely to be very large, possibly resulting in more autoconversion than expected and lower LWC values in this simulation. This conclusion is further supported by the results of the simulation, which does not include autoconversion and precipitation (the “no rain” case). Without autoconversion and precipitation, the simulated LWC is generally much higher than observed, but high values of LWC are still associated with greater CDNC (see Fig. 2). The no rain case has a larger slope and smaller R² than the other test cases, supporting the hypothesis that autoconversion is an important contributor to the observed linearity between LWC and CDNC compared to the other processes represented by the model. However, the relatively small number of flight profiles substantially affects the robustness of the statistical relationship between CDNC and LWC. Consequently, the model results indicate that a larger number of measurements would be required in order to minimize the impact of meteorological variability on LWC and relationship with CDNC.

Overall, the K–K scheme reproduced the observed LWC better at CDNC below 20 cm⁻³ while the L–D scheme reproduced it better at higher CDNC, suggestive of a regime change like that described by Mauritsen et al. (2011). Below the Mauritsen limit, clouds are CCN-limited and any droplet that forms can drizzle out. This process seems to be better represented by the K–K scheme, which continuously converts cloud droplets to raindrops with no threshold for conversion, compared to the other schemes which have a constant threshold, i.e. the L–D and Wood schemes. At higher CDNC, the K–K scheme overpredicts the LWC compared to the L–D scheme. To capture this change in regime, we combined the L–D and K–K schemes by using the K–K scheme to model the three profiles with CDNC below 20 cm⁻³ and the L–D scheme for the rest. This combination performed the best at obtaining the lowest variance, and the overall slope is similar to the observations (Table 2, L–D and K–K case). The exact cut-off for the tenuous cloud regime is likely dependent on the environment. In the original observations of Mauritsen et al. (2011), they discussed a threshold of 10 cm⁻³. However, both Mauritsen et al. (2011) and Leaitch et al. (2016a) suggested that this limit is more reflective of a change in regime than a specific numerical cut-off and that the actual threshold depends on location and time. The three lowest mean CDNC values used in our modelling were all less than or equal to 17 cm⁻³, similar to the limit suggested by Leaitch et al. (2016a) of 16 cm⁻³. We stress, however, that our data set is limited to only three profiles with CDNC in the tenuous cloud regime and that further work would be needed before these results could be generalized. Nevertheless, our findings are consistent with the observational results from Mauritsen et al. (2011) and Leaitch et al. (2016a) and further demonstrate the possible importance of this regime change at low CDNC. Other models may also need to consider this regime change to better represent Arctic low clouds.

The two observed profiles for which the model consistently underpredicted the LWC (at CDNC concentrations of 49 and 87 cm⁻³) had lower wind speeds in the cloud and less of a difference in wind speed between in-cloud and above the cloud than some of the other profiles. This may have prevented sufficient water vapour from mixing into the cloud, thereby preventing conversion of cloud water vapour to liquid water.

Other studies have previously noted that autoconversion schemes often do not represent the rain rates in the Arctic very well (Croft et al., 2016; Zhang et al., 2002; Olsson et al., 1998). Olsson et al. (1998) speculated that the discrepancy between modelled and observed rain rates may be due to the size of droplets, as small droplets can fail to initialize autoconversion when the threshold is too large. Our results support this theory at low CDNC: the K–K scheme, which has no threshold for autoconversion, performs the best at low CDNC, suggesting that the thresholds for autoconversion may be too high in the L–D and Wood schemes at these droplet concentrations, resulting in overpredicted LWC. We found that the L–D scheme performs best at higher CDNC, so there may be a regime change between low and high CDNC. Although the model comparisons carried out by Stevens et al. (2018) did not directly compare autoconversion schemes, they demonstrated that both large eddy simulation and numerical weather prediction models showed pronounced tendencies to increase LWP with increasing CDNC and that LWP is highly sensitive to CDNC, consistent with our results.

Although the L–D scheme best reproduces the nearly linear relationship between the observed LWC and CDNC, the linearity appears to be well-reproduced by all three of the autoconversion schemes that we examined. This indicates that autoconversion is indeed an important driver of the linearity between LWC and CDNC in this instance, since the no-autoconversion case is much less linear and has lower R² (see Fig. 2 and Table 2). Since the linear fit for the no rain case explains less of the variability than the linear fits for the simulations with autoconversion parameterizations, we surmise that autoconversion is a driver of the linear relationship. As such, autoconversion appears to be sufficient to drive the linearity observed between LWC and CDNC by Leaitch et al. (2016a), based on our modelling. This is consistent with the second aerosol indirect effect and similar to the findings by Stevens et al. (2018). There is no evidence of strong turbulent mixing in the observations. Further, we are assuming that turbulence affects the LWC but not the CDNC in the simulations, as we do not account for cloud inhomogeneities. As such, the simulated relationship between LWC and CDNC may be incomplete. Future work may have to better incorporate subgrid-scale cloud mixing processes in models.

3.2 Radiative fluxes

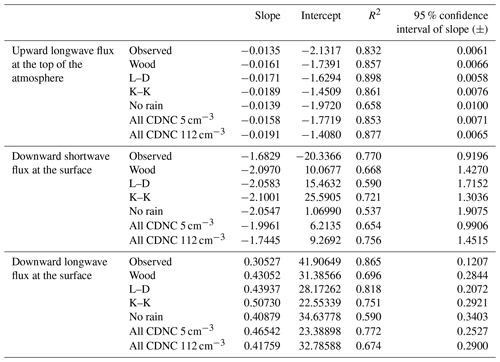
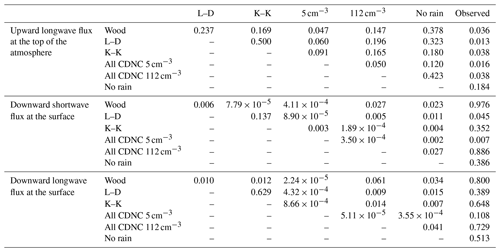
The offline radiative transfer model was run using simulated profiles of liquid water path and effective radius from the SCM-ABLC as input for the flights on 8 July, as well as with the clouds removed, to compute the cloud radiative effect (CRE). For these calculations, all profiles were assumed to be over open ocean. The green triangles in Fig. 3 are the longwave CRE at the top of the atmosphere calculated from the observed liquid water path and effective radius, while the other symbols represent the longwave CRE calculated from the model output using the different autoconversion schemes in the SCM-ABLC. Since the effective radii are roughly constant over all of the cases that were considered and the LWC was found to linearly increase with the CDNC, the optical depth, and therefore the extinction, estimated from the plane-parallel approximation, also varies linearly at these relatively low CDNC (see Table 3). This results in the longwave CRE at the top of the atmosphere linearly decreasing with increasing CDNC. We find that slopes are slightly larger for the simulations than for observations, with the exception of the no rain case (see Table 3). The R² value indicates that the relationships are linear to a very good approximation for each case but lowest for the no rain case (see Table 3). Further, using a t test, the longwave calculations showed no significant difference at p=0.05 in the CRE between the different autoconversion schemes (see Table 4). However, there is a significant difference between the CRE modelled and those based on observations at p=0.05, due to the differences in modelled and observed effective radii and LWC for all autoconversion schemes, except for the no rain case, where no autoconversion was included (see Table 4).

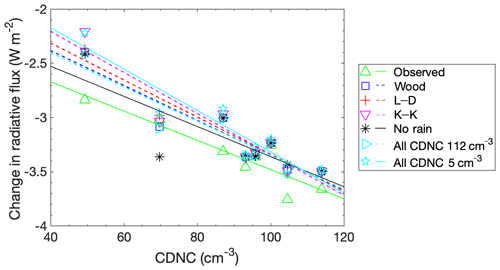
Figure 3 Change in upward longwave radiation at the top of the atmosphere due to the presence of cloud on 8 July only, wherein the input cloud variables were from the SCM-ABLC output or based on observations. The radiative flux for the “observed” case is calculated using the radiative transfer model with observed cloud properties.

Table 3 Summary of linear fits of radiation model CRE. See the main text for description of cases.

Table 4 The t test results for the change in CRE for 8 July.

A similar decreasing linear relationship exists for the downward shortwave CRE at the surface (Fig. 4). However, there is no significant difference at p=0.05 (see Table 4) in the downward shortwave CRE at the surface between each scheme and the observation-based radiative transfer calculations on 8 July, except for the L–D and all CDNC 5 cm⁻³ cases.

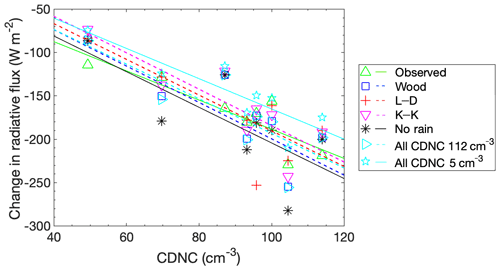
Figure 4 Change in downward shortwave radiation at the surface due to the presence of cloud, wherein the input cloud variables were from the SCM-ABLC output or based on observations. The radiative flux for the “observed” case is calculated using the radiative transfer model with observed cloud properties.

An increasing linear relationship exists for the downward longwave CRE at the surface (Fig. 5), indicating that clouds with higher CDNC result in greater longwave radiative fluxes when compared to the case with no cloud. The calculation based on observations results in the highest R² value (see Table 3), implying that autoconversion schemes do not replicate this result quite as well, although the L–D scheme does quite well at linearizing despite having a very different slope and intercept (Table 3). The t tests show, however, that none of the autoconversion schemes result in downward longwave radiation values that differ significantly (p=0.05) from observation-based calculations, though the all CDNC 5 cm⁻³ case and the no rain case differ significantly (p=0.05) from all other autoconversion-based cases (Table 4).

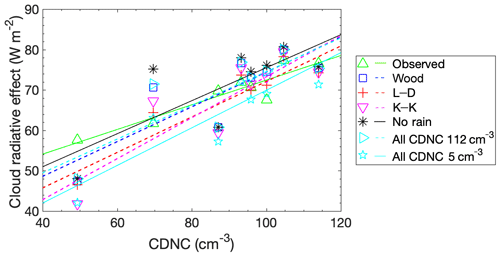
Figure 5 Change in downward longwave radiation at the surface due to the presence of cloud, wherein the input cloud variables were from the SCM-ABLC output or based on observations. The radiative flux for the “observed” case is calculated using the radiative transfer model with observed cloud properties.

From these comparisons of the 8 July data, the most important result is that there is an offset in the CRE based on the observations versus the SCM-ABLC model output for the upward longwave CRE at the top of the atmosphere, which is significant at p=0.05 for all cases but no rain, which had no autoconversion processes. However, the downward shortwave CRE at the model surface shows that all autoconversion schemes but the all CDNC 5 cm⁻³ and L–D cases produce CRE that are not significantly different (p=0.05) from those calculated based on observed cloud profiles. A final takeaway from the t tests was that the Wood autoconversion produced small but statistically significantly different downward shortwave CRE at the surface from the other two autoconversion schemes from the literature at a significance of p=0.05, while the L–D and K–K schemes did not significantly differ from each other. This may require further investigation as the L–D and Wood schemes differ only by a constant, while the K–K scheme uses an additional variable as well as different constants. In addition to this, the no rain case with no autoconversion processes differed significantly at p=0.05 from all other SCM-ABLC-based input to the downward shortwave CRE at the surface, thus the presence of an autoconversion scheme in the cloud model produces a significant change in the resulting CRE.

A sample calculation was carried out to test the radiative effects of extending the cloud to the surface, as was surmised to occur by observers during the 8 July flight. The extension of the cloud was assumed to have a LWP and effective radii equal to the average of those values in the observed portion of the cloud. This resulted in a decrease of less than 1 % in the longwave CRE at the top of the atmosphere. Similarly, the change in the downward longwave CRE at the surface was also small, with the newly modelled cloud increasing the CRE by almost 4 %. The results were most sensitive in the downward shortwave CRE at the surface, with the thicker cloud decreasing the original CRE by approximately 35 %. The small changes in the longwave CRE indicate that the temperatures of the ground and the cloud top are similar. The larger change in the downward shortwave CRE at the surface indicates that the observed portion of the cloud is insufficiently thick to estimate the effect on the shortwave CRE on its own.

Overall, the results from Table 3 show that the model-based CREs produce more negative slopes than those based on observations, suggesting that the model overestimates the relationship between CDNC and shortwave CRE and that the first aerosol indirect effect may be overestimated by the three autoconversion parameterizations used in this study. The first aerosol indirect effect depends on a realistic sensitivity of fluxes to changes in CDNC in response to changes in CCN concentrations. However, the best agreement in slopes for the change in shortwave CRE is found in the simulations which assume a constant CDNC in parameterizations of autoconversion (see Table 3). In particular, the change in shortwave CRE is much greater for the K–K parameterization than calculation based on observations, which is consistent with the particularly strong non-linear dependency of this parameterization on CDNC.

4 Conclusion

Our model simulations show that the linear relationship between LWC and CDNC observed by Leaitch et al. (2016a) in summer Arctic low clouds is consistent with parameterizations of autoconversion, although other processes, such as variability in meteorological conditions, entrainment of dry air without mixing and increased condensation rates, may contribute to the observed relationship. The choice of autoconversion scheme in the SCM-ABLC changes the simulated relationships between LWC and CDNC, with the best simulated linear relationship (highest R²) obtained from a combination of the K–K scheme at CDNC below 20 cm⁻³ and the L–D scheme at higher concentrations. These results are consistent with a regime change between very low and higher CDNC corresponding to the Mauritsen limit. Below this limit, droplet concentrations are CCN-limited and droplets are expected to grow and fall out quickly, consistent with the constantly drizzling K–K scheme. In contrast, the L–D and Wood schemes have threshold radii before drizzle occurs, consistent with our understanding of drizzle formation in regions with greater CDNC. Due to a lack of observational data, the exact transition above which the L–D scheme performed better could only be constrained to a range of 17–48 cm⁻³. It is important to note that our observations below the Mauritsen limit only consisted of three profiles and that our conclusions are dependent on this limited data set. It would be of interest to examine whether this regime change can be reproduced with more data in other parts of the summer Arctic and with other models. The observational data examined in this study have shown that cloud properties, such as effective radius, vary somewhat between the regimes, with an average observed effective radius of 12 µm below the Mauritsen limit versus 10 µm above it, which may also be interesting to re-examine with a larger data set. The choice of autoconversion scheme is most relevant when examining the cloud microphysical properties for their own sake, as opposed to radiation, and the combination of K–K and L–D schemes should be used for these conditions.

The modelled downward shortwave and longwave cloud radiative effects at the surface mostly did not differ significantly at p=0.05 from those due to the observations using the three autoconversion schemes from the literature, except for the L–D scheme, which had p=0.045 for the downward shortwave CRE. The modelled upward longwave CRE at the surface did differ significantly from those due to the observations for these schemes at p=0.05. This suggests that the microphysical parameters such as LWP and effective radius simulated by all the autoconversion schemes were sufficiently similar to observations for shortwave calculations but not for upward longwave calculations. The Wood autoconversion scheme simulated downward shortwave radiation at the surface that was significantly different from the K–K and L–D schemes but not from the observations. This appears to be due to the higher modelled LWC in the Wood scheme and indicates that this scheme may be less suitable for modelling low clouds in the summer Arctic, which tend to have low LWC.

Future work should determine the prevalence of a linear relationship between LWC and CDNC in other clouds, and whether autoconversion, and therefore the second aerosol indirect effect, is one of its primary drivers. Since part of our results were highly dependent on CDNC below the Mauritsen limit, determining the prevalence of clouds in a CCN-limited regime is needed to understand the importance of implementing different autoconversion schemes in clouds. There remain large uncertainties in the radiative effect of low clouds in the summer Arctic and ensuring that cloud microphysical properties are properly represented in models is one way to begin to reduce that uncertainty. Another important component of reducing the uncertainty in the radiative effect of clouds like these in the summer Arctic involves comparing the calculated radiative effect to observations. Remote sensing or in situ observations would allow us to improve our understanding of modelled cloud radiative effects. These results could be relevant for other regions with low CDNC, such as clean marine clouds and fogs. It may also be of interest to compare these findings to a large eddy simulation model. Another interesting future direction would be to probe our assumption that the cloud is in equilibrium. This could be accomplished by changing the CDNC abruptly after the model spin-up to observe the transient behaviour of the model microphysics, as performed by Gettelman (2015).