the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Constraining the Twomey effect from satellite observations: issues and perspectives
Johannes Quaas
Antti Arola
Brian Cairns
Matthew Christensen
Hartwig Deneke
Annica M. L. Ekman
Graham Feingold
Ann Fridlind
Edward Gryspeerdt
Otto Hasekamp
Zhanqing Li
Antti Lipponen
Po-Lun Ma
Johannes Mülmenstädt
Athanasios Nenes
Joyce E. Penner
Daniel Rosenfeld
Roland Schrödner
Kenneth Sinclair
Odran Sourdeval
Philip Stier
Matthias Tesche
Bastiaan van Diedenhoven
Manfred Wendisch
The Twomey effect describes the radiative forcing associated with a change in cloud albedo due to an increase in anthropogenic aerosol emissions. It is driven by the perturbation in cloud droplet number concentration (ΔNd, ant) in liquid-water clouds and is currently understood to exert a cooling effect on climate. The Twomey effect is the key driver in the effective radiative forcing due to aerosol–cloud interactions, but rapid adjustments also contribute. These adjustments are essentially the responses of cloud fraction and liquid water path to ΔNd, ant and thus scale approximately with it. While the fundamental physics of the influence of added aerosol particles on the droplet concentration (Nd) is well described by established theory at the particle scale (micrometres), how this relationship is expressed at the large-scale (hundreds of kilometres) perturbation, ΔNd, ant, remains uncertain. The discrepancy between process understanding at particle scale and insufficient quantification at the climate-relevant large scale is caused by co-variability of aerosol particles and updraught velocity and by droplet sink processes. These operate at scales on the order of tens of metres at which only localised observations are available and at which no approach yet exists to quantify the anthropogenic perturbation. Different atmospheric models suggest diverse magnitudes of the Twomey effect even when applying the same anthropogenic aerosol emission perturbation. Thus, observational data are needed to quantify and constrain the Twomey effect. At the global scale, this means satellite data. There are four key uncertainties in determining ΔNd, ant, namely the quantification of (i) the cloud-active aerosol – the cloud condensation nuclei (CCN) concentrations at or above cloud base, (ii) Nd, (iii) the statistical approach for inferring the sensitivity of Nd to aerosol particles from the satellite data and (iv) uncertainty in the anthropogenic perturbation to CCN concentrations, which is not easily accessible from observational data. This review discusses deficiencies of current approaches for the different aspects of the problem and proposes several ways forward: in terms of CCN, retrievals of optical quantities such as aerosol optical depth suffer from a lack of vertical resolution, size and hygroscopicity information, non-direct relation to the concentration of aerosols, difficulty to quantify it within or below clouds, and the problem of insufficient sensitivity at low concentrations, in addition to retrieval errors. A future path forward can include utilising co-located polarimeter and lidar instruments, ideally including high-spectral-resolution lidar capability at two wavelengths to maximise vertically resolved size distribution information content. In terms of Nd, a key problem is the lack of operational retrievals of this quantity and the inaccuracy of the retrieval especially in broken-cloud regimes. As for the Nd-to-CCN sensitivity, key issues are the updraught distributions and the role of Nd sink processes, for which empirical assessments for specific cloud regimes are currently the best solutions. These considerations point to the conclusion that past studies using existing approaches have likely underestimated the true sensitivity and, thus, the radiative forcing due to the Twomey effect.
- Article
(1506 KB) - Full-text XML
- BibTeX
- EndNote
Cloud droplets in liquid-water clouds form on cloud condensation nuclei (Aitken, 1880), a subset of the atmospheric aerosol particle population. The formation of cloud droplets in thermodynamic equilibrium is established textbook knowledge (Köhler, 1936). Whether an aerosol particle acts as cloud condensation nuclei (CCN) at a given supersaturation depends on its size and chemical composition, which determine the particle hygroscopicity (Dusek et al., 2006; Ma et al., 2013). If CCN concentrations at one supersaturation level are known, CCN concentrations at other supersaturation levels approximately scale with it according to the Twomey (1959) parameterisation. Here, we implicitly consider a supersaturation level of 0.2 % unless otherwise stated. Supersaturation is generated in the large majority of clouds by updraughts. The rare exceptions are formation due to radiative cooling (mainly fog events) or the mixing of cold and dry with warm and moist air masses. Cloud-scale updraughts originate in most cases from turbulence, convection or gravity waves. Updraught velocity, w, exhibits a large heterogeneity across temporal and spatial scales (Tonttila et al., 2011; Moeng and Arakawa, 2012). For a given probability density function (PDF) of updraughts, in an adiabatic air parcel with no active collision and coalescence, the addition of extra CCN will generally lead to a monotonic increase in cloud droplet number concentration, Nd (Twomey and Warner, 1967). The approximate functional form of the dependence of Nd on CCN concentration is then logarithmic, since the increase in Nd associated with activation of additional aerosol leads to a depletion of the maximum supersaturation (Twomey, 1959).
The CCN concentration in the atmosphere is increased by anthropogenic emission of aerosols and aerosol precursor gases (Boucher et al., 2013). This leads to enhanced Nd, unless aerosol particle concentrations are high and updraughts weak (Ghan et al., 1998; Feingold et al., 2001; Reutter et al., 2009). In turn, cloud albedo (αc, the fraction of solar radiative energy reflected back to space by clouds in relation to that incident at the cloud top) increases, as it is a monotonically increasing function of Nd. Following Platnick and Twomey (1994) and Ackerman et al. (2000),
a formulation which relies on (i) a two-stream radiative transfer approximation and (ii) the assumption that clouds obey vertical stratification that scales with an adiabatic one and that is horizontally homogeneous. Equation (1) is expressed as a partial derivative: other quantities – notably cloud water path – are considered constant.
These two facts – Nd is a monotonic function of CCN and αc in the partial-derivative sense is a monotonic function of Nd – imply that the anthropogenic increase in CCN concentrations causes a negative (cooling) radiative forcing due to aerosol–cloud interactions, RFaci (Boucher et al., 2013), denoted as ℱaci (Bellouin et al., 2020b). It can be approximately (neglecting absorption in the column above the cloud after scattering at cloud top) written as (Quaas et al., 2008; Bellouin et al., 2020b)
with the downward solar radiative flux density (irradiance) above clouds, , and a quantitative description of CCN denoted here as a. The relative anthropogenic perturbation to a is denoted Δln aant. This formulation assumes (i) that only the solar spectrum is relevant, which is well justified for the optically thick, liquid water clouds considered here, since an Nd perturbation only marginally changes the cloud radiative effect in the terrestrial spectrum of an optically thick cloud and (ii) that there is one liquid water cloud layer that determines the effect so that the problem can be considered purely horizontal in space. In contrast to the formulation by Bellouin et al. (2020b), we consider the problem as horizontally variable in space (x, y) and in time (t), i.e. . If Eq. (2) is assessed from temporally sparse satellite data, a proper integration over temporally varying solar zenith angles and cloud diurnal cycles is necessary.
RFaci is often referred to as the “Twomey effect” (Twomey, 1974) and also called the “(first) aerosol indirect effect” or “cloud albedo effect” (Lohmann and Feichter, 2001). Atmospheric models simulate a large range for RFaci (Gryspeerdt et al., 2020; Smith et al., 2020). It is, thus, necessary to constrain the Twomey effect quantitatively based on observations. Only satellites can provide global observational data that could be used to quantify the global RFaci (Stephens et al., 2019).
The Twomey effect has been assessed in many studies (starting with Bréon et al., 2002) in terms of cloud droplet effective radius, re, rather than using Nd. This is plausible as, for idealised vertical profiles of droplet size distributions (e.g. vertically constant or adiabatically increasing profiles), cloud optical depth and cloud albedo are easily expressed in terms of re (Hansen and Travis, 1974; Stephens, 1978). Given that re is closely related to light-scattering properties of clouds in the visible and near-infrared, this quantity is operationally retrieved from remote-sensing observations (Nakajima and King, 1990). However, re is not just a function of Nd but also varies with cloud liquid water path, L (Brenguier et al., 2000). It is thus necessary to formulate the problem for constant L, which is difficult to realise in data analysis from observations that are limited in time and space, or for selected cloud scenarios, so that datasets stratified by L become too small for meaningful analysis (Quaas et al., 2006; McComiskey and Feingold, 2012; Liu and Li, 2019). Specifically, in Eq. (2), the middle term, , would be formulated as , in which case the evaluation of the partial derivative requires stratification by L, in addition to the updraught regime, which adds substantial complexity.
Among the four factors on the right-hand side of Eq. (2), the first one, , is well quantified for each given latitude, longitude and time. The second one, , can be evaluated using Eq. (1) (Bellouin et al., 2020b; Hasekamp et al., 2019a), or alternatively by radiative-transfer simulations (Mülmenstädt et al., 2019). This implies that the two key problems in determining RFaci are the quantification of the anthropogenic perturbation of CCN, Δln aant, and the sensitivity of Nd to CCN perturbations, (Feingold et al., 2001). Taken together, this is the distribution of the anthropogenic perturbation of Nd (here expressed in absolute, not relative, terms):
The plausible range of the sensitivity is , except for heavily polluted situations (where it may become negative; Feingold et al., 2001), or when giant CCN play an important role (Ghan et al., 1998; Morales Betancourt and Nenes, 2014; Gryspeerdt et al., 2016; McCoy et al., 2017) where competition for water vapour during droplet formation is at its strongest. Such conditions represent a significant challenge to models and parameterisations of the process (Morales Betancourt and Nenes, 2014).
The aerosol forcing has to be evaluated at a scale much larger than an individual cloud. One of the key reasons for this is that there is currently no way to use satellite data to determine the anthropogenic fraction of the CCN population for a single air parcel. Methods applying model information, or data-tied approaches such as Bellouin et al. (2013) instead use the scale of model resolution or aggregate data resolution which is typically of the order of (or about 100×100 km2). The problem formulated in Eq. (3) then has to be reformulated, using an overbar to denote the averaging over a grid box as
which considers the mean sensitivity of Nd to CCN, , given the probability density function (PDF) of cloud base updraught velocity, w in the grid box, 𝒫(w); the PDF of CCN at cloud base within the scene, 𝒫(a); and the anthropogenic perturbation of the CCN concentration at the grid-box scale, . Note in the above equation, β is assumed independent of ln aant, which assumes that 𝒫(w) is independent of cloud properties (primarily, liquid water content), which applies to stratus clouds (Morales and Nenes, 2010) but not in general. Similarly, the covariance of 𝒫(w) and 𝒫(a) may not be zero (e.g. Kacarab et al., 2020 – in addition to Bougiatioti et al., 2020). All of the above suggest that observation of β at a cloud parcel scale is not directly transferrable to the large scale for an assessment of the Twomey effect. Rather, has to be estimated.
Beyond RFaci, aerosol–cloud interactions also lead to rapid adjustments: once cloud droplet size distributions are altered due to anthropogenic CCN, cloud microphysical and dynamical processes are modified as well (Albrecht, 1989; Ackerman et al., 2000; Wang et al., 2003; Heyn et al., 2017; Mülmenstädt and Feingold, 2018). Aerosols can induce transitions between cloud regimes, for instance by changing drizzle behaviour (Rosenfeld et al., 2006; Feingold et al., 2010; Wood et al., 2011). The direction and magnitude of these changes depends on the cloud state and regime, because responses to aerosol changes occur due to processes spanning a range from microphysics to the mesoscale (Christensen and Stephens, 2012; Kazil et al., 2011; Wang et al., 2011). These processes include precipitation suppression (Albrecht, 1989), rapid feedbacks involving cloud-top entrainment (Ackerman et al., 2004; Bretherton et al., 2007; Hill et al., 2009; Bulatovic et al., 2019) and rapid feedbacks involving cloud lateral entrainment (Xue and Feingold, 2006; Small et al., 2009) as well as responses in dynamics (Xue et al., 2008; Stevens and Feingold, 2009; Wang and Feingold, 2009). If one also considers deep clouds, further intricate cloud adjustments may occur that are not considered here (e.g. Ekman et al., 2011; Fan et al., 2013; Yan et al., 2014). As a result of these adjustment processes, cloud horizontal extent (Gryspeerdt et al., 2016) and liquid water path (Gryspeerdt et al., 2019) respond to perturbations in Nd. The sum of RFaci and the radiative effects of these adjustments is the effective radiative forcing due to aerosol–cloud interactions, ERFaci (Boucher et al., 2013). Based on modelling and data analysis, it is evident that the adjustments and, thus, also ERFaci scale with ΔNd, ant (Bellouin et al., 2020b; Gryspeerdt et al., 2020; Mülmenstädt et al., 2019). Analysis of model data shows that the rapid adjustments due to other contributions (small-scale to mesoscale circulation changes, thermodynamic changes) are small (Heyn et al., 2017; Mülmenstädt et al., 2019). Even so, thermodynamic and dynamic adjustments to aerosol changes can still have an important impact on droplet formation – especially under conditions where droplet formation is largely velocity-limited (Kacarab et al., 2020; Bougiatioti et al., 2020).
Despite the fact that the activation of an individual CCN to form a droplet is well understood in thermodynamic equilibrium (Köhler, 1936), it is not clear how Nd responds to perturbations of CCN at the scale of a cloudy air parcel, an entire cloud or of a cloud field up to the large scale of the order of as used in Eq. (4). A one-to-one relationship between CCN in the updraught below cumulus and Nd above the cloud base within the cumulus has been observed (Werner et al., 2014); although even at the cloud updraught scale, this relationship could be a convolution of the effect of CCN on droplet number, vertical velocity variability and lateral entrainment (Morales et al., 2011). At a larger scale, this relation is less pronounced (Boucher and Lohmann, 1995), consistent with the expectation from Eq. (4). In turn, there may be co-variability of updraughts and aerosol concentrations that lead to larger compared to situations with constant w (Kacarab et al., 2020; Bougiatioti et al., 2017, 2020).
Ground-based remote-sensing methods provide data to infer the sensitivity term β from long-term observations (Feingold et al., 2003; McComiskey et al., 2009; Schmidt et al., 2015; Liu and Li, 2018). However, this approach is limited to individual sites and cloud regimes. In consequence, when investigating the global radiative forcing relevant for climate studies, the sensitivity term necessarily is derived from satellite remote sensing (Nakajima and Schulz, 2009).
This leads to a number of problems and challenges discussed in more detail in the following sections.
- -
Retrieval of CCN. The first issue is the missing coincidence of cloud and aerosol retrievals. Usually, no aerosol is retrieved below or within clouds. It is thus questionable how representative aerosol in cloudless scenes is for (neighbouring) cloud base CCN. The second issue is the imperfect nature of proxies for CCN. Often the aerosol optical depth (AOD; see below) or a variant thereof is used, which can only imperfectly be related to CCN due to differences in sensitivity and the lack of vertical resolution.
- -
Retrieval of Nd. There are (i) retrieval errors and biases in Nd, which depend on cloud regimes, and (ii) one needs to consider the link between Nd as formed by CCN activation at cloud base and the retrieved cloud-top Nd. Cloud-top Nd (Nd, top) is the one that determines the scattering of sunlight and, thus, is relevant for the top-of-atmosphere cloud radiative effect. It differs from cloud base Nd (Nd, base) in conditions where Nd sinks such as precipitation or mixing play a role. When using re rather than Nd the additional problem of stratification by retrieved L arises.
- -
Cloud-regime dependence. Cloud base droplet concentration, Nd, base, is a function of both CCN and updraught, and Nd, top is further a function of Nd sinks such as precipitation formation and entrainment mixing. Thus, one needs to understand how the characteristics of w and its PDF, as well as precipitation and mixing processes, depend on cloud regime and how this may be used for an empirical estimation of .
- -
Aggregation scale. The relation of aggregate quantities is not the same as the aggregate relation, and, thus, one needs to determine how to derive optimally from remote-sensing data (Grandey and Stier, 2010; McComiskey and Feingold, 2012).
In practical terms, one further needs to assess to which extent a simple scalar sensitivity metric is sufficient, or whether a joint-PDF approach is preferable (McComiskey and Feingold, 2012; Gryspeerdt et al., 2017).
Beyond these questions which are discussed in the following sections, it is necessary to quantify the anthropogenic perturbation to CCN, Δln aant, which is not easily quantified from observations. The key problem is that there is little potential to observe an atmosphere unperturbed by anthropogenic emissions (Carslaw et al., 2013, 2017). Some studies attempt to quantify the anthropogenic perturbation to the column aerosol light extinction, or aerosol optical depth (AOD; τa), in a data-tied approach (Kaufman et al., 2005; Bellouin et al., 2005, 2013; Kinne, 2019). Such approaches rely on simplifying parameterisations, such as the assumption that small-mode aerosol particles are predominantly anthropogenic. The other option is to estimate it from simulations (Quaas et al., 2009b; Gryspeerdt et al., 2017). There are some indirect ways to infer the anthropogenic impacts on Nd (Quaas, 2015), such as from trends (Krüger and Graßl, 2002; Bennartz et al., 2011) or periodicity in anthropogenic emissions such as the weekly cycle (Quaas et al., 2009a). Hence, models are involved in determining an anthropogenic perturbation of CCN concentrations, which can even be attempted for individual weather events (Schwartz et al., 2002). In any case, it seems impossible to know the anthropogenic perturbation to the aerosol at the scale of an air parcel; rather it is possible only at larger, aggregate scales. The remainder of this review will focus on the sensitivity term .
The aerosol quantity most accessible to passive satellite remote sensing is AOD (Kaufman et al., 2002). It is derived from the multi-spectral reflectance of the Earth–atmosphere system using the incident solar radiation and retrieving or assuming surface albedo characteristics as well as aerosol absorption coefficient and scattering phase functions. There are four key issues with using the retrieved AOD for estimating the Nd to CCN sensitivity, which will be discussed in the following subsections.
- -
AOD is the vertical integral of the extinction coefficient. For the sensitivity of Nd to the aerosol, one needs to know the vertical distribution of the CCN concentration, most importantly the CCN at cloud base.
- -
AOD is an optical integral and does not provide information on the aerosol size distribution and its hygroscopicity. The use of AOD does not isolate aerosol particles that have the size and chemical composition to serve as CCN. It is also affected by aerosol swelling due to hygroscopic growth.
- -
AOD can be derived only for pixels determined to be cloud-free. The degree to which this correlates with the CCN at the base of (neighbouring) clouds is questionable. In addition, retrieved AOD can show a positive bias due to enhanced reflectance from neighbouring cloudy pixels or due to the lack of detecting spurious clouds in a retrieval scene.
- -
The optical signal is very weak at low concentrations. Therefore, retrievals become more and more uncertain below a certain aerosol load, especially over land and in situations with variable or uncertain surface albedo.
At aggregate scales, i.e. for monthly averages over regions, AOD from ground-based remote-sensing retrievals (AERONET; Holben et al., 2001) correlates well with CCN surface measurements (Andreae, 2009; Shen et al., 2019). Similar results were also reported for aircraft measurements (Clarke and Kapustin, 2010; Shinozuka et al., 2015). However, at shorter timescales or less spatial aggregation, there are significant deviations from a perfect correlation (Liu and Li, 2014). AOD due to aerosol light extinction is determined by the vertical integral of the extinction cross section, proportional to the vertical integral of the second moment of the aerosol size distribution. In turn, for a given chemical composition of aerosol particles, the CCN concentration is the zeroth moment of the size distribution for particles exceeding a size threshold that depends on supersaturation. In the following, the different problems are discussed in more detail, together with options for a better proxy for CCN from satellite remote sensing.
2.1 Vertical co-location
Stier (2016) investigated the correlation between AOD and CCN as represented in a climate model. He confirmed a mostly positive correlation of the temporal variability of the two quantities, although in some regions the correlation is low or even negative. A key reason for the partly low correlation is the fact that AOD is a vertically integrated quantity and may include aerosol layers that are not interacting with clouds. A similar result was reported from a statistical analysis of satellite data: cloud microphysical parameters correlate well with aerosol properties only if the vertical alignment of the aerosol and cloud layers is accounted for (Costantino and Bréon, 2010, 2013). More recently, Painemal et al. (2020) demonstrate a much higher correlation between Nd and aerosol extinction coefficients below cloud top sampled from satellite lidar compared to Nd vs. AOD. Ship measurements of CCN and microwave-retrieved Nd at cloud base between Los Angeles and Hawaii show a weaker β metric as the boundary layer deepens, thus indicating that surface aerosol measurements become less representative for aerosol variability at cloud base as the boundary layer deepens (Painemal et al., 2017), or that the updraughts become high enough to activate smaller aerosols than the accumulation mode. In situ observations suggest that AOD may even be anticorrelated with CCN at cloud base (Kacarab et al., 2020).
A way forward is the use of spaceborne vertically resolved observations such as lidar measurements (Shinozuka et al., 2015; Stier, 2016). The Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO; Winker et al., 2009) lidar retrieves aerosol backscatter profiles and thus is capable of identifying aerosol layers (Costantino and Bréon, 2010). Profiles of aerosol particle extinction are inferred from these backscatter profiles by using typical extinction-to-backscatter ratios based on aerosol type. However, the signal is not sensitive to smaller aerosol concentrations, which hampers a quantitative analysis at the large scale (Watson-Parris et al., 2018; Ma et al., 2018). For situations with sufficient aerosol loading for reliable CALIPSO aerosol profile observations, methods for retrieving CCN concentrations from ground-based lidar measurements can be adapted (Feingold and Grund, 1994; Lv et al., 2018; Haarig et al., 2019). These methods apply empirical extinction-to-particle-concentration relationships to obtain input for CCN concentrations for different aerosol types (Mamouri and Ansmann, 2016). In the future, the EarthCARE satellite mission currently scheduled for launch in 2022 (Illingworth et al., 2015; Hélière et al., 2017) shows promise to extend and improve upon the success of the CALIPSO mission. Its Atmospheric Lidar (ATLID) is a linearly polarised high-spectral-resolution lidar (HSRL) operating at a wavelength of 355 nm. The instrument allows the direct inference of profiles of aerosol backscatter and extinction coefficients, thereby substantially increasing the retrieval accuracy. The direct retrieval of the extinction-to-backscatter (lidar) ratio (Müller et al., 2007) with ATLID (compared to the use of pre-set values in the CALIPSO retrieval; Kim et al., 2018) and the large difference between lidar ratios of aerosols (20–80 sr) and clouds (20–30 sr) are also expected to provide better distinction between optically thin cirrus clouds and aerosols than CALIPSO (Reverdy et al., 2015). While a similar sensitivity to aerosol load is expected for ATLID and CALIOP observations during nighttime, ATLID promises a better daytime sensitivity. EarthCARE is also expected to provide better distinction between optically thin clouds and aerosols than CALIPSO (Reverdy et al., 2015). Airborne measurements have shown that further utilising HSRL at more than one wavelength (extending beyond ATLID) would provide substantial additional information content for retrieving vertically resolved aerosol parameters, especially when combined with polarimeter measurements (Burton et al., 2016). From the passive-remote-sensing perspective, promising results have been obtained for retrievals of aerosol vertical information from near-ultraviolet polarimetry (Wu et al., 2016), although the quality degrades for small aerosol concentrations. Passive observations with high spectral resolution within the oxygen A absorption band around 760 nm can also be used to infer aerosol layer height (Hollstein and Fischer, 2014; Geddes and Bösch, 2015). In particular, an operational aerosol layer height product is now available from the Tropospheric Monitoring Instrument (TROPOMI) flown on the Sentinel-5p mission (Sanders et al., 2015). Also, a recent study presents promising results based on Orbiting Carbon Observatory 2 (OCO-2) observations (Zeng et al., 2020). In particular, a combination of such approaches, e.g. passive polarimetry and active lidar observations (Stamnes et al., 2018) or multi-angle polarimetry and oxygen A band observations as planned for NASA's Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission (Remer et al., 2019), shows potential. Retrievals could also combine observations and model adjoints to constrain below-cloud aerosol number, which is directly relevant for aerosol–cloud interactions (Saide et al., 2012).
In summary, the lack of vertical co-location between retrieved CCN proxy and clouds leads to an underestimate in Nd–CCN sensitivity (Costantino and Bréon, 2010). Model studies suggest that this bias may be approximately cancelled by a corresponding bias in the anthropogenic component of the cloud base CCN (Gryspeerdt et al., 2017). However, the extent of this cancellation in current observational studies is unknown and requires further investigation. For an accurate estimation of , the use of lidar retrievals seems to be the best way forward, while additional information on the vertical distribution of aerosol can also be gained from present and upcoming passive satellite instruments.
2.2 Horizontal co-location
In studies examining β from satellite data, spatial aggregates are considered (i.e. as in Eq. 4), in which the aerosol retrievals in the cloud-free pixels are averaged at a coarse resolution (such as 1∘) and taken to define the relation with Nd retrievals in the same grid box (Quaas et al., 2008). This assumes that the aerosol population is horizontally homogeneous at such large scales. According to Anderson et al. (2003), this is often the case. It has been confirmed from aircraft data for the stratocumulus cases investigated by Shinozuka et al. (2020). However, CCN is consumed when droplets activate, and aerosol is scavenged when clouds precipitate. Hence, the assumption of aerosol concentration horizontal homogeneity is questionable, at least in precipitating clouds.
It is the aerosol in air masses before cloud particles form that is relevant to compute the aerosol impact on Nd (Gryspeerdt et al., 2015). In one of the early aerosol–cloud interaction studies from satellite data Bréon et al. (2002) used trajectories to identify cloudless situations in which aerosol retrievals were possible for air masses that later formed clouds. This is a promising solution but it requires much more effort than the simpler co-location assumptions. It also requires reliable, high-resolution information about atmospheric trajectories. Another complication is that the formation rate of secondary aerosol is enhanced by aqueous phase reactions, potentially enhancing aerosol concentrations in the vicinity of clouds (Jeong and Li, 2010). Such trajectory approaches are particularly useful when they exploit the high temporal resolution that is available from geostationary satellites. Aerosol retrievals from geostationary satellites may be combined using trajectory modelling to link these to clouds that form in these air masses (Kikuchi et al., 2018), or also the aerosol retrieval from a polar orbiter could be related to clouds retrieved from geostationary satellites that form in the same air masses (Christensen et al., 2020).
Altogether, the lack of horizontal co-location may imply somewhat too low due to the potential de-correlation of CCN concentrations and Nd in situations with spatially heterogeneous aerosol. The consideration of backward trajectory analysis seems the best option to address the issue since there is no solution yet to retrieve aerosols below or within clouds from satellite.
2.3 Hygroscopic growth of aerosol particles
The extinction of solar radiation by aerosol particles is a strong function of the hygroscopic growth of the particles. Haze particles attenuate much more sunlight compared to the same aerosol particle ensemble in dry conditions. AOD is thus heavily influenced by the variability of relative humidity. The light extinction caused by dry particles (at relative humidities below 30 %) is much better correlated to CCN concentrations than the extinction of particles at ambient relative humidity (Shinozuka et al., 2015). Liu and Li (2018) showed that using total AOD compared to dry AOD as a CCN proxy when estimating from measurements at different Atmospheric Radiation Measurements (ARM) sites resulted in a 23 % underestimate. A way forward is to apply parameterisations in terms of retrievals of relative humidity to account for the aerosol swelling. These need information about aerosol hygroscopicity and relative humidity at the appropriate scale. Hygroscopicity information could rely on the kappa-Köhler parameterisation approach (Petters and Kreidenweis, 2007; Pringle et al., 2010), and a parameterisation of small-scale to mesoscale humidity variability could make use of approaches exploited in general circulation models (GCMs) (Quaas, 2012; Petersik et al., 2018). Another alternative would be to retrieve the amount of aerosol water, making use of the real part of the refractive index (Schuster et al., 2009). This would allow the translation of the size distribution of humidified aerosol particles to the corresponding dry size distribution. In the near future, accurate refractive index retrievals are expected from polarimeters such as the SPEXone instrument on the NASA PACE mission (Hasekamp et al., 2019b; Werdell et al., 2019), to be launched in 2022.
Summarising, using AOD as a proxy for CCN results in low-biased estimates of due to aerosol swelling. Approaches to parameterise the dry aerosol properties on the basis of the humidified one can help alleviate the problem.
2.4 Approaches using aerosol index, column-CCN, reanalysis or cloud base updraught
The aerosol index (AI1) is defined as the product of AOD and the Ångström exponent (Deuzé et al., 2001). This latter quantity is the slope of the spectral variation in AOD and is typically larger for smaller particles (Ångström, 1929). AI is more weighted towards smaller particles, which makes it better suited as a proxy for CCN concentration at typical supersaturations than AOD. For log-normal size distributions, AI is approximately proportional to the column aerosol number concentration (Nakajima et al., 2001). Studies using models concluded that AI is a better predictor for CCN (Stier, 2016) and that AI–Nd relationships are better suited to predict ΔNd, ant than AOD–Nd relationships (Penner et al., 2011; Gryspeerdt et al., 2017). However, retrievals of the Ångström exponent, and thus of AI, over land are not reported in operational products such as the MODIS dark target algorithm and are in general not as reliable as they are over ocean (Lee and Chung, 2013; Sayer et al., 2013).
Further refining this idea, Hasekamp et al. (2019a) aimed to retrieve the column CCN concentrations over oceans. The analysis of polarimetric observations allowed us to account for some aspects of the aerosol particle size distribution, and for particle sphericity, which is related to particle hygroscopicity. This column-CCN retrieval implied larger , increasing the resulting RFaci by almost 50 %. It is an example of how additional information from polarimetry is useful for studying the CCN-to-Nd relationship.
However, neither the approach of Hasekamp et al. (2019a) nor the use of AI overcomes the problem of lack of horizontal and vertical coincidence of CCN and Nd retrievals. An option to overcome this problem is to make use of additional model information. Satellite-retrieved AOD is assimilated into aerosol models, e.g. in the Copernicus Atmosphere Monitoring Service (CAMS, Benedetti et al., 2009; Inness et al., 2019) or the Modern-Era Retrospective Analysis for Research and Applications (version 2; MERRA-2 Gelaro et al., 2017). The model predictions are applied to obtain aerosol information beneath clouds. Such aerosol re-analysis information has been used for assessing RFaci in several studies (Bellouin et al., 2013; McCoy et al., 2017; Bellouin et al., 2020a). However, assessing the validity of model results requires extensive and rigorous evaluation, especially for coarsely resolved models with regard to aerosol scavenging below clouds. For this, independent data are required such as from ground-based observations or satellite observations from sensors other than those that are assimilated.
Yet another solution initially proposed by Feingold et al. (1998) and applied to satellite retrievals by Rosenfeld et al. (2016) is to parameterise the cloud base updraught, w, on the basis of cloud retrievals, rather than to retrieve the aerosol. For convective clouds, Zheng et al. (2015) suggested that w scales with cloud base altitude, which can be retrieved from satellites. For stratocumulus clouds, Zheng et al. (2016) proposed that updraught is a function of cloud-top radiative cooling, and that this can be computed by radiative transfer modelling on the basis of cloud quantities retrieved from passive sensors and thermodynamic profiles from meteorological re-analyses. The retrieved profiles of re together with derivations of supersaturation as a function of w and Nd (Rosenfeld et al., 2016) then allow the parameterisation of the CCN concentration at any given supersaturation. This approach does not suffer from the problem of a lower detection limit. However, it has not yet been used to quantify the Twomey effect.
Concluding, all four approaches alleviate many problems encountered when using AOD. An ideal solution may be the combination of several of these by also assimilating, in addition to AOD, polarimetric satellite observations, as well as lidar measurements, into the analysis of the atmospheric state in high-resolution models.
The problem of the remotely sensed Nd as used to estimate has three different facets to it, which will be discussed in this section, namely the following.
- -
Consideration of re rather than Nd in aerosol–cloud interaction studies. In many studies, the droplet effective radius, re, is used, and the datasets are stratified with respect to L in order to estimate . This is very difficult to perform adequately and leads to biases.
- -
Biases in the retrieved Nd. For the assessment of sensitivity, systematic (rather than random) errors in retrieved Nd are relevant. Also, Nd is not retrieved in standard operational procedures, so that inconsistencies between the retrieval of standard components and in the computation of Nd on the basis of retrievals can lead to additional errors.
- -
Relationship of Nd formed at activation with retrieved and radiation-relevant Nd, top. Retrieved Nd, top refers to the drop concentration within the top one to two optical depths of the clouds, and it is Nd, top that is relevant for determining the cloud radiative effect. Nd sink processes such as coagulation imply that Nd, top is smaller than the one resulting from activation above cloud base, Nd, base.
Nd is vertically constant for single-layer, purely liquid-water clouds with (i) a vertically homogeneous droplet size spectrum, (ii) for adiabatically stratified clouds or (iii) for sub-adiabatic clouds in which mixing is homogeneous. However, in many situations, precipitation formation or entrainment can lead to reduction of Nd above cloud base. In such situations, it is Nd, top that is relevant to determine the cloud radiative effect (cloud albedo in Eq. 2). Building on Eq. (4) thus gives
When estimating as a regression coefficient from, for example, satellite-retrieved Nd and a proxy for CCN such as AOD, it is thus this that is inferred.
3.1 Considering re rather than Nd
Many past studies have used operationally retrieved re rather than Nd in aerosol–cloud interaction studies. However, re is a function of both Nd and L. This introduces the requirement for stratifying the data with respect to L in order to estimate . To further complicate matters, Nd and L have been found to be correlated (e.g. Michibata et al., 2016; Gryspeerdt et al., 2019). A precise estimation of is thus only possible for a large amount of data combined with suitable binning by L. Errors in this approach that are related to a lack of data increase at aggregated scales (McComiskey and Feingold, 2012). Using derived Nd is therefore preferable to avoid unnecessary complications.
3.2 Biases in the Nd retrieval
Satellite retrievals of Nd were extensively reviewed by Grosvenor et al. (2018). Since Nd currently is not retrieved by operational algorithms and new developments to retrieve Nd (e.g. from polarimetry) are still in their infancy, the most frequently used method is to infer Nd from retrieved re and cloud optical depth, τc, using the relationship
where m−0.5 is a parameter provided as a constant here but more realistically depending on cloud base temperature and pressure, the adiabatic fraction, and the drop size distribution breadth (Boers et al., 2006; Quaas et al., 2006; Grosvenor et al., 2018). The relationship in Eq. (6) assumes that clouds are adiabatic or nearly adiabatic (i.e. adiabatic clouds or sub-adiabatic clouds with homogeneous mixing only; Brenguier et al., 2000). The most common method uses a bispectral approach to retrieve re and τc (Nakajima and King, 1990). Various error sources lead to an overall retrieval error for Nd (Grosvenor et al., 2018; Wolf et al., 2019). As can be deduced form Eq. (6), the most important contributions are from retrieval errors in re. Other error sources are the uncertainty in sub-adiabatic factor, the cloud model used in the retrieval, and the droplet size distribution width. Satellite retrievals of the vertical profile of cloud droplet size may help to improve the retrieval (Chang and Li, 2002; Chen et al., 2008). Grosvenor et al. (2018) identified biases of retrieved Nd in particular for broken cloud regimes and at large solar zenith angles. In stratocumulus, it was suggested that the retrieval yields the most trustworthy results when considering only the brightest pixels (Zhu et al., 2018). For the ideal case of homogeneous, low-latitude stratiform clouds, relative errors in the Nd retrieval at pixel scale are quantified as 78 % (Grosvenor et al., 2018). In such cases, the error was assumed to be random. However, systematic errors occur in particular in broken cloud regimes and for large solar zenith angles, leading to an underestimation (broken cloudiness) and overestimation (large solar zenith angles), respectively, of Nd. Painemal et al. (2020) addressed the Nd bias for broken clouds by only sampling Nd retrieved for large clouds (larger than 5 km × 5 km) to find that the relation between Nd and aerosols is substantially enhanced.
For improvements in estimates of Nd, it would be beneficial to formulate a retrieval in terms of Nd directly rather than in terms of re and τc. It is also possible to reduce uncertainties in retrievals of re and τc, or to reduce uncertainties related to assumptions of the vertical structure of the cloud and particle size distribution shape. Approaches to quantify and partly correct for retrieval biases as discussed in Grosvenor et al. (2018) include accounting for cloud heterogeneity by using those channels in passive imagers that provide spatial resolution that exceeds the one at which the standard retrieval products are provided (Zhang et al., 2016). The combination of passive observations with radar may further improve the retrieval (Posselt et al., 2017). Substantially more accurate retrievals of re and additional relevant information about droplet size distributions may also come from multi-angular polarimetric measurements (Alexandrov et al., 2012a, b; Shang et al., 2019), which will be possible from orbit at pixel level from the Hyper-Angular Rainbow Polarimeter-2 (HARP-2) on the NASA PACE mission (Martins et al., 2018; McBride et al., 2019). Polarimetric retrievals allow the inference of the spectral width or general shape of the droplet size distribution at cloud top (Hu et al., 2007). This approach is not substantially sensitive to sub-pixel cloudiness, mixed-phase conditions and 3D radiative effects (Alexandrov et al., 2012b). The sensitivity of derived Nd to uncertainties in re from polarimetric retrievals may further be reduced by additionally inferring cloud physical thickness. In this case, Nd can be inferred to be linear in τc and inversely linear in geometrical thickness and mean droplet extinction cross section at cloud top (Sinclair et al., 2019). The geometrical thickness may also be inferred from total and/or polarised reflectances measured in oxygen or water vapour absorption bands (Desmons et al., 2013; Sanghavi et al., 2015; Richardson et al., 2019; Sinclair et al., 2019) or by retrieving cloud base using lidar (Mülmenstädt et al., 2018) or using multi-angle observations (Böhm et al., 2019). When exploiting passive observations together with lidar, Nd at cloud top can be robustly inferred as the ratio of in-cloud extinction (lidar) and extinction cross section (passive). A slightly less direct approach using depolarisation to estimate extinction and effective radius to estimate extinction cross section has been presented by Hu et al. (2007).
3.3 Relationship between Nd formed at CCN activation and retrieved radiation-relevant Nd
In stratiform clouds, droplets form in updraughts near cloud base which is where Nd most closely relates to CCN. In convective clouds, updraught in some cases increases with height above cloud base. Hence, additional CCN may activate above cloud base and lead to vertically increasing Nd in the lower third of the cloud with a decrease further up (Endo et al., 2015). However, in most cumulus clouds, and in stratiform clouds, Nd is found to be largest at cloud base and to slightly decrease above it (Jiang et al., 2008; Small et al., 2009; vanZanten et al., 2011). In the approach discussed by Grosvenor et al. (2018), the retrieved Nd is representative of the cloud-top reflectance, and thus the relevant proxy for the Nd that matters for cloud albedo and RFaci (Platnick, 2000). To which extent the microphysical structure of lower parts of a cloud exactly impacts radiation (weighting function) depends on the multiple scattering and thus on the vertical structure of Nd itself (Platnick, 2000; Krisna et al., 2018). For vertically constant Nd, the retrieved Nd represents the droplet concentration formed by CCN activation. However, there are Nd sinks, in particular due to collision and coalescence (in liquid clouds, the autoconversion and accretion, or “warm rain” processes) that lead to droplet depletion. Wood (2006) demonstrated that the depletion is exponential in precipitation rate and estimated a loss in Nd of 100 cm−3 d−1 for precipitation rates of 1 mm d−1. There may also be lateral and vertical mixing (of heterogeneous type; Lehmann et al., 2009) of cloud air with environmental cloud-free air that can lead to the full evaporation of droplets. In both sinks for Nd, the one due to precipitation formation and the one due to mixing, the retrieved Nd is expected to be smaller than the Nd formed at activation of CCN. In an aged cloud, however, updraughts may have decayed such that no additional droplets are formed, while existing droplets persist, or may be advected from elsewhere. Also, in case they are very large, raindrops may break up into droplets, in which case Nd is increased. Arguably, it is the right choice to relate the retrieved Nd, as the radiation-relevant one, to CCN, i.e. to use , when computing the Nd-to-CCN sensitivity with the aim to constrain RFaci.
Cloud-resolving models are a good tool to investigate these interpretations (McComiskey and Feingold, 2012). Figure 1 shows an analysis of a large-domain large-eddy simulation with the ICON-LEM model (Heinze et al., 2017; Costa-Surós et al., 2020). CCN concentrations in these simulations are relaxed towards pre-computed spatially and temporally varying fields and are consumed at activation. In the 22 million grid columns, the droplet concentration at cloud top (what is retrieved from satellites) is compared to the maximum droplet concentration (approximately the concentration of activated CCN divided by formed droplets). This demonstrates that there is a link between the droplet concentration formed at activation and Nd determining the cloud radiative effect at its top. These two quantities correlate rather well in the joint histogram, though that link is far from one to one. The second plot (Fig. 1b) assesses the possibility to infer cloud-top Nd from cloud-top re and τc (Grosvenor et al., 2018). For this, the MODIS simulator (Pincus et al., 2012) that is part of the Cloud Feedback Model Intercomparison Project (CFMIP) Observational Simulator Package (COSP; Bodas-Salcedo et al., 2011) is applied to the model output to compute cloud-top re and τc. From these, Nd is computed as in Eq. (6). This approach mimics the satellite retrieval but assumes no retrieval errors; i.e. the comparison is a lower bound on the accuracy of the retrieved Nd in representing the actual Nd at cloud top. There is a meaningful co-variation in the two quantities, but it is far from perfect. In particular, there is a systematic overestimation of Nd in the retrieval approach, especially at low Nd. The relative error even is a function of Nd, with larger relative errors at low Nd.
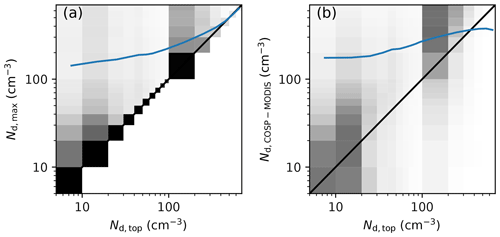
Figure 1Analysis of Nd in the “virtual reality” of a cloud-resolving simulation: droplet number concentration (cm−3) from the ICON large-eddy simulation (156 m horizontal resolution) over the domain of Germany for 2 May 2013 (Heinze et al., 2017), for the overpass times of the Terra and Aqua satellites for which the swath of the MODIS instrument covered the domain (twice around 10:30 local solar time for Terra, twice around 13:30 for Aqua) even if no actual data are used in this analysis (Costa-Surós et al., 2020). Joint histograms, normalised along the y axis as in Gryspeerdt et al. (2016) for (a) column-maximum (proxy for activated CCN) vs. cloud-top Nd (taken at τc=1 integrated from cloud top) and (b) Nd derived from re and τc as in Grosvenor et al. (2018) vs. cloud-top Nd, where both quantities are computed as seen from a satellite using the Cloud Feedback Model Intercomparison project (CFMIP) Observational Simulator Package COSP (Bodas-Salcedo et al., 2011). The blue line is the mean in each bin for cloud-top Nd.
In conclusion, the fact that cloud-top Nd is in general lower than Nd at activation height implies that is indeed somewhat smaller than unity. This is not a problem but rather a desired analysis result when studying the Twomey effect. However, Nd obtained from retrieval products is biased high for low values of Nd, top. This relative error, which is a function of Nd, implies that the regression between satellite-derived Nd and CCN yields a sensitivity that is too weak.
Aerosol–cloud interactions depend on cloud regime (Stevens and Feingold, 2009; Mülmenstädt and Feingold, 2018). When it comes to RFaci, there are three reasons for this: (i) the radiative sensitivity (Oreopoulos and Platnick, 2008; Alterskjær et al., 2012), i.e. the first two terms on the right-hand-side of Eq. (2) (in particular the sensitivity expressed in Eq. 1); (ii) the updraught dependence of ; and (iii) the dependence of the relation of cloud-top to cloud base Nd to characteristics of turbulence and rain. The latter two are of interest here. “Cloud regime” thus here means, a cluster of clouds with similar 𝒫(w) and similar in Eq. (5). When considering CCN at a certain supersaturation level, is larger at larger updraught, w (MacDonald et al., 2020). Broadly, cumulus clouds have larger w than stratiform clouds. In addition, clouds over land usually have larger w than clouds over ocean. Building on Eq. (5), this suggests a regime-based analysis expressed as
Figure 2 shows the spatial distribution of the Nd – AI regression coefficient from its temporal variability within grid boxes. The large spatial heterogeneity is not straightforward to interpret. Some problems may be due to the lack of aerosol retrieval sensitivity (e.g. in regions with low CCN concentrations such as the southern oceans) or lack of vertical or horizontal co-incidence (e.g. in regions with heterogeneous aerosol and large cloud coverage such as mid-latitude storm tracks). However, aspects of the geographical heterogeneity may indeed be attributable to physical and relevant reasons. However, it is difficult to determine any attributable factors in the spatial and cloud-regime variations in (Gryspeerdt and Stier, 2012) before retrieval errors are remedied.
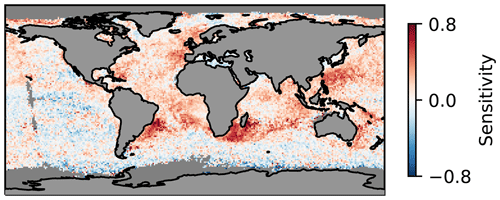
Figure 2Regression coefficients of Nd computed on the basis of retrievals of the MODerate Resolution Imaging Spectroradiometer (MODIS; Platnick et al., 2017) as in Grosvenor et al. (2018) and AI from MODIS (Levy et al., 2013) from the daily temporal variability in grid boxes of .
In precipitating situations, the two-way interactions can lead to large challenges in determining the term (Ekman et al., 2011). Precipitation scavenges aerosol and, in certain situations, the interplay between aerosol, droplet concentrations and precipitation determines both aerosol and droplet concentrations. This may yield bifurcations between situations with large Nd in which no drizzle forms and very low Nd and cloud dissolution when precipitation forms (e.g. Yamaguchi et al., 2017). In such situations, it is particularly challenging to identify the Nd–CCN concentration sensitivity.
The impact of aggregation scale on estimates of β has been discussed in detail by McComiskey and Feingold (2012). Their key conclusion is that at scales larger than the cloud variability scale of about 1 to 10 km, aerosol and cloud data become de-correlated so that the diagnosed β becomes less and less representative for individual cloud parcels. In turn, Sekiguchi et al. (2003) computed for different aggregation scales and demonstrated that it actually increases with larger scales. An analysis of spatio-temporal vs. temporal-only co-variability of Nd and AOD by Grandey and Stier (2010) found that is larger when considering spatio-temporal variability over entire regions compared to only temporal variability at individual grid boxes. These results are opposite to those expected from the process-based conclusions of McComiskey and Feingold (2012). A possible problem in the Sekiguchi et al. (2003) study is their use of re rather than Nd, and the subsequent need to stratify by L. McComiskey and Feingold (2012) demonstrated that this approach becomes more problematic with increasing aggregation scale. However, their analysis suggested a low-bias in β at coarser scales due to stratification by L. Reduced at small scales could occur if aerosol conditions become too homogeneous to diagnose the full range of co-variability due to smaller sample sizes at smaller scales.
Concluding, from a process point of view, aggregation over larger scales is expected to lead to a decrease in estimated . In turn, to study the large-scale Twomey effect, an aggregate Nd–CCN relationship is desired as it is the large-scale ΔNd, ant that matters for the radiation perturbation and because the anthropogenic aerosol perturbation can only be inferred at a large scale. The often adopted choice of a gridding is somewhat motivated by the suggestion that this is a scale at which aerosol concentrations are considered homogeneous (Anderson et al., 2003) and loosely (to within a factor of about 2 in each horizontal direction; re-analyses are to closer ∼50 km scales, and many general circulation models still are as coarse as 200 km) related to the scale at which models infer the anthropogenic perturbation of CCN. A rigorous study on the scale dependency of and the consequences thereof for RFaci would be desirable.
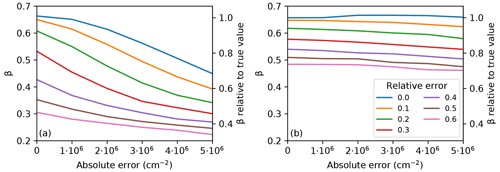
Figure 3Nd–column CCN sensitivity as a function of the stochastic error in column CCN (absolute additive error) in an emulated analysis as in Hasekamp et al. (2019a), for different relative (multiplicative) errors, for (a) the full range of data, including low NCCN values and (b) excluding NCCN<107 cm−2. Hasekamp et al. (2019a) suggest a realistic error is about cm−2.
When sensitivities are approximated by linear regression coefficients from an ordinary least-squares (OLS) line fitting method, rather than derived in the form of joint histograms, the problem of regression dilution arises to the extent that the aerosol quantity shows errors: the regression coefficient becomes gradually smaller as the stochastic error increases (Cantrell, 2008; Pitkänen et al., 2016; Wu and Yu, 2018). Regression dilution, also known as regression attenuation, is a problem if the independent variable (x axis) in the regression is subject to a statistical error. If the regression method does not take the statistical error into account, which is often the case (for example in OLS), the regression coefficient is always systematically biased low. In turn, statistical error on the dependent variable (y axis) only causes uncertainty in the regression coefficient but no systematic bias. This is quantified for the column-CCN vs. Nd sensitivity evaluated as a regression coefficient in Fig. 3. Due to the regression dilution, the sensitivity decreases by factors of 2 to 3 as the error in column CCN increases when considering relative errors of 50 %. This can to a large extent be remedied by ignoring data points at low CCN concentrations from the regression (Fig. 3b). However, this solution is limited to regions not dominated by low aerosol concentrations. Figure 3 also illustrates that an absolute bias in the data translates to relative bias in logarithmic scale. Therefore, if no bias correction is applied, an absolute bias in the data will cause a bias in the sensitivity estimates. As shown by Pitkänen et al. (2016), the regression dilution in turn becomes weaker at coarser aggregation scales in cases of auto-correlated data, which is the case for aerosol concentrations. This is of relevance in the case of both temporal and spatial aggregation. In other words, the systematic low-bias in the sensitivity is reduced if data are aggregated. This could partly explain some previous findings of increasing sensitivity with decreasing resolution (see discussion in the previous section), in addition to the actual bias due to the aggregation over a smaller scale of cloud processes. These considerations imply that it is necessary to either analyse the full variability of aerosol–cloud interactions, e.g. in the form of joint histograms, or to account for the regression dilution using established mathematical approaches that properly consider measurement uncertainties, as discussed in Mikkonen et al. (2019), for instance.
The radiative forcing due to aerosol–cloud interactions, or the Twomey effect, requires quantification based on observational data, since models are associated with large uncertainties. At a large scale, this calls for satellite retrievals. There are, however, large challenges when using satellite data and this review summarises these challenges and suggests some potential ways forward. The key data-related question is the sensitivity of droplet concentration, Nd, to perturbations in the cloud-active aerosol, i.e. the cloud condensation nuclei (CCN) concentration at or above cloud base. The most widely used proxy of the cloud base CCN concentration is the aerosol optical depth (AOD), or alternatively the aerosol index (AI), taken from cloud-free pixels in the vicinity of the locations of the cloud retrievals. The four main caveats with AOD are the lack of vertical resolution, the additional influence of hygroscopic swelling, the fact that the detected aerosol might be not active as CCN nd the impossibility to retrieve it below clouds. In terms of the vertical resolution, satellite-based lidar offers help. However, current lidar retrievals are even more constrained to large aerosol concentrations than passive AOD retrievals. EarthCARE's ATLID lidar will allow direct inference of the ratio of backscatter to extinction, enabling greatly improved retrievals of aerosol extinction profile. Adding a second wavelength with ATLID capabilities and combining it with polarimetric measurements would substantially extend vertically resolved aerosol information content. In terms of horizontal co-location, trajectory computations may help to identify the aerosol representative of that affecting specific clouds. However, this requires extra effort and reliable information about trajectories. The hygroscopic swelling can be addressed by parameterisations that use retrievals and ancillary data to compute the swelling. Further relevant information is possible from polarimetric measurements.
Cloud droplet number concentration, Nd, is only indirectly available from current operational satellite retrievals. It is generally computed from retrieved cloud-top droplet effective radius, re, and cloud optical thickness, τc, leading to substantial biases in comparison to the cloud-top droplet number concentration, especially in inhomogeneous, broken and/or precipitating cloud regimes. Sink processes for Nd and variability due to atmospheric dynamics, including turbulent mixing, imply that the radiatively relevant cloud-top Nd relates imperfectly to the Nd formed by CCN activation. In addition, at a given CCN concentration, the updraught variability also leads to sensitivities of Nd to CCN that are much less than 1. These latter two facts are not problematic when assessing the Nd to aerosol sensitivity from data for the estimation of the Twomey effect. In fact, it is desirable to quantify at a large scale the net impact of aerosol perturbations of the (radiatively relevant) cloud-top Nd that accounts for updraught and Nd sink variability. However, it is necessary to operationally retrieve Nd, rather than to indirectly compute it from re and τc retrievals. It is also necessary to improve these retrievals in particular for low droplet concentrations and broken cloud conditions. In addition, these retrievals should take into account additional information, e.g. about the onset of drizzle.
Regression dilution influences the statistically inferred sensitivity as a result of stochastic retrieval errors in CCN concentration. On the one hand, at aggregate scales, this problem becomes less relevant due to the autocorrelation of the aerosol concentrations. The relationship between Nd, which varies at cloud-dynamics scales, and CCN proxies becomes weaker at aggregate scales. Relative retrieval errors in Nd that depend on actual Nd (with larger high-biases at low true Nd) lead to a further reduction in the estimated sensitivity. It is thus necessary to account for the impact of CCN errors in the statistics and to optimise the resolution of Nd and CCN retrievals towards cloud-scale resolutions.
The recent study by Hasekamp et al. (2019a) made use of polarimetric satellite measurements to suggest a global-ocean average Nd-to-CCN sensitivity of 0.66. This, combined with anthropogenic column-CCN concentrations and radiative sensitivities, translates into a global Twomey effect of −1.1 W m−2. The net effect of the remaining problems laid out above suggests that this likely is still too low an estimate for the Nd–CCN sensitivity, implying a stronger Twomey effect. However, the estimate is in line with an independent observation-based estimate of McCoy et al. (2020) that used differences in Nd between pristine and polluted regions in combination with GCM results as an emergent constraint. In any case, it is desirable to add the extra steps to improve the quantification supported by data for process understanding as well as for evaluating and improving climate models.
In situ and ground-based observations, as well as analysis of cloud-resolving dynamical models, may be a path forward for the evaluation of critical aspects in the satellite-based analysis. Important steps would be the quantification of updraught PDFs for different cloud regimes and the assessment of horizontal homogeneity of aerosol concentrations.
The data used in Fig. 1 are the simulation data as described in Costa-Surós et al. (2020, https://doi.org/10.5194/acp-20-5657-2020) and available upon request due to the large amount of data; it is securely saved in tape archives at the Deutsches Klimarechenzentrum (DKRZ), which will be accessible for 10 years. The MODIS data used in Fig. 2 was downloaded from the Level-1 and Atmosphere Archive & Distribution System (LAADS) Distributed Active Archive Center (DAAC), located in the Goddard Space Flight Center in Greenbelt, Maryland (https://ladsweb.nascom.nasa.gov/, last access: 19 November 2020, LAADS DAAC, 2020). The data used for Fig. 3 are archived and available at https://cera-www.dkrz.de/WDCC/ui/cerasearch/entry?acronym=DKRZ_LTA_1002_ds00001 (last access: 19 November 2020, Hasekamp and Quaas, 2020).
JQ led the writing of the manuscript with significant contributions from all authors.
The authors declare there are no competing interests.
The work of Johannes Quaas, Annica M. L. Ekman, Athanasios Nenes and Philip Stier was supported by the European Union via its Horizon 2020 project FORCeS. The work of Athanasios Nenes was further supported by the European Research Council via the project PyroTRACH. Philip Stier was also supported by the European Research Council (ERC) project constRaining the EffeCts of Aerosols on Precipitation (RECAP). This review originated from discussions at the 2019 Nanjing workshop of the Aerosols-clouds-precipitation and climate (ACPC) initiative (http://acpcinitiative.org/, last access: 13 November 2020) and benefited from discussions within the group “Study of aerosol–cloud interactions based on satellite observations of the terrestrial underlying surface–atmosphere system: a new frontier of atmospheric science”, hosted by the International Space Science Institute (ISSI). We thank the German Climate Computing Centre (Deutsches Klimarechenzentrum, DRKZ) and the German Federal Ministry of Education and Research (BMBF) within the framework programme “Research for Sustainable Development (FONA)”, https://www.fona.de/ (last access: 13 November 2020) for making the ICON-LEM simulations available. Po-Lun Ma and Johannes Mülmenstädt were supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Earth System Modeling program. Johannes Quaas is grateful to the NASA Goddard Institute for Space Studies, New York, for hospitality during a research stay. We thank Andrew Ackerman and Patrick Chuang for constructive discussions. We thank the three anonymous reviewers and David Painemal for helpful comments on the earlier version of the manuscript. We acknowledge support from Leipzig University for Open Access Publishing.
This research has been supported by the European Union's Horizon 2020 research and innovation programme via H2020-EU.3.5.1. – Fighting and adapting to climate change (FORCeS (grant agreement no. 821205)), the European Research Council (ERC) via H2020-EU.1.1. – Excellent Science program (PyroTRACH (grant agreement no. 726165) and RECAP (grant agreement no. 724602)), the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research, Earth System Modeling program by the “Enabling Aerosol-cloud interactions at GLobal convection-permitting scalES (EAGLES) (project no. 74358), and the Pacific Northwest National Laboratory is operated for the U.S. Department of Energy by Battelle Memorial Institute (contract no. DE-AC05-76RL01830).
This paper was edited by Frank Dentener and reviewed by three anonymous referees.
Ackerman, A., Toon, O., Taylor, J., Johnson, D., Hobbs, P., and Ferek, R.: Effects of aerosols on cloud albedo: Evaluation of Twomey's parameterization of cloud susceptibility using measurements of ship tracks, J. Atmos. Sci., 57, 2684–2695, https://doi.org/10.1175/1520-0469(2000)057<2684:EOAOCA>2.0.CO;2, 2000. a, b
Ackerman, A., Kirkpatrick, M., Stevens, D., and Toon, O.: The impact of humidity above stratiform clouds on indirect aerosol climate forcing, Nature, 432, 1014–1017, https://doi.org/10.1038/nature03174, 2004. a
Aitken, J.: On dust, fogs, and clouds, Proceedings of the Royal Society of Edinburgh, 11, 122–126, 1880. a
Albrecht, B.: Aerosols, cloud microphysics, and fractional cloudiness, Science, 245, 1227–1230, https://doi.org/10.1126/science.245.4923.1227, 1989. a, b
Alexandrov, M., Cairns, B., and Mishchenko, M.: Rainbow Fourier transform, J. Quant. Spectrosc. Ra., 113, 2521–2535, https://doi.org/10.1016/j.jqsrt.2012.03.025, 2012a. a
Alexandrov, M. D., Cairns, B., Emde, C., Ackerman, A. S., and van Diedenhoven, B.: Accuracy assessments of cloud droplet size retrievals from polarized reflectance measurements by the research scanning polarimeter, Remote Sens. Environ., 125, 92–111, 2012b. a, b
Alterskjær, K., Kristjánsson, J. E., and Seland, Ø.: Sensitivity to deliberate sea salt seeding of marine clouds – observations and model simulations, Atmos. Chem. Phys., 12, 2795–2807, https://doi.org/10.5194/acp-12-2795-2012, 2012. a
Anderson, T. L., Charlson, R. J., Winker, D. M., Ogren, J. A., and Holmen, K.: Mesoscale variations of tropospheric aerosols, J. Atmos. Sci., 60, 119–136, https://doi.org/10.1175/1520-0469(2003)060<0119:MVOTA>2.0.CO;2, 2003. a, b
Andreae, M. O.: Correlation between cloud condensation nuclei concentration and aerosol optical thickness in remote and polluted regions, Atmos. Chem. Phys., 9, 543–556, https://doi.org/10.5194/acp-9-543-2009, 2009. a
Ångström, A.: On the Atmospheric Transmission of Sun Radiation and on Dust in the Air, Geografiska Annaler, 11, 156–166, https://doi.org/10.1080/20014422.1929.11880498, 1929. a
Bellouin, N., Boucher, O., Haywood, J., and Reddy, M. S.: Global estimate of aerosol direct radiative forcing from satellite measurements, Nature, 438, 1138–1141, https://doi.org/10.1038/nature04348, 2005. a
Bellouin, N., Quaas, J., Morcrette, J.-J., and Boucher, O.: Estimates of aerosol radiative forcing from the MACC re-analysis, Atmos. Chem. Phys., 13, 2045–2062, https://doi.org/10.5194/acp-13-2045-2013, 2013. a, b, c
Bellouin, N., Davies, W., Shine, K. P., Quaas, J., Mülmenstädt, J., Forster, P. M., Smith, C., Lee, L., Regayre, L., Brasseur, G., Sudarchikova, N., Bouarar, I., Boucher, O., and Myhre, G.: Radiative forcing of climate change from the Copernicus reanalysis of atmospheric composition, Earth Syst. Sci. Data, 12, 1649–1677, https://doi.org/10.5194/essd-12-1649-2020, 2020a. a
Bellouin, N., Quaas, J., Gryspeerdt, E., Kinne, S., Stier, P., Watson-Parris, D., Boucher, O., Carslaw, K., Christensen, M., Daniau, A.-L., Dufresne, J.-L., Feingold, G., Fiedler, S., Forster, P., Gettelman, A., Haywood, J. M., Malavelle, F., Lohmann, U., Mauritsen, T., McCoy, D., Myhre, G., Mülmenstädt, J., Neubauer, D., Possner, A., Rugenstein, M., Sato, Y., Schulz, M., Schwartz, S. E., Sourdeval, O., Storelvmo, T., Toll, V., Winker, D., and Stevens, B.: Bounding global aerosol radiative forcing of climate change, Rev. Geophys., 58, e2019RG000660, https://doi.org/10.1029/2019RG000660, 2020b. a, b, c, d, e
Benedetti, A., Morcrette, J.-J., Boucher, O., Dethof, A., Engelen, R. J., Fisher, M., Flentje, H., Huneeus, N., Jones, L., Kaiser, J. W., Kinne, S., Mangold, A., Razinger, M., Simmons, A. J., and Suttie, M.: Aerosol analysis and forecast in the European Centre for Medium-Range Weather Forecasts Integrated Forecast System: 2. Data assimilation, J. Geophys. Res., 114, D13205, https://doi.org/10.1029/2008JD011115, 2009. a
Bennartz, R., Fan, J., Rausch, J., Leung, L. R., and Heidinger, A. K.: Pollution from China increases cloud droplet number, suppresses rain over the East China Sea, Geophys. Res. Lett., 38, L09704, https://doi.org/10.1029/2011GL047235, 2011. a
Bodas-Salcedo, A., Webb, M. J., Bony, S., Chepfer, H., Dufresne, J.-L., Klein, S. A., Zhang, Y., Marchand, R., Haynes, J. M., Pincus, R., and John, V. O.: COSP: Satellite simulation software for model assessment, B. Am. Meteorol. Soc., 92, 1023–1043, https://doi.org/10.1175/2011BAMS2856.1, 2011. a, b
Boers, R., Acarreta, J. R., and Gras, J. L.: Satellite monitoring of the first indirect aerosol effect: Retrieval of the droplet concentration of water clouds, J. Geophys. Res., 111, D22208, https://doi.org/10.1029/2005JD006838, 2006. a
Böhm, C., Sourdeval, O., Mülmenstädt, J., Quaas, J., and Crewell, S.: Cloud base height retrieval from multi-angle satellite data, Atmos. Meas. Tech., 12, 1841–1860, https://doi.org/10.5194/amt-12-1841-2019, 2019. a
Boucher, O. and Lohmann, U.: The sulfate‐CCN‐cloud albedo effect, Tellus B, 47, 281–300, https://doi.org/10.1034/j.1600-0889.47.issue3.1.x, 1995. a
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S., Sherwood, S., Stevens, B., and Zhang, X.: Clouds and Aerosols, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T., Qin, D., Plattner, G.-K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, chap. 7, 571–658, https://doi.org/10.1017/CBO9781107415324.016, 2013. a, b, c
Bougiatioti, A., Argyrouli, A., Solomos, S., Vratolis, S., Eleftheriadis, K., Papayannis, A., and Nenes, A.: CCN activity, variability and influence on droplet formation during the HygrA-CD campaign in Athens, Atmosphere, 8, 108, https://doi.org/10.3390/atmos8060108, 2017. a
Bougiatioti, A., Nenes, A., Lin, J. J., Brock, C. A., de Gouw, J. A., Liao, J., Middlebrook, A. M., and Welti, A.: Drivers of cloud droplet number variability in the summertime in the southeastern United States, Atmos. Chem. Phys., 20, 12163–12176, https://doi.org/10.5194/acp-20-12163-2020, 2020. a, b, c
Brenguier, J.-L., Pawlowska, H., Schüller, L., Preusker, R., Fischer, J., and Fouquart, Y.: Radiative properties of boundary layer clouds: Droplet effective radius versus number concentration, J. Atmos. Sci., 57, 803–821, 2000. a, b
Bréon, F.-M., Tanré, D., and Generoso, S.: Aerosol effect on cloud droplet size monitored from satellite, Science, 295, 834–838, 2002. a, b
Bretherton, C. S., Blossey, P. N., and Uchida, J.: Cloud droplet sedimentation, entrainment efficiency, and subtropical stratocumulus albedo, Geophys. Res. Lett., 34, L03813, https://doi.org/10.1029/2006GL027648, 2007. a
Bulatovic, I., Ekman, A. M. L., Savre, J., Riipinen, I., and Leck, C.: Aerosol Indirect Effects in Marine Stratocumulus: The Importance of Explicitly Predicting Cloud Droplet Activation, Geophys. Res. Lett., 46, 3473–3481, https://doi.org/10.1029/2018GL081746, 2019. a
Burton, S. P., Chemyakin, E., Liu, X., Knobelspiesse, K., Stamnes, S., Sawamura, P., Moore, R. H., Hostetler, C. A., and Ferrare, R. A.: Information content and sensitivity of the 3β + 2α lidar measurement system for aerosol microphysical retrievals, Atmos. Meas. Tech., 9, 5555–5574, https://doi.org/10.5194/amt-9-5555-2016, 2016. a
Cantrell, C. A.: Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems, Atmos. Chem. Phys., 8, 5477–5487, https://doi.org/10.5194/acp-8-5477-2008, 2008. a
Carslaw, K. S., Lee, L. A., Reddington, C. L., Pringle, K. J., Rap, A., Forster, P. M., Mann, G. W., Spracklen, D. V., Woodhouse, M. T., Regayre, L. A., and Pierce, J. R.: Large contribution of natural aerosols to uncertainty in indirect forcing, Nature, 503, 67–71, https://doi.org/10.1038/nature12674, 2013. a
Carslaw, K. S., Gordon, H., Hamilton, D. S., Johnson, J. S., Regayre, L. A., Yoshioka, M., and Pringle, K. J.: Aerosols in the Pre-industrial Atmosphere, Curr. Clim. Change Rep., 3, 1–15, https://doi.org/10.1007/s40641-017-0061-2, 2017. a
Chang, F.-L. and Li, Z.: Estimating the vertical variation of cloud droplet effective radius using multispectral near‐infrared satellite measurements, J. Geophys. Res., 107, AAC 7-1–AAC 7-12, https://doi.org/10.1029/2001JD0007666, 2002. a
Chen, R., Wood, R., Li, Z., Ferraro, R., and Chang, F.-L.: Studying the vertical variation of cloud droplets effective radius using ship and space-borne remote sensing data, J. Geophy. Res., 113, D00A02, https://doi.org/10.1029/2007/JD009596, 2008. a
Christensen, M., Jones, W. K., and Stier, P.: Aerosols Enhance Cloud Lifetime and Brightness along the Stratus-to-Cumulus Transition, P. Natl. Acad. Sci. USA, 117, 17591–17598, https://doi.org/10.1073/pnas.1921231117, 2020. a
Christensen, M. W. and Stephens, G. L.: Microphysical and macrophysical responses of marine stratocumulus polluted by underlying ships: 2. Impacts of haze on precipitating clouds, J. Geophys. Res., 117, D11203, https://doi.org/10.1029/2011JD017125, 2012. a
Clarke, A. and Kapustin, V.: Hemispheric aerosol vertical profiles: anthropogenic impacts on optical depth and cloud nuclei, Science, 330, 1047–1047, 2010. a
Costantino, L. and Bréon, F.-M.: Analysis of aerosol-cloud interaction from multi-sensor satellite observations, Geophys. Res. Lett., 37, L11801, https://doi.org/10.1029/2009GL041828, 2010. a, b, c
Costantino, L. and Bréon, F.-M.: Aerosol indirect effect on warm clouds over South-East Atlantic, from co-located MODIS and CALIPSO observations, Atmos. Chem. Phys., 13, 69–88, https://doi.org/10.5194/acp-13-69-2013, 2013. a
Costa-Surós, M., Sourdeval, O., Acquistapace, C., Baars, H., Carbajal Henken, C., Genz, C., Hesemann, J., Jimenez, C., König, M., Kretzschmar, J., Madenach, N., Meyer, C. I., Schrödner, R., Seifert, P., Senf, F., Brueck, M., Cioni, G., Engels, J. F., Fieg, K., Gorges, K., Heinze, R., Siligam, P. K., Burkhardt, U., Crewell, S., Hoose, C., Seifert, A., Tegen, I., and Quaas, J.: Detection and attribution of aerosol–cloud interactions in large-domain large-eddy simulations with the ICOsahedral Non-hydrostatic model, Atmos. Chem. Phys., 20, 5657–5678, https://doi.org/10.5194/acp-20-5657-2020, 2020. a, b, c
Desmons, M., Ferlay, N., Parol, F., Mcharek, L., and Vanbauce, C.: Improved information about the vertical location and extent of monolayer clouds from POLDER3 measurements in the oxygen A-band, Atmos. Meas. Tech., 6, 2221–2238, https://doi.org/10.5194/amt-6-2221-2013, 2013. a
Deuzé, J. L., Bréon, F.-M., Devaux, C., Goloub, P., Herman, M., Lafrance, B., Maignan, F., Marchand, A., Nadal, F., Perry, G., and Tanré, D.: Remote sensing of aerosols over land surfaces from POLDER-ADEOS-1 polarized measurements, J. Geophys. Res., 106, 4913–4926, https://doi.org/10.1029/2000jd900364, 2001. a
Dusek, U., Frank, G. P., Hildebrandt, L., Curtius, J., Schneider, J., Walter, S., Chand, D., Drewnick, F., Hings, S., Jung, D., Borrmann, S., and Andreae, M. O.: Size Matters More Than Chemistry for Cloud-Nucleating Ability of Aerosol Particles, Science, 312, 1375–1378, https://doi.org/10.1126/science.1125261, 2006. a
Ekman, A. M. L., Engström, A., and Söderberg, A.: Impact of Two-Way Aerosol–Cloud Interaction and Changes in Aerosol Size Distribution on Simulated Aerosol-Induced Deep Convective Cloud Sensitivity, J. Atmos. Sci., 68, 685–698, https://doi.org/10.1175/2010JAS3651.1, 2011. a, b
Endo, S., Fridlind, A. M., Lin, W., Vogelmann, A. M., Toto, T., Ackerman, A. S., McFarquhar, G. M., R.C.Jackson, Jonsson, H. H., and Liu, Y.: RACORO continental boundary layer cloud investigations: 2. Large-eddy simulations of cumulus clouds and evaluation with in situ and ground-based observations, J. Geophys. Res.-Atmos., 120, 5993–6014, https://doi.org/10.1002/2014JD022525, 2015. a
Fan, J., Leung, L. R., Rosenfeld, D., Chen, Q., Li, Z., Zhang, J., and Yan, H.: Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds, P. Natl. Acad. Sci. USA, 110, E4581–E4590, https://doi.org/10.1073/pnas.1316830110, 2013. a
Feingold, G. and Grund, C. J.: Feasibility of Using Multiwavelength Lidar Measurements to Measure Cloud Condensation Nuclei, J. Atmos. Ocean. Tech., 11, 1543–1558, https://doi.org/10.1175/1520-0426(1994)011<1543:FOUMLM>2.0.CO;2, 1994. a
Feingold, G., Yang, S., Hardesty, R. M., and Cotton, W. R.: Retrieving cloud condensation nucleus properties from Doppler cloud radar, microwave radiometer, and lidar, J. Atmos. Ocean. Tech., 15, 1189–1196, 1998. a
Feingold, G., Remer, L. A., Ramaprasad, J., and Kaufman, Y.: Analysis of smoke impact on clouds in Brazilian biomass burning regions: An extension of Twomey's approach, J. Geophys. Res., 106, 22907–22922, https://doi.org/10.1029/2001JD000732, 2001. a, b, c
Feingold, G., Eberhard, W. L., Veron, D. E., and Previdi, M.: First measurements of the Twomey indirect effect using ground-based remote sensors, Geophys. Res. Lett., 30, 1287, https://doi.org/10.1029/2002GL016633, 2003. a
Feingold, G., Koren, I., Wang, H. L., Xue, H. W., and Brewer, W. A.: Precipitation-generated oscillations in open cellular cloud fields, Nature, 466, 849–852, 2010. a
Geddes, A. and Bösch, H.: Tropospheric aerosol profile information from high-resolution oxygen A-band measurements from space, Atmos. Meas. Tech., 8, 859–874, https://doi.org/10.5194/amt-8-859-2015, 2015. a
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Ghan, S., Guzman, G., and Abdul-Razzak, H.: Competition between sea-salt and sulfate particles as cloud condensation nuclei, J. Atmos. Sci., 55, 3340–3347, 1998. a, b
Grandey, B. S. and Stier, P.: A critical look at spatial scale choices in satellite-based aerosol indirect effect studies, Atmos. Chem. Phys., 10, 11459–11470, https://doi.org/10.5194/acp-10-11459-2010, 2010. a, b
Grosvenor, D. P., Sourdeval, O., Zuidema, P., Ackerman, A., Alexandrov, M. D., Bennartz, R., Boers, R., Cairns, B., Chiu, J. C., Christensen, M., Deneke, H., Diamond, M., Feingold, G., Fridlind, A., Hünerbein, A., Knist, C., Kollias, P., Marshak, A., McCoy, D., Merk, D., Painemal, D., Rausch, J., Rosenfeld, D., Russchenberg, H., Seifert, P., Sinclair, K., Stier, P., van Diedenhoven, B., Wendisch, M., Werner, F., Wood, R., Zhang, Z., and Quaas, J.: Remote Sensing of Droplet Number Concentration in Warm Clouds: A Review of the Current State of Knowledge and Perspectives, Rev. Geophys., 56, 409–453, https://doi.org/10.1029/2017RG000593, 2018. a, b, c, d, e, f, g, h, i, j
Gryspeerdt, E. and Stier, P.: Regime-based analysis of aerosol-cloud interactions, Geophys. Res. Lett., 39, L21802, https://doi.org/10.1029/2012GL053221, 2012. a
Gryspeerdt, E., Stier, P., White, B. A., and Kipling, Z.: Wet scavenging limits the detection of aerosol effects on precipitation, Atmos. Chem. Phys., 15, 7557–7570, https://doi.org/10.5194/acp-15-7557-2015, 2015. a
Gryspeerdt, E., Quaas, J., and Bellouin, N.: Constraining the aerosol influence on cloud fraction, J. Geophys. Res.-Atmos., 121, 3566–3583, https://doi.org/10.1002/2015JD023744, 2016. a, b, c
Gryspeerdt, E., Quaas, J., Ferrachat, S., Gettelman, A., Ghan, S., Lohmann, U., Morrison, H., Neubauer, D., Partridge, D. G., Stier, P., Takemura, T., Wang, H., Wang, M., and Zhang, K.: Constraining the instantaneous aerosol influence on cloud albedo, P. Nat. Acad. Sci. USA, 114, 4899–4904, https://doi.org/10.1073/pnas.1617765114, 2017. a, b, c, d
Gryspeerdt, E., Goren, T., Sourdeval, O., Quaas, J., Mülmenstädt, J., Dipu, S., Unglaub, C., Gettelman, A., and Christensen, M.: Constraining the aerosol influence on cloud liquid water path, Atmos. Chem. Phys., 19, 5331–5347, https://doi.org/10.5194/acp-19-5331-2019, 2019. a, b
Gryspeerdt, E., Mülmenstädt, J., Gettelman, A., Malavelle, F. F., Morrison, H., Neubauer, D., Partridge, D. G., Stier, P., Takemura, T., Wang, H., Wang, M., and Zhang, K.: Surprising similarities in model and observational aerosol radiative forcing estimates, Atmos. Chem. Phys., 20, 613–623, https://doi.org/10.5194/acp-20-613-2020, 2020. a, b
Haarig, M., Walser, A., Ansmann, A., Dollner, M., Althausen, D., Sauer, D., Farrell, D., and Weinzierl, B.: Profiles of cloud condensation nuclei, dust mass concentration, and ice-nucleating-particle-relevant aerosol properties in the Saharan Air Layer over Barbados from polarization lidar and airborne in situ measurements, Atmos. Chem. Phys., 19, 13773–13788, https://doi.org/10.5194/acp-19-13773-2019, 2019. a
Hansen, J. E. and Travis, L. D.: Light scattering in planetary atmospheres, Space Sci. Rev., 16, 527–610, https://doi.org/10.1007/BF00168069, 1974. a
Hasekamp, O. and Quaas, J.: Twomey parameter uncertainty, World Data Center for Climate (WDCC) at DKRZ, available at: http://cera-www.dkrz.de/WDCC/ui/Compact.jsp?acronym=DKRZ_LTA_1002_ds00001, last access: 19 November 2020. a
Hasekamp, O., Gryspeerdt, E., and Quaas, J.: Analysis of polarimetric satellite measurements suggests stronger cooling due to aerosol-cloud interactions, Nature Comm., 10, 5405, https://doi.org/10.1038/s41467-019-13372-2, 2019a. a, b, c, d, e, f
Hasekamp, O. P., Fu, G., P.Rusli, S., Wu, L., Noia, A. D., aan de Brugh, J., Landgraf, J., Smit, J. M., Rietjens, J., and van Amerongen, A.: Aerosol measurements by SPEXone on the NASA PACE mission: expected retrieval capabilities, J. Quant. Spectrosc. Ra., 227, 170–184, https://doi.org/10.1016/j.jqsrt.2019.02.006, 2019b. a
Heinze, R., Dipankar, A., Carbajal Henken, C., Moseley, C., Sourdeval, O., Trömel, S., Xie, X., Adamidis, P., Ament, F., Baars, H., Barthlott, C., Behrendt, A., Blahak, U., Bley, S., Brdar, S., Brueck, M., Crewell, S., Deneke, H., Di Girolamo, P., Evaristo, R., Fischer, J., Frank, C., Friederichs, P., Göcke, T., Gorges, K., Hande, L., Hanke, M., Hansen, A., Hege, H.-C., Hoose, C., Jahns, T., Kalthoff, N., Klocke, D., Kneifel, S., Knippertz, P., Kuhn, A., van Laar, T., Macke, A., Maurer, V., Mayer, B., Meyer, C. I., Muppa, S. K., Neggers, R. A. J., Orlandi, E., Pantillon, F., Pospichal, B., Röber, N., Scheck, L., Seifert, A., Seifert, P., Senf, F., Siligam, P., Simmer, C., Steinke, S., Stevens, B., Wapler, K., Weniger, M., Wulfmeyer, V., Zängl, G., Zhang, D., and Quaas, J.: Large-eddy simulations over Germany using ICON: A comprehensive evaluation, Q. J. Roy. Meteor. Soc., 143, 69–100, https://doi.org/10.1002/qj.2947, 2017. a, b
Hélière, A., Gelsthorpe, R., Hors, L. L., and Toulemont, Y.: ATLID, the atmospheric lidar on board the Earthcare Satellite, in: International Conference on Space Optics – ICSO 2012, Ajaccio, Corsica, France, 9–12 October 2012, Proc. SPIE 10564, https://doi.org/10.1117/12.2309095, 2017. a
Heyn, I., Block, K., Mülmenstädt, J., Gryspeerdt, E., Kühne, P., Salzmann, M., and Quaas, J.: Assessment of simulated aerosol effective radiative forcings in the terrestrial spectrum, Geophys. Res. Lett., 44, 1001–1007, https://doi.org/10.1002/2016GL071975, 2017. a, b
Hill, A. A., Feingold, G., and Jiang, H. L.: The Influence of Entrainment and Mixing Assumption on Aerosol-Cloud Interactions in Marine Stratocumulus, J. Atmos. Sci., 66, 1450–1464, 2009. a
Holben, B. N., Tanré, D., Smirnov, A., Eck, T. F., Slutsker, I., Abuhassan, N., Newcomb, W. W., Schafer, J. S., Chatenet, B., Lavenu, F., Kaufman, Y. J., Castle, J. V., Setzer, A., Markham, B., Clark, D., Frouin, R., Halthore, R., Karneli, A., O'Neill, N. T., Pietras, C., Pinker, R. T., Voss, K., and Zibordi, G.: An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET, J. Geophys. Res., 106, 12067–12097, https://doi.org/10.1029/2001JD900014, 2001. a
Hollstein, A. and Fischer, J.: Retrieving aerosol height from the oxygen A band: a fast forward operator and sensitivity study concerning spectral resolution, instrumental noise, and surface inhomogeneity, Atmos. Meas. Tech., 7, 1429–1441, https://doi.org/10.5194/amt-7-1429-2014, 2014. a
Hu, Y., Vaughan, M., McClain, C., Behrenfeld, M., Maring, H., Anderson, D., Sun-Mack, S., Flittner, D., Huang, J., Wielicki, B., Minnis, P., Weimer, C., Trepte, C., and Kuehn, R.: Global statistics of liquid water content and effective number concentration of water clouds over ocean derived from combined CALIPSO and MODIS measurements, Atmos. Chem. Phys., 7, 3353–3359, https://doi.org/10.5194/acp-7-3353-2007, 2007. a, b
Illingworth, A. J., Barker, H. W., Beljaars, A., Ceccaldi, M., Chepfer, H., Clerbaux, N., Cole, J., Delanoë, J., Domenech, C., Donovan, D. P., Fukuda, S., Hirakata, M., Hogan, R. J., Huenerbein, A., Kollias, P., Kubota, T., Nakajima, T., Nakajima, T. Y., Nishizawa, T., Ohno, Y., Okamoto, H., Oki, R., Sato, K., Satoh, M., Shephard, M. W., Velázquez-Blázquez, A., Wandinger, U., Wehr, T., and van Zadelhoff, G.-J.: The EarthCARE Satellite: The Next Step Forward in Global Measurements of Clouds, Aerosols, Precipitation, and Radiation, B. Am. Meteorol. Soc., 96, 1311–1332, https://doi.org/10.1175/bams-d-12-00227.1, 2015. a
Inness, A., Ades, M., Agustí-Panareda, A., Barré, J., Benedictow, A., Blechschmidt, A.-M., Dominguez, J. J., Engelen, R., Eskes, H., Flemming, J., Huijnen, V., Jones, L., Kipling, Z., Massart, S., Parrington, M., Peuch, V.-H., Razinger, M., Remy, S., Schulz, M., and Suttie, M.: The CAMS reanalysis of atmospheric composition, Atmos. Chem. Phys., 19, 3515–3556, https://doi.org/10.5194/acp-19-3515-2019, 2019. a
Jeong, M. and Li, Z.: Separating real and apparent effects of cloud, humidity, and dynamics on aerosol optical thickness near cloud edges, J. Geophys. Res., 115, D00K32, https://doi.org/10.1029/2009JD013547, 2010. a
Jiang, H., Feingold, G., Jonsson, H. H., Lu, M.-L., Chuang, P. Y., Flagan, R. C., and Seinfeld, J. H.: Statistical comparison of properties of simulated and observed cumulus clouds in the vicinity of Houston during the Gulf of Mexico Atmospheric Composition and Climate Study (GoMACCS), J. Geophys. Res. 113, D13205, https://doi.org/10.1029/2007JD009304, 2008. a
Kacarab, M., Thornhill, K. L., Dobracki, A., Howell, S. G., O'Brien, J. R., Freitag, S., Poellot, M. R., Wood, R., Zuidema, P., Redemann, J., and Nenes, A.: Biomass burning aerosol as a modulator of the droplet number in the southeast Atlantic region, Atmos. Chem. Phys., 20, 3029–3040, https://doi.org/10.5194/acp-20-3029-2020, 2020. a, b, c, d
Kaufman, Y. J., Tanré, D., and Boucher, O.: A satellite view of aerosols in the climate system, Nature, 419, 215–223, https://doi.org/10.1038/nature01091, 2002. a
Kaufman, Y. J., Boucher, O., Tanré, D., Chin, M., Remer, L. A., and Takemura, T.: Aerosol anthropogenic component estimated from satellite data, Geophys. Res. Lett., 32, L17804, https://doi.org/10.1029/2005GL023125, 2005. a
Kazil, J., Wang, H., Feingold, G., Clarke, A. D., Snider, J. R., and Bandy, A. R.: Modeling chemical and aerosol processes in the transition from closed to open cells during VOCALS-REx, Atmos. Chem. Phys., 11, 7491–7514, https://doi.org/10.5194/acp-11-7491-2011, 2011. a
Kikuchi, M., Murakami, H., Suzuki, K., Nagao, T. M., and Higurashi, A.: Improved Hourly Estimates of Aerosol Optical Thickness Using Spatiotemporal Variability Derived From Himawari-8 Geostationary Satellite, IEEE T. Geosci. Remote, 56, 3442–3455, https://doi.org/10.1109/TGRS.2018.2800060, 2018. a
Kim, M.-H., Omar, A. H., Tackett, J. L., Vaughan, M. A., Winker, D. M., Trepte, C. R., Hu, Y., Liu, Z., Poole, L. R., Pitts, M. C., Kar, J., and Magill, B. E.: The CALIPSO version 4 automated aerosol classification and lidar ratio selection algorithm, Atmos. Meas. Tech., 11, 6107–6135, https://doi.org/10.5194/amt-11-6107-2018, 2018. a
Kinne, S.: Aerosol radiative effects with MACv2, Atmos. Chem. Phys., 19, 10919–10959, https://doi.org/10.5194/acp-19-10919-2019, 2019. a
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, T. Faraday Soc., 32, 1152–1161, 1936. a, b
Krisna, T. C., Wendisch, M., Ehrlich, A., Jäkel, E., Werner, F., Weigel, R., Borrmann, S., Mahnke, C., Pöschl, U., Andreae, M. O., Voigt, C., and Machado, L. A. T.: Comparing airborne and satellite retrievals of cloud optical thickness and particle effective radius using a spectral radiance ratio technique: two case studies for cirrus and deep convective clouds, Atmos. Chem. Phys., 18, 4439–4462, https://doi.org/10.5194/acp-18-4439-2018, 2018. a
Krüger, O. and Graßl, H.: The indirect aerosol effect over Europe, Geophys. Res. Lett., 29, 1925, https://doi.org/10.1029/2001GL014081, 2002. a
Level-1 and Atmosphere Archive & Distribution System (LAADS), Distributed Active Archive Center (DAAC), Goddard Space Flight Center, Greenbelt, Maryland, available at: https://ladsweb.nascom.nasa.gov/, last access: 19 November 2020. a
Lee, K. and Chung, C. E.: Observationally-constrained estimates of global fine-mode AOD, Atmos. Chem. Phys., 13, 2907–2921, https://doi.org/10.5194/acp-13-2907-2013, 2013. a
Lehmann, K., Siebert, H., and Shaw, R. A.: Homogeneous and Inhomogeneous Mixing in Cumulus Clouds: Dependence on Local Turbulence Structure, J. Atmos. Sci., 66, 3641–3659, https://doi.org/10.1175/2009JAS3012.1, 2009. a
Levy, R. C., Mattoo, S., Munchak, L. A., Remer, L. A., Sayer, A. M., Patadia, F., and Hsu, N. C.: The Collection 6 MODIS aerosol products over land and ocean, Atmos. Meas. Tech., 6, 2989–3034, https://doi.org/10.5194/amt-6-2989-2013, 2013. a
Liu, J. and Li, Z.: Estimation of cloud condensation nuclei concentration from aerosol optical quantities: influential factors and uncertainties, Atmos. Chem. Phys., 14, 471–483, https://doi.org/10.5194/acp-14-471-2014, 2014. a
Liu, J. and Li, Z.: Significant underestimation in the optically based estimation of the aerosol first indirect effect induced by the aerosol swelling effect, Geophys. Res. Lett., 45, 5690–5699, https://doi.org/10.1029/2018GL077679, 2018. a, b
Liu, J. and Li, Z.: Aerosol properties and their influences on low warm clouds during the Two-Column Aerosol Project, Atmos. Chem. Phys., 19, 9515–9529, https://doi.org/10.5194/acp-19-9515-2019, 2019. a
Lohmann, U. and Feichter, J.: Can the direct and semi-direct aerosol effect compete with the indirect effect on a global scale?, Geophys. Res. Lett., 28, 159–161, https://doi.org/10.1029/2000GL012051, 2001. a
Lv, M., Wang, Z., Li, Z., Luo, T., Ferrare, R., Liu, D., Wu, D., Mao, J., Wan, B., Zhang, F., and Wang, Y.: Retrieval of cloud condensation nuclei number concentration profiles from lidar extinction and backscatter data, J. Geophys. Res.-Atmos., 123, 6082–6098, https://doi.org/10.1029/2017JD028102, 2018. a
Ma, P.-L., Rasch, P. J., Chepfer, H., Winker, D. M., and Ghan, S. J.: Observational constraint on cloud susceptibility weakened by aerosol retrieval limitations, Nat. Commun., 9, 2640, https://doi.org/10.1038/s41467-018-05028-4, 2018. a
Ma, Y., Brooks, S. D., Vidaurre, G., Khalizov, A. F., Wang, L., and Zhang, R.: Rapid modification of cloud-nucleating ability of aerosols by biogenic emissions, Geophys. Res. Lett., 40, 6293–6297, https://doi.org/10.1002/2013GL057895, 2013. a
MacDonald, A. B., Hossein Mardi, A., Dadashazar, H., Azadi Aghdam, M., Crosbie, E., Jonsson, H. H., Flagan, R. C., Seinfeld, J. H., and Sorooshian, A.: On the relationship between cloud water composition and cloud droplet number concentration, Atmos. Chem. Phys., 20, 7645–7665, https://doi.org/10.5194/acp-20-7645-2020, 2020. a
Mamouri, R.-E. and Ansmann, A.: Potential of polarization lidar to provide profiles of CCN- and INP-relevant aerosol parameters, Atmos. Chem. Phys., 16, 5905–5931, https://doi.org/10.5194/acp-16-5905-2016, 2016. a
Martins, J. V., Fernandez-Borda, R., McBride, B., Remer, L., and Barbosa, H. M. J.: The Harp Hype Ran Gular Imaging Polarimeter and the Need for Small Satellite Payloads with High Science Payoff for Earth Science Remote Sensing, in: IGARSS 2018 – 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018, IEEE, 6304–6307, https://doi.org/10.1109/IGARSS.2018.8518823, 2018. a
McBride, B. A., Martins, J. V., Barbosa, H. M. J., Birmingham, W., and Remer, L. A.: Spatial distribution of cloud droplet size properties from Airborne Hyper-Angular Rainbow Polarimeter (AirHARP) measurements, Atmos. Meas. Tech., 13, 1777–1796, https://doi.org/10.5194/amt-13-1777-2020, 2019. a
McComiskey, A. and Feingold, G.: The scale problem in quantifying aerosol indirect effects, Atmos. Chem. Phys., 12, 1031–1049, https://doi.org/10.5194/acp-12-1031-2012, 2012. a, b, c, d, e, f, g, h
McComiskey, A., Feingold, G., Frisch, A. S., Turner, D. D., Miller, M. A., Chiu, J. C., Min, Q., and Ogren, J. A.: An assessment of aerosol-cloud interactions in marine stratus clouds based on surface remote sensing, J. Geophys. Res., 114, D09203, https://doi.org/10.1029/2008JD011006, 2009. a
McCoy, D. T., Bender, F. A.-M., Mohrmann, J. K. C., Hartmann, D. L., Wood, R., and Grosvenor, D. P.: The global aerosol-cloud first indirect effect estimated using MODIS, MERRA, and AeroCom, J. Geophys. Res.-Atmos., 122, 1779–1796, https://doi.org/10.1002/2016JD026141, 2017. a, b
McCoy, I. L., McCoy, D. T., Wood, R., Regayre, L., Watson-Parris, D., Grosvenor, Daniel P. an d Mulcahy, J. P., Hu, Y., Bender, F. A.-M., Field, P. R., Carslaw, K. S., and Gordon, H.: The hemispheric contrast in cloud microphysical properties constrains aerosol forcing, P. Natl. Acad. Sci. USA, 117, 18998–19006, https://doi.org/10.1073/pnas.1922502117, 2020. a
Michibata, T., Suzuki, K., Sato, Y., and Takemura, T.: The source of discrepancies in aerosol–cloud–precipitation interactions between GCM and A-Train retrievals, Atmos. Chem. Phys., 16, 15413–15424, https://doi.org/10.5194/acp-16-15413-2016, 2016. a
Mikkonen, S., Pitkänen, M. R. A., Nieminen, T., Lipponen, A., Isokääntä, S., Arola, A., and Lehtinen, K. E. J.: Technical note: Effects of uncertainties and number of data points on line fitting – a case study on new particle formation, Atmos. Chem. Phys., 19, 12531–12543, https://doi.org/10.5194/acp-19-12531-2019, 2019. a
Moeng, C.-H. and Arakawa, A.: Representation of Boundary Layer Moisture Transport in Cloud-Resolving Models, Mon. Weather Rev., 140, 3682–3698, https://doi.org/10.1175/MWR-D-12-00046.1, 2012. a
Morales, R., Nenes, A., Jonsson, H., Flagan, R., and Seinfeld, J.: Evaluation Of An Entraining Droplet Activation Parameterization Using In-Situ Cloud Data, J. Geophys. Res., 116, D15205, https://doi.org/10.1029/2010JD015324, 2011. a
Morales Betancourt, R. and Nenes, A.: Understanding the contributions of aerosol properties and parameterization discrepancies to droplet number variability in a global climate model, Atmos. Chem. Phys., 14, 4809–4826, https://doi.org/10.5194/acp-14-4809-2014, 2014. a, b
Mülmenstädt, J. and Feingold, G.: The radiative forcing of aerosol-cloud interactions in liquid clouds: Wrestling and embracing uncertainty, Curr. Clim. Change Rep., 4, 23–40, https://doi.org/10.1007/s40641-018-0089-y, 2018. a, b
Mülmenstädt, J., Sourdeval, O., Henderson, D. S., L'Ecuyer, T. S., Unglaub, C., Jungandreas, L., Böhm, C., Russell, L. M., and Quaas, J.: Using CALIOP to estimate cloud-field base height and its uncertainty: the Cloud Base Altitude Spatial Extrapolator (CBASE) algorithm and dataset, Earth Syst. Sci. Data, 10, 2279–2293, https://doi.org/10.5194/essd-10-2279-2018, 2018. a
Mülmenstädt, J., Gryspeerdt, E., Salzmann, M., Ma, P.-L., Dipu, S., and Quaas, J.: Separating radiative forcing by aerosol–cloud interactions and rapid cloud adjustments in the ECHAM–HAMMOZ aerosol–climate model using the method of partial radiative perturbations, Atmos. Chem. Phys., 19, 15415–15429, https://doi.org/10.5194/acp-19-15415-2019, 2019. a, b, c
Müller, D., Ansmann, A., Mattis, I., Tesche, M., Wandinger, U., Althausen, D., and Pisani, G.: Aerosol-type-dependent lidar ratios observed with Raman lidar, J. Geophys. Res., 112, D16202, https://doi.org/10.1029/2006JD008292, 2007. a
Nakajima, T. and King, M. D.: Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I: Theory, J. Atmos. Sci., 47, 1878–1893, https://doi.org/10.1175/1520-0469(1990)047<1878:DOTOTA>2.0.CO;2, 1990. a, b
Nakajima, T. and Schulz, M.: What do we know about large-scale changes of aerosols, clouds, and the radiation budget?, Clouds in the Perturbed Climate System, Proceedings Ernst Strüngmann Forum, https://doi.org/10.7551/mitpress/9780262012874.003.0017, 2009. a
Nakajima, T., Higurashi, A., Kawamoto, K., and Penner, J. E.: A possible correlation between satellite-derived cloud and aerosol microphysical parameters, Geophys. Res. Lett., 28, 1171–1174, https://doi.org/10.1029/2000gl012186, 2001. a
Oreopoulos, L. and Platnick, S.: Radiative susceptibility of cloudy atmospheres to droplet number perturbations: 2. Global analysis from MODIS, J. Geophys. Res., 113, D14S21, https://doi.org/10.1029/2007JD009655, 2008. a
Painemal, D., Chiu, J.-Y. C., Minnis, P., Yost, C., Zhou, X., Cadeddu, M., Eloranta, E., Lewis, E. R., Ferrare, R., and Kollias, P.: Aerosol and cloud microphysics covariability in the northeast Pacific boundary layer estimated with ship-based and satellite remote sensing observations, J. Geophys. Res.-Atmos., 122, 2403–2418, https://doi.org/10.1002/2016JD025771, 2017. a
Painemal, D., Chang, F.-L., Ferrare, R., Burton, S., Li, Z., Smith Jr., W. L., Minnis, P., Feng, Y., and Clayton, M.: Reducing uncertainties in satellite estimates of aerosol–cloud interactions over the subtropical ocean by integrating vertically resolved aerosol observations, Atmos. Chem. Phys., 20, 7167–7177, https://doi.org/10.5194/acp-20-7167-2020, 2020. a, b
Penner, J. E., Xu, L., and Wang, M.: Satellite methods underestimate indirect climate forcing by aerosols, P. Natl. Acad. Sci. USA, 108, 13404, https://doi.org/10.1073/pnas.1018526108, 2011. a
Petersik, P., Salzmann, M., Kretzschmar, J., Cherian, R., Mewes, D., and Quaas, J.: Subgrid-scale variability in clear-sky relative humidity and forcing by aerosol–radiation interactions in an atmosphere model, Atmos. Chem. Phys., 18, 8589–8599, https://doi.org/10.5194/acp-18-8589-2018, 2018. a
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a
Pincus, R., Platnick, S., Ackerman, S., Hemler, R., and Hofmann, R. P.: Reconciling Simulated and Observed Views of Clouds: MODIS, ISCCP, and the Limits of Instrument Simulators, J. Climate, 25, 4699–4720, https://doi.org/10.1175/JCLI-D-11-00267.1, 2012. a
Pitkänen, M. R. A., Mikkonen, S., Lehtinen, K. E. J., Lipponen, A., and Arola, A.: Artificial bias typically neglected in comparisons of uncertain atmospheric data, Geophys. Res. Lett., 43, 10003–10011, https://doi.org/10.1002/2016GL070852, 2016. a, b
Platnick, S.: Vertical photon transport in cloud remote sensing problems, J. Geophys. Res., 105, 22919–22935, https://doi.org/10.1029/2000JD900333, 2000. a, b
Platnick, S. and Twomey, S.: Determining the Susceptibility of Cloud Albedo to Changes in Droplet Concentration with the Advanced Very High Resolution Radiometer, J. Appl. Meteorol., 33, 334–347, https://doi.org/10.1175/1520-0450(1994)033<0334:DTSOCA>2.0.CO;2, 1994. a
Platnick, S., Meyer, K. G., King, M. D., Wind, G., Amarasinghe, N., Marchant, B., Arnold, G. T., Zhang, Z., Hubanks, P. A., Holz, R. E., Yang, P., Ridgway, W. L., and Riedi, J.: The MODIS Cloud Optical and Microphysical Products: Collection 6 Updates and Examples From Terra and Aqua, IEEE T. Geosci. Remote, 55, 502–525, https://doi.org/10.1109/TGRS.2016.2610522, 2017. a
Posselt, D. J., Kessler, J., and Mace, G. G.: Bayesian Retrievals of Vertically Resolved Cloud Particle Size Distribution Properties, J. Appl. Meteorol. Clim., 56, 745–765, https://doi.org/10.1175/JAMC-D-16-0276.1, 2017. a
Pringle, K. J., Tost, H., Pozzer, A., Pöschl, U., and Lelieveld, J.: Global distribution of the effective aerosol hygroscopicity parameter for CCN activation, Atmos. Chem. Phys., 10, 5241–5255, https://doi.org/10.5194/acp-10-5241-2010, 2010. a
Quaas, J.: Evaluating the “critical relative humidity” as a measure of subgrid-scale variability of humidity in general circulation model cloud cover parameterizations using satellite data, J. Geophys. Res., 117, D09208, https://doi.org/10.1029/2012JD017495, 2012. a
Quaas, J.: Approaches to observe effects of anthropogenic aerosols on clouds and radiation, Curr. Clim. Change Rep., 1, 297–304, https://doi.org/10.1007/s40641-015-0028-0, 2015. a
Quaas, J., Boucher, O., and Lohmann, U.: Constraining the total aerosol indirect effect in the LMDZ and ECHAM4 GCMs using MODIS satellite data, Atmos. Chem. Phys., 6, 947–955, https://doi.org/10.5194/acp-6-947-2006, 2006. a, b
Quaas, J., Boucher, O., Bellouin, N., and Kinne, S.: Satellite-based estimate of the direct and indirect aerosol climate forcing, J. Geophys. Res., 113, D05204, https://doi.org/10.1029/2007JD008962, 2008. a, b
Quaas, J., Boucher, O., Jones, A., Weedon, G. P., Kieser, J., and Joos, H.: Exploiting the weekly cycle as observed over Europe to analyse aerosol indirect effects in two climate models, Atmos. Chem. Phys., 9, 8493–8501, https://doi.org/10.5194/acp-9-8493-2009, 2009a. a
Quaas, J., Ming, Y., Menon, S., Takemura, T., Wang, M., Penner, J. E., Gettelman, A., Lohmann, U., Bellouin, N., Boucher, O., Sayer, A. M., Thomas, G. E., McComiskey, A., Feingold, G., Hoose, C., Kristjánsson, J. E., Liu, X., Balkanski, Y., Donner, L. J., Ginoux, P. A., Stier, P., Grandey, B., Feichter, J., Sednev, I., Bauer, S. E., Koch, D., Grainger, R. G., Kirkevåg, A., Iversen, T., Seland, Ø., Easter, R., Ghan, S. J., Rasch, P. J., Morrison, H., Lamarque, J.-F., Iacono, M. J., Kinne, S., and Schulz, M.: Aerosol indirect effects – general circulation model intercomparison and evaluation with satellite data, Atmos. Chem. Phys., 9, 8697–8717, https://doi.org/10.5194/acp-9-8697-2009, 2009b. a
Remer, L. A., Knobelspiesse, K., Zhai, P.-W., Xu, F., Kalashnikova, O. V., Chowdhary, J., Hasekamp, O., Dubovik, O., Wu, L., Ahmad, Z., Boss, E., Cairns, B., Coddington, O., Davis, A. B., Dierssen, H. M., Diner, D. J., Franz, B., Frouin, R., Gao, B.-C., Ibrahim, A., Levy, R. C., Martins, J. V., Omar, A. H., and Torres, O.: Retrieving Aerosol Characteristics From the PACE Mission, Part 2: Multi-Angle and Polarimetry, Frontiers in Environmental Science, 7, 94, https://doi.org/10.3389/fenvs.2019.00094, 2019. a
Reutter, P., Su, H., Trentmann, J., Simmel, M., Rose, D., Gunthe, S. S., Wernli, H., Andreae, M. O., and Pöschl, U.: Aerosol- and updraft-limited regimes of cloud droplet formation: influence of particle number, size and hygroscopicity on the activation of cloud condensation nuclei (CCN), Atmos. Chem. Phys., 9, 7067–7080, https://doi.org/10.5194/acp-9-7067-2009, 2009. a
Reverdy, M., Chepfer, H., Donovan, D., Noel, V., Cesana, G., Hoareau, C., Chiriaco, M., and Bastin, S.: An EarthCARE/ATLID simulator to evaluate cloud description in climate models, J. Geophys. Res.-Atmos., 120, 11090–11113, https://doi.org/10.1002/2015JD023919, 2015. a, b
Richardson, M., Leinonen, J., Cronk, H. Q., McDuffie, J., Lebsock, M. D., and Stephens, G. L.: Marine liquid cloud geometric thickness retrieved from OCO-2's oxygen A-band spectrometer, Atmos. Meas. Tech., 12, 1717–1737, https://doi.org/10.5194/amt-12-1717-2019, 2019. a
Rosenfeld, D., Kaufman, Y. J., and Koren, I.: Switching cloud cover and dynamical regimes from open to closed Benard cells in response to the suppression of precipitation by aerosols, Atmos. Chem. Phys., 6, 2503–2511, https://doi.org/10.5194/acp-6-2503-2006, 2006. a
Rosenfeld, D., Zheng, Y., Hashimshoni, E., Pöhlker, M. L., Jefferson, A., Pöhlker, C., Yu, X., Zhu, Y., Liu, G., Yue, Z., Fischman, B., Li, Z., Giguzin, D., Goren, T., Artaxoi, P., Barbosai, H. M. J., Pöschl, U., and Andreae, M. O.: Satellite retrieval of cloud condensation nuclei concentrations by using clouds as CCN chambers, P. Natl. Acad. Sci. USA, 113, 5828–5834, https://doi.org/10.1073/pnas.1514044113, 2016. a, b
Saide, P., Carmichael, G., Spak, S., Minnis, P., and Ayers, J.: Improving aerosol distributions below clouds by assimilating satellite-retrieved cloud droplet number, P. Natl. Acad. Sci. USA, 109, 11939–11943, 2012. a
Sanders, A. F. J., de Haan, J. F., Sneep, M., Apituley, A., Stammes, P., Vieitez, M. O., Tilstra, L. G., Tuinder, O. N. E., Koning, C. E., and Veefkind, J. P.: Evaluation of the operational Aerosol Layer Height retrieval algorithm for Sentinel-5 Precursor: application to O2 A band observations from GOME-2A, Atmos. Meas. Tech., 8, 4947–4977, https://doi.org/10.5194/amt-8-4947-2015, 2015. a
Sanghavi, S., Lebsock, M., and Stephens, G.: Sensitivity analysis of polarimetric O2 A-band spectra for potential cloud retrievals using OCO-2/GOSAT measurements, Atmos. Meas. Tech., 8, 3601–3616, https://doi.org/10.5194/amt-8-3601-2015, 2015. a
Sayer, A. M., Hsu, N. C., Bettenhausen, C., and Jeong, M.-J.: Validation and uncertainty estimates for MODIS Collection 6 “Deep Blue” aerosol data, J. Geophys. Res., 118, 7864–7872, https://doi.org/10.1002/jgrd.50600, 2013. a
Schmidt, J., Ansmann, A., Bühl, J., and Wandinger, U.: Strong aerosol–cloud interaction in altocumulus during updraft periods: lidar observations over central Europe, Atmos. Chem. Phys., 15, 10687–10700, https://doi.org/10.5194/acp-15-10687-2015, 2015. a
Schuster, G. L., Lin, B., and Dubovik, O.: Remote sensing of aerosol water uptake, Geophys. Res. Lett., 36, L03814, https://doi.org/10.1029/2008GL036576, 2009. a
Schwartz, S. E., Harshvardhan, and Benkovitz, C. M.: Influence of anthropogenic aerosol on cloud optical depth and albedo shown by satellite measurements and chemical transport modeling, P. Natl. Acad. Sci. USA, 99, 1784–1789, https://doi.org/10.1073/pnas.261712099, 2002. a
Sekiguchi, M., Nakajima, T., Suzuki, K., Kawamoto, K., Higurashi, A., Rosenfeld, D., Sano, I., and Mukai, S.: A study of the direct and indirect effects of aerosols using global satellite data sets of aerosol and cloud parameters, J. Geophys. Res., 108, 4699, https://doi.org/10.1029/2002JD003359, 2003. a, b
Shang, H., Letu, H., Bréon, F.-M., Riedi, J., Ma, R., Wang, Z., Nakajima, Y. T., Wang, Z., and Chen, L.: An improved algorithm of cloud droplet size distribution from POLDER polarized measurements, Remote Sens. Environ., 228, 61–74, https://doi.org/10.1016/j.rse.2019.04.013, 2019. a
Shen, Y., Virkkula, A., Ding, A., Luoma, K., Keskinen, H., Aalto, P. P., Chi, X., Qi, X., Nie, W., Huang, X., Petäjä, T., Kulmala, M., and Kerminen, V.-M.: Estimating cloud condensation nuclei number concentrations using aerosol optical properties: role of particle number size distribution and parameterization, Atmos. Chem. Phys., 19, 15483–15502, https://doi.org/10.5194/acp-19-15483-2019, 2019. a
Shinozuka, Y., Clarke, A. D., Nenes, A., Jefferson, A., Wood, R., McNaughton, C. S., Ström, J., Tunved, P., Redemann, J., Thornhill, K. L., Moore, R. H., Lathem, T. L., Lin, J. J., and Yoon, Y. J.: The relationship between cloud condensation nuclei (CCN) concentration and light extinction of dried particles: indications of underlying aerosol processes and implications for satellite-based CCN estimates, Atmos. Chem. Phys., 15, 7585–7604, https://doi.org/10.5194/acp-15-7585-2015, 2015. a, b, c
Shinozuka, Y., Kacenelenbogen, M. S., Burton, S. P., Howell, S. G., Zuidema, P., Ferrare, R. A., LeBlanc, S. E., Pistone, K., Broccardo, S., Redemann, J., Schmidt, K. S., Cochrane, S. P., Fenn, M., Freitag, S., Dobracki, A., Segal-Rosenheimer, M., and Flynn, C. J.: Daytime aerosol optical depth above low-level clouds is similar to that in adjacent clear skies at the same heights: airborne observation above the southeast Atlantic, Atmos. Chem. Phys., 20, 11275–11285, https://doi.org/10.5194/acp-20-11275-2020, 2020. a
Sinclair, K., van Diedenhoven, B., Cairns, B., Alexandrov, M., Moore, R., Crosbie, E., and Ziemba, L.: Polarimetric retrievals of cloud droplet number concentrations, Remote Sens. Environ., 228, 227–240, https://doi.org/10.1016/j.rse.2019.04.008, 2019. a, b
Small, J. D., Chuang, P. Y., Feingold, G., and Jiang, H.: Can aerosol decrease cloud lifetime?, Geophys. Res. Lett., 36, L16806, https://doi.org/10.1029/2009GL038888, 2009. a, b
Smith, C. J., Kramer, R. J., Myhre, G., Alterskjær, K., Collins, W., Sima, A., Boucher, O., Dufresne, J.-L., Nabat, P., Michou, M., Yukimoto, S., Cole, J., Paynter, D., Shiogama, H., O'Connor, F. M., Robertson, E., Wiltshire, A., Andrews, T., Hannay, C., Miller, R., Nazarenko, L., Kirkevåg, A., Olivié, D., Fiedler, S., Lewinschal, A., Mackallah, C., Dix, M., Pincus, R., and Forster, P. M.: Effective radiative forcing and adjustments in CMIP6 models, Atmos. Chem. Phys., 20, 9591–9618, https://doi.org/10.5194/acp-20-9591-2020, 2020. a
Stamnes, S., Hostetler, C., Ferrare, R., Burton, S., Liu, X., Hair, J., Hu, Y., Wasilewski, A., Martin, W., van Diedenhoven, B., Chowdhary, J., Cetinic, I., Berg, L., Stamnes, K., and Cairns, B.: Simultaneous polarimeter retrievals of microphysical aerosol and ocean color parameters from the “MAPP” algorithm with comparison to high spectral resolution lidar aerosol and ocean products, Appl. Optics., 57, 2394–2413, https://doi.org/10.1364/AO.57.002394, 2018. a
Stephens, G.: Radiation profiles in extended water clouds. II: Parameterization schemes, J. Atmos. Sci., 35, 2123–2132, https://doi.org/10.1175/1520-0469(1978)035<2123:RPIEWC>2.0.CO;2, 1978. a
Stephens, G., Christensen, M., Andrews, T., Haywood, J., Malavelle, F. F., Suzuki, K., Jing, X., Lebsock, M., Li, J. F., Takahashi, H., and Sy, O.: Cloud physics from space, Q. J. Roy. Meteor. Soc., 145, 2854–2875, https://doi.org/10.1002/qj.3589, 2019. a
Stevens, B. and Feingold, G.: Untangling aerosol effects on clouds and precipitation in a buffered system, Nature, 461, 607–613, 2009. a, b
Stier, P.: Limitations of passive remote sensing to constrain global cloud condensation nuclei, Atmos. Chem. Phys., 16, 6595–6607, https://doi.org/10.5194/acp-16-6595-2016, 2016. a, b, c
Tonttila, J., O'Connor, E. J., Niemelä, S., Räisänen, P., and Järvinen, H.: Cloud base vertical velocity statistics: a comparison between an atmospheric mesoscale model and remote sensing observations, Atmos. Chem. Phys., 11, 9207–9218, https://doi.org/10.5194/acp-11-9207-2011, 2011. a
Torres, O., Bhartia, P., Herman, J., Ahmad, Z., and Gleason, J.: Derivation of aerosol properties from satellite measurements of backscattered ultraviolet radiation: Theoretical basis, J. Geophys. Res., 103, 17099–17110, 1998. a
Twomey, S.: The nuclei of natural cloud formation part II: The supersaturation in natural clouds and the variation of cloud droplet concentration, Geofisica Pura e Applicata, 43, 243–249, https://doi.org/10.1007/BF01993560, 1959. a, b
Twomey, S.: Pollution and the planetary albedo, Atmos. Environ., 8, 1251–1256, https://doi.org/10.1016/0004-6981(74)90004-3, 1974. a
Twomey, S. and Warner, J.: Comparison of measurements of cloud droplets and cloud nuclei, J. Atmos. Sci., 24, 702–703, https://doi.org/10.1175/1520-0469(1967)024<0702:COMOCD>2.0.CO;2, 1967. a
vanZanten, M. C., Stevens, B., Nuijens, L., Siebesma, A. P., Ackerman, A. S., Burnet, F., Cheng, A., Couvreux, F., Jiang, H., Khairoutdinov, M., Kogan, Y., Lewellen, D. C., Mechem, D., Nakamura, K., Noda, A., Shipway, B. J., Slawinska, J., Wang, S., and Wyszogrodzki, A.: Controls on precipitation and cloudiness in simulations of trade-wind cumulus as observed during RICO, J. Adv. Model. Earth Sy., 3, M06001, https://doi.org/10.1029/2011MS000056, 2011. a
Wang, H. and Feingold, G.: Modeling Mesoscale Cellular Structures and Drizzle in Marine Stratocumulus. Part II: The Microphysics and Dynamics of the Boundary Region between Open and Closed Cells, J. Atmos. Sci., 66, 3257–3275, 2009. a
Wang, H., Rasch, P. J., and Feingold, G.: Manipulating marine stratocumulus cloud amount and albedo: a process-modelling study of aerosol-cloud-precipitation interactions in response to injection of cloud condensation nuclei, Atmos. Chem. Phys., 11, 4237–4249, https://doi.org/10.5194/acp-11-4237-2011, 2011. a
Wang, S., Wang, Q., and Feingold, G.: Turbulence, Condensation, and Liquid Water Transport in Numerically Simulated Nonprecipitating Stratocumulus Clouds, J. Atmos. Sci., 60, 262–278, https://doi.org/10.1175/1520-0469(2003)060<0262:TCALWT>2.0.CO;2, 2003. a
Watson-Parris, D., Schutgens, N., Winker, D., Burton, S. P., Ferrare, R. A., and Stier, P.: On the Limits of CALIOP for Constraining Modeled Free Tropospheric Aerosol, Geophys. Res. Lett., 45, 9260–9266, https://doi.org/10.1029/2018GL078195, 2018. a
Werdell, P. J., Behrenfeld, M. J., Bontempi, P. S., Boss, E., Cairns, B., Davis, G. T., Franz, B. A., Gliese, U. B., Gorman, E. T., Hasekamp, O., Knobelspiesse, K. D., Mannino, A., Martins, J. V., McClain, C. R., Meister, G., and Remer, L. A.: The Plankton, Aerosol, Cloud, Ocean Ecosystem Mission: Status, Science, Advances, B. Am. Meteorol. Soc., 100, 1775–1794, https://doi.org/10.1175/BAMS-D-18-0056.1, 2019. a
Werner, F., Ditas, F., Siebert, H., Simmel, M., Wehner, B., Pilewskie, P., Schmeissner, T., Shaw, R. A., Hartmann, S., Wex, H., Roberts, G. C., and Wendisch, M.: Twomey effect observed from collocated microphysical and remote sensing measurements over shallow cumulus, J. Geophys. Res.-Atmos., 119, 1534–1545, https://doi.org/10.1002/2013JD020131, 2014. a
Winker, D. M., Vaughan, M. A., Omar, A., Hu, Y. X., Powell, K. A., Liu, Z. Y., Hunt, W. H., and Young, S. A.: Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms, J. Atmos. Ocean. Tech., 26, 2310–2323, https://doi.org/10.1175/2009jtecha1281.1, 2009. a
Wolf, K., Ehrlich, A., Jacob, M., Crewell, S., Wirth, M., and Wendisch, M.: Improvement of airborne retrievals of cloud droplet number concentration of trade wind cumulus using a synergetic approach, Atmos. Meas. Tech., 12, 1635–1658, https://doi.org/10.5194/amt-12-1635-2019, 2019. a
Wood, R.: Rate of loss of cloud droplets by coalescence in warm clouds, J. Geophys. Res., 111, D21205, https://doi.org/10.1029/2006JD007553, 2006. a
Wood, R., Bretherton, C. S., Leon, D., Clarke, A. D., Zuidema, P., Allen, G., and Coe, H.: An aircraft case study of the spatial transition from closed to open mesoscale cellular convection over the Southeast Pacific, Atmos. Chem. Phys., 11, 2341–2370, https://doi.org/10.5194/acp-11-2341-2011, 2011. a
Wu, C. and Yu, J. Z.: Evaluation of linear regression techniques for atmospheric applications: the importance of appropriate weighting, Atmos. Meas. Tech., 11, 1233–1250, https://doi.org/10.5194/amt-11-1233-2018, 2018. a
Wu, L., Hasekamp, O., van Diedenhoven, B., Cairns, B., Yorks, J. E., and Chowdhary, J.: Passive remote sensing of aerosol layer height using near‐UV multiangle polarization measurements, Geophys. Res. Lett., 43, 8783–8790, https://doi.org/10.1002/2016GL069848, 2016. a
Xue, H. W. and Feingold, G.: Large-eddy simulations of trade wind cumuli: Investigation of aerosol indirect effects, J. Atmos. Sci., 63, 1605–1622, 2006. a
Xue, H. W., Feingold, G., and Stevens, B.: Aerosol effects on clouds, precipitation, and the organization of shallow cumulus convection, J. Atmos. Sci., 65, 392–406, 2008. a
Yamaguchi, T., Feingold, G., and Kazil, J.: Stratocumulus to Cumulus Transition by Drizzle, J. Adv. Model. Earth Sy., 9, 2333–2349, https://doi.org/10.1002/2017MS001104, 2017. a
Yan, H., Li, Z., Huang, J., Cribb, M., and Liu, J.: Long-term aerosol-mediated changes in cloud radiative forcing of deep clouds at the top and bottom of the atmosphere over the Southern Great Plains, Atmos. Chem. Phys., 14, 7113–7124, https://doi.org/10.5194/acp-14-7113-2014, 2014. a
Zeng, Z.-C., Chen, S., Natraj, V., Le, T., Xu, F., Merrelli, A., Crisp, D., Sander, S. P., and Yung, Y. L.: Constraining the vertical distribution of coastal dust aerosol using OCO-2 O2 A-band measurements, Remote Sens. Environ., 236, 111494, https://doi.org/10.1016/j.rse.2019.111494, 2020. a
Zhang, Z., Werner, F., Cho, H. M., Wind, G., Platnick, S., Ackerman, A. S., Di Girolamo, L., Marshak, A., and Meyer, K.: A framework based on 2-D Taylor expansion for quantifying the impacts of subpixel reflectance variance and covariance on cloud optical thickness and effective radius retrievals based on the bispectral method, J. Geophys. Res.-Atmos., 121, 7007–7025, https://doi.org/10.1002/2016JD024837, 2016. a
Zheng, Y., Rosenfeld, D., and Li, Z.: Satellite inference of thermals and cloud base updraft speeds based on retrieved surface and cloud base temperatures, J. Atmos. Sci., 72, 2411–2428, 2015. a
Zheng, Y., Rosenfeld, D., and Li, Z.: Quantifying cloud base updraft speeds of marine stratocumulus based on cloud top radiative cooling, Geophys. Res. Lett., 43, 11407–11413, https://doi.org/10.1002/2016GL071185, 2016. a
Zhu, Y., Rosenfeld, D., and Li, Z.: Under what conditions can we trust retrieved cloud drop concentrations in broken marine stratocumulus?, J. Geophys. Res.-Atmos., 123, 8754–8767, https://doi.org/10.1029/2017JD028083, 2018. a
The difference in the measured radiance in the ultraviolet spectral range from a purely Rayleigh-scattering atmosphere is also called the UV-AI (Torres et al., 1998), but the UV-AI is different from the AI as used in this review.
- Abstract
- Introduction
- Remote sensing of CCN concentrations
- Remote sensing of cloud droplet concentrations
- Cloud-regime dependence
- Aggregation scale
- Quantification for the regression coefficient
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Remote sensing of CCN concentrations
- Remote sensing of cloud droplet concentrations
- Cloud-regime dependence
- Aggregation scale
- Quantification for the regression coefficient
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References





