Heterogeneous nucleation of water vapor on different types of black carbon particles

The heterogeneous nucleation of water vapor on insoluble particles affects cloud formation, precipitation, the hydrological cycle, and climate. Despite its importance, heterogeneous nucleation remains a poorly understood phenomenon that relies heavily on empirical information for its quantitative description. Here, we examine the heterogeneous nucleation of water vapor on different types of soots as well as cloud drop activation of different types of soots, including both pure black carbon particles and black carbon particles mixed with secondary organic matter. We show that the recently developed adsorption nucleation theory quantitatively predicts the nucleation of water and droplet formation upon particles of the various soot types. A surprising consequence of this new understanding is that, with sufficient adsorption site density, soot particles can activate into cloud droplets – even when completely lacking any soluble material.

1 Introduction

When water vapor becomes supersaturated – i.e., its relative humidity exceeds 100 % – it is in a metastable state and can form liquid water or ice. External surfaces can facilitate the phase transition via a process known as heterogeneous nucleation. Industrial processes (e.g., dropwise condensation), biological systems (e.g., infection strategy of plant pathogens), everyday situations (e.g., fogging of glasses and windshields), and fundamentally important atmospheric phenomena (clouds, frost, and hoar frost) are all driven by the heterogeneous nucleation of water (Pruppacher and Klett, 1997; Franks, 2003).

Despite its ubiquity and importance, the heterogeneous nucleation of water vapor remains poorly understood, even after more than a century of research (Pruppacher and Klett, 1997; Möller, 2008). This poor understanding is expressed by the lack of an established heterogeneous nucleation theory that provides quantitative comprehension of the process, and it translates into large uncertainty regarding the role of aerosol–cloud interactions in the climate system (Seinfeld et al., 2016). All traditional formulations are variants of classical nucleation theory, CNT (Fletcher, 1958), which provide notoriously poor predictions of water drop nucleation (Mahata and Alofs, 1975). Molecular simulations (Lupi et al., 2014) are able to reveal aspects of heterogeneous nucleation phenomena, but they cannot provide a theoretical framework for describing heterogeneous nucleation in atmospheric and climate models on their own – and are impractical for implementation in models themselves.

A shortcoming of CNT is that it does not recognize the existence of any water on surfaces prior to the formation of a macroscopic droplet (Fig. 1a). Another shortcoming is that all of the energetics of interaction between the surface and the nucleating droplet are expressed by one parameter – the contact angle (Fletcher, 1958). In reality, water already adsorbs to the surface under subsaturated conditions (relative humidity below 100 %), which can play a critical role in the nucleation process. Notably, the energetics of adsorbed water differs considerably from what is implied by the single value provided by the contact angle. In fact, the heat of adsorption changes with increasing adsorption layer thickness (Hill, 1949a). Therefore, not describing the process of water adsorption omits important physics that may hinder a quantitative description of heterogeneous nucleation. Unlike CNT, the adsorption nucleation theory, ANT (Laaksonen, 2015; Laaksonen and Malila, 2016), accounts for water adsorption prior to the onset of heterogeneous nucleation (Fig. 1a, b).

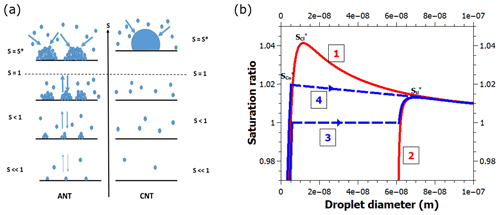
Figure 1 (a) A schematic showing the principal differences between ANT and CNT. ANT is based on the premise that vapor molecules are already adsorbed on the surface at subsaturation, and the molecular nature of adsorption is reflected in the values of the FHH parameters A and B that are obtained from experimental adsorption equilibria. The premise of CNT is that liquid droplets appear on the surface once the vapor becomes supersaturated. When experimental contact angles are used, CNT predicts higher critical supersaturations S^* (at which unlimited condensation starts) than ANT. In practice, the contact angle used for CNT is an adjustable parameter to fit experiments, whereas for ANT it is the bulk (observed) value, adjusted owing to the interaction of adsorbed water molecules on the surface. (b) Schematic Köhler-type curves for various heterogeneous nucleation pathways of water on a 60 nm spherical particle. Curve 1 depicts the saturation ratio as a function of the diameter of individual droplets with a contact angle of 30^∘. Nucleation takes place at the maximum of the curve. Curve 2 is the Köhler curve for the FHH activation mechanism, corresponding to a contact angle of 0^∘. Curve 3 corresponds to a situation where the droplets fill the surface of the solid particle just below S=1 and coalesce to form a uniform liquid film, which then grows along curve 2 until nucleation occurs at the maximum. Curve 4 is similar to curve 3, but the droplets fill the surface at S=1.02 and nucleation occurs instantaneously because the saturation ratio is higher than the maximum of curve 2. Note that the blue curves have been slightly offset along the x axis for clarity.

Soot particles formed in combustion processes often contain sufficient amounts of water-soluble impurities so that their cloud condensation nuclei (CCN) activity can be described using κ-Köhler theory (Petters and Kreidenweis, 2007), provided that the κ value is known. An exception is the major fraction of soot particles produced by aircraft engines, which contain only small amounts of impurities and are rather hydrophobic (Demirdjian et al., 2007). As those particles may participate in contrail or cirrus ice formation (Ikhenaze et al., 2020), either directly after emission or at some later point in time, it is important to be able to characterize their water uptake and nucleation properties theoretically as well as possible.

Water-insoluble atmospheric particles often have rough surfaces characterized by cavities that display physical and chemical heterogeneity. This means that nucleation is not equally likely for all locations on the surface, which is another challenge for CNT. Here, we show that when both adsorption and appropriate geometric considerations are included in the theoretical description of water nucleation, a quantitative theory of heterogeneous nucleation of water on aerosol is established. We demonstrate the new framework for different types of black carbon (BC) particles, which have long been known to be climate active – but with large uncertainty on their impact on direct radiative forcing and on their cloud formation ability and lifetime.

2 Theoretical framework

Using atomic force microscopy (Cao et al., 2011), it has been shown that adsorbed water exists as discrete “patches” (droplets) of liquid water, rather than a uniform film, on non-wettable surfaces. These patches then grow with increasing relative humidity (RH). Unless they fill the surface and coalesce to form a film, the growth continues past 100 % RH into the supersaturated regime (Rowley and Innes, 1942), owing to the Kelvin effect, which causes the equilibrium vapor pressure to increase over curved surfaces. At a characteristic level of supersaturation (the so-called “critical supersaturation”), however, the droplets experience heterogeneous nucleation, where the unconstrained condensation of water vapor ensues to form a water droplet.

To account for the above considerations, we develop a theory that is based on physisorption and captures the progressive accumulation of water, from monolayer “patches” on a surface (at low RH) up to macroscopic amounts of condensed material throughout the adsorption–nucleation transition (at the critical supersaturation). For this, we adopt a multilayer formulation that has minimal coefficients and can be informed by standard adsorption experiments. Our formulation (Laaksonen, 2015; Laaksonen and Malila, 2016; Laaksonen et al., 2016) uses a combination of the Frenkel–Halsey–Hill (FHH) multilayer adsorption theory (Frenkel, 1946; Halsey, 1948; Hill, 1949b) and the Kelvin effect (Defay et al., 1966). We treat the surface as being covered with individual, adsorbed droplets with an average distance s from their nearest neighbors. If the average droplet size and the average distance between them is known, the experimentally observable adsorption layer thickness can be calculated. Surface heterogeneities imply droplets with a distribution of radii and contact angles; however, as a first approximation, we assume that all droplets have the same size and contact angle (these can be considered as average values). The equilibrium condition for a single droplet is given by

$$\begin{array}{}\text{(1)}& \ln \left(S\right)=-{\displaystyle \frac{A}{\stackrel{\mathrm{‾}}{N_{\mathrm{d}}^B}}}+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }{v}_{\mathrm{w}}}{kTR}},\end{array}$$

where S denotes saturation ratio, γ is surface tension, v_w is the volume of a water molecule, k is the Boltzmann constant, T is temperature, R is the droplet radius, and A and B are FHH parameters. The average number of monolayers, $\stackrel{\mathrm{‾}}{N_{\mathrm{d}}}$, over the droplet projection area on the adsorbent surface is given by $\stackrel{\mathrm{‾}}{N_{\mathrm{d}}}=\stackrel{\mathrm{‾}}{\mathit{\delta }}/{\mathit{\delta }}_{\mathrm{m}}$; here, $\stackrel{\mathrm{‾}}{\mathit{\delta }}$ denotes the average water layer thickness, and δ_m is the thickness of a monolayer given as v_w∕σ, where σ is the cross-sectional area of an adsorbed water molecule. $\stackrel{\mathrm{‾}}{N_{\mathrm{d}}}$ and R can be related via a relation that depends on the contact angle θ and the curvature of the adsorbent surface (see Sect. 2.1 for details of the theory). Thus, unlike in CNT, the contact angle is a purely geometric parameter describing the behavior of bulk water on the surface. Molecular simulations have shown that the contact angle of a water nanodroplet on a graphitic surface equals the macroscopic value for droplets with radii larger than about 4 nm (Sergi et al., 2012). For nanodroplets on hydrophilic clays, the contact angle does not vary for droplets containing 256–1000 molecules (Zheng et al., 2017) – which means that any change in the contact angle refers to nanodroplets with radii of the order of 1 nm. The sizes of critical clusters calculated using our theory are typically much larger than that, justifying the use of experimental contact angles in the heterogeneous nucleation calculations. In case of a zero contact angle, water forms a uniform film on the adsorbent surface. If uniform adsorption occurs on spherical particles with radius R_p, the average number of monolayers is $\stackrel{\mathrm{‾}}{N}=(R-R_{\mathrm{p}})/{\mathit{\delta }}_{\mathrm{m}}$ (Sorjamaa and Laaksonen, 2007; Laaksonen and Malila, 2016).

The FHH interaction parameters A and B describe the strength of molecular interaction between the adsorbent and the first adsorption layer, and the exponential decay of the interaction strength as a function of distance, respectively. With the van der Waals model fluid, A and B have well-defined values (note, however, that A depends on the assumed molecular cross section of the adsorbing molecule), but in real systems they must be treated as empirical constants that can be determined from measured adsorption isotherms. In the case of droplet-wise adsorption, the macroscopically determined adsorption layer thickness is a statistical measure that can be related to the droplet size if the average distance between the adsorbed droplets, s, and the contact angle are known. In practice, s can be obtained along with A and B from the adsorption isotherms (Laaksonen, 2015; Laaksonen and Malila, 2016).

We note that there is considerable uncertainty regarding the value of the experimental contact angle, due to contact angle hysteresis (Tadmor, 2004). The difference between the advancing and receding angles can be of the order of 10^∘ or even more. In any case, with graphite the critical supersaturation is surprisingly insensitive to an uncertainty of around $\pm \mathrm{10}{}^{\circ }$ in the value of θ. The reason for this is that the contact angle is included in the equations used when the theory is fitted to adsorption experiments in order to determine the values of the FHH parameters A and B. Thus, if the contact angle is changed by a few degrees, the model has to be refitted to the adsorption data, which can be done by simply changing the value of the A parameter. It turns out that this does not compromise the quality of the fit to the adsorption experiments nor noticeably change the calculated critical supersaturation unless the contact angle is changed by more than about $\pm \mathrm{10}{}^{\circ }$ (see Fig. B3).

Figure 1b shows a schematic picture of the nucleation of water vapor on a spherical particle in our model framework. A single droplet on a BC particle grows along the red curve 1 until it reaches the critical supersaturation $S_{\mathrm{Cl}}^{*}$ and nucleates. However, if there are several similar droplets growing on the particle, and the average distance between them is small enough that they coalesce to form a uniform liquid film at a sufficiently low saturation ratio (blue curve 3), the new equilibrium and the new critical supersaturation $S_{\mathrm{U}}^{*}$ can be calculated by simply using a zero contact angle (red curve 2). Depending on the value of s, it is also possible that the droplet coalescence occurs at some supersaturation $S_{\mathrm{Co}}^{*}$ between $S_{\mathrm{U}}^{*}$ and $S_{\mathrm{Cl}}^{*}$, in which case nucleation is immediate (blue curve 4).

Classical nucleation theory is based on the idea that nucleation is a stochastic phenomenon, whereas ice nucleation theories that assume specific temperature-dependent ice nucleation sites are deterministic. The adsorption nucleation theory is deterministic, as one of its premises is that nucleation occurs on specific adsorption sites, and there is no stochastic element included in the theory. Such an element could be introduced in a similar fashion to the soccer ball model (Niedermeier et al., 2014) – by assuming a distribution of contact angles between the adsorption sites. However, without knowledge of factors such as the possible widths of such distributions, we prefer not to include this idea at present. In the future, we aim to use molecular dynamics to explore this issue with chemically and physically heterogeneous surfaces.

2.1 Adsorption nucleation theory

The starting point of the theory is that adsorbing vapor molecules are assumed to cluster around adsorption sites to form spherical caps of liquid drops with a contact angle θ. The equilibrium condition is given by Eq. (1). The geometry for a spherical seed particle is as shown in Fig. 2. The average over δ^B is given by

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{‾}}{{\mathit{\delta }}^B}={\left[\mathrm{1}-\cos \mathrm{\Phi }\right]}^{-\mathrm{1}}\underset{\mathrm{0}}{\overset{\mathrm{\Phi }}{\int }}{\mathit{\delta }}^B\sin \mathit{\alpha }d\mathit{\alpha }\end{array}$$

with

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }\mathit{\delta }=-R_{\mathrm{p}}+R\cos \mathit{\beta }+\sqrt{{\left(R\cos \mathit{\beta }\right)}^{\mathrm{2}}-R^{\mathrm{2}}+d^{\mathrm{2}}}\text{(4)}& {\displaystyle }& {\displaystyle }d=\sqrt{R_{\mathrm{p}}^{\mathrm{2}}+R^{\mathrm{2}}-\mathrm{2}{R}_{\mathrm{p}}R\cos \mathit{\theta }}\text{(5)}& {\displaystyle }& {\displaystyle }\cos \mathrm{\Phi }=\left(R_{\mathrm{p}}-R\cos \mathit{\theta }\right)/d\text{(6)}& {\displaystyle }& {\displaystyle }\cos \mathit{\beta }=\left(R_{\mathrm{p}}+\mathit{\delta }-d\cos \mathit{\alpha }\right)/R\end{array}$$

S can now be computed as a function of R using Eq. (1) with $\stackrel{\mathrm{‾}}{N_{\mathrm{d}}^B}=\stackrel{\mathrm{‾}}{{\mathit{\delta }}^B}/{\mathit{\delta }}_{\mathrm{m}}^B$ evaluated numerically from Eqs. (2)–(6). The resulting curve shows a maximum at the critical supersaturation S^* (and critical radius R^*), marking the onset of heterogeneous nucleation.

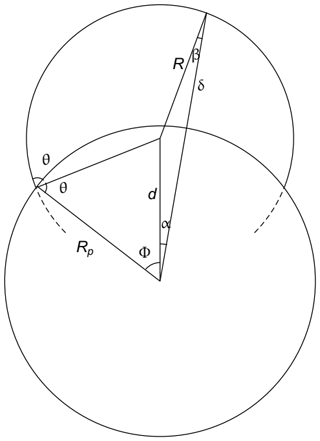
Figure 2 The geometry used in deriving equations for the nucleation of a spherical drop on a spherical nanoparticle.

The values of the adsorption parameters A and B as well as that of the distance between active sites s can be obtained from measured adsorption isotherms. If a portion of the adsorption data is clearly in the multilayer regime and the data points align linearly when ln (−ln (S)) is plotted vs. ln (N), parameters A and B can be determined by fitting the classical FHH equation $\ln \left(S\right)=-A{N}^B$ to the data (here, N denotes the macroscopically observable surface coverage). If the contact angle is known, the distance between active sites can be obtained from the sub-monolayer part of the adsorption isotherm. To do that, a relation is needed between the size of an individual adsorbed droplet and the macroscopic surface coverage. Making the approximation $\stackrel{\mathrm{‾}}{N_{\mathrm{d}}^B}\approx \stackrel{\mathrm{‾}}{N_{\mathrm{d}}^B}$, Eq. (1) can be translated into

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }\ln \left(S\right)=-A{\left[{\displaystyle \frac{\mathit{\pi }{\mathit{\zeta }}^{\mathrm{2}}}{{\mathit{\eta }}^{\mathrm{2}}N}}\right]}^{B/\mathrm{3}}+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }}{\mathrm{3}kT}}{\left[{\displaystyle \frac{\mathit{\pi }\mathit{\eta }{\mathit{\zeta }}^{\mathrm{2}}}{N}}\right]}^{\mathrm{1}/\mathrm{3}},\mathit{\theta }\le \mathrm{90}{}^{\circ },\text{(8)}& {\displaystyle }& {\displaystyle }\ln \left(S\right)=-A{\left({\displaystyle \frac{\mathit{\eta }}{\mathit{\beta }}}\right)}^B{\left[{\displaystyle \frac{\mathit{\pi }g\left(\mathit{\theta }\right)}{\mathrm{3}{s}^{\mathrm{2}}N}}\right]}^{\frac{B}{\mathrm{3}}}+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }\mathit{\nu }}{\mathrm{3}kT}}{\left[{\displaystyle \frac{\mathit{\pi }g\left(\mathit{\theta }\right)}{\mathrm{3}{s}^{\mathrm{2}}N}}\right]}^{\frac{\mathrm{1}}{\mathrm{3}}},\mathit{\theta }>\mathrm{90}{}^{\circ },\end{array}$$

with $\mathit{\zeta }=\mathrm{3}\mathit{\nu }\sin \mathit{\theta }/s$, η=σf(θ), $g\left(\mathit{\theta }\right)=\mathrm{4}-{\left(\mathrm{1}+\cos \mathit{\theta }\right)}^{\mathrm{2}}\left(\mathrm{2}-\cos \mathit{\theta }\right)$, and $f\left(\mathit{\theta }\right)=\frac{{\left(\mathrm{1}-\cos \mathit{\theta }\right)}^{\mathrm{2}}\left(\mathrm{2}+\cos \mathit{\theta }\right)}{{\sin }^{\mathrm{2}}\mathit{\theta }}$, $\mathit{\theta }\le \mathrm{90}{}^{\circ }$; $f\left(\mathit{\theta }\right)=\mathrm{2}-\mathrm{3}\cos \mathit{\theta }$, $\mathit{\theta }>\mathrm{90}{}^{\circ }$.

The distance between adsorption sites s can now be determined by fitting Eq. (7) or Eq. (8) to the sub-monolayer data. (Note that it is best to use the portion of the data just below a monolayer, as the low-coverage data may be affected by pores or other factors not taken into account in the above equations.)

When the adsorbent surface is poorly wettable, the adsorption data may not extend to the multilayer regime at all. In such a case, all of the parameters need to be obtained from a best fit of either Eq. (7) or Eq. (8) to the data set.

As noted in relation to Fig. 1b, nucleation can also occur due to the coalescence of adsorbed droplets. The criteria we use for the coalescence nucleation are that (i) the projection areas of adsorbed droplets equal the surface area of the seed particle and that (ii) the supersaturation exceeds the critical supersaturation calculated for a seed particle that is perfectly wettable.

2.2 Liquid drop nucleation on insoluble particles mixed with soluble material

If $\mathit{\theta }=\mathrm{0}{}^{\circ }$, i.e., the seed particle is completely wettable, the saturation ratio can be written in terms of dry and wet particle radii as follows:

$$\begin{array}{}\text{(9)}& \ln \left(S\right)=-A{\left({\displaystyle \frac{R-R_{\mathrm{p}}}{D_{\mathrm{w}}}}\right)}^{-B}+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }{v}_{\mathrm{w}}}{kTR}},\end{array}$$

where we have approximated monolayer thickness with the diameter of a water molecule, D_w (Laaksonen and Malila, 2016). For a partially soluble seed particle – for example, a black carbon particle coated with low-volatility organic or inorganic substances after atmospheric processing – Eq. (9) needs to be further modified to take the hygroscopicity of solution into account. The following equation (Kumar et al., 2011) can be written in terms of the hygroscopicity parameter κ (Petters and Kreidenweis, 2007):

$$\begin{array}{}\text{(10)}& \ln \left(S\right)=-A{\left({\displaystyle \frac{R-R_{\mathrm{p}}}{D_{\mathrm{w}}}}\right)}^{-B}-{\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{s}}{R}_{\mathrm{p}}^{\mathrm{3}}\mathit{\kappa }}{\left(R^{\mathrm{3}}-{\mathit{\epsilon }}_{\mathrm{i}}{R}_{\mathrm{p}}^{\mathrm{3}}\right)}}+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }{v}_{\mathrm{w}}}{kTR}},\end{array}$$

where ε_s and ε_i are the volume fractions of soluble and insoluble species in the seed particles, respectively.

3 Results and discussion

3.1 Constraining water adsorption parameters on carbon

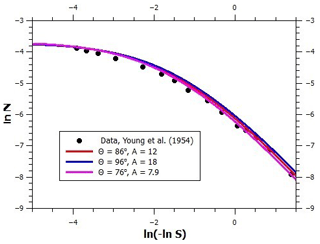
We now focus on the determination of water vapor adsorption parameters on graphite and on black carbon (BC) particles. Figure 2 shows a logarithmic FHH plot of several adsorption isotherms. The logarithm of the number of monolayers is shown as a function of ln (−ln S) because, according to the FHH adsorption model, the multilayer adsorption data should align linearly in such a plot (note that saturation ratio decreases from left to right). Starting from the bottom, the lowermost measurement data set (Young et al., 1954) shows adsorption on graphitized carbon black treated at 400 ^∘C for 12 h prior to the measurements. Based on the minute amounts of water adsorbed at even the highest relative humidity and information obtained from heat of immersion measurements, Young et al. (1954) suggested that clusters of water adsorb at hydrophilic surface sites which are far apart and may arise from surface oxides formed at the edge atoms of graphite, which has since been corroborated by quantum chemical calculations (Oubal et al., 2010). This description is in complete agreement with the droplet-wise FHH adsorption model (see the lowermost solid line in Fig. 3 where the model reproduces the data). The model parameters are shown in Fig. 3; the contact angle value was obtained from Fowkes and Harkins (1940), and the parameters A, B, and s were determined by optimizing the model fit to the experimental data.

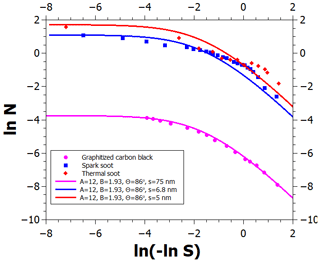
Figure 3 An FHH plot of experimental (markers) and modeled (lines) adsorption isotherms of water vapor on graphite and different soots. Note that increasing supersaturation is to the left on the abscissa. See text for details.

When BC is exposed to atmospheric conditions, the number of hydrophilic surface sites is expected to increase with time as different contaminants adsorb on the carbon and may undergo oxidation (Tritscher et al., 2011; Aria et al., 2016; Grimonprez et al., 2018; Friebel and Mensah, 2019). Contaminants may also be present due to imperfect combustion if the carbon was produced by burning. This suggests that adsorption isotherms of BC containing impurities can be accounted for by increasing the density of the adsorption sites in the FHH model (without changing the other adsorption parameters), which can be constrained by observations.

The data in the upper part of Fig. 3 (Kuznetsov et al., 2003; Popovicheva, 2008) show water adsorption on spark discharge soot as well as thermal soot produced by natural gas pyrolysis. The materials were not treated at high temperature prior to the adsorption measurements and are, thus, likely to contain more adsorption sites from surface contaminants than the graphitized carbon black used by Young et al. (1954). The blue and red solid curves represent the corresponding adsorption isotherms, which were obtained by simply reducing the average distance of adsorption sites in the FHH model from 75 to 6.8 and 5 nm, respectively, and keeping the other parameters at the graphitized carbon black values. The data for RH>80 % $\left(\ln \right(-\ln \left(S\right))<-\mathrm{1.5})$ agree well with the theoretical curves, whereas the data show more adsorption than the model at lower relative humidities. The latter is caused by the effects of soot porosity, which is indicated by a hysteresis between the measured adsorption and desorption curves.

When the density of hydrophilic adsorption sites is sufficiently high, the growing water clusters will start coalescing as the RH increases above some threshold value, and a liquid film will be formed on the BC surface. If the film formation occurs at an RH below 100 %, the conditions for the activation of a BC particle into a cloud droplet (where the particle is said to act as a CCN) can be described using a zero contact angle and the total surface area of the particle, whereas the full adsorption nucleation theory with a nonzero contact angle is required when the active site density is low (curve 3 in Fig. 1b). We next examine whether the CCN activation of different types of BC particles can be described with the theoretical framework as constrained above, using model parameters shown in Fig. 3.

3.2 Water nucleation on black carbon particles

Figure 4 depicts CCN activation data for hydrophobic and hydrophilic BC particles. The most hydrophobic particles (Kotzick et al., 1997) were produced using a spark discharger. The particles were only in contact with argon and nitrogen gases prior to the activation measurements (black spheres) and, thus, contained very few adsorption sites. As can be seen, all model curves are below the spark discharger data. However, the model with parameters obtained using the adsorption data for graphitized carbon black (Fig. 3) is in excellent agreement with the CCN activation data for spark discharger particles that were subjected to ozonolysis prior to the activation measurement (Kotzick et al., 1997) (red squares) and, therefore, have an increased density of adsorption sites.

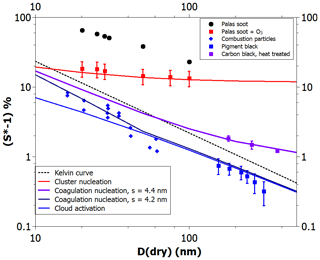
Figure 4 Experimental (markers) and theoretical (lines) critical supersaturations as a function of particle size for the cloud drop activation of hydrophobic and hydrophilic soot particles. See text for details.

Palas soot consists of agglomerates of primary soot spherules with a diameter of the order of 5–10 nm (Gysel et al., 2012). There is a possibility that the heterogeneous nucleation measurements would be explained by the nucleation of capillary-condensed pendular water rings formed around the contact points of primary spherules. Such pendular rings would not be formed much below 100 % RH, as the contact angle is close to 90^∘; thus, in practice, the meniscus cannot be concave. Crouzel and Marlow (1995) modeled water ring nucleation assuming spheres of equal size that are in contact. For a contact angle of 85^∘, they calculated that the critical supersaturation is about 2 % for 400 nm diameter spheres, about 4 % for 200 nm particles, and about 8 % for 100 nm particles. The size dependence is so strong that it is unlikely that the nucleation would take place at significantly lower supersaturation with 5–10 nm spheres than we have calculated for Fig. 4 (red line).

The blue diamonds in Fig. 4 show the activation of soot particles produced by burning camp stove fuel (white gas; Hagen et al., 1989). Such particles can be expected to contain a large amount of oxidized species on their surfaces and may, therefore, already have a liquid film of water at activation. The blue curve shows the model prediction with the same FHH parameters A and B as the red curve but with a zero contact angle. It appears that the model has somewhat gentler size dependence than the rather scattered data, but otherwise the agreement is quite satisfactory. The CCN activation of pigment black particles (Dalirian et al., 2018) also matches the theoretical line within uncertainty limits (with the exception of the largest particle size, which has an uncertainty range just below the theoretical line).

Very interestingly, the three data points of Dusek et al. (2006) are clearly above those of Dalirian et al. (2018). The principal difference between the soots used in these two studies is that Dusek et al. (2006) applied heat treatment, thereby very likely reducing the adsorption site density. Indeed, a theoretical line calculated with an average adsorption site distance of 4.4 nm and assuming that coagulation nucleation occurs matches the data perfectly. When a site distance of just 0.2 nm less is assumed, the theoretical prediction becomes equal to the CCN activation prediction for particles larger than about 50 nm. With smaller particles, the coagulation nucleation appears to match the camp stove gas soot data better than the CCN activation theory. In general, accounting for droplet-wise adsorption and the resulting alternative pathways for heterogeneous nucleation (Fig. 1) allows us to obtain a much improved description of the nucleation of water on BC particles compared with CNT (Kotzick et al., 1997) or ANT not considering initial adsorption on distinct sites (Henson, 2007; Sorjamaa and Laaksonen, 2007).

Further enhancement in BC hydrophilicity, on top of increased adsorption site density due to contaminant oxidation, may occur, e.g., as a result of heterogeneous chemistry leading to a substantial amount of water-soluble material on the BC particles. The red diamonds in Fig. 5 (Wittbom et al., 2014) represent particles aged in a smog chamber prior to the activation measurements and were estimated to contain between 8 % and 91 % by mass of water-soluble substance (the data points were deciphered from Figs. 10 and 11 in Wittbom et al., 2014). The blue crosses were calculated using the theory that describes the combined effect of adsorption and water-soluble material when the volume fraction ε and the hygroscopicity parameter κ of the water-soluble material are known (Kumar et al., 2011; Petters and Kreidenweis, 2007; see Sect. 2.2 for details). The FHH parameters were kept the same as for the pure black carbon particles, and the κ value was assumed to be 0.13 (Wittbom et al., 2014). The model predictions, shown by the blue crosses, are once again in excellent agreement with the data. The theory only provides clear underestimates in three cases, with the worst underestimate occurring at the lowest secondary organic aerosol (SOA) mass fraction of about 0.08, as can be seen in Fig. 5b, while Fig. 5a shows that the experimental point is very close to the Kelvin line. Comparison to Fig. 4 indicates that this data point is compatible with the activation of particles that do not contain water-soluble material.

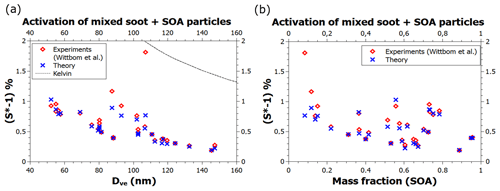
Figure 5 Experimental and theoretical critical supersaturations of water vapor on mixed soot particles containing BC and SOA as a function of (a) the volume equivalent diameter of dry particles and (b) the SOA mass fraction. The data are a subset of the data shown in Figs. 10 and 11 of Wittbom et al. (2014) and were identified by matching supersaturations (to a precision of <0.01 %) in the two figures.

4 Conclusions

In this study, we have shown that ANT can predict the critical supersaturations for heterogeneous nucleation and CCN activation of water vapor on different types of black carbon particles, using a single set of experimental adsorption and contact angle parameters.

It is quite obvious that surface heterogeneities cause adsorbed droplets to have a range of radii and contact angles; however, to make the theory usable, we assume that we can resort to average values. This applies to the FHH parameters A and B as well; it is likely that there would be variability if isolated surface regions were examined. However, the variability of the heterogeneities – whether chemical or physical – is reflected in the values of the “average” adsorption parameters obtained from macroscopic adsorption isotherms. Our hypothesis is that the same parameters can be made use of when extending the theory to the supersaturated regime to predict critical supersaturations. The good match between our theoretical predictions and the experimental critical supersaturations provides a clear indication that our hypothesis is well supported. This also implies that the heterogeneities occur at a spatial scale smaller than the surface area covered by the critical nuclei.

Our findings concerning adsorption nucleation on BC have a direct relevance for climate studies, as even the sign of the radiative forcing due to BC aerosol–cloud interactions remains uncertain (Bond et al., 2013). Notably, the atmospheric lifetime of BC particles is regulated by the condensation of water and subsequent cloud processes, which contribute further to the uncertainty of the total radiative forcing (Samseth et al., 2018).

Appendix A: Water properties used in the calculations

T denotes absolute temperature (K), T^′ is temperature ( ^∘C), and R_g is the molar gas constant.

The equilibrium vapor pressure of liquid water (Pa) is calculated as follows (Murphy and Koop, 2005):

$$\begin{array}{rl}{p}_{\mathrm{w}}=& \exp \mathit{\{}\mathrm{54.842763}-\mathrm{6763.22}/T-\mathrm{4.21}\ln (T)+\mathrm{0.000367}T\\ & +\tanh \left[\mathrm{0.0415}\right(T-\mathrm{218.8}\left)\right][\mathrm{53.878}-\mathrm{1331.22}/T\\ & -\mathrm{9.44523}\ln \left(T\right)+\mathrm{0.014025}T\left]\mathit{\right\}}\end{array}$$

The density of liquid water (g cm⁻³) is calculated as follows (Marcolli, 2017):

$$\begin{array}{rl}{\mathit{\rho }}_{\mathrm{w}}=& \mathrm{1.8643535}-\mathrm{0.0725821489}T+\mathrm{2.5194368}\times {\mathrm{10}}^{-\mathrm{3}}{T}^{\mathrm{2}}\\ & -\mathrm{4.9000203}\times {\mathrm{10}}^{-\mathrm{5}}{T}^{\mathrm{3}}+\mathrm{5.860253}\times {\mathrm{10}}^{-\mathrm{7}}{T}^{\mathrm{4}}\\ & -\mathrm{4.5055151}\times {\mathrm{10}}^{-\mathrm{9}}{T}^{\mathrm{5}}+\mathrm{2.2616353}\times {\mathrm{10}}^{-\mathrm{11}}{T}^{\mathrm{6}}\\ & -\mathrm{7.3484974}\times {\mathrm{10}}^{-\mathrm{14}}{T}^{\mathrm{7}}+\mathrm{1.4862784}\times {\mathrm{10}}^{-\mathrm{16}}{T}^{\mathrm{8}}\\ & -\mathrm{1.6984748}\times {\mathrm{10}}^{-\mathrm{19}}{T}^{\mathrm{9}}+\mathrm{8.3699379}\times {\mathrm{10}}^{-\mathrm{23}}{T}^{\mathrm{10}}\end{array}$$

The surface tension of water (N m⁻¹) is calculated as follows (Hrubý et al., 2014):

$$\begin{array}{rl}{\mathit{\gamma }}_{\mathrm{w}}=& \mathrm{0.2358}{\left(\mathrm{1}-T/\mathrm{647.096}\right)}^{\mathrm{1.256}}\\ & \left[\mathrm{1}-\mathrm{0.625}\left(\mathrm{1}-T/\mathrm{647.096}\right)\right]\end{array}$$

Appendix B: Sensitivity analysis

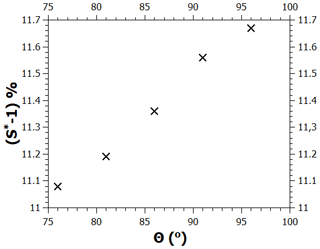
The contact angle value used in the calculations shown above is 86^∘; here, we examine how much the critical supersaturation is affected by changing the contact angle by up to $\pm \mathrm{10}{}^{\circ }$. As noted in the main text, when the contact angle is given a new value, the model needs to be refitted to the adsorption data by changing the value of the FHH parameter A. Figure B1 shows the values of A as a function of the contact angle in the range between 76 and 96^∘ when this is done (the values of the parameters B and s were kept at 1.93 and 75 nm, respectively). Figure B2 shows the experimental adsorption data and the model for $(\mathit{\theta },A)=(\mathrm{76}{}^{\circ },\mathrm{7.9})$, (86^∘, 12), and (96^∘, 18). As can be seen, all curves fit the data well, although there is some deviation at low saturation ratios. Figure B3 shows the calculated critical supersaturations for water nucleation. The dry particle diameter (100 nm) was chosen based on the experimental nucleation data of Kotzick et al. (1997). A change in the contact angle of 20^∘ (and the simultaneous change of the A parameter as shown in Fig. B1) causes a change of less than 0.7 % in the critical supersaturation. This is much less than the experimental uncertainty of the critical supersaturations of ozonized Palas soot particles (Fig. 4).

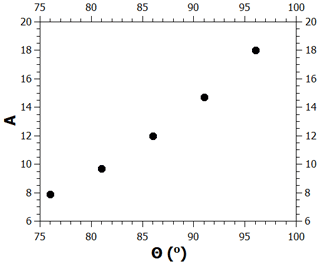
Figure B1 Pairs of contact angle and FHH parameter A values that produce good model fits to the adsorption data.

Figure B2 Model fits to adsorption data for three pairs of θ and A.

Figure B3 Critical supersaturations in water nucleation as a function of contact angle. The A-parameter values used in the calculations are as shown in Fig. B1. The nucleation temperature is +25 ^∘C, and the dry particle diameter is 100 nm.