Reaction between CH₃C(O)OOH (peracetic acid) and OH in the gas phase: a combined experimental and theoretical study of the kinetics and mechanism

Peracetic acid (CH₃C(O)OOH) is one of the most abundant organic peroxides in the atmosphere; yet the kinetics of its reaction with OH, believed to be the major sink, have only been studied once experimentally. In this work we combine a pulsed-laser photolysis kinetic study of the title reaction with theoretical calculations of the rate coefficient and mechanism. We demonstrate that the rate coefficient is orders of magnitude lower than previously determined, with an experimentally derived upper limit of $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹. The relatively low rate coefficient is in good agreement with the theoretical result of $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ at 298 K, increasing to $\sim \mathrm{6}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ in the cold upper troposphere but with associated uncertainty of a factor of 2. The reaction proceeds mainly via abstraction of the peroxidic hydrogen via a relatively weakly bonded and short-lived prereaction complex, in which H abstraction occurs only slowly due to a high barrier and low tunnelling probabilities. Our results imply that the lifetime of CH₃C(O)OOH with respect to OH-initiated degradation in the atmosphere is of the order of 1 year (not days as previously believed) and that its major sink in the free and upper troposphere is likely to be photolysis, with deposition important in the boundary layer.

1 Introduction

The processes leading to the formation and loss of two classes of atmospheric trace gases, organic acids and organic peroxides, have been the subject of numerous field, laboratory and model-based investigations (Atkinson et al., 2006; Calvert et al., 2011; Gunz and Hoffmann, 1990; Jackson and Hewitt, 1999; Lee et al., 2000; Paulot et al., 2011; Reeves and Penkett, 2003). By comparison, ambient measurements of the acidic peroxide, peracetic acid (CH₃C(O)OOH), in the gas phase are still relatively scarce. Measurements in the boundary layer (Crowley et al., 2018; Fels and Junkermann, 1994; He et al., 2010; Liang et al., 2013; Phillips et al., 2013; Walker et al., 2006; Zhang et al., 2010) and from aircraft (Crounse et al., 2006; Wang et al., 2019) indicate that it is present throughout the troposphere, where it is observed to be the second most abundant organic peroxide (after CH₃OOH). Like other organic peroxides, CH₃C(O)OOH can contribute to the formation and ageing of secondary organic aerosol (Docherty et al., 2005), which enhances its removal through wet deposition.

Unlike its non-peroxidic analogue, CH₃C(O)OH (acetic acid), the direct emission of CH₃C(O)OOH by the biosphere has not been documented, and its formation during biomass burning has not been reported (Andreae, 2019), although elevated CH₃C(O)OOH mixing ratios have been observed in air masses impacted by biomass burning (Crowley et al., 2018; Phillips et al., 2013). Apart from leakage during industrial production and application as an indoor disinfectant (Henneken et al., 2006; Pacenti et al., 2010), the only significant source of CH₃C(O)OOH in the atmosphere is the radical terminating channel (Reaction R1a) in the reaction between the acetylperoxy and hydroperoxyl radicals.

$$\begin{array}{}\text{(R1a)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}+{\mathrm{HO}}_{\mathrm{2}}& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{O}}_{\mathrm{2}}\text{(R1b)}& {\displaystyle }& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+{\mathrm{O}}_{\mathrm{3}}\text{(R1c)}& {\displaystyle }& {\displaystyle }\to \mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{CO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}\end{array}$$

The CH₃C(O)O₂ radical is formed in the degradation of acetaldehyde (mainly via reaction with OH), acetone and methylglyoxal (both via photolysis), all of which are common secondary products of the degradation of biogenic and anthropogenic volatile organic compounds (VOCs) including isoprene, monoterpenes, alkenes and alkanes. Globally, biogenic emissions account for >60 % of CH₃C(O)O₂ formation (Fischer et al., 2014).

The highest production rates of CH₃C(O)OOH are thus expected in regions which are impacted by biogenic emissions in which HO₂ levels are high enough to compete with NO₂ (Reaction R2) and NO (Reaction R3) for reaction with CH₃C(O)O₂:

$$\begin{array}{}\text{(R2)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{OONO}}_{\mathrm{2}}+M\text{(R3)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}+\mathrm{NO}\to {\mathrm{CH}}_{\mathrm{3}}{\mathrm{CO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}.\end{array}$$

As CH₃C(O)OONO₂ (peroxyacetyl nitric anhydride, PAN) is thermally unstable with respect to re-dissociation to reactants, high temperatures also favour CH₃C(O)OOH formation.

Laboratory studies, summarized by IUPAC, indicate that the overall rate coefficient (k₁) for Reactions (R1a)–(R1c) (at 298 K) is $(\mathrm{2}\pm \mathrm{1})\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molec.⁻¹ s⁻¹ and that CH₃C(O)OOH is formed with a branching ratio (k_1a∕k₁) of 0.37±0.09 at this temperature. At lower temperatures, such as those found in the upper troposphere, the rate coefficient increases ($k_{\mathrm{1}}\left(\mathrm{240}\mathrm{K}\right)=\mathrm{3.7}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molec.⁻¹ s⁻¹) while the branching ratio to CH₃C(O)OOH decreases: $k_{\mathrm{1}\mathrm{a}}/k_{\mathrm{1}}\left(\mathrm{240}\mathrm{K}\right)=\mathrm{0.31}$ (IUPAC Task Group, 2020).

As for other soluble organic acids and peroxides, deposition will be an important sink for CH₃C(O)OOH in the boundary layer, where (in the absence of measurements) an exchange velocity comparable to that of H₂O₂ (which has a similar solubility; Crowley et al., 2018) may be assumed and which results in a local lifetime of several hours. Further, wet deposition, either by direct dissolution or through particle formation and subsequent scavenging by clouds and rain, additionally reduces its lifetime. In analogy to other peroxides, reaction with OH is believed to be the dominant gas-phase loss process for CH₃C(O)OOH.

$$\begin{array}{}\text{(R4a)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{OH}& {\displaystyle }\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OO}\text{(R4b)}& {\displaystyle }& {\displaystyle }\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}\end{array}$$

The Master Chemical Mechanism (MCM v3.3.1: http://mcm.york.ac.uk/, last access: July 2020) presently uses an overall rate coefficient of $k_{\mathrm{4}}=\mathrm{3.6}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molec.⁻¹ s⁻¹, which is based on reactions of OH with other organic trace gases containing the –OOH group (Orlando and Tyndall, 2003) whereby abstraction of the peroxidic H atom (Reaction R4a), is expected to dominate. A single study of the rate coefficient has been published to date (Wu et al., 2017), in which the authors, deriving a rate coefficient of $\approx \mathrm{1}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molec.⁻¹ s⁻¹ in a relative rate study, confirm the dominance of the OH sink. There are no experimental studies of the branching ratio for the reaction between OH and CH₃C(O)OOH, though a theoretical study indicates that k_4a and k_4b are comparable (Rypkema and Francisco, 2013). Absorption cross-sections of CH₃C(O)OOH in the actinic region (λ>320 nm) are lower than those of, for example, CH₃OOH and H₂O₂ (Burkholder et al., 2015; IUPAC Task Group, 2020; Orlando and Tyndall, 2003), and noontime, mid-latitude photolysis rate coefficients are ≈ 5–7 × 10⁻⁷ s⁻¹. Assuming noontime OH radical densities of 2×10⁶ molec. cm⁻³ and $k_{\mathrm{4}}=\mathrm{3.6}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molec.⁻¹ s⁻¹ results in a first-order loss rate coefficient of $\approx \mathrm{7}\times {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹, which implies that the photolysis of CH₃C(O)OOH is not a significant atmospheric sink compared to the reaction with OH. The relative importance of the various atmospheric loss processes for CH₃C(O)OOH in the light of the present results is discussed in more detail in Sect. 4.6.

Measurements of ambient CH₃C(O)OOH mixing ratios have been used to gain insight into peroxy radical chemistry in the boreal forest during summer (Crowley et al., 2018; Phillips et al., 2013) and also to constrain the atmospheric budget of acetaldehyde, which is an important precursor of CH₃C(O)OOH (Travis et al., 2020; Wang et al., 2019). Such studies require accurate estimates of the lifetime of atmospheric CH₃C(O)OOH and thus the rate coefficient for its reaction with OH. The conclusions reached by Wang et al. (2019) based on aircraft data taken from remote sources of CH₃CHO are valid if CH₃C(O)OOH is much shorter lived than PAN and has a comparable lifetime to CH₃CHO. Likewise, the concentrations of CH₃C(O)OOH modelled by Crowley et al. (2018) are partially dependent on the OH rate coefficient for the title reaction. In addition, the degree to which the formation of CH₃C(O)OOH from the reaction between HO₂ and CH₃C(O)O₂ represents a permanent sink of peroxy radicals (and thus loss of oxidation capacity) depends on whether the photochemical degradation of CH₃C(O)OOH to reform organic radicals can compete with deposition processes.

In the following, we describe the results of laboratory experiments and theoretical calculations that show that CH₃C(O)OOH is much less reactive towards OH than presently believed. We also report rate coefficients (k₅) for the reaction of OD + CH₃C(O)OOH (Reaction R5), which was required to examine the potential role of OH reformation, and rate coefficients (k₆, k₇) for the reaction between both OH and OD with CH₃C(O)OH (Reactions R6, R7), which were required to apply corrections for the presence of CH₃C(O)OH in the CH₃C(O)OOH samples:

$$\begin{array}{}\text{(R5)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{OD}\to \mathrm{products}\text{(R6)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+\mathrm{OH}\to \mathrm{products}\text{(R7)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+\mathrm{OD}\to \mathrm{products}.\end{array}$$

Finally, we examine the site specificity of the H abstraction reaction (Reactions R4a versus R4b).

2 Experimental methods

The laboratory kinetic studies of the title reactions used the method of pulsed laser photolytic (PLP) generation of OH combined with real time detection based on pulsed laser induced fluorescence (LIF). The concentrations of CH₃C(O)OOH and CH₃C(O)OH were measured online using infrared absorption spectroscopy. The set-up is illustrated in Fig. 1.

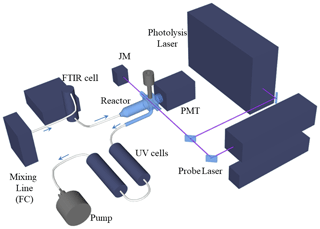
Figure 1 PLP-LIF experimental set-up. PMT is the photomultiplier, JM the joule meter and FC the flow controller. The IR and UV absorption cells are at room temperature. The photolysis laser is an excimer laser (Compex 205 F, 248 nm) and the probe laser a YAG-pumped dye laser (Quantel Brilliant B and Lambda Physik Scanmate, 281.99 and 287.68 nm). The arrows indicate the direction of gas flow.

2.1 PLP-LIF

The details of the experimental set-up have been described in detail previously (Wollenhaupt et al., 2000), and only a brief description of the central features and modifications is given here. The experiments were carried out in a double-jacketed quartz reactor of volume ∼500 cm³, which was held at the desired temperature by circulating a 60 : 40 mixture of ethylene glycol ∕ water through the outer jacket. The pressure in the reactor, generally between ∼50 and 100 Torr N₂, was monitored with 100 and 1000 Torr capacitance manometers (1 Torr = 1.333 HPa). For all experiments, the axial flow velocity in the reactor was kept roughly constant at ∼10 cm s⁻¹ by adjusting the flow rate. As the ∼ 8 mm wide laser beam propagated orthogonally to the direction of flow, this ensured that a fresh gas sample was available for photolysis at each laser pulse. Pulses of 248 nm laser light (∼20 ns) for OH generation from H₂O₂ and CH₃C(O)OOH or OD generation from DONO₂ were provided at 10 Hz by an excimer laser (Compex 205 F, Coherent) operated with KrF.

$$\begin{array}{}\text{(R8)}& {\displaystyle }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+h\mathit{\nu }\to \mathrm{2}\mathrm{OH}\text{(R9)}& {\displaystyle }{\mathrm{DONO}}_{\mathrm{2}}+h\mathit{\nu }\to \mathrm{OD}+{\mathrm{NO}}_{\mathrm{2}}\text{(R10)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+h\mathit{\nu }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{O}+\mathrm{OH}\end{array}$$

The laser fluence (typically ∼15 mJ cm⁻² per pulse) was measured using a calibrated joule meter located behind the exit window of the reactor. Concentrations of the OH precursors, H₂O₂, DONO₂ and CH₃C(O)OOH, were in the range ∼ 2–20 × 10¹³, 4–8 × 10¹⁴ molec. cm⁻³ and ∼ 6–60 × 10¹⁴ molec. cm⁻³, respectively (see Tables S1 and S2 in the Supplement). The initial OH concentrations were calculated using 248 nm cross-sections (units of cm² molec.⁻¹) from Vaghjiani and Ravishankara (1989a) (σ_248 nm(H₂O₂) = $\mathrm{9.3}\times {\mathrm{10}}^{-\mathrm{20}}$), Burkholder et al. (1993) (σ_248 nm(HNO₃) = $\mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{20}}$) and Orlando and Tyndall (2003) (σ_248 nm(CH₃C(O)OOH) = $\mathrm{3.41}\times {\mathrm{10}}^{-\mathrm{20}}$, and were ∼ 2–20 × 10¹¹ molec. cm⁻³.

Radiation for excitation of the OH $A^{\mathrm{2}}\mathrm{\Sigma }(v^{\prime }=\mathrm{1})\leftarrow X^{\mathrm{2}}\mathrm{\Pi }(v^{\prime \prime }=\mathrm{0})$ transition (Q₁₁(1)) at 281.99 nm and OD $A^{\mathrm{2}}\mathrm{\Sigma }(v^{\prime }=\mathrm{1})\leftarrow X^{\mathrm{2}}\mathrm{\Pi }(v^{\prime \prime }=\mathrm{0})$ transition at 287.68 nm was generated by a tuneable (YAG-pumped) dye laser (Quantel Brilliant B and Lambda Physik Scanmate). The fluorescence of OH and OD was detected using a photomultiplier tube screened by a 309 nm interference filter and a BG 26 glass cut-off filter. The fluorescence signal of OH was accumulated using a boxcar integrator triggered at different delay times prior to and after the 248 nm laser to build up a time-dependent concentration profile.

2.2 Online optical absorption measurements

The experiments to determine the rate coefficient of the title reaction were performed under pseudo-first-order conditions (i.e. [acid]₀ ≫ [OH]₀), and the overall uncertainty in the rate coefficients was determined largely by the accuracy with which the concentration of the excess reagent was measured. The concentrations of CH₃C(O)OH and CH₃C(O)OOH were therefore continuously measured upstream of the reactor by flowing the sample through an absorption cell (l=45 cm) made of glass, which was equipped with silicon windows for transmission of infrared (IR) light and a port for pressure measurement (using the same pressure gauges mentioned in Sect. 2.1). With this set-up, absorption features in the range 600–4000 cm⁻¹ were constantly monitored (2 cm⁻¹ resolution, 16 co-added interferograms with 128 scans for the background) using a Fourier-transform infrared (FTIR) spectrometer (Bruker Vector 22) with an external, liquid N₂ cooled HgCdTe detector. A low spectral resolution was chosen to reduce scan times (∼20 s) and enable rapid changes in concentration to be followed. OPUS software was used to analyse and manipulate the IR spectra. Interferograms were phase-corrected (Mertz) and boxcar-apodized with a zero-filling factor of 4. The concentrations of CH₃C(O)OH and CH₃C(O)OOH were calculated using reference spectra obtained in this work (see Sect. 2.2).

A further, in-line optical absorption system was located downstream of the reactor. An absorption cell operated at 184.95 nm (l=43.8 cm, low-pressure Hg lamp screened by a 185 nm interference filter) served to detect H₂O. The VUV absorption optical system is dual-beam so that drifts in light intensity could be accounted for and low optical densities could be measured over extended periods.

2.3 Offline IR spectrum measurements

Reference spectra for CH₃C(O)OOH and CH₃C(O)OH were obtained with the Bruker Vector 22 coupled to two further IR absorption cells. These were a 44.39 L cylindrical quartz chamber equipped with a White-type, multiple-reflection mirror system with an 86.3 m optical path and external (HgCdTe) detector at liquid N₂ temperature (Berasategui et al., 2020; Bunkan et al., 2018) and a 570 mL glass cell with a 15 cm optical path, located in the internal optical path of the FTIR using an internal DTGS detector. The pressure in both absorption cells was monitored using 1000 or 100 Torr capacitance manometers.

2.4 Chemicals

N₂ (Westfalen 99.999 %) was used without further purification. H₂O₂ (AppliChem, 50 wt %) was concentrated to >90 wt % by vacuum distillation. Anhydrous DONO₂ was prepared by partial vacuum distillation of deuterated nitric acid formed by the addition of D₂SO₄ to KNO₃. Liquid CH₃C(O)OH and CH₃C(O)OOH solutions (32 wt % in acetic acid) were used following purification by partial vacuum distillation.

3 Theoretical methods

The potential energy surface of the title reaction was characterized first at the M06-2X/cc-pVDZ level of theory (Dunning, 1989; Zhao and Truhlar, 2008). An exhaustive search for all conformers of reactants, transition states (TSs) and products was performed by systematic variations of the dihedral angles for the degrees of freedom for internal rotation. Likewise, we attempted to find all conformers of the prereaction and post-reaction complexes by positioning the two complexing compounds at a wide variety of relative orientations and optimizing the geometry from each of these starting positions. All geometries were subsequently re-optimized at the M06-2X-D3/aug-cc-pVTZ level of theory (Dunning, 1989; Goerigk et al., 2017; Grimme et al., 2011), improving the description of the long-distance interactions by including diffuse orbitals and dispersion corrections. The energy of the transition state for the abstraction of the peracidic H atom proved to be more dependent on the basis set than expected, changing by ∼4.3 kcal mol⁻¹ as opposed to ∼2 kcal mol⁻¹ for the methyl H abstraction, so to ensure full convergence with respect to the basis set, we re-optimized all structures again at the M06-2X-D3/aug-cc-pVQZ level of theory, confirming basis set convergence at the DFT (density functional theory) level within a few tenths of a kilocalorie per mole (kcal mol⁻¹) and no significant change in the geometries. Zero-point energy (ZPE) corrections are done at this level, with vibrational wavenumbers scaled by 0.971 (Alecu et al., 2010; Bao et al., 2018). Finally, the relative energies were refined using CCSD(T) single-point calculations (Purvis and Bartlett, 1982), extrapolated to the complete basis set using the aug-Schwartz6(DTQ) method by Martin (1996), based on calculations using the aug-cc-pVxZ ($x=D,T,Q$) basis sets. The T₁ diagnostics do not suggest multi-reference character in any of the structures. The strong dependence on the basis set size is assumed to be the main reason for the difference between our barrier heights and those predicted by Rypkema and Francisco (2013) who found submerged transition states incompatible with the experimental data.

The temperature-dependent rate coefficient of the reaction was calculated using multi-conformer canonical transition state theory (Truhlar et al., 1996; Vereecken and Peeters, 2003), including all conformers of reactants and transition states characterized at our highest level of theory. The spin-orbit splitting for OH of 27.95 cm⁻¹ was taken into account (Huber and Herzberg, 1979). Tunnelling was accounted for by asymmetric Eckart barrier corrections based on the reactant, the TS and product energy and the TS imaginary frequency (Eckart, 1930; Johnston and Heicklen, 1962). The rate coefficient is calculated in the high-pressure limit; i.e. the prereaction complex is assumed to be in thermal equilibrium with the reactants. The main impact of the prereaction complex on the kinetics is then to allow additional tunnelling through a wider energy range of the TS barrier for H abstraction. This is discussed in more detail below.

4 Results and discussion

4.1 Infrared absorption cross-sections

Accurate IR absorption cross-sections of CH₃C(O)OH, its dimer and CH₃C(O)OOH are required to derive accurate concentrations of reactants during kinetic experiments on OH + CH₃C(O)OOH in which both acids are unavoidably present because the commercially available sample of CH₃C(O)OOH is a ∼ 32 % solution in CH₃C(O)OH. Note that all IR cross-sections we quote are “base e”.

4.1.1 CH₃C(O)OH and CH₃C(O)OH dimer

In order to obtain the cross-sections of the CH₃C(O)OH monomer, the long-path cell was used in conjunction with low pressures of CH₃C(O)OH to avoid the formation of the dimer. A known pressure of the CH₃C(O)OH sample (in total typically 3–18 Torr) was first measured in a section of the vacuum line (volume 126.6 cm³) and then flushed into the long-path cell in a flow of N₂ until 700 Torr of total pressure was reached. The pressure of CH₃C(O)OH in the long-path cell (volume 44 390 cm³) was calculated from the sum of monomer pressure plus twice the dimer pressure in the vacuum line (both calculated from the total pressure using the 298 K equilibrium coefficient $K_{\mathrm{eq}}=\mathrm{2.5}\pm \mathrm{0.3}$ Torr⁻¹; Crawford et al., 1999) and the dilution factor, which is related to the relative volumes of the mixing line and the long-path cell. The concentration of CH₃C(O)OH in the long-path cell was (1–10) × 10¹⁴ molec. cm⁻³, where the equilibrium dimer concentration can be considered negligible. The CH₃C(O)OH dimer spectrum was measured in the small optical absorption cell (l=15 cm) using up to 1.36 Torr (dosed directly into the cell) of the CH₃C(O)OH ∕ CH₃C(O)OH dimer mixture to favour dimer formation. At the highest total pressure, the ratio of dimer to monomer (calculated using the equilibrium constant listed above) was 1.4.

The CH₃C(O)OH spectrum (Fig. 2) reveals features at 991, 1185, 1279, 1385, 1790 and 3583 cm⁻¹, with only the band at 3583 cm⁻¹ free of overlap with any of the CH₃C(O)OOH or CH₃C(O)OH dimer bands. The spectra obtained for the CH₃C(O)OH and CH₃C(O)OH dimer are in excellent agreement with those available in the literature: at 1117 cm⁻¹ we derive σ(CH₃C(O)OH = $\mathrm{6.0}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molec.⁻¹, which can be compared to σ(CH₃C(O)OH = $\mathrm{5.9}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molec.⁻¹ reported by Crawford et al. (1999). Our value of σ(CH₃C(O)OH dimer) = $\mathrm{1.8}\times {\mathrm{10}}^{-\mathrm{18}}$ cm² molec.⁻¹ at 1295 cm⁻¹ is identical to that reported by Crawford et al. (1999).

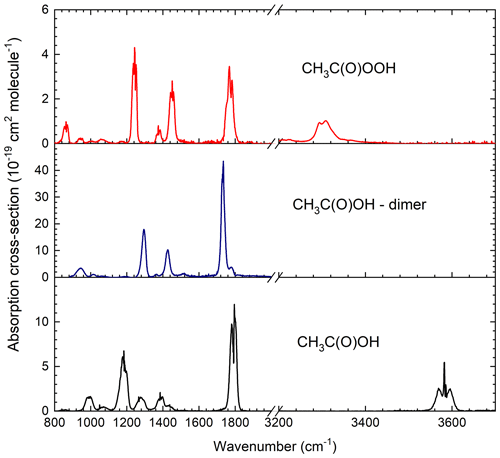
Figure 2 IR absorption cross-sections (base e) obtained in the long-path absorption cell. A comparison of the CH₃C(O)OOH spectrum with the literature is given in Fig. S2.

Beer–Lambert plots for the 3583 cm⁻¹ band of CH₃C(O)OH and the 1734 cm⁻¹ band of CH₃C(O)OH dimer were constructed by expanding different pressures of CH₃C(O)OH into the long-path cell at room temperature and 700 Torr of total pressure. The results, displayed in Fig. S1 in the Supplement, indicate a strictly linear relationship between band intensity and concentration over the range of concentrations investigated.

4.1.2 CH₃C(O)OOH

The liquid sample (32 % (wt) CH₃C(O)OOH in CH₃C(O)OH) is prepared commercially by the oxidation of CH₃C(O)OH using H₂O₂ and is a four-component equilibrium mixture:

$$\begin{array}{}\text{(R11)}& \begin{array}{rl}& {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\left(\mathrm{l}\right)+{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}\left(\mathrm{l}\right)\\ & \rightleftharpoons {\mathrm{H}}_{\mathrm{2}}\mathrm{O}\left(\mathrm{l}\right)+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}\left(\mathrm{l}\right)\end{array}.\end{array}$$

In order to obtain a quantitative IR spectrum of CH₃C(O)OOH, headspace mixtures were dosed into the mixing line, where the total pressure (${\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\text{-dimer}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}$) was recorded before the mixture was flushed into the long-path cell. At the low concentrations of CH₃C(O)OH in the long-path cell, there is no evidence for the CH₃C(O)OH dimer. In the absence of any absorption features of H₂O₂, the IR absorption due to CH₃C(O)OH and H₂O was converted to a vacuum-line pressure of CH₃C(O)OH + CH₃C(O)OH dimer + H₂O and the residual pressure assigned to CH₃C(O)OOH, enabling quantification of the CH₃C(O)OOH spectrum (Fig. 2). As noted by Crawford et al. (1999), there was no evidence for dimerization of CH₃C(O)OOH. These experiments were repeated using the 45 cm path-length absorption cell, which has the disadvantage that significantly higher concentrations of CH₃C(O)OOH are needed to obtain good quality spectra, and the CH₃C(O)OH dimer is therefore also present. However, it provides the advantage of eliminating uncertainty related to the optical path length. Additionally, using this set-up we obtained an accurate IR absorption spectra of H₂O relative to its VUV absorption 185 nm using a cross-section of $\mathrm{7.1}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molec.⁻¹ (Cantrell et al., 1997).

Using both set-ups, we derived a CH₃C(O)OOH cross-section at 1251 cm⁻¹ of $\mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molec.⁻¹, with an uncertainty of 15 %. This analysis neglects the contribution of H₂O₂ to the total headspace pressure. In offline experiments, whereby the headspace was sampled into an enzyme/fluorescence-based instrument for determination of H₂O₂ and organic peroxides (Fischer et al., 2015), we found that H₂O₂ was present at about 1 % of the CH₃C(O)OOH concentration, consistent with the low vapour pressure of H₂O₂ compared to CH₃C(O)OOH.

Our CH₃C(O)OOH absorption cross-sections are much larger (factor 2.1) than those reported by Crawford et al. (1999) whose spectrum has σ(CH₃C(O)OOH) = $\mathrm{1.81}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molec.⁻¹ at 1251.5 cm⁻¹. The only other published IR cross-sections of CH₃C(O)OOH of which we are aware were reported by Orlando et al. (2000b) in which a value of $\mathrm{5.3}\times {\mathrm{10}}^{-\mathrm{19}}$ cm² molec.⁻¹ at 1251 cm⁻¹ is reported (∼40 % larger than our value), which was subsequently confirmed by the same group by comparison with high-performance liquid chromatography (HPLC) measurements (Hasson et al., 2004). Note that both Orlando et al. (2000b) and Hasson et al. (2004) mistakenly listed this cross-section as being at 1295 cm⁻¹ instead of 1251 cm⁻¹, which was confirmed in private communication with the authors (John Orlando and Geoff Tyndall, personal communication, 2020), who kindly provided their spectrum. Our spectrum, that of Orlando et al. (2000b) and one obtained by digitizing Fig. 2 of Crawford et al. (1999) are displayed in Fig. S3.

We do not have an explanation for the divergent values of the IR absorption spectrum of CH₃C(O)OOH but note that this will, in part, be related to working with a multi-component mixture that requires accurate determination of the contributions of the H₂O, CH₃C(O)OH and CH₃C(O)OH dimer. As our experimental result could be reproduced in a series of experiments in two different experimental set-ups, we use our own cross-sections to calculate CH₃C(O)OOH concentrations and consider the use of the larger value when estimating potential uncertainty in our rate coefficients. A Beer–Lambert plot for the 3306 cm⁻¹ band of CH₃C(O)OH (which we used to determine its concentration in kinetic experiments) is displayed in Fig. S1. As for the CH₃C(O)OH and CH₃C(O)OH dimer, the integrated band intensity was strictly proportional to concentration.

4.2 OH/OD + CH₃C(O)OH: determination of k₆ and k₇ at 298 K

We show later (Sect. 4.3) that the reaction of OH with CH₃C(O)OH (Reaction R6) contributes to OH losses in the experiments designed to derive the rate coefficient for the title reaction, and accurate rate coefficients under our experimental conditions are necessary to account for this. We therefore carried out a set of experiments to measure the rate coefficients for the reactions of OH and OD with CH₃C(O)OH. k₆ was determined at a total pressure (N₂) of 57 and 102 Torr; k₇ was examined at 66 Torr (N₂).

In these experiments, OH was generated by the photolysis of H₂O₂ ((0.3–1.8) × 10¹⁴ molec. cm⁻³), and OD was generated by the photolysis of DONO₂ (5×10¹⁴ molec. cm⁻³), both at 248 nm. Initial hydroxyl radical concentrations were [OH]₀ ≈ (1–6) × 10¹¹ and [OD]₀ ≈ 2×10¹¹ molec. cm⁻³. The PLP-LIF studies were thus carried out under pseudo-first-order conditions with [CH₃C(O)OH] ≫ [OH], so that the OH profiles are described by

$$\begin{array}{}\text{(1)}& {\left[\mathrm{OH}\right]}_t={\left[\mathrm{OH}\right]}_{\mathrm{0}}{e}^{-k^{\prime }t},\end{array}$$

where [OH]_t is the concentration (molec. cm⁻³) at time t after the laser pulse, and k^′ is the pseudo-first-order rate coefficient and is defined as

$$\begin{array}{}\text{(2)}& k^{\prime }=k_{\mathrm{6}}\left[{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\right]+k_d,\end{array}$$

where k₆ is the bimolecular rate coefficient (cm³ molec.⁻¹ s⁻¹) for the reaction between OH and CH₃C(O)OH. k_d (s⁻¹) accounts for OH loss due to transport out of the reaction zone and reaction with H₂O₂ or DONO₂. Similar expressions (switch OD for OH and k₇ for k₆) apply to the OD experiments.

Figure 3 displays representative data obtained at 295 K in N₂ bath gas for reaction of OH and OD with CH₃C(O)OH. The OH (OD) decays are strictly exponential, and the plots of k^′ versus [CH₃C(O)OH] (Fig. 4) are straight lines as expected from Eq. (2). This analysis assumes that reaction of OH or OD with the CH₃C(O)OH dimer does not contribute significantly to its loss. In our experiments, the CH₃C(O)OH dimer ∕ CH₃C(O)OH ratio in the reactor varied between 0.04 and 0.32. The strict linearity observed when plotting the first-order loss constant of OH or OD versus [CH₃C(O)OH] is consistent with an insignificant contribution of the CH₃C(O)OH dimer to loss of OH, as also concluded by Singleton et al. (1989).

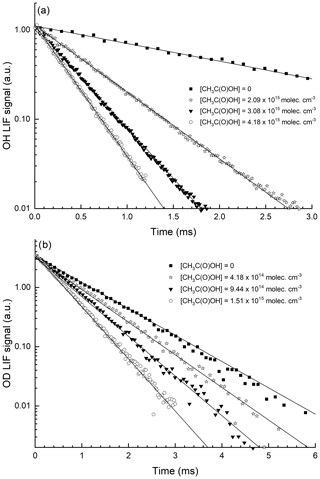
Figure 3 Exponential decay of the OH (a) and OD (b) LIF signals in 150 Torr N₂, at 293 K and at four different CH₃C(O)OH concentrations. OH was generated by the photolysis of H₂O₂, and OD was generated by the photolysis of DNO₃, both at 248 nm. The lines are fits to the datasets using Eq. (1).

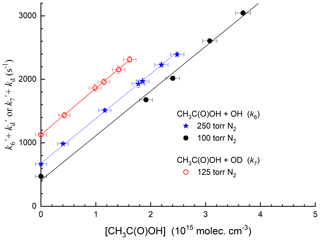
Figure 4 Plots of k^′ versus [CH₃C(O)OH] from the decays of OH and OD at different pressures of N₂ and 295 K. The lines are least-squares fits to the data using Eq. (2). Error bars represent 2σ statistical uncertainty. The different intercepts are due to use of different concentrations of H₂O₂ (OH source) or DONO₂ (OD source).

The values of k₆ and k₇ derived from these datasets typically have a statistical uncertainty (2σ) of less than 5 %, so that the overall uncertainty is dominated by a potential systematic error in the determination of CH₃C(O)OH concentration, i.e. in the in situ measurement of IR absorption by CH₃C(O)OH and its absorption cross-sections. During measurement of OH ∕ OD decay, the CH₃C(O)OH concentration was measured between five and eight times using the 45 cm IR cell located upstream of the reactor and a small correction (∼3 %) for pressure differences between the IR absorption cell and the reactor applied. Typically, [CH₃C(O)OH] varied by <3 % during the time required to measure the OH or OD decay and therefore did not contribute significantly to overall uncertainty.

Experimental details (e.g. identity and concentration of OH precursor and pressure) as well as the values of the rate coefficients k₆ and k₇ at 298 K are presented in Table S1. We obtained values of $k_{\mathrm{6}}=(\mathrm{6.95}\pm \mathrm{0.08})\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molec.⁻¹ s⁻¹ at 100 Torr total pressure and $k_{\mathrm{6}}=(\mathrm{7.04}\pm \mathrm{0.28})\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molec.⁻¹ s⁻¹ at 250 Torr. The result for OH is thus in excellent agreement (2 %) with the 298 K value of $\mathrm{6.9}\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molec.⁻¹ s⁻¹ presently recommended by the IUPAC panel (IUPAC Task Group, 2020). The IUPAC panel recommendation carries an uncertainty of ±25 % (Δlog k=0.1) at 298 K. The very close agreement with our data may indicate that an uncertainty of ±12 % (Δlog k=0.05) is more reasonable, and in the calculations below, we use the IUPAC-recommended expression $k_{\mathrm{4}}=\mathrm{8.40}\times {\mathrm{10}}^{-\mathrm{20}}{T}^{\mathrm{2}}\exp (\mathrm{1356}/T)$ cm³ molec.⁻¹ s⁻¹.

For the reaction between OD and CH₃C(O)OH, we obtain $k_{\mathrm{7}}=(\mathrm{7.3}\pm \mathrm{0.3})\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molec.⁻¹ s⁻¹ at 298 K and a pressure of 125 Torr N₂, i.e. within 5 % of the values obtained for OH. We are unaware of other measurements of this parameter with which to compare our value.

4.3 OH + CH₃C(O)OOH: determination of k₄ (298–353 K)

The experiments to measure k₄ were performed as described in Sect. 4.2 for CH₃C(O)OH with the difference that it was not necessary to add H₂O₂ as an OH precursor, as the photolysis of CH₃C(O)OOH itself provided sufficient OH. The experiments were conducted at a total pressure of ∼100 Torr (N₂).

Taking a 248 nm laser fluence of ∼12 mJ cm⁻² per pulse and a 248 nm cross-section of σ(CH₃C(O)OOH) = $\mathrm{3.4}\times {\mathrm{10}}^{-\mathrm{20}}$ cm² molec.⁻¹ (Orlando and Tyndall, 2003), and assuming unity quantum yield, we calculate that [OH]₀ varied in the range ∼ (3–20) × 10¹¹ molec. cm⁻³ when the CH₃C(O)OOH concentration was varied within the range (6.17–38.5) × 10¹⁴ molec. cm⁻³.

IR absorption due to the CH₃C(O)OOH, CH₃C(O)OH and CH₃C(O)OH dimer was monitored online in the 45 cm absorption cell (at 298 K). The concentrations of the CH₃C(O)OOH, CH₃C(O)OH and CH₃C(O)OH dimer were quantified by the scaling reference spectrum (Sect. 4.1.1 and 4.1.2) of each component to the measured composite spectrum as illustrated in Fig. S3. Typically, the concentrations of CH₃C(O)OH vary between 3×10¹⁴ and 2×10¹⁵ molec. cm⁻³ and those for CH₃C(O)OOH between 6×10¹⁴ and 6×10¹⁵ molec. cm⁻³. When the reactor was operated at high temperatures, some of the CH₃C(O)OH dimer present in the IR absorption cell was converted to CH₃C(O)OH in the reactor, and correction was done to account for this using the temperature-dependent equilibrium constant.

The pseudo-first-order conditions for both [CH₃C(O)OOH] ≫ [OH] and [CH₃C(O)OH] ≫ [OH] are thus guaranteed, and the decay of OH is described by

$$\begin{array}{}\text{(3)}& {\left[\mathrm{OH}\right]}_t={\left[\mathrm{OH}\right]}_{\mathrm{0}}{e}^{-\left(k_{\mathrm{4}}^{\prime }+k_{\mathrm{6}}^{\prime }+k_d\right)t},\end{array}$$

where $k_{\mathrm{6}}^{\prime }$ and $k_{\mathrm{4}}^{\prime }$ are the pseudo-first-order rate coefficients for loss of OH via Reactions (R6) and (R4), respectively.

Typical OH decays (at 298 and 353 K) in the presence of CH₃C(O)OH and CH₃C(O)OOH are displayed in Fig. 5a. As expected, the initial OH concentration varies with [CH₃C(O)OOH], and OH decays are strictly exponential. The contribution of CH₃C(O)OH to the decay of OH can be calculated as k₆[CH₃C(O)OH]. For this purpose, we use the IUPAC-recommended parameterization of k₆, the accuracy of which we have validated at 298 K as described above.

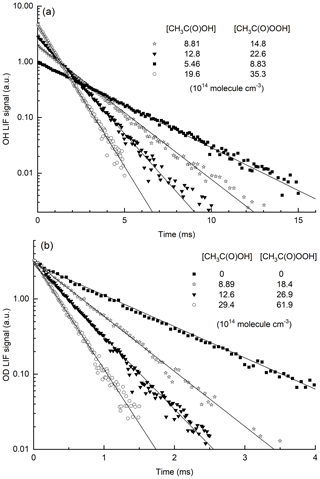
Figure 5 (a) Exponential decay of the OH LIF signal in the presence of CH₃C(O)OOH and CH₃C(O)OH in ≈150 Torr N₂ at 353 K. OH was generated by the photolysis of CH₃C(O)OOH at 248 nm. (b) Exponential decay of the OD LIF signal in the presence of CH₃C(O)OOH and CH₃C(O)OH in N₂ at 298 K. OD was generated from the 248 nm photolysis of DONO₂.

When k₆[CH₃C(O)OH] is subtracted from the total first-order loss rate coefficient, we obtain k₄[CH₃C(O)OOH] + k_d. The rate coefficient k₄ can thus be derived from the slope of plots of k₄[CH₃C(O)OOH] + k_d versus [CH₃C(O)OOH] as illustrated in Fig. 6, which contains the data obtained at all temperatures. A least-squares fit to the entire dataset yields $k_{\mathrm{4}}=(\mathrm{3.25}\pm \mathrm{0.46})\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹, independent of temperature. The complete dataset, listing the experimental conditions and the contribution of CH₃C(O)OH to the total OH decay constant, is found in Table S2. The uncertainty associated with the rate coefficient k₄ (listed in Table S2 and plotted in Fig. 6) considers the statistical error in deriving $k_{\mathrm{6}}^{\prime }$ and $k_{\mathrm{4}}^{\prime }$ as well as the uncertainty in the concentration of CH₃C(O)OH (10 %–15 %) (which is larger at high [CH₃C(O)OH] owing to uncertainty in the dimer : monomer ratio, i.e. in K_eq) and in the rate coefficient k₆ (12 %; see above). It does not consider systematic error [CH₃C(O)OOH], which is discussed below in deriving the final value for k₄ and its total uncertainty.

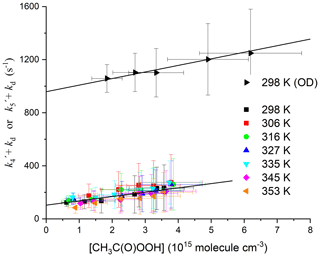
Figure 6 Pseudo-first-order rate coefficient for the loss of OH ($k_{\mathrm{4}}^{\prime }$) or OD ($k_{\mathrm{5}}^{\prime }$) (after subtraction of the contribution of CH₃C(O)OH) versus [CH₃C(O)OOH]. The slopes of the solid black lines are k₄ (lower dataset, with intercept ∼100 s⁻¹) and k₅ (uppermost dataset with intercept ∼900 s⁻¹). The larger intercept for the OD reaction is due to the reaction with DONO₂.

4.4 Potential for systematic error in determining k₄ (298–353 K)

The values we obtain for k₄ are clearly much lower than the one previous relative rate determination of Wu et al. (2017), who report a room temperature rate coefficient of $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{11}}$ cm³ molec.⁻¹ s⁻¹. Below, we examine potential sources of systematic bias in our experiments and analysis.

4.4.1 Uncertainty in the IR cross-sections of CH₃C(O)OOH

The accuracy of rate coefficients measured using the PLP-LIF method under pseudo-first-order conditions depends predominantly on the accuracy of the measurement of the excess reagent, in this case CH₃C(O)OOH. Any systematic error in the IR cross-sections used to calculate [CH₃C(O)OOH] propagates directly into a systematic error in k₄. Although our measurements of the IR cross-sections of CH₃C(O)OOH were in good agreement, irrespective of the absorption cell used, we noted divergence between our value and the values published previously (see Sect. 4.1.2). For this reason, we expand the uncertainty on our cross-sections to ±25 % so that the results agree (within combined experimental uncertainty) with those reported by Orlando et al. (2000a). This implies an additional uncertainty of 25 % for k₄.

4.4.2 Reformation of OH

A possible cause of the low rate coefficient measured in our direct study is the reformation of OH via decomposition of a reaction product, as has been observed (Vaghjiani and Ravishankara, 1989b) in the reaction of OH with another organic peroxide, CH₃OOH (Reactions R12a, R13):

$$\begin{array}{}\text{(R12a)}& {\displaystyle }\mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{OOH}& {\displaystyle }\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{2}}\mathrm{OOH}\text{(R12b)}& {\displaystyle }& {\displaystyle }\to {\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{CH}}_{\mathrm{3}}{\mathrm{O}}_{\mathrm{2}}\end{array}$$

$$\begin{array}{}\text{(R13)}& {\mathrm{CH}}_{\mathrm{2}}\mathrm{OOH}\to \mathrm{OH}+\mathrm{HCHO}.\end{array}$$

In analogy, if the decomposition to OH of any reaction product of CH₃C(O)OOH + OH were sufficiently rapid, our experiment would underestimate the rate coefficient. In order to rule this out, we conducted experiments in which OH was replaced with OD. In this case, the reformation of OH via dissociation of the O–OH bond would not impact the kinetic measurement.

The results of experiments (at ∼57 Torr N₂) in which the 248 nm photolysis of DONO₂ was used to generate OD and measure the rate coefficient (k₅) are displayed in Fig. 5. Following the same procedure as outlined above to subtract the contribution of CH₃C(O)OH from the OH decay constant (but using our value of k₇ for reaction between OD and CH₃C(O)OH), we derive values of k₅[CH₃C(O)OOH] + k_d versus [CH₃C(O)OOH]. These are plotted in Fig. 6. From Table S2 we see that, within experimental scatter, the rate coefficients for reaction of OH and OD with CH₃C(O)OOH are identical, and we conclude that OH reformation is not responsible for the divergence between our low rate coefficient and the literature value. Theoretical calculations (Sect. 4.5) also indicate that the reformation of OH in this system is energetically disfavoured.

4.4.3 Secondary reactions of OH

As the contribution of CH₃C(O)OOH to the overall loss rate of OH is small, there is potential for overestimation of the rate coefficient if OH can react with products. In this case, we consider the reaction of OH with CH₃, which is formed in the photolysis of CH₃C(O)OOH (Reactions R10, R15) and in the dominant loss process for OH, reaction with CH₃C(O)OH (Reactions R14, R15), respectively. OH may also react with the CH₃C(O)O₂ radical (Reaction R17), formed in the title reaction:

$$\begin{array}{}\text{(R10)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+h\mathit{\nu }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{O}+\mathrm{OH}\text{(R14)}& {\displaystyle }\mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OH}\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{O}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\text{(R15)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{O}\to {\mathrm{CH}}_{\mathrm{3}}+{\mathrm{CO}}_{\mathrm{2}}\text{(R16)}& {\displaystyle }\mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}+M\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{OH}+M\end{array}$$

$$\begin{array}{}\text{(R17a)}& {\displaystyle }\mathrm{OH}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right){\mathrm{O}}_{\mathrm{2}}& {\displaystyle }\to {\mathrm{HO}}_{\mathrm{2}}+{\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{O}\text{(R17b)}& {\displaystyle }& {\displaystyle }\to {\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOOH}.\end{array}$$

The rate coefficient for reaction of OH with CH₃ is at the high-pressure limit, with a value close to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ cm³ molec.⁻¹ s⁻¹ (Pereira et al., 1997; Sangwan et al., 2012) under our experimental conditions. There appear not to be any kinetic studies of the reaction between OH and CH₃C(O)O₂, but, by analogy to OH + CH₃O₂ and OH + C₂H₅O₂ (Assaf et al., 2018; IUPAC Task Group, 2020), Reactions (R17a) and (R17b) will also have a rate coefficient close to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ cm³ molec.⁻¹ s⁻¹. In order to assess the role of Reactions (R16) and (R17a), we performed numerical simulations of the chemistry subsequent to the generation of OH (and thus CH₃) in the photolysis of CH₃C(O)OOH ∕ CH₃C(O)OH mixtures. The simulations were initiated with the concentrations of CH₃C(O)OOH, CH₃C(O)OH and OH listed in Table S2. As the decomposition of CH₃C(O)O to CH₃ + CO₂ is rapid, we set the initial CH₃ concentration equal to that of OH. Along with Reactions (R16), (R17a) and (R17b), we considered inter-radical reactions (e.g. self- and cross-reactions of CH₃, HO₂ and CH₃C(O)O₂) as listed in Table S3.

For each set of experimental conditions, simulations were carried out in which k₄ was varied between zero and $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{13}}$ cm³ molec.⁻¹ s⁻¹. The simulated decays of OH thus obtained were fitted to an exponential function to obtain the total decay constant, from which the contribution of CH₃C(O)OH was subtracted (k₆[CH₃C(O)OH]), as in the experimental data. The results of the simulations are displayed in Fig. 7 along with one set of experimental data obtained at 298 K. Immediately apparent from the simulations is that values of $k_{\mathrm{4}}\ge \mathrm{3}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ overpredict the measured slope. Indeed, setting k₄ to zero gives the closest agreement between the simulation and measurement. A better match between the observation and simulation could be obtained by either reducing the initial OH concentration (and thus the concentrations of CH₃ and CH₃C(O)O₂) or lowering the rate coefficients for Reactions (R16), (R17a) and (R17b). The simulated loss of OH was mainly (>90 %) via reaction with CH₃, which reflects the fact that only a small fraction of OH generated reacts with CH₃C(O)OOH to form CH₃C(O)O₂.

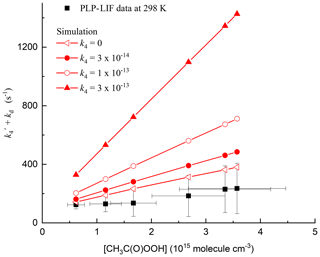
Figure 7 Results of 24 simulations (in red) of the chemistry initiated by the photolysis of CH₃C(O)OOH in the presence of CH₃C(O)OH including reactions of OH with CH₃ and CH₃C(O)O₂ radicals. As in the experimental data (only those obtained at 298 K are plotted), the contribution of CH₃C(O)OH to the OH decay constant has been subtracted from each data point. In addition, a diffusion term of 100 s⁻¹ has been added to the simulations so that the same intercept (at zero CH₃C(O)OOH) is obtained.

Given the uncertainty associated with the determination of the initial radical concentration (based on laser fluence), and with the rate coefficients of the inter-radical reactions involved, it is not possible to use the simulations to correct the experimental data. Instead, recognizing that a large fraction of the OH decay constant may be due to unwanted secondary processes, we prefer to quote the value of k₄ obtained experimentally as an upper limit.

4.4.4 Presence of H₂O₂ impurity

As indicated in Sect. 4.1.2, the CH₃C(O)OOH ∕ CH₃C(O)OH mixture is actually an equilibrium mixture containing H₂O₂ and H₂O (Reaction R11). Analysis of headspace samples of CH₃C(O)OOH and H₂O₂ indicates that H₂O₂ is present at ≈1 % the concentration of CH₃C(O)OOH (see Sect. 4.1.2). The IR absorption cross-sections of H₂O₂ are generally too weak to detect low-level impurities, so we were unable to unambiguously detect and quantify H₂O₂ during our kinetic measurements. However, unlike CH₃C(O)OOH, H₂O₂ reacts rapidly with OH, with a rate coefficient of $\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{12}}$ cm³ molec.⁻¹ s⁻¹ at 298 K. Initially assuming that $k_{\mathrm{4}}=\mathrm{3.2}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ as derived above from the PLP-LIF experiments would imply that a 1 % H₂O₂ “impurity” in our CH₃C(O)OOH sample would result in an overestimation of k₄ by ∼50 %. Together with the considerations of secondary, radical chemistry discussed in Sect. 4.4.2, this leads us to interpret our measurement of k₄ as an upper limit, and we prefer to quote a value of $k_{\mathrm{4}}\le \mathrm{4}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹.

4.5 Comparison with the previous determination of k₄

Our experimental upper limit of $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ is a factor ∼300 lower than the single, previous experimental determination (Wu et al., 2017). Wu et al. (2017) used a relative rate technique, which, in principle, offers the advantage that absolute concentrations of CH₃C(O)OOH need not be known as long as CH₃C(O)OOH and the reference reactant are removed solely via reaction with OH, and neither are reformed. However, the relative rate method does not lend itself readily to the study of this reaction, especially when the 254 nm photolysis of H₂O₂ is used as OH source, which results both in the photolysis of CH₃C(O)OOH and in formation of HO₂, which via reactions with CH₃C(O)O₂ can result in reformation of CH₃C(O)OOH. These issues were recognized by Wu et al. (2017), and corrections were applied to take both into account, which resulted in a slight increase in the rate coefficient. In some initial relative rate experiments in our laboratory, we were unable to derive consistent results as the large affinity of CH₃C(O)OOH for surfaces combined with its desorption from the walls during photolysis was too variable to allow analysis of the data.

In our theoretical study (Sect.4.6), we examine the reaction in detail and show that the low rate coefficient we measured with the PLP-LIF technique is in good agreement with the predictions.

4.6 Theoretical prediction of k₄ and the reaction mechanism

The potential energy surface for the CH₃C(O)OOH + OH reaction is shown in Fig. 8. The addition of OH radicals on a carbonyl double bond is known to have a high barrier and a negligible contribution and is ignored in this work (Anglada, 2004; De Smedt et al., 2005; Rypkema and Francisco, 2013; Vandenberk et al., 2002). The H abstraction reactions proceed through a prereaction complex and feature two protruding barriers for H abstraction at energies of 2.99 and 3.91 kcal mol⁻¹ above the free reactants, corresponding to the abstraction of the peracetic H atom and the methyl H atoms, respectively. The products are formed in a post-reaction complex that quickly dissociates to the free products. The rate coefficients calculated are found to be low, with a value of $k_{\mathrm{4}}=\mathrm{3}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ at 298 K. At 298 K, the branching ratio k_4a∕k₄ is predicted to be 0.78, and abstraction of the peracetic H atom dominates across the temperature range 200–450 K. Abstraction of the methyl H atoms ranges from 10 % at 200 K to 38 % at 450 K. The temperature dependence of the overall rate coefficient is given by $k_{\mathrm{4}}=\mathrm{3.16}\times {\mathrm{10}}^{-\mathrm{46}}$ T^10.90exp (3447 K∕T) cm³ molec.⁻¹ s⁻¹, with $k_{\mathrm{4}\mathrm{a}}\left(T\right)=\mathrm{1.43}\times$ ${\mathrm{10}}^{-\mathrm{43}}{T}^{\mathrm{9.87}}\exp (\mathrm{3287}\mathrm{K}/T)$ cm³ molec.⁻¹ s⁻¹ and k_4b $\left(T\right)=\mathrm{9.65}\times {\mathrm{10}}^{-\mathrm{47}}{T}^{\mathrm{11.10}}\exp (\mathrm{3000}\mathrm{K}/T)$ cm³ molec.⁻¹ s⁻¹. At the level of theory used, the expected uncertainty is a factor of 2 to 3. Given the slow product formation rate, the protruding reaction barriers and the fast formation and decomposition of the complex, k₄ is not expected to show a pressure dependence and should be at the high-pressure limit under the experimental conditions (50–100 Torr N₂).

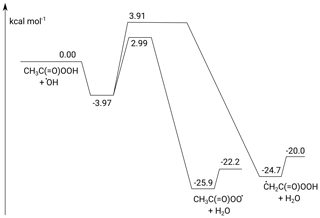
Figure 8 ZPE-corrected potential energy surface of the CH₃C(O)OOH + OH reaction calculated at the CCSD(T)/CBS(DTQ)//M06-2X-D3/aug-cc-pVQZ level of theory.

The theoretical predictions of k₄, k_4a and k_4b are plotted along with the experimental data from this work and the data of Wu et al. (2017) in Fig. 9. We also indicate the value of k₄ (based on comparison with CH₃OOH) that is presently used in the Master Chemical Mechanism. Our theoretical work shows that the Arrhenius plot for this reaction is curved, with a positive temperature dependence above room temperature and a negative T dependence below 280 K. At lower temperatures, abstraction of the peracetic H atom is dominant, but at higher temperatures the abstraction of methyl H atoms through the higher energy transition state rises in importance and is expected to become dominant at even higher temperatures. Similar to the reaction between OH and acetic acid (De Smedt et al., 2005; Khamaganov et al., 2006), the curvature in the Arrhenius plot is due to the formation of the prereaction complex and subsequent tunnelling to the products. With decreasing temperatures, the complex is increasingly populated with a longer lifetime, capturing ever more (per-)acetic acid + OH complexes and allowing them to tunnel through the barriers at energies below the reactant energies, leading to a negative T dependence of the rate coefficient. At high temperatures, the lifetime of the prereaction complex is too short for effective tunnelling, and the reaction proceeds predominantly over the protruding barriers, leading to a traditional positive T dependence.

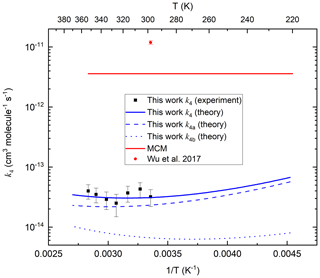
Figure 9 Rate coefficients (k₄, k_4a and k_4b) for the OH + CH₃C(O)OOH reaction. MCM is the value used in the Master Chemical Mechanism. The error bars in the present dataset include uncertainty in the value of $k_{\mathrm{4}}^{\prime }$ and IR absorption cross-sections of CH₃C(O)OOH. As described in the text, there are several reasons why the experimental rate coefficients should be regarded as upper limits.

With acetic and peracetic acids having similar mechanisms, this does not yet explain why the reaction with peracetic acid + OH is so much slower than the reaction of acetic acid + OH, despite the fact that the acidic H abstraction barrier height for CH₃C(O)OH, 3.3 kcal mol⁻¹ (De Smedt et al., 2005) is comparable within ∼ 0.3 kcal mol⁻¹ to that for CH₃C(O)OOH, 2.99 kcal mol⁻¹ (this work). The critical difference lies in the H bonding in the reactant and prereaction complex. In CH₃C(O)OH, the H bond between the acidic H atom and the carbonyl oxygen is very long, ∼2.25 Å, and thus weak. In CH₃C(O)OOH acid in contrast, this H bond is very short, 1.88 Å, and strong. Acetic acid can thus act without a penalty as a bidentate ligand for OH, forming two strong H bonds, leading to a planar complex with 7.3 kcal mol⁻¹ stability (De Smedt et al., 2005). CH₃C(O)OOH, in contrast, can either form a complex with only a single H bond on OH or needs to break the strong peracidic bond to form a geometrically unfavourable, non-planar complex with two OH hydrogen bonds. The peracidic complex is thus significantly less stable, by ≈4.0 kcal mol⁻¹, where the energy of the doubly H-bonded OH radical complex is 0.5 kcal mol⁻¹ higher than that of the most stable single-H-bonded complex, retaining the peracidic H bond. At room temperature, this weaker bonding decreases the lifetime of the prereactive complex by over 2 orders of magnitude compared to acetic acid, significantly reducing its equilibrium concentration and its ability to tunnel slowly through the barrier. This leads to a slower product formation rate compared to acetic acid, with a larger fraction of the prereaction complexes simply re-dissociating to the free reactants. Concomitantly, the deeper complex well for acetic acid + OH allows this latter reaction to show a negative T-dependent rate coefficient by sustained tunnelling even at higher temperatures, up to ∼500 K (Khamaganov et al., 2006), well beyond our predictions of a minimum of around 270 K for peracetic acid. Furthermore, we calculate a slightly wider energy barrier for peracetic acid, with a 1700 cm⁻¹ imaginary frequency, compared to that reported for acetic acid, 2000 cm⁻¹ (De Smedt et al., 2005), which further limits tunnelling for peracetic acid compared to acetic acid.

The strong H bond in peracetic acid also make its H abstraction reactions slower than in alkyl hydroperoxides such as CH₃OOH. These ROOH compounds can easily form complexes with OH radicals, and the H abstraction transition states are thus submerged by up to 1 kcal mol⁻¹ below the free reactants (Anglada et al., 2017), and even the somewhat less favourable H₂O₂ + OH reaction has energy barriers only ∼1 kcal mol⁻¹ above the reactants (Buszek et al., 2012). This enables the ROOH + OH reactions to proceed substantially faster than CH₃C(O)OOH + OH.

The dominant products of the OH-initiated degradation of CH₃C(O)OOH in air are the acetylperoxy radical, CH₃C(O)OO, the fate of which is described in Sect. 1, and includes formation of PAN or reformation of CH₃C(O)OOH. In air, the minor CH₂C(O)OOH product of Reaction (R4b) is expected to add O₂, forming a peracetic acid peroxy radical, OOCH₂C(O)OOH, which will also undergo reactions with NO, RO₂ and HO₂.

$$\begin{array}{}\text{(R18)}& {\displaystyle }{\mathrm{CH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{OOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}\text{(R19)}& {\displaystyle }\begin{array}{rl}& {\mathrm{OOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{NO}\\ & \to {\mathrm{OCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{NO}}_{\mathrm{2}}\end{array}\text{(R20)}& {\displaystyle }\begin{array}{rl}& {\mathrm{OOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{HO}}_{\mathrm{2}}\\ & \to {\mathrm{HOOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{O}}_{\mathrm{2}}\end{array}\text{(R21a)}& {\displaystyle }\begin{array}{rl}& {\mathrm{OOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+{\mathrm{RO}}_{\mathrm{2}}\\ & \to \mathrm{OCHC}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{ROH}+{\mathrm{O}}_{\mathrm{2}}\end{array}\text{(R21b)}& {\displaystyle }\to {\mathrm{HOCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{R}=\mathrm{O}+{\mathrm{O}}_{\mathrm{2}}\text{(R21c)}& {\displaystyle }\to \mathrm{OCHC}\left(\mathrm{O}\right)\mathrm{OOH}+\mathrm{RO}+{\mathrm{O}}_{\mathrm{2}}\end{array}$$

OCH₂C(O)OOH will quickly decompose to HCHO, CO₂ and OH (Vereecken and Peeters, 2009).

$$\begin{array}{}\text{(R22)}& {\mathrm{OCH}}_{\mathrm{2}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}\to \mathrm{HCHO}+{\mathrm{CO}}_{\mathrm{2}}+\mathrm{OH}\end{array}$$

Given that the slow abstraction of the peracetic H atom is a feature of the –C(O)OOH moiety and that the abstraction reaction is not influenced unduly by other functionalities in the molecules, we propose that the site-specific abstraction rate coefficient can be generalized to all peracids and used in group-additive structure–activity relationships. Only for long-chain oxygenated molecules, where an oxygenated group can reach the –C(O)OOH group and influence the H bonding with OH, can one expect a non-negligible deviation in the site-specific rate.

4.7 Atmospheric implications

Our experimental and theoretical results indicate that the reaction of CH₃C(O)OOH with OH has a rate coefficient of $\sim \mathrm{3}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ at temperatures prevalent in the lowermost atmosphere (i.e. in the boundary layer at mid-latitudes), doubling to $\sim \mathrm{6}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ at temperatures close to 230 K, as found in, for example, the upper troposphere. Assuming a global averaged OH abundance of 1×10⁶ molec. cm⁻³, these rate coefficients imply a lifetime of CH₃C(O)OOH with respect to degradation by OH of between about 6 months and 1 year. Given the low rate coefficient for reaction of CH₃C(O)OOH with OH, other loss processes are likely to dominate its atmospheric fate; these are wet and dry deposition, uptake to aerosols and photolysis so that its lifetime will be given by

$$\begin{array}{}\text{(4)}& \mathit{\tau }\left({\mathrm{CH}}_{\mathrm{3}}\mathrm{C}\left(\mathrm{O}\right)\mathrm{OOH}\right)={\displaystyle \frac{\mathrm{1}}{k_{\mathrm{4}}\left[\mathrm{OH}\right]+J+k_{\mathrm{dep}}+k_{\mathrm{het}}}},\end{array}$$

where J is the first-order rate coefficient for photolysis by actinic radiation, k_dep is the effective loss rate coefficient for removal by deposition and k_het is the loss rate coefficient for heterogeneous uptake to aerosol particles. The rate at which CH₃C(O)OOH will deposit on surfaces in the boundary layer is given by its deposition velocity and the boundary-layer height. Crowley et al. (2018) have assessed the terms k_dep (for dry deposition) and k_het for a summertime, mid-latitude, forested environment. Based on observations of CH₃C(O)OOH and H₂O₂, solubilities of CH₃C(O)OOH and H₂O₂ (Sander, 1999) actinic flux measurements, the UV absorption spectrum of CH₃C(O)OOH (Orlando and Tyndall, 2003) aerosol surface areas and an experimental uptake coefficient (Wu et al., 2015), they derived values of k_dep ∼ 3–5 × 10⁻⁵ s⁻¹, $k_{\mathrm{het}}\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ and J $\sim \mathrm{5}\times {\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ at local noon and concluded that, in the absence of rain, dry deposition is the dominant loss process in the boundary layer.

Above the boundary layer the loss of CH₃C(O)OOH via deposition and heterogeneous uptake to aerosol is less significant so that reaction with OH and photolysis will define its lifetime. A photolysis rate coefficient (J value) of $\approx \mathrm{5}\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ for CH₃C(O)OOH in the free and upper troposphere results in a lifetime of ∼ 3–4 weeks (Orlando and Tyndall, 2003). We note, however, that estimates of the photolysis rate coefficient are based on a single absorption spectrum measured to date (Orlando and Tyndall, 2003) and the assumption of a unity photodissociation quantum yield throughout the UV absorption spectrum, which remains unconfirmed by experiment or theory.

5 Conclusions

Both experimental and theoretical studies of the reaction between OH and CH₃C(O)OOH firmly establish that this is a slow process. The experimental work shows the rate coefficient is $<\mathrm{4}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ at 298 K, consistent with the theory-derived, temperature-dependent rate coefficients between 3 and $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{14}}$ cm³ molec.⁻¹ s⁻¹ for the entire troposphere. The low rate coefficient is rationalized in terms of a weakly bound (short-lived) prereaction complex combined with a sufficiently broad reaction barrier to reduce product formation by tunnelling. The site-specific rate coefficient for H abstraction from the –C(O)OOH moiety can be generalized to most reactions of OH with peracids, which will thus also be slow. The rate coefficient for the OH reaction is thus at least 2 orders of magnitude lower than previously reported and implies that the lifetime of CH₃C(O)OOH is dominated by deposition processes (notably dry deposition) in the boundary layer and photolysis in the free and upper troposphere, with OH-initiated degradation playing a minor role. The boundary-layer lifetime is expected to be of the order of 1 d, increasing to weeks in the free and upper troposphere. The longer than previously assumed chemical lifetime of CH₃C(O)OOH and probably of other peracids increases their potential to contribute to secondary organic aerosol formation.