Photooxidants from brown carbon and other chromophores in illuminated particle extracts

While photooxidants are important in atmospheric condensed phases, there are very few measurements in particulate matter (PM). Here we measure light absorption and the concentrations of three photooxidants – hydroxyl radical (^•OH), singlet molecular oxygen (${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$), and oxidizing triplet excited states of organic matter (³C^*) – in illuminated aqueous extracts of wintertime particles from Davis, California. ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^*, which are formed from photoexcitation of brown carbon (BrC), have not been previously measured in PM. In the extracts, mass absorption coefficients for dissolved organic compounds (MAC_DOC) at 300 nm range between 13 000 and 30 000 cm² (g C)⁻¹ are approximately twice as high as previous values in Davis fogs. The average (±1σ)^•OH steady-state concentration in particle extracts is $\mathrm{4.4}(\pm \mathrm{2.3})\times {\mathrm{10}}^{-\mathrm{16}}$ M, which is very similar to previous values in fog, cloud, and rain: although our particle extracts are more concentrated, the resulting enhancement in the rate of ^•OH photoproduction is essentially canceled out by a corresponding enhancement in concentrations of natural sinks for ^•OH. In contrast, concentrations of the two oxidants formed primarily from brown carbon (i.e., ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^*) are both enhanced in the particle extracts compared to Davis fogs, a result of higher concentrations of dissolved organic carbon and faster rates of light absorption in the extracts. The average ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentration in the PM extracts is $\mathrm{1.6}(\pm \mathrm{0.5})\times {\mathrm{10}}^{-\mathrm{12}}$ M, 7 times higher than past fog measurements, while the average concentration of oxidizing triplets is $\mathrm{1.0}(\pm \mathrm{0.4})\times {\mathrm{10}}^{-\mathrm{13}}$ M, nearly double the average Davis fog value. Additionally, the rates of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* photoproduction are both well correlated with the rate of sunlight absorption.

Since we cannot experimentally measure photooxidants under ambient particle water conditions, we measured the effect of PM dilution on oxidant concentrations and then extrapolated to ambient particle conditions. As the particle mass concentration in the extracts increases, measured concentrations of ^•OH remain relatively unchanged, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ increases linearly, and ³C^* concentrations increase less than linearly, likely due to quenching by dissolved organics. Based on our measurements, and accounting for additional sources and sinks that should be important under PM conditions, we estimate that [^•OH] in particles is somewhat lower than in dilute cloud/fog drops, while [³C^*] is 30 to 2000 times higher in PM than in drops, and [${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$] is enhanced by a factor of roughly 2400 in PM compared to drops. Because of these enhancements in ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* concentrations, the lifetimes of some highly soluble organics appear to be much shorter in particle liquid water than under foggy/cloudy conditions. Based on extrapolating our measured rates of formation in PM extracts, BrC-derived singlet molecular oxygen and triplet excited states are overall the dominant sinks for organic compounds in particle liquid water, with an aggregate rate of reaction for each oxidant that is approximately 200–300 times higher than the aggregate rate of reactions for organics with ^•OH. For individual, highly soluble reactive organic compounds it appears that ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ is often the major sink in particle water, which is a new finding. Triplet excited states are likely also important in the fate of individual particulate organics, but assessing this requires additional measurements of triplet interactions with dissolved organic carbon in natural samples.

1 Introduction

Photochemically generated oxidants largely drive atmospheric chemistry, both in the gas phase (Thompson, 1992; Finlayson-Pitts and Pitts Jr., 1999; Seinfeld and Pandis, 2012) and in aqueous drops, where they largely govern the reactions and lifetimes of organic compounds (Lim et al., 2005, 2010; Ervens et al., 2011; He et al., 2013; Herrmann et al., 2015; Blando and Turpin, 2000). Similarly, photooxidants can be important for transformations in water-containing particulate matter (PM): they make new PM mass by functionalizing gaseous volatile organics to oxygenated lower-volatility products and decrease PM mass by fragmenting large organics into smaller, more volatile species (Jimenez et al., 2009). Oxidants in condensed phases can come from the gas phase (e.g., the mass transport of hydroxyl radical, ^•OH) or can be formed photochemically within the particle or drop (Herrmann et al., 2010b). Our focus in this paper is on the latter pathway.

Of the photooxidants formed in airborne particles, hydroxyl radical (^•OH) is the most widely studied. While its concentrations have been measured in cloud/fog drops, rain, and dew (Arakaki and Faust, 1998; Arakaki et al., 1999; Anastasio and McGregor, 2001; Kaur and Anastasio, 2017), there are only four known measurements of ^•OH photoproduction rates, lifetimes, and steady-state concentrations in ambient particles, all from coastal or marine locations (Anastasio and Jordan, 2004; Arakaki et al., 2006, 2013; Anastasio and Newberg, 2007). Based on these and other measurements (e.g., Tong et al., 2017) and complementary modeling work (Herrmann et al., 2010b, 2015), the major sources of ^•OH include photolysis of nitrate, nitrite, and hydrogen peroxide (HOOH) as well as reactions of Fe(II) with HOOH or organic peroxides. The major sinks of ^•OH are organic molecules since these reactions typically have nearly diffusion controlled rate constants (Arakaki et al., 2013; Herrmann et al., 2010a, 2015).

Photoexcitation of organic chromophores, i.e., light-absorbing brown carbon (BrC), can also form oxidants in particles and drops. For example, sunlight absorption by organic chromophores can promote the molecules from their ground states to reactive triplet excited states (McNeill and Canonica, 2016; Kaur and Anastasio, 2018b). Triplets can both directly oxidize organics via electron-transfer reactions and form other photooxidants, including singlet molecular oxygen (${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$) (Zepp et al., 1985) and hydrogen peroxide (Anastasio et al., 1997). In this work we examine oxidizing triplets, which we refer to as ³C^* or simply “triplets” for simplicity. Such species are important in surface waters, where they rapidly oxidize several classes of compounds including phenols, anilines, phenylurea herbicides, and sulfonamide antibiotics (Canonica et al., 1995, 2006; Canonica and Hoigné, 1995; Boreen et al., 2005; Bahnmüller et al., 2014).

There has been growing interest in the role and reactivity of triplets formed from particulate brown carbon, especially their role in forming aqueous secondary organic aerosol (SOA(aq))(Smith et al., 2014, 2015; Yu et al., 2014, 2016; Laskin et al., 2015). There is evidence that triplet-forming, light-absorbing species, e.g., imidazoles and pyrazines, are formed in drops and particles (De Haan et al., 2009, 2010; Hawkins et al., 2018), and a few laboratory studies have examined how illuminated imidazole particles can oxidize isoprene or other alkenes to increase PM mass (Aregahegn et al., 2013; Rossignol et al., 2014). But the formation of SOA(aq) from such reactions appears not to be significant under environmentally relevant conditions where concentrations of triplet precursors are much lower (Tsui et al., 2017). While we recently made the first measurements of triplet concentrations in fog waters (Kaur and Anastasio, 2018b), there are no measurements of ³C^* in particles, making it difficult to assess their significance. This is doubly difficult because triplets are not a single oxidant but rather a suite of species with a wide range of reactivities (McNeill and Canonica, 2016).

Another important photooxidant in atmospheric and surface waters is singlet molecular oxygen (${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$), which is formed by energy transfer from a triplet excited state to dissolved oxygen and lost via deactivation by water (Zepp et al., 1977; Haag and Hoigné, 1986; Haag and Gassman, 1984; Faust and Allen, 1992). Similar to triplets, singlet oxygen has been studied widely in surface waters (Zepp et al., 1977; Haag and Gassman, 1984; Haag and Hoigné, 1986; Tratnyek and Hoigné, 1994) and reacts rapidly with electron-rich organics such as phenols, polycyclic aromatic hydrocarbons, amino acids, and reduced sulfur species (Wilkinson et al., 1995). However, there are only four measurements of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentrations in atmospheric waters (Anastasio and McGregor, 2001; Kaur and Anastasio, 2017; Albinet et al., 2010; Faust and Allen, 1992) and none in aqueous particles.

To address this gap, we measured ^•OH, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, and ³C^* in illuminated aqueous extracts of fine particles collected from the Central Valley of California during winter, a period of heavy residential wood burning. The goals of this study are to (1) quantify ^•OH, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, and ³C^* kinetics and concentrations in particle extracts; (2) compare light absorption and photooxidant kinetics with previous measurements made in fog; (3) measure the dependence of oxidant concentrations on particle dilution to predict photooxidant concentrations in ambient particle liquid water; and (4) assess the importance of particle photooxidants in processing organic compounds in the atmosphere.

2 Experimental

2.1 Chemicals

All chemicals were used as received. Furfuryl alcohol (98 %), syringol (99 %), methyl jasmonate (95 %), benzene (≥99.9 %), 2-methyl-3-buten-2-ol (98 %), deuterium oxide (99.9 % atom D), and 2-nitrobenzaldehyde (98 %) were from Sigma-Aldrich, and sulfuric acid (trace metal grade) was from Fisher. All chemical solutions and particulate matter extracts were prepared using purified water (Milli-Q water) from a Milli-Q Advantage A10 system (Millipore; ≥18.2 MΩ cm) with an upstream Barnstead activated carbon cartridge; total organic carbon concentrations were below 10 ppb C.

2.2 Particle collection and extraction

Wintertime particles were collected in a residential neighborhood in Davis, California, (38.5539^∘ N, 121.7381^∘ W; 16 m a.s.l.) during December 2015 and January 2016, a period with significant wood burning. PM_2.5 was collected on 20.3 cm × 25.4 cm (8 in. × 10 in.) Teflon-coated quartz filters (Pall Corporation, EmFab^™ filters, type TX40HI20-WW) using a high-volume sampler with a PM₁₀ inlet (Graseby Andersen) followed by two offset, slotted impactor plates (Tisch Environmental, Inc., 230 series) to remove particles greater than 2.5 µm. Due to technical difficulties, the air flow rate was variable and typically ranged between 1130 and 1560 L min⁻¹, corresponding to particle cut points of 2.5 to 1.6 µm. Particles were generally collected over two to three consecutive nights between 17:30 and 07:30 local time, but one sample (number 3) was collected continuously (day and night) for 72 h (Table S1 in the Supplement).

Immediately upon collection, samples were wrapped in aluminum foil (previously baked at 500 ^∘C for 8 h), sealed in Ziplock^™ bags, and stored at −20 ^∘C. On the day of extraction, several 2 cm × 2 cm pieces were cut (using stainless-steel tools) from the same filter, each was put into a separate pre-cleaned 10 mL amber glass vial, Milli-Q water was added (see below), and the vial was sealed and shaken for 3 h in the dark. The extracts were filtered (0.22 µm PTFE; Pall Corporation), combined, and labeled as particulate matter extract (PME). The standard condition was to use 1.0 mL of Milli-Q to extract each filter square, but in our initial work we used 2.5 mL of Milli-Q per filter square; these latter “dilute extracts” are indicated by an asterisk and footnotes in the figures and tables. We switched from dilute to standard conditions after PME1–3, but we include both results in this work to compare the two types of extracts.

In addition, to study the effect of PM mass concentration, separate portions of filter number 3 were extracted using five different extraction volumes between 0.5 and 10 mL (discussed later). Those extracts are labeled as PME3Dx, where “x” is the extraction volume (e.g., PME3D1.3 for filter squares extracted in 1.3 mL of Milli-Q). Upon extraction, each PME was stored in the refrigerator (5 ^∘C) until the day of the illumination experiments. All illumination experiments and analyses on a PME sample were completed within a week of its extraction.

2.3 Sample illumination and chemical analysis

For all illumination experiments except ^•OH measurements using benzene (discussed in Sect. 2.5.1), on the day of the experiment a 1.0 mL aliquot of an air-saturated particle extract was first acidified to pH 4.2±0.2 using 10 mM sulfuric acid (with sample dilution ≤10 %) to mimic the particle water acidity in wintertime PM in California's Central Valley (Parworth et al., 2017). The pH of the sample was measured using a pH microelectrode (MI-414 series, protected tip, 16 gauge needle, 6 cm length; Microelectrodes, Inc.). The acidified extract was then spiked with a single photooxidant probe and put into a silicone-plugged, fully filled GE021 quartz tube (4 mm inner diameter, 6 cm length, 1.0 mL volume) and illuminated with a 1000 W xenon arc lamp filtered with a water filter (to reduce sample heating), an AM 1.0 air mass filter (AM1D-3L, Sciencetech), and a 295 nm long-pass filter (20CGA-295, Thorlabs) to mimic tropospheric solar light (Kaur and Anastasio, 2017). Because of the small tube size, samples were not stirred, but the entire sample was illuminated in a chamber held at 20 ^∘C. 100 µL aliquots of illuminated (and parallel dark) samples were periodically removed and analyzed for the concentration of photooxidant probe (see below) using HPLC (high-performance liquid chromatography; Shimadzu LC-10AT pump, ThermoScientific BetaBasic-18 C₁₈ column (250×33 mm, 5 µM bead), and Shimadzu-10AT UV–Vis detector). The photon flux in the sample was measured on each experiment day using a 10 µM solution of 2-nitrobenzaldehyde (2NB) in the same type of quartz tube as the sample (Galbavy et al., 2010).

Major anions and cations in the extracts (Table S2) were quantified using two Metrohm ion chromatographs (881 Compact IC Pro) equipped with conductivity detectors (Ge et al., 2014; Kaur and Anastasio, 2017). Dissolved organic carbon (DOC) in the filtered extracts was measured using a Shimadzu TOC-VCPH analyzer (Yu et al., 2014).

2.4 Light absorbance

Light absorbance was measured immediately after extraction using a Shimadzu UV-2501PC spectrophotometer with 1 cm quartz cuvettes and a baseline of Milli-Q water. Absorbance (A_λ) was converted to light absorption coefficients using

$$\begin{array}{}\text{(1)}& {\mathit{\alpha }}_{\mathit{\lambda }}={\displaystyle \frac{A_{\mathit{\lambda }}}{l}},\end{array}$$

where l is the path length in centimeters. The rate of sunlight absorption (R_abs, mol photons L⁻¹ s⁻¹) in each extract was calculated as

$$\begin{array}{}\text{(2)}& R_{\mathrm{abs}}=\mathrm{2.303}\times {\displaystyle \frac{{\mathrm{10}}^{\mathrm{3}}}{N_{\mathrm{A}}}}\times \sum _{\mathrm{300}\mathrm{nm}}^{\mathrm{450}\mathrm{nm}}({\mathit{\alpha }}_{\mathit{\lambda }}\times I_{\mathit{\lambda }}\times \mathrm{\Delta }\mathit{\lambda }),\end{array}$$

where 2.303 is for base conversion, 10³ is for units conversion (cm³ L⁻¹), N_A is Avogadro's number, I_λ is the Davis winter-solstice actinic flux (photons cm⁻² s⁻¹ nm⁻¹) from the Tropospheric Ultraviolet and Visible (TUV) Radiation Model version 4.1 (Madronich et al., 2002), and Δλ is the interval between adjacent wavelengths in the TUV output (nm).

Wavelength-dependent mass absorption coefficients for DOC (MAC_DOC; cm² (g C)⁻¹) were estimated by subtracting the contributions of nitrite and nitrate from the measured absorbance at each wavelength (which were small, ≤7 % of the total absorbance) and then dividing the remainder by the DOC concentration:

$$\begin{array}{}\text{(3)}& {\mathrm{MAC}}_{\mathrm{DOC},\mathit{\lambda }}={\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{DOC},\mathit{\lambda }}\times \ln \left(\mathrm{10}\right)\times {\mathrm{10}}^{\mathrm{3}}\times {\mathrm{10}}^{\mathrm{3}}}{\left[\mathrm{DOC}\right]}},\end{array}$$

where α_DOC,λ(cm⁻¹) is the sample absorbance coefficient at wavelength λ due to DOC (Kaur and Anastasio, 2017), ln(10) is a base conversion factor, the two 10³ factors are for unit conversion (cm³ L⁻¹ and mg g⁻¹), and the DOC concentration is in milligrams of carbon per liter (mg C L⁻¹). Since the average organic-matter-to-organic carbon (OM/OC) ratio in California Central Valley particles is approximately 1.7 (Young et al., 2016), the absorption coefficients normalized by OM mass will be approximately 60 % of the MAC_DOC values.

2.5 Measurement of photooxidants

2.5.1 Hydroxyl radical (^•OH)

We quantified ^•OH kinetics using a benzene probe (Zhou and Mopper, 1990; Anastasio and McGregor, 2001; Kaur and Anastasio, 2017). Briefly, four aliquots of each extract were spiked with varying concentrations of benzene to trap ^•OH and form phenol (yield: 73 %), which is quantified (Fig. S1 in the Supplement). Each benzene stock was made a day before the illumination experiment. Similar to the other photooxidant experiments, all aliquots were air-saturated, acidified to an initial pH of 4.2(±0.2), capped, and then constantly stirred during illumination in airtight 5.0 mL, 1 cm path length, rectangular quartz cuvettes with no initial headspace. For all ^•OH measurements where benzene is used as a probe, we used this larger sample volume (5 mL instead of 1 mL) to minimize the headspace in the cuvette and prevent benzene loss due to volatilization. Throughout the illumination period, 100 µL aliquots were collected through the cap septum and analyzed for phenol using HPLC-UV (eluent of 30 % acetonitrile: 70 % Milli-Q, flow rate of 0.6 mL min⁻¹, detection wavelength of 210 nm, and column temperature of 35 ^∘C). As described in Kaur and Anastasio (2017), we use these results to determine three experimental quantities for ^•OH: the rate of photoproduction (P_OH,EXP), the rate constant for ^•OH loss due to natural sinks ($k_{\mathrm{OH}}^{\prime }$), and the steady-state concentration ([^•OH]_EXP). Measured rates of ^•OH formation and steady-state concentrations were normalized to values expected under midday, Davis winter-solstice sunlight and were corrected for the small amount of internal light screening due to light absorption by dissolved organic matter (DOM):

$$\begin{array}{}\text{(4)}& \left[{}^{\mathrm{•}}\mathrm{OH}\right]=\left({\displaystyle \frac{[{}^{\mathrm{•}}\mathrm{OH}{]}_{\mathrm{EXP}}}{{\mathrm{S}}_{\mathit{\lambda }}\times j_{\mathrm{2}\mathrm{NB},\mathrm{EXP}}}}\right)\times j_{\mathrm{2}\mathrm{NB},\mathrm{WIN}}.\end{array}$$

In this equation, S_λ is the internal light screening factor (Table S1), j_2NB,WIN is the rate constant for loss of 2-nitrobenzaldehyde at midday near the winter solstice in Davis (solar zenith angle = 62^∘, $j_{\mathrm{2}\mathrm{NB},\mathrm{WIN}}=\mathrm{0.0070}$ s⁻¹; Anastasio and McGregor, 2001), and j_2NB,EXP is the measured rate constant for loss of 2NB on the day of the experiment. ^•OH results are in Tables S3–S6.

We also measured ^•OH steady-state concentrations in squares of particle filter number 3 using five different dilutions with water (discussed later). Because these sample volumes were too small to use the benzene technique, we determined the steady-state concentration of ^•OH by measuring the loss of 2-methyl-3-buten-2-ol (MBO) (Sect. S1). We then measured P_OH in a 1 cm cuvette using a high benzene concentration (1.5 mM) and determined the rate constant for ^•OH loss due to natural sinks by dividing the rate of photoproduction by the steady-state concentration, $k_{\mathrm{OH}}^{\prime }=P_{\mathrm{OH}}/\left[{}^{\mathrm{•}}\mathrm{OH}\right]$ (Sect. S1.3). In contrast to the benzene technique, there was some quenching of ^•OH by the probe MBO in our PME3 samples; this quenching was most significant in the most dilute extract, PME3D10. We corrected measured ^•OH concentrations for quenching by MBO in the PME3 samples (Sect. S1), and the final, corrected values are given in the Tables mentioned above.

2.5.2 Singlet molecular oxygen (${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$)

Singlet oxygen was quantified by measuring the loss of a furfuryl alcohol (FFA) probe and using heavy water (D₂O) as a diagnostic tool (Kaur and Anastasio, 2017; Anastasio and McGregor, 2001). Briefly, each extract was divided into two aliquots, acidified to pH 4.2 (±0.2), and diluted 50:50 using H₂O or D₂O. Both aliquots were spiked to 10 µM FFA and illuminated in 1 mL quartz tubes. (At this concentration, FFA should decrease the steady-state concentration of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in air-saturated solutions by less than 1 %.) FFA loss was detected using HPLC-UV (eluent of 10 % acetonitrile: 90 % Milli-Q water, flow rate of 0.6 mL min⁻¹, detection wavelength of 210 nm, and column temperature of 35 ^∘C). The loss of FFA followed pseudo-first-order kinetics and the slope of the plot of ln ([FFA]_t∕[FFA]₀) versus time is the negative of the pseudo-first-order rate constant for loss of FFA (illustrated in Fig. S2). Loss of FFA in the D₂O-diluted aliquot is faster than in H₂O because H₂O is the dominant sink for ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, which reacts less quickly with D₂O (Bilski et al., 1997). The differences in the pseudo-first-order rate constants for loss of FFA between the two aliquots of sample were used to calculate the steady-state concentration of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and the rate of singlet oxygen photoproduction (Anastasio and McGregor, 2001). These were normalized to values expected in Davis winter-solstice sunlight (i.e., [${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$] and $P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$) and corrected for internal light screening using an equation analogous to Eq. (4). ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ measurements are in Table S7.

2.5.3 Oxidizing triplet excited states of organic matter (³C^*)

Triplets were measured using the dual-probe technique we developed recently for fog waters (Kaur and Anastasio, 2018b): two 1.0 mL, pH 4.2 aliquots of each extract were spiked to 10 µM of either syringol (SYR) or methyl jasmonate (MeJA), and the loss of each probe was measured during illumination in plugged quartz tubes (Sect. 2.3). The measured pseudo-first-order rate constant for probe loss ($k_{\mathrm{Probe},\mathrm{EXP}}^{\prime }$) was determined as the negative of the slope of the plot of ln([Probe]/[Probe]₀) versus illumination time. Values of $k_{\mathrm{Probe},\mathrm{EXP}}^{\prime }$ were normalized to Davis winter-solstice sunlight and corrected for internal light screening using an analog of Eq. (4); the resulting rate constants are termed $k_{\mathrm{Probe}}^{\prime }$ (s⁻¹) (Tables S8 and S9 of the SI). This pseudo-first-order rate constant for loss of probe represents the sum of all loss pathways:

$$\begin{array}{ll}{\displaystyle }{k}_{\mathrm{Probe}}^{\prime }& {\displaystyle }=k_{\mathrm{Probe}+\mathrm{OH}}\left[{}^{\mathrm{•}}\mathrm{OH}\right]+k_{\mathrm{Probe}+{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}\left[{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}\right]\\ {\displaystyle }& {\displaystyle }+\mathrm{\Sigma }\left(k_{\mathrm{Probe}+{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}}\left[{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}\right]\right)+j_{\mathrm{Probe}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }+\mathrm{\Sigma }\left(k_{\mathrm{Probe}+\mathrm{Other}}\left[\mathrm{Other}\right]\right),\end{array}$$

where the first two terms are the contributions of ^•OH and ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ to probe loss; $\mathrm{\Sigma }(k_{\mathrm{Probe}+{}^{\mathrm{3}}{\mathrm{C}}^{*}}$[³C^*]) represents the sum of all triplet contributions to probe loss; j_Probe is the first-order rate constant for direct photodegradation of the probe, which is negligible for our illumination times (< $\mathrm{4.3}\times {\mathrm{10}}^{-\mathrm{6}}{s}^{-\mathrm{1}}$ and $\mathrm{4.8}\times {\mathrm{10}}^{-\mathrm{7}}$ s⁻¹ for SYR and MeJA, respectively, under Davis winter conditions); and Σ(k_Probe+Other[Other]) is the sum of contributions from all other oxidants. As described in Sect. S3, we estimate that these other oxidants (hydroperoxyl radical/superoxide radical anion, ozone, carbonate radical, hydrogen ion/aquated electron) contribute 12 % or less of the average measured syringol loss (Sect. S3) and so are ignored. We can then simplify and rearrange Eq. (5) to determine the triplet contribution to probe loss:

$$\begin{array}{ll}{\displaystyle }{k}_{\mathrm{Probe},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }& {\displaystyle }=\mathrm{\Sigma }\left(k_{\mathrm{Probe}+{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}}\left[{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}\right]\right)=k_{\mathrm{Probe}}^{\prime }\\ \text{(6)}& {\displaystyle }& {\displaystyle }-\left(k_{\mathrm{Probe}+\mathrm{OH}}\left[{}^{\mathrm{•}}\mathrm{OH}\right]+k_{\mathrm{Probe}+{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}\left[{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}\right]\right).\end{array}$$

In other probe techniques, the equivalent of Eq. (6) is rearranged so that $\sum \left[{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}\right]$ can be determined based on the measured value of $k_{\mathrm{Probe},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$ and the literature value of the second-order rate constant $k_{\mathrm{Probe}+{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}}$. However, because triplets represent a suite of unidentified compounds, there is no one value of $k_{\mathrm{Probe}+{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}}$. To estimate this second-order rate constant in each sample, we used a combination of rate constants from four model triplets – 2-acetonaphthone (³2AN^*), 3'-methoxyacetophenone (³3MAP*), 3,4-dimethoxybenzaldehyde (³DMB*), and benzophenone (³BP^*) – that roughly span the range of triplet reactivities in natural samples. We first identified the “best match triplets”, i.e., the one or two model triplets that match the average oxidizing triplet reactivity in a given extract. To do this, we determined the model triplets whose mole-fraction-weighted ratio of second-order rate constants (i.e., $k_{\mathrm{SYR}+{}^{\mathrm{3}}{\mathrm{C}}^{*}}/k_{\mathrm{MeJA}+{}^{\mathrm{3}}{\mathrm{C}}^{*}}$) matches the ratio of the measured first-order probe loss rate constants due to triplets ($k_{\mathrm{SYR},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }/k_{\mathrm{MeJA},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$) in each extract (for more details, see Kaur and Anastasio, 2018b). Ratios of the second-order rate constants ($k_{\mathrm{SYR},{}^{\mathrm{3}}{\mathrm{C}}^{*}}/k_{\mathrm{MeJA}+{}^{\mathrm{3}}{\mathrm{C}}^{*}}$) of the model triplets range from 1.7 for the most reactive species (³BP^*) to 100 for the least reactive, ³2AN^* (Table S10). For each extract, we calculated two mole-fraction-weighted second-order rate constants for triplets (one for each probe) and used them to estimate the triplet steady-state concentration:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Sigma }{\left[{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}\right]}_{\mathrm{Probe}}=\\ \text{(7)}& {\displaystyle }& {\displaystyle \frac{k_{\mathrm{Probe},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }}{\mathit{\chi }{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{1}}}^{*}\times k_{\mathrm{Probe}+{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{1}}}^{*}}+\mathit{\chi }{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{2}}}^{*}\times k_{\mathrm{Probe}+{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{2}}}^{*}}}},\end{array}$$

where $\mathit{\chi }{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{1}}}^{*}$ and $\mathit{\chi }{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{2}}}^{*}$ are the mole fractions of the two best match triplets (${}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{1}}}^{*}$ and ${}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{2}}}^{*}$), and $k_{\mathrm{Probe}+{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{1}}}^{*}}$ and $k_{\mathrm{Probe}+{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{2}}}^{*}}$ are the second-order reaction rate constants of the best model triplet matches. Equation (7) gives us two estimates of the triplet steady-state concentration, one from each probe, i.e., $\sum [{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{i}}}^{*}{]}_{\mathrm{SYR}}$ and $\sum [{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{i}}}^{*}{]}_{\mathrm{MeJA}}$. We averaged the two to obtain the best value for the triplet steady-state concentration in each extract, $\sum \left[{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{i}}}^{*}\right]$.

We next estimated the rate of triplet photoformation ($P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$):

$$\begin{array}{}\text{(8)}& P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}=\mathrm{\Sigma }\left[{}^{\mathrm{3}}{\mathrm{C}}_{\mathrm{i}}^{*}\right]\times \left(k_{{}^{\mathrm{3}}{\mathrm{C}}^{*}+{\mathrm{O}}_{\mathrm{2}}}\right[{\mathrm{O}}_{\mathrm{2}}]+(k_{\mathrm{rxn}}+k_Q\left)\right[\mathrm{DOC}\left]\right),\end{array}$$

where $k_{{}^{\mathrm{3}}{\mathrm{C}}^{*}+{\mathrm{O}}_{\mathrm{2}}}$ is the average bimolecular rate constant for quenching of the model triplets by O₂ ($=\mathrm{2.8}\times {\mathrm{10}}^{\mathrm{9}}$ M⁻¹ s⁻¹: Table S11 and Canonica et al., 2000), [O₂] is the dissolved oxygen concentration of 284 µM at 20 ^∘C (USGS, 2018), k_rxn+k_Q is the overall reaction and quenching rate constant for triplets by DOC (9.3×10⁷ L (mol C)⁻¹ s⁻¹; see below), and [DOC] values are in Table S2. At the concentrations we used (10 µM), SYR and MeJA are negligible sinks for triplets. Measurements for triplets are in Tables S12 and S13.

For all three photooxidants, the quantum yield of formation was calculated as

$$\begin{array}{}\text{(9)}& {\mathrm{\Phi }}_{\mathrm{Ox}}={\displaystyle \frac{P_{\mathrm{Ox}}}{R_{\mathrm{abs}}}},\end{array}$$

where P_Ox is the Davis winter-solstice-normalized rate of oxidant photoproduction and R_abs is the rate of sunlight absorption by the extract.

2.5.4 PM mass concentration factor (CF)

Due to the volume required for our probe techniques, we extract particles into Milli-Q water, resulting in extracts that are approximately 1000 times more dilute than ambient particles. To examine the impact of dilution on photooxidant concentrations, we extracted sample number 3 in five different volumes of Milli-Q water (0.5 to 10 mL) and measured ^•OH, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, and ³C^* steady-state concentrations in the five extracts. We define the PM mass concentration factor (CF) as the ratio of (PM mass) ∕ (water mass) in a given extract relative to the most concentrated extract that we can make:

$$\begin{array}{}\text{(10)}& \mathrm{CF}={\displaystyle \frac{V_{\mathrm{MIN}}}{V_{\mathrm{EXT}}+V_{\mathrm{P}}}},\end{array}$$

where V_MIN is the minimum experimentally feasible volume of Milli-Q needed for extraction of one filter square (0.5 mL), V_EXT is the volume of Milli-Q used to extract a given filter square (0.5 to 10 mL), and V_P is the volume of probe stock solution added (typically 20 µL). Values of CF for the PME3D extracts ranged from 0.05 (least concentrated) to 0.96 (most concentrated) and are listed in Table S14.

2.5.5 Uncertainties

In figures, error bars represent ±1 standard error (SE) calculated by propagating the uncertainties in each term used to calculate the plotted value.

3 Results and discussion

3.1 General extract characteristics

Similar to Davis fogs collected in 1997–1998 (Anastasio and McGregor, 2001) and 2011 (Kaur and Anastasio, 2017), the most abundant ions in the particle extracts are ammonium (${\mathrm{NH}}_{\mathrm{4}}^{+}$, 280–2600 µM) and nitrate (${\mathrm{NO}}_{\mathrm{3}}^{-}$, 380–3300 µM) (Table S2). This is expected since ammonium nitrate is the most significant inorganic component of wintertime particles in the Central Valley (Herner et al., 2006; Heald et al., 2012; Young et al., 2016). The average values of ${\mathrm{NO}}_{\mathrm{3}}^{-}$ and ${\mathrm{NH}}_{\mathrm{4}}^{+}$ are not statistically different (p>0.5) between the current particle extracts (PME) and previous fogs, although the ranges are much wider in the particle extracts (Table S2). Similar to nitrate, nitrite is another important source of hydroxyl radical in the aqueous phase (Anastasio and McGregor, 2001), with an average concentration of 6.9(±2.9) µM in the particle extracts, again statistically similar to the 2011 fog average. On the other hand, the average concentration of potassium – commonly used as a tracer for biomass burning (Silva et al., 1999; Parworth et al., 2017) – is nearly 40 times higher in the particles than in the 2011 Davis fog samples (p=0.019), suggesting PME enrichment by residential wintertime wood-burning. This is reflected in the dilute PM extracts as well: even though most characteristics in the dilute extracts are similar to fog, the average K⁺ (38±7 µM) in the dilute PMEs is 10 times higher than the fog value. Dissolved organic carbon (DOC) in the standard extracts (mean: 3400(±760) µM C) is, on average, 3 times higher than both the dilute extracts and fog.

We employed two field blanks in this study, one each for dilute and standard extraction conditions. Ions and DOC in both field blanks are lower than 10 % of the corresponding PME sample averages, with a few exceptions (Table S2).

3.2 Light absorption in particle extracts

As shown in Fig. 1a and Table S1, the path-length-normalized absorbance (α, cm⁻¹) declines exponentially with wavelength, with values at 300 nm (α₃₀₀) between 0.27 and 0.58 cm⁻¹ for the standard extracts PME3–6. The average α₃₀₀ value is nearly 5 times higher in standard extracts than values in Davis fog samples (Table S1, Fig. S3, data available in Kaur and Anastasio, 2018a), while the dilute extracts (PME1*, PME2*, and PME3D2.5*) have absorbances very similar to fog samples. Values of the absorption Ångström exponent (AAE) for all PM extracts range between 6.2 and 7.9 (Table S1), similar to those reported previously for water-soluble particulate BrC from biomass burning (Hecobian et al., 2010; Kirchstetter and Thatcher, 2012). For both the fog and PM extracts the calculated rate of sunlight absorption between 300 and 450 nm (R_abs) is well correlated with dissolved organic carbon (DOC) (R²=0.89 and 0.67, respectively; Fig. S4), suggesting that BrC is mainly responsible for light absorption. The R_abs values for the standard extracts are high, with an average value of $\mathrm{9.1}(\pm \mathrm{4.1})\times {\mathrm{10}}^{-\mathrm{6}}$ mol photons L⁻¹ s⁻¹, 5 times higher than the dilute extracts and past Davis fogs (Table S1). Similar to fog (Kaur and Anastasio, 2018b), the average rate of sunlight absorbance in the standard particle extracts is 17 times higher than the total formation rates of the three photooxidants (discussed later), indicating that most of the (photo) energy absorbed is either dissipated via non-reactive pathways or leads to formation of other products.

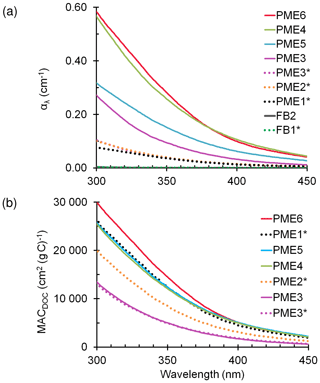
Figure 1 (a) Light absorption coefficients, α_λ, in particulate matter extracts (PME) (Eq. 1) and field blanks (FB). The legend shows the sample identities, arranged from the highest absorbing (top) to lowest absorbing (bottom) at 300 nm. Solid and dotted lines represent standard and dilute extracts, respectively (with the latter indicated with an asterisk; Sect. 2.2). (b) Mass absorption coefficients of DOC in the particle extracts (Eq. 3).

We next calculated mass absorption coefficients for the organics (MAC_DOC) by subtracting the absorbance contributions by nitrite and nitrate from α and dividing by the DOC concentration (Eq. 3). Across both standard and dilute extracts, the average (±σ) MAC_DOC value at 300 nm is $\mathrm{2.2}(\pm \mathrm{0.7})\times {\mathrm{10}}^{\mathrm{4}}$ cm² (g C)⁻¹, 1.7 times higher than the fog sample average (Figs. 1b and S3; data available at Kaur and Anastasio, 2018a). Both α and MAC_DOC in the PME are generally higher than in fog, especially at shorter sunlight wavelengths (Fig. S5), although AAE values are similar in the extracts and fog (Table S1). Since MAC_DOC accounts for dilution (Eq. 3), the higher values in PM extracts indicate that water-soluble organics in particles are either more strongly light-absorbing (on a per-carbon basis) and/or less diluted with non-absorbing DOC, compared to those in fog. Our PME mass absorption coefficients at 300 nm are very similar to values reported for the humic-like fraction of biomass-burning aerosols in the Amazon basin (Hoffer et al., 2006) and for the water-soluble organic fractions of rural aerosols (Varga et al., 2001; Sun et al., 2007).

Compared to the samples, light absorption in the field blanks is negligible, representing 0.7 % and 3 % of the average α₃₀₀ in the standard and dilute extracts, respectively (Table S1).

3.3 Hydroxyl radical

The average Davis winter-solstice-normalized rate of ^•OH photoproduction (P_OH) in the standard extracts is $\mathrm{1.2}(\pm \mathrm{0.5})\times {\mathrm{10}}^{-\mathrm{9}}$ M s⁻¹ (i.e., 4.2±1.7 µM h⁻¹), 3.3 times faster than the average of previous Davis fogs (Table S3). In Davis fog, the main sources of ^•OH were nitrite and nitrate photolysis, accounting for 70 %–90 % of measured P_OH (Anastasio and McGregor, 2001; Kaur and Anastasio, 2017). However, in the standard PM extracts, nitrite and nitrate together account for an average of only (34±14) % of P_OH (Table S4), while other unidentified species account for the remaining (66±14) %. While ${\mathrm{NO}}_{\mathrm{2}}^{-}$ and ${\mathrm{NO}}_{\mathrm{3}}^{-}$ concentrations in PME and fog are similar, measured ^•OH photoproduction rates are much higher in the particle extracts. The additional sources of ^•OH likely include photo-Fenton processes (Arakaki and Faust, 1998) and organic peroxides (Tong et al., 2016, 2017; Lim and Turpin, 2015), although there is only a modest correlation between DOC and P_OH due to unidentified sources (Fig. S6).

While organic compounds are potentially important sources of ^•OH in the particle extracts, they are almost certainly the main ^•OH sink, as found previously for atmospheric and surface waters (Brezonik and Fulkerson-Brekken, 1998; Dong et al., 2010; Arakaki et al., 2013). The average (±1σ) rate constant for ^•OH destruction, $k_{\mathrm{OH}}^{\prime }$, in the standard extracts is $\mathrm{2.5}(\pm \mathrm{1.1})\times {\mathrm{10}}^{\mathrm{6}}$ s⁻¹, 3 times higher than in dilute extracts and fog (Table S3); DOC concentrations in the standard PM extracts are similarly enhanced, ranging between 2350 and 4090 µM C (Table S2). Based on our calculations, inorganic species together account for no more than 10 % of $k_{\mathrm{OH}}^{\prime }$ in the PM extracts except for PME3D10, which is the most dilute sample and has the largest uncertainty (Tables S5 and S6). The rate constant for ^•OH destruction due to organics, i.e., $k_{\mathrm{OH},\mathrm{org}}^{\prime }$, obtained by subtracting contributions of the inorganic sinks from $k_{\mathrm{OH}}^{\prime }$, is well correlated with DOC concentrations (R²=0.73) (Fig. S6). Arakaki et al. (2013) showed that the ratio $k_{\mathrm{OH},\mathrm{org}}^{\prime }/\left[\mathrm{DOC}\right]$ is relatively constant in atmospheric waters, with an average (±1σ) value of $\mathrm{3.8}(\pm \mathrm{1.9})\times {\mathrm{10}}^{\mathrm{8}}$ L (mol C)⁻¹ s⁻¹. Our average (±1σ) measured ratio in all particle extracts is nearly twice as high, $\mathrm{7.1}(\pm \mathrm{2.7})\times {\mathrm{10}}^{\mathrm{8}}$ L (mol C)⁻¹ s⁻¹ but not statistically different (Table S3).

Davis winter-solstice-normalized ^•OH steady-state concentrations in all extracts are in the range of $(\mathrm{1.7}-\mathrm{7.9})\times {\mathrm{10}}^{-\mathrm{16}}$ M, with an average (±1σ) value of $\mathrm{5.1}(\pm \mathrm{2.4})\times {\mathrm{10}}^{-\mathrm{16}}$ M in the standard extracts (Fig. 2a, Table S3). While both the ^•OH photoproduction rate and rate constant for ^•OH loss are approximately 3 times higher in the standard PM extracts compared to the dilute extracts and fog, the two enhancements cancel out to give ^•OH steady-state concentrations that are similar across all three sample types. This relative consistency of ^•OH concentrations has been reported for a wide variety of atmospheric waters (Arakaki et al., 2013); our average concentration is similar to most of these past results (Fig. S7). As we discuss in Sect. 3.6, transport of ^•OH from the gas phase is also an important source to drops and particles, but its importance decreases with decreasing particle size.

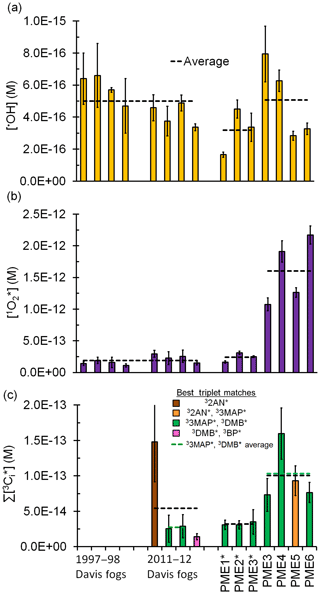
Figure 2 Measured steady-state concentrations of (a) hydroxyl radical, (b) singlet molecular oxygen, and (c) oxidizing triplet excited states of organic matter in particle extracts, along with previous measurements made in Davis fogs collected between 1997–1998 and 2011–2012 (Anastasio and McGregor, 2001; Kaur and Anastasio, 2017, 2018b). All concentrations are normalized to Davis midday, winter-solstice sunlight. Dilute particle extracts are indicated with an asterisk. Dashed lines represent sample averages.

We also calculated the quantum yield of hydroxyl radical formation, i.e., the fraction of absorbed photons that result in ^•OH formation (Eq. 9). The average (±1σ) value of Φ_OH in all particle extracts is (0.014±0.010) %, which is statistically similar to the average fog result (Table S3): while photoformation rates of ^•OH increase from fog to standard particle extracts (Table S3), light absorption shows a similar trend (Table S1).

The rate of ^•OH photoproduction in the field blanks is negligible, representing 1 % and 6 % of the average rate in standard and dilute extracts, respectively. The rate constants for ^•OH destruction ($k_{\mathrm{OH}}^{\prime }$) in the standard (FB2) and dilute (FB1) field blanks represent 10 % and 43 % of the corresponding PME averages. The latter result is puzzling, since the concentrations of ^•OH sinks measured in FB1 (i.e., DOC and ${\mathrm{NO}}_{\mathrm{2}}^{-}$; Table S2) are much lower relative to the extract. We discuss measurements of $k_{\mathrm{OH}}^{\prime }$ in the blanks in more detail in Sect. S2. We do not subtract the field blank results for $k_{\mathrm{OH}}^{\prime }$ from the corresponding PM extract values and thus our sample results are upper bounds.

3.4 Singlet molecular oxygen

The average (±1σ) Davis winter-solstice-normalized ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentration in the dilute extracts ($\mathrm{2.4}(\pm \mathrm{0.7})\times {\mathrm{10}}^{-\mathrm{13}}$ M) is very similar to the previous fog average (Fig. 2b). This is likely because brown carbon is the source of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ (Faust and Allen, 1992; Zepp et al., 1977) and the DOC concentrations in the fog and dilute extracts are very similar (Table S2). On the other hand, the average [${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$] in the more concentrated, standard PM extracts (PME3–6) is $\mathrm{1.6}(\pm \mathrm{0.5})\times {\mathrm{10}}^{-\mathrm{12}}$ M, nearly 7 times higher than the averages in Davis fog and dilute extracts (Fig. 2b, Table S7). This is because the standard extracts have higher DOC concentrations but the same major ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ sink, i.e., water. Across all fog and particle extracts, the rate of singlet oxygen formation ($P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$) is strongly correlated with the rate of sunlight absorption (R_abs) (R²=0.94; Fig. 3a), although this correlation is not evident in only the fog samples (Kaur and Anastasio, 2017). As seen for ^•OH, quantum yields of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ are similar in the extracts (standard and dilute) and fog (Table S7); the slope of the $P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$ versus R_abs correlation line (Fig. 3a) gives an overall quantum yield of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ of (3.8±0.2) %; i.e., across all samples roughly 4 % of the photons absorbed lead to the formation of singlet oxygen. This is nearly 260 times higher than the average quantum yield of ^•OH. Our quantum yields for singlet oxygen formation in PM extracts are similar to values previously reported for surface water organics (e.g., 2 %–5 % in Zhou et al. (2019).

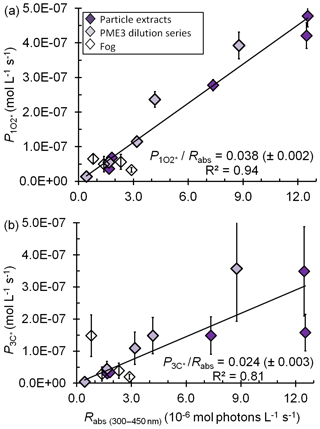
Figure 3 Correlations between (a) the rate of singlet oxygen photoproduction normalized to Davis winter-solstice sunlight ($P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$), (b) the rate of triplet photoproduction normalized to Davis winter-solstice sunlight ($P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$), and the rate of light absorption (R_abs) between 300 and 450 nm. Triplet rates for the fog samples were adjusted to account for the small DOC sink for triplets (Eq. 8). The P∕R_abs ratios (±1 SE) listed are unitless and represent the quantum yields.

3.5 Triplet excited states of organic matter (³C^*)

We also determined the kinetics and concentrations of oxidizing triplets by measuring the loss of two probes, syringol (SYR) and methyl jasmonate (MeJA) (Fig. S8). In the standard extracts, the average (±σ) Davis winter-normalized rate constants for loss of SYR and MeJA ($k_{\mathrm{Probe}}^{\prime }$) are $(\mathrm{4.3}\pm \mathrm{1.7})\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹ and $(\mathrm{2.6}\pm \mathrm{0.7})\times {\mathrm{10}}^{-\mathrm{5}}$ s⁻¹, which are equivalent to average lifetimes of 0.70(±0.20) and 11(±3) h, respectively (Tables S8 and S9). Triplet probe lifetimes in the dilute extracts are approximately 3 times longer and are very similar to fog values, indicating that the main source of triplet precursors to fog drops is the BrC present in the fog condensation nuclei rather than mass transport from the gas phase.

We correct the loss of triplet probes for oxidation by hydroxyl radical and singlet molecular oxygen (Eq. 6). In the standard extracts, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ^•OH account for an average of 13 % and 3 % of SYR loss, respectively (Table S8, Fig. S9); for methyl jasmonate, the corresponding contributions are 37 % and 13 %.

Next we use the ratio of the pseudo-first-order rate constants for probe losses by triplets, i.e., $k_{\mathrm{SYR},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }/k_{\mathrm{MeJA},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$, to characterize the average reactivity of the triplet species in each sample: a ratio close to 1 indicates higher reactivity, while a higher ratio indicates lower reactivity. The $k_{\mathrm{Probe},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$ ratio (i.e., $k_{\mathrm{SYR},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }/k_{\mathrm{MeJA},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$) in all extracts ranges between 7.9 and 37 (Table S12), which is a narrower range than in Davis fog samples (7.5 to 110) (Kaur and Anastasio, 2018b). Based on the $k_{\mathrm{Probe},{}^{\mathrm{3}}{\mathrm{C}}^{*}}^{\prime }$ ratios, triplets in the PM extracts generally have an average reactivity similar to model aromatic triplets 3'-methoxyacetophenone (³3MAP^*) and 3,4-dimethoxybenzaldehyde (³DMB^*) (Fig. 2c, Table S12). The average (±σ) triplet steady-state concentration in the standard extracts is $\mathrm{1.0}(\pm \mathrm{0.4})\times {\mathrm{10}}^{-\mathrm{13}}$ M (Fig. 2c, Table S13), which is nearly twice the fog average but not statistically significantly different. If we consider only the PM and fog samples that have triplet reactivities similar to ³3MAP^* and ³DMB^* (i.e., the green average lines in Fig. 2c), the average triplet concentration in the standard PM extracts is nearly 4 times greater than in fog (Table S2), similar to the ratio of DOC concentrations.

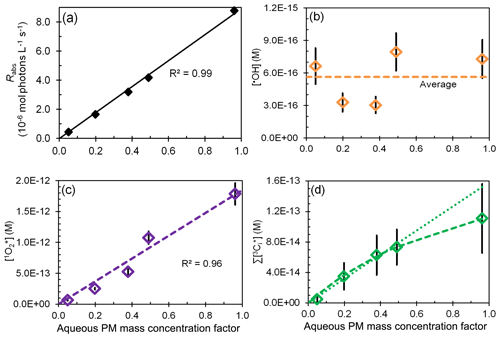
Figure 4 Effect of change in aqueous particle mass concentration (i.e., sample dilution) for sample PME3 on (a) rate of light absorption and the steady-state concentrations of (b) hydroxyl radical, (c) singlet molecular oxygen, and (d) oxidizing triplet excited states of organic matter. The last panel shows both linear (dotted) and hyperbolic (dashed) fits to the data. In each plot the x axis is a measure of sample dilution, with higher concentration factors corresponding to more concentrated particle extracts (Eq. 10).

In the standard extracts the average concentration of oxidizing triplets is 16 times lower than [${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$] but nearly 200 times higher than [^•OH] from in situ sources. Our measurements of oxidizing triplet concentrations lie at the higher end of measured and estimated concentrations of total (i.e., oxidizing and energy transfer) triplets in surface waters, 10⁻¹⁵–10⁻¹³ M (Zepp et al., 1985; Grebel et al., 2011). The average (±1σ) rate of triplet photoformation, $P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$, is $\mathrm{2.0}(\pm \mathrm{1.0})\times {\mathrm{10}}^{-\mathrm{7}}$ M s⁻¹ (i.e., 720(±360) µM h⁻¹) in the standard extracts (Table S13). Thus the ratios of the average production rates for ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, ³C^*, and ^•OH are $\mathrm{290}:\mathrm{170}:\mathrm{1}$. There is a fair correlation between $P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$ and R_abs(Fig. 3b), similar to the case for $P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$ (Fig. 3a), which is consistent with BrC as the source of triplets. Sample-to-sample variability in the fraction of the total triplet pool that can oxidize organics likely causes the $P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$ correlation (R²=0.81) to be weaker than that of $P_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}$ (R²=0.94). The average (±1σ) oxidizing triplet quantum yield in standard extracts is (2.4±1.0) % (Table S13), approximately 2 times lower than the value for ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ (Table S7) but 150 times higher than for ^•OH (Table S3). Our triplet quantum yields are within the wide range of values that has been reported for surface waters, approximately 0.4 %–7 % (Zepp et al., 1985; Grebel et al., 2011; Zhou et al., 2019).

Triplet excited states have two main reaction pathways: energy transfer (e.g., to make ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$) and electron transfer (e.g., to oxidize a phenol) (Zepp et al., 1985; McNeill and Canonica, 2016; Kaur and Anastasio, 2018b). Essentially all triplets possess enough energy to form ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ (McNeill and Canonica, 2016), but only a subset of the triplet pool can oxidize organics via electron transfer. Thus the quantum yield of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ can be used to estimate the total triplet quantum yield, while our measurements of ${\mathrm{\Phi }}_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$ constrain the smaller subset of oxidizing triplets (assuming energy transfer from triplets is the only source of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$). The quantum yield for all triplets can be estimated as ${\mathrm{\Phi }}_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}/f_{\mathrm{\Delta }}$, where f_Δ, the fraction of ³C^* interactions with dissolved O₂ that yield ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, is approximately 0.5 (McNeill and Canonica, 2016; Kaur and Anastasio, 2018b). For our standard extracts, the average value of ${\mathrm{\Phi }}_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}/f_{\mathrm{\Delta }}$ is 0.078±0.019; i.e., approximately 8 % of the photons absorbed by brown carbon chromophores make a triplet excited state. Next we use the ratio ${\mathrm{\Phi }}_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}/({\mathrm{\Phi }}_{{}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}}/f_{\mathrm{\Delta }})$ to estimate the fraction of all triplets that can participate in electron-transfer (oxidation) reactions. The average value of this fraction is 0.35±0.12 for all the PM extracts; i.e., on average, approximately a third of all triplets are oxidizing (range = 18 %–50 %; Table S13).

3.6 Predicting photooxidant concentrations in ambient particle water

Since our particle extracts are approximately 1000 times more dilute than ambient Davis particles during winter, we want to be able to estimate oxidant concentrations under ambient conditions. To do this we first measured photooxidant concentrations as a function of dilution for the same sample and then extrapolated our results to ambient particle conditions. For the first step, we extracted squares of filter number 3 using five different volumes of Milli-Q water, from 10 to 0.50 mL (Sect. 2.5.4), corresponding to aqueous PM mass concentration factors (CF) of 0.05 (most dilute) to 0.96 (most concentrated) (Eq. 10). For this sample, these are equivalent to PM solute mass/water mass ratios typical for dilute to very concentrated cloud or fog drops, i.e., $(\mathrm{0.35}-\mathrm{8.4})\times {\mathrm{10}}^{-\mathrm{4}}$ µg PM/µg H₂O; in comparison, ambient particles have ratios of approximately 1 µg PM/µg H₂O and higher (Table S14). The rate of light absorption increases linearly with CF (Fig. 4a), indicating that BrC and other chromophores are efficiently extracted for all Milli-Q volumes employed.

The change in photooxidant concentration with CF depends on how the ratio of sources and sinks varies with dilution. In the case of hydroxyl radical, P_OH and $k_{\mathrm{OH}}^{\prime }$ both increase as extracts get more concentrated (i.e., as CF increases), resulting in an ^•OH concentration that is noisy but essentially unchanged over the 20-fold increase in concentration factor (Fig. 4b). This result is consistent with the relatively constant [^•OH] in our particle extracts relative to fog (Fig. 3a, dashed black lines) and with prior results showing very similar concentrations for rain, cloud, fog, and marine PM extracts (Fig. S7 and Arakaki et al., 2013).

To estimate [^•OH] in particle liquid water, we use the measured linear dependences of the rate of ^•OH photoproduction (P_OH) and loss rate constant ($k_{\mathrm{OH}}^{\prime }$) on concentration factor, which corresponds to a measured PM mass/water mass ratio (Fig. S10). Under a typical wintertime, Central Valley ambient particle water condition (1 µg PM/µg H₂O), the in situ P_OH and $k_{\mathrm{OH}}^{\prime }$ are estimated to be $\mathrm{4.2}\times {\mathrm{10}}^{-\mathrm{6}}$ M s⁻¹ and 5.5×10⁹ s⁻¹, respectively (Fig. S10). This extrapolation of only aqueous processes gives an ^•OH concentration in particle water of $\mathrm{7.6}\times {\mathrm{10}}^{-\mathrm{16}}$ M, which is similar to the average of the measurements in Fig. 4b. However, this estimate does not include the contribution of mass transport of gas-phase ^•OH to the particles. As detailed in Sect. S4, we estimate that the rate of ^•OH gas-to-particle transport under particle conditions is $\mathrm{4.2}\times {\mathrm{10}}^{-\mathrm{7}}$M s⁻¹, which is approximately 10 % of the ^•OH photoformation rate from aqueous sources. Figure 5 shows estimated ^•OH steady-state concentrations considering both aqueous reactions and gas-phase mass transport across a wide range of drop-to-particle conditions: [^•OH] decreases from $\mathrm{5.4}\times {\mathrm{10}}^{-\mathrm{15}}$ M under dilute drop conditions ($\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ µg PM/µg H₂O) to $\mathrm{8.4}\times {\mathrm{10}}^{-\mathrm{16}}$ M under the much more concentrated particle conditions (1 µg PM/µg H₂O). The calculated [^•OH] values (orange line in Fig. 5) are higher than our measured values (orange points in Fig. 5) because of the gas-phase mass transport source. Changes in this source are also responsible for the slow decrease in calculated [^•OH] as conditions become more concentrated (i.e., as µg PM/µg H₂O increases). In the case of singlet oxygen, steady-state concentrations increase proportionally with PM mass concentration factor (Fig. 4c). Our interpretation of this result is that the concentrations of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ sources (i.e., BrC) increase proportionally with concentration factor, while the concentration of the main sink for ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ (i.e., water) is essentially unchanged. At higher PM mass/water mass ratios, we calculate that organic compounds become a significant sink for singlet oxygen (Sect. S4), leading to a plateau in [${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$] under the more concentrated conditions of particles (Fig. 5). This extrapolation for ambient PM conditions (1 µg PM/µg H₂O) predicts an ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentration in particle water of $\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{10}}$ M (Table S15, Fig. 5), which is 2400 times higher than our prediction for dilute fog/cloud drops. While there are no other measurements of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in particles, similar enhancements in ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentrations (up to a factor of roughly 10⁴) have been found in cases where ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ precursors become highly concentrated, e.g., in liquid-like regions of ice (Bower and Anastasio, 2013) and in regions of hydrophobic chromophoric dissolved organic matte (CDOM) in solution (Latch and McNeill, 2006).

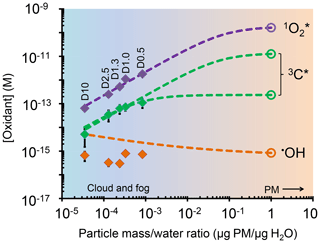
Figure 5 Dependence of photooxidant concentrations on particle mass/water mass ratio (i.e., aqueous particle concentration) in extracts of sample PME3. Solid diamonds are measured values under experimental dilution conditions (typical for clouds or fogs), while the open circles are values expected in more concentrated particle liquid water based on the dashed line extrapolations. For the solid symbols, error bars (±1σ) are often smaller than the symbols. Data labels on the diamonds (e.g., D10) represent the water volume used to extract the PME3 filter square (Sect. 2.5.4). The dashed line extrapolations include the contributions from both aqueous processes and interactions with the gas phase (Sect. S4). For oxidizing triplets, two extrapolation scenarios are shown: a best estimate (lower line) and a high estimate (upper line), as described in Sect. S4 and Table S15.

An increase in extract concentration (i.e., CF) also increases the triplet steady-state concentration (Fig. 4d), but there is greater uncertainty in this trend, in part because there is more uncertainty in measurements of $\mathrm{\Sigma }\left[{}^{\mathrm{3}}{{\mathrm{C}}_{\mathrm{i}}}^{*}\right]$. As described in Sect. S4, we fit the data in Fig. 4d with a hyperbolic regression under two cases: (1) a best fit, where parameters were adjusted to minimize the regression error; and (2) a high-estimate fit, where parameters were adjusted so that the regression line passed near the upper portion of the error bar for the CF 0.96 data point. These are the dashed and dotted lines in Fig. 4d, respectively. In both cases the triplet concentration initially rises more quickly with CF but then approaches a plateau at higher CF values. Our interpretation of this behavior is that as CF increases, [DOM] and $P_{{}^{\mathrm{3}}{\mathrm{C}}^{*}}$ increase linearly but the dominant triplet sink switches from dissolved O₂ at low CF to DOM at high CF. Wenk et al. (2011, 2013) have shown that surface water DOM can quench triplets when DOM concentrations are greater than 20 mg C L⁻¹; in the PME3D extracts of Fig. 4, DOM ranges from 4.3 to 86 mg C L⁻¹ (Table S2). Based on our previous work, we believe that phenols from wood combustion are reacting with (and physically quenching) triplets in our PM extracts (Smith et al., 2014, 2015). As described in Sect. S5, by fitting a kinetic model to our triplet dilution data we estimate that the total (reaction and quenching) rate constant for triplets with DOC in the PME3 extracts is $\mathrm{9.3}(\pm \mathrm{1.3})\times {\mathrm{10}}^{\mathrm{7}}$ L (mol C)⁻¹ s⁻¹.

These two extrapolations result in oxidizing triplet concentrations under PM conditions (1 µg PM/µg H₂O) of $\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{13}}$ M (best fit) and $\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{11}}$ M (high estimate). Taken together with the other oxidant measurements, we estimate that the ratio of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ : ³C^* : ^•OH concentrations in ambient particle water is approximately ${\mathrm{10}}^{\mathrm{5}}:{\mathrm{10}}^{\mathrm{4}}-{\mathrm{10}}^{\mathrm{2}}:\mathrm{1}$.

4 Implications

Our dilution experiments suggest that ^•OH, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, and ³C^* behave very differently as the PM/water ratio increases from cloud and fog drop conditions to water-containing particles (Fig. 5). To understand what this implies for the fate of organic compounds, we estimated the gas–aqueous partitioning and lifetimes of five model organic compounds for both fog and aqueous aerosol (Fig. 6). We consider reactions with two gas-phase oxidants (^•OH, O₃) and four aqueous-phase oxidants (^•OH, O₃, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, ³C^*) (Table S16). Our model organics represent two groups in terms of gas–aqueous partitioning: one group with modest Henry's law constants (K_H∼10⁴ M atm⁻¹) and one with much higher values ($K_{\mathrm{H}}={\mathrm{10}}^{\mathrm{9}}-{\mathrm{10}}^{\mathrm{11}}$ M atm⁻¹) (Fig. 6 and Table S17).

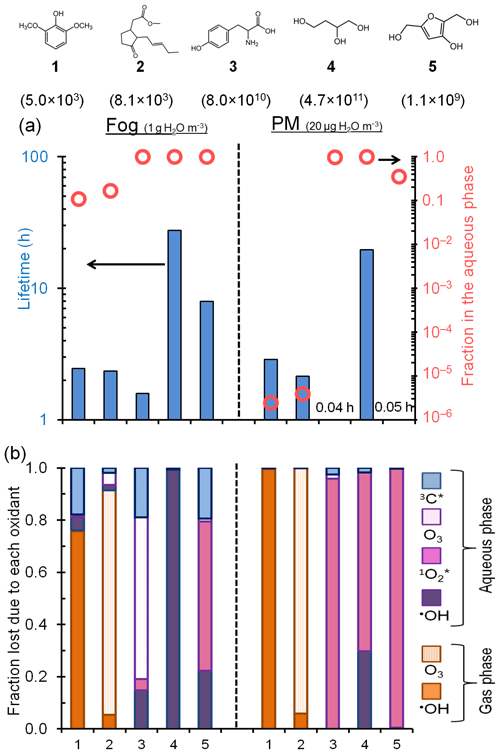
Figure 6 Fate of five model organic compounds – (1) syringol, (2) methyl jasmonate, (3) tyrosine, (4) 1,2,4-butanetriol, and (5) 3-hydroxy-2,5-bis(hydroxymethyl)furan – under liquid water content conditions for fog (left of vertical dashed line; 1 g H₂O/m³ air) and PM (right of line; 20 µg H₂O/m³ air). Estimated Henry's law constants for the compounds (in units of M atm⁻¹) are in parentheses beneath each structure. In panel (a) the columns represent overall lifetimes of the organics and the open circles represent the fractions in the aqueous phase. Panel (b) shows the fraction of each compound lost via various gas and aqueous pathways. The triplet contribution in PM is estimated using the lower-bound triplet concentration extrapolation, i.e., $\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{13}}$ M (Fig. 5). Oxidant concentrations and rate constants are in Tables S16 and S17.

Figure 6a shows the overall lifetimes of the five model organics and the fraction of each present in fog and PM. For the organics with the lowest K_H values, approximately 10 %–20 % is present in the aqueous phase under fog conditions, but almost none is present in the particle liquid water. Consequently, gas-phase reactions dominate their overall lifetimes, which are approximately 2 to 3 h for both fog and PM conditions. In contrast, the compounds with high K_H values are partitioned strongly to the aqueous phase for both the fog and PM scenarios (Fig. 6a). But due to the overall higher oxidant concentrations in PM, the lifetimes of these organics are predicted to be shorter – sometimes by large factors – in PM than in fog (Fig. 6a, Table S17). Additionally, their main sinks change from fog to PM, shifting from aqueous ^•OH, O₃, and ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in fog to being generally dominated by ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in PM water (Fig. 6b). For example, for tyrosine (compound 3), the predominant sink changes from aqueous O₃ in fog to ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in water-containing particles, while its lifetime decreases from 1.6 to 0.04 h (Fig. 6b and Table S17).

While triplets are negligible oxidants for individual organics in particles under the conditions of Fig. 6, the picture changes if we move from the Fig. 6 triplet concentration of $\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{13}}$ M to the high-estimate concentration ($\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{11}}$ M; Fig. 5). Under this condition aqueous oxidation still dominates the loss of the high-K_H compounds, but ³C^* becomes a much more important oxidant in PM and organic lifetimes get shorter by factors of 3 to 180 compared to fog (Fig. S11). While there is large uncertainty in the triplet concentrations in PM, Figs. 6 and S11 both indicate that aqueous oxidants can control the fate of highly soluble species in aerosols and that organic lifetimes can be shorter in PM because of an enhancement in oxidant concentrations.

Finally, despite the uncertainty in triplet concentration under particle conditions, the formation rate of ³C^* is fast enough – and the fraction of triplets lost via reaction with organics is high enough – that triplets represent, in aggregate, a significant sink for organic compounds in particles. While these two ideas might seem contradictory, we propose that the suite of reactive organic compounds is suppressing the triplet concentrations enough that ³C^* are small sinks for individual organic compounds but are significant sinks when integrated over all of the reactive organics. As described in Sect. 3.5, the formation rates for ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, ³C^*, and ^•OH have a ratio of $\mathrm{290}:\mathrm{170}:\mathrm{1}$, respectively, in the PM extracts; based on our dilution experiments (Fig. 4), we expect similar ratios in ambient particle liquid water. Since organic compounds appear to be the major sinks for all three oxidants under ambient particle conditions, and since each oxidant is at a steady state, the ratio of formation rates is approximately the same as the ratio of total rates of organic compound oxidation by each oxidant. Thus, while the steady-state concentration of ³C^* might be significantly lower than that of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ in particle water, both oxidants appear to be similarly important in the overall processing of particulate organics. In contrast, the total rate of oxidation of organics by ^•OH appears to be 200–300 times slower, although ^•OH will be relatively more important for less reactive organics. This comparison suggests that both singlet molecular oxygen and triplet excited states are important for the processing of organic compounds in particle liquid water.

5 Conclusions and uncertainties

We have made the first measurements of singlet molecular oxygen and oxidizing triplet states in aqueous extracts of particles, in addition to measuring hydroxyl radical. Under our standard condition, the particle extracts are approximately 3 times more concentrated than wintertime Davis fog waters. The extracts contain significant amounts of brown carbon, with DOC-normalized mass absorption coefficients between roughly 15 000 and 30 000 cm² (g C)⁻¹ and absorption Ångström exponents of 6.2 to 7.9. Upon absorbing light, BrC and other chromophores in the samples form significant amounts of ^•OH, ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$, and ³C^*. While concentrations of ^•OH in the PM extracts are in the same range as found in fog waters, concentrations of the oxidants derived primarily from BrC – i.e., ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* – are higher in the extracts compared to in fog by factors of approximately 7 and 2, respectively.

Dilution experiments indicate that the ^•OH concentration is essentially independent of the PM mass concentration in solution, consistent with previous results, while ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* increase with increasing aqueous PM concentration. Extrapolating our findings to the much more concentrated conditions expected in ambient particle water suggests that hydroxyl radical concentrations in particles will be somewhat lower than values in fog and cloud drops, a result of size-dependent changes in mass transport from the gas phase. In contrast, oxidants formed from illumination of brown carbon will be enhanced in particles: moving from very dilute drops ($\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ µg PM/µg H₂O) to concentrated particles (1 µg PM/µg H₂O) we predict that the concentration of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ will increase by approximately a factor of 2400, while concentrations of oxidizing triplets will increase between a factor of 30 and 2000. The higher ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ concentrations predicted in particles lead to a large decrease in the lifetimes of highly water soluble organic compounds compared to foggy conditions, even though the liquid water content of the particles is roughly 10⁴ times lower than the fog. It appears that triplets are also more significant oxidants for individual organic compounds in PM than in fog, but there is too much uncertainty in our data to properly assess this increase. In contrast, ^•OH is important for the oxidation of organics that react only slowly with ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* but is otherwise a minor oxidant for the organics we considered since the particulate ^•OH concentration is quite low.

While our results suggest that oxidants derived from brown carbon are very significant in water-containing particles, there are several large uncertainties. Most significantly, because of experimental limitations on the maximum PM concentration in our extracts, we need to extrapolate oxidant measurements over a very large range (approximately a factor of 1000) to predict oxidant levels in ambient water-containing particles. This results in very large uncertainties. As part of this uncertainty, it is difficult to assess how reactions in the particles might suppress concentrations of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^*. Secondly, while calculations suggest that unaccounted oxidants are minor sinks for our triplet probes, if these species were important our triplet concentrations would be biased high. Finally, it is unclear how widely our results, which are for one season and one location, can be applied to other particles containing brown carbon. However, PME3, our one sample collected during both daytime (with little biomass burning) and night (with significant biomass burning), had similar reactivity to the other samples, which were collected only at night. Regardless, since these are the first measurements of ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* in particles, strengthening and improving our findings requires more measurements, especially for other seasons and locations. Measurements under much higher particle mass/water mass ratios, ideally under ambient conditions, are also needed.

Despite the uncertainties, our results indicate that BrC-derived photooxidants such as singlet molecular oxygen and organic triplet excited states can be important oxidants in atmospheric particles. Currently these oxidants are not included in atmospheric models, although our calculations suggest that ${}^{\mathrm{1}}{{\mathrm{O}}_{\mathrm{2}}}^{*}$ and ³C^* can dominate the processing of highly soluble organic molecules in aerosol particles.