Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 3: Aluminosilicates

Aluminosilicates and quartz constitute the majority of airborne mineral dust. Despite similarities in structures and surfaces they differ greatly in terms of their ice nucleation (IN) efficiency. Here, we show that determining factors for their IN activity include surface ion exchange, NH₃ or ${\mathrm{NH}}_{\mathrm{4}}^{+}$ adsorption, and surface degradation due to the slow dissolution of the minerals. We performed immersion freezing experiments with the (Na-Ca)-feldspar andesine, the K-feldspar sanidine, the clay mineral kaolinite, the micas muscovite and biotite, and gibbsite and compare their IN efficiencies with those of the previously characterized K-feldspar microcline and quartz. Samples were suspended in pure water as well as in aqueous solutions of NH₃, (NH₄)₂SO₄, NH₄Cl and Na₂SO₄, with solute concentrations corresponding to water activities a_w equal to 0.88–1.0. Using differential scanning calorimetry (DSC) on emulsified micron-sized droplets, we derived onset temperatures of heterogeneous (T_het) and homogeneous (T_hom) freezing as well as heterogeneously frozen water volume fractions (F_het). Suspensions in pure water of andesine, sanidine and kaolinite yield T_het equal to 242.8, 241.2 and 240.3 K, respectively, while no discernable heterogeneous freezing signal is present in the case of the micas or gibbsite (i.e., $T_{\text{het}}\approx T_{\text{hom}}\approx \mathrm{237.0}$ K). The presence of NH₃ and/or ${\mathrm{NH}}_{\mathrm{4}}^{+}$ salts as solutes has distinct effects on the IN efficiency of most of the investigated minerals. When feldspars and kaolinite are suspended in very dilute solutions of NH₃ or ${\mathrm{NH}}_{\mathrm{4}}^{+}$ salts, T_het shifts to higher temperatures (by 2.6–7.0 K compared to the pure water suspension). Even micas and gibbsite develop weak heterogeneous freezing activities in ammonia solutions. Conversely, suspensions containing Na₂SO₄ cause the T_het of feldspars to clearly fall below the water-activity-based immersion freezing description (Δa_w= const.) even in very dilute Na₂SO₄ solutions, while T_het of kaolinite follows the Δa_w= constant curve. The water activity determines how the freezing temperature is affected by solute concentration alone, i.e., if the surface properties of the ice nucleating particles are not affected by the solute. Therefore, the complex behavior of the IN activities can only be explained in terms of solute-surface-specific processes. We suggest that the immediate exchange of the native cations (K⁺, Na⁺, Ca²⁺) with protons, when feldspars are immersed in water, is a prerequisite for their high IN efficiency. On the other hand, excess cations from dissolved alkali salts prevent surface protonation, thus explaining the decreased IN activity in such solutions. In kaolinite, the lack of exchangeable cations in the crystal lattice explains why the IN activity is insensitive to the presence of alkali salts (Δa_w= const.). We hypothesize that adsorption of NH₃ and ${\mathrm{NH}}_{\mathrm{4}}^{+}$ on the feldspar surface rather than ion exchange is the main reason for the anomalous increased T_het in dilute solutions of NH₃ or ${\mathrm{NH}}_{\mathrm{4}}^{+}$ salts. This is supported by the response of kaolinite to NH₃ or ${\mathrm{NH}}_{\mathrm{4}}^{+}$, despite lacking exchangeable ions. Finally, the dissolution of feldspars in water or solutions leads to depletion of Al and formation of an amorphous layer enriched in Si. This hampers the IN activity of andesine the most, followed by sanidine, then eventually microcline, the least soluble feldspar.

1 Introduction

Clouds interacting with incoming solar radiation and outgoing longwave radiation influence the Earth's radiation budget (IPCC, 2013). Ice crystals are found in cold cirrus clouds as well as mixed-phase clouds, modulating their radiative properties (Sun and Shine, 1994; Sassen and Benson, 2001). Moreover, mixed-phase clouds are responsible for precipitation formation via the Wegener–Bergeron–Findeisen process (Rogers and Yau, 1989; Korolev and Field, 2008). Ice can either form homogeneously from liquid droplets supercooled to temperatures below about 237 K or heterogeneously at higher temperatures with the help of foreign particles, called ice nucleating particles (INPs), which lower the free energy required to form a critical ice embryo growing into crystalline ice (Vali et al., 2015). Heterogeneous ice nucleation (IN) can proceed via various pathways, namely (1) immersion freezing, when ice forms on an INP suspended inside a supercooled droplet; (2) condensation freezing, when IN is concurrent with the activation of an aerosol particle to a cloud droplet and (3) contact nucleation, when ice forms in a supercooled droplet upon collision with an INP (Pruppacher and Klett, 1994; Vali et al., 2015). These freezing mechanisms all occur under participation of a liquid phase. Ice may also form at conditions supersaturated with respect to ice but subsaturated with respect to liquid water, a process termed deposition nucleation (Vali et al., 2015). Traditionally, it has been ascribed to deposition of water molecules directly from the vapor phase onto a solid INP without involvement of a liquid phase. Though, it has been questioned whether this process actually occurs, or whether ice forms by pore condensation and freezing (PCF), after stabilizing water in pores by an inverse Kelvin effect (Marcolli, 2014). The most important IN mechanisms in mixed-phase clouds are viewed to be immersion and condensation freezing (Hoose et al., 2008; Ansmann et al., 2009; Twohy et al., 2010; de Boer et al., 2011).

Various studies have shown that mineral dust, typically composed of feldspars, clay minerals, quartz, micas, calcite and metal oxides, constitutes an important class of INPs (Pruppacher and Klett, 1994; Murray et al., 2011; Hoose and Möhler, 2012; Atkinson et al., 2013; Cziczo et al., 2013; Kanji et al., 2017). The impact of mineral dusts on cloud properties has been shown in several observational and modeling studies (Lohmann and Diehl, 2006; Hoose et al., 2010; Seifert et al., 2010). Feldspars have been reported to be the most IN active minerals although the individual members of the feldspar group exhibit very different IN efficiencies in immersion freezing mode (Atkinson et al., 2013; Zolles et al., 2015; Harrison et al., 2016; Kaufmann et al., 2016). During long-range transport in the atmosphere, mineral dust particles can acquire organic and inorganic coatings (Usher et al., 2003; Sullivan et al., 2007), which may change their IN efficiencies (Zuberi et al., 2002; Zobrist et al., 2008; Eastwood et al., 2009; Augustin-Bauditz et al., 2014, 2016; Kumar et al., 2018a; Kanji et al., 2019). When the INPs are fully covered by a water-soluble coating, IN may occur by an immersion freezing mechanism, typically after the aerosol particles experience increasing humidity (Augustin-Bauditz et al., 2014). Indeed, studies conducted with size-selected Arizona Test Dust (ATD, 300 nm) coated with sulfuric acid have shown irreversible impairment of its IN efficiency in both water-subsaturation and supersaturation regimes (Sullivan et al., 2010b; Niedermeier et al., 2011; Reitz et al., 2011). On the other hand, Sullivan et al. (2010a) also reported decreased IN efficiency of size-selected ATD particles (200 nm) coated with nitric acid at RH_w<97 %, which recovered at conditions with RH_w≥100 %. In addition, Sihvonen et al. (2014) discussed the hampering of IN efficiency of clay minerals (kaolinite and montmorillonite) treated with aqueous acids at conditions below water saturation on the basis of the reaction products and surface physicochemical changes generated on the mineral surface due to acid–mineral interaction. Although, Kanji et al. (2019) reported no effect of secondary organic aerosol (SOA) coating on the IN efficiency of two types of natural dust samples (Saharan and Asian) in immersion freezing mode.

Koop et al. (2000) provided observational evidence and theoretical underpinning that the homogeneous freezing temperatures of aqueous solution droplets can be described as a function of the water activity of solution (a_w) alone, namely by shifting the ice melting curve by a constant Δa_w to higher a_w values. A similar approach has been used, with a suitably reduced Δa_w, to describe the immersion freezing temperatures of various types of INPs as a function of a_w. While the water-activity-based description of homogeneous IN is well established, for heterogeneous IN this description assumes implicitly that there is no interaction between particle surface and solute (Zobrist et al., 2008). Several studies suggest that the IN efficiency of various INPs can indeed be approximated by such a water-activity-based description (Archuleta et al., 2005; Zobrist et al., 2006, 2008; Koop and Zobrist, 2009; Knopf et al., 2011; Knopf and Forrester, 2011; Knopf and Alpert, 2013; Rigg et al., 2013). However, recent studies by Whale et al. (2018) and Kumar et al. (2018a) showed independently that the IN temperatures of some minerals – including the K-feldspars microcline and sanidine – deviate significantly from a freezing point line with Δa_w= const., with a shift to higher temperatures in the presence of dilute NH₃- and ${\mathrm{NH}}_{\mathrm{4}}^{+}$-containing solutions and a shift to lower temperatures in the presence of alkali salts.

In the companion paper Part 1 (Kumar et al., 2018a) we discussed the interactions of inorganic solutes with the microcline surface and the effects on its IN efficiency. In this and the companion paper Part 2 (Kumar et al., 2019) we relate IN on mineral surfaces with the mineral surface properties by investigating the differences in IN activity of chemically and/or structurally similar minerals in pure water and aqueous solutions. The analysis of our previous freezing experiments suggests that heterogeneous IN does not occur on the whole surface of INPs with a uniform probability. Rather, there are preferred locations, so-called active sites, which are responsible for the IN activity of a surface (Fletcher, 1969; Marcolli et al., 2007; Vali, 2014; Vali et al., 2015; Kaufmann et al., 2017). Estimates based on classical nucleation theory suggests that minimum surface areas of these sites need to cover about 10–50 nm² (Kaufmann et al., 2017). In the present paper, for the discussion of IN activity of aluminosilicates we will assume that IN active surface structures need to be of such size. We will further assume that IN active sites exhibit surface functional groups that are characteristic of the mineral, but either occurring in a special 2-D arrangement (e.g., higher density of certain end groups on a flat surface) or with a special 3-D feature (e.g., a step, crack or wedge), making them IN active.

In our companion papers (Kumar et al., 2018a, 2019) we discuss the specific aluminosilicate microcline and various aluminum-free silicas (both amorphous and crystalline forms) with a special focus on quartz (a crystalline form of silica). The present study investigates the differences in IN activities of a number of other aluminosilicates, and offers an overall summary. The aluminosilicates investigated by immersion freezing include sanidine (K-feldspar), andesine (Na-Ca-feldspar), kaolinite, micas (muscovite and biotite) and gibbsite, dispersed in solution droplets containing ammonia or the inorganic salts ammonium sulfate, ammonium chloride and sodium sulfate.

2 Methodology

2.1 Sources of samples, mineralogical composition and particle size distribution

Feldspar (sanidine and andesine) and mica (muscovite and biotite) samples were obtained from the Institute of Geochemistry and Petrology of ETH Zurich and milled with a tungsten carbide disc mill. Particle number size distributions were obtained with a TSI 3080 scanning mobility particle sizer (SMPS) and a TSI 3321 aerodynamic particle sizer (APS). The dry particles were dispersed using a fluidized bed. The detailed size distribution and mineralogical composition (using X-ray diffraction, XRD) of the feldspars, kaolinite and muscovite are given in Kaufmann et al. (2016). Rietveld refinement using Profex software (Döbelin and Kleeberg, 2015) was performed for a quantitative analysis. The microcline sample (Si : Al ≈ 3.1; Al : K ≈ 1.4) consists of 86.33 % (±1.71 %) microcline, mixed with orthoclase (6.18 % ± 0.72 %) and albite (7.49 % ± 0.48 %) (Kumar et al., 2018a). The sanidine sample proved to be pure sanidine with Si : Al ≈ 3.1 and Al : K ≈ 1.6 while andesine proved to be pure andesine with Si : Al ≈ 1.7 and Ca ∕ (Ca + Na) = 64 %. Note that andesine would be a labradorite based on the Ca ∕ (Ca + Na) ratio, but crystallographically it fits best with an andesine. Also note that the andesine sample is termed as “plagioclase” in Kaufmann et al. (2016). Biotite shows a bimodal particle size distribution with mode diameters of 241 nm and 1.7 µm (see Supplement). XRD analysis showed no traces of tungsten carbide in any of the milled samples. The kaolinite used in this study was KGa-1b from the Clay Mineral Society. Gibbsite (Al(OH)₃⋅xH₂O, < 45 µm) was obtained from Sigma-Aldrich.

2.2 Emulsion freezing experiments with mineral dusts freshly suspended in pure water or solutions

We described the general setup of immersion freezing experiments in Part 1 of this series of papers (Kumar et al., 2018a). Here we repeat essential aspects for convenience. The experiments were carried out with the differential scanning calorimetry (DSC; TA Instruments, Q10) setup (Zobrist et al., 2008). Sanidine and andesine suspensions (2 wt %), kaolinite suspensions (5 wt %), mica (muscovite and biotite; 5 wt % and 10 wt %) suspensions and gibbsite (10 wt %) suspensions in water (molecular biology reagent water from Sigma-Aldrich) were prepared with varying concentrations (0–20 wt %) of (NH₄)₂SO₄ (Sigma-Aldrich, ≥ 99 %), NH₄Cl (Sigma-Aldrich, ≥ 99.5 %), Na₂SO₄ (Sigma-Aldrich, ≥ 99 %) and diluted NH₃ solutions (Merck, 25 %). To avoid particle aggregation, the suspensions were sonicated for 5 min before preparing the emulsions. The aqueous suspension and an oil/surfactant mixture (95 wt % mineral oil, Sigma-Aldrich, and 5 wt % lanolin, Fluka Chemical) taken in a ratio of 1 : 4 were mixed using a rotor–stator homogenizer (Polytron PT 1300D with a PT-DA 1307/2EC dispersing aggregate) for emulsification (40 s at 7000 rpm); 4–10 mg of this emulsion was placed in an aluminum pan, which was hermetically closed; and then, following the method developed and described by Marcolli et al. (2007), three freezing cycles in the DSC were performed. The first and the third freezing cycles were executed at a cooling rate of 10 K min⁻¹ to control the stability of the emulsion. The second freezing cycle was run at 1 K min⁻¹ cooling rate and used for evaluation (Zobrist et al., 2008; Pinti et al., 2012; Kaufmann et al., 2016; Kumar et al., 2018a). Emulsions prepared by this procedure exhibit droplet size distributions peaking at diameters of about 2–3 µm in number and a broad distribution in volume with highest contributions from particles with diameters between 4 and 12 µm similar to the ones shown in Fig. 1 of Marcolli et al. (2007), Pinti et al. (2012) and Kaufmann et al. (2016). For a clear heterogeneous signal, dust particles need to be of similar size or smaller than the droplets. Large particles (> 10 µm) present in dust samples contribute significantly to the dust mass but hardly to the heterogeneous freezing signal.

Typically, a DSC thermogram of the cooling cycle performed with an emulsion containing INPs features two freezing signals, as depicted in Kumar et al. (2018a). The first peak occurring at a warmer temperature displays the heat release accompanied by heterogeneous freezing and the second peak occurring at a colder temperature is due to homogeneous freezing. The freezing temperatures (T_het and T_hom) are determined as the onset of the freezing peaks (i.e., intersection of the tangent drawn at the point of greatest slope at the leading edge of the thermal peak with the extrapolated baseline). Droplets with diameters of about 12 µm are considered to be relevant for the freezing onset. The loading of these droplets with particles depends on the particle size distribution and the suspension concentration. For 2 wt %–5 wt % suspensions, 12 µm droplets contain about 100–1000 particles (Kumar et al., 2018a). The melting temperature (T_melt) was determined as the maximum of the ice melting peak. For the investigated samples, average precision in T_het was ±0.1 K with maximum deviations not exceeding 0.5 K. Precisions of T_hom and T_melt are precise within ±0.1 K.

The heat release is related to the frozen water volume and is given by the integral of the heat signal over time. Since the enthalpy of freezing is temperature dependent, this evaluation is only approximate (Speedy, 1987; Johari et al., 1994). F_het is defined as the ratio of the heterogeneous freezing signal to the total freezing signal (heterogeneous and homogeneous). More details about the evaluation of T_het and F_het can be found in Kumar et al. (2018a). Absolute uncertainties in F_het are on average ±0.02 and do not exceed ±0.1 in cases where the heterogeneous freezing signal is clearly distinguishable from the homogeneous freezing signal. It is important to highlight that F_het carries larger uncertainties ($>\pm$0.1) in cases where heterogeneous freezing signals are weak and overlap (forming a flattened shoulder; see the Supplement) with the homogeneous freezing signal (e.g., in case of strong hampering of IN ability of feldspars in alkali solutes; see Sect. 3.1.1). Spikes occurring before the appearance of the heterogeneous freezing signal are excluded from the evaluation as they originate from single droplets (mostly between 100 and 300 µm with some up to 500 µm in diameter) in the tail of the droplet size distribution, which are orders of magnitude larger in volume than the average droplets, and not representative for the sample.

For feldspars, freezing experiments were at least performed in duplicates with separate emulsions, prepared from a single suspension for each concentration and the means are reported. For kaolinite and micas, freezing experiments were performed with emulsions prepared from at least two separate suspensions for each solute concentration and means are reported. Representative DSC thermograms of all experiments are shown in the Supplement.

2.3 Aging experiments with kaolinite suspended in pure water or solutions

Similar to our experiments with microcline (Kumar et al., 2018a), we let kaolinite (5 wt % suspension) age in pure water, ammonia solution (0.005 molal), and ammonium sulfate solutions (0.1 wt % and 10 wt %) over a period of 5 days and its IN activity was tested during this period in emulsion freezing experiments with the DSC setup. For each solute concentration two separate suspensions were prepared and aged. Small portions were taken from the suspension and emulsified for freezing experiments (as described in the previous section) on the day of suspension preparation (fresh) and the subsequent 5 days in order to assess the long-term effect of ammonia- and ammonium-containing solutes on the IN efficiency of kaolinite.

3 Results and discussion

3.1 Feldspars

Feldspars are crystalline aluminosilicates, primarily of igneous origin, with the general formula $X{\mathrm{Al}}_{\mathrm{1}-\mathrm{2}}{\mathrm{Si}}_{\mathrm{3}-\mathrm{2}}{\mathrm{O}}_{\mathrm{8}}$, often written as XT₄O₈ with T = (Al, Si) in tetrahedral coordination with oxygen. X represents an alkali or alkaline earth metal, acting as a charge-compensating cation. The tetrahedra with Al at the center carry single negative charges that are compensated by ${\mathrm{K}}^{+}/{\mathrm{Na}}^{+}$ (for one Al atom) or Ca²⁺ (for two Al atoms). Microcline, sanidine and orthoclase (all K-rich feldspars) are polymorphs and form the potassium feldspar group (Hofmeister and Rossman, 1983). Ideally, all of them exhibit a Si : Al ratio of 3 : 1, while our microcline and sanidine samples exhibit a Si : Al ratio of 3.1. In sanidine, which forms at high temperatures, Al and Si are fully disordered with Al taking random positions in the aluminosilicate framework leading to monoclinic symmetry. In microcline, Al is fully ordered leading to triclinic symmetry while orthoclase takes an intermediate position with Al and Si being partially disordered (Brown and Parsons, 1989). Despite the difference in charge, Na⁺ and Ca²⁺ are sufficiently similar in ionic radius so that there is a complete solid solution series, the plagioclase series, between albite (NaAlSi₃O₈) and anorthite (CaAl₂Si₂O₈), with intermediate members divided arbitrarily on the basis of anorthite contribution (see Fig. 1). In this series, the Ca : Na and Si : Al ratios are linked with the Al content that changes according to the Ca content. Andesine takes an intermediate position of (Na-Ca)-feldspars with a Ca ∕ (Ca + Na) = 30 %–50 % (Greenwood and Earnshaw, 1998). Our andesine (Si : Al ≈ 1.7) crystallographically fits best with an andesine though it exhibits Ca ∕ (Ca + Na) = 64 %.

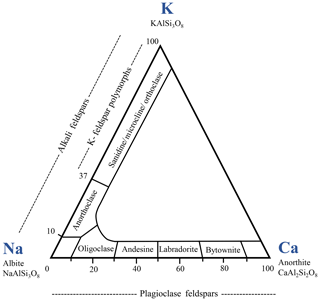
Figure 1 Feldspar classification diagram. Numbers are contributions of the end-member minerals in wt % (adapted from Greenwood and Earnshaw, 1998).

3.1.1 Dependence of the heterogeneous freezing temperatures and heterogeneously frozen fractions on water activity

Figure 2a and b show mean heterogeneous (T_het) and homogeneous freezing onsets (T_hom) and ice melting temperatures (T_melt) of the feldspars sanidine and andesine for all investigated solutes (NH₄Cl, (NH₄)₂SO₄, Na₂SO₄) as a function of a_w (water activity of solution). The water activity is defined as the ratio of the equilibrium vapor pressure of water over the flat surface of the solution and the saturation vapor pressure over the flat surface of pure water at the same temperature. We derive a_w from the melting point depression measured by DSC during the heating cycle (thus, the measured melting points, T_melt, lie by definition exactly on the melting curve). This procedure was not applicable to Na₂SO₄, because above the eutectic concentration of 4.6 wt % a hydrate of Na₂SO₄ crystallizes together with ice (Negi and Anand, 1985). Therefore, water activities for Na₂SO₄ solutions have been calculated based on the solute concentration using the AIOMFAC thermodynamic model at 298 K (Zuend et al., 2008, 2011). The homogeneous freezing curve (dotted black line) is obtained by a constant shift of the melting curve by $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{hom}}\left(T\right)=\mathrm{0.294}$, calculated to best fit the current dataset (see Kumar et al., 2018a, for more details of the derivation). This offset is in good agreement with $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{hom}}\left(T\right)=\mathrm{0.305}$ found by Koop et al. (2000). Following Koop et al. (2000), we assume a_w to be temperature independent between T_hom and T_melt.

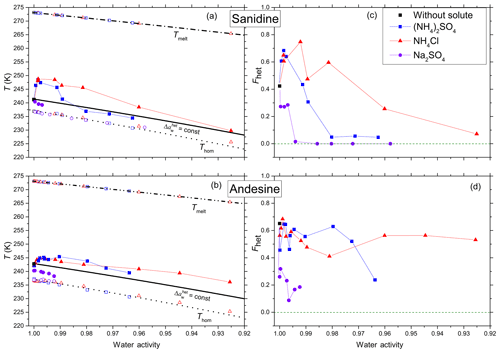
Figure 2 Measured freezing temperatures (a, b) and heterogeneously frozen fractions (c, d) of emulsion freezing experiments with 2 wt % feldspar, namely sanidine (a, c) and andesine (b, d), in various solutions (color coded). (a, b) Heterogeneous freezing onset temperatures, T_het (filled solid symbols connected by thin lines to guide the eye); homogeneous freezing onset temperatures, T_hom (open symbols at T<237 K); and ice melting temperatures, T_melt (open symbols at T>265 K) as functions of water activity of solutions, a_w, for various solutes (symbols and colors see insert). Dash-dotted black line: ice melting point curve. Dotted black line: homogeneous ice freezing curve for supercooled aqueous solutions obtained by horizontally shifting the ice melting curve by a constant offset $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{hom}}\left(T\right)=\mathrm{0.294}$. Solid black line: horizontally shifted from the ice melting curve by $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}\left(T\right)=\mathrm{0.264}$ and 0.254 for sanidine (a) and andesine (b), respectively, with offsets derived from the heterogeneous freezing temperature of the suspension of the mineral in pure water (filled black square at a_w=1). Symbols are the mean of at least two separate emulsion freezing experiments. Difference between the two measurements plus instrumental uncertainty in T_het and a_w are smaller than the symbol size (see Sect. 2.2). (c, d) Heterogeneously frozen fraction, F_het, as a function of a_w, for sanidine (c) and andesine (d). Measurement difference and uncertainty in F_het do not exceed ±0.1.

A constant offset $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}$ is also applied to the heterogeneous freezing temperatures. Here, the offset in a_w is chosen so that the heterogeneous freezing line passes through the freezing temperature of the pure water case. This yields the solid black lines with $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}=\mathrm{0.264}$ for sanidine and $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}=\mathrm{0.254}$ for andesine, which will be referred to as $T_{\text{het}}^{\mathrm{\Delta }{a}_{w,\mathrm{san}}}\left(a_{\text{w}}\right)$ and $T_{\text{het}}^{\mathrm{\Delta }{a}_{w,\mathrm{and}}}\left(a_{\text{w}}\right)$, respectively. The heterogeneous freezing behavior would be expected to follow these curves if specific chemical interactions between the solute and the ice-nucleating surface were absent, so that the only effect of the solute is a freezing point depression. However, as can be seen from Fig. 2a and b, the measured heterogeneous freezing onset temperatures, T_het, deviate from the $T_{\text{het}}^{\mathrm{\Delta }{a}_{\text{w}}}\left(a_{\text{w}}\right)$ curves for both feldspars. For both ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solute cases ((NH₄)₂SO₄ and NH₄Cl), sanidine shows a strong increase in T_het (by up to ≈ 7 K with respect to the pure water case) at low solute concentrations (a_w>0.99). This increase is followed by a decrease at higher concentrations back to $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{san}}}\left(a_{\text{w}}\right)$ in the case of NH₄Cl solutions (a_w≈0.925) and even slightly below $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{san}}}\left(a_{\text{w}}\right)$ in the case of (NH₄)₂SO₄ solutions (a_w≤0.98). Andesine also shows an increase in T_het, though smaller in magnitude (≈ 2.6 K with respect to the pure water case), but this enhancement persists to higher ${\mathrm{NH}}_{\mathrm{4}}^{+}$ concentrations. The observed enhancements with respect to $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{and}}}\left(a_{\text{w}}\right)$ are ∼ 5.1 and ∼ 4.0 K for NH₄Cl and (NH₄)₂SO₄, respectively.

In contrast to ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ solutions, freezing experiments in the presence of Na₂SO₄ as a non-${\mathrm{NH}}_{\mathrm{4}}^{+}$ solute show a strong decrease in T_het below $T_{\text{het}}^{\mathrm{\Delta }{a}_{\text{w}}}\left(a_{\text{w}}\right)$ by ∼ 1.7 K and ∼ 2.4 K for sanidine and andesine, respectively, at a_w≈0.99. No discernible heterogeneous freezing signal was observed for higher Na₂SO₄ concentrations (a_w<0.99).

Figure 2c and d show the heterogeneously frozen fraction F_het (the ratio of the heterogeneous freezing signal to the total freezing signal) as a function of a_w for sanidine and andesine. In dilute ${\mathrm{NH}}_{\mathrm{4}}^{+}$-containing solutions, sanidine shows an enhancement in F_het up to ≈ 0.75 at a_w≈0.99 compared to the suspension in pure water (F_het≈0.42 at a_w=1). With decreasing water activities, this enhancement reverses into a decline (for a_w<0.99 in case of (NH₄)₂SO₄ and for a_w<0.98 in case of NH₄Cl). In contrast, F_het of andesine is less influenced by the presence of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes since there is no significant enhancement at low concentrations and much less of a decrease at higher concentrations.

For both feldspars, the addition of Na₂SO₄ leads to a decrease of F_het for the lowest solute concentration (a_w≥0.99) and even to an almost complete inhibition of the IN activity for a_w<0.99.

3.1.2 Comparison with previous IN studies performed with feldspars

T_het and F_het trends for sanidine and andesine are similar to the ones of the K-feldspar microcline reported in our previous study, Kumar et al. (2018a), but with significant variations. All investigated feldspars show an increase in T_het at low concentrations of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes (a_w≥0.99). This increase is highest for sanidine and lowest for andesine. On the other hand, the decrease of T_het at higher solute concentration is most pronounced for microcline with values falling below the prediction from the water activity-based description. In case of non-${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes, T_het decreases below the prediction from the water activity-based approach for all investigated feldspars even at low solute concentrations. Similar trends among the feldspars are also observed for F_het. These findings are also in general agreement with droplet freezing experiments by Whale et al. (2018) who observed an increase of active-site densities for microcline and sanidine in the presence of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes and a decrease in alkali halide solutions.

The IN activity of feldspars has been investigated in numerous studies. All studies agree that the IN activity of K-feldspars is high among mineral dusts (Atkinson et al., 2013; Harrison et al., 2016; Kaufmann et al., 2016; Peckhaus et al., 2016; Welti et al., 2019). Kaufmann et al. (2016) and Welti et al. (2019) found that the IN activity of microcline is superior compared with other K-feldspars. Several studies have been dedicated to microcline. Niedermeier et al. (2015) and Burkert-Kohn et al. (2017) found frozen fractions of 0.5 at 244–245.5 K for condensation freezing on 300 nm microcline particles that were strongly reduced when the samples were aged under acidic conditions. A strong reduction of IN activity when feldspars were coated with sulfuric acid was also observed by Kulkarni et al. (2014). The IN activity of microcline after aging in pure water seems to depend on the specific sample. Samples with the highest onset freezing temperatures also show the strongest reduction in IN activity after aging, indicating that the best active sites might also be the most labile ones (Harrison et al., 2016; Peckhaus et al., 2016). Harrison et al. (2016) found that one sample of Na-feldspar (albite) was similarly active as microcline when freshly suspended in water, but lost its high IN activity after having been suspended for months in water, indicating that its IN activity may be related to sites with high solubility that are lost over time by dissolution. Kiselev et al. (2017) found that high-energy (100) surface patches of K-rich feldspars are best suited for deposition growth of aligned ice crystals below water saturation. However, it is not clear how resistant these high-energy sites are when immersed in water. Whale et al. (2017) related the exceptionally high IN ability of K-feldspars to microtextures, giving rise to topographic features with high IN temperatures. The IN site densities that they investigated with their setup were in the range from 10⁻¹ to 10³ cm⁻² with IN temperatures up to 271 K. With the DSC emulsion freezing experiments, we investigate the properties of sites that are common to submicrometer particles, i.e., with surface densities in the range from 10¹⁰ to 10⁵ cm⁻² nucleating ice up to 252 K. While the sites investigated by Whale et al. (2017) may be well correlated with perthitic structures, it is unlikely that such features are common enough in submicrometer particles to account for the IN activity observed in our emulsion freezing experiments. Welti et al. (2019) found a clear decrease in IN activity for all investigated feldspars (microclines, orthoclases, sanidine, pericline and labradorites) with decreasing particle size from 800–50 nm, indicating the better active sites are rarer.

3.1.3 Surface ion exchange

In pure water, the native charge-balancing surface cations (K⁺, Na⁺, Ca²⁺) immediately undergo cation exchange by ${\mathrm{H}}^{+}/{\mathrm{H}}_{\mathrm{3}}{\mathrm{O}}^{+}$ (Chardon et al., 2006; Lee et al., 2008), with hardly any simultaneous structural surface damage (Busenberg and Clemency, 1976). The native cation may also participate in ion exchange with an externally added cation depending on the size and charge compatibility of the latter with the crystal structure (Auerbach et al., 2003; Belchinskaya et al., 2013). Ammonium ions not only have a strong preference for cation exchange with K-feldspars and (Na-Ca)-feldspars but part of them remain fixed to the surface in nonexchangeable form (Nash and Marshall, 1957; Barker, 1964). In Kumar et al. (2018a), we have shown that the ion exchange is unlikely as a reason for the enhanced IN efficiency of microcline in dilute ${\mathrm{NH}}_{\mathrm{4}}^{+}$-containing solutions. Rather, hydrogen bonding of ammonia/ammonium with the surface hydroxyl groups seems to provide better ice-like template sites for the incoming water molecules (Anim-Danso et al., 2016), leading to an increase in IN efficiency.

3.1.4 Aluminum depletion and surface dissolution

When suspended in water or solutions, feldspars undergo slow dissolution, followed and accompanied by the precipitation of more stable phases like kaolinite, gibbsite or halloysite (Stillings and Brantley, 1995). Depending on the specific feldspar and solution pH, steady-state Si dissolution rates vary between 10⁻¹⁰ and 10⁻¹⁴ moles m⁻² s⁻¹ (Crundwell, 2015) with lowest values at near-neutral conditions. The solution pH during the emulsion freezing experiments reported in Fig. 2 are close to neutral with pH values ranging from 5.5 to 6.7. For the feldspars investigated in this study, steady-state dissolution rates are lowest for microcline with $\mathrm{4}\times {\mathrm{10}}^{-\mathrm{14}}$–$\mathrm{8}\times {\mathrm{10}}^{-\mathrm{14}}$ moles m⁻² s⁻¹ at pH ∼ 6 (Crundwell, 2015) followed by sanidine with a rate of ∼ $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{13}}$ moles m⁻² s⁻¹ at near-neutral conditions (Crundwell, 2015), while dissolution of andesine occurs with a steady-state rate of 10⁻¹²–10⁻¹¹ moles m⁻² s⁻¹ at pH ∼ 8 (Gudbrandsson et al., 2014). Hereby, initial dissolution rates of freshly suspended feldspar may be higher by up to 3 orders of magnitude than the rates at steady state (Zhu et al., 2016). With these rates, dissolution is in the range of one monolayer within the timescale of a DSC freezing experiment (1–1.5 h) for andesine, and below it for sanidine and microcline.

At near-neutral conditions, the dissolution proceeds via protonation of the oxygen of $\equiv \mathrm{Al}-\mathrm{O}-\mathrm{Si}\equiv$ bridges with subsequent release of Al³⁺ resulting in an incongruent (deviation of ratio of released Si to Al from stoichiometric ratio) initial dissolution for most feldspars when they are freshly suspended in water (Oelkers and Schott, 1995; Oelkers et al., 2009), and leading to a $\equiv \mathrm{Si}-\mathrm{OH}$ rich surface (Oxburgh et al., 1994; Stillings and Brantley, 1995; Oelkers et al., 2009). Oelkers et al. (2009) found aluminum surface depletion to occur readily in their 20 min titration experiments with the Na-feldspar albite. Thus, the feldspar surfaces in pure water suspensions can be considered at least partly or even completely depleted in aluminum with the dangling bonds replaced by silanol groups within the timescales of our experiments. The dissolution incongruence with respect to Al atoms depends on the Si∕Al ordering and the Si : Al ratio of the feldspar lattice (Yang et al., 2014a, b). Yang et al. (2014b) investigated the stoichiometry of feldspar dissolution under acidic conditions (pH 1.8) and found that microcline with Si : Al = 3.0 dissolved with a ratio of Si : Al = 2.1. Their sanidine sample with Si : Al = 2.87 released Al with Si :Al = 1.36, while their andesine sample with Si : Al = 1.95 dissolved at a ratio Si : Al = 0.76 : 1. This dissolution incongruence leads to a layer leached in Al, with a thickness that depends on the specific feldspar and increases with decreasing pH. At steady state, this Al-depleted layer is 6.6–8.5 nm thick for microcline at pH 1 (Lee et al., 2008), but only 1–2 nm at pH 3 (Stillings and Brantley, 1995). For andesine, it reaches 60–120 nm at pH 3.5 and still 15–30 nm at pH 5.7 (Muir et al., 1990). Since Al dissolution at steady-state conditions needs to occur through this layer, the andesine surface is considered to consist of somewhat loosened and distorted feldspar chains resulting in a porous amorphous-like structure (Marshall, 1962; Stillings and Brantley, 1995; Zhang and Lüttge, 2007). At pH 1, the first 5 nm of surface layer of microcline were found to be amorphous (Lee et al., 2008). Since amorphous silica shows barely any IN activity (see also the companion paper, Kumar et al., 2019), the loss of IN activity of microcline in the presence of H₂SO₄ (Kumar et al., 2018a) may be explained by the presence of an amorphous silica layer. Since T_het correlates with the thickness of the leached layer reported for the investigated feldspars, we hypothesize that amorphous surface layers exceeding a few nanometers in depth hamper the IN activity of feldspars.

3.1.5 Surface charge and surface protonation

Feldspars exhibit a negative surface charge over a wide pH range with a point of zero charge (PZC) < 2 (Karagüzel et al., 2005; Vidyadhar and Hanumantha Rao, 2007). Bringing the feldspar surface closer to the PZC by adding H₂SO₄ did not increase T_het but decreases F_het due to surface degradation as was shown for microcline (Kumar et al., 2018a). This shows that surface charge is only one among several factors influencing IN activity. We discuss the effect of surface charge on IN activity of mineral surfaces in more detail in Sect. 4.

Surface hydroxyl groups are considered to promote IN because they can form hydrogen bonds with water molecules and bring them in a suitable orientation for IN. In a recent molecular simulation study, Pedevilla et al. (2017) found that the OH density rather than a specific OH pattern is a useful descriptor of IN ability. The relevance of surface hydroxylation is in agreement with our observations that Na⁺ ions added to an aqueous feldspar suspension decrease T_het and F_het for all investigated feldspars since they replace the protons (Oelkers et al., 2009) thus decreasing the surface hydroxylation (see Fig. 2 of this paper; Kumar et al., 2018a). Ammonium on the other hand, can form hydrogen bonds with water molecules and therefore does not reduce the IN activity. In addition, ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ is not only involved in ion exchange but also binds to the feldspar surface (Kumar et al., 2018a). Therefore, it increases the capacity for hydrogen bonding even more and leads to an increased IN activity. A strong increase of proton concentration (low pH), on the other hand, hampers or even totally impedes IN because it promotes aluminum depletion and the formation of an amorphous silica surface layer.

3.1.6 Influence of sulfate

While we consider solute effects to be dominated by cations at low concentrations, the anions seem to become more relevant at higher concentrations. Aqueous phase complexes of dissolved aluminum with sulfate enhance the solubility of aluminum. Surface complexes of sulfate with surface aluminum can impede or enhance dissolution of aluminum. Bidentate surface complexes with sulfate do not enhance surface protonation and should stabilize aluminum at the surface, while the formation of mononuclear complexes should facilitate surface protonation and help dissolution of aluminum (Min et al., 2015). The effect of sulfate should therefore depend on the bonding strength of aluminum to the feldspar surface, which depends on the Si ∕ Al order and Si : Al ratio. Min et al. (2015) found that the dissolution rate of anorthite, a (Na-Ca)-feldspar with Si : Al = 1, is enhanced by the formation of monodentate complexes between the aluminum surface sites and sulfate. This seems to be also the case for the (Na-Ca)-feldspar andesine. On the other hand, surface complexation of aluminum sites with sulfate seems to decrease the removal of aluminum and block sites for IN in the case of microcline, while sanidine takes an intermediate position.

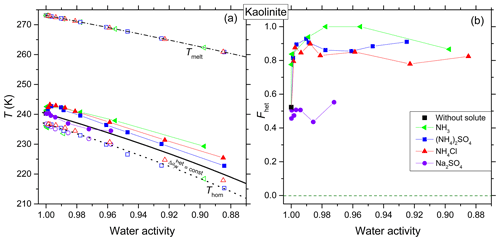
Figure 3 Same as Fig. 2, but for kaolinite (5 wt %). (a) Homogeneous ice freezing curve (dotted black line) characterized by a constant offset $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{hom}}\left(T\right)=\mathrm{0.294}$. Ice melting curve (dash-dotted black line) and the heterogeneous freezing curve (solid black line) horizontally shifted from the ice melting curve by $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}\left(T\right)=\mathrm{0.272}$ derived from the heterogeneous freezing temperature of the suspension of the mineral in pure water (filled black square at a_w=1). Measured differences and instrumental uncertainties in T_het and a_w are smaller than the symbol size (see Sect. 2.2). (b) F_het (heterogeneously frozen fraction) as a function of water activity of the solutions. Measurement difference and uncertainty in F_het do not exceed ±0.1.

3.2 Kaolinite and gibbsite

Kaolinite (Al₄[Si₄O₁₀](OH)₈) is a layered 1 : 1 (one tetrahedral sheet and one octahedral sheet forming stacked T–O layers) dioctahedral phyllosilicate and one of the most abundant clay minerals found in the Earth's crust (Murray, 1991). Each layer consists of a sheet of SiO₄ tetrahedra forming six-membered silicate rings connected via common oxygen atoms to a sheet of AlO₆ octahedra forming four-membered aluminate rings. Weak hydrogen bonds between Al−OH and Si–O–Si groups provide interlayer attraction preventing ions or molecules from entering the interlayer space and constituting the non-swelling nature of this mineral. Since ionic substitution of Si⁴⁺ with Al³⁺ is absent in the regular kaolinite lattice, exchangeable ions only occur at defects or at edges (Bibi et al., 2016). Cleavage of kaolinite preferentially occurs along the basal plane, resulting, on one side, in a hydroxylated Al surface with Al atoms arranged in a hexagonal pattern and on the other side in a siloxane surface with Si–O–Si bridges forming hexagonal rings (Bear, 1965).

Although particles of gibbsite are of rare abundance in atmospheric dusts (Boose et al., 2016; Kaufmann et al., 2016), we investigate this mineral because the hydroxylated Al sheets of kaolinite are structurally identical with gibbsite. Gibbsite is an aluminum hydroxide of the general formula Al(OH)₃ that exists as different polymorphs. The basal surface of gibbsite is comparable to the aluminol surface of kaolinite and, therefore, often used as a model surface to elucidate the physicochemical properties of the Al surface of kaolinite (Liu et al., 2015; Kumar et al., 2016).

3.2.1 Dependence of the heterogeneous freezing temperatures and frozen water volume fraction on water activity

Figure 3a presents T_het, T_hom and T_melt as a function of a_w for kaolinite. The offset in a_w applied to shift the melting curve so that it passes through the freezing temperature of the pure water case for kaolinite is $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}=\mathrm{0.272}$, here referred to as $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{kaol}}}\left(a_{\text{w}}\right)$. In the presence of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes, kaolinite shows an increase (≈ 2.4 K) in T_het compared to $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{kaol}}}\left(a_{\text{w}}\right)$ even at the lowest investigated solute concentration (0.1 wt %; a_w>0.99). The influence of NH₃ on the IN activity was found to be similar to the one of the ${\mathrm{NH}}_{\mathrm{4}}^{+}$-containing solutes. This enhancement relative to $T_{\text{het}}^{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{kaol}}}\left(a_{\text{w}}\right)$ persists over the complete concentration range probed in this study, similar to the case of andesine. For a_w<0.9, kaolinite shows an increase up to 2.9, 5.5 and 6.9 K in T_het compared to $T_{\text{het}}^{\mathrm{\Delta }{a}_{\text{w,kaol}}}\left(a_{\text{w}}\right)$ in solutions of (NH₄)₂SO₄, NH₄Cl and NH₃, respectively. In contrast to the feldspars, in Na₂SO₄ solutions T_het follows $T_{\text{het}}^{\mathrm{\Delta }{a}_{\text{w,kaol}}}\left(a_{\text{w}}\right)$ within the error range for all investigated concentrations.

Figure 3b shows F_het as a function of a_w for kaolinite. Interestingly, kaolinite shows a strong enhancement in F_het to 0.75–1.00 compared to the pure water case (F_het≈0.52) in the presence of NH₃ and ${\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes over the complete investigated concentration range (a_w=1–0.88). This enhancement is strongest for ammonia solutions, reaching F_het≈1 (F_het≈1 was assumed when it was not possible to discern a homogeneous freezing signal; see Fig. 5) at a_w=0.98–0.96, compared to F_het≈0.5 in pure water. In contrast, F_het seems to be unaffected by Na₂SO₄ within experimental uncertainties over the measured concentration range.

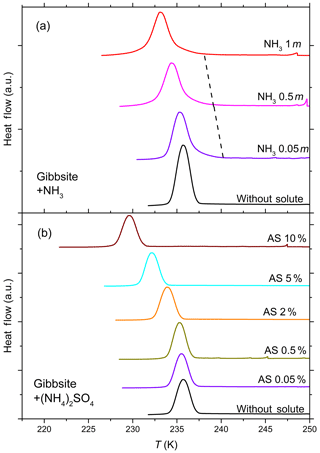
Figure 4 DSC thermograms of 10 wt % gibbsite suspended in ammonia solution droplets (a) of concentrations from 0 to 1 molal (a_w=1–0.981) and (NH₄)₂SO₄ solution droplets (b) from 0 to 10 wt % (a_w equal to 1–0.961). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. Gibbsite shows no discernible heterogeneous freezing signal in pure water and starts to show a weak heterogeneous freezing signal when suspended in ammonia solution (dashed black line connects the onset of heterogeneous freezing signals), while no heterogeneous IN is observed for gibbsite suspended in (NH₄)₂SO₄.

Figure 4 shows the DSC thermograms of the emulsion freezing experiments carried out with 10 wt % gibbsite suspensions in pure water, in NH₃- (panel a) and in (NH₄)₂SO₄-containing solutions (panel b). Gibbsite, exhibiting no heterogeneous freezing signal during emulsion freezing experiments in pure water, starts to show a weak heterogeneous freezing signal with increasing NH₃ concentration (indicated by the dashed black line in Fig. 4a). On the other hand, no heterogeneous freezing signal can be observed for gibbsite suspended in (NH₄)₂SO₄ solutions (0.05 wt %–10 wt %; a_w equal to 0.996–0.961.

3.2.2 Previous studies on the IN activity of kaolinite

Kaolinite has shown IN activity in various freezing modes (Hoose and Möhler, 2012; Murray et al., 2012; Kanji et al., 2017). Many studies investigated K-SA kaolinite from Sigma-Aldrich (Zuberi et al., 2002; Lüönd et al., 2010; Burkert-Kohn et al., 2017), while others used the KGa-1b kaolinite from the Clay Mineral Society with high mineralogical purity (96 %, minor impurities of anatase, crandallite, mica, and illite) (Murray et al., 2011; Pinti et al., 2012; Wex et al., 2014; Kaufmann et al., 2016). Pinti et al. (2012) found with their emulsion freezing experiments that K-SA exhibits a second freezing peak at higher temperatures with onset at ∼248 K that could be related to impurities of feldspars (Atkinson et al., 2013). On the other hand, KGa-1b features only one heterogeneous freezing peak with an almost constant onset at ∼ 240 K in emulsion freezing experiments irrespective of the kaolinite concentration in the aqueous suspension (Pinti et al., 2012), which is an indication of the homogeneous composition and mineralogical purity of the sample. Kaufmann et al. (2016) evaluated the active particle fraction of kaolinite KGa-1b to be only about 0.04 compared to values of 0.54–0.64 determined for microcline. A lower active fraction of kaolinite compared with the feldspar microcline was also confirmed by single particle immersion freezing experiments (Burkert-Kohn et al., 2017).

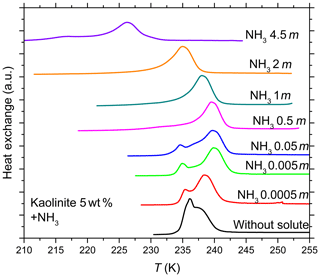
Figure 5 DSC thermograms of 5 wt % kaolinite particles suspended in ammonia solution droplets (0–4.5 molal; a_w equal to 1–0.922). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value.

The DSC curves for kaolinite suspended in NH₃ solution (Fig. 5) show that for a certain NH₃ concentration range (0.5–2 molal; a_w equal to 0.988–0.955) the heterogeneous freezing signal totally dominates the homogeneous one, indicating that initially IN inactive particles (contributing to the homogeneous freezing DSC signal) became IN active after addition of ammonia. Salam et al. (2007, 2008) have previously reported improved IN efficiency of the clay mineral montmorillonite below and above water saturation after the particles were exposed to NH₃ gas.

3.2.3 Which kaolinite surface is responsible for the IN activity?

As a sheet aluminosilicate, kaolinite exhibits two basal faces – the siloxane tetrahedral and the alumina octahedral – and hydroxylated edges. The overall surface charge of kaolinite in pure water is negative with a PZC < 2. The PZC increases when kaolinite is suspended in salt solutions (Yukselen-Aksoy and Kaya, 2011). However, this overall value determined from bulk experiments does not need to apply to the individual faces of kaolinite.

Recent surface force measurements have been able to probe the surface properties of the kaolinite faces individually. These measurements evidenced a negative charge of the siloxane surface with a PZC below pH 4 (Gupta and Miller, 2010). Isomorphic substitution of Si(IV) for Al(III) in tetrahedral layers is considered the main reason for the net permanent negative surface charge, which is balanced by the adsorption of cations (e.g., Na⁺, K⁺, Ca²⁺) (Cashen, 1959; Grim, 1968; Bolland et al., 1980). The oxygen atoms on the siloxane surface are relatively weak electron donors and incapable of forming hydrogen bonds with water molecules. Therefore, the near-surface water molecules interact predominantly with each other so that the surface is considered nearly hydrophobic (Jepson, 1984; Giese and van Oss, 1993; Braggs et al., 1994).

Unlike the siloxane surface, the hydroxyl-rich surface of the Al-octahedral layer is hydrophilic and forms hydrogen bonds with water (Schoonheydt and Johnston, 2006; Yin et al., 2012). The alumina face was found to be negatively charged at pH ≥ 8 and positively charged at pH ≤ 6 indicating a PZC of pH 6–8 (Gupta and Miller, 2010). The pH-dependent, nonpermanent surface charge arises from protonation or deprotonation of surface hydroxyl groups. While silanol groups mainly contribute to negative charge through the formation of SiO⁻ by deprotonation, aluminol groups undergo both protonation at low pH and deprotonation at high pH (Abendroth, 1970; Bleam et al., 1993).

Disruption of the kaolinite sheets leads to dangling oxygen atoms at the crystal edges that take up water molecules to transform into hydroxyl groups. This process produces a surface rich in silanols and aluminols, which terminate tetrahedral and octahedral layers, respectively (Brady et al., 1996; Liu et al., 2013). The PZC of the kaolinite edge surface was found to be below pH 4. The negative charge is considered to arise from deprotonation of Si sites, which is only partly counteracted by positively charged Al sites (Brady et al., 1996). The reactive hydroxyl groups, due to their charge, have the potential to chemisorb certain other ionic species (Schoonheydt and Johnston, 2006, 2013). Such hydroxyl groups are also present at steps and cracks.

First principles calculations and molecular dynamics simulations have indicated that hydrogen bonding to surface hydroxyl groups is an essential factor for providing IN activity to mineral surfaces (Hu and Michaelides, 2007; Sosso et al., 2016a; Glatz and Sarupria, 2018). The absence of sites for hydrogen bonding make the regular siloxane surface an unlikely candidate for IN (Freedman, 2015). The alumina surface, on the other hand, is OH-rich and has been probed in several modeling studies for its capability to nucleate ice. Based on a density-functional theory study, Hu and Michaelides (2007) concluded that the basal surfaces of kaolinite do not support epitaxial multilayer ice growth, rather they may promote the growth of the prism face of ice (Cox et al., 2013). Monte Carlo simulations carried out by Croteau et al. (2008, 2009) suggested that a rigid Al surface of kaolinite (001) is incapable of orienting water molecules into ice-like configurations, instead trenches and surface defects were suggested to be responsible for IN (Croteau et al., 2010a, b). Zielke et al. (2015) showed that both the Al surface and the Si surface can nucleate ice, by reorientation of hydroxyl groups in the former case and by ordered arrangement of hexagonal and cubic ice layers joined at their basal planes in the latter case. Glatz and Sarupria (2018), based on molecular dynamics simulations on kaolinite-like surfaces, argued that lattice matching and hydrogen bonding are necessary but not sufficient conditions for IN. Sosso et al. (2016b) found that IN on the hydroxylated basal surface of kaolinite proceeds exclusively via the formation of the hexagonal ice polytype but that this process crucially depends on very small structural changes upon kaolinite surface relaxation in the molecular dynamics simulations.

While most of these studies focused on the basal planes, experimental evidence suggests that the edges are preferred locations for IN. Indeed, Wang et al. (2016) found in IN experiments with a cell coupled to an environmental scanning electron microscope that ice preferentially nucleates at the edges of kaolinite particles when they were exposed to increasing relative humidity. The similar response of kaolinite and feldspars to ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ solutes indicates a similar chemical composition of IN active sites on the surfaces of these two mineral types, suggesting that the kaolinite edges, rich in both aluminol and silanol groups should be responsible for the observed IN activity.

Similar to the hydroxylated Al layers of kaolinite, gibbsite consists of stacked sheets of linked octahedra of aluminum hydroxide. Therefore, the gibbsite surface is often taken as a model for the Al surface of kaolinite (Liu et al., 2015; Kumar et al., 2016). The PZC of gibbsite falls in the pH range from 7.5 to 11.3 (Kosmulski, 2009; Liu et al., 2015), thus in a similar, yet somewhat higher, range than the one of the Al surface of kaolinite (pH 6–8). DSC thermograms of the emulsion freezing experiments with gibbsite (Fig. 4) show no heterogeneous freezing signal in pure water and (NH₄)₂SO₄ solutions up to 10 wt %. Only when suspended in NH₃ solutions (0.05–1 molal, a_w equal to 0.996–0.981), a weak heterogeneous freezing signal developed. This indicates that NH₃ hydrogen bonded to the hydroxylated Al surface provide IN activity to gibbsite, while the positively charged ${\mathrm{NH}}_{\mathrm{4}}^{+}$ does not adsorb on the positively charged Al surface. Given the inability of gibbsite to nucleate ice in water and (NH₄)₂SO₄, we conclude that the IN activity of kaolinite rather stems from the edges as suggested by Wang et al. (2016) and Croteau et al. (2010a). This conclusion is further supported by the finding that kaolinite indeed adsorbs NH₃ by forming hydrogen bonds with the hydroxyl groups at the edges (James and Harward, 1962).

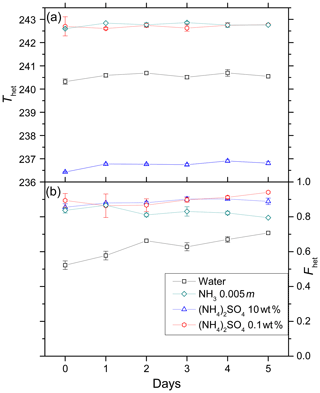
Figure 6 Development of T_het (a) and F_het (b) for 5 wt % kaolinite suspended in water, 10 wt % (NH₄)₂SO₄, 0.1 wt % (NH₄)₂SO₄, 0.005 molal ammonia solutions over a period of 5 days. Data points depict mean (with error bars representing min to max) for T_het and F_het measured for two aging experiments performed with two independently aged suspensions.

3.2.4 Aging effect

We carried out immersion freezing experiments with kaolinite (5 wt %) suspended in pure water, NH₃ solution (0.005 molal, a_w=0.999), and (NH₄)₂SO₄ solutions (0.1 wt % and 10 wt %; a_w=0.996, a_w=0.961, respectively) over a period of 5 days to assess the effect of aging on the IN efficiency of kaolinite. Figure 6 shows T_het (panel a) and F_het (panel b) as a function of time. T_het remains stable over the measured time period within the experimental measurement uncertainties. Similarly, F_het remains constant except in the pure water case where it shows a slight increase.

The dissolution rate of kaolinite depends on pH with the lowest values of 10⁻¹⁴–10⁻¹³ moles (of Si) m⁻² s⁻¹ realized at near-neutral conditions (Carroll and Walther, 1990; Huertas et al., 1999). At acidic conditions the dissolution increases because of H⁺ attack at the Si–O–Al linkages of the edges leading to the liberation of aluminum ions into the solution (Xiao and Lasaga, 1994; Fitzgerald et al., 1997). At alkaline conditions, dissolution is considered to occur dominantly at the basal octahedral face via deprotonation of aluminum sites (Huertas et al., 1999; Naderi Khorshidi et al., 2018). At near-neutral conditions, both mechanisms are inefficient leading to a minimum in the dissolution rate. Between pH 5 and 10, kaolinite dissolution is accompanied by the precipitation of an aluminum hydroxide phase (Huertas et al., 1999).

The pH of the solutions used for the aging experiments with kaolinite are in the slow dissolution near-neutral regime. Since there is no decrease in IN efficiency during the 5 days of aging in the aqueous solutions of ammonia and ammonium sulfate, surface alteration during this time period seems to be minor. Indeed, with a dissolution rate of 10⁻¹⁴–10⁻¹³ moles m⁻² s⁻¹, the Si dissolved during the 5 days of the experiments should be well below a monolayer and should not lead to a significant alteration of the surface composition. Nevertheless, when dissolution occurs preferentially on chemically more reactive sites that are likewise IN active, destruction of these sites might lead to a decrease in IN activity (Kumar et al., 2019). However, the increase of IN activity in pure water rather suggests the generation of new IN active sites due to surface changes in the presence of water.

3.3 Micas

Muscovite (KAl₂(AlSi₃O₁₀)(OH)₂) and biotite (K(Mg,Fe)₃AlSi₃O₁₀(OH)₂), both quite soft (on Mohs scale 2–3), are 2 : 1 layer phyllosilicates (one octahedral sheet sandwiched between two tetrahedral sheets, forming stacked T–O–T layers) belonging to the mica group with nearly perfect basal cleavage (Bower et al., 2016; Christenson and Thomson, 2016). The tetrahedral layer consists of Si and Al at a ratio of 3 : 1. The Al is randomly ordered avoiding Al–O–Al arrangements. The presence of Al in the tetrahedral layer introduces a negative charge that is neutralized by potassium ions acting as the bridge between the $\mathrm{T}-\mathrm{O}-\mathrm{T}$ layers. Muscovite and biotite differ in their octahedral layers, which in the case of muscovite is dioctahedral and occupied by Al³⁺. Biotite is part of a solid solution series within the mica group with trioctahedral layers occupied by Fe²⁺ and Mg²⁺. The end-members of the series are pure iron biotite called annite and pure magnesium biotite called phlogopite (Bray et al., 2015), while biotites take intermediate positions in terms of Fe : Mg ratios (Fleet et al., 2003).

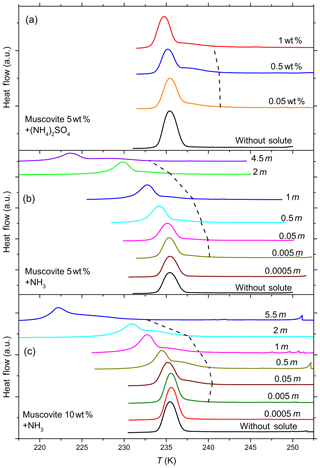
Figure 7 DSC thermograms of 5 wt % (a, b) and 10 wt % (c) muscovite particles suspended in ammonia (0–5.5 molal; a_w equal to 1–0.912) and ammonium sulfate (0–1 wt %; a_w equal to 1–0.988) droplets of different solution concentrations (given as inserts). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. The dashed black line connects the heterogeneous freezing onset temperatures (T_het) of the emulsions. With increasing ammonia concentration heterogeneous IN efficiency starts to develop, as can be noticed from the appearance of T_het, which was absent in pure water. The intensity of the heterogeneous freezing signal, hence F_het, becomes more prominent in 10 wt % suspensions (see Table 1).

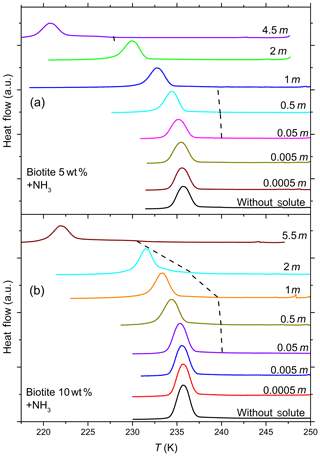
Figure 8 DSC thermograms of 5 wt % (a) and 10 wt % (b) biotite particles suspended in ammonia solution droplets (0–5.5 molal; a_w equal to 1–0.912). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. In contrast to muscovite, biotite becomes IN active only at very high concentrations of ammonia. In addition, the intensity of the heterogeneous freezing signal (hence F_het) is low, but becomes more prominent in 10 wt % suspensions (see Table 2).

3.3.1 Heterogeneous freezing of aqueous solution droplets containing micas

Figure 7 shows DSC thermograms of muscovite particles suspended in (NH₄)₂SO₄ and NH₃ solution droplets of increasing concentration, and Fig. 8 the same for biotite in NH₃ solution droplets. T_het and F_het from these measurements for muscovite and biotite are summarized in Tables 1 and 2, respectively. Interestingly, when suspended in pure water, neither muscovite nor biotite exhibit a discernible heterogeneous freezing signal in the DSC thermograms. Considering the particle size distributions of the two minerals, which peaks at about 335 nm in the case of the muscovite sample (Kaufmann et al., 2016) and is bimodal with maxima at 241 nm and 1.7 µm for biotite (see the Supplement), the lack of a heterogeneous freezing signal cannot be ascribed to the predominance of empty emulsion droplets. Indeed, both start to develop IN activity when immersed in ammonia or ammonium solutions (indicated by the dashed black lines in Figs. 7 and 8). The frozen fraction, F_het, is a strong function of NH₃ or ${\mathrm{NH}}_{\mathrm{4}}^{+}$ concentration. For muscovite (5 wt %), F_het increases from 0.138 in 0.005 molal NH₃ (a_w=0.997) to 0.387 in 4.5 molal NH₃ (a_w=0.922) solutions. In the case of biotite (5 wt %), suspensions do not reveal a heterogeneous freezing signal in pure water or in dilute ammonia solutions. A well discernable heterogeneous freezing signal appears only in concentrated ammonia (4.5 molal, a_w=0.922, Fig. 8a). For 10 wt % biotite suspensions, the heterogeneous freezing signal becomes visible already in 2 molal ammonia (a_w=0.968; Table 2), yet the signals are clearly weaker than those from muscovite suspensions at similar solute concentrations.

Table 1 Summary of the freezing experiments with emulsified aqueous solution droplets containing muscovite (5 wt % and 10 wt %). Note that the absolute uncertainty in F_het may be up to ±0.1. Only F_het values above this threshold are clear evidence of heterogeneous IN.

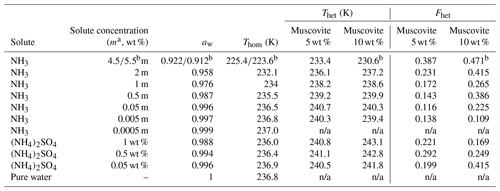
^a molality; ^b 10 wt % muscovite suspended in 5.5 molal NH₃ solution; n/a: no T_het and F_het can be reported due to absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments.

Table 2 Summary of the freezing experiments with emulsified aqueous solution droplets containing biotite (5 wt % and 10 wt %). Note that the absolute uncertainty in F_het may be up to ±0.1. Only F_het above this threshold are clear evidence of heterogeneous IN.

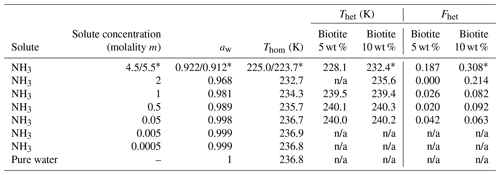
^* 10 wt % biotite suspended in 5.5 molal NH₃ solution; n/a: no T_het and F_het can be reported due to absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments

3.3.2 Previous studies on IN activities of micas

Micas have been tested for IN activity in numerous studies, but with very diverse outcomes. Older studies have reported dentritic ice growth on the basal planes of freshly cleaved micas (muscovite and fluorophlogopite: KMg₃AlSi₃O₁₀F₂) when they were exposed to water saturation at cold temperatures (Bryant et al., 1959; Hallett, 1961; Layton and Harris, 1963). Shen et al. (1977) showed that fluorophlogopite and muscovite particles (44–74 µm) induce IN in bulk freezing experiments with onset temperatures of 272 and 268 K, respectively. Steinke (2013) investigated the freezing of water droplets on a muscovite surface in a cold stage and found IN activity around 250 K but with a much lower active site density compared with clay minerals. Atkinson et al. (2013), on the other hand, observed hardly any IN activity in immersion mode for a non-specified mica. Campbell et al. (2015) found freezing close to the homogeneous freezing temperature for droplets on muscovite. Surface imperfections on the basal plane of muscovite were found to promote IN on muscovite exposed to water vapor below the threshold temperature for homogeneous IN but had no effect when the surface was immersed in water above this threshold temperature. Overall, the IN activity of micas seems to be much lower than that of clay minerals such as kaolinite despite their similar structure.

3.3.3 IN activity in relation to the surface properties of micas

The basal surfaces of micas are dominated by Si–O–Si and Al–O–Si bridges exhibiting little hydroxylation. Due to the isomorphic substitution of Si(IV) for Al(III) in the tetrahedral layer, the basal surfaces are hydrophilic and carry a permanent negative charge that is neutralized by K⁺ ions (Zhao et al., 2008; Yan et al., 2013). When suspended in electrolyte solutions, K⁺ exposed to the surface undergo ion exchange within seconds (Cho and Komarneni, 2009; de Poel et al., 2017; Lee et al., 2017). In pure water, surface K⁺, and to a lesser degree also interlayer potassium ions, are lost to the suspension and replaced by protons introducing hydroxylation to the basal surface and widening the muscovite lamellae (Banfield and Eggleton, 1990). At the edges of the plate-like particles, the broken bonds of the disrupted sheets are saturated by –OH, resulting in a hydrophilic, hydroxylated surface with a surface charge that depends on pH (Zhao et al., 2008).

Micas slowly dissolve when suspended in water accompanied by precipitation of metal (hydr)oxides and kaolinite, which may form nanometer coatings on the mica surface blocking active sites (Pachana et al., 2012). The dissolution occurs with similar pH dependence as observed for feldspars with the lowest rates at near-neutral conditions (Oelkers et al., 2008; Bray et al., 2015; Lammers et al., 2017). Dissolution may occur via etch pits on the basal surface, but the dominating process seems to be corrosion of the edge surfaces (Oelkers et al., 2008; Pachana et al., 2012).

The Si dissolution rate of muscovite is about 10⁻¹³ to 10⁻¹² moles m⁻² s⁻¹ at neutral conditions (Brady and Walther, 1989; Lammers et al., 2017), which is sufficient to lead to surface alterations within the timescale of our experiments. The initial dissolution of Al is higher than the one of Si (Pachana et al., 2012), confirming that edges dissolve more readily than the basal faces. The basal plane of muscovite carries negative charge independent of pH while the edges carry a negative charge at high pH and a positive charge at low pH with a PZC at pH 7–8. The dissolution rate of biotite is 10⁻¹² to 10⁻¹¹ moles m⁻² s⁻¹ at neutral conditions. The initial dissolution at pH 6 was observed to be congruent with respect to Si and Al, but Mg and Fe positioned in the octahedral layer dissolved at a higher rate, resulting in a metal-depleted disordered octahedral layer (Pachana et al., 2012; Bray et al., 2015).

The absence of a heterogeneous freezing signal in emulsion freezing experiments suggests a low density of IN active sites. Thus, the IN activity seems to stem from very special features that are rare, while the regular mica surfaces are inactive despite the hydrophilicity of the basal surfaces and the dense hydroxylation of the edges, both characteristics of IN active surfaces. Indeed, sum-frequency-generation (SFG) spectra showed that water adsorbed at full monolayer coverage (90 % RH) forms an ice-like film on the basal muscovite surface (Miranda et al., 1998). Yet, this film does not seem to grow readily into bulk ice. The surface electric field of the negatively charged muscovite surface orders water molecules with the protons pointing towards the surface. SFG spectra show that this ordering decreases when the water freezes and increases again when the ice melts, suggesting that the ordered water layer adsorbed on the basal mica surface is unable to match ice (Anim-Danso et al., 2016). This finding is in line with Abdelmonem et al. (2017) who found that IN was not promoted by the presence of an ordered water layer on the hydroxylated sapphire (α-Al₂O₃) surface. On the contrary, IN was observed to occur at slightly warmer temperature close to the PZC when the water molecules were disordered. While at low and high pH, the aligning of the water molecules on the positively or negatively charged surface, respectively, was detrimental to IN.

While the absence of IN activity at the edges of biotite may be ascribed to the fast disintegration of this surface in the presence of water, it is not clear whether surface alteration at the edges of muscovite are sufficient to explain their lack of IN activity in pure water. In the presence of NH₃ and (NH₄)₂SO₄ solutions, both investigated micas show IN activity in the emulsion freezing experiments. This might be due to adsorption of ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ on the basal planes increasing the number of sites available for hydrogen bonding or due to adsorption at the edges that may influence the dissolution rate.

Table 3 IN activities in terms of T_het and F_het together with surface properties of minerals investigated in this study at near-neutral conditions (representative for pure water), microcline from Kumar et al. (2018a) and quartz from Kumar et al. (2019).

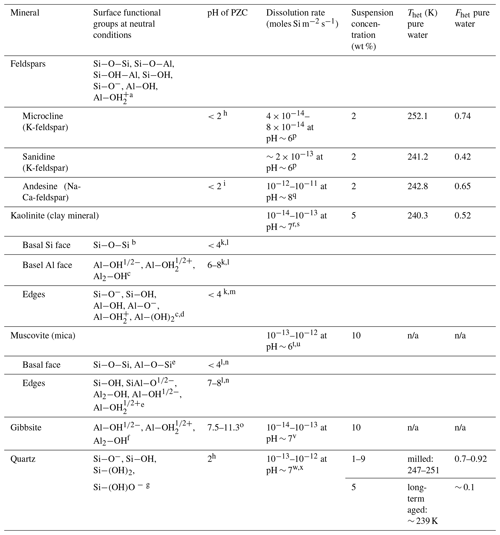
a: Teng et al., (2001); b: Schoonheydt and Johnston, (2006); c: Brady et al. (1996); d: Liu et al. (2013); e: Yan et al. (2011); f: Hiemstra et al. (1999); g: Liu et al. (2014); h: Vidyadhar and Hanumantha Rao (2007); i: Karagüzel et al. (2005); k: Gupta and Miller (2010); l: Kumar et al. (2017); m: Liu et al. (2014); n: Zhao et al. (2008); o: Kosmulski (2009); p: Crundwell (2015); q: Gudbrandsson et al. (2014); r: Carroll and Walther (1990); s: Huertas et al. (1999); t: Brady and Walther (1989); u: Lammers et al. (2017); v: Dietzel and Böhme (2005); w: Brady and Walther (1990); x: Berger et al. (1994); n/a: no T_het and F_het can be reported due to the absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments

4 Summary of IN activity of mineral surfaces

4.1 Influence of surface properties

Table 3 summarizes the IN activity of the minerals investigated in this study together with results of microcline from Part 1 (Kumar et al., 2018a) and quartz results from Part 2 (Kumar et al., 2019) and relates them to selected surface properties of the investigated minerals, namely the prevalent surface groups, the dissolution rates at near-neutral conditions and the PZC.

Although all investigated minerals possess hydroxylated surfaces, which are generally thought to promote IN (Hu and Michaelides, 2007; Sosso et al., 2016a; Glatz and Sarupria, 2018) (see Table 3), not all of them proved to be IN active in our emulsion freezing experiments. Namely, the gibbsite and mica (muscovite and biotite) samples did not show any heterogeneous freezing signal in pure water. Zeta potential measurements of these minerals show that the hydroxylated edges of muscovite and the surface of gibbsite carry a positive charge at neutral conditions due to protonation of aluminol groups (see Table 3). This is in contrast to the surfaces of quartz, feldspars and the hydroxylated edges of kaolinite, which all carry negative charge at neutral conditions due to partial deprotonation of the silanol groups. Thus, positively charged (due to protonation) hydroxylated surfaces seem to have a tendency to be IN inactive, while negatively charged surfaces tend to be IN active. However, long-term aged quartz surfaces (7 months; see Kumar et al., 2019) show hardly any IN activity while milled quartz surfaces are highly IN active, although the quartz surface is in both cases negatively charged and highly hydroxylated (Turci et al., 2016). On the other hand, AgI (Edwards and Evans, 1962; Marcolli et al., 2016) and sapphire (Abdelmonem et al., 2017) show the highest IN activity close to the point of zero charge. Conversely, pyroelectric LiTaO₃ and SrTiO₃ promote IN when their surfaces are positively charged (Ehre et al., 2010). This shows that the OH surface density together with the surface charge are not sufficient to predict IN activity.

4.2 Dissolution and growth in pure water

The surfaces of the investigated feldspars exhibit similar chemical compositions although with different Si : Al ratios and Si ∕ Al ordering, which both influence the aluminum depletion and the dissolution rate. The initial dissolution of most feldspars is incongruent with preferential dissolution of aluminum, resulting in a Si-rich amorphous layer. We hypothesize that the surface remains well-ordered over a longer period of time for microcline due to its lowest dissolution rate (compared to the other investigated feldspars). Indeed, our emulsion freezing experiments on a microcline suspension (2 wt %) in pure water, which was aged for 6 months, showed no significant change in IN efficiency compared with a freshly prepared sample (aged sample: T_het=251.4 K, F_het=0.71, see Fig. S15 in the Supplement; fresh sample: T_het=252.1 K, F_het=0.74; Kumar et al., 2018a). Peckhaus et al. (2016) observed a decrease in IN activity by 2 K for a K-feldspar over a time span of 5 months. This implies that the high initial IN activity of microcline degrades only slowly within days or months (Kumar et al., 2018a). Hydrogen bonding to the feldspar surface is a prerequisite to arrange water molecules in a suitable configuration for IN, but at the same time it is the first step to the disintegration of the feldspar surface. Feldspar dissolution occurs via protonation of Al–O–Si bridges followed by removal of Al³⁺ and protonation of the dangling bonds resulting in a silanol-rich surface. As the dissolution proceeds, the Al-depleted Si layer becomes thicker and more amorphous-like.

When the surface of milled quartz grows or dissolves, active sites are lost and the IN activity decreases (Kumar et al., 2019). Under growth conditions, i.e., when the dissolved Si concentration exceeds the saturation concentration with respect to quartz, a siliceous layer forms on the quartz surface within about a day, which hampers the IN activity of quartz. When this layer is washed away with pure water after several days of aging, the IN activity is restored. On timescales of months, quartz slowly grows within this layer resulting in an intact, grown quartz surface that is barely IN active. This suggests that the IN activity of silica mainly stems from activation through grinding and is absent in regular, grown quartz surfaces. We ascribe the absence of IN on the highly hydroxylated grown quartz surface to networks of interconnected hydrogen bonds that are too strong to be disrupted by water molecules. This implies that for a hydroxylated surface to be IN active the hydrogen bonds must be available for bonding to water molecules in order to direct them into an ice-like pattern.

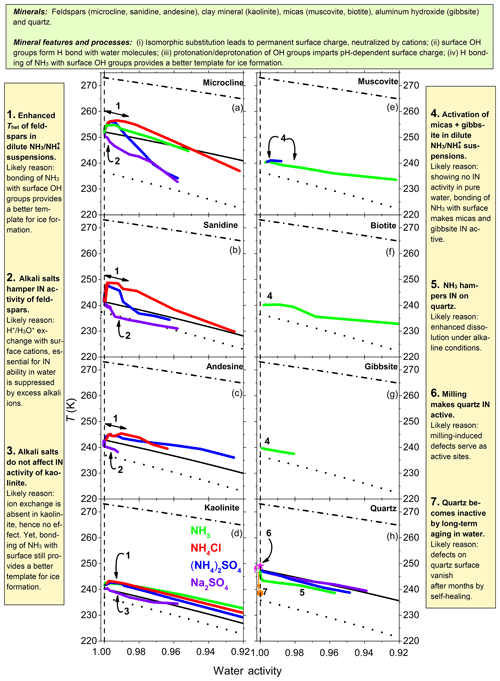
Figure 9 Annotated summary: heterogeneous IN onset temperatures, T_het, of various mineral dusts (2 wt %–10 wt %) as a function of water activity in NH₃, (NH₄)₂SO₄, NH₄Cl and Na₂SO₄ solutions (color coded) for a_w equal to 1.0–0.92. (a) Results for microcline from Kumar et al. (2018a). (b–g) Feldspars, kaolinite, micas and gibbsite investigated in the present study. (h) Results for quartz from Kumar et al. (2019). Dash-dotted black lines: ice melting point curves. Dotted black lines: homogeneous ice freezing curves for supercooled aqueous solutions. Solid black lines: expected heterogeneous freezing curves if the presence of solutes did not change the mineral surface properties. Lines result by horizontally shifting from the ice melting curve by a constant $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{het}}$ emanating from the heterogeneous freezing temperatures of the suspensions of the minerals in pure water (at a_w=1). Specifically, $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{microcline}}=\mathrm{0.296}$, $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{sanidine}}=\mathrm{0.264}$, $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{andesine}}=\mathrm{0.254}$, $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{kaolinite}}=\mathrm{0.272}$ and $\mathrm{\Delta }{a}_{\text{w}}^{\mathrm{quartz}}=\mathrm{0.221}$.

4.3 Influence of solutes

Figure 9 reviews the influence of solutes on the heterogeneous IN onset temperatures of the investigated aluminosilicates and quartz. The presence of ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ in the suspensions increases T_het of all investigated feldspars and kaolinite (Fig. 9, point 1). Moreover, it provides IN activity to the investigated micas and gibbsite, which showed no IN activity in our emulsion freezing experiments performed in pure water (Fig. 9, point 4). The increase in T_het of kaolinite with no exchangeable cations confirms the findings from Kumar et al. (2018a) that the enhanced IN activity in the presence of ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ is not due to ion exchange of ${\mathrm{NH}}_{\mathrm{4}}^{+}$ with the native cations but stems from the adsorption of ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ on the mineral surface. Water molecules can form hydrogen bonds with NH groups of adsorbed ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ that may promote their arrangement into an ice-like pattern. Moreover, this adsorption can decrease the feldspar dissolution by stabilizing the surface. While ${\mathrm{NH}}_{\mathrm{3}}/{\mathrm{NH}}_{\mathrm{4}}^{+}$ also interact with silica surfaces, these interactions do not lead to an increase in T_het. Rather, a decrease is observed in the presence of NH₃ due to the enhanced dissolution of quartz under alkaline conditions (Fig. 9, point 5).

The alkali salt Na₂SO₄ strongly decreases the IN activity of feldspars (Fig. 9, point 2) but does not influence that of kaolinite (Fig. 9, point 3). This indicates that alkali ions influence the IN activity of feldspars through ion exchange, which does not take place in kaolinite. Dissolved Na⁺ may take the positions of the protons on the surface and thus impede IN. This shows that the replacement of the charge balancing cations with protons taking place in pure water is crucial for the IN activity of feldspars.

4.4 Influence of milling

Milling increases the IN activity of quartz (Fig. 9, point 6), while the growth of an intact quartz layer on top of the milled quartz surface strongly hampers it (Fig. 9, point 7). Milling leads to an increase in surface irregularities and defects, which may lead to changes in the abundance and distribution of surface functional groups. These changes, in general, enhance IN efficiency but the enhancement depends on the type of mineral surface. Zolles et al. (2015) showed that additional milling of K-feldspar leads to only a slight increase in its high IN efficiency. Kaufmann et al. (2016) performed emulsion freezing experiments with a dust sample that was ground-collected in Antarctica (48 % feldspars, 24 % quartz) and observed an increase of the already high IN activity of the sieved sample when it was additionally milled. We ascribe the high IN activity of the sieved sample to the presence of the feldspars, whereas an additional increase after milling is most likely due to activation of the quartz component. Together with the finding that K-feldspars aged in pure water over months (see Sect. 4.2) kept their IN activity, we conclude that mechanical activation, e.g., due to milling, is not a prerequisite for the IN activity of feldspars. This is in contrast to our findings for quartz surfaces presented here (Fig. 9) and in Kumar et al. (2019). Boose et al. (2016) found a slightly higher active site density of the milled fraction of their Atacama dust sample (65 % feldspars, 10 % quartz) compared with the sieved fraction (51 % feldspars, 16 % quartz). On the other hand, they observed a decreased IN activity of their Israel dust sample after milling (80 % calcite, 6 % quartz) compared with the sieved fraction (67 % calcite, 7 % quartz). A natural quartz sample from Zolles et al. (2015) showed a very strong enhancement in IN efficiency due to milling. Moreover, milled samples from Boose et al. (2016) collected in Australia and Morocco, which primarily consisted of quartz, showed a very high IN activity, corroborating our results on quartz and amorphous silica in the companion paper (Kumar et al., 2019). Therefore, it seems likely that milling is a prerequisite for the IN activity of quartz. A natural process, closest to milling, would be dry erosion, yet it is unclear whether the forces exerted by fracturing during erosion are sufficient to generate similar defects as milling.

5 Conclusions and atmospheric implications

Immersion freezing experiments with aluminosilicates, namely feldspars, kaolinite, micas and gibbsite presented in this study and in Kumar et al. (2019) have shown that modifications of the mineral surfaces in the presence of water and solutes influence their IN activity.

The interaction of water with mineral surfaces is complex and manifold. It depends not only on the type of mineral but also on the exposure time of the surfaces to water and solutes. Factors influencing the IN ability of aluminosilicate surfaces are adsorption and ion exchange with solute molecules influencing the density of OH and NH groups that provide sites for hydrogen bonding with water molecules, permanent and pH-dependent surface charge influencing the orientation of water molecules and surface changes generated by the slow dissolution of the minerals. Therefore, for an improved understanding of IN, the specific surface properties of each mineral and the processes modifying the mineral surfaces in water and aqueous solutions need to be investigated by experimental surface techniques. In addition, molecular dynamics simulations of IN may contribute to clarifying these processes, but only if interactions of the mineral surface with water, e.g., surface ion exchange, protonation or deprotonation of the surface and slow dissolution, are taken into account.

Aluminosilicates constitute the majority of airborne mineral dust. Dust particles can be exposed to reactive gases like NH₃ or SO₂ during long-range transport, resulting in a coating and surface modification (Sullivan et al., 2007; Kolb et al., 2010; Fitzgerald et al., 2015). The modifications introduced by chemical coatings depend on the particle mineralogy, transport pathway and exposure duration (Matsuki et al., 2005; Sullivan et al., 2007; Rodríguez et al., 2011). Our results suggest that the IN activity of dust aerosols not only depend on their composition but also on their chemical exposure history. In Part 1 (Kumar et al., 2018a) we discussed in detail the fate of microcline in atmospheric solution droplets (especially (NH₄)₂SO₄ and H₂SO₄) following various atmospheric air parcel trajectories with increasing moisture. This discussion is applicable to the aluminosilicates shown in this study and can hence be extended. A coating of aqueous (NH₄)₂SO₄ solution may enhance the IN efficiency in condensation mode of aluminosilicates in general, but only when sulfuric acid and ammonia are deposited concomitantly. Aluminosilicates, especially feldspars, are sensitive to highly acidic conditions due to enhanced dissolution. This might hamper their relevance in the case of long-range transport when they are exposed to acidic air masses (e.g., acquiring sulfuric acid coatings prior to neutralization by ammonia). Moreover, in Part 2 (Kumar et al., 2019) we have shown that the relevance of quartz particles as atmospheric INPs is uncertain. To assess the IN activity of naturally eroded quartz, IN experiments need to be carried out with quartz-rich natural dust samples that are just sieved and not milled.