the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Aqueous reactions of organic triplet excited states with atmospheric alkenes
Richie Kaur
Brandi M. Hudson
Joseph Draper
Dean J. Tantillo
Triplet excited states of organic matter are formed when colored organic matter (i.e., brown carbon) absorbs light. While these “triplets” can be important photooxidants in atmospheric drops and particles (e.g., they rapidly oxidize phenols), very little is known about their reactivity toward many classes of organic compounds in the atmosphere. Here we measure the bimolecular rate constants of the triplet excited state of benzophenone (3BP∗), a model species, with 17 water-soluble C3–C6 alkenes that have either been found in the atmosphere or are reasonable surrogates for identified species. Measured rate constants () vary by a factor of 30 and are in the range of (0.24–7.5) ×109 M−1 s−1. Biogenic alkenes found in the atmosphere – e.g., cis-3-hexen-1-ol, cis-3-hexenyl acetate, and methyl jasmonate – react rapidly, with rate constants above 1×109 M−1 s−1. Rate constants depend on alkene characteristics such as the location of the double bond, stereochemistry, and alkyl substitution on the double bond. There is a reasonable correlation between and the calculated one-electron oxidation potential (OP) of the alkenes (R2=0.58); in contrast, rate constants are not correlated with bond dissociation enthalpies, bond dissociation free energies, or computed energy barriers for hydrogen abstraction. Using the OP relationship, we estimate aqueous rate constants for a number of unsaturated isoprene and limonene oxidation products with 3BP∗: values are in the range of (0.080–1.7) ×109 M−1 s−1, with generally faster values for limonene products. Rate constants with less reactive triplets, which are probably more environmentally relevant, are likely roughly 25 times slower. Using our predicted rate constants, along with values for other reactions from the literature, we conclude that triplets are probably minor oxidants for isoprene- and limonene-related compounds in cloudy or foggy atmospheres, except in cases in which the triplets are very reactive.
- Article
(3177 KB) - Full-text XML
-
Supplement
(1276 KB) - BibTeX
- EndNote
Photochemical processes in atmospheric aqueous phases (e.g., cloud and fog drops and aqueous particles) are important sources and sinks of secondary organic species (Blando and Turpin, 2000; Lim et al., 2010; Kroll and Seinfeld, 2008; Volkamer et al., 2009; Gelencsér and Varga, 2005), which represent a large fraction of aerosol mass (Zhang et al., 2007; Hallquist et al., 2009). Many of these reactions involve photooxidants, including the hydroxyl radical (•OH), which is widely considered to be the dominant aqueous oxidant (Herrmann et al., 2010, 2015). But there are numerous other aqueous photooxidants, such as singlet molecular oxygen, the hydroperoxyl radical–superoxide radical anion, hydrogen peroxide, and triplet excited states of organic matter (3C∗ or triplets) (Lee et al., 2011; Anastasio and McGregor, 2001; Kaur and Anastasio, 2017, 2018; Anastasio et al., 1994, 1996; Zepp et al., 1977; Wilkinson et al., 1995). Formed from the photoexcitation of colored organic matter (i.e., brown carbon), triplets are important oxidants in surface waters for several classes of organic compounds, including phenols, anilines, amines, phenylurea herbicides, and heterocyclic sulfur-containing compounds (Canonica et al., 1995, 2006; Canonica and Hoigné, 1995; Arnold, 2014; Bahnmüller et al., 2014; Boreen et al., 2005); however, very little is known about atmospheric triplets.
Recent studies have shown that aqueous triplets can be the dominant oxidants for phenols emitted during biomass combustion (Smith et al., 2014), with phenol lifetimes on the order of a few hours in fog drops (Kaur and Anastasio, 2018) and aqueous particle extracts (Kaur et al., 2018). There is also evidence that triplets can oxidize some unsaturated aliphatic compounds. Richards-Henderson et al. (2014) measured rate constants for five unsaturated biogenic volatile organic compounds (BVOCs) with the model triplets 3,4-dimethoxybenzaldhyde and 3'-methoxyacetophenone, and they found that rate constants ranged between 107 and 109 M−1 s−1. Other laboratory studies have shown that triplet states of photosensitizers such as imidazole-2-carboxaldehyde and 4-benzoylbenzoic acid can oxidize gaseous aliphatic BVOCs, e.g., isoprene and limonene, and model aliphatic compounds, e.g., 1-octanol, at the air–water interface to form low-volatility products that increase particle mass (Fu et al., 2015; Rossignol et al., 2014; Li et al., 2016; Laskin et al., 2015). However, the atmospheric importance of these types of processes is unclear (Tsui et al., 2017). Additionally, we recently reported that natural triplets in illuminated fog waters and particle extracts are significant oxidants for methyl jasmonate, an unsaturated aliphatic BVOC, accounting for 30 %–80 % of its aqueous loss during illumination (Kaur et al., 2018; Kaur and Anastasio, 2018).
Abundant BVOCs such as isoprene and limonene are rapidly oxidized in the gas phase to form unsaturated C3–C6 oxygenated volatile organic compounds (OVOCs) that include isoprene hydroxyhydroperoxides, isoprene hydroxynitrates, and isoprene and limonene aldehydes (Surratt et al., 2006; Paulot et al., 2009a, b; Crounse et al., 2011; Ng et al., 2008; Walser et al., 2008). Several of these first-generation products have high Henry's law constants, above 104 M atm−1 (Marais et al., 2016), and partition significantly into cloud and fog drops and, to a smaller extent, into aerosol liquid water. There, they can undergo further oxidation by aqueous photooxidants, including •OH, ozone (Wolfe et al., 2012; St. Clair et al., 2015; Khamaganov and Hites, 2001; Schöne and Herrmann, 2014; Lee et al., 2014), and possibly triplets. Our past measurements have shown that steady-state concentrations of 3C∗ are orders of magnitude higher than •OH in fog waters and aqueous particles (Kaur et al., 2018; Kaur and Anastasio, 2018), and thus they might contribute significantly to the loss of OVOCs derived from isoprene and other precursors. However, testing this hypothesis requires rate constants for the reactions of triplets with alkenes, which are scarce.
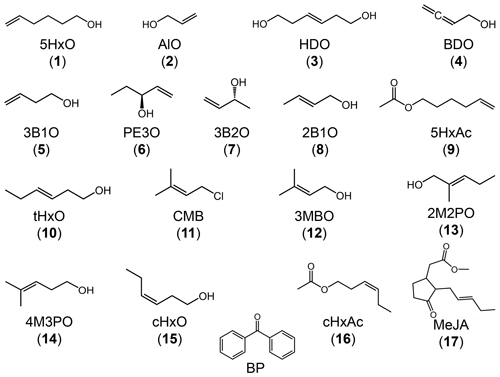
To address this gap, we studied the reactions of 17 C3–C6 unsaturated compounds with the triplet state of the model compound benzophenone (Fig. 1). While our 17 unsaturated compounds include alcohols, esters, and chlorinated compounds, for simplicity we refer to them all as “alkenes”. The tested alkenes include BVOCs emitted into the atmosphere as well as surrogates for some of the small unsaturated gas-phase products formed as secondary OVOCs. The goals of this study are to (1) measure rate constants for reactions of the alkenes with the triplet excited state of benzophenone, (2) explore quantitative structure–activity relationships (QSARs) between the measured rate constants and calculated alkene properties (e.g., the one-electron oxidation potential), and (3) use a suitable QSAR to estimate rate constants for triplets with some unsaturated isoprene and limonene oxidation products to predict whether or not triplets are significant oxidants for these species in cloud and fog drops.
2.1 Chemicals
All chemicals were purchased from Sigma-Aldrich with purities of 95 % and above and were used as received: the compound numbers, compound names, and abbreviated names are listed in Table 1. All chemical solutions were prepared using purified water (Milli-Q water) from a Milli-Q Plus system (Millipore; ≥18.2MΩ cm) with an upstream Barnstead activated carbon cartridge. To mimic fog drop acidity (Kaur and Anastasio, 2017), the pH of each reaction solution was adjusted to 5.5(±0.2) using a 1.0 mM phosphate buffer.
Table 1Measured alkene–benzophenone triplet reaction rate constants, predicted OVOC–benzophenone triplet reaction rate constants, and computed parameters for the alkenes.
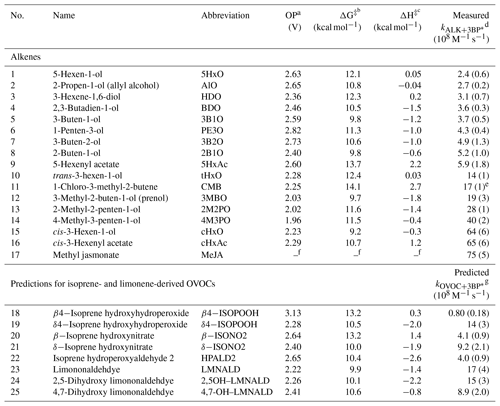
a One-electron oxidation potential calculated using the CBS–QB3 compound method. b,c Lowest transition-state energy barrier for H abstraction by triplet benzophenone; calculated using uB3LYP/6-31+G(d,p). d Measured bimolecular rate constant for alkene reacting with 3BP∗ with uncertainties of ±1 standard deviation; determined from triplicate measurements (Table S1 in the Supplement). e Listed uncertainty is ±1 standard error; n=1. f The oxidation potential and energy barriers could not be computed for MeJA (17). Because the CB3–QB3 method scales at N7 (where N is the number of atoms), the larger compound required more computational power than available. g Predicted bimolecular rate constant for select isoprene- and limonene-derived OVOCs reacting with 3BP∗; determined from the correlation between OP and . Listed uncertainties are ±1 standard error propagated from the error of the slope of the quantitative structure–activity relationship between oxidation potential and (Fig. 3).
2.2 Kinetic experiments
Bimolecular rate constants of the alkenes with the triplet state of benzophenone (3BP∗) were measured using a relative rate technique, as described in the literature (Richards-Henderson et al., 2014; Finlayson-Pitts and Pitts Jr., 1999). The technique involves illuminating a solution containing the triplet precursor (BP), a reference compound with a known second-order rate constant with 3BP∗, and one test alkene for which the rate constant is unknown. The reference compound for each alkene was chosen so that the triplet-induced loss rates for the test alkene and reference compound were similar. Buffered, air-saturated solutions containing 50 µM each of the reference and test compounds and 100 µM of BP were prepared, and then 10 mL of this solution was illuminated in a stirred 2 cm, airtight quartz cuvette (Spectrocell) at 25 ∘C. Samples were illuminated with a 1000 W Xenon arc lamp filtered with an AM 1.0 air mass filter (AM1D-3L, Sciencetech) and 295 nm long-pass filter (20CGA-295, Thorlabs) to mimic tropospheric solar light (Fig. S1 in the Supplement). At various intervals, aliquots of illuminated sample were removed and analyzed for the concentration of the reference compound and test alkene using HPLC (Shimadzu LC-10AT pump, Thermo Scientific BetaBasic 18 C18 column (250×33 mm, 5 µM bead), and Shimadzu-10AT UV–Vis detector). For each alkene, illumination experiments were performed in triplicate (Table S1) using total illumination times typically between 60 and 150 min. Parallel dark controls were employed with every experiment using an aluminum-foil-wrapped cuvette containing the same solution and analyzed in the same manner as the illuminated solutions. The dark cuvette was placed in a corner of the sample chamber, out of the path of the light beam. As a direct photodegradation control, each alkene was also illuminated (separately) in solution without benzophenone; there was no loss for any of the compounds.
In every case, loss of test and reference compounds followed first-order kinetics. Plotting the change in concentration of the test alkene against that of the reference compound yields a linear plot that is represented by
where [Reference]0, [Reference]t, [ALK]0, and [ALK]t are the concentrations of the reference and test alkenes at times zero and t, respectively, and and are the bimolecular rate constants for the reaction of the reference and test alkenes with 3BP∗, respectively. A plot of Eq. (1) (with the y intercept fixed at the origin) gives a slope equal to the ratio of the bimolecular rate constants; dividing by the slope gives . The measurement technique is illustrated in Fig. S2. While 3BP∗ makes singlet molecular oxygen (), the latter is an insignificant oxidant of alkenes in our solutions: the concentrations of the two oxidants are similar (McNeill and Canonica, 2016), but our measured rate constants of alkenes with 3BP∗ are approximately 2500 times faster than the corresponding rate constants with (Richards-Henderson et al., 2014).
2.3 Calculation of oxidation predictor variables
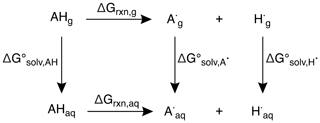
All calculations were completed using the Gaussian 09 software suite (Frisch et al., 2009). Structures of alkenes were optimized using uB3LYP/6-31+G(d,p) (Becke, 1992, 1993; Lee et al., 1988; Stephens et al., 1994; Tirado-Rives and Jorgensen, 2008) for reaction coordinate calculations and the CBS–QB3 (Montgomery Jr. et al., 1999) method for predicting bond dissociation enthalpies (BDEs), bond dissociation free energies (BDFEs), and oxidation potentials (OPs). This method has a mean absolute deviation of approximately 1 kcal mol−1, which corresponds to 0.04 V in Eox (i.e., OP). Transition-state structures (TSSs) were optimized in the triplet state using uB3LYP/6-31+G(d,p) (Becke, 1992, 1993; Lee et al., 1988; Stephens et al., 1994; Tirado-Rives and Jorgensen, 2008). TSSs were confirmed by the presence of an imaginary frequency, and minima (reactants and products) were confirmed by the absence of imaginary frequencies. Free energy (ΔG) and enthalpy (ΔH) differences were determined by comparing TSS energies relative to their reactant energies. For solvent-phase calculations, the solvent model density (SMD) (Marenich et al., 2009) continuum model was used with water as the solvent. To calculate BDEs, the neutral (AH) and radical species (A•) (resulting from H atom abstraction) of each alkene and the H radical (H•) were optimized in the gas phase. Using the computed enthalpies (H) and Eq. (2), the predicted BDEs of each alkene were determined.
To determine the predicted BDFEs, the neutral (AHg, AHaq) and radical species (, ) of each alkene and the H radical (, ) were optimized in the gas and solvent phases and their differences taken to give , , and , respectively. Based on the thermodynamic cycle shown (Scheme 1), these values were used in Eqs. (3) and (4) to calculate the BDFEs of C–H and O–H bonds.
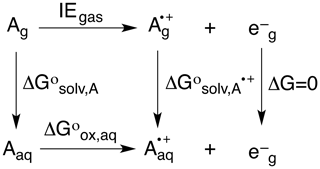
To predict OPs, the neutral (Ag, Aaq) and radical cation (, ) forms of each alkene were optimized in the gas and solvent phase, their difference giving ΔG∘solv,A and ΔG∘. Based on the thermodynamic cycle shown below (Scheme 2), these values were used in Eqs. (5)–(7) to calculate the OP (i.e., Eox) of each alkene.
Here, n is the number of electrons, F is Faraday's constant (96485.3365 C mol−1), and SHE is the potential of the standard hydrogen electrode (4.28 V) (Tripkovic et al., 2011).
Subsequent MP2–CBSB3 (Petersson et al., 1988, 1991; Petersson and Al-Laham, 1991; Mayer et al., 1998) single-point calculations were used to compute the highest occupied molecular orbitals (HOMOs) and singly occupied molecular orbitals (SOMOs). Structural drawings were produced using CYLView (Legault, 2009).
3.1 Alkene–triplet bimolecular rate constants ()
Figure 1 shows the chemical structures for all 17 alkenes and the triplet precursor benzophenone. The alkenes have molecular weights ranging between 58 and 220 g mol−1 and include 13 alcohols, three esters, and one chlorinated compound. The model triplet precursor benzophenone (BP) has been previously employed in surface water studies, and its triplet state rapidly reacts with aromatics such as substituted phenols and phenyl urea herbicides with rate constants faster than 109 M−1 s−1 (Canonica et al., 2000, 2006).
The bimolecular rate constants for the alkenes with the excited triplet state of BP () vary by a factor of 30, spanning the range of (0.24–7.5) ×109 M−1 s−1. Values are shown in Tables 1 and S1 in the Supplement and in Fig. S3, in which the alkenes are numbered in ascending order of their reactivity towards 3BP∗. Based on their rate constants, the alkenes appear to be broadly split into two groups: the slower alkenes (1–9), whose rate constants lie below 1×109 M−1 s−1 and span a range of only a factor of 2.5, and the faster alkenes (10–17), which vary by a factor of 5. Notably, three of the four BVOCs identified in emissions to the atmosphere – 3MBO (12), cHxO (15), cHxAc (16) and MeJA (17) – react rapidly with 3BP∗, with rate constants greater than 1×109 M−1 s−1.
Three alkene characteristics appear to increase reactivity: internal (rather than terminal) double bonds, methyl substitution on the double bond, and alkene stereochemistry. To more specifically examine the impact of these variables, we compare the rate constants for three sets of alkenes (Fig. 2). The lowest free energy and enthalpy barriers for the abstraction of a hydrogen atom are also shown in Fig. 2 (and in Table 1); while overall these computed barriers are not well-correlated with rate constants (discussed below), lower barriers generally correspond to higher rate constants for the sets of alkenes in Fig. 2. The first two sets of compounds in Fig. 2 indicate that internal alkenes react faster with 3BP∗ than do terminal isomers: cHxAc (16), an internal hexenyl acetate, has a reaction rate constant 11 times faster than its terminal isomer 5HxAc (9). The corresponding alcohols also exhibit the same trend: the internal alkenes cHxO (15) and tHxO (10) react 27 and 5.8 times faster, respectively, than the terminal isomer 5HxO (1). This dependence of reactivity on double bond location has implications for isoprene hydroxyhydroperoxides (ISOPOOHs) and hydroxynitrate (ISONO2), which have both terminal (β-) and nonterminal (δ-) isomers formed from gas-phase oxidation (Marais et al., 2016; Paulot et al., 2009a, b). Based on our results we expect the δ-isomers to react more quickly with organic triplets than the β-isomers.
Alkene stereochemistry also affects the triplet–alkene reaction rate constant. The data in the middle of Fig. 2 show that cis-HxO (15) reacts nearly 5 times more quickly with 3BP∗ than does trans-HxO (10), consistent with the lower predicted energy barrier for hydrogen atom abstraction from the cis-isomer. Finally, the addition of electron-donating substituents (methyl groups) on an unsaturated carbon atom also increases the rate constant. This is evident from comparing 2B1O (8) and its methyl-substituted analog 3MBO (12): is 3.7 times faster with the methyl group (Fig. 2). Mechanistically, triplet-induced oxidation can proceed via either hydrogen atom transfer or a proton-coupled electron transfer (Canonica et al., 1995; Warren et al., 2010; Erickson et al., 2015), and the presence of an electron-donating substituent on the double bond likely selectively stabilizes the intermediates (e.g., radical or radical cation) formed from these two processes, as well as the transition-state structures for their formation.
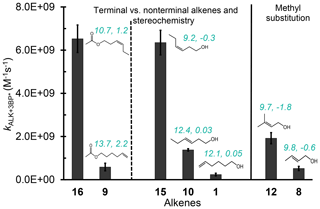
Figure 2Comparison of three sets of alkenes to illustrate how rate constants with the benzophenone triplet state vary with double bond location, stereochemistry, and methyl substitution. The teal numbers on each alkene represent the lowest free energy (ΔG‡) and enthalpy (ΔH‡) transition-state barriers in kcal mol−1 for H abstraction by the triplet benzophenone; these were calculated at the uB3LYP/6-31+G(d,p) level of theory. Though computed barriers (Table 1) are not correlated with the overall rates measured, they broadly match the rate trends within a given set of alkenes in this figure.
3.2 Relationship between k and one-electron oxidation potential
Our next goal was to develop a quantitative structure–activity relationship (QSAR) so that we can predict rate constants for alkene–triplet reactions. To use as predictor variables in the QSARs we computed several properties of the alkenes: bond dissociation enthalpy and free energy for various hydrogen atoms (Fig. S4), free energy and enthalpy barriers for hydrogen atom abstraction (Table 1), and one-electron oxidation potentials (Table 1). Apart from the oxidation potential, none of the other properties correlate well with the measured rate constants (Figs. S5 and S6). While there is no correlation between the rate constants and predicted energy barriers, alkenes with lower predicted free energy barriers (ΔG‡) are predicted to be fast-reacting, with rate constants above 5×108 M−1 s−1 (Fig. S6). As shown in Fig. S6, computed barriers predict much larger variation in the rate than observed experimentally, suggesting that the breaking of the C–H or O–H bond does not occur in the rate-determining step for all alkenes.
Of all the properties examined, the one-electron oxidation potential of the alkenes best correlates with the (log of) measured rate constants, with rate constants generally increasing as the alkenes are more easily oxidized, i.e., at lower OP values (R2=0.58) (Fig. 3). Measured rate constants for 13 of the 16 alkenes lie within (or very near) the 95 % confidence interval (blue lines) of the regression fit, but there are three notable outliers: hexen-1,3-diol (3, HDO), cis-3-hexen-1-ol (15, cHxO), and cis-3-hexenylacetate (16, cHxAc). The measured HDO rate constant is 3.3 times lower than that predicted by the regression line, while measured rate constants for cHxO and cHxAc are 3.9 and 4.9 times higher, respectively, than predicted.
To try to assess why these compounds differ from the others, we calculated the highest occupied molecular orbital of the alkene and the singly occupied molecular orbital of the alkene radical cation (i.e., after oxidation) (Fig. 4). Depending on the system, oxidation is predicted to occur by removing an electron either from the π system of the C–C double bond or from a lone pair on the O atom. This is illustrated in Fig. 4, which shows the HOMO and SOMO structures for HDO (3), wherein the electron is removed from the C–C double bond, and 3B1O (5), wherein the electron is removed from the oxygen atom. However, the three outliers in the correlation do not all fall into just one of these categories: for cHxAc (16) the electron is most likely abstracted from the oxygen, while for HDO (3) and cHxO (15) the electron is likely removed from the π system (Tables S2 and S3). This suggests that the location of electron removal does not control the rate constants. We also examined if the rate of loss of cHxO might be enhanced due to oligomerization, whereby an initially formed cHxO radical leads to additional cHxO loss. Since the pseudo-first-order rate constant of oligomerization should increase with initial cHxO concentration, we measured the rate constant for cHxO loss over a range of initial concentrations (2–50 µM). However, as shown in Fig. S8, the rate constant for cHxO loss does not depend on its concentration, suggesting that oligomerization is an unimportant loss process for cHxO in our experiments. Thus, it is not clear why these three compounds do not fall closer to the regression line in Fig. 3. However, except for 16, all of the alkenes fall within a factor of 4 of the correlation line (gray lines). Finally, even though there is a good correlation between rate constant and OP in Fig. 3, it does not indicate whether these reactions proceed via pure electron transfer, proton-coupled electron transfer, or hydrogen transfer. As discussed earlier, since the predicted energy barriers for hydrogen abstraction do not correlate with measured rate constants (Fig. S6) and appear to split into two groups, uncertainty remains about the mechanism of triplet-induced oxidation of the alkenes.
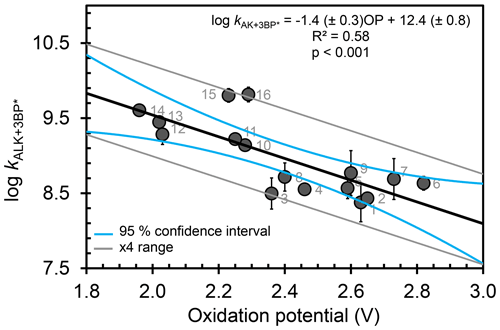
Figure 3Correlation between measured bimolecular rate constants for alkenes with the triplet excited state of benzophenone () and the computed one-electron oxidation potentials of the alkenes. Numbers on each point represent the alkene numbers in Table 1. Blue lines represent 95 % confidence intervals of the regression prediction. The gray lines bound the region that is within a factor of 4 of the regression prediction; all but one of the alkene values fall within this. Methyl jasmonate (17) is not included in this figure due to computational challenges in calculating its OP (see Table 1).
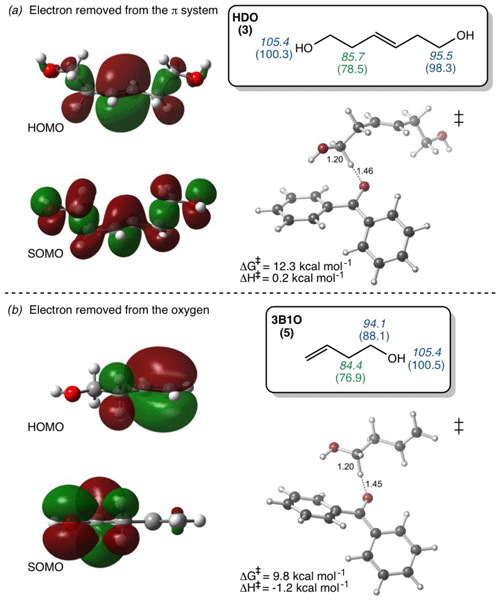
Figure 4Diagrams of the highest occupied molecular orbitals (HOMOs) of the alkenes before oxidation, the singly occupied molecular orbitals (SOMOs) after the removal of one electron from the alkenes, and the lowest-energy transition-state structures (‡) of alkenes 3 and 5. Bond dissociation enthalpy (italicized) and free energy (in parentheses) for various hydrogen atoms (in kcal mol−1) for each alkene are shown in the boxes. Numbers in green are the lowest values and thus represent the most labile hydrogen in each alkene. (a) The electron removed during H abstraction of HDO is predicted to come from the π system, but this results in delocalization due to hyperconjugation. (b) The electron removed from 3B1O during H abstraction is predicted to come from the oxygen. See Tables S2 and S3 for HOMO–SOMO structures and Fig. S4 for the bond dissociation enthalpies and free energies for other alkenes.
3.3 Predicted triplet–OVOC bimolecular rate constants
We next use the relationship in Fig. 3, along with calculated oxidation potentials, to predict second-order rate constants for 3BP∗ with a set of unsaturated oxygenated VOCs formed by the oxidation of isoprene and limonene. As shown in Fig. 5, we predict that limonene products generally react faster with 3BP∗ than do isoprene products. For the five isoprene-derived OVOCs that we considered, rate constants vary by a factor of 17 and range (0.080–1.4) ×109 M−1 s−1 (Table 1, Fig. 5). The δ-isomers of ISOPOOH and ISONO2, which contain internal double bonds, have lower computed one-electron oxidation potentials and thus higher predicted rate constants compared to the terminal β-isomers. This is similar to the trend observed with the other alkenes (Fig. 2). In the case of isoprene hydroperoxyaldehydes, we were able to determine the oxidation potential for only HPALD2 (22), and its predicted reaction rate constant (±1 SE) of M−1 s−1 is among the lowest of the isoprene-derived alkenes (Fig. 5).
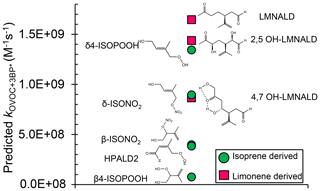
Figure 5Predicted bimolecular rate constants for a range of limonene and isoprene oxidation products (OVOCs) with the triplet state of BP. Rate constants are estimated from the QSAR with one-electron oxidation potentials (OPs) (Fig. 3). Oxidation potentials used to predict the rate constants here (and in Table 1) are for the lowest-energy isomers of the OVOCs, which are the structures shown here. The structures of some of the other higher-energy isomers are shown in Table S4.
We calculated OP values and triplet rate constants for three limonene-derived OVOCs: limonene aldehyde (LMNALD) and two dihydroxy-limonene aldehydes (2,5OH–LMNALD and 4,7OH–LMNALD). Compared to the isoprene-derived alkenes, the rate constants for all three limonene products are high and range (0.89–1.7) ×109 M−1 s−1. All of the limonene aldehydes (as well as the isoprene products) can have several isomers whose calculated oxidation potentials can vary, which affects the predicted rate constant. For example, for 4,7OH–LMNALD (25) the computed oxidation potential for five of its isomers vary between 2.17 and 2.48 V (Table S4), which leads to a relative standard deviation of 40 % in the predicted rate constants for the various isomers. For each OVOC, the predicted rate constants in Table 1 are for the lowest-energy isomers whose structures are shown in Fig. S9.
3.4 Role of triplets in the fate of isoprene- and limonene-derived OVOCs
Next, we use our estimated rate constants, along with previously published estimated values for rates of other loss processes (Table S5), to understand the importance of triplets as sinks for isoprene- and limonene-derived OVOCs in a foggy–cloudy atmosphere. For our simple calculations we use a liquid water content of L aq ∕ L g, a temperature of 25 ∘C, and calculated Henry's law constants from EPISuite (US EPA, Estimation Programs Interface Suite™ for Microsoft® Windows v4.1, 2016) (Table S6). From these inputs, we estimate that between 10 % and 97 % of the OVOCs will be partitioned into the aqueous phase under our conditions (Table S6). The OVOC sinks we consider are photolysis and reactions with the hydroxyl radical (•OH) and ozone (O3) in the gas phase as well as hydrolysis and reactions with •OH, O3, and triplets in the aqueous phase (Table S5). Based on typical oxidant concentrations in both phases and available rate constants with sinks, the overall pseudo-first-order rate constants for initial OVOC losses are estimated to be in the range of (0.27–3.0) s−1, corresponding to overall lifetimes of 0.93 to 10 h (Table S7). The only exception is δ-ISONO2, which is expected to undergo rapid hydrolysis to form its corresponding diol (Jacobs et al., 2014) with a lifetime of just 0.078 h (280 s).
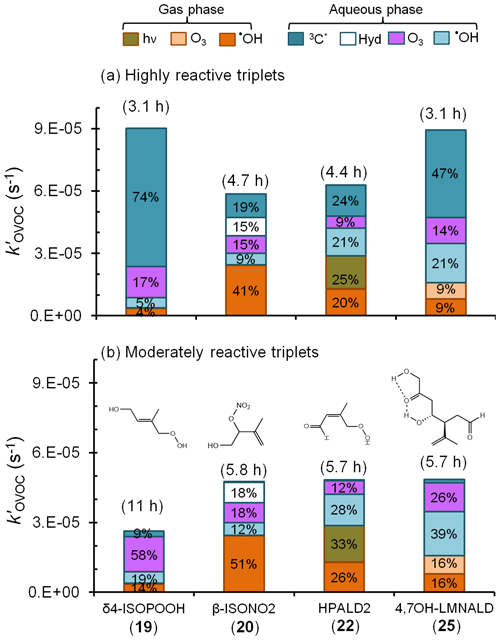
Figure 6Estimated pseudo-first-order loss rate constants and corresponding lifetimes (in parentheses) for representative isoprene- and limonene-derived oxidation products in a foggy atmosphere (Tables S5–S7). Colors and data labels indicate the percentage of OVOC lost via each gas and aqueous pathway, including direct photoreaction (hν) and hydrolysis (Hyd); pathways contributing less than 4 % are not labeled. Panel (a) is a likely upper bound for the triplet contributions to OVOC loss in which we assume that all fog triplets are highly reactive, like benzophenone. Panel (b) shows the more likely contribution from triplets, assuming moderately reactive triplets that are more representative of the average measured in fog waters and aqueous particle extracts (Kaur et al., 2018; Kaur and Anastasio, 2018) (Tables S5–S7).
Figure 6 shows the overall loss rate constants and the contribution from each pathway for four of these OVOCs: δ4-ISOPOOH (19), β-ISONO2 (20), HPALD2 (22), and 4,7-OH–LMNALD (25). Overall, aqueous-phase processes dominate the fate of these OVOCs, accounting for the bulk of their loss, but the contribution of aqueous triplets to OVOC loss depends strongly on the triplet reactivity. Panel (a) of Fig. 6 shows OVOC loss when we assume that the aqueous triplets are highly reactive, i.e., using rate constants estimated for 3BP∗ (Fig. 5). Since our recent measurements (Kaur et al., 2018; Kaur and Anastasio, 2018) indicate that, on average, ambient triplets are not this reactive, this scenario likely represents an upper bound for the triplet contribution. In this case highly reactive triplets are the dominant sinks for δ4-ISOPOOH and 4,7-OH–LMNALD, accounting for 74 % and 47 % of their total losses, respectively (Fig. 6a). For β-ISONO2 and HPALD2, triplets are not dominant but still significant, accounting for 19 % and 24 % of loss, respectively, while other sinks dominate. For the OVOCs for which we calculated rate constants with 3BP∗ (Fig. 5) but that are not shown in Fig. 6, the triplet contribution varies widely, from less than 1 % for δ-ISONO2 (21), for which hydrolysis dominates, to 59 % for 2,5-OH–LMNALD (24) (Table S7).
While 3BP∗ likely represents an upper bound of triplet reactivity in atmospheric waters, our recent measurements indicate that the triplets in fog waters and particles have an average reactivity that is typically similar to 3'-methoxyacetophenone (3MAP) and 3,4-dimethoxybenzaldehyde (DMB) (Kaur et al., 2018; Kaur and Anastasio, 2018). A comparison of our 3BP∗ rate constants (Table 1) with the average values for the 3MAP and DMB triplets for a subset of the alkenes (Richards-Henderson et al., 2014) indicates that the average 3MAP–DMB triplet rate constants are 1 %–18 % of the corresponding 3BP∗ values. Thus, to scale alkene–triplet rate constants from 3BP∗ to the 3MAP and DMB triplets we take the median value of 4 %, which is derived from the MeJA rate constants (Table S8). Figure 6b shows the calculated fates of the OVOCs in the case in which we consider “typical-reactivity” triplets; i.e., we multiply the 3BP∗ + OVOC rate constants (Fig. 5) by a factor of 0.04. Under these conditions, triplets are minor oxidants (Fig. 6b), accounting for 9 % and 3 % of the loss of δ4-ISOPOOH and 4,7-LMNALD, respectively, and approximately 1 % for the other two OVOCs. This suggests that aqueous triplets are generally minor sinks for OVOCs derived from isoprene and limonene, in contrast to the case for phenols, for which triplets appear to be the major sink (Smith et al., 2014; Yu et al., 2014; Kaur and Anastasio, 2018). However, there are several important uncertainties in our determination that triplets are likely minor sinks for oxygenated alkenes. First, the factor we used to adjust from 3BP∗ rate constants to triplet 3MAP–DMB rate constants (i.e., a factor of 0.04) is quite uncertain: values for the three BVOCs examined range from 0.01 to 0.18 (Table S8). Additionally, there are very few measurements of triplets in atmospheric drops or particles (Kaur et al., 2018; Kaur and Anastasio, 2018) and only from two sites, so it is possible that we are underestimating the average reactivity and/or concentrations of triplets in atmospheric drops and particles.
To explore whether triplet excited states of organic matter might be important sinks for unsaturated organic compounds in atmospheric drops, we measured rate constants for 17 C3–C6 alkenes with the triplet excited state of benzophenone (3BP∗). The resulting bimolecular rate constants span the range of (0.24–7.5) ×109 M−1 s−1. Notably, the rate constants are high (above 109 M−1 s−1) for some important green-leaf volatiles emitted from plants: 3MBO, cHxO, cHxAc, and MeJA. Rate constants appear to be enhanced by alkene characteristics such as an internal double bond, cis-stereochemistry, and alkyl substitution on the double bond.
To be able to predict rate constants for other alkenes, we examined QSARs between our measured rate constants and a variety of calculated properties for the alkenes and 3BP∗–alkene transition states. Rate constants are not correlated with bond dissociation enthalpies, free energies, or predicted energy barriers for the removal of various hydrogen atoms, but they are reasonably correlated with the one-electron oxidation potential of the alkenes (R2=0.58). Based on the relationship between rate constants and oxidation potential, we predict that highly reactive triplets will react with first-generation isoprene and limonene oxidation products with rate constants on the order of 108–109 M−1 s−1, with higher values for the δ-isomers compared to terminal β-isomer products. Using these rate constants in a simple model of OVOC chemistry in a foggy–cloudy atmosphere suggests that highly reactive aqueous triplets could be significant oxidants for some isoprene hydroxyhydroperoxides and limonene aldehydes. However, for our current best estimate of typical reactivities, triplets are a minor sink for isoprene- and limonene-derived OVOCs.
To more specifically quantify the contributions of triplet excited states towards the loss of alkenes in particles and drops requires more insight into both the reactivities and concentrations of atmospheric triplet species. In addition, assessing whether triplets might be important sinks for other organic species requires more measurements of reaction rate constants with atmospherically relevant organics.
Data are available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-5021-2019-supplement.
CA and RK conceptualized the research goals and designed the experiments. RK and JD performed the laboratory work, while BH and DT planned and performed the computational calculations. RK analyzed the experimental data and prepared the paper with contributions from all coauthors, particularly BH, who wrote the sections on computational calculations and prepared the corresponding figures. CA reviewed and edited the paper. CA and DT provided oversight during the entire process.
The authors declare that they have no conflict of interest.
We thank Jacqueline R. Labins for assistance with rate constant measurements, Ted Hullar for irradiance measurements, and Tran Nguyen for helpful discussions on the reactivity of isoprene oxidation products. This research was funded by the National Science Foundation (grants AGS-1105049 and AGS-1649212), the California Agricultural Experiment Station (Project CA-D-LAW-6403-RR), the University of California Davis Office of Graduate Studies, a UC Guru Gobind Singh Fellowship, and the Agricultural and Environmental Chemistry Graduate Group at UC Davis.
This paper was edited by Sergey A. Nizkorodov and reviewed by two anonymous referees.
Anastasio, C. and McGregor, K. G.: Chemistry of fog waters in California's central valley: 1. In situ photoformation of hydroxyl radical and singlet molecular oxygen, Atmos. Environ., 35, 1079–1089, 2001.
Anastasio, C., Faust, B. C., and Allen, J. M.: Aqueous-phase photochemical formation of hydrogen peroxide in authentic cloud waters, J. Geophys. Res.-Atmos., 99, 8231–8248, 1994.
Anastasio, C., Faust, B. C., and Rao, C. J.: Aromatic carbonyl compounds as aqueous-phase photochemical sources of hydrogen peroxide in acidic sulfate aerosols, fogs, and clouds. 1. Non-phenolic methoxybenzaldehydes and methoxyacetophenones with reductants (phenols), Environ. Sci. Technol., 31, 218–232, 1996.
Arnold, W. A.: One electron oxidation potential as a predictor of rate constants of N-containing compounds with carbonate radical and triplet excited state organic matter, Environ. Sci. Process. Impact., 16, 832–838, 2014.
Bahnmüller, S., von Gunten, U., and Canonica, S.: Sunlight-induced transformation of sulfadiazine and sulfamethoxazole in surface waters and wastewater effluents, Water Res., 57, 183–192, 2014.
Becke, A. D.: Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys, 96, 2155–2160, 1992.
Becke, A. D.: Becke's three parameter hybrid method using the LYP correlation functional, J. Chem. Phys., 98, 5648–5652, 1993.
Blando, J. D. and Turpin, B. J.: Secondary organic aerosol formation in cloud and fog droplets: A literature evaluation of plausibility, Atmos. Environ., 34, 1623–1632, 2000.
Boreen, A. L., Arnold, W. A., and McNeill, K.: Triplet-sensitized photodegradation of sulfa drugs containing six-membered heterocyclic groups: identification of an SO2 extrusion photoproduct, Environ. Sci. Technol., 39, 3630–3638, 2005.
Canonica, S. and Hoigné, J.: Enhanced oxidation of methoxy phenols at micromolar concentration photosensitized by dissolved natural organic material, Chemosphere, 30, 2365–2374, 1995.
Canonica, S., Jans, U., Stemmler, K., and Hoigne, J.: Transformation kinetics of phenols in water: Photosensitization by dissolved natural organic material and aromatic ketones, Environ. Sci. Technol., 29, 1822–1831, 1995.
Canonica, S., Hellrung, B., and Wirz, J.: Oxidation of phenols by triplet aromatic ketones in aqueous solution, J. Phys. Chem. A, 104, 1226–1232, 2000.
Canonica, S., Hellrung, B., Müller, P., and Wirz, J.: Aqueous oxidation of phenylurea herbicides by triplet aromatic ketones, Environ. Sci. Technol., 40, 6636–6641, 2006.
Crounse, J. D., Paulot, F., Kjaergaard, H. G., and Wennberg, P. O.: Peroxy radical isomerization in the oxidation of isoprene, Phys. Chem. Chem. Phys., 13, 13607–13613, 2011.
Erickson, P. R., Walpen, N., Guerard, J. J., Eustis, S. N., Arey, J. S., and McNeill, K.: Controlling factors in the rates of oxidation of anilines and phenols by triplet methylene blue in aqueous solution, J. Phys. Chem. A, 119, 3233–3243, 2015.
Finlayson-Pitts, B. J. and Pitts Jr., J. N.: Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications, Academic press, San Diego, 1999.
Frisch, M., Trucks, G., Schlegel, H. B., Scuseria, G., Robb, M., Cheeseman, J., Scalmani, G., Barone, V., Mennucci, B., and Petersson, G.: Gaussian 09, revision a. 02, gaussian, Inc., Wallingford, CT, 200, 2009.
Fu, H., Ciuraru, R., Dupart, Y., Passananti, M., Tinel, L., Rossignol, S. P., Perrier, S., Donaldson, D. J., Chen, J., and George, C.: Photosensitized production of atmospherically reactive organic compounds at the air/aqueous interface, J. Am. Chem. Soc., 137, 8348–8351, 2015.
Gelencsér and Varga: Evaluation of the atmospheric significance of multiphase reactions in atmospheric secondary organic aerosol formation, Atmos. Chem. Phys., 5, 2823–2831, https://doi.org/10.5194/acp-5-2823-2005, 2005.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Herrmann, H., Hoffmann, D., Schaefer, T., Bräuer, P., and Tilgner, A.: Tropospheric aqueous-phase free-radical chemistry: Radical sources, spectra, reaction kinetics and prediction tools, Chem. Phys. Chem., 11, 3796–3822, 2010.
Herrmann, H., Schaefer, T., Tilgner, A., Styler, S. A., Weller, C., Teich, M., and Otto, T.: Tropospheric aqueous-phase chemistry: Kinetics, mechanisms, and its coupling to a changing gas phase, Chem. Rev., 115, 4259–4334, 2015.
Jacobs, M. I., Burke, W. J., and Elrod, M. J.: Kinetics of the reactions of isoprene-derived hydroxynitrates: gas phase epoxide formation and solution phase hydrolysis, Atmos. Chem. Phys., 14, 8933–8946, https://doi.org/10.5194/acp-14-8933-2014, 2014.
Kaur, R. and Anastasio, C.: Light absorption and the photoformation of hydroxyl radical and singlet oxygen in fog waters, Atmos. Environ., 164, 387–397, 2017.
Kaur, R. and Anastasio, C.: First measurements of organic triplet excited states in atmospheric waters, Environ. Sci. Technol., 52, 5218–5226, 2018.
Kaur, R., Labins, J. R., Helbock, S. S., Jiang, W., Bein, K., Zhang, Q., and Anastasio, C.: Photooxidants from Brown Carbon and Other Chromophores in Illuminated Particle Extracts, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-1258, in review, 2018.
Khamaganov, V. G. and Hites, R. A.: Rate constants for the gas-phase reactions of ozone with isoprene, α-and β-pinene, and limonene as a function of temperature, J. Phys. Chem. A, 105, 815–822, 2001.
Kroll, J. H. and Seinfeld, J. H.: Chemistry of secondary organic aerosol: Formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 42, 3593–3624, 2008.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of atmospheric brown carbon, Chem. Rev., 115, 4335–4382, 2015.
Lee, A. K., Herckes, P., Leaitch, W., Macdonald, A., and Abbatt, J.: Aqueous OH oxidation of ambient organic aerosol and cloud water organics: Formation of highly oxidized products, Geophys. Res. Lett., 38, L11805, https://doi.org/10.1029/2011GL047439, 2011.
Lee, C., Yang, W., and Parr, R. G.: Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 37, 785, https://doi.org/10.1103/PhysRevB.37.785, 1988.
Lee, L., Teng, A. P., Wennberg, P. O., Crounse, J. D., and Cohen, R. C.: On Rates and Mechanisms of OH and O3 Reactions with Isoprene-Derived Hydroxy Nitrates, J. Phys. Chem. A, 118, 1622–1637, 2014.
Legault, C.: CYLview, 1.0 b, Université de Sherbrooke, 2009.
Li, W.-Y., Li, X., Jockusch, S., Wang, H., Xu, B., Wu, Y., Tsui, W. G., Dai, H.-L., McNeill, V. F., and Rao, Y.: Photoactivated production of secondary organic species from isoprene in aqueous systems, J. Phys. Chem. A, 120, 9042–9048, 2016.
Lim, Y. B., Tan, Y., Perri, M. J., Seitzinger, S. P., and Turpin, B. J.: Aqueous chemistry and its role in secondary organic aerosol (SOA) formation, Atmos. Chem. Phys., 10, 10521–10539, https://doi.org/10.5194/acp-10-10521-2010, 2010.
Marais, E. A., Jacob, D. J., Jimenez, J. L., Campuzano-Jost, P., Day, D. A., Hu, W., Krechmer, J., Zhu, L., Kim, P. S., Miller, C. C., Fisher, J. A., Travis, K., Yu, K., Hanisco, T. F., Wolfe, G. M., Arkinson, H. L., Pye, H. O. T., Froyd, K. D., Liao, J., and McNeill, V. F.: Aqueous-phase mechanism for secondary organic aerosol formation from isoprene: application to the southeast United States and co-benefit of SO2 emission controls, Atmos. Chem. Phys., 16, 1603–1618, https://doi.org/10.5194/acp-16-1603-2016, 2016.
Marenich, A. V., Cramer, C. J., and Truhlar, D. G.: Universal solvation model based on the generalized Born approximation with asymmetric descreening, J. Chem. Theory Comput., 5, 2447–2464, 2009.
Mayer, P. M., Parkinson, C. J., Smith, D. M., and Radom, L.: An assessment of theoretical procedures for the calculation of reliable free radical thermochemistry: A recommended new procedure, J. Chem. Phys., 108, 604–615, 1998.
McNeill, K. and Canonica, S.: Triplet state dissolved organic matter in aquatic photochemistry: Reaction mechanisms, substrate scope, and photophysical properties, Environ. Sci. Process. Impact., 18, 1381–1399, 2016.
Montgomery Jr., J. A., Frisch, M. J., Ochterski, J. W., and Petersson, G. A.: A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 110, 2822–2827, 1999.
Ng, N. L., Kwan, A. J., Surratt, J. D., Chan, A. W. H., Chhabra, P. S., Sorooshian, A., Pye, H. O. T., Crounse, J. D., Wennberg, P. O., Flagan, R. C., and Seinfeld, J. H.: Secondary organic aerosol (SOA) formation from reaction of isoprene with nitrate radicals (NO3), Atmos. Chem. Phys., 8, 4117–4140, https://doi.org/10.5194/acp-8-4117-2008, 2008.
Paulot, F., Crounse, J. D., Kjaergaard, H. G., Kroll, J. H., Seinfeld, J. H., and Wennberg, P. O.: Isoprene photooxidation: new insights into the production of acids and organic nitrates, Atmos. Chem. Phys., 9, 1479–1501, https://doi.org/10.5194/acp-9-1479-2009, 2009a.
Paulot, F., Crounse, J. D., Kjaergaard, H. G., Kürten, A., Clair, J. M. S., Seinfeld, J. H., and Wennberg, P. O.: Unexpected epoxide formation in the gas-phase photooxidation of isoprene, Science, 325, 730–733, 2009b.
Petersson, A., Bennett, A., Tensfeldt, T. G., Al-Laham, M. A., Shirley, W. A., and Mantzaris, J.: A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements, J. Chem. Phys., 89, 2193–2218, 1988.
Petersson, G. and Al-Laham, M. A.: A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms, J. Chem. Phys., 94, 6081–6090, 1991.
Petersson, G., Tensfeldt, T. G., and Montgomery Jr., J.: A complete basis set model chemistry. III. The complete basis set-quadratic configuration interaction family of methods, J. Chem. Phys., 94, 6091–6101, 1991.
Richards-Henderson, N. K., Pham, A. T., Kirk, B. B., and Anastasio, C.: Secondary organic aerosol from aqueous reactions of green leaf volatiles with organic triplet excited states and singlet molecular oxygen, Environ. Sci. Technol., 49, 268–276, 2014.
Rossignol, S. P., Aregahegn, K. Z., Tinel, L., Fine, L., Nozière, B., and George, C.: Glyoxal induced atmospheric photosensitized chemistry leading to organic aerosol growth, Environ. Sci. Technol., 48, 3218–3227, 2014.
Schöne, L. and Herrmann, H.: Kinetic measurements of the reactivity of hydrogen peroxide and ozone towards small atmospherically relevant aldehydes, ketones and organic acids in aqueous solutions, Atmos. Chem. Phys., 14, 4503–4514, https://doi.org/10.5194/acp-14-4503-2014, 2014.
Smith, J. D., Sio, V., Yu, L., Zhang, Q., and Anastasio, C.: Secondary organic aerosol production from aqueous reactions of atmospheric phenols with an organic triplet excited state, Environ. Sci. Technol., 48, 1049–1057, 2014.
St. Clair, J. M., Rivera-Rios, J. C., Crounse, J. D., Knap, H. C., Bates, K. H., Teng, A. P., Jørgensen, S., Kjaergaard, H. G., Keutsch, F. N., and Wennberg, P. O.: Kinetics and products of the reaction of the first-generation isoprene hydroxy hydroperoxide (ISOPOOH) with OH, J. Phys. Chem. A, 120, 1441–1451, 2015.
Stephens, P., Devlin, F., Chabalowski, C., and Frisch, M. J.: Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 98, 11623–1627, 1994.
Surratt, J. D., Murphy, S. M., Kroll, J. H., Ng, N. L., Hildebrandt, L., Sorooshian, A., Szmigielski, R., Vermeylen, R., Maenhaut, W., and Claeys, M.: Chemical composition of secondary organic aerosol formed from the photooxidation of isoprene, J. Phys. Chem. A, 110, 9665–9690, 2006.
Tirado-Rives, J. and Jorgensen, W. L.: Performance of B3LYP density functional methods for a large set of organic molecules, J. Chem. Theory Comput., 4, 297–306, 2008.
Tripkovic, V., Björketun, M. E., Skúlason, E., and Rossmeisl, J.: Standard hydrogen electrode and potential of zero charge in density functional calculations, Phys. Rev. B, 84, 115452, https://doi.org/10.1103/PhysRevB.84.115452, 2011.
Tsui, W. G., Rao, Y., Dai, H.-L., and McNeill, V. F.: Modeling photosensitized secondary organic aerosol formation in laboratory and ambient aerosols, Environ. Sci. Technol., 51, 7496–7501, 2017.
US EPA: Estimation Programs Interface Suite™ for Microsoft® Windows v 4.1: Estimation Programs Interface Suite™ for Microsoft® Windows, v 4.1, United States Environmental Protection Agency, Washington, DC, USA, 2016.
Volkamer, R., Ziemann, P. J., and Molina, M. J.: Secondary Organic Aerosol Formation from Acetylene (C2H2): seed effect on SOA yields due to organic photochemistry in the aerosol aqueous phase, Atmos. Chem. Phys., 9, 1907–1928, https://doi.org/10.5194/acp-9-1907-2009, 2009.
Walser, M. L., Desyaterik, Y., Laskin, J., Laskin, A., and Nizkorodov, S. A.: High-resolution mass spectrometric analysis of secondary organic aerosol produced by ozonation of limonene, Phys. Chem. Chem. Phys., 10, 1009–1022, 2008.
Warren, J. J., Tronic, T. A., and Mayer, J. M.: Thermochemistry of proton-coupled electron transfer reagents and its implications, Chem. Rev., 110, 6961–7001, 2010.
Wilkinson, F., Helman, W. P., and Ross, A. B.: Rate constants for the decay and reactions of the lowest electronically excited singlet-state of molecular-oxygen in solution – an expanded and revised compilation, J. Phys. Chem. Ref. Data, 24, 663–1021, 1995.
Wolfe, G. M., Crounse, J. D., Parrish, J. D., Clair, J. M. S., Beaver, M. R., Paulot, F., Yoon, T. P., Wennberg, P. O., and Keutsch, F. N.: Photolysis, OH reactivity and ozone reactivity of a proxy for isoprene-derived hydroperoxyenals (HPALDs), Phys. Chem. Chem. Phys., 14, 7276–7286, 2012.
Yu, L., Smith, J., Laskin, A., Anastasio, C., Laskin, J., and Zhang, Q.: Chemical characterization of SOA formed from aqueous-phase reactions of phenols with the triplet excited state of carbonyl and hydroxyl radical, Atmos. Chem. Phys., 14, 13801–13816, https://doi.org/10.5194/acp-14-13801-2014, 2014.
Zepp, R. G., Wolfe, N. L., Baughman, G. L., and Hollis, R. C.: Singlet oxygen in natural waters, Nature, 267, 421–423, 1977.
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced northern hemisphere midlatitudes, Geophys. Res. Lett., 34, L13801, https://doi.org/10.1029/2007GL029979, 2007.