the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Experimental study of the aerosol impact on fog microphysics
Frédéric Burnet
Cyrielle Denjean
Gregory C. Roberts
Martial Haeffelin
Jean-Charles Dupont
Thierry Elias
Comprehensive field campaigns dedicated to fog life cycle observation were conducted during the winters of 2010–2013 at the Instrumented Site for Atmospheric Remote Sensing Research (SIRTA) observatory in a suburb of Paris. In order to document their properties, in situ microphysical measurements collected during 23 fog events induced by both radiative cooling and stratus lowering are examined here. They reveal large variability in number, concentration and size of both aerosol background before the fog onset and fog droplets according to the different cases. The objective of this paper is to evaluate the impact of aerosol particles on the fog microphysics. To derive an accurate estimation of the actual activated fog droplet number concentration Nact, we determine the hygroscopicity parameter κ, the dry and the wet critical diameter and the critical supersaturation for each case by using an iterative procedure based on the κ-Köhler theory that combines cloud condensation nuclei (CCN), dry particle and droplet size distribution measurements.
Our study reveals low values of the derived critical supersaturation occurring in fog with a median of 0.043 %. Consequently, the median dry and wet activation diameters are 0.39 and 3.79 µm, respectively, leading to a minor fraction of the aerosol population activated into droplets. The corresponding Nact values are low, with median concentrations of 53.5 and 111 cm−3 within the 75th percentile. The activated fraction of aerosols exhibits remarkably low correlation with κ values, which reflects the chemical composition of the aerosols. On the contrary, the activated fraction exhibits a strong correlation with the inferred critical diameter throughout the field campaigns. This suggests that the variability in the activated fraction is mostly driven by particle size, while variations in aerosol composition are of secondary importance. Moreover, our analysis suggests that the supersaturation reached in fog could be lowered by the aerosol number concentration, which could contribute to the sink term of water vapor during the radiative cooling. Although radiative fogs are usually associated with higher aerosol loading than stratus-lowering events, our analysis also reveals that the activated fraction at the beginning of the event is similar for both types of fog. However, the evolution of the droplet concentration during the fog life cycle shows significant differences between both types of fog.
This work demonstrates that an accurate calculation of supersaturation is required to provide a realistic representation of fog microphysical properties in numerical models.
- Article
(1451 KB) - Full-text XML
- BibTeX
- EndNote
As they reduce visibility, fog events strongly perturb the aviation, marine and land transportation. Gultepe et al. (2009) pointed out the extremely high level of human losses and financial cost related to fog and low-visibility events. Moreover, present numerical weather prediction models are usually unable to predict the exact location and time evolution of the life cycle of a fog layer (Zhou and Ferrier, 2008; Van der Velde et al., 2010; Bergot, 2013; Boutle et al., 2018).
The occurrence and development of fog result from the nonlinear interaction of competing radiative, thermodynamic, microphysical and dynamical processes (see the review of Gultepe et al., 2007b). Water droplets are formed by heterogeneous nucleation of aerosol particles when the relative humidity (RH) exceeds 100 %. The Köhler theory (Köhler, 1936) forms the basis of our understanding of cloud droplet formation. The ability of aerosol particles to act as cloud condensation nuclei (CCN) depends largely on their size, composition and phase state. The number size distribution of the droplets activated during the cloud formation phase depends on the supersaturation values reached by the air mass (Pruppacher et al., 1998). Particles having a critical supersaturation below the maximum value are activated and will then further grow by water vapor diffusion as long as the RH remains high enough, while the others particles remain at their equilibrium diameter. At the same time, water droplets are the particles whose diameters are larger than the critical threshold corresponding to that critical supersaturation.
Because of the weak supersaturation inside the fog layers (Hudson, 1980; Pandis et al., 1990; Svenningsson et al., 1992; Hammer et al., 2014; Boutle et al., 2018), the separation between activated fog droplets and non-activated particles, so-called hydrated aerosols, is not explicit (Frank et al., 1998). To date, the microphysics in numerical weather prediction (NWP) models takes into account activated droplets only. Recently, a two-moment microphysical cloud scheme, which relies on the prognostic evolution of an aerosol population to predict cloud droplets, has been developed for low supersaturation clouds (Thouron et al., 2012) and needs to be tested against observations. It is thus essential to precisely evaluate total droplet number concentration values and their corresponding size range. Currently, their definition mainly deals with the instrumentation limitation that generally begins at 2 µm in diameter to measure droplet size distribution. However, Hammer et al. (2014) and Elias et al. (2015) experimentally determined threshold diameter higher than 2 µm to characterize droplets. As the smallest hydrated particles are more numerous, considering a smallest threshold diameter could lead to a significant overestimation of the droplet concentration. Moreover, as shown by Boutle et al. (2018), an accurate representation of droplet concentration for fog could also impact climate projection.
As a general rule in cloud physics, increase in aerosols causes an increase in the droplet number concentration for a given cloud type (Gultepe and Isaac, 1996; Ramanathan et al., 2001). Hudson (1980) and Liu et al. (2017) found systematic differences in the fog microstructure between fogs formed in maritime, continental and urban air masses with a simultaneous increase of fog condensation nuclei and aerosol concentration. Recent numerical simulations exhibit a strong positive correlation between aerosol and droplet concentrations (Zhang et al., 2014; Stolaki et al., 2015; Maalick et al., 2016). They also predict fog events with high values of droplet concentrations, typically a few hundred per cm−3 or more. By contrast, numerical study of Bott (1991) shows that an increase in aerosol particles leads to a decrease of the supersaturation that in turn decreases the activated droplet number.
Recently, Boutle et al. (2018) have obtained impressively low droplet concentrations with large eddy simulation (LES) by numerically solving the condensation equation at every time step and grid point, but they had very few activable aerosol particle.
In this study, we examined in situ microphysical measurements collected during the three winter campaigns to derive typical fog droplet concentrations in semi-urban conditions. From October 2010 to March 2013, a suite of active and passive remote sensing and in situ sensors was deployed at the Instrumented Site for Atmospheric Remote Sensing Research (SIRTA) in a suburb of Paris (Haeffelin et al., 2010). Dupont et al. (2016) analyzed 117 fog events to provide typical values of thermodynamical and radiative variables for the fog formation and the mature and dissipation phases. Burnet et al. (2012) have shown that, in terms of droplet number concentration and effective diameter, the microphysical properties of fog events sampled at SIRTA present a large variability. Elias et al. (2015) examined the data collected during November 2011 and assessed the contribution of hydrated aerosols that led to the extinction of the visible radiation in the mist–fog–mist cycle. Hammer et al. (2014) focused on the activation properties of developed fog events observed during the winter of 2012/2013, but they did not provide activated particle concentrations values.
Here, we determine the hygroscopicity parameter, the dry and wet critical diameters and the critical supersaturation by using an iterative procedure based on the κ-Köhler theory that combines CCN measurements, dry particle size distribution and composite wet particle size distribution at ambient humidity. The objectives are to derive accurate estimations of the fog droplet concentrations and to investigate the impact of aerosols on the fog microphysics. This paper provides a comprehensive data set on activation properties and an explanation of the aerosol impact on the activation process.
Data and methods are described in Sects. 2 and 3, respectively. Results are presented in Sect. 4, with first the statistics of fog activation properties of the 23 fog events analyzed in this study. The link between aerosol particles and fog droplets is examined in Sect. 4.2, and the impact of CCN concentration on fog microstructure is discussed in Sect. 5. Conclusions are finally given in Sect. 6.
2.1 Instrumentation
Data presented here were collected at the SIRTA observatory in the framework of the ParisFog field campaigns (Haeffelin et al., 2010). During the winters of 2010 to 2013, specific instrumentation were deployed for the PreViBOSS project (Elias et al., 2012) to provide continuous observation of aerosol and fog microphysics. The experimental setup was already presented in Burnet et al. (2012), Hammer et al. (2014), Elias et al. (2015) and Dupont et al. (2016). The instruments used in this study are listed in Table 1.
Particle size distribution at ambient humidity is derived from a combination of two optical spectrometers: the WELAS-2000 (Palas GmbH, Karlsruhe, Germany) and the FM-100 (Droplet Measurement Technologies Inc., Boulder, CO, USA), which do not cover the same size range. The WELAS-2000 (hereafter referred to as WELAS) provides particle size spectrum between 0.4 and 40 µm in diameter according to the constructor. However, the detection efficiency decreases drastically below ∼1 µm (Heim et al., 2008; Elias et al., 2015), resulting in a strong underestimation of the concentration of the submicronic particles. Hammer et al. (2014) choose to consider only data with diameters larger than 1.4 µm. Statistics over the whole data set reveal that the most frequent mode diameter of the WELAS size distribution is 0.96 µm. Thus, we choose to use this value as the lowest threshold and only measurements for bin diameter larger than 0.96 µm will be considered in this study. Note that the activated diameter in fog is expected to be larger than 1 µm; thus, this instrumental bias will not affect the results presented here, which is confirmed next in this study for SIRTA's fog. The sampling time period was fixed to 5 min as a compromise between time resolution and statistical significance of the measurements. Indeed, this corresponds to a volume of air of 6.40 cm−3 per sample.
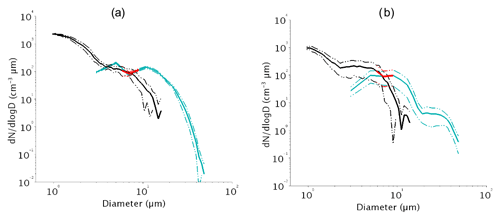
Figure 1The 1 h average composite number size distributions at ambient humidity derived from WELAS (black) and FM-100 (cyan) at the beginning of the fog event for cases (a) f6 and (b) f20. The solid line represents mean value and the dotted lines indicate ± 1 standard deviation. The red segments correspond to the result of merging both distributions between 6 and 8 µm.
The FM-100 provides 1 Hz droplet size distribution from 2 to 50 µm in diameter according to the constructor, hence providing a large overlapping range with the WELAS measurements. However, Burnet et al. (2012) and Elias et al. (2015) show that these distributions only overlap each other at a diameter which fluctuates between 5 and 9 µm. Their comparisons reveal a high discrepancy between both these probes with a large underestimation by the FM-100 for particles lower than about 5 µm but conversely a large underestimation by the WELAS for droplets larger than 10 µm (Burnet et al., 2012; Elias et al., 2015). This is illustrated in Fig. 1, which shows the size distributions measured by the WELAS (black) and FM-100 (cyan) for two fog cases with contrasting properties. Figure A1 in Appendix A shows comparisons of the particle number concentration values of the FM-100 vs. the integrated WELAS measurement over 2–10 µm diameter range that correspond to the four first bins of the FM-100. The default manufacturer's first four bins of the FM-100 are 2–4, 4–6, 6–8 and 8–10 µm, which correspond to 9, 7, 4 and 3 class bins of the WELAS, respectively. Following the WELAS sampling time period, FM-100 and WELAS data points are a 5 min average that represents 2851 samples for the whole data set. Figure A1 confirms that the FM-100 strongly underestimates the particle counts in the first size bin and that the WELAS underestimates the concentration of particles larger than 8 µm. The measurements of the two instruments do not match perfectly in the size range of 4 and 8 µm, which reflects the large fluctuations of the crossing diameter over this range. To derive a composite size distribution, Elias et al. (2015) chose a constant value of 7 µm. Because of this high variability, we compute here the composite size distribution by using WELAS data up to 6 µm, FM-100 data above 8 µm and the average of both from 6 to 8 µm. Results are illustrated in Fig. 1 with red segments corresponding to the junction between the WELAS and FM-100 distribution. This procedure allows us to take advantage of the finer bin resolution of the WELAS for the smaller particles and also to reduce uncertainties of the FM-100 due to Mie ambiguities for smaller diameter, as described by Spiegel et al. (2012), since our FM-100 was using the default manufacturer's bin threshold. Indeed, particularly for smaller diameter, the droplet concentration may be overestimated or underestimated; a few droplets from adjacent classes can be included or some can be counted in an adjacent class (Gonser et al., 2012). Nevertheless, because of the large discrepancies between the two sensors on the crossing diameter, the next calculation using this crossing diameter also considers a standard deviation using the minimum and the maximum size distributions over this size range. Both instruments are located on a scaffolding about 2.5 m high, close to a PVM-100 from Gerber Scientific Inc. used as a reference for the liquid water content (hereafter LWC) measurements, which measures on the 2–50 µm diameter. Measurements of visibility and its vertical evolution are given by two Degreanne diffusometers (DF20+ and DF320) located at 4 and 18 m above ground, respectively. Confidence is given in FM-100 measurements by comparison of the integrated LWC over its size range with the LWC measured by the PVM-100 and the visibility trend; see Burnet et al. (2012) for winter 2010–2011. A paper will follow on that issue.
Aerosol particle measurements are performed under dry conditions by instruments placed in a shelter. The sampled air mass enters through an aerodynamic size discriminator PM2.5 inlet and a dryer which reduces the relative humidity to less than 50 %. This value could be higher than the efflorescence point for some particles (Tang et al., 1995). A scanning mobility particle sizer (SMPS), which provides the dry aerosol particle number size spectrum, consists of a differential mobility analyzer (DMA; TSI 3071) which selects particles from 10.6 to 496 nm and of a condensation particle counter (TSI CPC 3022). Hydrophilic filters in the DMA circuit should lower the relative humidity to less than 30 % (Denjean et al., 2014), which should be enough to avoid water uptake issues. Another CPC (TSI 3025) measures the total particle number concentration from 2.5 nm to 2.5 µm. Finally, a continuous-flow streamwise thermal gradient CCN chamber (CCNC) (Roberts and Nenes, 2005) is used to measure the CCN number concentration at five different supersaturations from 0.1 to 0.5 %, by steps of 0.1 %.
2.2 Selected fog cases and aerosol properties
During the three winter campaigns of 2010–2013, Dupont et al. (2016) report the occurrence of 117 fog events. However, due to instrument failures and technical difficulties in operating the whole set of instruments on a 24/7 mode, 42 events were sampled simultaneously with both the WELAS and the FM-100, and only a subset of 23 cases was also sampled with both the CCNC and the SMPS. They are listed in Table 2 with their classification type (RAD for radiative cooling fog and STL for stratus-lowering ones), as determined by the scheme of Tardif (2007) and their vertical development based on the comparison of both diffusometers: a developed fog produces low-visibility conditions simultaneously at 4 and 18 m, while a thin fog produces low-visibility conditions at 4 m only (Elias et al., 2009; Dupont et al., 2016). About the same proportion (40 %) of RAD and STL fog events occurred at the SIRTA site (Haeffelin et al., 2010; Dupont et al., 2016). Among the 23 fog events analyzed here, 13 are radiation fogs and 10 stratus-lowering fogs, 19 are developed and 4 thin. Thermodynamics conditions during the field campaigns are described by Dupont et al. (2016).
Table 2List of fog events analyzed here. Type RAD corresponds to radiation fog and STL to stratus lowering, “thick” to fog developed on the vertical and “thin” to fog layer with top altitude lower than 18 m. Na is the number concentration of aerosol particles derived from SMPS data. The 25th, 50th and 75th percentiles are computed from the distribution of 5 min samples over the last hour before the fog beginning. NFM is the droplet number concentration as measured by the FM-100 over the range 2–50 µm. Statistics of NFM are computed with minute average data of samples with LWC > 0.005 g m−3 collected during the whole fog event. The last column provides the minimum of visibility observed during the event.
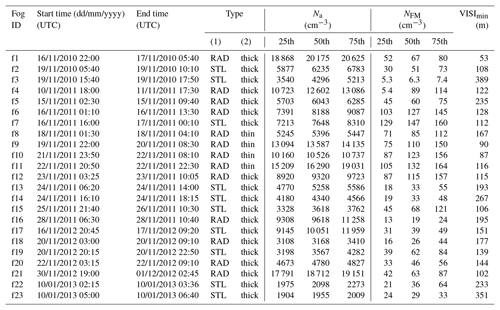
To characterize the aerosol background prior to a fog event, statistics of the total number aerosol particle concentration, Na, as measured by the SMPS between 10 and 496 nm diameter, are computed over the last hour before the beginning of the fog event. This time lapse is chosen to characterize aerosol before a fog event because CCNC, which allows to characterize aerosol chemistry, has a sampling time of 20 min; thus, a 1 h time lapse is supposed to provide reliable measurements. Median, 25th and 75th percentiles are reported in Table 2. Na values range from ≈2000 to ≈20 000 cm−3. Consistent with Haeffelin et al. (2010), the smallest values are observed in westerly flow conditions, while highest values are associated mostly with an easterly flow when SIRTA is exposed to continental conditions. Indeed, SIRTA is located 25 km southwest of Paris in a semi-urban environment, composed of agricultural fields, wooded areas, housing and industrial developments (Haeffelin et al., 2005), and is exposed to air mass charged with pollution originating from regional background according to Crippa et al. (2013).
These various conditions are reflected on the statistics that reveal a large case-to-case variability. This is illustrated in Fig. 2, which shows the scatterplot of the droplet number concentration derived by the FM-100, NFM on 2–50 µm diameter range as a function of Na, that represent the aerosol loading, for the 23 fog events (data in Table 2). Symbols depend on the fog type: blue and red colors for STL and RAD fogs, respectively, and open and solid symbols for thin and developed fogs, respectively. For STL fogs, Na ranges from 2000 to 11 000 cm−3 with a median value of 4340 cm−3 and 25th and 75th percentiles of 2833 and 6942 cm−3, respectively, while for RAD cases, Na values are spread over a larger range from 3000 to 20 000 cm−3 with a median value of 8822 cm−3 and 25th and 75th percentiles of 5719 and 13 094 cm−3, respectively. Thus, over this 3-year campaign, it appears that at SIRTA STL fogs are associated with lower aerosol loading than RAD ones, as already reported by Elias et al. (2015) for the month of November 2011.
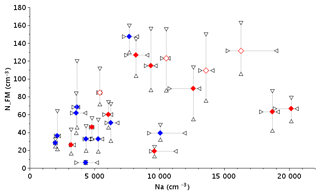
Figure 2Droplet number concentration as derived from the FM-100 collected during the whole fog event as a function of the aerosol number concentration as derived from the SMPS measurements collected over the last hour before the fog beginning. Median values (diamonds) are indicated for each case of Table 2, with the 25th and 75th percentiles (triangles) to represent the variability. Symbols depend on the fog types, STL (blue) and RAD (red), with open and solid symbols for thin and developed fogs, respectively.
There is also a significant difference between a STL and RAD fog with respect to NFM. Despite the maximum value being reached for a STL fog (147 cm−3 for the case of f7), NFM for a STL fog is generally lower, with median values between 38 and 83 cm−3 and 25th–75th percentiles of 31–63 and 53–118 cm−3, for STL and RAD, respectively. Moreover, for a RAD fog, thin cases exhibit higher values of NFM with a median and 25th–75th percentiles of 97 and 73–131 cm−3 compared to 64 and 49–81 cm−3 for a developed fog. Therefore, it appears that a radiative fog is also associated with higher droplet concentrations than stratus-lowering fog over the range 2–50 µm as measured by the FM-100. One can note that these values are rather low for continental conditions (Wendisch et al., 1998; García-García et al., 2002; Gultepe and Milbrandt, 2007a; Niu et al., 2012; Price, 2011; Liu et al., 2011; Lu et al., 2013; Zhao et al., 2013; Boutle et al., 2018).
As shown in Fig. 2, the general trend points towards a slight increase in the number of droplets with the aerosol loading but the scatter is very large. In cloud physics, the connection between an increase in aerosol particles and an increase in the cloud droplet number concentration (CDNC) has been supported by many in situ observations (Twohy et al., 2005; Lu et al., 2007; Levin and Brenguier, 2009) and even if the discrepancy is large in the compilation of the diverse results (Ramanathan et al., 2001), the general trend is much more pronounced to what is presently observed in Fig. 2. However, CDNC is derived here from FM-100 measurements only between 2 and 50 µm diameter. In warm clouds, the supersaturation at the cloud base is high enough to activate droplets whose size will increase by water vapor condensation during the ascent of the air parcel. The spectrum then gets narrower because the growth rate of a droplet is inversely proportional to its size, while the remaining interstitial particles keep their own equilibrium diameter at 100 % relative humidity. Higher up in the cloud, the spectrum is widened by different processes such as turbulent mixing and collision–coalescence and new CCN can also be activated. Droplet spectra vary considerably in space and in time but the general trend is that the activated droplet population is clearly separated from the interstitial non-activated particles. See, for example, measurements into stratocumulus cloud as reported in Martin et al. (1994), Brenguier et al. (2011) and Ditas et al. (2012). Measurements by optical counters such as FSSP (Forward Scattering Spectrometer Probe) or CDP (Cloud Droplet Probe) over the range (about 2–50 µm) are considered to provide an accurate estimation of the droplet size distribution.
In contrast, supersaturation in fog is much lower and, as already pointed out by Hudson (1980), in continental air the droplet number size distribution does not exhibit a clear separation. This is clearly illustrated in Fig. 1. To derive an accurate estimate of the CDNC, it is thus essential to determine carefully the wet activation diameter in order to integrate the composite size distribution derived from both WELAS and FM-100 measurements. The method used to discriminate the droplets from the hydrated aerosol particles using κ-Köhler theory is described in the next section.
There are different methods to separate fog droplets from non-activated aerosol particles. A fixed value can be used as a rough estimate, as described in previous studies by Noone et al. (1992), Hoag et al. (1999) and Elias et al. (2009), among others, with thresholds ranging from 2.5 to 5 µm. To take into account case-to-case variability, Elias et al. (2015) used WELAS measurements. The volume size distribution is fitted with two log-normal distributions and the transition diameter is defined as the intersection between them. Hammer et al. (2014) investigated the activation properties by measuring the total and interstitial dry particle number size distribution behind two different inlet systems, and with WELAS and CCN measurements. They compared two methods: one by fitting surface distributions of SMPS+WELAS measurements similar to Elias et al. (2014) and one by retrieving the dry activation diameter from the difference between interstitial and total particle size distribution measurements.
In this study, we use a different approach based on an iterative procedure that combines dry particle distribution from SMPS and composite wet particle size distribution derived from both WELAS and FM-100 measurements. The CCN measurements are also used to derive the hygroscopicity parameter (κ) needed to link the dry and wet activation diameters (Dd and Dw) with the critical supersaturation peak (SSpeak) using the κ-Köhler theory.
3.1 κ-Köhler theory
The Köhler theory (Köhler, 1936) expresses the equilibrium saturation vapor pressure over a solution droplet considering the solute effect (Raoult) and water surface tension effect (Kelvin). Accurate information is needed on the particle dry diameter and about the chemical composition to determine whether or not it can act as a CCN. Recently, Petters and Kreidenweis (2007) developed a method, named κ-Köhler, to describe the relationship between particle dry diameter and CCN using a single hygroscopic parameter, κ. This method allows to study the activation process without considering aerosols' complex chemical composition (McFiggans et al., 2006). The formulation of the method is expressed in Eq. (1):
where S is the saturation ratio over a solution droplet, D is the droplet diameter, Dd is the dry droplet diameter, ρw is the density of water, Mw is the molar mass of water, σs∕a is the surface tension of the solution air/interface (of pure water here), R is the universal gas constant, T is the temperature, and κ is the hygroscopicity parameter. κ represents a quantitative measure of aerosol particles water uptake characteristics and CCN activity. The critical supersaturation SSc and critical wet activation diameter Dw correspond to values at the maximum supersaturation. They are linked to a couple (Dd, κ) through the following relation:
SSpeak represents the maximum supersaturation that the air mass experienced for a sufficiently long time (Hammer et al., 2014); all particles whose SSc is less than SSpeak are activated and will further grow by water vapor condensation as long as RH remains high enough, while other particles remain stable at their equilibrium diameter at the actual RH value.
3.2 Method to determine fog activation properties
The iterative procedure used to derive fog activation properties is illustrated in Fig. 3. To derive Dd and Dw simultaneously, measured CCN concentration (Nccn), dry and wet aerosols' size distributions were used. From that, it follows that all particles become activated to droplets when their dry or wet size is similar to or larger than Dd and Dw. Indeed, there can only exist one trio (Nccn, Dw and Dd) that is linked to κ and SSpeak through Eq. (2). For each fog event, the activation properties are determined as follows: Nccn is set corresponding to a value of Dd. Dw and SSpeak are further calculated by using Eq. (2) for SSpeak and by numerically searching for the maximum of Eq. (1) for Dw for a given value of κ. Then the integral of the droplet distribution from Dw provides the droplet concentration Nd. Iterations are made on Nccn until Nccn equals Nd: this is the activated aerosol number concentration for this case, hereafter referred to as Nact. Nact corresponds to the concentration of activated aerosols at SSpeak. Two sets of iterations are made with the two κ values and the average particle size distribution. To take into account the size distribution variability within the selected time period, two other sets of iterations are made by using the average size distribution ± 1 standard deviation corresponding to the extrema of the WELAS and FM-100 crossing diameter, respectively, and with the κ value maximizing the scatter.
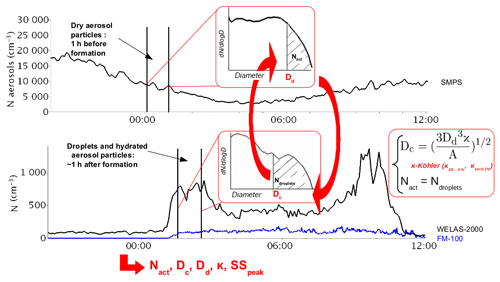
Figure 3Schematic of the iterative method used to retrieve fog activation properties from dry and ambient humidity particle size distributions.
Our method to determine fog activation properties has to assume that the aerosol particles are internally mixed. However, atmospheric aerosols are frequently externally mixed with particles of different sizes exhibiting different chemical composition. Discussion on this hypothesis is presented in Sect. 3. Moreover, surface tension properties (surface tension) of atmospheric aerosols could be modified by surfactant. This effect has largely been attributed to organics when the organic concentration in the aerosol population is sufficiently large (Facchini et al., 2000; Noziere et al., 2014). The extent to which this will occur is strongly dependent upon the specific molecular properties of the organic molecules. Unfortunately, exploring these aspects would need to combine CCN measurements and a detailed analysis of the molecular species contained in organic particles. This is out of the scope of this paper. In addition, number concentration of aerosol particles larger than 496 nm was assumed to be negligible in our calculation.
The air mass is sampled through a PM2.5 head and is dried to RH < 50 % before entering the SMPS and the CCN chamber. Hence, during a fog event, activated aerosols larger than 2.5 µm are missed. Aerosol properties of the air mass must thus be characterized before the occurrence of a fog event. In addition, the aerosol particle distribution changes continuously according to the boundary layer evolution and aerosol sources (wood burning, road traffic, etc.). This is illustrated in Fig. A2, showing a large variability in the aerosol particle distribution along the diurnal cycle for the fog event f6. There is a large variability along the diurnal cycle. To characterize the air mass just before the fog event, we average data recorded during the last hour before the fog onset. This corresponding time interval is delimited by red segments in Fig. A2.
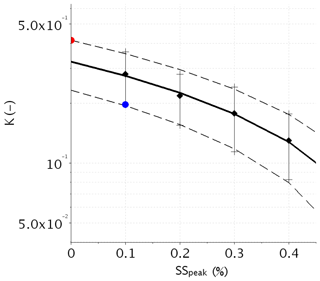
CCN chamber measurements are used to derive κ by using Eq. (2) knowing SSc and Dd. The chamber supplies the concentration of activated aerosol particles Nccn at five supersaturations from 0.1 % to 0.5 %. Scanning takes about 20 min. Therefore, three scans can be made during the 1 h interval and thus provide meaningful estimation of the aerosol hygroscopicity. However, supersaturation values in the chamber are greater than 0.1 % and it is well known that SSpeak in fog is generally lower than 0.1 % (Hammer et al., 2014; Ming and Russell, 2004; Svenningsson et al., 1992; Hudson, 1980). Therefore, assumptions must be made to extrapolate κ at lower supersaturation. This is illustrated in Fig. A3, which shows statistics of κ as a function of supersaturation for the selected time period of Fig. A2. Data points correspond to calculations with CCN data at each supersaturation and the SMPS aerosol size distribution averaged over the 1 h time interval. Solid and dashed lines superimposed on the data points correspond to mean and mean ± 1 standard deviation values, respectively. Two extrema of κ are defined. κinf, which is computed as the mean value of κ at 0.1 % minus the standard deviation, corresponds to the lowest expected value. κsup is calculated as the linear extrapolation of the mean κ at 0 % plus the standard deviation and corresponds to the highest expected value. Both values are indicated in Fig. A3 by blue and red dots, respectively. These two extreme values of κ will then provide extreme values of activation properties for a given dry activation diameter.
Once droplets have been activated, their size distribution evolves during the fog life cycle. They can grow by water vapor diffusion or by coalescence with other droplets due to gravitational and turbulent motions and they can also evaporate in the case of mixing with clear air or changes in temperature. Following Noone et al. (1992), the mixing with clear air has similar consequences to an external mixture for aerosols, which means that some particles can deactivate and their diameter can be under the critical wet diameter because of evaporation. In convective clouds, the activation occurs mainly within the first tenth of meters above the cloud base, and it is thus possible to directly sample the resulting droplet spectra with instrumented aircraft. By contrast, in the case of fog, the activation first occurs at the fog onset; the ensuing vertical development of the fog layer depends on many processes, among which the radiative cooling at the fog top plays a key role. The fog onset is generally defined by a drop of visibility below the 1 km threshold, but this is still subject to debate (see discussion in Elias et al., 2015). Time series show indeed various case-to-case CDNC evolution during the first fog hour of the fog event, with an instantaneous formation, or conversely, a slower increase towards a stable value as illustrated in Fig. A2. To estimate the most representative fog droplet size distribution of the activated distribution, we average the composite wet particle size distribution derived from both WELAS and FM-100 measurements over a time interval from the beginning of the fog event during which the CDNC reaches a stable value for a sufficiently long time. On average, this time period is selected from 30 min to 1 h after the fog beginning. It is delimited by blue segments in Fig. A2. We therefore also assume that local measurements at 2 m height are representative of the fog layer.
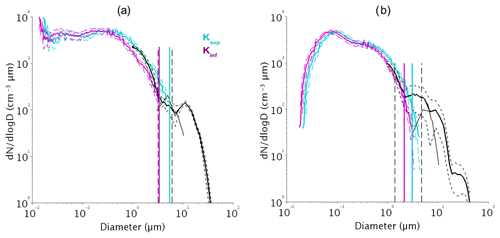
Figure 4The 1 h wet number size distribution before the fog event resulting from the hygroscopic grow at RH=100 % of the dry distribution measured by the SMPS calculated with κinf (purple) and κsup (cyan) for cases (a) f6 and (b) f20. The in-fog composite size distribution of Fig. 1 is superimposed (black). The solid lines represent mean values and the dashed lines show ± 1 standard deviation. The vertical segments indicate the mean values of Dw corresponding to each κ (solid color lines) and the extreme values (dashed lines).
3.3 Method validation
Figure 4 illustrates the impact of κ variability for two fog cases of Fig. 1. The average aerosol dry size distribution measured by the SMPS recalculated at 100 % RH with the κinf and κsup values (blue and purple lines, respectively) is superimposed on the composite fog droplet number size distribution. Vertical segments indicate the corresponding Dw diameters. These values are 3.37 and 5.45 µm, corresponding to Nact of 91 and 61 cm−3, respectively, for the f6 case (Fig. 4a), and 2.15 and 3.08 µm, which correspond to Nact of 116 and 86 cm−3, respectively, for the f20 case (Fig. 4b). The dashed lines correspond to the two calculations which produce extreme values and thus delimit the range of possible values. If the spectrum remains constant as in Fig. 4a, these values are rather identical. But if the shape of the spectrum evolves during the 1 h time period, the range of possible values increases as in Fig. 4b, with extreme values of 1.4 and 4.75 µm corresponding to Nact of 266 and 21 cm−3, respectively, leading to an uncertainty of a factor of 10 for Nact. There is good agreement between both distributions on the overlap area corresponding to hydrated (non-activated) particles. This indicates that the hygroscopic growth of all dry particles measured before the fog event with the derived κ values is consistent with the ambient measurements at the beginning of the fog. This also allows to neglect the mixture issue. Indeed, the dry (growth) and wet aerosol particles' shape could not fit with our assumption for a significant external mix, as there is no reason for an external mix to be homogenously distributed on the dry aerosol number size distribution. Nevertheless, a significant external mix would have implied less aerosol particles activated per diameter with our method that would lead to an overestimation of Dd.
Our method provides a satisfactory estimation of κ, and the selected time periods are adequate to estimate the activation properties.
4.1 Fog activation properties
Table 3 presents results for the 23 fog events with mean values and uncertainty intervals for each parameter (κ, Dd, Dw, SSpeak and Nact). The mean value is the average between the two values obtained from the above procedure with the average wet composite size distribution and the two κ values. The uncertainty interval is determined by the extreme values resulting from the average wet composite size distribution minus (plus) 1 standard deviation and the lowest (highest) κ value, respectively.
Table 3Activation properties of the 23 fog events: hygroscopicity parameters κinf and κsup, mean values and uncertainty intervals of the dry diameter Dd, the wet diameter Dw, the supersaturation SSpeak and the number concentration of activated particles Nact. The 5th, 25th, 50th, 75th and 95th percentiles of the distribution of the 23 cases are indicated on the last lines for each parameter.
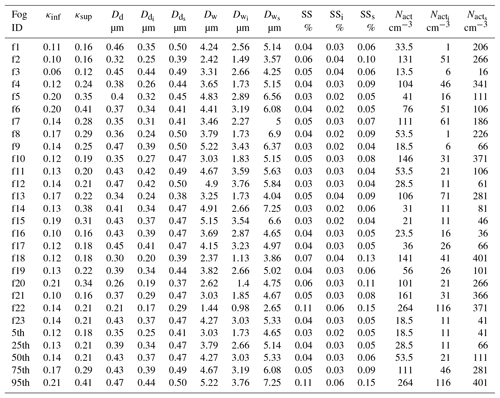
Values of κinf and κsup are relatively close. Indeed, the relative standard deviation to the average value κmean ranges between 9 % and 25 %, except for the f14 case, which reaches 35 %. It follows that κmean which corresponds roughly to κ value at SS≈0.05 %, is representative of the κ value at the actual supersaturation. As a result, κmean values range from 0.09 to 0.3 with a median of 0.17. They are in agreement with those determined by Hammer et al. (2014), who found κ between 0.06 and 0.27 centered at 0.14 (SS≤0.11 %), and Jurányi et al. (2013), who reported κ between 0.08 and 0.24 (SS=0.1–1 %) at the same site. They are slightly lower than those observed for continental aerosols; Andreae and Rosenfeld (2008), for example, suggested to use . As already pointed out by Hammer et al. (2014), local emissions of road traffic and residential wood burning are likely responsible for these low values of κ. Figure 5 shows the scatterplot of the hygroscopic parameter as a function of the critical supersaturation for each of the 23 fog events with their uncertainty interval. Overall, the variability of κ remains very low, since 80 % of the κ values range between 0.13 and 0.27. This suggests that the possible variations in aerosol composition occurring during the campaign due to variations in air mass type or source contributions have limited effect on the CCN ability of aerosol in fog conditions. Based on this study, a single κ value of 0.17 could be used for further modeling studies in this area.
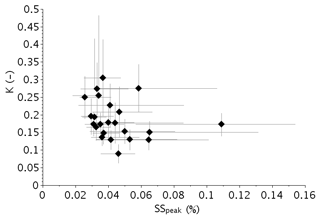
Figure 5Hygroscopicity parameter κ as a function of the critical supersaturation for the 23 fog events. Diamonds correspond to mean values and error bars to uncertainty intervals.
The mean dry activation diameter values, 0.39 µm for the median and 0.35–0.43 µm for the 25th–75th percentiles, are rather high, which indicates that only largest aerosol particles are activated. This is in agreement with previous studies of Noone et al. (1992), Ming and Russell (2004) and Hammer et al. (2014) of the supersaturation occurring in fog. The wet activation diameter Dw is 3.79 µm in median and range from 3.03 and 4.67 µm for the 25th and 75th percentiles. These values are slightly higher than the median value of 2.6 µm reported by Hammer et al. (2014) but are consistent with the mean value of 4 µm by Elias et al. (2015). The latter determined from a November 2011 data set as the intersection between the two log-normal distributions fitting the particle volume distribution measured by the WELAS. That is also highly consistent with statistics on a no-fog event at SIRTA, whereby particle diameters as measured by WELAS do not exceed 2 µm. Except for the f22 event, mean values of Dw are larger than 2.37 µm throughout the field campaign. The differences between hydrated and activated particles can be seen in Fig. 4a and b, and correspond fairly well to the average wet activation diameters derived for such cases that are equal to 4.41 and 2.62 µm, respectively. Moreover, it appears that the extreme values indicated by the dashed vertical segments largely maximize the uncertainty of the retrieval.
Critical supersaturation occurring in fog is very low with a median value of 0.043 % and 25th–75th percentiles of 0.035 %–0.051 %. This result was expected for fog conditions, as already shown in experimental and modeling studies (Hudson, 1980; Svenningsson et al., 1992; Ming and Russell, 2004; Hammer et al., 2014; Shen et al., 2018; Boutle et al., 2018).
Finally, the corresponding concentration of activated particles (Nact) is 53.5 cm−3 for the median and 28.5–111 cm−3 for the 25th–75th percentiles. These values are slightly lower than the NFM ones derived from FM-100 data (reported in Fig. 2) which give a median and 25th–75th percentiles of 61 and 34–103 cm−3, respectively. Moreover, the median of the average concentration values of particles with diameter in the range of 0.96–50 µm at the beginning of the fog events reaches 389 cm−3 with 25th–75th percentiles of 260–660 cm−3. It follows that only a small fraction of the fog hydrated particles can be activated to droplets due to low critical supersaturations encountered in fog. Obviously, because of the uncertainty interval, Nact is very broad. For instance, this uncertainty is twice the Nact value itself on average but could be as high as a factor of 6 for the f1 event. However, as mentioned before, and are the extreme possible values derived by cumulating uncertainties on κ and on the variability of measurements during the 1 h time period.
4.2 Impact of aerosol particles on fog droplet concentration
Mean values of Nact are shown in Fig. 6 as a function of the other activation parameters (SSpeak, Dd and κ) for the 23 fog events. Nact values increase with SSpeak (Fig. 6a) and consequently decreased with Dd (Fig. 6b). In contrast to Fig. 6b, Fig. 6c reveals no trend between Nact and κ, suggesting that size matters more than chemical composition for a particle to be activated. Indeed, the largest aerosol particles are activated at low SS independently of their κ values. There is some scatter in Fig. 6b for values of Dd≤0.4 µm, which suggests that some variability of the dry aerosol size number distribution between the different cases occurs mainly below this threshold.
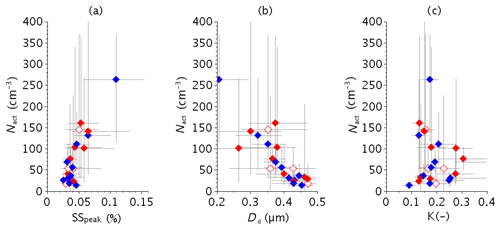
Figure 6Number concentration of activated particles Nact as a function of (a) the critical supersaturation, (b) the dry critical diameter and (c) κ for the 23 fog cases. Diamonds correspond to mean values and error bars to uncertainty intervals. The same symbols as in Fig. 2 are used.
Our results extend to the lower supersaturation conclusion of Fitzgerald (1973) and Andreae and Rosenfeld (2008) on clouds that particle size plays a much greater role than composition in regulating cloud droplet nucleation. The fundamental reason is that soluble mass changes with the third power of particle diameter but only linearly with soluble fraction (Andreae and Rosenfeld, 2008). The color code in Fig. 7a shows that, at a given supersaturation, the highest values of the CCN ratio are associated with the highest values of the hygroscopic parameter (i.e., chemical composition), and that at a given CCN ratio, decrease as the supersaturation increases. However, more samples are needed before a robust interpretation of that feature is to be established.
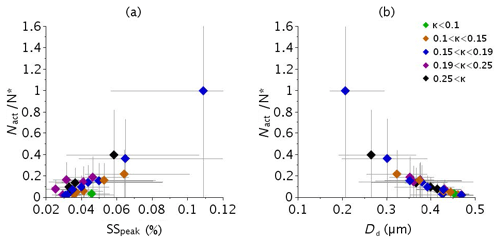
Figure 7Ratio of activated particles to concentration of aerosol particles with diameter >200 nm (activated fraction) for the 23 fog cases as a function of (a) the critical supersaturation and (b) the dry critical diameter. Diamonds correspond to mean values and error bars to uncertainty intervals. Color as a function of κ is indicated in the legend.
To remove the influence of the aerosol number concentration, we normalize Nact by the number concentration of activable aerosols (N*), defined as the number concentration of aerosol particles with diameter ≥200 nm, which corresponds to the smallest dry diameter of Table 3. Figure 7b shows a good correlation between Nact normalized by N* and the inferred critical diameter. We obtained similar correlation when N* was calculated for the range of critical diameter inferred during the campaign (150 to 400 nm). This suggest that N* using a single critical diameter can be considered as a good proxy of the number of activable particles. This can be understood since the supersaturation occurring in fog has a narrow range of value. CCN at a supersaturation between 0.02 % and 0.11 % are mostly composed of accumulation-mode particles.
Figure 8 reveals that almost no relationship exists between Nact and N*. This surprising behavior demonstrates that the concentration of fog droplets was roughly independent of the aerosol number concentration. This is most likely due to the low SS occurring in fog leading to very selective criteria on particle diameter for droplet activation. This is also consistent with the very large derived dry diameter. Nevertheless, this figure also shows that, for high concentration of activable particles (N*), lower Nact values are obtained. It follows that the number concentration of fog droplets is mainly controlled by the peak supersaturation with low influence from the aerosol loading. This is illustrated in Fig. 9, where Nact values are plotted as a function of SSpeak in log scale (black diamonds, same data as Fig. 6a) superimposed on the statistics of CCN measurements (grey diamonds). Compared to the compilation of CCN spectra reported in Andreae and Rosenfeld (2008) (their Fig. 2), our CCN data are spread between SCMS (Small Cumulus Microphysics Study) data (Hudson and Yum, 2001) and continental cases. However, we observe a strong decrease of Nact for SSpeak≤0.1 %, similar to the ASTEX (Atlantic Stratocumulus Transition Experiment) data collected in maritime stratocumuli and to Hudson (1980) fog activation spectra measurements. This indicates that only a very small fraction of aerosols is activated for such low values of supersaturation.
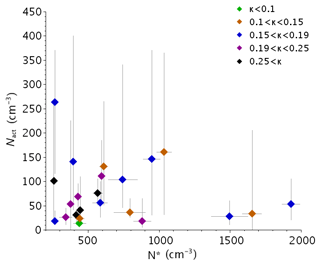
Figure 8Number concentration of activated particles (Nact) as a function of N*, the concentration of aerosol particles with diameter >200 nm for the 23 fog events. For N*, diamonds correspond to median values and error bars to 25th–75th percentile intervals. Color as a function of κ is indicated in the legend.
These results have been fitted using three different equations commonly used in modeling. The typical CCN parameterization is proposed by Twomey (1959): NCCN=CSk, where C represents the CCN number concentration at SS=1 % and the parameter k that varies significantly (Martins et al., 2009). The next formula is suggested by Ji et al. (1998): , where N is the total number concentration of CCN and B and k are empirical coefficients to be determined. Finally, the more general description of the activation spectra is proposed by Cohard et al. (1998): , where C is proportional to NCCN that would be activated when supersaturation tends to infinity and parameters k, μ and β are adjustable parameters depending on the aerosol properties. Figure 9 shows that the parameterization of Ji et al. (1998) (green line), with parameters as indicated by the legend, better reproduces the decrease of Nact for SS<0.1 % compared to the Twomey expression (blue line) but the drop is not as sharp as in the data. In contrast, the parameterization of Cohard et al. (1998) (red line) provides the best fit of the data for lower values of SS.
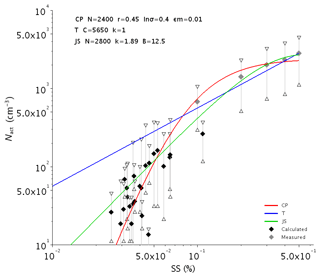
Figure 9Number concentration of activated particles Nact as a function of the critical supersaturation for the 23 fog events (black) superimposed for the statistics of CCN chamber measurements (grey). For CCN measurements, diamonds correspond to median values and error bars to 25th–75th percentile intervals. Color lines correspond to fitted results of (red), NCCN=CSk (blue) and (green), with parameters as indicated in the legend.
Figure 10 shows the CCN concentration that would be activated at SS=0.1 % as a function of the aerosol activable concentration for the 23 fog events. The expected strong correlation between activated particles and aerosol concentration then clearly appears. This confirms that the apparent independence observed in Fig. 8 is simply due to the low supersaturation values experienced in fogs. The symbol color depends on κ as the preceding figures. Data are aligned according to their hygroscopic parameter. For a given aerosol particle's activable concentration, the number of activated particles at SS=0.1 % increases with κ, which is consistent with Fig. 7a.
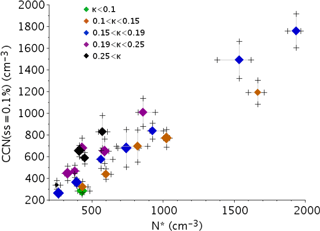
Figure 10Median values for the 23 fog events of the number concentration measured by the CCN chamber at SS=0.1 % as a function of the concentration of aerosol particles with diameter >200 nm. Color as a function of κ is indicated as in Fig. 8. Symbol size is proportional to the mean diameter.
One can note in Fig. 8 that the highest values of Nact decrease as N* increases. Indeed, while aerosol particles' activable concentration increases (N*), variability of SSpeak decreases and tends toward low values as reported in Fig. 11; thus, less particles can be activated. This suggests that the supersaturation reached in fog could be limited by the activable aerosol concentration; if numerous aerosol particles are available, they are efficient enough to uptake the water vapor excess and therefore limit the supersaturation. Hudson (1980) found that aerosol particle concentration values do not have a great effect on fog supersaturation. Our result however supports the conclusions drawn by the numerical study performed by Bott (1991) that the higher the particle concentration is, the lower the supersaturation is. Note that no trend appears with κ in Fig. 8, which means that the sensitivity of this process to the hygroscopicity is very weak. As suggested by Bott et al. (1990), this could be due to a lowering of vapor supersaturation with the hydration of the numerous aerosol particles.
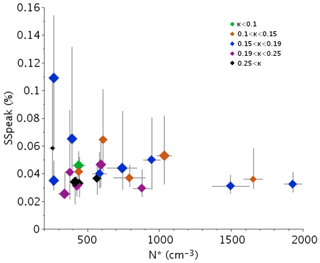
Figure 11Critical supersaturation as a function of the concentration of aerosol particles with diameter >200 nm for the 23 fog cases. Diamonds correspond to mean values and error bars to uncertainty intervals. Color and size of symbols are as in Fig. 10.
Figure 6 compared to Fig. 2 shows that there are no obvious differences between STL and RAD cases. As a result, the median values of Nact are 40 and 58 cm−3, and the 25th–75th percentiles are 25–115 and 33–109 cm−3, for STL and RAD cases, respectively. Radiative cases have thus higher values of activated particles but the percentile intervals are rather similar and the difference is less pronounced than the factor of 2 obtained from NFM derived from the FM-100 measurements only.
4.3 Impact of CCN concentration on fog microstructure
The mean fog droplet concentration () averaged over the 1 h time interval at the beginning of the fog event is plotted in Fig. 12a as a function of Nact. Obviously, they are almost identical, apart from small deviations that come from averaging the Nact values derived for both κ values. The color code in Fig. 12a shows no differences between radiative (red diamonds) and stratus-lowering (blue diamonds) fogs during the formation phase.
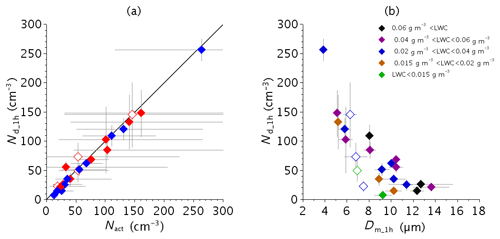
Figure 12Droplet number concentration at the beginning of the fog for the 23 cases as a function of (a) the activated particle concentration (Nact) and (b) the mean fog diameter. Diamonds correspond to median values and error bars to 25th–75th percentile intervals. Symbol colors are as a function of (a) fog type as in Fig. 2 and (b) LWC values as indicated in the legend.
Once droplets have been activated, they compete for the available water vapor; when their number increases, the size they can reach by water vapor diffusion growth decreases. This inverse relationship between the number and the size of droplets is clearly depicted in Fig. 12b, which displays the concentration vs. the corresponding mean diameter Dm. Indeed, the highest of 255 cm−3 corresponds to the lowest Dm of 4 µm, and for fog events with cm−3 the mean diameter cannot exceed 7 µm, while it reaches twice this value for concentration as low as 25 cm−3. However, some scatter appears for samples with cm−3. The symbol color corresponds to the mean LWC values, as indicated by the legend. Lowest values of Dm are associated with lowest values of LWC, which suggests that a lack of available liquid water could also limit the droplet growth, even when there are few of them.
During a fog life cycle, several processes contribute to the droplet size distribution. Droplets can grow by water vapor diffusion or by collision–coalescence with other droplets due to gravitational and turbulent motions. Conversely, they can evaporate if the supersaturation decreases due to heating of the air mass, for example, or in the case of mixing with clear air. Figure 13a and b show the same plots except that Nd, Dm and LWC correspond to mean values over the complete fog life cycle. The mean droplet concentration values are significantly lower, especially for cases with high Nact values. For instance, for cases with Nact>50 cm−3, the ratio ranges from 0.25 to 0.92, with an average value of 0.58. Values reported in Brenguier et al. (2011) exhibit a clear separation between cumulus and stratocumulus clouds, with values from 0.32 to 0.56 (0.46 on average) and from 0.72 to 0.96 (0.87 on average), respectively, that were attributed to differences in entrainment–mixing processes in both cloud types. Here, it appears that values are spanned over a large range with an intermediate average value. It is noteworthy that Fig. 13b reveals that for a radiative fog cannot exceed 70 cm−3, which suggests that this reduction is more pronounced in the case of a radiative fog, while STL cases seem less affected. Indeed, for cases with Nact>100 cm−3, the average is 0.80 for a STL fog, a value close to stratocumulus clouds, while it drops down to 0.45 for RAD cases. This suggests that the processes involved in the reduction of the CDNC in a radiative fog are as efficient as the entrainment–mixing occurring in cumulus clouds. Note that many studies (Pilié et al., 1975; Choularton et al., 1981; Gerber, 1991; Bergot, 2013; Maronga and Bosveld, 2017), among others, pointed out the key mechanism of the turbulent mixing in fogs. Recent work of Bergot (2016) has shown, with a LES study, evidence of the key role of dry downdraught at the top of the fog layer on dissipation. These downdraughts would even then reach the surface, allowing the Sun to warm it. Wærsted et al. (2017), using experimental data, confirmed the importance of top processes for the fog evolution. The dilution ratio being as high as in cumulus clouds in radiative fog brings a new element on that point, meaning that turbulent mixing must be of importance.
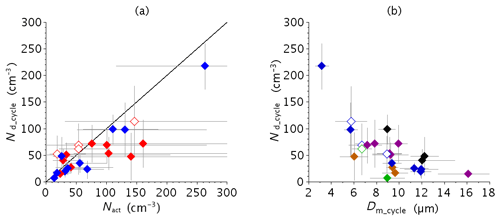
Figure 13Same as Fig. 12 except that statistics of Nd, Dm and LWC are computed over the complete fog life cycle.
Figure 13b shows that mean diameter values averaged over the fog life cycle are similar to the previous ones. The resulting cluster of data points does not reveal any general trend and the anticorrelation between size and number of droplets is no longer noticeable. Indeed, the evolution of microphysical properties during the fog life cycle is complex and highly varies from case to case and depends on many parameters. As already noticed by Burnet et al. (2012) in their Fig. 3, various values of Deff and NFM can be observed for a given LWCFM. A comprehensive analysis on this topic has been performed and will appear in a forthcoming paper.
In this experimental study, we derived accurate estimations of the activated droplet concentration at the beginning of a fog event. This was done through a careful estimation of the critical supersaturation and of the wet critical diameter, which allowed us to integrate the composite size distribution derived from WELAS and FM-100 measurements. We have shown that the derived parameters are consistent with the parameterization of Cohard et al. (1998). They are also consistent with measurements reported in Hudson (1980), who developed the isothermal haze chamber to extend the CCN measurements to supersaturation range below 0.1 % and derived fog condensation nuclei (FCN). Indeed, the author found effective supersaturation between 0.06 % and 0.1 % as well as sharp changes in FCN spectra below 0.1 % with activated concentration at SS=0.4 % ranging from 0.8 cm−3 over the sea to 250 cm−3 for polluted cases.
To our knowledge, no other study has experimentally retrieved concentration of activated particles (and thus droplets) in fog. Usually, measurements of droplet spectra reported in the literature were performed by single particle counters such as FSSP, CDP or FM-100 over the range 2–50 µm. Figure 1 shows typical droplet size distributions observed during the campaign with measures from 2 up to 50 µm.
The corresponding droplet concentrations are in the range of a tenth to several hundred cm−3 (Wendisch et al., 1998; García-García et al., 2002; Gultepe and Milbrandt, 2007a; Niu et al., 2012; Price, 2011; Liu et al., 2011; Burnet et al., 2012; Lu et al., 2013; Zhao et al., 2013; Boutle et al., 2018). In our study, droplet concentrations are rather low for semi-urban conditions, with a maximum value of 150 cm−3. For instance, Liu et al. (2017) reported values in China as high as 1000 cm−3. Moreover, our values of critical diameter are large, with a median value of 3.8 µm. Consequently, the use of FM-100 data over the range 2–50 µm will lead to an overestimation of the droplet concentration, because it includes deliquescent aerosol particles that are not activated. A noticeable exception comes from the f22 case with a maximum value of 264 cm−3. Surprisingly, the median NFM value for this case is only 36 cm−3, which is rather low. This is explained by the fact that this case also corresponds to the lowest critical diameter (Dw=1.44 µm); therefore, the contribution from WELAS data is the most important and emphasizes the underestimation of the FM-100 in the first classes (see Fig. A1). Thus, for cases with low Dw, WELAS data must be taken into account to avoid an underestimation of the concentration. In a modeling purpose, distinguishing hydrated aerosol particles from droplets allows to calculate an accurate repartition of the vapor deposition on the droplet size distribution. Indeed, behavior of hydrated particles and droplets is quite different: the second one grows as long as there is vapor in excess, while the first one stays at an equilibrium diameter. The second one may grow enough to produce drizzle and have strong interaction with radiation. A clear distinction should improve the representation of processes in numerical weather prediction models and thus on the visibilities' forecast.
A surprising result is the observed decrease of droplet concentrations with increasing aerosol loading. This is in contrast with recent numerical simulations that exhibit a strong positive correlation between aerosol and droplet concentrations in fog (Zhang et al., 2014; Stolaki et al., 2015; Maalick et al., 2016). This could be due to a limitation of the supersaturation according to Bott (1991). The sensitivity study of Stolaki et al. (2015) indicates that the fog droplet concentration during the mature stage is 2.6 times greater (2.9 times lower) when doubling (halving) the CCN number concentration of the accumulation mode. Indeed, at the fog onset, the droplet concentration at the surface reaches 467 cm−3 in their simulation with a double CCN concentration. This value is much larger than that of our estimations, which is ≤150 cm−3, except in one case where it reaches 264 cm−3. For their reference run, also this value is as high as 304 cm−3. The CCN activation scheme used by the model follows the expression of Cohard et al. (1998). Given the CCN activation spectrum derived from their values of CCN size distribution parameters (geometric mean radius and standard deviation of 0.1525 µm and 2.33, respectively) and concentration (540 cm−3) and solubility of aerosols (0.4), this corresponds to an estimation of the maximum supersaturation of 0.15 %. Even for activated concentration of 250 cm−3, the corresponding SS is still ≃0.1 %. We have shown that CCN measurement at SS=0.1 % exhibits a linear increase of the droplet concentration with the activable aerosol concentration. Consequently, with such high supersaturation values, it is consistent that their simulations produce a strong positive correlation between aerosol and droplet concentration.
More generally, one shall keep in mind that the use of the CCN activation spectra provides a satisfactory estimation of the activated concentration, providing that the maximum supersaturation is correctly diagnosed. For instance, a current limitation of schemes with adjustment to saturation with parameterized peak supersaturation is that the formulae do not take into account pre-existing liquid water in the model grid box (Thouron et al., 2012). This leads to a significant overestimation of the supersaturation peak value that in turn will overestimate the activated concentration. Another limitation is the use of minimum values for vertical velocities in typical supersaturation parameterization as pointed out by Boutle et al. (2018). They are not necessarily consistent with fog dynamics and can lead to an overestimation of the supersaturation peak value. The same overestimation could occur while using the saturation adjustment assumption instead of a diffusion growth/evaporation equation according to Khain et al. (2015). Moreover, in a sensitivity study in which the CCN concentration is increased (or decreased) while keeping other parameters constant, it intrinsically introduces a strong dependency between droplet and aerosol particles. Indeed, the pre-existing hygroscopic aerosol particles contribute to the sink term of water vapor during the radiative cooling that will also reduce the supersaturation peak value at the fog onset and then limits the number of activated particles. Thus, changing the aerosol properties in models using such a scheme provides a useful way to modify the droplet concentration and study the impact of this latter on the fog life cycle. However, it should not be used to assess the impact of aerosol properties themselves on the fog life cycle.
In situ microphysical measurements collected during 23 wintertime fog events sampled from October 2010 to March 2013 at the semi-urban SIRTA site near Paris have been examined to document their properties. They reveal a large variability of their characteristic values in terms of number concentration and size of fog droplets depending on the different cases, as well as various evolution of these properties during the fog life cycle. The aerosol background exhibits also a highly variable number concentration of particles >10 nm before the fog onset. The objective of this paper was to evaluate the impact of aerosol particles on the fog microphysics. As a first step, we focused on the relationship between aerosol and fog droplet number concentrations, as we expected that they follow the same trend with a greater number of fog droplets with an increase of the aerosol loading.
To derive accurate estimations of the actual activated fog droplet number concentration (Nact), we determined the hygroscopicity parameter, the dry and wet critical diameters, and the critical supersaturation for the 23 events by using an iterative procedure based on the κ-Köhler theory which combined CCN measurements, dry particle distribution from an SMPS and composite wet particle size distribution at ambient humidity derived from WELAS and FM-100 measurements. These data are averaged over a 1 h time period before and during the fog onset to characterize the air mass and the fog properties, respectively.
Values of the hygroscopicity parameter κ extrapolated at SS≃0.05 % were found to range from 0.09 to 0.3 which are characteristics for urban aerosol. They are rather similar from case to case; thus, we recommended to use for fog modeling studies in this urban area. Our study reveals low values of the derived critical supersaturations with a median of 0.043 % and 25th–75th percentiles of 0.035 %–0.051 %. Consequently, wet and dry activation diameters are high and the corresponding Nact values are low for continental conditions, with a median concentration of 53.5 cm−3 and 25th–75th percentiles of 28.5–111 cm−3. Our results depict a sharp drop of Nact as critical supersaturations decrease which is best fitted by the parameterization of Cohard et al. (1998).
Concentration of activated particles using a single critical diameter can be considered as a good proxy of the number of activable particles. No detectable trend between concentration of aerosol particles with diameter >200 nm and Nact was observed. But Nact could be modulated for high concentration of aerosol particles. Hydration of numerous aerosol particles could indeed lower the supersaturation. Our analysis corroborates the modeling study by Bott (1991) suggesting that an increase of the aerosol concentration limits the SS values. In contrast, the CCN data at 0.1 % supersaturation exhibit a strong correlation with these aerosol concentrations. We therefore conclude that the droplet number concentration is roughly independent of the aerosol one because the actual supersaturations reached in these fog events are too low. Given the very diverse origin of atmospheric particles, the complexity of their composition has long been seen as a major obstacle to modeling aerosol effects on fog properties. Understanding that particles' ability to act as CCN at the supersaturation reached in fog is largely controlled by aerosol size rather than composition greatly facilitates the treatment of aerosol impacts on fog microphysics in NWP models. Nevertheless, some reservation must be issued on that point. Aerosol size distribution impacts fog microphysics more than chemical composition on the measured range on the hygroscopic parameter during the three winters of observations. Higher or lower values of this parameter could bias this conclusion. Other measurements of aerosol and fog microphysics in other environmental conditions would be needed to pursue this issue.
Despite a stratus-lowering fog appearing to be associated with lower aerosol loading than a radiation fog event, no significant differences were observed with respect to the droplet number concentration at the fog formation when calculations were performed by taking into account the wet critical diameter. In contrast, statistics over the complete life cycle indicate that a radiation fog is subject to a pronounced decrease in the droplet concentration, while stratus-lowering cases seem unaffected. In a radiation fog, this decrease, which occurs mainly for events with Nact>50 cm−3, is significant with a ratio of average droplet concentration to Nact ranging from 0.25 to 0.67. This reduction is similar to the dilution which results from entrainment–mixing in cumulus clouds, meaning that mixing with clear air may be of importance for fog microphysical evolution. The expected inverse relationship between the number and the size of the droplets at the formation phase is clearly depicted, except for some cases with low liquid water content values. However, this trend is less pronounced on average over the fog life cycle.
Nenes and Seinfeld (2003) have shown that kinetic limitations in droplet activation may retard the growth of CCN sufficiently to limit the number of activated droplets formed. The extent to which potential kinetic limitations to droplet formation exist in fog conditions will be explored in a subsequent publication focusing on the temporal evolution of droplet spectra and visibility during fog life cycle.
Advanced data are available in Tables 2 and 3. Data are available upon request to the authors.
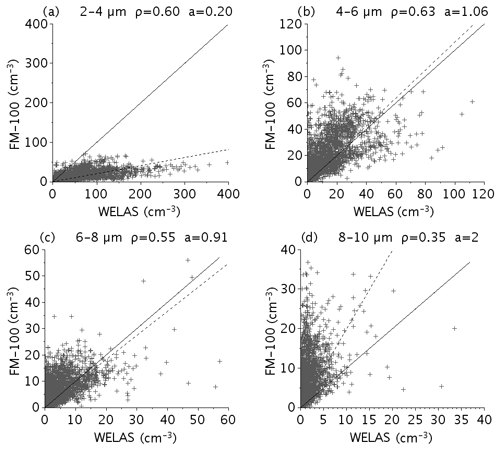
Figure A1Scatterplot of the 5 min average particle number concentration values as measured by the FM-100 for the four first bins vs. the integrated WELAS measurement over the corresponding diameter range (a) 2–4 µm, (b) 4–6 µm, (c) 6–8 µm and (d) 8–10 µm. The solid line corresponds to 1:1 line and the dashed line corresponds to best-fit line with correlation coefficient ρ and slope a, as indicated in the legend.
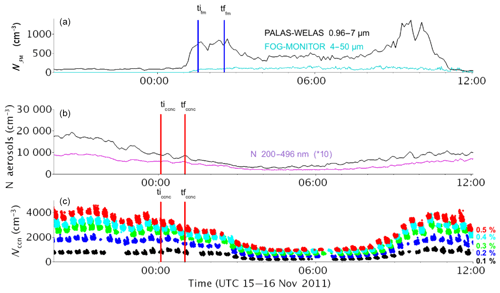
Figure A2Time series of measurements for the f6 case: (a) particle number concentration at ambient humidity from FM-100 (cyan) and WELAS (black); (b) dry particle number concentration from SMPS: total (black) and particle with diameter >200 nm (purple); and (c) Nccn from the CCN chamber at each supersaturation with color as indicated on the label. Vertical segments indicate the selected time periods before (red) and during (blue) the beginning of the fog event.
| CCN | Cloud condensation nuclei |
| Nd | Concentration of particles above the wet critical diameter (derived from WELAS+FM-100) |
| CN | Condensation nuclei |
| NFM | Concentration of particles measured by the FM-100 between 2 and 50 µm diameter |
| Na | Concentration of dry particles measured by the SMPS between 10 and 495 nm diameter |
| Nact | Concentration of activated particles |
| N* | Concentration of dry particles between 200 and 496 nm diameter (derived from SMPS) |
| Nccn | Concentration of activated aerosol measured by the CCN at different supersaturation |
| Dd | Dry critical diameter |
| Dw | Wet critical diamter |
| Dm | Median diameter |
| SSpeak | Critical supersaturation peak |
| SS | Supersaturation |
This work is a part of the PhD of MM. MM and FB analyzed the data and wrote the paper. FB, MH, JCD and TE organized the field campaign. TE coordinated the field campaign. GCR helped to process the CCNC data. MM and CD performed the review process.
The authors declare that they have no conflict of interest.
The authors are very grateful to all SIRTA operators and database managers. This campaign was held in the framework of the PreViBOSS project, supported by DGA/DGIS. This research was partially funded by the European Commission's Seventh Framework Programme (FP7/2007-2013) under the SESAR WP 11.2.2 project, under grant agreement 11-120809-C.
This paper was edited by Barbara Ervens and reviewed by four anonymous referees.
Andreae, M. and Rosenfeld, D.: Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols, Earth-Sci. Rev., 89, 13–41, 2008. a, b, c, d
Bergot, T.: Small-scale structure of radiation fog: a large-eddy simulation study, Q. J. Roy. Meteor. Soc., 139, 1099–1112, 2013. a, b
Bergot, T.: Large-eddy simulation study of the dissipation of radiation fog, Q. J. Roy. Meteor. Soc., 142, 1029–1040, 2016. a
Bott, A.: On the influence of the physico-chemical properties of aerosols on the life cycle of radiation fogs, Bound.-Lay. Meteorol., 56, 1–31, 1991. a, b, c, d
Bott, A., Sievers, U., and Zdunkowski, W.: A radiation fog model with a detailed treatment of the interaction between radiative transfer and fog microphysics, J. Atmos. Sci., 47, 2153–2166, 1990. a
Boutle, I., Price, J., Kudzotsa, I., Kokkola, H., and Romakkaniemi, S.: Aerosol–fog interaction and the transition to well-mixed radiation fog, Atmos. Chem. Phys., 18, 7827–7840, https://doi.org/10.5194/acp-18-7827-2018, 2018. a, b, c, d, e, f, g, h
Brenguier, J.-L., Burnet, F., and Geoffroy, O.: Cloud optical thickness and liquid water path – does the k coefficient vary with droplet concentration?, Atmos. Chem. Phys., 11, 9771–9786, https://doi.org/10.5194/acp-11-9771-2011, 2011. a, b
Burnet, F., Gomes, L., Haeffelin, M., Dupont, J., and Elias, T.: Analysis of the microphysical structures of fog during the ParisFog project, in: Proceedings of the 16th international conference of clouds and precipitation (ICCP), Leipzig, Germany, Vol. 30, 2012. a, b, c, d, e, f, g
Choularton, T., Fullarton, G., Latham, J., Mill, C., Smith, M., and Stromberg, I.: A field study of radiation fog in Meppen, West Germany, Q. J. Roy. Meteor. Soc., 107, 381–394, 1981. a
Cohard, J.-M., Pinty, J.-P., and Bedos, C.: Extending Twomey's analytical estimate of nucleated cloud droplet concentrations from CCN spectra, J. Atmos. Sci., 55, 3348–3357, 1998. a, b, c, d, e
Crippa, M., DeCarlo, P. F., Slowik, J. G., Mohr, C., Heringa, M. F., Chirico, R., Poulain, L., Freutel, F., Sciare, J., Cozic, J., Di Marco, C. F., Elsasser, M., Nicolas, J. B., Marchand, N., Abidi, E., Wiedensohler, A., Drewnick, F., Schneider, J., Borrmann, S., Nemitz, E., Zimmermann, R., Jaffrezo, J.-L., Prévôt, A. S. H., and Baltensperger, U.: Wintertime aerosol chemical composition and source apportionment of the organic fraction in the metropolitan area of Paris, Atmos. Chem. Phys., 13, 961–981, https://doi.org/10.5194/acp-13-961-2013, 2013. a
Denjean, C., Formenti, P., Picquet-Varrault, B., Katrib, Y., Pangui, E., Zapf, P., and Doussin, J. F.: A new experimental approach to study the hygroscopic and optical properties of aerosols: application to ammonium sulfate particles, Atmos. Meas. Tech., 7, 183–197, https://doi.org/10.5194/amt-7-183-2014, 2014. a
Ditas, F., Shaw, R. A., Siebert, H., Simmel, M., Wehner, B., and Wiedensohler, A.: Aerosols-cloud microphysics-thermodynamics-turbulence: evaluating supersaturation in a marine stratocumulus cloud, Atmos. Chem. Phys., 12, 2459–2468, https://doi.org/10.5194/acp-12-2459-2012, 2012. a
Dupont, J. C., Haeffelin, M., Stolaki, S., and Elias, T.: Analysis of dynamical and thermal processes driving fog and quasi-fog life cycles using the 2010–2013 ParisFog dataset, Pure Appl. Geophys., 173, 1337–1358, 2016. a, b, c, d, e, f
Elias, T., Haeffelin, M., Drobinski, P., Gomes, L., Rangognio, J., Bergot, T., Chazette, P., Raut, J.-C., and Colomb, M.: Particulate contribution to extinction of visible radiation: Pollution, haze, and fog, Atmos. Res., 92, 443–454, 2009. a, b
Elias, T., Jolivet, D., Dupont, J.-C., Haeffelin, M., and Burnet, F.: Preliminary results of the PreViBOSS project: description of the fog life cycle by ground-based and satellite observation, in: SPIE Remote Sensing, 853 406–853 406, International Society for Optics and Photonics, 2012. a
Elias, T., Dupont, J.-C., Hammer, E., Hoyle, C. R., Haeffelin, M., Burnet, F., and Jolivet, D.: Enhanced extinction of visible radiation due to hydrated aerosols in mist and fog, Atmos. Chem. Phys., 15, 6605–6623, https://doi.org/10.5194/acp-15-6605-2015, 2015. a, b, c, d, e, f, g, h, i, j, k
Facchini, M. C., Decesari, S., Mircea, M., Fuzzi, S., and Loglio, G.: Surface tension of atmospheric wet aerosol and cloud/fog droplets in relation to their organic carbon content and chemical composition, Atmos. Environ., 34, 4853–4857, 2000. a
Fitzgerald, J. W.: Dependence of the supersaturation spectrum of CCN on aerosol size distribution and composition, J. Atmos. Sci., 30, 628–634, 1973. a
Frank, G., Martinsson, B., Cederfelt, S.-I., Berg, O., Swietlicki, E., Wendish, M., Yuskiewicz, B., Heintzenberg, J., Wiedensohler, A., Orsini, D., Stratmann, F., Laj, P., and Ricci, L.: Droplet formation and growth in polluted fogs, Contributions to Atmospheric Physics, 71, 65–85, 1998. a
García-García, F., Virafuentes, U., and Montero-Martínez, G.: Fine-scale measurements of fog-droplet concentrations: A preliminary assessment, Atmos. Res., 64, 179–189, 2002. a, b
Gerber, H.: Supersaturation and droplet spectral evolution in fog, J. Atmos. Sci., 48, 2569–2588, 1991. a
Gonser, S. G., Klemm, O., Griessbaum, F., Chang, S.-C., Chu, H.-S., and Hsia, Y.-J.: The relation between humidity and liquid water content in fog: An experimental approach, Pure Appl. Geophys., 169, 821–833, 2012. a
Gultepe, I. and Isaac, G.: The relationship between cloud droplet and aerosol number concentrations for climate models, Int. J. Climatol., 16, 941–946, 1996. a
Gultepe, I. and Milbrandt, J.: Microphysical observations and mesoscale model simulation of a warm fog case during FRAM project, in: Fog and Boundary Layer Clouds: Fog Visibility and Forecasting, 1161–1178, Springer, Birkhäuser Basel, 2007a. a, b
Gultepe, I., Tardif, R., Michaelides, S., Cermak, J., Bott, A., Bendix, J., Müller, M., Pagowski, M., Hansen, B., Ellrod, G., Jacobs, W., Toth, G., and Cober, S. G.: Fog research: A review of past achievements and future perspectives, Pure Appl. Geophys., 164, 1121–1159, 2007b. a
Gultepe, I., Hansen, B., Cober, S., Pearson, G., Milbrandt, J., Platnick, S., Taylor, P., Gordon, M., and Oakley, J.: The fog remote sensing and modeling field project, B. Am. Meteorol. Soc., 90, 341–359, 2009. a
Haeffelin, M., Barthès, L., Bock, O., Boitel, C., Bony, S., Bouniol, D., Chepfer, H., Chiriaco, M., Cuesta, J., Delanoë, J., Drobinski, P., Dufresne, J.-L., Flamant, C., Grall, M., Hodzic, A., Hourdin, F., Lapouge, F., Lemaître, Y., Mathieu, A., Morille, Y., Naud, C., Noël, V., O'Hirok, W., Pelon, J., Pietras, C., Protat, A., Romand, B., Scialom, G., and Vautard, R.: SIRTA, a ground-based atmospheric observatory for cloud and aerosol research, Ann. Geophys., 23, 253–275, https://doi.org/10.5194/angeo-23-253-2005, 2005. a
Haeffelin, M., Bergot, T., Elias, T., Tardif, R., Carrer, D., Chazette, P., Colomb, M., Drobinski, P., Dupont, E., Dupont, J., Gomes, L., Musson-Genon, L., Pietras, C., Plana-Fattori, A., Protat, A., Rangognio, J., Raut, J.-C., Rémy, S., Richard, D., Sciare, J., and Zhang, X.: PARISFOG: shedding new light on fog physical processes, B. Am. Meteorol. Soc., 91, 767–783, 2010. a, b, c, d
Hammer, E., Gysel, M., Roberts, G. C., Elias, T., Hofer, J., Hoyle, C. R., Bukowiecki, N., Dupont, J.-C., Burnet, F., Baltensperger, U., and Weingartner, E.: Size-dependent particle activation properties in fog during the ParisFog 2012/13 field campaign, Atmos. Chem. Phys., 14, 10517–10533, https://doi.org/10.5194/acp-14-10517-2014, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m
Heim, M., Mullins, B. J., Umhauer, H., and Kasper, G.: Performance evaluation of three optical particle counters with an efficient “multimodal” calibration method, J. Aerosol Sci., 39, 1019–1031, 2008. a
Hoag, K. J., Collett Jr., J. L., and Pandis, S. N.: The influence of drop size-dependent fog chemistry on aerosol processing by San Joaquin Valley fogs, Atmos. Environ., 33, 4817–4832, 1999. a
Hudson, J. G.: Relationship between fog condensation nuclei and fog microstructure, J. Atmos. Sci., 37, 1854–1867, 1980. a, b, c, d, e, f, g, h
Hudson, J. G. and Yum, S. S.: Maritime-continental drizzle contrasts in small cumuli, J. Atmos. Sci., 58, 915–926, 2001. a
Ji, Q., Shaw, G. E., and Cantrell, W.: A new instrument for measuring cloud condensation nuclei: Cloud condensation nucleus “remover”, J. Geophys. Res.-Atmos., 103, 28013–28019, 1998. a, b
Jurányi, Z., Tritscher, T., Gysel, M., Laborde, M., Gomes, L., Roberts, G., Baltensperger, U., and Weingartner, E.: Hygroscopic mixing state of urban aerosol derived from size-resolved cloud condensation nuclei measurements during the MEGAPOLI campaign in Paris, Atmos. Chem. Phys., 13, 6431–6446, https://doi.org/10.5194/acp-13-6431-2013, 2013. a
Khain, A., Beheng, K., Heymsfield, A., Korolev, A., Krichak, S., Levin, Z., Pinsky, M., Phillips, V., Prabhakaran, T., Teller, A., van den Heever, S. C., and Yano, J.-I.: Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parameterization, Rev. Geophys., 53, 247–322, 2015. a
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, T. Faraday Soc., 32, 1152–1161, 1936. a, b
Levin, Z. and Brenguier, J.-L.: Effects of Pollution and Biomass Aerosols on Clouds and Precipitation: Observational Studies, in: Aerosol Pollution Impact on Precipitation, 205–241, Springer, Dordrecht, 2009. a
Liu, D., Yang, J., Niu, S., and Li, Z.: On the evolution and structure of a radiation fog event in Nanjing, Adv. Atmos. Sci., 28, 223–237, 2011. a, b
Liu, D., Li, Z., Yan, W., and Li, Y.: Advances in fog microphysics research in China, Asia-Pac. J. Atmos. Sci., 53, 131–148, 2017. a, b
Lu, C., Liu, Y., Niu, S., Zhao, L., Yu, H., and Cheng, M.: Examination of microphysical relationships and corresponding microphysical processes in warm fogs, Acta Meteorol. Sin., 27, 832–848, 2013. a, b
Lu, M.-L., Conant, W. C., Jonsson, H. H., Varutbangkul, V., Flagan, R. C., and Seinfeld, J. H.: The Marine Stratus/Stratocumulus Experiment (MASE): Aerosol-cloud relationships in marine stratocumulus, J. Geophys. Res.-Atmos., 112, D10209, https://doi.org/10.1029/2006JD007985, 2007. a
Maalick, Z., Kühn, T., Korhonen, H., Kokkola, H., Laaksonen, A., and Romakkaniemi, S.: Effect of aerosol concentration and absorbing aerosol on the radiation fog life cycle, Atmos. Environ., 133, 26–33, 2016. a, b
Maronga, B. and Bosveld, F.: Key parameters for the life cycle of nocturnal radiation fog: a comprehensive large-eddy simulation study, Q. J. Roy. Meteor. Soc., 143, 2463–2480, 2017. a
Martin, G., Johnson, D., and Spice, A.: The measurement and parameterization of effective radius of droplets in warm stratocumulus clouds, J. Atmos. Sci., 51, 1823–1842, 1994. a
Martins, J. A., Gonçalves, F. L. T., Morales, C. A., Fisch, G. F., Pinheiro, F. G. M., Júnior, J. B. V. L., Oliveira, C. J., Silva, E. M., Oliveira, J. C. P., Costa, A. A., and Silva Dias, M. A. F.: Cloud condensation nuclei from biomass burning during the Amazonian dry-to-wet transition season, Meteorol. Atmos. Phys., 104, 83–93, 2009. a
McFiggans, G., Artaxo, P., Baltensperger, U., Coe, H., Facchini, M. C., Feingold, G., Fuzzi, S., Gysel, M., Laaksonen, A., Lohmann, U., Mentel, T. F., Murphy, D. M., O'Dowd, C. D., Snider, J. R., and Weingartner, E.: The effect of physical and chemical aerosol properties on warm cloud droplet activation, Atmos. Chem. Phys., 6, 2593–2649, https://doi.org/10.5194/acp-6-2593-2006, 2006. a
Ming, Y. and Russell, L. M.: Organic aerosol effects on fog droplet spectra, J. Geophys. Res.-Atmos., 109, D10206, https://doi.org/10.1029/2003JD004427, 2004. a, b, c
Nenes, A. and Seinfeld, J. H.: Parameterization of cloud droplet formation in global climate models, J. Geophys. Res.-Atmos., 108, 4415, https://doi.org/10.1029/2002JD002911, 2003. a
Niu, S., Liu, D., Zhao, L., Lu, C., Lü, J., and Yang, J.: Summary of a 4-year fog field study in northern Nanjing, Part 2: Fog microphysics, Pure Appl. Geophys., 169, 1137–1155, 2012. a, b
Noone, K. J., Ogren, J. A., Hallberg, A., Heintzenberg, J., Ström, J., Hansson, H.-C., Svenningsson, B., Wiedensohler, A., Fuzzi, S., Facchini, M. C., Arends, B. G., and Berner, A.: Changes in aerosol size-and phase distributions due to physical and chemical processes in fog, Tellus B, 44, 489–504, 1992. a, b, c
Noziere, B., Baduel, C., and Jaffrezo, J.-L.: The dynamic surface tension of atmospheric aerosol surfactants reveals new aspects of cloud activation, Nat. Commun., 5, 3335, https://doi.org/10.1038/ncomms4335, 2014. a
Pandis, S. N., Seinfeld, J. H., and Pilinis, C.: Chemical composition differences in fog and cloud droplets of different sizes, Atmos. Environ. A-Gen., 24, 1957–1969, 1990. a
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a
Pilié, R., Mack, E., Kocmond, W., Rogers, C., and Eadie, W.: The life cycle of valley fog. Part I: Micrometeorological characteristics, J. Appl. Meteorol., 14, 347–363, 1975. a
Price, J.: Radiation fog. Part I: observations of stability and drop size distributions, Bound.-Lay. Meteorol., 139, 167–191, 2011. a, b
Pruppacher, H. R., Klett, J. D., and Wang, P. K.: Microphysics of clouds and precipitation, Springer, Dordrecht, https://doi.org/10.1007/978-0-306-48100-0_2, 1998. a
Ramanathan, V., Crutzen, P., Kiehl, J., and Rosenfeld, D.: Aerosols, climate, and the hydrological cycle, Science, 294, 2119–2124, 2001. a, b
Roberts, G. and Nenes, A.: A continuous-flow streamwise thermal-gradient CCN chamber for atmospheric measurements, Aerosol Sci. Tech., 39, 206–221, 2005. a
Shen, C., Zhao, C., Ma, N., Tao, J., Zhao, G., Yingli, Y., and Kuang, Y.: Method to Estimate Water Vapor Supersaturation in the Ambient Activation Process using Aerosol and Droplet Measurement Data, J. Geophys. Res.-Atmos., 123, 10606–10619, https://doi.org/10.1029/2018JD028315, 2018. a
Spiegel, J. K., Zieger, P., Bukowiecki, N., Hammer, E., Weingartner, E., and Eugster, W.: Evaluating the capabilities and uncertainties of droplet measurements for the fog droplet spectrometer (FM-100), Atmos. Meas. Tech., 5, 2237–2260, https://doi.org/10.5194/amt-5-2237-2012, 2012. a
Stolaki, S., Haeffelin, M., Lac, C., Dupont, J.-C., Elias, T., and Masson, V.: Influence of aerosols on the life cycle of a radiation fog event. A numerical and observational study, Atmos. Res., 151, 146–161, 2015. a, b, c
Svenningsson, I., Hansson, H.-C., Wiedensohler, A., Ogren, J., Noone, K., and Hallberg, A.: Hygroscopic growth of aerosol particles in the Po Valley, Tellus B, 44, 556–569, 1992. a, b, c
Tang, I., Fung, K., Imre, D., and Munkelwitz, H.: Phase transformation and metastability of hygroscopic microparticles, Aerosol Sci. Tech., 23, 443–453, 1995. a
Tardif, R. M.: Characterizing fog and the physical mechanisms leading to its formation during precipitation in a coastal area of the northeastern United States, ProQuest, University of Colorado, Boulder, 2007. a
Thouron, O., Brenguier, J.-L., and Burnet, F.: Supersaturation calculation in large eddy simulation models for prediction of the droplet number concentration, Geosci. Model Dev., 5, 761–772, https://doi.org/10.5194/gmd-5-761-2012, 2012. a, b
Twohy, C. H., Petters, M. D., Snider, J. R., Stevens, B., Tahnk, W., Wetzel, M., Russell, L., and Burnet, F.: Evaluation of the aerosol indirect effect in marine stratocumulus clouds: Droplet number, size, liquid water path, and radiative impact, J. Geophys. Res.-Atmos., 110, D08203, https://doi.org/10.1029/2004JD005116, 2005. a
Twomey, S.: The nuclei of natural cloud formation part II: The supersaturation in natural clouds and the variation of cloud droplet concentration, Geofisica Pura e Applicata, 43, 243–249, 1959. a
Van der Velde, I., Steeneveld, G., Wichers Schreur, B., and Holtslag, A.: Modeling and forecasting the onset and duration of severe radiation fog under frost conditions, Mon. Weather Rev., 138, 4237–4253, 2010. a
Wærsted, E. G., Haeffelin, M., Dupont, J.-C., Delanoë, J., and Dubuisson, P.: Radiation in fog: quantification of the impact on fog liquid water based on ground-based remote sensing, Atmos. Chem. Phys., 17, 10811–10835, https://doi.org/10.5194/acp-17-10811-2017, 2017. a
Wendisch, M., Mertes, S., Heintzenberg, J., Wiedensohler, A., Schell, D., Wobrock, W., Frank, G., Martinsson, B., Fuzzi, S., Orsi, G., Kos, G., and Berner, A.: Drop size distribution and LWC in Po Valley fog, Contributions to Atmospheric Physics, 71, 87–100, 1998. a, b
Zhang, X., Musson-Genon, L., Dupont, E., Milliez, M., and Carissimo, B.: On the Influence of a Simple Microphysics Parametrization on Radiation Fog Modelling: A Case Study During ParisFog, Bound.-Lay. Meteorol., 151, 293–315, 2014. a, b
Zhao, L., Niu, S., Zhang, Y., and Xu, F.: Microphysical characteristics of sea fog over the east coast of Leizhou Peninsula, China, Adv. Atmos. Sci., 30, 1154–1172, 2013. a, b
Zhou, B. and Ferrier, B. S.: Asymptotic analysis of equilibrium in radiation fog, J. Appl. Meteorol. Clim., 47, 1704–1722, 2008. a