the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Kinetic mass-transfer calculation of water isotope fractionation due to cloud microphysics in a regional meteorological model
I-Chun Tsai
Wan-Yu Chen
Mao-Chang Liang
In conventional atmospheric models, isotope exchange between liquid, gas, and solid phases is usually assumed to be in equilibrium, and the highly kinetic phase transformation processes inferred in clouds are yet to be fully investigated. In this study, a two-moment microphysical scheme in the National Center for Atmospheric Research (NCAR) Weather Research and Forecasting (WRF) model was modified to allow kinetic calculation of isotope fractionation due to various cloud microphysical phase-change processes. A case of a moving cold front is selected for quantifying the effect of different factors controlling isotopic composition, including water vapor sources, atmospheric transport, phase transition pathways of water in clouds, and kinetic-versus-equilibrium mass transfer. A base-run simulation was able to reproduce the ∼ 50 ‰ decrease in δD that was observed during the frontal passage. Sensitivity tests suggest that all the above factors contributed significantly to the variations in isotope composition. The thermal equilibrium assumption commonly used in earlier studies may cause an overestimate of mean vapor-phase δD by 11 ‰, and the maximum difference can be more than 20 ‰. Using initial vertical distribution and lower boundary conditions of water stable isotopes from satellite data is critical to obtain successful isotope simulations, without which the δD in water vapor can be off by about 34 ‰ and 28 ‰, respectively. Without microphysical fractionation, the δD in water vapor can be off by about 25 ‰.
- Article
(11343 KB) - Full-text XML
- BibTeX
- EndNote
The water stable isotopes (1H2O, 1H2D16O, and 1) differ in molecular symmetry and weight. These differences in physical properties lead to a change in the stable isotope composition of water, due to fractionation during phase changes. When water vapor condenses and forms liquid or solid particles, it becomes depleted in 2D and 18O, because heavy isotopes condense preferentially to light ones. Information about the stable water stable isotopes is thus useful for understanding the water cycle (Dansgaard, 1964; Dawson and Ehleringer, 1998; Lorius et al., 1985; Risi et al., 2012; Sturm et al., 2010).
Isotope fractionation, as measured in precipitation, has been studied for decades. The observed isotope concentrations generally exhibit significant variations in either time or space. Factors such as the effects of surface type (e.g., land versus ocean), latitude, temperature, and precipitation amount are commonly considered to be key to the relationship between isotope fractionation and meteorological parameters (Dansgaard, 1964; Gonfiantini, 1985; Rozanski et al., 1993; Yurtsever and Gat, 1981; Kurita, 2013; Zwart et al., 2018). These factors are related to various physical processes, such as the surface water vapor source, atmospheric transport, phase changes in clouds, and gravitational sorting of precipitation hydrometeors. For example, the water stable isotopic ratios decreased inland from the coast and the so-called continental effect (Clark and Fritz, 1997). The precipitation amount effect states that isotopic contents of tropical precipitation decrease as the amount of local precipitation increases (Dansgaard, 1964; Kurita, 2013), and the cause of which could either be the preferential removal during condensation (Cole et al., 1999; Yoshimura et al., 2003) or stronger downdraft in more intense convection (Risi et al., 2008). Untangling the intertwined effects of the various physical processes is essential to understanding isotope fractionation and the atmospheric water cycle.
The variations in isotope concentrations usually have multiple causes, and it is difficult to understand the impacts of different factors by measurements alone. Therefore, numerical models have been used to simulate isotope fractionation in the atmosphere. The Rayleigh-type models, in which the air mass is continuously cooled down and the condensation process is assumed to occur in isotopic equilibrium, are widely used in discussing isotope measurements (Aldaz and Deutsch, 1967; Dansgaard, 1964). Such models can explain the linear relationship between the surface temperature and isotopic composition of precipitation (Rozanski et al., 1993), and they have been expanded to incorporate more processes since the publication of Dansgaard (1964). For example, Jouzel and Merlivat (1984) reported that the isotopic equilibrium assumption led to an overestimation of the temperature-isotope gradients of polar snow, so they included isotopic kinetic effects at snow formation in the models. However, the Rayleigh-type models greatly simplify the complexity of the hydrological cycle, and Joussaume et al. (1984) introduced the concept of building isotopes into an atmospheric general circulation model (AGCM). AGCMs can calculate the transport and mixing of air masses from different sources (which cannot be addressed by the Rayleigh-type models), and have been used in studying the hydrological cycle in the troposphere (Hoffmann et al., 1998; Lee et al., 2007; Sjolte and Hoffmann, 2014; Yoshimura et al., 2008). In conventional AGCMs, isotope exchange between liquid or ice and gas phases is usually assumed to be in a partial or full equilibrium state (Hoffmann et al., 1998; Risi et al., 2010; Nusbaumer et al., 2017; Werner et al., 2011; Yoshimura et al., 2010). In a synoptic weather system such as a front or typhoon, thermal equilibrium fractionation may not be appropriate for describing fractionation during phase change, since the clouds are usually not in vapor equilibrium (Laskar et al., 2014). Therefore, in recent years, several regional models start to consider the kinetic fractionation during evaporation from open water, condensation from vapor to ice, or isotope exchange from raindrops to unsaturated air (Hoffmann et al., 1998; Yoshimura et al., 2010; Blossey et al. 2010; Pfahl et al., 2012; Dütsch et al., 2016). However, the microphysics in these global or regional models is usually described with single-moment schemes. This study developed a kinetic fractionation scheme for water stable isotopes using a two-moment microphysical scheme that coupled into the National Center for Atmospheric Research (NCAR) Weather Research and Forecasting (WRF) model (Skamarock, 2008) to understand the role of different factors in the fractionation of the stable isotopes of water at the synoptic scale.
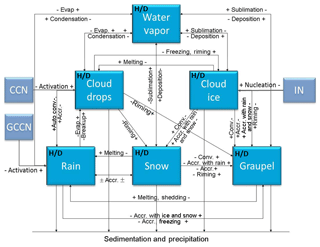
Figure 1Schematics of the modified NTU scheme. The blue boxes are the six hydrometeor categories considered in the model, and H∕D indicates that both H2O and HDO are included. The arrows represent the microphysical conversion processes, and the light blue boxes represent aerosol categories, including cloud condensation nuclei (CCN), giant CCN (GCCN), and ice nuclei (IN). Here Accr. denotes accretion, and Evap denotes evaporation. (Figure modified from Cheng et al., 2010.)
Because the αl-v of 18O (grey line in Fig. 2) does not deviate significantly from unity, the signal of 18O fractionation is generally much less pronounced. Therefore, we focus on deuterium for demonstrating the fractionation processes. The microphysical processes of deuterium such as condensation and collision were incorporated into the WRF model. A moving frontal system is selected to demonstrate the effect of microphysical fractionation versus other controlling factors such as air mass origins and surface sources. The effects of microphysical processes, including kinetic-versus-equilibrium treatments, are discussed in more detail, whereas the importance of initial and boundary conditions of the vapor-phase isotope is also investigated.
In this study, the WRF model version 3.4.1 coupled with a two-moment bulk-water microphysical scheme (cf. Cheng et al., 2010, 2015; Dearden et al., 2016) that was developed at the National Taiwan University (hereafter, the NTU scheme) was selected for simulations. The NTU scheme shown in Fig. 1 is modified to handle the isotope fractionation due to various cloud microphysical phase-change processes. The hydrodeoxygenation (HDO) cycle and its initial and boundary conditions were incorporated into the model and more details were provided in Sect. 2.1. The simulation setup and observation data are given in Sect. 2.2 and 2.3, respectively.
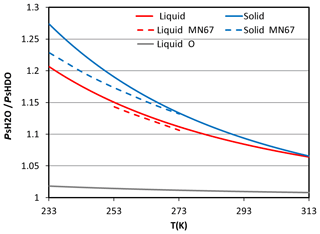
Figure 2The ratio between saturation pressure of H2O and HDO in different phases (liquid: red line, solid: blue line) at different temperatures. The grey line is the ratio of 18O based on Horita and Wesolowski (1994). The dashed lines are the formulas from Merlivat and Nief (1967).
2.1 Description of the isotopic microphysical model
In modified NTU scheme, isotope mass transfer between vapor-, liquid-, and ice-phase hydrometeors during microphysical processes such as deposition, sublimation, evaporation, and condensation were considered explicitly (cf. Fig. 1). For processes of collision collection or melting and freezing, the masses of isotopes of the involving particles are simply combined or conserved, respectively, without worrying about the fractionation.
Thermal equilibrium fractionation has been widely used in conventional models. In such schemes, the HDO concentration can be determined from the (hereafter, H2O) concentration for both gas and liquid phases, because it is assumed that HDO is always in equilibrium with H2O, irrespective of their phase states. The equilibrium between stable isotopes in liquid water and vapor phases is commonly expressed using the isotopic fractionation factor αl-v:
where R is the ratio of the heavy (HDO) to light (H2O) isotopes. This ratio can be explained with the Raoult's law, which states that the activity (saturation ratio) of each species in the vapor phase equals its activity in the liquid phase. For the HDO–H2O system, this relationship can be expressed as the following:
where n is the number of moles in the liquid phase, P is vapor pressure, and Ps is saturation vapor pressure, whereas x represents all other chemical species. By dividing Eq. (2a) by (2b), one can derive the following:
One can see that the left-hand-side term is exactly αl-v, while the right-hand-side term tells us that this factor is actually the ratio between the saturation vapor pressure of H2O and HDO. Thus the isotopic fractionation factor αl-v is a function of temperature only and can be determined experimentally. In this study, we adopted the temperature dependence of αl-v from Horita and Wesolowski (1994):
whereas that between ice and water vapor was adapted from Ellehoj et al. (2013):
where the subscript “s” means solid phase.
When the kinetic process is considered, isotopic fractionation is not only related to temperature but also factors such as the diffusion coefficient and water vapor concentration. The calculation of kinetic fractionation during condensation/evaporation is based on the two-stream Maxwellian kinetic equation:
where m is HDO mass in the particle, t is time, r is hydrometeor particle size, D is the mass diffusivity in air, ρenv is vapor density in the air, and ρp is vapor density at the particle surface. The latter two terms can be rewritten as:
where RHDO is the gas constant of HDO, aHDO and Ps,HDO are the activity and saturation vapor pressure of HDO, respectively, and Tair and Tp are temperatures of the air and particle surface, respectively. Equation (5) is for a single particle, but the bulk-water microphysical schemes commonly used in regional weather models deal with a population of hydrometeor particles (thus called bulk water). Conventional bulk-water schemes apply a mathematical function to represent the size distribution of any hydrometeor category, and the mathematical function is solved by knowing several bulk properties (moments) of the size distribution. The NTU scheme is a two-moment scheme that predicts both the number and mass concentrations of each bulk-water category, which allows better presentation of microphysical processes than the commonly used 1-moment schemes (Taufour et al., 2018). In contrast to the conventional bulk-water schemes that must assume a certain size distribution function, the NTU scheme derived the warm-cloud parameterization by analyzing results from bin model simulations and is thus rather accurate and comprehensive in microphysical processes, while the cold-cloud parameterization still follows the conventional approach. Another advantage of the NTU scheme is that it does not apply the “saturation adjustment” strategy, as done in most global and regional models. This saturation adjustment treatment assumes that water vapor and liquid (or ice) water are in thermodynamic equilibrium once water (or ice) saturation is reached in non-mixed-phase clouds (i.e., all hydrometeors are either liquid or ice). Therefore, for models applying the saturation adjustment strategy, condensation is not calculated explicitly but rather by converting all excess water vapor into condensate, regardless of the cloud drop size and number concentration or the time needed for condensing all supersaturated water. So, under the saturation adjustment assumption, the kinetic effect as described in Eq. (5) cannot be solved fully and explicitly. In mixed-phase clouds (i.e., where water and ice coexist), the equilibrium is maintained by assuming either water saturation or ice saturation (e.g., Sundqvist, 1978) or by varying linearly from water saturation to ice saturation between two specified temperature thresholds (e.g., Tiedtke, 1993). Then, condensation on ice can be calculated following the kinetic approach, but the condensation on cloud drops still follows the saturation adjustment in most models. If the air is subsaturated but cloud drops (or cloud ice) are present, the cloud drops (or cloud ice) are forced to evaporate to maintain the equilibrium until they are all evaporated. As the saturation adjustment strategy conventionally is not applied in subsaturated conditions for precipitation particles (e.g., raindrops, snow), it should be denoted as a partial equilibrium assumption.
The kinetic effect might have significant impacts on isotope fractionation, thus there is a need for it to be considered in models. For example, Hoffmann et al. (1998) tried to consider the kinetic effect during deposition growth in the ECHAM AGCM model, which was developed at the Max Planck Institute for Meteorology. Due to the saturation adjustment assumption in ECHAM model, an effective factor which is function of temperature only is used to express the kinetic effect (Jouzel and Merlivat, 1984). In Wernet et al. (2011), the condensation on ice is also calculated with an effective factor, but the condensation on cloud drops is in equilibrium fractionation. In reality, deviation from equilibrium is rather common in clouds, and its magnitude depends on factors such as updraft speed and hydrometeors' size spectra. These factors usually are not considered in existing models but are included in the NTU scheme.
Key parameters such as the HDO saturation vapor pressure, Ps,HDO, and diffusion coefficient, DHDO, are modified to handle HDO in the NTU scheme. The HDO saturation pressure, which is needed for the kinetic mass-transfer calculation in Eq. (5), can be obtained by equating Eqs. (3) to (4). The derived HDO saturation vapor pressure is generally lower than that of H2O, and the differences increase as temperature gets lower (Fig. 2). The mass diffusivity of HDO in air, DHDO in Eq. (5), was obtained based on the relationship proposed by Hirschfelder et al. (1954):
where x represents any gas molecule. Assuming that the proportionality constants are the same for DHDO and , one can obtain the following:
with which we can relate DHDO to .
In Eq. (6), the activity of water stable isotope depends on the composition of the particle. For ice particles, the model cannot trace the history of water stable isotope deposition and thus cannot distinguish between the surface layer from the inner core of the ice particles. Therefore, the water stable isotope activity of ice-phase hydrometeor is assumed to depend on its bulk composition (i.e., assuming that it is well mixed). In reality, however, there is no homogenization of isotopes in ice particles due to the low diffusivities of molecules in ice. Blossey et al. (2010), Pfahl et al. (2012), and Dütsch et al. (2016) dealt with this problem by setting the ice particle's isotope ratio equal to that produced by vapor deposition. This is an effective approach, as only the most recently deposited ice is exposed to the vapor. However, during evaporation the mass exchange depends heavily on the residual composition, making the treatment rather tricky. Before a better solution is devised, this study adopted the bulk composition approach for both condensation and evaporation processes.
2.2 Simulation setup
Frontal systems are not only rich in cloud microphysical processes but also involve air mass transitions and atmospheric circulation. As a result, they are ideal for evaluating the relative contribution of various physical processes to isotopic fractionation. The case selected for this study is a frontal system that passed through Northern Taiwan on 11 June 2012, with moderate to heavy rainfall from the night of 11 June until noon on 12 June. Special focus will be placed on Northern Taiwan because of the availability of isotope measurements for verification.
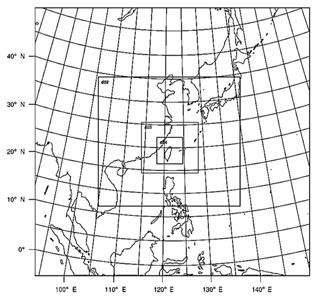
Figure 3Map of the model domains for the simulations in this study. The resolutions are 81, 27, 9, and 3 km in the outmost, 2nd, 3rd, and inmost domains, respectively.
The simulation domain is shown in Fig. 3. The resolution of the coarse domain was set at 81 km, covering the region from 90 to 150∘ E and 0 to 50∘ N. The resolutions of the nested domains were set at 27, 9, and 3 km. The innermost domain covers Taiwan and the surrounding ocean. Twenty-eight vertical layers were used, eight of which were below 1.5 km (roughly the height of the planetary boundary layer), with a maximum model height at 50 hPa. For the initial and boundary conditions, we applied the National Centers for Environmental Prediction (NCEP) final global analysis (FNL) data with a 1∘ by 1∘ resolution. FNL data for wind properties and temperatures were nudged into domains 1 and 2 only every 6 h for better simulation of the meteorology. The physical options used in the WRF model included the NTU microphysical scheme, the rapid radiative transfer model (RRTM) longwave and shortwave radiation scheme (Mlawer et al., 1997), and the Yonsei University (YSU) planetary-boundary-layer scheme (Hong et al., 2006). Cumulus parameterization was turned off in the simulations.
To examine different factors that control the water stable isotopes concentration, six simulations were conducted: the control run (CTRL) used the kinetic approach for cloud microphysical processes, the EQ run used the thermal equilibrium approach, NoIce was conducted to examine the differences between liquid- and ice-phase fractionations, NoLnd inspected the land–sea contrast of water vapor sources, and NoVh was for investigating the vertical exchange of isotope composition between lower and upper troposphere. We also conducted a blank test (NoFrac) in which isotopic microphysical fractionation was turned off. Descriptions of these numerical experiments is listed in Table 1.
The isotopic value for water vapor or condensates is conventionally expressed as δD (conventionally expressed in ‰):
where R is the HDO∕H2O ratio in the sample, and RSMOW is the Vienna Standard Mean Ocean Water isotopic ratio (Craig, 1961). The lower boundary condition of δD over land and ocean are calculated by relating HDO flux to H2O flux according to Eqs. (3) and (4). In such a conversion, the ratio Rl over land is set to be that in surface precipitation according to observed mean climatology in June from the Global Network of Isotopes in Precipitation (GNIP; Johnson and Ingram, 2004; Rozanski et al., 1993). The obtained initial near-surface distribution of water vapor δD (δDV) is shown in Fig. 4a.
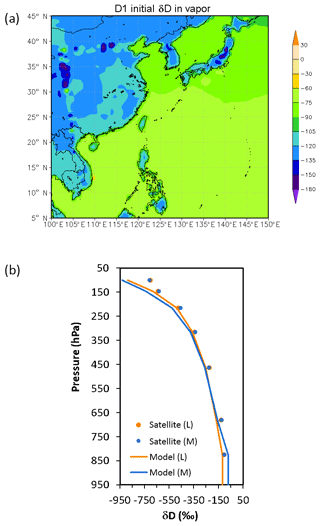
Figure 4The initial distribution of water vapor δD (in ‰). (a) Surface distribution in the coarse domain; (b) vertical profiles fitted from satellite data (dots) of water vapor δD. Orange is for land (L), and blue is for marine (M).
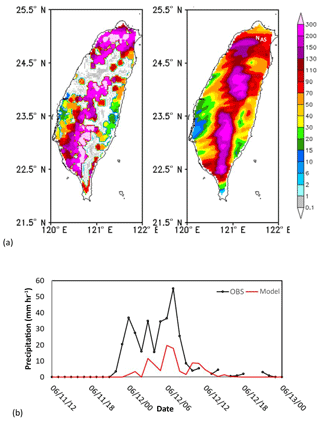
Figure 5(a) Comparison between observed (left) and simulated (right) accumulated precipitation (mm h−1) in Taiwan on 12 June 2012. Mark N and A denotes the location of NTU and AS. (b) Simulated (red line) and observed (black line) precipitation of 680 (mm h−1) at Taipei station on 11–13 June 2012.
The vertical distribution of initial atmospheric water stable isotope concentrations (Fig. 4b) was obtained from the NASA TES Aura Level 3 data (http://tes.jpl.nasa.gov/data/products/, last access: 1 December 2018). We took the data for the month of June and averaged over the years 2006–2012. Although the concentrations of water vapor (QV) and HDO (QIV) usually decrease exponentially with height, their ratios (i.e., QV : QIV) vary rather linearly with height. So, for areas over land, the vertical profile is fitted as the following:
where QIVsrf and QVsrf are the near-surface values of QIV and QV, respectively. For marine environments, the profile is fitted as
Note that these formulas apply only to the free troposphere; within the planetary boundary layers, QIV is assumed to be well mixed (see Fig. 4b for the full profiles).
2.3 Observations
The isotopic water vapor and rainwater δD data from 11–12 June 2012 were recorded using a cavity ring-down spectroscopy analyzer (CRDS; Picarro L2120-i), following Gupta et al. (2009). The measurement of rainwater was conducted on the fourth floor of the building of the Department of Geography, National Taiwan University (NTU, 25.02∘ N, 121.53∘ E). The isotopic water vapor measurements were conducted at Academia Sinica (AS), which is about 10 km east of the rainwater collection site. The two sites are marked as N and A, respectively, in Fig. 5a. The uncertainties in δD for liquid and vapor samples were found to be less than 0.3 ‰ and 1.0 ‰, respectively (Laskar et al., 2014). The precision of water vapor concentration measurements made using a Picarro CRDS is less than 100 ppmv (Crosson, 2008); this is applicable to all of the data presented here. In addition to these experimental data, the NCEP Reanalysis II (R2) data and precipitation data from the Central Weather Bureau of Taiwan (https://www.cwb.gov.tw/eng/index.htm, last access: 1 December 2018) were used to verify the simulations. Unfortunately, the NASA TES Aura satellite daily data during this case are not available for verification over the studied region.
3.1 Model verification
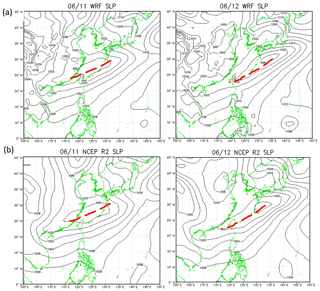
Comparison of the model results with the NCEP R2 data shows that the model captured the locations of the cold front and associated low-pressure system reasonably well; the front was over the East China Sea on 11 June and moved to Taiwan on 12 June (Fig. 6). However, the simulated precipitation was generally lower than observed, especially over northwestern Taiwan (Fig. 5a). Additionally, the first peak in rainfall during the early morning of 11 June (Fig. 5b), was not obvious in the simulated results. The impact of these discrepancies will be discussed in Sect. 4.
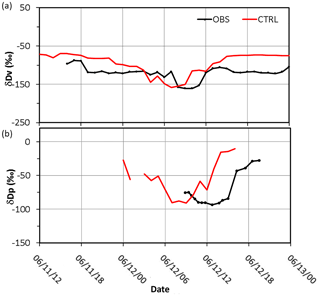
Figure 7Simulated (CTRL: red line) and observed (OBS: black line) (a) water vapor δDv (in ‰) at AS and (b) precipitation δDp (in ‰) at NTU on 11–13 June 2012.
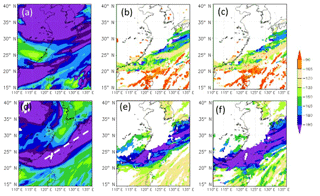
Figure 8Simulated δD (in ‰) of water vapor (a, d), liquid-phase condensates including cloud and rainwater (b, e), and ice-phase condensates, including cloud 697 ice, snow, and graupel (c, f) in the CTRL run at 500 hPa (a, c) and 850 hPa (d, f) on 12 June 2012.
The observed δDV was about −90 ‰ to −120 ‰ during the pre- and post-frontal periods and decreased to a minimum of −160 ‰ on 12 June. The simulated δDV (from −70 ‰ to −100 ‰) values were about 20 ‰ higher than observed during the pre- and post-frontal periods (Fig. 7), whereas the minimum δDV of −150 ‰ was slightly higher than the observed during the rainy period. Observation of δD in precipitation (δDL) was available only after 09:00 LT (local time) on 12 June (Fig. 7b). It decreased slightly from −70 ‰ to −90 ‰ before 16:00 LT and then recovered to around −30 ‰ by the evening on 12 June. The simulated minimum is also around −90 ‰ but occurred a few hours earlier than observed. The classic amount effect cannot be assessed from observations. For model simulations, the simulated δD in precipitation (Fig. 7b) decreased with the amount precipitation that occurred (Fig. 5b). The negative correlation is similar to the amount effect in other studies. Overall, the model captured the pattern and magnitude of changes in δD during the frontal passage reasonably well, except that the timing is off by a few hours.
3.2 Factors affecting isotopic fractionation
The simulated spatial distribution of δDV in Fig. 8a and d shows two main zones of the minimum δDV, one over the midlatitudes and the other over the latitudes of Taiwan. The former is mainly due to the low δD of the surface vapor source (cf. Fig. 4a), whereas the latter is associated with the frontal rainband and corresponds to the observed minima shown in Fig. 7a. At a first glance, one may deduce two main causes for the minima. Firstly, the near-surface air in the frontal zone is basically of continental origin, where the δDV is lower than over the oceans (cf. Fig. 4a). Secondly, precipitation microphysics inside the frontal system caused a strong reduction (fractionation) in δD of hydrometeors, as can be seen in Fig. 8e and f; therefore, the evaporation of hydrometeors would produce a low δDV in the lower troposphere. The above results are in agreement with the finding of Dütsch et al. (2016), who pointed out that horizontal transport determines the large-scale pattern of water stable isotope in both vapor and precipitation, while fractionation and vertical transport are more important on a smaller scale, near the fronts. Note that the location of the hydrometeor's δD minima at 500 and 850 hPa is shifted due to the structure of the frontal system. However, the relatively high δDV behind (to the north of) the frontal system may seem a bit strange, as the air mass there should be of continental origin. This suggests more complicated mechanisms. Besides the water vapor source and microphysical fractionation, other factors such as the initial vertical distribution may also contribute to the variation in δD values. So, in order to decipher all possible controlling factors and to evaluate their relative contributions, we need to examine results from the five sensitivity experiments that are listed in Table 1.
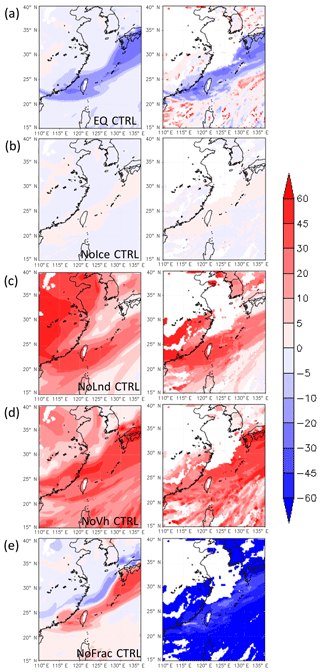
Figure 9Difference in simulated δD (in ‰) of water vapor (left panel) and liquid-phase condensates, including clouds and rainwater (right panel), between CTRL and other runs: (a) EQ CTRL, (b) NoIce CTRL, (c) NoLnd CTRL, and (d) NoVh CTRL, and (e) NoFrac CTRL, at 850 hPa on 12 June 2012.
The most obvious differences between the CTRL and other simulations in terms of δD in the vapor (δDV) and liquid (δDL) phases at 850 hPa occurred near the front, because that is the location of the richest microphysical fractionation and largest contrast in air mass properties (Fig. 9). Isotopic fractionation due to phase change in the CTRL run was weaker than that calculated in the EQ run (Fig. 9a), because the isotopic compositions were not always in equilibrium between the different phases in the CTRL run. That led to slower isotopic fractionation under severe phase changes.
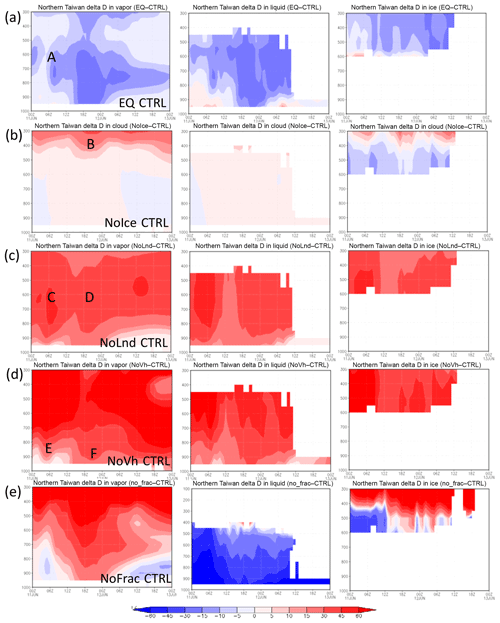
Figure 10Time evolution of the vertical distribution of water vapor δD (left), liquid-phase water (cloud water and rainwater; middle), and ice-phase water (including cloud ice, snow and graupel; right) over Northern Taiwan (121.123∘ E, 25.27∘ N) in different simulations: (a) EQ CTRL, (b) Nolce CTRL, (c) NoLnd CTRL, (d) NoVh CTRL, and (e) NoFrac CTRL on 11–12 June 2012. The ordinate is pressure (hPa), and abscissa is time.
The vertical distribution of the δDV between the CTRL and EQ runs over Northern Taiwan (121–123∘ E, 25–27∘ N) is shown in Fig. 10a. The differences in water vapor δD at around 850 hPa or higher prior to the passing of the front (point A, Fig. 10a) are associated with cloud formation due to mesoscale lifting in the warm air sector. When the frontal system passed through Northern Taiwan in the early morning of 12 June, low δDL extended almost down to the surface. The δDL in the EQ run was about 30 ‰ lower than that in the CTRL run during this period. These results suggest that the equilibrium assumption may lead to large biases in δD for a synoptic-scale weather system, as mentioned in other studies (e.g., Risi et al., 2010), and kinetic calculation is crucial to isotope modeling.
The degree of isotopic fractionation is related to temperature. As the ratio between the saturation pressure of H2O and HDO in different phases deviates more from unity at lower temperatures (cf. Fig. 2), a higher degree of fractionation will occur at lower temperatures. The significance of ice-phase fractionation is tested with the NoIce run, for which the saturation vapor pressure of ice-phase HDO was assumed to be the same as that of the liquid phase, which leads to weaker HDO vapor deposition on ice. The resulting differences in the δDV are small near the surface (Figs. 9b and 10b) but become significant at higher altitudes where the ice fractionation deviates more from that of liquid. Reduced δD in the ice phase (δDI) can be seen immediately above the 0 ∘C level (Fig. 10b), causing more heavy water isotopes to remain in the gas phase and then be transported to higher altitudes. This results in an elevated δD in both the vapor and the ice phase. The increase in the δDV and δDI can reach over 50 ‰ and 30 ‰, respectively, near the tropopause. Such changes may also affect the lower troposphere, because snow and graupel particles may fall to lower levels and bring down high δDI water. The amount of changes due to such gravitational sorting depends on whether snow and graupel were formed in the lower or higher mixed-phase zone; the former leads to lower δDI, while the latter increases it. However, the changes were generally within 10 ‰. Due to the temperature dependence of the isotopic value and the structure of the atmosphere, ignoring the difference between liquid- and ice-phase fractionations will lead to a vertical redistribution of the isotopes.
The initial and boundary conditions are also important in determining the isotope levels. Based on the IAEA data, precipitation δD decreases from marine to inland areas, indicating that the water source is important in determining the initial water stable isotope content. In the NoLnd run, the initial δD over land was set to be the same as that over the ocean, and this resulted in a higher δD not only over land but also in the frontal system (Fig. 9c). Ahead of the front, the vapor-phase δD in the NoLnd run increased by about 40 ‰ relative to the CTRL run. The initial vertical distribution of the δDV, which was based on satellite data, showed large vertical decay into the free troposphere. In the NoVh run, the initial δD in the free troposphere is assumed to be the same as that in the planetary boundary layer. This caused a 20 ‰–50 ‰ overestimation of the δDV at the near surface (Fig. 9d).
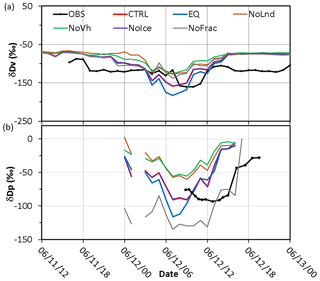
Figure 11Same as Fig. 7 but for sensitivity simulations: the control run (CTRL; red line), thermodynamic equilibrium run (EQ; blue line), no-ice run (NoIce; purple line), no-land run (NoLnd; orange line), constant initial vertical profile run (NoVh; green line), and no-fractionation run (NoFrac; grey line).
When the observed and simulated δDV values at AS and precipitation δDL at NTU are compared (Fig. 11), one can see that the full simulation (i.e., the CTRL run, red line) is rather close to the observation in terms of the peak values during the time of frontal passage (06:00–12:00 LT on 12 June). In contrast, the decrease in the δDV was overestimated by 11 ‰ in the equilibrium run and underestimated by 28 ‰ and 34 ‰ in the NoLnd, and NoVh runs, respectively. The simulated δDV in the NoIce run is rather close to that in the CTRL run, which is consistent with the vertical profile shown in Fig. 10b, suggesting that the ice-phase process does not have a significant effect on δD at lower altitudes; however, the changes in the upper troposphere are significant. The importance of microphysical fractionation is elucidated with the NoFrac run (grey line in Fig. 11), which yields 25 ‰ and more than 50 ‰ differences in the minimum δDV and δDL, respectively.
Combining the observations and simulations results of the water stable isotopes can be used to understand the water cycle. The observed δDV decreased after 06:00 LT on 12 June (black line in Fig. 11), much later than the onset of the precipitation. The observations suggested that the source of water vapor before this time is the ocean (Wang et al., 2016) and that the microphysical processes related to the precipitation did not substantially affect the δDV during this period. Model simulations can help with further understanding such isotopic fractionation. The δDV on 11 June varied little among different tests (Fig. 11), because the air mass was from nearby areas (i.e., no significant advection effect) and no cloud microphysical processes occurred during this period. However, the water vapor δDV decreased from −80 ‰ to −100 ‰ at midnight of 11–12 June in the control run, but not in the NoLnd run, indicating that the decreases in the δDV were due to advection of the continental air mass. When the front passed through during the early morning of 12 June, the δDV decreased from −100 ‰ to −170 ‰ in the control run but not in the NoFrac run (grey line in Fig. 10), indicating that the additional differences were caused by cloud microphysical processes. After the passage of frontal system, the δDV returned to its background level, around −80 ‰. The results of these sensitivity tests suggest that the changes in the δDV due to cloud microphysical processes, initial vertical distribution, and lower boundary conditions are of a similar order and are all important to isotopic fractionation.
Although the model seems to adequately reproduced changes in δD in this frontal case, there are some minor inconsistencies between the simulation results and observations. Some discrepancies originated from the meteorological model itself and the initial meteorological conditions, which caused inaccuracies in the intensity or timing of surface precipitation. In fact, most models including ours failed to simulate the strong precipitation over land for this system (Wang et al., 2016). The observed water vapor and precipitation δD values were not in phase, and the water vapor δD decreased prior to precipitation (black line in Fig. 11). In contrast, the decreases in the simulated precipitation and water vapor δD were almost simultaneous, starting around 03:00 LT on 12 June (red line in Fig. 11). This again suggests that the model missed an earlier local convection system occurred during the early morning, so the simulation can reflect only the δD variation due to the frontal system. The simulated δDV decreased and returned to its previous level earlier than the observed δDV (∼ 03:00–10:00 LT compared to ∼ 07:00–13:00 LT). This also suggests that the arrival time of the frontal system to Taipei was earlier than observed, although the speed of the simulated system was close to that of the observed one, taking about 7 h to pass through Taipei.
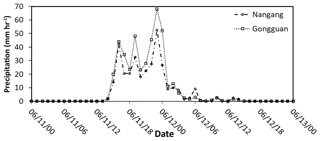
Figure 12Precipitation (mm h−1) at Nangang (dashed line) and Gongguan (dotted line) stations on 11–13 June 2012.
Uncertainties may also exist in the observation data, as the vapor and precipitation measurements were taken at different locations, separated by about 10 km. A comparison of precipitation at different sites (Fig. 12; Nangang station is close to AS, and Gongguan station is close to NTU) suggests that the difference in sampling locations would not significantly affect the results in this study. Another uncertainty is the parameterization of isotopic fractionation factor α. In this study, the temperature dependence of αl-v and αs-v was adopted from Horita and Wesolowski (1994) and Ellehoj et al. (2013) , respectively. In most models, the formulation for ice and vapor by Merlivat and Nief (1967) is still used. From Fig. 2 one can estimate that the differences in αs-v between Ellehoj et al. (2013) and Merlivat and Nief (1967) are around 1 % between −10 to 20 ∘C and 4 % at −40 ∘C; whereas the differences of αl-v between Horita and Wesolowski (1994) and Merlivat and Nief (1967) are less than 1 %.
There are also uncertainties in the treatment of microphysical processes. The isotopic value for water vapor at the lower boundary condition was assumed to be in equilibrium with surface precipitation in this study. Rangarajan et al. (2017) analyzed the isotopic ratios in water vapor from measurements over Taipei, and they found that isotopic values were not always in equilibrium. This suggests that the assumed lower boundary condition might not always be applicable for Taipei. Moreover, since the lower boundary condition can be affected by fresh precipitation, the δDV might decrease after the precipitation event which brings in low δDL to the soil; however, our model does not update the surface δDV flux accordingly. This might partially explain the discrepancy in the δDV after the frontal passage that shown in Fig. 7a. In addition, the evaporation from the ocean is assumed to be in equilibrium between liquid and vapor phases. This assumption may also affect the simulation of δD in the model, and the process needs to be explicitly considered in the future study. Finally, whether the nonequilibrium effects are important for the second-order isotope parameter, deuterium excess, is an interesting subject worthy of further investigation by including the description of the δ18O isotope in the model.
Exploring physical processes controlling the stable isotopic composition of water, including details such as water vapor source, atmospheric circulation, and cloud microphysical processes, is useful for understanding the water cycle. In this study, we modified the NCAR WRF model to understand the role of different factors in the fractionation of the stable isotopes of water. The experimental stable isotope thermal equilibrium data were converted into isotope saturation vapor pressure, which was then used in the two-stream Maxwellian kinetic equation for calculating the condensation and evaporation or deposition and sublimation of HDO, parallel to that for H2O. Mass conservation was also considered explicitly for the collection processes as well as during freezing and melting.
A frontal system event was selected to reveal the complexity of isotope fractionation. The model captured the location of the front adequately, although the estimated precipitation was less than observed. The simulated results showed fairly good agreement with water vapor and rainwater stable isotope measurements and suggested that the decreases in water vapor δD before the front arrived in Taiwan were due to an air mass of continental origin. When the front passed during the early morning of 12 June, both the water vapor sources and the cloud microphysical processes contributed to a decrease in water vapor δD, which returned to background levels after the front had passed.
Additional sensitivity experiments showed that the thermal equilibrium assumption commonly used in earlier studies might significantly overestimate the decrease of mean δD by about 11 ‰, while the maximum difference can be more than 20 ‰, during the precipitation event. Cloud microphysical processes, including ice-phase processes, have substantial effects on isotopic fractionation, especially on the vertical redistribution of isotopes. Furthermore, the sensitivity tests suggest that the initial vertical profile and the land–sea contrast in surface sources are quite important in simulating atmospheric stable isotopic composition and should be estimated from observations such as satellite data, without which the underestimation in the decrease of water vapor δD could reach about 34 ‰ and 28 ‰, respectively. The problem in determining the activity of water stable isotope in ice particles without knowing the inhomogeneity of chemical composition in the bulk ice, as mentioned at the end of Sect. 2.1, is another issue worthy of further study. To accommodate the different conditions between condensation and evaporation, it might be feasible to assume that the water stable isotope activity is determined by the vapor phase during condensation following the approach of Blossey et al. (2010), Pfahl et al. (2012), and Dütsch et al. (2016), whereas for the evaporation process, one may assume a well-mixed bulk composition for determining the isotope activity, as done in this study. In summary, this study suggests that a better understanding of the relationship between water stable isotope variation and hydrological cycle can be achieved with a combination of multiplatform observations and detailed cloud model simulations.
Data available on request from the authors.
JP and IC designed the research. IC wrote the paper with further contributions from all co-authors. WY performed the WRF simulations. MC provided measurements. JP supervised the research. All authors discussed the results and contributed to the final paper.
The authors declare that they have no conflict of interest.
Acknowledgment. This study was supported by the projects MOST 105-2119-M-002-028-MY3, 105-2119-M-002-035,
106-2111-M-001-008, and 107-2111-M-001-006.
The suggestions provided by anonymous reviewers are highly appreciated.
Edited by: Eliza Harris
Reviewed by: two anonymous referees
Aldaz, L. and Deutsch, S.: On a relationship between air temperature and oxygen isotope ratio of snow and firn in the south pole region, Earth Planet. Sci. Lett., 3, 267–274, 1967.
Blossey, N. P., Kuang, Z., and Romps, D. M.: Isotopic composition of water in the tropical tropopause layer in cloud-resolving simulations of an idealized tropical circulation, J. Geophys. Res., 115, https://doi.org/10.1029/2010JD014554, 2010.
Chen, J. P. and Liu, S. T.: Physically based two-moment bulkwater parametrization for warm-cloud microphysics, Q. J. Roy. Meteorol. Soc., 130, 51–78, 2004.
Chen, S. H., Liu, Y. C., Nathan, T. R., Davis, C., Torn, R., Sowa, N., Cheng, C. T., and Chen, J. P.: Modeling the effects of dust-radiative forcing on the movement of Hurricane Helene (2006), Q. J. Roy. Meteorol. Soc., 141, 2563–2570, 2015.
Cheng, C.-T., Wang, W.-C., and Chen, J.-P.: A modeling study of aerosol impacts on cloud microphysics and radiative properties, Q. J. Roy. Meteorol. Soc., 133, 283–297, 2007.
Cheng, C.-T., Wang, W.-C., and Chen, J.-P.: Simulation of the effects of increasing cloud condensation nuclei on mixed-phase clouds and precipitation of a front system, Atmos. Res., 96, 461–476, 2010.
Clark, I. and Fritz, P.: Environmental Isotopes in Hydrogeology, Boca Raton, CRC Press, 328 pp., ISBN 1-56670-249-6, 1997.
Cole, J. E., Rind, D., Webb, R. S., Jouzel, J., and Healy, R.: Climatic controls on interannual variability of precipitation δ18O: Simulated influence of temperature, precipitation amount, and vapor source region, J. Geophys. Res., 104, 14223–14236, 1999.
Craig, H.: Isotopic Variations in Meteoric Waters, Science, 133, 1702–1703, 1961.
Crosson, E. R.: A cavity ring-down analyzer for measuring atmospheric levels of methane, carbon dioxide, and water vapor, Appl. Phys., 92, 403–408, 2008.
Dansgaard, W.: Stable isotopes in precipitation, Tellus, 16, 436–468, 1964.
Dawson, T. E. and Ehleringer, J. R.: Plants, isotopes and water use: a catchment-scale perspective, in: Isotope tracers in catchment hydrology, 165–202, 1998
Dearden, C., Vaughan, G., Tsai, T.-C., and Chen, J.-P.: Exploring the diabatic role of ice microphysical processes in UK summer cyclones, Mon. Weather Rev., 144, 1249–1272, 2016.
Dütsch, M., Pfahl, S., and Wernli, H.: Drivers of δ2H variations in an idealized extratropical cyclone, Geophys. Res. Lett., 43, 5401–5408, 2016.
Ellehoj, M., Steen-Larsen, H. C., Johnsen, S. J., and Madsen, M. B.: Ice-vapor equilibrium fractionation factor of hydrogen and oxygen isotopes: Experimental investigations and implications for stable water isotope studies, Rapid Commun. Mass Sp., 27, 2149–2158, 2013.
Gonfiantini, R.: On the isotopic composition of precipitation in tropical stations, Acta Amazon., 15, 121–140, 1985.
Gupta, P., Noone, D., Galewsky, J., Sweeney, C., and Vaughn, B. H.: Demonstration of high-precision continuous measurements of water vapor isotopologues in laboratory and remote field deployments using wavelength-scanned cavity ring-down spectroscopy (WS-CRDS) technology, Rapid Commun. Mass Sp., 23, 2534–2542, 2009.
Hirschfelder, J. O., Curtiss, C. F., Bird, R. B., and Mayer, M. G.: Molecular theory of gases and liquids, Wiley & Sons, Inc., New York, 1219 p., 1954.
Hoffmann, G., Werner, M., and Heimann, M.: Water isotope module of the ECHAM atmospheric general circulation model: A study on timescales from days to several years, J. Geophys. Res., 103, 16871–16896, 1998.
Hong, S.-Y., Noh, Y., and Dudhia, J.: A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes, Mon. Weather Rev., 134, 2318–2341, 2006.
Horita, J. and Wesolowski, D. J.: Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature, Geochim. Cosmochim. Ac., 58, 3425–3437, 1994.
Johnson, K. R. and Ingram, B. L.: Spatial and temporal variability in the stable isotope systematics of modern precipitation in China: implications for paleoclimate reconstructions, Earth Planet. Sci. Lett., 220, 365–377, 2004.
Joussaume, S., Sadourny, R., and Jouzel, J.: A general circulation model of water isotope cycles in the atmosphere, Nature, 311, 24–29, 1984.
Jouzel, J. and Merlivat, L.: Deuterium and oxygen 18 in precipitation: Modeling of the isotopic effects during snow formation, J. Geophys. Res., 89, 11749–11757, 1984.
Kurita, N.: Water isotopic variability in response to mesoscale convective system over the tropical ocean, J. Geophys. Res., 118, 10376–10390, https://doi.org/10.1002/jgrd.50754, 2013.
Laskar, A. H., Huang, J.-C., Hsu, S.-C., Bhattacharya, S. K., Wang, C.-H., and Liang, M.-C.: Stable isotopic composition of near surface atmospheric water vapor and rain-vapor interaction in Taipei, Taiwan, J. Hydrol., 519, 2091–2100, 2014.
Lee, J.-E., Fung, I., DePaolo, D. J., and Henning, C. C.: Analysis of the global distribution of water isotopes using the NCAR atmospheric general circulation model, J. Geophys. Res., 112, D16306, https://doi.org/10.1029/2006JD007657, 2007.
Lorius, C., Ritz, C., Jouzel, J., Merlivat, L., and Barkov, N.: A 150 000-year climatic record from Antarctic ice, Nature, 316, 591–596, 1985.
Merlivat, L. and Nief, G.: Fractionnement isotopique lors des changements d'etat solide-vapeur et liquide-vapeur de l'eau a des temperatures inferieures a 0 ∘C. Tellus, 19, 122–127, 1967.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res., 102, 16663–16682, 1997.
Pfahl, S., Wernli, H., and Yoshimura, K.: The isotopic composition of precipitation from a winter storm – a case study with the limited-area model COSMOiso, Atmos. Chem. Phys., 12, 1629–1648, https://doi.org/10.5194/acp-12-1629-2012, 2012.
Rangarajan, R., Laskar, A. H., Bhattacharya, S. K., Shen, C.-C., and Liang, M.-C.: An insight into the western Pacific wintertime moisture sources using dual water vapor isotopes, J. Hydrol., 547, 111–123, 2017.
Risi, C., Noone, D., Worden, J., Frankenberg, C., Stiller, G., Kiefer, M., Funke, B., Walker, K., Bernath, P., Schneider, M., Bony, S., Lee, J., Brown, D., and Sturm, C.: Process-evaluation of tropospheric humidity simulated by general circulation models using water vapor isotopologues: 1. Comparison between models and observations, J. Geophys. Res., 117, D05303, 2012.
Rozanski, K., Araguás-Araguás, L., and Gonfiantini, R.: Isotopic Patterns in Modern Global Precipitation, in: Climate Change in Continental Isotopic Records, American Geophysical Union, 1–36, https://doi.org/10.1029/GM078p0001 1993.
Sjolte, J. and Hoffmann, G.: Modelling stable water isotopes in monsoon precipitation during the previous interglacial, Quat. Sci. Rev., 85, 119–135, 2014.
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D. M., Duda, M., Huang, X.-Y., Wang, W., and Powers, J. G.: A Description of the Advanced Research WRF Version 3, NCAR Technical Note, 2008.
Sturm, C., Zhang, Q., and Noone, D.: An introduction to stable water isotopes in climate models: benefits of forward proxy modelling for paleoclimatology, Clim. Past, 6, 115–129, https://doi.org/10.5194/cp-6-115-2010, 2010.
Taufour, M., Vié, B., Augros, C., Boudevillain, B., Delanoë, J., Delautier, G., Ducrocq, V., Lac, C., Pinty, J.-P., and Schwarzenböck, A.: Evaluation of the two-moment scheme LIMA based on microphysical observations from the HyMeX campaign, Q. J. Roy. Meteorol. Soc., 144, 1398–1414, 2018.
Sundqvist, H.: A parameterization scheme for non-convective condensation including prediction of cloud water content, Q. J. Roy. Meteorol. Soc., 104, 677–690, 1978.
Tiedtke, M.: Representation of clouds in large-scale models, Mon. Weather Rev., 121, 3040–3061, 1993.
Werner, M., Langebroek, P. M., Carlsen, T., Herold, M., and Lohmann, G.: Stable water isotopes in the ECHAM5 general circulation model: Toward high-resolution isotope modeling on a global scale, J. Geophys. Res., 116, D15109, doi:10.1029/2011JD015681, 2011.
Wang, C.-C., Chiou, B.-K., Chen, G. T.-J., Kuo, H.-C., and Liu, C.-H.: A numerical study of back-building process in a quasistationary rainband with extreme rainfall over northern Taiwan during 11–12 June 2012, Atmos. Chem. Phys., 16, 12359–12382, https://doi.org/10.5194/acp-16-12359-2016, 2016.
Yoshimura, K., Kanamitsu, M., Noone, D., and Oki, T.: Historical isotope simulation using Reanalysis atmospheric data, J. Geophys. Res., 113, D10198, https://doi.org/10.1029/2008JD010074, 2008.
Yoshimura, K., Kanamitsu, M., and Dettinger, M.: Regional downscaling for stable water isotopes: A case study of an atmospheric river event, J. Geophys. Res., 115, D18114, https://doi.org/10.1029/2010JD014032, 2010.
Yoshimura, K., Oki, T., Ohte, N., and Kanae, S.: A quantitative analysis of short-term 18O variability with a Rayleigh-type isotope circulation model, Journal of Geophysical Research: Atmospheres, 108, 4647, doi:10.1029/2003JD003477, 2003.
Yoshimura, K.: Stable water isotopes in climatology, meteorology, and hydrology: A review, J. Meteor. Soc. Japan, 93, 513–533, https://doi.org/10.2151/jmsj.2015-036, 2015.
Yurtsever, Y. and Gat, J. R.: Atmospheric waters, of IAEA, Stable Isotope Hydrology: Deuterium and Oxygen-18 in the Water Cycle, Vienna, IAEA, 210, 103–142, ISBN:92-0-145281-0, 1981.
Zwart, C., Munksgaard, N. C., Protat, A., Kurita, N., Lambrinidis, D., and Bird, M. I.: The isotopic signature of monsoon conditions, cloud modes, and rainfall type, Hydrol. Proc., 32, 2296–2303, 2018.